Optimising precision and power by machine learning in randomised trials with ordinal and time‐to‐event outcomes with an application to COVID‐19

Abstract

The rapid finding of effective therapeutics requires efficient use of available resources in clinical trials. Covariate adjustment can yield statistical estimates with improved precision, resulting in a reduction in the number of participants required to draw futility or efficacy conclusions. We focus on time‐to‐event and ordinal outcomes. When more than a few baseline covariates are available, a key question for covariate adjustment in randomised studies is how to fit a model relating the outcome and the baseline covariates to maximise precision. We present a novel theoretical result establishing conditions for asymptotic normality of a variety of covariate‐adjusted estimators that rely on machine learning (e.g., ${\ell }_1$‐regularisation, Random Forests, XGBoost, and Multivariate Adaptive Regression Splines [MARS]), under the assumption that outcome data are missing completely at random. We further present a consistent estimator of the asymptotic variance. Importantly, the conditions do not require the machine learning methods to converge to the true outcome distribution conditional on baseline variables, as long as they converge to some (possibly incorrect) limit. We conducted a simulation study to evaluate the performance of the aforementioned prediction methods in COVID‐19 trials. Our simulation is based on resampling longitudinal data from over 1500 patients hospitalised with COVID‐19 at Weill Cornell Medicine New York Presbyterian Hospital. We found that using ${\ell }_1$‐regularisation led to estimators and corresponding hypothesis tests that control type 1 error and are more precise than an unadjusted estimator across all sample sizes tested. We also show that when covariates are not prognostic of the outcome, ${\ell }_1$‐regularisation remains as precise as the unadjusted estimator, even at small sample sizes ($n=100$). We give an R package adjrct that performs model‐robust covariate adjustment for ordinal and time‐to‐event outcomes.

1. INTRODUCTION

Coronavirus disease 2019 (COVID‐19) has affected more than 125 million people and caused more than 2.7 million deaths worldwide (World Health Organization, 2021). Governments and scientists around the globe have deployed an enormous amount of resources to combat the pandemic with remarkable success, such as the development in record time of highly effective vaccines to prevent disease (e.g., Baden et al., 2021; Polack et al., 2020). Global and local organisations are launching large‐scale collaborations to collect robust scientific data to test potential COVID‐19 treatments, including the testing of drugs re‐purposed from other diseases as well as new compounds (Kupferschmidt & Cohen, 2020). For example, the World Health Organization launched the SOLIDARITY trial, enrolling almost 12,000 patients in 500 hospital sites in over 30 countries (WHO Solidarity Trial Consortium, 2021). Other large initiatives include the RECOVERY trial (The RECOVERY Collaborative Group, 2021) and the ACTIV initiative (Collins & Stoffels, 2020). To date, there are approximately 2400 randomised trials for the treatment of COVID‐19 registered in clinicaltrials.gov.

The rapid finding of effective therapeutics for COVID‐19 requires the efficient use of available resources. One area where such efficiency is achievable at little cost is in the statistical design and analysis of the clinical trials. Specifically, a statistical technique known as covariate adjustment may yield estimators with increased precision (compared to unadjusted estimators), and may result in a reduction of the time, number of participants, and resources required to draw futility or efficacy conclusions. This results in faster trial designs, which may help accelerate the delivery of effective treatments to patients who need them (and may help rule out ineffective treatments faster).

Covariate adjustment refers to pre‐planned analysis methods that use data on patient baseline characteristics to correct for chance imbalances across study arms, thereby yielding more precise treatment effect estimates. The ICH E9 Guidance on Statistical Methods for Analyzing Clinical Trials (FDA & EMA, 2019) states that ‘Pretrial deliberations should identify those covariates and factors expected to have an important influence on the primary variable(s), and should consider how to account for these in the analysis to improve precision and to compensate for any lack of balance between treatment groups’. Even though its benefits can be substantial, covariate adjustment is underutilised; only 24%–34% of trials use covariate adjustment (Kahan et al., 2014).

We focus on estimation of marginal treatment effects, defined as a contrast between study arms in the marginal distribution of the outcome. Many approaches for estimation of marginal treatment effects using covariate adjustment in randomised trials invoke a model relating the outcome and the baseline covariates within strata of treatment. Recent decades have seen a surge in research on the development of model‐robust methods for estimating marginal effects that remain consistent even if this outcome regression model is arbitrarily mis‐specified (e.g., Austin et al., 2010; Benkeser et al., 2020; Moore & van der Laan, 2009a; Tsiatis et al., 2008; Yang & Tsiatis, 2001; Zhang & Gilbert, 2010; Zhang et al., 2008). We focus on a study of the model‐robust covariate‐adjusted estimators for time‐to‐event and ordinal outcomes developed by Moore and van der Laan (2009a), Díaz et al. (2016, 2019).

All potential adjustment covariates must be pre‐specified in the statistical analysis plan. At the end of the trial, a pre‐specified prediction algorithm (e.g., random forests, or using regularisation for variable selection) will be run and its output will be used to construct a model‐robust, covariate‐adjusted estimator of the marginal treatment effect for the trial's primary efficacy analysis. We aim to address the question of how to do this in a model‐robust way that guarantees consistency and asymptotic normality, under some regularity conditions weaker than related work (described below). We also aim to demonstrate the potential value added by covariate adjustment combined with machine learning, through a simulation study based on COVID‐19 data.

As a standard regression method for high‐dimensional data, ${\ell }_1$‐regularisation has been studied by several authors in the context of covariate selection for randomised studies. For example, Wager et al. (2016) present estimators that are asymptotically normal under strong assumptions that include linearity of the outcome–covariate relationship. Bloniarz et al. (2016) present estimators under a randomisation inference framework and show asymptotic normality of the estimators under assumptions similar to the assumptions made in this paper. Both of these papers present results only for continuous outcomes. The method of Tian et al. (2012) is general and can be applied to continuous, ordinal, binary, and time‐to‐event data, and its asymptotic properties are similar to the properties of the methods we discuss for the case of ${\ell }_1$‐regularisation, under similar assumptions.

More related to our general approach, Wager et al. (2016) also present a cross‐validation procedure that can be used with arbitrary non‐parametric prediction methods (e.g. ${\ell }_1$‐regularisation, random forests, etc.) in the estimation procedure. Their proposal amounts to computation of a cross‐fitted augmented inverse probability weighted estimator (Chernozhukov et al., 2018). Their asymptotic normality results, unlike ours, require that their predictor of the outcome given baseline variables converges to the true regression function. Wu and Gagnon‐Bartsch (2018) proposed a ‘leave‐one‐out‐potential outcomes’ estimator where automatic prediction can also be performed using any regression procedure such as linear regression or random forests, and they propose a conservative variance estimator. It is unclear as of yet whether Wald‐type confidence intervals based on the normal distribution are appropriate for this estimator. As in the above related work that compares the precision of covariate‐adjusted estimators to the unadjusted estimator, we assume that outcomes are missing completely at random (since otherwise the unadjusted estimator is generally inconsistent).

In Section 3.3, we present our main theorem. It shows that any of a large class of prediction algorithms (e.g. ${\ell }_1$‐regularisation, random forests, XGBoost, and MARS) can be combined with the covariate‐adjusted estimator of Moore and van der Laan (2009b) to produce a consistent, asymptotically normal estimator of the marginal treatment effect, under regularity conditions. These conditions do not require consistent estimation of the outcome regression function (as in key related work described above); instead, our theorem requires the weaker condition of convergence to some (possibly incorrect) limit. We also give a consistent, easy to compute variance estimator. This has important practical implications because it allows the use machine learning coupled with Wald‐type confidence intervals and hypothesis tests, under the conditions of the theorem. The above estimator can be used with ordinal or time‐to‐event outcomes.

We next conduct a simulation study to evaluate the performance of the aforementioned machine learning algorithms for covariate adjustment in the context of COVID‐19 trials. We simulate two‐arm trials comparing a hypothetical COVID‐19 treatment to standard of care. The simulated data distributions are generated by re‐sampling longitudinal data on approximately 1500 patients hospitalised at Weill Cornell Medicine New York Presbyterian Hospital prior to 15 May 2020. We present results for two types of endpoints: time‐to‐event (e.g. time to intubation or death) and ordinal (e.g., WHO scale, see Marshall et al., 2020) outcomes. For survival outcomes, we present results for two different estimands (i.e. targets of inference): the survival probability at any given time and the restricted mean survival time. For ordinal outcomes we present results for the average log‐odds ratio, and for the Mann–Whitney estimand, interpreted as the probability that a randomly chosen treated patient has a better outcome than a randomly chosen control patient (with ties broken at random).

Benkeser et al. (2020) used simulations based on the above data source to illustrate the efficiency gains achievable by covariate adjustment with parametric models including a small number of adjustment variables (and not using machine learning to improve efficiency). In this paper we evaluate the performance of four machine learning algorithms (${\ell }_1$‐regularisation, random forests, XGBoost, and MARS) in several sample sizes, and compare them in terms of their bias, mean squared error, and type‐1 and type‐2 errors, to unadjusted estimators and to fully adjusted main terms logistic regression with all available variables included. Furthermore, we introduce a new R package adjrct (Díaz & Williams, 2021) that can be used to perform model‐robust covariate adjustment for ordinal and time‐to‐event outcomes, and provide R code that can be used to replicate our simulation analyses with other data sources.

2. ESTIMANDS

The ICH E9(R1) addendum on Estimands and Sensitivity Analysis in Clinical Trials (U.S. Food and Drug Administration, 2021b) postulates several attributes that may be used in the construction of an estimand. In addition to the specification of a treatment, an endpoint, and a population of interest, these attributes include the specification of a population‐level summary and methods for handling intercurrent events such as treatment discontinuation or terminal events that preclude the occurrence of the endpoint of interest (e.g. death).

We assume the target population is the entire trial population, and construct estimands as marginal summaries (e.g. means or probabilities) across the entire population. We focus on estimation of marginal treatment effects, defined as a contrast between study arms in the marginal distribution of the outcome.

Non‐terminal intercurrent events such as post‐randomisation changes in treatment or non‐compliance with the assigned treatment arm are handled using a treatment policy strategy, under the intention‐to‐treat principle. The estimands we consider do not take into account terminal intercurrent events that preclude observation of the endpoint of interest. The literature on competing risks and truncation by death discusses several estimands that may be used for such cases, such as the sub‐distribution risk, the survivor average causal effect, etc. (Comment et al., 2019; Young et al., 2020).

We further assume that we have data on $n$ trial participants, represented by $n$ independent and identically distributed copies of data $O_i:i=1,\dots ,n$. We assume $O_i$ is distributed as P, where we make no assumptions about the functional form of P except that treatment is independent of baseline covariates (by randomisation). We denote a generic draw from the distribution P by $O$. We use the terms ‘baseline covariate’ and ‘baseline variable’ interchangeably to indicate a measurement made before randomisation.

We are interested in making inferences about a feature of the distribution P. We use the word estimand to refer to such a feature. We describe example estimands, which include those used in our simulations studies, below.

2.1. Ordinal outcomes

For ordinal outcomes, assume the observed data is $O=(W,A,Y)$, where $W$ is a vector of baseline covariates, $A$ is the treatment arm, and $Y$ is an ordinal variable that can take values in $\{1,\dots ,K\}$. Let $F(k,a)=\mathsf{P}(Y\le k|A=a)$ denote the cumulative distribution function (CDF) for patients in arm $A=a$, and let $f(k,a)=F(k,a)-F(k-1,a)$ denote the corresponding probability mass function. For notational convenience we will sometimes use the ‘survival’ function instead: $S(k,a)=1-F(k,a)$. The average log‐odds ratio is then equal to

$$\mathsf{LOR}=\frac{1}{K-1}\sum _{k=1}^{K-1}\log \left[\frac{F(k,1)/\{1-F(k,1)\}}{F(k,0)/\{1-F(k,0)\}}\right],$$

and the Mann–Whitney estimand is equal to

$$\mathsf{MW}=\sum _{k=1}^K\left\{F(k-1,0)+\frac{1}{2}f(k,0)\right\}f(k,1).$$

The Mann–Whitney estimand can be interpreted as the probability that a randomly drawn patient from the treated arm has a better outcome than a randomly drawn patient from the control arm, with ties broken at random (Ahmad, 1996). The average log‐odds ratio may be interpreted as a non‐parametric extension of the parameter $\beta$ estimated by the commonly used proportional odds model $\text{logit}\{F(k,a)\}={\alpha }_k+\beta a$ (Díaz et al., 2016).

While the $\mathsf{MW}$ statistic may seem more desirable than the $\mathsf{LOR}$ statistic because its interpretation does not depend on a parametric model, the $\mathsf{MW}$ also has drawbacks that may be undesirable in some situations. For example, it is a non‐transitive measure, meaning that in a multi‐arm trial, superiority of treatment A to treatment B and superiority of treatment B to treatment C do not guarantee that treatment A is superior to treatment C.

2.2. Time to event outcomes

For time to event outcomes, we assume the observed data is $O=(W,A,\mathrm{\Delta }=\mathbb{1}\{Y\le C\},\tilde{Y}=\min (C,Y))$, where $C$ is a right‐censoring time denoting the time that a patient is last seen, and $\mathbb{1}\{E\}$ is the indicator variable taking the value 1 on the event $E$ and 0 otherwise. We further assume that events are observed at discrete time points $\{1,\dots ,K\}$ (e.g. days) as is typical in clinical trials. For a restriction time $\tau \le K$, the difference in restricted mean survival time is given by

$$\begin{array}{llll}\mathsf{RMST}& =E(\min (Y,\tau )|A=1)-E(\min (Y,\tau )|A=0)& & \\ & =\sum _{k=1}^{\tau -1}\{S(k,1)-S(k,0)\},& & \end{array}$$

and can be interpreted as a contrast comparing the expected survival time within the first $\tau$ time units for the treated arm minus the control arm (Chen & Tsiatis, 2001; Royston & Parmar, 2011). The risk difference at a user‐given time point $k$ is defined as

$$\mathsf{RD}=S(k,1)-S(k,0),$$

and is interpreted as the difference in survival probability for a patient in the treated arm minus the control arm. We note that the $\mathsf{MW}$ and $\mathsf{RD}$ parameters may be meaningful for both ordinal and time‐to‐event outcomes.

3. ESTIMATORS

For the sake of generality, in what follows we use a common data structure $O=(W,A,\mathrm{\Delta }=\mathbb{1}\{Y\le C\},\tilde{Y})$ for both ordinal and survival outcomes, where for ordinal outcomes $C=K$ if the outcome is observed and $C=0$ if it is missing.

Many approaches for estimation of marginal treatment effects using covariate adjustment in randomised trials invoke a model relating the outcome and the baseline covariates within strata of treatment. It is important that the consistency and interpretability of the treatment effect estimates do not rely on the ability to correctly posit such a model. Specifically, in a recent draft guidance (U.S. Food and Drug Administration, 2021a), the FDA states: ‘Sponsors can perform covariate adjusted estimation and inference for an unconditional treatment effect $\dots$ in the primary analysis of data from a randomized trial. The method used should provide valid inference under approximately the same minimal statistical assumptions that would be needed for unadjusted estimation in a randomized trial’. The assumption of a correctly specified model is not typically part of the assumptions needed for an unadjusted analysis, and should therefore be avoided when possible.

All estimands described in this paper can be computed from the CDF $F(·,a)$ for $a\in \{0,1\}$, which can be estimated using the empirical cumulative distribution function (ECDF) or the Kaplan–Meier estimator. Model‐robust, covariate adjusted estimators have been developed for the CDF, including, for example, Chen and Tsiatis (2001), Rubin and van der Laan (2008), Moore and van der Laan (2009b), Stitelman et al. (2011), Lu and Tsiatis (2011), Brooks et al. (2013), Zhang (2014), Parast et al. (2014), Benkeser et al. (2018), Díaz (2019).

We focus on the model‐robust, covariate‐adjusted estimators of Moore and van der Laan (2009b), Díaz et al. (2016, 2019). These estimators have at least two advantages compared to unadjusted estimators based on the ECDF or the Kaplan–Meier estimator. First, with time‐to‐event outcomes, some adjusted estimators can achieve consistency under an assumption of censoring being independent of the outcome given study arm and baseline covariates ($C⫫Y\hspace{0.17em}|\hspace{0.17em}A,W$), rather than the assumption of censoring in each arm being independent of the outcome marginally ($C⫫Y\hspace{0.17em}|\hspace{0.17em}A$) required by unadjusted estimators. The former assumption is arguably more likely to hold in typical situations where patients are lost to follow‐up due to reasons correlated with their baseline variables. Second, in large samples and under regularity conditions, the adjusted estimators of Díaz et al. (2016, 2019) can be at least as precise as the unadjusted estimator (this requires that missingness/censoring is completely at random, i.e., that in each arm $a\in \{0,1\}$, $C⫫(Y,W)|A=a$), under additional assumptions.

Additionally, under regularity conditions, the three aforementioned adjusted estimators are asymptotically normal. This allows the construction of Wald‐type confidence intervals and corresponding tests of the null hypothesis of no treatment effect.

3.1. Prediction algorithms

While we make no assumption on the functional form of the distribution P (except that treatment is independent of baseline variables by randomisation), implementation of our estimators requires a working model for the following conditional probability

$$m(k,a,W)=\mathsf{P}(\tilde{Y}=k,\mathrm{\Delta }=1|\tilde{Y}\ge k,A=a,W).$$

In time‐to‐event analysis, this probability is known as the conditional hazard. The expression working model here means that we do not assume that the model represents the true relationship between the outcome and the treatment/covariates. Fitting a working model for $m$ is equivalent to training a prediction model for $m$ (specifically, a prediction model for the probability of $\tilde{Y}=k,\mathrm{\Delta }=1$ given $\tilde{Y}\ge k,A=a,W$), and we sometimes refer to the model fit as a predictor.

In our simulation studies, we will use the following working models, fitted in a dataset where each participant contributes a row of data corresponding to each time $k=1$ through $k=\tilde{Y}$:

• The following pooled main terms logistic regression (LR) $\text{logit}\{m_{\beta }(k,a,W)\}={\beta }_{a,0,k}+{\beta }_{a,1}^{\top }W$ estimated with maximum likelihood estimation. Note that this model has (i) separate parameters for each study arm, and (ii) in each arm, intercepts for each possible outcome level $k$.

• The above model fitted with an ${\ell }_1$ penalty on the parameter ${\beta }_{a,1}$, where the ${\ell }_1$ penalty is chosen using five‐fold cross‐validation (${\ell }_1$‐LR, Tibshirani, 1996; Park & Hastie, 2007).

• A random forest classification model (RF, Breiman, 2001), with hyper‐parameters chosen based on five‐fold cross‐validation.

• An extreme gradient boosting tree ensemble (XGBoost, Friedman, 2001), with hyper‐parameters chosen based on five‐fold cross‐validation.

• MARS(MARS, Friedman, 1991).

For RF, XGBoost, and MARS, the algorithms are trained in the whole sample $\{1,\dots ,n\}$. For these algorithms, we also assessed the performance of cross‐fitted versions of the estimators. Cross‐fitting is sometimes necessary to guarantee that the regularity assumptions required for asymptotic normality of the estimators hold when using data‐adaptive regression methods (Chernozhukov et al., 2018; Klaassen, 1987; Zheng & van der Laan, 2011), and is performed as follows. Let ${𝒱}_1,\dots ,{𝒱}_J$ denote a random partition of the index set $\{1,\dots ,n\}$ into $J$ prediction sets of approximately the same size. That is, ${𝒱}_j\subset \{1,\dots ,n\}$; ${\bigcup }_{j=1}^J{𝒱}_j=\{1,\dots ,n\}$; and ${𝒱}_j\cap {𝒱}_{j^{\prime }}=\varnothing$. In addition, for each $j$, the associated training sample is given by ${𝒯}_j=\{1,\dots ,n\}\setminus {𝒱}_j$. Let ${\widehat{m}}_j$ denote the prediction algorithm trained in ${𝒯}_j$. Lett $j(i)$ denote the index of the prediction set which contains observation $i$, cross‐fitting entails using only observations in ${𝒯}_{j(i)}$ for fitting models when making predictions about observation $i$. That is, the outcome predictions for each subject $i$ are given by ${\widehat{m}}_{j(i)}(u,a,W_i)$. We let ${\widehat{\eta }}_{j(i)}=({\widehat{m}}_{j(i)},{\widehat{\pi }}_A,{\widehat{\pi }}_C)$ for cross‐fitted estimators and ${\widehat{\eta }}_{j(i)}=(\widehat{m},{\widehat{\pi }}_A,{\widehat{\pi }}_C)$ for non‐cross‐fitted ones. RF, XGBoost, and MARS were fit using the ranger (Wright & Ziegler, 2017), xgboost (Chen et al., 2021) and earth (Milborrow, 2020) R packages, respectively. Hyperparameter tuning was performed using cross‐validation with the origami (Coyle & Hejazi, 2020) R package.

3.2. Targeted minimum loss‐based estimation

Our simulation studies use the targeted minimum loss‐based estimation (TMLE) procedure presented in Díaz et al. (2019). We will refer to that estimator as TMLE with improved efficiency, or IE‐TMLE. We will first present the TMLE of (Moore & van der Laan, 2009b), which constitutes the basis for the construction of the IE‐TMLE.

In Appendix S1 we present some of the efficiency theory underlying the construction of the TMLE. Briefly, TMLE is a framework to construct estimators ${\widehat{\eta }}_{j(i)}$ that solve the efficient influence function estimating equation $n^{-1}{\sum }_{i=1}^n{D}_{{\widehat{\eta }}_{j(i)}}(O_i)=0$, where $D_{\eta }(O)$ is the efficient influence function for $S(k,a)$ in the non‐parametric model that only assumes treatment $A$ is independent of baseline variables $W$ (which holds by design), defined in the supplementary materials. TMLE enjoys desirable properties such as local efficiency, robustness to mis‐specification of the outcome model under censoring completely at random, and asymptotic normality, under regularity assumptions.

3.2.1. TMLE estimator definition

Given a predictor $\widehat{m}$ constructed as in the previous subsection and any $k,a$, the corresponding TMLE estimation procedure for $F(k,a)$ can be summarised in the next steps:

1. Create a long‐form dataset where each participant $i$ contributes the following row of data corresponding to each time $u=0$ through $k$:

   $$\left(u,W_i,A_i,1\{\widetilde{Y_i}\ge u\},1\{\widetilde{Y_i}=u,{\mathrm{\Delta }}_i=0\},1\{\widetilde{Y_i}=u,{\mathrm{\Delta }}_i=1\}\right),$$

   where $1\{X\}$ is the indicator variable taking value 1 if $X$ is true and 0 otherwise.

2. For each individual $i$, obtain a prediction $\widehat{m}(u,a,W_i)$ for each pair in the set $\{(u,a):a=0,1;u=0,\dots ,k\}$.

3. Fit a model ${\pi }_A(a,W)$ for the probability $\mathsf{P}(A=a|W)$. Note that, in randomised trials, this model may be correctly specified by a LR $\text{logit}{\pi }_A(1,W)={\alpha }_0+{\alpha }_1^{\top }W$. Let ${\widehat{\pi }}_A(a,W_i)$ denote the prediction of the model for individual $i$.

4. Fit a model ${\pi }_C(u,a,W)$ for the censoring probabilities $\mathsf{P}(\tilde{Y}=u,\mathrm{\Delta }=0|\tilde{Y}\ge u,A=a,W)$. For time‐to‐event outcomes, this is a model for the censoring probabilities. For ordinal outcomes, the only possibilities are that $C=0$ (outcome missing) or $C=K$ (outcome observed); in this case we only fit the aforementioned model at $u=0$ and we set ${\pi }_C(u,a,W)=0$ for each $u>0$. For either outcome type, if there is no censoring (i.e. if $P(\mathrm{\Delta }=1)=1$), then we set ${\pi }_C(u,a,W)=0$ for all $u$. Let ${\widehat{\pi }}_C(u,a,W_i)$ denote the prediction of this model for individual $i$, that is, using the baseline variable values from individual $i$.

5. For each individual $i$ and each $u\le k$, compute a ‘clever’ covariate $H_{Y,k,u}$ as a function of $\widehat{m}$, ${\widehat{\pi }}_A$, and ${\widehat{\pi }}_C$ as detailed in Appendix S1. The outcome model fit $\widehat{m}$ is then updated by fitting the following LR ‘tilting’ model with single parameter $ϵ$ and offset based on $\widehat{m}$:

   $$\mathsf{P}(\tilde{Y}=u,\mathrm{\Delta }=1|\tilde{Y}\ge u,A=a,W)={\text{logit}}^{-1}\left\{\text{logit}\widehat{m}(u,a,W)+\epsilon H_{Y,k,u}\right\}.$$

   This can be done using standard statistical software for fitting a LR of the indicator variable $1\{\tilde{Y}=u,\mathrm{\Delta }=1\}$ on the variable $H_{Y,k,u}$ using offset $\text{logit}\widehat{m}(u,a,W)$ among observations with $\tilde{Y}\ge u$ and $A=a$ in the long‐form dataset from step 1. The above model fitting process is iterated where at the beginning of each iteration we replace $\widehat{m}$ in the above display and in the definition of $H_{Y,k,u}$ by the updated model fit. We denote the maximum number of iterations that we allow by $i_{\max }$.

6. Let $\tilde{m}(u,a,W_i)$ denote the estimate of $m(u,a,W_i)$ for individual $i$ at the final iteration of the previous step. Note that this estimator is specific to the value $k$ under consideration.

7. Compute the estimate of $S(k,a)=1-F(k,a)$ as the following standardised estimator

   $${\tilde{S}}_{\text{TMLE}}(k,a)=\frac{1}{n}\sum _{i=1}^n\prod _{u=1}^k\{1-\tilde{m}(u,a,W_i)\},$$ (1)

   and let the estimator of $F(k,a)$ be $1-{\tilde{S}}_{\text{TMLE}}(k,a)$.

This estimator was originally proposed by Moore and van der Laan (2009b). The role of the clever covariate $H_{Y,k,u}$ is to endow the resulting estimator $\tilde{S}(k,a)$ with properties such as model‐robustness and more efficiency compared to unadjusted estimators, by means of producing a solution to the efficient influence function estimating equation $n^{-1}{\sum }_{i=1}^n{D}_{{\tilde{\eta }}_{j(i)}}(O_i)=0$ (see technical details for this in Moore & van der Laan, 2009b). In particular, it can be shown that this estimator is efficient when the working model for $m$ is correctly specified. The specific form of the covariate $H_{Y,k,u}$ is given in Appendix S1. Throughout, the notation $\widehat{m}$ is used to represent the predictor constructed as in Section 3.1 and which is an input to the above TMLE algorithm, while $\tilde{m}$ denotes the updated version of this predictor that is output by the above TMLE algorithm at step 6.

3.2.2. IE‐TMLE estimator definition

In Section 4 we will compare several machine learning procedures for estimating $m$ in finite samples. The estimators used in the simulation study are the IE‐TMLE of Díaz et al. (2019), where in addition to updating the initial estimator for the outcome regression $m$, we also update the estimators of the treatment and censoring mechanisms. Specifically, we replace step 5 of the above procedure with the following:

1. For each individual $i$ construct ‘clever’ covariates $H_{Y,k,u}$, $H_A$, and $H_{C,k,u}$ (defined in Appendix S1) as a function of $\widehat{m}$, ${\widehat{\pi }}_A$, and ${\widehat{\pi }}_C$. For each $k=1,\dots ,K$, the model fits are then iteratively updated using LR ‘tilting’ models:

   $$\begin{array}{llll}\text{logit}{m}_{\epsilon }(u,a,W)& =\text{logit}\widehat{m}(u,a,W)+\epsilon H_{Y,k,u}& & \\ \text{logit}{\pi }_{\gamma ,A}(1,W)& =\text{logit}{\widehat{\pi }}_A(1,W)+\gamma H_A& & \\ \text{logit}{\pi }_{\upsilon ,C}(u,a,W)& =\text{logit}{\widehat{\pi }}_C(u,a,W)+\upsilon H_{C,k,u},& & \end{array}$$

   where the iteration is necessary because $H_{Y,k,u}$, $H_A$, and $H_{C,k,u}$ are functions of $\widehat{m}$, ${\widehat{\pi }}_A$, and ${\widehat{\pi }}_C$ that must be updated at each step. As before, for ordinal outcomes we only fit the aforementioned model at $u=0$ and we set ${\pi }_C(u,a,W)=0$ for each $u>0$.

We use ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ to denote this estimator. The updating step above combines ideas from Moore and van der Laan (2009b), Gruber and van der Laan (2012) and Rotnitzky et al. (2012) to produce an estimator with the following properties:

• (i)Consistency and at least as precise as the Kaplan–Meier and inverse probability weighted estimators;
• (ii)Consistency under violations of independent censoring (unlike the Kaplan–Meier estimator) when either the censoring or survival distributions, conditional on covariates, are estimated consistently and censoring is such that $C⫫Y|W,A$; and
• (iii)Non‐parametric efficiency (meaning achieving the smallest possible variance among a class of admissible estimators) when both of these distributions are consistently estimated at rate $n^{1/4}$.

Please see Díaz et al. (2019) for more details on these estimators, which are implemented in the R package adjrct (Díaz & Williams, 2021).

Next, we present a result (Theorem 1) stating asymptotic normality of ${\tilde{S}}_{\text{TMLE}}$ using machine learning for prediction that avoids some limitations of existing methods, and present a consistent estimator of its variance. In Section 4 we present simulation results where we evaluate the performance of ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ for covariate adjustment in COVID‐19 trials for hospitalised patients. We favour ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ in our numerical studies because, unlike ${\tilde{S}}_{\text{TMLE}}$, it satisfies property (ii) above. The simulation uses Wald‐type hypothesis tests based on the asymptotic approximation of Theorem 1, where we note that the variance estimator in the theorem is consistent for ${\tilde{S}}_{\text{TMLE}}$ but it is conservative for ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ (Moore & van der Laan, 2009b).

3.3. Asymptotically correct confidence intervals and hypothesis tests for TMLE combined with machine learning

Most available methods to construct confidence intervals and hypothesis tests in the statistics literature are based on the sampling distribution of the estimator. While using the exact finite‐sample distribution would be ideal for this task, such distributions are notoriously difficult to derive for our problem in the absence of strong and unrealistic assumptions (such as linear models with Gaussian noise). Thus, here we focus on methods that rely on approximating the finite‐sample distribution using asymptotic results as $n$ goes to infinity.

In order to discuss existing methods, it will be useful to introduce and compare the following assumptions:

Assumption A1

Censoring is completely at random, that is, $C⫫(Y,W)|A=a$ for each treatment arm $a$.

Assumption A2

Let $\Vert f|{|}^2$ denote the $L_2(\mathsf{P})$ norm $\int f^2(o)\mathrm{d}\mathsf{P}(o)$, for $O=(W,A,\mathrm{\Delta }=\mathbb{1}\{Y\le C\},\tilde{Y})$. We abbreviate $m(k,a,W)$ and $\widehat{m}(k,a,W)$ by $m$ and $\widehat{m}$, respectively. Assume the estimator $\widehat{m}$ is consistent in the sense that $\Vert \widehat{m}-m\Vert =o_P(1)$ for all $k\in \{1,\dots ,K\}$ and $a\in \{0,1\}$. We also assume that there exists a $\delta >0$ such that $\delta <m<1-\delta$ with probability 1.

Assumption A3

Assume the estimator $\widehat{m}$ converges to a possibly mis‐specified limit $m_1$ in the sense that $\Vert \widehat{m}-m_1\Vert =o_P(1)$ for all $k\in \{1,\dots ,K\}$ and $a\in \{0,1\}$, where we emphasise that $m_1$ can be different from the true regression function $m$. We also assume that there exists a $\delta >0$ such that $\delta <m_1<1-\delta$ with probability 1.

For estimators $\widehat{m}$ of $m$ that use cross‐fitting, the function $\widehat{m}$ consists of $J$ maps (one for each training set) from the sample space of $O$ to the interval $[0,1]$. In this case, by convention we define $||\widehat{m}-m||$ in A2 as the average across the $J$ maps of the $L_2(\mathsf{P})$ norm of each such map minus $m$. Convergence of $\Vert \widehat{m}-m\Vert$ to 0 in probability is then equivalent to the same convergence where $\widehat{m}$ is replaced by the corresponding map before cross‐fitting is applied. The same convention is used in A3.

There are at least two results on asymptotic normality for ${\tilde{S}}_{\text{TMLE}}$ relevant to the problem we are studying. The first result is a general theorem for TMLE (see appendix A.1 of van der Laan & Rose 2011), stating that the estimator is asymptotically normal and efficient under regularity assumptions which include A2. Among other important implications, this asymptotic normality implies that the variance of the estimators can be consistently estimated by the empirical variance of the efficient influence function. This means that asymptotically correct confidence intervals and hypothesis tests can be constructed using a Wald‐type procedure. As stated above, it is often undesirable to assume A2 in the setting of a randomised trial, as it is a much stronger assumption than what would be required for an unadjusted estimator.

The second result of relevance to this paper establishes asymptotic normality of $\tilde{S}(k,a)$ under assumptions that include A3 (Moore & van der Laan, 2009a). The asymptotic variance derived by these authors depends on the true outcome regression function $m$, and is thus difficult to estimate. As a solution, the authors propose to use a conservative estimate of the variance whose computation does not rely on the true regression function $m$. While this conservative method yields correct type 1 error control, its use is not guaranteed to fully convert precision gains from covariate adjustment into power gains.

We note that the above asymptotic normality results from related works rely on the additional condition that the estimator $\widehat{m}$ lies in a Donsker class. This assumption may be violated by some of the data‐adaptive regression techniques that we consider. Furthermore, we note that resampling methods such as the bootstrap cannot be safely used for variance estimation in this setting. Their correctness is currently unknown when the working model for $m$ is based on data‐adaptive regression procedures such as those described in Section 3.1 and used in our simulation studies.

In what follows, we build on recent literature on estimation of causal effects using machine learning to improve upon the aforementioned asymptotic normality results on two fronts. First, we introduce cross‐fitting (Chernozhukov et al., 2018; Klaassen, 1987; Zheng & van der Laan, 2011) to avoid the Donsker condition. Second, and most importantly, we present a novel asymptotic normality result that avoids the above limitations of existing methods regarding strong assumptions (specifically A2) and conservative variance estimators (that may sacrifice power).

The following are a set of assumptions about how components of the TMLE are implemented, which we will use in our theorem below:

Assumption A4

The initial estimator of ${\pi }_A(1)$ is set to be the empirical mean $n^{-1}{\sum }_{i=1}^n{A}_i$.

Assumption A5

For time‐to‐event outcomes, the initial estimator ${\widehat{\mathrm{\Pi }}}_C(a,u)$ is set to be the Kaplan–Meier estimator estimated separately within each treatment arm $a$. For ordinal outcomes, ${\widehat{\mathrm{\Pi }}}_C(a,0)$ is the proportion of missing outcomes in treatment arm $a$ and ${\widehat{\mathrm{\Pi }}}_C(a,u)=0$ for $u>0$.

Assumption A6

The initial estimator $\widehat{m}(u,a,W)$ is constructed using one of the following:

1. Any estimator in a parametric working model (i.e. a model that can be indexed by a Euclidean parameter) such as maximum likelihood, ${\ell }_1$ regularisation, etc.

2. Any data‐adaptive regression method (e.g., random forests, MARS, XGBoost, etc.) estimated using cross‐fitting as described above.

Assumption A7

The regularity conditions in theorem 5.7, p. 45 of van der Vaart (1998) hold for the maximum likelihood estimator corresponding to each LR model fit in step (5) of the TMLE algorithm.

Theorem 1

Assume A1 and A3–A7 above. Recall that $D_{\eta }$ is the efficient influence function for estimation of $S(k,a)$ (given in Appendix S1). Define the variance estimator

$${\tilde{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n{[D_{{\tilde{\eta }}_{j(i)}}(O_i)]}^2.$$

Then we have for all $k\in \{1,\dots ,K\}$ and $a\in \{0,1\}$ that

$$\sqrt{n}\{{\tilde{S}}_{\text{TMLE}}(k,a)-S(k,a)\}/\tilde{\sigma }⇝N(0,1).$$

Theorem 1 is a novel result establishing the asymptotic correctness of Wald‐type confidence intervals and hypothesis tests for the covariate‐adjusted estimator ${\tilde{S}}_{\text{TMLE}}(k,a)$ based on machine learning regression procedures constructed as stated in A6. For example, the confidence interval ${\tilde{S}}_{\text{TMLE}}(k,a)\pm 1.96\times \tilde{\sigma }/\sqrt{n}$ has approximately 95% coverage at large sample sizes, under the assumptions of the theorem. The theorem licenses the large sample use of any regression procedure for $m$ when combined with the TMLE of Section 3.2, as long as the regression procedure is either (i) based on a parametric model (such as ${\ell }_1$‐regularisation) or (ii) based on cross‐fitted data‐adaptive regression, and the assumptions of the theorem hold. The theorem states sufficient assumptions under which Wald‐type tests from such a procedure will be asymptotically correct.

Insight into the correctness of the variance estimator proposed in Theorem 1 may be gained as follows. Under Assumption A2, standard theory for the TMLE (e.g., Zheng & van der Laan, 2011) shows that ${\tilde{S}}_{\text{TMLE}}(k,a)$ is asymptotically normal with asymptotic variance given by the variance of the efficient influence function $D_{\eta }(O)$. When Assumption A2 does not hold, and if ${\pi }_A$ and ${\pi }_C$ are estimated using correctly specified parametric models, the TMLE is still asymptotically normal, but its variance is now equal to the variance of $D_{{\eta }_1}(O)-C_{{\eta }_1}(O)$, where ${\eta }_1=(m_1,{\pi }_A,{\pi }_C)$ and $C_{{\eta }_1}(O)$ is a correction term that must be subtracted to account for inconsistent estimation of $m$ (see section 4.1.3 of Moore & van der Laan, 2009b). This correction terms is equal to zero in two circumstances: if either A2 holds such that $m_1=m$, or if ${\pi }_A$ and ${\pi }_C$ are known and we use ${\widehat{\pi }}_A={\pi }_A$ and ${\widehat{\pi }}_C={\pi }_C$. The crux of the proof of Theorem 1 is to show that this correction term also equals zero under Assumptions A4 and A5, namely when ${\pi }_A$ and ${\pi }_C$ are estimated using non‐parametric maximum likelihood estimators that do not use covariates under censoring completely at random. Readers interested in more technical details are encouraged to consult the proof of this theorem in Appendix S1.

Assumption A3 states that the predictions given by the regression method used to construct the adjusted estimator converge to some arbitrary function (i.e., not assumed to be equal to the true regression function). This assumption is akin to Condition 3 assumed by Bloniarz et al. (2016) in the context of establishing asymptotic normality of a covariate‐adjusted estimator based on ${\ell }_1$‐regularisation. We note that this is an assumption on the predictions themselves and not on the functional form of the predictors. Therefore, issues like collinearity do not necessarily cause problems. While this assumption can hold for many off‐the‐shelf machine learning regression methods under assumptions on the data‐generating mechanism, general conditions have not been established and the assumption must be checked on a case‐by‐case basis.

We note that assumption A1 is stronger than the assumption $C⫫Y|A=a$ required by unadjusted estimators such as the Kaplan–Meier estimator. However, if $W$ is prognostic (meaning that $W\perp \perp /Y|A=a$), then the assumption $C⫫Y|A=a$ required by the Kaplan–Meier estimator cannot generally be guaranteed to hold, unless A1 also holds. Thus, our theorem aligns with the recent FDA draft guidance on covariate adjustment in the sense that ‘it provides valid inference under approximately the same minimal statistical assumptions that would be needed for unadjusted estimation in a randomized trial’ (U.S. Food and Drug Administration, 2021a).

The construction of estimators based on A5 such as ${\tilde{S}}_{\text{TMLE}}$ and the unadjusted estimator should be avoided if A1 does not hold. In these cases, we recommend the use of the estimator ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$, which can achieve consistency if censoring at random holds (i.e. $C⫫Y|W,A$). The variance estimator given in Theorem 1 is conservative for ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ (see Moore & van der Laan, 2009b).

Consistency of ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ under $C⫫Y|W,A$ will typically require that at least one of two assumptions hold: (a) that the censoring probabilities ${\pi }_C(u,a,w)$ are estimated consistently, or that (b) the outcome regression $m(u,a,w)$ is estimated consistently. To maximise the chances of either of these conditions being true, we recommend the use of flexible machine learning for both of these regressions, including model selection and ensembling techniques such as the Super Learner (van der Laan et al., 2007). The conditions for asymptotic normality of ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}$ under these circumstances are much stronger than those for Theorem 1, and typically include consistent estimation of both ${\pi }_C(u,a,w)$ and $m(u,a,w)$ at certain rates (e.g., each of them converging at $n^{1/4}$‐rate is sufficient, see appendix A.1 of van der Laan and Rose (2011).

4. SIMULATION STUDIES

We performed a Monte Carlo simulation study with the following goals: (1) to evaluate the performance of the covariate‐adjusted estimators based on machine learning discussed in Section 3, and compare them to unadjusted estimators in terms of efficiency and bias, (2) to illustrate the performance of hypothesis tests based on the asymptotic approximation of Theorem 1, and (3) to provide preliminary evidence to help guide the choice of regression algorithm for covariate adjusted estimators. Code to reproduce our simulations may be found at https://github.com/nt‐williams/covid‐RCT‐covar.

4.1. Data generating mechanisms

Our data generating distribution is based on a database of over 1500 patients hospitalised at Weill Cornell Medicine New York Presbyterian Hospital prior to 15 May 2020. The database includes information on patients 18 years of age and older with COVID‐19 confirmed through reverse‐transcriptase‐polymerase‐chain‐reaction assays. For a full description of the clinical characteristics and data collection methods of the initial cohort sampling, see Goyal et al. (2020).

We evaluate the potential to improve efficiency by adjustment for subsets of the following baseline variables: age, sex, BMI, smoking status, whether the patient required supplemental oxygen within 3 h of presenting to the emergency department, number of comorbidities (diabetes, hypertension, COPD, CKD, ESRD, asthma, interstitial lung disease, obstructive sleep apnea, any rheumatological disease, any pulmonary disease, hepatitis or HIV, renal disease, stroke, cirrhosis, coronary artery disease, active cancer), number of relevant symptoms, presence of bilateral infiltrates on chest X‐ray, dyspnea, and hypertension. These variables were chosen because they have been previously identified as risk factors for severe disease (Goyal et al., 2020; Guan et al., 2020; Gupta et al., 2020), and therefore are likely to improve efficiency of covariate‐adjusted effect estimators in randomised trials in hospitalised patients.

We consider two types of outcomes: a time‐to‐event outcome defined as the time from hospitalisation to intubation or death, and a six‐level ordinal outcome at 14 days post‐hospitalisation based on the WHO Ordinal Scale for Clinical Improvement (Marshall et al., 2020). The categories are as follows: 0, discharged from hospital; 1, hospitalised with no oxygen therapy; 2, hospitalised with oxygen by mask or nasal prong; 3, hospitalised with non‐invasive ventilation or high‐flow oxygen; 4, hospitalised with intubation and mechanical ventilation; 5, dead.

We simulate datasets for four scenarios where we consider two effect sizes (null vs. positive) and two baseline variable settings (prognostic vs, not prognostic, where prognostic means marginally associated with the outcome). For each sample size $n\in \{100,500,1500\}$ and for each scenario, we simulated $R=5000$ datasets as follows. To generate datasets where covariates are prognostic, we draw $n$ pairs $(W,Y)$ randomly from the original dataset with replacement. This generates a dataset where the covariate prognostic strength is as observed in the real dataset. To simulate datasets where covariates are not prognostic, we first draw outcomes $Y$ at random with replacement from the original dataset, and then draw covariates $W$ at random with replacement and independent of the value $Y$ drawn.

For each scenario, a hypothetical treatment variable is assigned randomly for each patient with probability 0.5 independent of all other variables. This produces a data generating distribution with zero treatment effect, used to assess type 1 error. Next, a positive treatment effect is simulated for time‐to‐event outcomes by adding an independent random draw from a ${\chi }^2$ distribution four degrees of freedom to each patient's observed survival time in the treatment arm. To simulate outcomes being missing completely at random, $5\%$ of the patients are selected at random to be censored, and the censoring times are drawn from a uniform distribution between 1 and 14. A positive treatment effect is simulated for ordinal outcomes by subtracting from each patient's outcome in the treatment arm an independent random draw from a four‐parameter Beta distribution with support $(0,5)$ and parameters $(3,15)$, rounded to the nearest nonnegative integer. This approach to generating positive treatment effects implies no treatment effect heterogeneity in the linear scale, but does not imply this on other scales.

4.2. Estimands

For time‐to‐event outcomes, we focus on evaluating the effect of treatment on the $\mathsf{RMST}$ at 14 days and the $\mathsf{RD}$ at 7 days after hospitalisation, and for ordinal outcomes we evaluate results for both the $\mathsf{LOR}$ and the Mann–Whitney statistic (see Section 3). For survival outcomes, the data generating mechanisms of Section 4.1 yield an effect size for $\mathsf{RMST}$ difference of 1.04, and $\mathsf{RD}$ of 0.10, respectively. For ordinal outcomes, the data generating mechanism of Section 4.1 yields effect sizes for $\mathsf{LOR}$ of 0.60 and for $\mathsf{MW}$ of 0.46. These values were approximated using formulas given in Section 2, with population quantities replaced by empirical quantities in a dataset of size $10^7$ generated according to the data generated processes of the previous subsection.

4.3. Estimators and methods evaluated

We evaluate several estimators. First, we evaluate unadjusted estimators based on substituting the empirical CDF for ordinal outcomes and the Kaplan–Meier estimator for time‐to‐event outcomes in the parameter definitions of Section 2. We then evaluate adjusted estimator ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}(k,a)$ where the working models are:

LR:

a fully adjusted estimator using LR including all the variables listed in the previous section,

ℓ ₁‐LR:

${\ell }_1$ regularisation of the previous LR,

RF:

random forests,

MARS:

multivariate adaptive regression splines, and

XGBoost:

extreme gradient boosting tree ensembles.

For estimators RF, MARS, and XGBoost, we further evaluated cross‐fitted versions of the working model. For all adjusted estimators the propensity score ${\pi }_A$ is estimated with an intercept‐only model (A4), and the censoring mechanism ${\pi }_C$ is estimated using a Kaplan–Meier estimator fitted independently for each treatment arm (A5) (or equivalently for ordinal outcomes the proportion of missing outcomes within each treatment arm).

Confidence intervals and hypothesis tests are performed using Wald‐type statistics, which use an estimate of the standard error based on the asymptotic Gaussian approximation described in Theorem 1. We compare the performance of the estimators in terms of the probability of type 1 error, power, the bias, the variance, and the mean squared error. Monte Carlo errors in these estimates resulting from using $R=5000$ are computed using the formulas discussed in Morris et al. (2019). These formulas assume normality of the effect estimators and therefore may not be accurate at the smaller sample sizes where our asymptotic normality results may not provide a good approximation.

4.4. Simulation results

We compute the relative efficiency $\mathsf{RE}$ of each estimator compared to the unadjusted estimator as a ratio of the mean squared errors. This relative efficiency can be interpreted as the ratio of sample sizes required by the estimators to achieve the same power at local alternatives, asymptotically (van der Vaart, 1998). Equivalently, one minus the relative efficiency is the relative reduction (due to covariate adjustment) in the required sample size to achieve a desired power, asymptotically; for example, a relative efficiency of 0.8 is approximately equivalent to needing 20% smaller sample size when using covariate adjustment.

In the presentation of the results, we append the prefix CF to cross‐fitted estimators. For example, CF‐RF will denote cross‐fitted random forests.

Tables containing the comprehensive results of the simulations are presented in Appendix S1. The maximum Monte Carlo SE for each quantity is presented for each scenario. Figures 1 and 2 show results for relative efficiency, power, and type 1 error for two of the scenarios evaluated. Figures for the other two scenarios are available in Appendix S1.

FIGURE 1.

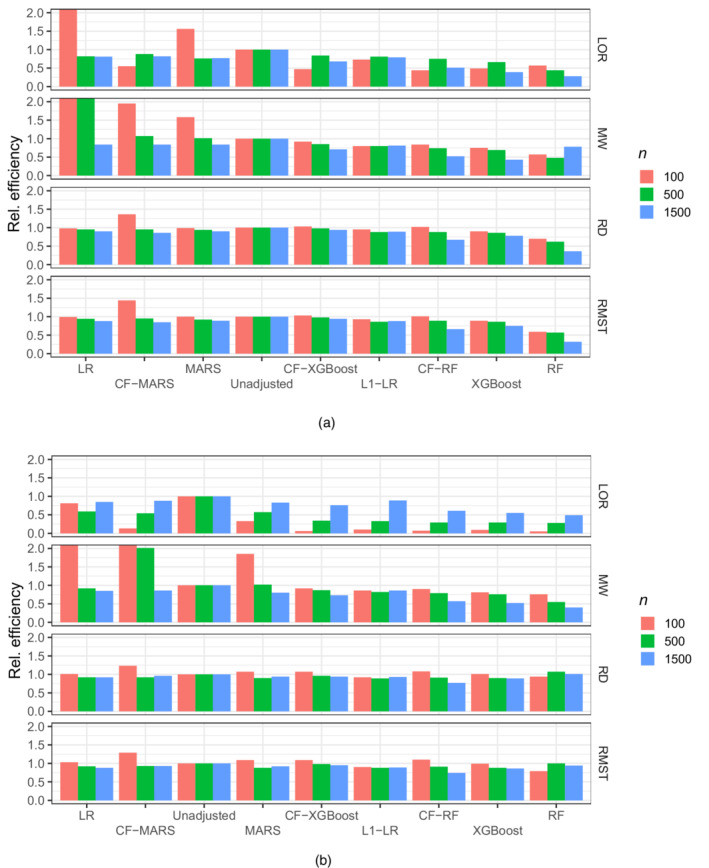
Efficiency of adjusted estimators relative to an unadjusted estimator for $\mathsf{LOR}$, $\mathsf{MW}$, $\mathsf{RD}$, and $\mathsf{RMST}$ when there is (a) no effect of the exposure on the outcome and (b) when there is a positive effect of the exposure on the outcome and covariates are prognostic of the outcome. Estimators are ordered by decreasing order of efficiency and efficiency is truncated at two.

FIGURE 2.

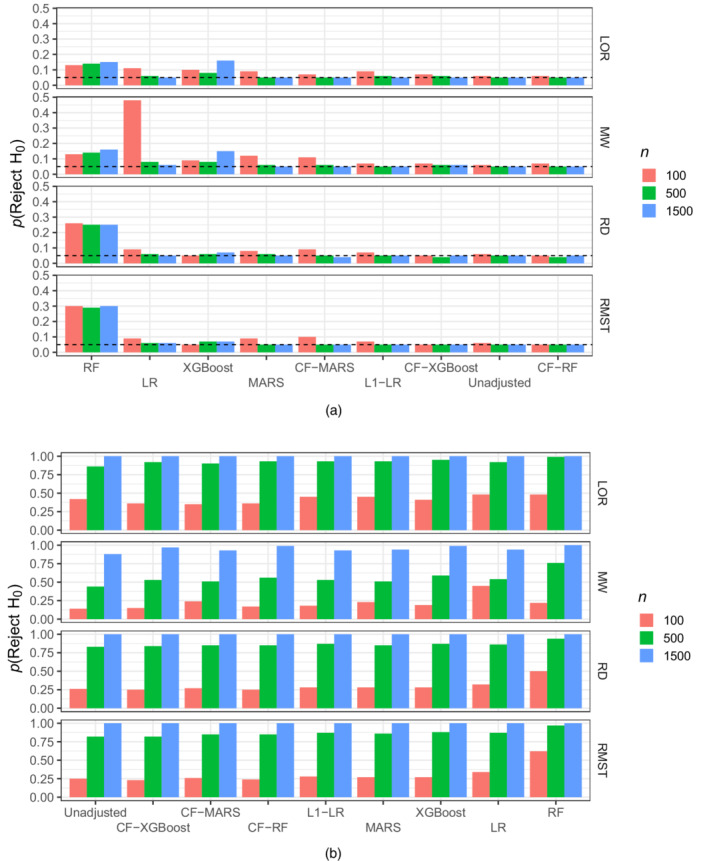
Probability of rejecting H${\hspace{0.17em}}_0$ for $\mathsf{LOR}$, $\mathsf{MW}$, $\mathsf{RD}$, and $\mathsf{RMST}$ when covariates are prognostic of the outcome and there is (a) no effect of the exposure on the outcome–estimators ordered by decreasing probability–and (b) when there is a positive effect of the exposure on the outcome–estimators ordered by increasing probability

In the remainder of this section we present a summary of the results. First, we note that the use of random forests without cross‐fitting exhibits very poor performance, failing to appropriately control type 1 error when the effect is null, and introducing significant bias when the effect is positive. We observed this poor performance across all simulations. Thus, in what follows we omit a discussion of this estimator.

At large sample sizes all cross‐fitted estimators along with LR estimators yield correct type I error, illustrating the correctness of Wald‐type tests proved in Theorem 1. Our simulation results also show that Wald‐type hypothesis tests based on data‐adaptive machine learning procedures fail to control type 1 error if the regressions procedures are not cross‐fitted.

Results for the $\mathsf{LOR}$ in Tables S3 and S11 show that covariate adjusted estimators have better performance than the unadjusted estimator at small sample sizes, even when the covariates are not prognostic. In these cases, the unadjusted estimator is unstable with large variance due to near‐empty outcome categories in some simulated datasets, which causes division by near‐zero numbers in the unadjusted $\mathsf{LOR}$ estimator. Some covariate adjusted estimators fix this problem by extrapolating model probabilities to obtain better estimates of the probabilities in the near‐empty cells.

Tables S1–S4 display the results for the difference in $\mathsf{RMST}$, $\mathsf{RD}$, $\mathsf{LOR}$, and $\mathsf{MW}$ estimands when covariates are prognostic and there is a positive effect size. At sample size $n=1500$ all adjusted estimators yield efficiency gains, with CF‐RF offering the best $\mathsf{RE}$ ranging from 0.51 to 0.67 compared to an unadjusted estimator, while appropriately controlling type 1 error. In contrast, the $\mathsf{RE}$ of ${\ell }_1$‐LR at $n=1500$ ranged from 0.79 to 0.89.

At sample size $n=500$, ${\ell }_1$‐LR, CF‐RF, and XGBoost offer comparable efficiency gains, ranging from 0.29 to 0.99. As the sample size decreases to $n=100$ most adjusted estimators yield efficiency losses and the only estimator that retains efficiency gains is ${\ell }_1$‐LR, with $\mathsf{RE}$ from 0.86 to 0.92. (An exception is in estimation of the $\mathsf{LOR}$, where the $\mathsf{RE}$ of ${\ell }_1$‐LR was 0.1 due to the issue discussed above.)

Efficiency gains for ${\ell }_1$‐LR did not always translate into power gains of a Wald‐type hypothesis test compared to other estimators (e.g. LR at $n=100$), possibly due to biased variance estimation and/or a poor Gaussian approximation of the distribution of the test statistic. At small sample size $n=100$ power was uniformly better for a Wald‐type test based on LR compared to ${\ell }_1$‐LR. At sample size $n=500$ a Wald‐type test based on ${\ell }_1$‐LR seemed to dominate all other algorithms, whereas at $n=1500$ all algorithms had comparable power very close to one.

Results when the true treatment effect is zero and covariates are prognostic are presented in Tables S5–S8. At sample size $n=1500$, CF‐RF generally provides large efficiency gains with relative efficiencies ranging from 0.66 to 0.77. For comparison, ${\ell }_1$‐LR has $\mathsf{RE}$ ranging from 0.88 to 0.92. As the sample size decreases to $n=500$, ${\ell }_1$‐LR and CF‐RF both offer the most efficiency gains while retaining type 1 error control, with $\mathsf{RE}$ ranging from 0.74 to 0.88. At small sample sizes $n=100$, ${\ell }_1$‐LR consistently leverages efficiency gains from covariate adjustment ($\mathsf{RE}$ ranging from 0.73 to 0.95) but its type 1 error (ranging from 0.07 to 0.09) is slightly larger than that of the unadjusted estimator. For estimation of $\mathsf{LOR}$ and $\mathsf{MW}$, XGBoost has similar results at sample size $n=100$.

Tables S9–S12 show results for scenarios where the covariates are not prognostic of the outcome but there is a positive effect. This case is interesting because it is well known that adjusted estimators can induce efficiency losses (i.e. $\mathsf{RE}>1$) by adding randomness to the estimator when there is nothing to be gained from covariate adjustment. We found that ${\ell }_1$‐LR uniformly avoids efficiency losses associated with adjustment for independent covariates, with a maximum $\mathsf{RE}$ of 1.03. All other covariate adjustment methods had larger maximum $\mathsf{RE}$. At sample size $n=100$, the superior efficiency of the ${\ell }_1$‐LR estimator did not always translate into better power (e.g. compared to LR) due to the use of a Wald‐test which relies on an asymptotic approximation to the distribution of the estimator.

Results when the true treatment effect is zero and covariates are not prognostic are presented in Tables S13–S16. In this case, ${\ell }_1$‐LR also avoids efficiency losses across all scenarios, while maintaining a type 1 error that is comparable to that of the unadjusted estimator.

5. RECOMMENDATIONS AND FUTURE DIRECTIONS

In our numerical studies we found that ${\ell }_1$‐regularised LR offers the best trade‐off between type I error control and efficiency gains across sample sizes, outcome types, and estimands. We found that this algorithm leverages efficiency gains when efficiency gains are feasible, while protecting the estimators from efficiency losses when efficiency gains are not feasible (e.g., adjusting for covariates with no prognostic power). A direction of future research is the evaluation of bootstrap estimators for the variance and confidence intervals of covariate‐adjusted estimators, especially for cases where the Wald‐type methods evaluated in this manuscript did not perform well (e.g. ${\ell }_1$‐LR at $n=100$).

We also found that LR can result in large efficiency losses for small sample sizes, with relative efficiencies as large as 1.17 for the $\mathsf{RMST}$ estimand, and as large as 7.57 for the $\mathsf{MW}$ estimand. Covariate adjustment with ${\ell }_1$‐regularised LR solves this problem, maintaining efficiency when covariates are not prognostic for the outcome, even at small sample sizes. However, Wald‐type hypothesis tests do not appropriately translate the efficiency gains of ${\ell }_1$‐regularised LR into more powerful tests. This requires the development of tests appropriate for small samples.

We recommend against using the $\mathsf{LOR}$ parameter since it is difficult to interpret and the corresponding estimators (even unadjusted ones) can be unstable at small sample sizes. Covariate adjustment with ${\ell }_1$‐LR, CF‐MARS, CF‐RF, or CF‐XGBoost can aid to improve efficiency in estimation of the $\mathsf{LOR}$ parameter over the unadjusted estimator when there are near‐empty cells at small sample sizes. This improvement in efficiency did not translate into an improvement in power when using Wald‐type hypothesis tests, due to poor small‐sample Gaussian approximations or poor variance estimators.

We discourage the use of non‐cross‐fitted versions of the machine learning methods evaluated (i.e., RF, XGBoost, MARS) for covariate adjustment. Specifically, we found in simulations that non‐cross‐fitted random forests can lead to overly biased estimators in the case of a positive effect, and to anti‐conservative Wald‐type hypothesis tests in the case of a null treatment effect. We found that cross‐fitting the random forests alleviated this problem and was able to produce small bias and acceptable type 1 error at all sample sizes. This is supported at large sample sizes by our main theoretical result (Theorem 1) which establishes asymptotic correctness of cross‐fitted procedures under regularity conditions. In fact, we found that random forests with cross‐fitting provided the most efficiency gains at large sample sizes.

Based on the results of our simulation studies, we recommend that cross‐fitting with data‐adaptive estimators such as random forests and extreme gradient boosting be considered for covariate selection in trials with large sample sizes ($n=1500$ in our simulations). In large sample sizes, it is also possible to consider an ensemble approach such as Super Learning (van der Laan et al., 2007) that allows one to select the predictor that yields the most efficiency gains. Traditional model selection with statistical learning is focused on the goal of prediction, and an adaptation of those tools to the goal of maximising efficiency in estimating the marginal treatment effect is the subject of future research.

We have developed estimators that leverage efficiency gains from covariate adjustment while delivering correct inference under approximately the same conditions as an unadjusted estimator. Those conditions include A1. When A1 does not hold, neither our approach based on Theorem 1 nor an unadjusted estimator delivers correct inference. In these cases, consistency of the ${\tilde{S}}_{\text{TMLE}}(k,a)$ and ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}(k,a)$ estimators requires that censoring at random holds (i.e. $C⫫Y|W,A$), and that either the outcome regression or censoring mechanism is consistently estimated. Thus, it is recommended to also estimate the censoring mechanism with machine learning methods that allow for flexible regression. Standard asymptotic normality results for the ${\tilde{S}}_{\text{TMLE}}(k,a)$ and ${\tilde{S}}_{\mathrm{IE}-\mathrm{TMLE}}(k,a)$ require consistent estimation of both the censoring mechanism and the outcome mechanism at certain rates (e.g. both estimated at a $n^{1/4}$ rate is sufficient). The development of estimators that remains asymptotically normal under the weaker condition that at least one of these regressions is consistently estimated has been the subject of recent research (e.g., Avagyan & Vansteelandt, 2021; Benkeser et al., 2017; Díaz, 2019; Díaz & van der Laan, 2017; Dukes & Vansteelandt, 2021). These recent methods require assumptions that are more restrictive than those required by an unadjusted estimator under A1. Thus, our approach is preferable to the above methods when A1 holds, such as when non‐administrative censoring is minimal.

Lastly, our methods are developed in a discrete‐time setting. Outcomes in most trials (e.g. in clinical research) are measured in discrete‐time (e.g. survival is measured in days). When the time‐to‐event outcomes are measured in continuous time, application of our methods will require the discretisation of time. The optimal time‐window for discretisation is an open question, but we recommend discretising time in terms of a time unit that is relevant for the scientific question at hand. For example, for A/B testing a web page design it may be most relevant to measure the number of seconds required for the users to complete a given task.

Supporting information

Appendix S1. Supporting information

Williams, N. , Rosenblum, M. & Díaz, I. (2022) Optimising precision and power by machine learning in randomised trials with ordinal and time‐to‐event outcomes with an application to COVID‐19. Journal of the Royal Statistical Society: Series A (Statistics in Society), 1–23. Available from: 10.1111/rssa.12915

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.