Regressive changes of crown‐root morphology and their volumetric segmentation for adult dental age estimation

Abstract

Cone‐beam computed tomography (CBCT) enables the assessment of regressive morphological changes in teeth, which can be used to predict chronological age (CA) in adults. As each tooth region is known to have different correlations with CA, this study aimed to segment and quantify the sectional volumes of the tooth crown and root from CBCT scans to test their correlations with the chronological age (CA). Seventy‐five CBCT scans from individuals with age between 20 and 60 years were collected retrospectively from an existing database. A total of 192 intact maxillary anterior teeth fulfilled the eligibility criteria. The upper tooth volume ratio (UTVR), lower tooth volume ratio (LTVR), and sex were used as predictor variables. The UTVR and LTVR parameters were both found to be differently correlated to CA and independent from each other. Regression models were derived from each tooth, with the highest R ² being the maxillary lateral incisor (R ² = 0.67). Additional single predictor models using each ratio were capable of reliably predicting the CA. The segmentation approach in volumetric adult dental age estimation proved to be beneficial in enhancing the reliability of the regression model.

Highlights.

• The relationship between age and segmented dental morphological changes in adults was examined.

• The ratios of upper and lower tooth volume regions were differently correlated with age.

• The maxillary lateral incisor achieved the highest R ² value (R ² = 0.67).

• Volumetric ratio parameters showed a nonlinear and linear relationship with age.

1. INTRODUCTION

Age estimation has a significant role in human identification [1]. In practice, the estimated age can refine the antemortem data and reduce the time‐consuming comparative reconciliation processes [2]. Dental development is a parameter known for its reliability in estimating the age of children and adolescents [3, 4]. In adults, however, dental age estimation does not rely on development. Instead, regressive morphological parameters are used, such as attrition, secondary dentin deposition, periodontosis, cementum apposition, root resorption, and translucency changes [5, 6, 7, 8]. These regressive changes—known for their high error rates [9]—were initially explored via destructive analysis [5] and later employed (nondestructive) radiographic assessment [10, 11].

With the evolution of advanced imaging tools, such as cone‐beam computed tomography (CBCT), a more realistic noninvasive assessment of dental morphology has been made possible, offering three‐dimensional (3D) visualization and navigation. Current trends using CBCT‐based methods for dental age estimation of adults highlight the advantages of the volumetric quantification of dental structure [12, 13, 14]. The most common approach quantifies the ratio between pulp and tooth volumes (PTV) [15]. In this approach, the whole volume of the pulp is calculated and divided by the volume of the tooth [16]. Although the PTV method provides a more reliable dental age estimation outcome [15], specific age‐related changes will be ignored when the whole tooth volumetric information is not segmented. In other words, the detailed correlation between regressive morphological changes and chronological age (CA) can be adequately assessed if the tooth region is analyzed separately [7]. For example, the dental crown is mainly affected by attrition, while the root is more affected by resorption. Similarly, secondary dentin deposition leads to distinct reductions in the pulp volume in different tooth regions [17].

Considering the limitations of the PTV approach, which quantifies volumetric information across different tooth regions as an aggregate, this study aimed to segment and quantify the volume of the crown and root separately and test their correlation with the chronological age (CA). The proposed approach was intended to promote a more comprehensive analysis of the regressive morphological changes as a function of age.

2. MATERIALS AND METHODS

This analytical, cross‐sectional study was approved by the Ethics Committee of Universitas Padjajaran (899/UN6.KEP/EC/2021). The study sample was collected retrospectively and consisted of 75 CBCT scans recorded at the Universitas Padjajaran Dental Hospital, Bandung, West Java, Indonesia. All CBCT data were obtained for varied diagnostic and therapeutic purposes, and no patient was exposed to radiation for the sole purpose of research.

The inclusion criteria consisted of fully erupted, mature (closed apex), and sound anterior maxillary teeth with a visible cementoenamel junction (CEJ). Maxillary canines (C), lateral incisors (Li), and central incisors (Ci) on the right side were observed. Left side teeth were observed only if the contralateral maxillary right could not fulfill the inclusion criteria. Only one tooth type per region in a CBCT scan was sampled (i.e., if left Ci was measured, right Ci was not used). The exclusion criteria consisted of teeth with restorations, caries, significant wear, resorption, impaction, and presence of traumatic lesions, cysts, tumors, two or more root canals, pulp calcification, and any internal or external interventions affecting tooth formation or structure. To specify the extent of “significant wear,” we used Lovejoy stages of attrition for maxillary tooth “Phase G” through dentine exposure observation in the CBCT scans [18].

An a‐priori sample size calculation using G*Power linear multiple regression function, with an effect size of 0.3, the alpha error probability of 0.05, power of 0.95, and 3 predictors resulted in a minimum sample of 62 teeth per regression model [19]. The selected subjects were divided into eight age groups from 20 to 59.99 years (Table 1). Subsequently, 192 intact teeth which fulfilled the study criteria were selected. CBCT scans were acquired using Instrumentarium Dental OP300 (Instrumentarium Dental, Tuusula, Finland). The energy protocol for image acquisition had exposure parameters of 85 kV, tube current of 3–8 mA, and exposure time of 1.7–8.7 s.

TABLE 1.

Sample distribution based on sex, age group, and tooth position

Group	Age (years)	M			F
		Ci	Li	C	Ci	Li	C
1	20–24.99	4	4	4	4	4	4
2	25–24.99	4	4	4	4	4	4
3	30–34.99	4	4	4	4	4	4
4	35–35.99	4	4	4	4	4	4
5	40–44.99	4	4	4	4	4	4
6	45–49.99	4	4	4	4	4	4
7	50–54.99	4	4	4	4	4	4
8	55–59.99	4	4	4	4	4	4

Abbreviations: Ci, maxillary central incisor; Li, maxillary lateral incisor; C, maxillary canine.

CBCT scans in DICOM (Digital Imaging and Communication in Medicine) format were then imported into ITK‐SNAP 3.8 (ITK‐SNAP, UPenn & UNC) for segmentation. Primary settings in ITK‐SNAP were set with 3D brush options turned on, “all labels opacity” was set to 20, and the “initialize with current segmentation” option (in the active contour menu) switched on.

The morphology‐based segmentation method was accomplished by segmenting the volumetric tooth region into four groups: upper hard tissue volume (UHTV), lower hard tissue volume (LHTV), upper root chamber volume (URCV), and lower root chamber volume (LRCV) (Figure 1) using built‐in Region of Interest (ROI) inside the Active Contour Segmentation Function menu. The volumetric measurement results were given by ITK‐SNAP in cubic millimeters (mm³). The separation between UHTV and LHTV, URCV and LRCV was defined by placing the ROI limits in the highest (or most apical) portion of the cementoenamel junction (CEJ) seen in the sagittal view.

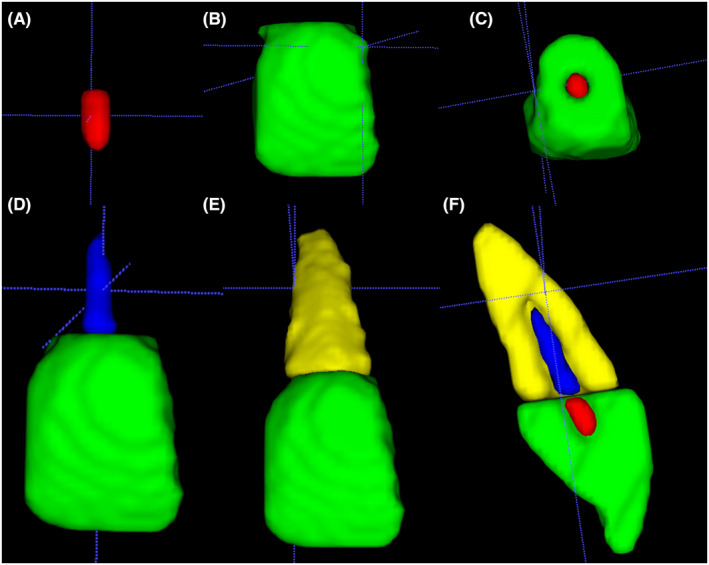
FIGURE 1.

Tooth region in the segmentation‐based volumetric method. The image shows the upper hard tissue volume (UHTV) in green, upper root chamber volume (URCV) in red, lower root chamber volume (LRCV) in blue, and lower hard tissue volume (LHTV) in yellow. The cementoenamel junction defined the separation between the measured parameters.

The segmentation was done in a pair of measured regions, namely, URCV‐UHTV and LRCV‐LHTV (Figure 2). The ROI placement in the LRCV‐LHTV pair needs to overlap the previous measured parameters pair (URCV‐UHTV) to ensure the continuation of the segmentation.

FIGURE 2.

Segmentation sequence used to calculate measured parameters volume. The segmentation starts from the upper root chamber volume (A, red) and upper hard tissue volume (B, Green). The section of volumetric segmentation was not overlapping (C, Axial View). The volumetric segmentation continued to the lower root chamber volume (D, Blue) and lower hard tissue volume (E, Yellow). The cross‐sectional view of the fully segmented tooth represents secondary dentine and root resorption is presented in F.

After the desired measured parameters were selected inside the region of interest (ROI), segmentation was performed by setting the threshold in presegmentation mode. It is important to note that ITK‐SNAP begins the segmentation of one slice after the ROI; therefore, the ROI needs to be placed one slice outside the desired area (Figure 3). The UHTV and LHTV segmentation threshold was set to minimum in the lower and upper thresholds set by the observer. Furthermore, URCV and LRCV segmentation threshold was set to maximum for the upper and lower threshold set by the observer. After a bubble was added inside the ROI, contour evolution was executed. Note that bubbles placed outside the ROI field of view will cause a leakage outside the ROI (Figure 3). The finalization of the segmentation can be performed by deleting the 3D label leakage outside the desired measured parameter or by adding labels manually using a 3D brush if the semi‐automated 3D segmentation does not cover a measured parameter region. The “continuous update” feature in the 3D model window may also be used to increase the segmentation accuracy further. The measured parameters were then calculated as a ratio as the upper tissue volume ratio $\left(\text{UTVR}=\frac{\text{URCV}}{\text{UHTV}}\right)$ and the lower tissue volume ratio $\left(\text{LTVR}=\frac{\text{LRCV}}{\text{LHTV}}\right)$ to be used in the final regression modeling.

FIGURE 3.

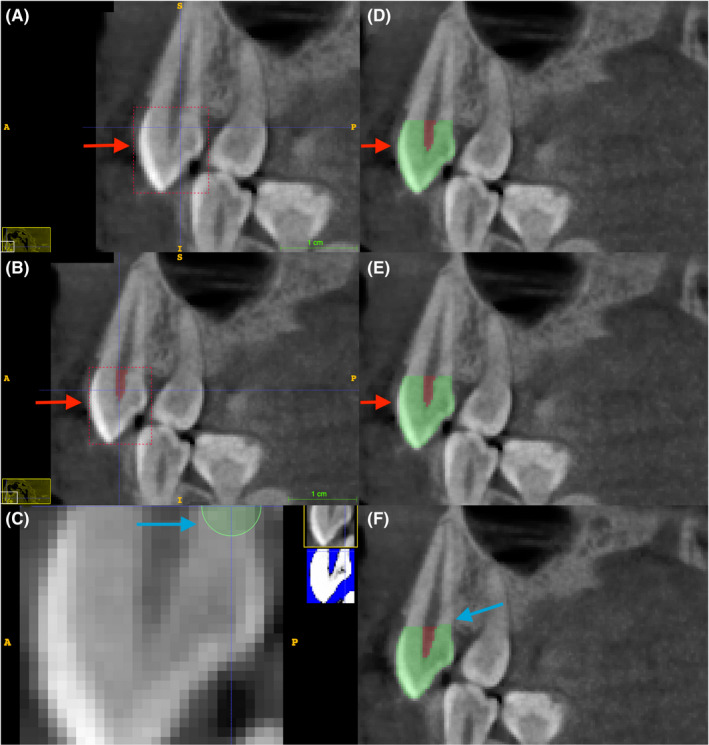
The placement of Region of Interest (ROI) (red box, A,B) and contour bubbles (green circle, C) in the ITK‐SNAP sagittal section affects the final volumetric measurement accuracy. Note in A (red arrow) that the placement of the ROI in one slice outside the measured parameter will result in a correctly segmented region (C). In B (red arrow), the ROI is placed in the same position as the desired measured parameter, resulting in inaccuracy in segmentation with partially segmented crown hard tissue (E, red arrow). The bubble was placed outside the ROI (C, blue arrow), resulting in a volumetric label leak outside the measured parameter (F, blue arrow).

Intraclass correlation coefficient (ICC) for the intra‐ and inter‐observer agreement was calculated using 20 randomly selected teeth with a 1‐week interval between observations 1 and 2. The correlation between ratio parameters and CA was quantified using a correlation matrix and visualized using the Locally Weighted Scatterplot Smoothing (LOWESS) line. Furthermore, multiple linear regression models were created for each tooth, with CA as a dependent variable, ratio parameters as a predictor, and gender as a covariate. Additionally, a single predictor linear model was tested in each significant ratio parameter to CA. The model's reliability was measured using R ², root mean squared error (RMSE), and mean average error (MAE) value.

Further performance evaluation was accomplished through Variance Inflation Factor (VIF) and Variable Importance Measures (VIM) to detect multicollinearity in the model [20] and predictive power of the independent variables [21], respectively. The statistical analyses were performed using R (R Foundation for Statistical Computing Version 4.0.5) with irr for ICC evaluation and caret for regression modeling [22, 23]. Regression model tuning parameters in caret were set using the training method “repeated cross‐validation” and 5‐fold cross‐validation with two repetitions [24].

3. RESULTS

The mean age of the sample was 40.34 ± 11.84 years. The overall inter‐and intra‐observer agreement in the measured parameters was reported in Table 2. Each tooth segmentation was accomplished in approximately 10 min.

TABLE 2.

Inter and intra‐class correlation coefficient between measured and ratio parameters

	Measured parameters					Ratio parameters
	Overall (n = 80)	UHTV (n = 20)	LHTV (n = 20)	URCV (n = 20)	LRCV (n = 20)	Overall (n = 40)	UTVR (n = 20)	LTVR (n = 20)
Inter‐observer	0.992 CI [0.986–0.996]	0.889 CI [0.581–0.972]	0.972 CI [0.893–0.993]	0.741 CI [0.023–0.935]	0.897 CI [0.61–0.974]	0.942 CI [0.842–0.974]	0.775 CI [0.048–0.928]	0.942 CI [0.83–0.978]
Intra‐observer	0.975 CI [0.937––0.99]	0.942 CI [0.856–0.977)	0.875 CI [0.682–0.951]	0.975 CI [0.937–0.99]	0.958 CI [0.894–0. 9983]	0.925 CI [0.858–0.96]	0.889 CI [0.748–0.96]	0.827 CI [0.57–0.931]

Abbreviations: UHTV, upper hard tissue volume; LHTV, lower hard tissue volume; URCV, upper root chamber volume; LRCV, lower root chamber volume; n, number of measured parameters; CI, 95% confidence interval; UTVR, upper tooth volume ratio; LTVR, lower tooth volume ratio.

The overall trend between ratio parameters and CA are displayed in Figure 4. The trend between UTVR and LTVR to CA indicated by the LOWESS line gives a different downtrend movement along with the increased CA.

FIGURE 4.

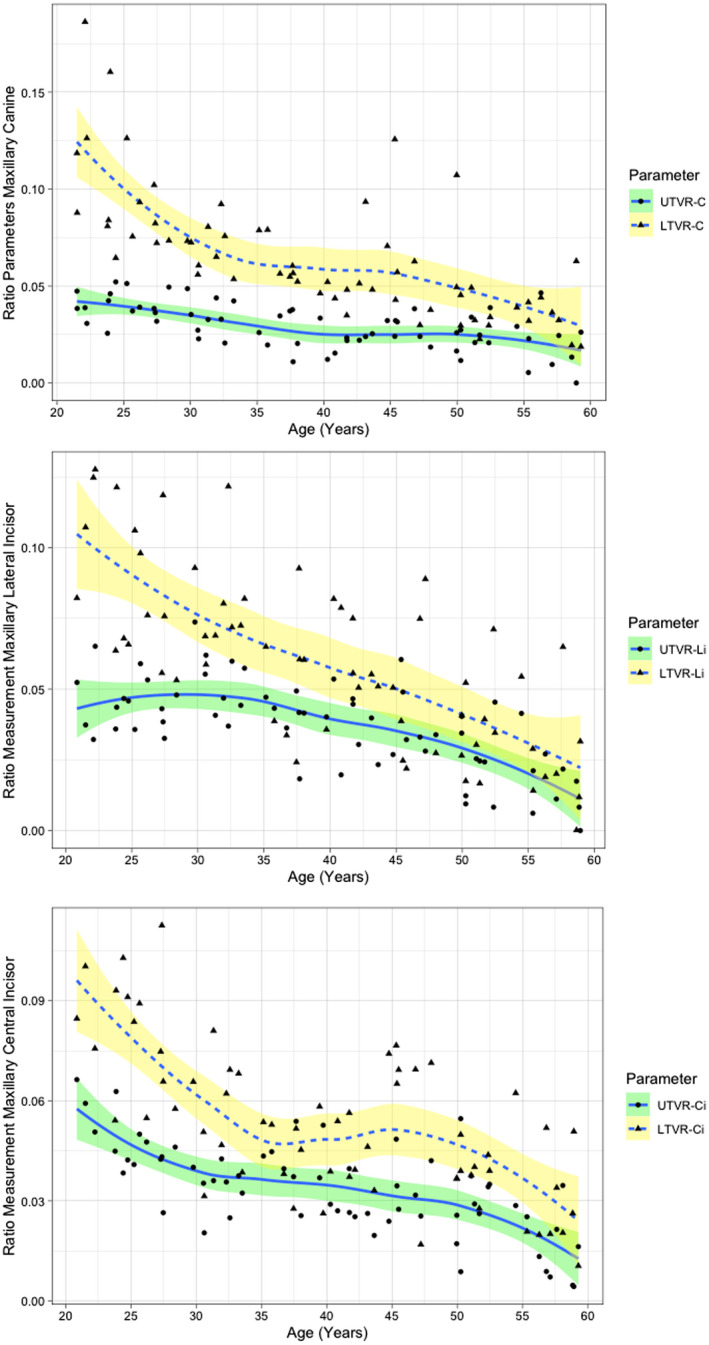
Relationship between chronological age (years) and ratio measurement in anterior maxillary tooth depicted by locally weighted scatterplot smoothing line. UTVR, upper tooth volume ratio; LTVR, lower tooth volume ratio; C, maxillary canine; Li, maxillary lateral incisor; Ci, maxillary central incisor.

The overall r‐values were significant (p < 0.001) between all the ratio parameters to CA (Table 3). The r‐value varies between −0.59 and −0.69, with the highest r‐value achieved by LTVR‐C and the lowest r‐value by UTVR‐C and LTVR‐Ci.

TABLE 3.

Correlation matrix between ratio parameters in each tooth

Tooth		CA	UTVR	LTVR
C	CA	–	−0.59	−0.69
	UTVR	−0.59	–	0.43
	LTVR	−0.69	0.43	–
Li	CA	–	−0.65	−0.63
	UTVR	−0.65	–	0.5
	LTVR	−0.63	0.5	–
Ci	CA	–	−0.68	−0.59
	UTVR	−0.68	–	0.46
	LTVR	−0.59	0.46	–

Note: All correlation value is significant (p < 0.001).

Abbreviations: C, maxillary canine; Li, maxillary lateral incisor; Ci, maxillary central incisor; CA, chronological age; UTVR, upper tooth volume ratio; LTVR, lower tooth volume ratio.

The regression models displayed a varied performance between each tooth, with all parameters being significant (p < 0.05), except sex was only found to be significant in the C model after a polynomial variable was introduced to the model (Table 4). In the multiple regression model, Li model gives the best R ² value of 0.67, and the Ci model shows the lowest R ² value of 0.59. No multicollinearity was detected in the multiple linear models given by the low VIF value (<5) [25]. VIM evaluation gives the highest value to LTVR in every multiple linear models.

TABLE 4.

Regression models for the observed teeth and ratio parameters

Tooth	Predictors	Model	Performance
			R 2	RMSE	MAE
C	UTVR‐C, LTVR‐C, & Sex	77.393−348.379 UTVR‐C−565.709 LTVR‐C + 2140.073 (LTVR‐C)2−3.961 s	0.66	6.88	5.45
	UTVR‐C	56.77−583.095 UTVR‐C	0.38	9.3	7.5
	LTVR‐C	68.923−628.93 LTVR‐C + 2217.17 (LTVR‐C)2	0.62	7.5	5.83
Li	UTVR‐Li & LTVR‐Li	63.09−301.38 UTVR‐Li−204.65 LTVR‐Li	0.67	6.67	5.3
	UTVR‐Li	57.31−475.26 UTVR‐Li	0.44	8.6	7
	LTVR‐Li	55.95−271.38 LTVR‐Li	0.56	7.76	6.27
Ci	UTVR‐Ci & LTVR‐Ci	64.21−368.32 UTVR‐Ci−214.41 LTVR‐Ci	0.59	7.6	6.19
	UTVR‐Ci	59.48−568.93 UTVR‐Ci	0.5	8.5	6.9
	LTVR‐Ci	58.4−337.25 LTVR‐Ci	0.46	8.5	7.19

Abbreviations: C, maxillary canine; Li, maxillary lateral incisor; Ci, maxillary central incisor; UTVR, upper tooth volume ratio; LTVR, lower tooth volume ratio; s, sex (M = 1; F = 0); R ², coefficient of determination; RMSE, root mean squared error; MAE, mean average error.

Considering that all predictors were significant, a linear regression model can be derived from each measured parameter (Table 4). In the single predictor linear model, the highest R ² value was given by LTVR‐Li (R ² = 0.56), and the lowest R ² value was provided by UTVR‐C (R ² = 0.38). As observed in the multiple regression in the C model, a second‐degree polynomial regression line can be derived for LTVR‐C, resulting in an R ² value of 0.62.

4. DISCUSSION

Regressive morphological dental changes in adults are guided by time. Therefore, quantifying this process accurately could allow forensic odontologists to estimate dental age [26]. The accurate quantification can be achieved by observing volumetric features in CBCT [27, 28]. More recently, the practice of dental age estimation in adults using CBCT scans has become more common and demonstrates satisfactory results when compared to more traditional 2D methods [15, 29]. CBCT scans also eliminate image acquisition limitations that affect 2D imaging (ie mesiodistal or buccolingual visualization in radiographs). Dahal et al [30] endorses this finding by explaining that different periapical viewing angles can result in different R ² values.

Our current approach to segment tooth regions aims to understand how each regressive morphological change differs from one another—namely, attrition, root resorption, and, most importantly, secondary dentine formation. This study suggests that segmentation may prove beneficial for age estimation in adults. In this research, the ratio related to the root region (LTVR) was more closely correlated to CA. Previous studies have explored the value of pulp chamber reduction alongside CA. Oi et al [31] found that the functional cusp has more secondary dentin than other tooth sites due to the heavier mastication activity. Nudel et al [32] stated that the secondary dentine formation begins in the crown region in older age. These findings support our current result that the UTVR had a reduced predictive performance since the secondary dentine formation varied differently due to multiple external factors. These factors might have affected the secondary dentine formation in the crown region rather than the root region.

The LOWESS line in Figure 4 depicts a different relationship between UTVR and LTVR. It must be noted that the usage of the LOWESS line itself can be applied to visualize the trend of the relationship between age‐related parameters and CA—whether it is linear or nonlinear. A LOWESS line function uses data cluster weight to draw the correlation line; therefore, the movement of the line can accurately allow the visualization of the relationship between each parameter without including observer bias [33]. More importantly, the timing of the decline or sideways movement from the parameter can also be observed, contributing to the (non)linear model selection. Additionally, the relationship between each parameter and CA is different from one another. The nonlinear relationship was observed in LTVR‐C, UTVR‐Li, and LTVR‐Ci, while UTVR‐Ci, LTVR‐Li, and UTVR‐Ci had a linear relationship to CA. This distinction between each parameter is in‐line with the findings of Johanson et al [7], in which each tooth part has a different r‐value to CA. However, contrary to their findings, our root ratio parameter gives an overall better result in the regression model. This observation can be explained by the utilization of ratios in our study parameters, combining the root resorption parameter and secondary dentine build‐up in the pulp chamber. By using ratios, the measurement's reliability can be improved [34]. For example, when a tooth is tilted, the ROI will calculate more volume in the measured parameter pairs (ie UHTV and URCV) as the ROI boundary will always be in the highest area of the CEJ seen in the sagittal view. However, a more optimized outcome could emerge from a fully controlled scenario—where tooth angulation was uniform. However, this scenario does not reflect current practice. We assessed the eventual bias of tooth angulation by measuring the correlation between sagittal tooth angles using Fiji ImageJ software (National Institutes of Health, Maryland, USA). This procedure had a quality‐control purpose of guaranteeing that tooth angulation (tilting) would not affect our outcomes. No significant correlation between dental angulation and volumetric information was detected, accordingly [35]. We recommend that future studies examine the effect of tooth angulation on ratio parameters in each of the study cohorts.

In this research, sex did not play a significant part except for the C model. The inclusion of sex in the regression model in the previous studies was diverse. For example, the same approach using upper canine pulp volume by De Angelis et al [3] found that sex was not significant, but Kazmi et al [36] found the opposite. It is important to note that our inclusion of sex in the C model was only significant after a nonlinear variable was used in the LTVR‐C parameter. Zilberman et al [37] found that in children (4–16 years old) that secondary dentin formation was greater in males, while our C model suggests that males have a slower progression of secondary dentin formation as indicated by the negative prediction parameter (−3.961 years old for males). Although LTVR‐Ci depicts a similar nonlinear movement to LTVR‐C (Figure 4), adding the quadratic or cubic LTVR‐Ci variable did not improve the Ci model. The choice of using the normalization method (ie logarithmic transformation) [38] or the non‐linear model when confronted with non‐linear data needs to be considered when observing the secondary dentine formation concerning CA in adults.

An in‐depth model evaluation was accomplished using VIF and VIM. VIF evaluates the multicollinearity in the model, a phenomenon that happens when two or more parameters in a regression model are highly correlated [39]. Reference VIF threshold values for multicollinearity are 10 [25]—or even 5 (with a more conservative approach) [40]. Nevertheless, our VIF value is smaller than both thresholds, indicating that UTVR and LTVR were independent of each other. Furthermore, the VIM value can quantitatively evaluate which parameter gives more predictive power in a multiple regression model, which is collectively found to be LTVR. Therefore, both evaluation methods need to be considered when building a regression model. Additionally, as each parameter is significantly correlated to CA, a single predictor regression model can be derived (Table 4). This additional model can be used if a tooth is fractured with the CEJ visible in the CBCT scan, for instance.

In conclusion, regressive morphological changes in the crown and root region were differently correlated to CA with linear and non‐linear variations. The segmentation approach in volumetric dental age estimation of adults proved to be beneficial in enhancing the reliability of the regression model. The segmentation of the tooth may offer a plethora of routine forensic applications, especially if teeth are found fractured or fragmented. Future research might consider independent evaluation of regressive dental morphological changes visible in radiographic imaging, such as enamel segmentation [41]. Furthermore, country‐specific samples can be addressed as testing datasets to enable the external validation of the current approach.

FUNDING INFORMATION

R. Merdietio Boedi received a tuition scholarship by the Ministry of Education and Culture, Universitas Diponegoro no. 497/UN7.P/HK/2021.

Merdietio Boedi R, Shepherd S, Oscandar F, Mânica S, Franco A. Regressive changes of crown‐root morphology and their volumetric segmentation for adult dental age estimation. J Forensic Sci. 2022;67:1890–1898. 10.1111/1556-4029.15094