How Are Mixed‐Phase Clouds Mixed?

Abstract

Mixed‐phase clouds are recognized as significant contributors to the modulation of precipitation and radiation transfer on both regional and global scales. This study is focused on the analysis of spatial inhomogeneity of mixed‐phase clouds based on an extended data set obtained from airborne in situ observations. The lengths of continuous segments of ice, liquid, and mixed‐phase clouds present a cascade of scales varying from 10² km down to a minimum scale of 100 m determined by the spatial resolution of measurements. It was found that the phase composition of mixed‐phase clouds is highly intermittent, and the frequency of occurrence of ice, liquid, and mixed‐phase regions increases with the decrease of their spatial scales. The distributions of spatial scales have well‐distinguished power‐law dependencies. The results obtained yield insight into the morphology of mixed‐phase clouds and have important implications for improvement in representing subgrid inhomogeneity of mixed‐phase clouds in weather and climate models.

Key Points

• In mixed‐phase clouds droplets and ice particles may be uniformly distributed (genuinely mixed) or spatially separated (conditionally mixed)

• Horizontal lengths of genuine mixed‐phase and single‐phase ice and liquid clouds present a cascade of scales from 100 km down to 100 m or less

• At small scales mixed‐phase clouds have high spatial intermittency, which is currently unconstrained in weather and climate models

1. Introduction

Mixed‐phase clouds represent a three‐phase colloidal system consisting of water vapor, ice particles, and supercooled liquid droplets. Mixed‐phase clouds are ubiquitous in the troposphere, occurring at all latitudes from the polar regions to the tropics (e.g., D’Alessandro et al., ²⁰¹⁹; Wang et al., ²⁰¹³). Because of their widespread nature, mixed‐phase clouds play important roles in precipitation formation, and the radiative energy balance on both regional and global scales.

One of the important characteristics of mixed‐phase clouds is the degree of homogeneity of mixing ice particles and liquid droplets. There are two possible extremes of mixing. The first one is when ice particles are uniformly mixed (Figure 1a). The second one is when ice particles and liquid droplets are clustered in single‐phase liquid or ice cloud regions with a complex morphology (Figure 1b). The first type of mixed‐phase clouds is referred to as “genuine” mixed‐phase and the second type is “conditional” mixed‐phase (A. Korolev et al., ²⁰¹⁷).

Figure 1.

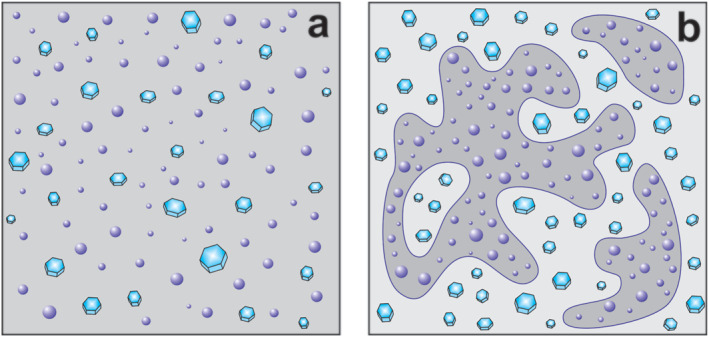
Conceptual diagrams of (a) genuine and (b) conditional mixed‐phase clouds, representing two extremes of spatial intermittency of ice and liquid phase.

In genuine mixed‐phase clouds, ice particles and liquid droplets are interacting with each other through the molecular diffusion of water vapor. In absence of dynamic forcing genuine mixed‐phase clouds are colloidally unstable enabling the Wegener‐Bergeron‐Findeisen (WBF) process (Bergeron, 1935; Findeisen, ¹⁹³⁸; Wegener, ¹⁹¹¹), which results in the growth of ice particles and evaporation of droplets, and eventually leads to the glaciation of a mixed‐phase cloud. Theoretical analysis suggests that glaciation time depending on temperature, ice particle concentration, and liquid water content (LWC) may vary from few minutes to tens of minutes (Korolev & Mazin, 2003). Therefore, the WBF process is an important factor limiting the endurance of genuine mixed‐phase clouds.

However, in conditional mixed‐phase clouds, the interaction between ice crystals and liquid droplets is hindered because of their spatial separation (Figure 1b). Therefore, under the assumption of inhibited turbulent mixing between ice and liquid cloud regions, the WBF process in such clouds will be suppressed, and conditional mixed‐phase clouds would be colloidally stable. The endurance of such clouds is determined by processes other than the WBF mechanism. Since the WBF process enhances the growth rate of ice particles, then for the same amount of ice and liquid in the same volume the rate of precipitation formation in conditional mixed‐phase clouds will be slower compared to that in genuine mixed‐phase clouds.

Radiative properties of genuine and conditional mixed‐phase clouds are also different due to the spatial clustering of ice and liquid phase (e.g., Ruiz‐Donoso et al., ²⁰²⁰). The liquid water, initially distributed among a large number of liquid droplets, by the end of glaciation will be depleted by fewer ice particles. Therefore, the WBF process will result in a reduction of the extinction coefficient, optical thinning, cloud coverage and lifetime of genuine mixed‐phase clouds. In contrast to the above, in conditional mixed‐phase, the glaciation process is hindered, and therefore, the radiative properties will be more stable compared to the genuine mixed‐phase clouds. Therefore, the net radiative effect for genuine and conditional mixed‐phase clouds integrated over time will be different.

Understanding the spatial phase intermittency of clouds has great importance both for fundamental cloud physics and numerical simulations of clouds. Several climate and numerical weather prediction (NWP) models use representations of cloud fractions for liquid and ice contents that are then used to determine the in‐cloud hydrometeor values, from which microphysical process rates are computed (e.g., Bogenschutz et al., ²⁰¹²; Walters et al., ²⁰¹⁹). However, the degree of overlap of the in‐cloud liquid and ice within grid cells, that is, the mixed‐phase cloud fraction, is unconstrained. The type of mixed‐phase cloudiness that is represented will impact the calculations of cloud optical properties and the WBF process rate, and thus the rate of glaciation. This also depends on the horizontal grid spacing which, depending on modeling system, varies widely. For example, NWP systems use grid spacings ranging from approximately 3 km to 15 km (e.g., McTaggart‐Cowan et al., ²⁰¹⁹), with some experiment systems on the hectometer scale (e.g., Joe et al., ²⁰¹⁸), whereas global climate models run with grid spacings ranging from 60 to 300 km (Almazroui et al., 2020). The assumption about homogeneously mixed liquid droplets and ice particles may result in biases in precipitation production and radiation transfer.

In situ observations showed high spatial phase variability of clouds. Thus, Hallett (1999) observed well‐separated regions of ice and liquid in sea‐breeze‐front clouds with a mixed‐phase interface of only a few hundreds of meters wide. A. V. Korolev et al. (2003) showed that clusters of ice and liquid phase clouds can exist at the scale of the order of kilometers. Field et al. (2004) obtained statistics of contiguous ice, liquid, and mixed‐phase cloud segments from in situ observations in frontal clouds. They pointed out that liquid intrusion into surrounding ice clouds can be as small as 100 m. A. V. Korolev et al. (2003) hypothesized that phase intermittency may exist down to a meter, that is, fine‐scale clusters of liquid (ice) embedded in a glaciated (liquid) cloud.

This study is aimed to address the following questions: (a) what are the typical spatial scales of genuinely mixed‐phase and single‐phase ice, liquid clouds? (b) what is the spatial intermittency of single‐phase ice, liquid, and genuinely mixed‐phase cloud segments?

2. Methodology and the Data Set

The cloud phase composition was studied with a set of airborne instruments installed by Environment and Climate Change Canada (ECCC) in collaboration with the National Research Council (NRC) on the NRC Convair‐580 research aircraft.

The phase composition of clouds was identified with the help of a set of instruments: Nevzorov probe (A. V. Korolev et al., ¹⁹⁹⁸), Rosemount Icing Detector (Baumgardner & Rodi, 1989; Mazin et al., ²⁰⁰¹), Forward Scattering Spectrometer Probe (FSSP) (Knollenberg, 1976; McFarquhar et al., ²⁰¹⁷), Optical Array Probe 2DC (OAP‐2DC) (Baumgardner et al., 2017; Knollenberg, ¹⁹⁷⁶), and Optical Array Probe 2DP (OAP‐2DP) (Knollenberg, 1976).

The Nevzorov probe was primarily used for the assessment of liquid water (LWC) and ice water content (IWC). The methodology of Nevzorov probe data processing and phase discrimination was described in detail in (Korolev & Strapp, 2002; A. V. Korolev et al., ¹⁹⁹⁸). The Nevzorov probe liquid water sensor measurements were corrected on the residual effect of ice (Field et al., 2004; A. V. Korolev et al., ¹⁹⁹⁸, ²⁰⁰³) and the total water sensor measurements were corrected on the ice bouncing effect (A. V. Korolev et al., ²⁰¹³). The Rosemount Icing Detector was used to identify the presence of the liquid phase and exclude false liquid signals in ice clouds. The FSSP was employed to identify the presence of liquid droplets smaller than 45 μm in diameter. The OAP‐2DC and 2DP were used for justification of the presence or absence of ice particles based on identification of non‐circular shapes of their binary images.

In the present study the thresholds for liquid water content and ice water content (IWC) were set as LWC > 0.01 g m⁻³, IWC > 0.01 g m⁻³, respectively. The phase composition of clouds was identified based on the assessment of the ice water fraction $\mu =IWC/\left(LWC+IWC\right)$. Thus, clouds with $\mu >$ 0.9 were considered as ice, clouds with $\mu <$ 0.1 were defined as liquid, and clouds 0.1 $\le \mu \le$ 0.9 were determined as mixed‐phase clouds. The smallest spatial scale was limited by 100 m, and it was determined by the temporal resolution of the Nevzorov probe (∼1 s) and average aircraft sampling speed (∼100 m s⁻¹).

The objective of the data processing was the identification of continuous ice, liquid, and mixed‐phase cloud segments along the flight path of the research aircraft. Following the above definitions of clouds and cloud phase, the time series of LWC and IWC were converted into three discrete cloud phase categories of “ice,” “liquid,” and “mixed‐phase.” The processing algorithm started counting the cloud length when LWC or IWC exceeded the threshold value 0.01 g m⁻³, and the cloud length counting was interrupted, when the cloud phase changed, or LWC and IWC became lower the predetermined cloud water content threshold. Isolated single‐phase ice or liquid clouds were defined as continuous clouds, which were not interrupted by cloud segments with another phase. Such clouds were excluded from the subsequent analysis. The mixed‐phase clouds at the smallest resolved scale (100 m) were assumed as genuinely mixed. Therefore, the ensemble of clouds used in this study consists of continuous conditional and genuine mixed‐phase cloud segments.

The analyzed data set includes seven flight campaigns lead by ECCC and extended over a period of 10 years from 1994 to 2004: Beaufort Arctic Storm Experiment (BASE), Canadian Freezing Drizzle Experiment (Phase 1 and 3) (CFDE 1 and 3), the First International Satellite Cloud Climatology Project (ISCCP) Regional Experiment Arctic Cloud Experiment (FIRE‐ACE), Alliance Icing Research Study (Phase 1, 1.5, 2) (AIRS 1, 1.5, 2). The description of the time frames, map of areas of operations, number of flights, and sampled cloud lengths for each campaign are available from Table S1 and Figure S1 in Supporting Information S1.

Most of the data was collected in stratiform clouds associated with mesoscale frontal systems. The altitude and temperature of the sampled clouds varied in the ranges 0.5 km < H < 7.3 km and −50 < $T$ < +10°C, respectively. However, in the frame of this study the measurements were limited by the temperature range −35 < $T$ < 0°C due to the low statistics of mixed and liquid clouds in the range −40 < $T$ < −35°C, and the absence of liquid phase at $T$ < −40°C due to homogeneous freezing.

The entire flight operations include 117 research flights. The endurance of each flight varied from 3 to 5 hr. The total length of sampled in‐cloud space extended over 55,381 km. After elimination of isolated single‐phase clouds and applying temperature limitations, the total length of the clouds, which were included in the statistics, was reduced to 32,488 km.

3. Results

Figure 2 shows frequency distributions of ice, liquid, and mixed‐phase contiguous cloud segments in three temperature subranges −10 < $T$ < 0°C, −20 < $T$ < −10°C, and −30 < $T$ < −20°C. The distributions were normalized on the total length of clouds in each phase category to facilitate their intercomparisons with each other. As it is seen from Figure 2 the ice, liquid, and mixed‐phase cloud regions are represented by a cascade of scales ranging from tens and hundreds of kilometers down to the minimum scale $L_{\min }$∼100 m. The minimum scale $L_{\min }$ is limited by the instrumental resolution.

Figure 2.

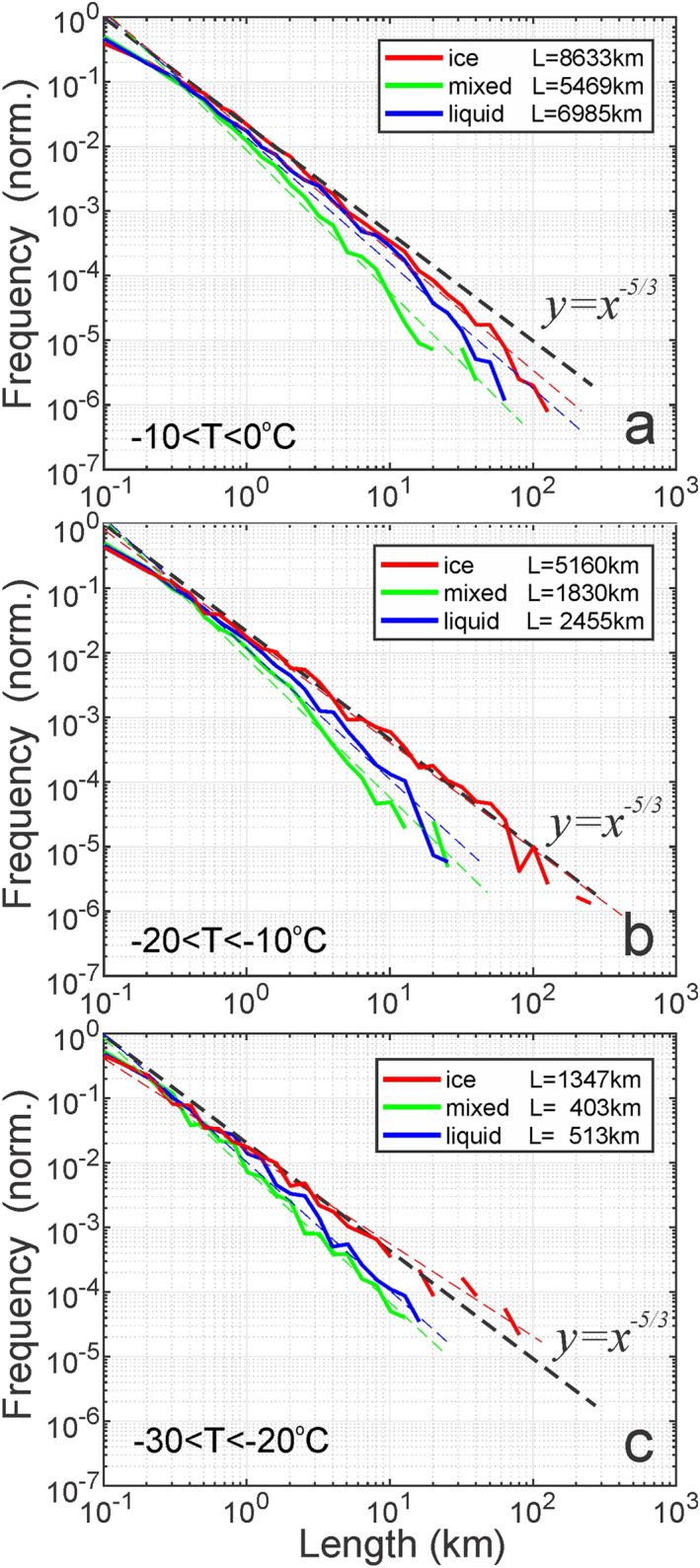
Distributions of continuous ice, liquid, and mixed‐phase cloud segments in three temperature intervals (a) −10 < T < 0°C; (b) −20 < T < −10°C; (c) −20 < T < −30°C. “L” indicates total sampled cloud length. Power law fitting curves (as in Table 1) are indicated by red (ice), blue (liquid), and green (mixed phase) dashed lines.

The maximum scale of ice clouds ($L_{\max }^{\left(i\right)}$) varies from tens kilometers at cold temperatures (−30 < $T$ < −20°C) (Figure 2c) to 100–300 km at $T$ > −20°C (Figures 2a and 2b). The maximum scales of liquid ($L_{\max }^{\left(w\right)}$) and mixed‐phase ($L_{\max }^{\left(m\right)}$) cloud segments are systematically lower than $L_{\max }^{\left(i\right)}$ for ice clouds. As follows from Figure 2, $L_{\max }^{\left(w\right)}$ and $L_{\max }^{\left(m\right)}$ decrease from 40 to 60 km at −10 < $T$ < 0°C to 10–15 km at −30 < $T$ < −20°C.

The spatial scale distributions of continuous ice, liquid, and mixed‐phase segments are well described by the power law $F\left(L\right)=a{L}^b$. The weighted least squares fit coefficients $a$ and $b$ are presented in Table 1. The Pearson correlation coefficient for each parameterization in Table 1 are higher 0.99.

Table 1.

Coefficients for the Power Law Fitting of the Normalized Frequency Distributions of Spatial Scales of Ice, Liquid, and Mixed‐Phase Cloud Regions $F\left(L\right)=a{L}^b$

Cloud type	−30 < T < −20°C		−20 < T < −10°C		−10 < T < 0°C
	a	b	a	b	a	b
Ice	10.5 10−3	−1.44	18 10−3	−1.66	17.4 10−3	−1.86
Mixed	7.85 10−3	−2.03	8.06 10−3	−2.17	8.75 10−3	−2.19
Liquid	24.4 10−3	−1.97	11.5 10−3	−2.03	13.8 10−3	−1.94

As it is seen from Table 1 the slope of lengths distributions for mixed‐phase and liquid (Figure 2) remains nearly constant in all temperature intervals, and it changes withing 3%–4%. However, the slope of lengths distributions for ice has a clear tendency to increase toward low temperatures.

Figure 3 shows temperature dependences of average continuous lengths of ice, liquid, and mixed phase cloud segments. As it is seen from Figure 3 the average length of mixed‐phase segments has a weak dependence on temperature and it varies between 300 and 500 m. The mean length of liquid cloud segments is systematically larger than that of mixed‐phase segments, and it gradually decreases with the decrease of temperature from approximately 900m down to 500 m. However, average lengths of continuous ice cloud segments turned out to be the largest compared to liquid and mixed‐phase segments. The average length of ice cloud segments increases from 1 km at 0°C to 5 km at −25 < $T$ < −20°C and then decrease to approximately 1 km at −35°C.

Figure 3.

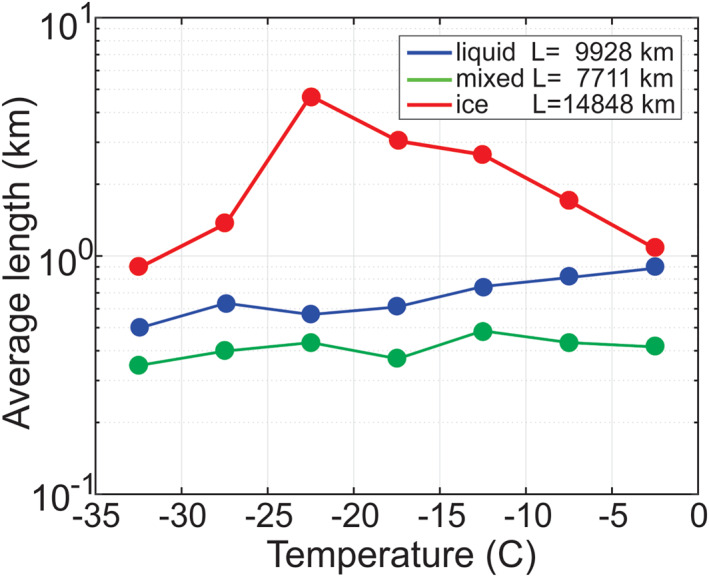
Average lengths of ice, liquid, and mixed‐phase cloud segments versus temperature.

4. Discussion

The slopes of obtained frequency distributions or some of their parts in Figure 2 are close to −5/3. In the atmosphere, the −5/3 power law is underlying numerous processes, including turbulence, storm intensity, ocean wave growth, etc. The proximity of distributions of cloud spatial scales to the universal −5/3 power law is indicative of the linkage between formation of mixed‐phase clouds and turbulence.

Turbulence is one of the major mechanisms mixing environments with different phases. The result of the turbulent mixing of clouds with a different phase composition is a mixed‐phase cloud. The characteristic time scale (${\tau }_t$) of mixing of a cloud volume with a spatial scale $L$ can be assessed as (Landau & Lifshitz, 1987)

$${\tau }_t={\left(\frac{L^{\mathrm{2}}}{\epsilon }\right)}^{\raisebox{1ex}{$\mathrm{1}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{3}$}\right.}$$ (1)

where $\epsilon$ is the turbulence energy dissipation rate.

However, cloud particles are an active admixture and during mixing they are interacting with each other through water vapor. Such interaction results in activation of the WBF mechanism, if the vertical velocity of the cloud $u_z$ does not exceed a critical velocity $u_z^{\ast }$ (i.e., $u_z<u_z^{\ast }$) (A. Korolev, ²⁰⁰⁷). The WBF process leads glaciation of the mixed phase cloud within the glaciation time (Korolev & Mazin, 2003)

$${\tau }_{\mathrm{g}\mathrm{l}}=k{\left(\frac{W}{N_i}\right)}^{\mathrm{2}/\mathrm{3}}$$ (2)

Here $W$ is the liquid water content, $N_i$ is the concentration of ice particles; $k=\frac{{\rho }_i}{\mathrm{4}\pi c{S}_i\left(T\right)}{\left(\frac{\mathrm{9}\pi {\rho }_i}{\mathrm{2}}\right)}^{\mathrm{1}/\mathrm{3}}\left(\frac{L_i^{\mathrm{2}}}{K{R}_v{T}^{\mathrm{2}}}+\frac{R_{v}T}{E_i\left(T\right)D}\right)$; ${\rho }_i$ is the density of ice; $S_i\left(T\right)=\frac{E_w\left(T\right)}{E_i\left(T\right)}-\mathrm{1}$ is the supersaturation over ice at saturation pressure over water at temperature $T$; $E_w\left(T\right)$, $E_i\left(T\right)$ is the saturating pressure of water vapor over liquid and ice, respectively, at temperature $T$; $R_v$ is the specific gas constant of water vapor; $L_i$ is the latent heat for ice sublimation; $K$ is the coefficient of air heat conductivity; $D$ is the coefficient of water vapor diffusion in the air.

Thus, turbulent mixing and glaciation are two processes working in opposite directions. The turbulent mixing is tending to homogenize and maintain a mixed‐phase environment. Whereas the glaciation process tends to turn a mixed‐phase cloud into an ice cloud. Therefore, a mixed‐phase environment may be maintained by turbulent mixing, if the glaciation time ${\tau }_{\mathrm{g}\mathrm{l}}$ exceeds the mixing time ${\tau }_t$, that is,

$${\tau }_{\mathrm{g}\mathrm{l}}>{\tau }_t$$ (3)

Substituting Equations 1 and 2 in Equation 3 yields a threshold spatial scale,

$$L_{\mathrm{p}\mathrm{h}}={\left(k^{\mathrm{3}}\epsilon \right)}^{\mathrm{1}/\mathrm{2}}\frac{W}{N_i}$$ (4)

such that mixed‐phase environment can exist at scales ${L<L}_{\mathrm{p}\mathrm{h}}$ at time scales satisfying Equation 3.

Substituting $\epsilon$ = 10⁻³–10⁻⁴ m² s⁻³, $W=$ 0.01–1.0 g m⁻³, $N_i=$10¹–10² L⁻¹, −35 < $T$ < −5°C yields the range of spatial phase scales $L_{\mathrm{p}\mathrm{h}}$ ∼ 10¹–10⁴ m. This obtained assessment of $L_{\mathrm{p}\mathrm{h}}$ remarkably consistent with the range of spatial scales covered by mixed‐phase clouds in Figure 2. However, the obtained assessment, also suggests that $L_{\mathrm{p}\mathrm{h}}$ may extend toward the small‐scale end. As it is seen from Equation 4, the spatial scale of mixed‐phase clouds depends on LWC. Therefore, it is anticipated that the frequency function $F\left(L\right)$ should be related on a frequency of occurrence of LWC ($F\left(W\right)$). Figure 4 shows a probability density functions $F\left(W\right)$ at different temperatures. As it is seen from Figure 4 $F\left(W\right)$ increases with the decrease of LWC. Therefore, following Equation 4 the increase of occurrence of small‐scale mixed‐phase clouds may be explained by the increase of occurrence of LWC with the decrease of LWC. Even though $F\left(W\right)$ has a quasi‐exponential dependence, whereas $F\left(L\right)$ is described by a power‐law, the behavior of LWC generally explains the behavior of $F\left(L\right)$.

Figure 4.

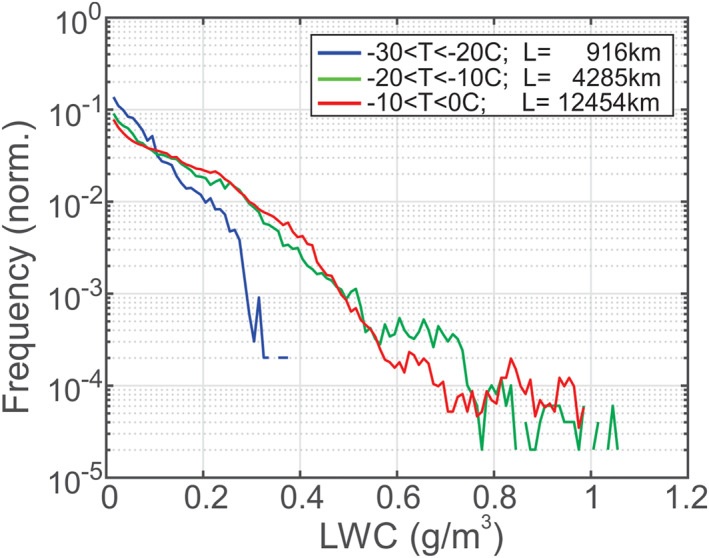
Normalized frequency of occurrences of liquid water content in liquid and mixed‐phase clouds averaged over all sampled clouds. Isolated single‐phase clouds were not included in these statistics.

It should be noted that the above simplified consideration is relevant for isotropic turbulence in the inertial subrange, which in free atmosphere is limited by approximately 1 km (Honnert et al., 2020; Wyngaard, ²⁰¹⁰). The spatial scales of the cloud phase composition at larger scales are controlled by convection and mesoscale dynamics (Wood & Field, 2011). The above consideration also did not account for cloud processes such as riming, ice sedimentation, and entrainment of out‐of‐cloud air. The later was in detail discussed in Pinsky et al. (2018). However, the above approach allows to generally predict the behavior and the range of spatial scales of genuinely mixed‐phase clouds.

In the present study the smallest spatial scale of genuine mixed‐phase cloud segments was limited by the instrumental resolution (100 m). In fact, these clouds can be conditionally mixed at spatial scales ${L<L}_{\min }$. It should be noted that at present, the smallest scale of the spatial phase intermittency ($L_{\min }$) remains an open question.

The size of the smallest single‐phase cluster can be assessed as $L_{\min }\sim n∆x$, where $∆x=N^{-\mathrm{1}/\mathrm{3}}$ is the average distance between particles, $N$ is the average concentration of cloud particles in the cluster, and $n$ is the number of particles across the cluster. Assuming, that the cluster has a compact shape (i.e., the fractal dimension is ∼3), and the total number of particles in the cluster $n_{\mathrm{t}\mathrm{o}\mathrm{t}}>\mathrm{10}$, which mitigates statistical fluctuations, we obtain $L_{\min }\sim {\left(n_{\mathrm{t}\mathrm{o}\mathrm{t}}/N\right)}^{\mathrm{1}/\mathrm{3}}$. Thus, for typical ice particle concentrations $N_i$ ∼ 0.01–10 L⁻¹ the minimum scale of ice is expected to be 0.1 m < $L_{\min }$ < 1 m. For the cases of ice multiplication (i.e., $N_i$ ∼ 10³ L⁻¹) $L_{\min }$ for ice may go down to a centimeter scale. However, for cloud droplet with concentration $N_{\mathrm{d}\mathrm{r}}$ ∼ 10–1,000 cm⁻³ the minimum cluster scale is estimated to vary in the range 2 mm < $L_{\min }$ < 10 mm.

As seen, the obtained estimates of $L_{\min }$ for ice particle and liquid droplet clusters are much smaller than that in this study. The question of $L_{\min }$ is of great importance, and its future addressing requires advanced in situ observations.

5. Conclusions

This study presents observed spatial phase intermittency in mixed phase clouds based on a large data set collected in midlatitude and Arctic clouds. It was shown that in the temperature range −35 < T < 0°C clouds containing ice and liquid may form regions with genuinely or conditionally mixed‐phase environments. The lengths of continuous segments of ice, liquid, and mixed‐phase cloud present a cascade of scales varying from 10^1–10² km down to a minimum scale $L_{\min }$ ∼ 100 m determined by the spatial resolution of the measurements. It is hypothesized that $L_{\min }$ of the genuine conditionally mixed‐phase cloud regions may go down to scale of 1–10 m or even smaller.

The results obtained yield insight on the spatial morphology of mixed‐phase clouds. These results also suggest the potential of using in situ observations to validate and calibrate atmospheric models in terms their ability to represent subgrid‐scale phase heterogeneity. They also suggest that even in cloud‐resolving and high‐resolution mesoscale models (with horizontal grid spacings on the order of a few km or less) whose microphysics schemes typically do not consider cloud fractions, subgrid‐scale heterogeneity of mixed‐phase clouds is likely not well represented, biased toward genuinely mixed, and is a potential source of model error. Improving the type of mixing for mixed‐phase clouds in models of all types will improve the calculation of cloud optical properties, thereby improving radiative transfer calculations, and modify the WBF process, which ultimately determines the glaciation time and impacts the production of precipitation and cloud brightness.

Supporting information

Supporting Information S1

Korolev, A. , & Milbrandt, J. (2022). How are mixed‐phase clouds mixed? Geophysical Research Letters, 49, e2022GL099578. 10.1029/2022GL099578

Data Availability Statement

Data supporting this research are available from https://doi.org/10.5281/zenodo.6558498.