The Deep Ocean's Carbon Exhaust

Abstract

The deep ocean releases large amounts of old, pre‐industrial carbon dioxide (CO₂) to the atmosphere through upwelling in the Southern Ocean, which counters the marine carbon uptake occurring elsewhere. This Southern Ocean CO₂ release is relevant to the global climate because its changes could alter atmospheric CO₂ levels on long time scales, and also affects the present‐day potential of the Southern Ocean to take up anthropogenic CO₂. Here, year‐round profiling float measurements show that this CO₂ release arises from a zonal band of upwelling waters between the Subantarctic Front and wintertime sea‐ice edge. This band of high CO₂ subsurface water coincides with the outcropping of the 27.8 kg m⁻³ isoneutral density surface that characterizes Indo‐Pacific Deep Water (IPDW). It has a potential partial pressure of CO₂ exceeding current atmospheric CO₂ levels (∆PCO₂) by 175 ± 32 μatm. Ship‐based measurements reveal that IPDW exhibits a distinct ∆PCO₂ maximum in the ocean, which is set by remineralization of organic carbon and originates from the northern Pacific and Indian Ocean basins. Below this IPDW layer, the carbon content increases downwards, whereas ∆PCO₂ decreases. Most of this vertical ∆PCO₂ decline results from decreasing temperatures and increasing alkalinity due to an increased fraction of calcium carbonate dissolution. These two factors limit the CO₂ outgassing from the high‐carbon content deep waters on more southerly surface outcrops. Our results imply that the response of Southern Ocean CO₂ fluxes to possible future changes in upwelling are sensitive to the subsurface carbon chemistry set by the vertical remineralization and dissolution profiles.

Key Points

• Deep ocean CO₂ release arises from high potential CO₂ partial pressure in subsurface water between the Subantarctic Front and sea‐ice edge

• Maximum subsurface potential CO₂ is connected to the outcrop of upwelling Indo‐Pacific Deep Water (IPDW), rich in remineralized organic carbon

• High alkalinity and low temperature limit CO₂ release from higher carbon‐content deep water outcropping south of IPDW

1. Introduction

Based on year‐round biogeochemical measurements with profiling floats that resolve the seasonal cycle, recent work has identified a larger than previously estimated release of carbon dioxide (CO₂) from the Southern Ocean to the atmosphere during austral winter (black line in Figure 1; Bushinsky et al., ²⁰¹⁹; Gray et al., ²⁰¹⁸). While there has been a broad consensus that the region south of about 50°S releases old, pre‐industrial CO₂ to the atmosphere (Gruber et al., 2019; Mikaloff Fletcher et al., ²⁰⁰⁷; Morrison et al., ²⁰¹⁵; Wu et al., ²⁰¹⁹), the magnitude and extent of this CO₂ release have been substantially smaller in previous estimates, which were derived from ship‐board measurements (gray and red lines in Figure 1; Landschützer et al., ²⁰¹⁶, ²⁰²⁰; Takahashi et al., ²⁰⁰⁹). These previous estimates most likely underestimate the CO₂ release due to a lack of data during austral winter. Therefore, analysis of data that are unaffected by seasonal biases is required to better understand the Southern Ocean's potential to release CO₂. In this study, we analyze ship and float measurements from depths that are not subject to large seasonal variations in order to address the question of whether such a large outgassing from the Southern Ocean during winter can be expected when deep waters are brought to the surface.

Figure 1.

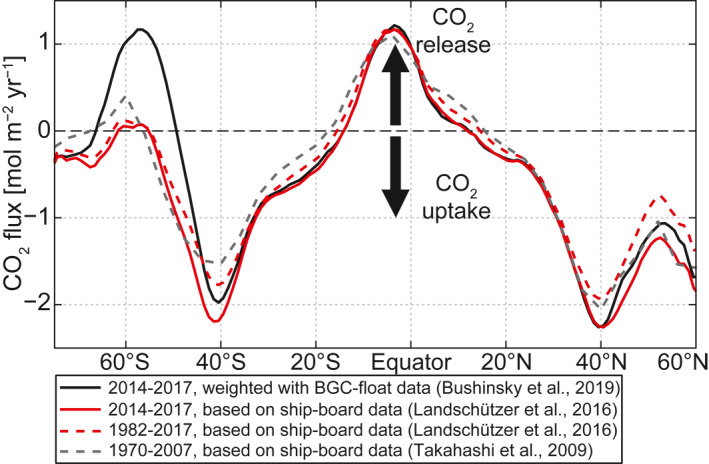
Zonal and annual mean global ocean to atmosphere CO₂ flux (positive values denote ocean CO₂ release to the atmosphere) from different data products for different time periods. Black: Neural‐network estimate, weighted with biogeochemical Argo float data (Bushinsky et al., 2019; Landschützer et al., ²⁰¹⁹). Red: Neural‐network estimate, based on ship‐board observations from the SOCAT database (Landschützer et al., 2016, ²⁰²⁰). Gray: Climatology based on ship‐board observations from the CDIAC database (Takahashi et al., 2009).

In the Southern Ocean (south of about 50°S), CO₂ is naturally released from the ocean to the atmosphere due to the upwelling of carbon‐rich waters from the deep layers of the global ocean (Mikaloff Fletcher et al., 2007; Morrison et al., ²⁰¹⁵; Takahashi et al., ²⁰⁰⁹) that elevate the surface dissolved inorganic carbon (DIC) content in this region (Wu et al., 2019). Globally, this Southern Ocean CO₂ release is balanced by natural CO₂ uptake in the subtropics and northern subpolar oceans (Figure 1; Gruber et al., ²⁰⁰⁹; Takahashi et al., ²⁰⁰², ²⁰⁰⁹). This CO₂ uptake is driven in part by cooling of the surface water as it is being transported to higher latitudes, which increases its capacity to hold CO₂, and in part by the sinking of biologically produced organic matter out of the surface layer (Gruber et al., 2009; Takahashi et al., ²⁰⁰², ²⁰⁰⁹). The biologically produced organic carbon sinks through the thermocline and is remineralized at depth, where it feeds the deep waters with inorganic carbon, which is then transported to the Southern Ocean (Sarmiento & Gruber, 2006). Therefore, the upwelling and CO₂ release in the Southern Ocean closes the global ocean carbon cycle.

The leakage of old, pre‐industrial CO₂ from the deepest ocean layers is unique to the high‐latitude Southern Ocean, because this is the only region where deep waters ascend to the surface along rising, steep isopycnals (Morrison et al., 2015; Speer et al., ²⁰⁰⁰; Talley, ²⁰¹³; Toggweiler & Samuels, ¹⁹⁹⁵). Deep waters exit the Indian, Pacific and Atlantic basins in both western and eastern boundary currents, and spiral southeastward and upward until reaching the base of the mixed layer in the southern Antarctic Circumpolar Current (ACC; Tamsitt et al., ²⁰¹⁷, ²⁰¹⁹). This upwelling process is thought to be the major return pathway for remineralized carbon from the ocean's interior to the surface (Kwon et al., 2009; Sarmiento et al., ¹⁹⁸⁸; Skinner et al., ²⁰¹⁰). Estimates of ocean transport show that a supply of DIC to the Southern Ocean surface comes from a southward and upward flux of Circumpolar Deep Water (Iudicone et al., 2011; Wu et al., ²⁰¹⁹). This southward transport consists of North Atlantic Deep Water (NADW), Lower Circumpolar Deep Water (LCDW) in the Indian and Pacific basins, and somewhat less dense Indo‐Pacific Deep Water (IPDW) that all carry DIC from sinking and remineralization of biogenic carbon, and, in the case of NADW, DIC from air‐sea gas exchange (Aldama‐Campino et al., 2020; Broecker & Peng, ¹⁹⁹²).

The upwelling of the DIC‐rich waters as well as the low surface temperature are responsible for a strong meridional surface DIC increase toward the high latitudes, as recently shown by Wu et al. (2019). Moreover, the study shows that an elevated Southern Ocean DIC is maintained by a larger capacity of the water to hold carbon due to the cold conditions and elevated alkalinity (Alk) associated with the upwelled waters. In contrast to DIC that is high throughout most of the Southern Ocean surface waters (Wu et al., 2019), the CO₂ release is concentrated to a relatively narrow band between about 50° and 65°S (Figure 1). The latter is driven by an elevated surface ocean partial pressure of CO₂ (pCO₂) over atmospheric pCO₂ ($p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$), whereas the ocean's pCO₂ is set by the seawater properties such as DIC, Alk, temperature, and salinity. Therefore, a more detailed understanding of the pCO₂ of the upwelling deep waters is required to explain the deep ocean's CO₂ release through Southern Ocean upwelling.

In this study, we aim to further our understanding of the underlying mechanisms of this deep ocean CO₂ release in the Southern Ocean and to identify its sources. We seek to explain the characteristic meridional patterns of surface CO₂ fluxes in the Southern Ocean (Figure 1), to explain why CO₂ release peaks in a zonal band between 55° and 65°S, and to identify the pathway and sources of how the deep ocean loses carbon to the atmosphere. For this purpose, we assess factors that could affect the deep ocean's outgassing potential using subsurface DIC, Alk, dissolved oxygen, nutrient, temperature, and salinity data from ship‐based observations (Key et al., 2004, ²⁰¹⁵; Lauvset et al., ²⁰¹⁶; Olsen et al., ²⁰¹⁶) and biogeochemical floats (Johnson et al., 2017). In order to relate these ocean observational data to the Southern Ocean surface CO₂ fluxes, in a first step, we here make use of the interior ocean potential pCO₂ (PCO₂; Broecker & Peng, ¹⁹⁸²; Skinner et al., ²⁰¹⁰) excess above the approximate current (year 2015) global‐mean $p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$ (400 μatm), that is, ∆PCO₂ = PCO₂ − $p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$. Thus, we calculate the seawater PCO₂ as the pCO₂ that a water parcel would attain if it were adiabatically brought to the surface (Broecker & Peng, 1982) using its DIC, alkalinity, potential temperature ($\theta$Al) and sea‐level pressure. The resulting ∆PCO₂ is then a more accurate measure of the capability of upwelling water to release CO₂ to the present‐day atmosphere than DIC alone. In a second step, we analyze the drivers of the spatial patterns of ∆PCO₂ in the interior ocean by estimating the different contributions of the dissolution, solubility, ocean circulation and ventilation, and biological carbon pump processes (Gruber & Sarmiento, 2002; Sarmiento & Gruber, ²⁰⁰⁶; Volk & Hoffert, ¹⁹⁸⁵). In a third step, we decompose ∆PCO₂ vertical gradient into components associated with DIC, temperature, and Alk. Using this decomposition, we demonstrate the importance of considering the full vertical carbon chemistry structure, in particular Alk, when assessing the influence of the carbon‐rich deep ocean on the surface Southern Ocean CO₂ fluxes.

2. Methods

2.1. Potential pCO₂ and Neutral Density

Potential pCO₂ (PCO₂) is defined as the pCO₂ that a water parcel would attain if it was brought to the surface adiabatically (Broecker & Peng, 1982; Sarmiento & Gruber, ²⁰⁰⁶; Skinner et al., ²⁰¹⁰), thus correcting for the pressure effects on temperature and partial pressure. PCO₂ is computed following Williams et al. (2017) using CO2SYS (van Heuven et al., ²⁰¹¹) and by using dissociation constants of carbonate from Lueker et al. (2000), of sulfate from Dickson (1990), and of fluoride from Perez and Fraga (1987), and the boron to salinity ratio of Lee et al. (2010). Here, PCO₂ is a function of Alk, DIC, potential temperature (θ, referenced to 0 dbar), practical salinity (S), the reference pressure (p^ref = 0 dbar), silicate (Si), and phosphate (PO₄). For biogeochemical float data (Section 3), we use nitrate (NO₃) and convert it to PO₄ and Si using stoichiometric phosphate‐to‐nitrate and silicate‐to‐nitrate ratios of 1:16 and 2.5, respectively (Anderson & Sarmiento, 1994). Note that we here use the deviation of the interior ocean PCO₂ from the approximate current (year 2015) atmospheric pCO₂ of 400 μatm (∆PCO₂), which differs from past or future atmospheric conditions, to illustrate the present‐day outgassing potential of an interior ocean water masses.

We here evaluate the interior ocean ∆PCO₂ structure considering neutral density surfaces. For this purpose, we have calculated the neutral density (γ ⁿ) for all data sets (Section 3) based on Jackett and McDougall (1997; version 3.05.12; 17 June 2019; http://www.teos-10.org/preteos10_software/neutral_density.html). Since in this code γ ⁿ is not defined for temperatures below −2.5°C, the small set of temperatures below this value is set to −2.5°C.

2.2. Temperature and Salinity Effects on ∆PCO₂

In a first step, we estimate the effect of dilution of ocean tracers through freshwater fluxes on PCO₂ ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$) by evaluating the difference between PCO₂ and sPCO₂ derived from salinity normalized (s) quantities:

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}=\mathrm{P}\mathrm{C}{\mathrm{O}}_2-\mathrm{s}\mathrm{P}\mathrm{C}{\mathrm{O}}_2.\end{array}$$ (1)

Here, sPCO₂ is derived using sAlk, sDIC, sSi, and sPO₄, whereas salinity normalization of a given variable X to a reference salinity (S^ref = 34.7) is performed through (Broecker & Peng, 1992; Chen & Millero, ¹⁹⁷⁹)

$$\begin{array}{l}\mathrm{s}\mathrm{X}=\frac{\mathrm{X}}{\mathrm{S}}{\mathrm{S}}^{\mathrm{r}\mathrm{e}\mathrm{f}}.\end{array}$$ (2)

The only exception here is sDIC, which we obtain by first salinity normalizing its preindustrial value and then adding the anthropogenic component (see Section 3).

In a second step, we estimate the effect of solubility on the interior ocean PCO₂ distribution ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$) through

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}=\mathrm{s}\mathrm{P}\mathrm{C}{\mathrm{O}}_2-\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}.\end{array}$$ (3)

Here, ${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ is the PCO₂ arising from variations in sDIC and sAlk and it is computed as a function of sAlk, sDIC, θ ^ref (2.5°C), S^ref (34.7), p^ref (0 dbar), sSi, and sPO₄. Reference values θ ^ref and S^ref are arbitrary values that depend on the purpose of the analysis (Table 1). The resulting $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$ provides a measure for the contribution of mostly temperature differences relative to the location of the reference value. Since we are interested in the ocean interior structure of PCO₂, we chose these reference values to reflect deep water properties. If for example, θ ^ref was set to 20°C, which is closer to global surface water temperatures, the interior ocean ${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ would become much larger than the actual PCO₂ and $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$ strongly negative everywhere. We note that these solubility effects on PCO₂ should not be confused with solubility effects on DIC through air‐sea exchange in response to surface heat fluxes, that is, the so‐called solubility pump. We further note that the separation of the DIC and Alk into the pump components (Sections 2.3 and 2.4) is not affected by the choice of θ ^ref.

Table 1.

Reference Values Used in This Study for the Estimation of the Drivers of Interior Ocean PCO₂ Variations, in Part Derived From Gridded GLODAPv2 Data (Lauvset et al., 2016)

Variable	Value	Description
pref	0 dbar	Reference pressure
Sref	34.7	Reference ocean salinity
θ ref	2.5°C	Reference ocean temperature
${\mathrm{p}\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$	400 µatm	Approximate atmospheric partial pressure of CO2 in 2015
${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}$	131 µatm	Partial pressure of CO2 using reference values of this table
sAlkref	2,298 μmol kg−1	Reference surface ocean alkalinity
${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$	0.1 μmol kg−1	Reference surface ocean phosphate concentration
sSiref	6.3 μmol kg−1	Reference surface ocean silicate concentration
sDICref	1,967 μmol kg−1	Reference preindustrial surface ocean dissolved inorganic carbon concentration

2.3. Biological Pumps and Effects of Ocean Ventilation and Circulation on ∆PCO₂

We further attribute the interior ocean ∆PCO₂ variations to the driving biological pump components, that is, the soft‐tissue and carbonate pumps that are associated with the photosynthesis and remineralization of organic matter as well as the precipitation and dissolution of calcium carbonate (CaCO₃), respectively, and provide an interpretation of the residual term. We make use of a concept that has been developed to separate the interior ocean DIC variations into these contributions (Gruber & Sarmiento, 2002; Sarmiento & Gruber, ²⁰⁰⁶; Volk & Hoffert, ¹⁹⁸⁵) to estimate their effect on ∆PCO₂. In order to achieve this goal, we first separately estimate the sDIC, sAlk, sPO₄, and sSi deviations from their reference values, which are listed in Table 1, defined as ∆X = sX − sX^ref, for any variable X. For sDIC^ref, we use the estimated pre‐industrial surface mean value, since the effect of anthropogenic carbon is estimated separately (below and Section 3). Consistent with Gruber and Sarmiento (2002) that used a ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$ of 0.07 μmol kg⁻¹, representing the surface PO₄ at lower latitudes, we here use a ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$ of 0.1 μmol kg⁻¹. This value is at the upper bound of sPO₄ in the subtropical gyre regions where nutrient consumption is high and from where organic matter is exported to the deep ocean. This value is substantially smaller than the actual global mean surface value of 0.47 μmol kg⁻¹. The elevated mean global surface ocean ${\mathrm{sPO}}_4$ largely arises from regions with incomplete nutrient consumption. We also ran sensitivity tests to evaluate the effect of the choice of ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$ on the deep ocean ∆PCO₂ using 0.07, 0.1, and 0.47 μmol kg⁻¹ (Figure S1 in Supporting Information S1). We found that a ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$ of 0.47 μmol kg⁻¹ leads to a strong positive residual $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ (defined below) with a maximum in the deep northern Pacific (around 1,500 m)—a signal that would rather be expected from the soft‐tissue pump. In contrast, this region should exhibit a local minimum $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ due to the poor ventilation of this region (Holzer et al., 2021). Note that this region may include a large ∆PCO₂ component that arises from disequilibrium carbon (Eggleston & Galbraith, 2018), which is not included in our estimate of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ as discussed below. Our sensitivity analysis suggests that a ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$ of 0.1 μmol kg⁻¹ minimizes the effect of a positive $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ in the poorly ventilated deep Pacific, and seems to be a suitable choice. Nevertheless, we note that the separation of ∆PCO₂ is sensitive to the choice ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$. Therefore, our results should be interpreted as qualitative rather than quantitative estimates.

We estimate the contributions of the soft‐tissue pump to ∆DIC and ∆Alk by using ∆PO₄, which results in an estimate of the maximum potential of the soft‐tissue pump in the absence of air‐sea equilibration, that is, the amount of carbon that would be retained in the ocean by the soft‐tissue pump (rsoft) if there was no equilibration at the surface:

$$\begin{array}{l}∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}=r_{\mathrm{C}:\mathrm{P}}∆\mathrm{P}{\mathrm{O}}_4,\end{array}$$ (4)

$$\begin{array}{l}∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}=-r_{\mathrm{N}:\mathrm{C}}∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}},\end{array}$$ (5)

Here, r _C:P and r _N:C are the carbon‐to‐phosphate and nitrate‐to‐carbon stoichiometric ratios set to 117/1 and 16/117, respectively (Anderson & Sarmiento, 1994). The latter ratio is applied because a molar increase in seawater nitrate due to for example, the remineralization of organic matter equals the molar decline in Alk (Sarmiento & Gruber, 2006).

We note that this approach makes the assumption that the entire ∆PO₄ pool in the deep ocean is associated with a corresponding soft‐tissue ∆DIC. In practice, only a fraction of ∆PO₄ is directly accumulated through remineralization in the deep ocean (so‐called regenerated PO₄), whereas another fraction of ∆PO₄ is recirculated through transport and mixing processes after its exposure to the surface ocean (so‐called preformed PO₄). The latter process is very prominent in the Southern Ocean, where nutrient consumption is incomplete. In order to illustrate this process, we here compute the fraction of the soft‐tissue pump that is associated with directly accumulated carbon (F^accum) and the fraction that is associated with recirculated carbon (F^recirc) using the apparent oxygen utilization (AOU) following Williams and Follows (2011) as

$$\begin{array}{l}{\mathrm{F}}^{\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{m}}=\frac{r_{\mathrm{P}:\mathrm{O}}\left({\mathrm{O}}_2^{\mathrm{s}\mathrm{a}\mathrm{t}}-{\mathrm{O}}_2\right)}{∆\mathrm{P}{\mathrm{O}}_4},\end{array}$$ (6)

and

$$\begin{array}{l}{\mathrm{F}}^{\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}}=1-{\mathrm{F}}^{\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{m}},\end{array}$$ (7)

respectively. Here, the difference between the saturated (${\mathrm{O}}_2^{\mathrm{s}\mathrm{a}\mathrm{t}}$) and observed (O₂) dissolved oxygen concentrations corresponds to AOU, and r _P:O is the phosphate‐to‐oxygen stoichiometric ratio set to 1/170 (Anderson & Sarmiento, 1994).

While the fraction of ∆PO₄ that is not consumed by biological production at the surface gets recirculated (F^recirc), some of the associated DIC is released to the atmosphere through air‐sea equilibration and another part is retained in the ocean as so‐called disequilibrium carbon due to an incomplete air‐sea equilibration at the surface (Eggleston & Galbraith, 2018; Ito & Follows, ²⁰¹³). Thus, we are here considering the entire history of a water parcel (derived from ∆PO₄; Sarmiento & Gruber, ²⁰⁰⁶) and not just the history of the water parcel since it was last at the surface (derived from AOU; Williams & Follows, ²⁰¹¹). While disequilibrium carbon in the existing literature is largely interpreted as an air‐sea gas exchange process, in our study, the retained soft‐tissue pump includes the portion of this disequilibrium carbon that originates from biological sources in the deep ocean, which is not equilibrated at the surface. Moreover, since we attribute all ∆PO₄ to the soft‐tissue pump, our estimate should be interpreted as the maximum potential of the soft‐tissue pump in the absence of air‐sea equilibration. In contrast to estimating the soft‐tissue pump through AOU (Williams & Follows, 2011), our approach therefore provides the opportunity to estimate the equilibrated DIC at the surface, that is, the fraction of deep ocean carbon that has been released to the atmosphere, through the residual term discussed below.

Subsequently, the contributions of the carbonate pump to the ∆DIC and ∆Alk are estimated as

$$\begin{array}{l}∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}=∆\mathrm{A}\mathrm{l}\mathrm{k}-∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}},\end{array}$$ (8)

and

$$\begin{array}{l}∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}=0.5∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}},\end{array}$$ (9)

respectively.

We proceed to estimate and interpret the pre‐industrial residual DIC term (∆DIC^res) as:

$$\begin{array}{l}∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{s}}=\mathrm{s}\mathrm{D}\mathrm{I}\mathrm{C}-\mathrm{s}\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{f}}-∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}-∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}-∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}},\end{array}$$ (10)

where ∆DIC^cant is the anthropogenic DIC estimate (Lauvset et al., 2016; see Section 3). ∆DIC^res represents a combination of factors: To first order it includes the part of DIC that has been released to the atmosphere due to incomplete air‐sea equilibration at the surface, that is, ventilation, before the water is subducted again. Since disequilibrium carbon is included in the retained soft‐tissue component, this residual component thus expresses where CO₂ is actually being gained or lost from the ocean by gas exchange due to equilibration. The residual component also includes effects of the so‐called solubility pump that is associated with DIC changes at the surface due to heating and cooling and subsequent CO₂ release and uptake, respectively. Moreover, the residual term also includes any errors in our attempt to decompose the DIC pool. In particular, such errors arise from our choice of ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$ and uncertainties and variations in the stoichiometric ratios. Therefore, our results only provide a qualitative measure.

In contrast to DIC and Alk, PCO₂ is not a conserved tracer but depends on current carbon chemistry and solubility of the water. Therefore, separating ∆PCO₂ deviations into its components is not straightforward. Nevertheless, we can quantify the range of values by calculating each contribution, that is, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$, and $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$ under four scenarios, during which we vary processes that modify the PCO₂ sensitivity to DIC and Alk, and using p^ref, S^ref, and θ ^ref. We run these four scenarios four times for each of the terms above by replacing the terms x, y, and z in Equations (11), (12), (13), (14) below. In the first run, in order to obtain an estimate for $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$, x ≡ rsoft, y ≡ carb, and z ≡ res + cant. In the second run, in order to obtain an estimate for $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$, x ≡ carb, y ≡ rsoft, z ≡ res + cant. In the third run, in order to obtain an estimate for $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$, x ≡ res, y ≡ rsoft, z ≡ carb. In the fourth run, in order to obtain an estimate for $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$, x ≡ cant, y ≡ rsoft, and z ≡ carb. For runs where there is no corresponding Alk^x,y,z, because the process only affects DIC, it is set to zero.

The first scenario for $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{x}}$ assumes that only this one process influences DIC and Alk deviations from the reference values. As such, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{x}}$ is calculated by using sDIC, sAlk, sPO₄, and sSi fields that are driven by process x alone:

$$∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{x}}=\mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{x}},\mathrm{s}\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{x}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4,\mathrm{s}\mathrm{S}\mathrm{i}\right)-\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}},$$ (11)

where ${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}$ is the ocean PCO₂ calculated using all reference values (Table 1). The second and third scenarios assume that one of the two other processes y or z influencing DIC and Alk has occurred prior to process x to determine the PCO₂ sensitivity to DIC and Alk:

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{x}}=\\ \mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{y}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{x}},\mathrm{s}\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{y}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{x}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4,\mathrm{s}\mathrm{S}\mathrm{i}\right)-\\ \mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{y}},\mathrm{s}\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{y}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}},\mathrm{s}\mathrm{S}{\mathrm{i}}^{\mathrm{r}\mathrm{e}\mathrm{f}}\right),\end{array}$$ (12)

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{x}}=\\ \mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{z}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{x}},\mathrm{s}\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{z}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{x}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4,\mathrm{s}\mathrm{S}\mathrm{i}\right)-\\ \mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{z}},\mathrm{s}\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{e}\mathrm{f}}+∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{z}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}},\mathrm{s}\mathrm{S}{\mathrm{i}}^{\mathrm{r}\mathrm{e}\mathrm{f}}\right).\end{array}$$ (13)

The last scenario is that process x occurs after all the other processes. Therefore, we have

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{x}}=\mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{s}\mathrm{A}\mathrm{l}\mathrm{k},\mathrm{s}\mathrm{P}{\mathrm{O}}_4,\mathrm{s}\mathrm{S}\mathrm{i}\right)-\\ \mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}\mathrm{C}-∆\mathrm{D}\mathrm{I}{\mathrm{C}}^{\mathrm{x}},\mathrm{s}\mathrm{A}\mathrm{l}\mathrm{k}-∆\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{x}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}},\mathrm{s}\mathrm{S}{\mathrm{i}}^{\mathrm{r}\mathrm{e}\mathrm{f}}\right).\end{array}$$ (14)

We then use the mean of the four scenarios (Equations (11), (12), (13), (14)) as an estimate for the contribution of the $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{x}}$ to the interior ocean ∆PCO₂ distribution.

2.4. Impact of Carbon Chemistry on the Vertical ∆PCO₂ Distribution

To estimate how the seawater carbon chemistry drives the vertical ∆PCO₂ distribution, we separately estimate the departure of ∆PCO₂ due to deviations of DIC and Alk from the respective reference values (Table 1). The increasing DIC with depth is the primary source of the elevated ∆PCO₂ in the deeper layers of the ocean, which is then modified by Alk. Therefore, we first estimate PCO₂ variations due to DIC alone ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C}}$):

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C}}=\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C}}-\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}=\\ \mathrm{P}\mathrm{C}{\mathrm{O}}_2\left(\mathrm{s}\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{s}\mathrm{A}\mathrm{l}{\mathrm{k}}^{\mathrm{r}\mathrm{e}\mathrm{f}},{\theta }^{\mathrm{r}\mathrm{e}\mathrm{f}},{\mathrm{S}}^{\mathrm{r}\mathrm{e}\mathrm{f}},\mathrm{s}\mathrm{P}{\mathrm{O}}_4,\mathrm{s}\mathrm{S}\mathrm{i}\right)-\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}.\end{array}$$ (15)

We then estimate the impact of Alk variations ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{A}\mathrm{l}\mathrm{k}}$) as

$$\begin{array}{l}∆\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{A}\mathrm{l}\mathrm{k}}=\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}-\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C}}-\mathrm{P}\mathrm{C}{\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}\end{array}$$ (16)

where ${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ is defined in Section 2.2. Moreover, we define $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}={\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}-p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$.

3. Data

Our conclusions are drawn from ship‐based measurements and measurements by profiling floats. We use physical and biogeochemical data from the gridded Global Ocean Data Analysis Project version 2 (GLODAPv2; Key et al., ²⁰⁰⁴, ²⁰¹⁵; Lauvset et al., ²⁰¹⁶; Olsen et al., ²⁰¹⁶) climatology, which are provided at a 1° by 1° spatial resolution. GLODAPv2 is based on shipboard measurements from 724 hydrographic cruises from 1972 to 2013. Estimates of anthropogenic DIC provided in the mapped GLODAPv2 data (Lauvset et al., 2016) were used to assess the anthropogenic contribution to DIC. The GLODAPv2 DIC and ∆DIC^cant estimates are referenced to the year 2002. In addition, we use biogeochemical profiling float data from a broad region in the Southern Ocean (Johnson et al., 2021), which were deployed as part of the Southern Ocean Carbon and Climate Observations and Modeling (SOCCOM) project (Johnson et al., 2017). Here, we use a total of 8,332 profiles from 174 floats with measurements of high‐quality pH (Johnson et al., 2016; Williams et al., ²⁰¹⁷), NO₃, and estimated Alk (Carter et al., 2018) to estimate PCO₂.

Surface CO₂ flux data stems from two neural‐network estimates; one is weighted toward biogeochemical Argo float data (Bushinsky et al., 2019; Landschützer et al., ²⁰¹⁹) and one uses only shipboard observations from the SOCAT database (Landschützer et al., 2016, ²⁰²⁰). A third product is a climatology based on shipboard observations from the CDIAC database (Takahashi et al., 2009). Climatological frontal positions stem from Orsi et al. (1995) and the sea‐ice edge position is the annual mean 1% sea‐ice concentration derived from the NSIDC Climate Data Record (1979–2018; Meier et al., ²⁰¹⁷; Peng et al., ²⁰¹³).

4. Results

4.1. Spatial Patterns of CO₂ Release Linked to Subsurface ∆PCO₂ Maximum

The float‐weighted annual mean surface CO₂ flux estimate (Bushinsky et al., 2019; Landschützer et al., ²⁰¹⁹) reveals a distinct ring feature (Figures 2a and 2b), with strong CO₂ release occurring within the ACC, roughly between the Subantarctic Front and the winter‐time sea‐ice edge. The highest outgassing occurs in the Pacific and Indian Ocean sectors, regionally exceeding 3 mol m⁻² yr⁻¹ (positive values are a CO₂ flux from the ocean to the atmosphere; see also Prend et al. (2022)). In these regions, intensive CO₂ release is observed in the fall and winter, followed by weaker, yet non‐negligible, outgassing fluxes in the remaining seasons (Bushinsky et al., 2019; Gray et al., ²⁰¹⁸). North of the ACC, CO₂ fluxes are characterized by a broad region of CO₂ uptake. The highest annual uptake, below −3 mol m⁻² yr⁻¹, is found in the Argentine Basin in the Atlantic. In the seasonally ice‐covered region, annual mean surface CO₂ fluxes are generally small. In summary, the largest CO₂ release occurs roughly between the sea‐ice edge and the Subantarctic Front during wintertime, a region that is dominated by a wind‐driven divergence at the surface and deep mixing in winter (Bushinsky et al., 2019; Gray et al., ²⁰¹⁸; Prend et al., ²⁰²²) and during strong storms (Nicholson et al., 2022).

Figure 2.

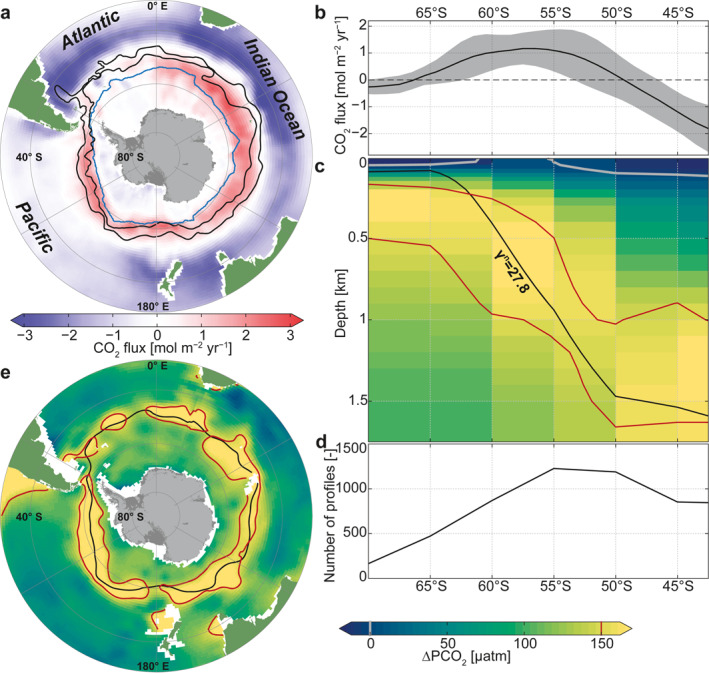
Southern Ocean CO₂ release and its subsurface source. (a) Annual mean surface CO₂ flux from a neural‐network estimate that is weighted with biogeochemical Argo float data (Bushinsky et al., 2019; Landschützer et al., ²⁰¹⁹). Positive values (red) indicate CO₂ degassing from the ocean to the atmosphere. Black contours denote the mean position of the Subantarctic and Polar Fronts (Orsi et al., 1995). The light blue contour line represents the annual mean sea‐ice edge (1% mean sea‐ice concentration). (b) Zonally averaged annual mean surface CO₂ flux (as in panel (a)). Gray shading denotes ±1 standard deviation in the zonal direction. (c) Zonally averaged annual‐mean potential pCO₂ excess with respect to current atmospheric levels (400 μatm; ∆PCO₂) from profiling floats (in 5° latitudinal bins). (d) Number of float profiles per 5° latitudinal bins. (e) ∆PCO₂ at 800 m from gridded GLODAPv2. In panels (c and e), the 27.8 kg m⁻³ isoneutral surface is shown in black, and the 150 and 0 μatm ∆PCO₂ isolines in red and gray, respectively.

The ring pattern of outgassing evident from the surface CO₂ fluxes aligns with the region of upward sloping isopycnal surfaces in the Southern Ocean subsurface between about 55° and 65°S (Figures 2c and 2d). In this region, the zonal mean ∆PCO₂ from the float profiles reveals a signature of high‐∆PCO₂ deep water that upwells along isopycnals. The vertical ∆PCO₂ maximum appears along the 27.8 kg m⁻³ neutral density surface, which shoals toward the south within the ACC; this is coincident with the core of the oxygen minimum layer that is characteristic of, and defines, IPDW (Talley, 2013; see also Figures 3g–3i). The sign of the surface CO₂ fluxes (Figure 2b) closely tracks this shoaling of the subsurface ∆PCO₂ maximum (Figure 2c), switching from CO₂ uptake north of 50°S to CO₂ outgassing between about 50°S and 65°S (Figure 2b). Maximum outgassing, between 55° and 60°S, encompasses the latitude range of positive ∆PCO₂ at the surface (gray contour lines in Figure 2c). This picture of highest surface outgassing in the region where high‐∆PCO₂ waters upwell, as derived from the profiling floats, is corroborated by a ring pattern in the ∆PCO₂ constructed from gridded shipboard observations (Section 3) at 800 m depth (Figure 2e). It reflects the high annual‐mean surface CO₂ fluxes, with highest values occurring between the Polar and Subantarctic Fronts. The core of the subsurface high‐∆PCO₂ ring coincides with the outcropping of the 27.8 kg m⁻³ neutral density surface (black in Figures 2c and 2e). Both the surface CO₂ fluxes and the subsurface ∆PCO₂ at 800 m decrease further south of the outcropping 27.8 kg m⁻³ neutral density surface. Therefore, the reduced CO₂ outgassing south of its maximum is in part related to a decrease of the subsurface ∆PCO₂ south of 60°S. In addition, the inhibition of gas exchange by sea‐ice cover, a potentially high biological carbon export efficiency (Arteaga et al., 2018), reduced mixing (Wilson et al., 2019), and cold surface temperatures could further limit the mixed‐layer ∆PCO₂ and thereby surface CO₂ fluxes in this seasonally ice‐covered region. In summary, the outcropping of the isopycnal surfaces in the Southern Ocean acts to project the vertical ∆PCO₂ structure with its maximum on the 27.8 kg m⁻³ neutral density surface onto a horizontal plane, resulting in the meridional ∆PCO₂ maximum between the sea‐ice edge and Subantarctic Front.

Figure 3.

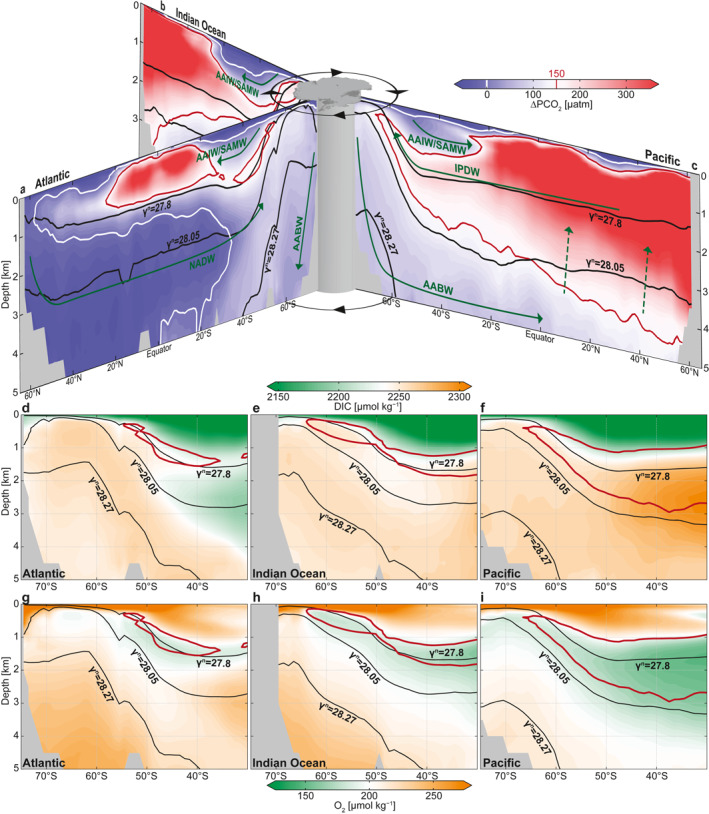
Potential pCO₂ excess above current atmospheric levels (400 μatm; ∆PCO₂) and dissolved inorganic carbon (DIC) in the ocean interior from gridded GLODAPv2. Meridional sections of zonally averaged ∆PCO₂ in the Atlantic (a), Indian (b), and Pacific (c) Oceans, overlaid with a schematic representation of the subsurface water pathways (white arrows) and the Antarctic Circumpolar Current (black arrows). Zonally averaged DIC in the Atlantic (d), Indian (e), and Pacific (f) sectors of the Southern Ocean (south of 30°S). Zonally averaged dissolved oxygen (O₂) in the Atlantic (g), Indian Ocean (h), and Pacific (i) sectors of the Southern Ocean (south of 30°S). Isoneutral surfaces are shown in black (γ ^N = 27.8 and 28.05 kg m⁻³ characterizing Indo‐Pacific Deep Water [IPDW] and North Atlantic Deep Water [NADW], respectively), and the 150 and 0 μatm ∆PCO₂ isolines in red and white, respectively.

4.2. Sources of the Subsurface ∆PCO₂ Maximum

Where does the high subsurface ∆PCO₂ water in the Southern Ocean come from? In order to address this question, in the following, we base our analysis on ∆PCO₂ derived from a global data set (GLODAPv2; Lauvset et al., ²⁰¹⁶; see Section 3) as displayed in Figure 3. Note that this data has several advantages, such as higher accuracy ship‐board observations compared to the float data, actual alkalinity observations, and being a gridded product. However, major differences occur at the Southern Ocean surface. Here, the float data suggest an outcrop of the zero ∆PCO₂ contour (gray in Figure 2c), whereas the the zero ∆PCO₂ contour from ship‐data (white in Figures 3a–3c) does not outcrop. This difference most likely occurs from the lack of wintertime observations in GLODAPv2. In this study, we are mostly interested in the subsurface ∆PCO₂, where both data sets largely agree.

We now assume that, to a first order, water masses spread along isoneutral density surfaces (denoted as γ ^N)—an assumption that has been widely used to identify the deep water circulation pathways (Jackett & McDougall, 1997). The ∆PCO₂ maximum follows the 27.8 kg m⁻³ isoneutral surface, which characterizes the IPDW core as identified by the vertical oxygen minimum (Talley, 2013, Figure 3); hence the vertical oxygen and ∆PCO₂ extrema appear to have the same biological and physical forcing. The ∆PCO₂ maximum can be traced back from the Southern Ocean subsurface to its source region in the deep northern Indian and Pacific basins (Figures 3a–3c). Here, the ocean is pervaded by PCO₂‐rich waters, with ∆PCO₂ much larger than 150 μatm extending from the thermocline to about 4 km depth (red contour line in Figures 3b and 3c).

The highest ∆PCO₂ waters, indicated by a ∆PCO₂ larger than 800 μatm, are located in the North Pacific between 50° and 60°N and between 500 and 1,500 m, where the oldest subsurface waters occur in the global ocean, supplied by slow vertical diffusion from below (dashed white lines in Figure 3c; Holzer et al., ²⁰²¹; Talley, ²⁰¹³). These waters with high ∆PCO₂ spread southward and outcrop at the sea surface in the Southern Ocean (Gent & McWilliams, 1990; Holzer et al., ²⁰²¹; Talley, ²⁰¹³). They enter the Southern Ocean as a layer of elevated ∆PCO₂ that extends southward and upward across 50°S, where the zonal mean PCO₂ exceeds atmospheric levels by about 175 ± 32 μatm (averaged between 27.7 and 27.9 kg m⁻³; Table 2). Both advective and diffusive eddy transport can play an important role in pulling these high ∆PCO₂ signals to the Southern Ocean subsurface (Dufour et al., 2015; Tamsitt et al., ²⁰¹⁷), with the final step being entrainment into the surface mixed layer (Prend et al., 2022). This chimney of elevated ∆PCO₂ is narrowly constrained along the IPDW core (27.8 kg m⁻³ isoneutral surface; Figure 3c). As these waters reach the Southern Ocean, the ∆PCO₂ signal is strongly attenuated as a result of diapycnal mixing with ambient low ∆PCO₂ waters, yet its magnitude is still strongly elevated and forms a clear local vertical maximum in all three ocean basins. South of the Polar Front, where the 27.8 kg m⁻³ isoneutral surface outcrops, the high ∆PCO₂ signals originated from the IPDW are circumpolarly distributed, again mirroring the oxygen minimum layer (Figures 3g–3i; Talley, ²⁰¹³), and control the subsurface ∆PCO₂ around Antarctica.

Table 2.

Deep Ocean ∆PCO₂ (in µatm), Reference Values (Ref), and the Estimated Sources From Temperature (T) and Salinity (S), and Dissolved Inorganic Carbon (DIC) and Alkalinity (Alk) Variations

Water mass		IPDW	LCDW/NADW	AABW	LCDW/NADW–IPDW	AABW–IPDW
Range		27.7 kg m−3–27.9 kg m−3	27.9 kg m−3–28.2 kg m−3	>28.2 kg m−3
∆PCO2		175 ± 32	104 ± 33	77 ± 16	−70 ± 46	−97 ± 36
Ref	$p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$	−400	−400	−400	0	0
	${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}$	+131	+131	+131	0	0
T, S	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$	−1 ± 1	0 ± 0	0 ± 0	+2 ± 1	+1 ± 1
	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$	−4 ± 7	−23 ± 11	−53 ± 8	−19 ± 13	−48 ± 10
DIC, Alk	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$	+595 ± 59	+506 ± 59	+530 ± 22	−89 ± 84	−65 ± 63
	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$	−112 ± 22	−104 ± 24	−114 ± 6	+8 ± 32	−2 ± 23
	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$	+39 ± 17	+18 ± 9	+25 ± 9	−21 ± 19	−13 ± 19
	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$	−78 ± 29	−25 ± 19	−46 ± 16	+53 ± 34	+33 ± 33
	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{c}}$	+699 ± 92	+676 ± 105	+707 ± 31	−23 ± 140	+8 ± 98
	$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{l}\mathrm{k}}$	−253 ± 70	−283 ± 83	−312 ± 24	−30 ± 108	−59 ± 74

Note. DIC and Alk variations are also split into contributions by the retained soft‐tissue (rsoft) and carbonate (carb) pumps, as well as the anthropogenic and residual contributions. Values are averaged for different water masses (columns 2, 3, and 4) and differences between water masses and IPDW (columns 5 and 6). All values are averaged between 45° and 55°S. Note that the components do not add up to zero due to non‐linearities in the PCO₂ estimation and should be understood as a qualitative measure. Uncertainties are reflected by the respective standard deviation.

In contrast to the maximum ∆PCO₂ found in IPDW, the lowest value of deep‐ocean ∆PCO₂, of less than −50 μatm, is located in the northern Atlantic, where NADW is formed from surface sources, and hence has higher oxygen and lower ∆PCO₂ than IPDW (Figures 3a and 3g). The NADW core in the Southern Ocean has been identified by its salinity maximum, which roughly follows the 28.05 kg m⁻³ isoneutral surface (Talley, 2013). While the ∆PCO₂ of NADW increases continuously due to diapycnal mixing and biological processes as the NADW moves southward, much less CO₂ outgassing would be expected if NADW were the primary water mass being ventilated in the Southern Ocean. In the Southern Ocean, NADW mixes with higher ∆PCO₂ LCDW from the Indo‐Pacific (Figure 3c). Between 45° and 55°S, the circumpolar average of LCDW/NADW has a ∆PCO₂ that is about 70 ± 46 μatm lower than the ∆PCO₂ of IPDW (Table 2). This LCDW/NADW mixture then upwells primarily in the region covered by the seasonal sea ice (Talley, 2013), where the local environment further hinders the air‐sea CO₂ exchange. In conclusion, our analysis shows that the characteristic pattern of a high ΔPCO₂ ring below the mixed layer, which causes the Southern Ocean CO₂ outgassing, is induced by the southward and upward transport of IPDW through a narrow and relatively light isoneutral density band and cannot be explained by the upwelling of LCDW, such as NADW.

4.3. Drivers of High ∆PCO₂ in Indo‐Pacific Deep Water

Why is ∆PCO₂ particularly elevated along the circulation pathway of IPDW? A larger CO₂ outgassing potential in deep waters has generally been linked to a higher DIC content. However, IPDW has no clear vertical DIC maximum in the Southern Ocean (Figures 3d–3f). Instead, vertically, the DIC peaks are located at a much greater depth and higher density than those of ∆PCO₂. For example, DIC maxima in the Southern Ocean occur on isoneutral surfaces that are associated with the Antarctic Bottom Water (AABW; γ ^N ∼28.27 kg m⁻³; Orsi et al., ¹⁹⁹⁹) in the Atlantic and Indian Ocean (Figures 3d and 3e), and on isoneutral density surfaces of about 28.0 kg m⁻³ in the Pacific north of 50°S (Figure 3f). Since the IPDW ∆PCO₂ maximum cannot simply be explained by its carbon content (DIC), we here consider the different temperature and salinity effects (dilution and solubility; Section 4.3.1; Figure 4), and DIC and Alk variations arising from biological and ventilation processes (Section 4.3.2; Figures 5 and 6), as well as the carbonate chemistry (Section 4.3.3; Figure 7) that determine the interior Southern Ocean PCO₂ structure (see Section 2 for methods). For this purpose, we evaluate these contributions on depth levels (Figures 4, 5, 6, 7a and 7b) and on neutral density surfaces that represent the corresponding water masses (Figures 7c and 7d, Table 2). We vertically separate the subsurface ocean into three neutral density layers: IPDW (27.7–27.9 kg m⁻³), LCDW/NADW (27.9–28.2 kg m⁻³), and AABW (>28.2 kg m⁻³) (Figure 7, Table 2).

Figure 4.

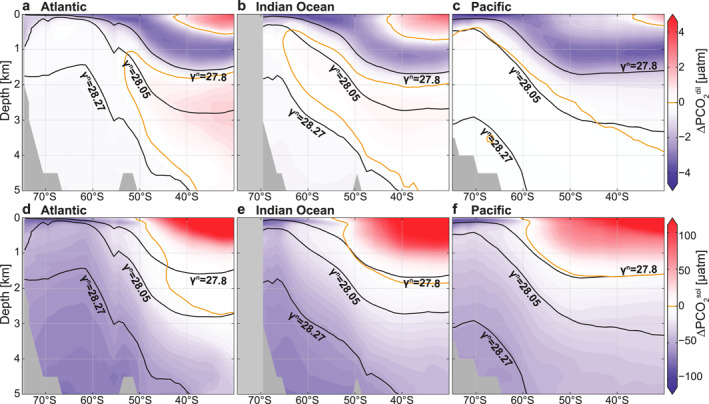
Temperature and salinity effects on the subsurface ∆PCO₂ structure. (a–c) Dilution effects ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$) relative to a salinity of 34.7. (d–f) Solubility effects ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$) with respect to a reference temperature and salinity of 2.5°C and 34.7°C, respectively. Panels show the Atlantic (left), Indian (middle), and Pacific (right) sectors of the Southern Ocean. Isoneutral surfaces are shown in black, and the 0 μatm ∆PCO₂ isoline in orange.

Figure 5.

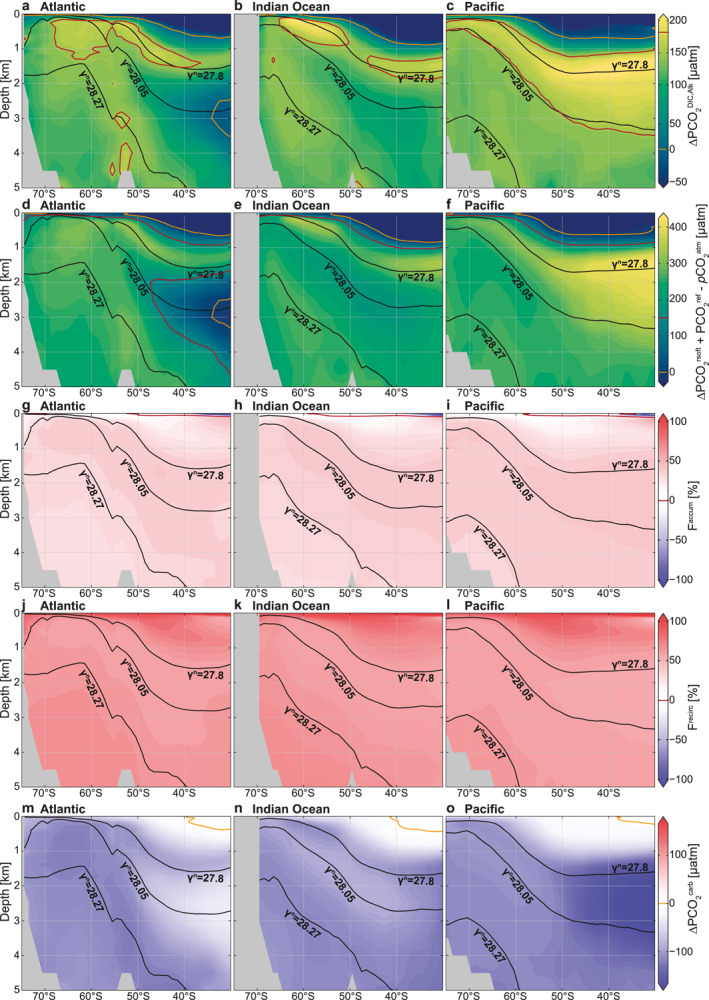
Biological drivers of the subsurface ∆PCO₂ structure. (a–c) ∆PCO₂ structure due to interior ocean dissolved inorganic carbon (DIC) and Alk variations alone ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$), after removing dilution and solubility effects. (d–f) Expected ∆PCO₂ driven by the retained soft‐tissue pump ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$) due to photosynthesis and remineralization of organic matter plus ${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}$ (131 μatm) minus $p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$ (400 μatm). (g–i) Fraction of the retained soft‐tissue pump associated with accumulated remineralized carbon in the deep ocean (F^accum). (j–l) Fraction of the retained soft‐tissue pump recirculated remineralized carbon (F^recirc). (m–o) Carbonate pump ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$) due to precipitation and dissolution of calcium carbonate. Panels show the Atlantic (left), Indian (middle), and Pacific (right) sectors of the Southern Ocean. Isoneutral surfaces are shown in black, and the 150 and 0 μatm ∆PCO₂ isolines in red and orange, respectively.

Figure 6.

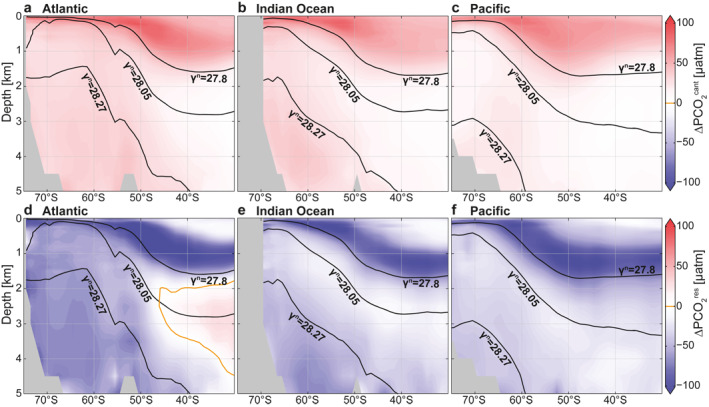
Ventilation effects on the subsurface ∆PCO₂ structure. (a–c) Influence of anthropogenic carbon uptake ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$). (d–f) Influence of air‐sea gas exchange due to equilibration and other residual effects ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$). Panels show the Atlantic (left), Indian (middle), and Pacific (right) sectors of the Southern Ocean. Isoneutral surfaces are shown in black, and the 0 μatm ∆PCO₂ isoline in orange.

Figure 7.

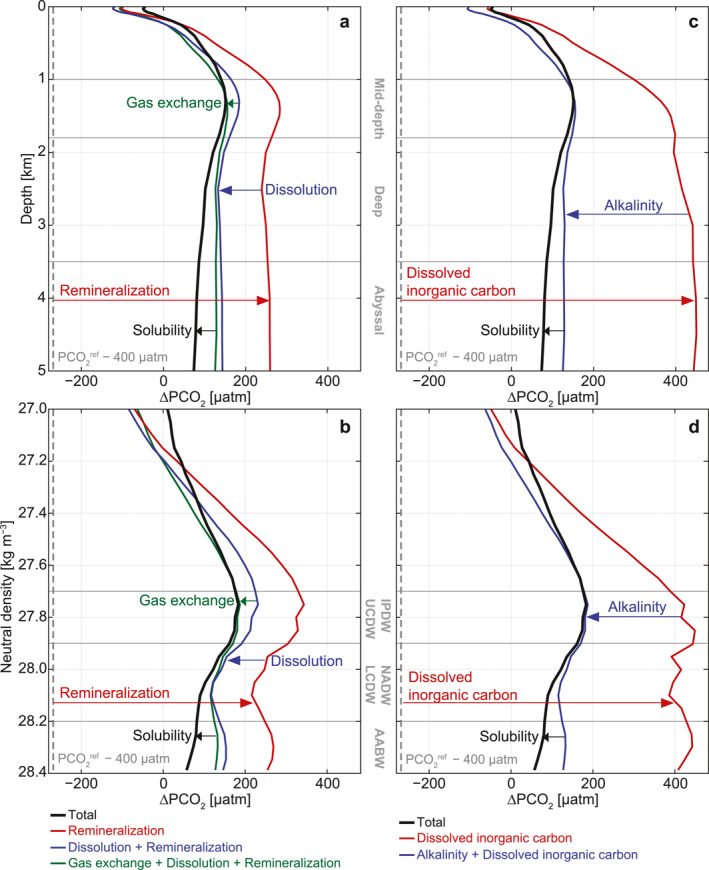
Drivers of the vertical ∆PCO₂ profile between 45° and 55°S. Decomposition of ∆PCO₂ profiles into biological and physical processes in (a) depth and (b) neutral density coordinates. Decomposition of ∆PCO₂ profiles into chemical (dissolved inorganic carbon, Alk) and physical components in (c) depth and (d) neutral density coordinates. Note that in this figure, for simplicity, gas exchange is the combination of anthropogenic and natural components and dilution effects are neglected.

4.3.1. Temperature and Salinity Effects on Interior Ocean ∆PCO₂ Structure

Physical effects of interior ocean temperature and salinity variations on ∆PCO₂ include the dilution of ocean tracers by surface freshwater fluxes, and changes in CO₂ solubility (Section 2.2). Dilution effects (∆${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$; Figures 4a–4c, Table 2) are generally small (<5 μatm). Compared to our chosen reference salinity of 34.7, the LCDW/NADW layer (γ ^N ∼ 28.05 kg m⁻³) and the subtropical surface waters have an elevated $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$ due to evaporation effects on those waters. Antarctic surface waters, Antarctic Intermediate Water (AAIW), and Subantarctic Mode Water (SAMW) experience a reduced $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$ due to a net freshwater input at the Southern Ocean surface. However, this pattern cannot explain the interior ocean ∆PCO₂ structure and the order of magnitude of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{d}\mathrm{i}\mathrm{l}}$ is negligible.

Solubility effects ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$; Figures 4d–4f), which are mostly associated with the interior Southern Ocean temperature distribution and to a lesser degree with the salinity distribution, are on the order of about 20–100 μatm. They become very large in the much warmer subtropical thermocline waters. Overall, the colder temperatures in the deepest layers, in particular AABW, as well as the high‐latitude Antarctic surface waters, reduce ∆PCO₂ and enhance the ability of these waters to hold CO₂ or reduce their outgassing potential. Thus, solubility effects have a substantial influence on the interior Southern Ocean ∆PCO₂ structure and act to contribute to the observed vertical ∆PCO₂ decrease, especially in the deepest layers (Figures 7a and 7b, Table 2), with the most negative values occurring in the deep southern Atlantic (Figure 4d). However, vertical $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{s}\mathrm{o}\mathrm{l}}$ gradients around the ∆PCO₂ maximum (27.8 kg m⁻³) are weaker than in the abyssal ocean, suggesting that other processes control the ∆PCO₂ decrease with depth, especially between the IPDW and LCDW/NADW layers. In summary, dilution effects are small and solubility effects on ∆PCO₂, arising from interior ocean temperature variations, enforce the IPDW ∆PCO₂ maximum (Table 2).

4.3.2. Biological and Ventilation Effects on Interior Ocean ∆PCO₂ Structure

In order to better understand the biological and ventilation contribution to the subsurface ∆PCO₂ structure in the Southern Ocean, we compare the contributions of the retained soft‐tissue pump ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$), carbonate pump ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$), and residual ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$) to ∆PCO₂ variations that arise from variations in sDIC and sAlk alone ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$; Figures 5a–5c), that is, for fixed reference values of temperature, salinity, and pressure (Section 2). It should be noted that while these reference values affect the actual value of ∆PCO₂, they do not affect the relative partitioning between the factors driving $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$. We also note that $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ approximately equals the sum of ${\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{f}}$, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$, and $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$ minus $p{\mathrm{C}\mathrm{O}}_2^{\mathrm{a}\mathrm{t}\mathrm{m}}$ (Section 2). These contributions are discussed in this section.

The retained soft‐tissue pump ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$) is the most efficient mechanism to increase the deep ocean's ∆PCO₂ through the accumulation and subsequent recirculation of remineralized carbon (DIC; Figure 7, Table 2). The contribution of this mechanism to ∆PCO₂ explains most of the interior ocean structure of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ (Figures 5a–5f), as well as the occurrence of very high $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ in IPDW, which is especially prominent in the Pacific (Figure 5f). High values of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ in the rather shallow IPDW (Table 2), as compared to the deeper LCDW/NADW (Table 2), partially occur because IPDW accumulates respired carbon over long timescales (DeVries & Primeau, 2011), which is related to the long route that newly ventilated AABW takes through the Indian and Pacific, upwelling diffusively to produce IPDW, which then returns to the Southern Ocean surface (Holzer et al., 2021; Talley, ²⁰¹³). In addition to the difference in accumulation time, IPDW receives more organic carbon from remineralization as a result of its rather shallow depth in the water column (shallower than 1,500 m) compared to LCDW/NADW and AABW (Kwon et al., 2009; Martin et al., ¹⁹⁸⁷). The organic matter received by IPDW could be about twice as large as in the layers below when using a vertical organic carbon remineralization curve that follows a classic power‐law relationship (Martin et al., 1987) and ignoring possible spatial differences in the production of organic matter at the surface. A secondary peak in both $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ and $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ occurs around the 28.27 kg m⁻³ isoneutral surface, which marks the upper bound of AABW (Orsi et al., 1999), in particular in the Weddell Sea (Atlantic south of 50°S; Figures 5a and 5d). This secondary $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ peak arises from local production and remineralization within the Weddell Gyre (MacGilchrist et al., 2019). A local minimum is found in the core of the relatively young NADW around the 28.05 kg m⁻³ isoneutral surface in the Atlantic (Figure 5d; DeVries & Primeau, ²⁰¹¹), which disappears toward the south as this water masses mixes with other waters in the Southern Ocean. In conclusion, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ dominates the vertical ∆PCO₂ decline below IPDW, which also explains the colocation of the vertical ∆PCO₂ maximum and the dissolved oxygen minimum in the deep ocean (Section 4.2), because both quantities are dominated by the soft‐tissue pump.

Our estimate of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ should be interpreted as the maximum potential of the retained soft‐tissue pump in the absence of air‐sea equilibration at the surface, since it is estimated from the total ∆PO₄. In practice, when the upwelling water masses reach the surface of the Southern Ocean, PO₄ that is not utilized by biological production becomes recirculated into the ocean interior with the subduction of AAIW, SAMW, and AABW. In the absence of air‐sea equilibration this recirculated PO₄ would also be associated with recirculated biogenic DIC^rsoft. However, a partial air‐sea equilibration of DIC occurs at the surface. The equilibrated DIC portion is part of our residual estimate ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$), further discussed below, and the portion of soft‐tissue carbon associated with the incomplete equilibration (so‐called disequilibrium carbon; Eggleston & Galbraith, ²⁰¹⁸; Ito & Follows, ²⁰¹³) is part of our $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ and is thus interpreted as biogenic carbon in our context (see Section 2.3). Further insight into the contribution of the directly accumulated fraction (F^accum) and the recirculated fraction (F^recirc) to $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ is gained by partitioning them using AOU (Section 2.3; Williams & Follows, ²⁰¹¹). These two contributions (Figures 5g–5l) highlight the important potential of the ocean circulation to recirculate carbon in the ocean in the absence of air‐sea equilibration since F^recirc dominates $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ in AABW, AAIW, and SAMW. In the IPDW core, between the 27.7 and 27.9 kg m⁻³ isoneutral surfaces, F^accum becomes as large as 39% but still remains smaller than F^recirc. This overall large contribution of F^recirc implies that any long‐term changes in the surface equilibration due to, for example, changes in the surface residence time, sea ice cover, or solubility of these waters could alter the carbon storage in the deep ocean. In addition, a shift in the occupied deep ocean volume from NADW (low recirculated soft‐tissue carbon) to AABW (high recirculated soft‐tissue carbon), as implied for glacial times (Curry & Oppo, 2005), could substantially impact the total CO₂ balance between the ocean and the atmosphere due to an increased recirculation of soft‐tissue carbon in the deep ocean (Eggleston & Galbraith, 2018; Skinner, ²⁰⁰⁹).

The magnitude of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ (Figures 5d–5f) is substantially larger than $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$ (Figures 5a–5c), because the carbonate pump ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$; Figures 5m–5o) and residual terms ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$; Figures 5g–5i) counter the retained soft‐tissue pump effect on $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{D}\mathrm{I}\mathrm{C},\mathrm{A}\mathrm{l}\mathrm{k}}$. The negative $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$ in the deep ocean arises from the dissolution of mineral carbonates, which increases alkalinity twice as much as it increases DIC. The most negative values of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$ are located in the deep Pacific (Figure 5o), where dissolution of mineral carbonate is enhanced by the metabolic CO₂ release that drives the deep water to be undersaturated with respect to calcite (Broecker & Peng, 1987; Jiang et al., ²⁰¹⁵; Kwon et al., ²⁰¹¹; Sarmiento et al., ¹⁹⁸⁸). As the dissolution process strongly depends on pressure and preferentially happens at greater depth compared to organic matter remineralization (Broecker & Peng, 1987; Kwon et al., ²⁰¹¹; Sarmiento et al., ¹⁹⁸⁸), the $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$ deficit appears to peak at greater depth than the $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}$ maximum in the Pacific (Figure 5o). However, due to compensatory effects between the Atlantic and the Pacific basins (Figures 5m and 5o), the $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$ contribution to the overall zonal mean vertical ∆PCO₂ decrease with depth is small (Figure 7a; between 45° and 55°S) and even of opposite sign when averaged over neutral density layers (Table 2). Therefore, the overall effects of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}}$ in setting the vertical ∆PCO₂ maximum in IPDW are small, but are critical to understanding the differences between the vertical ∆PCO₂ and DIC profiles, as we show in Section 4.3.3.

The effect of anthropogenic carbon on ∆PCO₂ ($∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$; Figures 6a–6c) is estimated based on GLODAPv2 (Section 2.3). $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$ is elevated in the AAIW, SAMW, and subtropical surface waters and also has some smaller positive values in the AABW, due to an uptake of anthropogenic carbon by these waters before they are subducted (Gruber et al., 2019). However, a substantial amount of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$ is also found in IPDW, and the decline of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$ with depth contributes to the overall vertical ∆PCO₂ decline below IPDW (Table 2). Such an invasion of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{t}}$ to the IPDW layer could arise from along‐isopycnal stirring by mesoscale eddies, connecting the surface outcrop of the isopycnal with the older, upwelling deep waters (Abernathey & Ferreira, 2015). Overall, anthropogenic carbon reinforces the IPDW ∆PCO₂ maximum (Table 2).

$∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ (Figures 6d–6f) includes all residual effects of unexplained subsurface DIC variations. These effects include carbon release at the ocean surface due to air‐sea equilibration which acts to lower the subsurface $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ because the recirculated DIC pool becomes depleted by carbon outgassing to the atmosphere compared to the recirculated PO₄ pool (see discussion above). Therefore, negative $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ values reflect CO₂ that was released from the ocean due to ventilation processes. The most negative values of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ are associated with AAIW. This water is formed by transforming the upwelling IPDW into lighter waters at the Southern Ocean surface, mostly through freshening by sea ice melt and precipitation (Abernathey et al., 2016; Haumann et al., ²⁰¹⁶). The surface water experiences a substantial loss of biogenic CO₂ to the atmosphere (Figure 2a) before being subducted as AAIW. Similarly to its anthropogenic component, these natural ventilation effects also reach into the IPDW layer (γ _N ∼ 27.8 kg m⁻³). The negative peak of $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ just above the 27.8 kg m⁻³ isoneutral surface contributes to the sharp decline of ∆PCO₂ just above the IPDW layer, but counteracts the decline below this layer (Figure 7, Table 2). Moreover, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ also includes air‐sea gas exchange effects related to DIC exchange at the surface that are the result of cooling or heating of a water mass at the surface before subduction. Such a signal of the so‐called solubility pump is visible in the positive values of the NADW core (Figure 6d). The arise from an uptake of carbon in the North Atlantic, driven by surface cooling, before the subduction of NADW to the deep ocean. This positive $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ signature of NADW is lost southward within the Southern Ocean as these waters mix with waters ventilated in the Southern Ocean. Other residual effects included in $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ arise from the choice of reference values, in particular ${\mathrm{s}\mathrm{P}\mathrm{O}}_4^{\mathrm{r}\mathrm{e}\mathrm{f}}$, as discussed in Section 2.3. Overall, $∆{\mathrm{P}\mathrm{C}\mathrm{O}}_2^{\mathrm{r}\mathrm{e}\mathrm{s}}$ tends to increase ∆PCO₂ below IPDW (Table 2) and therefore cannot explain the vertical ∆PCO₂ maximum in IPDW.

4.3.3. Vertical Difference Between DIC and ∆PCO₂ Maxima Between 45° and 55°S

We now separately consider the effects of DIC and alkalinity on the vertical ∆PCO₂ structure (Figures 7c and 7d) to better understand why ∆PCO₂ decreases below the 27.8 kg m⁻³ isoneutral surface despite an equally high or higher carbon content (DIC) below this layer in the Southern Ocean (Figure 3). While the retained soft‐tissue and carbonate pumps both act to enhance the DIC storage in the interior ocean, the carbonate pump adds DIC to a greater depth than the retained soft‐tissue pump (Broecker & Peng, 1987; Kwon et al., ²⁰¹¹; Sarmiento et al., ¹⁹⁸⁸). The difference between the vertical ∆PCO₂ and DIC structure then largely results from the vertical alkalinity structure, since the retained soft‐tissue pump decreases the deep ocean alkalinity (increasing ∆PCO₂) and the carbonate pump increases it (decreasing ∆PCO₂). This impact of alkalinity on the zonal mean vertical ∆PCO₂ structure between 45° and 55°S is shown in Figures 7c and 7d (see Section 2.4). Compared to the ∆PCO₂ maximum of 175 ± 32 μatm in IPDW, ∆PCO₂ in LCDW/NADW waters is 70 ± 46 μatm lower (Table 2). The largest contributor to this reduction, that is, 43%, is alkalinity, while the remainder is explained by a colder temperature (27%) and lower DIC (33%; Table 2; Figure 7d). The DIC contribution arises from low‐DIC NADW, which vanishes in depth coordinates, where alkalinity and temperature effects are the sole drivers of the vertical ∆PCO₂ decline with depth (Figure 7c). These roles of alkalinity (61%) and temperature (49%) in driving a vertical ∆PCO₂ decline become even larger when comparing the IPDW layer to AABW. Thus, the vertical DIC gradient cannot explain the lower ∆PCO₂ in deeper and denser waters, except for the NADW core (γ ^N ∼ 28.05 kg m⁻³) that exhibits a DIC decrease with depth. In conclusion, the separation between the deeper DIC and shallower ∆PCO₂ maxima is caused by the shallower depth of remineralization of organic carbon compared to the depth of dissolution of calcium carbonate that sets the relative contributions of DIC and alkalinity in driving ∆PCO₂, reinforced by a decreasing temperature with depth.

5. Summary and Conclusions

We here show that the upwelling of high‐ΔPCO₂ IPDW occurs along the 27.8 kg m⁻³ isoneutral surface in the Southern Ocean, which we identify as the major global pathway for old, pre‐industrial carbon to return to the surface and as the key source of Southern Ocean outgassing. The importance of this isopycnal and pathway for supply of old, nutrient‐rich IPDW to the surface of the Southern Ocean was previously identified through the location of the IPDW oxygen minimum (Talley, 2013). Here we highlight its relevance as the major return pathway of CO₂ from the deep ocean to the atmosphere. This pathway draws from a high‐ΔPCO₂ pool in the middepth northern Indo‐Pacific basins, which exceeds current atmospheric CO₂ levels (400 μatm) by more than 800 μatm and is the result of a slow accumulation of carbon due to the remineralization of organic matter and its subsequent recirculation. The resulting high‐PCO₂ IPDW propagates southward, where it subsequently upwells in the high‐latitude Southern Ocean, retaining a high‐ΔPCO₂ signal that exceeds current atmospheric levels by 175 ± 32 μatm. Our findings thus provide observational evidence that there is a substantial transport of old, pre‐industrial CO₂ from the deep ocean to the atmosphere through the Southern Ocean surface under present‐day conditions. Therefore, interior ocean measurements support the recent argument for a large natural CO₂ release at the surface in the open waters around Antarctica (Bushinsky et al., 2019; Gray et al., ²⁰¹⁸), sourced from relatively high PCO₂ water that has upwelled to just beneath the mixed layer; this outgassing signal is best observed in winter when deep mixing entrains the high‐ΔPCO₂ IPDW to the surface (Prend et al., 2022).

We find that the vertical subsurface ΔPCO₂ gradient, and in particular the isopycnal that best characterizes its subsurface maximum, directly controls the meridional pattern of the Southern Ocean surface CO₂ fluxes. The maximum outgassing between the Subantarctic Front and the winter‐time sea‐ice edge is caused by a circumpolar band of high‐ΔPCO₂ IPDW just beneath the surface mixed layers. This characteristic ring pattern of Southern Ocean outgassing and high subsurface ΔPCO₂ is due to the southward‐rising isopycnal surfaces that project the vertical ΔPCO₂ maximum in IPDW onto the horizontal plane. The ring is circumpolar because the deep waters spiral southeastward with the ACC while they are rising, and are thus found all around Antarctica even though the original sources are localized boundary outflows from the Indian and Pacific basins (Tamsitt et al., 2017). Denser waters, such as NADW and the denser portion of IPDW (LCDW), reach the surface south of the maximum outgassing region in the ACC, and exhibit a much weaker outgassing, in part due to their lower ΔPCO₂. Thus, the vertical ΔPCO₂ distribution at mid‐latitudes directly explains the characteristic ring structure of Southern Ocean CO₂ release (Figures 2a and 2e). Next to the source water properties investigated in this study, this pattern of CO₂ release is further influenced by other surface processes, such as vertical mixing (Nicholson et al., 2022; Prend et al., ²⁰²²), solubility (Wu et al., 2019), biological production (Arteaga et al., 2019), and air‐sea gas exchange. In particular, storm driven mixing (Nicholson et al., 2022) and seasonal sea ice cover (Gupta et al., 2020; Loose & Schlosser, ²⁰¹¹; Rysgaard et al., ²⁰¹¹; Shadwick et al., ²⁰²¹) might play an important role in modulating the seasonal rate of CO₂ release.

Deep and surface ocean carbon content (DIC) are often used as a measure for potential Southern Ocean CO₂ release. While the sources of elevated surface DIC in the Southern Ocean have been recently investigated (Wu et al., 2019), we here have shown that only considering DIC can lead to misinterpretations when it comes to surface CO₂ fluxes, since the subsurface DIC structure critically differs from the subsurface ΔPCO₂ structure that controls the surface CO₂ fluxes. The DIC maximum occurs much deeper in the water column and remains high all the way to the bottom of the ocean, whereas ΔPCO₂ peaks shallower and declines with depth. In our analysis, we show that the vertical distribution of ΔPCO₂ and dissolved oxygen in the deep ocean are controlled primarily by the soft‐tissue pump, whereas the vertical distribution of DIC is influenced by both the retained soft‐tissue and the carbonate pumps, offsetting its maximum to deeper layers. This elevated carbon content (DIC) in the denser and deeper water masses, such as LCDW and AABW, is buffered by their carbon chemistry (high alkalinity) and colder temperatures, which limits CO₂ outgassing from these waters. This reduced outgassing potential from higher alkalinity in the deeper waters is the result of a deeper depth of calcium carbonate dissolution compared to organic matter remineralization in the global ocean, which has been identified as a key mechanism for actively retaining carbon at depth over long time scales (Broecker & Peng, 1987; Hain et al., ²⁰¹⁰; Krumhardt et al., ²⁰²⁰; Kwon et al., ²⁰¹¹; Toggweiler, ¹⁹⁹⁹). Consequently, next to adequate ocean circulation and gas‐exchange kinetics, a realistic representation of the vertical remineralization and dissolution profiles in the global ocean is an important pre‐requisite for Earth System Models to accurately simulate Southern Ocean CO₂ fluxes and the global ocean carbon cycle, as well as their response to climatic changes (Kwon et al., 2009).

Model simulations project an enhanced future upwelling of deep waters in the Southern Ocean (Downes & Hogg, 2013) due to a poleward intensification of westerly winds (Bracegirdle et al., 2020) and changes in the surface buoyancy forcing (Bishop et al., 2016; Downes et al., ²⁰¹⁸). Such increased upwelling could substantially amplify the leakage of pre‐industrial CO₂ from the deep ocean (Lovenduski et al., 2007; Toggweiler & Russell, ²⁰⁰⁸) and lead to a “saturation” of the anthropogenic CO₂ uptake by the ocean (Le Quéré et al., 2007; Lovenduski et al., ²⁰⁰⁷). However, there is still limited confidence in future projections of upwelling in the Southern Ocean (Meredith et al., 2019) since these models do not resolve mesoscale eddies (Bishop et al., 2016; Meredith et al., ²⁰¹²; Morrison & Hogg, ²⁰¹³) that are important for the ocean's carbon transport (Abernathey & Ferreira, 2015; Dufour et al., ²⁰¹⁵) and suffer from large biases in their water mass structure (Beadling et al., 2020; Downes et al., ²⁰¹⁸). In addition, global climate models struggle to produce the correct patterns, magnitudes (Lenton et al., 2013; Mongwe et al., ²⁰¹⁸), and temporal variability (Gruber et al., 2019) of surface CO₂ fluxes in the Southern Ocean. Observational evidence derived from chlorofluorocarbon measurements points toward an increased upwelling since the early 1990s (Ting & Holzer, 2017; Waugh et al., ²⁰¹³). However, recent findings also show that the relation between upwelling deep waters and changes in the surface CO₂ fluxes is much more complex and exhibits strong fluctuations on decadal time scales (DeVries et al., 2019; Landschützer et al., ²⁰¹⁵). Our results imply that not only the strength of circulation and ventilation changes in the Southern Ocean play an important role in altering the release of CO₂ from the deep ocean to the atmosphere, but also the depth level from which waters are upwelled. Moreover, they also imply that changes in subsurface carbon chemistry could impact the CO₂ release from the deep ocean. These implications of our results highlight the importance of improving the subsurface carbon chemistry, water‐mass structure, and circulation in global climate models in order to better assess future changes in atmospheric CO₂ in response to ocean circulation changes.

Supporting information

Supporting Information S1

Chen, H. , Haumann, F. A. , Talley, L. D. , Johnson, K. S. , & Sarmiento, J. L. (2022). The deep ocean's carbon exhaust. Global Biogeochemical Cycles, 36, e2021GB007156. 10.1029/2021GB007156

Data Availability Statement

All data and tools underlying this analysis are openly available: Mapped Global Ocean Data Analysis Project version 2 (https://www.glodap.info/index.php/mapped-data-product; https://doi.org/10.5194/essd-8-325-2016); Southern Ocean Carbon and Climate Observations and Modeling float data (Snapshot 2021‐05‐05; https://doi.org/10.6075/J0T43SZG); globally mapped CO₂ flux estimate based on the Surface Ocean CO₂ Atlas Database and Southern Ocean Carbon and Climate Observations and Modeling biogeochemistry floats (1982–2017, NCEI Accession 0191304, Version 2.2; https://doi.org/10.25921/9hsn-xq82); Global monthly gridded sea surface pCO₂ product from 1982 onward and its monthly climatology (NCEI Accession 0160558, Version 5.5; https://doi.org/10.7289/V5Z899N6); CDIAC CO₂ flux estimated from air‐sea difference in CO₂ partial pressure (revised October 2009; https://www.ldeo.columbia.edu/res/pi/CO2/carbondioxide/pages/air_sea_flux_2010.html); MATLAB Program Developed for CO₂ System Calculations (https://doi.org/10.3334/CDIAC/otg.CO2SYS_MATLAB_v1.1); and NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration (Version 3, 1979–2018; https://doi.org/10.7265/N59P2ZTG).