Abstract
The Earth's magnetosheath (MSH) is governed by numerous physical processes which shape the particle velocity distributions and contribute to the heating of the plasma. Among them are whistler waves which can interact with electrons. We investigate whistler waves detected in the quasi‐parallel MSH by NASA's Magnetospheric Multiscale mission. We find that the whistler waves occur even in regions that are predicted stable to wave growth by electron temperature anisotropy. Whistlers are observed in ion‐scale magnetic minima and are associated with electrons having butterfly‐shaped pitch‐angle distributions. We investigate in detail one example and, with the support of modeling by the linear numerical dispersion solver Waves in Homogeneous, Anisotropic, Multicomponent Plasmas, we demonstrate that the butterfly distribution is unstable to the observed whistler waves. We conclude that the observed waves are generated locally. The result emphasizes the importance of considering complete 3D particle distribution functions, and not only the temperature anisotropy, when studying plasma wave instabilities.
Keywords: quasi‐parallel magnetosheath, whistler waves, electron butterfly distribution
Key Points
Whistler waves in the quasi‐parallel magnetosheath exist in regions unstable and stable to the whistler temperature anisotropy instability
When whistlers are observed in regions predicted stable, electrons often have butterfly pitch‐angle distributions located in local B minima
Using a dispersion solver, we show that the butterfly distribution can excite the whistler waves observed in the data
1. Introduction
The Earth's magnetosheath (MSH) is the space plasma region downstream of the bow shock where solar wind plasma is heated, slowed down, and deflected around the magnetosphere. Numerous physical processes take place in the MSH, among which are pitch‐angle scattering from wave‐particle interactions (He et al., 2019), and particle trapping (Ahmadi et al., 2018; Yao et al., 2018), which shape the velocity distributions of the electrons and ions and contribute to the heating of the plasma. Understanding these processes and the conditions in which they arise is an active research topic.
The conditions in the MSH depend on the geometry of the bow shock, where it is common to differentiate between two different cases: quasi‐parallel (Q ‖) and quasi‐perpendicular (Q ⊥). In the Q ⊥ case, the shock normal angle θ bn (the angle between the bow shock normal direction and the interplanetary magnetic field (IMF)) is larger than 45° (Balogh et al., 2005). Typical for this region is ion pressure anisotropy which favors the mirror mode instability (Dimmock et al., 2015), and particle energization is mainly caused by compression. In the Q ‖ case, θ bn < 45°. Since the MSH is magnetically connected to the IMF, it strongly interacts with the upstream transients and discontinuities hitting the bow shock. The Q ‖ MSH is characterized by significant variations in the magnetic field, particle velocity, density, and temperature. The fluctuations of the plasma parameters have larger amplitude than in the Q ⊥ case. Current sheets (Vörös et al., 2016; Yordanova et al., 2020), high speed jets (Hietala et al., 2009; Plaschke et al., 2020), energetic ions (Fuselier, 1994), and magnetic holes (Huang, Du, et al., 2017) are common in the Q ‖ MSH geometry.
The Q ‖ MSH is rich in waves and among the most common waves are whistlers. Whistler waves are right hand polarized with frequencies between the ion and electron cyclotron frequencies. They were first observed in the MSH by Smith et al. (1969). MSH whistlers propagate quasi‐parallel to the background magnetic field (Y. Zhang et al., 1998; Baumjohann et al., 1999), and are correlated with minima in magnetic field magnitude (Smith & Tsurutani, 1976). Whistler waves are found in several space plasma regions including the radiation belts (Li et al., 2017), the magnetotail (Huang, Yuan, et al., 2017; Khotyaintsev et al., 2011), and the dayside magnetopause (Vaivads et al., 2007). They have been attributed to heating of non‐thermal electrons in the MSH (Breuillard et al., 2018) and electron acceleration at the bow shock (Oka et al., 2017). In the solar wind, whistlers can interact with electrons by pitch‐angle scattering of strahl electrons at 0.3 AU (Cattell et al., 2021), and have also been detected in magnetic holes at heliospheric distances ranging from 1.2 to 5 AU (Lin et al., 1995; Stone et al., 1995).
Whistlers are thought to play a crucial role in heating electrons in the MSH via wave‐particle interaction. One of the ways in which whistlers interact with electrons is through cyclotron resonance. For example, whistler generation can occur when the electron distribution is bi‐Maxwellian with a high temperature anisotropy (Kennel & Petschek, 1966), which has been observed in the MSH (Huang et al., 2018). When whistler waves are found in regions with low temperature anisotropy, this can be interpreted as the waves being generated remotely and propagating to the point of observation (Masood et al., 2006).
However, considering only temperature anisotropy can lead to misleading conclusions. Electron distributions in the turbulent MSH can be highly non‐Maxwellian (Graham et al., 2021). For example, non‐Maxwellian electron distributions can form in ion scale magnetic dips (Yao et al., 2017), where whistler waves are commonly observed (Yao et al., 2019). Different types of non‐Maxwellian distributions can excite whistlers in the MSH, including so‐called butterfly distributions occurring in mirror modes in the Q ⊥ MSH (Kitamura et al., 2020) and in magnetic holes close to the magnetopause (H. Zhang et al., 2021), and bi‐directional, anisotropic electron beams at the edge of a magnetic hole (Huang et al., 2020). Whistlers can also be excited via Landau resonance with electron beams, in which case they tend to propagate obliquely to the background magnetic field (An et al., 2016; Mourenas et al., 2015). However, the generation of whistler waves in the more turbulent MSH region downstream of a Q ‖ shock has not been studied in detail.
In this Letter, we use in‐situ data from NASA's Magnetospheric Multiscale (MMS) mission (Burch et al., 2016) to analyze the resonant interaction between electrons and whistler waves in the turbulent Q ‖ MSH. We adopt a kinetic approach, using full 3D distribution functions. We find that characteristics in the electron velocity distribution other than temperature anisotropy are fundamental for wave generation.
2. Whistler Observations
We consider a one‐hour interval, 11:00–12:00 UTC on 5 April 2019, shown in Figure 1. During this interval in, MMS is located at (12, 10, 1)R E (GSE coordinates are used here and throughout the paper) and stays mainly in the MSH. For our analysis, we use burst mode data from MMS. The flux‐gate magnetometer (FGM) (Russell et al., 2016) provides the magnetic field vector B (128 samples/s). Wave measurements with 8,192 samples/s are made by the search coil magnetometer (SCM) (Le Contel et al., 2016) and the electric double probe (EDP) (Ergun et al., 2016; Lindqvist et al., 2016). The fast plasma investigation (FPI) (Pollock et al., 2016) instruments provide 3D particle velocity distributions and the derived ion bulk velocity, electron density, and temperature, with time resolution of 30 ms for electrons and 150 ms for ions.
Figure 1.
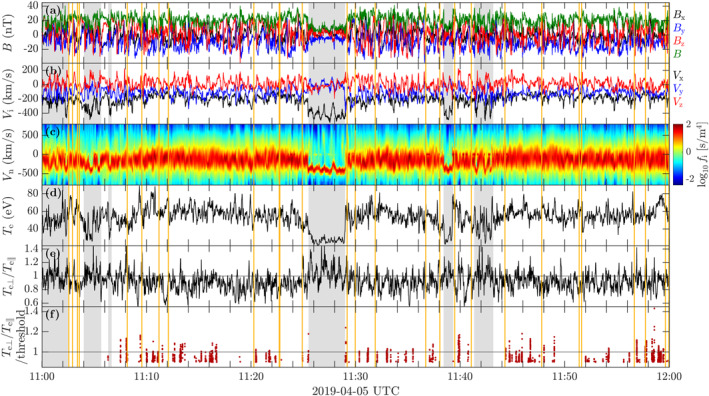
One‐hour interval in the Q ‖ magnetosheath (MSH). (a) Magnetic field vector B and magnitude B. (b) Ion velocity V i. (c) Reduced ion velocity distribution along the bow shock normal (fast data). (d) Electron temperature T e. (e) Electron temperature anisotropy T e⊥/T e‖. (f) T e⊥/T e‖ divided by the whistler instability threshold for γ = 0.01Ωce (Equation 1); only values above 0.9 are shown. Shaded intervals show regions with solar wind plasma which are excluded from the analysis. Vertical orange lines indicate when the butterfly‐shaped electron distribution was observed simultaneously with whistler waves.
Even though MSH is observed for the majority of the considered interval, bow shock crossings are observed on several occasions, suggesting that MMS stays close to the shock. The intervals with solar wind plasma, for example, between 11:25:30 and 11:29:00, are characterized by a lower magnetic field magnitude B compared to the MSH (Figure 1a) and a mainly negative x component of the ion velocity (Figure 1b) peaking at 500 km/s. The shock crossings were identified from the reduced ion velocity distribution along the bow shock normal (Figure 1c), and are shaded gray in Figure 1. We want to focus on the MSH and therefore exclude the shock/solar wind intervals from the statistical analysis presented later. The shock normal used to produce the reduced ion distribution in Figure 1c was estimated from magnetic coplanarity of the upstream field B u ≈ (3.2, −4.9, 1.7) nT, obtained from the OMNI database (Papitashvili & King, 2020), and the downstream field B d ≈ (−2.0, −17, 5.8) nT, a one‐minute average of the measured field before the crossing at 11:25:30. The estimated shock normal angle is therefore θ bn ≈ 36°, corresponding to a Q ‖ shock. In the MSH, B (Figure 1a) has an average magnitude 〈B〉 = 21 nT and fluctuations of , which falls in the range of statistically observed fluctuation levels in the MSH (Stawarz et al., 2022).
In Figure 1d, the electron temperature T e is shown. It has larger variations in the MSH than in the solar wind intervals. We also show the electron temperature anisotropy, T e⊥/T e‖, in Figure 1e. These quantities are derived from the electron temperature tensor, and represent the average internal energy (perpendicular and parallel to B in the case of T e⊥/T e‖) of the velocity distribution. The physical interpretation of T e and T e⊥/T e‖ should be done with caution when the distribution significantly deviates from a Maxwellian.
We can compare T e⊥/T e‖ to theoretical thresholds for the whistler temperature anisotropy instability (which we will refer to as the whistler instability) derived by Gary and Wang (1996). These give the anisotropy required for the waves to achieve a given growth rate γ, assuming that the electron distribution is bi‐Maxwellian. The thresholds are of the form:
| (1) |
where β e‖ = 2μ 0 n e T e‖/B 2 is the parallel electron plasma beta, μ 0 the vacuum permeability, and n e the electron density. For γ = 0.01Ωce, S = 0.36 and α = 0.55, and for γ = 0.10Ωce, S = 1.00, and α = 0.49. Here, Ωce = eB/m e is the angular electron cyclotron frequency, e the elementary charge, and m e the electron mass. Figure 1f shows the ratio between T e⊥/T e‖ and the whistler instability threshold (Equation 1) for γ/Ωce = 0.01. When this ratio is above 1, whistler wave generation is expected. However, when we analyze the whistler occurrence in detail (details presented later in this section) we find that whistler wave activity is often observed in the regions where the threshold is not reached (marked with vertical orange lines in Figure 1).
We now show one such interval of whistler wave observations occurring between 11:29:10.4 and 11:29:14.0 UTC (vertical dashed lines in Figure 2). During this interval, the average β e‖ and T e⊥/T e‖ are 0.7 and 0.9, respectively, predicting the plasma to be stable to whistler generation. Whistlers can be seen in Figures 2b–2e which show wavelet spectra of the fluctuating magnetic field in the frequency range 6–600 Hz. In order to detect whistlers, we only include points with high planarity and degree of polarization (>0.5). The wave between the vertical dashed lines exhibits increased intensity between 0.1f ce (solid white curve) and 0.5f ce (dashed white curve) (Figure 2b), and a right‐hand polarization (Figure 2c). Here, f ce = Ωce/(2π) is the electron cyclotron frequency. The wave vector is quasi‐parallel to B since the wave normal angle θ k with respect to B (Figure 2d) is smaller than 30°, and θ k < 10° where the fluctuations are the most intense. Figure 2e shows the direction of the Poynting flux, S ‖, computed by the singular value decomposition method (Santolík et al., 2003). It reverses at 11:29:12 (between the solid black lines), which means that waves propagating both parallel and anti‐parallel to B are detected. Given the frequency of 0.1–0.5f ce, right‐hand polarization and small θ k, the observed waves are consistent with whistler‐mode waves.
Figure 2.
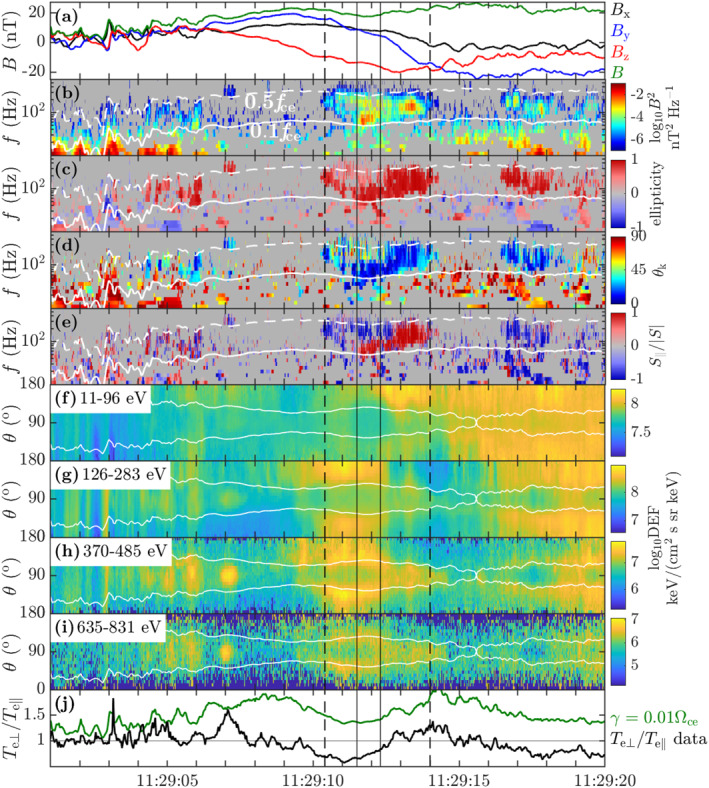
Observation of whistler waves together with the electron butterfly distribution. (a) Magnetic field vector B and magnitude B. (b)–(e) Magnetic field wavelet spectra: (b) power, (c) ellipticity, (d) wave normal angle θ k, (e) Poynting flux direction S ‖/|S|. (f)–(i) Electron pitch‐angle evolution in four different energy ranges. (j) Electron temperature anisotropy T e⊥/T e‖ (black); whistler instability threshold (Equation 1, green). Vertical lines: wave observation interval (dashed); interval used for the electron distribution in Section 3 (solid).
During this interval, B (Figure 2a) rotates as B y changes sign, and B reaches a local minimum (17.5 nT at 11:29:12 compared to 22 nT at the dashed lines). The velocity of this structure was estimated to be ∼80(−0.9, 0.5, 0) km/s, applying the timing method (Harvey, 1998) on the B y reversal at 11:29:13. The spatial scale of the B minimum is therefore estimated to be 3.6 s × 80 km/s ≈ 290 km which corresponds to ∼4d i (d i ≈ 81 km is the ion inertial length).
Figures 2f–2i show the electron differential energy flux as a function of pitch‐angle for four different energy ranges. In the thermal energy range (see Figure 2f), an anti‐parallel electron beam is observed at 11:29:13, seen in the enhancement at θ = 180°. When the whistlers are observed (between the vertical dashed lines), the distribution has the so‐called butterfly shape, defined by local minima for θ = 0°, 90°, and 180° (West Jr. et al., 1973), in the higher energy ranges (Figures 2h and 2i). We compute the non‐Maxwellianity ϵ, as defined in Graham et al. (2021), where ϵ ranges from 0 to 1 with ϵ = 0 corresponding to a perfect bi‐Maxwellian. In their work, based on ∼85 million electron distributions measured in different regions of the magnetosphere, it has been found that statistically ϵ depends on the plasma density. In our case we obtain ϵ ≈ 0.16 during the wave observation, which is in the top part of the statistically observed range considering that n e ≈ 8 cm−3. The distribution in Figures 2h and 2i also depends on B, as the maximum occurs for lower θ (close to 0° and 180°) at the B minimum at 11:29:12 but approaches higher θ further from the B minimum. The white curves show the trapping angle θ tr, defined by sin2 θ tr = B/B max, where B max = 27 nT is the maximum value of B taken at 11:29:15.6. In a magnetic bottle, particles with pitch‐angles above θ tr are reflected by an increasing magnetic field and become trapped in the B minimum (Yao et al., 2018). Trapping has been proposed as one of the mechanisms responsible for the butterfly distribution, which we discuss in Section 4. We note that the pitch‐angle evolution in Figures 2h and 2i approximately follows the shape of θ tr. Figure 2j shows that T e⊥/T e‖ < 1, far below the whistler instability threshold for γ = 0.01Ωce. Thus, in Figure 2 we observe whistler waves together with the butterfly distribution in a local B minimum, where the whistler instability threshold is not exceeded.
We identify 27 similar events across the interval, the centers of which are marked with vertical orange lines in Figure 1. In these events, whistler waves are observed in local dips of B simultaneously with butterfly‐shaped electron distribution functions. These dips correspond to different structures, such as current sheets or magnetic holes. For the purpose of our analysis, the type of B minimum is not crucial, and the characterization of the different types of structures is beyond the scope of this study. The duration for each event was between 1 and 5.5 s, with an average of 2 s. Summary plots of all 27 events are provided in the Supporting Information S1.
Figure 3a shows the distribution of β e‖ and T e⊥/T e‖ in the Q ‖ MSH during the one‐hour interval from Figure 1, together with the whistler instability thresholds (Equation 1) corresponding to growth rates γ/Ωce = 0.01 (solid green curve) and 0.10 (dashed green curve). More than half (54%) of the data points have β e‖ ranging between 0.2 and 1 and T e⊥/T e‖ between 0.7 and 1. Few points (0.3%) exceed the γ/Ω ce = 0.01 threshold, which suggests that the whistler instability plays a role in shaping the electron distribution function.
Figure 3.
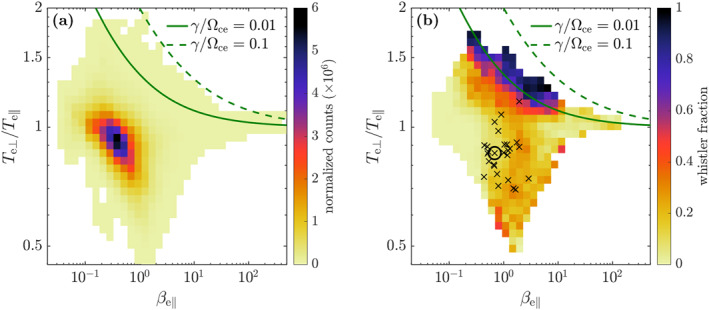
(a) Distribution of β e‖ and T e⊥/T e‖ (counts scaled with bin size). (b) Fraction of data points where whistler waves are observed. The green curves show the whistler instability threshold (Equation 1) for growth rates γ/Ω ce = 0.01 (solid) and 0.10 (dashed). Black crosses indicate when the butterfly‐shaped electron distribution was observed simultaneously with whistler waves. The circle marks the example in Figure 2.
We search for whistler waves by performing wavelet analysis on the entire interval and applying the following criteria: ellipticity above 0.7 (right hand polarization), degree of polarization and planarity above 0.5, and θ k < 45°. The points in the magnetic field spectra meeting these criteria are then integrated over frequency between 0.1f ce and f ce to estimate the whistler wave power in each time step. Only wave powers above 10−4 nT2 are considered (the maximum value was ∼2 nT2). In Figure 3b, the fraction of data points meeting the whistler criteria is shown. For this comparison, the particle data were resampled to the time resolution of the wavelet. We observe a whistler fraction close to unity around the γ/Ωce = 0.01 threshold (green solid curve in Figure 3b), which is expected for bi‐Maxwellian distributions. In the data points exceeding the threshold, whistler wave activity is observed 73% of the time, with an average power of 0.05 nT2. Remarkably, whistler waves are also observed below the threshold in 14% of the time, with the average power 0.01 nT2, comparable with the wave power in the data points exceeding the threshold.
The black crosses in Figure 3b mark T e⊥/T e‖ and β e‖ averaged over the duration of each of the 27 events identified by the vertical orange lines in Figure 1, and the black circle represents the event in Figure 2. For all these events, we recall that the butterfly shape in the electron pitch‐angle distribution is observed simultaneously with whistler waves. We note that these data points tend to be far from the whistler instability thresholds. In summary, Figure 3 shows that the electron temperature anisotropy is limited by the whistler instability and that, despite the lower amplitude, the presence of whistlers is significant even in regions predicted stable by the linear theory.
3. Modeling the Whistler Growth
In this section we demonstrate that the butterfly‐shaped electron distribution in Figure 2 is unstable to whistler waves. The measured phase space density is shown as a function of θ in Figure 4a (solid curves), and has been averaged over the interval 11:29:11.5–11:29:12.3 (vertical solid black lines in Figure 2), where we note that T e⊥/T e‖ (Figure 2j) is far below the whistler instability threshold.
Figure 4.
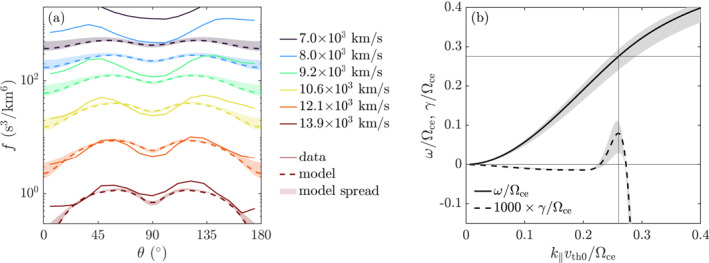
WHAMP model and result. (a) Measured pitch‐angle distribution (solid) and model distribution (dashed). (b) Whistler‐mode frequency ω (solid) and growth rate γ (dashed). The shaded regions in both figures show variation in the input for the model distribution and the resulting range of frequencies and growth rate.
To analyze the stability of this distribution, we use the numerical dispersion solver Waves in Homogeneous, Anisotropic, Multicomponent Plasmas (WHAMP) (Rönnmark, 1982). Since WHAMP only takes bi‐Maxwellian distributions as input, we construct a butterfly shape by subtracting two bi‐Maxwellians f par, f perp from an isotropic Maxwellian f 0 with density n 0 = 5.04 cm−3 and temperature T 0 = 62 eV. The subtracted distributions had densities n par = 2.1 cm−3 and n perp = 0.84 cm−3, f par had T e⊥/T e‖ = 0.73 with T e‖ = 66 eV and f perp had T e⊥/T e‖ = 2.5 with T e⊥ = 66 eV. The parameters were chosen manually by visual comparison with the measured distribution. In cyclotron resonance, the particles interacting with the waves satisfy the resonance condition, v ‖ = v ph − Ωce/k ‖ (Treumann & Baumjohann, 1997). For our case, this only happens for v > 10 × 103 km/s (see Section 4). Therefore, when matching the distributions, we focused on getting a good agreement above this value. The full model distribution f = f 0 − f par − f perp, shown with dashed curves in Figure 4a is used as input in the WHAMP solver.
WHAMP gives the angular frequency ω and growth rate γ as a function of a two‐dimensional wave vector k = (k ‖, k ⊥). For the case analyzed here, γ is largest for wave vectors parallel to B . Figure 4b therefore shows the dispersion relation for k ⊥ = 0. We find that γ (dashed) is positive for 0.23 ≤ k ‖ v th0/Ωce ≤ 0.27 (where ), and reaches its maximum at k ‖max = 0.26Ωce/v th0, indicated by the vertical line, where ω (solid curve) is ω max = 0.27Ωce (horizontal line). With B = 17.9 nT (averaged over the interval), this corresponds to a frequency of 138 Hz. The phase velocity is v ph = ω max/k ‖max = 4.7 × 103 km/s. We estimate the frequency observed in the spacecraft frame through 2πf obs = ω + k ⋅ V i, using the average ion velocity V i = (−209, −180, 125) km/s as plasma bulk velocity and assuming that the wave vector is parallel or anti‐parallel to B = (9.05, 6.53, −13.9) nT. We then find that the observed frequencies should be f obs+ = 130 Hz for parallel and f obs− = 146 Hz for anti‐parallel propagation. These estimations fall within the range of the observations (50–200 Hz) in Figure 2b.
The shaded regions in Figure 4a represent small variations in the model distribution, varying the slope at lower pitch‐angles. The resulting ranges of ω and γ are shown with shaded regions in Figure 4b, where the largest γ comes from the distribution with the largest slope. We find that the observed butterfly distribution is indeed unstable to whistler waves, and that changes in input parameters for the particle distributions still give wave growth consistent with observations.
To investigate whether the electron beam observed at 11:29:13 in Figure 2f could contribute to the whistler wave growth, we also modeled this distribution in WHAMP. The results, which are given in the Supporting Information S1, show that the beam is not associated with whistler wave generation.
4. Discussion
In this work, we have analyzed whistler waves in the Earth's MSH downstream of a Q ‖ shock. We observed that whistler wave activity can occur both in regions predicted to be unstable to the temperature anisotropy instability, as well as in regions predicted to be stable. Our focus has been on the generation of whistler waves which cannot be explained by the temperature anisotropy instability. We found that when such waves are observed the electron velocity distributions often exhibit the butterfly shape, characterized by minima at pitch‐angles 0°, 90°, and 180°. During a one‐hour interval we observed 27 such events with the average duration 2 s.
Within a source region whistler waves are generally expected to propagate away from the source, so for quasi‐parallel whistlers this implies propagation both parallel and anti‐parallel to the magnetic field direction (Y. Zhang et al., 1998). The observed reversal of the Poynting flux in Figure 2e indicates such propagation in both directions, and is therefore consistent with observation of a wave source region. This is further supported by the results of the WHAMP solver (Figure 4), where we found that a model distribution mimicking the one measured by MMS is unstable to generation of whistlers with characteristics close to the ones observed by MMS. Considering the Doppler shift, the parallel‐to‐ B waves are expected to have a lower measured frequency than the anti‐parallel ones. This is consistent with the observed Poynting flux (Figure 2e). We also confirmed using WHAMP that the electron beam observed at 11:29:13 (see Figure 2f) is not associated with whistler generation. In addition, beam generated whistlers are expected to be very oblique (An et al., 2016), which is not consistent with the observed small wave normal angle (see Figure 2d). Hence, we conclude that the electron butterfly distribution is likely the source of the observed whistler waves.
The WHAMP model predicts the highest growth at ω max ∈ (0.24, 0.30)Ωce (see Figure 4b), where the spread in frequency comes from the variations we introduced in the model distribution to account for the observed variations. Consequently, the cyclotron resonance condition is satisfied for |v ‖| ∈ (10, 15) × 103 km/s. Since the particle flux drops significantly with increasing energy, there are more electrons available to contribute to wave growth at small v ⊥, namely with θ close to 0° and 180°. To achieve a positive growth rate, the slope in the pitch‐angle distribution f must satisfy tan θ ∂ θ f > 0 (Kennel & Petschek, 1966). The butterfly distribution in Figure 4a has the required slope for θ < 45° and θ > 135°. The minimum at θ = 90° leads to reduction of T e⊥ (and thus of T e⊥/T e‖), but does not contribute to the wave growth. A bi‐Maxwellian distribution with T e⊥ > T e‖ lacks the 90° minimum and therefore it has the slope required for wave growth at all pitch angles; all electrons meeting the resonance condition can give energy to the wave. In the butterfly distribution the required slope exists only for pitch‐angles close to 0° and 180°. This could mean that the butterfly distribution generates weaker waves than a bi‐Maxwellian since a smaller portion of the electron population contributes to wave growth. This is consistent with the lower average whistler wave power observed for small T e⊥/T e‖ in Figure 3.
The origin of the butterfly distributions has been studied in previous works through theory and observations. Yao et al. (2018) analyzed mechanisms responsible for such distributions observed inside mirror modes in the Q ⊥ MSH. They explained the minima at low θ by trapping of electrons with θ tr < θ < 180° − θ tr in the mirror structure of a local B minimum. The minimum at θ = 90° was attributed to a combination of betatron cooling and Fermi deceleration, conserving the first and second adiabatic invariants as the mirror mode grows deeper. Since in our case, the observed pitch‐angle evolution in Figures 2h and 2i is approximately limited by θ tr, we consider it as a signature of the electrons being trapped in the B minimum. The existence of electrons outside this limit can be attributed to pitch‐angle scattering from the interaction with the whistler waves. The origin of the minimum at θ = 90° depends on the time evolution of B and could be different in our B minimum observed in Figure 2 compared to the mirror modes studied by Yao et al. (2018). In the Q ‖ MSH, mirror modes are less common, and the B minima causing the butterfly distributions can come from other processes such as current sheets and discontinuities which are characteristic for this MSH geometry.
The concept of the electron butterfly distribution generating MSH whistlers has recently been explored in cases of large‐scale magnetic minima. Kitamura et al. (2020) observed whistlers inside mirror modes of size ∼2,600 km ≈ 43d i in the Q ⊥ MSH, and simultaneously observed butterflies which they identified as the source of the waves. H. Zhang et al. (2021) found whistler waves generated by electron butterfly distributions inside a magnetic hole of size ∼2,400 km ≈ 26d i close to the magnetopause. These previous reports have mainly been focused on the Q ⊥ MSH, where magnetic minima (of size tens of ion inertial lengths) due to mirror modes are common. The size of the magnetic minimum we observe (Figure 2a) is ∼300 km ≈ 4d i, which is significantly smaller than what has previously been observed. To our knowledge, this is the first report on this phenomenon in the highly non‐stationary Q ‖ MSH, showing that electron butterfly distributions generating whistler waves are not limited to the ones related to magnetic holes, or mirror modes in the Q ⊥ MSH.
5. Conclusions
We analyzed MMS observations during a one‐hour interval in the Q ‖ MSH and we found that the whistler temperature anisotropy instability shapes the electron velocity distributions via pitch‐angle scattering. We observed whistler wave activity both in regions predicted to be unstable (high‐β e‖ and high‐T e⊥/T e‖ plasmas), as well as in regions predicted to be stable. In the regions which are predicted to be stable, the electron pitch‐angle distributions often have a butterfly shape, with minima both parallel and perpendicular to the background magnetic field. By comparing observations with the results of the kinetic solver WHAMP, we demonstrated that butterfly‐shaped distribution functions can be unstable to whistler wave growth and that only the θ = 0° and 180° minima of the distribution contribute to wave growth. In addition, we find that butterfly‐shaped distribution functions are observed in local minima of the magnetic field having spatial scales of a few ion inertial lengths. Previously, whistler generation associated with butterfly‐shaped distributions has only been reported for much broader magnetic minima of mirror modes in the case of Q ⊥ MSH geometry.
Our results underline the importance of considering the complete 3D particle distribution function to advance our understanding of wave‐particle interactions. Temperature anisotropy is an averaged quantity only unambiguously defined for bi‐Maxwellian distributions, and the moments derived from an arbitrary distribution can give an anisotropy of unity even when the distribution is far from stable. Wave growth occurs in a much broader area in parameter space than it is predicted by the temperature anisotropy instability.
Supporting information
Supporting Information S1
Acknowledgments
The authors thank the entire MMS team and instrument PI:s for data access and support. Thank you to Daniel Graham for helpful discussions. This work is supported by the Swedish Research Council Grant 2016‐0550 and the Swedish National Space Agency Grant 158/16. EY is supported by the Swedish National Space Agency Grant 145/18. GC is supported by the European Research Council Consolidator Grant 682068‐PRESTISSIMO. YK is supported by the Swedish Research Council Grant 2016‐05507.
Svenningsson, I. , Yordanova, E. , Cozzani, G. , Khotyaintsev, Yu. V. , & André, M. (2022). Kinetic generation of whistler waves in the turbulent magnetosheath. Geophysical Research Letters, 49, e2022GL099065. 10.1029/2022GL099065
Data Availability Statement
Magnetospheric multiscale data are available at https://lasp.colorado.edu/mms/sdc/public/data/ following the directories: mms#/fgm/brst/l2 for FGM data, mms#/scm/brst/l2 for SCM data, mms#/edp/brst/l2 for EDP data, mms#/fpi/brst/l2/dis‐dist for FPI ion distributions, mms#/fpi/brst/l2/dis‐moms for FPI ion moments, mms#/fpi/brst/l2/des‐dist for FPI electron distributions, and mms#/fpi/brst/l2/des‐moms for FPI electron moments. Data analysis was performed using the IRFU‐Matlab analysis package. No new data has been produced as part of this project.
References
- Ahmadi, N. , Wilder, F. D. , Ergun, R. E. , Argall, M. , Usanova, M. E. , Breuillard, H. , et al. (2018). Generation of electron whistler waves at the mirror mode magnetic holes: MMS observations and pic simulation. Journal of Geophysical Research: Space Physics, 123(8), 6383–6393. 10.1029/2018JA025452 [DOI] [Google Scholar]
- An, X. , Van Compernolle, B. , Bortnik, J. , Thorne, R. M. , Chen, L. , & Li, W. (2016). Resonant excitation of whistler waves by a helical electron beam. Geophysical Research Letters, 43(6), 2413–2421. 10.1002/2015GL067126 [DOI] [Google Scholar]
- Balogh, A. , Schwartz, S. J. , Bale, S. D. , Balikhin, M. A. , Burgess, D. , Horbury, T. S. , et al. (2005). Cluster at the bow shock: Introduction. Space Science Reviews, 118(1–4), 155–160. 10.1007/s11214-005-3826-1 [DOI] [Google Scholar]
- Baumjohann, W. , Treumann, R. A. , Georgescu, E. , Haerendel, G. , Fornacon, K.‐H. , & Auster, U. (1999). Waveform and packet structure of lion roars. Annales Geophysicae, 17(12), 1528–1534. 10.1007/s00585-999-1528-9 [DOI] [Google Scholar]
- Breuillard, H. , Le Contel, O. , Chust, T. , Berthomier, M. , Retino, A. , Turner, D. L. , et al. (2018). The properties of lion roars and electron dynamics in mirror mode waves observed by the magnetospheric multiscale mission. Journal of Geophysical Research: Space Physics, 123(1), 93–103. 10.1002/2017JA024551 [DOI] [Google Scholar]
- Burch, J. , Moore, T. , Torbert, R. , & Giles, B. (2016). Magnetospheric multiscale overview and science objectives. Space Science Reviews, 199(1–4), 5–21. 10.1007/s11214-015-0164-9 [DOI] [Google Scholar]
- Cattell, C. , Breneman, A. , Dombeck, J. , Short, B. , Wygant, J. , Halekas, J. , et al. (2021). Parker solar probe evidence for scattering of electrons in the young solar wind by narrowband whistler‐mode waves. The Astrophysical Journal Letters, 911(2), L29. 10.3847/2041-8213/abefdd [DOI] [Google Scholar]
- Dimmock, A. P. , Osmane, A. , Pulkkinen, T. I. , & Nykyri, K. (2015). A statistical study of the dawn‐dusk asymmetry of ion temperature anisotropy and mirror mode occurrence in the terrestrial dayside magnetosheath using themis data. Journal of Geophysical Research: Space Physics, 120(7), 5489–5503. 10.1002/2015JA021192 [DOI] [Google Scholar]
- Ergun, R. E. , Tucker, S. , Westfall, J. , Goodrich, K. A. , Malaspina, D. M. , Summers, D. , et al. (2016). The axial double probe and fields signal processing for the MMS mission. Space Science Reviews, 199(1–4), 167–188. 10.1007/s11214-014-0115-x [DOI] [Google Scholar]
- Fuselier, S. A. (1994). Suprathermal ions upstream and downstream from the Earth’s bow shock. In Solar wind sources of magnetospheric ultra‐low‐frequency waves (pp. 107–119). American Geophysical Union (AGU). 10.1029/GM081p0107 [DOI] [Google Scholar]
- Gary, S. P. , & Wang, J. (1996). Whistler instability: Electron anisotropy upper bound. Journal of Geophysical Research, 101(A5), 10749–10754. 10.1029/96JA00323 [DOI] [Google Scholar]
- Graham, D. B. , Khotyaintsev, Y. V. , André, M. , Vaivads, A. , Chasapis, A. , Matthaeus, W. H. , et al. (2021). Non‐Maxwellianity of electron distributions near earth’s magnetopause. Journal of Geophysical Research: Space Physics, 126(10), e2021JA029260. 10.1029/2021JA029260 [DOI] [Google Scholar]
- Harvey, C. C. (1998). Spatial gradients and the volumetric tensor. In Paschmann G. & Daly P. W. (Eds.), Analysis methods for multi‐spacecraft data (pp. 307–322). ESA/ISSI. [Google Scholar]
- He, J. , Duan, D. , Wang, T. , Zhu, X. , Li, W. , Verscharen, D. , et al. (2019). Direct measurement of the dissipation rate spectrum around ion kinetic scales in space plasma turbulence. The Astrophysical Journal, 880(2), 121. 10.3847/1538-4357/ab2a79 [DOI] [Google Scholar]
- Hietala, H. , Laitinen, T. V. , Andréeová, K. , Vainio, R. , Vaivads, A. , Palmroth, M. , et al. (2009). Supermagnetosonic jets behind a collisionless quasiparallel shock. Physical Review Letters, 103(24), 245001. 10.1103/PhysRevLett.103.245001 [DOI] [PubMed] [Google Scholar]
- Huang, S. Y. , Du, J. W. , Sahraoui, F. , Yuan, Z. G. , He, J. S. , Zhao, J. S. , et al. (2017). A statistical study of kinetic‐size magnetic holes in turbulent magnetosheath: MMS observations. Journal of Geophysical Research: Space Physics, 122(8), 8577–8588. 10.1002/2017JA024415 [DOI] [Google Scholar]
- Huang, S. Y. , Sahraoui, F. , Yuan, Z. G. , Contel, O. L. , Breuillard, H. , He, J. S. , et al. (2018). Observations of whistler waves correlated with electron‐scale coherent structures in the magnetosheath turbulent plasma. The Astrophysical Journal, 861(1), 29. 10.3847/1538-4357/aac831 [DOI] [Google Scholar]
- Huang, S. Y. , Xu, S. B. , He, L. H. , Jiang, K. , Yuan, Z. G. , Deng, X. H. , et al. (2020). Excitation of whistler waves through the bidirectional field‐aligned electron beams with electron temperature anisotropy: MMS observations. Geophysical Research Letters, 47(14), e2020GL087515. 10.1029/2020GL087515 [DOI] [Google Scholar]
- Huang, S. Y. , Yuan, Z. G. , Sahraoui, F. , Fu, H. S. , Pang, Y. , Zhou, M. , et al. (2017). Occurrence rate of whistler waves in the magnetotail reconnection region. Journal of Geophysical Research: Space Physics, 122(7), 7188–7196. 10.1002/2016JA023670 [DOI] [Google Scholar]
- Kennel, C. F. , & Petschek, H. E. (1966). Limit on stably trapped particle fluxes. Journal of Geophysical Research, 71(1), 1–28. 10.1029/JZ071i001p00001 [DOI] [Google Scholar]
- Khotyaintsev, Y. V. , Cully, C. M. , Vaivads, A. , André, M. , & Owen, C. J. (2011). Plasma jet braking: Energy dissipation and nonadiabatic electrons. Physical Review Letters, 106(16), 165001. 10.1103/PhysRevLett.106.165001 [DOI] [PubMed] [Google Scholar]
- Kitamura, N. , Omura, Y. , Nakamura, S. , Amano, T. , Boardsen, S. A. , Ahmadi, N. , et al. (2020). Observations of the source region of whistler mode waves in magnetosheath mirror structures. Journal of Geophysical Research: Space Physics, 125(5), e2019JA027488. 10.1029/2019JA027488 [DOI] [Google Scholar]
- Le Contel, O. , Leroy, P. , Roux, A. , Coillot, C. , Alison, D. , Bouabdellah, A. , et al. (2016). The search‐coil magnetometer for MMS. Space Science Reviews, 199(1–4), 257–282. 10.1007/s11214-014-0096-9 [DOI] [Google Scholar]
- Li, L. Y. , Yu, J. , Cao, J. B. , Yang, J. Y. , Li, X. , Baker, D. N. , et al. (2017). Roles of whistler mode waves and magnetosonic waves in changing the outer radiation belt and the slot region. Journal of Geophysical Research: Space Physics, 122(5), 5431–5448. 10.1002/2016JA023634 [DOI] [Google Scholar]
- Lin, N. , Kellogg, P. , Macdowall, R. , Balogh, A. , Forsyth, R. , Phillips, J. , et al. (1995). Observations of plasma waves in magnetic holes. Geophysical Research Letters, 22(23), 3417–3420. 10.1029/95GL03266 [DOI] [Google Scholar]
- Lindqvist, P.‐A. , Olsson, G. , Torbert, R. , King, B. , Granoff, M. , Rau, D. , et al. (2016). The spin‐plane double probe electric field instrument for MMS. Space Science Reviews, 199(1–4), 137–165. 10.1007/s11214-014-0116-9 [DOI] [Google Scholar]
- Masood, W. , Schwartz, S. J. , Maksimovic, M. , & Fazakerley, A. N. (2006). Electron velocity distribution and lion roars in the magnetosheath. Annales Geophysicae, 24(6), 1725–1735. 10.5194/angeo-24-1725-2006 [DOI] [Google Scholar]
- Mourenas, D. , Artemyev, A. V. , Agapitov, O. V. , Krasnoselskikh, V. , & Mozer, F. S. (2015). Very oblique whistler generation by low‐energy electron streams. Journal of Geophysical Research: Space Physics, 120(5), 3665–3683. 10.1002/2015JA021135 [DOI] [Google Scholar]
- Oka, M. , Wilson, L. B. W., III , Phan, T. D. , Hull, A. J. , Amano, T. , Hoshino, M. , et al. (2017). Electron scattering by high‐frequency whistler waves at Earth’s bow shock. The Astrophysical Journal, 842(2), L11. 10.3847/2041-8213/aa7759 [DOI] [Google Scholar]
- Papitashvili, N. E. , & King, J. H. (2020). Omni hourly data. NASA Space Physics Data Facility. 10.48322/1shr-ht18 [DOI] [Google Scholar]
- Plaschke, F. , Hietala, H. , & Vörös, Z. (2020). Scale sizes of magnetosheath jets. Journal of Geophysical Research: Space Physics, 125(9), e2020JA027962. 10.1029/2020JA027962 [DOI] [Google Scholar]
- Pollock, C. J. , Moore, T. E. , Jacques, A. D. , Burch, J. L. , Gliese, U. , Saito, Y. , et al. (2016). Fast plasma investigation for magnetospheric multiscale. Space Science Reviews, 199(1–4), 331–406. 10.1007/s11214-016-0245-4 [DOI] [Google Scholar]
- Rönnmark, K. (1982). Whamp – waves in homogeneous, anisotropic, multicomponent plasmas (KGI Report No. 179). Kiruna Geophysical Institute. [Google Scholar]
- Russell, C. T. , Anderson, B. J. , Baumjohann, W. , Bromund, K. R. , Dearborn, D. , Fischer, D. , et al. (2016). The magnetospheric multiscale magnetometers. Space Science Reviews, 199(1–4), 189–256. 10.1007/s11214-014-0057-3 [DOI] [Google Scholar]
- Santolík, O. , Parrot, M. , & Lefeuvre, F. (2003). Singular value decomposition methods for wave propagation analysis. Radio Science, 38(1), 10‐1–10‐13. 10.1029/2000RS002523 [DOI] [Google Scholar]
- Smith, E. J. , Holzer, R. E. , & Russell, C. T. (1969). Magnetic emissions in the magnetosheath at frequencies near 100 hz. Journal of Geophysical Research, 74(11), 3027–3036. 10.1029/JA074i011p03027 [DOI] [Google Scholar]
- Smith, E. J. , & Tsurutani, B. T. (1976). Magnetosheath lion roars. Journal of Geophysical Research, 81(13), 2261–2266. 10.1029/JA081i013p02261 [DOI] [Google Scholar]
- Stawarz, J. E. , Eastwood, J. P. , Phan, T. D. , Gingell, I. L. , Pyakurel, P. S. , Shay, M. A. , et al. (2022). Turbulence‐driven magnetic reconnection and the magnetic correlation length: Observations from magnetospheric multiscale in Earth’s magnetosheath. Physics of Plasmas, 29(1), 012302. 10.1063/5.0071106 [DOI] [Google Scholar]
- Stone, R. , Macdowall, R. , Fainberg, J. , Kaiser, M. , Desch, M. , Goldstein, M. , et al. (1995). Ulysses radio and plasma wave observations at high southern heliographic latitudes. Science, 268(5213), 1026–1029. 10.1126/science.268.5213.1026 [DOI] [PubMed] [Google Scholar]
- Treumann, R. A. , & Baumjohann, W. (1997). Electromagnetic instabilities. In Advanced space plasma physics (Vol. 5). Imperial College Press. 10.1142/p020 [DOI] [Google Scholar]
- Vaivads, A. , Santolík, O. , Stenberg, G. , André, M. , Owen, C. J. , Canu, P. , & Dunlop, M. (2007). Source of whistler emissions at the dayside magnetopause. Geophysical Research Letters, 34(9). 10.1029/2006GL029195 [DOI] [Google Scholar]
- Vörös, Z. , Yordanova, E. , Echim, M. M. , Consolini, G. , & Narita, Y. (2016). Turbulence‐generated proton‐scale structures in the terrestrial magnetosheath. The Astrophysical Journal, 819(1), L15. 10.3847/2041-8205/819/1/l15 [DOI] [Google Scholar]
- West, H. I., Jr. , Buck, R. M. , & Walton, J. R. (1973). Electron pitch angle distributions throughout the magnetosphere as observed on OGO 5. Journal of Geophysical Research, 78(7), 1064–1081. 10.1029/JA078i007p01064 [DOI] [Google Scholar]
- Yao, S. T. , Shi, Q. Q. , Liu, J. , Yao, Z. H. , Guo, R. L. , Ahmadi, N. , et al. (2018). Electron dynamics in magnetosheath mirror‐mode structures. Journal of Geophysical Research: Space Physics, 123(7), 5561–5570. 10.1029/2018JA025607 [DOI] [Google Scholar]
- Yao, S. T. , Shi, Q. Q. , Yao, Z. H. , Li, J. X. , Yue, C. , Tao, X. , et al. (2019). Waves in kinetic‐scale magnetic dips: MMS observations in the magnetosheath. Geophysical Research Letters, 46(2), 523–533. 10.1029/2018GL080696 [DOI] [Google Scholar]
- Yao, S. T. , Wang, X. G. , Shi, Q. Q. , Pitkänen, T. , Hamrin, M. , Yao, Z. H. , et al. (2017). Observations of kinetic‐size magnetic holes in the magnetosheath. Journal of Geophysical Research: Space Physics, 122(2), 1990–2000. 10.1002/2016JA023858 [DOI] [Google Scholar]
- Yordanova, E. , Vörös, Z. , Raptis, S. , & Karlsson, T. (2020). Current sheet statistics in the magnetosheath. Frontiers in Astronomy and Space Sciences, 7, 2. 10.3389/fspas.2020.00002 [DOI] [Google Scholar]
- Zhang, H. , Zhong, Z. , Tang, R. , Deng, X. , Li, H. , & Wang, D. (2021). Modulation of whistler mode waves by ultra‐low frequency wave in a macroscale magnetic hole: MMS observations. Geophysical Research Letters, 48(22), e2021GL096056. 10.1029/2021GL096056 [DOI] [Google Scholar]
- Zhang, Y. , Matsumoto, H. , & Kojima, H. (1998). Lion roars in the magnetosheath: The Geotail observations. Journal of Geophysical Research, 103(A3), 4615–4626. 10.1029/97JA02519 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1
Data Availability Statement
Magnetospheric multiscale data are available at https://lasp.colorado.edu/mms/sdc/public/data/ following the directories: mms#/fgm/brst/l2 for FGM data, mms#/scm/brst/l2 for SCM data, mms#/edp/brst/l2 for EDP data, mms#/fpi/brst/l2/dis‐dist for FPI ion distributions, mms#/fpi/brst/l2/dis‐moms for FPI ion moments, mms#/fpi/brst/l2/des‐dist for FPI electron distributions, and mms#/fpi/brst/l2/des‐moms for FPI electron moments. Data analysis was performed using the IRFU‐Matlab analysis package. No new data has been produced as part of this project.


