Can In Vitro In Vivo Extrapolation (IVIVE) Be Successful? Recognizing the Incorrect Clearance Assumptions

Abstract

For a number of years, our laboratory has been investigating the underlying reasons for the published poor in vitro in vivo extrapolation (IVIVE) predictability of human clearance both from a theoretical and from an experimental perspective. Here, we critically examine clearance concepts and commonly-employed IVIVE approaches, concluding that there is no theoretical reason that IVIVE should work, just as it does not. Our analysis, however, has identified 10 misconceptions and/or poorly understood aspects of clearance that are listed in the Conclusion section of this manuscript. Chief among these are that all published human drug clearance values are arterial clearances, clearance calculated as organ blood flow multiplied by the extraction ratio is the arterial clearance of the organ of elimination (and not the published drug clearance value) and that the well-stirred model equation taught in all pharmacokinetic courses that relates organ blood flow, fraction unbound in blood and intrinsic clearance has no validity. We further list 10 Conclusions relating to the IVIVE process. The primary IVIVE-related conclusions are that the intrinsic clearance value determined from an in vitro incubation is an arterial intrinsic clearance, there is no theoretical basis upon which an arterial intrinsic clearance can be related to a whole-body arterial clearance to accomplish IVIVE, there are no published data demonstrating that in vitro intrinsic metabolic clearance can predict in vivo organ clearance as IVIVE assumes, and the scientific basis for the hypothesized albumin mediated hepatic uptake phenomenon is invalid. We further propose three IVIVE process recommendations.

INTRODUCTION

For the past 6 years our laboratory has been focused on understanding the explanation for the poor in vitro in vivo extrapolation (IVIVE) predictability of hepatic clearance both from theoretical and from experimental evaluations. Correct and accurate prediction of human pharmacokinetic characteristics of a new chemical entity (NCE) is a critical aspect of the drug development process. Of primary importance in drug development is prediction of human drug clearance, which will determine the drug exposure in a patient and relates to both efficacy and toxicity of an NCE. The IVIVE process is employed to predict hepatic clearance, where characteristics of an in vitro incubation of the NCE with human hepatocytes or microsomes are scaled-up to predict those characteristics in an intact human. The IVIVE process utilizes a model of hepatic elimination that includes measures of blood flow to the organ of elimination, fraction of drug unbound in the systemic circulation and a measure of the intrinsic ability of the liver to eliminate drug independent of organ blood flow and protein binding. It is this intrinsic elimination measure that is scaled-up from the in vitro hepatocyte and microsome studies as we recently reviewed¹. However, IVIVE is not sufficiently successful, with only about 1/3^rd of human drug hepatic clearance being predicted within 2-fold of measured human drug clearance values^2,3. During these past 6 years, our laboratory has published 16 papers, addressing a multitude of issues, slowly peeling the onion-like problem, recognizing today that the failure of IVIVE is due primarily to theoretical issues and realizing now that our laboratory, in good part, may be responsible for the failure of the IVIVE process. In this manuscript, we attempt to demonstrate to the reader why this is true.

DEFINING HUMAN DRUG CLEARANCE

Clearance is the fundamental parameter in pharmacokinetics that is a measure of the rate of drug elimination divided by the systemic exposure driving that elimination⁴. It is defined at steady-state from the equality of rate in = rate out, with its equivalence in drug dosing as dosing rate equal to the steady-state systemic concentration (C_ss) multiplied by clearance (CL). Therefore, for steady-state drug dosing

$$CL=\frac{DosingRate}{C_{ss}}$$ (1)

Clearance may also be defined for a single dose as the amount that reaches the systemic circulation intact divided by the systemic exposure driving that elimination (AUC, area under the systemic concentration time curve). Therefore, for an intravenous bolus dose, over all time, zero to infinity

$$CL=\frac{Dose}{{AUC}_{0-\mathrm{\infty }}}$$ (2)

For a drug following linear pharmacokinetics, calculated clearance by Eq. 1 should equal clearance calculated by Eq. 2.

For the IVIVE process depicted in Fig. 1, an intrinsic clearance (CL_int) value is determined by measuring the elimination of the drug in the in vitro human hepatocyte or microsome incubation mixture, which is then scaled up to whole-body values in terms of the hepatocellularity per gram of liver tissue or the microsomal protein per gram of liver, respectively for hepatocyte and microsome incubations, and corrected for gram liver per kg of body weight, to determine a predicted whole-body intrinsic clearance. This whole-body intrinsic clearance is then inserted into an equation believed to predict organ hepatic clearance, such as the hypothesized well-stirred model (Eq. 3) in Fig. 1, which includes the organ blood flow (Q_H), the fraction unbound in blood (f_u,B) and the fraction unbound in the in vitro incubation mixture (f_u,inc) as presented by Obach⁵. Equation 3 is then used to predict the drug hepatic clearance (CL_H) that would be expected for Eqs. 1 or 2 in humans.

Figure 1.

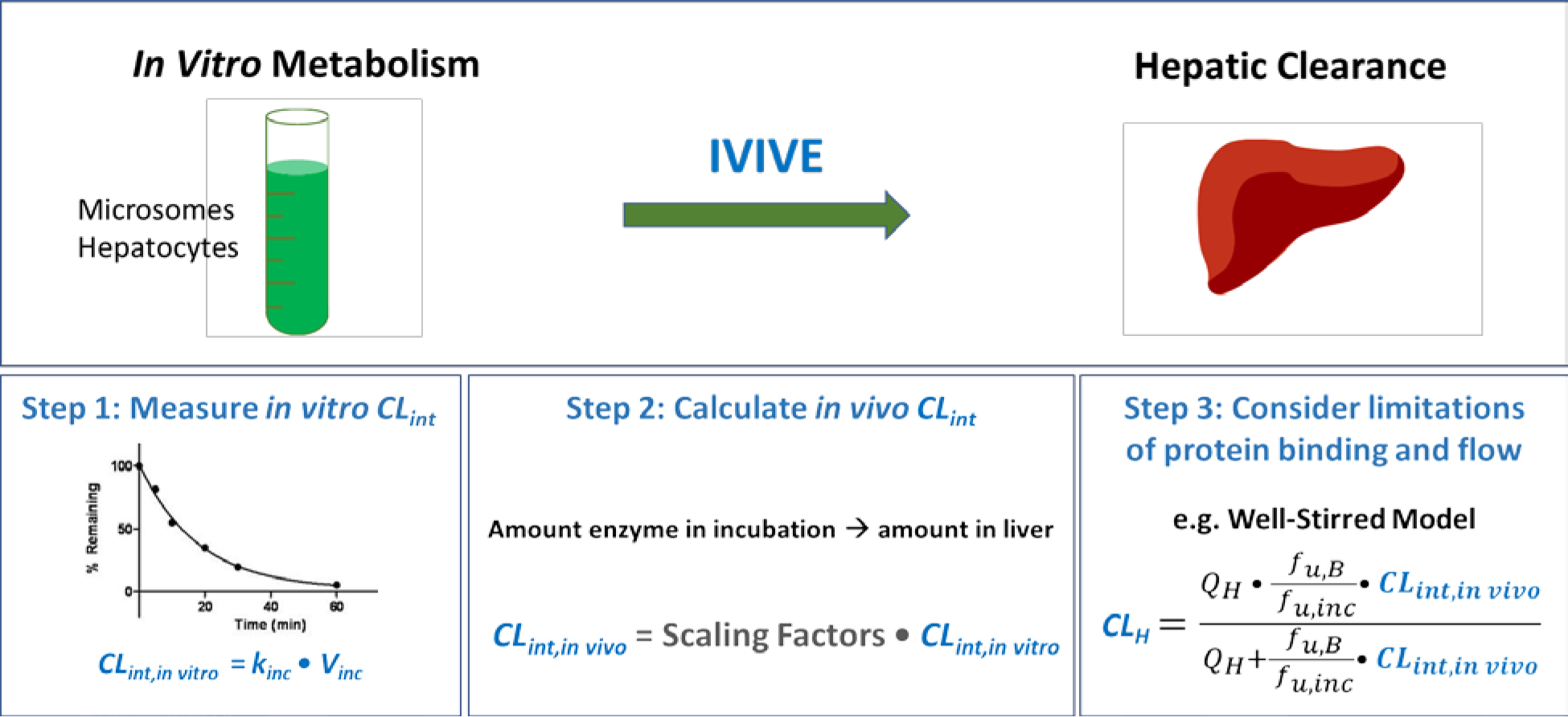
In vitro-in vivo extrapolation (IVIVE) scheme where an in vitro incubation of hepatocytes or microsomes allows determination of the half-life of drug elimination and an estimate of the in vitro drug intrinsic clearance (CL_int), which is then scaled up to whole organism liver intrinsic clearance. This value is then inserted into an equation representing a model of hepatic elimination, here the purported well-stirred model incorporating whole organism liver blood flow (Q_H) and fraction unbound in blood (f_u,B), with correction for fraction unbound in the incubation mixture (f_u,inc), to predict an in vivo liver clearance (CL_H).

$${CL}_H=Q_H·\frac{\frac{f_{u,B}}{f_{u.inc}}·{CL}_{int}}{Q_H+\frac{f_{u,B}}{f_{u.inc}}·{CL}_{int}}$$ (3)

WHAT CONCENTRATIONS ARE BEING MEASURED IN EQUATIONS 1 AND 2?

Here we encounter the first issue concerning the relevance of the IVIVE approach that is not well recognized by our field. Figure 2 depicts a physiologically based pharmacokinetic model (PBPK) where each of the organs in the body that can affect systemic drug concentrations and/or is relevant for pharmacodynamic outcomes is depicted. We will assume initially here that liver elimination is the only excretory process of relevance in the PBPK model. If as done originally by Bischoff and colleagues in one of the papers introducing the PBPK model⁶, hepatic elimination is acharacterized by the well-stirred model of organ elimination. However, in measuring systemic concentrations for Eqs. 1 and 2, we do not measure the exit concentration from the liver (C_{H, out}) depicted in Fig. 2. Rather, in determining clearance from Eqs. 1 and 2 we measure a venous concentration that is better represented as the whole-body venous concentration (C_{venous, whole-body}) shown in Fig. 2, the venous concentration entering the lungs. That is, the parameter we measure in calculating human venous clearance by either Eqs. 1 or 2, is the blend of concentrations exiting the organ of elimination and the concentrations exiting the non-eliminating organs, which at steady-state will of course be greater than the concentration coming out of the organ of elimination alone, especially for high extraction ratio (ER) drugs. Therefore, over all time, the average measured venous concentration will be greater than the average venous concentration coming out of the liver, (C_{venous measured} > C_{H, out}), while over all time the integrated concentrations exiting non-eliminating organs will equal the integrated concentrations entering, and thus the clearance values published in the literature will be less that the clearance for the eliminating organ, (CL_{Eqs. 1&2} < CL_{Elim Organ}), especially for high ER drugs. However, although IVIVE utilizes Eq. 3 to predict the whole-body clearance (when hepatic elimination is the only route of elimination), the equation does not theoretically predict whole-body clearance. Thus, to be more explicit, clearance is determined by Eqs. 1 or 2 in humans by measuring venous concentrations, for example from an arm vein, and these are concentrations of drug after the elimination/reaction has occurred. However, IVIVE has been predicated on predicting organ of elimination clearance, but the clearance values in the literature are not the organ of elimination clearances, they are the whole-body clearance, which are a result of concentrations coming from organs of elimination blended with concentrations coming from non-eliminating organs.

Figure 2.

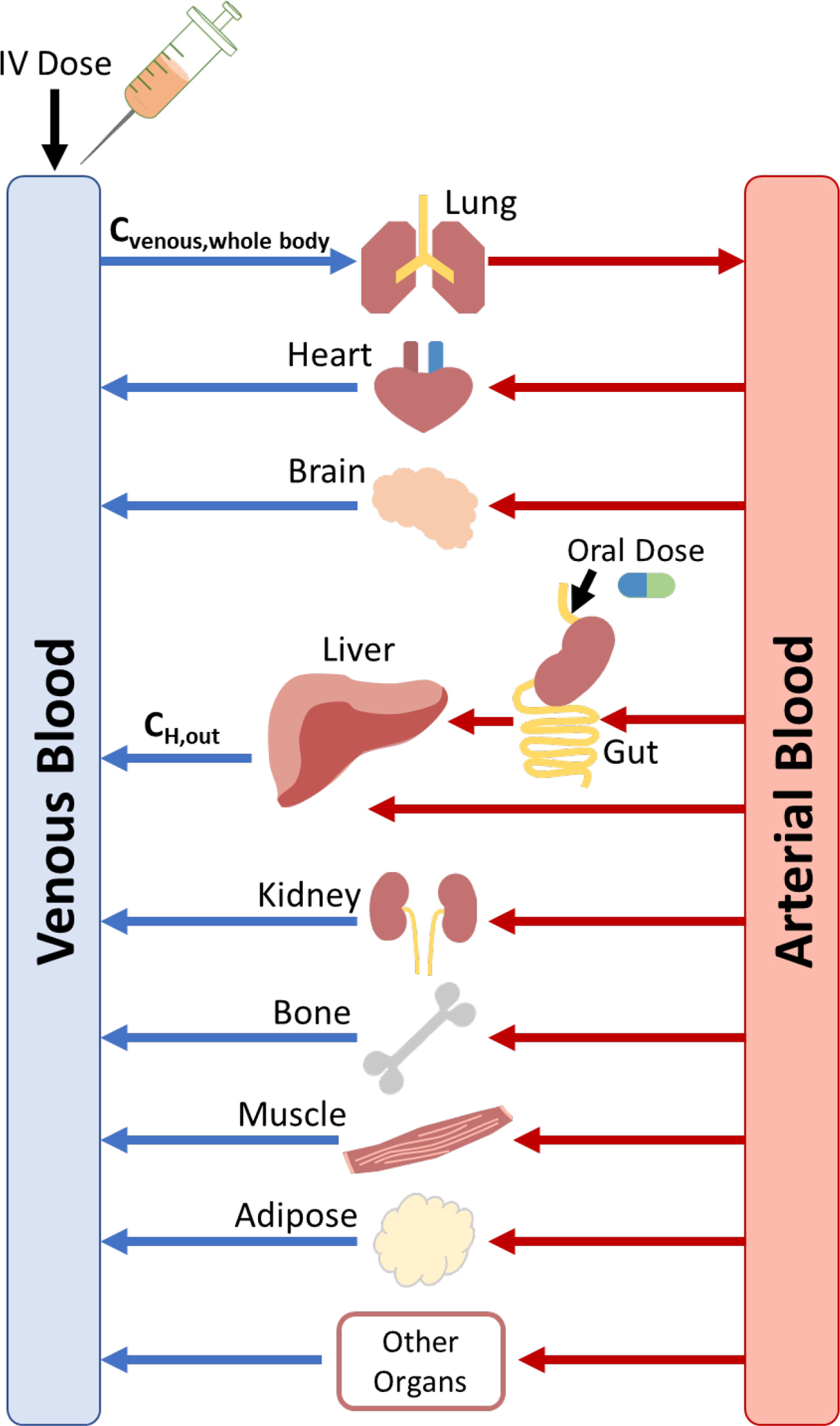
Physiologic based pharmacokinetic (PBPK) model depicting the exit concentration from the liver (C_{H, out}) and the whole-body venous concentration (C_{venous, whole-body}).

THE GREAT MAJORITY OF PUBLISHED HUMAN CLEARANCE VALUES ARE ARTERIAL CLEARANCES

In fact, the blended venous concentration going into the lung will closely approximate the arterial concentration coming out of the lung (if there is no lung or cardiac elimination, which is true for the great majority of human drugs). That is, the venous concentrations that are measured clinically are a close approximation of the arterial concentration driving elimination. Thus, the published human clearance values for Eq. 2 (and Eq. 1) are

$${CL}_{arterial}=\frac{Dose}{{AUC}_{0-\mathrm{\infty },venous}}$$ (4)

Since this arterial clearance is a whole-body parameter, the relevant blood flow limiting this value is cardiac output, not blood flow to elimination organs.

Clearance is defined in terms of where and how we measure the concentration driving elimination. If we measure in blood, then we determine blood clearance; if we measure in plasma, we determine plasma clearance; if we measure unbound concentrations, we determine unbound clearance. Human pharmacokinetic clearance values listed in the literature are measured as venous concentrations, and pharmacokinetic dose adjustments are usually based on changes in this measured clearance. But let’s examine a 1973 study in dogs with lidocaine where the authors did measure arterial concentrations. Figure 3 reproduced from the 1973 study of Branch et al.⁷ depicts the steady-state infusion of lidocaine and the measurements made. Readers will be familiar with this study since it was the first to show that changing hepatic blood flow by concomitant administration of propranolol would change the clearance of the high ER drug lidocaine. But for our purposes here, we will initially only consider the pre-propranolol steady-state measurements. The authors calculated the in vivo pharmacokinetic clearance using Eq. 1: the steady-state dosing rate (the amount lost) divided by the exposure driving that elimination (here the steady state arterial concentration).

Figure 3.

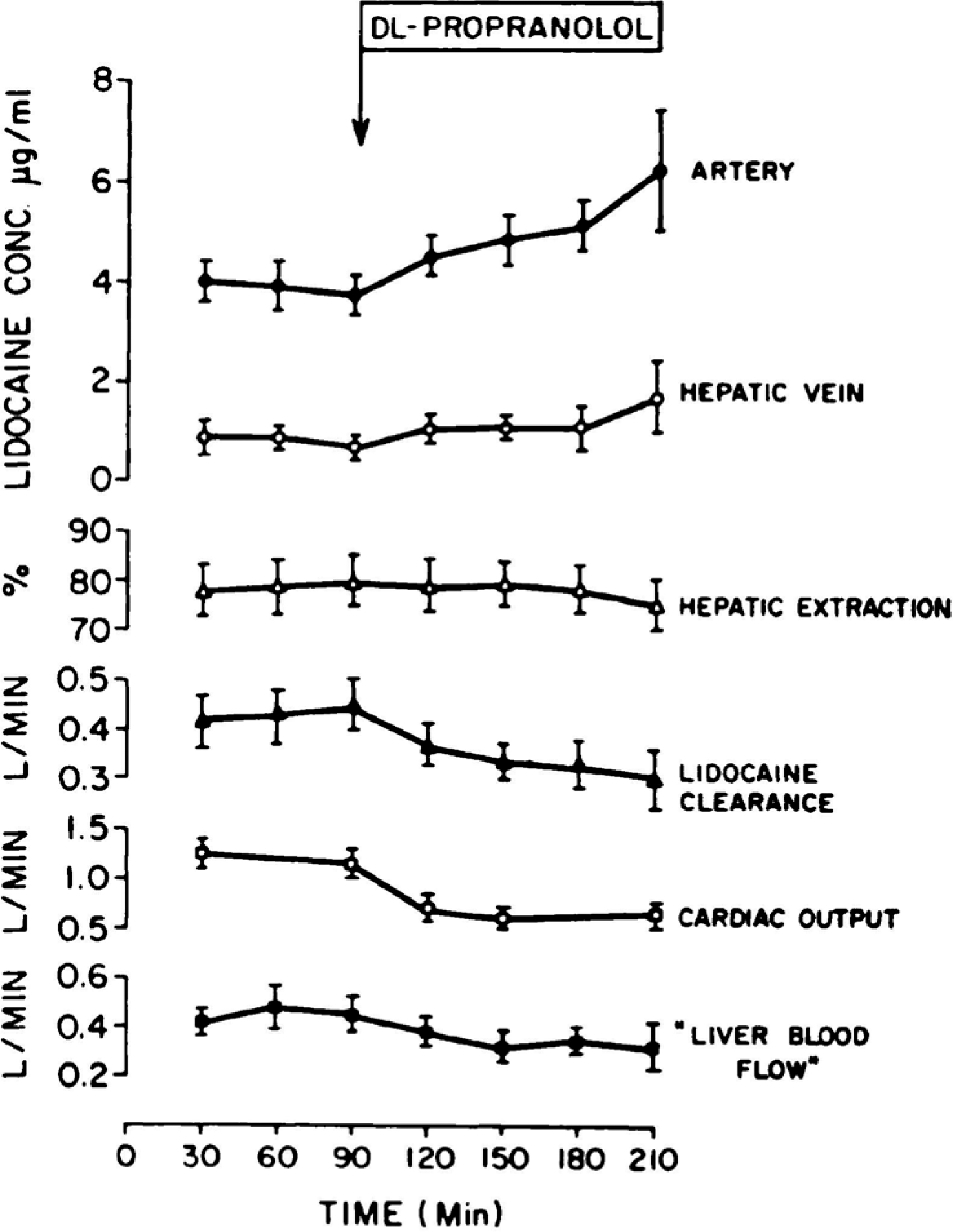
The effect of dl-propranolol on the disposition of lidocaine under steady-state conditions. Each point represents the mean ± S.E. for 6 dogs⁷.

$${CL}_{arterial}=\frac{{DosingRate}_{ss}}{C_{ss,arterial}}=\frac{0.14\frac{mg}{min·kg}·12.12kg}{3.92\mu g/ml}=433\frac{ml}{min}=35.7\frac{ml}{min·kg}$$

The dosing rate (0.14 mg/min kg), the average steady-state arterial concentration (3.92 μg/ml) and the average arterial clearance (433 ml/min) are stated in the paper, we inserted the average weight for the 6 dogs studied. Branch et al.⁷ also depicted the average lidocaine venous plasma concentration time curve following a 30 mg/kg i.v. bolus dose as depicted here in Fig. 4. Branch et al. did not calculate the lidocaine clearance for this data, but it can easily be done using Eq. 2.

Figure 4.

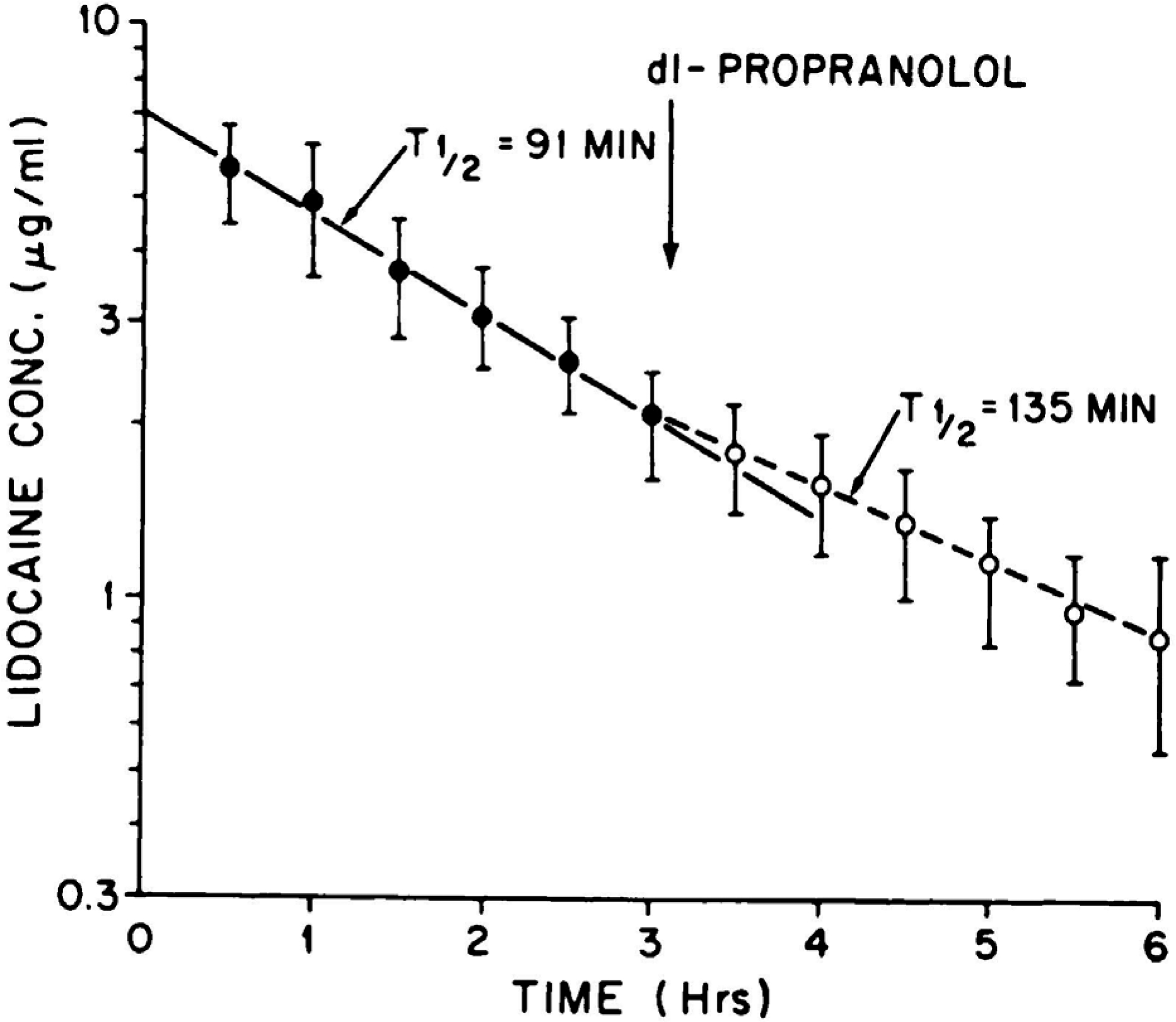
Plasma concentrations of lidocaine (30 mg/kg i.v.) before (solid circles) and after (open circles) 0.5 mg/kg of propranolol i.v. Each point represents the mean ± S.E. for 5 dogs⁷.

$${CL}_{i.v.Bolus}=\frac{Dose}{{AUC}_{0-\mathrm{\infty },venous}}=\frac{\frac{30mg}{kg}}{\frac{\frac{7\mu g}{ml}}{\frac{0.693}{91min}}}=32.6\frac{ml}{min·kg}$$

The AUC_0−∞ for a one-compartment model can be approximated by dividing the initial concentration by the rate constant of elimination. The initial concentration (7 μg/ml) can be estimated from the y-axis intercept of this apparent one-compartment body model fit of the data, and the rate constant of elimination can be determined from the 91 min half-life. This 32.6 ml/min kg value is only 8.7% different than the steady-state arterial clearance of 35.7 ml/min kg calculated from the steady-state infusion data, independent of any measure of C_out. The relevance of these calculations is that both the determination of clearance using Eq. 1 measuring arterial concentrations at steady state and using Eq. 2 measuring venous concentrations following an i.v. bolus dose yield the same clearance value as hypothesized here, because both measurements are determining whole-body arterial clearance. A further example of the equivalence of clearance following arterial and venous sampling was demonstrated by Lee et al.⁸, who only observed a 6.6% difference in clearance of azosemide in rabbits following an i.v. bolus dose when calculated from venous versus arterial measurements.

Till now, we have not mentioned Eq. 5, the 1972 Rowland equation⁹

$${CL}_{Rowland}=Q_H·ER=Q_H·\frac{C_{in}-C_{out}}{C_{in}}$$ (5)

where C_in and C_out are the entering arterial and exiting venous concentrations in an isolated perfused organ study at steady-state, nor have we calculated lidocaine clearance using that equation, but that can be done now based on the Branch et al. data⁷.

$${CL}_{Eq.5}=Q_H·ER=532·0.786=418\frac{ml}{min}\mathrm{or}34.5\frac{ml}{min·kg}$$

The hepatic blood flow of 532 ml/min and the extraction ratio of 0.786 are reported in Branch et al.⁷

Clearance can also be calculated using Eq. 5 by utilizing the steady-state arterial and venous concentrations.

$${CL}_{Eq.5}=Q_H·\frac{C_{in}-C_{out}}{C_{in}}=532·\frac{3.92-0.73}{3.92}=433\frac{ml}{min}$$

As noted previously the steady-state arterial (C_in) concentration of 3.92 μg/ml was stated by Branch et al.⁷, but we estimated the steady-state venous (C_out) concentration of 0.73 μg/ml from Fig. 3. Therefore, there are slight differences in the average calculated clearance values, but overall, it is obvious that the Rowland Eq. 5 also calculates the arterial whole-body clearance.

Thus, there is no theoretical reason that IVIVE should work since the outcome of IVIVE is to predict the organ of elimination clearance. The IVIVE process cannot predict the clearances published in the literature, which should always differ from the in vivo organ of elimination clearances, especially for high extraction ratio drugs. Additionally, our analysis led to the recognition of a number of incorrect assumptions beyond IVIVE related to clearance, its calculation and its use in making predictions, as we now detail.

UNDERSTANDING MODELS OF HEPATIC ELIMINATION

If there is no theoretical reason that IVIVE should work, why did the field think it would, and further why did the field believe that different models of hepatic elimination could provide better predictions of IVIVE? What assumptions did we make about clearance for the past 50 years that may be incorrect? Since the pharmacokinetic models of hepatic elimination were based on concepts from chemical reaction engineering we contacted experts in this field from the Chemical and Biomolecular Engineering Department at the University of California, Berkeley. Our paper, with the Chemical Engineers, “There is Only One Valid Definition of Clearance: Critical Examination of Clearance Concepts Reveal the Potential for Errors in Clinical Drug Dosing Decisions” makes two major points⁴. First, of primary relevance to this manuscript, there is only one valid definition of clearance: the amount eliminated divided by the exposure driving that elimination, is consistent with Eqs. 1 and 2. But, this definition of clearance is not consistent with Eq. 5, if as proposed by Rowland and Pang¹⁰, C_in is only a reference concentration and not driving elimination. The second major point is that defining organ clearance based solely on systemic blood concentrations (e.g., AUC) can lead to drug dosing errors when drug effect sites reside either in an eliminating organ exhibiting incremental clearance (e.g., liver) or in a non-elimination organ where intraorgan concentration is governed by transporter actions (e.g., brain). This is an important issue for clinical pharmacologists and recommend reviewing our paper where we give several examples⁴.

Our Chemical Engineer colleagues markedly assisted us in understanding the basic principles of models of reaction chemical engineering and their translation to pharmacokinetic models as depicted in Fig. 5. As we note in the Supplementary Material to our 2021 paper⁴: “From a chemical reaction engineering point of view, as shown in Fig. 5, WSM (well-stirred model) corresponds to a well-mixed CSTR (continuous-stirred tank reactor), whereas PTM (parallel tube model) corresponds to a PFR (plug flow reactor) where only convective flow is considered. The notation here follows the common chemical reaction engineering notation. Consider the steady-state equation for a CSTR

$$Q{C}_{in}-Q{C}_{out}-k{VC}_{out}=0$$ (6)

which is a mass balance based on the assumption that the concentration is homogenous within the volume V of the reactor, and k is a first-order rate constant expressed in units of inverse time.”

Figure 5.

Chemical engineering reaction (pharmacokinetic) models at steady-state (logarithmic concentration on Y axis)⁴

To what should k V in the CSTR model of Chemical Engineering be converted in the well-stirred Pharmacokinetic model? The senior author of this paper, together with Professor Rowland and Dr. Graham, through a series of convoluted derivations¹¹ in 1973, concluded k V should be equivalent to a newly defined term CL_int multiplied by f_u,B

$$Q·C_{in}-Q·C_{out}={CL}_{int}·f_{u,B}·C_{out}$$ (7)

where the exiting concentration (C_out) was equal to the concentration throughout the reactor, and at steady-state the amount lost per unit time was equal to the intrinsic clearance, a flow independent parameter, multiplied by the unbound C_out (Eq. 7). Today, 48 years later, it is so easy to see the error we made. Unknowingly, we had set a flow dependent rate on the left-hand side of Eq. 7 equal to a flow independent rate on the right-hand side of Eq. 7. Rowland and Pang appear not to recognize in their publications that their construct of the well-stirred model can be simply described by Eq. 7 and that that they have set the k V term in the flow incorporating CSTR model of chemical engineering equal to a flow independent clearance in pharmacokinetics. There is no validity to Eq. 7. It is not the well-stirred model. And our field knows well to what the product k V is equivalent in pharmacokinetics, it is clearance, not intrinsic clearance. It is argued that Eq. 7 meets mass balance considerations¹⁰, but that is not an argument for validity since the correct well-stirred model clearance equation also meets mass balance criteria as given in Eq. 8

$$Q·C_{in}-Q·C_{out}={CL}_{H,WSM}·C_{out}$$ (8)

This is a critical point of this manuscript. The field, including Rowland and Pang in their publications, assume that the k V term in the CSTR Eq. 6 can be represented by a flow independent hypothetical intrinsic clearance as given in Eq. 7, even though the left side of Eq. 7 is a flow dependent relationship. In contrast, we believe that the k V term in the CSTR Eq. 6 should be represented by the flow dependent well-stirred model clearance, CL_H,WSM, as in Eq. 8. We maintain that Eq. 7 is an invalid WSM equation, while Eq. 8 is the valid WSM equation. Although the Eq. 7 relationship has been accepted for almost 50 years, we can see no justification or conceptual advantage for setting a flow dependent elimination equal to a flow independent elimination, while there are a number of disadvantages to this assumption, as we will detail.

But, we and the field made another big error. Until now, our laboratory assumed in our publications, even earlier this year⁴, that the Rowland Eq. 5 was the well-stirred model, and in 1973 Rowland, Benet and Graham¹¹ used this assumption, as we will detail subsequently, to derive what our entire field today believes is the general well-stirred model independent of the incubation fraction unbound in IVIVE (Eq. 3).

$$CL=Q_H·\frac{f_{u,B}·{CL}_{int}}{Q_H+f_{u,B}·{CL}_{int}}$$ (3)

(Equation 3 above differs from what was presented earlier as Eq. 3 since the equation here was believed to be the general theoretical basis of the WSM, while the earlier version that included the correction for protein binding in the incubation mixture was the application of the WSM to IVIVE prediction.) Why did our laboratory and many in the field believe this? To understand that, we must review the 1977 publication of Pang and Rowland¹² as represented in Fig. 6. Here the authors carried out isolated perfused rat liver (IPRL) studies with lidocaine, changing the hepatic blood flow from 10 ml/min to 12, 14, 16 ml/min and back and forth. Their excellent experimental work yielded the black dots in Fig. 6 when they plotted the ratio of C_out at varying flow rates to C_out at a flow rate of 10 ml/min. They presented two theoretical lines that they attributed to Models I and II, to which we have added the equations for the Model I and Model II lines. The following is a quote from the conclusion of the paper¹² deleting the references in the quote

Figure 6.

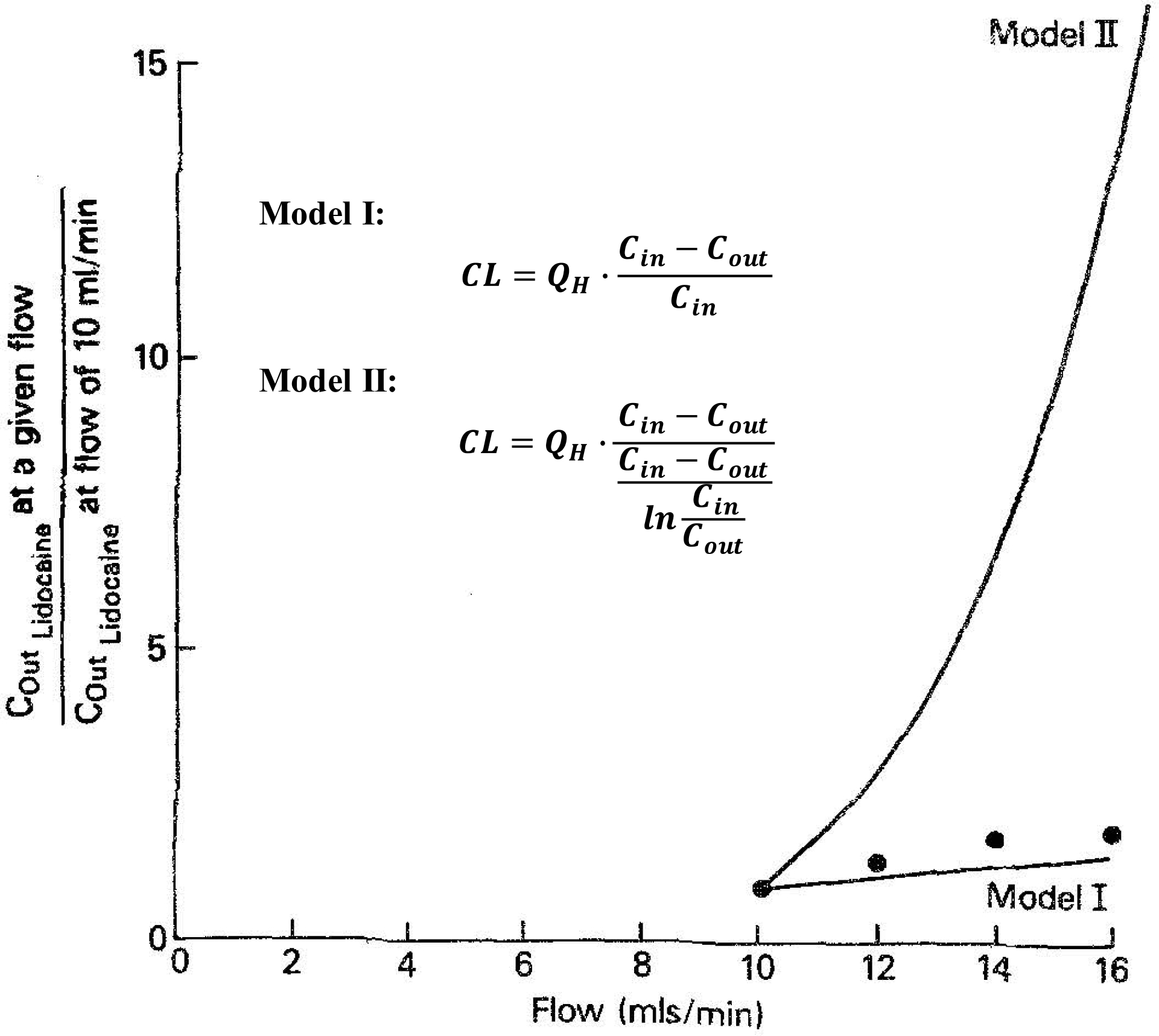
Plot of the predicted and the observed lidocaine concentrations in the effluent blood for models I and II when hepatic blood flow was changed from the control flow rate of 10 to 12, 14, and 16 ml/min per liver. The lines represent predicted data from models I and II, and the points represent observations¹².

“The portal vein, the hepatic artery, and the sinusoids are interconnected by both direct and obscure pathways. In this respect, the liver can be viewed operationally as a well-stirred compartment (model I), a situation analogous to a mixed reactor such that the exit stream (unbound drug concentration in emergent blood) has the same composition as the fluid within the reactor (unbound drug concentration in liver). A similar assumption exists in the models used by Kety and by Bischoff et al., in that the effluent drug concentration is assumed to be in equilibrium with that within the tissues. … An attempt to discriminate between two models of hepatic drug clearance has elucidated that the ‘well-stirred’ model is a better predictor of changes in clearance and in some other pharmacokinetic parameters with changes in hepatic blood flow.”

But there is no assumption in Eq. 5, i.e., model I in Fig. 6, that “the exit stream (unbound drug concentration in emergent blood) has the same composition as the fluid within the reactor (unbound drug concentration in liver)”. Measurement of the exit stream concentration is unnecessary to determine arterial clearance in Eq. 5, since Eq. 5 can also be written as

$$CL=Q_H·ER=Q_H·\frac{C_{in}-C_{out}}{C_{in}}=\frac{RateofElimination}{C_{in}}$$ (5a)

and the rate of elimination is equivalent to the rate of infusion at steady-state. Therefore, any steady-state isolated perfused organ study, either the study of Pang and Rowland¹² or the many published IPRL studies, as we recently reviewed¹³, must always be described by Eq. 5 if there are no methodological errors in carrying out the experimental measurements. And if the data from the isolated perfused organ studies do not correspond to Eq. 5, then those experimental outcomes cannot be trusted. Sodhi et al.¹³ identified a number of such highly cited unreliable studies. In fact, concordance with Eq. 5 is the “litmus test” for the validity of IPRL studies. More recently, Rowland and Pang did report¹⁰ that Eq. 5 was not the well-stirred model. Yet inexplicitly, when these authors try to define which hepatic model of organ elimination is consistent with IPRL steady-state studies, they continue to maintain that if the experimental data are consistent with Eq. 5, the data fit the well-stirred model.

Returning to Fig. 1, what is the theoretical basis of Eq. 3, the well-stirred model equation? What Rowland, Benet (an author of the current manuscript), Graham, Shand, Wilkinson did in 1973–75 ^{11, 14} was take Eq. 5, which they believed was the well-stirred model (but we now know is the arterial clearance equation) and set C_out/C_in in that equation equal to C_out/C_in in Eq. 7, believing it to also be the well-stirred model but which we now know is not the well-stirred model and is invalid, because it is not possible to have an equality between a term that is influenced by blood flow and a term that is not influenced by blood flow. After setting C_out/C_in in Eqs. 5 and 7 equal and rearranging, these authors presented the resulting relationship as Eq. 3, which we now know has no validity. However, Eq. 3 is the equation that today we teach all our students and fellows and by which we try to relate measures of in vitro elimination to measures of in vivo clearance published in the literature. Repeating again, the k V term in Eq. 6 is the well-stirred model clearance, which is a function of blood flow, and when multiplied by C_out gives the rate of elimination.

It is now apparent that the authors referenced above did not realize that a flow dependent elimination was being equated to a flow independent elimination, and an arterial clearance equated to a well-stirred model clearance. These errors, however, have led to a series of incorrect relationships between measured in vivo clearance determined by Eqs. 1 and 2 and the hypothesized organ clearance equations employed by our field and taught in all beginning pharmacokinetic courses for the past half-century. Of major importance is the recognition that it is not possible to calculate what we call intrinsic clearance from in vivo clearance studies. The reader can understand now, why at the end of the introductory paragraph, we acknowledge that “Our laboratory, in good part, may be responsible for the failure of the IVIVE process”.

It seems so simple and obvious; one cannot set an elimination rate that is dependent on blood flow equal to an elimination rate that is independent of blood flow, but apparently no one in pharmacokinetics or drug metabolism has recognized it prior to today. The correct relationships to define a metabolic clearance dependent on C_out measures are:

$$Q_H·C_{in}-Q_H·C_{out}={CL}_{art}·C_{in}={CL}_{WSM}·C_{out}$$ (8)

$$Q_H·C_{in}-Q_H·C_{out}={CL}_{art}·C_{in}={CL}_{PTM}·\frac{C_{in}-C_{out}}{ln\frac{C_{in·}}{C_{out}}}$$ (9)

$$Q_H·C_{in}-Q_H·C_{out}={CL}_{art}·C_{in}={CL}_{Disp}·C_{avg}$$ (10)

So that for each of the hepatic models of elimination, clearances will be different. We have previously pointed out that each of the models in Fig. 5 will exhibit different mean residence times for drug within the organ¹⁵, consistent with chemical engineering principles that all the reactors in Fig. 5 will exhibit different mean residence times within the reactor⁴, and therefore also consistent with the model clearances being different in Eqs. 8–10. The implications of the relationship between the rate of elimination and CL_PTM and CL_Disp were also presented by Kochak¹⁶. Returning to the 1973 paper of Branch et al.⁷ we can see the steady-state lidocaine measurements in Fig. 3 pre- and post- propranolol administration. Notice that although propranolol caused a 23% decrease in lidocaine clearance as reported by Branch et al.⁷ (third series of measurements from the bottom of Fig. 3), hepatic extraction ratio was unchanged (third series of measurements from the top on Fig. 3). We will return to this later. Pre-propanol for a steady-state lidocaine dosing rate of 0.14 mg/min kg the values are: hepatic artery concentration 3.92 μg/ml; hepatic vein concentration 0.73 μg/ml; liver blood flow 532 ml/min or 44.0 ml/min kg; lidocaine clearance 433 ml/min or 35.7 ml/min kg. Using Eq. 8 and the hepatic vein concentration we may now calculate the well-stirred model clearance

$${CL}_{WSM}=\frac{0.14\frac{mg}{min·kg}}{0.73\frac{\mu g}{ml}}=192\mathrm{m}\mathrm{l}/\mathrm{m}\mathrm{i}\mathrm{n}·\mathrm{k}\mathrm{g}$$

And from Eq. 9 and hepatic artery and hepatic vein concentration, we may now calculate the parallel tube model clearance

$${CL}_{PTM}=\frac{0.14\frac{mg}{min}/kg}{1.90\mu g/ml}=73.7ml/min·\mathrm{k}\mathrm{g}$$

The field believes that for a high clearance drug the calculated venous clearance will be much greater than the arterial clearance, as seen above. All the Branch et al.⁷ values are for plasma measurements. However, the Blood/Plasma ratio for lidocaine in all species is close to 1.0 (e.g., humans 0.91¹⁷; dogs 1.04¹⁸) so these plasma clearances can reasonably reflect blood clearance values. Then it becomes obvious that the well-stirred and parallel tube model clearance values exceed hepatic blood flow, which in the dog is reported between 30 and 50 ml/min kg. But this is not true for the arterial clearance (35.7 ml/min kg), which does not exceed hepatic blood flow (reported to be 44.0 ml/min kg in this study). It has not been generally recognized in the literature that for high hepatic extraction ratio drugs, organ clearance values dependent on venous concentration measurements will exceed liver blood flow. Table 1 demonstrates this principle. The numerical values in the table for extraction ratios varying from 0.05 to 0.95 must be multiplied by the hepatic blood flow to yield the clearance values for the arterial, parallel tube and well-stirred models of hepatic elimination. For the well-stirred model, the calculated hepatic clearance equals hepatic blood flow at an ER of 0.5 and exceeds hepatic blood flow for ERs greater than 0.5. For the parallel tube model, ER must reach 0.632 before calculated hepatic clearance equals hepatic blood flow. At an ER of 0.95 the calculated well-stirred model clearance is 19-fold greater than hepatic blood flow, while parallel tube clearance is 3-fold hepatic blood flow. Of course, arterial liver clearance can never exceed hepatic blood flow.

Table 1.

For varying extraction ratios, the values to be multiplied by hepatic blood flow to obtain clearances for arterial, parallel tube venous and well-stirred venous models

Extraction Ratio	Arterial CL $\frac{{\mathit{C}}_{\mathit{a}\mathit{r}\mathit{t}}-{\mathit{C}}_{\mathit{v}\mathit{e}\mathit{i}\mathit{n}}}{{\mathit{C}}_{\mathit{a}\mathit{r}\mathit{t}}}$	Parallel Tube Venous CL $\frac{{\mathit{C}}_{\mathit{a}\mathit{r}\mathit{t}}-{\mathit{C}}_{\mathit{v}\mathit{e}\mathit{i}\mathit{n}}}{\frac{{\mathit{C}}_{\mathit{a}\mathit{r}\mathit{t}}-{\mathit{C}}_{\mathit{v}\mathit{e}\mathit{i}\mathit{n}}}{\mathit{l}\mathit{n}\frac{{\mathit{C}}_{\mathit{a}\mathit{r}\mathit{t}}}{{\mathit{C}}_{\mathit{v}\mathit{e}\mathit{i}\mathit{n}}}}}$	Well-Stirred Venous CL $\frac{{\mathit{C}}_{\mathit{a}\mathit{r}\mathit{t}}-{\mathit{C}}_{\mathit{v}\mathit{e}\mathit{i}\mathit{n}}}{{\mathit{C}}_{\mathit{v}\mathit{e}\mathit{i}\mathit{n}}}$
0.05	0.050	0.051	0.053
0.10	0.100	0.105	0.111
0.30	0.300	0.357	0.429
0.50	0.500	0.693	1.000
0.632	0.632	1.000	1.72
0.70	0.700	1.20	2.33
0.90	0.900	2.30	9.00
0.95	0.950	3.00	19.0

Reviewing the lidocaine dog clearance values (arterial clearance 35.7, Rowland equation 34.5 from the Q_H ER values, parallel tube 73.7 and well-stirred 192 ml/min kg), it is obvious that the Rowland equation (Eq. 5 and Model I in Fig. 6) is an arterial clearance calculation, has no relationship with the well-stirred or parallel tube models, and can be calculated without ever measuring C_out concentrations as shown in Eq. 5a. The arterial clearance equation is model independent, as there is no dependence upon what happens within the organ of elimination and concentration measurements within the organ are unnecessary to obtain this arterial clearance value. Thus, the assumption that the field has made that this unchanged clearance can allow calculation of a model dependent intrinsic clearance is not valid. That is, the proposal of Rowland, Benet, Graham, Wilkinson and Shand^{11, 14} with respect to the well-stirred model is invalid:

$$CL=Q_H·\frac{C_{in}-C_{out}}{C_{in}}\ne Q_H·\frac{f_{u,B}·{CL}_{int}}{Q_H+f_{u,B}·{CL}_{int}}$$

The proposal of Pang and Rowland¹² with respect to the parallel tube model is invalid:

$$CL=Q_H·\frac{C_{in}-C_{out}}{C_{in}}\ne Q_H·\left(1-e^{-\frac{f_{u,B}·{CL}_{int}}{Q_H}}\right)$$

The proposal of Roberts and Rowland¹⁹ with respect to the dispersion model is invalid:

$$CL=Q_H\cdot \frac{C_{in}-C_{out}}{C_{in}}\ne Q_H\cdot (1-\frac{4a}{{(1+a)}^2\cdot e^{\frac{(a-1)}{2D_N}}-{(1-a)}^2\cdot e^{\frac{(a+1)}{2D_N}}})$$

where $=\sqrt{1+4D_N·R_N}$, D_N is the dispersion number, and $R_N=\frac{f_{u,B}·{CL}_{int}}{Q_H}$

Why would one believe that a model independent arterial clearance, which does not require knowledge of C_out, could be equivalent to any model dependent organ clearance that requires measurement of C_out? These nonequalities are consistent with the report of Sodhi et al.¹³ who found no experimental perfusion data that preferentially supported the dispersion and parallel tube models over Eq. 5, the left-hand side of the nonequality relationships above. In Fig. 6, Pang and Rowland¹² concluded that the lidocaine IPRL data was consistent with the well-stirred model (Model I) and not the parallel tube model (Model II), but their analysis had done nothing of the kind. What Fig. 6 confirms is the relationship above, the arterial clearance calculation cannot be used to determine the intrinsic clearance of the parallel tube model. All IPRL data must be consistent with Eq. 5, the arterial clearance relationship, or the experimental methods are flawed. There was no testing of the well-stirred model. However, the experimental data in Fig. 6 and the theoretical line for model I are consistent with the point raised previously with respect to the effect of propranolol as reported by Branch et al.⁷ As seen for the Fig. 6 experimental data, clearance increased 58.7% when blood flow increased 60%, i.e., from 10 ml/min to 16 ml/min, but extraction ratio remained unchanged (0.995 to 0.992). That is, for high ER drugs changes in clearance are driven almost exclusively by blood flow.

THE INVALIDITY OF THE ALBUMIN MEDIATED HEPATIC UPTAKE HYPOTHESIS AND THE LACK OF IVIVE RELEVANCE DUE TO HEPATIC ORGAN CLEARANCE MISREPRESENTATION

Here we address the unfortunate downstream consequences of not recognizing that a) what was falsely believed to be a well-stirred model clearance (Eq. 5) was actually an arterial clearance; b) the invalid assumption that the clearance determined by Eq. 5 could be taken as the clearance for the various models of hepatic elimination; and c) intrinsic clearance cannot be determined from in vivo studies. In 1981, Forker and Luxon²⁰ reported that the addition of albumin to an IPRL study with the high extraction ratio compound taurocholate did not decrease metabolism to the degree that would be expected just due to protein binding changes. They identified this new finding as an “albumin-facilitated uptake” phenomenon, and since that time a multitude of investigators have carried out innumerable studies to understand and predict how this may aid in IVIVE predictions, as we recently reviewed²¹. The results of their study are presented in Fig. 7 where Forker and Luxon examined the disappearance of radiolabeled taurocholate, a high ER compound, from a steady-state reservoir of cold taurocholate in a recirculating IPRL experiment. The open circles represent the disappearance of radiolabeled taurocholate in the presence of 0.5 g/dl albumin, while the solid circles depict the disappearance in the presence of a 10-fold higher, 5.0 g/dl, albumin. The dashed “Expected Rate of Loss” line was derived by Forker and Luxon believing that the rate of loss for the high ER compound taurocholate should be described by the dispersion model of hepatic elimination.

Figure 7.

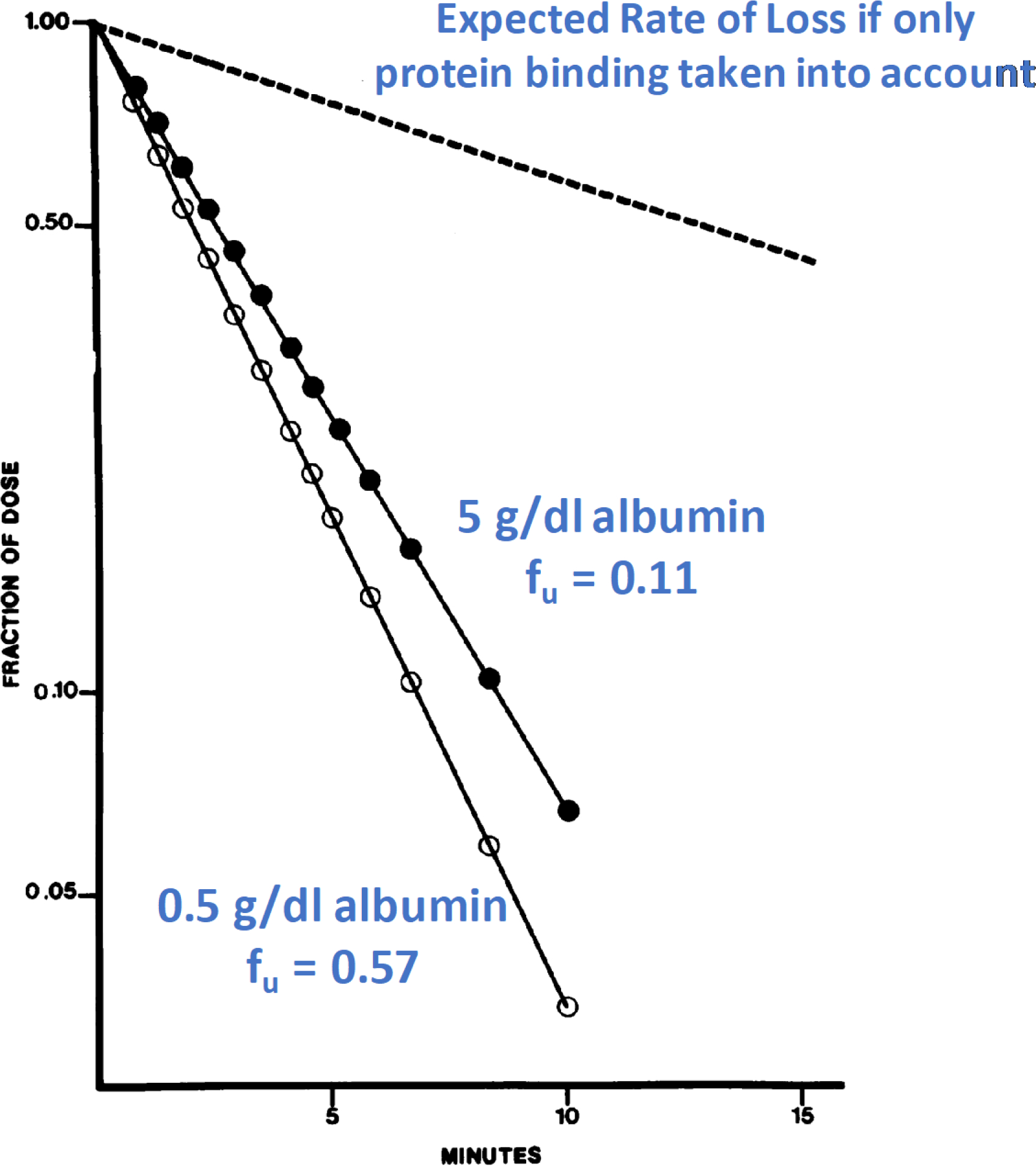
IPRL steady-state cold taurocholate studies depicting radioactive dose taurocholate disappearance curves obtained when perfusate albumin concentration was 0.5 g/dl (open circles) and 5.0 g/dl (solid circles). The broken line represents the predicted result for an albumin concentration of 5.0 g/dl based on the assumption that uptake is determined by the perfusate concentration of free bile salt utilizing a dispersion model of hepatic elimination²⁰.

A year later Coburn²² reanalyzed the data using the well-stirred model (Eq. 3) reporting that CL_int had only changed by 7% between the two albumin additions and that the data are ”consistent with, rather than divergent from, conventional pharmacokinetic theory and liver uptake can be predicted from free fraction in the perfusate.” In Forker and Luxon’s response²³ they “conclude that although Coburn’s analysis of the data appears to confirm a widely held preconception, it is physiologically irrelevant. His model simply does not describe a real liver.” This controversy has not been further addressed until today. The unnecessarily complicated Forker and Luxon presentation and the Coburn analysis exemplify the unsupported machinations our field has undertaken because of our false belief that intrinsic clearance can be determined from in vivo studies. Theoretically, unbound clearance should not change with the change in protein binding. For this study, the change in unbound clearance is 20%. Is this difference just experimental error or alternatively if the 20% difference is real, is there any clinical relevance to the finding? This analysis can be simply understood by recognizing that unbound clearance will be calculated as the product of the unbound volume of distribution and the rate constant for elimination. The change in protein binding will change the total volume of distribution but should not change the unbound volume of distribution. By normalizing each plot to fraction of dose as shown in Fig. 7, the authors have corrected for the change in volume of distribution and therefore the change in clearance is reflected by the change in rate constant, which here is 20%. Furthermore, the addition of albumin decreases the clearance, rather than enhancing clearance.

Forker and Luxon assumed that the results from an IPRL study can be described by a dispersion model, then concluded their data appeared to support an albumin-enhanced uptake outcome because their experimental data did not fit the dispersion model that they selected. But Forker and Luxon had not addressed the question of relevance: Has the addition of albumin changed the unbound drug clearance? The answer is 20% at most. Not recognizing that the Forker and Luxon analysis is based on this invalid assumption has been damaging to our field through the generation of unsupported studies and wasting of research dollars. The Forker and Luxon study does not support an albumin-mediated hepatic uptake phenomenon. Other recent analyses suggest that addition of albumin to in vitro incubation media provides only a minimal increase in IVIVE predictability.

INVALIDITY OF THE CLEARANCE EQUATION BASED ON THE EXTENDED CLEARANCE CONCEPT

As demonstrated above, the incorrect assumption of setting clearance of Eq. 5 equal to the clearance of Eq. 3 led to the derivation of Eq. 6, an invalid relationship, yet it is the equation that the field utilizes to predict IVIVE and that we teach all our students and fellows. It is not possible to derive a relationship between CL_{in vivo, measured}, CL_int and Q_H. Unless one incorporates these invalid assumptions, it is also not possible to derive a relationship between CL_{in vivo measured}, CL_{H,int,metabolic} (the intrinsic hepatic metabolic clearance), CL_{H,int,biliary} (the intrinsic hepatic biliary clearance) and PS_inf,int and PS_eff,int (the transporter influx and efflux intrinsic clearances, respectively) for the extended clearance model of organ elimination as shown in Fig. 8, as we summarized²⁴ from the extensive literature. There is no way to derive the equation relating measured in vivo clearance to these extended clearance model parameters, just as it is not possible to derive in vivo clearance in the simple well-stirred model in terms of the intrinsic clearance parameter and hepatic blood flow, unless arterial clearance does approximate well-stirred or parallel tube venous clearance. And when will this happen? Only for low extraction ratio drugs where, as seen in Table 1, it is not possible to differentiate an experimentally measurable difference between the clearances of the arterial and other models of hepatic elimination (see ER = 0.05 and 0.10 values). However, since the value IVIVE attempts to predict is the whole-body clearance calculated by Eqs. 1 or 2; even for low extraction ratio drugs will this be predicted by the intrinsic clearance multiplied by f_u,B?

Figure 8.

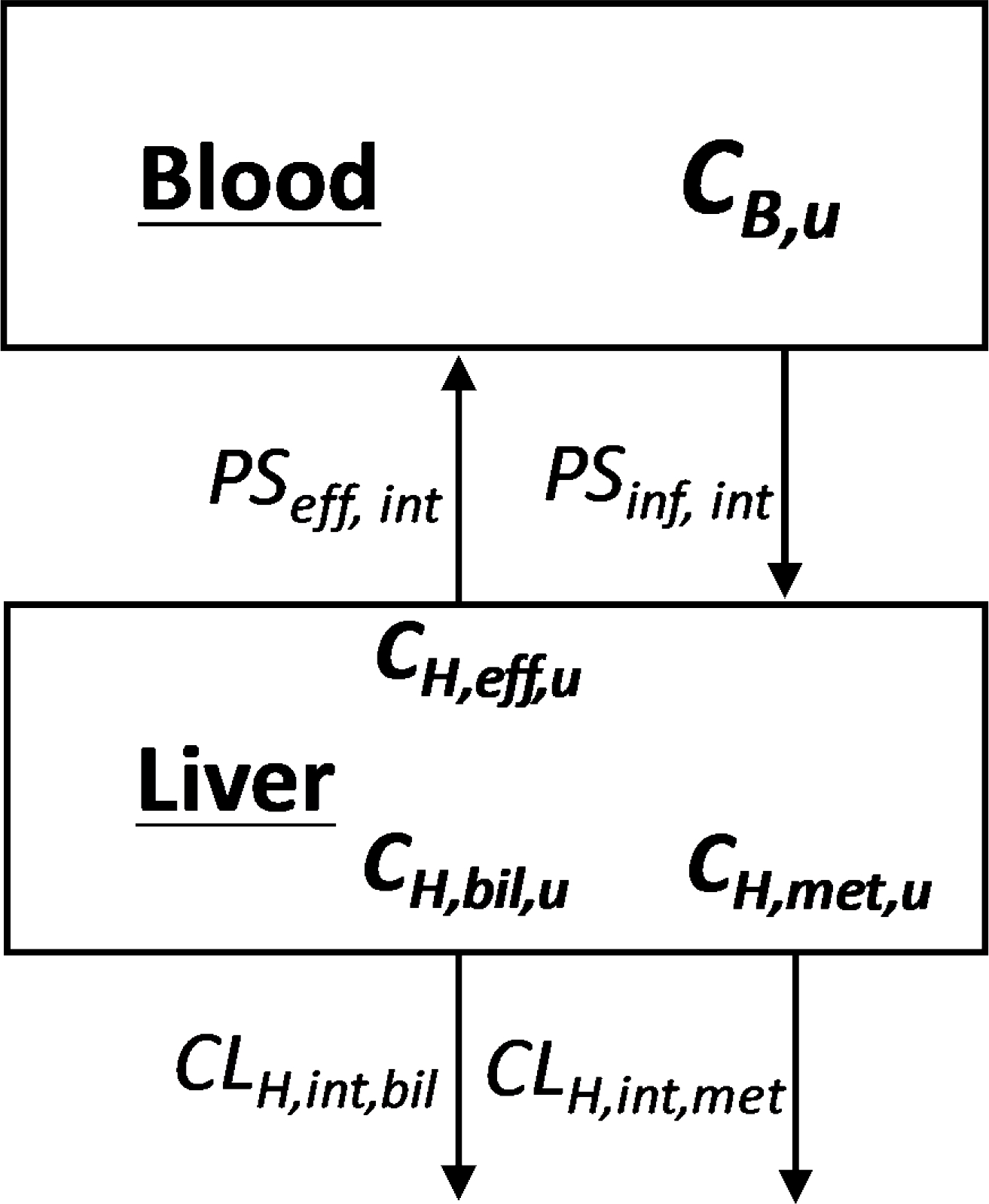
Schematic representation of blood and liver concentrations (C_B & C_H) in the extended clearance model where unbound concentrations (C_u) drive hepatic intrinsic metabolic (met), biliary (bil) and transporter efflux (eff) intrinsic clearances and blood transporter influx (inf) intrinsic clearance, as presented by Sodhi et al.²⁴

EVEN FOR LOW EXTRACTION RATIO DRUGS THE IN VITRO SCALED-UP INTRINSIC CLEARANCE MAY NOT PREDICT THE IN VIVO MEASURED CLEARANCE

As described previously in terms of Fig. 2, the PBPK model, the mixing of venous concentrations for the in vivo measurements that are made will not be equal to the in vivo venous concentration from the organ of elimination and this will be especially true as ER increases. Therefore, the in vitro scaled-up intrinsic clearance would not be expected to provide a good estimate of total body published clearance. However, in our review of the literature, the field does not even have evidence that the in vitro scaled-up intrinsic clearance will predict the in vivo organ of elimination clearance. To prove if this is true or to analyze the variability, one must evaluate for low extraction ratio compounds if scaled-up in vitro rat intrinsic clearance measurements with hepatocytes or microsomes will accurately predict in vivo isolated perfused rat liver clearances, that is, the organ clearance alone without the other in vivo organs modulating the measured concentrations. As far as we can tell from the literature this has never been adequately tested. However, there are potential theoretical reasons that for such studies the scale-up of CL_{int,in vitro} may still underpredict CL_{in vivo measured}, as will be presented in a subsequent section.

DRUG-DRUG INTERACTION, DISEASE STATE AND PHARMACOGENOMIC PREDICTIONS

Although here we report that there is no possibility to derive equations that will predict clearance based on IVIVE measurements, except possibly for low extraction ratio drugs where the arterial clearance will not differ significantly from clearance calculated for any metabolic venous clearance model or for the well-stirred model when transporters are relevant, it appears that changes in clearance, or more correctly changes in concentration-time curves, due to DDIs, disease state or pharmacogenomic differences can be reasonably predicted. This is certainly true for low extraction ratio drugs and appears to also be true for all drugs. However, not necessarily on a direct proportionate basis for high extraction ratio drugs. This exemplifies why PBPK models are so valuable. If the concentration-time curve and its change with dose can be validated based on a PBPK model, then it is possible to predict changes in concentration with modulating factors and this is the justification for regulatory agencies requiring/recommending that sponsors of NCEs validate the PBPK model and use the model to predict when certain studies may or may not be required prior to regulatory approval.

PREDICTION OF HEPATIC FIRST-PASS LOSS IS AN ARTERIAL CLEARANCE CONCEPT

There is another interesting outcome of this analysis that has not been previously considered with respect to F_H, the fraction of an oral dose that escapes first pass liver metabolism. F_H is predicted in Eq. 11 as 1 minus the measured hepatic clearance (CL_H) divided by Q_H

$$F_H=1-\frac{{CL}_H}{Q_H}$$ (11)

The calculation of F_H is an organ arterial clearance concept since the concentration driving the hepatic first pass loss is the entering concentration, so that the CL_H term in Eq. 11 should be an arterial clearance. If the measured organ clearance was a well-stirred or parallel tube model clearance, CL_H would be a larger value and we would be underestimating F_H and overestimating the gut first pass loss, 1-F_G. This possibility has not been presented previously, but it is not a major concern since we now recognize that published clearance values are arterial clearances.

THE INTRINSIC CLEARANCE VALUE DETERMINED IN THE IN VITRO INCUBATION IS AN ARTERIAL INTRINSIC CLEARANCE

Returning to Fig. 1, what are the characteristics of the intrinsic clearance value determined in the in vitro incubation? It is a measured rate of elimination (clearance) independent of protein binding and hepatic blood flow. Certainly, it is an intrinsic clearance. But the definition of intrinsic clearance as first proposed in 1973 in the derivation¹¹ of Eq. 6 is the amount eliminated at steady-state divided by the unbound concentration exiting the IPRL (C_out,u). How can the CL_int in the isolated perfused organ of elimination at steady-state have any equivalence to the measure of the rate of elimination in an in vitro incubation mixture? There is no C_out,u to measure in a test tube. Rather the in vitro rate of elimination is driven by the concentration in the incubation mixture, where just as in the PBPK model, the concentration after the reaction has occurred is the same concentration driving the reaction. That is, CL_{int,incubation} is the arterial intrinsic clearance. What the field has been attempting to do in IVIVE, without recognizing it, is use CL_int,arterial to predict CL_{in vivo,arterial.}

This now brings a completely different perspective to IVIVE. We are trying to predict an in vivo arterial clearance. The in vitro CL_int,arterial determined from the incubations when multiplied by f_u,B will be the lower limit of the prediction and cardiac output the upper limit, but it is not possible to derive the equation relating these parameters. Thus, investigating the models of hepatic elimination has no relevance for predicting whole-body arterial clearance values. The only reason that one would want to use a model of hepatic extraction would be to predict the possible exposure of drug within the liver, when liver exposure drives either efficacy or toxicity, as recently discussed⁴. This is where the belief that organ clearance is model independent^{10, 12, 19} becomes most confounding. If organ clearance is model independent, then organ exposure is model independent, and therefore it would not possible to evaluate the relationship between organ exposure and pharmacodynamics.

IS THE FAILURE OF IVIVE DUE TO METHODOLOGIC ISSUES?

As discussed above, we believe that the failure of IVIVE is due to theoretical not methodologic issues. It is useful to review some of these data. Bowman and Benet² analyzed data for 5 human hepatocyte studies and 6 human microsome studies for 664 individual measurements, finding that 2/3rds of the IVIVE clearance predictions fell outside of 2-fold predictability, with no difference in poor predictability for microsomes vs hepatocytes. Wood et al.³ compared scaled-up in vitro CL_int with “observed” CL_int (calculated from the measured human clearance values using Eq. 3) as shown in Fig. 9 for literature data for human and rat hepatocyte and microsome measurements with obvious poor predictability. Many authors have argued the poor IVIVE outcome is due to methodologic problems with the IVIVE incubations. Looking at the 29 drugs investigated by Dr. Obach in his 1999 publication⁵, a data set included in both the Bowman and Benet² and Wood et al.³ analyses, Obach reports that 16 predictions based on in vitro human microsome intrinsic clearance utilizing Eq. 6 were within 2-fold of CL_{in vivo measured}, while for 13 drugs, the prediction was not within 2-fold. It is the Obach data set that leads us to believe that poor IVIVE predictability is not a methodologic problem. All 29 drugs were investigated by Dr. Obach following the same experimental procedures. We do not believe there is a methodologic problem with the 13 poorly predicted drugs, but not for the 16 drugs well predicted.

Figure 9.

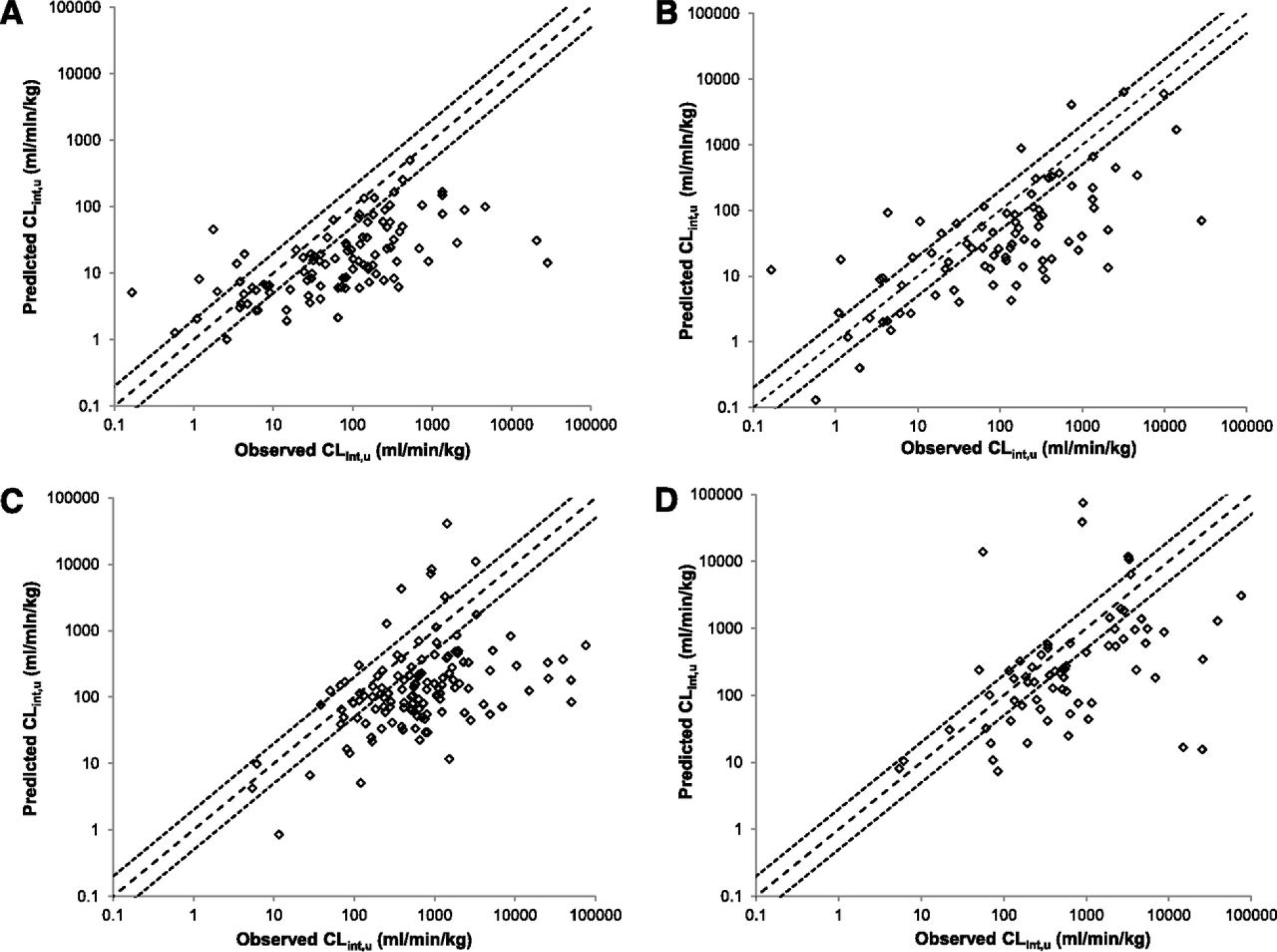
Prediction by Wood et al.³ of CL_int,u in hepatocytes (A and C) and microsomes (B and D) in human (A and B) and rat (C and D). Dashed lines represent unity and dotted lines a 2-fold margin of error.

In the Wood et al.³ data set, the marked decrease in predictability with increasing “Observed” CL_int is obvious in Fig. 9. Benet and Sodhi²⁵ suggested that for high ER (high “Observed” CL_int) drugs, clearance was rate limited by organ blood flow and noted that the underprediction disappeared as organ blood flow approached 50 ml/ml kg, from the generally recognized human hepatic blood flow of 21 ml/min kg. The authors wrote “Please note that we are not suggesting that the measured hepatic blood flows are incorrect, nor do we have a physiologic explanation for the hepatocytes and microsomes seeing an apparent flow that exceeds the measured value coming into the liver. However, based on the boundary conditions, increased under prediction with increasing intrinsic clearance or measured in vivo hepatic clearance is only consistent with an increased apparent flow. This is obviously an area requiring further investigation.” This manuscript now provides the explanation for the finding. As demonstrated above, CL_{in vivo measured} is a whole-body arterial clearance with the upper blood flow boundary equal to cardiac output, a value approached by our previous analysis²⁵.

IVIVE MAY NOT PROVIDE 2-FOLD PREDICTION EVEN FOR ORGAN CLEARANCE OF LOW EXTRACTION RATIO DRUGS

As pointed out above, the reliability of an animal model in vitro scaled-up intrinsic clearance to predict the isolated perfused animal liver clearance has not been adequately evaluated. Consider how the in vitro intrinsic clearance is determined as illustrated in Fig. 1. As presented by Obach⁵, the rate constant for elimination in the in vitro incubation is multiplied by the volume of fluid in the incubation mixture to obtain the intrinsic clearance value. Why should the volume of fluid in the in vitro incubation mixture have any correlation with the volume of distribution of the drug within an in vivo liver? Certainly, some of the lipophilic drug within the liver may distribute into lipophilic portions of the liver into which the enzymes in the liver cannot partition. Yet, in the in vitro mixture the hepatocytes/microsomes see the same volume of distribution for the drug and the enzymes. We believe that this discrepancy is the major reason for the IVIVE underprediction, because the blending of organ concentrations would tend to lead to overprediction. Our argument is often countered by scientists who state that the intrinsic clearance in the liver is not calculated by the in vitro rate constant of elimination multiplied by the volume of fluid of the incubation mixture, but rather by the direct measurement of intrinsic clearance calculated as V_max divided by K_m, i.e., CL_{int,in vitro} = V_max/K_m. Those scientists are ignoring the derivation of the Michaelis-Menten equation. In Biochemistry the equation is derived where V_max is the maximum change in concentration with time, leading to the units of V_max/K_m being time⁻¹. But that was not useful to pharmacokineticists, who decreed that although the Michaelis-Menten equation was derived in terms of concentrations, it is justifiable to change the units of V_max to the maximum change of amount with time, so that the units of V_max/K_m become volume/time, a clearance. This arbitrary conversion of units is not valid, but the theoretical derivations related to these two issues will be presented in a subsequent publication. We raise the point here, however, to indicate that even when trying to predict organ clearance, not whole-body clearance, it is possible that IVIVE may fail.

HOW SHOULD THE LIVER BE MODELED?

PBPK models (Fig. 2) should get it right, since if we could predict organ clearance correctly, PBPK models recognize that the venous concentration leaving the organ of elimination is not the venous concentration that is measured in vivo. Liver clearance (CL_H) at steady-state is given by Eq. 12

$${CL}_H·C_H=Q_H·\left(C_{in}-C_{out}\right)$$ (12)

but we don’t know its value or how to determine it, except possibly for low extraction ratio compounds. C_H is the liver concentration, but it differs across the liver, even at steady-state, due to incremental elimination. We could assume the arterial clearance model.

$${CL}_{H,arterial}·C_{in}=Q_H·(C_{in}-C_{out})\frac{C_{out}}{C_{in}}=\frac{Q_H-C{L}_{H,arterial}}{Q_H}$$ (13)

But we don’t know CL_{H, arterial}; it is the value we are trying to predict by using IVIVE and as noted earlier we cannot derive the relationship between this clearance term and the intrinsic PS_inf, PS_eff, CL_H,met, CL_H,bil and f_u,B parameters. We only have an estimate of CL_{H,int, arterial} from the in vitro hepatocyte or microsome incubations. If we substitute f_u,B CL_{H,int, arterial} for CL_{H, arterial}, we could markedly underpredict C_out/C_in, especially for high ER drugs and even have negative values.

We can only manipulate the value of CL_{int, arterial} in a bottom-up PBPK model based on our belief of the importance of the various parameters. But in a top-down PBPK model we can estimate the change in C_out/C_in when these parameters are altered. This is why PBPK modeling is so useful and required/recommended by regulatory agencies in the drug approval process.

WHERE ARE WE IN IVIVE TODAY?

PBPK models should get it right. But we have not recognized that we are trying to use an arterial intrinsic clearance measured in vitro to predict an in vivo arterial drug clearance. Rather we use an invalid equation to convert this arterial intrinsic clearance into a dispersion (or well-stirred or parallel tube) model clearance, resulting in markedly mispredicting the appropriate organ clearance for 2/3rds of NCEs. Further, the in vitro intrinsic clearance may not even correctly predict the in vivo clearance of the organ of elimination as opposed to the whole-body clearance. We attempt to overcome this organ clearance error by putting 5 liver compartments in a row in PBPK models, which decreases predicted C_venous, without really knowing why we did it. So, is it useful to carry out these in vitro incubations as depicted in Fig. 2? Yes, but one should stop after the in vitro half-life determination. There is no theoretical relationship that will allow one to predict human pharmacokinetics from these measurements, so there is no advantage in converting the half-life measure into an intrinsic clearance. The in vitro measures will alert drug development scientists to high ER, short t½ drugs versus low ER, longer t½ drugs, as they do now, and give information concerning potential enzymatic and transporter relevance that then can be used to adjust PBPK data fitting.

We might expect that organ-on-a-chip in vitro methodologies incorporating flow would allow determination of in vitro arterial CL_int and provide potentially better predictions, as published results seem to indicate. Yet, this does not negate the difficulties discussed here of trying to use an organ of elimination clearance to predict a whole-body measured clearance determined by Eqs. 1 and 2, as well as the potential that the in vitro incubation where both drug and enzymes exhibit the same volume of distribution may not mimic the in vivo condition where some drug in the liver will not always have access to the enzymes.

CONCLUSIONS

In our quest to understand the published poor ability of IVIVE to successfully predict in vivo drug clearance, we identified a number of misconceptions and/or poorly understood aspects of clearance, which we summarize first.

• 1Published human drug clearances determined by measuring venous drug concentrations (as well as steady-state measures of arterial concentrations) are all arterial clearances (except for drugs eliminated in the lung or heart).
• 2These published arterial clearance measures will always be less than the sum of the organ of elimination clearances since the systemic concentrations measured are a blend of concentrations exiting the organs of elimination plus the concentrations exiting organs where no elimination occurs. The greater the extraction ratio of the organs of elimination, the greater the difference between the measured systemic concentrations and the exiting concentrations from the organs of elimination. This difference for drugs following linear pharmacokinetics occurs equally for clearance calculations following a single dose of a drug and following steady-state dosing.
• 3The upper boundary condition for measured arterial whole-body clearance is cardiac output, not blood flow to the organs of elimination.
• 4The equation $CL=Q_{organ}·ER=Q_{organ}\frac{C_{in}-C_{out}}{C_{in}}$ (Eq. 5) defines the arterial clearance of an organ of elimination. It is not the equation for the well-stirred model.
• 5The equation generally recognized as the well-stirred model relationship in pharmacokinetics $CL=Q_{organ}·\frac{f_{u,B}·{CL}_{int}}{Q_{organ}+f_{u,B}·{CL}_{int}}$ (Eq. 3) was derived based on two invalid assumptions: a) that a flow dependent clearance relationship could be equated with a flow independent clearance relationship, and b) that the organ arterial equation (Eq. 5) was the well-stirred model equation. There is no validity to Eq. 3 above and it is not the well-stirred model intrinsic clearance equation; it is not possible to derive a relationship between measured clearance in humans, organ blood flow and fraction unbound in blood; it is not possible to calculate an organ intrinsic clearance from a measured human clearance value.
• 6Just as it is not possible to derive an equation for the simple organ of elimination clearance in point 5 above, it is not possible to derive the clearance equation for the extended clearance model when transporters can potentially become rate limiting as represented in Fig. 8.
• 7Although it is not possible to derive the relationship between measured clearance, organ blood flow and intrinsic clearances, predictions of changes in clearance or more correctly changes in concentration time curves, based on changes in individual parameters will be successful.
• 8The clearance determined from the arterial organ of elimination equation, CL=Q_organ ER (Eq. 5), is not the clearance for the models of hepatic elimination (well-stirred, dispersion, parallel tube) and will not allow intrinsic clearance for these various models to be calculated.
• 9Prediction of hepatic first pass elimination is an arterial clearance concept, but since published human clearances are arterial clearances, these predictions are accurate.
• 10For models of hepatic elimination involving measurements of venous concentrations exiting the organs of elimination (well-stirred, dispersion and parallel tube), clearance will exceed organ blood flow for high extraction ratio drugs.

Obviously, many of the conclusions above contradict what is taught in basic pharmacokinetic courses and what is generally believed by the field.

The following conclusions relate to IVIVE prediction.

• 11The intrinsic clearance value determined from the in vitro incubation is an arterial intrinsic clearance.
• 12Thus, IVIVE attempts to predict a whole-body arterial clearance based on an arterial intrinsic clearance.
• 13However, there is no theoretical basis upon which an arterial intrinsic clearance can be related to a whole-body arterial clearance to accomplish IVIVE.
• 14Investigating different models of hepatic elimination in IVIVE analyses has no relevance for predicting whole-body arterial clearance values.
• 15For low extraction ratio drugs, where organ blood flow has little or no effect on organ clearance, IVIVE might be expected to be successful if the in vitro intrinsic metabolic clearance, the in vitro intrinsic biliary clearance and/or the intrinsic influx and efflux transporter clearances from the in vitro incubation can be expected to be the relevant values in vivo.
• 16There are no published data demonstrating that in vitro intrinsic metabolic clearance can predict in vivo organ clearance as IVIVE assumes. A study validating such a prediction would entail an animal in vitro microsome or hepatocyte determination of intrinsic metabolic clearances for a number of low extraction ratio drugs that then are consistent with an in vivo isolated organ metabolic clearance for these drugs.
• 17The poor predictability of IVIVE is due to theoretical reasons not experimental methodology reasons.
• 18Theoretical reasons for a lack of IVIVE predictability include the potential that in vivo in the liver, drug can distribute into portions of the liver that are not in contact with the enzymes, while in vitro this is not a possibility. Furthermore, the intrinsic clearance determination assuming that one may change the units of V_max in the Michaelis-Menten equation to maximum amount of drug eliminated when the derivation is maximum concentration of drug eliminated is not valid.
• 19A generally unrecognized assumption in IVIVE is that the possible prediction of the organ of elimination clearance is not the value equivalent to the whole-body arterial clearance, and this difference increases as extraction ratio increases.
• 20Albumin addition to in vitro incubations does not improve IVIVE predictability in a meaningful manner and there is no theoretical basis as to why it should. The albumin facilitated uptake phenomenon as originally observed was only based on a false belief of the equivalence of the arterial clearance in an IPRL experiment to the clearance of a hypothetical dispersion model of organ elimination. In that early study, unbound clearance only changed at most 20% with a 10-fold increase in albumin concentration and unbound clearance was not even evaluated by the investigators.

IVIVE RECOMMENDATIONS

1. We have presented the theoretical reasons that IVIVE should not give good predictability and cited the published compilations suggesting that good predictability is not obtained. We believe that it would be very useful for companies to separate out those compounds exhibiting good IVIVE predictability and those that do not. Then determine if quantitative structure activity relationship (QSAR) regressions may give clues as to NCE characteristics that may favor both good and poor predictability. These initial evaluations should be carried out for long in vitro half-life (potentially low extraction ratio) compounds, where organ blood flow would not be expected to play a roll.

2. It may also be useful to explore such analyses for compounds where both static and flow incorporated organ-on-a-chip in vitro measures are obtained.

3. Without such discoveries, an alternate approach is to utilize a PBPK model to determine the relationship between f_u,B CL_int and CL_whole-body for an animal model such as a rat where CL_int is determined from an in vitro incubation and CL_whole-body from in vivo dosing. Then apply this relationship to the human f_u,B CL_int. It is obvious that this is not a high throughput methodology and will possibly only be used for very few NCEs that may appear to be the optimum half-life measure from a set of NCEs tested in vitro using human hepatocytes or microsomes.