Indicators to assess physiological heat strain – Part 1: Systematic review

ABSTRACT

In a series of three companion papers published in this Journal, we identify and validate the available thermal stress indicators (TSIs). In this first paper of the series, we conducted a systematic review (registration: INPLASY202090088) to identify all TSIs and provide reliable information regarding their use (funded by EU Horizon 2020; HEAT-SHIELD). Eight databases (PubMed, Agricultural and Environmental Science Collection, Web of Science, Scopus, Embase, Russian Science Citation Index, MEDLINE, and Google Scholar) were searched from database inception to 15 April 2020. No restrictions on language or study design were applied. Of the 879 publications identified, 232 records were considered for further analysis. This search identified 340 instruments and indicators developed between 200 BC and 2019 AD. Of these, 153 are nomograms, instruments, and/or require detailed non-meteorological information, while 187 can be mathematically calculated utilizing only meteorological data. Of these meteorology-based TSIs, 127 were developed for people who are physically active, and 61 of those are eligible for use in occupational settings. Information regarding the equation, operating range, interpretation categories, required input data, as well as a free software to calculate all 187 meteorology-based TSIs is provided. The information presented in this systematic review should be adopted by those interested in performing on-site monitoring and/or big data analytics for climate services to ensure appropriate use of the meteorology-based TSIs. Studies two and three in this series of companion papers present guidance on the application and validation of these TSIs, to guide end users of these indicators for more effective use.

Introduction

Billions of people perform their daily activities in ambient conditions that exceed their bodies’ capacity for maintaining a safe body temperature [1]. This often leads to the development of severe conditions that they have to carry throughout their life [2]. Even worse, heat stress can be fatal in many cases [1,3,4]. For instance, three to four occupational heat stress fatalities are currently occurring every hour across the world [5]. While heat stress is more prevalent in working populations [2,6–11], athletes [12,13] and other civilians, especially heat-vulnerable older adults and individuals with chronic health conditions who perform intense manual tasks are also affected by hyperthermia and heat-related illnesses. Older individuals [4,14,15] and people with underlying cardiovascular diseases [4,15–17] face significant heat-related morbidity and mortality, even when sitting or resting in hot conditions. To tackle this problem, effective heat mitigation strategies should be designed and implemented. But first, it is crucial to assess the magnitude of heat stress.

The idea of having a single value characterizing the heat stress and strain experienced by individuals was incubated in the early scientific research. The importance of this topic has inspired numerous scientists to develop sophisticated thermal stress indicators (TSI) aiming to safeguard health and well-being of humans exposed to a wide range of environments [18–21]. A total of 167 TSIs have been identified and listed in reviews published to date [18–23], but we are aware of many that have not been included in these articles. To enhance our understanding on the development and use of TSI developed throughout history, it is necessary to overview the extensive collection of TSIs so that we may build and/or expand their development.

In a series of three companion papers published in this Journal, we identified the TSIs developed since the dawn of scientific research (part 1), we conducted a Delphi exercise to understand what is important to consider when adopting a TSI to protect individuals who work in the heat (part 2)[24], and we performed field experiments across nine countries to evaluate the efficacy of each TSI for quantifying the physiological strain experienced by individuals who work in the heat (part 3) [25]. The present article is the first in this series, and our aim was to conduct a systematic review to identify the TSIs developed since the dawn of scientific research and provide reliable information regarding their computation, as well as to publish a valid and reliable software to calculate them. This information is important to ensure appropriate use of TSIs. To inform the subsequent parts of this series of companion papers, we were particularly interested in TSIs that can be calculated using only meteorological data (air temperature, relative humidity, wind speed, and solar radiation), as we aimed to enhance the quality and relevance of on-site monitoring (e.g., field evaluation) and big-data analytics (e.g., satellite data) used in climate services for the athletic, occupational, and the general populations.

Methodology

To reduce bias and the likelihood of duplication, as well as to maximize the validity of the procedures involved, we registered our systematic review in the international platform of registered systematic review and meta-analysis protocols (INPLASY) database (registration number: INPLASY202090088).

Search strategy and selection criteria

We searched eight databases from the date of their inception to 15 April 2020, for studies evaluating the capacity of TSIs to quantify the magnitude of thermal stress and strain experienced by humans. Studies published in any language were included. The following databases were searched: Pubmed, Agricultural and Environmental Science Collection, Web of Science, Scopus, Embase, Russian Science Citation Index, MEDLINE, Google Scholar. No date or other study limits (e.g., original articles, review articles, and conference papers) were applied in our search. The search algorithms used in each database are provided in the Appendix. We supplemented the electronic database searches with manual searches for published and unpublished papers, websites of international agencies (i.e., World Health Organization, World Meteorological Organization, and World Migration Organization), national bureaus of meteorology, international standards, reports (e.g., International Organization for Standardization, and American Society of Heating, Refrigerating and Air-Conditioning Engineers), and relevant books in the field. The screening was conducted independently by two investigators (LGI and KM) and any conflicts were resolved through consensus by a third researcher (ADF). We excluded studies focusing on animal-, crop-, engineering-, geology-, oil-, and clinical-related indicators. Detailed information regarding the included and excluded papers is provided in the Appendix.

Sensitivity analysis for the search algorithm

The term “index” is part of the name in 96 out of 340 TSIs; (Tables 1–2 e.g., Universal Thermal Climate Index, Belding-Hatch Index, Discomfort Index, Environmental Stress Index). Therefore, using “index” in a systematic search returns tens of thousands of eligible articles that adopted a TSI which happened to include “index” as part of its name. To ensure that our search is specific to the issue at hand, we opted out of using “index” within the search algorithm. To confirm that this did not limit the sensitivity of our search, we performed a sensitivity analysis as follows..

1. The reference lists of all eligible articles were extracted.

2. Duplicates were removed.

3. The titles and abstracts of all unique citations were screened for eligibility.

4. Sensitivity was defined as the percent of eligible articles resulting from the search algorithm out of all the known eligible articles that were included in the systematic review (articles from the search algorithm + articles added from detailed reference list search + articles added manually).

Table 1.

| List of 153 non-meteo-based thermal stress indicators identified in the systematic search. These are complex models requiring some or all the meteorological parameters (air temperature, relative humidity, wind speed, and solar radiation) in addition to other information. Nomograms and other instruments were also considered non-meteo based indicators. The fourth column titled “Literature” cites the eligible article that was used to extract data for the present thermal stress indicator. Precise information regarding the original article of each thermal stress indicator can be found in the supplementary material.

ID		Thermal Stress Indicator	First Authors; Year	Literature	Reason for considered as non-meteo-based
					Parameter	Type
1		Acclimatization Thermal Strain Index	de Freitas; 2009	[19]
2		Adaptation Strain Index	Blazejcztk; 2014	[18,19]
3		Air Cooling Power	Mitchell; 1971	[19]
4		Air Diffusion performance Index	ASHRAE; 1989	[35]
5		Air Pressure Thermometer	Amonton; 1702	[36]
6		Air Thermometer	Dulong; 1815	[36]
7		Air Thermometer	Galileo; 1592	[36]
8		Apparatus for Thermal Expansion of Gasses	Gay-Lussac; 1802	[36]
9		Berkeley Comfort Model	Huizenga; 2001
10		Bioclimatic Contrast Index	Blazejczyk; 2011	[19]
11		Bioclimatic Distance Index	Mateeva; 2003	[19]
12		Bioclimatic Index	Olgyay; 1963	[37]
13		Black Sphere Actinograph	Poschmann; 1932	[19,38]
14		Body Temperature Index	Dayal; 1974	[19]
15		Body-atmosphere Energy Exchange Index	de Freitas; 1989	[19]
16		Classification of Weather in Moments	Rusanov; 1973	[19]
17		Climate Index	Becker; 2000	[19]
18		Closed Air Thermometer	Amonton; 1702	[36]
19		Climatic Heat	Hubac, 1989	[39]
20		Clothing Insulation	Mount;1982	[19]
21		Cold Strain Index	Moran; 1999	[19]
22		COMfort formulA (COMFA)	Brown; 1986
23		Comfort Chart	Mochida; 1979	[19]
24		Comfort Index	Terjung; 1966	[19,23,40]
25		Corrected Effective Temperature (basic)	Vernon; 1932	[19]
26		Corrected Effective Temperature (normal)	Vernon; 1932	[19]
27		Corrected Humid Operative Temperature	Horikoshi; 1985	[41]
28		Craig Index	Craig; 1950	[42]
29		Cumulative Discomfort Index	Tennenbaum; 1961	[43]
30		Cumulative Effective Temperature	Sohar; 1962	[22]
31		Cumulative Heat Strain Index	Frank; 1996	[19,44]
32		Cylinder	Brown;1986	[19]
33		Daily Weather Types	Lecha; 1998	[19,23]
34		Effective Draft Temperature	Koestel; 1955	[35]
35		Effective Heat Strain Index	Kamon;1981	[19]
36		Ellipsoid index	Blazejczyk; 1998	[19,23]
37		Equilibrating Columns	Dulong; 1802	[36]
38		Equilibrium Rectal Temperature	Givoni; 1972	[19]
39		Equivalent Uniform Temperature	Wray; 1980
40		Eupathescope	Dufton; 1929	[19,38]
41		Evans Scale	Evans; 1980	[18,19]
42		Exceedance	Borgeson; 2011
43		Facial Cooling Index	Tikuisis; 2002	[45]
44		Frigorimeter	Dorno; 1928	[19,38]
45		Globe Thermometer	Vernon; 1932	[46]
46		Grade of Heat Strain	Hubac; 1989	[19]
47		Heart Rate Index	Dayal; 1974	[19]
48		Heart Rate Index	Givoni; 1973	[19]
49		Heat Budget Index	de Freitas; 1985	[19]
50		Heat Strain Decision Aid Model	Cadarette; 1999	[19]
51		Heat Strain Index (corrected)	McKarns; 1966	[22]
52		Heat Strain Predictive Systems	Lustinec; 1965	[20]
53		Heat Stress Index	Watts; 2004	[19]
54		Heat Stress Prediction Model	Pandolf; 1986	[19]
55		Heat Tolerance Index	Hori; 1978	[19]
56		Heat Tolerance Limits	Vogt;1982	[19]
57		Heated Thermometer	Heberden; 1826	[47]
58		Heat Load	Blazejczyk; 1994	[48]
59		Humid Operative Temperature	Nishi; 1971	[19]
60		Hybrid Thermometer	Kircher; 1643	[36]
61		Hypso-barometer	Fahrenheit; 1724	[36]
62		Increment Temperature Equivalent to Radiation Load	Lee; 1964	[19]
63		Index of Clothing Required for Comfort	de Freitas; 1986	[19]
64		Index of Pathogenicity of Meteorological Environment	Latyshev; 1965	[19]
65		Index of Physiological Effect	Robinson; 1945	[19]
66		Index of Thermal Stress	Givoni; 1969	[19]
67		Index of Thermal Stress	Kondratyev; 1957	[19]
68		Integral Index of Cooling Conditions	Afanasieva; 2009	[19,49]
69		Integral Load Index	Matyukhin; 1987	[19]
70		Kata Thermometer	Hill; 1916	[19,50]
71		Mahani Climate Index / Mahoney Scale	Mahoney; 1967	[51]
72		Maximum Exposure Time	Brauner; 1995	[19]
73		Maximum Recommended Duration of Exercises	Young; 1979	[19]
74		Mean Equivalence Lines	Wenzel; 1978	[19]
75		MENEX model	Blazejczyk; 1994	[22]
76		Mercury Weight Thermometers	Dulong; 1815	[36]
77		Metal Man (thermal manikin)	Pedersen; 1948	[19]
78		Meteorological Health Index	Bogatkin; 2006	[19]
79		Modified Effective Temperature	Smith; 1952	[19]
80		Modified Physiological Equivalent Temperature	Lin; 2019	[52]
81		Munich Energy Balance Model	Hope; 1984	[22]
82		New Effective Temperature	Gagge; 1971	[19]
83		Outdoor Comfort Zone	Ahmed; 2003	[53]
84		Outdoor Neutral Temperature	Aroztegui; 1995	[54]
85		Outdoor Thermal Environment Index	Nagano; 2011	[19]
86		Optimum Summer Weather Index	Davis; 1968	[55]
87		Overheating Risk	Nicol; 2009	[22]
88		Overheating Risk	Robinson; 2008	[22]
89		Perceived Temperature	Jendritzky; 2000	[19]
90		Perceptual Hyperthermia Index	Gallagher; 2012	[19]
91		Physiological Equivalent Temperature	Mayer; 1987	[19]
92		Physiological Heat Exposure Limit	Chart; 1977	[19]
93		Physiological Index of Strain	Hall; 1960	[19]
94		Physiological Strain	Blazejczyk; 2005	[19]
95		Physiological Strain Index	Moran; 1998	[19]
96		Physiological Subjective Temperature	Blazejczyk; 2007	[19]
97		Predicted Effects of Heat Acclimatization	Givoni; 1973	[19]
98		Predicted Four-Hour Sweat Rate	McArdle; 1947	[19]
99		Predicted Heat Strain	Malchaire; 2001	[19]
100		Predicted Mean Vote—Fuzzy	Hamdi; 1999	[19]
101		Predicted Mean Vote—Indoors	Fanger; 1970	[19]
102		Predicted Mean Vote—Outdoors	Gagge; 1986	[19]
103		Predicted Mean Vote—Outdoors	Jendritzky; 1981	[19]
104		Predicted Percentage Dissatisfied	Index Fanger; 1970	[19]
105		Predicted Rectal Temperature	Givoni; 1972	[21]
106		Predicted Sweat Loss	Shapiro; 1982	[22]
107		Prescriptive Zone	Lind; 1970	[22]
108		Qs Index	Rublack; 1981	[19]
109		Quotient of Heat Stress	Hubac; 1989	[19]
110		Reference Index	Pulket; 1980	[19]
111		Relative Heat Strain	Lee; 1966	[19]
112		Required Clothing Insulation	Holmer; 1984	[19]
113		Required Sweat Rate	Vogt; 1981	[19]
114		Respiratory Heat Loss	Rusanov; 1989	[19]
115		Resultant Thermometer	Missenard; 1935	[38]
116		Santorio’s Thermometer	Santorio; 1612	[56]
117		Skin Temperature	Mehnert; 2000	[19]
118		Skin Temperature Energy Balance Index	de Freitas; 1985	[19]
119		Skin Wettedness	Gonzalez; 1978	[19,23]
120		Skin Wettedness	Kerslake; 1972	[22]
121		Spatial Synoptic Classification	Kalkstein; 1996	[19]
122		Standard Effective Temperature	Gonzalez; 1974	[19]
123		Standard Effective Temperature	Gagge; 1986	[21]
124		Standard Effective Temperature for Outdoors	Pickup; 2000	[19]
125		Still Shade Temperature	Burton; 1955	[19]
126		Subjective Temperature Index	Blazejczyk; 2005	[19]
127		Summer Severity Index	McLaughlin; 1977	[19]
128		Survival Time Outdoors in Extreme Cold	de Freitas; 1987	[19,23]
129		Temperature Load	cited by Kioka; 2006	[57]
130		Thermal Acceptance Ratio	Ionides; 1945	[19,23]
131		Thermal Balance	Rusanov; 1981	[19]
132		Thermal Discomfort	Gagge; 1986	[19]
133		Thermal Insulation of Clothing	Aizenshtat; 1964	[18,19]
134		Thermal Insulation of Clothing	Budyko; 1960	[19]
135		Thermal Insulation of Clothing	Rusanov; 1981	[19]
136		Thermal Insulation of Protective Clothing	Afanasieva; 1977	[19]
137		Thermal Sensation	Fountain; 1995	[54]
138		Thermal Sensation	Givoni; 2003	[19,23]
139		Thermal Sensation Index	Kiuchi; 2001	[57]
140		Thermal Strain Index	Lee; 1958	[19,23]
141		Thermal Work Limit	Brake; 2002	[19]
142		Thermal-Insulation Characteristics of Clothing	Kondraty; 1957	[19]
143		Thermo-Integrator	Winslow; 1935	[19,23]
144		Thermoscope	Hero; 40 AD	[36]
145		Thermoscope	Philo; 200 BC	[36]
146		Total Heat	Hubac, 1989	[39]
147		Total Thermal Stress	Auliciems; 1981	[19]
148		Tourism Climate Index	Mieczowski; 1985	[55]
149		Weather Stress Index	Kalkstein; 1986	[19]
150		Weather–Climate Contrasts	Rusanov; 1987	[19]
151		Wet Bulb Thermometer	Haldane; 1905	[58]
152		Wet Globe Thermometer	Botsford; 1971	[59]
153		Wind Effect Index	Terjung; 1966	[19,23,40]

Metabolic Rate

Elevation / Barometric Pressure

Skin Temperature

Clothing Insulation

Cloud Level

Duration of Effort

Long-wave Radiation

Acclimatization status

Heart Rate

Precipitation

No Environmental Data

Water Intake

Core Temperature

Covered Distance

Specialized Equipment

Sweat Rate / Water loss / Vapor Pressure at Skin Surface

Evaporative Heat Loss from Skin

Questionnaire

Delta Data (fluctuation throughout the time)

No Fitted Equation / Nomogram

average temperature over multiple measures

Table 2.

The environmental parameters used by the 187 meteo-based thermal stress indicators. Meteo-based indicators were defined as those that can be calculated using only meteorological data (air temperature, relative humidity, wind speed, and solar radiation).

ID	Thermal Stress Indicator	First Author	Year	Unit	Temperature	Humidity	Radiation	Wind
1	Accepted Level of Physical Activity [60]	Blazejczyk	2010	W/m²	✓	✓
2	Actual Sensation Vote [61]	Nikolopoulou	2003	[-]	✓	✓	✓	✓
3	Actual Sensation Vote [62]	Nikolopoulou	2004	[-]	✓	✓	✓	✓
4	Actual Sensation Vote (Europe) [62]	Nikolopoulou	2004	[-]	✓	✓	✓	✓
5	Air Enthalpy [63]	Boer	1964	Kcal/kg	✓	✓	✓	✓
6	Apparent Temperature [64]	Almeida	2010	°C	✓	✓
7	Apparent Temperature [65]	Arnoldy	1962	°C	✓			✓
8	Apparent Temperature [66]	Fischer	2010	°C	✓	✓
9	Apparent Temperature [67]	Kalkstein	1986	°C	✓	✓
10	Apparent Temperature [68]	Smoyer-Tomic	2001	°C	✓	✓
11	Apparent Temperature (indoor) [69]	Steadman	1994	°C	✓	✓
12	Apparent Temperature (indoors) [70]	Steadman	1984	°C	✓	✓
13	Apparent Temperature (shade) [70]	Steadman	1984	°C	✓	✓		✓
14	Apparent Temperature (shade) [69]	Steadman	1994	°C	✓	✓		✓
15	Apparent Temperature (sun) [70]	Steadman	1984	°C	✓	✓	✓	✓
16	Apparent Temperature (sun) [69]	Steadman	1994	°C	✓	✓	✓	✓
17	Approximated Subjective Temperature [71]	Auliciems	2007	°C	✓	✓	✓	✓
18	Belding-Hatch Index [72]	Belding	1955	[-]	✓	✓	✓	✓
19	Belgian Effective Temperature [38]	Bidlot	1947	°C	✓	✓	✓	✓
20	Bioclimatic Index of Severity [73]	Belkin	1992	[-]	✓	✓		✓
21	Biologically Active Temperature [74]	Tsitsenko	1971	°C	✓	✓		✓
22	Biometeorological Comfort Index [75]	Rodriguez	1985	°C	✓	✓	✓	✓
23	Bodman’s Weather Severity Index [76]	Bodman	1908	[-]	✓			✓
24	Clothing Thickness	Steadman	1971	mm	✓		✓	✓
25	Comfort Vote [77]	Bedford	1936	[-]	✓	✓	✓	✓
26	Cooling Power [78]	Becker	1972	mcal/cm²/s	✓			✓
27	Cooling Power [79,80]	Bedford	1933	mcal/cm²/s	✓			✓
28	Cooling Power [79,80]	Bider	1931	mcal/cm²/s	✓			✓
29	Cooling Power [79,80]	Bradtke	1926	mcal/cm²/s	✓			✓
30	Cooling Power [79,80]	Buttner	1934	mcal/cm²/s	✓			✓
31	Cooling Power [79,80]	Cena	1966	mcal/cm²/s	✓			✓
32	Cooling Power [79,80]	Dorno	1925	mcal/cm²/s	✓			✓
33	Cooling Power [79,80]	Dorno	1934	mcal/cm²/s	✓			✓
34	Cooling Power (eq. 1) [79,80]	Goldschmidt	1952	mcal/cm²/s	✓			✓
35	Cooling Power (eq. 2) [79,80]	Goldschmidt	1952	mcal/cm²/s	✓			✓
36	Cooling Power [79]	Henneberger	1948	mcal/cm²/s	✓			✓
37	Cooling Power [76,81]	Hill	1916	W/m²	✓			✓
38	Cooling Power (eq. 1) [79]	Hill	1937	mcal/cm²/s	✓			✓
39	Cooling Power (eq. 2) [79]	Hill	1937	mcal/cm²/s	✓			✓
40	Cooling Power [79]	Lahmayer	1932	mcal/cm²/s	✓			✓
41	Cooling Power (eq. 1) [79]	Matzke	1954	mcal/cm²/s	✓			✓
42	Cooling Power (eq. 2) [79]	Matzke	1954	mcal/cm²/s	✓			✓
43	Cooling Power [79]	Meissner	1932	mcal/cm²/s	✓			✓
44	Cooling Power [82]	Vinje	1962	mcal/m²/hr	✓			✓
45	Cooling Power [79]	Weiss	1926	mcal/cm²/s	✓			✓
46	Cooling Power [82]	Angus	1930	mcal/cm²/s	✓			✓
47	Cooling Power [82]	Lehmann	1936	mcal/cm²/s	✓			✓
48	Cooling Power [82]	Joranger	1955	mcal/cm²/s	✓			✓
49	Cooling Power (Wet Air Temperature) [76,81]	Hill	1916	W/m²	✓	✓		✓
50	Corrected Effective Temperature (Basic) [71]	Auliciems	2007	°C	✓	✓	✓	✓
51	Corrected Effective Temperature (Normal) [71]	Auliciems	2007	°C	✓	✓	✓	✓
52	Dew Point [83]	Bruce	1916	°C	✓	✓
53	Discomfort Index [84]	Giles	1990	°C	✓	✓
54	Discomfort Index [79]	Kawamura	1965	[-]	✓	✓
55	Discomfort Index [79]	Tennenbaum	1961	°C	✓	✓	✓	✓
56	Discomfort Index (eq. 1) [85]	Thom	1959	[-]	✓	✓	✓	✓
57	Discomfort Index (eq. 2) [54,86]	Thom	1959	[-]	✓	✓	✓	✓
58	Discomfort Index [87]	Weather Services of South Africa	2018	[-]	✓	✓
59	Draught Risk Index [88]	Fanger	1987	% of people dissatisfied	✓			✓
60	Dry Kata Cooling [89]	Maloney	2011	W/m²	✓			✓
61	Effective Radiant Field [90]	Gagge	1967	W/m²	✓	✓	✓	✓
62	Effective Radiant Field [90]	Nishi	1981	W/m²	✓	✓	✓	✓
63	Effective Temperature [71]	Houghten	1923	°C	✓	✓
64	Effective Temperature [91]	Missenard	1933	°C	✓	✓
65	Environmental Stress Index [86]	Moran	2001	°C	✓	✓	✓
66	Equatorial Comfort Index [79]	Webb	1960	°C	✓	✓	✓	✓
67	Equivalent Effective Temperature [23]	Aizenshtat	1974	°C	✓	✓		✓
68	Equivalent Effective Temperature [92]	Aizenshtat	1982	°C	✓	✓		✓
69	Equivalent Temperature [77]	Bedford	1936	°C	✓	✓	✓	✓
70	Equivalent Temperature [93]	Brundl	1984	°C	✓	✓
71	Equivalent Warmth [77]	Bedford	1936	°C	✓	✓	✓	✓
72	Exposed Skin Temperature [94]	Brauner	1995	°C	✓			✓
73	Facial Skin Temperature (Cheek) [95]	Adamenko	1972	°C	✓			✓
74	Facial Skin Temperature (Ear Lobe) [95]	Adamenko	1972	°C	✓			✓
75	Facial Skin Temperature (Nose) [95]	Adamenko	1972	°C	✓			✓
76	Fighter Index of Thermal Stress (Direct Sunlight) [96]	Stribley	1978	°C	✓	✓	✓	✓
77	Fighter Index of Thermal Stress (Moderate Overcast) [96]	Stribley	1978	°C	✓	✓	✓	✓
78	Globe Temperature [97]	Liljegren	2008	°C	✓	✓	✓	✓
79	Heart Rate [98]	Fuller	1966	beats/min	✓	✓
80	Heart Rate Safe limit [98]	LaFleur	1971	beats/min	✓	✓
81	Heat Index [91]	Blazejczyk	2012	°C	✓	✓
82	Heat Index [99,100]	Stull	2000	°C	✓	✓
83	Heat Index [101]	National Oceanic and Atmospheric Administration	2014	°C	✓	✓
84	Heat Index [102]	Patricola	2010	°C	✓	✓
85	Heat Index [103]	Rothfusz	1990	°C	✓	✓
86	Humidex [91]	Masterson	1979	°C	✓	✓
87	Humisery [104]	Weiss	1982	°C	✓	✓		✓
88	Humiture [105]	Lally	1960	°C	✓	✓
89	Humiture [104]	Weiss	1982	°C	✓	✓
90	Humiture [106]	Hevener	1959	°C	✓	✓	✓	✓
91	Humiture revised	Wintering	1979	°F	✓	✓
92	Insulation Predicted Index [107]	Blazejczyk	2011	Clo	✓			✓
93	Integrated Index (indoor) [108]	Junge	2016	[-]	✓	✓		✓
94	Integrated Index (outdoor) [108]	Junge	2016	[-]	✓	✓	✓	✓
95	Internal Comfort Temperature [109]	Xavier	2000	°C	✓	✓	✓	✓
96	Kata Index [110]	Zhongpeng	2012	[-]	✓	✓	✓	✓
97	Mean Radiant Temperature (approximated) [111]	Ramsey	2001	°C	✓	✓	✓	✓
98	Mean Skin Temperature [112]	McPherson	1993	°C	✓
99	Meditteranean Outdoor Comfort Index [113]	Salata	2016	[-]	✓	✓	✓	✓
100	Missenard’s Index [114]	Missenard	1969	°C	✓	✓
101	Modified Discomfort Index [115]	Moran	1998	°C	✓	✓	✓	✓
102	Modified Environmental Stress Index [116]	Moran	2003	°C	✓	✓	✓
103	Natural Wet Bulb Temperature [89]	Maloney	2011	°C	✓	✓	✓	✓
104	Nett Radiation [117]	Cena	1984	W/m²	✓	✓	✓	✓
105	New Wind Chill [118]	NOAA	2001	[-]	✓			✓
106	Normal Equivalent Effective Temperature [74]	Boksha	1980	°C	✓	✓		✓
107	Operative Temperature [119]	ASHRAE	2004	°C	✓	✓	✓	✓
108	Operative Temperature [120]	ISO 7726:1998	1998	°C	✓	✓	✓	✓
109	Operative Temperature [121]	ISO 7730:1994	1994	°C	✓	✓	✓	✓
110	Operative Temperature [122]	Winslow	1937	°C	✓	✓	✓	✓
111	Outdoor Standard Effective Temperature [123]	Skinner	2001	°C	✓	✓	✓	✓
112	Oxford Index [124]	Lind	1957	[-]	✓	✓	✓	✓
113	Perceived Equivalent Temperature [125]	Monteiro	2010	°C	✓	✓	✓	✓
114	Perceived Temperature [38]	Linke	1926	°C	✓		✓	✓
115	Predicted Percentage Dissatisfied [109]	Xavier	2000	% of dissatisfied people	✓	✓	✓	✓
116	Predicted Thermal Sensation Vote [126]	Cheng	2008	[-]	✓	✓	✓	✓
117	Psychrometric Wet Bulb Temperature [127]	Malchaire	1976	°C	✓	✓	✓	✓
118	Psychrometric Wet Bulb Temperature [30]	McPherson	2008	°C	✓	✓		✓
119	Radiative Effective Temperature [128]	Blazejczyk	2004	°C	✓	✓	✓	✓
120	Radiation Equivalent Effective Temperature (Non-Pigmented) [129]	Sheleihovskyi	1948	°C	✓	✓	✓	✓
121	Radiation Equivalent Effective Temperature (Pigmented) [129]	Sheleihovskyi	1948	°C	✓	✓	✓	✓
122	Relative Humidity Dry Temperature [130]	Wallace	2005	°C	✓	✓
123	Relative Strain Index [54]	Kyle	1992	[-]	✓	✓
124	Relative Strain Index [131]	Lee	1966	[-]	✓	✓
125	Revised Wind Chill Index [132]	Court	1948	kg cal/m²/hr	✓			✓
126	Robaa’s Index [114]	Robaa	2003	[-]	✓	✓	✓	✓
127	Saturation Deficit [38]	Flugge	1912	kPa	✓	✓
128	Severity Index [129]	Osokin	1968	[-]	✓	✓		✓
129	Simple Index [86]	Moran	2001	[-]	✓	✓	✓
130	Simplified Radiation Equivalent Effective Temperature [74]	Boksha	1980	°C	✓	✓		✓
131	Simplified Tropical Summer Index [71]	Auliciems	2007	°C	✓	✓	✓	✓
132	Simplified Universal Thermal Climate Index [133]	Blazejcyk	2011	°C	✓	✓	✓	✓
133	Simplified Wet Bulb Globe Temperature [134]	American College of Sports Medicine	1984	°C	✓	✓
134	Simplified Wet Bulb Globe Temperature [30]	Gagge	1976	°C	✓	✓
135	Skin Temperature [135]	Blazejczyk	2005	°C	✓	✓	✓	✓
136	Skin Wettedness [135]	Blazejczyk	2005	[-]	✓	✓	✓	✓
137	Standard Operative Temperature [136]	Gagge	1940	°C	✓	✓	✓	✓
138	Subjective Temperature [137]	McIntyre	1973	°C	✓	✓	✓	✓
139	Sultriness Index [138]	Scharlau	1943	Torr		✓
140	Sultriness Intensity [139]	Akimovich	1971	[-]		✓
141	Summer Scharlau Index [140]	Scharlau	1950	[-]	✓	✓
142	Summer Simmer Index [141]	Pepi	1987	°C	✓	✓
143	Swedish Wet Bulb Globe Temperature [142]	Eriksson	1974	°C	✓	✓	✓	✓
144	Temperature Humidity Index [99]	Schoen	2005	°C	✓	✓
145	Temperature Humidity Index [143]	Costanzo	2006	°C	✓	✓
146	Temperature Humidity Index [144]	INMH	2000	[-]	✓	✓
147	Temperature Humidity Index [144]	Kyle	1994	°C	✓	✓
148	Temperature Humidity Index [145]	Nieuwolt	1977	°C	✓	✓
149	Temperature Humidity Index (eq. 1) [141]	Pepi	1987	°C	✓	✓
150	Temperature Humidity Index (eq. 2) [141]	Pepi	1987	°C	✓	✓
151	Temperature of the Exhaled air [112]	McPherson	1993	°C	✓	✓
152	Temperature Resultante Miniere [38]	Vogt	1978	°C	✓	✓	✓	✓
153	Temperature Wind Speed Humidity Index [146]	Zaninovic	1992	kJ/kg	✓	✓	✓	✓
154	Thermal Comfort [147]	Givoni	2000	[-]	✓		✓	✓
155	Thermal Comfort (Humid-Tropical environments) [148]	Sangkertadi	2014	[-]	✓	✓	✓	✓
156	Thermal Resistance of Clothing (1 Clothing Layer) [149]	Jokl	1982	W/m [2]/K				✓
157	Thermal Sensation [125]	Monteiro	2010	[-]	✓	✓	✓	✓
158	Thermal Sensation (eq 1.) [150]	Rohles	1971	[-]	✓	✓
159	Thermal Sensation (eq. 2) [151]	Rohles	1971	[-]	✓	✓
160	Thermal Sensation [152]	Givoni	2004	[-]	✓		✓	✓
161	Thermal Sensation Index [109]	Xavier	2000	[-]	✓	✓	✓	✓
162	Thermal Sensation Vote (Summer) [153]	Yahia	2013	[-]	✓	✓	✓	✓
163	Thermal Sensation Vote (Winter) [153]	Yahia	2013	[-]	✓	✓	✓	✓
164	TPV index (Baghdad) [72]	Nicol	1975	[-]	✓	✓	✓	✓
165	TPV index (Roorkee) [72]	Nicol	1975	[-]	✓	✓	✓	✓
166	Tropical Summer Index [154]	Sharma	1986	°C	✓	✓	✓	✓
167	Universal Thermal Climate Index [155]	Jendritzky	2012	°C	✓	✓	✓	✓
168	Wet Bulb Globe Temperature (eq. 1) [156]	Ono	2014	°C	✓	✓	✓	✓
169	Wet Bulb Globe Temperature (eq. 2) [156]	Ono	2014	°C	✓	✓	✓	✓
170	Wet Bulb Globe Temperature (indoors)[appr:30]	Yaglou	1956	°C	✓	✓		✓
171	Wet Bulb Globe Temperature (outdoors) [appr:30]	Yaglou	1956	°C	✓	✓	✓	✓
172	Wet Bulb Temperature [97]	Liljegren	2008	°C	✓	✓	✓	✓
173	Wet Bulb Temperature [127]	Malchaire	1976	°C	✓	✓	✓	✓
174	Wet Bulb Temperature [157]	Stull	2011	°C	✓	✓
175	Wet Cooling Power [79]	Landsberg	1972	mcal/cm²/s	✓	✓	✓	✓
176	Wet Globe Temperature (Botsball)[[appr:158]]	Botsford	1971	°C	✓	✓	✓	✓
177	Wet Kata Cooling [89]	Maloney	2011	W/m²	✓	✓	✓	✓
178	Wet Kata Cooling Power [112]	Chamber of Mines of South Africa	1972	mcal/cm²/s	✓	✓	✓	✓
179	Wet Kata Cooling Power [159]	Krisha	1996	W/m²	✓	✓	✓	✓
180	Wet Kata Cooling Power [160]	Hill	1919	mcal/cm²/s	✓	✓		✓
181	Wet-Bulb Dry Temperature [130]	Wallace	2005	°C	✓	✓	✓	✓
182	Wind Chill [161]	OFCM/NOAA	2003	°C	✓			✓
183	Wind Chill [162]	Siple	1945	kg cal/m²/hr	✓			✓
184	Wind Chill [163]	Steadman	1971	cal/m²/s	✓	✓	✓	✓
185	Wind Chill Equivalent [164]	Quayle	1998	°C	✓			✓
186	Wind Chill Equivalent Temperature (wind of 1.34 m/s) [165]	Falconer	1968	°C	✓			✓
187	Winter Scharlau Index [140]	Sharlau	1950	[-]	✓	✓

Notes:
[-] no unit available for this thermal index
✓ environmental parameter required for the calculation of this thermal index
[cit:] no original article found; the equation for the identified thermal index was found in the cited publication
[appr:] the current index requires specialized equipment; an equation found in the cited publication was used for its approximation
Information on complex parameters used for the computation of some thermal indices.
In case where the calculation of a thermal index requires any of the following parameter, that parameter was translated as follows:
	Temperature	Humidity	Radiation	Wind
Mean Radiant Temperature (approximated). Proper measurement considers short- and long-wave radiation.	✓	✓*	✓	✓
Dew point	✓	✓
Wet Bulb Temperature	✓	✓	✓	✓*
Globe Temperature	✓	✓	✓	✓*
Vapor Pressure	✓	✓
Saturated Vapor Pressure	✓
Wet Bulb Globe Temperature	✓	✓	✓	✓
Psychrometric Wet Bulb Temperature	✓	✓	✓
*indirect use of a parameter incorporating that factor

Risk of bias assessment

There is no tool to assess the risk of bias in modelling studies (i.e., studies that use mathematics to describe the effect of physical phenomena on humans, on the absence of human participants). Therefore, we assessed the sources of funding for the eligible studies, as an indicator of bias. Also, we assessed the strength of the evidence presented in each study using the Evidence for Policy and Practice Information (EPPI) approach [26], which is a recommended methodology for assessing methodological quality [27]. This tool employs four criteria to evaluate each study: (1) trustworthiness (assessed as the percent of TSIs cited and described appropriately in each study; scores: 0 = 0%, 1 = 20%, 2 = 40%, 3 = 60%, 4 = 80%, and 5 = 100%), (2) appropriateness (assessed as the appropriateness of the study's research design in addressing the current review question; scores: 0 = conference abstract, 1 = book/report, 2 = meteorology/modelling article, 3 = human study, 4 = narrative review, and 5 = systematic review), (3) relevance (assessed as the relevance of each study to the current review question; all articles were given the highest score [5] in this criterion), and (4) the overall weight of each study (assessed as the average score of the previous three criteria). For instance, a study receiving a relevance score of 5 (as it has been screened for eligibility), an appropriateness score of 4 (because it is a narrative review), and a trustworthiness score of 3 (because it provides appropriate citation and description for 60% of the TSIs mentioned in its text), will have an overall weight of 4 = (5 +4 +3)/3.

Data extraction and analysis

As described in the Introduction, we present a comprehensive list of different types of TSIs in the current systematic review, yet our analysis focused primarily on indicators requiring only meteorological data (air temperature, relative humidity, wind speed, and solar radiation), as we aimed to enhance the quality and relevance of big-data analytics used in climate services for the occupational and the general populations. Independent data extraction was performed by two investigators (LGI and KM) and conflicts were resolved through consensus and supervision by a third researcher (ADF). When necessary, additional information was requested from the journals and/or the study authors via email. For all studies, we extracted the author name(s), year of publication, country of the first author, as well as all the relevant information regarding the TSIs used to describe the heat stress/strain experienced by humans. The equations describing each TSI were retrieved from the original publication or, in case where the original manuscript was not available, the equations were cross-referenced with multiple sources in scientific literature. Formulas having the same name but considering different environmental factors and/or using different equations for their computation were considered unique TSIs and were treated as such in the present systematic review. Data for non-English articles were extracted based on the provided English abstracts and the mathematical equations presented in the original manuscript. No professional English translation of these articles was performed. When deemed necessary, Google Translator was used to improve understanding and provide context.

Development of a software to calculate all meteo-based thermal stress indicators

A software titled “Thermal Stress Indicators calculator” was developed to calculate all the meteo-based TSIs using the Visual Basic programming language (Microsoft; USA). In its core, the software incorporates the assumptions and equations required for each TSI. The user can edit the assumed default values in each case by clicking “options”. In addition, the software includes a number of features to optimize practicality and user-friendliness, including a method to estimate solar radiation using geographical and chronological data [28], as well as to adjust it for cloud cover [29].

The “Thermal Stress Indicators calculator” software can be freely downloaded using the following link: www.famelab.gr/meteo-TSI.html. It runs on Microsoft Windows operating systems (XP/Vista/Win7/Win10/Win11). With the use of Windows emulators, the software can also run on Linux and Apple Macintosh platforms. The calculated data are provided in numeric format and can be exported in *.csv format.

We assessed the criterion-related validity, construct validity, and reliability of the “Thermal Stress Indicators calculator” to compute all the identified meteo-based TSIs. Criterion-related validity refers to comparing a measurement against some known quantity, while construct validity refers to the property of a measurement being associated with variables assessing the same (or similar) characteristics. Reliability in this case assessed the degree to which the calculated TSIs were consistent from one test to the next.

Qualitative assessment of meteo-based TSIs for work in hot environments

Part of our analysis focused on TSIs targeting working environments and different population groups to support research on this front and the development of effective heat mitigation measures. We used the following criteria to determine whether a TSI can assess the heat stress/strain in working people:

1. Evaluation of the activity level (i.e., whether a TSI was developed for “active” or “passive” metabolic state) [19]. Indicators developed only for passive conditions were considered non-eligible for assessing the heat stress/strain experienced by workers in occupational settings.

2. Evaluation of environmental conditions to ensure that a TSI applies to environments typically found in outdoor and indoor occupational settings.

   1. Evaluation of the operating temperature range [parameters used: air temperature, globe temperature, operative temperature, wet bulb temperature, and Wet-Bulb Globe Temperature (WBGT)] identified for each TSI: A recent systematic review identified that 62 out of 88 studies that examined health-related outcomes due to occupational heat strain reported WBGT ranges of 19.3 to 52.0°C [2]. This WBGT range was translated to air temperature by using a published method to calculate WBGT from meteorological data [30]. The environmental data we utilized were 600 W/m² solar radiation, 50 % relative humidity, and 0.5 m/s wind speed, while keeping constant WBGT values (i.e., 19.3 and 52.0°C) and solving for air temperature. It is important to note that an infinite range of environmental conditions lead to the same WBGT value. Here we chose to use environmental data which characterize the heat stress experienced by outdoor workers. The computed air temperature range was 18.2 to 56.5°C. The same environmental data were employed for the computation of the remaining parameters used to describe the operating temperature range of some thermal indices [globe temperature (32.5 to 72.0°C), operative temperature (34.8 to 72.0°C), and wet bulb temperature (15.7 to 45.7°C)]. Thereafter, these data were used to calculate the percentage of overlap between the identified operating temperature range of each TSI and the temperature ranges used in the literature for examining health-related outcomes in occupational settings. Indicators covering less than two-thirds (66.6%) of the temperature range found in the literature were considered non-eligible for assessing the heat stress and strain experienced by workers in occupational settings.
   2. Evaluation of the operating wind speed range identified for each TSI: Indicators with an operative wind speed range lower than half (50%) of the wind speed range that the United States of America Occupational Safety and Health Administration (OSHA) considers safe for work and it is not immediately dangerous for life or health. Specifically, we assumed that typical wind speed in occupational settings ranges between negligible (0 m/s) and high (17.9 m/s) air flow conditions also defined as “high wind” according to OSHA [31]. It is important to note that the majority of outdoor workplaces are characterized by much lower wind speed than the extreme value of 17.9 m/s, while working indoors involves wind speeds ranging between negligible to very low air flows (i.e., 0 to 1 m/s) [32].

3. Evaluation of the environmental parameters used by each TSI: Indicators incorporating less than two (2) environmental parameters were considered non-eligible for assessing the heat stress/strain experienced by workers in occupational settings.

Results

A total of 228 publications from the search algorithms met the eligibility criteria and were considered in the analysis (Table S1), while 664 publications were excluded as non-eligible (Table S2). Full manuscripts written in 11 languages (English: 178; Iranian: 7; Chinese: 6; French: 3; Spanish: 3; Russian: 2; Korean: 2; Japanese: 1; Polish: 1; Italian: 1; and Czech: 1) were retrieved for 89.9% (205/228; Table S1) of the identified eligible publications. An additional set of 18 publications found in the reference lists of the eligible articles as well as 14 publications (e.g., standards, reports from reputable organizations, books) were manually included in the analysis (Table S3). Overall, 237 unique publications were included in the current systematic review as shown in the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) flow-chart (Figure 1). The associated PRISMA checklist is presented in the Appendix.

Figure 1.

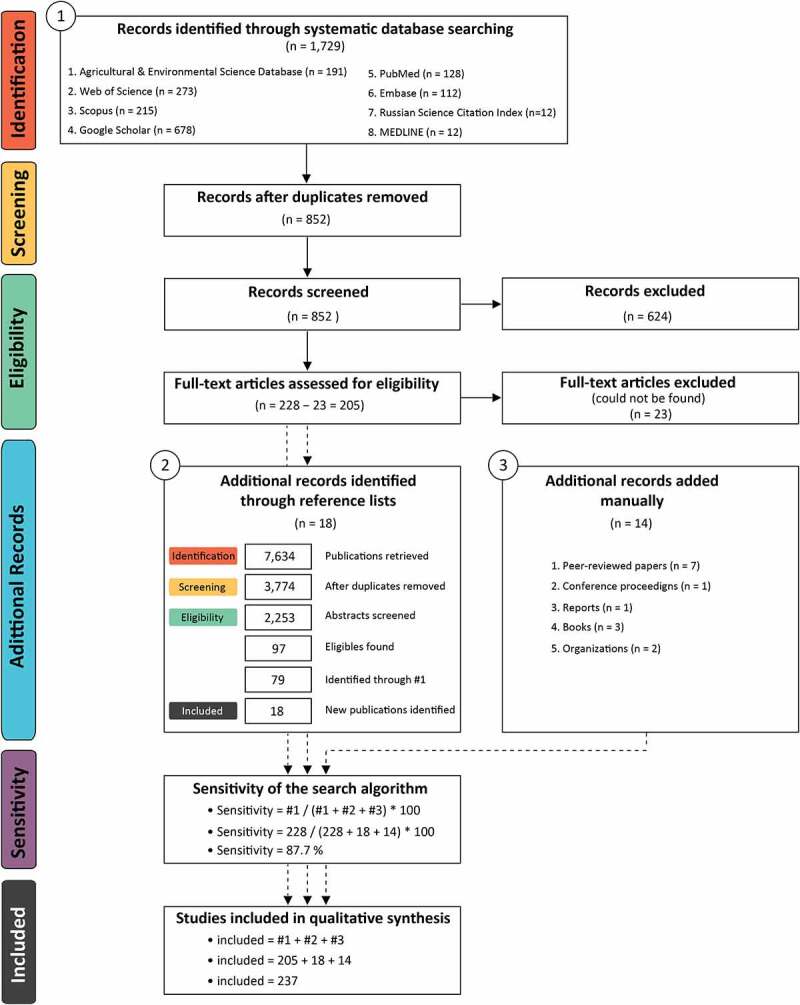
Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) flow diagram detailing the different steps of selection process, in line with PRISMA recommendation, as well as the procedures involved in the calculation of the sensitivity of the search algorithm.

The sensitivity analysis conducted demonstrated that the search algorithm captured 87.7% of all the known eligible articles that were included in the systematic review (i.e., articles from the search algorithm + articles added from detailed reference list search + articles added manually; Figure 1).

In the following subsections, we adopt established recommendations [27] to ensure a high quality of evidence synthesis in this systematic review, in a way that brings together research evidence to give an overall picture of the existing knowledge that can be used to inform policy and decisions.

Overview of thermal stress indicator literature

The majority of the analysed studies aimed to compare the technical characteristics of different TSIs – for instance, the response of different TSIs as one or more environmental, physiological, clothing, or behavioural parameters changes. In most cases, the technical characteristics for each TSI were retrieved from the original publication cited in the eligible articles (Table S4).

Analysis of the sources of funding for the eligible studies, as an indicator of bias, demonstrated that 65.4% of studies received no funding, 29.1% of studies were funded by government/public organizations, 4.2% of studies were funded by private/industry stakeholders, and 1.3% of studies received funding from governmental organizations and the industry.

In total, the average score in the EPPI tool across all studies was 3.8 ± 0.6 (mean ± sd), indicating high strength of evidence (0–1: low; 2: medium; 3–5: high). Of the 237 unique studies included in the current systematic review, 222 received a “high” score, eight studies were classified as “medium” and seven were given an overall score of “low”. More specifically, 221 studies scored “high” in the “trustworthiness” item, while five studies were classified as “medium” and 11 studies were classified as “low” in this item. With regards to the “appropriateness” item, 22 studies scored “high”, 133 studies were classified as “medium” and 57 were classified as “low”. Finally, all 237 studies were classified as “high” in the “relevance” item of the EPPI tool.

In total, our search identified 340 unique TSIs developed between 200 BC and 2019 AD. Of these, 153 TSIs required data for some or all the meteorological parameters in addition to other detailed information (Table 1), while 187 utilize only meteorological data (Table 2). The majority (123) of these meteo-based TSIs were identified through the algorithmic database search, while 64 were identified through publications found in the reference lists of the eligible studies and the manually added articles (Table S4).

The meteo-based TSIs identified in the current systematic review are widely applicable because their calculation requires freely-available weather data and their development considered the characteristics of the local populations across 35 countries in all six geographical regions (Africa, eastern Mediterranean, Europe, America, south-east Asia, and western Pacific; Figure 2). 75.4 % percent of these TSIs assess heat and/or physiological strain using air temperature and humidity, while 41.2 % utilize all four meteorological parameters (Figure 2). The first meteo-based TSI identified in our search was developed in 1905 while the last one was published in 2018 (Figure 3).

Figure 2.

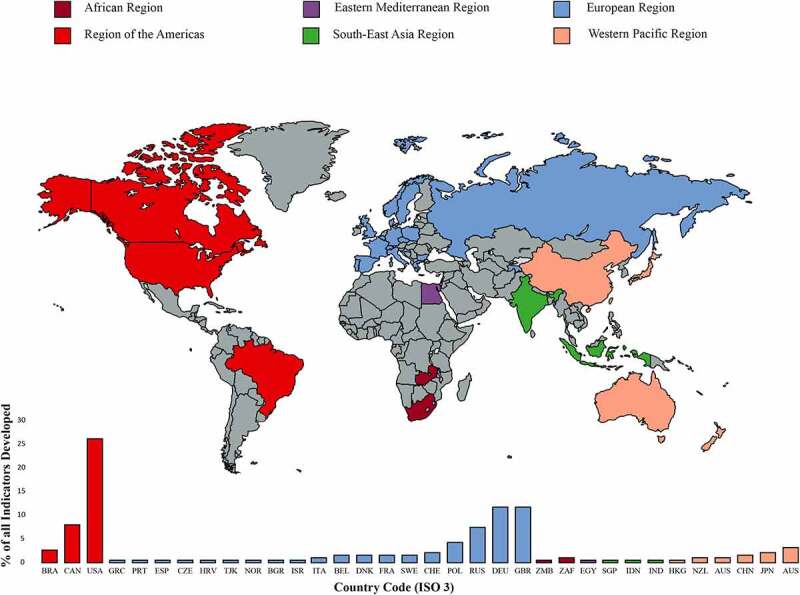
Countries (Alpha-3 code) in which the 187 meteo-based thermal stress indicators originated from, based on the affiliation of the first author. Bars represent the number of indicators developed in each country. Detailed information regarding the number of thermal stress indicators developed by each country can be found in www.famelab.gr/meteo-TSI.html.

Figure 3.

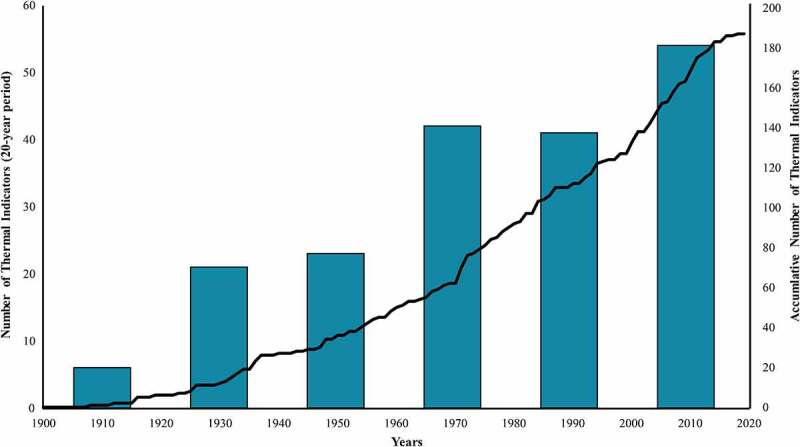
Development of the 187 thermal stress indicators (TSIs) that use only meteorological data. Bars represent the number of indices developed in chronological groups of 20 years. The black line indicates the cumulative number of TSIs developed during the last 120 years.

Preliminary synthesis

While tabulating the data, it became apparent that there were some discrepancies between the information presented in the eligible articles and those in the cited original papers. Specifically, our analysis identified nine common misconceptions regarding the use of meteo-based TSIs which are listed below with references to Table S4:

1. More than one equation, providing different results, has been reported under the same TSI name (e.g., TSI #6-16, #26-49, #81-85, #88-90, #107-110, #133-135).

2. Location-specific equations, providing different results, are given for the same TSI (e.g., TSIs #164-165).

3. Original papers provide more than one equation to calculate the same TSI (e.g., TSIs #158-159, #168-169).

4. The same equation, providing identical results, has been reported under different TSI names (e.g., TSI #176).

5. Nomograms have been partially converted to equations under the same TSI name (e.g., TSI #50-51).

6. TSIs were developed to predict the reading of specialized instruments (e.g., the Wet Bulb Thermometer) under the same TSI name based on meteorological data (e.g., TSIs #172-174).

7. Mistakes in a TSI equation are carried over in subsequent publications (e.g., TSI #56-57).

8. Reference to TSIs that do not appear in the original article (e.g., #73-75).

9. Erroneous citation of the original paper introducing a TSI (e.g., #112, #133).

All the above discrepancies were addressed upon reviewing the original article, and/or contacting the eligible article authors. To harmonize knowledge for each individual TSI identified in our search, we provide the equation, operating range, interpretation categories, as well as the physical activity mode (active or passive) that it has been designed for in Tables 5 & S5.

We found that almost all meteo-based TSIs incorporate air temperature (98.4 %), about three quarters of them incorporate humidity (76.8 %) and wind (71.9 %), while less than half incorporate sunlight (44.9 %) (Table 2; Figure 4). Even fewer TSIs incorporate all four environmental parameters (Table 2). The lists of the assumptions (Table 3), abbreviations (Table 4), equations (Table 5) , as well as the limits and categories (Table S5) required for the calculation of each of the 187 meteo-based indicators are presented below.

Figure 4.

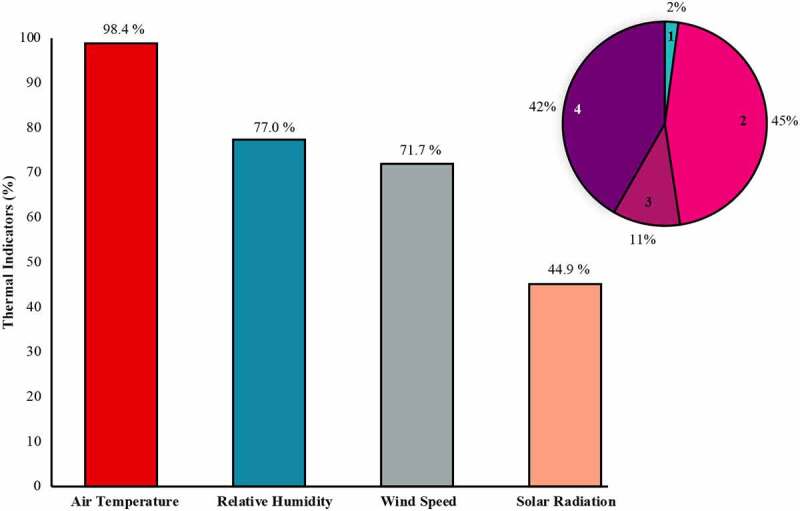
Usage of different meteorological parameters in the 187 meteorology-based thermal stress indicators (TSIs) (bars) and complexity (pie chart; i.e., number of meteorological parameters utilized by these TSIs).

Table 3.

Recommended assumptions in the calculation the meteo-based 187 TSIs for practicality or when no data are available.

ID	Assumption	Value	Assumption
1	We calculated wind at altitude using a friction coefficient for “high crops, hedges and shrubs”. [166]	α = 0.20
2	We set a standard value for workers’ body stature. [167]	Height = 1.80 m
3	We set a standard value for workers’ body mass. [168]	Weight = 75 kg
4	We assume a comfortable barometric pressure (sea level). [169]	P = 1016 hPa
5	Mean skin temperature was estimated as a function of air temperature. [112]	Tsk = f (Ta)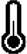
6	We set a constant emissivity of the body / clothing. [167]	ε = 0.97
7	We set a constant effective radiating area of the body (standing posture). [167]	Ar = 0.77
8	We assume a constant core temperature. This can be modified as needed.	Tcr = 37.3
9	Clothing insulation was estimated as a function of air temperature.	Icl = f (Ta)

Note: Assumptions were not adopted for the computation of all TSIs

Table 4.

| List of abbreviations used for the computation of the 187 meteo-based thermal stress indicators.

ID	Variable	Abbreviation	Formula / Value	Assumption/s
1	Air Temperature (undefined unit)	Ta	Input value
2	Relative Humidity (%)	RH	Input Value
3	Air Velocity (undefined unit)	WS	Input Value
4	Solar Radiation (undefined unit)	SR	Input Value
5	Wet Bulb Globe Temperature (undefined unit) [30]	WBGT	TSI # 171
6	Vapor Pressure (undefined unit) [168]	VP	= 6.11 * (10 ^ ((7.5 * Td[°C]) / (237.3 + Td[°C]))) ⇒ Td = TSI # 52
7	Barometric Pressure (hPa)	P	= 1016
8	Mean Radiant Temperature (undefined unit)	Tmrt	TSI # 97
9	Absolute Humidity (g/kg) [169], [170]	h	= (6.112 * Exp((17.56 * Ta[°C]) / (Ta[°C] + 243.5)) * RH * 2.1674) / ((273.15 + Ta[°C]) * 1.204 * 10 ^ 3) * 1000
10	Wet Bulb Temperature [97] (undefined unit)	Tw	TSI # 172
11	Radiant heat exchange coefficient (w/m2)	Hr	= 4 * ε * σ * Ar/ADu * ((273.2 + ((Tsk[°C] + Tmrt[°C]) / 2)) ^ 3)
12	Mean Skin Temperature [112]	Tsk	TSI # 98
13	Friction coefficient (unitless)	α	= 0.20
14	Emissivity of skin (unitless)	ε	= 0.97
15	Universal radiation constant (w/m2·K4) [171]	σ	= (5.67 * (10 ^ -8))
16	Fraction of the body affected by radiation	Ar	= 0.77
17	Globe Temperature (undefined unit) [97]	Tg	TSI # 78
18	Latent heat released by water vaporization (cal/g) [172]	r	= 585
19	Real mixture ratio (g/kg) [172]	w	= RH * ((6.112 * 10 ^ (7.5 * Ta[°C] / (237.7 + Ta[°C]))) / P) / 100
20	Specific heat of air at constant pressure (cal/°C/g) [172]	Cp	= 0.24
21	Specific heat of water (cal/°C/g) [172]	Cw	= 1
22	Body tissue thermal resistance (kcal/h/°C/m2)	Rb	= 0.08
23	Convection heat transfer coefficient (w/m2)	Hc	⇒ if WS < 1 Then = 8.7 * WS[m/s] ^ 0.6 ⇒ if WS >= 1 Then = 3.5 + 5.2 * WS[m/s]
24	Psychrometric wet bulb (undefined unit)	Tpw	TSI # 118
25	Metabolic rate (w/m2)	Met	low intensity = 100; moderate intensity = 165; and high intensity = 230
26	Body surface area (m2) [173]	ADu	= 0.202 * height[m] ^ 0.725 * weight[kg] ^ 0.425
27	Clothing insulation (clo)	Icl	Icl = 1.691 - 0.0436 * Ta[°C] ⇒ if Ta[°C] < -30 Then = 3 ⇒ if Ta[°C] > 25 Then = 0.6
28	Saturated vapor pressure (undefined unit)	SVP	= (2.7150305 * Log(Ta[k]) - 2836.5744 * Ta[k] ^ (-2) - 6028.076559 / Ta[k] + 19.54263612 - 0.02737830188 * Ta[k] + 0.000016261698 * Ta[k] ^ 2 + 7.0229056E-10 * Ta[k] ^ 3 - 1.8680009E-13 * Ta[k] ^ 4) * 0.01
29	Core temperature (°C)	Tcr	= 37.3
	Notes: “undefined unit” indicates that the variable is not characterized by the same unit for all TSIs. [subscript] condition which characterizes the variable (e.g., V10m = air velocity at a height of 10 m). [superscript] unit of the variable:
	[°C]	degrees Celsius
	[°F]	degrees Fahrenheit
	[hPa]	hectopascal
	[kPa]	kilopascal
	[mmHg]	millimeter of mercury
	[ft/min]	feet per minute
	[m/s]	meters per second
	[cm/s]	Centimeters per second
	[Btu/hr]	British thermal units per hour
	[mb]	millibar
	[mph]	miles per hour
	[cal/cm2/min]	calories per square centimeter per minute
	[Torr]	unit of pressure, Torr
	[kw/m2]	kilowatts per square meter
	[w/m2]	watts per square meter
	[K]	Kelvin
	[km/h]	kilometers per hour

Table 5.

Computation of the 187 meteo-based thermal stress indicators in BASIC programming language (^ = power notation and sqr = square root).

ID	Thermal Stress Indicator	Formula/s	Assumption/s
1	Accepted Level of Physical Activity (Blazejczyk; 2010)	= (90 - 22.4 - 0.25 * ((5 * Ta[°C]) + (2.66 * VP[hPa]))) / 0.18
2	Actual Sensation Vote (Nikolopoulou; 2003)	= 0.061 * Ta[°C] + 0.091 * TGA - 0.324 * WS[ms] + 0.003 * RH - 1.455 ⇒ TGA = Tg[°C] - Ta[°C]
3	Actual Sensation Vote (Nikolopoulou; 2004)	= 0.034 * Ta[°C] + 0.0001 * SR[w/m2] - 0.086 * WS[m/s] - 0.001 * RH - 0.412
4	Actual Sensation Vote (Europe) (Nikolopoulou; 2004)	= 0.049 * Ta[°C] + 0.001 * SR[w/m2] - 0.051 * WS[m/s] + 0.014 * RH - 2.079
5	Air Enthalpy (Boer; 1964)	= 0.24 * (Tw[°C] + (1555 / P[hPa]) * SVP[hPa])
6	Apparent Temperature (Almeida; 2010)	= -2.653 + (0.994 * Ta[°C]) + (0.0153 * Td[°C] ^ 2)
7	Apparent Temperature (Arnoldy; 1962)	= Ta[°C] - (2 * WS[m/s])
8	Apparent Temperature (Fischer; 2010)	= c1 + (c2 * Ta[°C]) + (c3 * (Ta[°C] ^ 2)) + (RH * (c4 + (c5 * Ta[°C]) + (c6 * (Ta[°C] ^ 2)))) + ((RH ^ 2) * (c7 + (c8 * Ta[°C]) + (c9 * (Ta[°C] ^ 2)))) c1 = -8.7847; c2 = 1.6114; c3 = -0.012308; c4 = 2.3385; c5 = -0.14612; c6 = 2.2117 * (10 ^ -3); c7 = -0.016425; c8 = 7.2546 * (10 ^ -4); and c9 = -3.582 * (10 ^ -6)
9	Apparent Temperature (Kalkstein; 1986)	reported by Kalkstein;1986: = -2.653 + (0.994 * Ta[°C]) + (0.368 * Td[°C]) ^ 2 ⇒ Erroneous reported by Kwon;1990:174 = -2.653 + (0.994 * Ta[°C]) + (0.368 * Td[°C])
10	Apparent Temperature (Smoyer-Tomic; 2001)	= -2.719 + 0.994 * Ta[°C] + 0.016 * Td[°C] ^ 2 ⇒ if Ta[°C] < 25 Then = Ta[°C]
11	Apparent Temperature (indoor) (Steadman; 1994)	= (0.89 * T a[°C]) + (3.82 * VP[kPa]) - 2.56
12	Apparent Temperature (indoor) (Steadman; 1984)	= -1.3 + 0.92 * Ta[°C] + 2.2 * VP[kPa]
13	Apparent Temperature (shade) (Steadman; 1984)	= -2.7 + 1.04 * Ta[°C] + 2 * VP[kPa] - 0.65 * WS10m[m/s]
14	Apparent Temperature (shade) (Steadman; 1994)	= Ta[°C] + (3.3 * VP[kPa]) - (0.7 * WS10m[m/s]) - 4
15	Apparent Temperature (sun) (Steadman; 1984)	= -1.8 + 1.07 * Ta[°C] + 2.4 * VP - 0.92 * WS + 0.044 * Qg ⇒ Qg = Hr * (Tmrt[°C] - Ta[°C])
16	Apparent Temperature (sun) (Steadman; 1994)	= Ta[°C] + (3.48 * VP[kPa]) - (0.7 * WS10m[m/s]) + (0.7 * Qg / (WS10m[m/s] + 10)) - 4.25 ⇒ Qg = Hr * (Tmrt[°C] - Ta[°C])
17	Approximated Subjective Temperature (Auliciems; 2007)	= Tg[°C] + 2.8 * (1 - Sqr(10 * WS[m/s])) / (0.44 + 0.56 * Sqr(10 * WS[m/s]))
18	Belding-Hatch Index (Belding; 1955)	= E / Emax ⇒ E = 110 + 11.6 * (1 + 1.3 * (WS[m/s] ^ 0.5)) * (Tg[°C] - 35) ⇒ Emax = 25 * (WS[m/s] ^ 0.4) * (42 – VP[mmHg])
19	Belgian Effective Temperature (Bidlot; 1947)	= 0.9 * Tw[°C] + 0.1 * Ta[°C]
20	Bioclimatic Index of Severity (Belkin; 1992)	= (Ti * (P - 266) * (1 - (0.02 * WS))) / (Ri * S * 75) Temperature coefficient (Ti): ⇒ if Ta[°C] < -90 Or Ta[°C] > 60 Then Ti = 0 ⇒ if Ta[°C] = 22 Then Ti = 1 ⇒ if Ta[°C] > 22 And Ta[°C] <= 60 Then Ti = 1 - 0.0263 * (Ta[°C] - 22) ⇒ if Ta[°C] < 22 And Ta[°C] > -90 Then Ti = 1 - 0.0089 * (22 - Ta[°C]) Relative humidity coefficient (Ri): ⇒ if RH = 50 Then RH = 50.0001 ⇒ if RH > 50 Then Ri = 1 + (0.6 * ((RH - 50) / 100)) ⇒ if RH < 50 Then Ri = 1 + (0.6 * ((50 - RH) / 100)) Radiation Coefficient (S): ⇒ S = 1 (we assume low altitude / comfortable barometric pressure) ⇒ if altitude > 2000 m then S = 1 + (0.045 * ((altitude - 2000)/ 1000))
21	Biologically Active Temperature (Tsitsenko; 1971)	= 0.8 * EET + 9 ⇒ EET = Ta[°C] * (1 - 0.003 * (100 - RH)) - (0.385 * WS2m[m/s]) ^ 0.59 * ((36.6 - Ta[°C]) + 0.622 * (WS2m[m/s] - 1)) + ((0.0015 * WS2m[m/s] + 0.0008) * (36.6 - Ta[°C]))
22	Biometeorological Comfort Index (Rodriguez; 1985)	= (Taero + Tw[°C]) / 2 ⇒ Vr[km/day] = 150 km / day (air speed relative to a person while walking in calm air) ⇒ Tcr[°C] = 37.3 ⇒ n = 0.6 * Exp(-0.01 * Ta[°C]) ⇒ cited by Garcia:1994 [175] ⇒ if Vr[km/day] >= WS[km/day] Then Taero = Ta[°C] ⇒ if Vr[km/day] < WS[km/day] Then Taero = Tcr[°C] - (((0.9311 + 0.0295 * (WS ^ n)) * (Tcr[°C] - Ta[°C])) / (0.0411 + 0.0295 * (Vr[km/day] ^ n)))
23	Bodman’s Weather Severity Index (Bodman; 1908)	= (1 - 0.04 * Ta[°C]) * (1 + 0.272 * WS[m/s])
24	Clothing Thickness (Steadman; 1971)	45 = 3.9 + 0.053 * (37 - Ta[°C]) + ((0.03 * (30 - Ta[°C])) / Rs) + ((0.12 * (30 - Ta[°C])) / (0.5 + Rs)) + ((0.85 * (30 - Ta[°C])) / (Rf + Rs)) Rs = 1 / (Hr + Hc) ⇒ surface resistance, in m2/sec/°C Rf = clothing thickness / thermal conductivity ⇒ clothing resistance in m2/sec/°C 1.3s
25	Comfort Vote (Bedford; 1936)	= 11.16 - 0.0556 * Ta[°F] - 0.0538 * Tmrt[°F] - 0.0372 * VP[mmHg] + 0.00144 * Sqr(WS[ft/min]) * (100 - Ta[°F])
26	Cooling Power (Becker; 1972)	= (0.26 + 0.34 * (WS[m/s] ^ 0.622)) * (36.5 - Ta[°C])
27	Cooling Power (Bedford; 1933)	= (0.123 + 0.465 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
28	Cooling Power (Bider; 1931)	= (0.31 + 0.112 * WS[m/s])) * (36.5 - Ta[°C])
29	Cooling Power (Bradtke; 1926)	= (0.1 + 0.403 * Sqr(WS[m/s])) * (36.5 - Ta[°C]) ^ 1.06
30	Cooling Power (Buttner; 1934)	= (0.23 + 0.47 * WS[m/s] ^ 0.52) * (36.5 - Ta[°C])
31	Cooling Power (Cena; 1966)	= (0.412 + 0.087 * WS[m/s]) * (36.5 - Ta[°C])
32	Cooling Power (Dorno; 1925)	= (0.22 + 0.25 ^ 1.5 * Sqr(WS[m/s])) * (33 - Ta[°C])
33	Cooling Power (Dorno; 1934)	= (0.22 + 0.25 ^ 1.5 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
34	Cooling Power (eq. 1) (Goldschmidt; 1952)	= (0.25 + 0.2 ^ 1.1 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
35	Cooling Power (eq. 2) (Goldschmidt; 1952)	= (0.3 + 0.16 * WS[m/s]) * (36.5 - Ta[°C])
36	Cooling Power (Henneberger; 1948)	= (0.276 + 0.117 * WS[m/s]) * (36.5 - Ta[°C])
37	Cooling Power (Hill; 1916)	⇒ if WS[m/s] =< 1 then = (36.5 - Ta[°C]) * (0.2 + 0.4 * Sqr(WS[m/s])) * 41.868 ⇒ if WS[m/s] > 1then = (36.5 - Ta[°C]) * (0.13 + 0.47 * Sqr(WS[m/s])) * 41.868
38	Cooling Power (eq. 1) (Hill; 1937)	= (0.105 + 0.485 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
39	Cooling Power (eq. 2) (Hill; 1937)	= (0.205 + 0.385 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
40	Cooling Power (Lahmayer; 1932)	= (0.22 + 0.2 ^ 1.3 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
41	Cooling Power (eq. 1) (Matzke; 1954)	= (0.249 + 0.258 * WS[m/s] ^ 0.616) * (36.5 - Ta[°C])
42	Cooling Power (eq. 2) (Matzke; 1954)	= (0.441 + 0.096 * WS[m/s]) * (36.5 - Ta[°C])
43	Cooling Power (Meissner; 1932)	= (0.275 + 0.251 * WS[m/s] ^ 0.7) * (36.5 - Ta[°C])
44	Cooling Power (Vinje; 1962)	⇒ if WS[m/s] > 1 And WS[m/s] <= 12 Then = 0.57 * (WS[m/s] ^ 0.42) * (36.5 - Ta[°C]) ⇒ if WS10m[m/s] > 12 Then = (0.46 + 0.08 * WS10m[m/s]) * (36.5 - Ta[°C])
45	Cooling Power (Weiss; 1926)	= (0.14 + 0.49 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
46	Cooling Power (Angus; 1930)	= Sqr(0.29 * (0.26 + WS[m/s])) * (36.5 - Ta[°C])
47	Cooling Power (Lehmann; 1936)	= (0.113 + 0.34 * WS[m/s] ^ 0.622) * (36.5 - Ta[°C])
48	Cooling Power (Joranger; 1955)	= (0.375 + 0.316 * Sqr(WS[m/s])) * (36.5 - Ta[°C])
49	Cooling Power (Wet Air Temperature) (Hill; 1916)	= h + 41.868 * (0.085 + 0.102 * (WS[m/s] ^ 0.3)) * (61.1 – VP[hPa]) ^ 0.75 ⇒ if WS[m/s] =< 1 then h = (36.5 - Ta[°C]) * (0.2 + 0.4 * Sqr(WS[m/s])) * 41.868 ⇒ if WS[m/s] > 1 then h = (36.5 - Ta[°C]) * (0.13 + 0.47 * Sqr(WS[m/s])) * 41.868
50	Corrected Effective Temperature (Basic) (Auliciems; 2007)	= (0.944 * Tg[°C] - 0.056 * Tw[°C]) / (1 + 0.022 * (Tg[°C] - Tw[°C]))
51	Corrected Effective Temperature (Normal) (Auliciems; 2007)	= (1.21 * Tg[°C] - 0.21 * Tw[°C]) / (1 + 0.029 * (Tg[°C] - Tw[°C]))
52	Dew Point (Bruce; 1916)	= 237.3 * (Log(RHD) / 17.27 + Ta[°C] / (237.3 + Ta[°C])) / (1 - Log(RHD) / 17.27 - Ta[°C] / (237.3 + Ta[°C])) ⇒ RHD = RH / 100
53	Discomfort Index (Giles; 1990)	= Ta[°C] - 0.55 * (1 - 0.01 * RH) * (Ta[°C] - 14.5)
54	Discomfort Index (Kawamura; 1965)	= 0.99 * Ta[°C] + 0.36 * Td[°C] + 41.5
55	Discomfort Index (Tennenbaum; 1961)	= (Ta[°C] + Tw[°C]) / 2
56	Discomfort Index (eq. 1) (Thom; 1959)	= (0.4 * Tw[°C]) + (0.4 * Ta[°C]) + 8.3
57	Discomfort Index (eq. 2) (Thom; 1959)	= 0.4 * (Ta[°F] + Tw[°F]) + 15
58	Discomfort Index (Weather Services of South Africa; 2018)	= (2 * Ta[°C]) + (RH / 100 * Ta[°C]) + 24
59	Draught Risk Index (Fanger; 1987)	= (3.143 * (34 - Ta[°C]) * (WS[m/s] - 0.05) ^ 0.6233) + (0.3696 * WS[m/s] * Tu * (34 - Ta[°C]) * (WS[m/s] - 0.05) ^ 0.6233) ⇒ if result > 100 then result = 100 ⇒ if WS[m/s] < 0.05 Then WS[m/s] = 0.05 “The parameter Tu can simply be defined as the ratio between standard deviation of instantaneous air speeds (Vsd) and the mean air speed (V), both of which are derived from anemometry, having time-constants of 1/10 S or faster” [176]
60	Dry Kata Cooling (Maloney; 2011)	⇒ if WS[m/s] = 0 Then = 0.27 * ((36.5 - Ta[°C]) ^ 1.06) * 41.84 ⇒ if WS[m/s] > 0 And WS[m/s] < 1 Then = 0.2 + 0.4 * (WS[m/s] ^ 0.5) * (36.5 - Ta[°C]) * 41.84 ⇒ if WS[m/s] >= 1 Then = 0.13 + 0.47 * (WS[m/s] ^ 0.5) * (36.5 - Ta[°C]) * 41.84
61	Effective Radiant Field (Gagge; 1967)	= Hr * (Tmrt[°C] - Ta[°C])
62	Effective Radiant Field (Nishi; 1981)	= 0.76 * (6.1 + 13.6 * Sqr(WS[m/s])) * (Tg[°C] - Ta[°C])
63	Effective Temperature (Houghten; 1923)	= Ta[°C] - 0.4 * (Ta[°C] - 10) * (1 - (RH / 100))
64	Effective Temperature (Missenard; 1933)	= 37 - ((37 - Ta[°C]) / (0.68 - 0.0014 * RH + (1 / (1.76 + (1.4 * (WS[m/s] ^ 0.75)))))) - 0.29 * Ta[°C] * (1 - (0.01 * RH))
65	Environmental Stress Index (Moran; 2001)	= (0.63 * Ta[°C]) - (0.03 * RH) + (0.002 * SR[w/m2]) + (0.0054 * (Ta[°C] * RH)) - (0.073 * (0.1 + SR[w/m2]) ^ -1)
66	Equatorial Comfort Index (Webb; 1960)	= Tw[°F] + 0.447 * (Ta[°F] - Tw[°F]) - 0.231 * (WS[ft/min] ^ 0.5)
67	Equivalent Effective Temperature (Aizenshtat; 1974)	= Ta[°C] * (1 - 0.003 * (100 - RH)) - 0.385 * (WS[m/s] ^ 0.59) * ((36.6 - Ta[°C]) + 0.662 * (WS[m/s] - 1)) + ((0.0015 * WS[m/s] + 0.0008) * (36.6 - Ta[°C]) - 0.0167) * (100 - RH)
68	Equivalent Effective Temperature (Aizenshtat; 1982)	= Ta[°C] * (1 - 0.003 * (100 - RH)) - (0.385 * WS2m[m/s]) ^ 0.59 * ((36.6 - Ta[°C]) + 0.622 * (WS2m[m/s] - 1)) + ((0.0015 * WS2m[m/s] + 0.0008) * (36.6 - Ta[°C]))
69	Equivalent Temperature (Bedford; 1936)	= (0.522 * Ta[°F]) + (0.478 * Tmrt[°F]) - 0.0147 * Sqr(WS[ft/min]) * (100 - Ta[°F])
70	Equivalent Temperature (Brundl; 1984)	= Ta[°C] * w * (r - 2.326 * Ta[°C]) / (cp + w * cw) ⇒ if Ta[°C] = 0 then = 0
71	Equivalent Warmth (Bedford; 1936)	= 9.979 * x - 0.1495 * (x ^ 2) - 2.89 ⇒ x = ((0.0556 * Ta[°F]) + (0.0538 * Tmrt[°F]) + (0.0372 * VP[mmHg]) - (0.00144 * Sqr(WS[ft/min]) * (100 - Ta[°F])))
72	Exposed Skin Temperature (Brauner; 1995)	= Tcr[°C] – (Qs * Rb) ⇒ Qs = (Tcr[°C] - Ta[°C]) / (Rb + (1 / Hc))
73	Facial Skin Temperature (Cheek) (Adamenko; 1972)	= 0.4 * Ta[°C] - 3.3 * Sqr(WS[m/s]) + 19
74	Facial Skin Temperature (Ear Lobe) (Adamenko; 1972)	= 0.4 * Ta[°C] - 3.3 * Sqr(WS[m/s]) + 12
75	Facial Skin Temperature (Nose) (Adamenko; 1972)	= 0.4 * Ta[°C] - 3.3 * Sqr(WS[m/s]) + 17
76	Fighter Index of Thermal Stress (Direct Sunlight) (Stribley; 1978)	= (0.8281 * Tpw[°C]) + (0.3549 * Ta[°C]) + 5.08
77	Fighter Index of Thermal Stress (Moderate Overcast) (Stribley; 1978)	= (0.8281 * Tpw[°C]) + (0.3549 * Ta[°C]) + 2.23
78	Globe Temperature (Liljegren; 2008)	= Solve by iteration method: f (Ta, RH, SR, WS)
79	Heart Rate (Fuller; 1966)	= 0.029 * Met[Btu/hr] + 0.7 * (Ta[°F] + VP[mmHg])
80	Heart Rate Safe limit (LaFleur; 1971)	= (206.4 - 0.63 * (Ta[°F] + VP[mmHg])) - 10
81	Heat Index (Blazejczyk; 2012)	= -8.784695 + 1.61139411 * Ta[°C] + 2.338549 * RH - 0.14611605 * Ta[°C] * RH - (1.2308094 * (10 ^ -2)) * (Ta[°C] ^ 2) - (1.6424828 * (10 ^ -2)) * (RH ^ 2) + (2.211732 * (10 ^ -3)) * (Ta[°C] ^ 2) * RH + (7.2546 * (10 ^ -4)) * Ta[°C] * (RH ^ 2) - (3.582 * (10 ^ -6)) * (Ta[°C] ^ 2) * (RH ^ 2)
82	Heat Index (Stull; 2000)	= 16.923 + ((1.85212 * 10 ^ -1) * Ta[°F]) + (5.37941 * RH) - ((1.00254 * 10 ^ -1) * Ta[°F] * RH) + ((9.41695 * 10 ^ -3) * Ta[°F] ^ 2) + ((7.28898 * 10 ^ -3) * RH ^ 2) + ((3.45372 * 10 ^ -4) * Ta[°F] ^ 2 * RH) - ((8.14971 * 10 ^ -4) * Ta[°F] * RH ^ 2) + ((1.02102 * 10 ^ -5) * Ta[°F] ^ 2 * RH ^ 2) - ((3.8646 * 10 ^ -5) * Ta[°F] ^ 3) + ((2.91583 * 10 ^ -5) * RH ^ 3) + ((1.42721 * 10 ^ -6) * Ta[°F] ^ 3 * RH) + ((1.97483 * 10 ^ -7) * Ta[°F] * RH ^ 3) - ((2.18429 * 10 ^ -8) * Ta[°F] ^ 3 * RH ^ 2) + ((8.43296 * 10 ^ -10) * Ta[°F] ^ 2 * RH ^ 3) - ((4.81975 * 10 ^ -11) * Ta[°F] ^ 3 * RH ^ 3)
83	Heat Index (National Oceanic and Atmospheric Administration; 2014)	If Ta[°F] <= 40 Then = Ta[°F] ElseIf Ta[°F] < 80 Then = A ElseIf (RH <= 13) = True And (80 <= Ta[°F] And Ta[°F] <= 112) = True Then = B - ((13 - RH) / 4) * Sqr((17 - Abs(Ta[°F] - 95)) / 17) ElseIf (RH > 85) = True And (80 <= Ta[°F] And Ta[°F] <= 87) = True Then = B + ((RH - 85) / 10) * ((87 - Ta[°F]) / 5) Else = B End If ⇒ A = 0.5 * (Ta[°F] + 61 + ((Ta[°F] - 68) * 1.2) + (RH * 0.094)) ⇒ B = -42.379 + 2.04901523 * Ta[°F] + 10.14333127 * RH - 0.22475541 * Ta[°F] * RH - 0.00683783 * Ta[°F] * Ta[°F] - 0.05481717 * RH * RH + 0.00122874 * Ta[°F] * Ta[°F] * RH + 0.00085282 * Ta[°F] * RH * RH - 0.00000199 * Ta[°F] * Ta[°F] * RH * RH
84	Heat Index (Patricola; 2010)	= -42.4 + 2.05 * Ta[°F] + 10.1 * RH - 0.225 * (Ta[°F] * RH) - 6.84 * (10 ^ -3) * (Ta[°F] ^ 2) - 5.48 * (10 ^ -2) * (RH ^ 2) + 1.23 * (10 ^ -3) * (Ta[°F] ^ 2 * RH) + 8.53 * (10 ^ -4) * (Ta[°F] * RH ^ 2) - 1.99 * (10 ^ -6) * (Ta[°F] ^ 2 * RH ^ 2) ⇒ if Ta[°F] <= 80 Or RH <= 40 Then = Ta[°F]
85	Heat Index (Rothfusz; 1990)	= -42.379 + 2.04901523 * Ta[°F] + 10.14333127 * RH - 0.22475541 * Ta[°F] * RH - 0.00683783 * Ta[°F] * Ta[°F] - 0.05481717 * RH * RH + 0.00122874 * Ta[°F] * Ta[°F] * RH + 0.00085282 * Ta[°F] * RH * RH - 0.00000199 * Ta[°F] * Ta[°F] * RH * RH
86	Humidex (Masterson; 1979)	= Ta[°C] + 0.5555 * (6.11 * Exp(5417.753 * ((1 / 273.15) - (1 / (Td[°C] + 273.15)))) - 10)
87	Humisery (Weiss; 1982)	= Ta[°C] + Tda + WSa + Ea Dew point adjustment (Tda): ⇒ If Td[°C] <= 20 Then Tda = 0 ⇒ If Round(Td[°C], 0) = 21 Then Tda = 1 ⇒ If Round(Td[°C], 0) = 22 Then Tda = 3 ⇒ if Round(Td[°C], 0) = 23 Then Tda = 4 ⇒ if Round(Td[°C], 0) = 24 Then Tda = 6 ⇒ if Round(Td[°C], 0) = 25 Then Tda = 7 ⇒ if Round(Td[°C], 0) = 26 Then Tda = 9 ⇒ if Round(Td[°C], 0) = 27 Then Tda = 11 ⇒ if Round(Td[°C], 0) = 28 Then Tda = 13 ⇒ if Round(Td[°C], 0) = 29 Then Tda = 14 ⇒ if Round(Td[°C], 0) = 30 Then Tda = 16 ⇒ if Round(Td[°C], 0) = 31 Then Tda = 18 Wind Speed adjustment (WSa): ⇒ if WS[m/s] = 0 Then WSa = 0 ⇒ if Round(WS[m/s], 0) = 1 Then WSa = 0 ⇒ if Round(WS[m/s], 0) = 2 Then WSa = 0 ⇒ if Round(WS[m/s], 0) = 3 Then WSa = -2 ⇒ if Round(WS[m/s], 0) = 4 Then WSa = -3 ⇒ if Round(WS[m/s], 0) >= 5 Then WSa = -4 Elevation adjustment (Ea): ⇒ if Elevation = 0 then Ea = 0 (in the current study we assume no elevation) ⇒ if Elevation = 300 then Ea = -1 ⇒ if Elevation = 600 then Ea = -1 ⇒ if Elevation = 900 then Ea = -2 ⇒ if Elevation = 1200 then Ea = -2 ⇒ if Elevation = 1500 then Ea = -3
88	Humiture (Lally; 1960)	= Ta[°F] + humits ⇒ humits = VP[mb] - 10
89	Humiture (Weiss; 1982)	= Ta[°C] + Td[°C] - 18
90	Humiture (Hevener; 1959)	= (Ta[°C] + Tw[°C]) / 2
91	Humiture (Wintering; 1979)	= Ta[°F] + (VP[mb] – 21)
92	Insulation Predicted Index (Blazejczyk; 2011)	= Itot – Ia ⇒ Itot = 0.082 * (91.4 - (1.8 * Ta[°C] + 32)) / 2.3274 ⇒ Insulation of clothing and surrounding air layer ⇒ Ia = 1 / (0.61 + 1.9 * (WS[m/s] ^ 0.5)) ⇒ Insulation of air layer
93	Integrated Index (indoor) (Junge; 2016)	= (Ta[°C] * RH) / Sqr(WS[m/s])
94	Integrated Index (outdoor) (Junge; 2016)	= ((0.7 * Ta[°C] + 0.3 * Tg[°C]) * RH) / Sqr(WS[m/s])
95	Internal Comfort Temperature (Xavier; 2000)	= (S + 4.8689) / 0.2107 ⇒ S = 0.219 * OT + 0.012 * RH - 0.547 * WS[m/s] - 5.83 ⇒ OT = (Ta[°C] + Tmrt[°C]) / 2
96	Kata Index (Zhongpeng; 2012)	If WS < 1 Then = (0.35 + 0.85 ^ 3 * (WS[m/s]/ (1/3)) * (36.5 - Tw[°C])) If WS >= 1 Then = (0.1 + 1.1 ^ 3 * (WS[m/s]/ (1/3)) * (36.5 - Tw[°C]))
97	Mean Radiant Temperature (approximated) (Ramsey; 2001)	= ((Tg[°C] + 273.15) ^ 4 + 1.335 * WS[m/s] ^ 0.71 * (Tg[°C] - Ta[°C]) / (0.95 * 0.15 ^ 0.4) * 100000000) ^ 0.25 - 273.15
98	Mean Skin Temperature (McPherson; 1993)	= 24.85 + 0.322 * Ta[°C] - 0.00165 * (Ta[°C] ^ 2)
99	Meditteranean Outdoor Comfort Index (Salata; 2016)	= -4.068 - 0.272 * WS[m/s] + 0.005 * RH + 0.083 * Tmrt[°C] + 0.058 * Ta[°C] + 0.264 * Icl
100	Missenard’s Index (Missenard; 1969)	= Ta[°C] - 0.4 * (Ta[°C] - 10) * (RH / 100)
101	Modified Discomfort Index (Moran; 1998)	= (0.75 * Tw[°C]) + (0.3 * Ta[°C])
102	Modified Environmental Stress Index (Moran; 2003)	= 0.62 * Ta[°C] - 0.007 * RH + 0.002 * SR[w/m2] + 0.0043 * (Ta[°C] * RH) - 0.078 * (0.1 + SR[w/m2]) ^ -1
103	Natural Wet Bulb Temperature (Maloney; 2011)	= 0.85 * Ta[°C] + 0.17 * RH - 0.61 * (WS[m/s] ^ 0.5) + 0.0016 * SR[w/m2] - 11.62
104	Nett Radiation (Cena; 1984)	= Hr * (Tmrt[°C] - Tsk[°C])
105	New Wind Chill (NOAA; 2001)	= 35.74 + 0.6215 * Ta[°F] - 35.75 * (WS[mph] ^ 0.16) + 0.4275 * Ta[°F] * (WS[mph] ^ 0.16)
106	Normal Equivalent Effective Temperature (Boksha; 1980)	= 0.8 * EET + 7 ⇒ EET = Ta[°C] * (1 - 0.003 * (100 - RH)) - (0.385 * WS2m[m/s]) ^ 0.59 * ((36.6 - Ta[°C]) + 0.622 * (WS2m[m/s] - 1)) + ((0.0015 * WS2m[m/s] + 0.0008) * (36.6 - Ta[°C]))
107	Operative Temperature (ASHRAE; 2004)	= (Tmrt[°C] + Ta[°C]) / 2
108	Operative Temperature (ISO 7726:1998; 1998)	= (Ta[°C] * Sqr(10 * WS[m/s]) + Tmrt[°C]) / (1 + Sqr(10 * WS[m/s]))
109	Operative Temperature (ISO 7730:1994; 1994)	= A * Ta[°C] + (1 - A) * Tmrt[°C] ⇒ A = 0.73 * (WS[m/s] ^ 0.2) Note: ISO 7730:1994 proposes a simplified approximation of coefficient A as function of air velocity. Hence, we used a simplified approximation found in literature.; [177]
110	Operative Temperature (Winslow; 1937)	= ((Hr * Tmrt[°C]) + (Hc * Ta[°C])) / (Hr + Hc)
111	Outdoor Standard Effective Temperature (Skinner; 2001)	= (WBGT - 11.76) / 0.405
112	Oxford Index (Lind; 1957)	= 0.85 * Tw[°C] + 0.15 * Ta[°C]
113	Perceived Equivalent Temperature (Monteiro; 2010)	= -3.777 + 0.4828 * Ta[°C] + 0.5172 * Tmrt[°C] + 0.0802 * RH - 2.322 * WS[m/s]
114	Perceived Temperature (Linke; 1926)	= Ta[°C] - (4 * WS) + (12 * SR[cal/cm2/min])
115	Predicted Percentage Dissatisfied (Xavier; 2000)	= 18.94 * (S ^ 2) - 0.24 * S + 24.41 ⇒ S = 0.219 * OT + 0.012 * RH - 0.547 * WS[m/s] - 5.83 ⇒ OT = (Ta[°C] + Tmrt[°C]) / 2 ⇒ if S > 2 OR S < -2 then = 100
116	Predicted Thermal Sensation Vote (Cheng; 2008)	= 0.1895 * Ta[°C] - 0.7754 * WS[m/s] + 0.0028 * SR[w/m2] + 0.1953 * h - 8.23
117	Psychrometric Wet Bulb Temperature (Malchaire; 1976)	= ((0.16 * (Tg[°C] - Ta[°C]) + 0.8) / 200) * (560 - 2 * RH - 5 * Ta[°C]) - 0.8 + Tw[°C]
118	Psychrometric Wet Bulb Temperature (McPherson; 2008)	Solve by iteration method: [30] = f (Ta, RH, WS)
119	Radiative Effective Temperature (Blazejczyk; 2004)	= TE[°C] + (1 - 0.01 * albedo) * SR[w/m2] * ((0.0155 - 0.00025 * TE[°C]) - (0.0043 - 0.00011 * TE[°C])) ⇒ If WS <= 0.2 Then TE = Ta[°C] - 0.4 * (Ta[°C] - 10) * (1 - 0.01 * RH) ⇒ If WS > 0.2 Then TE = 37 - ((37 - Ta[°C]) / (0.68 - 0.0014 * RH + (1 / (1.76 + (1.4 * (WS ^ 0.75)))))) - 0.29 * Ta[°C] * (1 - (0.01 * RH)) ⇒ We assume skin albedo for pigmented individuals = 0.11, based on index #120 below
120	Radiation Equivalent Effective Temperature (Non-Pigmented) (Sheleihovskyi; 1948)	= 125 * Log(1 + 0.02 * Ta[°C] + 0.001 * (Ta[°C] - 8) * (RH - 60) - 0.045 * (33 - Ta[°C]) * Sqr(WS[m/s]) + 0.185 * X) ⇒ X = SR[cal/cm2/min] * (1 – albedo) ⇒ Skin albedo for pigmented individuals = 0.11
121	Radiation Equivalent Effective Temperature (Pigmented) (Sheleihovskyi; 1948)	= 125 * Log(1 + 0.02 * Ta[°C] + 0.001 * (Ta[°C] - 8) * (RH - 60) - 0.045 * (33 - Ta[°C]) * Sqr(WS[m/s]) + 0.185 * X) ⇒ X = SR[cal/cm2/min] * (1 – albedo) ⇒ Skin albedo for non-pigmented individuals = 0.28
122	Relative Humidity Dry Temperature (Wallace; 2005)	= (0.1 * RH) + (0.9 * Ta[°C])
123	Relative Strain Index (Kyle; 1992)	= (Ta[°C] - 21) / (58 – VP[hPa])
124	Relative Strain Index (Lee; 1966)	= (10.7 + 0.74 * (Ta[°C] - 35)) / (44 – VP[mmHg])
125	Revised Wind Chill Index (Court; 1948)	= (10.9 * Sqr(WS[m/s]) + 9 - WS[m/s]) * (33 - Ta[°C])
126	Robaa’s Index (Robaa; 2003)	= (1.53 * Ta[°C]) - (0.32 * Tw[°C]) - (1.38 * WS[m/s]) + 44.65
127	Saturation Deficit (Flugge; 1912)	= SVP[hPa] – VP[hPa]
128	Severity Index (Osokin; 1968)	= (1 - 0.06 * Ta[°C]) * (1 + 0.2 * WS[m/s]) * (1 + 0.0006 * Elevation) * Kb * AC Elevation = 0 m (we assume sea level altitude) Relative humidity: ⇒ if RH <= 60 Then Kb = 0.9 ⇒ if RH > 60 And RH <= 70 Then Kb = 0.95 ⇒ if RH > 70 And RH <= 80 Then Kb = 1 ⇒ if RH > 80 And RH <= 90 Then Kb = 1.05 ⇒ if RH > 90 And RH <= 100 Then Kb = 1.1 Diurnal temperature (DTR): (e.g., the variation between a high temperature and a low temperature that occurs during the same day). ⇒ if DTR <= 4 °C then AC = 0.85 ⇒ if DTR > 4 °C And DTR <= 6 °C Then AC = 0.90 ⇒ if DTR > 4 °C And DTR <= 6 °C Then AC = 0.90 ⇒ if DTR > 6 °C And DTR <= 8 °C Then AC = 0.95 ⇒ if DTR > 8 °C And DTR <= 10 °C Then AC =1.00 ⇒ if DTR > 10 °C And DTR <= 12 °C Then AC = 1.05 ⇒ if DTR > 12 °C And DTR <= 14 °C Then AC = 1.10 ⇒ if DTR > 14 °C And DTR <= 16 °C Then AC = 1.15 ⇒ if DTR > 18 °C And DTR <= 20 °C Then AC = 1.20 ⇒ if DTR > 18 °C Then AC = 1.25
129	Simple Index (Moran; 2001)	= 0.66 * Ta[°C] + 0.09 * RH + 0.0035 * SR[w/m2]
130	Simplified Radiation Equivalent Effective Temperature (Boksha; 1980)	= 0.8 * EET + 12 ⇒ EET = Ta[°C] * (1 - 0.003 * (100 - RH)) - (0.385 * WS2m[m/s]) ^ 0.59 * ((36.6 - Ta[°C]) + 0.622 * (WS2m[m/s] - 1)) + ((0.0015 * WS2m[m/s] + 0.0008) * (36.6 - Ta[°C]))
131	Simplified Tropical Summer Index (Auliciems; 2007)	= ((1 / 3) * Tw[°C]) + ((3 / 4) * Tg[°C]) - (2 * Sqr(WS[m/s]))
132	Simplified Universal Thermal Climate Index (Blazejcyk; 2011)	= 3.21 + 0.872 * Ta[°C] + 0.2459 * Tmrt - 2.5078 * WS[m/s] - 0.0176 * RH
133	Simplified Wet Bulb Globe Temperature (American College of Sports Medicine; 1984)	= 0.567 * Ta[°C] + 0.393 * VP[hPa] + 3.94
134	Simplified Wet Bulb Globe Temperature (Gagge; 1976)	= 0.567 * Ta[°C] + 0.216 * VP[hPa] + 3.38
135	Skin Temperature (Blazejczyk; 2005)	= (26.4 + 0.02138 * Tmrt[°C] + 0.2095 * Ta[°C] - 0.0185 * RH - 0.009 * WS) + 0.6 * (Icl - 1) + 0.00128 * Met ⇒ Met = 135 W/m2 ⇒ “metabolism in standard applications” [135].
136	Skin Wettedness (Blazejczyk; 2005)	= 1.031 / (37.5 - Tsk[°C]) - 0.065 ⇒ if Tsk[°C] > 36.5 Then = 1 ⇒ if Tsk[°C] < 22 Then = 0.001 Tsk[°C] = (26.4 + 0.02138 * Tmrt[°C] + 0.2095 * Ta[°C] - 0.0185 * RH - 0.009 * WS) + 0.6 * (Icl - 1) + 0.00128 * Met Met = 135 W/m2 ⇒ “metabolism in standard applications” [135].
137	Standard Operative Temperature (Gagge; 1940)	= Tsk[°C] - (Heat_Loss / 5.2) ⇒ Heat_Loss = Ko * (Tsk[°C] - OT) ⇒ Ko = 0.75 * (4 * 4.92 * 10 ^ -8) * ((Tmrt[°C] ^ 3 + (273 + 35) ^ 3) / 2) + 1 ⇒ OT = ((Hr * Tmrt[°C]) + (Hc * Ta[°C])) / (Hr + Hc)
138	Subjective Temperature (McIntyre; 1973)	⇒ if WS[m/s] <= 0.1 Then = 0.56 * Ta[°C] + 0.44 * Tmrt[°C] ⇒ if WS[m/s] > 0.1 Then = (0.44 * Tmrt[°C] + 0.56 * (5 - Sqr(10 * WS[m/s]) * (5 - Ta[°C]))) / (0.44 + 0.56 * Sqr(10 * WS[m/s]))
139	Sultriness Index (Scharlau; 1943)	⇒ if VP[Torr] > 14.08 Then = Sultriness ⇒ if VP[Torr] <= 14.08 Then = Comfort
140	Sultriness Intensity (Akimovich; 1971)	⇒ if VP < 18.8 Then = 0 ⇒ if VP = 18.8 Then = 1 ⇒ if VP > 18.8 Then =((VP - 18.8) / 2) + 1
141	Summer Scharlau Index (Scharlau; 1950)	= Tc - Ta[°C] ⇒ Tc = (-17.089 * Log(RH)) + 94.979 ⇒ critical temperature
142	Summer Simmer Index (Pepi; 1987)	= 1.98 * (Ta[°F] - (0.55 - 0.55 * (RH / 100)) * (Ta[°F] - 58)) - 56.83
143	Swedish Wet Bulb Globe Temperature (Eriksson; 1974)	⇒ if WS[m/s] >= 0.5 Then = 0.7 * Tpw[°C] + 0.3 * Tg[°C] ⇒ if WS[m/s] < 0.5 Then = 0.7 * Tpw[°C] + 0.3 * Tg[°C] + 2
144	Temperature Humidity Index (Schoen; 2005)	= Ta[°C] - 1.0799 * Exp(0.03755 * Ta[°C]) * (1 - Exp(0.0801 * (VP[hPa] - 14)))
145	Temperature Humidity Index (Costanzo; 2006)	= Ta[°C] - 0.55 * (1 - 0.001 * RH) * (Ta[°C] - 14.5)
146	Temperature Humidity Index (INMH; 2000)	= (Ta[°C] * 1.8 + 32) - (0.55 - 0.0055 * RH) * ((Ta[°C] * 1.8 + 32) - 58)
147	Temperature Humidity Index (Kyle; 1994)	= Ta[°C] - (0.55 - 0.0055 * RH) * (Ta[°C] - 14.5)
148	Temperature Humidity Index (Nieuwolt; 1977)	= 0.8 * Ta[°C] + ((RH * Ta[°C]) / 500)
149	Temperature Humidity Index (eq. 1) (Pepi; 1987)	= Ta[°F] - (0.55 - 0.55 * (RH / 100)) * (Ta[°F] - 58)
150	Temperature Humidity Index (eq. 2) (Pepi; 1987)	= 0.55 * Ta[°F] + 0.2 * Td[°F] + 17.5
151	Temperature of the exhaled air (McPherson; 1993)	= 32.6 + 0 / 66 * Ta[°C] + 0.0002 * VP[hPa]
152	Temperature Resultante Miniere (Vogt; 1978)	= (0.7 * Tw[°C]) + (0.3 * Ta[°C]) – WS[m/s]
153	Temperature Wind Speed Humidity Index (Zaninovic; 1992)	= 1.004 * (Th1 + ((1555 / P) * ETH)) ⇒ Th1 =36.5 - (((0.902 + 0.063 * (WS[m/s] ^ 1.072)) * (36.5 - Tw[°C])) / 0.902) ⇒ Th2 = 36.5 - (((0.902 + 0.063 * (WS[m/s] ^ 1.072)) * (36.5 - Ta[°C])) / 0.902) ⇒ ETH[hPa] = saturated vapour pressure at temperature Th2.
154	Thermal comfort (Givoni; 2000)	= 1.2 + 0.1115 * Ta[°C] + 0.0019 * SR[w/m2] - 0.3185 * WS[m/s]
155	Thermal Comfort (Humid-Tropical environments) (Sangkertadi; 2014)	= -7.91 - 0.52 * WS[m/s] + 0.05 * Ta[°C] + 0.17 * Tg[°C] - 0.0007 * RH + 1.43 * ADu
156	Thermal Resistance of Clothing (Jokl; 1982)	= (0.0053 + 0.035 * Layers) ^ 0.61 * Exp(-0.147 * WS[m/s]) + 0.054 * Exp((-0.23 * Layers) - (1.07 + 0.06 * Layers) * WS[m/s]) ⇒ Layers = number of clothing layer someone wears
157	Thermal Sensation (Monteiro; 2010)	= -3.557 + 0.0632 * Ta[°C] + 0.0677 * Tmrt[°C] + 0.0105 * RH - 0.304 * WS[m/s]
158	Thermal Sensation (eq. 1) (Rohles; 1971)	= (0.245 * Ta[°C]) + (0.033 * VTd[hPa]) - 6.471 VTd = saturated vapor pressure at dew point temperature
159	Thermal Sensation (eq. 2) (Rohles; 1971)	= (0.245 * Ta[°C]) + (0.248 * VP[kPa]) - 6.475
160	Thermal Sensation (Givoni; 2004)	= (1.83 - 0.05 * GTa[°C]) + (0.135 * Ta[°C]) + (0.00195 * SR[w/m2] - 0.6) - (0.4915 * Log(WS[m/s])) ⇒ GTa[°C] = average temperature of season
161	Thermal Sensation Index (Xavier; 2000)	= 0.219 * OT + 0.012 * RH - 0.547 * WS[m/s] - 5.83 ⇒ OT = (Ta[°C] + Tmrt[°C]) / 2
162	Thermal Sensation Vote (Summer) (Yahia; 2013)	= 0.134 * SET - 3.208 ⇒ SET = (WBGT - 11.76) / 0.405 ⇒ Outdoor Standard Effective temperature based on a formula (e.g., TSI #111) found in literature [123].
163	Thermal Sensation Vote (Winter) (Yahia; 2013)	= 0.082 * SET - 2.928 ⇒ SET = (WBGT - 11.76) / 0.405 ⇒ Outdoor Standard Effective temperature based on a formula (e.g., TSI #111) found in literature [123].
164	TPV index (Baghdad) (Nicol; 1975)	= 0.214 * Tg[°C] + 0.031 * VP[mmHg] - 0.545 * (WS[m/s] ^ 0.5) - 2.85
165	TPV index (Roorkee) (Nicol; 1975)	= 0.186 * Tg[°C] + 0.032 * VP[mmHg] - 0.366 * (WS[m/s] ^ 0.5) - 0.82
166	Tropical Summer Index (Sharma; 1986)	= (0.308 * Tw[°C]) + (0.745 * Tg[°C]) - (2.06 * Sqr(WS[m/s])) + 0.841
167	Universal Thermal Climate Index (Jendritzky; 2012)	= f (Ta[°C], Tmrt[°C], WS10m[m/s], VP[hPa])
168	Wet Bulb Globe Temperature (eq. 1) (Ono; 2014)	= 0.718 * Ta[°C] + 0.0316 * RH + 0.00321 * Ta[°C] * RH + 4.363 * SR[kW/m2] - 0.0502 * WS[m/s] - 3.623
169	Wet Bulb Globe Temperature (eq. 2) (Ono; 2014)	= 0.735 * Ta[°C] + 0.0374 * RH + 0.00292 * Ta[°C] * RH + 7.619 * SR[kW/m2] - 4.557 * (SR[kW/m2] ^ 2) - 0.0572 * WS[m/s] - 4.064
170	Wet Bulb Globe Temperature (indoors) (Yaglou; 1956)	= 0.67 * Tpw[°C] + 0.33 * Ta[°C] - 0.048 * Log(WS) / Log(10) * (Ta[°C] – Tpw[°C]) Calculation based on meteorological data according to the literature. [30]
171	Wet Bulb Globe Temperature (outdoors) (Yaglou; 1956)	= 0.7 * Tw[°C] + 0.2 * Tg[°C] + 0.1 * Ta[°C] Calculation based on meteorological data according to the literature. [30]
172	Wet Bulb Temperature (Liljegren; 2008)	= f (Ta, SR, WS, RH)
173	Wet Bulb Temperature (Malchaire; 1976)	= ((0.16 * (Tg[°C] - Ta[°C]) + 0.8) / 200) * (560 - 2 * RH - 5 * Ta[°C]) - 0.8 + Tw[°C]
174	Wet Bulb Temperature (Stull; 2011)	= Ta[°C] * Atn(0.151977 * ((RH + 8.313659) ^ 0.5)) + Atn(Ta[°C] + RH) - Atn(RH - 1.676331) + 0.00391838 * (RH ^ (3 / 2)) * Atn(0.023101 * RH) - 4.686035
175	Wet Cooling Power (Landsberg; 1972)	= (0.37 + 0.51 * (WS[m/s] ^ 0.63)) * (36.5 - Tw[°C])
176	Wet Globe Temperature (Botsball) (Botsford; 1971)	= (WBGT + 2.64) / 1.044
177	Wet Kata Cooling (Maloney; 2011)	= (0.648 * (36.4 - Tn) + 0.833 * (36.4 - Tn) * (WS[m/s] ^ 0.5)) * 41.84 ⇒ Tn = 0.85 * Ta[°C] + 0.17 * RH - 0.61 * (WS[m/s] ^ 0.5) + 0.0016 * SR[w/m2] - 11.62 ⇒ Tn = natural wet bulb temperature as described in the paper [89].
178	Wet Kata Cooling Power (Chamber of Mines of South Africa; 1972)	= (0.7 + (RH ^ 0.5)) * (36.5 - Tw[°C])
179	Wet Kata Cooling Power (Krisha; 1996)	⇒ If WS[m/s] < 1 Then = (14.65 + (35.59 * (WS[m/s] ^ (1 / 3)))) * (309.65 – Tw[K]) ⇒ If WS[m/s] >= 1 Then = (4.19 + (46.05 * (WS[m/s] ^ (1 / 3)))) * (309.65 - Tw[K])
180	Wet Kata Cooling Power (Hill; 1919)	⇒ If WS[m/s] <= 1 Then = (36.5 - Ta[°C]) * (0.2 + 0.4 * Sqr(WS[m/s])) * 41.868 ⇒ If WS[m/s] > 1 Then = (36.5 - Ta[°C]) * (0.13 + 0.47 * Sqr(WS[m/s])) * 41.868
181	Wet-Bulb Dry Temperature (Wallace; 2005)	= (0.4 * Tw[°C]) + (0.6 * Ta[°C])
182	Wind Chill (OFCM/NOAA; 2003)	= 13.12 + 0.6215 * Ta[°C] - 11.37 * (WS10m[km/h] ^ 0.16) + 0.3965 * Ta[°C] * (WS10m [km/h] ^ 0.16)
183	Wind Chill (Siple; 1945)	= ((Sqr(WS[m/s] * 100)) + 10.45 – WS[m/s]) * (33 - Ta[°C])
184	Wind Chill (Steadman; 1971)	= (30 - Ta[°C]) / RS ⇒ RS = 1 / (Hr + Hc) ⇒ Surface resistance
185	Wind Chill Equivalent (Quayle; 1998)	= 1.41 - 1.162 * WS[m/s] + 0.98 * Ta[°C] + 0.0124 * (WS[m/s] ^ 2) + 0.0185 * (WS[m/s] * Ta[°C])
186	Wind Chill Equivalent Temperature (wind of 1.34 m/s) (Falconer; 1968)	= Solve by iteration method: = f (Ta, WS) ⇒ WC = ((Sqr(WS[m/s] * 100)) + 10.45 – WS[m/s]) * (33 - Ta[°C]) ⇒ Wind Chill According to the authors the Wind Chill Equivalent Temperature is “the equivalent temperature that would be felt on exposed flesh in a 3 mph wind – the amount of ventilation one might experience in walking in an otherwise calm wind condition” [165].
187	Winter Scharlau Index (Sharlau; 1950)	= Ta[°C] - Tc ⇒ Tc = (-0.0003 * (RH ^ 2)) + (0.1497 * RH) - 7.7133 ⇒ critical temperature

For our sub-analysis regarding occupational settings, each meteo-based TSI was scored based on whether it satisfied or not each of the qualitative criteria described in the Methodology section. The results showed that 33.0 % (61/187) of the identified TSIs fulfilled all qualitative criteria for assessing the heat stress and strain experienced by workers in occupational settings (Table S6).

Validity and reliability of the thermal stress indicators calculator

The criterion-related validity of the “Thermal Stress Indicators calculator” to compute the meteo-based TSIs identified in our search was assessed by comparing the results calculated for 13 TSIs (we could not identify tools to computing the remaining 172 indicators) using the developed software against other published tools computing the same TSIs. Detailed description of the equations and the information used for the calculation of the 13 TSIs is provided in the Appendix. The construct validity of the “Thermal Stress Indicators calculator” to compute the meteo-based TSIs was assessed for all 187 TSIs by comparing the calculated values from the developed software against the identified limits and categories for each TSI. Specifically, we tested whether a TSI value can be considered cold, neutral, or hot after testing cold, neutral, and hot environments, respectively.

The above analyses returned perfect (i.e., null differences between our software and the 13 available calculators) criterion-related validity, construct validity, and reliability for the “Thermal Stress Indicators calculator” under environmental consistent conditions. Moreover, we confirmed that the software returns null value for a TSI when the provided meteorological data fall outside its operating range.

It is important to note that this criterion-related validation does not examine the predictive (the extent to which TSIs predict the physiological strain experienced during heat stress by someone) and concurrent (the extent to which TSIs correlate with the physiological strain experienced during heat stress by someone) validities of the identified TSIs, but, instead, it was performed to ensure that the developed software provides valid and reliable output.

Discussion

Our systematic search identified 340 unique TSIs that have been developed between 200 BC and 2019 AD to assess the heat stress and physiological strain experienced by people performing various activities over a wide operating range and conditions. Of these TSIs, 153 represent nomograms, specific instruments, and complex models, while the remaining 187 TSIs are formulas that can be mathematically calculated utilizing only meteorological data (air temperature, relative humidity, wind speed, and solar radiation). We focused primarily on the TSIs requiring only meteorological data, as we aimed to enhance the quality and relevance of big-data analytics used in climate services to inform the public of possible health risks during physical activity in warm – hot conditions. To foster popularization of the meteo-based TSIs, we developed a valid and reliable software to calculate them, which can be freely downloaded.

The identified TSIs included unique and sometimes abbreviated names in multiple languages across multiple sources. For instance, TSIs such as the Actual Sensation Vote (#2), Belding-Hatch Index (#18), Dry Kata Cooling (#60), Humisery (#87), Humiture (#88), Robaa's Index (#126), Universal Thermal Climate Index (#167), and Wet-Bulb Globe Temperature (#170), are some of the unique names that we had to identify. It is nearly impossible for a search algorithm to include all the possible unique names and abbreviations, especially since these are unknown at the time of the search. This may be the reason why the only systematic review [23] on this topic identified just 32 eligible articles. Together with the available narrative reviews on TSIs [18–22], a total of 165 TSIs had been identified in previous searches. We were able to expand this and identify 340 unique TSIs by searching for articles introducing individual TSIs as well as those incorporating and comparing multiple TSIs. For instance, our searches included the term “indices”, targeting papers involving multiple TSIs, as well as the previous systematic reviews [23] on the topic that used the term “index”. We performed an exhaustive search in the reference lists of the articles identified through our search algorithm. Our analysis revealed that this search algorithm was 87.7 % sensitive, indicating that our search has likely missed many TSIs that have been developed across the centuries in different languages and publication modalities. We did not place language or publication year limits, yet our searchers were done mostly in databases including English literature. Also, we only searched journal publications, but grey literature likely presents with many additional TSIs.

We did not detect significant evidence for bias. Nearly all (94.5 %) the analysed studies either received no funding or were supported by government/public funding. Also, 94 % of the studies were classified as “high” in the EPPI tool which assessed the strength of the evidence presented. Nevertheless, as indicated in the Results section, our analysis identified nine common misconceptions regarding the use of meteo-based TSIs. We made every effort to harmonize knowledge regarding the adoption and use of each individual TSI identified in our search, providing the equation (Table 5), operating range, interpretation categories, as well as the physical activity mode (active or passive) that it has been designed for (Table S5). Critical evaluation of these operational characteristics of the 187 meteo-based TSIs showed that 127 TSIs were developed for people who are physically active and 61 those are eligible for use in occupational settings. The classification of occupational TSIs was compiled after critical evaluation of all 187 meteo-based TSIs against their operational characteristics, including grading whether a TSI (1) was developed for “active” metabolic state, (2) operates to environments typically found in occupational settings, and (3) incorporates more than one environmental factor.

It is important for future studies to assess the validity of the 153 complex models identified in the present search for describing the heat stress and strain experienced by non-occupational populations performing various activities over a wide operating range of ecologically valid conditions. In this exercise, it is important to consider the impact of interindividual and intraindividual factors that modify the heat strain response and the associated health outcomes [14,176,177].

In conclusion, the information presented in this systematic review should be adopted by those interested to perform on-site monitoring and/or big data analytics for climate services to ensure valid use of the meteo-based TSIs. The present systematic search identified 340 unique TSIs that have been designed to assess the heat stress experienced by people performing various activities over a wide range of ambient conditions. Of these, 187 TSIs can be calculated utilizing only meteorological data and, therefore, are relevant for big-data analytics used in climate services. These TSIs are the most important component for heat-health guidelines, and as such, they should be included in future legislation and climate change policy.

This study is led by the FAME Laboratory, which stands for (F)unctional (A)rchitecture of (M)ammals in their (E)nvironment. It is part of the University of Thessaly and is situated in Trikala, Greece. It was founded in 2008 and currently employs 18 researchers with backgrounds in physiology, molecular biology, epidemiology, medicine, and data science. Together, they publish widely on the effects of different environmental factors on human health and performance, with particular focus on the effects of heat. The lab is also contributing to efforts aiming to translate scientific evidence to environmental, climate, and health policies for international organizations, including the World Health Organization, the International Labour Organization, the Greek Ministry of Labour, and the Qatari Ministry of Administrative Development, Labour and Social Affairs.

Biography

Leonidas G. Ioannou This study is led by the FAME Laboratory, which stands for (F)unctional (A)rchitecture of (M)ammals in their (E)nvironment. It is part of the University of Thessaly and is situated in Trikala, Greece. It was founded in 2008 and currently employs 18 researchers with backgrounds in physiology, molecular biology, epidemiology, medicine, and data science. Together, they publish widely on the effects of different environmental factors on human health and performance, with particular focus on the effects of heat. The lab is also contributing to efforts aiming to translate scientific evidence to environmental, climate, and health policies for international organizations, including the World Health Organization, the International Labour Organization, the Greek Ministry of Labour, and the Qatari Ministry of Administrative Development, Labour and Social Affairs.

Funding Statement

This work was supported by the Horizon 2020 [668786].

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplementary material

Supplemental data for this article can be accessed here.

AUTHOR CONTRIBUTIONS

Conceptualization: LGI, ADF, LN, GH, GPK; Data curation: LGI, ADF; Formal Analysis: LGI, ADF; Funding acquisition: ADF; Investigation: LGI, KM, LT, ADF; Methodology: LGI, GH, GPK, LN, ADF; Project administration: LGI, ADF; Software: LGI, KM, ADF; Supervision: ADF; Validation: ADF; Visualization: LGI, ADF; Writing – original draft: LGI, ADF; Writing – review & editing: LGI, KM, LT, SRN, PCD, MB, YE, GH, MS, PB, IM, GPK, TEB, LN, ADF.