Abstract
The potentials of mean force (PMFs) along the end‐to‐end distance of two different helical peptides have been obtained and benchmarked using the adaptive steered molecular dynamics (ASMD) method. The results depend strongly on the choice of force field driving the underlying all‐atom molecular dynamics, and are reported with respect to the three most popular CHARMM force field versions: c22, c27 and c36. Two small peptides, and 1PEF, serve as the particular case studies. The comparisons between the versions of the CHARMM force fields provides both a qualitative and quantitative look at their performance in forced unfolding simulations in which peptides undergo large changes in structural conformations. We find that ASMD with the underlying c36 force field provides the most robust results for the selected benchmark peptides.
Keywords: Adaptive Steered Molecular Dynamics, Jarzynski's Equality, Peptide Structure, CHARMM
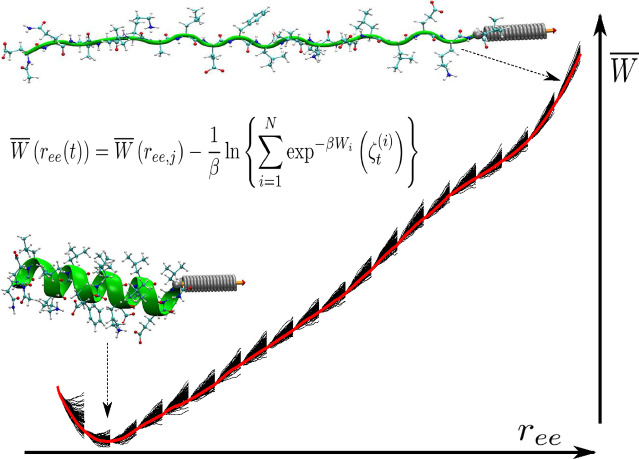
Adaptive steered molecular dynamics method (ASMD) is used to mechanically unfold the α‐helix 1PEF (green ribbon) as its end‐to‐end distance (r ee, the pulling coordinate) is gradually increased from 22 to 62 Å. The solid black lines represent the work for each trajectory, W( ), in several stages whose average (thick‐red‐highlighted black‐dashed curve) represents the overall PMF, . We found that CHARMM36 produced the most accurate result among various CHARMM variants.
Introduction
The energetic interactions within biomolecules and their role in structure‐function relationships can be partially understood through the determination of their associated work functions – thermodynamics – along the characteristic path between the interacting components. Computational methods for obtaining these work functions include, but are not limited to, replica exchange molecular dynamics, [1] free energy perturbation molecular dynamics, [2] and steered molecular dynamics (SMD).[ 3 , 4 , 5 , 6 ] We have focused on SMD approaches in combination with the Jarzynski's nonequilibrium work relation [7] because it offers the possibility of general applicability as long as the sampling of nonequilibrium trajectories converges. [8]
The SMD method has been seen to accurately describe the free energy profile of a biological system transitioning between stable states along a predefined steering pathway (e. g., a predefined unfolding or pulling coordinate).[ 3 , 4 , 5 , 9 ] Unfortunately, as we found in our previous Neuropeptide Y studies[ 10 , 11 ] and in other cases,[ 12 , 13 ] the convergence of the nonequilibrium trajectories can be slow and worsens as the overall extension along the nonequilibrium pulling coordinate is increased. As the extension grows, many of the underlying nonequilibrium trajectories wander increasingly far from the dominant unfolding pathways, requiring significantly higher work, and hence contribute little to the average of the exponential work in the Jarzynski Equality. This leads to the need for an extraordinarily large and increasing number of nonequilibrium work trajectories that must be calculated in order to converge the resulting potential of mean force (PMF). Our previously developed method, adaptive steered molecular dynamics (ASMD),[ 10 , 14 , 15 ] rectifies these obstacles by dividing the pulling coordinate into a series of smaller segments over which the work distribution is narrower and hence requires many fewer nonequilibrium work trajectories to converge. We have previously demonstrated the accuracy of this approach for the mechanical unhinging of Neuropeptide Y, [10] for the mechanical unfolding of the hydrophobic‐homopolymer ,[ 14 , 15 , 16 ] and the unfolding of two small β‐hairpin peptides.[ 12 , 17 ] The approach has also been adopted by several other groups to, for example, reveal mutagenesis effects of calcium binding affinity in cardic troponin c, [18] and kinetic selectivity in anion encapsulation. [19]
The quality and reliability of these simulations are largely dependent upon the accuracy of the underlying empirical force field (FF) of choice. There are many available choices for the all‐atom, additive potential functions, such as the CHARMM,[ 20 , 21 , 22 , 23 ] AMBER,[ 24 , 25 ] and OPLS‐AA FFs.[ 26 , 27 ] These empirical FFs are continuously being improved, resulting in more accurate quantitative energy calculations ranging from structure information to thermodynamic properties, while unfortunately creating questions as to which version is most accurate for a particular observable. In particular, recent refinements to additive FFs have focused on the reparameterization of the torsion angles and corresponding degrees of freedom. The effects of polarizable force fields on the underlying SMD approach was recently shown to also be significant in certain cases by Piquenal and coworkers, [28] but here we consider only the nonpolarizable variants of CHARMM as we focus on the effects on helical proteins.
For example, ff99 was seen to over stabilize the α‐helical secondary structure conformation. [29] Through a reparameterization of the backbone ϕ and ψ torsions obtained by fitting the energies of glycine and alanine tetrapeptides from high level ab initio quantum mechanical calculations, Simmerling and coworkers were able to make improvements and developed ff99SB. [30] Thereafter, ff14SB included additional corrections to the backbone and side‐chain torsion potentials. [31] The reparameterization of the original OPLS‐AA FF involved generating a set of energies for all amino acids on the basis of geometry optimizations and single point LMP2/cc‐pVTZ(‐f) calculations. [27] Afterward, the backbone ϕ and ψ angle parameters were refit to this data. The CHARMM FF potential c36 – also known as CHARMM36 – is a reparameterization the internal parameters associated with the peptide backbone via the CMAP and dihedral terms. [32] The most recent CHARMM36m force field [23] was not tested, even though it has notable improvements to address polypeptide chains, because the present set of peptides are neither polypeptides nor intrinsically disordered, and thereby unlikely to show much difference relative to c36 in the reported results or interpretation. Through the above mentioned series of very subtle modifications to the FFs potential energy functions and corresponding parameters, significant changes in the computed biological behavior with respect to the overall stabilization or destabilization of the peptide system can occur. An additional challenge to the accuracy of FF based methods is that forty‐three percent of the proteins in the Protein Data Bank (PDB) are of unknown function and therefore have little or no experimental data Thus, the uncertainty in the choice of FF makes it difficult to perform a single calculation of the potential of mean force without consideration of the other FFs.
The aim of this article is to clarify which version of the recent CHARMM family of FFs is most appropriate for the use of ASMD, and to provide additional evidence for the efficacy of the approach through the determination of the potential of mean force for a peptide not previously addressed using ASMD. Specifically, we focus on a de novo designed amphiphilic 18‐residue peptide, 1PEF (EQLLKALEFLLKELLEKL) that possesses a high degree of helicity and self‐associates into hexamers in aqueous solvent. [33] It forms aggregates and is a possible model for mimicking the peptide aggregation processes seen in many neurodegenerative diseases, such as Alzheimer's and Parkinson's. [34] However, the time scales needed to characterize peptide aggregation and self‐assembly can be long, and thereby pose a challenge for atomic‐scale molecular dynamic simulations. [35] Nevertheless, the structure and stability of the single 1PEF peptide is germane to the larger complex. We address it using ASMD so as to provide a physically realizable alternative to that is structurally larger and contains significant helical character.
In this work, we performed a rigorous evaluation of the ASMD methodology with several established CHARMM FFs: c22, [20] c27,[ 21 , 36 ] and c36.[ 22 , 32 , 37 ] Specifically, we compared and analyzed the energetics and conformational sampling of two small α‐helical peptides, and 1PEF, along a predefined pulling coordinate to improve the general understanding of the FF parameters and benchmark the effects of our method on relevant conformational changes and the corresponding mechanical unfolding energetics. For simplicity, we employ ASMD using stages with constant time intervals, and do not optimize the staging using recently introduced criteria.[ 8 , 38 , 39 ] In particular, we confirmed that our ASMD methodology correctly captures, through efficient sampling and averaging, the previously reported π‐helical structural artifacts observed for c22, the α‐helical bias reported for c27, and the corrections reparameterized in the CMAP term for c36.
This article is organized as follows: The results for the collective observables along the unfolding (or pulling) coordinate such as energetics, secondary structure, and hydrogen bonding profiles are reported in the next section. The present implementation of the ASMD method[ 10 , 13 , 14 ] is summarized in the Theory, Materials and Methods section. Notably, for convenience throughout this work, we use ASMD to refer to the naive NASMD version of the method unless specified otherwise. The selected CHARMM FF potentials, c22, c27, and c36 are reviewed within the Simulation Protocols subsection. The simulation parameters and protocols are provided thereafter. A detailed structural analysis of the small single‐motif α‐helical peptides, and 1PEF, obtained by minimization of the equilibrium free energy is available in the Supporting Inf.
Results and Discussion
Structural Analysis
Each of the CHARMM force fields – c22, c27 and c36 – in this study give rise to very different weightings in the structures of the corresponding equilibrium ensemble. These differences can be characterized by comparison of the representative structures of the ensembles and the minimum energy structures found in the ASMD‐generated PMFs. These structures also differ from the corresponding structures in the PDB (1PEF) because the latter are generally obtained under different conditions, and there may also be systematic error due to the differences in the force fields. Nevertheless, in order to ensure consistency and reproducibility, protein structures from the literature serve to initiate all of the structural determinations in the numerical experiments described here.
Minimum Energy Structures: 1PEF
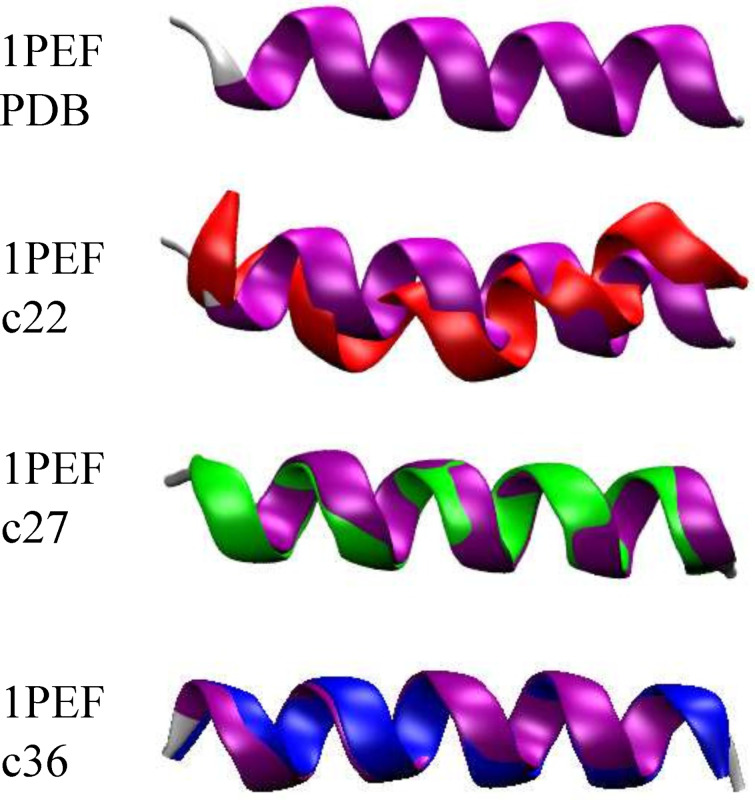
According to the published XRD structure, [33] 1PEF has significant helical character and contains critical intramolecular contacts, while exhibiting some helical deformations. Utilizing the PMF generated for each ASMD simulation (in particular, the 100 tps at 1 Å/ns in each CHARMM FF) such as those shown in Figure 1, the minimum energy structure was determined. For each nonequilibrium trajectory, there exists a minimum energy structure which can be assigned according to the one whose extension matches that at which the PMF has a minimum. An average minimum energy structure ( ) was obtained by averaging 100 minimum energy structures using custom scripts and VMD. The XRD 1PEF structure is illustrated as a purple ribbon in Figure 2. It is compared through backbone alignment to the average minimum energy c22 structure ( , red ribbon), the average minimum energy c27 structure ( , green ribbon), and the average minimum energy c36 structure ( , blue ribbon). These 1PEF backbone alignments form the basis for the metrics listed in Table 1. A similar comparison for is not shown because all the ASMD simulations for this peptide have been initiated with the same structure as that initially used by Park and Schulten.[ 4 , 5 ] It has been inserted into an explicit water box as outlined in the Methods. The minimum energy structures do differ across the selected CHARMM FFs as indicated by the differing values of the corresponding distance listed in Table S1 and illustrated in Figure S1, both in Supporting Inf.
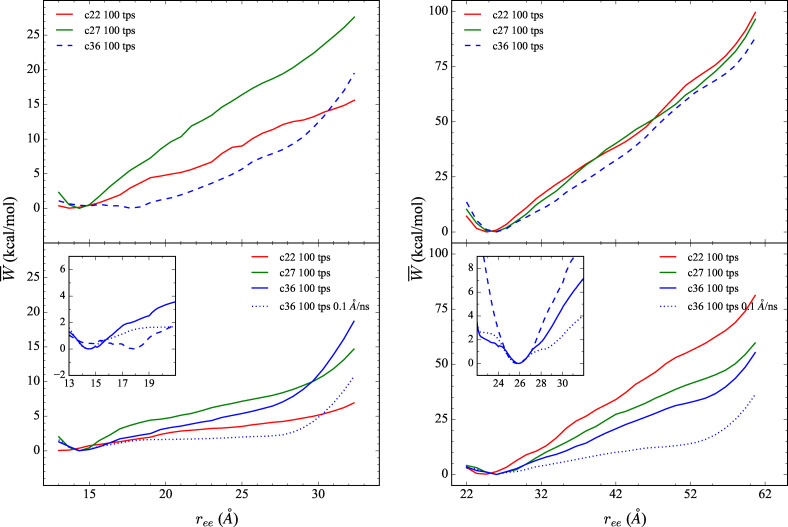
Figure 1.
The comparison of the explicit PMFs obtained using the CHARMM family of potentials for the forced stretching of ALA10 (left) and 1PEF (right) using ASMD, with c22 (in red), c27 (in green) and c36 (in blue) FFs. The PMFs are displayed for three stretching velocities, 10 Å/ns (top panels), 1 Å/ns (bottom panels), and 0.1 Å/ns (inset in bottom panels). Each PMFs is obtained by averaging over 100 trajectories per stage (tps). More specifically, each data inset in the bottom panel displays the behavior of the PMFs obtained using the c36 FF at each velocity: 10 (blue dashed curve), 1 (blue solid curve), and 0.1 Å/ns velocity (blue dotted curve) near the respective peptide's energy minimum structure.
Figure 2.
Comparison between the XRD 1PEF peptide (purple) and the average minimum energy structures – (red), (green) and (blue) – obtained using ASMD simulations with and 100 tps.
Table 1.
Comparison between the XRD 1PEF peptide and the average minimum energy structures ( ) shown in Figure 2 calculated for each ASMD simulation with and 100tps. Values displayed include: the end‐to‐end distance (in Å) of the averaged minimum energy structure, the RMSD (in Å) between the experimentally determined 1PEF coordinates and minimum energy structures, and the ϕ and ψ backbone torsional angles. The specific angles for residues 2 through 15 are nearly the same and hence only the averages, , and corresponding RMSDs are shown for θ being ϕ and ψ, and .
|
|
|
RMSD |
|
|
ϕ 16 |
ψ 16 |
ϕ 17 |
ψ 17 |
|||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Exptl. [33] |
26.9 Å |
– |
−62±3° |
−42±4° |
−87° |
−4° |
−63° |
−16° |
|||
|
|
24.3 Å |
2.02 Å |
−64±9° |
−43±6° |
−71° |
−57° |
−84° |
−53° |
|||
|
|
25.5 Å |
0.86 Å |
−63±1° |
−41±3° |
−65° |
−45° |
−84° |
−26° |
|||
|
|
25.8 Å |
0.58 Å |
−63±3° |
−40±3° |
−66° |
−38° |
−74° |
−30° |
The end‐to‐end distance (r ee ), the RMSD when compared to the XRD structure, and the average ϕ and ψ angles along the backbone of 1PEF for the experimental and computed peptide structures are listed in Table 1. The character of the possible backbone (not side‐chain) intrapeptide hydrogen bond contacts for the experimental minimum energy structures of 1PEF are provided in Table 2. The ψ and ϕ angles in the XRD structure of 1PEF in residues 2 through 15 consistent with α‐helical character as indicated by the average values of those angles, and in Table 1, and more precisely by each pair of angles (not shown.) Also typical of α‐helices is the observation that 12 of the 14 main chain intramolecular hydrogen bonds, between residues 1 and 16, involve contacts, as indicated in Table 2. 1PEF exhibits a distortion away from the ideal α‐helical structure in residues 16 through 18. One pair of ϕi and ψi angles at has a slightly distorted stereochemistry, while the second pair at is more consistent with the typical range of angles observed for 310‐helical conformations. The relative poses of the final residues – at positions 16 to 18 – give rise to hydrogen bond contacts exhibiting 310‐helical character. This overall structural motif – in which α‐helical character dominates in the middle of the stable helix while 310‐helix character dominates near the C‐terminus – is not uncommon for small peptides as it has been observed in several others.[ 40 , 41 , 42 , 43 ]
Table 2.
All main chain intrapeptide hydrogen bond contacts for the experimental structure of 1PEF, and the minimum energy structures of 1PEF in each CHARMM FF. π‐helical contacts are , α‐helical contacts are , and 310‐helical contacts are .
|
Donor |
Acceptor |
Exptl. [33] |
|
|
|
|||
|---|---|---|---|---|---|---|---|---|
|
LEU18 |
GLU13 |
– |
π |
– |
– |
|||
|
LEU18 |
LEU15 |
310 |
– |
– |
– |
|||
|
LEU18 |
LEU14 |
– |
– |
α |
α |
|||
|
LYS17 |
LEU14 |
310 |
– |
– |
– |
|||
|
LYS17 |
GLU13 |
– |
α |
α |
α |
|||
|
GLU16 |
GLU13 |
310 |
– |
– |
– |
|||
|
GLU16 |
LYS12 |
α |
α |
α |
α |
|||
|
LEU15 |
LEU11 |
α |
α |
α |
α |
|||
|
LEU14 |
LEU10 |
α |
α |
α |
α |
|||
|
GLU13 |
PHE9 |
α |
– |
α |
α |
|||
|
LYS12 |
GLU8 |
α |
– |
α |
α |
|||
|
LEU11 |
LEU7 |
α |
α |
α |
α |
|||
|
LEU10 |
ALA6 |
α |
α |
α |
α |
|||
|
PHE9 |
LYS5 |
α |
α |
α |
α |
|||
|
PHE9 |
ALA6 |
– |
310 |
– |
– |
|||
|
GLU8 |
LEU4 |
α |
α |
α |
α |
|||
|
LEU7 |
LEU3 |
α |
α |
α |
α |
|||
|
ALA6 |
GLN2 |
α |
α |
α |
α |
|||
|
LYS5 |
GLU1 |
α |
– |
α |
α |
|||
|
|
Numbers of Contacts: |
12: α |
10: α |
14: α |
14: α |
|||
|
|
|
3: 310 |
1: 310 |
|
|
|||
|
|
|
|
1: π |
|
|
The secondary structural elements of the experimental 1PEF peptide are generally captured by each CHARMM FF in the average minimum energy structure although there are some differences. The and structures contain only α‐helical backbone intrapeptide hydrogen bonds, as indicated in Table 2. This finding is further supported by the results on the secondary structure evolution during the mechanical unfolding event, and those on the hydrogen bonds explicitly accounted for along the forced unfolding pathway. However, the structure only differs by a RSMD of 0.58 Å from the experimental structure, and the ψ 16 and ψ 17 torsional angles are closer to the XRD structure. On the other hand, the average 1PEF structure from the c22 ASMD simulations ( ) exhibits some unusual structural features. The distance is approximately 2.5 Å shorter than the experimental structure, in addition to the ψ 16 and ψ 17 torsional angles being overestimated (Table S1 of the Supporting Inf.) Furthermore, the structure has an RMSD difference from the XRD structure by over 2 Å. The decrease in distance of the 1PEF peptide is a consequence of two factors: (i) a single 310‐helical contact ( .) occurring between Ala6 and Phe9, which causes the helix to bend, and (ii) a π‐helical contact ( ) between residues Glu13 and Leu18 which increases the pitch or width of the helix (Table 2). The formation of the π‐helical contact in the minimum energy structure of 1PEF in the c22 FF is expected, and is further supported by our hydrogen bonding data (see Figure 6 and our secondary structure analysis (see Figure 5.)
Figure 6.
The average number of α‐, 310‐, and π‐helical contacts as a function of the end‐to‐end distance are shown for the mechanical unfolding of (left) and 1PEF (right) in explicit solvent using the c22 (top), c27 (middle), and c36 (bottom) FFs as obtained by ASMD with vs =1 Å/ns with 100 tps. Red curves represents The (310‐helix), (α‐helix) and (π‐helix) contacts are shown in red, blue and green, respectively.
Figure 5.
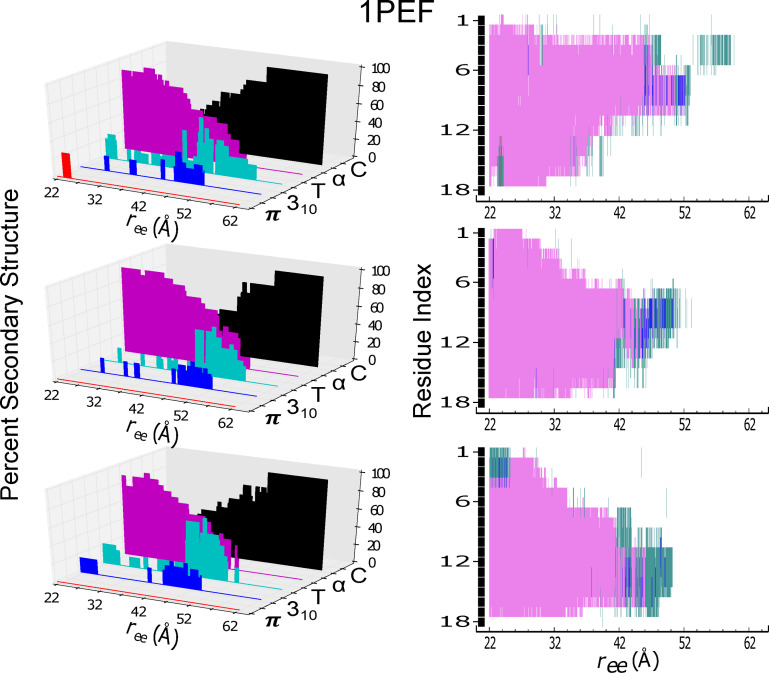
Secondary structure content and individual residue structural assignment for the helical peptide 1PEF are shown as in Figure 4. In the right column panels, the secondary structural assignment of each amino acid residue is indexed from 1 to 18 corresponding to its sequence: Glu, Gln, Leu, Leu, Lys, Ala, Leu, Glu, Phe, Leu, Leu, Lys, Glu, Leu, Leu, Glu, lys, Leu.
Energetics
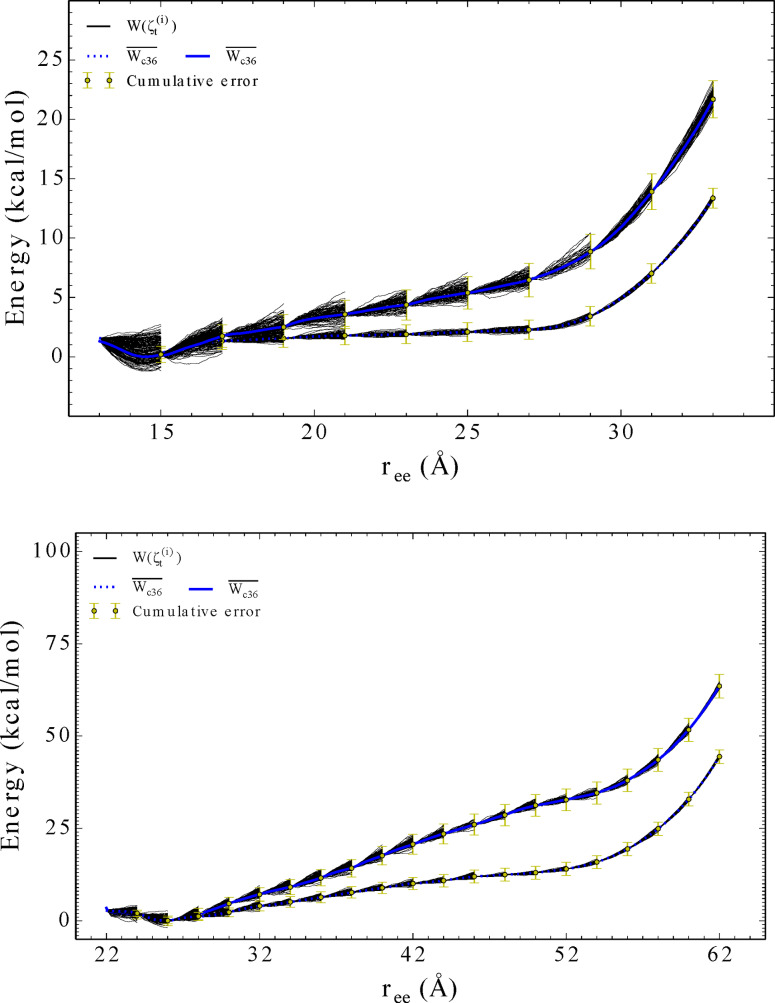
The energetics along the forced unfolding pathway of and 1PEF in an explicit (water) solvent has also been obtained using ASMD at two pulling velocities vs , 10 and 1 Å/ns, with 100 trajectories per stage (tps) for each CHARMM force field. The PMFs for each peptide in explicit (water) solvent using the c36 force field were obtained at an even slower pulling velocity: vs =0.1 Å/ns with 100 trajectories per stage. The simulations are performed in 10 equally‐spaced incremental stages covering a change in the overall pulling coordinate of 20 Å. The peptide is pulled from the initially compressed α‐helical structure with an distance of 13 Å to a fully extended structure with a final distance of 33 Å. Twenty equally‐spaced incremental stages are employed for the ASMD simulations of 1PEF covering a change in the overall pulling coordinate of 40 Å. The 1PEF peptide is pulled from the initially compressed α‐helical structure with distance of 22 Å to a fully extended structure with a final distance of 62 Å. The PMFs obtained by ASMD are shown in Figure 1 according to Eq. 2. Several pulling velocities have been employed because earlier work on SMD[ 3 , 4 , 5 , 44 ] and ASMD[ 14 , 15 ] indicated that it can affect the overall energetics and pathways. The slowest pulling velocity employed here ( ) was seen to be sufficient for confirming convergence in our previous work on the peptide[ 14 , 15 , 16 ] and two β‐turn peptides. [17] It appears to be sufficient here as the insets in Figure 1 displaying the first 10 Å of the pull obtained at are in agreement with the pulls.
The structures of and 1PEF at the start of the ASMD pulling simulations are not the minimum energy structures as can be seen from the PMFs in Figure 1 for each pulling velocities. The initial structures for and 1PEF are therefore seemingly arbitrary in the sense that they do not correspond to a set point such as the minimum of the PMF. This is a consequence of the fact that the peptides are intentionally made more compact, following the original procedure of Park and Schulten,[ 4 , 5 ] so as to allow SMD (and ASMD) to find the minimum through the pulling procedure. Meanwhile, the extension (ASMD) of the peptide at which the ASMD PMF is a minimum is not quite equal to the typical extension at which the peptide is freely equilibrated as can be seen in Table 1 of the Supporting Inf. The discrepancies likely arises from the relative numerical error in the two methods. It is also possible that the SMD or ASMD procedure could limit the sampling of structures in such a way as to bias the nonequilibrium average. To mitigate and expose these effects, we have used slow pulling speeds while displaying comparisons to the results obtained from faster pulling speeds. The fact that convergence is possible has already been seen in the case of .[ 4 , 5 , 14 ]
For the steered unfolding velocity simulations of in Figure 1, the C22 PMF does not exhibit a free energy minimum for either pulling velocity, while the C27 and C36 PMFs exhibit minima at r ee equal to 14.3 Å and 14.4 Å (and 14.5 Å for 0.1 Å/ns pulling velocity), respectively. The secondary structure of in all three simulations near this extension is that of an α‐helix except for the small percentage of π‐helical character in the C22 trajectories. The latter was also observed by Feig and coworkers [45] when using c22.
As in , the c22 simulations of 1PEF exhibits a minimum energy structure with a shorter than that obtained by the c27 and c36 simulations. The starting structures are, in this case, sufficiently compact that a minimum is explicitly found in all three cases, as shown in Figure 1. The c22 minimum energy structure (at 24.30 Å) is approximately 1.5 Å shorter from end‐to‐end than the structures from the c27 and c36 simulations. As previously discussed, the c22 minimum energy structure is also 2.5 Å shorter from end‐to‐end than the experimental XRD structure. The shortening of 1PEF in c22 results from a terminal π‐helical contact, defined as , making the helical peptide shorter and fatter, and a centrally located 310‐helix contact causing a bend that leads to an additional shortening. Meanwhile, the c27 and c36 1PEF vs =1 Å/ns minimum energy structures follow the same trend as the model system . The two structures have very similar values, 25.50 Å and 25.80 Å, respectively (25.84 Å for vs =0.1 Å/ns). These minimum energy structures posses α‐helical contacts, but unlike in , the c27 and c36 1PEF minimum energy structures have the same amount and type of hydrogen bonds: 14 α‐helical contacts. This 1PEF c27 result more clearly illustrates the reported α‐helical bias of the FF, and suggests that short range interactions do not fully account for their stability as remarked earlier.
There is a drop in the overall magnitude of PMF along the pull for both the and 1PEF peptide systems as the vs is decreased from 10 Å/ns to 1 Å/ns. The drop in the PMF relative to the minimum at the end of the pull (at 32 Å) for was approximately 10 kcal/mol in the c22 FF. The corresponding drop for 1PEF is approximately 20 kcal/mol. This is consistent with the fact that the latter has a helix that is twice as long, and that the stabilization energy is approximately additive. It is notable that the corresponding drops in the PMFs upon decreasing the pulling speeds for the c27 and c36 FFs are somewhat different. Nevertheless, across the CHARMM family of potentials for the slow vs extension of , the thermodynamically accessible states remain fairly structured in the sense that there is an initial fast rise from the energy minimum conformation, and then a subsequent flattening of the PMF up to ≈23 Å , where the peptide becomes completely unstructured. The homopolymer is primarily stabilized through backbone hydrogen bond contacts. The secondary structure analysis shown below clearly supports this observation. Moreover, (leftmost column) has little to no remaining secondary structural characteristics after approximately the first 10 Å of extension.
On the other hand, the lack of a flattening of the PMFs for 1PEF suggest that it remains highly structured along the induced unfolding pathway by way of retention of secondary structural elements. The 1PEF PMFs across each CHARMM potential have a fairly consistent positive slope for both vs . A positive and consistent slope across all FFs, for both vs , demonstrates a positive correlation between the energetics and , which directly correlates to the observed secondary structure along 1PEF's induced unfolding pathway.
Finally, the convergence of the PMFs with respect to the pulling velocity is indicated in the insets of Figure 1 and further detailed in Figure 3. Evidently, the slower pulling speeds provides a lowere and more accurate PMF given the time intervals of each of the stages. This is refleced in the reduced widths in the spreads of the work functions across the nonequilibrium trajectories at the slower pulling speeds. While pulling at even slower pulling speeds is cost prohibitive, the trends suggest that PMFs at 0.1 Å/ns are converged.
Figure 3.
The comparison of the explicit PMFs obtained using the CHARMM36 potential for the forced stretching of (top) and 1PEF (bottom) using ASMD at two different pulling velocities: 1 Å/ns (solid blue curves) and 0.1 Å/ns (dotted blue curves). Each PMFs is obtained by averaging over 100 trajectories per stage (tps) for each peptides predetermined reaction coordinate: More specifically, the error, illustrated using yellow bars, was calculated at the end of each ASMD stage and weighted using the computed Jarzynski average for that corresponding stage. This error is cummulative across each stage for the entire ASMD simulation.
Secondary Structure Evolution
In the following, we compare variations in the secondary structure as a function of peptide extension during ASMD simulations of and 1PEF. The STRIDE algorithm from VMD, in conjunction with customs scripts, was used to generate the and 1PEF results displayed in Figures 4 and 5, respectively. In particular, the ASMD explicit 1 Å/ns trajectory with 100 tps that was nearest to the computed JA was chosen for this analysis. In both figures, the percent composition of secondary structure of each peptide is shown as a function of . The contribution of each peptide to a given secondary structure is also reported as a function of of .
Figure 4.
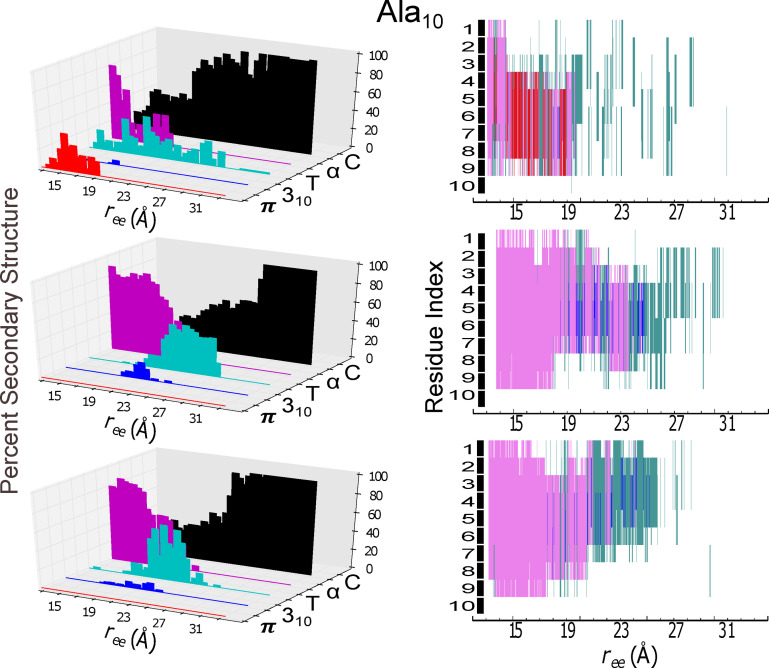
Secondary structure content (panels at left) and individual residue structural assignment (panels at right) for the model helical peptide are shown as a function of extension, . The trajectory for the protein in explicit solvent obtained at 1 Å/ns with ASMD that was nearest to the computed Jarzynski average was chosen for analysis using the STRIDE algorithm in VMD in c22 (top panels), in c27 (middle panels), and in c36 (bottom panels). The evolution of the secondary structure character as a function of mechanical unfolding is displayed as: π‐helical (red), 310‐helical (blue), turn (T in teal), α‐helical (purple), and random coil (C in black). In the right column panels, the secondary structural assignments of each amino acid residue is indexed from 1 to 10, starting with the amino‐terminal (N) end.
The model peptide displays a clear helix‐to‐coil transition for the c27 and c36 FF mechanical unfolding simulations. For the c27 FF ASMD simulation, the α‐helix is the primary secondary conformation, with at least 40 % composition, up to approximately 23 Å of extension. Beyond this extension, the secondary structure transforms primarily into a mix of turn and coil for 5 Å, and then becomes a complete random coil. A similar unfolding pathway is observed for the c36 FF; the primary difference in pathway being the duration of the α‐helix secondary structure during extension. For the c36 FF ASMD simulation, the α‐helix unravels much faster, giving way to a random coil. Both the c27 and c36 FF ASMD unfolding pathways give rise to a very small degree of 310‐helical characteristics with i→i+3 hydrogen bond contacts predominately occurring centrally within the model helical peptide. The presence of these 310‐helical contacts during the helix‐to‐coil transition supports a proposed mechanism for helix denaturation which involves passing through a 310‐helix like conformation.[ 43 , 46 , 47 ] The mechanical unfolding of in the c22 FF however exhibits a distinctively different pathway. The initial helical conformation is not entirely α‐helical, as it was in the c27 and c36 ASMD simulations. The initial structure of in the c22 FF has a significant proportion of π‐helical characteristics, which have i→i+5 contacts. The π‐helical non‐native contacts occur toward the C‐termini, and then rapidly become frayed to a disordered structure at ≈ of 19 Å. Unlike the mechanical unfolding pathway of in the c27 and c36 FFs, the ASMD simulation in the c22 FF does not exhibit any significant degree of 310‐helical characteristics, and favors instead the turn structural motif. In the c22 FF, the presence of the π‐helix and turn predominate until the peptide is completely unstructured. For the ASMD numerical experiments of the model peptide , there is a mixed preference for the mode of mechanical unfolding. Meaning for the c27 and c36 FFs simulations there is mechanical unwinding progressing from the C‐terminus to the N‐terminus. There is a slight difference in the mechanical unfolding pathway of 1PEF in the c27 and in the c36 FF. In the c27 FF the mechanical unfolding occur lastly towards the C‐termini in residues 12–18, whereas in the c27 FF the final mechanical unfolding of the α‐helix occurs slightly more centrally, affecting residues 8–14. For the c22 ASMD mechanical unfolding, the appears to occur from both the N‐ and C‐termini simultaneously, leaving the central area of the peptide structured briefly.
Across all FFs, 1PEF maintains primarily α‐helical secondary structural components up to an of 52 Å. Because of the strong propensity of 1PEF to retain α‐helical contacts, the induced unfolding pathway of 1PEF remains highly structured. This retention of α‐helical secondary structure and the similarity of mechanical unfolding pathway across all FFs is illustrated with the positive and consistent slope across both vs , demonstrating a positive correlation between the energetics and . This correlates directly to the observed secondary structure along 1PEF's induced unfolding pathway. For the ASMD simulations in the c27 and c36 FFs, the loss of secondary structure is generally proceeding from the N‐terminus toward the C‐terminus, which is the opposite for what was observed in the ASMD simulations of the model peptide . Although a variety of mechanisms are involved in the breaking of helical hydrogen bonds, the formation of transient turn structures and structures with mixed α‐ and turn, or α‐ and 310 structure is a common motif observed along the 1PEF mechanical unfolding pathway. Primarily for the c22 and c27 forced unfolding simulations, the formation of the 310‐helical contacts occurs more centrally within the 1PEF peptide, starting at an of 42 Å and ending at an of roughly 50 Å. The c36 1PEF mechanical unfolding pathway exhibits similar 310‐helical contacts starting at an of 42 Å and ending at an of roughly 50 Å. But additionally, and uniquely to this FF, 310‐helical contacts are found in the initial starting structure of 1PEF, located near the N‐termini. As seen with , the c22 initial 1PEF structure is not entirely α‐helical, and exhibits π‐helical contacts. Albeit 1PEF's π‐helical contacts consist of a smaller percent composition of the peptide, and persist for a much shorter duration in the unfolding pathway when compared to . Furthermore, the mechanical unfolding of 1PEF in the c22 FF proceeds with a loss of secondary structure from the C‐terminus towards the N‐terminus. This behavior is opposite what is observed during the mechanical unfolding of 1PEF in the c27 and c36 FFs.
Hydrogen Bonding
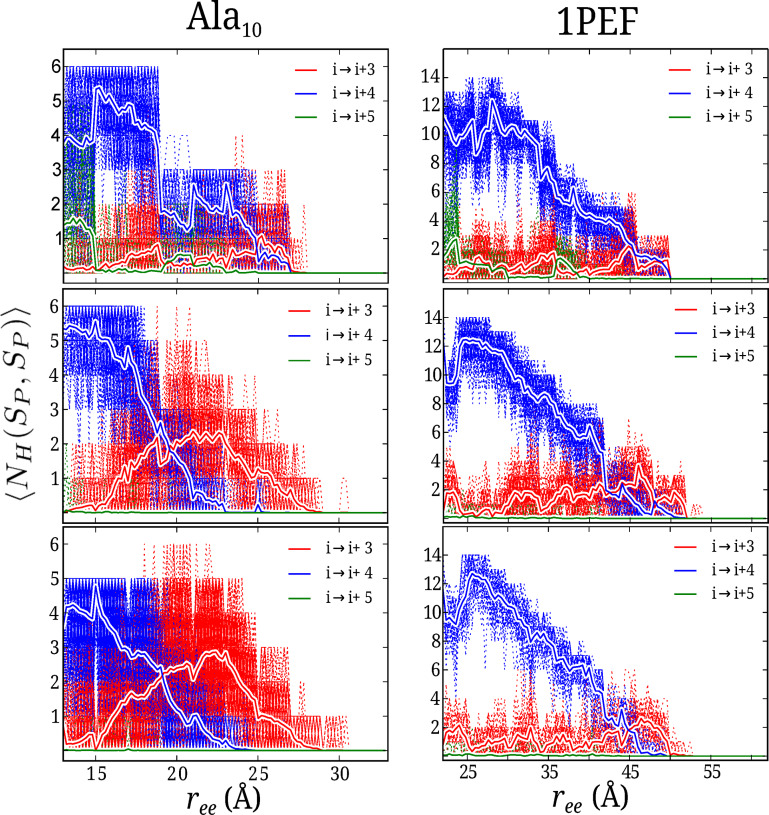
The converged PMF shown in Figure 1, and the secondary structural analysis shown in Figures 4 and 5 reveal important structural properties of the helix‐to‐coil transition of and 1PEF in water across the family of CHARMM potentials. To more clearly examine the helical preferences and other structural properties of the peptides along the PMFs, a hydrogen bond analysis of the nonequilibrium ASMD ensembles was performed. The instantaneous number of intrapeptide hydrogen bonds, , was obtained using Eq. 8. For Figure 6, N (=100) is the number of trajectories for trajectory i at the extension ζt of the peptide backbone.
The hydrogen bonding profiles across each FF seen in Figure 6, although weighted in accordance with the work values, still have significant fluctuations. The hydrogen bond profiles for the mechanical unfolding of are on the left hand side, and the hydrogen bond profiles for the mechanical unfolding of 1PEF are on the right hand side of Figure 6. The top panels are for the mechanical unfolding using the c22 FF, the central panels are the profiles from the c27 FF, and the last panels are for the ASMD simulations in the c36 FF. The sum of hydrogen bonds for a given structure along the pulling coordinate was partitioned into sums of those hydrogen bonds linking residues separated by a given number of residues along the peptide backbone. In Figure 6, the i→i+4 hydrogen bonds (the blue curves) correspond to those bonds an α‐helix. Additionally, the i→i+3 hydrogen bond contacts (the red curves) and i→i+5 hydrogen bond contacts (the green curves) correspond to those bonds observed in an 310‐helix and π‐helix respectively.
For , the average number of hydrogen bonds seen in the initial compact form of the peptide varies across the FFs. In the c22 FF ASMD simulations (top panel, left hand side of Figure 6), the initial compact conformation has a mixture of four i→i+4 contacts and one to two i→i+5 hydrogen bonds. As was previously discussed and shown in Figure 4, the π‐helical contacts observed in the c22 FF are centrally located within the compact conformation, and are present until an of 19 Å. The hydrogen bond analysis of in the c22 FF shows a reorganization and reformation of α‐helical contacts very suddenly during the initial mechanical stretching to an of 15 Å. This reformation of the i→i+4 contacts increases the α‐helical character of the peptide, from having initially only four contacts to a maximum of six contacts. After this initial reformation of i→i+4 contacts, the α‐helical character of the peptide in c22 FF drops dramatically at an of 19 Å. This dramatic drop in α‐helical character corresponds directly to the formation of 310‐ and π‐helical contacts. After this sudden drop in α‐helical character, there is little to no restructuring of the intrapeptide hydrogen bond contacts. The loss of these weak hydrogen bonds, and the lack of secondary structure during the second half of the overall PMF, gives rise to a small free energy increase. For in c27, (middle left hand side panel) there exists approximately six i→i+4 contacts in the starting‐compact helical structure. The previously reported α‐helical bias of the c27 FF becomes more clear with the hydrogen bond analysis, in combination with the secondary structural analysis. These six α‐helical contacts are fairly stable and therefore present, on average, to approximately an of 19 Å, after which there is a cross‐over to predominately i→i+3 character, see Figure 6. After the model peptide has reached an of 19 Å the secondary structure is dominated by 310 and turn motifs, but some α‐helical character remains until an extension of 23 Å. The c27 FF clearly has the most α‐helical character observed for the model system across the family of CHARMM potentials. The PMF for the model peptide in the c27 FF (green curve in Figure 1) has the minimum energy conformation with the lowest energy and demonstrates a free energy landscape with the highest energy plateau. This plateau in the free energy surface represents the extension past 19 Å that has the most α‐helical character of any of the FFs, with the greatest energy bias. Lastly, the hydrogen bond profile for in the c36 FF closely resembles that of the hydrogen bond profile from the c27 FF, with one major exception; the total number of α‐helical contacts along the pulling coordinate is lower. in the c36 FF has five i→i+4 contacts in the compact structure, and this number declines rapidly upon the peptide unraveling. On the other hand, in the c36 FF becomes characterized by an equal number of α‐helical and 310‐helical contacts at a cross‐over point on the pulling coordinate, of approximately 19 Å at around 23 Å. This cross‐over point matches the cross‐over of secondary structure observed in the c27 simulations. At this cross‐over point there are an equal number of α‐helical and 310‐helical hydrogen bonds present in the ensemble. All α‐helical contacts, across all FFs for the mechanical unfolding of are ruptured at around 23 Å. The ASMD hydrogen bond profiles of are further substantiated with the secondary structural analysis. There are no π‐helical contacts observed during the peptide extension in the c27 or c36 FF as there was in the c22 FF. The α‐helical contacts are mostly replaced by 310 contacts within the first 10 Å of peptide backbone extension in the c27 and c36 FFs at which the cross‐over point is reached. This would explain how the energy in the PMF – refer to Figure 1, – remains nearly constant and flat up to approximately 23 Å , where the peptide becomes completely unstructured.
In the XRDs of 1PEF, twelve of the fourteen main chain intra‐molecular hydrogen bonds are seen to be α‐helical in character and the last two main chain intra‐molecular hydrogen bonds have 310‐character. The initial conformation of 1PEF for each ASMD simulation is a compact helix with unspecified helical contacts with an of 22 Å. Similarly to , 1PEF displays π‐helical contacts in the c22 FF ASMD pulling experiments, resulting with a shorter and fatter helix. These π‐helical contacts shift the minimum energy to the right, making the energy minimum occur at 24.06 Å (with a well depth of 3.2 kcal/mol, refer to Figure 1). Furthermore, just like in the c22 FF, there are very little to no 310‐helical contacts in the compressed or minimum energy structure. The mechanical unfolding pathway experienced by 1PEF in the c27 and c36 FF are very similar to one another, just as the two pathways were similar to one another in the two FFs for . There is a clear shift of the hydrogen bonds from α‐helical to 310‐helical for the c27 and c36 FF ASMD simulations of 1PEF, occurring near 45 Å of extension. Furthermore, there is a slight reorganization of hydrogen bonds in the c27 and c36 FF for the mechanical unfolding of 1PEF. The restructuring of these hydrogen bond contacts increase the number of α‐helical contacts within the peptide at the minimum energy structure observed along the PMF. The minimum energy structure of 1PEF in the c27 FF occurs with an of 25.93 Å at a well depth of 4.1 kcal/mol. In the c36 FF, the minimum energy conformation occurs with an of 25.80 Å at a well depth of 3.5 kcal/mol. The c27 FF ASMD simulation shows the over stabilization of the α‐helical peptide with a constant 12–14 α‐helical contacts formed, and no 310 contacts. Likewise in the c36 FF, during the mechanical unfolding of 1PEF, there is a reorganization of the α‐helical hydrogen bonds that increases the overall number within 1PEF. But the duration of the maximum number of hydrogen bonds is shorter than in the c27 FF. As further reflected in Figure 5, the secondary structure of 1PEF remains α‐helical until ≈42–44 Å for both the c27 and c36 FF. However, the unraveling in the c36 FF occurs more towards the C‐termini (residues 12–18), whereas in the c27 FF the final unraveling of the α‐helix occurs slightly more centrally (residues 8–14). For 1PEF, the α‐helical contacts are replaced by 310 contacts within the last 10 Å of peptide backbone extension in c27 and in c36 at which the cross‐over point is reached. However, unlike , the α‐helical bonds are not completely replaced by 310‐helical contacts in the c27 or c36 FF. This would explain how the energy in the PMF – see Figure 1, – remains constantly increasing and flat up to about 52 Å , where the peptide becomes completely unstructured. For our model system, all secondary structure (excluding turn motifs) is lost after approximately 15 Å of steering the peptide backbone. Whereas for 1PEF, all secondary structure, again excluding turn motifs, is lost after approximately 30 Å of steering the peptide backbone. This provides an explanation for the cross‐over point occurring roughly twice as far along the pulling coordinate: at about twice as far along the pulling coordinate; 19 Å for and approximately 45 Å for 1PEF. The c36 FF results are about the same as the c27 FF results; the free energy results in the c27 FF are higher than the results from the c36 FF. The similarities of the mechanical unfolding pathways between our model system and the biological relevant system 1PEF demonstrate how the corrections from the CMAP reparameterization take affect.
Conclusions
Molecular simulation routinely offers atomic‐detail of key processes in chemistry and biology, but its accuracy depends on the underlying energy potentials and the MD methodology. Here, we compare two very different α‐helical peptides, and 1PEF, across a CHARMM family of molecular dynamic potentials utilizing our ASMD methodology. We found that the transition between α‐helical and random coil states for these linear peptides follow similar pathways of mechanical unfolding across the potentials despite their sequence differences: one is a homopolymer and one is amphiphilic.
Our ASMD methodology is robust enough to capture expected behavior across the CHARMM family of FFs. This includes the presence of π‐helical artifacts in the c22 FF, and the bias of the c27 FF toward α‐helical secondary structures. Furthermore, we find that even though 1PEF is an 18‐mer, and is comprised of about twice as many amino acids as , convergence can be reached using 100 tps with a pulling velocity of 1 Å/ns. These thermodynamic results, in combination with the detailed structural and electrostatic analysis as a function of , shows that while 1PEF has a well defined forced pathway of unfolding, it unexpectedly resembles the unfolding pathway of the homopolymer . The thermodynamic results of and 1PEF suggest a concerted unfolding of the hydrogen bond contacts, and transient intermediate structures that have mostly 310‐helical characteristics and hydrogen bonds. [46] This unfolding behavior helps stabilize secondary structures relative to the random coil, and plays a key role in helix stability.
Thus the observed energetics of both proteins across the three force fields, c22, c27 and c36, obtained using ASMD reassuringly follows the pattern of corrections across them. Namely, in both proteins, the degree of helical structure (as seen here through the hydrogen bond contacts) moves substantially towards more alpha‐helical content in the c27 trajectories with a smaller reduction in the c36 trajectories. Through ASMD, we also observe that the relative stability of the protein structure is somewhat reduced when measured with the c36 force field which is significant as one moves to look at the relative stability of other peptides/proteins (or species in a thermodynamic system) rather than to itself. When ASMD is obtained using the CHARMM family of potentials, it is consequently advisable to use the c36 force field (or perhaps newer variants, such as CHARMM36 m, [23] which includes the corrections in c36) in order to obtain energetics and characteristic structure along the end‐to‐end distance.
Theory, Materials and Methods
Adaptive Steered Molecular Dynamics (ASMD)
Potential of Mean Force (PMF)
In SMD, [4] the steering force is applied through an auxiliary particle that is attached to a specified atom (or set of atoms) on the peptide by a harmonic spring. When the auxiliary particle is held fixed, the specified atom fluctuates with average position as that of the auxiliary particle and no net work is done on the peptide. When the auxiliary particle is moved along a specified time‐dependent path, the atoms in the rest of the peptide must rearrange accordingly. For example, the steering paths can include conformational changes, [48] ligand dissociation, [49] or the forced unfolding of a peptide by pulling along two ends. [48] The work performed on the system can be obtained directly from the integral of the force of the spring. If the motion is sufficiently slow and adiabatic, then the work change between the endpoints is equal to the free energy difference. Unfortunately, these conditions are usually not met. Nevertheless, the SMD simulation can provide information about the structural changes (and time scales) of the degrees of freedom orthogonal to the steered path as long as the time scales of the steering pathway match those of the MD simulations and the intermolecular peptide motions.
The Jarzynski Equality:[ 50 , 51 , 52 , 53 ]
| (1) |
involving an average over an ensemble of nonequilibrium trajectories (available from an SMD simulation) allows for the free energy difference and non‐equilibrium work to be related exactly. It offered the possibility of revolutionizing the determination of the free energy because it no longer required the nearly reversible paths initially considered in SMD. Indeed, Schulten and coworkers[ 4 , 5 ] demonstrated that the method could lead to accurate potentials of mean force (PMFs) in several model systems over specified reduced dimensional configuration spaces. However, since the exponential‐Boltzmann‐weighted ensemble average is computed, many trajectories are needed to converge the potential mean of force. [54] Furthermore, there is a direct relationship between size of the system and the number of trajectories that need to be simulated. The computational cost of this large sampling problem has significantly limited the use of SMD to calculate free energies through the Jarzynski Equality.
In order to circumvent the sampling problem, Hernandez and coworkers [10] developed the adaptive steered molecular dynamics (ASMD) approach. Its accuracy has been benchmarked on several small model helical‐peptides. in vacuum, [14] in an implicit (water) solvent, [16] and in an explicit (water) solvent. [15] In ASMD, the overall steering path is partitioned into ns smaller consecutive paths with support where the ( ) endpoints run from the initial position to final position of the steered path. In the present work, the end points of each window are equally spaced across the steered path but they could be generalized to include varying distances. Similarly, the steered path is primarily the end‐to‐end vector as signaled by the “ee“ subscript in the notation for the endpoints. The PMF is calculated within each window using the Jarzynski Equality. The peptide is stretched along the end‐to‐end vector at a constant velocity, vs , such that the auxiliary particle's position is defined as . At a given position in the range , the average work assumes the form,
| (2) |
where ζ i is the i th trajectory in the nonequilibrium ensemble stretched from . At the completion of each stage, the work of the trajectories has spread across several kT, and the final configurations are also quite dissimilar. In order to accelerate the convergence in the next step, the space of final configurations must be contracted by effectively removing those configurations that would not contribute to the free energy. [14] In naive ASMD, the contraction of the swarm of nonequilibrium trajectories maps the final configurations from a given stage to a single structure corresponding to the trajectory whose nonequilibrium work is the closest to the Jarzynski average (JA). As we have previously shown,[ 10 , 14 , 15 ] this choice is intuitive and takes advantage of the results from the trajectories that have already been calculated, effectively picking a structure from the mode of the nonequilibrium work distribution. Naive ASMD has also been shown to converge much faster than conventional SMD simulations with respect to the overall number of trajectories required for convergence, thus reducing the computational cost. [10] An important requirement of the contraction of the trajectory space spanned by the final structures in a given previous stage is that it not add energy to the system. This criteria is satisfied by naive ASMD by construction, and would also be satisfied if the contraction simply evolved the relaxation of the trajectories under a constrained endpoint. [14]
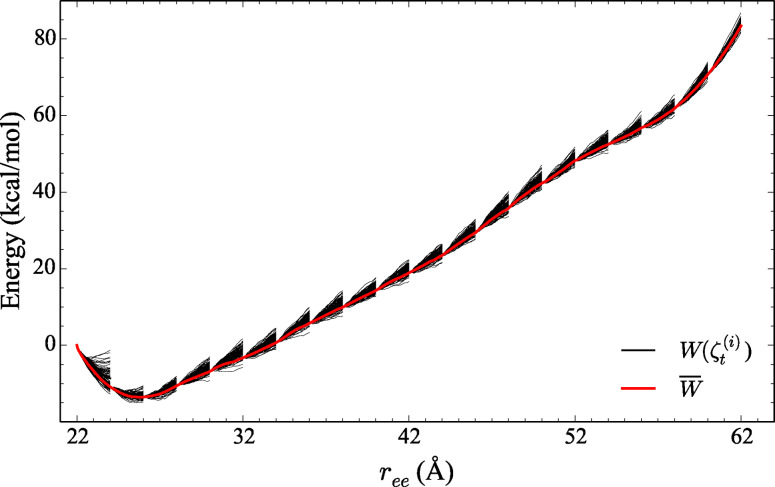
During each iteration after the contraction, the initial velocities for each trajectory in a given window are randomly distributed according to the Boltzmann distribution allowing for faster resampling of the trajectory space. The PMF is thus fully constructed through the iteration of nS pairs of contraction and expansion stages. The stages in ASMD are illustrated in Figure 7. The potential of mean force, shown in red, is obtained from the Jarzynski average while the nonequilibrium work associated with each trajectory in a steered stage, shown in black, spreads in energy within increasing pulling distance. The contraction is also visible as the work distribution is initially narrow at the beginning of each stage. As the present work uses only naive ASMD, and not any of the other recent variants[ 14 , 15 , 16 , 55 ] with differing choices for the contraction, we refer to the naive ASMD simply as ASMD throughout as also noted in the introduction.
Figure 7.
A typical ASMD simulation is divided into 20 stages, as shown, and sampled from 100 trajectories per stage at a stretching velocity, vs , of 10 Å/ns. for the α‐helical peptide 1PEF. The solid black lines represent the work for each trajectory, W( ), whereas the thick red curve represents the overall PMF, , from Eq. 2.
To quantify the precision of the naive ASMD method with the given velocity and associated number of individual trajectories, the Jarzynski weighted cumulative error was computed at the end of each stage over all work trajectories where w denotes work during the stage and denotes a Jarzynski weighted average over all work trajectories, see Figure 3:
| (3) |
| (4) |
| (5) |
Cumulative errors are the square root of:
| (6) |
Observables
The potentials of mean force (PMFs) for and 1PEF are obtained by averaging the nonequilibrium work trajectories using equation 1. The potentials of mean force determined for and 1PEF in an explicit (water) solvent – that is, one in which the waters are treated with an all‐atom representation – CHARMM family of potentials for 100 trajectories per stage with several pulling velocities are reported herein.
The significance of solvent interactions in the stabilization of specific peptide structure has long been recognized and heavily investigated. The hydrophobic effect and the burial of hydrophobic amino acid side chains could stabilize proteins and play a role in determining their structure is viewed as a highly critical, if not the primary cause of how a protein folds.[ 56 , 57 ] Likewise, additional peptide‐solvent interactions such as van der Waals, polar, charged, ionic, and hydrogen bonding are equally as critical to fully understanding the structure‐energetic relationship. [58] Since peptides posses a small proportion of the primary and thus secondary structure of the larger protein systems, small peptides, such as and 1PEF, albeit more computational advantageous, lack a well‐defined hydrophobic core, and nearly all atoms have high solvent exposure. This suggests that peptides are fundamental indicators of the solvent effects on the conformations and energetics which can be observed in large proteins systems.
To investigate the direct role of solvent in the mechanical unfolding of the α‐helical peptides and 1PEF, expectation values of observables along the stretching pathway are obtained using the weight for the work associated with the nonequilibrium paths. These observables are obtained through the use of an ASMD Boltzmann‐weighted‐average. For example, the average number NH of hydrogen bonds between two sets of atoms for a given structure along the pulling coordinate is
| (7) |
where the sets of atoms, S 1 and S 2, contain the indices in the positions of the selected atoms and/or collective variables in , N is the number of trajectories, and is the given observable count for trajectory i at the extension ζt of the peptide. The instantaneous number of hydrogen bonds between the two sets can then be written as
| (8) |
where (ζk , ζl ) is 1 if ζk and ζl are hydrogen bonded positions and 0 otherwise, and the prime in the sum excludes the case that k=l. The hydrogen bonding criteria is set at ≤4 Å and ≥140° for the distance and angle cutoffs. The average number of hydrogen bonds between the peptide and water is determined by and likewise, the average number of intrapeptide hydrogen bonds is determined by letting S P and S W denote the sets of position of oxygen atoms in the peptide and water solvent respectively. The sum of the hydrogen bonds for a given structure along the forced unfolding pathway were partitioned into sums of those bonds linking residues separated by a specific number of residues along the peptide chain. For instance, the hydrogen bonds correspond to a hydrogen bond between the ith and ( residues, as would be observed in an α‐helix. Detailed structural information about the steered unfolding pathway is reported below through a count of hydrogen bonds within the α‐helix and those between the α‐helix and surrounding water molecules.
A detailed analysis of the evolution and change in secondary structure of each α‐helical peptide was determined as a function of the end‐to‐end extension of the peptide so as to further examine the differences between the CHARMM FF potentials. As a peptide unfolds, a variety of conformations are explored before the peptide is completely unstructured. The peptide twists, bends and turns as it is steered along a predetermined pulling coordinate at a constant velocity, and ultimately leading to the breaking of stabilizing intramolecular hydrogen bonds and van der Waals interactions. As these key intramolecular interactions rupture, they can simultaneously be replaced with alternative intramolecular interactions when the peptide is sufficiently compact in an effort to retain some secondary structure. [16] Otherwise, the intramolecular interactions are replaced by stabilizing peptide‐water interactions assisting the peptide in unfolding. The correct identification of secondary structure elements is a major step in the proper characterization of the mechanical unfolding pathway. The percent of secondary structure as a function of end‐to‐end distance (ree) is computed using custom in‐house scripts in conjunction with VMD, [59] STRIDE, [60] and the computed JA trajectory from the ASMD simulations.
Materials
The present work focuses on two peptides, and 1PEF because they contain a high degree of helicity. In particular, the mechanical unfolding of α‐helical peptides presents a challenge to the accuracy of the FFs and is relevant to the correct characterization of the helix‐to‐coil transition. [61] There also exists a large amount of numerical and empirical data about and 1PEF useful for the benchmarking of the methods being investigated here. Specifically, ASMD is used in conjunction with various versions of the CHARMM potential to determine the PMFs for the mechanical unfolding of two small α‐helical peptides, and 1PEF. The former has been thoroughly investigated by many groups in a range of environments.[ 4 , 5 , 9 , 14 , 15 , 16 ] This α‐helical hydrophobic‐homopolymer therefore provides a suitable benchmark for assessing the role of the CHARMM potentials in ASMD.
The initial coordinates of 1PEF were obtained from the PDB (PDB code: 1PEF) and the sequence of 1PEF is as follows: EQLLKALEFLLKELLEKL. [33] 1PEF is an 18‐amino acid α‐helix that is composed of 334 atoms with an acetylated N‐terminus and an amidated C‐terminus, and all hydrogens are explicitly defined. All MD simulations were performed with NAMD [62] and the c22, c22 with CMAP (c27), and c36 family of potentials. 1PEF was placed along the z‐axis of a periodic box composed of approximately 12,600 TIP3P [63] water molecules with the dimensions of 50 Å×60 Å×120 Å. The longest side of this square cuboid is chosen so as to ensure that sufficient solvation layers separate the periodic boundary when the peptide is fully extended.
Simulation Protocols
Although the results for in vacuum, implicit solvent, and explicit solvent using ASMD with the c22 potential were previously published,[ 14 , 15 , 16 ] we have reproduced them in the current work using updated scripts. In addition to the reproduced c22 data, the new c27 and c36 ASMD data results in a robust benchmark for the comparison of the CHARMM family of potentials using our ASMD methodology. This benchmark provides a standard for the hydrophobic, homopolymer helical structure‐energetic relationship, and characteristics in each FF. The ASMD simulations of 1PEF also provided new insight into the complex role of short and long‐range noncovalent interactions, which are critical in the folding and unfolding of all macromolecular systems. The simulation protocols for equilibration and ASMD mechanical unfolding of the homopolymer across the family of CHARMM potentials remained unchanged from the original publications.[ 14 , 15 , 16 ] The following sections detail the simulation protocols for the 1PEF peptide in an explicit (water) solvent.
Equilibration Protocol
In all equilibrium and ASMD mechanical unfolding simulations of 1PEF, the temperature is regulated using the Langevin thermostat, the van der Waals interaction cutoff distance was set at 12 Å, the smooth switching function beginning at 8 Å, and long‐range electrostatic forces were computed using the particle‐mesh Ewald summation method with a gird size of <1 Å. To prepare the peptide‐water system for the ASMD simulations, a minimization and equilibration protocol was followed.
The peptide‐water system was initially energy‐minimized to remove bad contacts by carrying out a minimization, 10,000 steps of each steepest descent and conjugate gradient method. The system was then slowly heated from 100–300 K during a 500 ps simulation (NVT Ensemble) with the solute restrained using a 10 kcal/molÅ2 harmonic potential. The system then underwent 1 ns of constant pressure equilibration at 300 K (NPT ensemble) through the Nose‐Hoover Langevin piston method. A damping coefficient of 5 ps−1 with a decay period of 100 fs and a damping time constant of 50 fs was employed. The helical peptide's backbone was constrained during the NPT equilibration using a stiff harmonic potential, allowing the water to reach a density of approximately 0.9987 g/cm3 while allowing the side‐chains to reach energetically favorable conformations within the TIP3P water. Next, the peptide‐water system underwent a constant volume equilibration (NVT ensemble) at 300 K. A series of 100 ps constraint relaxations were performed where the backbone was constrained with a harmonic potential of 10.0 kcal/mol Å2, 5.0 kcal/mol Å2, and 1.0 kcal/mol Å2 consecutively. After the final constraint of 1.0 kcal/mol Å2 was released, the peptide‐water system was allowed to freely equilibrate in the NVT ensemble for 500 ps.
Production Phase
In the production stage of the ASMD simulations, 1PEF is mechanically unfolded such that the end‐to‐end ( ) distance between the α‐carbon of the N‐terminus (ACN) and the α‐carbon of the C‐terminus (ACC) is gradually increased from 22 to 62 Å. The ACN is kept fixed and the ACC is steered along the longest axis of the periodic square cuboid box, defined to be the z‐axis, while harmonically attached to a pseudo particle using a biased Hamiltonian. [15] The harmonic force constant, k, is set to be 7.2 kcal/mol. The pulling coordinate for the forced stretching of 1PEF is defined as the end‐to‐end distance between the ACN and ACC ( ). This pulling coordinate was partitioned into 20 stages, such that was perturbed 2 Å/stage. To obtain good statistics, multiple trajectories at each stage have been generated over the equilibrated initial configuration by varying the forces in the Langevin bath. These resulting trajectories are then analyzed numerically and visually with in‐house scripts and by using the VMD package. [59]
Empirical Force Fields
In many currently available all‐atom additive FFs, all‐inclusive many‐body effects are generally missing even though they make a large contribution to the total energy in the condensed phase. [64] For the helix‐to‐coil transition, missing contributions to the total energy may come from stabilizing hydrogen bonds, [37] charge transfer effects [65] or electronic polarization. [66] Through the use of a single family of FFs, we have shown in this paper that ASMD is sensitive to the underlying FF and improves systematically with the evolution of the FF parameterization; both with respect to the mechanical‐unfolding energetics and the pathway of each α‐helical peptide system.
The oldest of the CHARMM FFs of interest to this study is c22 (also known as CHARMM22). c22 differed significantly from it's predecessor EF2, [67] and was the first to provide reasonable agreement with experiment. It was parameterized to include TIP3P water, [68] nucleic acids, [69] proteins, [20] and lipids. [70] The c22 FF has been used to study the mechanical unfolding of peptides solvated in explicit (TIP3P) water. In 1999, for example, Schulten and coworkers examined the force‐induced unfolding of the α‐helical domain IGB and the β‐sandwich domain CAD2. [71] Likewise, our earlier work on neuropeptide Y [10] and [ 14 , 15 ] ASMD simulations were carried out with c22. However, despite its broad adoption, c22 has been seen to have some shortcomings, including its improper handling of protein conformations leading to the incorrect prediction of π‐helical structures. [45]
To address the shortcomings of c22, improvements in the backbone energetics were undertaken by MacKerell et al. [21] through the introduction of a two‐dimensional energy correction map (CMAP) that could be applied to the functions of c22 that depend on the dihedral angles, ϕ and ψ. The CMAP grid correction was applied to all residues in the c22 FF with the same parametric dependence, except glycine and proline for which different CMAP corrections were implemented. The c27 FF (also known as CHARMM22 with CMAP or CHARMM27) has been used to study the dynamics of various biological systems, ranging from structural‐function studies of proteins[ 72 , 73 , 74 ] and long scale MD simulations, [75] to SMD simulations. [76]
Even though the CMAP correction to c22 resulted in better agreement with NMR measurements, c27 has been shown by several groups to have too strong a bias toward α‐helical conformations.[ 77 , 78 ] This bias is largely due to relatively small inaccuracies in the backbone potential.[ 61 , 77 , 79 , 80 ] To correct this issue, CMAP was reparameterized by MacKerell and coworkers [81] in creating c36. The grid correction map was adjusted to provide a better fit to experimental NMR structure data for the peptides and Ac‐(AAQAA)3‐NH2 within common residues, and to the QM energy surfaces computed with a higher level of theory for the glycine and proline residues. In addition, the side‐chain dihedral parameters χ 1 and χ 2 for each amino acid were fitted to QM surfaces.[ 32 , 82 ] Gumbart and coworkers [9] characterized the thermodynamics of decaalanine folding in water using both the c27 and c36 FFs. They determined that c36 agreed well with previously reported PMFs and significantly improved agreement with helix‐formation experiments.
Supporting Information
Supporting information reporting the end‐to‐end distances and relative structures of the ALA10 and 1PEF peptices equilibrated for each of the CHARMM force fields – c22, c27 and c36 – reported here is available on line.
Conflict of interest
The authors declare no conflict of interest.
1.
Supporting information
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
Supporting Information
Acknowledgements
This work has been partially supported by the National Science Foundation (NSF) through Grant No. CHE 2102455. The computing resources necessary for this work were provided in part by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (NSF) grant number ACI‐1548562 through allocation CTS090079, and the Advanced Research Computing at Hopkins (ARCH) high‐performance computing (HPC) facilities supported by NSF grant number OAC‐1920103.
C. Allen, H. R. Bureau, T. D. McGee, S. Quirk, R. Hernandez, ChemPhysChem 2022, 23, e202200175.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- 1. Sugita Y., Okamoto Y., Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar]
- 2. Zwanzig R. W., J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar]
- 3. Isralewitz B., Baudry J., Gullingsrud J., Kosztin D., Schulten K., J. Mol. Graphics Modell. 2001, 19, 13–25. [DOI] [PubMed] [Google Scholar]
- 4. Park S., Khalili-Araghi F., Tajkhorshid E., Schulten K., J. Chem. Phys. 2003, 119, 3559–3566. [Google Scholar]
- 5. Park S., Schulten K., J. Chem. Phys. 2004, 120, 5946–5961. [DOI] [PubMed] [Google Scholar]
- 6. Ramírez C., Martí M., Roitberg A., in Computational Approaches for Studying Enzyme Mechanism Part B, Vol. 578 of Methods in Enzymology, pp. 123–143, Academic Press, 2016. [DOI] [PubMed] [Google Scholar]
- 7. Jarzynski C., Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar]
- 8. Zhuang Y., Bureau H., Quirk S., Hernandez R., Mol. Simul. 2021, 47, 408–419. [Google Scholar]
- 9. Hazel A., Chipot C., Gumbart J. C., J. Chem. Theory Comput. 2014, 10, 2836–2844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Ozer G., Valeev E., Quirk S., Hernandez R., J. Chem. Theory Comput. 2010, 6, 3026–3038. [DOI] [PubMed] [Google Scholar]
- 11. Quirk S., Hopkins M., Bureau H., Lusk R., Hernandez R., Bain D., ACS Omega 2018, 3, 2141–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Bureau H., Quirk S., Hernandez R., RSC Adv. 2020, 10, 6520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Zhuang Y., Bureau H. R., Lopez C., Bucher R., Quirk S., Hernandez R., Biophys. J. 2021, 120, 2009–2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Ozer G., Quirk S., Hernandez R., J. Chem. Phys. 2012, 136, 215104. [DOI] [PubMed] [Google Scholar]
- 15. Ozer G., Quirk S., Hernandez R., J. Chem. Theory Comput. 2012, 8, 4837–4844. [DOI] [PubMed] [Google Scholar]
- 16. Bureau H. R., Merz D. Jr., Hershkovits E., Quirk S., Hernandez R., PLoS One 2015, 10, e0127034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bureau H. R., Hershkovits E., Quirk S., Hernandez R., J. Chem. Theory Comput. 2016, 12, 2028–2037. [DOI] [PubMed] [Google Scholar]
- 18. Hantz E. R., Lindert S., J. Chem. Inf. Model. 2021, 61, 3052–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Xie H., Gunawardana V. W. L., Finnegan T. J., Xie W., Badjić J. D., Angew. Chem. Int. Ed. 2022, 61, e202116518. [DOI] [PubMed] [Google Scholar]
- 20. MacKerell A. D. Jr., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., Karplus M., J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- 21. A. D. MacKerell, Jr. , Feig M., Brooks C. L. III, J. Comput. Chem. 2004, 25, 1400–1415. [DOI] [PubMed] [Google Scholar]
- 22. Huang J., A. D. MacKerell, Jr. , J. Comput. Chem. 2013, 34, 2135–2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Huang J., Rauscher S., Nawrocki G., Ran T., Feig M., de Groot B. L., Grubmüller H., A. D. MacKerell, Jr. , Nat. Methods 2017, 14, 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Case D. A., Cheatham T. E., Darden T., Gohlke H., Luo R., Merz K. M., Onufriev A., Simmerling C., Wang B., Woods R. J., J. Comput. Chem. 2005, 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Salomon-Ferrer R., Case D. A., Walker R. C., WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar]
- 26. Jorgensen W. L., Maxwell D. S., Tirado-Rives J., J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar]
- 27. Kaminski G. A., Friesner R. A., Tirado-Rives J., Jorgensen W. L., J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar]
- 28. Célerse F., Lagardère L., Derat E., Piquemal J.-P., J. Chem. Theory Comput. 2019, 15, 3694–3709. [DOI] [PubMed] [Google Scholar]
- 29. Garcia A. E., Sanbonmatsu K. Y., Proc. Natl. Acad. Sci. USA 2002, 99, 2782–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Hornak V., Abel R., Okur A., Strockbine B., Roitberg A., Simmerling C., Proteins Struct. Funct. Bioinf. 2006, 65, 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Maier J., Martinez C., Kasavajhala K., Wickstrom L., Hauser K., Simmerling C., J. Chem. Theory Comput. 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Best R. B., Zhu X., Shim J., Lopes P. E. M., Mittal J., Feig M., A. D. Mackerell, Jr , J. Chem. Theory Comput. 2012, 8, 3257–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Taylor K. S., Chin M. Z., Yang N. C., Garavito R. M., Protein Sci. 1996, 5, 414–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Ross C. A., Poirier M. A., Nat. Med. 2004, 10, S10–S17. [DOI] [PubMed] [Google Scholar]
- 35. Ghosh T., Garde S., Garcia A. E., Biophys. J. 2003, 85, 3187–3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. A. D. MacKerell, Jr. , Feig M., Brooks C. L. III, J. Am. Chem. Soc. 2004, 126, 698–699. [DOI] [PubMed] [Google Scholar]
- 37. Best R. B., Mittal J., Feig M., A. D. MacKerell, Jr. , Biophys. J. 2012, 103, 1045–1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Arrar M., Boubeta F. M., Szretter M. E., Sued M., Boechi L., Rodriguez D., J. Chem. Theory Comput. 2018, 40, 688–696. [DOI] [PubMed] [Google Scholar]
- 39. Wang X., Tu X., Deng B., Zhang J. Z. H., Sun Z., J. Chem. Theory Comput. 2019, 40, 1270–1289. [DOI] [PubMed] [Google Scholar]
- 40. Sheinerman F. B., Brooks C. L. III, J. Am. Chem. Soc. 1995, 117, 10098–10103. [Google Scholar]
- 41. Millhauser G. L., Stenland C. J., Hanson P., Bolin K. A., van de Ven F. J. M., J. Mol. Biol. 1997, 267, 963–974. [DOI] [PubMed] [Google Scholar]
- 42. Barlow D. J., Thornton J. M., J. Mol. Biol. 1988, 201, 601–619. [DOI] [PubMed] [Google Scholar]
- 43. Young W. S., Brooks C. L. III, J. Mol. Biol. 1996, 259, 560–572. [DOI] [PubMed] [Google Scholar]
- 44. Bryant Z., Pande V. S., Rokhsar D. S., Biophys. J. 2000, 78, 584–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Feig M., Mackerell A. D., Brooks C. L., J. Phys. Chem. B 2003, 107, 2831–2836. [Google Scholar]
- 46. Soman K. V., Karimi A., Case D. A., Biopolymers 1991, 31, 1351–1361. [DOI] [PubMed] [Google Scholar]
- 47. Tirado-Rives J., Jorgensen W. L., Biochemistry 1991, 30, 3864–3871. [DOI] [PubMed] [Google Scholar]
- 48. Lu H., Isralewitz B., Krammer A., Vogel V., Schulten K., Biophys. J. 1998, 75, 662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Sadiq S., Wan S., Coveney P., Biochemistry 2007, 46, 14865–14877. [DOI] [PubMed] [Google Scholar]
- 50. Jarzynski C., Phys. Rev. E 1997, 56, 5018–5035. [Google Scholar]
- 51. Jarzynski C., Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar]
- 52. Jarzynski C., Phys. Rev. E 1997, 56, 5018–5035. [Google Scholar]
- 53. Crooks G. E., J. Stat. Phys. 1998, 90, 1481–1487. [Google Scholar]
- 54. Jiang W., Roux B., J. Chem. Theory Comput. 2010, 6, 2559–2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Ozer G., Keyes T., Quirk S., Hernandez R., J. Chem. Phys. 2014, 141, 064101. [DOI] [PubMed] [Google Scholar]
- 56. Dill K. A., Biochemistry 1990, 29, 7133–7151. [DOI] [PubMed] [Google Scholar]
- 57. Kauzmann W., Adv. Protein Chem. 1959, 16, 1–64. [DOI] [PubMed] [Google Scholar]
- 58. Prabhu N., Sharp K., Chem. Rev. 2006, 106, 1616–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Humphrey W., Dalke A., Schulten K., J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
- 60. Frishman D., Argos P., Proteins Struct. Funct. Genet. 1995, 23, 566–579. [DOI] [PubMed] [Google Scholar]
- 61. Best R. B., Hummer G., J. Phys. Chem. B 2009, 113, 9004–9015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kale L., Schulten K., J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L., J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- 64. Stone A. J., Science 2008, 321, 787–789. [DOI] [PubMed] [Google Scholar]
- 65. Bartlett G. J., Choudhary A., Raines R. T., Woolfson D. N., Nat. Chem. Biol. 2010, 6, 615–620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Morozov A. V., Tsemekhman K., Baker D., J. Phys. Chem. B 2006, 110, 4503–4505. [DOI] [PubMed] [Google Scholar]
- 67. Nilsson L., Karplus M., J. Comput. Chem. 1986, 7, 591–616. [Google Scholar]
- 68. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klien M. L., J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- 69. Mackerell A. D. Jr., Wiorkiewicz-Kuczera J., Karplus M., J. Am. Chem. Soc. 1995, 117, 11946–11975. [Google Scholar]
- 70. Schlenkrick M., Brickmann J., Mackerell A. D. Jr., Karplus M., in In Biological Membranes: A Molecular Perspective from Computation and Experiment, (Eds. Pastor R. W., Feller S. E., Merz Jr K. M., Roux B.), Birkhauser, Boston, MA, 1996, pp. 31–81. [Google Scholar]
- 71. Lu H., Schulten K., Proteins Struct. Funct. Bioinf. 1999, 35, 453–463. [PubMed] [Google Scholar]
- 72. Buck M., Bouguet-Bonnet S., Pastor R., M. A. D. Jr., Biophys. J. 2006, 90, L36–L37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Guvench O., Qu C. K., M. A. D. Jr., BMC Struct. Biol. 2007, 7, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Aleksandrov A., Simonson T. A., J. Comput. Chem. 2010, 31, 1550–1560. [DOI] [PubMed] [Google Scholar]
- 75. Gleeson M. P., Deechongkit S., Ruchirawat S., J. Mol. Model. 2011, 17, 769–775. [DOI] [PubMed] [Google Scholar]
- 76. Liu Y., Hsin J., Kim H., Selvin P. R., Schulten K., Biophys. J. 2011, 100, 2964–2973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Best R. B., Buchete N.-V., Hummer G., Biophys. J. 2008, 95, L7–L9. [Google Scholar]
- 78. Cino E. A., Choy W.-Y., Karttunen M., J. Chem. Theory Comput. 2012, 8, 2725–2740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Mittal J., Best R. B., Biophys. J. 2010, 99, L26–L28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Best R. B., Mittal J., J. Phys. Chem. B 2010, 114, 8790–8798. [DOI] [PubMed] [Google Scholar]
- 81. Best R. B., Zhu X., Shim J., Lopes P. E. M., Mittal J., Feig M., MacKerell A. D. Jr., J. Chem. Theory Comput. 2012, 8, 3257–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Zhu X., Lopes P. E. M., Shim J., Alexander J., Mackerell D., J. Chem. Inf. Model. 2012, 52, 2317–2318. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
Supporting Information
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.