Abstract
The use of deep learning (DL) to improve cone‐beam CT (CBCT) image quality has gained popularity as computational resources and algorithmic sophistication have advanced in tandem. CBCT imaging has the potential to facilitate online adaptive radiation therapy (ART) by utilizing up‐to‐date patient anatomy to modify treatment parameters before irradiation. Poor CBCT image quality has been an impediment to realizing ART due to the increased scatter conditions inherent to cone‐beam acquisitions. Given the recent interest in DL applications in radiation oncology, and specifically DL for CBCT correction, we provide a systematic theoretical and literature review for future stakeholders. The review encompasses DL approaches for synthetic CT generation, as well as projection domain methods employed in the CBCT correction literature. We review trends pertaining to publications from January 2018 to April 2022 and condense their major findings—with emphasis on study design and DL techniques. Clinically relevant endpoints relating to image quality and dosimetric accuracy are summarized, highlighting gaps in the literature. Finally, we make recommendations for both clinicians and DL practitioners based on literature trends and the current DL state‐of‐the‐art methods utilized in radiation oncology.
Keywords: adaptive radiotherapy, AI, cone‐beam CT, CT, deep learning, image synthesis, synthetic CT
1. INTRODUCTION
Artificial intelligence (AI) is expected to both disrupt and transform standard practices in healthcare. Radiation oncology has traditionally been at the forefront of medical technology adoption, a tradition that demands expertise in both theoretical and practical aspects of a given technology. 1 Hence, this review aims to broaden both clinicians’ and researchers’ understanding of state‐of‐the‐art (SoTA) deep learning (DL) methods currently employed in cone‐beam CT (CBCT) image correction, summarize clinically relevant results, and offer constructive considerations in advancing the research.
Adaptive radiation therapy (ART) has shown tremendous promise in improving patient outcomes by sparing healthy tissues and escalating dose‐to‐tumor volumes. 2 , 3 , 4 , 5 CBCT‐driven dose monitoring enables the recalculation of the dose on updated patient anatomy prior to irradiation. Hence, clinicians can monitor the validity of the plan and decide to trigger an adaptive protocol if dosimetric deviations from the initial prescription are deemed clinically relevant. The irradiation parameters are then modified, either online or offline, to achieve optimal tumor coverage whilst minimizing dose to healthy tissues. Online ART has not been widely adopted into the clinical workflow due to practical limitations involving the integration of specialized tools for patient assessment, plan adoption, and quality assurance. 6 Of critical importance to the first consideration is CBCT image quality. In their most rudimentary implementation, CBCT images are unable to reproduce accurate tissue density, suffer from artifacts capable of undermining subsequent clinical application, and have inferior contrast relative to diagnostic grade CT imaging. 7 The focus of this investigation is to review DL methods for correcting CBCT image quality, placing emphasis on methodological novelties such as loss functions and architectural/model design.
The article is divided into five parts consisting of background information, methods, results, discussion, and conclusion. Background information introduces readers to fundamental DL components necessary to understand SoTA approaches in medical image synthesis, along with detailed descriptions of the most common evaluation metrics for assessing image quality and dose accuracy. The methods section outlines what criteria were used in compiling the review. The results section summarizes the most salient trends throughout the literature, whereas the discussion section draws on these trends to make recommendations for both clinicians and DL practitioners.
2. BACKGROUND
A theoretical understanding of the basic components that underlies SoTA algorithms provides a foundation for researchers to build on and allows clinicians to appreciate the technology that could underpin future workflows. What follows is a brief discussion introducing the concept of DL (1), convolution operations and layers (2), model optimization and the role of loss functions (3), and a description of the most popular image synthesis architectures (4). Table 1 summarizes the strengths and limitations of these architectures.
TABLE 1.
Benefits and limitations of three common deep learning (DL) architectures: U‐Net, GAN (generative adversarial network), and cycle‐GAN
| Architecture | Strengths | Limitations |
|---|---|---|
| U‐Net |
|
|
| GAN |
|
|
| Cycle‐GAN |
|
|
2.1. Deep learning
Machine learning (ML) is a field of computer science interested in developing algorithms that accomplish complex tasks without being explicitly programed to do so by observing data. DL is a subfield of ML that specifically uses artificial neural networks—computational units inspired by biological synaptic responses—to process data into desired outputs. 8 The stacking of many such neuronal hidden layers gives “depth” to the network, thus reflecting the term “deep” in DL. The convolutional neural network (CNN) is a specialized framework that excels in computer vision problems. The interested reader can refer to Yamashita et al. 9 for an accessible overview of general mechanisms and building blocks comprising CNNs in the radiological context.
In the context of medical image synthesis (also termed image‐to‐image translation or domain transfer), four major components are required, namely, the convolution layer, a model architecture, and the loss function and optimizer.
2.2. The convolution layer
The convolution operation—not limited to DL—is a linear function used for image‐based feature extraction. For example, early attempts at modeling scatter from primary signals in radiographic systems used a convolution‐filtering method. 10 Figure 1a depicts how image features are extracted by convolution between the image and filter (also known as kernel). During convolution, an element‐wise multiplication between the kernel and image is followed by a summation over each of the values. The convolution output, also known as a feature map, contains the results of all convolution operations. The spatial dimensions of the feature map depend on the image padding, size of the filter, and stride of the filter. The stride controls the distance between two adjacent convolutions (stride = 3 in Figure 1a). The filter size controls how much information is extracted per convolution, with smaller feature maps resulting from larger filters. Finally, image dimensions may be increased by applying border padding (typically zero pixels), enabling a precise control of the output feature map spatial dimension. The choice of padding, filter size, and stride are hyperparameters set by the practitioner and remain unchanged during training. Conversely, the parameters contained within the filters are learned during the optimization stage. 11
FIGURE 1.
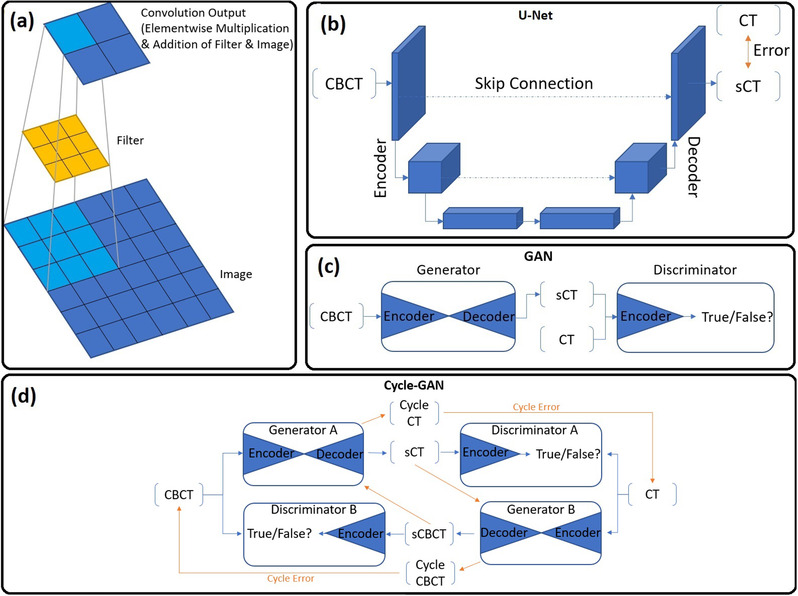
(a) The convolution output (feature map) results from element‐wise multiplication followed by summation between the filter and image. Note how image information is encoded into a reduced spatial dimension. (b) Depiction of the U‐Net architecture. Note how the input spatial dimensions are progressively reduced, whereas the feature dimension increases with network depth. (c) The GAN architecture comprising a generator and discriminator. Generators are typically U‐Net‐type architectures with encoder/decoder arms, whereas discriminators are encoder classifiers. (d) The Cycle‐GAN network comprising two generators and discriminators capable of unpaired image translation via computation of the cycle error. The orange arrows indicate the backward synthesis cycle path.
The convolution layer, whose task is to extract meaningful features, is defined by the application of an arbitrary number of these filters per layer, each followed by a nonlinear processing unit (or activation function). Chemical synapses activate by forming a potential difference between junctions and breaching a threshold voltage. 12 So to do neurons in a CNN “activate” by satisfying a nonlinear function—the simplest being the rectified linear unit (ReLU). ReLU outputs zero (no signal) if the input is a negative value, else mapping the input as output. Each filter contained in a layer outputs a unique feature map, which is stacked into a 3D feature map volume ready to be processed by a deeper convolutional layer. Hence, deeper convolution layers extract hierarchically more complex feature representations, where each filter in deeper layers has a “depth” dimension matching the input feature map depth. The impressive expressivity of neural networks stems from the combined use of such nonlinear functions and deep network architectures. 9
Equally important in the image translation literature is the transposed convolution layer. Typically, a series of convolution layers will downsample the spatial dimensions of an image (by virtue of the convolution operation), whilst increasing the feature dimensions (controlled by the number of filters per layer). The role of transposed convolutions is to upsample the feature map spatial dimensions such that we may return an output image with the same dimensions as the input. In transposed convolution, each element of the kernel is multiplied by a single element in the input feature map for a given position. The result is stored in the output feature map before moving to the next input feature map element. Any overlapping regions of each transposed convolution operation are summed to form the final output feature map. Furthermore, in transposed convolution the padding decreases the output spatial dimensions, whereas the stride determines the number of zero elements inserted between each input element, hence increasing the output dimensions. Finally, a larger kernel size will form a larger transposed convolution output, thereby increasing the output feature map dimensions. 11
2.3. Loss function and optimization
Training a model requires discovering the optimal parameters that process the input data into a satisfactory output. Hence, the model must have a measure of how wrong its predictions are—the loss function; and a strategy to adjust its parameters to minimize this loss—gradient descent optimization. The loss function computes a distance metric between the model prediction and the ground‐truth data which it is trying to approximate. A typical loss function for paired training arrangements is the mean absolute error (MAE), also known as L1 distance. Here, the average absolute magnitude difference between predicted and ground‐truth data is computed on a per‐pixel basis. This loss is a function of the millions or billions of trainable parameters contained in the model, and each unique configuration of the parameters in turn has its own loss value. Hence, the loss with respect to each parameter can be thought of as a hyperdimensional plane, which contains local peaks and troughs and a global minimum and maximum. 13
In gradient descent optimization, the task is to adjust the network parameters in the direction that reduces the loss. Ideally, we stop training when model weights arrive at the global minimum, which represents the lowest achievable loss value for the given dataset and architecture. In practice, the model may not reach the global minimum but a local trough. Regardless, gradient descent operates by computing the partial derivative of each parameter with respect to the loss. This indicates the local slope of the loss with respect to that parameter. A given parameter is then updated by subtracting it with its partial derivative, which effectively moves the model state toward a lower loss state. The learning rate is a hyperparameter that controls the size of steps taken toward that minima. 13
2.3.1. U‐Net
With the basic building blocks and optimization frameworks in mind, it becomes possible to define the most widely used medical DL architecture, U‐Net, as depicted in Figure 1b. Based on the autoencoder architecture, U‐Net is suitable for both classification or regression tasks, capable of pixel‐wise predictions (as opposed to image‐wide) by utilizing skip connections and a fully convolutional framework. The encoding portion of the network passes the input image through consecutive convolution layers with serially increasing numbers of output feature maps. The image is encoded in a compressed latent space with a reduced spatial dimension but increased feature dimension. The decoding portion of the network reassembles an output image using consecutive transpose convolution layers that restore the input spatial image dimensionality while reducing feature dimensions. U‐Net differs from autoencoders by enabling the accurate reconstruction of spatial information during upsampling by the use of skip connections from encoder‐side convolution layers to the corresponding decoder‐side layers. These connections, which concatenate encoder feature maps to the decoder side, propagate spatial and contextual information across the network to help the decoder reassemble a more accurate output using queues from the input. The fully convolutional structure of U‐Net means that no fully connected dense layers are needed at the output, drastically reducing model parameters while enabling a per‐pixel prediction. Hence, more computational resources can be directed to expanding model depth, in turn, increasing predictive capacity. 14
U‐Net‐based image translation tasks typically require pixel‐wise loss functions for supervision; hence, input and target domain images must be paired to achieve satisfactory results. In the medical context, perfectly aligned imaging data is only attainable through post‐processing corruption of the target domain to resemble the input domain. 15 Alternatively, same‐day scans offer the best anatomical match but are logistically difficult to acquire. Else, data pairing is achieved through a rigid and deformable registration of same‐patient scans. When coupled with per‐pixel losses, anatomical discrepancies in the training data imbed an unavoidable error into the model that is propagated to future predictions typically manifesting as a loss of boundary sharpness or false anatomy artifacts. 16 , 17 , 18 , 19
2.3.2. Generative adversarial networks
Unlike U‐Net, which can be considered a single generator constrained by hand‐crafted loss functions, the generative adversarial network (GAN) instead consists of two networks: a generator and a discriminator that each minimizes their own loss in a competitive two‐player setting. 20 In a GAN framework (shown in Figure 1c), the discriminator is a classification network whose task is to discern real from generated samples, meanwhile the generator is tasked with generating samples that can fool the discriminator. During a single pass, GAN training is performed sequentially: First, the discriminator is trained to minimize its classification loss between real and generated samples (discriminator loss). Next, the generator is trained to maximize the likelihood that a generated sample will be classified as real by the discriminator (adversarial loss). In turn, the discriminator loss and adversarial loss are dynamic as each network improves and provides impetus for the other. GAN optimality is reached when a Nash equilibrium is established: where a networks loss cannot be minimized further without altering the other networks parameters. 21 At this equilibrium, the discriminator will equally classify real and generated samples with a probability of 0.5. 22
The GAN framework discussed so far has been purely generative in nature: synthesizing realistic outputs from input noise. For the special case of medical image synthesis, conditional GANs are introduced. They function in the same way but accept images as input rather than noise. 23
Compared with U‐Net, the GAN framework has several advantages. For one, the adversarial loss minimizes differences in the data distribution and deep features between the two domains. Consequently, paired training data is not required, and the resulting synthetic images are perceptually more realistic. In practice, unsupervised GAN implementations are highly unconstrained as the set of realistic generator outputs that can fool the discriminator is large. This is problematic for medical image synthesis as the patient anatomy may not be preserved, or density information may not be retained even if the style of the target image is attained. To remedy this, a GAN may be constrained using paired data and per‐pixel losses. Other issues associated with GAN optimization include difficulty balancing generator and discriminator hyperparameters for stable training, uncertainty as when to cease training as Nash equilibrium convergence rarely manifests, longer training, and higher hardware requirements.
2.3.3. Cycle‐GAN
Cycle‐GAN is a variant of the conditional‐GAN framework that introduces forward and backward domain synthesis to enforce a “cycle‐consistency” loss using two generators and two discriminators. 24 The major benefit of cycle‐consistency is the preservation of anatomic information during synthesis for unpaired datasets. Figure 1d demonstrates the cycle‐loss for the CBCT and CT wings of the network. For a given CBCT image, generator A outputs a synthetic CT (sCT), after which generator B transforms the sCT back into a cycle‐synthetic CBCT. By enforcing a pixel‐wise loss between the original CBCT and cycle‐synthetic CBCT, anatomic preservation is encouraged during the initial generator A transformation. The same set of transformations is applied to the input CT.
Cycle‐GAN achieves SoTA performance on unpaired data owing to the combination of cycle‐consistency and adversarial losses. However, cycle‐consistency is a strict regularization technique that constrains the generator to output images that can be easily inverted to the original domain. Although desirable for anatomic preservation, cycle‐consistency becomes problematic where large changes to the output are desired, 25 such as in the presence of motion artifacts. In these instances, the generator preserves aspects of the artifact as a prompt to recover them during the backward synthesis cycle. 26 , 27 Generally, the issues that inflict GANs are present for cycle‐GAN, albeit more severely as greater computational resources are required, more precise fine‐tuning of hyperparameters is needed, and training times are further increased.
2.4. Evaluation metrics
Typical evaluation metrics for assessing image quality between ground truth and corrected image sets are presented in Table 2. Ground‐truth data consists of CT images that have undergone deformable image registration (DIR) to the CBCT, or CBCT images that have been scatter corrected using Monte Carlo (MC) or a previously validated CT‐prior method. 28 , 29 , 30 The most cited metric is MAE, which linearly compares the average absolute pixel‐wise error deviations over the entire image or within specific regions of interest (ROI) or the patient body contour. Mean error (ME) and (root) mean squared error ((R)MSE) assess the degree of systematic error shift, and prominence of large error deviations, respectively. The peak signal‐to‐noise ratio (PSNR) is a measure used to quantify the magnitude of noise relative to signal affecting the CBCT in comparison to the ground truth. Finally, the structural similarity (SSIM) index is used to assess perceptual qualities of corrected and ground‐truth images based on statistical measures of luminance, contrast, and structure. 31 Recently, the Dice similarity score, 32 used to quantify segmentation accuracy, has been used as a surrogate metric for image quality. The Dice score measures the area of overlap between ground truth and automated segmentations. In the context of CBCT image quality, automated segmentations performed on corrected and non‐corrected CBCT images are compared to manual or automatic segmentations performed on DIR CT.
TABLE 2.
Summary of common image and dose based similarity metrics
| Metric | Formula | |
|---|---|---|
| Image similarity | MAE/ME ↓ | / |
| MSE/RMSE ↓ | / | |
| PSNR ↑ |
|
|
| SSIM ↑ |
with ; ; ; ; ; ; ; |
|
| DICE ↑ |
with |
|
| Dosimetric similarity | DPR ↑ |
Fraction of voxels where DD ⩽ x% with where |
| DVH ↑ | Cumulative histogram of dose–volume frequency distribution for a given volume | |
| GPR ↑ | Fraction of voxels where |
Note: Arrows indicate better result.
Abbreviations: DPR, dose difference pass rate; DVH, dose–volume histogram; GPR, gamma pass rate; MAE, mean absolute error; ME, mean error; MSE, mean squared error; PSNR, peak signal‐to‐noise ratio; RMSE, root mean square error; SSIM, structural similarity.
The ART process can involve the recalculation of treatment dose on the corrected CBCT images. In investigating the suitability of corrected CBCT images for ART, the dosimetric accuracy can be validated by applying the same clinical plan used during treatment planning on the ground‐truth CT and corrected CBCT images. A variety of metrics such as dose difference pass rate (DPR), dose–volume histogram (DVH) metrics, and Gamma pass rates (GPR) are commonly used. The DPR is a pixel‐wise metric that quantifies the percentage of pixels that satisfy a set dose difference threshold between corrected and ground truth images. The DVH compares the cumulative dose to different structures as a function of volume. 33 Comparisons to clinically relevant criteria can be made, such as the volume of tissue receiving a given prescription dose, the percentage difference of which can be compared between corrected and ground truth volumes. Finally, the Gamma index is a composite function of dose difference and distance‐to‐agreement criteria used to gauge the similarity of two dose distributions. Calculated in either 2D or 3D, the GPR measures the percentage of points that satisfy the specified criteria. 34
3. METHODS
PubMed, Scopus, and Web of Science were searched using the terms and inclusion/exclusion criteria outlined in Figure 2. The goal was to review the CBCT‐specific literature and include any investigations that used DL to improve image quality suitable for ART. Criteria were narrowed to exclude CBCT acquisitions that do not comport with ART, for example: Studies using low‐dose scans that do not explicitly strive for ART, 4D scans, and C‐arm or dental modalities. We did not limit our investigation to methods that only sought to generate sCT images using DL as alternative approaches in the projection domain show promising results and are worthy of discussion. Finally, we restricted our criteria to only include peer‐reviewed journal articles.
FIGURE 2.
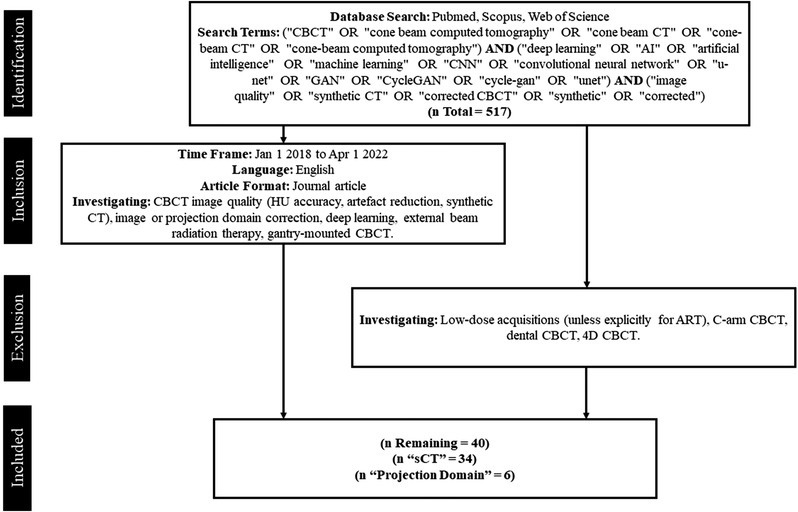
Flowchart of study selection process
An initial selection screening was performed based on the title and abstract of the articles returned after the database search. Duplicate results or items that did not meet the inclusion criteria were removed. Post screening, the full‐text articles were retrieved for a review. The methods of each investigation were reviewed and information pertaining to model architecture, loss functions, cohort size and split, anatomical region, training configuration, augmentations, and preprocessing were extracted. When available, the corresponding results that reported image similarity metrics (MAE, (R)MSE, SSIM, ME, PSNR) and dose accuracy (GPR, DVH, DPR) were also extracted. The information is summarized in separate tables under categories “sCT generation” (Tables 3A, 3B, 3C) and “projection based” (Table 4) based on the authors’ aims. Studies defined under “sCT generation” set their target domain as CT images, whereas studies under “projection based” employ a range of DL‐driven scatter correction techniques to improve CBCT image quality.
TABLE 3A.
Summary of synthetic CT (sCT) generation methods
| Author and year | Anatomic site | Model | Loss function | Augmentation | Preprocessing | (train/val/test) | Training configuration | Image similarity (input CBCT) | Dose similarity |
|---|---|---|---|---|---|---|---|---|---|
| Kida et al. 2018 53 | Pelvis | U‐Net | MAE |
|
5‐CV (16/0/4) | Paired axial 2D | SSIM: 0.967 (0.928). PSNR: 50.9 (31.1). RMSE: 13 (232) | ||
| Xie et al. 2018 62 | Pelvis | Deep‐CNN | MSE |
|
15/0/5 | Paired axial patch 2D | PSNR: 8.823 (7.889). Anatomy ROI mean HU | ||
| Chen et al. 2019 54 | HN | U‐Net |
|
|
30/7/7 | Dual‐input paired axial 2D | MAE: 18.98 (44.38). PSNR: 33.26 (27.35). SSIM: 0.8911 (0.7109). RMSE: 60.16 (126.43) | ||
| Pelvis | 6/0/7 | Paired axial 2D | MAE: 42.40 (104.21). PSNR: 32.83 (27.59). SSIM: 0.9405 (0.8897). RMSE: 94.06 (163.71) | ||||||
| Harms et al. 2019 35 | Brain | Cycle‐GAN |
|
|
LoO‐CV (23/0/1) | Paired patch 3D | MAE: 13.0 ± 2.2 (23.8 ± 5.1). PSNR: 37.5 ± 2.3 (32.3 ± 5.9) | ||
| Pelvis | LoO‐CV (19/0/1) | MAE: 16.1 ± 4.5 (56.3 ± 19.7). PSNR: 30.7 ± 3.7 (22.2 ± 3.4) | |||||||
| Kida et al. 2019 36 | Pelvis | Cycle‐GAN |
|
Gaussian noise |
|
16/0/4 | Unpaired axial 2D | Average ROI HU. Volume HU histograms. Self‐SSIM | |
| Kurz et al. 2019 37 | Pelvis | Cycle‐GAN |
|
|
|
4‐CV (25/0/8) | Unpaired axial 2D | MAE: 87 (103) a . ME: −6 (24) a |
DD1: 89%. DD2: 100%. DVH < 1.5%. DD2: 80%. DD3: 86%. GPR2: 96%. GPR3: 100%. DVH < 1% |
| Lei et al. 2019 38 | Brain | Cycle‐GAN |
|
Intra‐subject RR | LoO‐CV (11/0/1) | Paired patch 3D | MAE: 20.8 ± 3.4 (44.0 ± 12.6). PSNR: 32.8 ± 1.5 (26.1 ± 2.5) | ||
| Li et al. 2019 55 | Nasopharynx | U‐Net | MAE |
|
|
50/10/10 | Paired axial 2D | MAE: 6–27 (60–120). ME: −26–4 (−74–51) | DVH < 0.2% (0.8%). GPR1: 95.5% (90.8%) |
| Liang et al. 2019 39 | HN | Cycle‐GAN |
|
|
81/9/20 | Unpaired axial 2D | MAE: 29.85 ± 4.94 (69.29 ± 11.01). RMSE: 84.46 ± 12.40 (182.8 ± 29.16). SSIM: 0.85 ± 0.03 (0.73 ± 0.04). PSNR: 30.65 ± 1.36 (25.28 ± 2.19) | GPR2: 98.40% ± 1.68% (91.37% ± 6.72%). GPR1: 96.26% ± 3.59% (88.22% ± 88.22%) | |
| Barateau et al. 2020 61 | HN | GAN |
|
Random translations, rotations, shears | Intra‐patient RR and DIR | 30/0/14 | Paired axial 2D | MAE: 82.4 ± 10.6 (266.6 ± 25.8) a . ME: 17.1 ± 19.9 (208.9 ± 36.1) a | GPR2: 98.1% (91.0%). DVH (OAR) < 99 cGy. DVH (PTV) < 0.7% |
| Eckl et al. 2020 40 | HN | Cycle‐GAN |
|
|
25/0/15 | Paired axial 2D | MAE: 77.2 ± 12.6 a . ME: 1.4 ± 9.9 a | GPR3: 98.6 ± 1.0%. GPR2: 95.0 ± 2.4%. DD2: 91.5 ± 4.3%. DVH < 1.7% | |
| Thorax | 53/0/15 | MAE: 94.2 ± 31.7 a . ME: 29.6 ± 30.0 a | GPR3: 97.8 ± 3.3%. GPR2: 93.8 ± 5.9%. DD2: 76.7 ± 17.3%. DVH < 1.7% | ||||||
| Pelvis | 205/0/15 | MAE: 41.8 ± 5.3 a . ME: 5.4 ± 4.6 a | GPR3: 99.9 ± 0.1%. GPR2: 98.5 ± 1.7%. DD2: 88.9 ± 9.3%. DVH < 1.1% |
Note: Dose similarity in italics suggests proton plans, otherwise photon plans. GPR3 = 3%/3 mm; GPR2 = 2%/2 mm.
Abbreviations: CBCT, cone‐beam CT; CNN, convolutional neural network; CV, cross‐validation; DIR, deformable image registration; DVH, dose–volume histogram; GAN, generative adversarial network; HN, head and neck; LoO‐CV, leave on out cross‐validation; MAE, mean absolute error; ME, mean error; MSE, mean squared error; P/C/GTV, planning/clinical/gross target volume; PSNR, peak signal‐to‐noise ratio; RMSE, root mean square error; ROI, regions of interest; RR, rigid registration; SSIM, structural similarity.
Image similarity metrics computed within body contour.
TABLE 3B.
Summary of synthetic CT (sCT) generation methods
| Author and year | Anatomic site | Model | Loss function | Augmentation | Preprocessing | (train/val/test) | Training configuration | Image similarity (input CBCT) | Dose similarity |
|---|---|---|---|---|---|---|---|---|---|
| Liu et al. 2020 41 | Abdomen | Cycle‐GAN |
|
|
LoO‐CV (29/0/1) | Paired patch 3D | MAE: 56.89 ± 13.84 (81.06 ± 15.86) a . PSNR: 28.80 ± 2.46 (22.89 ± 2.89) a . SSIM: 0.71 ± 0.032 (0.60 ± 0.063) a | DVH < 0.8% | |
| Maspero et al. 2020 42 |
HN Lung Breast |
Cycle‐GAN |
|
|
|
15/8/10 15/8/10 15/8/10 |
Unpaired axial 2D |
MAE: 51 ± 12 (195 ± 20) a . ME: −6 ± 6 (−122 ± 33) a |
GPR3: 99.3 ± 0.4%. GPR2: 97.8 ± 1% GPR3: 98.2 ± 1%. GPR2: 94.9 ± 3% GPR3: 97 ± 4%. GPR2: 92. ± 8% |
| Park et al. 2020 43 | Lung | Cycle‐GAN |
|
CT and CBCT resampled to 384 × 384 | 8/0/2 | Unpaired sagittal and coronal 2D | PSNR: 30.60 (26.13). SSIM: 0.8977 (0.8173) | ||
| Thummerer et al. 2020 56 | HN | U‐Net | MAE |
|
3‐CV (16/2/9) | Paired axial, sagittal and coronal 2D | MAE: 40.2 ± 3.9 a . ME: −1.7 ± 7.4 a | GPR3: 98.77 ± 1.17%. GPR2: 96.57 ± 3.26% | |
| Thummerer et al. 2020 57 | HN | U‐Net | MAE |
|
|
3‐CV (11/11/11) | Paired axial, sagittal, coronal 2D | MAE: 36.3 ± 6.2 a . ME: 1.5 ± 7.0 a | GPR3: 99.95%. GPR2: 99.30% |
| Xie et al. 2020 63 | Pelvis | Deep‐CNN | Contextual loss | Random rotations | Intra‐patient DIR | 499/64/64 (slices) | Paired axial 2D | MAE: 46.01 ± 5.28 (51.01 ± 5.38). PSNR: 23.07 (22.66). SSIM: 0.8873 (0.8749) | |
| Yuan et al. 2020 58 | HN | U‐Net | MAE |
|
5‐CV (40/5/10) | Paired axial 2D | MAE: 49.24 (167.46). SSIM: 0.85 (0.42) | ||
| Zhang et al. 2020 18 | Pelvis | GAN |
|
|
|
150/0/15 | Paired multi‐slice axial 2.5D | MAE: 23.6 ± 4.5 (43.8 ± 6.9). PSNR: 20.09 ± 3.4 (14.53 ± 6.7) | DVH < 1% |
| Dahiya et al. 2021 15 | Thorax | GAN |
|
Geometric augmentation (scale, sheer, rotation) |
|
140/0/15 | Paired 3D | MAE: 29.31 ± 12.64 (162.77 ± 53.91). RMSE: 78.62 ± 78.62 (328.18 ± 84.65). SSIM: 0.92 ± 0.01 (0.73 ± 0.07). PSNR: 34.69 ± 2.41 (22.24 ± 2.40) | |
| Dai et al. 2021 51 | Breast | Cycle‐GAN |
|
52/0/23 | MAE: 71.58 ± 8.78 (86.42 ± 10.12) a . ME: 8.46 ± 11.88 (−37.71 ± 15.49) a . PSNR: 23.34 ± 3.63 (20.19 ± 5.26). SSIM: 0.92 ± 0.02 (0.88 ± 0.04) | GPR3: 91.46 ± 4.63%. GPR2: 85.09 ± 6.28%. DVH (CTV) < 3.58% | |||
| Dong et al. 2021 50 | Pelvis | Cycle‐GAN |
|
|
46/0/9 | Unpaired axial 2D | MAE: 14.6 ± 2.39 (49.96 ± 7.21). RMSE: 56.05 ± 13.05 (105.9 ± 11.52). PSNR: 32.5 ± 1.87 (26.82 ± 0.638). SSIM: 0.825 ± 1.92 (0.728 ± 0.36) | ||
| Gao et al. 2021 49 | Thorax | Cycle‐GAN |
|
|
136/0/34 | Unpaired axial 2D | MAE: 43.5 ± 6.69 (92.8 ± 16.7). SSIM: 0.937 ± 0.039 (0.783 ± 0.063). PSNR: 29.5 ± 2.36 (21.6 ± 2.81) | GPR3: 99.7 ± 0.39% (92.8 ± 3.86%). GPR2: 98.6 ± 1.78% (84.4 ± 5.81%). GPR1: 91.4 ± 3.26% (50.1 ± 9.04%) | |
| Liu et al. 2021 27 | Thorax | Modified ADN |
|
Random horizontal flip |
|
32/8/12 | Unpaired axial 2D patch | MAE: 32.70 ± 7.26 (70.56 ± 11.81). RMSE: 60.53 ± 60.53 (112.13 ± 17.91). SSIM: 0.86 ± 0.04 (0.64 ± 0.04). PSNR: 34.12 ± 1.32 (28.67 ± 1.41) |
Note: Dose similarity in italics suggests proton plans, otherwise photon plans. GPR3 = 3%/3 mm; GPR2 = 2%/2 mm.
Abbreviations: ADN, artifact disentanglement network; CBCT, cone‐beam CT; CNN, convolutional neural network; CV, cross‐validation; DIR, deformable image registration; DVH, dose–volume histogram; GAN, generative adversarial network; HN, head and neck; LoO‐CV, leave on out cross validation; MAE, mean absolute error; ME, mean error; P/C/GTV, planning/clinical/gross target volume; PSNR, peak signal‐to‐noise ratio; RMSE, root mean square error; RR, rigid registration; SSIM, structural similarity.
Image similarity metrics computed within body contour.
TABLE 3C.
Summary of synthetic CT (sCT) generation methods
| Author and year | Anatomic site | Model | Loss function | Augmentation | Preprocessing | (train/val/test) | Training configuration | Image similarity (input CBCT) | Dose similarity |
|---|---|---|---|---|---|---|---|---|---|
| Qiu et al. 2021 48 | Thorax | Cycle‐GAN |
|
|
Intra‐patient RR and DIR | 5‐CV (16/0/4) | Paired axial 2D | MAE: 66.2 ± 8.2 (110.0 ± 24.9) a . PSNR: 30.3 ± 6.1 (23.0 ± 4.0) a . SSIM: 0.91 ± 0.05 (0.85 ± 0.05) | |
| Rossi et al. 2021 60 | Pelvis | U‐Net | MAE |
|
|
4‐CV (42/0/14) | Paired axial 2D | MAE: 35.14 ± 13.19 (93.30 ± 59.60). PSNR: 30.89 ± 2.66 (26.70 ± 3.36). SSIM: 0.912 ± 0.033 (0.887 ± 0.048) | |
| Sun et al. 2021 47 | Pelvis | Cycle‐GAN |
|
|
5‐CV (80/20/20) | Paired patch 3D | MAE: 51.62 ± 4.49. SSIM: 0.86 ± 0.03. PSNR: 30.70 ± 0.78 (27.15 ± 0.57) | GPR2: 97% | |
| Thummerer et al. 2021 59 | Thorax | U‐Net | MAE |
|
3‐CV (22/0/11) | Paired axial, sagittal, coronal 2D | MAE: 30.7 ± 4.4 a . ME: 2.4 ± 3.9 a . SSIM: 0.941 ± 0.019. PSNR: 31.2 ± 3.4 | GPR3: 96.8 ± 2.4%. GPR2: 90.7%. DVH (CTV/GTV) < 0.5% | |
| Tien et al. 2021 44 | Breast | Cycle‐GAN |
|
|
|
12/0/3 | Paired axial 2D | Average ROI HU. ROI MAE. ROI PSNR. ROI SSIM | |
| Uh et al. 2021 45 |
Abdomen Pelvis |
Cycle‐GAN |
|
|
21/0/7 29/0/7 |
Paired axial 2D |
GPR2: 98.4% (83.0%) GPR2: 98.5% (80.9%) |
||
| Xue et al. 2021 19 | Nasopharynx | Cycle‐GAN |
|
|
135/0/34 | Paired axial 2D | MAE: 23.8 ± 8.6 (42.2 ± 17.4). RMSE: 79.7± 20.1 (134.3 ± 31.0). PSNR: 37.8 ± 2.1 (27.2 ± 1.9). SSIM: 0.96 ± 0.01 (0.91 ± 0.03) | GPR3 > 98.52% ± 3.09%. GPR2 > 96.82% ± 1.71% | |
| Zhao et al. 2021 46 | Pelvis | Cycle‐GAN |
|
Added noise |
|
100/0/10 | Unpaired axial 2D | MAE: 52.99 ± 12.09 (135.84 ± 41.59). SSIM: 0.81 ± 0.03 (0.44 ± 0.07). PSNR: 26.99 ± 1.48 (21.76 ± 1.95). | DVH < 50 cGy (< 350 cGy) |
| Wu et al. 2022 64 | Pelvis | Deep‐CNN |
|
|
5‐CV (90/30/23) | Paired 2D | MAE: 52.18 ± 3.68 (352.56) a . SSIM: 0.67 ± 0.02 (0.56). ME: 21.72 ± 14.18 (352.41). PSNR: 29.27 ± 0.37 (20.21) | ||
| Lemus et al. 2022 52 | Abdomen | Cycle‐GAN |
|
Random 256 × 256 image sampling |
|
10‐CV (11/0/6) | Paired 2D | MAE: 54.44 ± 16.39 (72.95 ± 6.63). RMSE: 108.765 ± 40.54 (137.29 ± 21.19) | DVH (PTV): 1.5% (3.6%). GPR3/2: 98.35% (96%) |
Note: Dose similarity in italics suggests proton plans, otherwise photon plans. GPR3 = 3%/3 mm; GPR2 = 2%/2 mm.
Abbreviations: CBCT, cone‐beam CT; CNN, convolutional neural network; CV, cross validation; DIR, deformable image registration; DVH, dose–volume histogram; GAN, generative adversarial network; HN, head and neck; LoO‐CV, leave on out cross validation; MAE, mean absolute error; ME, mean error; P/C/GTV, planning/clinical/gross target volume; PSNR, peak signal‐to‐noise ratio; RMSE, root mean square error; ROI, regions of interest; RR, rigid registration; SSIM, structural similarity.
Image similarity metrics computed within body contour.
TABLE 4.
Miscellaneous approaches for cone‐beam CT (CBCT) correction
| Author and year | Anatomic site | Model | Loss function | Augmentation | Preprocessing | (train/val/test) | Training configuration | Image similarity (input CBCT) | Dose similarity |
|---|---|---|---|---|---|---|---|---|---|
| Hansen et al. 2018 73 | Pelvis | U‐Net | MSE | Linear combination of two random inputs (Mixup) | A priori scatter correction for target projections | 15/8/7 | Paired projection 2D | MAE: 46 (144). ME: −3 (138) | GPR2: 100%. GPR1: 90%. GPR2: 53% |
| Jiang et al. 2019 74 | Pelvis | U‐Net | MSE | MC scatter correction for target CBCTs | 15/3/2 | Paired axial 2D | RMSE: 18.8 (188.4). SSIM: 0.9993 (0.9753) | ||
| Landry et al. 2019 75 | Pelvis | U‐Net 1 | MSE | Mixup | A priori scatter correction for target projections | 27/7/8 | Paired projection 2D | MAE: 51 (104). ME: 1 (30) |
DPR2 > 99.5%. DPR1 > 98.4%. GPR2 > 99.5% GPR3 > 95%. GPR2 > 85%. DPR3 > 75%. DPR2 > 68% |
| U‐Net 2 |
|
|
Paired axial 2D | MAE: 88 (104). ME: 2 (30) |
DPR2 > 99.5%. DPR1 > 98.4%. GPR2 > 99.5% GPR3 > 97%. GPR2 > 89%. DPR3 > 81%. DPR2 > 76% |
||||
| U‐Net 3 | Voxels outside body set to −1000 HU | MAE: 58 (104). ME: 3 (30) | DPR2 > 99.5%. DPR1 > 98.4%. GPR2 > 99.5%. GPR3 > 98%. GPR2 > 91%. DPR3 > 85%. DPR2 > 79% | ||||||
| Nomura et al. 2019 79 | HN | U‐Net | MAE |
|
|
Training: 5 phantoms. Validation: HN phantom. Testing: 1 HN, 1 Thorax patient |
Paired projections 2D | MAE: 17.9 ± 5.7 (21.8 ± 5.9). SSIM: 0.9997 ± 0.0003 (0.9995 ± 0.0003). PSNR: 37.2 ± 2.6 (35.6 ± 2.3) | |
| Thorax | MAE: 29.0 ± 2.5 (32.5 ± 3.2). SSIM: 0.9993 ± 0.0002 (0.9990 ± 0.0003). PSNR: 31.7 ± 0.8 (30.6 ± 0.9) | ||||||||
| Lalonde et al. 2020 80 | HN | U‐Net | MAPE | Vertical and horizontal flips |
|
29/9/10 | Paired projections 2D | MAE: 13.41 (69.64). ME: −0.801 (−28.61) | GPR2: 98.99% (68.44%) |
| Rusanov et al. 2021 81 | HN | U‐Net | MAE | Random vertical/horizontal flips | Bowtie filter removal via projection normalization using flood field scan | 4/0/2 | Paired projection 2D | MAE: 74 (318) a . SSIM: 0.812 (0.750) |
Note: GPR3 = 3%/3 mm; GPR2 = 2%/2 mm; GPR1 = 1%/1‐mm criteria. DPR2 = 2% DD threshold; DPR1 = 1% DD threshold.
Abbreviations: DIR, deformable image registration; HN, head and neck; MAE, mean absolute error; MC, Monte Carlo; ME, mean error; MSE, mean squared error; PSNR, peak signal‐to‐noise ratio; RMSE, root mean square error; SSIM, structural similarity.
Image similarity metrics computed within body contour.
4. RESULTS
4.1. Study identification
The initial identification search returned 218 investigations on Scopus, 119 on PubMed, and 180 on Web of Science for a total of 517 investigations. After screening for eligibility, 40 studies qualified, of which 34 investigated sCT generation and 6 utilized projection domain approaches. The distribution of the total number of investigations per year is presented in Figure 3 and is further broken down into network type. The number of investigations in DL‐based CBCT correction has grown each year, with the first investigations performed in 2018. U‐Net was the preferred architecture in 2018; however, preference for cycle‐GAN grew rapidly in 2019 which kept it tied with U‐Net from 2019 to 2020, thereafter becoming the most popular architecture. Figure 4 depicts the share of anatomic regions investigated by percentage, with the pelvic and head‐and‐neck (HN) region being the most thoroughly covered, both making up 70% of all sites. The thoracic region made up 23% of all studies includes both lung and breast patients. The least investigated region was the abdomen comprising just 7% of all studies.
FIGURE 3.
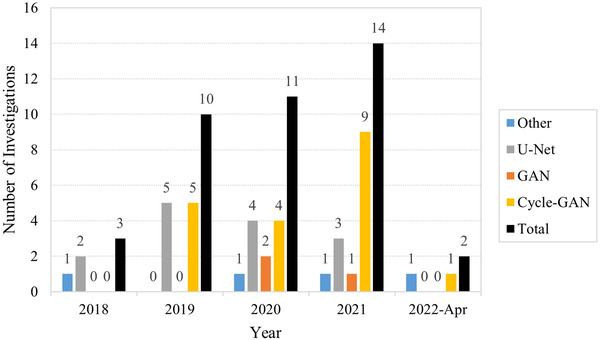
Distribution of total and per architecture investigations per year
FIGURE 4.
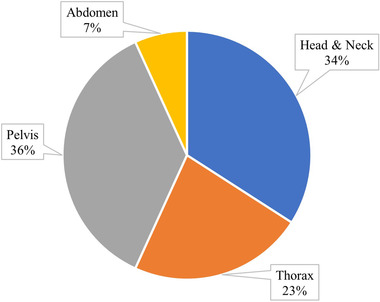
Pie chart of distribution of anatomic sites investigated
4.2. sCT generation
4.2.1. Network architectures
Tables 3a–c show that a total of nineteen studies investigated sCT generation primarily using cycle‐GAN for their translation task, 19 , 35 , 36 , 37 , 38 , 39 , 40 , 41 , 42 , 43 , 44 , 45 , 46 , 47 , 48 , 49 , 50 , 51 , 52 compared to eight utilizing U‐Net, 53 , 54 , 55 , 56 , 57 , 58 , 59 , 60 three implementing GANs, 15 , 18 , 61 three exploring deep‐CNNs, 62 , 63 , 64 and one study utilizing a novel architecture called artifact disentanglement network (ADN). 27 Deep‐CNNs maintain the input image dimensions as the feature maps flow through the network. ADN, originally used for metal artifact reduction in CT imaging, has been utilized for sCT generation. By “disentangling” domain‐specific features corresponding to style, whilst mapping a common structure feature space between CT and CBCT data, a transformation can be learnt that decomposes CBCT style from structure then reassembles an sCT image using CT style and CBCT structure.
The most objective comparisons of image quality can be found in studies that compare multiple architectures or correction techniques for generating sCT images using the same datasets. 18 , 19 , 27 , 35 , 39 , 41 , 44 , 47 , 49 , 57 , 60 , 61 , 63 Where DL methods were compared to classical CBCT correction methods, Barateau et al. 61 demonstrated that their GAN sCT achieved a lower MAE than DIR of the CT (82.4 ± 10.6 vs. 95.5 ± 21.2 HU), which was found to be consistent with the results in Thummerer et al. (36.3 ± 6.2 vs. 44.3 ± 6.1 HU). 57 Similarly in Liang et al., 39 cycle‐GAN showed improved image quality metrics over DIR of the CT when a saline‐adjustable phantom was used in a controlled experiment. In terms of photon dosimetry, Barateau et al., 61 Lemus et al., 52 and Maspero et al. 42 concluded that sCT images perform similarly to deformed CT images for HN, lung, and breast regions, whereas Thummerer et al. 57 found that the same was also true for proton plans in the HN region.
When comparisons were made between architectures, Liang et al. 39 reported an improved MAE for cycle‐GAN over two GAN implementations (29.85 ± 4.94 vs. 39.71 ± 10.79 and 40.64 ± 6.99 HU), along with superior anatomical preservation for an adjustable saline‐fillable HN phantom. Likewise, Sun et al. 47 showed that their cycle‐GAN could produce lower MAE than an equivalent GAN (51.62 ± 4.49 vs. 56.53 ± 5.26 HU) and resulted in better Dice score agreement for various structures. Gao et al. 49 also demonstrated a lower MAE for their unpaired cycle‐GAN implementation over a paired GAN network (43.5 ± 6.69 vs. 53.4 ± 9.34 HU). Visual inspection showed bone, air, and certain lung structures were incorrectly synthesized for the GAN, with poor structural continuity along sagittal and coronal images.
Liu et al. 41 compared U‐Net to Cycle‐GAN and noted a substantial reduction in MAE (66.71 ± 15.82 vs. 56.89 ± 13.84 HU) and reduced artifact severity for the latter network. Similarly, Tien et al. 44 reported better HU agreement within lung region ROIs for cycle‐GAN over U‐Net and undertook a blind observer test which scored cycle‐GAN sCT images at 4.5/5 and U‐Net sCT images at 1.3/5 based on image realism.
Xue et al. 19 and Zhang et al. 18 tested cycle‐GAN, GAN, and U‐Net on the same datasets and demonstrated the lowest MAE for cycle‐GAN over GAN when model configurations were kept constant (23.8 ± 8.6 vs. 24.3 ± 8.0 HU 19 and 8.9 ± 3.1 vs. 9.4 ± 1.2 HU 18 ). The U‐Net‐based models, however, performed noticeably worse with MAEs increasing to 26.8 ± 10.0 HU in Xue et al. 19 and 19.2 ± 6.4 HU in Zhang et al. 18 Aside from image quality, Xue et al. 19 showed explicitly the anatomy preserving capacity of cycle‐GAN over GAN and U‐Net: Structures pertaining to contrast enhancement solution present in CT images were falsely generated on U‐Net/GAN sCT images but were suppressed in cycle‐GAN sCT images.
Liu et al. 27 demonstrated the effectiveness of their unpaired ADN network over three variants of cycle‐GAN. Their approach to image disentanglement reduced CBCT MAE from 70.56 ± 11.81 to 32.70 ± 7.26 HU, whereas three cycle‐GAN approaches resulted in sCT MAEs of 42.04 ± 8.84 HU (base cycle‐GAN), 43.90 ± 8.23 HU (cycle‐GAN with larger generator), and 36.26 ± 7.00 HU (cycle‐GAN with attention gating). Furthermore, visual inspection showed reduced noise and motion artifacts for ADN over the cycle‐GAN variants.
Figure 5 shows the mean percent improvement in sCT MAE over the base CBCT for different networks when a common dataset was used. The greatest disparity was observed between cycle‐GAN and U‐Net (51.0% vs. 36.8% respectively, p = 0.37), 18 , 19 , 41 whereas a smaller difference was noted between cycle‐GAN and GAN networks (58.3% vs. 51.5% respectively, p = 0.24). 18 , 19 , 39 , 49
FIGURE 5.
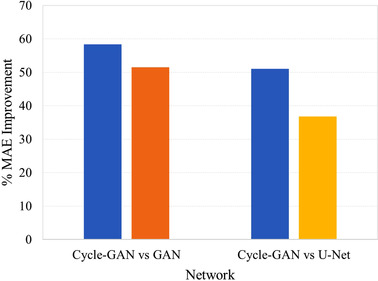
Percent mean absolute error (MAE) improvement per network for studies utilizing common data
4.2.2. Training configuration
Ten cycle‐GAN studies were trained with paired training configurations, whereas eight were not. Figure 6 shows the mean percentage MAE improvement for the two most common anatomical regions, as well as the overall percentage improvement for all studies that reported the original CBCT and sCT MAE metric. For the pelvic region, two studies used paired data, 35 , 45 whereas three utilized unpaired images to train their cycle‐GAN. 37 , 46 , 50 Subsequently, three investigations focusing on the HN region used paired data, 19 , 35 , 38 whereas two used unpaired. 39 , 42 The paired studies showed a greater improvement (61.41% vs. 51.35%, p = 0.32) in the pelvic region, whereas the unpaired networks performed better in the HN region (65.38% vs. 47.24%, p = 0.04). Comparing all studies that trained either with paired or unpaired data, unpaired implementations recovered a better improvement in MAE on average (55.98% vs. 47.61%, p = 0.16). However, it must be noted that among other network nuances, unpaired networks were trained on an average of ∼54 patients, compared to an average of ∼33 for paired networks. By selecting studies with training set sizes within ±4 patients between the two groups, 19 , 35 , 37 , 38 , 42 , 45 , 48 , 49 the difference between paired and unpaired networks is reduced, with paired networks performing slightly better (53.65% vs. 51.83%, p = 0.29).
FIGURE 6.
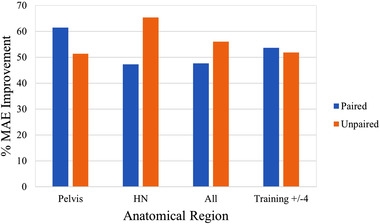
Percent mean absolute error (MAE) improvement for cycle‐generative adversarial network (GAN) models trained with paired or unpaired datasets, controlling for pelvic, head and neck (HN), and all anatomical regions, as well as training set sizes within four patients
Most networks were trained using axial 2D slices, with the exception of 35 , 38 , 41 , 47 that utilized 3D patch‐based training, and Dahiya et al. 15 who used entire 3D volumes. The main advantage of 3D training is improved feature extraction as medical images are volumetric in nature. Zhang et al. 18 trained in 2.5D, utilizing adjacent axial slices to help the model predict the central slice. Alternatively, Thummerer et al. 56 , 57 trained three separate models on the same data organized in sagittal, coronal, and axial planes. The median value for a given pixel was taken as the prediction.
Within the GAN literature, all studies were performed using paired data, with Barateau et al. 61 training in 2D, Zhang et al. 18 in 2.5D, and Dahiya et al. 15 in 3D. The respective improvement in MAE over the original CBCT was 69.09%, 46.12%, and 81.99%, suggesting that the use of 3D convolutions on entire image volumes is highly advantageous. Interestingly, in the Zhang et al. 18 study, no difference was observed between training in 2D and 2.5D.
For studies utilizing cycle‐GAN, the mean percentage improvement in MAE for 2D approaches 19 , 37 , 39 , 42 , 45 , 46 , 48 , 49 , 50 , 52 was slightly higher than 3D‐patch based approaches 35 , 38 , 41 (52.08% vs. 49.83%, p = 0.41). When controlling for training set sizes within ± 4 patients, a similar trend was observed with 2D networks 37 , 42 still slightly outperforming patched 3D networks 35 , 38 , 41 (51.51% vs. 49.83%, p = 0.46). On the contrary, Sun et al. 47 did note a slight increase in PSNR of their patched 3D cycle‐GAN over a 2D implementation (30.70 ± 0.78 vs. 29.72 ± 0.59), although the analysis was not comprehensive and lacked other image quality analyses.
One novel approach by Chen et al. 54 used a dual‐channel input U‐Net to create sCT images using intensity information from CT images and structural information from CBCT images. Having access to original planning CTs and same‐day replan CT images, the authors created a dual channel dataset containing the RR CBCT and corresponding planning CT images. This dataset was fed into the network, with replan CT images used as the ground truth for optimization. The authors noted a visual reduction in artifacts using the dual channel over the standard approach, with percentage MAE improvement increasing from 50.68% to 56.80%.
4.2.3. Preprocessing
Image registration and resampling is used to bring images into the same coordinate space such that voxels between two datasets contain compatible biological information. Hence, image registration is necessary to provide the most anatomically accurate ground truth for both training and inference. As such, image registration is used ubiquitously, with DIR being used for training in most U‐Net and deep‐CNN architectures, with the exception of 55 , 58 , 60 which used RR only. GAN‐based studies all used DIR given their susceptibility of generating false anatomies. Cycle‐GAN, originally designed for unpaired data, was most commonly coupled with RR, for both paired 19 , 35 , 38 , 40 , 45 , 52 and unpaired approaches 36 , 37 , 42 , 46 , 49 . Alternatively, Liu et al. 41 and Qiu et al. 48 applied DIR to their training set for better anatomical correspondence, whereas Liang et al. 39 and Dong et al. 50 did not apply any registration to their training data, only resampling to the same grid. Liu et al. 41 was the only cycle‐GAN study to investigate the impact of DIR and RR preprocessing on the same dataset and found that DIR produced slightly better HU agreement (56.89 ± 13.84 vs. 58.45 ± 13.88 HU), with substantially less noise and sharper organ boundaries upon visual inspection. 41 Some authors applied a secondary intersubject RR to a common patient such that all volumes were closely centered, allowing for substantial truncation of air regions to reduce the computational load. 35 , 38 Meanwhile Uh et al. 45 performed a novel body normalization technique to equalize the extent of pediatric patients’ lateral anatomy that significantly reduced the MAE of their composite model (47 ± 7 vs. 60 ± 7 HU, p < 0.01).
Other than registration, the most common preprocessing techniques involved clipping and normalizing HU values to between [0,1] or [−1,1], 15 , 19 , 27 , 36 , 39 , 40 , 42 , 44 , 46 , 49 , 50 , 54 , 60 or alternatively standardizing 18 intensities to minimize biasing gradients. Dong et al. 50 investigated slice‐wise versus patient‐wise normalization and found the former resulted in slice discontinuity artifacts, whereas the latter resulted in superior image quality. Another common technique was to replace voxels outside the patient body contour with air to minimize the impacts from nonanatomical structures. 19 , 36 , 37 , 42 , 45 , 46 , 50 , 53 , 56 , 57 , 59 , 60
4.2.4. Loss metrics
With the exception of Xie et al., 63 all U‐Net‐ and deep‐CNN‐based architectures were constrained by pixel‐wise loss functions with the most common being L1 loss. Chen et al. 54 applied the SSIM image quality assessment metric as a loss function. SSIM computes statistical terms corresponding to structure, luminance, and contrast 31 and discovered that SSIM alone improved the percentage MAE by 47.05%, whereas L1 loss alone increased it to 50.68%. By utilizing both losses, the percent improvement increased to 51.15% suggesting an additive relationship that was corroborated in a natural image restoration study. 65
Of the studies investigating cycle‐GAN, four made no alterations to the standard loss, 37 , 42 , 45 , 51 whereas fifteen made substantial alterations. 19 , 35 , 36 , 38 , 39 , 40 , 41 , 44 , 46 , 47 , 48 , 49 , 50 , 52 Networks considered unmodified used the default adversarial and cycle losses. The percent MAE improvement for cycle‐GAN networks using standard versus extended loss functions was 49.08 ± 21.85 and 49.90 ± 14.37 HU, respectively (p = 0.46). The perceptual SSIM metric is better able to quantify changes in image appearance relating to artifacts and image realism. The percentage SSIM improvement for networks using standard versus extended loss functions was 10.5 ± 5.95% and 12.8 ± 5.73%, respectively (p = 0.35), suggesting that sCTs from the latter networks were perceptually closer to real CT images.
Extensions to the cycle‐GAN global loss included identity loss, 19 , 39 , 49 , 50 gradient loss, 35 , 36 , 44 , 46 , 47 , 48 , 52 synthetic loss, 35 , 38 , 40 , 41 , 44 , 48 L1.5 loss, 35 histogram matching loss, 48 idempotent loss, 36 , 52 air loss, 36 total variation loss, 36 , 52 feature matching loss, 18 and perceptual loss. 48 The identity loss 19 , 39 , 49 , 50 aids network stability and generator accuracy by ensuring no additional effect occurs to real images when they are input into generators tasked to output images in the same domain. In their larger ablation experiment, Zhang et al. 18 compared cycle‐GAN with and without the identity loss, demonstrating a slight improvement in sCT MAE (8.9 ± 3.1 vs. 9.2 ± 1.5 HU).
The gradient loss is used to either preserve structural details during conversion or enhance edge sharpness. One approach uses the Sobel operator 66 to compute the gradient map of sCT and CBCT images during optimization. The pixel‐wise error between the two gradient maps is then minimized to maintain the same edge boundaries between CBCT and sCT images. The second approach attempts to equalize the neighboring pixel‐wise intensity variations between cycle/real and synthetic/real image pairs, thereby maintaining the same level of noise and edge sharpness in both cycle and synthetic images as real images. 35 , 47 This technique was utilized by Sun et al. 47 resulting in a noticeable visual improvement in edge sharpness in sCT images generated by a network trained with and without gradient loss.
In cases where data is paired and well registered, the synthetic loss is applied in a similar fashion to U‐Net implementations to enforce pixel‐wise similarity between generated and target domain images, typically using the L1 distance. Alternatively, the histogram matching loss used in Qiu et al. 48 attempts to maximize the similarity between input and cycle‐synthetic histogram distributions globally, further constraining the model parameters to output accurate tissue densities. Their cycle‐GAN network trained with histogram matching achieved an sCT MAE of 66.2 ± 8.2 HU compared to 72.8 ± 11.5 HU without the loss. Visual inspection confirmed a more uniform soft tissue distribution reflecting real tissue densities.
Tien et al. 44 incorporated both gradient and synthetic losses into their cycle‐GAN model and performed a blind observer test to assess how closely sCT perceptual image quality matched the CT. The unmodified cycle‐GAN achieved 3.3/5 in the blind test, whereas the proposed method scored 4.5/5.
The L1.5 loss used in Harms et al. 35 merges the benefits of L1 and L2 losses. L1 loss may lead to inconsistent HU reproduction as it is more difficult to optimize (tends toward sparse solutions and results in a noncontinuous optimization function). Conversely, L2 is easier to solve as solutions to all parameters lie on a continuous function in optimization space. However, heightened sensitivity to outliers results in blurring of anatomical boundaries primarily because outliers lie at the boundaries. The L1.5 norm produces a more stable optimization function whilst not weighing outliers as heavily as L2 norm, resulting in greater model stability and increased output accuracy. 35 , 67 , 68
The idempotent, air, and total variation losses were introduced in Kida et al. 36 The idempotent loss is similar to the identity loss, but functions by minimizing the difference between a synthetic image, and the same image fed through a generator tasked to output images in the same domain as the original synthetic image. The air loss is a piece‐wise function that encourages the preservation of air pockets and the body contour by penalizing mismatches. The function equals zero if respective densities of both sCT and CBCT images are greater than −465 HU, else the output error is equal to the density of the L1 norm of CBCT and sCT density differences. The total variation loss is used as an image denoising technique that works by minimizing the absolute difference of pixel intensities in an image and its vertically and horizontally translated version.
Zhang et al. 18 introduced the feature matching loss that modifies the typical adversarial loss used in GANs. Instead of using the classification output of the discriminator as the minimization target for the generator, intermediate level feature maps for real and synthetic inputs at the discriminator are extracted and used as a minimization criterion while optimizing the generator. Hence, the network can be optimized by exploiting levels of abstraction and not just the image domain, in turn aiding network stability. 69
Finally, Qiu et al. 48 and Barateau et al. 61 incorporated a content‐based perceptual loss function into their model, whereas Zhang et al. 18 combined a style and content‐based function in their perceptual loss. Content‐based perceptual loss is said to minimize the structure or content differences between two images based on their deep feature representations, rather than in the image domain. The loss is computed by finding the L2‐norm of selected deep feature maps contained in a pretrained CNN that is fed both images. The style‐based perceptual loss is based on the same principle; however, spatial information is lost by first computing the Gram matrix of selected feature maps, followed by the minimization of the Frobenius norm between the Gram matrix of each image. 70 , 71 The MAE for a cycle‐GAN trained with and without the content‐based perceptual loss improved from 82.0 ± 17.3 to 72.8 ± 11.5 HU in the work by Qiu et al., 48 whereas Zhang et al. 18 found their style and content‐based perceptual loss disturbed training and resulted in an increased MAE from 8.1 ± 1.3 to 9.2 ± 1.5 HU. This was likely because Qiu et al. 48 used a segmentation CNN pretrained on medical images, whereas Zhang et al. 18 used VGG‐16 (Visual Geometry Group) pretrained on natural images that failed to adequately capture feature peculiarities of medical images.
4.2.5. Network blocks
CNNs typically contain parameter counts in the order of tens or hundreds of millions. However, a major issue resulting from high parameter counts is the degradation of network performance in proportion to network depth—a phenomenon not caused by overfitting. 72 Hence, deeper models are more difficult to optimize and may converge at a higher error than shallower models. The residual block, 72 used by many authors, 27 , 35 , 36 , 37 , 38 , 44 , 45 , 46 , 47 , 52 , 55 , 64 , 73 , 74 , 75 solves the degeneration of deep models by introducing a skip connection that circumvents one or more convolution layers by transmitting upstream signals downstream via element‐wise addition. Hence, the residual block encourages the local mapping, H(x), to learn a residual function, F(x) = H(x) − x, if x is the upstream signal. It is empirically shown that learning the residual version of the mapping is easier than learning an unreferenced mapping as the optimal function tends to be close to an identity mapping, necessitating only a small response in H(x). 72
The inception block was designed to detect features at different scales by extracting image information using multiple kernel sizes. 76 Typically, a single convolution filter size is used throughout the network. With inception blocks, multiple filters are arranged in parallel. For example, Tien et al. 44 combined 1 × 1, 5 × 5, 9 × 9, and 13 × 13 filters in to extract features at multiple resolutions, concatenating the results into a single feature map volume, and performing dimensionality reduction using a 1 × 1 convolution. In addition, the inclusion of 1 × 1 convolutions enables the network to learn cross‐channel patters. The resulting operation has a higher capacity to extract useful features hence improve network performance. 76
Attention gates give priority to salient anatomical information while suppressing feature responses pertaining to noise or background information. Integrated into the U‐Net architecture, attention gates operate along the skip connections that propagate encoder‐side features to the decoder. The skip connections may propagate many redundant features that compromise the accuracy of the decoder. The attention gate learns to suppress redundant features by applying an element‐wise multiplication of incoming encoder‐side feature maps with attention coefficients that range between [0, 1]. These coefficients are learnt during backpropagation, thereby allowing only relevant information to reach the decoder. 41 , 47 , 77 The impact of attention‐gated cycle‐GAN was analyzed in Liu et al. (2020) 41 and Liu et al. (2021). 27 In both studies, the addition of attention gates over an unmodified cycle‐GAN improved the MAE from 63.72 ± 10.55 to 56.89 ± 13.84 HU 41 and 42.04 ± 8.84 to 36.26 ± 7.00 HU. 27
Gao et al. 49 infused attention guidance into their GAN to prompt the network to pay more attention to specific problematic regions. The decoder arm of their generator outputs both foreground attention masks and background attention masks. Foreground masks prompt the network to focus on image regions that change during synthesis, whereas background masks contain unchanging regions. By separating network attention to changing and unchanging regions, network performance improved over a base cycle‐GAN from 47.1 ± 6.65 to 43.5 ± 6.45 HU.
4.2.6. Cohort size
The impact of cohort sizes can most readily be appreciated by examining studies that used the same model. Yuan et al. 58 conducted an explicit analysis on the impact of training sizes where they trained a U‐Net using different permutations of 50, 40, and 30 patients. The authors split the 50 patients into 5 groups of 10 and subsequently trained 5 models with 50 patients (all data), 5 models with 40 patients (omitting one group of 10 for each model), and 5 models with 30 patients (omitting 2 groups of 10 for each model) for a total of 15 models. The authors concluded that 30 patients were insufficient to obtain a well‐trained model as significant differences were noted between using 30 compared to 40 and 50 patients (p < 0.05). Conversely, no significant difference was observed between models trained with 40 or 50 patients (p > 0.1). Mean MAE across models trained with 50, 40, and 30 patients were 53.90 ± 0.79, 53.20 ± 1.06, and 54.65 ± 0.43 HU respectively, indicating that larger training sets do not necessarily result in lower MAE.
Eckl et al. 40 investigated training a cycle‐GAN model on HN and pelvic images. The mean MAE for HN sCT images was 77.2 ± 12.6 HU for a model trained on 25 patients, whereas the same model trained on 205 pelvic patients achieved an MAE of 41.8 ± 5.3 HU. Although the HN region incurs less scatter contamination and anatomical variability compared to the pelvis, the pelvic sCT images were of higher absolute quality as a result of the eightfold increase in training data.
The mean number of training and testing patients for all studies and studies broken down into anatomic regions is presented in Table 5, along with the mean CBCT MAE, mean sCT MAE, and relative percentage MAE improvement of the sCT. Note that the asterisk signifies only studies that reported base CBCT and sCT MAE. For all studies reviewed, the size of training sets ranged from 8 to 205 for any given anatomic region, with an average of 47.74 ± 47.11 patients. Testing sets ranged from 3 to 34 and had a mean of 11.02 ± 7.90 patients. Studies investigating the HN region utilized on average the smallest training size (45.63 ± 39.38) but produced the largest percent improvement in MAE (58.67 ± 10.75%). Investigations of the pelvic and thoracic region used more training data (62.63 ± 43.20 and 59.00 ± 56.18, respectively) but resulted in similar improvements in MAE to the HN region. However, studies focusing on the abdomen typically used less than half of the training data as other regions (20.33 ± 7.36) and produced the lowest percent MAE improvement of 41.33 ± 19.51% on average. In absolute terms, HN studies started with the lowest CBCT MAE of 106.59 ± 84.63 HU and likewise synthesized CT images with the lowest MAE of 36.13 ± 21.76 HU. The pelvic region had a slightly higher sCT average of 41.58 ± 22.73 HU, followed by the abdomen at 51.78 ± 5.59 HU, and the thorax at 54.12 ± 20.47 HU.
TABLE 5.
Mean cohort size and model performance statistics for all publications
| Training size (no patients) | Testing size (no. patients) | CBCT MAE (HU) | sCT MAE (HU) | % MAE improvement | |
|---|---|---|---|---|---|
| All studies | 47.74 ± 47.11 | 11.02 ± 7.90 | – | 46.83 ± 22.23 | – |
| All studies* | 51.27 ± 44.27 | 11.77 ± 8.77 | 114.66 ± 75.84 | 45.13 ± 22.01 | 54.60 ± 17.90 |
| Pelvis* | 62.63 ± 43.20 | 10.88 ± 6.11 | 117.47 ± 93.73 | 41.58 ± 22.73 | 57.97 ± 19.68 |
| HN* | 45.63 ± 39.38 | 12.13 ± 10.17 | 106.59 ± 84.63 | 36.13 ± 21.76 | 58.67 ± 10.75 |
| Thorax* | 59.00 ± 56.18 | 14.17 ± 9.46 | 134.52 ± 49.45 | 54.12 ± 20.47 | 57.54 ± 12.65 |
| Abdomen* | 20.33 ± 7.36 | 4.67 ± 2.62 | 98.34 ± 30.35 | 51.78 ± 5.59 | 41.33 ± 19.51 |
Note: * indicates studies which reported CBCT and sCT MAE values.
Abbreviations: CBCT, cone‐beam CT; HN, head and neck; MAE, mean absolute error; sCT, synthetic CT.
To analyze the impact of training set sizes and model performance across studies, the scatter plot in Figure 7 presents the best linear fit to the data. The regression line shows a small but positive relationship between training set size and relative MAE improvement, but large variability between studies. The small r‐squared value indicates that training set size alone is a poor predictor for model performance. Majority of points are concentrated between 15 and 45 patients and show a high variance. The variance decreases at higher cohort sizes, whereas MAE improvements are marginal. This suggests a saturation of model performance with diminishing returns as training set size increases beyond 50.
FIGURE 7.
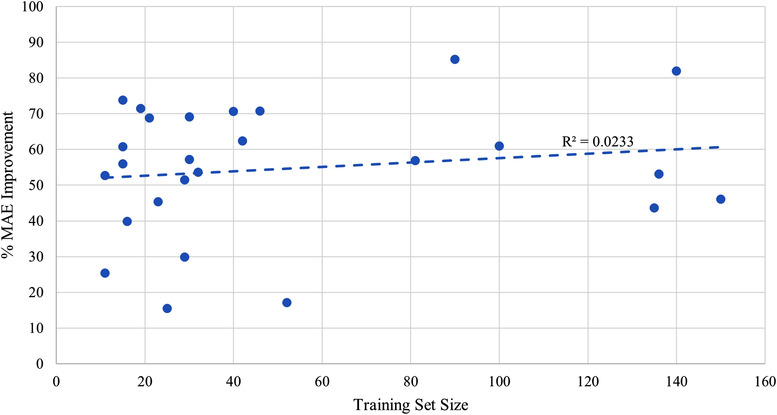
Scatter plot demonstrating the relationship between training cohort size and percent mean absolute error (MAE) improvement
Figure 8 lists the absolute MAE for every publication ordered from highest to lowest. Superimposed for each study is the number of training patients used, along with information pertaining to network architecture, training arrangement, network modifications, and anatomical site. No clear relationship between sCT MAE and training size is evident given that raw MAE values are strongly influenced by the original CBCT image quality, anatomical site, and whether or not the MAE was calculated over the entire image or the body contour. Figure 9 looks at the percentage improvement in MAE for every publication that listed the original CBCT MAE ordered from lowest to highest, along with the training set size. Aside from noting that the top two networks by Wu et al. 64 and Dahiya et al. 15 used relatively large cohorts of 90 and 140 patients, respectively (compared to the mean of 51.27 ± 44.27), no discernible trend could be noted among the other works, corroborating the relationship in Figure 7. Figure 10 visualizes the percentage SSIM improvement against training set size to assess whether perceptual image quality improved with greater training cohorts. Once again, no clear relationship presents itself as the performance of a model seems less dependent on training set size compared to other study nuances.
FIGURE 8.
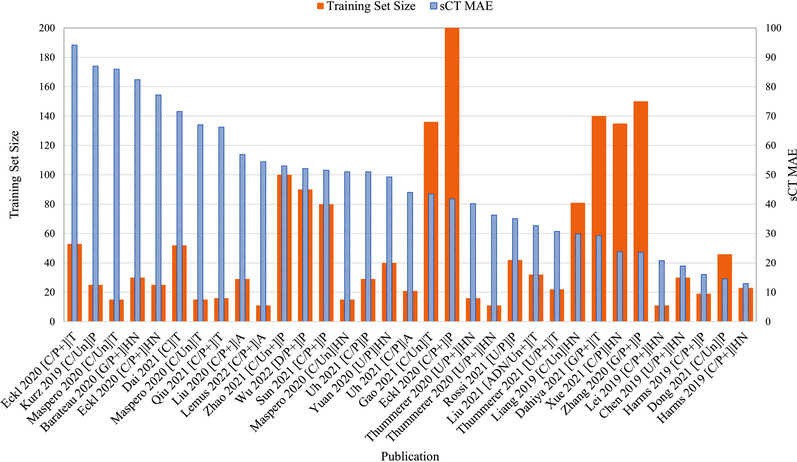
Absolute synthetic CT (sCT) mean absolute error (MAE) ordered from highest to lowest compared against training set size. Publication format describes: (model architecture/supervision type + additional loss functions and/or 3D training) | anatomical region. +, additional loss functions/3D input; A, abdomen; ADN, artifact disentanglement network; C, cycle‐GAN; CNN, convolutional neural network; D, deep CNN; G, GAN; GAN, generative adversarial network; HN, head and neck; P, paired training; P, pelvis; T, thorax; U, U‐Net; Un, unpaired training.
FIGURE 9.

Percentage mean absolute error (MAE) improvement ordered from lowest to highest compared against training set size. Publication format describes: (model architecture/supervision type + additional loss functions and/or 3D training) | anatomical region. +, additional loss functions/3D input; A, abdomen; ADN, artifact disentanglement network; C, cycle‐GAN; CNN, convolutional neural network; D, deep CNN; G, GAN; GAN, generative adversarial network; HN, head and neck; P, paired training; P, pelvis; T, thorax; U, U‐Net; Un, unpaired training
FIGURE 10.
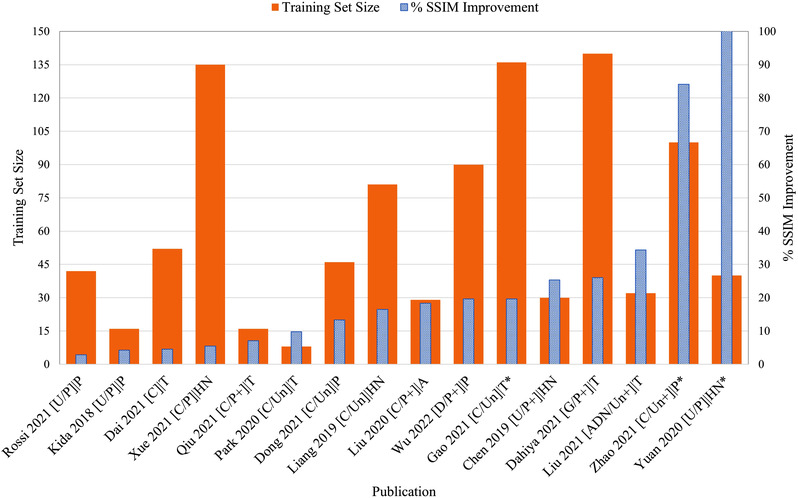
Percentage structural similarity (SSIM) improvement ordered from lowest to highest compared against training set size. Publication format describes: (model architecture/supervision type + additional loss functions and/or 3D training) | anatomical region. *, low dose CBCT; +, additional loss functions/3D input; A, abdomen; ADN, artifact disentanglement network; C, cycle‐GAN; CNN, convolutional neural network; D, deep CNN; G, GAN; GAN, generative adversarial network; HN, head and neck; P, paired training; P, pelvis; T, thorax; U, U‐Net; Un, unpaired training
4.2.7. Augmentation
Augmentation of training data is a strategy used to synthetically increase the number of examples to prevent overfitting to the specific variance of the training set and improve model generalizability. The most popular augmentation techniques were random horizontal flips, 18 , 27 , 37 , 42 , 44 , 48 , 55 , 57 , 60 followed by random rotations. 15 , 18 , 44 , 60 , 61 , 63 The addition of noise, 18 , 36 , 46 translational shifts, 55 , 57 , 61 random crops, 37 , 42 , 44 random shears, 15 , 61 and scaling 15 were also utilized in the literature. Although most augmentation strategies consist of simple linear transformation of the image, the addition of random noise at every iteration degrades image quality yet aids in the learning of salient features by making the network more robust to overfitting (small changes in latent space do not alter the output) while improving generalizability (multiple representations of the same feature are mapped to same output). 78 Random crops present a more functional augmentation strategy that simultaneously increases training set size whilst reducing computational load by reducing input image dimensions.
4.2.8. Model generalizability
Of the studies that examined multiple anatomies, several authors further investigated whether composite models (trained/tested using multiple anatomic sites) could generalize as well as intra‐anatomy models (trained/tested using single anatomic site). 42 , 45 Other authors explored whether inter‐anatomy models (tested on different anatomic site) would improve image quality at all. 18 , 39 In Maspero et al., 42 the composite models were outperformed by intra‐anatomy models by a very small margin (51 ± 12 vs. 53 ± 12 HU), leading the authors to conclude that a single composite model could generalize as well as intra‐anatomy models. On the contrary, Uh et al. 45 found that a single composite model outperformed their intra‐anatomy model (47 ± 7 vs. 51 ± 8 HU), suggesting that single‐composite models benefit from training on multiple anatomic regions.
Liang et al. 39 and Chen et al. 54 showed that their HN trained models could generalize well on pelvic data, demonstrating a percent MAE improvement of 58.10% and 55.11%, respectively. Meanwhile, Zhang et al. 18 used their pelvic trained GAN on HN data to recover a 25.39% improvement in MAE. This implies that the HN rather than pelvic region contains richer features for more generalizable inter‐anatomic models. Furthermore, Chen et al. 54 utilized transfer learning by retraining the intra‐anatomy HN model weights on a small subset of inter‐anatomy pelvic data and compared that strategy to no model tuning. The transfer learning strategy further reduced sCT MAE from 46.78 to 42.40 HU.
4.2.9. Segmentation accuracy
Segmentation accuracy can be thought of as a proxy measure for image quality and a useful metric for assessing the extent of anatomical preservation during image synthesis. To compare the preservation of anatomical structures, Lemus et al. 52 manually contoured CBCT, sCT, and DIR CT images of abdominal patients, with the CBCT used as reference. The sCT images consistently outperformed the DIR CT for each anatomical structure, with a mean Dice coefficient of 0.92 ± 0.04 for the sCT and 0.82 ± 0.06 for the DIR CT.
Eckl et al. 40 compared a manual segmentation performed on the sCT to the one performed on the CT image and later deformed to the sCT as an indirect measure of image quality. The HN region scored the lowest Dice scores ranging from 60.6 ± 10.4 to 79.3 ± 5.8, whereas thoracic and pelvic regions did not go below 81.0%, with the exception of the seminal vesicles. The mean Dice for HN, thoracic, and pelvic regions was 73.33 ± 7.83, 87.03 ± 10.30, and 81.03 ± 18.50, respectively. This suggests that smaller structures in the HN and pelvis were more prone to errors, with the seminal vesicles scoring 66.7 ± 8.3. However, it is difficult to differentiate image quality from improper DIR.
Sun et al. 47 and Zhao et al. 46 compared automatically generated segmentations of organs at risk (OAR) to manual delineations for the pelvic region. In Sun et al., 47 auto‐segmentation Dice scores for sCT images generated by cycle‐GAN did not fall below 87.23 ± 2.01, with a mean of 89.89 ± 1.01 when compared to manually segmented structures on the CT. In comparison, the mean Dice coefficient for a GAN was 87.84 ± 1.23. Zhao et al. 46 also reported high Dice scores for the pelvic region using an auto‐segmented ground truth CT, with a mean of 0.93 ± 0.03, whereas auto‐segmentation performed on CBCT images routinely failed to segment certain structures. When the same sCT auto‐segmentation was compared to a manually segmented ground truth dataset, the Dice score improved to 0.96 ± 0.04, suggesting that only small modifications are necessary. Dai et al. 51 trained a separate segmentation network on sCT and CT images with respective manually generated ground truth labels for the thoracic region. The sCT and CT datasets performed comparably, with sCT Dice scores ranging from 0.63 ± 0.08 to 0.95 ± 0.01, compared to CT Dices scores of 0.73 ± 0.08 to 0.97 ± 0.01. Importantly, the mean Dice score for the CTV was 0.88 ± 0.03 for the CT and 0.83 ± 0.03 for the sCT.
4.2.10. sCT dosimetry
The dosimetric accuracy of sCT images is a clinically important endpoint for ART. Table 6 summarizes the number of investigations above and below a 95% GPR threshold for differing anatomical sites, gamma criteria, and radiation modalities.
TABLE 6.
Studies reporting mean gamma pass rates for different anatomical regions and radiation modalities
| Head and neck | Pelvis | Abdomen | Breast | Lung | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| γ 3 | γ 2 | γ 1 | γ 3 | γ 2 | γ 1 | γ 3/2 | γ 2 | γ 1 | γ 3 | γ 2 | γ 1 | γ 3 | γ 2 | γ 1 | |
| Photon | [2, 0] | [5, 0] | [2, 0] | [1, 0] | [2, 0] | – | [1, 0] | – | – | [1, 1] | [0, 1] | – | [3, 0] | [1, 2] | – |
| Proton | [2, 0] | [2, 0] | – | [1, 0] | [2, 0] | – | – | [1, 0] | – | – | – | – | [1, 0] | [0, 1] | – |
Note: Mean gamma rates above 95% are considered clinically acceptable. Reporting format: [N > 95%, N < 95%] with N = number of evaluations. γ 3 = 3%/3 mm; γ 2 = 2%/2 mm; γ 1 = 1%/1 mm; γ 3/2 = 3%/2 mm. Light green = 1 validation; medium green = 2 validations; dark green = 3+ validations.
The HN site was the most investigated region for both photon and proton plans and recorded no rates below 95%. 19 , 39 , 40 , 42 , 55 , 56 , 57 , 61 Furthermore, it was the only region to be assessed under a 1%/1‐mm stringency and pass for photon plans. 39 , 55 Meanwhile, multiple studies showed the acceptability of proton plans in the HN region for both 2%/2‐ and 3%/3‐mm criteria. 56 , 57
The pelvic region was validated for photon 40 , 47 and proton plans, 37 , 45 showing acceptable pass rates for both 3%/3‐ and 2%/2‐mm criteria.
A single study reported passing 3%/2‐mm GPR for the abdominal region for photon plans 52 ; however, Liu et al. 41 did conduct a DVH analysis on OAR and PTV volumes for pancreatic cancer and concluded that there was no significant difference between sCT and DIR CT plans. The abdominal region was investigated once for pediatric proton patients in Uh et al. 45 with passing 2%/2‐mm rates.
Photon breast cancer plans failed under the 2%/2‐mm criteria in Maspero et al. 42 ; however, the more permissible 3%/3‐mm criteria passed in their investigation. Conversely, Dai et al. 51 reported failing plans at 3%/3 mm. No proton dosimetric analyses were conducted for the breast region.
The lung site was well validated for photon plans 40 , 42 , 49 for a 3%/3‐mm criteria; however, two investigations noted failing 2%/2‐mm rates. A single study by Thummerer et al. 59 investigated the lung site for proton ART and reported passing rates only for 3%/3‐mm criteria.
4.3. Projection domain corrections
A total of six projection domain–based CBCT correction methods are summarized in Table 4. Studies operating strictly in the projection domain attempted to approximate the scatter signal contained in raw projections by using either MC‐derived scatter maps, 79 , 80 or a CT‐prior‐based correction approach as the ground truth. 73 , 75 , 81 Meanwhile, one study looked at predicting MC‐corrected CBCT images from uncorrected CBCT images. 74 For all studies, U‐Net was used as training was performed using paired data.
Nomura et al. 79 utilized a U‐Net to learn how the scatter distribution within five simulated non‐anthropomorphic phantom projections generalized to patient projections simulated using MC. The DL approach was compared to an analytical kernel‐based scatter correction method fASKS 82 and was shown to significantly improve the resulting MAE. Similarly, Rusanov et al. 81 trained a network to learn the scatter distribution resulting from four anthropomorphic phantoms. When applied on real patient scans, the MAE improved compared to vendor reconstructions (74 vs. 117 HU). Residual learning 72 of the scatter signal rather than the corrected projection was hypothesized by Nomura et al. 79 to be a more efficacious training strategy, a fact later confirmed by Lalonde et al. 80 in their patient‐based MC study (13.41 vs. 20.23 HU), and Rusanov et al. 81 in their scatter correction study (74 vs. 77 HU). These authors also investigated the use of MSE and MAE loss functions, with Lalonde et al. 80 and Rusanov et al. 81 both reporting an improved MAE for the latter loss (13.41 vs. 15.48 HU and 74 vs. 86 HU, respectively). Nomura et al. concluded that MAE penalized anatomic regions more than MSE, which tended to penalize noisy regions primarily in air, thereby leading to more inaccurate scatter correction in anatomic regions.
The a priori scatter correction technique is well validated in the CBCT literature 28 , 29 , 30 , 83 and has served as the ground truth for the Hansen et al. 73 and Landry et al. 75 studies investigating projection domain correction. The technique is predicated on simulating virtual projections of the planning CT through forward projection using the scanning geometry of the CBCT. CT projections are assumed to be scatter‐free and are used to estimate the scatter signal in raw CBCT projections by extracting the low frequency signal contained in the residual projection. In both studies, raw projections were synthesized into synthetic a priori corrected projections that, once reconstructed, deviated in MAE from the ground truth by 51 HU for Landry et al. 75 and 48 HU for Hansen et al. 73 Landry et al. 75 further compared projection domain synthesis to two image domain synthesis approaches: transforming uncorrected CBCT images to a priori corrected CBCT images, and generating sCTs. In terms of MAE, the projection domain approach performed best (51‐HU projection vs. 88‐HU sCT and 58‐HU a priori image). However, in terms of proton dosimetry, the sCT produced the highest mean 2%/2‐mm GPR (96.1%), followed by synthetic a priori (95.3%), and projection domain synthesis (93.0%). Even though the ground truth was a priori corrected CBCTs, the sCT produced the best dosimetric agreement, likely due to the more uniform HU and smooth distribution unlike the other two approaches.
Lalonde et al. 80 and Jiang et al. 74 used MC to create scatter‐free ground‐truth data for their image synthesis studies. Although Lalonde et al. trained a network to predict the scatter contribution in raw projections, Jiang et al. synthesized MC‐corrected CBCTs from input‐uncorrected CBCTs. As ground truth and input CBCT images show perfect alignment, a one‐to‐one mapping can be learned using U‐Net without suffering blurring and artifact‐related shortcomings common in sCT generation. Their proposed network outperformed the a priori 28 , 29 , 30 correction method in terms of RMSE (18.8 vs. 30.3 HU). Lalonde et al. 80 found good agreement between U‐Net‐corrected CBCTs and MC‐synthesized images for proton HN plans (2%/2‐mm gamma mean of 98.89%). When the same model was compared against real patient HN scans using the a priori correction as ground truth, the 2%/2‐mm GPR dropped to 78.15%. This result is lower than what was reported in Landry et al. 75 for the same criteria (2%/2‐mm gamma > 85%), possibly because MC simulations do not model system realism to the same degree achieved in a priori corrections.
5. DISCUSSION
This review has sought to provide an in‐depth summary of the current state of the literature involved with CBCT‐based sCT generation and projection‐based scatter correction using DL. Studies from 1 January 2018 to 1 April 2022 were reviewed with a focus on DL methods and relevant clinical endpoints relating to image quality, dosimetry, and segmentation accuracy. The primary motivation for improving CBCT image quality is to provide accurate pretreatment anatomical information to facilitate online ART. By minimizing inter‐fractional anatomic uncertainty, clinical benefits accrue from the reduction of dose to OAR and escalation of dose to target volumes. 3 , 4 , 84 , 85 , 86 , 87 The following discussion aims to summarize best practices that may be of interest to DL practitioners and inform clinicians on the current state of CBCT‐based ART.
5.1. Recommendations for researchers
The literature summary showed that among studies that controlled for training data, cycle‐GAN generally outperformed GAN‐based approaches by 6.81% and U‐Net by 14.25% in terms of relative MAE improvement (see Figure 5). In terms of anatomical preservation, cycle‐GAN was explicitly compared to GAN models in Gao et al. 49 and Liang et al. 39 using anthropomorphic phantoms as true ground truth data. In both studies, GAN‐based sCT images failed to preserve the underlying anatomy. Importantly, phantom inserts were erased and false anatomic information such as the heart and bronchioles were superimposed in Gao et al., 49 showing that GAN‐based synthesis produces the most likely anatomy based on the specific context of the region, rather than explicitly maintaining the structure from the input. Given that GANs are trained to approximate the probability density distribution of the target domain, 20 without further constraints such as cycle consistency, this result is not surprising. U‐Net‐based synthesis relies on data alignment to learn a direct mapping using a hand‐crafted loss function. In the absence of perfectly paired data, the resulting sCT is blurred as boundary differences are averaged and perceptually unrealistic given the simplicity of the loss function. 16 , 17 , 18 , 19 Although the resulting sCT images may be viable for dose calculations, their MAE is generally higher than GAN‐based architectures and they may fall short in downstream tasks necessary for ART such as manual or automatic segmentation that requires sharp organ boundaries.
One other unpaired translation network was investigated, ADN, which outperformed cycle‐GAN in terms of MAE (32.70 ± 7.26 vs. 42.04 ± 8.84 HU), 27 and scored the highest percentage SSIM improvement out of studies not using low‐dose CBCTs as input (see Figure 10). ADN does not rely on cycle‐consistency to enforce anatomical information, rather, image content and style are disentangled using multiple encoders. A common content feature space is established between CT and CBCT images, whereas style embeddings relating to CBCT and CT images are separated. It then becomes possible to combine CT style with CBCT content. One advantage of the ADN network, and disentangled unsupervised image translation approaches in general, is that their outputs do not depend on the strict cycle‐consistency constraint, in turn producing more realistic images. Although cycle‐consistency helps maintain content information, it also encourages the preservation of some artifacts during sCT generation such that the backward cycle has useful prompts to accurately recreate the cycle images (which contain those artifacts). 88 A recent work aimed to loosen the cycle loss constraint by replacing the pixel‐wise error between input and cycle images with another discriminator. The authors show that this strategy provides sufficient constraints for the generators to maintain the input structure while minimizing any residual prompts in the synthetic image. 89 In the DL literature, many supervised and unsupervised image translation architectures exist, but only a small subset have been applied to medical data. A more complete review of these architectures can be found in Alotaibi et al. 90 and Pang et al., 91 with benchmarks of various networks on some of the most common datasets in Saxena et al. 92
Interestingly, unpaired training configurations outperformed paired training for cycle‐GAN in terms of relative MAE improvements (see Figure 6; 55.98% vs. 47.61%, p = 0.16). However, the results narrowed when studies with similar training set sizes were compared, with paired implementations performing slightly better (53.65% vs. 51.83%, p = 0.29). Given that all studies used CBCT and CT data from the same patients, similar levels of variance, and therefore model performance, should exist whether paired or unpaired configurations were applied. However, it is anticipated that faster convergence could be achieved using paired data, as discriminators are better able to determine real from fake samples when anatomic position is controlled for. Hence, domain‐specific features such as artifacts may be easier to identify when real and fake data distributions are structurally similar.
Similarly, no clear advantage was observed for cycle‐GAN studies utilizing patch‐based 3D networks over 2D variants (52.08% 2D vs. 49.83% 3D, p = 0.41). It is suspected that the benefits of 3D feature representations are somewhat negated by two factors: (1) 3D networks contain more trainable parameters than their 2D counterparts; hence, more training data is required to avoid overfitting and to capture the increased data complexity. (2) Creating patch‐based volumes destroys the global feature representations otherwise available at the encoder‐decoder bottleneck, thereby losing access to important contextual information for modeling long range dependencies. To overcome these drawbacks, the GAN used in Dahiya et al. 15 used full 3D image volumes and was trained on a large cohort of 140 patients. Accordingly, the authors achieved the second‐best relative MAE improvement of 81.99%, likely due to addressing the abovementioned concerns.
Whether using paired or unpaired data, preprocessing images using intra‐patient RR is always beneficial as it allows excess air regions to be truncated. It is hypothesized that network performance may further increase with inter‐patient RR as the extent of each patient's anatomy is grouped to a common center, similar to the improvement in results in Uh et al. 45 after pediatric body normalization (47 ± 7 vs. 60 ± 7 HU, p < 0.01). The only study to compare the use of DIR and RR on training a cycle‐GAN concluded that minimal benefits accrue in terms of MAE improvement (56.89 ± 13.84 HU DIR vs. 58.45 ± 13.88 HU RR); however, visual inspection showed noticeably less noise, fewer motion artifacts, and superior boundary preservation for the model trained with DIR pre‐processing. 41 Finally, applying normalization on a patient‐wise level is recommended over slice‐wise normalization, as demonstrated by Dong et al. 50 in which the latter resulted in intensity discontinuity between slices.
Data augmentation is used to prevent overfitting and improve model generalization when limited data is available. One important augmentation strategy is the addition of Gaussian noise during optimization, which has been shown to improve the learning of salient features. 78 A further benefit of noise injection relates closely to the phenomenon described earlier regarding the preservation of artifacts during the forward cycle in cycle‐GAN. Bashkirova et al. 26 showed how generators imbed a low amplitude structured noise in synthetic images that is used during the backward cycle as a prompt to reproduce the input domain more accurately. The addition of this structured noise, which is imperceptible by humans, is like cheating and prevents the generator from learning the optimal translation parameters. The authors discovered that the addition of low amplitude Gaussian noise during training inhibits the generators capacity to cheat, encourages the learning of more robust features, leads to visually more realistic images, and reduces model sensitivity to noise perturbations by a factor of 6. As a result, their cycle‐GAN trained with noise augmentation produced synthetic images with an MSE 31.86% lower than the baseline. 26
Virtually no difference in percent MAE improvement was observed between studies utilizing the standard cycle‐GAN loss compared with extended loss configurations (49.08 ± 21.85‐HU standard vs. 49.90 ± 14.37‐HU extended, p = 0.35). However, for studies investigating different loss functions, perceptual and MAE improvements in image quality were reported for identity, SSIM, feature matching, gradient, synthetic, histogram, and perceptual losses. 18 , 44 , 47 , 48 , 54 Furthermore, the SSIM—a perceptual image quality metric—improved by a greater margin in studies using additional loss functions over studies using baseline losses (10.5 ± 5.95% vs. 12.8 ± 5.73%, p = 0.35). As a consequence for ART, automatic segmentation models (pre‐)trained on CT images should perform better on sCT images that are perceptually more similar to CT images. Hence, more time‐effective ART protocols requiring fewer manual corrections could be achieved if perceptual differences are minimized.
For this reason, it is important to adopt more sophisticated perceptual image quality metrics alongside SSIM, which has been shown to fail under certain circumstances. 93 The Fréchet inception distance (FID) is the most common metric used in the DL community to measure image quality in the absence of a ground truth image. 94 FID uses a pretrained inception v3 network to extract features from real and generated data. Statistical measures are then compared between deep feature maps to assess image similarity, a technique shown to correlate well with the human visual system. 95 Another benefit of FID is that data alignment is not required, thereby removing the bias entrenched in MAE assessments that are highly dependent on anatomical correspondence. Newer and more robust deep‐feature‐based perceptual metrics include LPIPS (Learned Perceptual Image Patch Similarity) 95 and DISTS (Deep Image Structure and Texture Similarity), 96 both of which are commonly used to compare generative model image quality. Hence, using these metrics as optimization criteria or merely to compare models can aid in the selection of the most suitable sCT data in terms of CT/sCT feature similarity for downstream ART auto‐segmentation tasks.
One shortcoming of fully convolutional networks is their inability to model long range dependencies well. This is due to the use of small convolution kernels that can only “see” a portion of the image at any given time. The use of inception blocks, as in Tien et al. to merge smaller and larger kernels, is one method to capture features at different resolutions. 44 Alternatively, global attention mechanisms such as attention gating used in Liu et al. aim to downweigh less relevant spatial regions. 27 , 41 Recently, the emergence of vision transformers (ViT) has challenged the notion that convolutions are the best way to drive learning‐based computer vision tasks. 97 Based on patch‐tokenization of the image, ViTs are capable of modeling global contextual information, in effect learning how each patch relates to every other patch directly. 97 The downside, however, is that local information is coarsely modeled, which motivated researchers to create hybrid models that utilize ViTs to model global information in the encoder wing, while synthesizing high resolution outputs using a CNN decoder wing. 98 Currently, segmentation‐based networks such as Trans‐U‐Net use this configuration to outperform comparable pure CNN architectures. 98 The first hybrid image synthesis architecture, ResViT, utilizes a series of ViTs at the encoder‐decoder bottleneck to better aggregate global features. 99 The authors noted that SSIM and PSNR for ResViT (0.931 ± 0.009 and 28.45 ± 1.35) improved over Trans‐U‐Net (0.914 ± 0.009 and 27.76 ± 1.03), attention U‐Net (0.913 ± 0.004 and 27.80 ± 0.63), and pix2pix GAN (0.898 ± 0.004 and 26.53 ± 0.45) for an MRI to CT synthesis task. 99 Hybrid architecture approaches to image synthesis offer a new and exciting research direction; however, issues around higher ViT training data requirements still need to be addressed.
That learning‐based models benefit from increased trained set sizes is well known. As evident in Figure 7, a small but positive relationship was found between training cohort size and relative improvement in MAE. The relationship was poorly modeled by linear regression; however, a moderate upward trend is seen from 11 to 46 patients, which then forms a plateau as further increases in cohort size offer diminished, or no benefit. Comparable MAE reductions, around ∼70%, were achieved using anywhere from 15 to 46 patients; however, less variance in model performance was observed for higher cohort sizes indicating a stronger relationship. The two largest improvements in MAE used 90 and 140 patients, respectively, showing that much larger training sets can push the SoTA. Although reliance only upon data size is not guaranteed for success, as seen by studies that showed comparable improvements using sub 40 and greater than 120 patients. In general, the interplay between model performance and training set size follows this pattern across different medical tasks such as segmentation 100 , 101 and classification102,103: rapid improvements with high variance initially, followed by saturation with any further increases in training set size. 104 The optimal number of training cases is unique for every class of problem and dependent on the quality of the data itself. Nevertheless, given the high cost of medical data collection, suitable sCT image quality can be achieved using anywhere between 15 and 46 patients, with preference for higher cohort sizes if reasonably possible.
Table 5 shows the thoracic, pelvic, and HN regions were widely investigated and showed similar levels of MAE improvement (57.54 ± 12.65%, 57.97 ± 19.68%, 58.67 ± 10.75% respectively). These may be considered well validated in the context of image quality. However, studies investigating the abdominal region accounted for only 7% of all sites and also showed the lowest relative MAE improvement (41.33 ± 19.51%) while using less than half of the training data of other sites. Given the large extent of motion artifacts present in abdominal scans, larger training cohorts and more sophisticated translation approaches such as in Dahiya et al. 15 may be necessary. There, CBCT‐specific artifacts were infused into CT images using a physics‐based augmentation to create perfectly aligned training data which aided sCT synthesis for the artifact‐prone thoracic region. 15
Beyond sCT generation, projection domain corrections warrant further attention given the impressive results in Landry et al. 75 which showed that DL‐driven a priori corrected images possessed lower MAE than sCT images (51 HU a priori vs. 88 HU sCT), and comparable proton dose accuracy (96.1% sCT vs. 93.0% a priori). Performing corrections in the projection domain has several advantages over the image domain: First, scatter and associated intensity deviations are well localized in each projection, whereas these errors manifest non‐trivially in the image domain making them more difficult to learn. Thus, projection data compliments how convolution operations extract features locally. Second, projection data is far more numerous than reconstructed data for a given patient—a beneficial characteristic for DL. Unpaired translation networks have not yet been investigated in the projection domain. The a priori correction currently requires well‐aligned CT and CBCT data to mitigate high‐frequency errors during reconstruction. Alternatively, the use of unpaired data with cycle‐GAN mitigates the need to perform any smoothing operations during a priori correction, allowing the network to learn both low and high frequency sources of intensity errors—a characteristic not possible under the original a priori implementation. 28 , 29 , 30 , 83
The use of DL techniques for CT reconstruction has predominantly involved sparse‐view and low‐dose acquisitions as there is no ideal tomographic ground truth for learning strategies. 105 , 106 , 107 , 108 , 109 , 110 Iterative reconstruction (IR) applications utilizing DL can be categorized into “plug‐and‐play” and “unrolling” methods. 109 Plug‐and‐play methods utilize a CNN that is first trained in the image domain to act as a regularizer during IR. 111 Unrolling methods aim to model the various components of a reconstruction algorithm using convolutional and fully connected networks (FCN). 107 For example, Wurfl et al. 107 explicitly modeled the discrete Feldkamp–Davis–Kress (FDK) 112 algorithm using convolutional and neuronal neural network components. Direct reconstruction using DL has been achieved by utilizing FCN, 105 or a combination of CNN and FCNs. 107 , 110 In these latter approaches, raw data is first preprocessed with CNNs then reconstructed by utilizing an FCN that connects each pixel in the measured domain to all voxels in the image domain to learn a direct domain transformation mapping. For example, Li et al. 110 performed reconstruction directly on sinogram data previously preprocessed by a CNN. Specifically for cone‐beam reconstruction, global FCN mapping showed to be computationally expensive; hence, Lu et al. 105 developed a geometry‐guided framework containing an array of much smaller FCNs, each of which connects a pixel in the projection domain to a beamlet in the image domain based on the specific beamlet geometry incident from the X‐ray source. Thus, each beamlet traversing the object is modeled by a small FCN. Chen et al. 113 showed that a pretrained natural image denoising CNN could denoise real cone‐beam projections. The CNN replaced classical hand‐crafted regularization terms in statistical‐IR reconstruction and resulted in reduced artifacts compared to total‐variation 114 and FDK 112 reconstructions. Meanwhile Han et al. 115 proposed a novel reconstruction method using differentiated backprojection (DBP). Projection data is first transformed to a DBP form, 116 with coronal and sagittal views fed into a CNN that learns to solve a Hilbert transform deconvolution task. The output consists of coronal and sagittal reconstructed images that exhibit higher image quality than FDK and CNN‐aided FDK reconstructions.
Adhering to good practices in the reporting of results will help standardize the literature and make comparisons more consistent. Dose distribution comparisons of clinical plans between ground truth and corrected CBCTs should be performed using the recommendations defined by regulatory bodies such as AAPM (American Association of Physicists in Medicine). The latest AAPM Task Group 218 guidelines suggest using the 3%/2‐mm GPR criteria, calculated using a 10% low‐dose threshold for comparing dose distributions. 117 Evaluating image quality is typically assessed using MAE; however, authors are sometimes ambiguous on how the metric is calculated. Most authors report MAE over the entire image volume, yet, these approaches can be biased against volumes with large amounts of air that artificially reduce the MAE. Recently, some authors have calculated MAE within the patient body contour, 37 , 40 , 41 , 45 , 48 , 51 , 56 , 57 , 59 , 61 whereas others went a step further and found the MAE for specific anatomic regions such as bone or soft tissue. 40 , 44 We recommend good practice in data reporting by defining all pixel‐wise metrics within the patient body contour to eliminate bias. Furthermore, reporting uncorrected CBCT image quality is necessary to gauge the relative improvement. Similar recommendations were recently echoed for SSIM: The authors recommended reporting the average SSIM within the patient body contour and ensuring that an appropriate dynamic range is used. 118 As previously discussed, the FID is a popular image quality metric used in assessing generative models that lack a ground truth. 94 The distance metric compares the distribution of deep features between two datasets irrespective of their pixel‐wise alignment, thereby addressing the inherent flaw of using MAE.
5.2. Recommendations for clinicians
A recent review of AI applications in radiotherapy listed sCT generation as one of the top three most popular use cases—and provided practical steps in commissioning, clinical implementation, and quality assurance. 119 A best practice workflow for AI, and sCT generation specifically, is many years away given the rapid pace of technical progress; however, clinicians have begun investigating novel ways of ensuring quality control (QC). For example, as suggested by Thummerer et al. 59 and shown in Oria et al., 120 proton range probing fields can be used as a QC tool by comparing the difference between simulated and CT/sCT mean relative range errors in retrospective patient scans. Hence, in vivo data may be preferable to using conventional image quality phantoms for QA/QC applications as training data used for sCT generation does not contain any phantoms.
The preferred method for implementing CBCT‐based dose monitoring protocols has relied on DIR of the planning CT to the CBCT. 121 , 122 , 123 With the emergence of sCT generation, the authors have demonstrated better agreement in terms of MAE 39 , 57 , 61 and anatomical accuracy 52 over using deformed planning CTs, whilst maintaining comparable dose accuracy for proton and photon plans. 42 , 52 , 61 Hence, the use of sCT for dose monitoring will enhance the accuracy of research conclusions and result in improved decision‐making for both online and offline ART.
The acceptance criteria outlined in AAPM‐TG 218 for tolerance and action limits are defined as greater than 95% and less than 90% for a 3%/2‐mm GPR criterion, respectively. 117 In adopting these thresholds, the current literature has thoroughly demonstrated adequate sCT dose accuracy for photon and proton plans in the HN region. 19 , 39 , 40 , 42 , 55 , 56 , 57 , 61 (see Table 6) Likewise, multiple‐photon 40 , 47 and proton 37 , 45 studies in the pelvic region demonstrated pass rated above 95% for the stricter 2%/2‐mm criterion. The abdominal, breast, and lung regions were less researched. Proton 45 and photon 52 abdominal plans were validated once, and a single‐photon lung plan was validated for the stricter 2%/2‐mm criteria. 49 However, no study has investigated sCT accuracy for proton breast plans, whereas the single study that analyzed proton lung plans failed to demonstrate sufficient dosimetric accuracy. 59
Automatic segmentation is an important intermediary step toward the development of online CBCT‐guided ART workflows. Although not the focus of this review, several authors did analyze the performance of sCTs in auto‐segmentation tasks. The suitability of sCT images for autosegmentation was compared to CT images in the thoracic region by training a separate model for each dataset. Dice scores indicated comparable performance on both datasets, with CT images retaining slightly higher mean CTV overlap. 51 Generally, good auto‐segmentation performance is achieved if results are as good or better than interobserver variability, which was shown to range from 0.8 to 0.99 for the pelvic region. 124 Consequently, Sun et al. and Zhao et al. demonstrated Dice score agreement greater than 0.89 for the pelvic region. 46 , 47 Recently, segmentation‐specific studies have compared the performance of CBCT‐derived sCT images for abdominal segmentations, reporting Dice scores above 0.8. 125 , 126 The validation of sCT‐based auto‐segmentation for all anatomic regions is an important step toward online ART.
The nascent field of sCT generation is attracting attention from vendors, with Elekta releasing a research version of their Advanced Medical Image Registration Engine (ADMIRE) (Elekta AB, Sweden) software capable of producing sCT images using their implementation of cycle‐GAN. 40 The model must be trained locally to adhere to consistent CT acquisition parameters. To this end, the recent retrospective study by Eckl et al. 127 demonstrated the benefits of sCT‐driven ART using ADMIRE for stereotactic prostate cancer patients, showing statistically significant improvements in target coverage and organ sparing. Plan adaption varied from 2.6 ± 0.3 to 19.4 ± 4 min, depending on the ART protocol. Alternatively, the specialized ART module Ethos released by Varian (Varian Medical Systems, Palo Alto, CA, USA) 128 does not generate sCT for replanning but utilizes DL for rapid contour generation. A recent analysis showed that Ethos could improve CTV and PTV coverage whilst significantly reducing dose to all OAR in prostate cancer patients, with an average clinical treatment time of 19 min. 129 Looking forward, one may envision several DL models that make up the backbone of an ART engine that can quickly and accurately generate sCT images, automatically contour structures, predict new optimal dose distributions, and conduct QA assessments with minimal manual intervention.
6. CONCLUSION
Methods for improving CBCT image quality using DL have been reviewed, with emphasis placed on exploring the technical aspect of the current state of the art. Literature summaries and recommendations for DL practitioners and clinicians alike are made, ensuring that best practices are established in model development and clinical deployment moving forward. CBCT‐based sCTs were shown to accurately reflect real CT density information for the HN, pelvic, and thoracic regions, whereas the abdominal site received less attention. Cycle‐GAN models, on average, outperformed both U‐Net and GAN approaches in terms of image quality and anatomical preservation. Dosimetric performance of sCTs was thoroughly validated in the pelvic, and HN regions for both photon and proton plans, whereas other regions were less researched. Preliminary auto‐segmentation results demonstrate comparable performance for CT and sCT datasets alike. Looking ahead, large multicenter studies are needed to report their firsthand experiences implementing ART workflows, which include sCT generation, auto‐segmentation, plan adaption, and QA to help inform future protocols and highlight weaknesses.
CONFLICT OF INTEREST
The authors have no conflicts of interest to disclose.
ACKNOWLEDGMENTS
This work was supported by an Australian Government Research Training Program (RTP) scholarship and a Cancer Council WA PhD Top Up scholarship (ID: 1208). The authors would like to thank the Sir Charles Gairdner Department of Radiation Oncology and The University of Western Australia for supporting this research.
Open access publishing facilitated by The University of Western Australia, as part of the Wiley – The University of Western Australia agreement via the Council of Australian University Librarians.
Rusanov B, Hassan GM, Reynolds M, et al. Deep learning methods for enhancing cone‐beam CT image quality toward adaptive radiation therapy: A systematic review. Med Phys. 2022;49:6019–6054. 10.1002/mp.15840
REFERENCES
- 1. The Royal Australian and New Zealand College of Radiologists . Artificial Intelligence in Radiology and Radiation Oncology: The State of Play 2019 . The Royal Australian and New Zealand College of Radiologists; 2019. [Google Scholar]
- 2. Castelli J, Simon A, Lafond C, et al. Adaptive radiotherapy for head and neck cancer. Acta Oncol. 2018;57:1‐9. [DOI] [PubMed] [Google Scholar]
- 3. Morgan H, Sher D. Adaptive radiotherapy for head and neck cancer. Cancers Head Neck. 2020;5:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Kataria T, Gupta D, Bisht S, et al. Adaptive radiotherapy in lung cancer: dosimetric benefits and clinical outcome. Br J Radiol. 2014;87:20130643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Thörnqvist S, Hysing L, Tuomikoski L, et al. Adaptive radiotherapy strategies for pelvic tumors – a systematic review of clinical implementations. Acta Oncol. 2016;55:1‐16. [DOI] [PubMed] [Google Scholar]
- 6. Green O, Henke L, Hugo G. Practical clinical workflows for online and offline adaptive radiation therapy. Semin Radiat Oncol. 2019;29:219‐227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Schulze R, Heil U, Groß D, et al. Artefacts in cbCT: a review. Dentomaxillofac Radiol. 2011;40:265‐273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Marblestone AH, Wayne G, Kording KP. Toward an integration of deep learning and neuroscience. Front Comput Neurosci. 2016;10:94‐94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Yamashita R, Nishio M, Do RKG, Togashi K. Convolutional neural networks: an overview and application in radiology. Insights Imaging. 2018;9(4):611‐629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Love LA, Kruger RA. Scatter estimation for a digital radiographic system using convolution filtering. Med Phys. 1987;14(2):178‐185. [DOI] [PubMed] [Google Scholar]
- 11. Dumoulin V, Visin F. A guide to convolution arithmetic for deep learning. ArXiv. 2016. doi: arXiv:1603.07285v2
- 12. Pereda AE. Electrical synapses and their functional interactions with chemical synapses. Nat Rev Neurosci. 2014;15(4):250‐263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Ruder S. An Overview of Gradient Descent Optimization Algorithms. ArXiv. 2016. 10.48550/arXiv.1609.04747 [DOI]
- 14. Ronneberger O, Fischer P, Brox T. U‐Net: convolutional networks for biomedical image segmentation. Medical Image Computing and Computer‐Assisted Intervention MICCAI 2015. 2015;9351:234‐241. 10.1007/978-3-319-24574-4_28 [DOI] [Google Scholar]
- 15. Dahiya N, Alam SR, Zhang P, et al. Multitask 3D CBCT‐to‐CT translation and organs‐at‐risk segmentation using physics‐based data augmentation. Med Phys (Lancaster). 2021;48(9):5130‐5141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Ghodrati V, Shao J, Bydder M, et al. MR image reconstruction using deep learning: evaluation of network structure and loss functions. Quant Imaging Med Surg. 2019;9(9):1516‐1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Mustafa A, Mikhailiuk A, Iliescu DA, Babbar V, Mantiuk RK. Training a Task‐Specific Image Reconstruction Loss. 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV). 2022;21‐30. 10.1109/WACV51458.2022.00010 [DOI] [Google Scholar]
- 18. Zhang Y, Yue N, Su M‐Y, et al. Improving CBCT quality to CT level using deep learning with generative adversarial network. Med Phys (Lancaster). 2020;48(6):2816‐2826. 10.1002/mp.14624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Xue X, Ding Y, Shi J, et al. Cone beam CT (CBCT) based synthetic CT generation using deep learning methods for dose calculation of nasopharyngeal carcinoma radiotherapy. Technol Cancer Res Treat. 2021;20:153303382110624‐15330338211062415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Goodfellow I, Pouget‐Abadie J, Mirza M, et al. Generative adversarial networks. Commun ACM. 2020;63(11):139‐144. [Google Scholar]
- 21. Fedus W, Rosca M, Lakshminarayanan B, Dai AM, Mohamed S, Goodfellow I. Many Paths to Equilibrium: GANs Do Not Need to Decrease a Divergence At Every Step. ArXiv. 2017. 10.48550/arXiv.1710.08446 [DOI]
- 22. Jolicoeur‐Martineau A. The Relativistic Discriminator: A Key Element Missing from Standard GAN. ArXiv. 2018. 10.48550/arXiv.1807.00734 [DOI]
- 23. Isola P, Zhu J, Zhou T, Efros AA. Image‐to‐image translation with conditional adversarial networks. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2017; 5967‐5976. 10.1109/CVPR.2017.632 [DOI] [Google Scholar]
- 24. Zhu J, Park T, Isola P, Efros AA. Unpaired Image‐to‐Image Translation Using Cycle‐Consistent Adversarial Networks. 2017 IEEE International Conference on Computer Vision (ICCV) . 2017; 2242‐2251. 10.1109/ICCV.2017.244 [DOI]
- 25. Amodio M, Krishnaswamy S. TraVeLGAN: Image‐to‐image Translation by Transformation Vector Learning. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) . 2019; 8975‐8984. 10.1109/CVPR.2019.00919 [DOI]
- 26. Bashkirova D, Usman B, Saenko K. Adversarial self‐defense for cycle‐consistent GANs. Proceedings of the 33rd International Conference on Neural Information Processing Systems . 2019; 637‐647. 10.5555/3454287.3454345 [DOI]
- 27. Liu J, Yan H, Cheng H, et al. CBCT‐based synthetic CT generation using generative adversarial networks with disentangled representation. Quant Imaging Med Surg. 2021;11(12):4820‐4834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Niu T, Al‐Basheer A, Zhu L. Quantitative cone‐beam CT imaging in radiation therapy using planning CT as a prior: first patient studies. Med Phys. 2012;39:1991‐2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Niu T, Sun M, Star‐Lack J, Gao H, Fan Q, Zhu L. Shading correction for on‐board cone‐beam CT in radiation therapy using planning MDCT images. Med Phys. 2010;37:5395‐5406. [DOI] [PubMed] [Google Scholar]
- 30. Park Y‐K, Winey B, Sharp G. Proton dose calculation on scatter‐corrected CBCT image: feasibility study for adaptive proton therapy. Med Phys. 2015;42:4449‐4459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Zhou W, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13(4):600‐612. [DOI] [PubMed] [Google Scholar]
- 32. Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297‐302. [Google Scholar]
- 33. Drzymala RE, Mohan R, Brewster L, et al. Dose‐volume histograms. Int J Radiat Oncol Biol Phys. 1991;21(1):71‐78. [DOI] [PubMed] [Google Scholar]
- 34. Low D, Harms W, Mutic S, Purdy J. A technique for the quantitative evaluation of dose distributions. Med Phys. 1998;25(5):656‐661. [DOI] [PubMed] [Google Scholar]
- 35. Harms J, Lei Y, Wang T, et al. Paired cycle‐GAN‐based image correction for quantitative cone‐beam computed tomography. Med Phys (Lancaster). 2019;46(9):3998‐4009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Kida S, Kaji S, Nawa K, et al. Visual enhancement of cone‐beam CT by use of CycleGAN. Med Phys. 2019;47(3):998‐1010. [DOI] [PubMed] [Google Scholar]
- 37. Kurz C, Maspero M, Savenije MHF, et al. CBCT correction using a cycle‐consistent generative adversarial network and unpaired training to enable photon and proton dose calculation. Phys Med Biol. 2019;64(22):225004‐225004. [DOI] [PubMed] [Google Scholar]
- 38. Lei Y, Wang T, Harms J, et al. Image quality improvement in cone‐beam CT using deep learning. Proceedings of SPIE – The International Society for Optical Engineering. 2019. 10.1117/12.2512545:78 [DOI] [PMC free article] [PubMed]
- 39. Liang X, Chen L, Nguyen D, et al. Generating synthesized computed tomography (CT) from cone‐beam computed tomography (CBCT) using CycleGAN for adaptive radiation therapy. Phys Med Biol. 2019;64(12):125002‐125002. [DOI] [PubMed] [Google Scholar]
- 40. Eckl M, Hoppen L, Sarria G, et al. Evaluation of a cycle‐generative adversarial network‐based cone‐beam CT to synthetic CT conversion algorithm for adaptive radiation therapy. Physica Med. 2020;80:308‐316. [DOI] [PubMed] [Google Scholar]
- 41. Liu Y, Lei Y, Wang T, et al. CBCT‐based synthetic CT generation using deep‐attention CycleGAN for pancreatic adaptive radiotherapy. Med Phys. 2020;47(6):2472‐2483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Maspero M, Houweling A, Savenije M, et al. A single neural network for cone‐beam computed tomography‐based radiotherapy of head‐and‐neck, lung and breast cancer. Phys Imaging Radiat Oncol. 2020;14:24‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Park S, Ye JC. Unsupervised cone‐beam artifact removal using CycleGAN and spectral blending for adaptive radiotherapy. Paper presented at: 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI). 2020.
- 44. Tien H‐J, Yang H‐C, Shueng P‐W, Chen J‐C. Cone‐beam CT image quality improvement using Cycle‐Deblur consistent adversarial networks (Cycle‐Deblur GAN) for chest CT imaging in breast cancer patients. Sci Rep. 2021;11:1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Uh J, Wang C, Acharya S, Krasin MJ, Hua C‐h. Training a deep neural network coping with diversities in abdominal and pelvic images of children and young adults for CBCT‐based adaptive proton therapy. Radiother Oncol. 2021;160:250‐258. [DOI] [PubMed] [Google Scholar]
- 46. Zhao J, Chen Z, Wang J, et al. MV CBCT‐based synthetic CT generation using a deep learning method for rectal cancer adaptive radiotherapy. Front Oncol. 2021;11:655325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Sun H, Fan R, Li C, et al. Imaging study of pseudo‐CT synthesized from cone‐beam CT based on 3D CycleGAN in radiotherapy. Front Oncol. 2021;11:603844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Qiu RLJ, Lei Y, Shelton J, et al. Deep learning‐based thoracic CBCT correction with histogram matching. Biomed Phys Eng Express. 2021;7(6):65040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Gao L, Xie K, Wu X, et al. Generating synthetic CT from low‐dose cone‐beam CT by using generative adversarial networks for adaptive radiotherapy. Radiat Oncol (London, England). 2021;16(1):1‐202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Dong G, Zhang C, Liang X, et al. A deep unsupervised learning model for artifact correction of pelvis cone‐beam CT. Front Oncol. 2021;11:686875‐686875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Dai Z, Zhang Y, Zhu L, et al. Geometric and dosimetric evaluation of deep learning‐based automatic delineation on CBCT‐synthesized CT and planning CT for breast cancer adaptive radiotherapy: a multi‐institutional study. Front Oncol. 2021;11:725507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Lemus OMD, Wang Y‐F, Li F, et al. Dosimetric assessment of patient dose calculation on a deep learning‐based synthesized computed tomography image for adaptive radiotherapy. J Appl Clin Med Phys. 2022:e13595. 10.1002/acm2.13595:e13595-e13595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Kida S, Nakamoto T, Nakano M, et al. Cone beam computed tomography image quality improvement using a deep convolutional neural network. Curēus. 2018;10(4):e2548‐e2548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Chen L, Liang X, Shen C, Jiang S, Jing W. Synthetic CT generation from CBCT images via deep learning. Med Phys. 2019;47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Li Y, Zhu J, Liu Z, et al. A preliminary study of using a deep convolution neural network to generate synthesized CT images based on CBCT for adaptive radiotherapy of nasopharyngeal carcinoma. Phys Med Biol. 2019;64(14):145010. [DOI] [PubMed] [Google Scholar]
- 56. Thummerer A, Jong B, Zaffino P, et al. Comparison of the suitability of CBCT‐ and MR‐based synthetic CTs for daily adaptive proton therapy in head and neck patients. Phys Med Biol. 2020;65:235036. [DOI] [PubMed] [Google Scholar]
- 57. Thummerer A, Zaffino P, Meijers A, et al. Comparison of CBCT based synthetic CT methods suitable for proton dose calculations in adaptive proton therapy. Phys Med Biol. 2020;65:095002. [DOI] [PubMed] [Google Scholar]
- 58. Yuan N, Dyer B, Rao S, et al. Convolutional neural network enhancement of fast‐scan low‐dose cone‐beam CT images for head and neck radiotherapy. Phys Med Biol. 2020;65(3):035003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Thummerer A, Oria CS, Zaffino P, et al. Clinical suitability of deep learning based synthetic CTs for adaptive proton therapy of lung cancer. Med Phys (Lancaster). 2021;48(12):7673‐7684. 10.1002/mp.15333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Rossi M, Cerveri P. Comparison of supervised and unsupervised approaches for the generation of synthetic CT from cone‐beam CT. Diagnostics (Basel). 2021;11(8):1435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Barateau A, De Crevoisier R, Largent A, et al. Comparison of CBCT‐based dose calculation methods in head and neck cancer radiotherapy: from Hounsfield unit to density calibration curve to deep learning. Med Phys (Lancaster). 2020;47(10):4683‐4693. [DOI] [PubMed] [Google Scholar]
- 62. Xie S, Yang C, Zhang Z, Li H. Scatter artifacts removal using learning‐based method for CBCT in IGRT system. IEEE Access. 2018;6:78031‐78037. [Google Scholar]
- 63. Xie S, Liang Y, Yang T, Song Z. Contextual loss based artifact removal method on CBCT image. J Appl Clin Med Phys. 2020;21(12):166‐177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Wu W, Qu J, Cai J, Yang R. Multiresolution residual deep neural network for improving pelvic CBCT image quality. Med Phys (Lancaster). 2022;49(3):1522‐1534. [DOI] [PubMed] [Google Scholar]
- 65. Hang Z, Gallo O, Frosio I, Kautz J. Loss functions for image restoration with neural networks. IEEE Trans Comput Imaging. 2017;3(1):47‐57. [Google Scholar]
- 66. Sobel I. An isotropic 3×3 image gradient operator. Presentation at Stanford AI Project 1968. 2014.
- 67. Hastie T, Tibshirani R, Wainwright M. Statistical Learning with Sparsity: The Lasso and Generalizations. New York: Chapman and Hall/CRC. 2015; 22‐22. 10.5555/2834535 [DOI] [Google Scholar]
- 68. Zhou W, Bovik AC. Mean squared error: love it or leave it? A new look at signal fidelity measures. IEEE Signal Process Mag. 2009;26(1):98‐117. [Google Scholar]
- 69. Salimans T, Goodfellow I, Zaremba W, Cheung V, Radford A, Chen X. Improved techniques for training GANs. Proceedings of the 30th International Conference on Neural Information Processing Systems . 2016; 2234‐2242. 10.5555/3157096.3157346 [DOI]
- 70. Gatys LA, Ecker AS, Bethge M. Image Style Transfer Using Convolutional Neural Networks. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) . 2016; 2414‐2423. 10.1109/CVPR.2016.265 [DOI]
- 71. Johnson J, Alahi A, Fei‐Fei L. Perceptual Losses for Real‐Time Style Transfer and Super‐Resolution. Springer International Publishing; 2016:694‐711. 10.1007/978-3-319-46475-6_43 [DOI] [Google Scholar]
- 72. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. Paper presented at: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 12/10, 2015.
- 73. Hansen DC, Landry G, Kamp F, et al. ScatterNet: a convolutional neural network for cone‐beam CT intensity correction. Med Phys (Lancaster). 2018;45(11):4916‐4926. [DOI] [PubMed] [Google Scholar]
- 74. Jiang Y, Yang C, Yang P, et al. Scatter correction of cone‐beam CT using a deep residual convolution neural network (DRCNN). Phys Med Biol. 2019;64(14):145003‐145003. [DOI] [PubMed] [Google Scholar]
- 75. Landry G, Hansen D, Kamp F, et al. Comparing Unet training with three different datasets to correct CBCT images for prostate radiotherapy dose calculations. Phys Med Biol. 2019;64(3):035011. [DOI] [PubMed] [Google Scholar]
- 76. Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions. Paper presented at: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 09/16, 2014.
- 77. Oktay O, Schlemper J, Folgoc L, et al. Attention U‐Net: learning where to look for the pancreas. ArXiv. 2018. doi: arXiv:1804.03999v3. [Google Scholar]
- 78. Shorten C, Khoshgoftaar TM. A survey on image data augmentation for deep learning. J Big Data. 2019;6(1):1‐48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Nomura Y, Xu Q, Shirato H, Shimizu S, Xing L. Projection‐domain scatter correction for cone beam computed tomography using a residual convolutional neural network. Med Phys. 2019;46:3142‐3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Lalonde A, Winey B, Verburg J, Paganetti H, Sharp G. Evaluation of CBCT scatter correction using deep convolutional neural networks for head and neck adaptive proton therapy. Phys Med Biol. 2020;65:245022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Rusanov B, Ebert MA, Mukwada G, Hassan GM, Sabet M. A convolutional neural network for estimating cone‐beam CT intensity deviations from virtual CT projections. Phys Med Biol. 2021;66(21):215007. [DOI] [PubMed] [Google Scholar]
- 82. Sun M, Star‐Lack JM. Improved scatter correction using adaptive scatter kernel superposition. Phys Med Biol. 2010;55(22):6695‐6720. [DOI] [PubMed] [Google Scholar]
- 83. Andersen A, Park Y‐K, Elstrøm U, et al. Evaluation of an a priori scatter correction algorithm for cone‐beam computed tomography based range and dose calculations in proton therapy. Phys Imaging Radiat Oncol. 2020;16:89‐94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Bylund K, Bayouth J, Smith M, Hass A, S Bhatia, Buatti J. Analysis of interfraction prostate motion using megavoltage cone beam computed tomography. Int J Radiat Oncol Biol Phys. 2008;72:949‐956. [DOI] [PubMed] [Google Scholar]
- 85. Hoegen P, Lang C, Akbaba S, et al. Cone‐beam‐CT guided adaptive radiotherapy for locally advanced non‐small cell lung cancer enables quality assurance and superior sparing of healthy lung. Front Oncol. 2020;10:564857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Huang T‐C, Chou K‐T, Yang S‐N, Chang C‐K, Liang J‐A, Zhang G. Fractionated changes in prostate cancer radiotherapy using cone‐beam computed tomography. Med Dosim. 2015;40:222‐225. [DOI] [PubMed] [Google Scholar]
- 87. Tanaka O, Seike K, Taniguchi T, Ono K, Matsuo M. Investigation of the changes in the prostate, bladder, and rectal wall sizes during external beam radiotherapy. Rep Pract Oncol Radiother. 2019;24:204‐207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Liao H, Lin W‐A, Zhou SK, Luo J. ADN: artifact disentanglement network for unsupervised metal artifact reduction. IEEE Trans Med Imaging. 2020;39(3):634‐643. [DOI] [PubMed] [Google Scholar]
- 89. Zhao Y, Wu R, Dong H. Unpaired Image‐to‐Image Translation Using Adversarial Consistency Loss. Springer International Publishing; 2020:800‐815. 10.1007/978-3-030-58545-7_46 [DOI] [Google Scholar]
- 90. Alotaibi A. Deep generative adversarial networks for image‐to‐image translation: a review. Symmetry (Basel). 2020;12(10):1705. [Google Scholar]
- 91. Pang Y, Lin J, Qin T, Chen Z. Image‐to‐image translation: methods and applications. IEEE Trans Multimedia. 2021. 10.1109/TMM.2021.3109419:1-1 [DOI] [Google Scholar]
- 92. Saxena S, Teli MN. Comparison and Analysis of Image‐to‐Image Generative Adversarial Networks: A Survey. ArXiv. 2021. 10.48550/arXiv.2112.12625 [DOI]
- 93. Nilsson J, Akenine‐Möller T. Understanding SSIM. ArXiv. 2020. doi: arXiv:2006.13846v2 [Google Scholar]
- 94. Heusel M, Ramsauer H, Unterthiner T, Nessler B, Hochreiter S. GANs trained by a two time‐scale update rule converge to a local nash equilibrium. Proceedings of the 31st International Conference on Neural Information Processing Systems. 2017;6629‐6640. 10.5555/3295222.3295408 [DOI] [Google Scholar]
- 95. Zhang R, Isola P, Efros AA, Shechtman E, Wang O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. ArXiv. 2018. 10.48550/arXiv.1801.03924 [DOI]
- 96. Ding K, Ma K, Wang S, Simoncelli EP. Image quality assessment: unifying structure and texture similarity. IEEE Trans Pattern Anal Mach Intell. 2022;44(5):2567‐2581. [DOI] [PubMed] [Google Scholar]
- 97. Dosovitskiy A, Beyer L, Kolesnikov A, et al. An Image Is Worth 16×16 Words: Transformers for Image Recognition at Scale. ArXiv. 2020. 10.48550/arXiv.2010.11929 [DOI]
- 98. Chen J, Lu Y, Yu Q, et al. TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation. ArXiv. 2021. 10.48550/arXiv.2102.04306 [DOI]
- 99. Dalmaz O, Yurt M, Çukur T. ResViT: residual vision transformers for multi‐modal medical image synthesis. IEEE Trans Med Imaging. 2022. 10.1109/TMI.2022.3167808 [DOI] [PubMed] [Google Scholar]
- 100. Neubauer A, Li HB, Wendt J, et al. Efficient claustrum segmentation in T2‐weighted neonatal brain MRI using transfer learning from adult scans. Clin Neuroradiol (Munich). 2022. 10.1007/s00062-021-01137-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Bardis M, Houshyar R, Chantaduly C, et al. Deep learning with limited data: organ segmentation performance by U‐Net. Electronics (Basel). 2020;9(8):1199. [Google Scholar]
- 102. Jafarian K, Vahdat V, Salehi S, Mobin M. Automating detection and localization of myocardial infarction using shallow and end‐to‐end deep neural networks. Appl Soft Comput. 2020;93:106383. [Google Scholar]
- 103. Schouten JPE, Matek C, Jacobs LFP, Buck MC, Bosnacki D, Marr C. Tens of images can suffice to train neural networks for malignant leukocyte detection. Sci Rep. 2021;11(1):7995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Cho J, Lee K, Shin E, Choy G, Do S. How Much Data Is Needed to Train a Medical Image Deep Learning System to Achieve Necessary High Accuracy?. ArXiv 2015. 10.48550/arXiv.1511.06348 [DOI]
- 105. Lu K, Ren L, Yin F‐F. A geometry‐guided deep learning technique for CBCT reconstruction. Phys Med Biol. 2021;66(15):15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106. Dai X, Bai J, Liu T, Xie L. Limited‐view cone‐beam CT reconstruction based on an adversarial autoencoder network with joint loss. IEEE Access. 2019;7:7104‐7116. [Google Scholar]
- 107. Wurfl T, Hoffmann M, Christlein V, et al. Deep learning computed tomography: learning projection‐domain weights from image domain in limited angle problems. IEEE Trans Med Imaging. 2018;37(6):1454‐1463. [DOI] [PubMed] [Google Scholar]
- 108. Yang H‐K, Liang K‐C, Kang K‐J, Xing Y‐X. Slice‐wise reconstruction for low‐dose cone‐beam CT using a deep residual convolutional neural network. Nucl Sci Tech. 2019;30(4):59. [Google Scholar]
- 109. Chen G, Hong X, Ding Q, et al. AirNet: fused analytical and iterative reconstruction with deep neural network regularization for sparse‐data CT. Med Phys (Lancaster). 2020;47(7):2916‐2930. [DOI] [PubMed] [Google Scholar]
- 110. Li Y, Li K, Zhang C, Montoya J, Chen G‐H. Learning to reconstruct computed tomography images directly from sinogram data under a variety of data acquisition conditions. IEEE Trans Med Imaging. 2019;38(10):2469‐2481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Gupta H, Kyong Hwan J, Nguyen HQ, McCann MT, Unser M. CNN‐based projected gradient descent for consistent CT image reconstruction. IEEE Trans Med Imaging. 2018;37(6):1440‐1453. [DOI] [PubMed] [Google Scholar]
- 112. Feldkamp LA, Davis LC, Kress JW. Practical cone‐beam algorithm. J Opt Soc Am A Opt Image Sci Vis. 1984;1(6):612. [Google Scholar]
- 113. Chen B, Xiang K, Gong Z, Wang J, Tan S. Statistical iterative CBCT reconstruction based on neural network. IEEE Trans Med Imaging. 2018;37(6):1511‐1521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114. Wang Y, Yang J, Yin W, Zhang Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J Imag Sci. 2008;1(3):248‐272. [Google Scholar]
- 115. Han Y, Kim J, Ye JC. Differentiated backprojection domain deep learning for conebeam artifact removal. IEEE Trans Med Imaging. 2020;39(11):3571‐3582. [DOI] [PubMed] [Google Scholar]
- 116. Lee M, Han Y, Ward JP, Unser M, Ye JC. Interior tomography using 1D generalized total variation. Part II: Multiscale implementation. SIAM J Imag Sci. 2015;8(4):2452‐2486. [Google Scholar]
- 117. Miften M, Olch A, Mihailidis D, et al. Tolerance limits and methodologies for IMRT measurement‐based verification QA: recommendations of AAPM Task Group No. 218. Med Phys. 2018;45(4):e53‐e83. [DOI] [PubMed] [Google Scholar]
- 118. Gourdeau D, Duchesne S, Archambault L. On the proper use of structural similarity for the robust evaluation of medical image synthesis models. Med Phys (Lancaster). 2022;49(4):2462‐2474. [DOI] [PubMed] [Google Scholar]
- 119. Liesbeth V, Michaël C, Dinkla A, et al. Overview of artificial intelligence‐based applications in radiotherapy: recommendations for implementation and quality assurance. Radiother Oncol. 2020;153:55‐66. [DOI] [PubMed] [Google Scholar]
- 120. Oria CS, Thummerer A, Free J, et al. Range probing as a quality control tool for CBCT‐based synthetic CTs: in vivo application for head and neck cancer patients. Med Phys. 2021;48(8):4498‐4505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Elstrøm UV, Wysocka BA, Muren LP, Petersen JBB, Grau C. Daily kV cone‐beam CT and deformable image registration as a method for studying dosimetric consequences of anatomic changes in adaptive IMRT of head and neck cancer. Acta Oncol. 2010;49(7):1101‐1108. [DOI] [PubMed] [Google Scholar]
- 122. Ayyalusamy A, Vellaiyan S, Shanmugam S, et al. Feasibility of offline head & neck adaptive radiotherapy using deformed planning CT electron density mapping on weekly cone beam computed tomography. Br J Radiol. 2017;90(1069):20160420‐20160420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Hay LK, Paterson C, McLoone P, et al. Analysis of dose using CBCT and synthetic CT during head and neck radiotherapy: a single centre feasibility study. Tech Innovations Patient Support Radiat Oncol. 2020;14:21‐29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124. Casati M, Piffer S, Calusi S, et al. Clinical validation of an automatic atlas‐based segmentation tool for male pelvis CT images. J Appl Clin Med Phys. 2022;23(3):e13507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Dai X, Lei Y, Wynne J, et al. Synthetic CT‐aided multiorgan segmentation for CBCT‐guided adaptive pancreatic radiotherapy. Med Phys (Lancaster). 2021;48(11):7063‐7073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Janopaul‐Naylor J, Lei Y, Liu Y, et al. Synthetic CT‐aided online CBCT multi‐organ segmentation for CBCT‐guided adaptive radiotherapy of pancreatic cancer. Int J Radiat Oncol Biol Phys. 2020;108(3):S7‐S8. [Google Scholar]
- 127. Eckl M, Sarria GR, Springer S, et al. Dosimetric benefits of daily treatment plan adaptation for prostate cancer stereotactic body radiotherapy. Radiat Oncol (London, England). 2021;16(1):1‐145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Archambault Y, Boylan C, Bullock D, et al. Making on‐line adaptive radiotherapy possible using artificial intelligence and machine learning for efficient daily re‐planning. Med Phys Intl J. 2020;8(2):77‐86. [Google Scholar]
- 129. Byrne M, Archibald‐Heeren B, Hu Y, et al. Varian ethos online adaptive radiotherapy for prostate cancer: early results of contouring accuracy, treatment plan quality, and treatment time. J Appl Clin Med Phys. 2022;23(1):e13479. [DOI] [PMC free article] [PubMed] [Google Scholar]


