Multimodal imaging shows fibrosis architecture and action potential dispersion are predictors of arrhythmic risk in spontaneous hypertensive rats

Abstract

Abstract

Hypertensive heart disease (HHD) increases risk of ventricular tachycardia (VT) and ventricular fibrillation (VF). The roles of structural vs. electrophysiological remodelling and age vs. disease progression are not fully understood. This cross‐sectional study of cardiac alterations through HHD investigates mechanistic contributions to VT/VF risk. Risk was electrically assessed in Langendorff‐perfused, spontaneously hypertensive rat hearts at 6, 12 and 18 months, and paced optical membrane voltage maps were acquired from the left ventricular (LV) free wall epicardium. Distributions of LV patchy fibrosis and 3D cellular architecture in representative anterior LV mid‐wall regions were quantified from macroscopic and microscopic fluorescence images of optically cleared tissue. Imaging showed increased fibrosis from 6 months, particularly in the inner LV free wall. Myocyte cross‐section increased at 12 months, while inter‐myocyte connections reduced markedly with fibrosis. Conduction velocity decreased from 12 months, especially transverse to the myofibre direction, with rate‐dependent anisotropy at 12 and 18 months, but not earlier. Action potential duration (APD) increased when clustered by age, as did APD dispersion at 12 and 18 months. Among 10 structural, functional and age variables, the most reliably linked were VT/VF risk, general LV fibrosis, a measure quantifying patchy fibrosis, and non‐age clustered APD dispersion. VT/VF risk related to a quantified measure of patchy fibrosis, but age did not factor strongly. The findings are consistent with the notion that VT/VF risk is associated with rate‐dependent repolarization heterogeneity caused by structural remodelling and reduced lateral electrical coupling between LV myocytes, providing a substrate for heterogeneous intramural activation as HHD progresses.

Key points

• There is heightened arrhythmic risk with progression of hypertensive heart disease.

• Risk is related to increasing left ventricular fibrosis, but the nature of this relationship has not been quantified.

• This study is a novel systematic characterization of changes in active electrical properties and fibrotic remodelling during progression of hypertensive heart disease in a well‐established animal disease model.

• Arrhythmic risk is predicted by several left ventricular measures, in particular fibrosis quantity and structure, and epicardial action potential duration dispersion.

• Age alone is not a good predictor of risk.

• An improved understanding of links between arrhythmic risk and fibrotic architectures in progressive hypertensive heart disease aids better interpretation of late gadolinium‐enhanced cardiac magnetic resonance imaging and electrical mapping signals.

Abstract figure legend Structure and function variables are extracted from spontaneously hypertensive rat (SHR) hearts using multiple recording and imaging modalities. Analysis shows that arrhythmic risk is reliably linked to fibrotic structure and the variability of action potential duration. Graphic created with BioRender.com.

Introduction

Heart failure (HF) is a leading cause of death and dysfunction worldwide and, despite improvements in treatment, long‐term prognosis remains poor (Savarese & Lund, 2017). Hypertensive heart disease (HHD) is an increasingly common cause of HF (Di Palo & Barone, 2020; Roth et al., 2017) and is characterized by extensive structural remodelling at the tissue level including marked hypertrophy of left ventricular (LV) muscle cells and increasing interstitial fibrosis, as well as myocyte disruption, necrosis and replacement or patchy fibrosis (Drazner, 2011). These changes compromise LV diastolic function, and the heart may progress to decompensated HF (Drazner, 2011; Rodrigues et al., 2016). HHD is also associated with ECG changes (Devereux & Reichek, 1982), increased susceptibility to ventricular tachycardia (VT) and ventricular fibrillation (VF), and sudden cardiac death (Devereux & Reichek, 1982; Verdecchia et al., 2019).

Myocardial fibrosis is widely viewed as a predictor of arrhythmic risk in heart disease (de Jong et al., 2011) and is linked with early afterdepolarizations that initiate and mediate VT/VF (Karagueuzian et al, 2013). Interstitial fibrosis may slow conduction via myocyte–fibroblast interactions (Miragoli et al., 2006) and indirect pathways (de Jong et al., 2011). Patchy fibrosis provides a source and substrate for re‐entrant activation by promoting tortuous conduction (de Bakker et al., 1993), focal delay and rate‐dependent conduction block (Smaill et al., 2013). Ageing is associated with interstitial rather than patchy fibrosis in animal models (de Jong et al., 2011). HHD has direct effects on cellular electrophysiology with ventricular myocyte hypertrophy consistently associated with prolongation of action potential duration (APD) (Brooksby et al., 1993; Clauss et al., 2019), while action potential kinetics in hypertension are modulated by changes in intracellular calcium handling (Cerbai et al., 1994). To date, the relative importance of electrical and structural remodelling to arrhythmogenesis in HHD and their contribution to VT/VF risk during the progression of this disease have not been comprehensively studied.

The spontaneously hypertensive rat (SHR) is a well‐established animal model that replicates key end‐points in the progression of human HHD (Saito et al., 1984), and it has been used extensively to investigate LV structural remodelling and mechanical dysfunction in chronic hypertension (Brooksby et al., 1993; Herrmann et al., 1995). Structural remodelling, particularly patchy fibrosis, electrical remodelling and VT/VF risk are all significantly different in SHRs compared to age‐matched normotensive rats from around 6 months (Chan et al., 2011; Herrmann et al., 1995; LeGrice et al., 2012; Nguyen et al., 2016; Sung et al., 2020; Tribulova et al., 2003).

Here, we present a cross‐sectional study relating VT/VF risk to structural and electrophysiological remodelling as HHD progresses in the SHR, prior to the development of end‐state HF. To achieve this, independent measures of two electrical activity signals and two image‐based structural features at multiple scales were used. These measures enable a new multimodal view of mechanisms contributing to VT/VF risk in this context.

Methods

Ethical approval

All procedures adhered to the guidelines of the University of Auckland Animal Ethics Committee under Project AEC 001602 and conform to the Guide for the Care and Use of Laboratory Animals (NIH publication No. 85‐23). The authors understand the ethical principles of The Journal of Physiology and this work complies with their policies.

Experimental protocol

This cross‐sectional study used SHRs (Harlan Laboratories, Indianapolis, IN, USA), weighed weekly and with unrestricted access to food and water. To remove sex variations from the study only male animals were used (Pahor et al., 1991). Studies have shown no significant inter‐sex differences in APD or LV collagen fraction from 3 months in the SHR (Chan et al., 2011).

SHRs at approximately 6 (n = 6), 12 (n = 6) and 18 (n = 5) months were deeply anaesthetized with isoflurane (delivered into the chamber, 5% in O₂ at 1 litre/min) until loss of paw withdrawal reflex then euthanized by cervical dislocation. The chest cavity was opened, and heparin (0.1 ml/kg, 100 IU/kg) was injected into the LV and allowed to circulate for 30 s. Hearts were quickly excised with ascending aorta intact, immersed in cold (4°C) phosphate‐buffered saline (PBS) and Langendorff‐perfused at a constant flow rate with carbogenated modified Krebs–Henseleit solution (in mM: NaCl 118, KCl 4.75, MgSO₄ 1.18, KH₂PO₄ 1.18, NaHCO₃ 24.8, glucose 10, CaCl₂ 2.5) until steady sinus rhythm was established. Two 10 mM boluses of the membrane potential‐sensitive dye Di‐4‐ANEPPS (15 μl of stock solution dissolved in 2 ml of carbogenated Krebs solution) were added to the perfusate 3 min apart followed by blebbistatin (12.5 μl in 15 ml of oxygenated Krebs solution). The heart was mounted in a purpose‐constructed imaging bath (Khwaounjoo et al., 2015), supported from the backplane and pressed against the glass front plane. A constant‐flow Langendorff perfusion was maintained at 37°C. The imaging bath was filled with Krebs–Henseleit solution also at 37°C. The heart was paced via a unipolar pacing electrode (2× stimulation threshold) near the equator on the mid‐anterior LV free wall epicardium. The stimulating electrode was carefully inserted through the wall from the endocardium to maintain an unobstructed optical field of view. Two electrograms were recorded from the lateral margins of the LV.

For optical mapping, the heart was excited by two arrays of light emitting diodes (LEDs) (LEDEngin, San Jose, CA, USA, LZ4‐00G110; 532 ± 15 nm) each directed through the side windows of the imaging bath. Fluorescence emission was acquired over an imaging field ∼12 × 12 mm² with a charge multiplying CCD camera (Photometrics, Tucson, AZ, USA, Cascade 128+, 64 × 64 pixels, 635 Hz) fitted with a wide aperture lens (Navitar, Ottawa, CA, NAV DO5095), a 2× close‐up lens and a 565 ± 10 nm long pass filter, giving a pixel resolution of 0.1875 mm (Khwaounjoo et al., 2015). Programmed stimulation was applied and electrograms recorded with a PowerLab 25T data acquisition system (ADInstruments, Dunedin, NZ). Hearts were paced between 3 and 12 Hz in an alternating sequence of high and low frequencies. Following capture loss, stimulation was then reduced in steps of 0.1 Hz to determine the maximum pacing frequency. Two‐second bursts of 2 ms pulse trains with increasing frequencies (×4) and amplitudes (×3) were applied until VT or VF (>15 sustained complexes on the electrogram following cessation of stimulation) was induced (Rossi et al., 2017; Yang et al., 2007). The total stimulus current, I _S (mA), was used to assign VT/VF risk index integer values from 12 (high risk: low total current) to 1 (low risk: high total current) according to the following relationship:

$$I_{\mathrm{S}}\propto \sigma \left(f\right)fV.$$

Here, σ is the local tissue conductivity (mS/mm) and a function of stimulus frequency, f is the pulse train frequency (10, 20, 50, 100 Hz) and V is the pulse amplitude (3, 5, 7.5 V). The local tissue conductivity dependence on frequency was modelled as $\sigma (f)\approx {10}^{-1.2}{f}^{0.1}$ (mS/mm) using data from Gabriel et al. (2009).

Analysis of experimental data

Instantaneous optical map signals were smoothed (Gaussian filter: 5 × 5 pixel kernel: σ = 0.5) and noise at each pixel was reduced with a low‐pass third order Savitsky–Golay filter (Savitzky & Golay, 1964). Signals from regions adjacent to the visible boundary of the ventricles (∼2 pixels) were excluded to minimize artifact introduced by surface curvature.

Activation time (AT) was found from the maximum upstroke gradient of optical APs. To estimate longitudinal and transverse conduction velocities (CV), ellipsoids were fitted to 1 ms AT isochrones between 3 and 6 ms. The CVs were determined using the average of major (longitudinal) and minor (transverse) apex‐to‐apex distances across the three isochrone pairs. Ellipsoid principal axes were assumed to coincide with subepicardial myofibre and cross myofibre directions (Caldwell et al., 2009). The anisotropy ratio (AR) is the ratio of longitudinal to transverse CV.

APD was measured as the difference between AT and the time where the optical signal amplitude returned to 30% of its peak value, that is APD70. Dispersion of APD (a measure of repolarization heterogeneity) was quantified by Annoni et al. (2015):

$$\mu =\frac{\mathrm{AP}{\mathrm{D}}_{95\mathrm{th}}-\mathrm{AP}{\mathrm{D}}_{5\mathrm{th}}}{\mathrm{AP}{\mathrm{D}}_{50\mathrm{th}}}.$$

Here APD_5th and APD_95th are the 5th and 95th percentiles of the APD distribution and APD_50th is the median across the region of interest.

Imaging and structural analysis

On completion of experiments, hearts were arrested by perfusing with St Thomas's solution and perfusion‐fixed with paraformaldehyde (PFA) (4% in PBS). Hearts were cut into short axis rings (2–3 mm thick) and immersed overnight in PFA at 4°C. Excess PFA was removed by washing with PBS and tissue was cryoprotected in 10, 20 and 30% sucrose solutions for 1 h each. Upper surfaces of each ring were levelled by cryomicrotome.

All labelling steps were conducted at room temperature on a laboratory platform rocker. Samples were blocked overnight in 10% goat serum, 0.3% Triton X‐100 in PBS (PBST) to reduce non‐specific staining and exposed to wheat germ agglutinin (WGA) (diluted 1:50 in 0.3% PBST and 5% goat serum (GS)) conjugated with AF488 (Sigma‐Aldrich, St Louis, MO, USA) to label cell membranes and extracellular matrix. WGA has previously been used to quantify fibrosis (Emde et al., 2014). Anti‐Cx43 (Thermo Fisher Scientific, Waltham, MA, USA) (diluted 1:250 in 0.3% PBST and 5% GS) conjugated with AF568 (Sigma) to label gap junction connexins. Labelled rings were left in primary antibody solution for 3 days. Subsequently, they were washed in PBS for 3 × 10 min between incubation stages to remove excess fluorescent label. The rings were dehydrated with successive 2 h washes through a graded ethanol series (25, 50, 75, 95% v/v in distilled water). They were placed in methyl salicylate to optically clear over 4 days (Fig. 1A ). This refractive index matching enabled 3D confocal microscopy imaging of cellular architecture.

Figure 1. Tissue imaging and analysis.

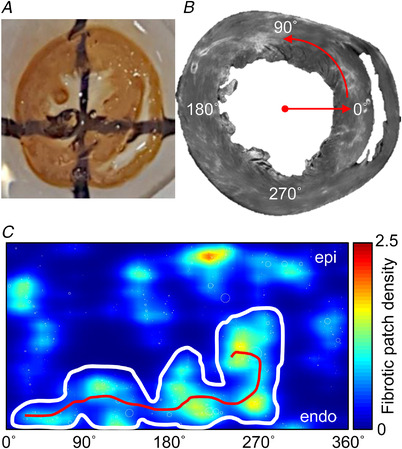
A, short axis ventricular ring (2–3 mm thick) optically cleared using methyl salicylate. Lines on the surface below indicate translucency. B, composite image of WGA fluorescence in upper surface of ventricular ring acquired using a confocal microscope (6.22 × 6.22 μm² pixels). C, patches of fibrosis from B mapped in polar coordinates and represented as a continuous distribution map. The white envelope bounds a region of aggregated fibrosis patch and the length of the skeletonization (red line) reflects the tortuosity of the region. [Colour figure can be viewed at wileyonlinelibrary.com]

Composite images of WGA fluorescence on upper surfaces of all short‐axis rings were constructed by montaging multiple images acquired with a Nikon TE2000 inverted confocal microscope system (excitation wavelength 488 nm; 4× objective: numerical aperture 0.13, working distance 16.4 mm; 6.22 × 6.22 μm² pixels). A typical image is presented in Fig. 1B . The tissue processing and imaging steps in this study were novel. To control for this, short‐axis tissue rings were excised from post‐mortem 18‐month normotensive Wistar Kyoto (WKY) rat hearts (n = 4), used for a non‐ventricular study. In that study, hearts were arrested with N‐methyl‐d‐glucamine solution, and diffusion fixed in PFA (4% in PBS). The fixed tissue was then cleared, labelled and imaged using methods identical to those described for the SHR short‐axis rings.

LV tissue, non‐tissue and fibrotic patch regions were segmented from the WGA intensity short‐axis images. Using a maximum entropy intensity filter (Zheng et al., 2017) higher intensity pixels were segmented to differentiate patches of fibrosis from the reminder of the tissue. Fibrosis density percentage was the total patch area relative to the LV area. Patch centroids were projected into polar coordinates (Fig. 1B ) and a heat map of patch densities constructed (Fig. 1C ). Aggregated regions with patch densities ≥1 were skeletonized and the region with the longest skeletonization (aggregated fibrosis patch density length (AFL)) was used as representative for that heart (an indirect measure of functional re‐entrant path length) (Fig. 1C ). The area of this region was normalized across all hearts in the study (0–1 range) to give an aggregated fibrosis patch density area (AFA) index. Additional data are available in Supporting information SI1. The AFA provides a measure of aggregated patchy fibrosis impact at scales commensurate with re‐entrant paths.

High‐resolution 3D image volumes were acquired in optically cleared tissue from representative regions of the anterior LV mid wall in each heart with a Nikon TE2000 confocal microscope. WGA was imaged at 488 nm and Cx43 at 568 nm excitation wavelengths using a ×60 oil immersion objective (numerical aperture 1.25, working distance 180 μm). The Cx43 label did not penetrate the tissue consistently, providing equivocal data unsuitable for quantitative purposes. This is attributed to the larger size of anti‐Cx43 antibody compared to WGA (Sands et al., 2022). Image stacks were typically 512 × 512 × 180 voxels with voxel dimensions 0.41 μm × 0.41 μm × 1 μm. Myocytes were segmented in 3D using ITK SNAP (Yushkevich et al., 2006). As many cells as possible were semi‐manually segmented from each image. For each complete cell (no intersection with image boundaries) the long axis through the centre of mass was found with eigenanalysis of the mask covariance matrix. Cross‐sectional area was computed by resampling the mask voxels at the centre of mass and orthogonal to the long axis and the cell volume was the sum of mask voxels. For each complete cell, adjacent cells were identified as connected when separated by not more than one image voxel (0.41 μm) (Seidel et al., 2016). Relative volumes occupied by the extracellular matrix were estimated using a Shanbhag filter in ImageJ (Rueden et al., 2017). Additional data are available in Supporting information SI1.

Statistical analysis

Between‐group differences were assessed using one‐ and two‐way ANOVA and post hoc Tukey tests. Pairwise comparisons between VT/VF risk, electrical function and structural change for each animal were made using univariate linear regression (MATLAB (The MathWorks, Natick, MA, USA) ‘fitlm’; null hypothesis: slope of linear model is zero). Data are presented as mean  ± SD and P‐values <0.05 are considered statistically significant.

Correlation and factor analysis

Sets of 10 variables were extracted from the data gathered across 12 SHRs: age, VT/VF risk, transverse CV (for pacing >5 Hz), AR (for pacing >5 Hz), APD (mean over field of view for pacing at 2.33 Hz), APD dispersion (for pacing >5 Hz), cell scale percentage fibrosis, number of adjacent cells, LV scale percentage fibrosis and AFA index. Data for each variable were normalized with mean 0 and standard deviation 1. Using the MATLAB ‘corr’ function, Pearson's linear correlation coefficients and corresponding P‐values from a Student's t‐distribution were found for all combinations. Approximate R ² values were the squared correlation coefficients. Exploratory factor analysis was used to investigate if there were emergent or latent groupings of variables into a small number of factors (Tabachnick & Fidell, 2019). Factor analysis used the MATLAB ‘factoran’ function with maximum likelihood factor extraction and promax oblique rotation. Key variables grouped in each factor were determined from scree plots of factor loadings and supported by the specific variable variance. Transformed factor scores were used to fit linear two and three factor data models. Additional data are available in Supporting information SI2.

Results

Structural remodelling

Mean LV free wall thickness in SHRs was 2.71 ± 0.48 mm (6 months), 3.18 ± 0.59 mm (12 months) and 2.60 ± 0.27 mm (18 months), but the 6−12 months and 12−18 months differences were not statistically significant (P = 0.16110 and P = 0.05340, two‐way ANOVA and post hoc Tukey test) (additional data are available in Supporting information SI3). Figure 2 shows distributions and organization of fibrosis revealed by short‐axis macroscopic imaging. Increased fibrosis density at 12 and 18 months was more marked in the LV free wall compared to interventricular septum (Fig. 2A ) and inner compared to outer LV wall (Fig. 2B ). LV fibrosis density was significantly greater at 12 and 18 months than 6 months (6 vs. 12 and 6 vs. 18 months, P = 0.03040 and 0.00280, respectively, one‐way ANOVA and post hoc Tukey test, Fig. 2C ) with no significant difference (P = 0.38080) between older cohorts. Figure 2D shows the AFA index (Fig. 1B and C ) for each cohort. Marked increases in the extent and complexity of patchy fibrosis occurred from 12 months. Measures were significantly greater at 12 and 18 months compared to 6 months (6 vs. 12 and 6 vs. 18 months, P = 0.04890 and 0.00810, respectively, one‐way ANOVA and post hoc Tukey test), but there was considerable overlap between 12‐ and 18‐month cohorts and no significant difference (P = 0.50280, one‐way ANOVA and post hoc Tukey test) between them. Imaging and analysis for 18‐month normotensive WKY rats showed no evidence of patchy fibrosis in the left ventricle (additional data are available in Supporting information SI3).

Figure 2. LV fibrosis distribution for 6 (n = 6), 12 (n = 6) and 18 (n = 5) months age groups.

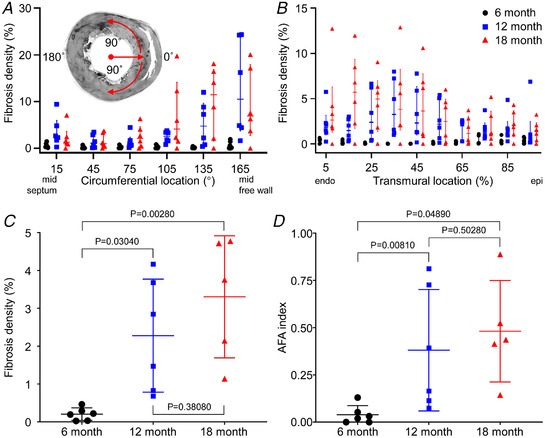
A, circumferential distributions of LV fibrosis density from mid septum to mid free wall. Data from ± angles are binned from 15° to 165°. Median and quartiles are also shown. B, transmural distributions of fibrosis density. Median and quartiles are also shown. C, fibrosis density varying with age cohort. One‐way ANOVA and post hoc Tukey test were used to calculate P‐values. D, aggregated fibrosis patch density area (AFA) index at 6, 12 and 18 months. One‐way ANOVA and post hoc Tukey test were used to calculate P‐values. [Colour figure can be viewed at wileyonlinelibrary.com]

High resolution 3D images of selected LV regions in SHRs showed changes in myocardial structure characteristic of the progression of HHD. These are illustrated in representative image volumes (Fig. 3A ) from 6‐, 12‐ and 18‐month SHRs, labelled with WGA (green). Auto‐fluorescence and orientation of the cell axes relative to the imaging plane varied across the image sets. This altered the contrast between myocytes and extracellular space, while the point‐spread function of the microscope objective (Sands et al., 2022) was anisotropic with 2−3 times better resolution in the imaging plane than transverse to it. At 12 months (Fig. 3A , middle panel), cell hypertrophy was evident with substantial increases in myocyte cross‐sectional area. The extracellular matrix surrounding individual cells thickened, as did perimysial connective tissue around groups of cells which appeared to be heavily cross‐linked. Fibrosis was markedly increased at 18 months (Fig. 3A , right panel) and in this example replaced substantial numbers of myocytes. Individual cells could be reliably segmented from 3D images and their morphology quantified (Fig. 3B ). While the extent and type of fibrosis varied within and between age‐group cohorts, particularly at 12 months, increases in myocyte cross‐sectional area between 6 and 12 months were consistent and significant (P = 0.00260, one‐way ANOVA and post hoc Tukey test) with no further change at 18 months (Table 1). In Fig. 3C , distributions of connected adjacent myocytes for each 3D image are plotted as a function of percentage fibrosis volume. While there is little evident difference in the number of adjacent myocytes associated with mid wall myocytes at 6 and 12 months, there was a significant inverse linear relationship between this measure and fibrosis volume (R ² = 0.69, P = 0.00060, linear regression, F‐statistic). This indicates that proximity connections between adjacent myocytes decreased with increased fibrosis (apparent in the sample images in Fig. 3A ). Additional data are available in Supporting information SI1.

Figure 3. Changes in LV mid wall 3D microstructure.

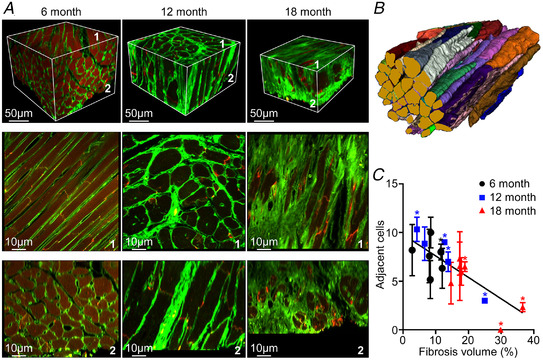
A, representative images from cleared tissue specimens from anterior LV mid wall labelled with WGA (green) at 6, 12 and 18 months. The dull red at 6 months is due to background auto‐fluorescence. The upper panel presents volume‐rendered 3D images, while the lower panels show mid‐block longitudinal and cross‐sectional image planes parallel to surfaces 1 and 2. B, segmented myocytes from 6 month SHR. C, connected adjacent cells as a function of 3D fibrosis density. Data for n = 39, 15 and 28 selected cells are presented as means ± SD at 6, 12 and 18 months, respectively. *Three selected myocytes. For best‐fit regression line shown, R ² = 0.692 and P = 0.00060 (linear regression, F‐statistic). [Colour figure can be viewed at wileyonlinelibrary.com]

Table 1.

Changes in mid wall LV myocyte geometry

	6 months (n = 39)	12 months (n = 15)	18 months (n = 28)
Length (μm)	153 ± 49	137 ± 38	142 ± 40
Cross‐section area (μm2)	300 ± 115	456 ± 135	466 ± 193
Volume (102 μm3)	377 ± 244	492 ± 225	528 ± 336

Data are presented as means ± SD. The significance of differences in cross‐section area are: 6 vs. 12 months P = 0.00260, 6 vs. 18 months P = 0.00100, 12 vs. 18 months P = 0.38080 (one‐way ANOVA, post hoc Tukey test).

Electrical remodelling

Data clustered by age cohort showed altered epicardial activation spread from focal stimuli (Fig. 4). In Fig. 4A , representative AT maps are given for 6‐, 12‐ and 18‐month‐old SHRs paced at a base cycle length (BCL) of 140 ms. They show slower and more anisotropic activation spread in the two older animal groups. In Fig. 4B and C longitudinal and transverse CV are plotted as functions of diastolic interval (DI). Both were significantly greater at 6 months than at 12 and 18 months across all stimulus rates (P = 0.00001 in both cases, two‐way ANOVA and post hoc Tukey test), but there was no significant difference (P = 0.08000 and 0.05390 for longitudinal and transverse CV respectively, two‐way ANOVA and post hoc Tukey test) between the older animals. Longitudinal and transverse CV decreased progressively in the range DI <150 ms at all ages and there was a rate‐dependent reduction in transverse CV relative to longitudinal CV at 12 and 18 months though not at 6 months. This is reflected in Fig. 4D . AR was greater for all stimulus rates at 12 and 18 months, compared to 6 months. In both of the older SHR groups, AR also increased linearly as DI was reduced, with no significant difference (P = 0.99900, two‐way ANOVA and post hoc Tukey test) between the older groups). Additional data are available in Supporting information SI4.

Figure 4. Variation of epicardial conduction with diastolic interval (DI).

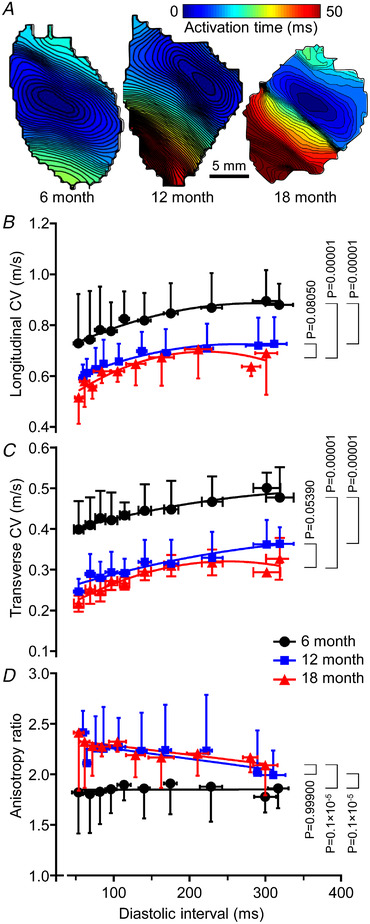
A, representative activation time maps for 6, 12 and 18 months at a base cycle length of 140 ms. B, longitudinal CV (in the direction of most rapid activation) at 6 months (44 measurements from five animals), 12 months (44 measurements from five animals) and 18 months (46 measurements from five animals). Two‐way ANOVA and post hoc Tukey test were used to calculate P‐values. C, transverse CV (in the direction of least rapid activation) at 6 months (44 measurements from five animals), 12 months (44 measurements from five animals) and 18 months (46 measurements from five animals). Two‐way ANOVA and post hoc Tukey test were used to calculate P‐values. D, anisotropy ratio (ratio of the means of longitudinal/transverse velocities) as functions of DI at 6 months (44 measurements from five animals), 12 months (44 measurements from five animals) and 18 months (46 measurements from five animals). Two‐way ANOVA and post hoc Tukey test were used to calculate P‐values. [Colour figure can be viewed at wileyonlinelibrary.com]

Beat‐to‐beat alternation of action potential amplitude and AT was observed at high stimulus rates (additional data are available in Supporting information SI4). The magnitude of these alternans rhythms was greatest at stimulus rates just below those at which block, conduction failure and VT occurred. The incidence of alternans increased with age and was more likely to be spatially discordant transverse to the direction of most rapid initial activation (discordant action potential amplitude and AT alternans occurred in 1/3, 2/6 and 3/5 SHRs and exhibited alternans at 6, 12 and 18 months, respectively).

Figure 5 summarizes the effects of cohort clustering and stimulus rate on APD. Representative APD70 maps at a BCL of 140 ms for 6‐, 12‐ and 18‐month‐old SHRs (Fig. 5A ) showed increasing APD and considerable APD variation across the mapping field in the 18‐month‐old example. These individual observations are reinforced in Fig. 5B and C where APD and APD dispersion are presented as functions of DI for the three age cohorts. APD increased with DI for all age groups and, for each DI, was progressively greater at 6, 12 and 18 months (P = 0.04270, 0.00010, 0.00270, for 6 vs. 12, 6 vs. 18 and 12 to 18, respectively, two‐way ANOVA and post hoc Tukey test). APD dispersion was greater at 12 months and 18 months than at 6 months (P = 0.00010 for both cases, two‐way ANOVA and post hoc Tukey test). Moreover, while there was little change in APD dispersion with stimulus rate in 6‐month‐old SHRs, there was a substantial and progressive increase at both 12 and 18 months in the range DI <150 ms. There was no significant difference (P = 0.87970, two‐way ANOVA and post hoc Tukey test) in APD dispersion between 12 and 18 months. Additional data are available in Supporting information SI4.

Figure 5. Variation of epicardial action potential duration (APD) with diastolic interval (DI).

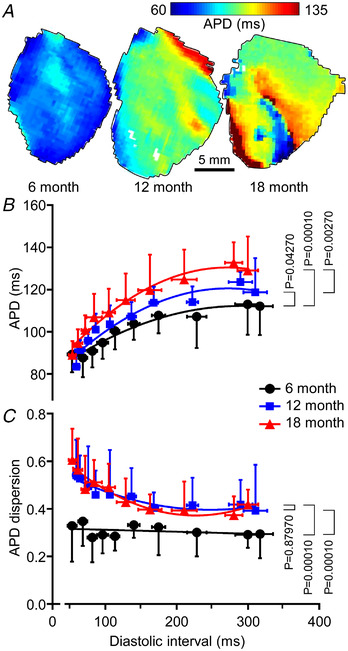
A, representative APD maps for 6, 12 and 18 months at a base cycle length of 140 ms. B, APD as a function of DI for the three age cohorts at 6 months (45 measurements from five animals), 12 months (45 measurements from five animals) and 18 months (46 measurements from five animals). Two‐way ANOVA and post hoc Tukey test were used to calculate P‐values. C, APD dispersion as functions of DI at 6 months (45 measurements from five animals), 12 months (45 measurements from five animals) and 18 months (46 measurements from five animals). Two‐way ANOVA and post hoc Tukey test were used to calculate P‐values. [Colour figure can be viewed at wileyonlinelibrary.com]

VT/VF risk and progression of HHD

Arrhythmia was induced in all SHRs. Compared to 6 months, arrhythmia duration was longer in 5/6 12‐month and 5/5 18‐month SHRs. Arrhythmia duration in 18‐month SHRs clustered into a shorter duration group (6.7–12.9 s compared to 2.4–17.3 s for 12 months) and a longer duration group (87–94.9 s) (additional data are available in Supporting information SI4). The effects of HHD progression on VT/VF risk are presented in Fig. 6. VT/VF risk (Fig. 6A ) exhibited considerable scatter in both 12‐ and 18‐month‐old groups. Despite this, the 18‐month cohort was significantly different from 6 months (P = 0.03790, one‐way ANOVA and post hoc Tukey test). VT/VF risk was positively correlated with LV fibrosis density (R ² = 0.61, P = 0.00025, linear regression, F‐statistic), but better modelled by the AFL and AFA measures quantifying the most significant regional feature of aggregated fibrosis patches. The VT/VF risk correlated strongly with the AFL index (R ² = 0.73, P = 0.00034, linear regression, F‐statistic) but better with the AFA index (R ² = 0.76, P = 0.000005, linear regression, F‐statistic) (Fig. 6B ). That is, ∼76% of the variability of VT/VF risk is explained by an index which reflects the aggregated density of LV patchy fibrosis, and ∼73% by an index that indirectly captures the tortuosity of those aggregated patches.

Figure 6. VT/VF risk, structural remodelling and rate‐dependent APD dispersion.

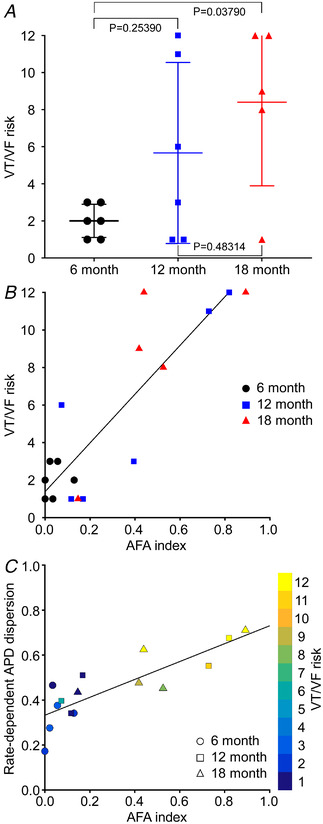
A, VT/VF risk at 6, 12 and 18 months (n = 6, 6 and 5, respectively). One‐way ANOVA and post hoc Tukey test were used to calculate P‐values. B, VT/VF risk as a function of aggregated fibrosis patch density area (AFA) index. For best‐fit regression line shown, R ² = 0.76, P = 0.00487 × 10⁻³, linear regression, F‐statistic. n = 17. C, VT/VF risk as a function of rate‐dependent APD dispersion and AFA index. For best‐fit regression line shown, R ² = 0.70 and P = 0.00103 × 10⁻¹, linear regression, F‐statistic. n = 15. [Colour figure can be viewed at wileyonlinelibrary.com]

The increase in VT/VF risk with structure paralleled observed changes in electrophysiological measures: CV, APD, APD dispersion. Figure 6C shows a strong linear relationship between rate‐dependent APD dispersion (pacing >5 Hz) and AFA index (R ² = 0.70, P = 0.00025, linear regression, F‐statistic). These data also predicted VT/VF risk (Fig. 6C , coloured symbols) and reinforced the reliability of the three independently obtained measures. Animals exhibiting discordant AT alternans were significantly more likely to have higher VT/VF risk and increased AFA index than those which displayed concordant alternans (P = 0.04800 and 0.04420 for VT/VF risk and AFA index respectively, one‐way ANOVA and post hoc Tukey test) or no alternans (P = 0.03430 for AFA index, one‐way ANOVA and post hoc Tukey test) (additional data are available in Supporting information SI2 and SI4).

Correlation and factor analysis

Ten variables collected over the three SHR age cohorts were analysed for cross‐correlations and for emergent factor groupings among all variables. Two 12‐month and one 6‐month animal were excluded as complete individual cells could not be segmented from the 3D images. Consequently, 10 variables over 12 animals were analysed (additional data are available in Supporting information SI2).

Linear regressions between a selection of the 10 variables are given in Fig. 7. Figure 7A and B shows the strong linear correlations between (1) transverse CV and the LV scale fibrosis density (R ² = 0.64; P = 0.00173, F‐statistic) and (2) rate‐dependent APD dispersion and the cell scale fibrosis density (R ² = 0.65; P = 0.00158, F‐statistic). In contrast, Fig. 7C–E illustrates moderate and non‐existent correlations. Transverse CV on the epicardium was less correlated with the cell scale fibrosis density (R ² = 0.48; P = 0.01230, F‐statistic) than with LV scale fibrosis density. Similarly, the anisotropy ratio (CV_L/CV_T) for pacing rates >5 Hz correlated only moderately with the AFA index (R ² = 0.48; P = 0.01260, F‐statistic), and APD at 2.33 Hz pacing did not correlate with AFA index (R ² = 0.10; P = 0.30440, F‐statistic). These plots, together with data in Figs 2, 3, 4, 5, 6, confirm that while the 6‐month cohort is clustered, the 12‐ and 18‐month cohorts are intermingled. This observation that age was not a good contributing predictor of the key components of arrhythmic risk was confirmed by the multi‐variable analysis summary. The summary is shown as a network of strong correlation links in Fig. 7F . Figure 7 also shows that VT/VF risk is most correlated with rate‐dependent APD dispersion (Fig. 7B ) and less so with the anisotropy ratio for pacing rates >5 Hz (Fig. 7D ).

Figure 7. Linear correlations between several key variables and multi‐variable analysis.

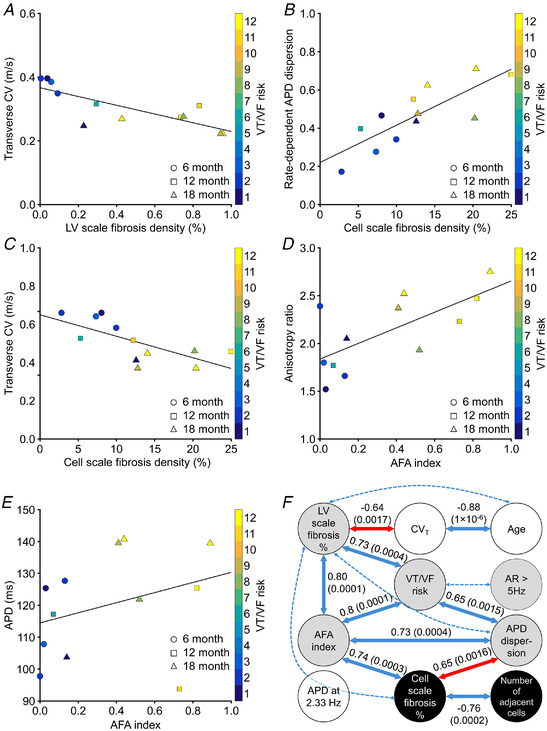
A, transverse conduction velocity at pacing rates >5 Hz as a function of short axis fibrosis density in the left ventricle. For the regression line shown, R ² = 0.64 and P = 0.00173, linear regression, F‐statistic. n = 12. B, rate‐dependent APD dispersion as a function of fibrosis density at the cell scale. For the regression line shown, R ² = 0.65 and P = 0.00158, linear regression, F‐statistic. n = 12. C, transverse conduction velocity at pacing rates >5 Hz as a function of fibrosis density at the cell scale. For the regression line shown, R ² = 0.48 and P = 0.01230, linear regression, F‐statistic. n = 12. D, conduction velocity anisotropy ratio at pacing rates >5 Hz as a function of the AFA index. For the regression line shown, R ² = 0.48 and P = 0.01220, linear regression, F‐statistic. n = 12. E, APD at a pacing rate of 2.33 Hz as a function of the AFA index. For the regression line shown, R ² = 0.10 and P = 0.30440, linear regression, F‐statistic. n = 12. F, inter‐variable Pearson's correlations and P‐values (in brackets, Student's t‐distribution) for the principal correlations (continuous links; approximate R ² ≥ 0.6) and lesser correlations (dotted links; 0.5 ≤ R ² < 0.6). The red links show relationships from sub‐figure A and B. All correlations shown are significant at 95% confidence interval. Inverse correlations are indicated by negative R ² values. Segmentation of variables into three factors using exploratory factor analysis is shown by shading (grey: factor 1; white: factor 2; black: factor 3). The APD variable is not strongly correlated with any other variable, but factor analysis associates it with factor 2 (age and transverse conduction velocity). AR, CV anisotropy ratio; CVT, transverse conduction velocity. [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 7F summarizes the strong cross‐correlation relationships between variables and their P‐values for approximate R ² ≥ 0.6 (continuous links) and 0.6 > R ² ≥ 0.5 (dotted links). The correlations of Fig. 7A and B are indicated by red links in Fig. 7F . All correlations shown were significant (P < 0.05, Student's t‐distribution). As suggested by Fig. 6B and C , VT/VF risk was significantly correlated with AFA index and APD dispersion. In addition, risk was linked to short axis fibrosis, but only indirectly to transverse CV (and consequently age) or cell scale fibrosis (and consequently number of adjacent cells). VT/VF risk was weakly linked to the anisotropy ratio with pacing faster than 5 Hz. APD was not significantly correlated with any of the other variables, with the strongest correlation being to APD dispersion (R ² = 0.3; not significant, P = 0.06430, Student's t‐distribution). Exploratory factor analysis (with 2 or 3 factors) always linked risk, AFA index, short axis percentage fibrosis, anisotropy ratio and APD dispersion into a leading descriptive factor (Fig. 7F : grey disc). Age, transverse CV and APD were clustered into a second factor (Fig. 7F : white disc). In two‐factor analysis cell percentage fibrosis and number of adjacent cells (Fig. 7F : black disc) were included in the leading factor, but in three‐factor analysis they became a separate third factor. The two variables least well described by the three‐factor analysis were anisotropy ratio and APD. Linear models were reliably fit to the variables reduced to two factors (R ² = 0.55; P = 0.00585, Student's t‐distribution) and three factors (R ² = 0.54; P = 0.03179, Student's t‐distribution). Additional data are available in Supporting Information SI2.

Discussion

We have investigated the relationships between VT/VF risk and key aspects of structural and electrophysiological remodelling in a well‐established animal model of HHD that progresses to heart failure over time (Herrmann et al., 1995; LeGrice et al., 2012; Li et al., 2019; Nguyen et al., 2016). Novel findings were that: (1) VT/VF risk was strongly associated with a measure that quantifies the extent and complexity of aggregated fibrosis patches throughout the LV wall, (2) both were independently associated with the development of rate‐dependent repolarization heterogeneity, (3) increased intramural fibrosis led to reduced lateral connections between cardiomyocytes, and (4) age was not a strong predictor of VT/VF risk.

Structural remodelling and HHD progression

The SHR recapitulates key features in progressive human HHD (Brooksby et al., 1993) and relationships between LV structure and function have been investigated extensively in this animal model (Chan et al., 2011; LeGrice et al., 2012; Li et al., 2019; Nguyen et al., 2016). SHRs are hypertensive at 3 months (LeGrice et al., 2012) and, despite subtle changes from 2 to 6 months compared with age‐matched controls (Nguyen et al., 2016), LV structure and pump function remain constant and relatively normal over this period (Kokubo et al., 2005). Previously, we quantified changes in LV structure and function in SHRs from 3 to 24 months compared to normotensive controls, and showed that for many measures, SHRs diverged from the control animals before 12 months (LeGrice et al., 2012). That study found animals progressed toward end‐stage HF from ∼18 months with increasing patchy fibrosis, LV dilatation and reduction in ejection fraction. This was associated with increased myocyte cross‐sectional dimensions and interstitial fibrosis. Similar observations have been made in other studies (Chan et al., 2011). With ageing, there is increased interstitial fibrosis but not patchy fibrosis in murine models (de Jong et al., 2011). At some time point between 6 and 12 months, the increase in interstitial fibrosis due to ageing diverges between normotensive WKY rats and SHRs (Herrmann et al., 1995). Unlike WKY rats, SHRs increasingly develop patchy fibrosis from 12 months, and this tends to localize mainly near the endocardium (Herrmann et al., 1995; Pahor et al., 1991). Our findings from both SHR and WKY tissue imaging are consistent with these earlier studies.

A novel feature of this study is that we have combined optical clearing with fluorescent labelled WGA to characterize LV fibrosis (Emde et al., 2014) at both cell and tissue levels. WGA diffused readily in cleared LV short‐axis rings, enabling us to quantify the extent and distribution of patchy fibrosis throughout the LV. The results were consistent with previous findings (Herrmann et al., 1995; LeGrice et al., 2012), but revealed that progression of HHD was associated not just with increased fibrosis density, but also with aggregation of fibrosis into larger effective patches, particularly in the inner LV free wall. For each SHR studied, 3D myocyte arrangement and extracellular connective tissue matrix content were also analysed at the microscale in representative LV mid wall specimens (Fig. 3). The number of adjacent connected myocytes was inversely related to fibrosis density in those patches (Figs 3C and 7). At low fibrosis density, connection ratios were ∼9:1, similar to those reported for normal canine LV (Saffitz et al., 1994), while the ∼3:1 connection ratios at the highest fibrosis density are similar to comparable data for the border zone of healed infarcts in rat (Rutherford et al., 2012) and rabbit (Seidel et al., 2016). While our measure of connected adjacent cells is based on proximity, some qualitative evidence of Cx43 plaques co‐located with points of contact between myocytes indicates that it may also reflect electrical coupling. Our results show that lateral coupling between myocytes is reduced by infiltration of patchy and interstitial fibrosis that occurs later in progression of HHD (Herrmann et al., 1995), but suggest that it is less affected by the interstitial fibrosis that occurs earlier in HHD (Herrmann et al., 1995; LeGrice et al., 2012). Structure measures are related across scales with correlations between the cell and ventricular scale measures (Fig. 7). But the data summarized in Fig. 7F indicate that structural measures are not strongly related to age, which also confirms the observations of Figs 2C , D and 3C . Multiscale structural measures like these at the cellular and tissue levels are novel.

Effects of age and HHD progression on LV electrophysiology

To date, there have been a few studies of how LV electrophysiology in SHRs changes with age and progression of HHD (Chan et al., 2011), but none have comprehensively considered a range of electrophysiological variables, in addition to quantitative structural variables, and the linkages between them. Related information is available from other animal models of hypertension (Clauss et al., 2019). These include mice (Boulaksil et al., 2010; Gao et al., 2016), rats (Boulaksil et al., 2016; Jin et al., 2010), guinea pigs (Botchway et al., 2003), rabbits (Wiegerinck et al., 2006) and cats (Kowey et al., 1991) following trans‐aortic constriction, and time‐course studies with Dahl salt‐sensitive hypertensive rats on high‐salt diets (Kamei et al., 2007). The effects of HHD on CV are unclear, with unaltered (Boulaksil et al., 2016), reduced (Kamei et al., 2007), more anisotropic (Boulaksil et al., 2010) and increased epicardial CV (Wiegerinck et al., 2006), reported following sustained LV pressure loading. In almost all cases, though, VT/VF risk was increased (Botchway et al., 2003; Boulaksil et al., 2016, 2010; Jin et al., 2010; Kowey et al., 1991; Wiegerinck et al., 2006). Furthermore, repolarization heterogeneity (Boulaksil et al., 2016; Kowey et al., 1991) and APD prolongation (Botchway et al., 2003; Gao et al., 2016; Jin et al., 2010; Kowey et al., 1991) were recorded following development of cellular and LV hypertrophy.

We found that epicardial CV decreased between 6 and 12 months with little change thereafter, while CV anisotropy increased and became rate‐dependent at 12 and 18 months (Fig. 4). While the transverse CV is inversely correlated with LV fibrosis (Fig. 7A and F ), it is only moderately correlated with cell scale fibrosis density (Fig. 7C ) (R ² = 0.48; P = 0.01230, linear regression, F‐statistic) and there is no complete explanation for cellular mechanisms causing the reduction in epicardial CV. For example, no difference in action potential upstroke rate during rapid depolarization has been found in isolated myocytes from 3‐ and 18‐month SHRs and age‐matched controls (Cerbai et al., 1994), suggesting that I _Na density is preserved with age and HHD progression. The extent of rate‐dependence in CV anisotropy could be related to altered lateral coupling, but our data show weak correlations with cell scale measures of fibrosis and cell connectivity, and there are only moderate correlations between CV anisotropy and AFA index (Fig. 7D ) (R ² = 0.48; P = 0.01260, linear regression, F‐statistic) and LV fibrosis (R ² = 0.40; P = 0.02850, linear regression, F‐statistic). These are both measures of global structural remodelling, suggesting anisotropy could be a phenomenon emerging with developing HHD (and hence linked with VT/VF risk).

Age‐related increase in ventricular APD has been observed previously (Botchway et al., 2003; Gao et al., 2016; Jin et al., 2010; Kowey et al., 1991). Prolongation of APD in hypertension is linked with down‐regulation of potassium ion channels that contribute to repolarization (Comollo et al., 2020), principally the transient outward current, I _to, in the rat (Cerbai et al., 1994). However, while we also found that mean APD was progressively longer at all pacing rates for older SHRs when data were clustered by age (Fig. 5B ), there was no strong correlation between age and APD when the SHRs were not clustered by age (Fig. 7E and F ). This suggests that age is not a dominant factor in observed APD change compared with disease progression.

In general, association between the measures of electrical activation and the extent and distribution of fibrosis was weak. This is not surprising, given that optical mapping recovered information on electrical activity from the subepicardial LV free wall, while the accumulation of patchy fibrosis in this region with age and HHD progression was substantially less marked than the inner wall. However, rate‐dependent APD dispersion was the exception, being strongly related to the extent of patchy fibrosis (Figs 6C and 7F ), but less so to age (Fig. 5C ). This suggests it is predominantly a feature of HHD progression and is discussed further in the next section.

Mechanisms of increasing VT/VF risk with HHD progression

Various studies show that SHRs are more susceptible to arrhythmic risk compared to normotensive animals by our control point of 6 months (Nguyen et al., 2016; Sung et al., 2020; Tribulova et al., 2003). We found this risk increased as HHD developed from 6 months. The striking associations among three independently collected variables, namely (1) electrically assessed VT/VF risk, (2) optical mapping derived rate‐dependent APD dispersion and (3) confocal microscopy indices of fibrosis, provide important insights into mechanisms underlying this progression. As discussed in previous sections, APD generally increases as hypertension develops (Chan et al., 2011), and focal or patchy fibrosis toward the endocardium is associated with progression of HHD in SHRs but not with ageing in normotensive rats (Herrmann et al., 1995). When all variables are considered together, APD does not appear as a predictor of arrhythmic risk and age does so only weakly, and then via transverse CV and LV scale fibrosis (Fig. 7F ). However, VT/VF risk strongly correlates with APD dispersion and AFA index. These measures form a remodelling‐risk triangle in the correlation network of Fig. 7F and are predominately associated with HHD development rather than age. The evidence for this is both from the strong correlative links and the factor analysis groupings (additional data are available in Supporting information SI2). The AFA measure captures both extent and complexity of fibrosis, and these have been recognized in prior studies as important predictors of VT/VF risk (de Bakker et al., 1990).

An explanation for these observations is that VT/VF risk is increased by repolarization heterogeneity resulting from extensive deposition of patchy fibrosis. Our 3D microscopic analyses show that lateral connections between adjacent mid wall myocytes were reduced with increasing fibrosis (Fig. 3), while extensive, closely apposed patches of fibrosis accumulated in the mid wall and sub‐endocardial LV as HHD progressed. The data variable correlations indicated strong links between cell scale fibrosis and the LV scale AFA index as well as APD dispersion (but not transverse CV or age). Regional repolarization gradients are an expected result of structural remodelling (Smaill et al., 2013), and the reduced repolarization reserve causing early afterdepolarizations that drive VT/VF is also linked to increased fibrosis (Karagueuzian et al, 2013). It has been demonstrated that disruption of cell networks and reduction of lateral connections between myocytes by interstitial fibrosis leads to tortuous impulse propagation (de Bakker et al., 1993), as do surviving tracts of viable myocardium through compact scar (de Bakker et al., 1990; Trew et al., 2019), causing activation pathway‐dependent repolarization heterogeneity (Rutherford et al., 2012). Furthermore, regional repolarization gradients are amplified by local accumulation of such barriers to normal propagation (Engelman et al., 2010).

These mechanisms relate to heterogeneous electrical propagation and electrotonic coupling in myocardium due to altered connections between adjacent myocytes. It has also been argued that the proliferation of myofibroblasts in fibrosis modulates cell electrical properties through both electrotonic loading between myocytes and non‐active cardiac tissue cells, and the release of paracrine mediators such as transforming growth factor β from the fibroblasts (de Jong et al., 2011; Kohl & Gourdie, 2014). Evidence has come from myocyte–fibroblast co‐culture studies (Miragoli et al., 2006), experimental studies in mice (Rubart et al., 2018) and computer modelling (Maleckar et al., 2009). However, the extent to which these factors contribute to electrical dysfunction in structural heart disease remains unclear.

Despite our previous caveat on the extent to which epicardial optical mapping can be related to predominantly intramural structural remodelling, we would expect the development of electrical instability to be reflected in epicardial electrical maps. This is supported by our finding that rate‐dependent APD dispersion and VT/VF risk were better predicted by the AFA index, a measure which reflects the extent of closely apposed patches of patchy fibrosis at the LV scale, than by fibrosis density alone. The observation of spatially discordant AT alternans with increasing stimulus rates prior to conduction failure or initiation of VT/VF is also noteworthy in this context, as is the fact that animals which exhibited discordant AT alternans had significantly higher VT/VF risk than those that had concordant alternans (P = 0.04800, one‐way ANOVA and post hoc Tukey test).

Clinical translation

We have demonstrated a strong association between VT/VF risk, in a well‐established animal model of progressive HHD, and a new metric quantifying the extent of aggregated patchy fibrosis. This fibrosis classification could be transferred directly to late gadolinium‐enhanced cardiac MR images to further substantiate its use as a robust basis for risk stratification in HHD. In addition, our results indicate that rate‐dependent APD variability and AT alternans mapped on an LV surface recording may also reveal the underlying substrate that contributes to risk of sudden cardiac death.

Limitations

This study does not address the predictors and mechanisms of VT/VF risk in normotensive animals or attempt to contrast and compare them with our findings in SHRs. Our focus is on risk development in HHD and it is well established that by 6 months, SHRs have diverged in structural and functional remodelling from normotensive animals. They are significantly more pro‐arrhythmic (Chan et al., 2011; LeGrice et al., 2012; Nguyen et al., 2016; Sung et al., 2020; Tribulova et al., 2003), with emerging sub‐endocardial patchy fibrosis that is not present in normotensive WKY rats (Herrmann et al., 1995). Consequently, we elected to conduct a cross‐sectional study referenced to the 6‐month SHR cohort and examined VT/VF risk with progression of age and HHD together with other structural and electrophysiological variables.

Our metrics which quantify both the density and 3D distribution of LV patchy fibrosis have enabled us to complete a far more robust statistical analysis than would have been possible based on age alone. We have established a strong relationship between structural remodelling, APD dispersion and VT/VF risk, but acknowledge there are challenges differentiating age and HHD contributions to these outcomes. However, supported by other studies (de Jong et al., 2011; Herrmann et al., 1995; Pahor et al., 1991), we argue that our findings are more consistent with mechanisms dominated by HHD progression rather than ageing.

In this study, epicardial optical mapping has been used to make mechanistic inferences about the effects of structural remodelling on APD dispersion and VT/VF risk when the substrate involved is most extensive in the inner LV wall. While it is possible to characterize intramural electrical activity using wedge preparations, for example, the rhythm disturbances addressed in this study are supported only in the intact LV. We acknowledge that the rate‐dependent repolarization dispersion and AT instability reported are likely to be an attenuated reflection of the underlying electrical behaviour that leads to VT/VF. Our preparation has the advantage that key aspects of the 3D structural remodelling contributing to these rhythms are preserved. However, we note that the interactions between intramural LV structural remodelling and electrical dysfunction are complex and incompletely understood. The patchy fibrosis identified here in the inner wall of the LV should, therefore, be viewed as marking a potential substrate for re‐entrant electrical activation.

Conclusions

We have completed a systematic and multimodal cross‐sectional study of VT/VF risk in a well‐established animal model of HHD, combining novel multiscale imaging methods with optical mapping to characterize structural and electrophysiological changes. VT/VF risk was stratified with high reliability employing a metric which quantifies the extent of closely apposed patches of LV fibrosis, and with APD dispersion. We conclude that VT/VF risk is associated with rate‐dependent repolarization heterogeneity caused by reduced lateral electrical coupling between LV myocytes with progression of HHD.

Competing interests

None.

Author contributions

P.K. designed the project, collected and analysed data and wrote the article; G.B.S., I.J.L. and A.M.G. designed the project, analysed the data and revised the article; G.R. helped with the collection of data and analysis and revised the article; J.A.A. and J.M.M. sourced and prepared normotensive tissue and helped with analysis; B.H.S. conceived the project, analysed the data and wrote the article; M.L.T. designed the project, analysed the data and wrote the article. All authors have read and approved the final version of this manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported by program grant 13/779 from the Health Research Council of New Zealand and by a grant from the Leducq Foundation.

Open access publishing facilitated by The University of Auckland, as part of the Wiley ‐ The University of Auckland agreement via the Council of Australian University Librarians.

Supporting information

Statistical Summary Document

Peer Review History

SI1 Image and Cell Segmentation Data: https://doi.org/10.17608/k6.auckland.16840198

SI2 Inter‐variable Relationships Data: https://doi.org/10.17608/k6.auckland.16840138

SI3 Image Data: https://doi.org/10.17608/k6.auckland.16829017

SI4 Arrhythmia and Alternans Data: https://doi.org/10.17608/k6.auckland.16829047

Biography

Prashanna Khwaounjoo has a PhD degree in Biomedical Engineering from the Auckland Bioengineering Institute (ABI), Auckland, New Zealand. He is a Research Fellow with the ABI and University of Otago, Dunedin, New Zealand. The research presented in this paper, highlights the multiscale relationships between arrhythmic risk and fibrotic architectures in progressive hypertensive heart disease. It also has potential to be investigated further in larger animal studies. His current research interests include translational sciences with a particular focus on non‐invasive cardiac diagnostic systems. He hopes to be able to develop patient specific tools and techniques to improve health outcomes.

Data availability statement

The data that support this study are presented within the paper and its Supporting information available in figshare (see URLs in Supporting information section).