Comparing hair tensile testing in the wet and the dry state: Possibilities and limitations for detecting changes of hair properties due to chemical and physical treatments

Abstract

Objectives

This investigation focuses, first, on the question to which extent wet and dry tensile tests on human hair may be considered as leading to independent results. Second, we try to assess the sensitivities of wet and dry‐testing to detect changes of mechanical properties. Specifically, we were interested in separating changes, which were induced by a combination of a chemical (oxidation/bleach) and a physical treatment (heat).

Methods

The basis for our study are data for the tensile properties (wet and dry) of a set of untreated and bleached hair tresses, which were submitted to the same schedule of thermal treatments. As characteristic tensile parameters, we chose modulus (E), break extension (BE), and break stress (BS). First, parameters were analysed across treatments for the correlations between wet and dry data. Second, we applied two‐factor analysis of variance to assess the effects of the factors and their potential interaction.

Results

Correlations for the dry versus wet data show only a weak relationship for E, while coefficients of determination (R ² ) are quite high for BE and BS. Two‐factor ANOVA enables to quantify the various contributions to the Total Sum‐of‐Squares for all three parameters. We show that the parameters respond quite differently to the chemical and the thermal treatments as well as to testing conditions (wet or dry). It is of interest to note that the interaction between the chemical and the physical treatment is generally quite weak. For the interpretation of the results, we use the concept of the humidity‐dependent as well as strain‐induced glass transition of the amorphous matrix.

Conclusions

The independence hypothesis for dry and wet tensile measurements only applies for modulus. Overall, we consider modulus (wet) as the best tensile measure of fibre damage when assessing chemical and/or physical treatments. Under ambient conditions (dry), break stress is shown to be a feasible alternative measure.

This investigation focusses, first, on the question to which extent wet and dry tensile tests on human hair may be considered as leading to independent results. Second, we try to assess the sensitivities of wet and dry testing to detect changes of mechanical properties. Specifically we were interested in separating changes, which were induced by a combination of a chemical (oxidation/bleach) and a physical treatment (heat).

INTRODUCTION

Tensile testing of keratin fibres, including human hair, is of academic as well as of practical (textile, cosmetic industries) importance. Concentrating for the current context on human hair, tensile tests may in practice be conducted either in water (wet) or under ambient, defined, or standard conditions. ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ The choice of conditions may on the one hand be a matter of convenience. On the other hand, investigators may decide to employ both conditions, assuming that sets of data are essentially independent and reflect different aspects of hair properties. ³ , ¹¹

The independence assumption is on the one hand plausible in view of the fact that hair is well below its glass transition under ambient or standard conditions (20°C/65% rh or 22°C/55% rh) and well above the transition in water. ¹² , ¹³ On the other hand, there is a pronounced similarity of the shape of the stress/strain curves, as investigated in detail for wool, ¹⁴ for the whole humidity range.

It is interesting to note that we know from conversations, that most colleagues within the hair cosmetics research community would agree that dry tensile testing has a lower sensitivity than wet testing to detect the effects of cosmetic treatments and processes (mainly chemical and thermal). ¹ , ² , ³ , ⁵ , ¹⁵ , ¹⁶ However, the use of dry‐testing may be justified by the argument that ambient environmental conditions represent the usual conditions of hair in practice. Another very practical reason is that an active agent under investigation may be rinsed off during testing. Despite this ambiguity with respect to tensile testing conditions and in view of the wide range of tensile variables, ¹⁵ , ¹⁷ we have not been able to find a comprehensive investigation to establish or dismiss reasons for a preference for one of the conditions.

Tensile data (wet & dry) have been available from a set of hair samples from a study on the effects of heating (thermal straightening) on untreated and bleached European hair. ¹⁸ , ¹⁹ This study was undertaken by the expert working group ‘Hair Care Products’ of the DGK (Deutsche Gesellschaft fuer Wissenschaftliche und Angewandte Kosmetik e.V.).

On the basis of common practice ¹ , ² , ³ , ⁶ , ⁸ , ¹⁰ , ¹¹ , ¹⁵ , ²⁰ , ²¹ , ²² as well as of a recent investigation of the information content of wet tensile testing, ¹⁷ we identified three specific variables as being especially suited for our investigation. These are elastic modulus (E), break extension (BE), and break stress (BS).

The current investigation focuses, first, on the question to which extend wet and dry tensile tests on human hair may be considered as independent for any of the variables. Second, we try to assess the sensitivity of the two variations of tensile testing to detect and possibly discriminate between changes of human hair mechanical properties, which were induced by a combination of a chemical (oxidation/bleach) and a physical treatment (heat).

For this aim, we use two‐factor analysis of variance (2F‐ANOVA). The method enables to separate the influences of the chemical and the thermal treatment on the tensile parameters (wet and dry) as well as to study potential interaction effects of the treatments.

With our investigation, we try to contribute to the discussion of the suitability of wet or dry tensile testing, respectively, to support research and development of hair cosmetic products and procedures.

EXPERIMENTAL

Materials and methods

A description of materials and methods for the samples used in this investigation have been given before in detail. ¹⁸ , ¹⁹ For this reason, we only provide a short summary here with a focus on the current context. Further details can be found in the Appendix S1.

The study was conducted with 16 commercial, mixed, Caucasian hair tresses (19 cm long, 1.5 cm wide, ≈ 2 mm thick) from the same hair batch. Half of the tresses were subjected twice to a bleach using a commercial product (Wella) and practically relevant conditions. This treatment defines the two levels of chemical treatment for each tress as either natural/untreated (N) and bleached (B), respectively.

Prior to the thermal treatment, the tresses were subjected to a standard wash and brought to a ‘towel‐dry’ state. Under these conditions, a tress is expected to contain about 60% water. At this stage, each tress was subjected to straightening through the repeated application of a commercial straightening iron set to 200 °C. Individual treatment times (1.67 s) added up to three total contact times, which defined four levels of thermal treatment (0: no thermal treatment; 1: 60s; 2: 300 s; 3: 800 s). Two tresses were produced for each combination of chemical and thermal treatment.

Tensile test were conducted on hair fibres, using the Fibre Dimensional Analysis Unit Model 765 (FDA765, Dia‐Stron) and a Miniature Tensile Tester Model 675 (MTT675, Dia‐Stron). The fibres were tested immersed in water at approx. 20°C (wet) and under standard room conditions (dry: 20°C, 65% rh). Thirty fibres were tested from each hair tress under wet and dry conditions. From each successful test, the software (UvWin – 3Phase –Dia‐Stron) extracts a wide variety of stress, strain, and work‐related parameters. ¹⁷

Choice of variables, basic data, and statistical analysis

Tensile testing provides a large number of variables, which relate to moduli, stresses, various types of work, and strains. ¹⁷ For our investigation, we selected as variables elastic modulus (E), break extension (BE), and break stress (BS). This is in line with the practice of tensile testing of hair ³ , ¹⁵ as well as consistent with the results of our recent investigation on the correlations between tensile variables (wet). ¹⁷ The chosen variables are further specified by subscripts to indicated wet (w) and dry (d) conditions of testing.

As already described elsewhere, ¹⁷ we checked the data distribution for each sample, applying normal‐probability plots. This approach revealed a small number of outliers. The final number of data for each tress was between 30 and 27. For our analyses, we pooled data obtained for pairs of tresses with equal treatments, yielding a maximum of 60 data points for each case. Table 1 summarizes the basic results underlying this analysis. The notation of the samples follows the levels of chemical and thermal treatment, as outlined above. On this basis, for example, N0 is untreated hair with no thermal treatment, while B3 is bleached hair with level 3 (800 s) thermal treatment, respectively (see Appendix S1).

TABLE 1.

Summary of basic statistics for the investigated variables for natural/chemically untreated (N) and bleached (B) hair

Sample	Ew ± q95%	Ed ± q95%	BEw ± q95%	BEd ± q95%	BSw ± q95%	BSd ± q95%
	GPa	GPa	%	%	MPa	MPa
N0	1.89 ± 0.05	3.95 ± 0.12	57.5 ± 1.0	46.9 ± 1.1	191 ± 3	229 ± 4
N1	1.82 ± 0.09	3.64 ± 0.10	53.2 ± 0.74	44.9 ± 0.83	175 ± 9	216 ± 5
N2	1.76 ± 0.04	3.73 ± 0.10	52.7 ± 0.59	45.1 ± 0.98	161 ± 3	205 ± 5
N3	1.58 ± 0.04	3.65 ± 0.09	49.1 ± 0.74	44.6 ± 0.96	125 ± 4	190 ± 3
B0	1.63 ± 0.04	4.15 ± 0.10	58.7 ± 1.1	50.3 ± 1.0	167 ± 6	223 ± 3
B1	1.45 ± 0.04	3.53 ± 0.10	60.0 ± 1.1	49.4 ± 0.92	160 ± 4	208 ± 3
B2	1.26 ± 0.04	3.71 ± 0.13	60.5 ± 1.2	51.1 ± 1.1	139 ± 5	192 ± 6
B3	1.02 ± 0.04	3.64 ± 0.11	59.0 ± 0.75	51.7 ± 0.91	114 ± 4	176 ± 3

Note: Numerals indicate the level of thermal treatment for each sample. q _95% are the 95% confidence limits. The number of underlying data is 53–60.

We analysed the data by a two‐factor analysis of variance (2F‐ANOVA), using the appropriate tool in Statistica ²³ and the following approach. A first factor, Factor 1, refers to the chemical state of a sample. Factor 1 has two levels (a = 2) for the chemical state of a sample (N = natural/chemically untreated, B = bleached). The second factor, Factor 2, describes the four levels (times) of thermal treatment (b = 4). The results represent a 2 × 4 ‘crossed’ ANOVA design with essentially equal numbers of replicas for each cell (sample). ²⁴

The measure of the variability within a given set of values for a chosen variable across all samples is the Total Sum of Squares (SS _T ), as given specifically by ²⁴ :

$${\mathrm{SS}}_T=\sum _{i=0}^1\sum _{j=0}^3\sum _{l=1}^n\left(x_{\mathit{ijl}}-\stackrel{̿}{x}\right)$$ (1)

where i (0, 1) signifies the two levels of chemical and j the four levels thermal treatment (0, 1, 2, 3). $x_{\mathit{ijl}}$ are all of the individual data across both factors. $\stackrel{̿}{x}$ is the mean for all data.

SS _T is related to the variance (Var) of a data set according to:

$$\mathrm{Var}={\mathrm{SS}}_T/\left(n-1\right)$$ (2)

where n is the number of data for a given variable across all samples.

The fraction of SS _T associated with the variability of the data for the individual samples – that is for the hairs taken from tress pairs N0 to B3 for testing – is described by the error‐SS as:

$${\mathrm{SS}}_E=\sum _{i=0}^1\sum _{j=0}^3\left[\sum _{l=1}^n{\left(x_{\mathit{ijl}}-{\overline{x}}_{\mathit{ij}}\right)}^2\right]$$ (3)

The fraction of SS _T specifically attributed to Factor 1 (SS₁: chemical treatment) is given by:

$${\mathrm{SS}}_1=bn\sum _{i=0}^1{\left({\overline{x}}_i-\stackrel{̿}{x}\right)}^2$$ (4)

${\overline{x}}_i$ is the mean across all samples for a given level of Factor 1. b is the number of levels for Factor 2 (b = 4).

The sum of squares attributed to Factor 2 (SS ₂ : thermal treatment) is accordingly given by:

$${\mathrm{SS}}_2=an\sum _{j=0}^3{\left({\overline{x}}_j-\stackrel{̿}{x}\right)}^2$$ (5)

${\overline{x}}_j$ is the mean across all samples for a given level of Factor 2. a is the number of levels for Factor 1 (a = 2).

The sum of the various contributions to SS _T may leave a rest SS _1x2 , which is attributed to the interaction of the Factors 1 and 2 as:

$${\mathrm{SS}}_{\mathit{\text{1x2}}}={\mathrm{SS}}_E-{\mathrm{SS}}_1-{\mathrm{SS}}_2$$ (6)

In summary, we have:

$${\mathrm{SS}}_T={\mathrm{SS}}_{\mathit{1}}+{\mathrm{SS}}_{\mathit{2}}+{\mathrm{SS}}_{\text{1x2}}+{\mathrm{SS}}_E$$ (7)

For the variables, the various components of SS _T , are determined and assessed for their statistical significance on the 95% level on the basis of their specific degrees of freedom. ²⁴ The various SS‐components are reported as fractions (%) of SS _T (see Table 3).

TABLE 3.

Summary of the various sum‐of‐squares (SS) components for the three chosen variables (wet and dry), according to Equations (1), (2), (3), (4), (5), (6), (7)

Variable	SS T , %	SS1, %	SS2, %	SS1 × 2, %	SS E , %
E w , GPa	50.78	41	26	3	30
E d , GPa	91.01	1	16	2	82
BE w , %	12.3*103	38	8	10	44
BE d , %	9.60*103	33	1	2	64
BS w , MPa	428*103	9	55	1	35
BS d , MPa	236*103	5	48	1	47

Note: SS _T is the total sum‐of‐squares. SS ₁ and SS ₂ relate to the chemical (Factor 1) and the thermal treatment (Factor 2), respectively. SS _1 × 2 gives the interaction component. SS _E is the unexplained (error) component of the sum‐of‐squares. Values for SS ₁ , SS ₂ , SS _1 × 2 , and SS _E are given as percentages of SS _T . The number of data for each variable is around 450 across all samples. Significant SS‐components (95%‐level) are marked (italics).

All calculations and graphs were done using Excel (2016, Microsoft) and Statistica. ²³

RESULTS

Correlations wet vs dry

As first part of the investigation, we consider the independence hypothesis for wet and dry‐testing across all chemically and thermally treated samples. For this, we assess the correlations between the variable means for each wet/dry‐pair. Figure 1a,b graphically summarize the results of the regression process for modulus (E) and break extension (BE), as examples. For Figure 1a,b, these two variables were specifically chosen, since they have been shown to be independent in the wet state. Break stress (BS), in contrast, was found to be a combination of E‐ and BE‐ properties. ¹⁷ Data sets for E, BE, and BS were analysed by linear regression, for which the parameters are summarized in Table 2.

FIGURE 1.

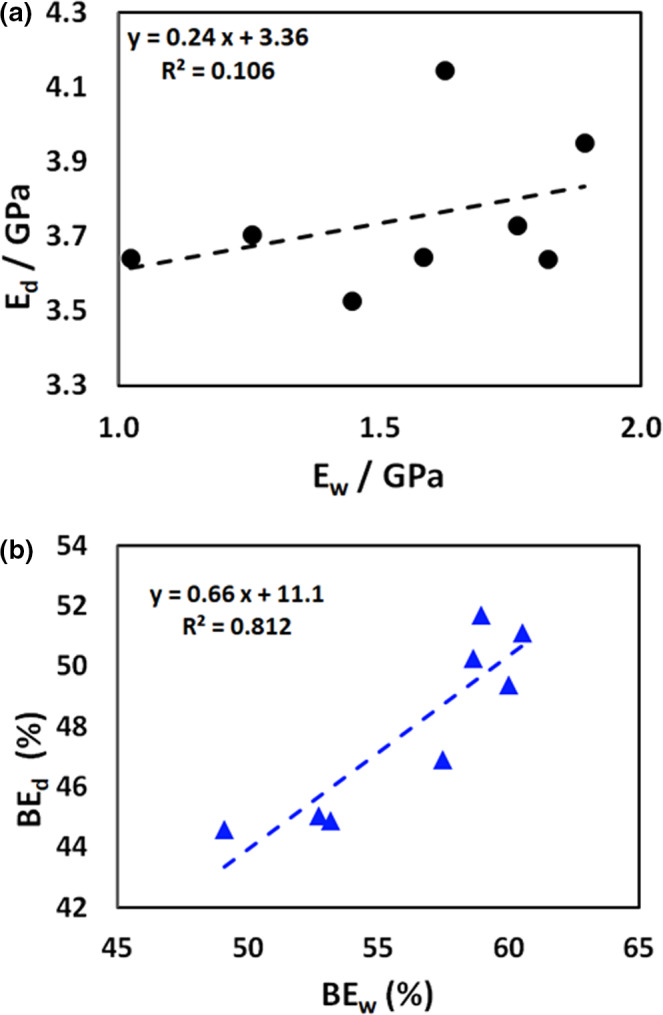
(a): Plot of means for moduli (●) for dry (E _d ) versus wet (E _w ) testing for natural and bleached hair. The linear regression line (− − ‐) is given. The related generic regression equation together with the coefficient of determination (R ² ) are inset. (b): As (a), but for break extension (BE ). For further details, see Table 2

TABLE 2.

Parameter values of the regression equations, when plotting variable means (n = 8) for dry vs wet testing (see Figure 1a,b)

Variable	ic ± SE; p	sl ± SE; p	R 2
E, GPa	3.36 ± 0.45; 0.001	0.24 ± 0.29; 0.43	0.106
BE, %	11.1 ± 7.2; 0.17	0.66 ± 0.13; 0.002	0.812
BS, MPa	99 ± 11; <0.001	0.69 ± 0.071; <0.001	0.940

Note: For each variable, the p‐value is given to quantify the statistical significance level. Values, which are significant on the 95%‐level are marked (italics).

Abbreviations: ic, intercept.; R ², coefficient of determination; SE, standard error; sl, slope of the regression line.

2‐Factor ANOVA

Table 3 summarises the results of the 2F‐ANOVA for all three variables.

DISCUSSION

The independence hypothesis

For the modulus, the analysis confirms that wet and dry measurements are not really correlated (see Figure 1a and Table 2). Means across all samples (see Table 1) for E _w (1.55 GPa) and E _d (3.75 GPa) differ by a factor of somewhat larger than two. Values for the thermally untreated samples (see Table 1) are in good agreement with literature values. This includes the drop of modulus with bleaching (compared with natural hair) when wet and its increase when dry. ¹ , ² , ⁵ , ¹¹ , ¹⁵ , ²⁵

The main components of the microscopic structure of human hair are an outer protective layer (cuticle) and a fibre core (cortex). The cortex is essentially a fibre/matrix composite, comprising partly α‐helical intermediate filaments (IF) embedded in amorphous IF‐associated material. The difference between wet and dry values for modulus is attributed to the low contribution of the matrix in the wet compared with a much larger effect in the dry/conditioned state. ³ , ¹⁵ , ²⁶ Under wet condition, the modulus is about 2 GPa (Table S1), in agreement with values for wool. ²⁷ For wool, the contributions (wet) of IFs (1.7 GPa) and the matrix (0.3 GPa) show a ratio of (5–6: 1). ²⁸ The IF contribution (1.7 GPa) to the elastic modulus is independent of humidity. ²⁷ , ²⁹ Under standard conditions, the modulus of a hair fibre is about 4 GPa (Table S1). With the humidity‐independent contribution of the IFs (1.7 GPa), this yields 2.3 GPa for the matrix contribution for the chosen experimental conditions, in good agreement with literature data. ²⁶ This represents a much different relation between the contributions of IF and matrix contributions to fibre modulus (1: 1.3). The strong increase of matrix modulus from wet to dry is due to a phase change. The matrix is a gel in the wet state and turns into a glass below about 80% relative humidity (RH). ¹³ , ²⁸

Against this background, in view of Figure 1a and the results given in Table 2, modulus measurements are thus considered as conforming to the hypothesis that wet and dry‐testing results are independent (independence hypothesis).

The situation is quite different for break extension (BE) were wet and dry measurements are highly correlated (R ²  = 0.812, see Table 2). For this variable, the independence hypothesis is thus not valid. Furthermore, the differences between means across all samples for the wet (56%) and the dry state (48%) (see Table 1) are quite small compared with modulus. BE‐results for the untreated hair (wet: 58%; dry: 47%) are in good agreement with the literature data. ¹¹ For break stress (BS), the significance of the correlation between dry and wet readings increases even further (R ²  = 0.94). BS‐values for the untreated hair show little difference (wet: 191 MPa; dry: 229 MPa), in accordance with the literature data. ³ , ¹¹

We attribute the strong dry vs wet correlations for the break variables BE and BS to a much smaller contribution of the matrix in dry state for these parameters compared with the dry elastic modulus. For this, we offer the following argument. Upon straining under dry conditions beyond the elastic limit of about 2%, the matrix undergoes a strain‐induced glass transition. ³⁰ , ³¹ It turns into a highly viscous liquid, which flows upon fibre extension, somewhat similar to wet conditions. The estimated viscosity for the matrix (in wool) drops for standard conditions (20°C, 65% rh) and low strains (<2%) from that for a glassy solid (η = 10¹⁹ Pa) to that of a highly viscous fluid at higher strains (>2%) (η ≈ 10¹⁴–10¹⁵ Pa). ³⁰ The strain‐induced reduced contribution of the matrix to BE _d and BS _d compared with modulus is thus the main factor of the strong dry/wet‐correlations for the two variables. Since the properties of the IFs are humidity‐independent, ³² the glass/liquid transition in the matrix explains the similarity of the stress/strain curves of keratin fibres across the humidity range ¹⁴ , including the humidity‐dependent glass transition. ¹² , ¹³

Two‐Factor ANOVA

Figure 2 summarizes the relative contributions to SS _T for the three variables (wet and dry) as detailed in Table 3.

FIGURE 2.

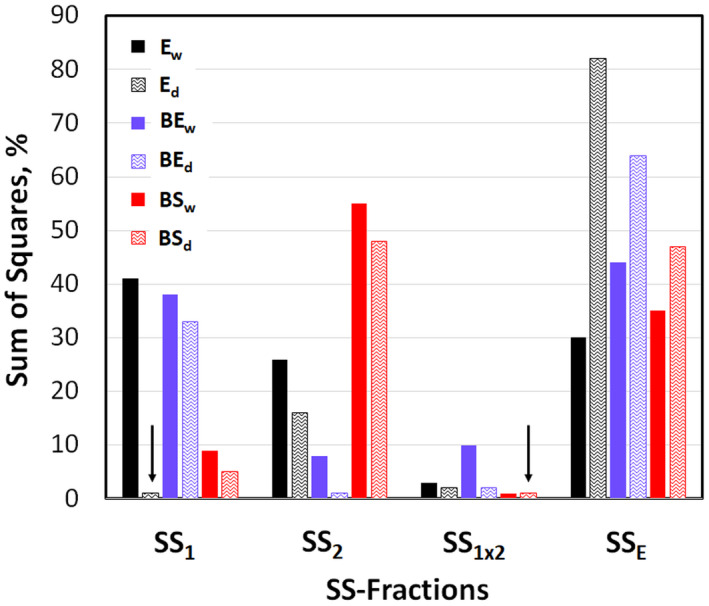
Fractions of the total sum‐of‐squares (SS _T ) for the three pairs of variables, as associated with the two factors and their interaction (see Equation 7 and Table 3). The arrows mark those two contributions, which are not significant on the 95%‐level

Most contributions to SS _T are significant. The two exceptions, as marked in Figure 2 are the effect of the chemical treatment (Factor 1) on the dry modulus (E _d ) and the interaction SS‐component for dry break stress (BS _d ).

Figure 3a,b summarize the results for the moduli (see Table 1) in detail.

FIGURE 3.

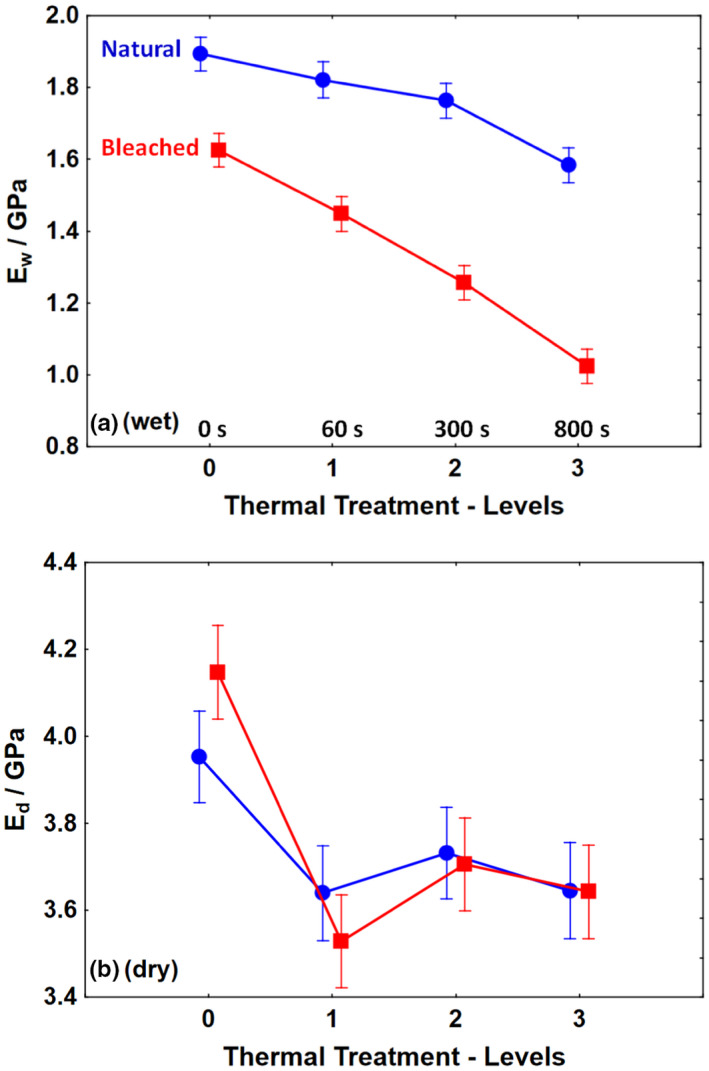
(a): Summary of thermal effects on wet modulus (E _w ) for natural () and bleached () hair. (b): As (a), but for dry modulus (E _d ). Symbols (arithmetic means), whiskers (95% confidence range). The x‐axis represents thermal treatment times on an ordinal scale, as shown in Figure 3a. The lines do not indicate a formal connection between data points, but are rather meant as a guide for the eye

For wet conditions, the moduli for natural are consistently higher than for bleached hair. This is in line with expectations. ¹ , ⁵ , ²¹ Prior to the thermal treatment, the difference is 14% and increases to 35% with the thermal treatment. Accordingly, the effect of the chemical treatment (bleach) on E _w is quite high (SS₁ = 41%) (see Table 3). The effect of the thermal treatment is smaller (SS ₂  = 26%) and comparable to the error component (SS _E  = 30). This shows that E _w is more sensitive to the chemical than to the thermal treatment. The interaction component is small (SS _1 × 2  = 3%), but significant. Both curves in Figure 3a follow first‐order kinetics with thermal treatment time. The increasing difference between the curves from 16% to 37% with the level of thermal treatment is due to the smaller rate constant and thus the higher heat‐sensitivity of bleached hair. ¹⁸

The results are quite different for the dry modulus E _d (see Figure 3b). For the start material, E _d is numerically somewhat higher (5%) for the bleached compared with the natural hair. ²⁶ The gap between the two curves vanishes with the first thermal treatment. Accordingly, the effect of the chemical pretreatment turns out to be not significant, overall (see Table 3). The thermal treatments show a moderate but significant effect (SS ₂  = 16%). This is, however, small compared with the residual error (SS _E  = 82%, see Table 3). Overall, dry modulus shows only a low sensitivity towards treatments, in line with observations in the literature. ¹⁵ , ²¹ , ²² , ³³ We attribute this lack of sensitivity to the large contribution of the matrix to E _d . The matrix is an amorphous, cross‐linked glass under these conditions, which will be rather insensitive to moderate changes of its molecular structure.

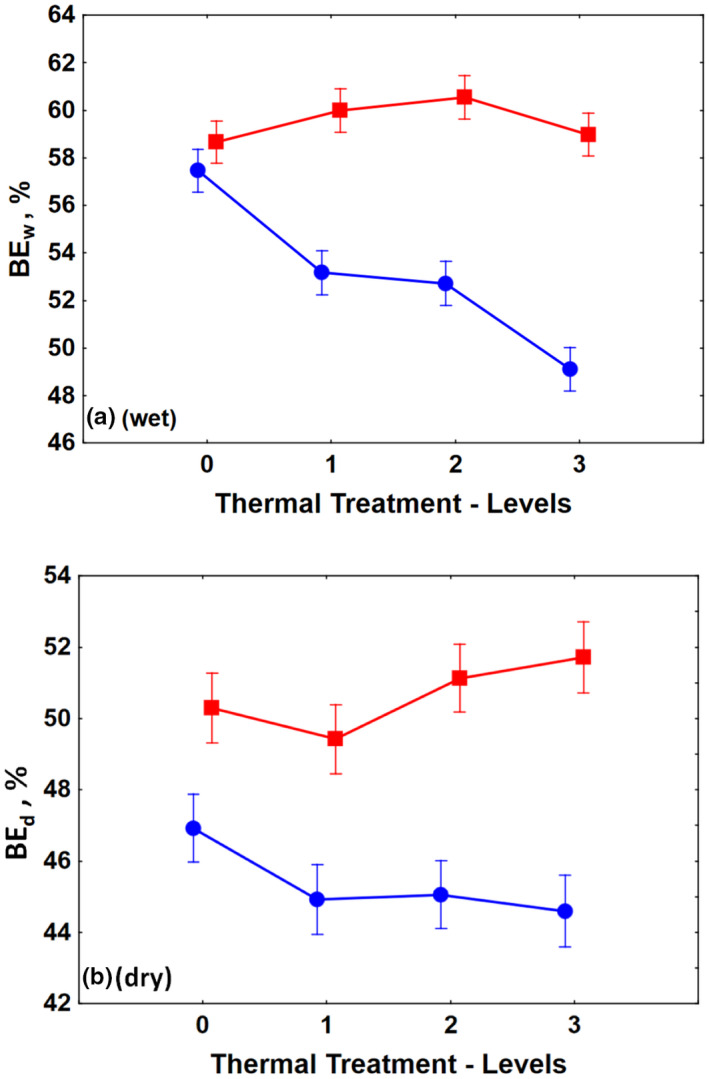
Figure 4 summarizes the results for break extension (see Table 1), complementing the results of Table 3.

FIGURE 4.

(a) Break extension (%) for wet conditions (BE _w ) for natural () and bleached () hair as it changes with the levels of thermal treatment (Factor 2). (b) as (a), but for dry conditions (BE _d ). For further specifics, see Figure 3

Initial wet break extension (BE _w ) (see Figure 4a) does not change significantly through the bleaching treatment. BE _w is about 58% for the natural as well as the bleached hair sample with a slight tendency towards higher values for the latter (see Table 1). Literature data would lead to expect a larger difference. ¹¹ , ¹⁵ For the untreated hair, BE _w decreases with the thermal treatments by 15% along a seemingly similar path as E _w (see Figure 3a). This is reflected in similar values for SS ₁ (see Table 3). In contrast, the thermal treatment does have no overall effect on the bleached hair (SS ₂  = 8%). This difference in performance explains the overall significant effect of bleaching (SS ₁  = 38%) as well as the moderate interaction effect (SS _1 × 2  = 10%). We hypothesize that this may be attributed to a specific, antagonistic effect between bleaching and thermal treatment for break extension. This contrast in performance for untreated and bleached hair would certainly merit further investigation. Under wet conditions, BE _W thus shows satisfactory sensitivity towards the thermal treatment only for natural hair. Bleaching appears to suppress the thermal effects.

For the dry state, break extension is somewhat smaller than for wet conditions for both hair types. This we again attribute to the fact that the matrix is below its glass transition when dry. However, the effect (BE _w  ≈ 58% vs. BE _d  ≈ 47–50%) is rather small compared with the effects for E _w versus E _d . We attributed this to the strain‐induced reduction of matrix viscosity, as discussed above. Break extension for bleached hair is 7% higher than for the untreated hair, in line with literature results. ¹¹ The overall ANOVA ‐effect of bleaching is similar to that for the wet state (SS ₁ = 33%). We attribute this to increased molecular mobility, namely, in the matrix due to broken/oxidized disulphide cross‐links. Though bleached and natural hair in the dry state show opposite trends with the thermal treatment, the effects of thermal treatment are small but significant (SS ₂  = 1%) for both types of samples. The interaction component is also small but significant (SS _1 × 2  = 2%). Comparing Figure 4a,b shows relevant sensitivity of BE _d towards the chemical treatment, which is only rather limited for the thermal treatment.

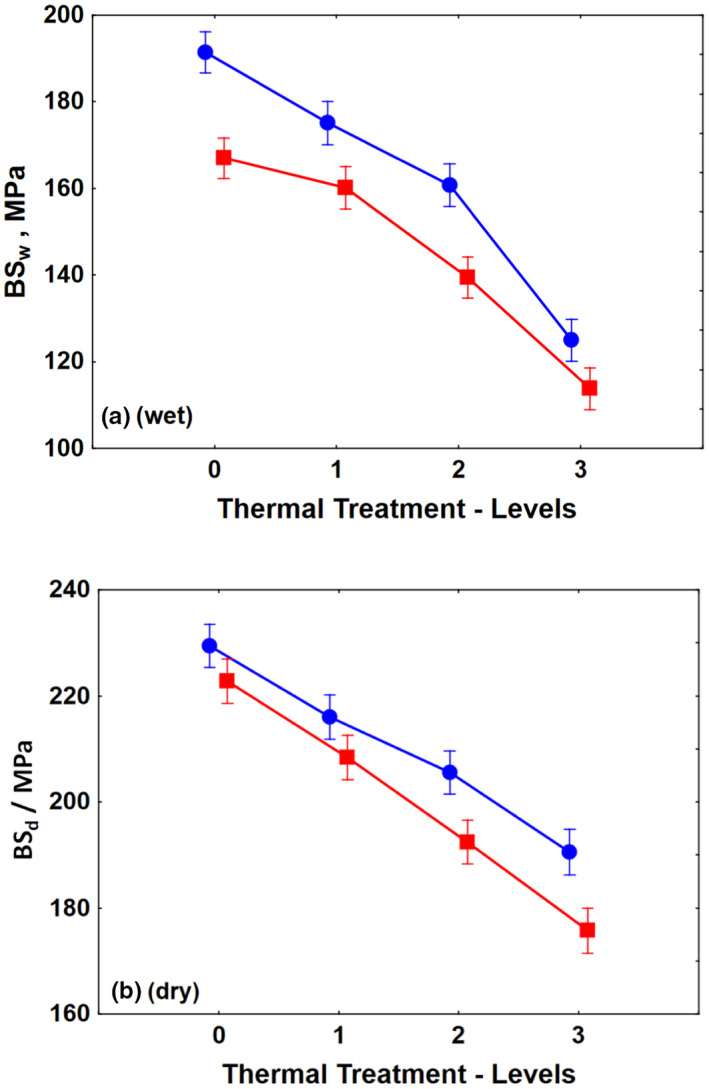
Figure 5 summarizes the results for break stress wet and dry from Table 1.

FIGURE 5.

Break stress for wet conditions (BS _w ) for natural () and bleached () hair as it changes with the levels of thermal treatment (Factor 2). (b) as (a), but for dry conditions (BS _d ). For further specifics, see Figure 3

Results for break stress (see Figure 5) show a striking qualitative similarity. Their change with thermal treatment ³⁴ appears to be comparable to that for E _w (see Figure 3a). This is in agreement with the underlying strong correlation between E _w and BS _w for untreated hair. ¹⁷ BS _w appears thus as a suitable parameter to assess both the chemical as well as the thermal treatment.

For wet (Figure 5a) and dry (Figure 5b), start values for natural are consistently higher than for bleached hair, though this effect is only small for the dry case. ¹¹ , ²¹ Initial values for dry compared with wet conditions are roughly 20% higher. The effects of the thermal treatment are 31%–35% for wet and 21%–17% for dry conditions. The overall low differentiation between wet and dry BS‐data, compared with modulus, we again attribute to the small contribution of the matrix, due to its strain‐induced low viscosity. In line with these observations, SS ₂ is comparable for wet (55%) and dry (48%) conditions and much larger than SS ₁ (wet:9%; dry:5%). Interaction effects are essentially negligible (see Table 3). Due to the closeness of the curves in Figure 5b, BS _d appears to be only of limited value to determine bleaching related effects ⁸ but appears suitable with respect to thermal damage.

CONCLUSIONS

Regarding the Independence Hypothesis for wet and dry tensile testing, the results show that it only applies for modulus. In contrast, correlations between dry and wet results are highly significant for break extension (BE) and stress (BS). We attribute this difference in performance to a strongly decreased contribution of the matrix due to a strain‐induced glass transition. For BE and BS, the assumption of independence between testing conditions is thus not supported.

Parameters show pronounced differences in their responses towards the chosen chemical (bleach) and physical (thermal) treatment as well as towards testing conditions. Overall, modulus measurements under wet conditions show the best sensitivity towards the chemical (bleach) as well as towards the physical (thermal) treatment. Dry modulus testing, in contrast, is rather insensitive overall. We attribute this to the large contribution of the matrix in this case, which shows a low sensitivity towards changes/damage in its glassy state. Break extension shows a rather complex behaviour across samples and testing conditions but generally low sensitivity, except when testing untreated hair samples under wet conditions. Break stress shows very similar behaviour for wet and dry conditions, somewhat analogous to wet modulus testing. This observation is attributed to the underlying correlation between E _w and B _w ¹⁷ as well as the strain‐induced glass/fluid transition of the matrix at strains beyond the elastic region. ³⁰ If testing under room conditions is preferred, determining break stress may thus be the best option to detect changes/damage of hair due to physical and/or chemical cosmetic processes.

In general, we expect these conclusions to be also applicable for other types of chemical and physical treatments of hair, leading to specific types of modification and/or damage.

Supporting information

Appendix S1

Wortmann FJ, Quadflieg JM, Wortmann G. Comparing hair tensile testing in the wet and the dry state: Possibilities and limitations for detecting changes of hair properties due to chemical and physical treatments. Int J Cosmet Sci. 2022;44:421–430. doi: 10.1111/ics.12796