Abstract
Objective:Coronavirus disease 2019 (COVID-19) targets several tissues of the human body; among these, a serious impact has been observed in the microvascular system. The aim of this study was to verify the presence of photoplethysmographic (PPG) signal modifications in patients affected by COVID-19 at different levels of severity.
Approach: The photoplethysmographic signal was evaluated in 93 patients with COVID-19 of different severity (46: grade 1; 47: grade 2) and in 50 healthy control subjects. A pre-processing step removes the long-term trend and segments of each pulsation in the input signal. Each pulse is approximated with a model generated from a multi-exponential curve, and a Least Squares fitting algorithm determines the optimal model parameters. Using the parameters of the mathematical model, three different classifiers (Bayesian, SVM and KNN) were trained and tested to discriminate among healthy controls and patients with COVID, stratified according to the severity of the disease. Results are validated with the leave-one-subject-out validation method.
Main results: Results indicate that the fitting procedure obtains a very high determination coefficient (above 99% in both controls and pathological subjects). The proposed Bayesian classifier obtains promising results, given the size of the dataset, and variable depending on the classification strategy. The optimal classification strategy corresponds to 79% of accuracy, with 90% of specificity and 67% of sensibility.
Significance:The proposed approach opens the possibility of introducing a low cost and non-invasive screening procedure for the fast detection of COVID-19 disease, as well as a promising monitoring tool for hospitalized patients, with the purpose of stratifying the severity of the disease.
Keywords: Microcirculation, COVID-19, Modelling, PPG
1. Introduction
Coronavirus disease 2019 (COVID-19) is a condition caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). COVID-19 was identified in Whuan (central China) in late 2019. Since then, this disease has spread worldwide and WHO declared COVID-19 a pandemic on March 11, 2020. The trend of the spread of the disease led to a severe global health crisis with a huge impact on health systems [1]. According to the data reported by the World Health Organization, as of 3 April 2022 there were more than 489 million cases and more than 6 million deaths worldwide [2].
The novel coronavirus SARS-CoV-2 manages to infect the human body mainly by binding to epithelial cells in the oral and nasal cavity. In particular, this infection acts through angiotensin-converting enzyme 2 (ACE2) receptors, widely distributed in the respiratory tract and in other tissues such as skin and arterial and venous endothelium [3], [4]. As a result, SARS-CoV-2 can induce several feared consequences in addition to respiratory complications. Among the non-respiratory complications, a high prevalence of cardiovascular diseases were found in patients with COVID-19 [5]. It was reported that over 7% of COVID-19 patients were affected by myocardial damage. This percentage can rise to 22% in the case of critically ill patients [6]. Moreover, SARS-CoV-2 infection can modify endothelial cells morphology as well as induce their apoptosis. As a result of the infection, the endothelial cells may trigger the immune system to release a storm of cytokine. This condition, in association with endothelial dysfunction, can induce microvascular damage and contribute to multiorgan failure [4].
Since endothelium has an important role in the regulation of vascular tone and the maintenance of vascular homeostasis, endothelial alteration may lead to important consequences such as microvascular abnormalities [7].
In this sense, it was reported that severe form of COVID-19 is a systemic disease that affects the microvessels of the body. Microvascular alterations have been observed both in skin and sublingual circulation [8]. In particular, the heterogeneity of circulation and reduction of flow velocity in addition to a deformation of red blood cells was found [7], [9].
The timely assessment of the microcirculation of patients with COVID-19 is important because the impairment of the microvascular response may be correlated with the severity of the disease [9]. In this sense, it is well documented how endothelial dysfunction and microcirculatory changes caused by COVID-19 are associated with poor prognosis in the acute phase [4], [10]. Furthermore, ensuring the best possible treatments is important because the effects of coronavirus disease 2019 can last for a long time after healing even in the case of patients with non-severe symptoms [10], [11].
All this highlights the importance of studying the effects of COVID-19 on the microcirculation. Since microvascular evaluation can be hampered by the condition and the treatments to which these patients may be subjected, the use of devices such as photoplethysmography (PPG) may represent a valid solution. PPG technique is a non-invasive, low cost and user-friendly method easy to perform. Furthermore, the use of PPG technique could allow a more precise assessment and monitoring of the microcirculation, even remotely, contributing to the detection of the disease and its severity [12]. The aim of the study was to define a mathematical model representing the microvascular flow starting from a PPG signal in order to detect early alterations in patients with COVID-19. The definition of this mathematical model could allow a timely detection of the presence of the disease and the evaluation of its severity.
2. Methods
A total of 143 subjects were enrolled in this study. The subjects considered were assigned to Control (50) and Covid (93) groups. The Covid group was, in turn, divided into Group 1 (47) and Group 2 (46) on the basis of the severity of the disease. Control group, referred as Group 0, was composed of healthy workers operating at the San Giuseppe hospital (Empoli - Italy) while groups 1 and 2 were composed of patients admitted to the same hospital. Only white Caucasian subjects were included in the study. The clinical classification and assignment of patients to group 1 and group 2 was carried out on the basis of ventilation support and/or oxygen therapy required for the treatment of respiratory failure caused by COVID-19. In particular, two indexes were adopted: the Horowitz index P/F or PaO2/FiO2: ratio of arterial oxygen partial pressure (PaO2 in mmHg) to fractional inspired oxygen (FiO2 expressed as a fraction, not a percentage) [13] and the ROX index [SpO2/FiO2]/respiratory rate, where SpO2 is the peripheral oxygen saturation [14].
Specifically the two groups of patients were defined as follow:
-
•
Group 1: Patients with and (Respiratory Rate) a/min. and at 2 h, at 6 h and at 12 h, receiving low flow oxygen therapy (nasal canula or face masks) or HFNC only without positive pressure ventilatory support.
-
•
Group 2: Patients with and/or , mmHg and/or a/min. and at 2 h, at 6 h and at 12 h, receiving non invasive positive pressure ventilatory support (CPAP - Continuous Positive Airway Pressure or NIV - Non Invasive Ventilation).
The acquisition procedure involved a commercial system, described in more detail in the paragraph 2.1, coupled with a small datalogger equipped with a custom software written in Python language. The elaboration steps foresaw a preprocessing and segmentation step for detecting individual cardiac cycles, a model of each cardiac cycle with mathematical function and the analysis of the model parameters. These elaboration steps were implemented offline on a dedicated workstation, using Matlab workspace (The Math Works, Inc., 2021).
Patients gave informed consent to the procedure according to the Declaration of Helsinki before the acquisitions of the PPG signal [15]. The study protocol was approved by the local ethics committee (CEAVC 19059).
Data was anonymized during the acquisition phase. The PPG waveform alone was considered and associated with the experimental groups.
2.1. Signal acquisition procedure
The system for the acquisition of the photoplethysmographic (PPG) signal was composed of three components: a finger pulse oximeter probe, Mindray touchscreen monitor (Mindray ePM 10 - Mindray, China), and a single-board computer - Raspberry Pi 3. The finger pulse oximeter probe was positioned on the right forefinger for 5 min. This device was wired to the SpO2 input of the monitor providing data acquisition and real-time visualization of the PPG signal. The monitor was also connected by means of Ethernet connection with the Raspberry. The first two components constitute the standard monitoring system in use in the hospital, while the third element acts only as a datalogger, allowing data to be collected easily. The connection between the monitor and the datalogger was based on the standard HL7 protocol, already present in the monitor. An HL7 server module was installed on the Pi 3 device which allowed the continuous data storage on the device itself. Collected data was downloaded using an offline procedure at the end of the acquisition phase. The monitor was programmed by entering a unique numerical identifier for patient identification before each acquisition. This identifier was transmitted along the HL7 stream and was thus associated with each signal. Consequently, no user intervention was required on the Pi 3 device for managing the recordings.
Each acquisition lasted 5 min, and was preceded by an acclimatization phase of 10 min. This phase was included in order to let the skin temperature of the patients reach a stable value to avoid any possible data bias caused by temperature variations that in turn, may have introduced different levels of vasodilation.
2.2. Signal preprocessing
The first preprocessing step consisted in an upsampling procedure, followed by a smoothing filter. The monitor provided a waveform sampled at 60 Hz that was upsampled to a frequency of 100 Hz to obtain a smoothing waveform. This increased the number of points available for the fitting procedure, without introducing higher frequency components, not present in the original signal. Subsequently, a low pass filter with a cutoff frequency of 30 Hz was applied in order to remove high-frequency noise that could affect data. Once the signals were upsampled and filtered, the waveform was segmented into single pulses: a local maximum detector identified possible candidates; those points (i.e. local maximums) could be either systolic peaks, or spurious detections usually related to the ripples present in the PPG waveform. A refinement step eliminated spurious detection using a set of heuristic rules as the amplitude and the temporal difference between peaks and variability of neighboring cycles. Diastolic valleys, constituting the separation points among consecutive cycles, were finally identified as the absolute minimum present between each pair of maximums.
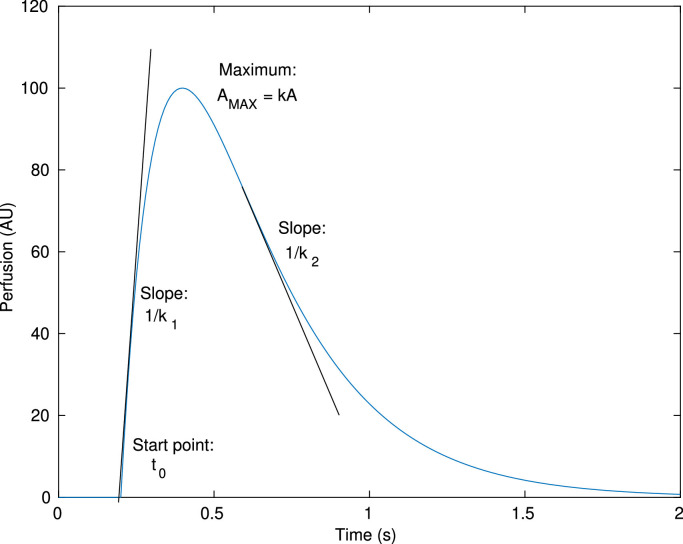
All the signal key points related to the preprocessing phase are shown in Fig. 1 . The segmentation algorithm was a derivation of the algorithm developed for the analysis of perfusion signals acquired using Laser Doppler Flowmeter (LDF) [16], [17], [18].
Fig. 1.
Signal key points of the preprocessing phase.
2.3. Pulse wave modelling
Each cardiac cycle is independently modeled by fitting a parametric function to the curve to obtain its best approximation. The performances of the fitting, thus, strictly depend on the structure of the chosen function. Several models have been proposed to this purpose [19]. The model presented in this study is based on the same structure we used in our recent studies focused on the effect of type 2 diabetes [20] and ageing [21] on microcirculation. In brief, the model assumes that the pulse waveform is generated by a linear system; this assumption helps to simplify the mathematical description of the system response, as the response of any linear system to an ideal pulse can be expressed as a sum of decreasing exponential functions. Thus, a single PPG cycle can be modelled by a sum of decreasing exponential functions , where can be expressed as:
| (1) |
where represents the maximum flow, that is measured at time , and is the time constant of the system. The expression above is valid up to the start of the next cardiac cycle. A similar approach is exploited in the well-known Windkessel model [22], which is focused on the diastolic part of the cardiac pulse. However this expression presents a discontinuity for that is physiologically implausible.
A possible workaround that ensures the continuity of the curve is based on coupling together a pair of exponential functions, thus creating an ”exponential pulse function”, defined as:
| (2) |
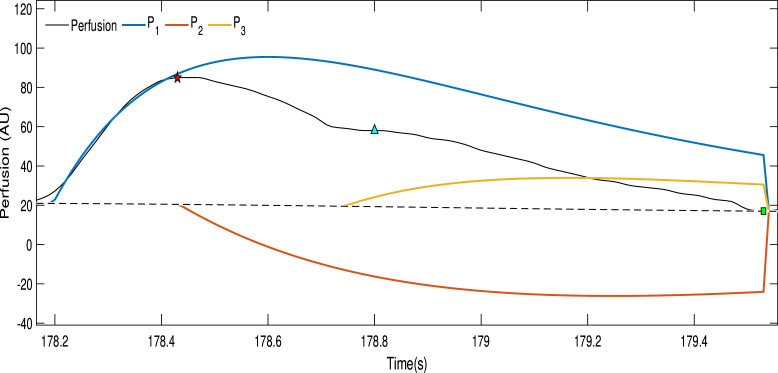
with , where represents the pulse amplitude, the slope of the rising phase and the slope of the falling phase. This definition does not present discontinuities, thus avoiding the main issue of Eq. 1. It also has an asymmetrical ”pulse like” shape, i.e. the curve tends to zero with large values of , with different slopes on the two sides of the peak. The approximate meaning of the parameters is graphically represented in Fig. 2 .
Fig. 2.
Exponential pulse with graphic representation of the parameters.
While a sum of exponential curves produces (in general) an unsuitable pattern for a physiological signal, any sum of exponential pulses has always a practically limited support, without any non-causal effect (assuming ). Using this auxiliary representation, we propose to model the cardiac cycle using a linear combination of three exponential pulses (, and ), each one modelling a specific phase of the PPG wave:
-
•
models the systolic wave;
-
•
models the diastolic wave, meaning the negative pulse generated by the closing of the aortic valve;
-
•
models the reflected wave.
Fig. 3 shows a combination of three exponential pulses, replicating the shape of the PPG signal.
Fig. 3.
The black curve represents a single pulse from the photoplethysmographic signal while the three exponential pulses are represented by the colored curves.
The resulting model expression thus becomes:
| (3) |
where , and are the parameters of the th pulse and is the start time of the same pulse. Thus, the proposed model needs to define a vector composed of twelve parameters, , to fully specify its shape.
The modeling procedure identifies, for each cardiac cycle , the optimal parameter vector that minimizes an objective function, defined as the sum of the squared differences between the measured waveform and the model . The minimization procedure adopts the Levemberg-Marquardt algorithm. This algorithm is an iterative procedure needing to specify a starting value for , called , that is refined until it reaches the optimal solution. This seed value was determined, for every cycle, using a set of heuristic rules on the curve waveform (i.e., position of dicrotic notch, maximum amplitude, cycle length). An acceptable range (maximum and minimum value) for every parameter was also defined.
The minimization procedures yield as output the optimal parameter vector as well as a quantification of the goodness of fitting, that is represented by the determination coefficient , defined as follow:
| (4) |
where SSR (Sum of Squared Regression) is the deviance explained from the model, , where is the mean value of over the cardiac cycle; SST (Sum of Squared Total) is the total deviance, ; and SSE (Sum of Squared Error) is the deviance not explained from the model, .
The determination coefficient quantifies the quality of the fit on a single cardiac cycle; an overall evaluation is provided by the mean determination coefficient defined as:
| (5) |
where is the determination coefficient for the subject , is the number of subjects and is the number of cardiac cycles of subject .
It is worthy of attention that the fitting interval is limited to a single cardiac cycle, disregarding both the ”tail” from the model describing the previous cycle and the error between the model and the physiological signal occurring after the starting of the following cycle.
The fitting procedure thus associates every cardiac cycle with the corresponding vector.
2.4. Statistical analysis
A preliminary statistical analysis allows the assessment of the capability of the proposed model for capturing variations of the PPG waveform correlated with the presence and severity of the disease.
We determined the statistical distribution for each parameter and for each group of subjects; differences among the groups where analysed by using t-test. This procedure also allows the identification of potential of variation of the parameters with the increase of the disease severity.
2.5. Classification technique and methods
The number of subjects involved in the trial is relatively large; however, the creation of separate training and test sets yields a number of subjects that is too small for an adequate evaluation of the system performance.
Although the number of cardiac cycles (and therefore the number of vector parameters ) is large, the consecutive cardiac cycles belonging to the same subject cannot be assumed to be unrelated to each other; thus, any strategy for creating training and test sets needs to consider possible correlations among the samples belonging to the same subject.
Therefore, it is advisable to use the Leave-One-Subject-Out (LOSO) [23] technique for testing the performance of the classifier: it consists in removing a subject from the dataset (composed by subjects), training the classifier on the remaining subjects and testing on the removed subject. Afterwards, the removed subject is reinserted into the dataset and the steps are repeated iteratively until all the N subjects have been removed once. The global performance of the classifier is evaluated by averaging the performance of every single iteration.
Moreover, the large number of consecutive data cycles available for each subject allows the design of three different strategies to classify each subject:
-
•
Single cycle: this strategy classifies the cardiac cycles composing the PPG signal of each patient, independently of each other. The patient classification is obtained, at a later stage, by an ensemble classifier, based on the majority of classifications on the single cycles. In this case, the classifier’s input is composed of the modelling parameters , the cycles length and the determination coefficients of each cycle .
-
•
Double cycle: the strategy is similar to the previous one, but in this case the cardiac variability is taken into account by providing the classifier with an input vector containing the parameter vectors of two consecutive cardiac cycles. Again, an ensemble classifier provides the final subject classification, as in the previous case.
-
•
Mean cycle: in this case, the classifier operates on each subject, and not on each cardiac cycle. Every subject is represented by one 24-component vector , containing information regarding the mean and standard deviation, over all cycles belonging to the subject , of each component of the vector.
Each one of those three strategies was tested on three different classifiers: Support Vector Machine (SVM) [24], Bayesian Classifier (BYM) [25] and K-Nearest Neighbor (KNN) [26].
The ensemble classifier used in the first two strategies, is based on a variant of the majority voting obtained by adding a voting threshold . It is assumed that the recording for a subject contains cycles (or pairs of cycles, in case of the second strategy described above), and that the classifier labels as healthy cycles, and the remaining as patients ones. Therefore, the subject, as a whole, is classified healthy if . When , the ensemble classifier corresponds to the classical hard majority voting classifier.
The latter strategy provides a single classification result for each patient, thus no ensemble classifier is possible. In this case, a variable per-class misclassification cost allows the balancing of sensibility and specificity. The cost represents the misclassification cost of a subject with Covid-19 (false negative), while the cost corresponding to a false positive is assumed unitary. Naive Bayes classifier corresponds to a value . Subsequently, further optimization procedures were performed only for the classifiers that achieved better results.
2.6. Threshold optimization
By selecting larger (or smaller) values of and , we may balance sensibility and specificity of the ensemble classifier in order to optimize classification results.
Since quick screening tests are very important due to the high contagiousness of the virus, we decided to reward sensibility at the expense of a few percentage values of specificity. To this aim, ROC curve of each classifier was evaluated in order to attempt new values of and that increase the sensibility keeping the specificity around the starting value.
2.7. Parameters optimization
The results obtained with the threshold optimization on the various classifiers suggest that the number of available subjects is not sufficient for completely avoiding overfitting issues; therefore, we introduced a regularization step aimed at removing the features that do not provide adequate discriminating power. The selected optimization strategy is similar to the backward feature selection (BFS) and follows the iterative procedure described below. In each procedure iteration, one of the parameters was removed from the input vector of the classifier, a new classifier was so designed and its performance evaluated. The best classifier was identified, and we moved to the next step. The entire procedure was repeated, by removing one more parameter, until we observed that the performance did not improve furtherly.
3. Results
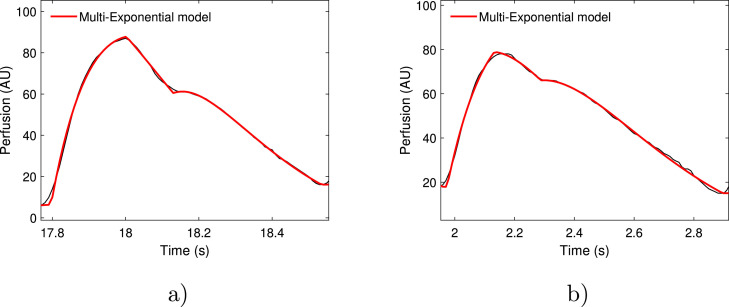
The proposed model provides a very good representation of the PPG signal. After the fitting procedure based on the Levemberg-Marquardt algorithm, we obtained very high values of the coefficient: = 98.99% (healthy group 0) and = 98.98% (Covid, groups 1 and 2); Fig. 4 .
Fig. 4.
Red curves represent multiexponential model that fits two cardiac cycles (in black): a) healthy subject and b) COVID-19 subject.
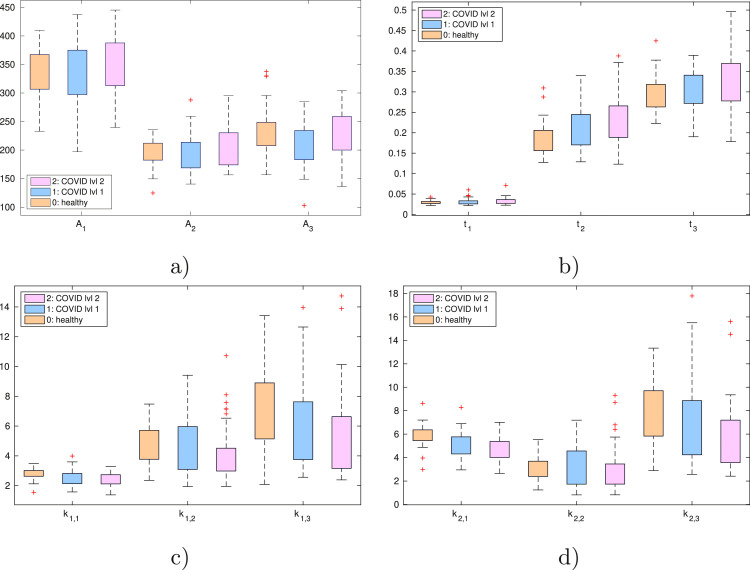
A visual evaluation of the capability of the proposed model to capture the differences among the different groups is shown in Fig. 5 , where a noticeable trend is present, as concerns parameters and , comparing the groups 0, 1 and 2; in particular, parameters tends to decrease from group 0 to group 2, while starting times and increase with the worsening of the disease.
Fig. 5.
Statistical distribution of the parameters given by the mean on each pulse of each subject: pulse amplitudes (a), starting times (b), rising slope (c) and falling slope (d).
According to the results observed in the boxplot, we performed a comparison of healthy subjects (group 0) and patients (group 1 and group 2), Table 1 .
Table 1.
Mean and standard deviation of the model parameters of all cardiac cycles in the control group (group 0) and mild-to-moderate Covid group (groups 1 and 2), respectively. The symbol * next to the p-value indicates statistically significant differences ().
| Parameter | Control | Covid | p-value |
|---|---|---|---|
| 0.332 | |||
| 0.389 | |||
| 0.189 | |||
| 0.144 | |||
| 1 | |||
| 1 | |||
| 0.236 |
A detailed analysis highlights a ”slower” response in the Covid case: all parameters, unless , decrease in the Covid group compared to the Control group. Thus, the corresponding exponential pulses are ”wider” with respect to the Control case. While the changes in the systolic wave and in the reflected wave are statistically significant, changes in (diastolic wave) are not significant. The amplitudes of the pulses do not present variation. Starting times of the pulses () present very small differences. In particular, parameter, namely the starting time of the diastolic pulse, is statistically significant. The increased value of in the case of patients with Covid-19 confirms the ”slower” increase of the waveform.
According to the data of Table 1, we tested the classifier on healthy vs Covid (group 0 vs groups 1 and 2). Moreover, we also evaluated the performances of a classifier trained at identifying healthy vs moderate Covid subjects (group 0 vs group 2), in order to avoid boundary situations between mild and moderate Covid patients, or between mild and healthy subjects. Among the groups considered in this study there was a threshold based only on clinical parameters. This condition may have complicated finding differences among the groups. However, a difference was present between groups 0 and 2, that is, in the case of groups with very different clinical parameters. In fact, as shown in Fig. 5, parameter values from Group 1 almost always assume values between Group 0 and Group 2. Thus, the retention of subjects affected by mild Covid-19 disease inside COVID-19 group could lead to a wrong classification.
The classification process was tested on three different classifiers. We observed that both KNN and SVM algorithms present unsatisfactory performances. The results obtained with the BYM classifier are reported in Table 2 . In Table 3 , the confusion matrix for the best classification case related to Table 2 is reported.
Table 2.
Classification results obtained with BYM classifier, hard voting ensemble classifier/naive Bayes classifier, with the different grouping and classification strategies. (1,2) is the sum of group 1 and group 2 (Covid group).
| Groups | Strategy | Sensibility | Specificity | Accuracy | |
|---|---|---|---|---|---|
| 0 vs (1, 2) | Single | = 1 | 77% | 56% | 70% |
| 0 vs (1, 2) | Double | = 1 | 71% | 66% | 69% |
| 0 vs (1, 2) | Mean | = 1 | 68% | 74% | 70% |
| 0 vs 2 | Single | = 1 | 80% | 66% | 73% |
| 0 vs 2 | Double | = 1 | 78% | 66% | 72% |
| 0 vs 2 | Mean | = 1 | 63% | 82% | 73% |
Table 3.
Confusion matrix obtained from the comparison between Group 0 and Group 2 adopting the mean pulse strategy and = 1.
| Group 0 | Group 2 | Total | |
|---|---|---|---|
| Group 0 | 41 | 9 | 50 |
| Group 2 | 17 | 29 | 46 |
The patient classification reported for the single and double classification strategy was obtained with the hard voting ensemble classifier, i.e. the patient was classified as ”Covid-19” if at least 50% ( = 1 or =1) of the cycles were classified correspondingly.
Results indicate that, although the classifier accuracy is quite low, it is able to achieve a good sensibility, up to 77% in the Control vs Covid classification, and up to 80% in the control vs moderate Covid classification, where ”boundary” conditions are not present. Then, we worked on the last classification, namely controls vs moderate Covid.
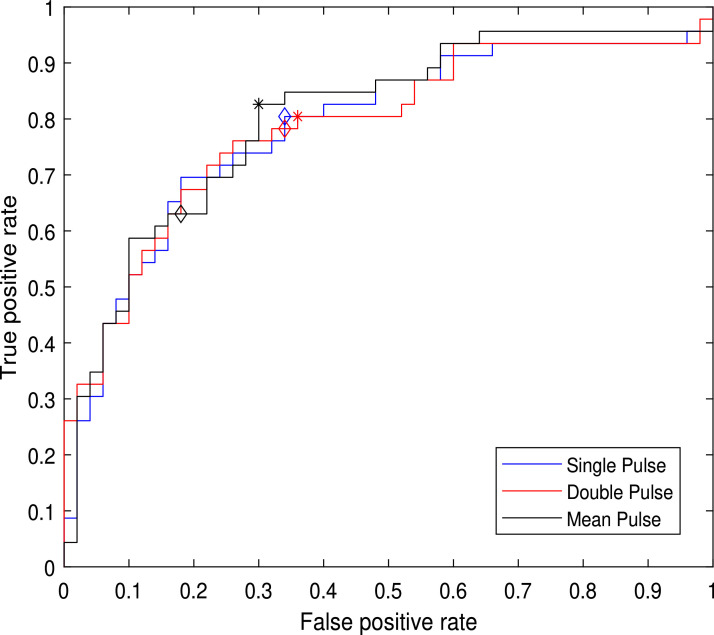
Given the difference between sensibility and specificity values, we optimized the classification on the basis of the analysis of the ROC curve, shown in Fig. 6 .
Fig. 6.
ROC curves, obtained with the complete feature vector: blue curve, BYM classifier with single cycle; red curve, BYM classifier with double cycle; black curve, BYM classifier on mean pulse. Diamonds () indicate the hard voting classifier, stars (*) indicate the optimized working point of each classifier.
Whereas the method appears to be more promising for a quick screening procedure, where it gives an early detection warning, the selection of the optimal threshold allows a higher sensibility value, without sensible degradation of the specificity. With these aims, the optimal value of for the double pulse classification, marked with the ”*” in the plot, corresponds to and for the mean pulse classifier. The analysis of the ROC curve confirmed that, for the single pulse classifier, corresponds to the optimal threshold.
The results obtained with the optimal threshold values were reported in Table 4 . In particular, with mean strategy we obtained an increase of sensibility up to 83% with a lower specificity value of 70%, and an accuracy value of 76%. In Table 5 , the confusion matrix for the best classification case related to Table 4 is reported.
Table 4.
Classification results, Bayes classifier, all classification strategies, optimized value, group 0 vs group 2.
| Strategy | Sensibility | Specificity | Accuracy | |
|---|---|---|---|---|
| Single | 80% | 66% | 73% | |
| Double | 80% | 64% | 72% | |
| Mean | 83% | 70% | 76% |
Table 5.
Confusion matrix obtained from the comparison between Group 0 and Group 2 adopting the mean pulse strategy and optimized value.
| Group 0 | Group 2 | Total | |
|---|---|---|---|
| Group 0 | 35 | 15 | 50 |
| Group 2 | 8 | 38 | 46 |
The reported results indicate that a Bayesian classifier, in the optimal conditions, i.e. dataset restricted to groups 0 and 2, tested with the LOSO technique, hard voting classifier and with mean pulse classification strategy, reaches an accuracy of 73%.
Subsequently, after the threshold optimization for the mean pulse classification strategy, an accuracy of 76% with a sensibility of 83% and a specificity of 70% were reached.
Given the architecture of the Bayesian classifier, however, we expect its performance may be negatively impacted by the presence of not significant, or even misleading, features. The parameters optimization procedure identifies the optimal parameter set, separately for each classification strategy, confirming that several parameters do not provide valuable information for the classification task. The resulting optimal feature sets are reported in Table 6 .
Table 6.
Leftover parameters for each classification strategy after the optimization process.
| Strategy | Feature set |
|---|---|
| Single | , , , , , , , , , , , , and |
| Double | , , , , , , and |
| Mean | , , , , , , , , and |
The optimization procedure identifies five features appearing to have a higher relevance, as those features were selected by the procedure in all classification strategies: , , , and . As expected, the elimination of the misleading features improves the classification results, as shown in Table 7 , which indicates that the overall accuracy improves about 3% in all the classification strategies except for the single pulse classification strategy where we can observe that all the parameters were preserved because the parameters optimization didn’t improve the performance of the classifier.
Table 7.
Classification results, Bayes classifier, optimized threshold, optimized parameter set.
| Groups | Strategy | Sensibility | Specificity | Accuracy | |
|---|---|---|---|---|---|
| 0 vs 2 | Single | = 1 | 80% | 66% | 73% |
| 0 vs 2 | Double | = 1.04 | 85% | 70% | 77% |
| 0 vs 2 | Mean | 87% | 72% | 79% |
4. Discussion
With this study, we investigated the feasibility of using photoplethysmographic signal for the recognition of patients hospitalized with COVID-19 as well as the severity of the disease itself.
In particular, the proposed multiexponential model showed an excellent representation of the PPG signals considering all the patients and controls investigated. This result was a good starting point for the pursuit of the objectives of the study. As a whole, the results of this study confirmed the presence of microvascular alterations in patients with COVID-19 [8], [27]. Significant differences between the patient group and the control group were found, as reported in Table 1. Regarding the systolic pulse and the reflected pulse wave, both the slope of the rising phase and the falling phase were lower in patients with COVID-19. An inverse relationship between the slope of the curves considered and the severity of the disease was found (Fig. 5).
The results of this study are in line with what was reported in previous studies with regards to the effects of COVID-19 on the microcirculatory flow [4], [10]. In particular, our results suggest that SARS-CoV-2 infection can lead to a “damper” microcirculatory response. The damping of the shape of the curve along with minor slopes confirms the possible effect of vasoconstriction that these patients may show [28], [29]. This condition can be the result of endothelial damage and cytokine storm induced over time by the SARS-COV-2 infection [4], [10], [30]. However, the alteration of several other microcirculatory parameters such as: vascular densities, heterogeneity index, functional capillary density, and microvascular flow index, in addition to red blood cells velocity, blood pressure variability and PPG dropout [8], [31], [32], [33], were associated with COVID-19 disease. A number of studies evaluated the usefulness of PPG signal analysis in the treatment of COVID-19 patients treated in ICU units. Peck et al. in a recent partially prospective, observational study used the PPG signal to confirm the presence in a large number of patients of PPG dropout threshold and PPG amplitude abnormalities [33]. Other studies have verified how PPG technology can be used for monitoring, even remotely, patients with COVID-19 at different levels of severity [34], [35], [36].
Regarding the ability to recognize between the groups of controls and patients, the best performances of the proposed model were obtained considering patients affected by a higher level of severity of the disease and by using the Bayesian classifier both with the mean pulse and single pulse strategies (Table 2).
However, the results achieved were not completely satisfactory. In particular, the objective of obtaining a good result in terms of specificity and sensibility with the same strategy was not fully achieved: in fact, with mean pulse strategy a sensibility lower then specificity was present, while with both single and double pulse strategy the opposite situation was present. The greater heterogeneity of PPG signals found in patients with COVID-19 could be one of the causes of this not fully satisfactory result. In this sense, some studies reported a greater heterogeneity in microcirculation in patients with COVID-19 treated in the intensive care unit [27], [37].
The subsequent use of the ROC curve allowed the further improvement of the performance of the classifier and overcoming the limits related to the evident difference between the sensibility and specificity values. In particular, through this procedure, the BYM classifier with the mean pulse strategy and cost allowed us to obtain a sensibility of 83% with a lower specificity value of 70% and accuracy value of 76% (Table 4). As a whole, this analysis enabled the defining of a more promising and rapid screening procedure with a high level of sensibility but a lower specificity.
Subsequently a procedure of parameter optimization was applied to the optimized threshold model in order to evaluate if some features could negatively impact on the accuracy of the classifiers. This optimization led to an accuracy of 77%, with sensibility and specificity values respectively at 85% and 70% regarding the double pulse strategy, while for the mean pulse strategy, an accuracy of 79% with a sensibility value of 87% and a specificity value of 72% were reached (Table 7).
Moreover, this procedure and the result showed the limits of using a BYM classifier, highlighting the importance of carrying out an appropriate management and selection of the characteristics to be considered. In particular, the optimization procedure allowed the identification of a set of parameters common to the different classification strategies proposed. In particular, five characteristics were found to be common to all classification strategies. Among these parameters, the presence of the rising slope of the systolic curve confirmed the possible role of COVID-19 disease in the cardiovascular condition [38]. Furthermore, the presence of two out of four parameters related to the reflected wave could confirm the presence of microvascular abnormalities.
The modifications of PPG signals found with this study may be less evident in patients with a different clinical picture. In fact, patients with severe clinical conditions could show more complex microcirculatory alterations with different characteristics of the PPG signal. In this sense, in our recent studies we have investigated the relationship between PPG signal and Sepsi conditions in addition to Covid-19 disease [39], [40]. The fact that many factors can contribute to hindering the analysis of individual PPGs obtained from patients with Covid-19 is to be considered. Among these, as reported in recent articles, skin color can also play an important role [41], [42]. In this regard, only white Caucasian subjects were considered in this study, favoring the appropriate analysis of the collected signals.
5. Conclusion
This study allowed us to use microcirculation analysis by photoplethysmography signal for the screening and classification of patients affected by COVID-19. The analysis of the PPG signal is important because Sars-Cov-2 infection can cause significant alterations in the microcirculation, particularly in patients with a more severe condition. The fact that PPG signal analysis consists of a simple, fast, painless and inexpensive bedside test may further increase clinical interest in this test for the treatment of patients even during the COVID-19 pandemic waves. The multi-exponential model proposed in this study showed a high ability to detect the physiological changes related to COVID-19, especially for the subjects showing moderate severity condition.
The final results achieved indicate how the analysis of the proposed PPG signals can play a role in the screening procedure in which it is important to identify a high rate of true positives.
Author credit statement
Eva Rossi: Data elaboration, Data modelling and results extraction, Writing: original draft-review-editing.
Cosimo Aliani: Data elaboration, Data modelling and results extraction, Writing: original draft-review-editing.
Piergiorgio Francia: Methodology, Writing: original draft-review-editing, Formal analysis, Reviewing.
Rossella Deodati: Data acquisition, Reviewing, Validation.
Italo Calamai: Data acquisition, Reviewing, Validation.
Marco Luchini: Data acquisition and curation, Writing: original draft.
Rosario Spina: Data acquisition, Supervision, Validation, Funding acquisition.
Leonardo Bocchi: Conceptualization, Data modelling, Writing: original draft-review-editing, Validation, Funding acquisition.
All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Regione Toscana, Italy (Bando Ricerca COVID-19 Toscana).
Ethical Approval
The study protocol was approved by the local ethics committee (CEAVC 19059).
Declaration of Competing Interest
None.
Acknowledgment
The authors thank Ian Webster B.A. (Hons) PGCE for revising the English content.
References
- 1.Zhou P., Yang X.-L., Wang X.-G., Hu B., Zhang L., Zhang W., et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579(7798):270–273. doi: 10.1038/s41586-020-2012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.World health organization: Modes of transmission of virus causing COVID-19: implications for IPC precaution recommendations. https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19---5-april-2022; 2022. Last access: 08-04-2022.
- 3.Kowalik M.M., Trzonkowski P., Łasińska Kowara M., Mital A., Smiatacz T., Jaguszewski M. Covid-19 – toward a comprehensive understanding of the disease. Cardiol J. 2020;27(2):99–114. doi: 10.5603/CJ.a2020.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Das S. Microcirculatory changes and thrombotic complications in COVID-19. Br J Community Nurs. 2021;26(10):474–480. doi: 10.12968/bjcn.2021.26.10.474. [DOI] [PubMed] [Google Scholar]
- 5.Mason R.J. Pathogenesis of COVID-19 from a cell biology perspective. Eur Respir J. 2020;55(4) doi: 10.1183/13993003.00607-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Clerkin K.J., Fried J.A., Raikhelkar J., Sayer G., Griffin J.M., Masoumi A., Jain S.S., Burkhoff D., Kumaraiah D., Rabbani L., Schwartz A., Uriel N. COVID-19 and cardiovascular disease. Circulation. 2020;141(20):1648–1655. doi: 10.1161/CIRCULATIONAHA.120.046941. [DOI] [PubMed] [Google Scholar]
- 7.Hohberger B., Ganslmayer M., Lucio M., Kruse F., Hoffmanns J., Moritz M., et al. Retinal microcirculation as a correlate of a systemic capillary impairment after severe acute respiratory syndrome coronavirus 2 infection. Front Med. 2021;8:1013. doi: 10.3389/fmed.2021.676554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kanoore Edul V.S., Caminos Eguillor J.F., Ferrara G., Estenssoro E., Siles D.S.P., Cesio C.E., et al. Microcirculation alterations in severe COVID-19 pneumonia. J Crit Care. 2021;61:73–75. doi: 10.1016/j.jcrc.2020.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mesquida J., Caballer A., Cortese L., Vila C., Karadeniz U., Pagliazzi M., et al. Peripheral microcirculatory alterations are associated with the severity of acute respiratory distress syndrome in COVID-19 patients admitted to intermediate respiratory and intensive care units. Crit Care. 2021;25(1):1–10. doi: 10.1186/s13054-021-03803-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Charfeddine S., Ibn Hadj Amor H., Jdidi J., Torjmen S., Kraiem S., Hammami R., et al. Long COVID 19 syndrome: is it related to microcirculation and endothelial dysfunction? Insights from tun-endcov study. Front Cardiovasc Med. 2021;8 doi: 10.3389/fcvm.2021.745758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lopez-Leon S., Wegman-Ostrosky T., Perelman C., Sepulveda R., Rebolledo P.A., Cuapio A., Villapol S. More than 50 long-term effects of COVID-19: a systematic review and meta-analysis. medRxiv. 2021 doi: 10.1101/2021.01.27.21250617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rovas A., Osiaevi I., Buscher K., Sackarnd J., Tepasse P.-R., Fobker M., Kühn J., Braune S., Göbel U., Thölking G., et al. Microvascular dysfunction in COVID-19: the mystic study. Angiogenesis. 2021;24(1):145–157. doi: 10.1007/s10456-020-09753-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Horovitz J.H., Carrico C.J., Shires G.T. Pulmonary response to major injury. Arch Surg. 1974;108(3):349–355. doi: 10.1001/archsurg.1974.01350270079014. [DOI] [PubMed] [Google Scholar]
- 14.Roca O., Messika J., Caralt B., García-de Acilu M., Sztrymf B., Ricard J.-D., et al. Predicting success of high-flow nasal cannula in pneumonia patients with hypoxemic respiratory failure: the utility of the rox index. Journal of Crit Care. 2016;35:200–205. doi: 10.1016/j.jcrc.2016.05.022. [DOI] [PubMed] [Google Scholar]
- 15.https://www.wma.net/policies-post/wma-declaration-of-helsinki-ethical-principles-for-medical-research-involving-human-subjects/, Last access: 27-12-2021; 2021.
- 16.Sorelli M., Perrella A., Bocchi L. Detecting vascular age using the analysis of peripheral pulse. IEEE Trans Biomed Eng. 2018;65(12):2742–2750. doi: 10.1109/TBME.2018.2814630. [DOI] [PubMed] [Google Scholar]
- 17.Sorelli M., Francia P., Bocchi L., De Bellis A., Anichini R. Assessment of cutaneous microcirculation by laser doppler flowmetry in type 1 diabetes. Microvasc Res. 2019;124:91–96. doi: 10.1016/j.mvr.2019.04.002. [DOI] [PubMed] [Google Scholar]
- 18.Morelli A., Sorelli M., Francia P., Bocchi L. In: 8th European medical and biological engineering conference. Jarm T., Cvetkoska A., Mahnič-Kalamiza S., Miklavcic D., editors. Springer International Publishing; Cham: 2021. Modelling of microcirculatory dynamics with auto-regressive models; pp. 824–832. [Google Scholar]
- 19.Fleischhauer V., Ruprecht N., Sorelli M., Bocchi L., Zaunseder S. Pulse decomposition analysis in photoplethysmography imaging. Physiol Meas. 2020;41(9):095009. doi: 10.1088/1361-6579/abb005. [DOI] [PubMed] [Google Scholar]
- 20.Rossi E., Aliani C., Francia P., Anichini R., Bocchi L. International conference on medical and biological engineering. Springer; 2021. An improved model for the assessment of cutaneous microcirculation in type 1 diabetes; pp. 37–46. [Google Scholar]
- 21.Aliani C., Rossi E., Francia P., Bocchi L. Vascular ageing and peripheral pulse: an improved model for assessing their relationship. Physiol Meas. 2021;42(12):125002. doi: 10.1088/1361-6579/ac3e87. [DOI] [PubMed] [Google Scholar]
- 22.Frank O. Die grundform des arteriellen pulses [basic shape of the arterial pulse] Z Biol. 1899;37:483–526. [Google Scholar]
- 23.Sammut C., Webb G.I., editors. Springer US; Boston, MA: 2010. Leave-one-out cross-validation; pp. 600–601. [DOI] [Google Scholar]
- 24.Cortes C., Vapnik V. Support-vector networks. Mach Learn. 1995;20(3):273–297. doi: 10.1023/A:1022627411411. [DOI] [Google Scholar]
- 25.Hand D.J., Yu K. Idiot’s bayes: not so stupid after all? Int Stat Rev. 2001;69(3):385–398. [Google Scholar]
- 26.Altman N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am Stat. 1992;46(3):175–185. doi: 10.1080/00031305.1992.10475879. [DOI] [Google Scholar]
- 27.Di Dedda U., Ascari A., Fantinato A., Fina D., Baryshnikova E., Ranucci M. Microcirculatory alterations in critically ill patients with COVID-19-associated acute respiratory distress syndrome. J Clin Med. 2022;11(4) doi: 10.3390/jcm11041032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ko C.J., Harigopal M., Gehlhausen J.R., Bosenberg M., McNiff J.M., Damsky W. Discordant anti-sars-cov-2 spike protein and rna staining in cutaneous perniotic lesions suggests endothelial deposition of cleaved spike protein. J Cutaneous Pathol. 2021;48(1):47–52. doi: 10.1111/cup.13866. [DOI] [PubMed] [Google Scholar]
- 29.Farinazzo E., Dianzani C., Zalaudek I., Conforti C., Grabbe S., Goldust M. Synthesis of the data on COVID-19 skin manifestations: underlying mechanisms and potential outcomes. Clin Cosmetic Investig Dermatol. 2021;14:991. doi: 10.2147/CCID.S325552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Martini R. The compelling arguments for the need of microvascular investigation in COVID-19 critical patients. Clin Hemorheol Microcirc. 2020;75:1–8. doi: 10.3233/CH-200895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Østergaard L. Sars COV-2 related microvascular damage and symptoms during and after COVID-19: consequences of capillary transit-time changes, tissue hypoxia and inflammation. Physiol Rep. 2021;9(3):e14726. doi: 10.14814/phy2.14726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li F.-K., An D.-W., Guo Q.-H., Zhang Y.-Q., Qian J.-Y., Hu W.-G., et al. Day-by-day blood pressure variability in hospitalized patients with COVID-19. J Clin Hypertension. 2021;23(9):1675–1680. doi: 10.1111/jch.14338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Peck J., Wishon M., Wittels H., Hasty F., Hendricks S., Lee S., Wittels S. COVID-19 causes changes in photoplethysmography. Preprint. 2021 doi: 10.21203/rs.3.rs-899550/v1. [DOI] [PubMed] [Google Scholar]
- 34.Dasari A., Arul Prakash S.K., Jeni L., Tucker C. Evaluation of biases in remote photoplethysmography methods. npj Digit Med. 2021;4 doi: 10.1038/s41746-021-00462-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chauhan A., Farmah K., Goel A., Gandotra A. 2021 5th international conference on computing methodologies and communication (ICCMC) 2021. A novel patient monitoring system using photoplethysmography and IOT in the age of COVID-19; pp. 427–437. [DOI] [Google Scholar]
- 36.Rohmetra H., Raghunath N., Narang P., Chamola V., Guizani M., Lakkaniga N.R. Ai-enabled remote monitoring of vital signs for COVID-19: methods, prospects and challenges. Computing. 2021:1–27. [Google Scholar]
- 37.Abou-Arab O., Beyls C., Khalipha A., Guilbart M., Huette P., Malaquin S., et al. Microvascular flow alterations in critically ill COVID-19 patients: a prospective study. PLoS One. 2021;16(2):1–11. doi: 10.1371/journal.pone.0246636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chung M.K., Zidar D.A., Bristow M.R., Cameron S.J., Chan T., Harding C.V., et al. COVID-19 and cardiovascular disease. Circ Res. 2021;128(8):1214–1236. doi: 10.1161/CIRCRESAHA.121.317997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lombardi S., Partanen P., Bocchi L. Proceedings of the IEEE engineering in medicine and biology society conference. 2022. Detecting sepsis from photoplethysmography: strategies for dataset preparation. [DOI] [PubMed] [Google Scholar]
- 40.Lombardi S., Partanen P., Francia P., Calamai I., Deodati R., Luchini M., Spina R., Bocchi L. Proceedings of health information science and systems. 2022. Classifying sepsis from photoplethysmography. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sinaki F.Y., Ward R., Abbott D., Allen J., Fletcher R.R., Menon C., et al. Ethnic disparities in publicly-available pulse oximetry databases. Commun Med. 2022;2(1):1–5. doi: 10.1038/s43856-022-00121-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Elgendi M., Fletcher R., Liang Y., Howard N., Lovell N.H., Abbott D., et al. The use of photoplethysmography for assessing hypertension. npj Digit Med. 2019;2(1):1–11. doi: 10.1038/s41746-019-0136-7. [DOI] [PMC free article] [PubMed] [Google Scholar]