Abstract
Mechanical properties of anterior anatomical structures of eye, such as the cornea and ciliary body, play a key role in ocular function and homeostasis. However, measuring the biomechanical properties of the anterior ocular structures, especially deeper structures such as the ciliary body, remains a challenge due to the lack of high-resolution imaging tools. Herein, we implemented a mechanical shaker-based high frequency ultrasound elastography technique that can track the induced elastic wave propagation to assess the linear and nonlinear elastic properties of anterior ocular structures. Findings of this study advance our understanding of the role of anterior ocular structures in the pathogenesis of different ocular disorders, such as glaucoma.
Keywords: Elastography, Cornea, Ciliary body, Elastic wave, Intraocular pressure
I. INTRODUCTION
Glaucoma is a leading cause of permanent vision loss worldwide, affecting 1% of the population overall and 2% of people over the age of 45 [1]. In clinical practice, glaucoma is often classified as primary or secondary [2] and open angle or angle closure according to etiology and status of the anterior chamber angle [3, 4]. Glaucoma commonly refers a group of disorders including the damage to the optic nerve head by various biomechanical and vascular factors [5]. An important risk factor for glaucoma is elevated intraocular pressure (IOP), which can result from impaired aqueous humor outflow from the eye [6, 7]. Mechanical features of anterior ocular structures, such as the cornea and ciliary body, play essential roles in determining glaucoma risk and maintaining IOP homeostasis [8].
Currently, measuring the biomechanical characteristics of anterior ocular structures remains a challenge due to the lack of high-resolution imaging tools. Early detection of patients with high risk of elevated IOP and glaucoma is crucial to prevent irreversible vision loss. Therefore, a reliable and convenient method to assess the mechanical characteristics of anterior ocular structures may help provide insight into mechanisms of disease and identify high-risk patients.
Numerous studies have shown that the internal stress and mechanical properties of tissues can dramatically and interactively influence each other [9–11]. In addition, most biological tissues have a nonlinear stress-strain behavior under variable amounts of pressure. This nonlinear elasticity can cause biological tissues to become more stressed under increased pressure. For example, studies have demonstrated that the stiffness of the cornea and sclera increases with increasing IOP [12–14]. Our group previously demonstrated that IOP modulates the inherent mechanical properties of the optic nerve head and parapapillary sclera [15]. The ciliary body produces aqueous humor and undergoes dynamic anatomical changes during accommodation [8, 16]. However, there is sparse knowledge about the influence of IOP on the mechanical properties of the ciliary body.
Elastography is an emerging, non-invasive imaging method that characterizes the biomechanical properties of soft tissue and provides critical clinically relevant information for the diagnosis of ocular diseases. With respect to ocular tissues, optical coherence elastography (OCE), developed in recently, uses optical coherence tomography (OCT) [17] to detect the propagation of induced elastic waves, and it has been widely used in the biomechanical characterization of the cornea [18], lens [19] and retina [20]. However, due to its limited penetration depth, OCE is poorly suited for imaging of deeper anterior ocular structures, such as the ciliary body.
High-frequency ultrasound elastography has become an essential technique for ophthalmic imaging due to its innate advantages of balancing spatial resolution and penetration depth [21–25]. Cho-Chiang Shih et al. [26]developed a dual frequency confocal transducer to obtain stiffness distributions of both healthy porcine corneas and cornea with localized sclerosis. Chen et al. [27]used a dual-element transducer to measure the GSWV of human cornea and reconstructed its Young’s modulus. C.-C. Shih et al. [28]combined the Lamb wave model with their previously developed an ultrasonic micro-elastography imaging system for determining viscoelastic properties in thin-layer tissues. To induce small vibrations in the ocular tissue, several excitation methods have been developed, including air-puff [29, 30], acoustic micro-tapping [31, 32], acoustic radiation force (ARF) [33–36], and mechanical shaker[37, 38]. However, air-puff has inherent limitations, including relatively narrow bandwidth of the induced mechanical wave and slower relaxation times. Micro-tapping is an alternative excitation method in which a sharp pressure is applied to the tissue surface in space and time by a focused, air-coupled ultrasonic transducer [35, 39]. In micro-tapping, very little force is applied to the tissue since most of the sound intensity is reflected at the boundaries, resulting in displacement waves at the nanometer or sub-micrometer scale. As a result, a higher driving power is typically required to induce sufficient tissue deformation, which makes it challenging for deeper ocular tissues. Similarly, ARF (regular transducer other than air-coupled transducer) based approaches suffers from high mechanical index or acoustic intensity issue when imaging the eye structure, which impede its potential deployment in clinical practice.
Among these propulsion strategies, mechanical vibrators are preferred due to their relative safety and the need to produce sufficient deformation of anterior ocular structures [40]. Recently, mechanical vibrators have been applied in human-based clinical studies [41]. In this study, we implemented a mechanical shaker-based high-frequency (30 MHz linear array) ultrasonic elastography technique to track elastic wave propagation and further assess biomechanical properties of anterior ocular structures. The proposed method has the capability to assess the elasticity of anatomical structures to provide information to guide detection of and risk-stratification for ocular disease.
II. Materials and methods
A. System setup
The diagram of the experimental configuration is shown in Fig. 1. A programmable high frequency ultrasound system (Vantage 256, Verasonics, Redmond, WA, USA) [42] was developed for imaging and data acquisition. A function generator (AFG 3252C, Tektronix, Beaverton, OR USA) was used to generate a single cycle tone burst of 2kHz with the amplitude of 500 mV, and then the signal was amplified by a power amplifier (Type 2718, Bruel & Kjaer, Duluth, Georgia, USA) to drive the shaker in order to induce single shot vibration at the target region. The shaker was synchronized with ultrasound system via the trigger out channel of the ultrasound system. A metal rod was attached to the shaker and the diameter of the contact surface was 1mm.
Fig. 1.

Schematic diagram of the experimental setup. A custom-built high frequency 30 MHz linear array transducer was used in this study.
B. Ultrasound high frequency array
A custom-built 30-MHz 256-element linear high frequency array utilizing an interdigitally bonded (IB) piezo-composite transducer was fabricated and used for imaging, as described in [43]. This array has a 50μm azimuth pitch, two matching layers, and 2 mm elevation length focused to 7.3 mm with a lens. The measured pulse-echo results indicated that the center frequency was 28 MHz and −6 dB bandwidth was 44% (a representative element results are shown in Fig. 2). To connect this probe with the Verasonics imaging system, a converter board of a L7–4 probe cable was used. Due to the limited elements of the L7–4 probe cable, only 128 elements of the array were used for this study.
Fig. 2.
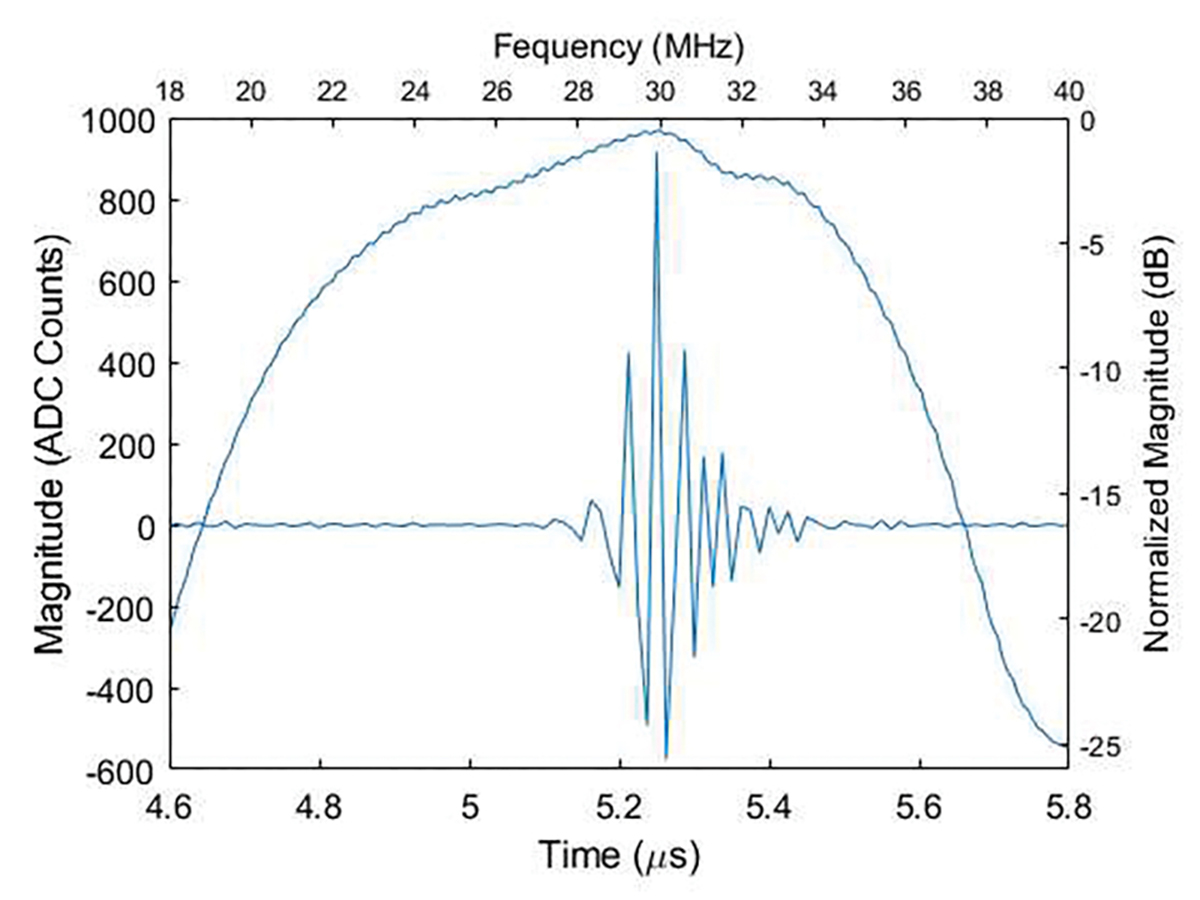
The Pulse-echo test of a representative element of the custom-built high frequency linear array.
C. Biological Tissue Preparation
Biological tissue experiments were performed on porcine eyeballs ex vivo. Fresh unscalded porcine eyeballs were collected from a local slaughter house (Sierra for Medical Science, Inc.), and all experiments being performed within 24h of collection. Ten unscalded porcine eyeballs were used for cornea measurements and another six eyeballs were used for ciliary body measurements. Each eyeball was fixed in a homemade plastic foam mold with agar and was placed in the container filled with saline solution.
The bottom of each eyeball was cannulated with two needles. One needle was connected to a saline infusion bag, which was used to modulate IOP by adjusting the height of the bag [44]. The other needle was connected to a pressure sensor, and IOP data was displayed using LabView software.
D. Data collection and post-processing
The transducer was placed on the top of the eyeball and the real-time B-mode image was first acquired at plane wave imaging mode with 15 angles compounding to identify the regions of interest.
To collect the elastography sequence, the array was employed in the plane wave imaging mode with 5 angles compounding at the pulse repetition frequency (PRF) of 13.3 K. The IQ Data were gathered by the Verasonics system and transferred to the disk for offline processing. Post-processing was performed using MATLAB 2021a (The MathWorks, Natick, MA, USA). IOP in each sample was increased from 5 mmHg to 30 mmHg in 5 mmHg increments.
For each IQ dataset, we applied the Kasai algorithm (1D autocorrelation) [45] to estimate the displacement curve for each image pixel. More specifically, we obtained 3D matrix data that was converted into a spatiotemporal map (a 2-D plot of lateral position over time). Motion data was averaged along the axial direction of the region of interest (ROI), and the slope of the spatial–temporal trajectory of the time shift (the time to reach the peak deformation at each displacement curve) was estimated to calculate the elastic wave speed. Then, we used the spline function in MATLAB to interpolate the time dimension in the 2D spatiotemporal map to smooth the data. A 50–500 Hz band-pass filter was also applied to suppress background motion and environmental noise. For each IOP, three measurements were performed separately for the cornea and ciliary body.
E. Mathematical model validation
For the shear wave that is initiated at a given value of IOP, we assume that the deformation gradient tensor is given by
| (1) |
This corresponds to a constant stretch, λ (defined as λ = 1 + ϵ, where ϵ is the strain), in the two circumferential directions and a strain of λ−2 in the radial direction which ensures incompressibility. The shear strain generated by the elastic wave in the cornea is given by γ(x1, t). In the development below we will also require an expression for the left Cauchy-Green strain tensor, B = FFT. Recognizing that the strain due to the elastic wave is much smaller than the strain induced by changing the IOP (that is, γ ≪ ϵ), the non-zero components of this tensor are given by
| (2) |
We model the tissue response as Blatz solid [46]whose strain energy density is given by
| (3) |
where I1 = tr(B) is the first invariant of the left Cauchy-Green strain tensor, and c1 and β are the two hyperelastic parameters. We chose the Blatz model for two main reasons. First, as described in [47] and the references therein, this type of model has proven to be very effective in modelling corneal mechanics. Second, it is a simple model with only two parameters that have a clear interpretation. The parameter c1 determines the shear modulus at small strains while β determines the nonlinear elastic behavior of the tissue. We note that several other popular strain energy density functions also include an exponential dependence on strain. These include the Veronda-Westmann model[48] and the Fung model[49]. Given this expression for the strain density function, the Cauchy stress can be determined from the relation (see for example [50, 51] Using the expression for strain energy density in this expression yields
| (4) |
Using this relation and the expression for B from (2), the non-zero components of stress are given by
| (5) |
| (6) |
| (7) |
We now link these stresses to our measurements of the IOP and the elastic wave speed and use this relation to determine the hyperelastic parameters c1 and β.
We did not observe significant strain below an IOP of 5 mm of Hg. Therefore, we assume that the cornea is unstretched when the IOP is equal to P0 = 5 mm of Hg and denote by ΔP = IOP − P0, any increment above it. From the continuity of normal traction between the vitreous chamber and the eye, we have σ33 = ΔP, which yields for pressure (from (6)),
| (8) |
Using this expression for pressure in (5), we have
| (9) |
We also recognize that σ11 is equal to the Hoop stress, that is , where R(λ) = R0λ, and τ(λ) = τ0λ−2 are the radius and the thickness of the eye at the given IOP, and R0 = 12 mm and τ0 = 1 mm are the corresponding unstretched values. This gives us another expression for σ11,
| (10) |
Equating the two expressions for σ11, that is (9) and (10), we finally arrive at
| (11) |
The equation above can be interpreted as a relation between λ and ΔP parametrized by c1 and β. That is , meaning thereby that for a given value of the IOP and the hyperelastic parameters, we can determine the base deformation state of the cornea.
We now turn to (7) and compute the tangent shear modulus by evaluating the derivative,
| (12) |
For a simple shear wave, the tangent shear modulus is equal to the product of density and the square of the elastic wave speed. Therefore, we have
| (13) |
where is the tissue density and cs is the measured elastic wave speed. From (11) and (13), we obtain
| (14) |
Substituting the relation between stretch and IOP increment obtained from (11) in the equation above we have
| (15) |
For our choice of hyperelastic constitutive model, the equation above represents the theoretical relation between the elastic wave speed and IOP. Given pairwise measurements of , ΔP(i), i = 1, … M, this equation may be used to determine the values of hyperelastic parameters c1, β that minimize the discrepancy between the measurements and the predictions. Performing this minimization for each sequence of measured IOP and elastic wave speed for the cornea gives us multiple values for c1 and β. Repeating this for 10 sequences we compute 10 different values for c1 and β. From these, we can compute the mean and standard deviations for these parameters.
III. results and Discussion
In this study, we demonstrate that it is feasible to measure the biomechanical properties of the cornea and the ciliary body using the high frequency ultrasound elastography system. Ten fresh porcine eyes were used to measure the response of the cornea to increasing IOP, and the response of the ciliary body was measured in six similar eyes. Fig. 4 shows the ultrasound B-mode image of the cornea and ciliary body.
Fig. 4.
B-mode images of the (a) cornea and (b) ciliary body. The red window indicated the location to obtain the reconstructed spatiotemporal map
For each eyeball, we estimated the elastic wave speed propagating through the cornea and ciliary body with increasing IOP from 5 mmHg to 30 mmHg in 5 mmHg increments. Fig. 5 shows the reconstructed spatiotemporal map of the cornea in response to IOP equal to 5, 15 and 30 mmHg. The mean and standard deviation of elastic wave speed averaged over six samples of the ciliary body was 1.31±0.14 m/s at 5 mmHg, 1.93±0.44 m/s at 10 mmHg, 2.39±0.52 m/s at 15 mmHg, 2.95±0.72 m/s at 20 mmHg, 3.04±0.74 m/s at 25 mmHg, 3.71±0.62 m/s at 30 mmHg. The mean and standard deviation of elastic wave speed averaged over ten samples of the cornea was 1.23±0.18 m/s at 5 mmHg, 2.33±0.59 m/s at 10 mmHg, 3.52±0.51 m/s at 15 mmHg, 4.57±0.28 m/s at 20 mmHg, 5.54±0.35 m/s at 25 mmHg, 6.34 ±0.45 m/s at 30 mmHg. The relationship between elastic wave velocity and IOP ranging between 5 mmHg to 30 mmHg are summarized for the cornea and the ciliary body in Fig. 6. We observed that the rate of increase of the elastic wave speed in the cornea is faster than in the ciliary body.
Fig. 5.
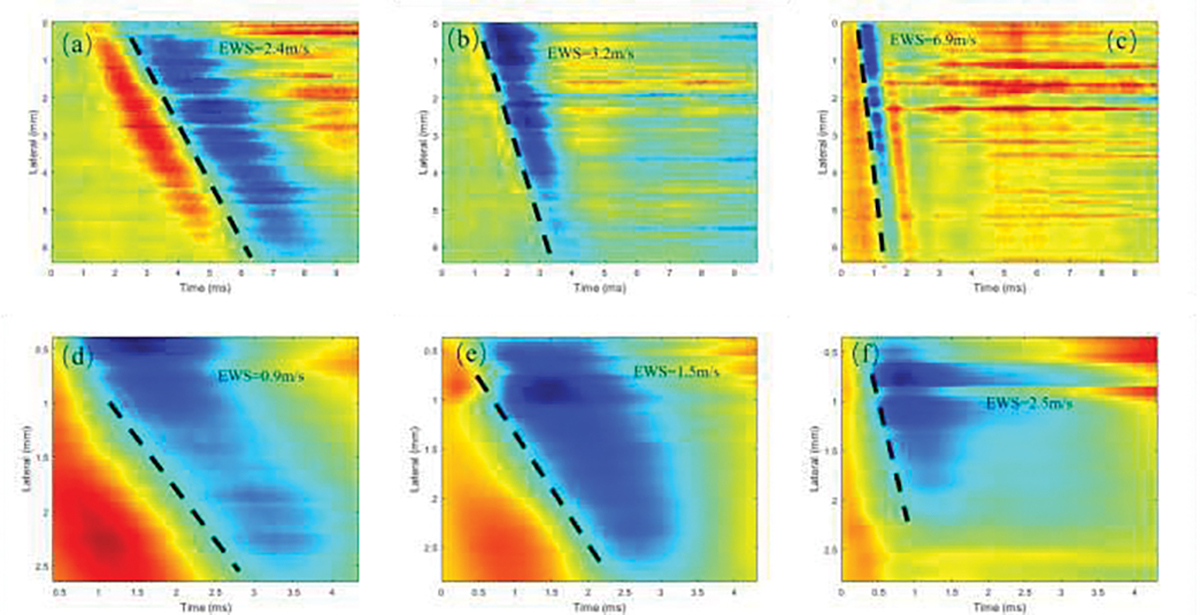
The reconstructed spatiotemporal map of the (a-c) cornea and (d-f) ciliary body of the porcine eye under three different IOPs – (a,d) 5 mmHg, (b,e) 15 mmHg and (c,f) 30 mmHg, respectively.
Fig. 6.
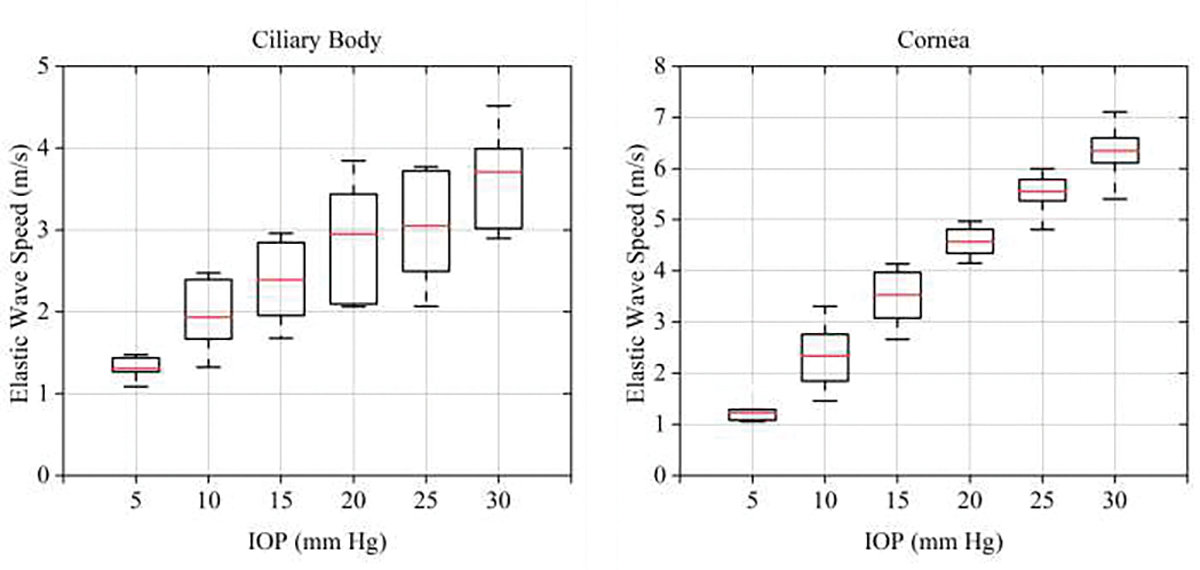
Relationship between elastic wave speed in the cornea/ciliary body, and IOP.
Many papers have been published for cornea elasticity measurement. By using the similar set up, Weng CC et al.[52] proposed a HFUS elastography system based on an external vibrator and ultrafast ultrasound imaging to estimate the viscoelasticity of porcine cornea ex vivo. In that study, a thin rod vibrator was used to generate stable elastic wave and the estimated elasticities of the healthy cornea was 9.1± 1.3 kPa by using the Lamb wave model..Ashofteh Yazd et al.[53] used three non-linear hyperelastic models (i.e. Hamilton-Zabolotskaya model, Ogden model and Mooney-Rivlin model) to fitted to the stress–strain curves obtained in the tensile tests of the cornea and decided that the Hamilton-Zabolotskaya model showed the highest discriminative capability of the nonlinear model parameter for the tissue structural changes changes between the two sample groups(control (non-treated) and NaOH-treated (damaged)). However, they did not measure the response of the corneal elasticity to various IOP nor did they measure the response of elasticity of ciliary body to increasing IOP.
To further validate our experimental results, we investigated a hyperelastic model to explain for this observation. We also demonstrate how measurements of the elastic wave velocity at multiple levels of IOP can be used to infer the hyperelastic parameters of the cornea and the ciliary body. We begin this demonstration with a discussion of the corneal microstructure.
The cornea has a complex microstructure which influences its mechanical behavior. It contains lamellae composed of collagen fibrils, embedded in a hydrated proteoglycan matrix [54]. The collagen lamellae are oriented in different directions within the corneal plane and their orientation varies from one corneal zone to the other [55]. It is widely recognized that fiber arrangement in the limbus region of the cornea for most mammals, including pigs, is in the circumferential direction. In the diagram shown in Fig. 3, this orientation corresponds to fibers running perpendicular to the plane; that is fibers running along the e2 direction. Further, in our measurements the excitation is such that we generate an elastic wave oriented along the e1 − e3 directions. Given this, and the fact that the fibers are oriented along the e2 direction, we anticipate that our measurement probes the properties of the matrix of the cornea rather than the collagen lamellae. Therefore, in the discussion below we use a hyperelastic constitutive model that is associated with the matrix, which is isotropic, and not the lamella, which are anisotropic [56–58].
Fig. 3.
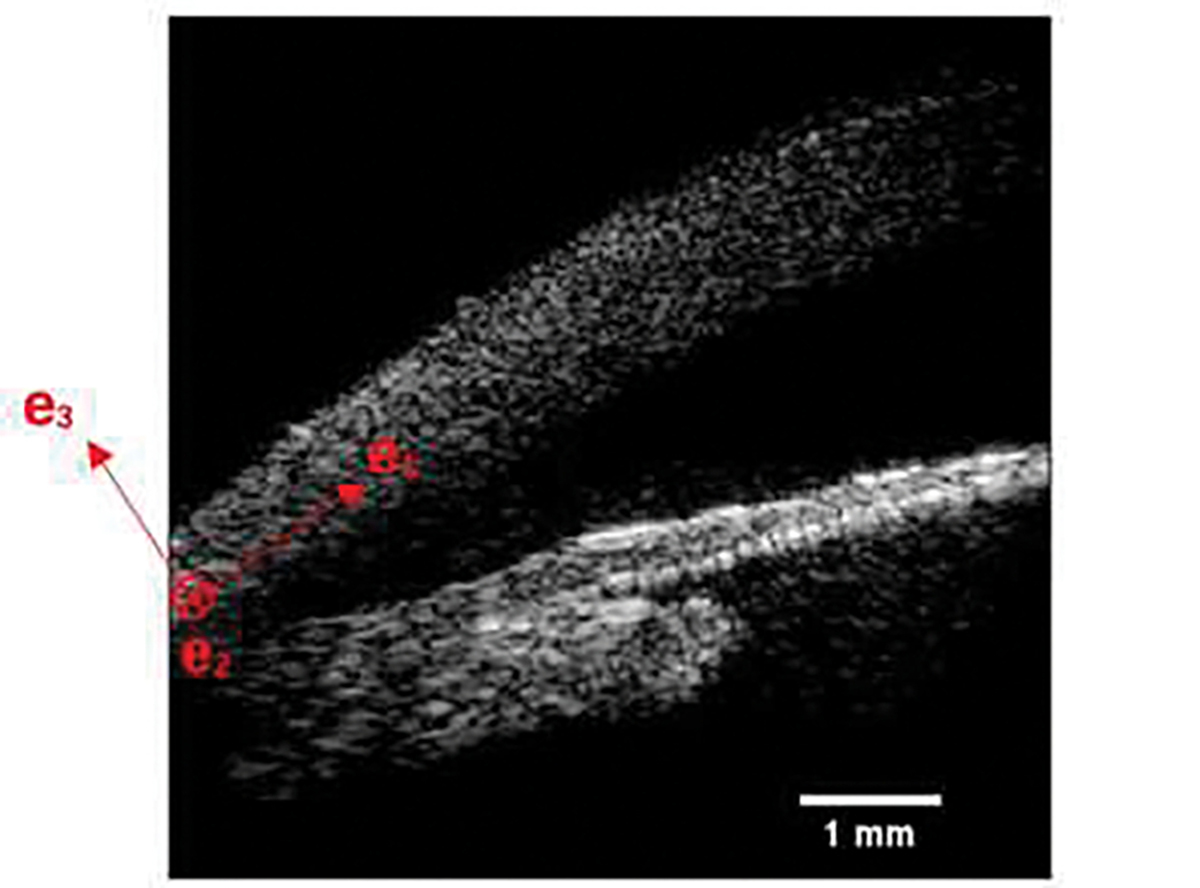
Illustration of the frame of reference considered in the hyperelastic model.
The cornea and the sclera form the outside of the globe and provide it with structural integrity. In contrast, the CB lies entirely within the globe, the shape of the CB is roughly triangular, where one vertex is attached to the scleral spur, another is contiguous with the choroid, and the third is attached to the zonular apparatus but otherwise moves freely. Any increase in IOP stretches the sclera and the CB, since the CB is connected to the sclera. Stretching forces on the CB are greatest in regions directly adjacent to the sclera (being roughly equal to the stretching forces in the sclera) and smallest at its free vertex, where they are almost zero. For this reason, we anticipate the average strain in the CB to be lower than in the cornea and sclera. Therefore, any strain induced stiffening, which is typically observed in biological materials, will be more pronounced in the cornea when compared with the CB. This is precisely what is observed in the experimental data for the elastic wave speed in the cornea and the CB as a function of IOP. The analysis described below makes this assertion more previse.
This analysis, which is described in detail in Methods section, is based on using the Blatz model for the matrix in the cornea and CB. We further recognize that the eye responds to increasing IOP as an elastic shell. This leads us to an implicit relation between the two measured quantities, the IOP and the elastic wave speed (Equation (15)). This relation is parameterized by the two parameters of the Blatz model. For each sequence of measured IOP and elastic wave speed data for the cornea, we determine the parameters that minimize the square of the difference between the theoretical and with these, we can compute the mean and μβ = 48.9. and standard deviation and σβ = 12.6. These values are in the same range as those reported by other researchers[47]. The relatively small value of variance c1 compared with the standard deviation in β indicates that the degree of uncertainty in the latter is higher. A mean coefficient of determination, R2, of 0.93 was obtained for the fitting between the experimental and theoretical values.
Using these values, in Figure 7a we have plotted the theoretical variation of the elastic wave speed with IOP for the cornea. We observe that it closely matches experimental data. Further, assuming the same hyperelastic parameters for the ciliary body, but a lower circumferential strain (mean = 78.5% and standard deviation 8.5%) due to its mechanical connection to the sclera, we obtain a similar curve for the CB (shown in Fig. 7b). The circumferential strain in the CB was estimated by minimizing the difference between the theoretical and experimental values of the elastic wave speed as a function of IOP. We observe that the simple hypotheses of lower strain in the ciliary body produces a good match with experimental data.
Fig. 7.

Experimental vs. theoretical IOP vs. elastic wave speeds in the cornea (a) and ciliary body (b). Box plots include the experimental elastic wave speed measured at each IOP level and the dashed line shows the estimated elastic wave speed using the obtained mean hyperelastic parameters.
In Figure 8, using the mean values of c1 and β, we have plotted the value of longitudinal stress as a function of the longitudinal strain ϵ = λ − 1 for the cornea. We can clearly observe that the stress increases with a small linear slope when the strain is small; this behavior is represented by the lower-order parameter c1. Thereafter, when the strain reaches around 5%, the high-order term attached to β becomes active, and the stress-strain relation becomes highly nonlinear. This type of behavior has been observed by other researchers in direct tensile tests conducted on corneal tissue (see[47], and references therein).
Fig. 8.

Strain vs. longitudinal stress (σ11) curve estimated using the procedure described in the Methods section. The mean hyperelastic parameters obtained from al experimental measurement sequences were used to estimate this curve.
In summary, although the overall mechanical behavior of the cornea and the CB is complex, using the results of this analysis, we have demonstrated that
The relation between elastic wave speed and IOP, determined using elastic wave ultrasound elastography, can be used to infer the nonlinear hyperelastic parameters of the cornea and CB.
The differing rates of increase of elastic wave speed with the IOP for the cornea and the CB can be explained on the basis of the lower circumferential strain in the latter.
In future studies, the measurement of the deformation of the cornea and ciliary body at different IOP levels, in addition to measuring the elastic wave speeds, would allow us to identify more accurate constitutive models for both tissues. It will also enable an in-depth analysis of the nonlinear elastic parameters in these tissues. Our results demonstrated the potential of high frequency ultrasound elastography for characterizing the nonlinear hyperelastic response of corneal and ciliary body in clinical applications[59].
IV. Conclusions
We demonstrate that the shaker-based high frequency ultrasound elastography system can be used to measure nonlinear hyperelastic response of the cornea and ciliary body. The mean and standard deviation of elastic wave speed averaged over six samples of the ciliary body was 1.31±0.14 m/s at 5 mmHg, 1.93±0.44 m/s at 10 mmHg, 2.39±0.52 m/s at 15 mmHg, 2.95±0.72 m/s at 20 mmHg, 3.04±0.74 m/s at 25 mmHg, 3.71±0.62 m/s at 30 mmHg. The mean and standard deviation of elastic wave speed averaged over ten samples of the cornea was 1.23±0.18 m/s at 5 mmHg, 2.33±0.59 m/s at 10 mmHg, 3.52±0.51 m/s at 15 mmHg, 4.57±0.28 m/s at 20 mmHg, 5.54±0.35 m/s at 25 mmHg, 6.34 ±0.45 m/s at 30 mmHg. We model the tissue response by using Blatz model and a mean coefficient of determination, R^2, of 0.93 was obtained for the fitting between the experimental and theoretical values. In the long term, this high frequency ultrasound elastography system can be used to assess the morphological and biomechanical properties of ocular tissue.
Acknowledgments
This work was supported by the National Institutes of Health (NIH) under grant R01EY028662, R01EY030126, R01EY032229 and NIH P30EY029220. Unrestricted departmental grant from research to prevent blindness.
Contributor Information
Junhang Zhang, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA.; Department of Ophthalmology, Keck School of Medicine, University of Southern California, Los Angeles, CA 90033, USA.
Javier Murgoitio-Esandi, Department of Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA..
Xuejun Qian, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA.; Department of Ophthalmology, Keck School of Medicine, University of Southern California, Los Angeles, CA 90033, USA.
Runze Li, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA.; Department of Ophthalmology, Keck School of Medicine, University of Southern California, Los Angeles, CA 90033, USA.
Chen Gong, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA..
Amir Nankali, Department of Ophthalmology, Keck School of Medicine, University of Southern California, Los Angeles, CA 90033, USA..
Liang Hao, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA..
Benjamin Y. Xu, Department of Ophthalmology, Keck School of Medicine, University of Southern California, Los Angeles, CA 90033, USA.
K. Kirk Shung, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA..
Assad Oberai, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA..
Qifa Zhou, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA.; Department of Ophthalmology, Keck School of Medicine, University of Southern California, Los Angeles, CA 90033, USA.
V. REFERENCE
- [1].Quigley HA, “Number of people with glaucoma worldwide,” British journal of ophthalmology, vol. 80, no. 5, pp. 389–393, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Lavia C, Dallorto L, Maule M, Ceccarelli M, and Fea AM, “Minimally-invasive glaucoma surgeries (MIGS) for open angle glaucoma: a systematic review and meta-analysis,” PloS one, vol. 12, no. 8, pp. e0183142, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].J. G, “Research progress and development trend of glaucoma,” Chinese Journal of Ophthalmology, vol. 36(3):5., 2000. [Google Scholar]
- [4].Thylefors B, and Negrel A, “The global impact of glaucoma,” Bulletin of the World Health Organization, vol. 72, no. 3, pp. 323, 1994. [PMC free article] [PubMed] [Google Scholar]
- [5].Burgoyne C, Downs J, Bellezza A, Suh J-K, and Hart R, “The optic nerve head as a biomechanical structure: A new paradigm for understanding the role of IOP-related stress and strain in the pathophysiology of glaucomatous optic nerve head damage,” Progress in retinal and eye research, vol. 24, pp. 39–73, 02/01, 2005. [DOI] [PubMed] [Google Scholar]
- [6].W.-y G. Sun xing-huai, “Etiology analysis and prevention of secondary glaucoma,” Chinese Journal of Practical Ophthalmology, vol. 1996 (8) : 469–471 (3), 1996 [Google Scholar]
- [7].Weinreb RN, Aung T, and Medeiros FA, “The pathophysiology and treatment of glaucoma: a review,” Jama, vol. 311, no. 18, pp. 1901–1911, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Goel M, Picciani RG, Lee RK, and Bhattacharya SK, “Aqueous humor dynamics: a review,” The open ophthalmology journal, vol. 4, pp. 52–59, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Voorhees AP, Hua Y, Brazile BL, Wang B, Waxman S, Schuman JS, and Sigal IA, “So-Called Lamina Cribrosa Defects May Mitigate IOP-Induced Neural Tissue Insult,” Investigative Ophthalmology & Visual Science, vol. 61, no. 13, pp. 15–15, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Sigal I, and Grimm J, “A few good responses: Which mechanical effects of IOP on the ONH to study?,” Investigative ophthalmology & visual science, vol. 53, pp. 4270–8, 05/08, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wu C, Aglyamov SR, Han Z, Singh M, Liu C-H, and Larin KV, “Assessing the biomechanical properties of the porcine crystalline lens as a function of intraocular pressure with optical coherence elastography,” Biomedical Optics Express, vol. 9, no. 12, pp. 6455–6466, 2018/12/01, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Elsheikh A, McMonnies CW, Whitford C, and Boneham GC, “In vivo study of corneal responses to increased intraocular pressure loading,” Eye Vis (Lond), vol. 2, pp. 20, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Girard MJ, Suh JK, Bottlang M, Burgoyne CF, and Downs JC, “Biomechanical changes in the sclera of monkey eyes exposed to chronic IOP elevations,” Invest Ophthalmol Vis Sci, vol. 52, no. 8, pp. 5656–69, Jul 29, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Downs JC, Suh JK, Thomas KA, Bellezza AJ, Hart RT, and Burgoyne CF, “Viscoelastic material properties of the peripapillary sclera in normal and early-glaucoma monkey eyes,” Invest Ophthalmol Vis Sci, vol. 46, no. 2, pp. 540–6, Feb, 2005. [DOI] [PubMed] [Google Scholar]
- [15].Qian X, Li R, Lu G, Jiang L, Kang H, Kirk Shung K, Humayun MS, and Zhou Q, “Ultrasonic elastography to assess biomechanical properties of the optic nerve head and peripapillary sclera of the eye,” Ultrasonics, vol. 110, pp. 106263, Feb, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Tamm E, “The Role of the Ciliary Body in Aqueous Humor Dynamics Structural Aspects,” Encyclopedia of the Eye, pp. 179–186, 12/31, 2010. [Google Scholar]
- [17].Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, Puliafito CA, and et al. , “Optical coherence tomography,” Science, vol. 254, no. 5035, pp. 1178–81, Nov 22, 1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Qu Y, Ma T, He Y, Zhu J, Dai C, Yu M, Huang S, Lu F, Shung KK, Zhou Q, and Chen Z, “Acoustic Radiation Force Optical Coherence Elastography of Corneal Tissue,” IEEE J Sel Top Quantum Electron, vol. 22, no. 3, May-Jun, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Li Y, Zhu J, Chen JJ, Yu J, Jin Z, Miao Y, Browne AW, Zhou Q, and Chen Z, “Simultaneously imaging and quantifying in vivo mechanical properties of crystalline lens and cornea using optical coherence elastography with acoustic radiation force excitation,” APL Photonics, vol. 4, no. 10, Oct, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].He Y, Qu Y, Zhu J, Zhang Y, Saidi A, Ma T, Zhou Q, and Chen Z, “Confocal Shear Wave Acoustic Radiation Force Optical Coherence Elastography for Imaging and Quantification of the In Vivo Posterior Eye,” IEEE J Sel Top Quantum Electron, vol. 25, no. 1, Jan-Feb, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Qian X, Ma T, Yu M, Chen X, Shung KK, and Zhou Q, “Multifunctional Ultrasonic Micro-elastography Imaging System,” Sci Rep, vol. 7, no. 1, pp. 1230, Apr 27, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Qian X, Ma T, Shih CC, Heur M, Zhang J, Shung KK, Varma R, Humayun MS, and Zhou Q, “Ultrasonic Microelastography to Assess Biomechanical Properties of the Cornea,” IEEE Trans Biomed Eng, vol. 66, no. 3, pp. 647–655, Mar, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Lay FY, Chen PY, Cheng HF, Kuo YM, and Huang CC, “Ex Vivo Evaluation of Mouse Brain Elasticity Using High-Frequency Ultrasound Elastography,” IEEE Trans Biomed Eng, vol. 66, no. 12, pp. 3426–3435, Dec, 2019. [DOI] [PubMed] [Google Scholar]
- [24].Hsiao YY, Yang TH, Chen PY, Hsu HY, Kuo LC, Su FC, and Huang CC, “Characterization of the extensor digitorum communis tendon using high-frequency ultrasound shear wave elastography,” Med Phys, vol. 47, no. 4, pp. 1609–1618, Apr, 2020. [DOI] [PubMed] [Google Scholar]
- [25].Chen PY, Yang TH, Kuo LC, Shih CC, and Huang CC, “Characterization of Hand Tendons Through High-Frequency Ultrasound Elastography,” IEEE Trans Ultrason Ferroelectr Freq Control, vol. 67, no. 1, pp. 37–48, Jan, 2020. [DOI] [PubMed] [Google Scholar]
- [26].Shih CC, Huang CC, Zhou Q, and Shung KK, “High-resolution acoustic-radiation-force-impulse imaging for assessing corneal sclerosis,” IEEE Trans Med Imaging, vol. 32, no. 7, pp. 1316–24, Jul, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen PY, Shih CC, Lin WC, Ma T, Zhou Q, Shung KK, and Huang CC, “High-Resolution Shear Wave Imaging of the Human Cornea Using a Dual-Element Transducer,” Sensors (Basel), vol. 18, no. 12, Dec 3, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Shih CC, Qian X, Ma T, Han Z, Huang CC, Zhou Q, and Shung KK, “Quantitative Assessment of Thin-Layer Tissue Viscoelastic Properties Using Ultrasonic Micro-Elastography With Lamb Wave Model,” IEEE Transactions on Medical Imaging, vol. 37, no. 8, pp. 1887–1898, 2018. [DOI] [PubMed] [Google Scholar]
- [29].Bekesi N, Dorronsoro C, de la Hoz A, and Marcos S, “Material Properties from Air Puff Corneal Deformation by Numerical Simulations on Model Corneas,” PLOS ONE, vol. 11, no. 10, pp. e0165669, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Koprowski R, and Wilczyński S, “Corneal Vibrations during Intraocular Pressure Measurement with an Air-Puff Method,” J Healthc Eng, vol. 2018, pp. 5705749, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ambroziński Ł, Song S, Yoon SJ, Pelivanov I, Li D, Gao L, Shen TT, Wang RK, and O’Donnell M, “Acoustic micro-tapping for non-contact 4D imaging of tissue elasticity,” Sci Rep, vol. 6, pp. 38967, Dec 23, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Pitre JJ Jr., Kirby MA, Li DS, Shen TT, Wang RK, O’Donnell M, and Pelivanov I, “Nearly-incompressible transverse isotropy (NITI) of cornea elasticity: model and experiments with acoustic micro-tapping OCE,” Sci Rep, vol. 10, no. 1, pp. 12983, Jul 31, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Qi W, Chen R, Chou L, Liu G, Zhang J, Zhou Q, and Chen Z, “Phase-resolved acoustic radiation force optical coherence elastography,” J Biomed Opt, vol. 17, no. 11, pp. 110505, Nov, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Mikula E, Hollman K, Chai D, Jester JV, and Juhasz T, “Measurement of corneal elasticity with an acoustic radiation force elasticity microscope,” Ultrasound Med Biol, vol. 40, no. 7, pp. 1671–9, Jul, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Qu Y, He Y, Saidi A, Xin Y, Zhou Y, Zhu J, Ma T, Silverman RH, Minckler DS, Zhou Q, and Chen Z, “In Vivo Elasticity Mapping of Posterior Ocular Layers Using Acoustic Radiation Force Optical Coherence Elastography,” Invest Ophthalmol Vis Sci, vol. 59, no. 1, pp. 455–461, Jan 1, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Maklad O, Eliasy A, Chen KJ, Theofilis V, and Elsheikh A, “Simulation of Air Puff Tonometry Test Using Arbitrary Lagrangian-Eulerian (ALE) Deforming Mesh for Corneal Material Characterisation,” Int J Environ Res Public Health, vol. 17, no. 1, Dec 19, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Qian X, Li R, Li Y, Lu G, He Y, Humayun MS, Chen Z, and Zhou Q, “In vivo evaluation of posterior eye elasticity using shaker-based optical coherence elastography,” Exp Biol Med (Maywood), vol. 245, no. 4, pp. 282–288, Feb, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Kashani K, Mao S, Safadi S, Amiot B, Glorioso J, Lieske J, Nyberg S, and Zhang X, “Association between kidney intracapsular pressure and ultrasound elastography,” Critical Care, vol. 21, 12/01, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Jin Z, Khazaeinezhad R, Zhu J, Yu J, Qu Y, He Y, Li Y, Gomez Alvarez-Arenas TE, Lu F, and Chen Z, “In-vivo 3D corneal elasticity using air-coupled ultrasound optical coherence elastography,” Biomedical optics express, vol. 10, no. 12, pp. 6272–6285, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Zhou B, Chen JJ, Kazemi A, Sit AJ, and Zhang X, “An Ultrasound Vibro-Elastography Technique for Assessing Papilledema,” Ultrasound Med Biol, vol. 45, no. 8, pp. 2034–2039, Aug, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Sit AJ, Lin SC, Kazemi A, McLaren JW, Pruet CM, and Zhang X, “In Vivo Noninvasive Measurement of Young’s Modulus of Elasticity in Human Eyes: A Feasibility Study,” J Glaucoma, vol. 26, no. 11, pp. 967–973, Nov, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Khalitov RS, Gurbatov SN, and Demin IY, “The use of the Verasonics ultrasound system to measure shear wave velocities in CIRS phantoms,” Physics of Wave Phenomena, vol. 24, no. 1, pp. 73–76, 2016/01/01, 2016. [Google Scholar]
- [43].Cannata JM, Williams JA, Zhang L, Hu CH, and Shung KK, “A high-frequency linear ultrasonic array utilizing an interdigitally bonded 2–2 piezo-composite,” IEEE Trans Ultrason Ferroelectr Freq Control, vol. 58, no. 10, pp. 2202–12, Oct, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Ma Y, Kwok S, Sun J, Pan X, Pavlatos E, Clayson K, Hazen N, and Liu J, “IOP-induced regional displacements in the optic nerve head and correlation with peripapillary sclera thickness,” Experimental eye research, vol. 200, pp. 108202–108202, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Deng Y, Rouze NC, Palmeri ML, and Nightingale KR, “Ultrasonic Shear Wave Elasticity Imaging Sequencing and Data Processing Using a Verasonics Research Scanner,” IEEE Trans Ultrason Ferroelectr Freq Control, vol. 64, no. 1, pp. 164–176, Jan, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Blatz PJ, Chu BM, and Wayland H, “On the Mechanical Behavior of Elastic Animal Tissue,” vol. 13, no. 1, pp. 83–102, 1969. [Google Scholar]
- [47].Kim W, Argento A, Rozsa FW, and Mallett K, “Constitutive behavior of ocular tissues over a range of strain rates,” J Biomech Eng, vol. 134, no. 6, pp. 061002, Jun, 2012. [DOI] [PubMed] [Google Scholar]
- [48].Veronda DR, and Westmann RA, “Mechanical characterization of skin—Finite deformations,” Journal of Biomechanics, vol. 3, no. 1, pp. 111–124, 1970/01/01/, 1970. [DOI] [PubMed] [Google Scholar]
- [49].Fung Y, “Elasticity of soft tissues in simple elongation,” vol. 213, no. 6, pp. 1532–1544, 1967. [DOI] [PubMed] [Google Scholar]
- [50].Gurtin ME, An Introduction to Continuum Mechanics: Elsevier Science, 1982. [Google Scholar]
- [51].Ferreira E, Oberai A, and Barbone P, “Uniqueness of the elastography inverse problem for incompressible nonlinear planar hyperelasticity,” Inverse Problems, vol. 28, pp. 065008, 05/02, 2012. [Google Scholar]
- [52].Weng CC, Chen PY, Chou D, Shih CC, and Huang CC, “High Frequency Ultrasound Elastography for Estimating the Viscoelastic Properties of the Cornea Using Lamb Wave Model,” IEEE Trans Biomed Eng, vol. 68, no. 9, pp. 2637–2644, Sep, 2021. [DOI] [PubMed] [Google Scholar]
- [53].Ashofteh Yazdi A, Melchor J, Torres J, Faris I, Callejas A, Gonzalez-Andrades M, and Rus G, “Characterization of non-linear mechanical behavior of the cornea,” Scientific Reports, vol. 10, no. 1, pp. 11549, 2020/07/14, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Cogan DG, “Applied anatomy and physiology of the cornea,” Trans Am Acad Ophthalmol Otolaryngol, vol. 55, pp. 329–59, Mar-Apr, 1951. [PubMed] [Google Scholar]
- [55].Meek KM, Blamires T, Elliott GF, Gyi TJ, and Nave C, “The organisation of collagen fibrils in the human corneal stroma: a synchrotron X-ray diffraction study,” Curr Eye Res, vol. 6, no. 7, pp. 841–6, Jul, 1987. [DOI] [PubMed] [Google Scholar]
- [56].Pinsky PM, van der Heide D, and Chernyak D, “Computational modeling of mechanical anisotropy in the cornea and sclera,” J Cataract Refract Surg, vol. 31, no. 1, pp. 136–45, Jan, 2005. [DOI] [PubMed] [Google Scholar]
- [57].Pandolfi A, and Holzapfel GA, “Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations,” J Biomech Eng, vol. 130, no. 6, pp. 061006, Dec, 2008. [DOI] [PubMed] [Google Scholar]
- [58].Nguyen TD, and Boyce BL, “An inverse finite element method for determining the anisotropic properties of the cornea,” Biomechanics and Modeling in Mechanobiology, vol. 10, no. 3, pp. 323–337, 2011/06/01, 2011. [DOI] [PubMed] [Google Scholar]
- [59].Rus G, Faris IH, Torres J, Callejas A, and Melchor J, “Why Are Viscosity and Nonlinearity Bound to Make an Impact in Clinical Elastographic Diagnosis?,” Sensors (Basel, Switzerland), vol. 20, no. 8, pp. 2379, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]



