Building viable stockpiles of personnel protective equipment

Abstract

Many stockpiled personnel protective equipment (PPE) were of no use during COVID-19 because they have expired. The need for rethinking past approaches of building PPE stockpiles without planning for their timely rotation has become clear. We develop a game-theoretic pandemic preparedness model for single and multiple PPE products for a budget-constrained governmental organization (GO) supplied by a manufacturer. The GO maximizes preparedness, measured by the service rate of PPE, whereas the manufacturer maximizes profit. The manufacturer supplies the PPE stockpile in the first year. Thereafter, the manufacturer buys back a quantity of older PPE from the GO annually and sells the GO the same quantity of new PPE. The manufacturer sells older PPE in the market place. We find that this approach induces the manufacturer to rotate inventory in the stockpile. Joint determination of the stockpile size and its rotation results in no waste from expired PPE and is better than separately determining the stockpile size and then determining how to rotate it. Using insights from the single PPE model, we examine the optimal budget allocation among multiple PPE products. We also consider the effect of spot market prices of PPE during a pandemic on the optimal stockpile sizes. We find that spot market prices of PPE can have a significant effect on the optimal stockpile sizes. We examine the performance of the proposed approach in a manufacturers-distributor-GO supply chain and with an option for the GO to invest in the manufacturer’s volume flexibility and show its effectiveness.

1. Introduction

On 2/05/2021, Mike Kaufmann, the CEO of Cardinal Health, said that his firm is already seeing changes in how its customers buy and store their personnel protective equipment (PPE). He also added “You will see increased storage,” and “I think you will see the federal government improve their national stockpile.” (Nathan-Kazis, 2021). He further explained that, over one year from the start of COVID-19, “Exam gloves are still an area where demand is outstripping supply.” Undoubtedly, building stockpiles of PPE will happen as it did with other pandemics and epidemics. For example, after the SARS epidemic, Ontario (Canada), built a PPE stockpile of millions of face masks. However, their budgeting allocated funds only to maintain the warehouses with no funding to replace expired products (Silverman, Clarke, & Stranges, 2020). As a result, about 50 million face masks stored after the SARS outbreak have expired (Martell & Warburton, 2020) before COVID-19.

Lessons that PPE stockpiles should be built seems to have been learned in many countries but the management of such stockpiles to keep them viable did not occur. Reports of expired PPE stockpiles are plentiful. Nearly 1.5 million N95 respirator masks in a warehouse in Indiana owned by the U.S. government were past their expiration date (Miroff 2020). Emergency stockpiles of N95 respirator masks at the Department of Veterans Affairs have deteriorated in storage and could not be used (Tozzi, 2020). In the U.K, out of the 26.3 million respirators in the stockpile, 20.9 million had expired (Finnis, 2020). In France, over 1.5 million masks were burned between January and March of 2020 because they were out of date (Ferguson, 2020). Clearly, a one-time large purchase of PPE products is insufficient to plan for a pandemic without a long range plan which schedules the rotation of the stockpile. Without such rotation, if a pandemic does not occur within the shelf life of the PPE, stockpiles of PPE products will be wasted at expiration of their viable life.

The problems faced by GOs in a pandemic can have many nuances. The GO may be managing a single PPE product (PPEP) or multiple PPEPs. The GO may purchase PPEPs from a manufacturer or a distributor. As observed during COVID-19, a pandemic has three phases:

• 1.Phase I: The PPEP is not available on the market for any price.
• 2.Phase II: The PPEP is available on the spot market for a price $p_h$ which is higher than the regular price $p_r$. The GO can satisfy demand from the stockpile and the spot market.
• 3.Phase III: During this phase, manufacturers have responded to the large demand spike with increased production capacity and supply of the PPEP and the price return to $p_r$.

The three phases of a pandemic can be illustrated for ventilators. Prior to COVID-19, annual global demand for ventilators was around 77,000. When Covid-19 hit New York city, the city alone needed an additional 33,000 ventilators (Dube, Li, Selviaridis, & Jahre, 2022). Due to global ventilator shortages, procurement from existing suppliers was going to be too slow for governments to meet rapidly growing demand. Furthermore, most supply chains were disrupted and could not make ventilators for several weeks. This is because ventilators range in complexity from basic models with 250–350 components to sophisticated models with 450–650 components (Gereffi, Pananond, & Pedersen, 2022), many of which were sourced globally and their supply was disrupted. The Federal Emergency Management Agency (FEMA) informed the public that they do not have enough ventilators in the strategic national stockpile (SNS) to meet demand by the states (Sadiq & Kessa, 2020). This period of ventilators shortage in the market place represents Phase I of the Pandemic. When ventilators were available, the state of New York found that prices for some models have increased from $20,000 to $50,000 (Voytko, 2020). This period of few months with high prices represents Phase II of the pandemic. U.S. and European government officials, facing this urgent need for ventilators, approached companies like General Motors, Ford, Airbus, Rolls-Royce, Jaguar, and Dyson to deploy their resources to build ventilators, which they did (Gereffi et al., 2022). Also, as Covid-19 restrictions eased and global logistics improved, manufacturers of ventilators ramped up their production. In March 2021 the ventilators market was expected to return to pre-pandemic levels before year’s end (GlobalData Healthcare, 2021), which begins Phase III of the pandemic.

The budgeting processes of different GOs may have some differences. It is reasonable to assume that a GO receives an initial budget to build PPEPs stockpiles. Thereafter, the GO receives annual budgets for holding and maintaining the stockpiles. If a pandemic occurs, the GO receives an emergency funding.

We begin by addressing the problem of a GO maximizing preparedness in Phase I for a single PPEP purchased from a manufacturer. We do not consider Phase II preparedness for a single PPEP because with a single PPEP, the GO can use the entire emergency funding to cover the needs for the PPEP and does not face a budget allocation decision among different PPEPs. Based on the results of the single PPEP model, we consider the problem of a GO maximizing Phase I preparedness for multiple PPEPs purchased from a single manufacturer. We then extend the model to a GO with a longer planning horizon that includes Phase II. In this extension, the decision of how to allocate Phase II’s emergency budget among PPEPs and the effects of pre-pandemic budget allocation on Phase II preparedness come into play. We do not consider phase III because during it, PPEPs’ availability and prices have returned to pre-pandemic levels. We investigate the following:

• 1.What should be the contract terms between the GO and the manufacturer for a single PPEP? The contract should increase preparedness for a pandemic.
• 2.How should the GO allocate its total budget among PPEPs to maximize preparedness given its budget constraint and different characteristics and importance of PPEPs?
• 3.What is the effect of considering Phase II of the pandemic, when PPEPs become available?
• 4.What should the contract terms be when the GO contracts with a distributor?
• 5.What effects does a GO option for investing in the manufacturer’s volume flexibility have?

This paper is organized as follows. In Section 2, we review relevant literature. We analyse the problem of a GO maximizing Phase I preparedness of a single PPEP in Section 3 where we consider two solution approaches by the GO. In the first approach, which we advocate, a single contract between the GO and the manufacturer covers the stockpile size and rotation decisions. In the second approach, the GO separates the decisions of building the stockpile from its rotation decisions. We extend the analysis to multiple PPEPs in Section 4 where we consider the budget allocation among PPEPs. In Section 5, we consider preparedness in Phase II which requires the consideration of spot market prices. We examine cases in which no single manufacturer has sufficient sales volume to rotate the stockpile and deal with different probability distributions of PPEPs demand in Section 6. We close with a discussion, conclusion, and suggestions for future research in Section 7.

2. Literature review

The operations management literature is rich in terms of analyzing inventory, logistics, and production decisions when disasters, e.g., earthquakes, epidemics, famine, hurricanes, and wars, occur, Dwivedi, Shareef, Mukerji, Rana, & Kapoor (2018); Song, Chen, & Lei (2018). Reviews of this vast literature prior to the COVID-19 can be found in Behl & Dutta (2019) and Kovacs & Moshtari (2019). However, as pointed out by Sodhi, Tang, & Willenson (2021), COVID-19 is the first genuinely global scale pandemic since the 1918 flu pandemic. While natural or man-made disasters hit a part of the world, COVID-19 was all over the world. Cross-border logistics which have been either stopped or severely curtailed because of border and port closures, flights shutdown, and quarantines’ requirements, further exacerbated an already bad situation. The inability to move materials from countries and regions at different stages of COVID-19 meant that those who needed medical and PPE supplies were unable to get them. Every part of the world experienced severe shortages of PPE and the demand surge completely overwhelmed the limited supply (Sodhi et al., 2021).

The events during the first six months of COVID-19 revealed gaps in the literature. The notion that a country or an organization can meet the demand for PPEPs in the first few months of a pandemic outbreak from increased production, onshore or offshore, has been proven wrong. In much of the disaster relief literature, demand spikes in an area or a region. This spike can be due to a disaster which increases demand and/or disrupts production. With COVID-19, demand spiked everywhere and production ceased, at least for some time. From a resiliency perspective, supply chains (SCs) should avoid PPEPs shortages at the different stages of a pandemic (Queiroz, Ivanov, Dolgui, & Wamba, 2020). Because some PPEPs were not available for purchase during the first few months of COVID-19, the only way to avoid shortages was to have ready to use viable stockpiles of PPEPs. While stockpiles were built to prepare for a pandemic, large proportions of these PPEPs stockpiles were unusable. In the U.S., masks, gloves, and other essential equipment sent from the strategic national stockpile to some states were expired (Sodhi et al., 2021). In rare cases were PPEPs were available early in the COVID-19, they were under-performing poor quality grey market products. The National Institute for Occupational Safety and Health found that 60% of 67 different types of imported N95 masks did not provide adequate protection. This indicates that a resilient approach to manage PPEPs must incorporate a period of time at the outset of a pandemic with a complete shortage of PPEPs in the market and full reliance on stored stockpiles. Such a reliance should not be viewed as a failure or a weakness of PPEPs SCs because pandemics are indeed unique. During the start of a pandemic, the spike in demand is sudden and very large, it occurs everywhere, production is disrupted, and panic sets in. SCs can not be expected to have such abundant excess capacity to utilize within a short time with constraints imposed by a pandemic. Moreover, having this costly capacity which may not be used for many years can be wasteful.

During COVID-19, PPEPs became available after some time at much higher prices than pre-pandemic prices. The World Health Organization (WHO) reported a six-fold increase in surgical masks’ prices. So, even after shortages begin to subside, GOs have to pay very high prices if their stockpiles are not large enough to outlast this high-price period. This also indicates that a resilient approach to managing medical supplies and PPEPs for pandemics must incorporate a period of time after the outbreak of a pandemic during which PPEPs are available at high prices. The existence of viable stockpiles may dampen the price shock PPEPs experience in the spot market.

Since the start of COVID-19, researcher began to focus their efforts on managing PPEPs during large scale disease breakout. A review of the literature on COVID-19 related studies can be found in Chowdhury, Paul, Kaisar, & Moktadir (2021). The authors find that most research on PPEPs management has focused on improving logistics by redesigning production facilities and diversifying their locations, improving transportation routes, implementing faster delivery modes, etc. While this research is needed to get the PPEPs to those who need it, it assumes that PPEPs are available or can be produced at a very large rate. Our work begins with making this assumption true by ensuring PPEPs availability using stockpiles. We first do not incorporate production capacity because the demand spike is very large, particularly when ordinary people start using PPEPs (Song, Zhang, Ran, & Ran, 2021), and because the pandemic may disrupt the production of PPEPs. The need for the stockpiles of PPEPs was echoed by Finkenstadt & Handfield (2021) who served in a variety of roles within the Department of Defense Joint Acquisition Task Force. They concluded that strategic national stockpile “will require on-site management, to drive appropriate turning of inventory and avoid large lot buying and large concurrent expiration dates for large parts of its contents”.

Zhang, Shi, Huang, Hua, & Teunter (2021) analyzed the use of capital reserves, a practice in China, for pandemic preparedness. Capital reserves are kept in addition to stockpiles of medical supplies. Their analysis included three policies, holding only safety stock, keeping only capital reserves, and mixed policy. They found that for products with more perishable nature, e.g., antiviral medicines, demand uncertainty may lead to lower safety stock levels and increased capital reserves to limit obsolescence. In our analysis, we focus on less perishable products, such as face masks and shields, whose shelf life is long. Hammami, Salman, Khouja, Nouira, & Alaswad (2023) also considered the stockpile size with government subsidy to the manufacturer for moving production on-shore. Their model does not consider the contract terms for building the stockpile, i.e., the GO is a price taker, and stockpile rotation was not considered.

We contribute to the literature by developing terms for contracts between GOs and PPEPs manufacturers to improve preparedness for pandemics. The contracts jointly determines the stockpile purchase and its rotation. The contracts include a buy back of PPEPs by the manufacturer from the GO. This is possible because the long shelf life of PPEPs enables PPEPs manufacturers to sell older PPEPs to other customers long before expiration. We consider a manufacturer-GO SC and different phases of pandemics. We show that relative to the common practice of GOs buying PPEPs to stockpile them and then developing a plan to maintain the stockpiles, our proposed contract increases the size of the stockpiles of PPEPs and eliminates waste and expiry of PPEPs without increasing cost. We also show that the proposed contract increases the manufacturer’s profit. We also develop an algorithm for maximizing preparedness which considers multiple PPEPs with different random demands during the different phases of a pandemic, different importance, and different pandemic surges in price. We extend the analysis for developing effective contract in a manufacturers-distributor-GO SC and with an option for investing in volume flexibility.

3. Single PPEP in a manufacturer-GO supply chain

3.1. The framework

The GO builds a stockpile of $Q$ units at the beginning of the planning horizon of $N$ years (which is the contract length if a pandemic does not occur). While building the stockpile may take some time, assuming it is instantaneous does not change the analysis, unless a pandemic begins during the buildup time. If no pandemic occurs during the $N$ years, the remaining PPEP inventory at contract’s end becomes part of the stockpile for a new contract. If a pandemic occurs at time $\Lambda$ from contract signing and $\Lambda <N$, then the GO begins depleting the stockpile, which no longer needs to be rotated as it is used up quickly. This implies that the manufacturer, knowing the possible disruption to its production capacity as well as potential profit from selling the PPEP at a high price in a pandemic-stricken spot market, avoids commitment for supplying PPEP in a pandemic. Thus, the effective planning horizon is $\text{min}[N,\Lambda ]$.

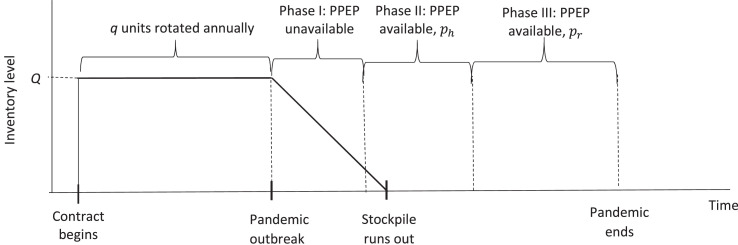
The inventory level of the PPEP over time is shown in Fig. 1 . Before the pandemic, $Q$ units are maintained by rotating $q$ units per year, i.e., replacing the oldest $q$ units. At the start of a pandemic, demand greatly outstrips supply and the GO draws from the stockpile. The stockpile can be sufficiently large to meet demand for the duration of Phases I and II and the GO does not have a PPEP shortage nor needs to buy PPEP at the high price. The stockpile can be sufficiently large to meet only the demand for the Phase I, which is the case shown in Fig. 1, and the GO does not have a PPEP shortage but needs to buy PPEP at the high price of Phase II. Finally, the stockpile can be insufficient to meet demand for the duration of Phase I and the GO will have a PPEP shortage until the start of Phase II when the GO has to pay a high price per unit of PPEP.

Fig. 1.

Sequence of events and PPEP availability, prices and inventory.

For simplicity, Fig. 1 shows the stockpile is procured instantaneously and, therefore, all these items would have the same age, and the manufacturer would not be able to find the oldest $q$ items to replace. However, in practice, the manufacturer supplies some quantity of $\overline{q}\ge q$ units each year with a shelf life of $N$ years. Then, if rotation starts after $n$ years ($n<N$), then a stable stockpile of size $Q=n\overline{q}$ will be created without affecting the mathematical development of the model depicted in Fig. 1.

With a single PPEP, since the GO is a price taker, the GO’s best action is to use all of Phases’ II and III funding to purchase more PPEP. Therefore, a GO managing a single PPEP considers only Phase I preparedness. For multiple PPEPs, the pre-pandemic budget allocation among PPEPs must be decided. Also, the GO receives an emergency budget in case of a pandemic and needs to decide how to allocate it among PPEPs in Phase II. Because pre-pandemic decisions determine the GO’s inventory levels of PPEPs at the start of Phase II, pre-pandemic budget allocation problem and the emergency funding allocation problem are linked. Define the following notation:

• $Q=$ PPEP stockpile size at the start of the contract, a decision variable of the GO.

• $q=$ quantity the GO sells back to the manufacturer (and buys $q$ new units) per year, a decision variable of the GO.

• $p=$ price per new unit of PPEP the GO pays the manufacturer.

• $p_r=$ regular (no pandemonic) price per unit of new PPEP prior to the GO entry into the SC.

• $b=$ price per unit of older PPEP the manufacturer pays the GO for buying back PPEP.

• $L=$ the shelf life of the PPEP in years.

• $V=$ number of years to expiration the PPEP must have to be considered new, i.e., can be sold in the market by the manufacturer for $p_r$.

• $T=$ L-V number of years available to rotate the $Q$ units in the stockpile to avoid expiration.

• $N=$ the length of the contract in years, $N>T$.

• $U=$ the initial budget of the GO to build the stockpile of $Q$ units.

• $B=$ the annual budget of the GO for holding and rotating the stockpile to keep it viable.

• $Y=U+NB$ the total budget of the GO for the PPEP for the $N$ years of the contract.

• $D_i,$$i=I,II,III$, a random variable denoting daily demand during phases $I$, $II$, and $III$, respectively.

• ${\mu }_i,$$i=I,II,III$, durations of phases $I$, $II$, and $III$ of the pandemic, respectively.

According to the above notation, we get

• $X=$$D_I{\mu }_I$, a random variable denoting demand during phase I, with probability density function (pdf) $f(·)$ and cumulative density function (cdf) $F(·)$.

• $Y=$$D_{II}{\mu }_{II}$, a random variable denoting demand during phase II, with pdf $g(·)$ and cdf $G(·)$.

• $S=$$D_{III}{\mu }_{III}$, a random variable denoting demand during phase III.

The GO can reasonably forecast $U$ and $B$. We also assume that without a pandemic the manufacturer can sell the rotated PPEP for the same price of new PPEP as long as its remaining shelf life is longer than $V,$ where $V$ is sufficiently large for the rotated PPEP to work its way through the SC before expiration. For example, the manufacturer may decide to buy back only a PPEP with $V=3$ years or more left to expiration. If the PPEP has a shelf life of $L=7$ years, then the PPEP in the stockpile can’t be more than $T=L-V=4$ years old to enable its rotation and avoid its expiration later. Therefore, the entire stockpile should be rotated within 4 years to avoid expiration. Assuming that the manufacturer sells rotated PPEP for a price slightly less than $p_r$ will not qualitatively change our results, however, it will increase the complexity of the model.

Two important aspects of a PPEP which determines its suitability for being rotated are its shelf life and the number of manufacturers. For a PPEP with a short shelf life, given a GO may want to have a year or two supply of the PPEP, a shelf life of 3 years or more will be needed. Table 1 shows the shelf life of some PPEPs. For products with $L=7$, if the rotated stock needs to have 2 viable years left, then there are 5 years available to rotate the stockpile. Similarly, for products with $L=5$, there are 3 years available to rotate the stockpile. For products with $L=3$ years, e.g., latex gloves, if the stock is rotated while it has 1 viable year left, which is an ample time for it to work its way through the SC and be used, then there are 2 years available to rotate the entire stockpile. For cases of $L\le 2$ there may not be sufficient time to rotate the stockpile. If a PPEP has a few large manufacturers, then one manufacturer may have enough volume to fully supply and rotate the stockpile. When a PPEP has several small manufacturers, the GO can deal with a distributor who consolidates inventory or the GO can invest in extra capacity of a manufacturer. Both of these possibilities are analyzed in the extensions section Table 1.1 ^, 2 ^, 3

Table 1.

Shelf life for some PPEPs.

During normal times, a GO has multiple sources for PPEPs, including its inventory, inventory in hospitals, and inventory held by manufacturers. The GO also has multiple demand sources during normal times at its own hospitals as well as other small scale public health emergencies, e.g., hurricanes. We consider managing these sources of supply and demand as “business as usual” for the GO. A world-wide pandemic is a rare phenomena which creates large demand shocks and production disruptions and a significant departure from “business as usual”. Therefore, demands imposed by a pandemic are in addition to those faced by usual PPEP management the GO has prepared for. Our focus is managing preparedness for a pandemic.

The GO pays for the holding cost of the PPEP stockpile. Since the GO is a not-for-profit organization, the holding cost does not include the cost of capital invested in inventory. Therefore, we assume a fixed annual holding cost $H$ that is independent of $Q$ and is mainly composed of the storage and insurance cost. The GO maximizes preparedness which is measured by the service level (fraction of satisfied demand) during phase $I$. Phases II is not considered since for a single PPEP, all emergency funds are used to purchase the PPEP at the prevailing market price. Thus, the GO’s problem is:

$$\text{Maximize}S{L}_I={\int }_0^{Q}f\left(x\right)dx=F\left(Q\right)$$ (1)

$$\text{Subject}\text{to}Qp\le U,$$ (2)

$$q(p-b)+H\le B.$$ (3)

We assume $B>H$, i.e., the GO’s annual PPEP budget is enough to pay for the holding cost and leaves an excess amount to rotate the stockpile. Constraint (2) limits the GO’s spending in year 1 to its budget. In Constraint (3), the GO spends $H$ annually on the holding cost and rotates $q$ PPEP units at a net unit cost of $(p-b)$ resulting in an annual cost of $q(p-b)$. The sum of the annual holding and rotation costs can’t exceed the GO’s annual budget $B$. The maximum PPEP quantity that can be rotated annually is $q=\frac{B-H}{p-b}$ and the total PPEP quantity rotated over $T$ years is $Tq=T\frac{B-H}{p-b}$. The maximum quantity that can be purchased in year 1 is $Q=\frac{U}{p}$. If $T\frac{B-H}{p-b}=\frac{U}{p}$ then all of $Q$ is rotated, no PPEP expire, and the GO spends all its budget. If $T\frac{B-H}{p-b}<\frac{U}{p}$ then the GO can’t rotate all of $Q$, some PPEP will expire, and the GO spends its entire budget. If $T\frac{B-H}{p-b}>\frac{U}{p}$ then the GO will rotate all of $Q$, no PPEP will expire, and the GO will not spend all its budget. We also assume that PPEP demand has a decreasing pdf (increasing concave CDF) with support on $[0,\infty ]$, which is true for exponential and gamma distribution with shape parameter less than one (Zhou & Wang, 2009). We relax this assumption in Section 6.3.

There are two approaches (contracts) for the GO to manage the PPEP inventory. In one approach, the GO separates the stockpile decision from its maintenance and rotation decisions. The GO uses $U$ to buy the PPEP stockpile. Thereafter, the annual budget is used for the holding cost and what remains is used to rotate as much inventory in the stockpile as possible. While empirical studies on approaches to PPEPs management are not available, this approach seems to be most commonly used by GOs prior to COVID-19. In analyzing causes behind PPEP shortages during COVID-19, Cohen & Rodgers (2020) write “Not only did the government poorly maintain already-inadequate supplies and... ”, which shows the disconnect between the stockpile decision and maintenance decisions. Reasons for separating the decisions may be that different GO units are responsible for the two decisions or that the budgeting process precludes long term commitments. We refer to this case as the separate stockpile and rotation contract (SSRC). In the second approach, the GO negotiates a single contract for the stockpile size and its rotation. We suggest this approach as means to integrate the stockpile decision and maintenance decisions. We refer to this case as the joint stockpile and rotation contract (JSRC).

In both the SSRC and JSRC, the manufacturer sells $Q$ units to the GO in year 1 and, thereafter, sells $q$ units of new PPEP to the GO annually and buys back $q$ units of older PPEP from the GO. The manufacturer sells the older $q$ PPEP units, with $V$ or more years to expiration, in the market. We begin by analyzing the JSRC, which serves as a benchmark. We then analyze the SSRC and compare its performance to the JSRC. The better-performing contract will then be used to solve the problem with multiple PPEPs.

3.2. Joint stockpile and rotation contract (JSRC)

The flow of materials and prices is shown in Fig. 2 (a). The GO pays a price of $p$ per unit of new PPEP for the entire contract, i.e., the GO negotiates a single contract with a duration of $N$ years. If a pandemic occurs before $N$, years, then the rotation of the stockpile is suspended because the GO is depleting the stockpile and rotation is no longer needed. Both parties know the budget for the $N$ years, which is the sum of year 1’s budget $\$U$, and the total annual budgets for maintaining and rotating it $\$NB$, resulting in total budget $Y=U+NB$. The GO must reserve the funds needed for the holding cost, $NH$. Thus, the maximum amount that can be paid to the manufacturer for new PPEP is $Y-NH$. Thus, the JSRC’s two constraints are combined into:

$$Qp+Nq(p-b)\le Y-NH\equiv Y_N,$$ (4)

which the manufacturer knows. To maintain a viable stockpile of $Q$, $q=\frac{Q}{T}$ units must be rotated per year and constraint (4) can be rewritten as $Q(p+\frac{N(p-b)}{T})\le Y-NH\equiv Y_N$. To maximize $Q$, the constraint must be binding and the optimal $Q$ is obtained by solving the equality which yields

$$Q^{*}=\frac{T{Y}_N}{p(N+T)-bN}$$ (5)

Fig. 2.

Material flow, prices, and information in the JSRC and SSRC.

The GO wants the manufacturer to sell new PPEP for a low price and also wants the manufacturer to buy back older PPEP for a high price. The GO does not ask for a specific price for buying new PPEP or a specific price for selling back old PPEP. The reason for not specifying one of the two prices is that if the GO only specifies a low price for new PPEP, the manufacturer responds by requiring a low buy-back price for older PPEP. Conversely, if the GO only specifies a high buy-back price for older PPEP, the manufacturer responds by requiring a high price for new PPEP. Therefore, the GO needs a scheme in which the manufacturer (he) has to increase the buy-back price of older PPEP when he increases the price of new PPEP. Therefore, we investigate scheme in which the GO makes the buy-back price of older PPEP it sells back to the manufacturer an increasing function of the price the manufacturer charges for new PPEP. The GO stipulates a buy-back price for rotated stock of $b=p\frac{p}{p_r}$, where $p$ is determined by the manufacturer and $p_r$ is market price. This price relationship means $b$ is determined when the manufacturer decides $p$. The buy-back price of the JSRC is shown in Fig. 3 for $p_r=1$. As can be seen, if the manufacturer decides to charge the GO the retail market price $p=p_r$ for building the stockpile, then $b=p_r$, which implies that the GO wants the manufacturer to rotate the stock at no cost. As the manufacturer decreases the price of new PPEP, the GO accepts a lower buy-back price for older PPEP. Also, in this contract, $\frac{db}{p}=\frac{2p}{p_r}>$ and $\frac{d^{2}b}{p^2}=\frac{2}{p_r}>0$, i.e., $b$ is increasing and convex in $p$, which means that the buy-back price increases at an increasing rate in the price of new PPEP. The manufacturer profit is:

$$MaxZ=Q(p-c)+N\frac{Q}{T}(p-c+(p_r-\frac{p}{p_r}p)-(p_r-c)).$$ (6)

Fig. 3.

Buy-back price of old PPEPs, $p_r=1$.

The first term in $Z$ is the profit from selling $Q$. In the second term, $N\frac{Q}{T}$ is the total rotated PPEP units over the contract. The manufacturer makes a profit of $p-c$ from selling a new PPEP unit to the GO and $p_r-\frac{p}{p_r}p$ from selling an older PPEP unit in the market but incurs a loss of $p_r-c$ per unit because an older PPEP is sold instead of a new unit. We can prove Proposition 1.

Proposition 1

The manufacturer charges$p^{*}=\frac{p_r(N+T)}{2N}$per unit of new PPEP and buys back older PPEP for$b^{*}=\frac{p_r{(N+T)}^2}{4N^2}$per unit and his profit for a given$Q$is$Z^{*}=\frac{Q(N^2{p}_r+2N(p_r-2c)T+p_r{T}^2)}{4NT}$.

Proposition 1 implies that the price of new and rotated PPEP are independent of the GO’s budget. Also, since $\frac{d{Z}^{*}}{Q}=\frac{1}{4}(\frac{p_r{(N+T)}^2}{NT}-4c)>0$, $Z^{*}$ is increasing in $Q$. Therefore, the manufacturer maximizes profit by maximizing the quantity he sells to the GO at those prices, i.e. exhausting the GO’s $N$-years budget. Also, since $\frac{d{p}^{*}}{dT}-\frac{d{b}^{*}}{dT}=-\frac{p_{r}T}{2N^2}<0$, the buy-back price increases faster than the price of new PPEP as the maximum rotatable age increases. This is a result of $b=\frac{p}{p_r}p$, which increases at an increasing rate. Using Eq. (5) and Proposition 1, we have Proposition 2.

Proposition 2

Under the JSRC, the GO stockpiles a quantity of$Q^{*}=\frac{4NT{Y}_N}{p_r{(N+T)}^2}$, no PPEP expires, and the manufacturer makes a total profit of$Z^{*}=\frac{(N^2{p}_r+2N(p_r-2c)T+p_r{T}^2)Y_N}{p_r{(N+T)}^2}$.

Proposition 2 shows that the manufacturer’s optimal profit and the stockpile size are increasing in $Y_N$. Therefore, both the manufacturer and the GO benefit from spending the entire budget. Even though $U$ and $B$ are separate budgets, the GO can negotiate based on $Y_N$. In other words, the contract is robust with respect to the distribution of $Y$ between $U$ and $B$. Corollary 1 follows directly from the expressions in Proposition 2 and shows some desirable properties of the JSRC.

Corollary 1

The outcomes of the JSRC have the following properties:

• 1.The unit price of new PPEP ($p^{*}$) and the buy-back unit price of old PPEP ($b^{*}$) are independent of the total budget$Y$and its distribution between$B$and$U$.
• 2.The optimal stockpile size ($Q^{*}$) and maximum manufacturer’s profit ($Z^{*}$) are a function of$Y$but are independent of the distribution of$Y$between$U$and$B$.

Property (1) allows the GO to spread its budget among different manufacturers to buy a PPEP without losing negotiation power and paying a higher price. Property (2) enables the GO to handle unbalanced budget allocation, e.g., the GO may get a large $U$ but small $B$.

From Proposition 2 we find $\frac{d{p}^{*}}{dT}=\frac{p_r}{2N}>0$ and the price of the PPEP is increasing in its maximum rotatable age. Since $q=\frac{Q}{T}$ units need to be rotated annually, a larger $T$ results in a smaller $q$, which means the manufacturer sells fewer PPEP to the GO and, therefore, raises the price to increase profit. Also, $\frac{d{b}^{*}}{dT}=\frac{p_r(N+T)}{2N^2}>0$, the buy-back price of the PPEP is increasing in the maximum rotatable age because the GO links the buy-back price to the price of new PPEP and the manufacturer increases the price of new PPEP as $T$ increases.

Also, from Proposition 2, $\frac{d{Q}^{*}}{dT}=\frac{4N(N-T)Y_N}{p_r{(N+T)}^3}>0$ and the stockpile size increases in the maximum rotatable age. As $T$ increases, the annual quantity of rotated PPEP decreases and less money is spent on stock rotation. The saved money is used to increase the size of the stockpile. For the manufacturer’s profit $\frac{d{Z}^{*}}{dT}=-\frac{4cN(N-T)Y_N}{p_r{(N+T)}^3}<0$ and the manufacturer’s profit decreases in $T$. As $T$ increases, the GO has less PPEP to rotate annually which decreases annual sales of new PPEP for the manufacturer and decreases profit. Since T=L-V, $T$ can be increased by increasing $L$ or decreasing $V$. It is reasonable to assume that the shelf life of a PPEP, $L$, depends on its nature and can be objectively determined. This leaves $V$ (and as a result $T$) to be negotiated. It is in the best interest of the manufacturer to increase $V$ to increase sales and profits from the GO, and to be sure that the rotated stock is far from expiration and can reach consumers before expiration. Decreasing $V$ increases the size of the PPEP stockpile and increases the service level. The GO can make $T$ part of its offer to the manufacturer and can allow a sufficient time for the manufacturer to sell the rotated PPEP. Given that much of the industry has adopted just-in-time inventory management, it is reasonable to assume that 1–2 years are sufficient for PPEP inventory to make its way through the SC and be used. Therefore, setting $V$ to 1 or 2 years is quite reasonable.

3.3. Separate stockpile and rotation contract (SSRC)

In the SSRC, there are two contracts as shown in Fig. 2(b). In year 1, the GO has a budget of $\$U$ to build the stockpile. The manufacturer knows $U$. The GO buys a stockpile with $U$ without considering its rotation. The GO may do so because two separate entities are involved in PPEP management, one for purchasing and the other for maintenance. Also, the GO may have a myopic view of “we should build the maximum stockpile with $U$”. After building the stockpile in year 1, a new contract is agreed on to rotate the stockpile. To evaluate the benefits from the JSRC relative to the SSRC, we assume that the GO can get the JSRC’s price, i.e., $p^{*}=\frac{p_r(N+T)}{2N}$, in the SSRC. This avoids giving the JSRC any advantage over the SSRC. Realistically, the JSRC is likely to have a price advantage over the SSRC because the JSRC has a larger budget and may give the GO more bargaining power. Since $p^{*}$ is determined and the manufacturer requires a buy-back price of $b=\frac{p}{p_r}p$, the buy-back price in the SSRC is the asme as in the JSRC. The GO purchases a quantity of $Q=\frac{U}{p^{*}}=\frac{2NU}{p_r(N+T)}$ in year 1. In subsequent years, the stockpile may be too large to be rotated with the annual budget or too small such that all of it can be rotated. Depending on the $U$ and $B$, the GO may be able the rotate all of $Q$ or only part of it depending on the annual constraint:

$$q(p^{*}-\frac{p^{*}}{p_r}p)+H\le B.$$ (7)

Constraint (7) is either binding for all $N$ years or not binding. If $U$ is large relative to $B$, the quantity needing rotation annually ($\frac{Q}{T}$) is greater than the quantity that can be rotated ($\frac{B-H}{p}$) and the constraint is binding. If $U$ is small relative to $B$, the quantity needing rotation annually is smaller than the quantity that can be rotated and the constraint is not binding. This is different from the JSRC where the joint consideration of the stockpile size and its rotation leads to the equality holding on the budget constraints. At equality, Constraint (7) can be rewritten as $q=\frac{4(B-H)N^2}{p_r(N-T)(N+T)}$. If $qT\ge Q$, then Constraint (7) is not binding and the GO is able to rotate all of $Q$ with $q_a^{*}=\frac{Q}{T}=\frac{2NU}{N{p}_{r}T(N+T)}$ units rotated annually. If $qT<Q$ then Constraint (7) is binding, the GO can’t rotate all of $Q$ in $T$ years, and $q_b^{*}=\frac{4(B-H)N^2}{p_r(N-T)(N+T)}$ units are rotated annually. Solving $q_{b}T=Q$, we obtain $B_c\equiv H+\frac{(N-T)U}{2NT}$ as the critical value of the annual budget below which Constraint (7) is binding, i.e., not all $Q$ can be rotated. Define $E=B-H$, which is the part of the annual budget in excess of the holding cost, i.e., the annual amount of money available for rotating PPEP in the stockpile. We formalize the results of the SSRC in Proposition 3.

Proposition 3

The solution to the SSRC problem is

• 1.If$B\ge B_c$the GO has$Q^{*}=\frac{2NU}{p_r(N+T)}$units of PPEP stockpile, rotates$q_a^{*}=\frac{2NU}{N{p}_{r}T(N+T)}$units annually, and no PPEP will expire. The manufacturer’s profit in year 1 is$U(1-\frac{2cN}{p_r(N+T)})$, annual profits in years$2toN$is$\frac{(N-T)U}{2NT}$, and the total contract profit is$\frac{(N^2{p}_r+2N(p_r-2c)T+p_r{T}^2)U}{2p_{r}T(N+T)}$.
• 2.If$B<B_c$the GO has a PPEP stockpile of$Q_L=\frac{2NU}{p_r(N+T)}$units in years$1toL$and$Q_N=\frac{4E{N}^{2}T}{p_r(N-T)(N+T)}$units in years$L+1toN$, for an average time-weighted stockpile level of$A_Q=\frac{4E(N-L)NT+2L(N-T)U}{p_r(N-T)(N+T)}$units.$W=\frac{2N\left(\right(N-T)U-2NTE)}{p_r(N-T)(N+T)}$units of PPEP will expire. The manufacturer’s profit in year 1 is$U(1-\frac{2cN}{p_r(N+T)})$and years$2toN$is$EN$and the total contract profit is$\frac{(N^2{p}_r+2N(p_r-2c)T+p_r{T}^2)Y_N}{p_r{(N+T)}^2}$.

Proposition 3 reveals a disadvantage of the SSRC in that its performance depends on the allocation of the N-year budget of $Y$ between the first year budget $U$ and subsequent $N-1$ years annual budget $B$, whereas the performance of the JSRC does not. This can be seen by comparing $Q^{*}$ in Proposition 2, which is a function of only $Y$, and the expressions for $Q^{*}$ in Proposition 3 which depend on $U$ and $B$. Also, Proposition 3 shows that the SSRC can generate waste, a conclusion supported by actual evidence of the many expired PPEP stock during COVID-19. For waste, $\frac{dW}{dT}=-\frac{4E{N}^2(N^2+T^2)+2N{(N-T)}^{2}U}{p_r{(N^2-T^2)}^2}<0$ and $\frac{dW}{dN}=\frac{8EN{T}^3+2{(N-T)}^{2}TU}{p_r{(N^2-T^2)}^2}>0$ which implies that waste is decreasing in the maximum rotatable age of the PPEP and increasing in the duration of the SSRC. Comparing Propositions 2 and Proposition 3, Corollary 2 follows.

Corollary 2

For$N>L$and a budget of$Y$or less, the SSRC changes relative to the JSRC:

• 1.
  If$B>B_c$then

  • (a)
    SSRC decreases the stockpile by$\frac{2N(2NTE-(N-T\left)U\right)}{p_r{(N+T)}^2}>0$for years 1 to$N$;
  • (b)
    SSRC decreases the manufacturer’s profit by$\frac{(N^2{p}_r+2N(p_r-2c)T+p_r{T}^2)(2NTE-(N-T)U)}{2p_{r}T{(N+T)}^2}>0.$
• 2.
  If$B\le B_c$then

  • (a)
    SSRC increases the PPEP stockpile by$\frac{2N\left(\right(N-T)U-2NTE)}{p_r{(N+T)}^2}>0$for years 1 to$L$and decreases the PPEP stockpile by$\frac{4NT\left(\right(N-T)U-2NTE)}{p_r(N-T){(N+T)}^2}>0$for years$L+1$to$N$. The time weighted average PPEP stockpile decreases by$\frac{2(2NT-L(N+T\left)\right)\left(\right(N-T)U-2NTE)}{p_r(N-T){(N+T)}^2}>0$;
  • (b)
    SSRC decreases the manufacturer’s profit by$\frac{2cN\left(\right(N-T)U-2NTE)}{p_r{(N+T)}^2}>0$.

Corollary 2 shows the importance of having a single contract covering both the PPEP stockpile and its rotation. Such a contract is better for the GO in the sense of increasing the average size of the PPEP stockpile. The key feature causing such improvement is that using a single contract allows the GO, without increasing PPEP unit cost, to avoid any waste of PPEP in the stockpile and to spend its entire budget

Corollary 2 also shows why the manufacture will agree to the JSRC. The JSRC does not let any PPEP expire and uses the entire budget of the GO for the $N$ years. Therefore, compared to the SSRC, the JSRC will provide one of two advantages for the manufacturer. In cases were the SSRC does not exhaust the entire $N$-years budget (i.e., small initial budget and large annual budgets in Case 1 of Corollary 2), the JSRC allows the manufacturer to exhaust all of the GO’s $N$-years budget, resulting in larger revenue and larger profit. In case the SSRC creates waste due to PPEP expiration (i.e., large initial budget and small annual budgets in Case 2 of Corollary 2), the JSRC allows the manufacture to buy back PPEP for a low price and sell them for $p_r$ as well as sell their replacement to the GO. In both cases, the manufacturer is better off with the JSRC.

It should be noted that the comparison in Corollary 2 was performed with the same price from the JSRC for new PPEP. It is unlikely that the GO will have the same bargaining power in the two-part SSRC as it does in the larger JSRC and will pay a higher price for the PPEP in the SSRC.

3.4. Example-single PPEP in a manufacturer-GO SC

Consider a PPEP with an exponentially distributed demand and a mean of 100,000 units (rate parameter of 1/100,000) in Phase I. Other parameters are $p_r=\$1$ per unit, $c=\$0.60$ per unit, $L=7$ years, $Y=\$250,000$, $N=15$ years, $T=5$ years, and $H=\$6000$ per year. Table 2 shows the solutions for the JSRC and two SSRCs, SSRC-1 and SSRC-2. In SSRC-1, the GO allocates $60,000 to the stockpile and $100,000 and for its rotation over 15 years. The remaining $90,000 is the holding cost for 15 years. In SSRC-2, the GO allocates $110,000 to the stockpile, and $50,000 for its rotation. The remaining $90,000 is used for the holding cost. As can be seen, the JSRC increases the manufacturer’s profit and the stockpile size by 33.3% over SSRC-1. This is because the budget allocated to build the stockpile in the SSRC is small and the remaining money for rotating and holding the stockpile is more than needed for a stockpile of this size. Compared to SSRC-2, the JSRC increases the average stockpile size and the manufacturer’s profit by 2.6% and 25.7%, respectively. This is because the budget allocated to build the stockpile is large and the remaining money is less than needed to rotate the stock and pay for the holding cost for a stockpile of this size. As a result, the viable stockpile in years 1 to 6 is 165,000 units and drops to 75,000 units starting in year 8 due to 90,000 units expiring at the end of year 7. The manufacturer is worse-off with the SSRC-2 because instead of rotating and making a profit on 24,000 units per year in the JSRC for 15 years, he is rotating and making a profit on 15,000 units per year in the SSRC.

Table 2.

Comparison of JSRC and SSRC solutions.

4. The multi-product stockpile and rotation problem (MPSRP)

A GO is usually responsible for a number of different PPEPs, e.g., masks, goggles, and face shields. The problem is allocating the N-year budget of $\Omega$ among $m$ different PPEPs and their associated costs. Part of $\Omega$ is allocated to building the stockpiles, which we denote by ${\Omega }_1$. The remaining, $\Omega -{\Omega }_1$, is allocated to holding and rotating the stockpiles. The GO also needs to determine how to allocate ${\Omega }_1$ among $m$ PPEPs, which in turn determines the allocation of $\Omega -{\Omega }_1$ among PPEPs. As we showed for a single PPEP, the JSRC is the better contact and, therefore, we use it in solving the MPSRP. The JSRC analysis shows that the stockpile size of a PPEP depends only on its N-year budget, $Y$. Thus, in the MPSRP, the GO determines the optimal values of $Y_j,j=1,2,\dots ,m,$ such that preparedness is maximized and ${\sum }_{j=1}^m{Y}_j=\Omega$, where $\Omega ={\Omega }_1+N\eta$ and $\eta$ is the annual rotation and holding budget for PPEPs.

PPEPs have different importance. Face masks are the first line of defense and the GO may give them higher importance. The service level for PPEP $j$ is ${\int }_0^{Q_j}{f}_j\left(x_j\right)d{x}_j$, where $x_j$ is demand for PPEP $j$ in Phase I. For decreasing $f_j\left(x_j\right)$ with support on $[0,\infty ]$, ${\int }_0^{Q_j}{f}_j\left(x_j\right)d{x}_j<1$. To reflect different importance of PPEPs, each PPEP is assigned a weight $0<{\omega }_j<1$ and ${\sum }_{j=1}^m{\omega }_j=1$. For example, for two PPEPs, if $j=1$ is most important, then the GO should determine the relative importance of PPEP $j=2$. This can be achieved by deciding the service level of $j=2$, $S{L}_2$ which, weighted by its importance, is equivalent to $S{L}_1\simeq 1$. If $S{L}_2=0.6$ is equivalent, then ${\omega }_1=\frac{1}{1+0.6}=0.625$ and ${\omega }_2=\frac{0.4}{1+0.6}=0.375$. Since the GO is using the JSRC, the quantity of any PPEP, $Q_j$, is determined once its budget allocation, $Y_j$, is determined, resulting in the GO’s MPSRP

$$\underset{Y_j}{\text{Maximize}}SL=\sum _{j=1}^m{\omega }_j{\int }_0^{Q_j}{f}_j\left(x_j\right)d{x}_j$$ (8)

$$\text{subject}\text{to}\frac{U_j(p_j-\frac{p_j}{p_{r,j}}{p}_j)}{p_j{T}_j}+H_j=B_{j}j=1,2,\dots ,m$$ (9)

$$U_j+N{B}_j=Y_j,j=1,2,\dots ,m$$ (10)

$$\sum _{j=1}^m{U}_j={\Omega }_1$$ (11)

$$\sum _{j=1}^{m}N{B}_j=\Omega -{\Omega }_1$$ (12)

Constraint (9) insures that funds for each PPEP are sufficient to hold and rotate the stockpile. The necessary and sufficient optimality condition is given in Proposition 4.

Proposition 4

The necessary and sufficient optimality condition for the MPSRP is

$$\frac{{\omega }_1{f}_1\left(\frac{U_1}{p_1}\right)}{p_1}=\frac{{\omega }_2{f}_2\left(\frac{U_2}{p_2}\right)}{p_2}=\dots =\frac{{\omega }_i{f}_j\left(\frac{U_j}{p_j}\right)}{p_j}=\dots =\frac{{\omega }_m{f}_m\left(\frac{U_m}{p_m}\right)}{p_m}$$ (13)

Eq. (13) implies that at optimality, the budget allocation among PPEPs is such that the increase in the service level of each PPEP from $1 increase in its budget weighted by the PPEP importance is equal to that of all other PPEPs. The manufacturer’s problem is

$$\underset{p_j}{Maximize}Z=\sum _{j=1}^m(\frac{U_j(p_j-c_j)}{p_j}+\frac{N{\sum }_{i=1}^{T_j}\frac{U_j(p_{r,j}-\frac{p_j}{p_{r,j}}{p}_j)}{p_j{T}_j}}{T_j})$$ (14)

The multi-PPEP manufacturer’s profit is the sum of $m$ PPEPs’ profits, i.e., separable, and, therefore, the optimal policy for each PPEP is given by Proposition (1). Substituting for the prices into Eq. (13) gives the following sufficient optimality condition:

$$\frac{{\omega }_1{f}_1\left(\frac{U_1}{\frac{p_{r,1}(N+T_1)}{2N}}\right)}{p_{r,1}}=\frac{{\omega }_2{f}_2\left(\frac{U_1}{\frac{p_{r,2}(N+T_2)}{2N}}\right)}{p_{r,2}}=\dots =\frac{{\omega }_j{f}_j\left(\frac{U_j}{\frac{p_{r,j}(N+T_j)}{2N}}\right)}{p_{r,j}}=\dots =\frac{{\omega }_m{f}_m\left(\frac{U_m}{\frac{p_{r,m}(N+T_m)}{2N}}\right)}{p_{r,m}}$$ (15)

The optimal $U_j$, $j=1,2,\dots ,m$ can be found using Eq. (15) with Constraint (11). Finding the optimal $U_j$ means finding the optimal $Q_j$ and $Y_j$. Closed-form solutions can be obtained for some PPEPs demand distributions, e.g., exponential. Pandemics severity varies significantly, which makes the exponential distribution suitable for modeling the demand. Proposition 9 in the Appendix shows the optimal solution for exponential PPEPs demand distributions with means of $\frac{1}{{\lambda }_j}$, $j=1,2,\dots ,m,$ during Phase I. We illustrate the solution using the following numerical example.

4.1. Example-multi-PPEP in a GO-manufacturer SC

We use a four-PPEPs MPSRP with demands, weights, and holding costs shown in Table 3 and a GO 12-year budget of $4,000,000. The GO and manufacturer agree to a rotation cycle of $T_j=L_j-2$, $j=1,2,3,4$. The solution illustrates some important features of the proposed method. PPEPs 1 and 2 have the same weight while the mean demand of PPEP 1 is 50% larger than the mean demand of PPEP 2, yet the budget allocation of PPEP 2 is smaller than PPEP 1 by only $20,853 (1.5%). This shows how the proposed method deals with PPEPs with different useful life which, in this case, causes the GO to allocate more expenditure to PPEP 2 with the shorter useful life to ensure the proper rotation of its stockpile. PPEPs 3 and 4 have identical parameters except that the retail price of PPEP 4 is twice that of PPEP 3. However, the budget allocation to PPEP 4 is only $118,419 (21.1%) larger than that of PPEP 3, which reflects the ability of the proposed method to get the largest “bang for the buck”. Both PPEPs 3 and 4 have the same importance but the mean demand in $ (instead of units of PPEP) for PPEP 3 is $200,000 and for PPEP 4 is $400,000. Therefore, allocating larger amount from the budget per $1 of mean demand to PPEP 3 than per $1 of mean demand to PPEP 4 is more effective.

Table 3.

Solution to a multi-product stockpile and rotation problem .

5. Planning for phase II and spot market prices

Prices of PPEPs are known to spike during pandemics after a period of no availability. It is prudent for GOs managing multiple PPEPs to consider Phase II during which PPEPs become available at much higher prices. At the start of the pandemic, there is usually an emergency budget allocation to GOs. For example, a supplementary budget in California appropriated $100 million for buying PPEPs and other COVID-19 related expenses. This allocation is usually limited and we denote it by $\Psi$. The GO wants to maximize its service level (preparedness) over Phases I and II. This presents additional complexity to the Phase I problem. The service level for PPEP $j$ in Phase II depends on the budget allocation it receives in Phases I and II. This is because the allocation in Phase I determines the PPEP’s inventory position at the end of Phase I and start of Phase II. This problem requires a two-stage solution approach. In the second stage, given any Phase I budget allocation, the optimal policy to Phase II budget allocation is determined. The first stage problem is determining the optimal Phase I policy, given the second stage optimal policy. We first solve the second stage optimal allocation of $\Psi$ among PPEPs. Depending on the initial stockpile and the demand during Phase I, the expected quantity of PPEP $j$ left in the stockpile at the end of Phase I for exponentially distributed PPEP demand is

$$L_j={\int }_0^{\frac{U_j}{p_j}}(\frac{U_j}{p_j}-x_j)f_j\left(x_j\right)d{x}_j=\frac{U_j}{p_j}-\frac{1-e^{-\frac{U_j{\lambda }_j}{p_j}}}{{\lambda }_j}>0for{\lambda }_j,U_j,p_j>0.$$

In phase II, PPEP $j$ receives a budget allocation of $S_j$, where $S_j$ is determined by the GO, for purchasing additional PPEPs. This results in a service level for PPEP $j$ in Phase II which depends on the ending inventory of PPEP $j$ in Phase I and the allocation it receives in Phase II as follows:

• 1.If $\frac{U_j}{p_j}\le x_j$ then there is no inventory of PPEP $j$ at the start of Phase II and the service level in Phase II is ${\int }_0^{\frac{S_j}{p_{h,j}}}{g}_j\left(y_j\right)d{y}_j$, where $g_j\left(y_j\right)$ is the pdf of the demand for PPEP $j$ during Phase II and $p_{h,j}$ is its spot market price in Phase II.
• 2.If $\frac{U_j}{p_j}>x_j$, then the inventory level of PPEP $j$ at the start of Phase II is $L_j>0$ units and its Phase II service level is ${\int }_0^{L_j+\frac{S_j}{p_{h,j}}}{g}_j\left(y_j\right)d{y}_j$.

The GO may consider satisfying demand in Phases I and II to have different importance and, therefore, the weight assigned to PPEP $j$ is denoted by ${\omega }_{j,k}$, where $k=I,II$ denotes Phases I and II, respectively, and ${\sum }_{j=1}^m({\omega }_{j,I}+{\omega }_{j,II})=1$. The GO’s problem is:

$$\begin{array}{c}\hfill \underset{Y_j,S_j}{\text{Maximize}}S{L}_T=\sum _{j=1}^m[{\omega }_{j,I}{\int }_0^{\frac{U_j}{p_j}}{f}_j\left(x_j\right)d{x}_j+{\omega }_{j,II}[{\int }_0^{\frac{U_j}{p_j}}{f}_j\left(x_j\right)d{x}_j{\int }_0^{L_j}\\ \hfill +\frac{S_j}{p_{h,j}}{g}_j\left(y_j\right)d{y}_j+{\int }_{\frac{U_j}{p_j}}^{\infty }{f}_j\left(x_j\right)d{x}_j{\int }_0^{\frac{S_j}{p_{h,j}}}{g}_j\left(y_j\right)d{y}_j\left]\right]\end{array}$$ (16)

$$\text{subject}\text{to}\text{Constraints}(9-12)$$ (17)

$$\sum _{j=1}^m{S}_j=\Psi$$ (18)

Constraint (18) implies the GO spends the entire emergency budget in Phase II. Proposition 5 characterizes the optimal solution to second stage problem of allocating the Phase II budget.

Proposition 5

The necessary and sufficient optimality condition for Phase II’s solution is

$$\frac{{\omega }_{j,II}\left[\right(1-F_j\left(\frac{U_j}{p_j}\right))g_j\left(\frac{S_j}{p_{h,j}}\right)+F_j\left(\frac{U_j}{p_j}\right)g_j(\frac{S_j}{p_{h,j}}+L_j)]}{p_{h,j}}=\frac{{\omega }_{i,II}\left[\right(1-F_i\left(\frac{U_i}{p_i}\right))g_i\left(\frac{S_i}{p_{h,i}}\right)+F_i\left(\frac{U_i}{p_i}\right)g_i(\frac{S_i}{p_{h,i}}+L_i)]}{p_{h,i}},\forall i\ne j$$ (19)

Eq. (19) implies that at optimality, the allocations, $S_j,j=1,2,\dots ,m$, must satisfy the condition: All PPEPs have the same increase in their service level, weighted by their importance, from a $1 increase in their Phase II budget allocation from the total Phase II budget of $\Psi$. Otherwise, a change in the allocation will result in an increase in the service level. Proposition 6 characterises the optimal budget allocation in Phase I for any Phase II budget allocation $S_j$ $j=1,2,\dots ,m$.

Proposition 6

For any Phase II budget allocation$S_j$$j=1,2,\dots ,m$, the optimal Phase I budget allocation must satisfy:

$$\frac{dS{L}_T}{d{U}_j}=\frac{dS{L}_T}{d{U}_i},forallj\ne i$$ (20)

Eq. (20) implies that at optimality, and for any Phase II budget allocations, Phase I budget allocations, $U_j$, $j=1,2,\dots ,m$, must satisfy the condition: All PPEPs have the same increase in their service level, weighted by their importance, from a $1 increase in their Phase I budget allocation from the total budget of $\Omega$. Otherwise, a change in the allocation will result in an increase in the service level. We provide closed-form solution for Phase II optimal budget allocation and the sufficient optimality condition for Phase I budget allocations for exponential demand distributions in Proposition 10 in the Appendix.

From Proposition 10, to solve the problem, Eqs. (33) and (34) in the Appendix are used to obtain the optimal expressions of $S_j^{*},j=1,2,\dots ,m$, as a function of $U_j,j=1,2,\dots ,m$, which eliminates $S_j$ in Eq. (35). A numerical procedure can be used to find the $U_j$, $j=1,2,\dots ,m$, which satisfy Eqs. (35) and (36). To do so, we rewrite Eq. (36) as

$$\sum _{j=1}^m{U}_j=\Omega -N\sum _{j=1}^m(\frac{U_j(p_j-p_j\frac{p_j}{p_{rj}})}{p_j{T}_j}+H_j)$$

For any $\Omega$, a value of ${\Omega }_1={\sum }_{j=1}^m{U}_j=\frac{\Omega }{2}$ can used to find $U_j$, $j=1,2,\dots ,m$, satisfying Eq. (35). If the equality is not satisfied, then the bisection method is used to obtain ${\Omega }_1={\sum }_{j=1}^m{U}_j=\frac{\frac{\Omega }{2}+\Omega }{2}$ as the new value to use in Eq. (35) to find each $U_j$. This bi-section search process is continued until a set of $U_j$, $j=1,2,\dots ,m$, satisfying Eqs. (35) and (36) are found.

5.1. Example-effect of spot market prices

We now reconsider the example in Section 4.1 with the additional data for Phase II of the pandemic as shown in Table 4 . Mean demands in Phase II of the pandemic for PPEPs 1, 2, and 4 are half of the mean demands in Phase I, whereas PPEP 3’s Phase II mean demand is two thirds of Phase I mean demand. The spot market prices of PPEPs 2 and 3 are three-fold the regular price. The spot market price of PPEP 1 is 50% above the regular price whereas PPEP 4 does not have an increase in price in Phase II. The GO estimates that if a pandemic occurs, then it will receive $2,000,000 to purchase PPEPs. First, we note from Table 4 that considering Phase II in making Phase I decisions results in significant changes to Phase I’s optimal solution. Second, we note that the proportions of the Phase I budget allocated to PPEPs 2 and 3 are much larger than the proportions of Phase II budget allocated to them. This can be seen in Table 5 , which is computed from Table 4, and shows the percent of the total budget allocation each PPEP received in Phases I and II. As can be seen, $\frac{\%ofPhaseIbudget}{\%ofPhaseIIbudget}$ for each PPEP is large when its $\frac{Spotmarketprice}{JSRCprice}$ is large. This shows how the proposed method enables the GO to avoid paying high PPEPs spot market prices by building larger stockpiles for these PPEPs at the regular prices.

Table 4.

Solution to a multi-product stockpile and rotation problem with spot market prices .

Table 5.

Phases I&II budget allocation among PPEPs.

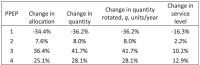
Comparing Phase I solutions in Tables 3 and 4, we obtain Table 6 , which illustrates some advantages of considering Phase II in making Phase I decisions. First, considering Phase II results in an increase in the budget allocations in Phase I to PPEPs 2 and 3, both of which have the largest increase in spot market prices over the regular prices. Therefore, the stockpiled quantities of both PPEPs 2 and 3 increase which decrease the expected quantities the GO needs to purchase at the expensive spot market prices in Phase II. Considering Phase II when making Phase I allocation also results in decreasing the budget allocation to PPEP 1 in Phase I by 34.4% and its stockpile by 36.2%. However, PPEP 1’s service level decreases by a smaller amount of 16.3%, from 0.871 to 0.729. This is because the stockpile size when only Phase I is considered was large and its size occurs at demand realizations where the pdf is weakly decreasing. As a result, reducing PPEP 1’s stockpile quantity in Phase I when Phase II is considered results in a small decrease in its service level which is traded off to get significant increases in the service level of other PPEPs.

Table 6.

Changes in Phases I allocation, quantities, and service levels of PPEPs

The proposed method focuses the GO on preparedness per $1 of spending. This can be seen by comparing PPEPs 3 and 4 in Tables 3 and 4. The difference between PPEPs 3 and 4 when only Phase I is considered is that PPEP 4’s regular price is twice the regular price of PPEP 3. However, when only Phase I is considered in Table 3, PPEP 4 is allocated $678,516, which is only $118,419 (21.1%) above PPEP 3’s allocation of $560,097. This disproportionably smaller allocation relative to the two-fold larger price of PPEP 4 shows how this approach gives “big bang for the buck”. Similar advantage is observed in Phases I&II allocations where PPEP 4 is allocated 848,906 + 451,339 = $1,300,245, which is $281,913 (27.7%) above PPEP 3’s Phases I&II allocation of 763,723+254,609=$1,018,332. The increase of $27.6-21.1=6.5\%$ in the Phases I&II vs. Phase I only allocation to PPEP 4 reflects the ability of the proposed method to adjust to the large spot market price of PPEP 3 which reduces its “big bang for the buck” relative to PPEP 4.

6. Extensions

In this section, we consider three situations that may be faced by the GO and how to address them using the proposed models. Some PPEPs have several manufacturers with insufficient sales volume to rotate a large stockpile. The GO in this case can invest in volume flexibility of a manufacturer and use the increased capacity in case of a pandemic or contract with a distributor who deals with many manufacturers. Also, PPEPs demand cdfs may not be increasing concave property. Last, the PPEPs supplied to the GO may have scrap which affects preparedness.

6.1. Investing in volume flexibility

Without a large manufacturer or distributor, no one entity in the SC is able to rotate the stockpile. In this one manufacturer-GO SC, in addition to rotating a quantity equal to the sales volume of the manufacturer, denoted by $D_r$, the GO needs additional PPEP in case of a pandemic. The GO can invest in the manufacturer’s volume flexibility which enables him to produce above regular capacity (at a cost) (Wei & Zhang, 2021). The GO invests in building volume flexibility of $\ell$ units per year and uses it in a pandemic. There are different functions for modeling the cost of volume flexibility, e.g., linear and quadratic, as well as modeling the premium increase in unit cost when utilizing it (Sapra & Jackson, 2013). We assume a linear investment cost in volume flexibility given by ${{\rm Y}}_1\left(\ell \right)=a_1\ell$, where $a_1$ is a PPEP specific parameter. Unit production cost increases as more of this capacity is used. Given a unit cost of $c$ at the manufacturers’ ideal volume, the cost per unit when producing on the extra capacity is ${{\rm Y}}_2\left(\ell \right)=c+a_2\ell$, where $a_2$ is a PPEP specific parameter. The GO agrees to provide the same margin the manufacturer gets at the price $p_r$ before a pandemic, i.e., $p_r-c$ and, therefore, the price per unit from extra capacity is $a_2\ell +p_r$. The GO determines how to allocate the initial budget between the stockpile and investment in volume flexibility. We incorporate the spot market prices in case of a pandemic with emergency budget $\Psi$. Let $Q_t$ denote spot-market quantity. To maximize preparedness for Phases I and II, the GO maximizes:

$$\underset{\ell }{\text{Maximize}}S{L}_I=Q+({\mu }_I+{\mu }_{II})\ell +Q_t$$ (21)

$$\text{Subject}\text{to}Qp+a_1\ell \le U,$$ (22)

$$({\mu }_I+{\mu }_{II})\ell (a_2\ell +p_r)+Q_t{p}_h\le \Psi$$ (23)

.

$$q(p-b)+H\le B$$ (24)

$$q\le D_r$$ (25)

Constraint (25) limits the rotated quantity to the manufacturer’s annual non-GO sales. We denote the JSRC with flexibility investment by (JSRCFI). The manufacturer maximizes

$$\begin{array}{ccc}\hfill Z& =& \frac{(U-a_1\ell )(p-c)}{p}+\frac{N(U-a_1\ell )(p-c+(p_r-\frac{p}{p_r}p)-(p_r-c))}{pT}\hfill \\ & & +a_1\ell +\ell ({\mu }_1+{\mu }_2)(p_r+a_2\ell -c)\hfill \end{array}$$ (26)

Define ${\rho }_h=p_h-p_r$ as the spot market price penalty, ${\mu }_e={\mu }_1+{\mu }_2$, $N_e=T+N$, and the quantities in Table 7 . Proposition 7 characterises the optimal solution to the JSRCFI.

Proposition 7

If the manufacturer non-Go annual sales satisfy$D_r\le {\overline{D}}_r$, then at equilibrium of the JSRCFI, the manufacturer charges a price of$p^{*}=\frac{p_r(N+T)}{2N}$and

• 1.If$a_1\ge {\overline{a}}_1\equiv \frac{{\rho }_h{p}_r{N}_e^2{\mu }_e}{4N{p}_{h}T}$, it is optimal not to invest in volume flexibility.
• 2.
  If$a_1<{\overline{a}}_1$then

  • (a)
    If$a_1\ge {\dot{a}}_1$, stockpile is$Q^{*}=T{D}_r$, capacity added is${\ell }^{*}\equiv \frac{{\rho }_h{p}_r{N}_e^2{\mu }_e-4a_{1}N{p}_{h}T}{2a_2{p}_r{N}_e^2{\mu }_e}$, and$Q_t^{*}=\frac{p_r{N}_e^2{\mu }_e(8a_{1}N{p}_h^{2}T+p_r{N}_e^2(4a_2\Psi -(p_h+p_r){\mu }_e{\rho }_h))-16a_1^2{N}_1^2{p}_h^2{T}^2}{4a_2{p}_h{p}_r^2{N}_e^4{\mu }_e}$are purchased on the spot market.
  • (b)
    If${\ddot{a}}_1\le a_1<{\dot{a}}_1$, stockpile is$Q^{*}=T{D}_r$, capacity added is${\ell }^{*}$and no PPEP is purchased on the spot market.
  • (c)
    If${\widehat{a}}_1\le a_1<{\ddot{a}}_1$, stockpile is$Q^{*}=\frac{N(4a_1^{2}N{p}_{h}T+{\mu }_e(4a_1{a}_{2}N{p}_{h}T-a_1{p}_r{C}_3{\rho }_h+a_2{p}_r{N}_e^2(2(BN-Y+\Psi )+{\mu }_e{\rho }_h)))}{a_2{p}_r^2{N}_e^3{\mu }_e}$, capacity added is${\ell }^{*}$and no PPEP is purchased on the spot market.
  • (d)
    If$0\le a_1\le {\widehat{a}}_1$, no PPEP stockpile is held or purchased on the spot market and capacity added is${\ell }^{*}=\frac{Y+\Psi }{a_1+a_2{\mu }_e}$.

Table 7.

Expressions for terms used in Proposition 7.

Quantity	Expression
${\overline{D}}_r$	$\frac{4N(Y-HN)}{p_r{N}_e^2}+\frac{4a_2\Psi +(p_h+p_r)(p_r{\mu }_e-\sqrt{{\mu }_e(4a_2\Psi +p_r^2{\mu }_e)})}{2a_2{p}_{h}T}$
${\dot{a}}_1$	$\frac{N_e^2{p}_r({\mu }_e-p_h^2\sqrt{{\mu }_e(4\Psi a_2+p_r^2{\mu }_e)})}{4NT}$
$C_1$	$\frac{p_r^2{N}_e{\mu }_e(3N{p}_h-N{p}_r+T{\rho }_h){}^2-8a_2{p}_h(4NT(HN-Y)-2N\Psi N_e+p_r{D}_{r}T{N}_e^2)(N{\rho }_h-p_{r}T)}{N_e{\mu }_e}$
${\ddot{a}}_1$	$\frac{p_r{N}_e^2{\mu }_e(2N{p}_h^2-N{p}_h{p}_r+N{p}_r^2-p_{r}T{\rho }_h-\sqrt{C_1})}{8N{p}_{h}T(N{\rho }_h-p_{r}T)}$
$C_2$	$\frac{{\mu }_e(4N{p}_{h}T+N_e^2{\rho }_h){}^2-32a_{2}N{p}_{h}T(Y+\Psi )(p_r(N^2+T^2)-2NT{\rho }_h)}{{\mu }_e}$
${\widehat{a}}_1$	$\frac{p_r{N}_e^2{\mu }_e(p_r{N}_e^2{\rho }_h-4N{p}_h^{2}T++p_r\sqrt{C_2})}{8N{p}_{h}T(p_r(N^2+T^2)-2NT{\rho }_h)}$
$C_3$	$N^2+2N{p}_{h}T+T^2$

Fig. 4 illustrates Proposition 7. The per unit cost of building volume flexibility can be very large (above ${\overline{a}}_1$) to make any investment suboptimal, even for zero penalty in unit production cost. The threshold ${\overline{a}}_1$ is decreasing in the spot market price penalty, i.e., when the PPEP is available in Phase II at a low price, building volume flexibility is suboptimal. Also, ${\overline{a}}_1$ is decreasing in $T$, i.e., investing in volume flexibility is more likely to be optimal if the time to rotate the stockpile is short. If $a_1<{\overline{a}}_1$, then the GO uses volume flexibility with the extent depending on the unit cost production premium, $a_2$. For an $a_1<{\overline{a}}_1$, as $a_2$ decreases, more volume flexibility is used until it first replaces spot market purchases in Phase II but fully utilizes the largest stockpile possible, followed by less than full utilization of the stockpile, and finally eliminating the stockpile.

Fig. 4.

Optimal PPEP sources for the GO.

6.2. Manufacturers-distributor-GO SC-single PPEP

In many SCs of PPEPs, supplies, and drugs, distributors play an important role. Hospitals and pharmacies frequently replenish many different products made by many manufacturers from a single distributor. For example, Cardinal Health, one of the largest distributors in the U.S., had a revenue of $152.9 billion in fiscal 2020, much of which was from distributing medical products, including PPEPs, of different manufacturers. In this SC, the distributor has sufficient volume to rotate the stockpile. We analyze the JSRC in this SC type and evaluate its effectiveness relative to buying the PPEP for the retail price.

The entry of the GO alters the equilibrium between the manufacturers and distributor in the SC shown in Fig. 5 , where the manufacturers are the leaders in a Stackelberg game. Without the GO, the distributor sells PPEP to non-GO customers, denoted by subscript $ng$. Since PPEPs of different manufacturers are similar, we assume the wholesale prices are the same. The non-GO market size is $\kappa$ and consumers’ reservation prices, $u$, are uniformly distributed on $[0,\overline{u}]$. Without the GO, it can be shown that the manufacturers’ optimal wholesale price is $w_s^{*}=\frac{c+\overline{u}}{2}$, where the subscript $s$ denotes the SC Stackelberg equilibrium. The optimal distributor’s price is $p_{r,s}^{*}=\frac{c+3\overline{u}}{4}$. The manufacturers’ and distributor’s profits are $Z_{M,s}^{*}=\frac{N\kappa {(\overline{u}-c)}^2}{8\overline{u}}$ and $Z_{D,s}^{*}=\frac{N\kappa {(\overline{u}-c)}^2}{16\overline{u}}$, respectively.

Fig. 5.

The supply chain with manufacturers and distributor for single PPEP.

If the manufacturer sells the PPEP directly to non-GO customers then the optimal price is $\frac{c+\overline{u}}{2}$, which implies that the addition of a distributor to the SC results in a double marginalization effect increase in price of $\frac{c+3\overline{u}}{4}-\frac{c+\overline{u}}{2}=\frac{\overline{u}-c}{4}$.

Suppose the GO pays $p_{r,s}^{*}=\frac{c+3\overline{u}}{4}$ per unit, which we refer to as the retail price contract (RPC), and buys PPEP with $\$U$ in year 1 and $\$E=B-H>0$ annually thereafter. Manufacturers are aware of sales to the GO and respond by changing $w$ resulting in a new SC equilibrium. In the new equilibrium, using the first and second order conditions on the manufacturers’ profits, we obtain a wholesale price and price for non-GO customers of $\frac{1}{2}(c+\overline{u}+\frac{8Y_n\overline{u}}{N(c+3\overline{u})\kappa })$ and $\frac{1}{4}(c+3\overline{u})+\frac{2Y_n\overline{u}}{N(c+3\overline{u})\kappa }$, respectively. Corollary 3 shows changes in the SC if the GO buys the PPEP for $p_{r,s}^{*}$.

Corollary 3

In a manufacturers-distributor-GO SC where the GO spends$U$in year 1 and$B-H>0$annually to purchase PPEP at price$p_{r,s}^{*}=\frac{c+3\overline{u}}{4}$per unit, the entry of the GO into the SC causes the following changes from the no-GO SC:

• 1.A$\frac{4Y_n\overline{u}}{N(c+3\overline{u})\kappa }>0$increase in the wholesale price.
• 2.A$\frac{2Y_n\overline{u}}{N(c+3\overline{u})\kappa }>0$increase in the retail price to non-GO customers.
• 3.A$\frac{2Y_n(4Y_n\overline{u}+N(\overline{u}-c)(c+3\overline{u})\kappa )}{N{(c+3\overline{u})}^2\kappa }>0$increase in the manufacturers’ profit.
• 4.A$\frac{12Y_n^2\overline{u}}{N{(c+3\overline{u})}^2\kappa }>0$decreases in the distributor’s profit.

Corollary 3 shows that, except for the manufacturers, all SC members are worse off because manufacturers raise $w$. The distributor increases $p_r$ which makes customers worse off. This is because manufacturers, empowered by the guaranteed sales to the GO for $p_{r,s}^{*}$, increase their share of the SC profit by increasing $w$, leaving the distributor worse off and with no incentive to sell to the GO. Taking the first derivative of the decrease in the distributor’s profit ($\frac{12Y_n^2\overline{u}}{N{(c+3\overline{u})}^2\kappa }$) with respect to $Y$ gives $\frac{24\overline{u}{Y}_n}{N{(c+3\overline{u})}^2\kappa }>0$. Therefore, as the GO’s budget increases, the distributor’s profit decreases, which can be explained by the manufacturers’ behavior. Because the GO agrees to buy $Y_n$ worth of a PPEP for $p_{r,s}^{*}$, a large $Y_n$ means more PPEP is sold to the GO, which encourages manufacturers to raise $w$. The GO pays for the double marginalization and has smaller stockpile.

We now examine the JSRC and denote this contract by JSRCD. The GO’s $N$-year budget is $U+NB=Y$, which is known to all SC parties. As Fig. 5 shows, the distributor sells $Q_o$ units of PPEP to the GO in year 1 for $p$ per unit and $\frac{Q_o}{T}$ units annually thereafter. The distributor buys back $\frac{Q_o}{T}$ units annually from the GO for $b$ per unit and sells them to non-GO customers for $p_r$. The distributor also sells $Q_{ng}$ annually to non-GO customers for $p_r$. Like the JSRC, the GO stipulates a buy-back price of $b=p\frac{p}{p_r}$. Manufacturers, knowing the terms of the contact between the GO and the distributor and the distributor’s optimal policy, determine $w$ to maximize their profit.

From Corollary 3, the distributor has no incentive to accept the RPC because the SC (manufacturers and distributor) increase in profit goes to the manufacturers and the distributor’s profit decreases. Therefore, the GO needs to change the profit distribution between the manufacturers and distributor. To achieve an acceptable profit for the distributor and avoid double marginalization, we introduce a GO-controlled parameter $\alpha >0$ to redistribute profits between the distributor and manufacturers. The distributor holds the PPEP stockpile and is compensated for it. Therefore, the GO agrees to pay $\alpha H$ annually to the distributor, and uses $\alpha$ to achieve the desired distribution of the SC’s profit. An $\alpha =1$ means the GO pays the distributor only the storage and maintenance cost of the PPEP and increasing $\alpha$ increases the distributor’s surplus. At contract negotiation time, the retail price is $p_{r,s}^{*}=\frac{c+3\overline{u}}{4}$. Also, the GO operates with the annual constraint:

$$\frac{\frac{U}{p}}{T}(p-\frac{p}{p_{r,s}}p)+\alpha H=B$$ (27)

The equilibrium for the SC with the JSRCD is shown in Proposition 8.

Proposition 8

In a manufacturers-distributor-GO SC using the JSRCD, the wholesale and retail prices are$w^{*}=\frac{1}{2}(c+\overline{u}+\frac{32\overline{u}(Y-HN\alpha )}{(N+T)(c+3\overline{u})\kappa })and{p}_r^{*}=\frac{1}{2}(\overline{u}+\frac{1}{2}(c+\overline{u}+\frac{32\overline{u}(Y-HN\alpha )}{(N+T)(c+3\overline{u})\overline{u}})),$respectively. The GO pays$p^{*}=\frac{(N+T)(c+3\overline{u})}{8N}$for new PPEP and sells back old PPEP for$b^{*}=\frac{{(N+T)}^2(c+3\overline{u})}{16N^2}$.

From Proposition 8, the price the GO pays for new PPEP and the buy back price are independent of $\alpha$. However, $\frac{d{w}^{*}}{d\alpha }=-\frac{16HN\overline{u}}{(N+T)\kappa (c+3\overline{u})}<0$, i.e., $w$ is decreasing in $\alpha$. Therefore, the GO can use $\alpha$ to cause manufacturers to reduce $w$ which increases the distributor’s share of the SC’s profit. This increase in the distributor’s profit comes partially at the cost of reducing the stockpile size as more money is paid to the distributor.

In determining $\alpha$, the GO wants to pay a price close to the coordinated SC price of $p_c=\frac{c+\overline{u}}{2}$, i.e., avoid double marginalization, while achieving an acceptable profit for the distributor. Therefore, we define two metrics for the GO to determine $\alpha$ and evaluate the effectiveness of the JSRCD

• 1.The premium, $\vartheta$, above the coordinated SC’s price the GO pays for new PPEP, which does not apply to PPEPs to rotate the stockpile. The price for new PPEP in $Q_o$ is $p=(1+\vartheta )p_c=(1+\vartheta )\frac{c+\overline{u}}{2}$ and the GO wants a small $\vartheta$ while getting the distributor to accept the contract.
• 2.The proportion of profit from the GO’s purchases allocated to the distributor, $\xi$. We show that decreasing $\vartheta$ decreases $\xi$ and decreases the distributor’s profit from the no-GO level.

The GO’s challenge is to find a ($\vartheta$, $\xi$) pair which provides the distributor with reasonable profit while building a large stockpile. We show how the GO can achieve a contract in which it pays a premium of $\vartheta p_c$ above the coordinated SC’s price for PPEP with free stock rotation and gives the distributor a proportion of $\xi$ of the SC’s profit increase due to the GO’s purchase. For the GO to give the distributor a share of $\xi$ of the increase in the SC profit from its purchases, it must pay a premium over the coordinated SC price, which is computed using the no-GO SC profit and GO-SC profit, of

$$\vartheta =\frac{\sqrt{N(16\overline{u}{Y}_n(3-\xi )\underset{\_}{\xi }+N{(c+3\overline{u}-(3c+\overline{u})\xi )}^2\kappa )}-N(3c+\overline{u}-(c+3\overline{u})\xi )\sqrt{\kappa }}{4N(c+\overline{u})\underset{\_}{\xi }\sqrt{\kappa }}.$$ (28)

Using the distributor’s profit function, the $\vartheta$ premium requires the GO to pay the distributor a holding cost multiple of

$$\alpha =\frac{HN{(N+T)}^2(c+3\overline{u})-cY(N^2+T^2-2NT(3+4\vartheta ))+\overline{u}Y(2N(T+4T\vartheta )-3N^2-3T^2)}{8H{N}^{2}T(c+\overline{u})(1+\vartheta )},$$ (29)

which results in a stockpile size of

$$Q=\frac{\sqrt{\kappa N(16\overline{u}{Y}_n(3-\xi )\underset{\_}{\xi }+N{(c(1-3\xi )+\overline{u}(3-\xi ))}^2\kappa )}-N(c(1-3\xi )+\overline{u}(3-\xi ))\kappa }{2\overline{u}(3-\xi )}.$$ (30)

Fig. 6 illustrates Eq. (28). A premium of $0.38p_c$ is needed to make the distributor indifferent (no change in profit) to the contract. To give the distributor a $\frac{1}{3}$ share of the SC profit increase, a premium of $0.726p_c$ is needed. While $0.726p_c$ may seem large, it is better viewed relative to the double marginalization price for which the premium is $3p_c$. Because the GO has to pay a premium above $p_c$, stockpile size in Eq. (30), is decreasing in the distributor’s share of SC profit $\xi$

Fig. 6.

Coordinated SC price premium to achieve a given profit distribution.

To allocate $1/3$ of the increase in the SC’s profit to the distributor, we set $\xi =\frac{1}{3}$ and use Eqs. (28)–(30) to obtain the threshold market size of non-GO customers

$${\kappa }_c\equiv \frac{4{(E(L-3)L+2EN+2LU)}^2\overline{u}}{N^2(c+3\overline{u})(N(3\overline{u}-c)Y_n-2(E(L-3)L+2EN+2LU)\overline{u})}.$$ (31)

If $\kappa >{\kappa }_c$, the JSRCD results in a larger stockpile and $1/3$ allocation of SC’s profit increase to the distributor. The larger the non-GO market size, the more likely the GO can increase its stockpile size with the JSRCD over the RPC while allocating the distributor $1/3$ profit share. This is because a larger non-GO market size makes the GO’s contribution to the SC’s profits smaller. As a result, sales to the GO are not as important to manufacturers as sales to other customers and manufacturers have a smaller incentive to increase $w$, which leaves the distributor and customers better off. Eq. (31) is illustrated in Fig. 7 where ${\kappa }_c$ is shown versus the PPEP’s shelf life ($L$) and the upper bound on the reservation prices ($\overline{u}$). As shown, ${\kappa }_c$ increases in $L$ because the average stockpile in the RPC increases due to the PPEP lasting longer. As a result, for the JSRCD to have a larger stockpile than the RPC requires that the GO does not pay a large premium over the coordinated SC’s price to increase the distributor’s profit. A large premium is required when manufacturers increase $w$ significantly. If the non-GO market size is large, manufacturers are focused on extracting surplus from non-GO customers and do not have a strong wholesale price response to the GO’s entry. Fig. 7 also shows that ${\kappa }_c$ decreases as $\overline{u}$ increases which can be explained by non-GO customers profit potential measured by $\kappa \times \overline{u}$. For a given $\kappa$, as $\overline{u}$ increases, there is more surplus to be extracted from non-GO customers. Therefore, a larger $\overline{u}$ makes manufacturers more focused on extracting surplus from the non-GO customers and decreases their wholesale price response to the GO’s entry.

Fig. 7.

Market size needed to have one third distributor profit share and increased stockpile size.

6.2.1. Example-single PPEP in a SC with a distributor

Using the example in Section 3.4, $\kappa =20,000$, and $\overline{u}=10$, Table 8 shows the results for the no-GO case, the RPC, and two JSRCDs. In JSRCD${}_{\xi =0.4}$, the distributor requires a $40\%$ share of the increase in the SC (manufacturers and distributor) profit, whereas in JSRCD${}_{\xi =0.5}$, the distributor requires a $50\%$ share. We first note that in the RPC, the addition of the GO results in a decrease in the distributor’s profit of $165,675-154,739=10,936$, ($6.6\%$) from the no-GO level and an increase in the manufacturers’ profit of $436,941-331,350=105,591$ ($31.7\%$). Therefore, the distributor is unlikely to accept the RPC. In addition, non-GO customers pay $\$8.0$ per PPEP, a $0.35 ($4.6\%$) increase from the no-GO price. The JSRCD remedies some of the problems by reallocating profits between the manufacturers and distributor. In JSRCD${}_{\xi =0.4}$, relative to the no-GO case, the distributor’s profit increases by $212,291-154,739=46,616$, ($28.1\%$) and the manufacturers’ profit increases by $401,274-331,350=69,924$ ($21.1\%$). Non-GO consumers pay $7.886 per unit, which is larger than the no-GO price by $0.236 but less than the RPC’s price by $0.114 ($1.4\%$). As described earlier, increasing the profit share of the distributor using $\alpha$ causes the manufacturers to decrease $w$ from $5.997 in the RPC to 5.772 in JSRCD${}_{\xi =0.4}$, which is a $0.225 ($3.8\%$) decrease. Increasing the distributor’s profit share by 10% in the JSRCD${}_{\xi =0.5}$ results in $0.0584 (1%) drop in $w$ from JSRCD${}_{\xi =0.4}$. Also, the stockpile size of JSRCD${}_{\xi =0.4}$ is $9161-5723=3438$ (60%) larger than the average stockpile of the RPC and larger than the JSRCD${}_{\xi =0.5}$ stockpile by $9161-8071=1090$ (13.5%). Fig. 8 shows how the stockpile size decreases as the GO increases the distributor’s share from the SC’s profit, i.e., increasing the distributor’s share of the SC’s profit comes at the cost of decreasing the stockpile size. Allocating $\xi =\frac{1}{3}$ of the SC’s profit increase to the distributor (which was the share in the no-GO SC) results in a stockpile of 15,227, which is $15,227-5723=9504$ units (166%) increase from the RPC.

Table 8.

Manufacturers-distributor supply chain example .

Fig. 8.

Stockpile size versus the distributor’s share of the SC profit increase.

6.3. Different demand functions

We now examine the implications of an increasing then decreasing unimodal PPEPs pdf. For the single PPEP, the solution does not change since maximizing the service level $F\left(Q\right)$, which is an increasing function of $Q$, is equivalent to maximizing $Q$. For the multi PPEP problem (MPPE), Eq. (13) (or (15)) can be rewritten as $\frac{{\omega }_i{f}_i(U_i/p_i)}{p_i}=\frac{{\omega }_j{f}_j(U_j/p_j)}{p_j},foralli\ne j$. In the case of deceasing pdf, this necessary condition is satisfied for a unique combination of $x_j,j=1,2,\dots ,m$. For example, for two PPEPs with exponentially distritbuted demands of $x_1$ and $x_2$ with means of ${\mu }_1$ and ${\mu }_2$, respectively, the optimality condition is $Q_1={\mu }_1(\frac{Q_2}{{\mu }_2}+\log \left(\frac{{\mu }_2}{{\mu }_1}\right))$, which together with the budget constraint results in a unique optimal solution.

For PPEPs with unimodal increasing then decreasing pdfs, $\frac{{\omega }_i{f}_i(U_i/p_i)}{p_i}=\frac{{\omega }_j{f}_j(U_j/p_j)}{p_j},\forall i\ne j$ does not have a unique solution. For example, for two PPEPs with normally distributed demands $x_1$ and $x_2$, means ${\mu }_1$ and ${\mu }_2$, and standard deviations ${\sigma }_1$ and ${\sigma }_2$, respectively, a given $\frac{{\omega }_1{f}_1(U_1/p_1)}{p_1}$ is satisfied at two values of $Q_1$ as shown in Fig. 9 (a). In this figure, an $\frac{{\omega }_1{f}_1(U_1/p_1)}{p_1}=0.00786$ is satisfied for $Q_1=$101.66 and 138.33 and, correspondingly, $\frac{{\omega }_2{f}_2(U_2/p_2)}{p_2}=0.00786$ is satisfied for $Q_2=$88.34 and 111.66. Thus, there are four $(Q_1,Q_2)$ values satisfying $\frac{{\omega }_1{f}_1(U_1/p_1)}{p_1}=\frac{{\omega }_2{f}_2(U_2/p_2)}{p_2}=0.0078$, $(138.33,88.34)$, $(138.33,111.66)$, $(101.66,88.34)$, and $(101.66,111.66)$, of which only one is optimal. In general, for a MPPE with $m$ PPEPs, the are $2^m$ candidate solutions satisfying Eq. (13). The following is a simple algorithm to solve the problem.

Fig. 9.

Sufficient optimality conditions for a 2 PPEP problem.

Step 1: Denote the PPEP with the largest weight as 1.

Step 2: Allocate $Y_1$ to PPEP 1 such that $Q_1<{\overline{m}}_1$, where ${\overline{m}}_i$ is the mode of the demand of PPEP $i$. Use $\frac{{\omega }_1{f}_1(U_1/p_1)}{p_1}=\frac{{\omega }_j{f}_j(U_j/p_j)}{p_j},\forall j\ne 1$ to obtain the two values of $Q_j$ satisfying this condition. The value of $Y_1$ should be sufficiently small such that the low values of $Q_j$ $\forall j\ne 1$ result in $Q_j<{\overline{m}}_j$ and ${\sum }_{j=1}^m{Y}_j<\Omega$.

Step 3: Increase the value of $Y_1$ by $\Delta$ until for one and only one $j\ne 1$, $\frac{{\omega }_1{f}_1(U_1/p_1)}{p_1}=\frac{{\omega }_j{f}_j\left({\overline{m}}_j\right)}{p_j}$. For this PPEP the optimal $Q_j$ is above its mode and this PPEP is moved to set $O$. If no new PPEP not in $O$ reaches $\frac{{\omega }_j{f}_j(U_j/p_j)}{p_j}=\frac{{\omega }_1{f}_1\left({\overline{m}}_1\right)}{p_1}$ until ${\sum }_{i=1}^m{Y}_i=\Omega$ then the solution is optimal.

Step 4: If all PPEPs optimal quantities are above their modes, then the solution with all quantities above the modes satisfying Eq. (13) and ${\sum }_{i=1}^m{Y}_i=\Omega$ is optimal. Otherwise, go to Step 3.

If demand for one or more PPEP has a finite support, then a modification to the above procedure is needed. For a single PPEP, $F\left[x\right]$ reaches a value of 1 at the upper support and remains 1. Thus, $F\left[Q\right]=1$ when $Q$ is above the upper support on $X$ and increasing $Q$ will not increase the service level. Therefore, if $X$ has finite upper support of $\overline{S}$, and $U$ and $B$ are sufficiently large to build and fully rotate a stockpile of $Q>\overline{S}$, then $Q^{*}=\overline{S}$. If $U$ and $B$ are not sufficiently large to build and rotate a stockpile of $Q\ge \overline{S}$, then $S{L}_I<1$, the budget constraints are binding, and maximizing $S{L}_I$ is equivalent to maximizing $Q$. For multiple PPEPs, the algorithm described above needs to take into account the possibility of the optimal stockpile of a PPEP reaching the upper support on its demand. This can be accomplished by adding a step between Steps 3 and 4 as follows.

Step 3.5. For all PPEPs with $Q_i\ge {\overline{S}}_i$, set the optimal order quantity to ${\overline{S}}_i$.

If all PPEPs have a finite upper support on their demand and the budget is sufficiently large, then the last step will terminate at a ${\sum }_{j=1}^m{Y}_j<\Omega$ because all PPEPs will have a stockpile size equal to the support on their demand and the budget constraint is not binding.

6.4. Quality considerations

For PPEPs with considerable scrap, the GO needs to consider the effect of scrap on preparedness as well as its cost. The contract may specify an acceptable proportion of scrap above which the GO is reimbursed. Managing the effects of scrap must consider that different PPEPs may have different proportion of scrap. For PPEP $i$ with a ${\Phi }_i$ proportion of scrap, the actual service level with a stockpile of $Q_i$ is ${\omega }_i{\int }_0^{(1-{\varphi }_i)Q_i}{f}_i\left(x_i\right)d{x}_i$ and the GO’s problem becomes maximizing $SL={\sum }_{j=1}^m{\omega }_j{\int }_0^{(1-{\varphi }_j)Q_j}{f}_j\left(x_j\right)$ subject to Constraints (9)–(12). PPEPs with large weight and high proportion of scrap will have larger proportional change in their stockpile size because of scrap.

The consideration of quality reveals another advantage of the JSRC. In the SSRC, much of the stockpile may be kept in storage until it is needed or it is expired. In the JSRC the entire stockpile is rotated and is sold to non-GO customers. As a result, scrap is discovered earlier and in case of bad quality, causes brand image damage and higher costs for the manufacturer. Therefore, the JSRC creates stronger incentive for the manufacturer to provide higher quality PPEPs.

7. Discussion, conclusion and future research

We demonstrated that the proposed joint determination of PPEPs’ stockpile sizes and rotation in a single contract (JSRC) results in a higher preparedness for pandemics, less waste, and higher manufacturer’s profit. The JSRC is a new approach that provides an incentive for manufacturers to rotate PPEPs stockpiles, which increases the GO’s pandemic preparedness. We showed that the JSRC will also work in a manufacturers-distributor-GO SC and can work with the option of investing in a manufacturer’s volume flexibility.

There are some practical and important issues for the JSRC. On the GO’s side, the budget over the planning horizon (contract length) needs to be known. However, budgets frequently change as administrations change. If a GO faces uncertainty about future budgets, then it may be prudent to use a pessimistic forecast of the budget. This allows the GO to allocate a large proportion of its budget most effectively. The GO must also plan for the proper holding and verification of the stockpiles. In this regard, wether the GO or the manufacturer store the stockpile, the annual rotation will insure that the viability of the stockpile is maintained.

On the manufacturer’s side, we assumed that he can sell older rotated PPEP in the market as new. There are two important considerations that make this possible. First, most PPEPs have a shelf life of few years, and second, just-in-time (JIT) inventory management has become pervasive among organizations, including health care organizations. JIT means a unit of a PPEP makes its way from production to being used by customers within several weeks or few months at most. The shelf life of most PPEPs is in the range of 3–8 years. This implies that reasonable rotation cycles of 2–7 years depending on the PPEP leaves amble time for rotated PPEPs to work their way through the SC to be used by the final customers much earlier than their expiration dates.

For multiple PPEPs, we find that incorporating spot market prices during Phase II is important to increasing preparedness. By focusing on Phase I (no PPEPs availability) alone, the GO may achieve very high service level in Phase I on important PPEPs but it may force the GO to pay very high prices for less important PPEPs whose price spikes are very large in Phase II. This is particularly important when the GO is financially constringed in Phase II.

In cases where no one manufacturer has sufficient sales volume to rotate the stockpile, the GO may contract with a distributor or invest in a manufacturer’s volume flexibility. We showed that the JSRC is effective in both cases. With a distributor, the JSRC reduces the effect of double marginalization. In the case of volume flexibility, the JSRC is likely to be used unless the cost of volume flexibility and per unit cost of utilizing it are very small.

Our models have some limiting assumptions. We assumed that supplies of PPEPs cease during Phase I. Extensions to immediate but constrained Phase I supply may be applicable for some PPEPs. Also, our approach is not applicable to some medical products with short shelf life of fewer than 3 years, such as antiviral drugs. For these products, holding a smaller stockpile with cash reserves (Zhang et al., 2021) is more effective.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

Proof of Proposition 1

Proof

Substituting for $Q$ from Eq. (5) in Eq. (6) and using $b=\frac{p}{p_r}p$, we obtain

$$Z=\frac{(Np(p_r-p)+(p-c)p_{r}T)(Y-HN)}{p(N(p_r-p)+p_{r}T)}$$

The second derivative of $Z$ with respect to $p$ is

$$\frac{d^{2}Z}{d{p}^2}=\frac{2c{p}_{r}T(N^2(3p{p}_r-3p^2-p_r^2)+N{p}_r(3p-2p_r)T-p_r^2{T}^2)(Y-HN)}{p^3(N(p_r-p)+p_{r}T){}^3}.$$

Since $p^3(N(p_r-p)+p_{r}T){}^3>0$ for $p<p_r$, the sign of $\frac{d^{2}Z}{d{p}^2}$ is determined by the numerator which can be written as

$$\begin{array}{ccc}& & 6c{N}^2{p}^2{p}_{r}T(HN-Y)-6cNp{p}_r^{2}T(N+T)(HN-Y)\hfill \\ & & +2c{p}_r^{3}T{(N+T)}^2(HN-Y).\hfill \end{array}$$

Dividing by $c{p}_r(HN-Y)<0$ gives

$$-6N^2{p}^{2}T+6Np{p}_{r}T(N+T)-2p_r^{2}T{(N+T)}^2,$$

with roots at $\frac{3N{p}_r(N+T)(3\pm \sqrt{3}\sqrt{-1})}{6N^2}$ which are imaginary and therefore $\frac{d^{2}Z}{d{p}^2}<0$ and the first order condition given by

$$\frac{dZ}{dp}=\frac{c{p}_{r}T(N(p_r-2p)+p_{r}T)(Y-HN)}{p^2(N(p_r-p)+p_{r}T){}^2}=0,$$

which gives $p^{*}=\frac{p_r(N+T)}{2N}$. Substituting for $p^{*}$ into $\frac{p}{p_r}p$ gives $b^{*}=\frac{p_r{(N+T)}^2}{4N^2}$. □

Proof of Proposition 2

Proof

Substituting $p^{*}$ and $b^{*}$ obtained in Proposition 1 into $Q$ in Eq. (5) and $Z$ in Eq. (6) yields the expressions in Proposition 2. □

Proof of Proposition 3

Proof

Using $p^{*}=\frac{p_r(N+T)}{2N}$, the GO buys $Q=\frac{U}{p}=\frac{2NU}{p_r(N+T)}$ in year 1. The maximum PPEP quantity that can be rotated annually satisfies $q(p-\frac{p}{p_r}p)+H=B$ resulting in $q=\frac{(B-H)p_r}{p(p_r-p)}$ which is increasing in $B$. Solving $qT=Q$ yields $B_c=H+\frac{(N-T)U}{2NT}$ as the annual budget at which the GO can rotate all of $Q$ in $T$ years and spends its entire annual budgets. Therefore, there are two possible cases:

• 1.If $B\ge B_c$, all of $Q=\frac{U}{p}=\frac{2NU}{p_r(N+T)}$ can be rotated over $T$ years and the GO maintains a stockpile of $Q_1=\frac{U}{p}=\frac{2NU}{p_r(N+T)}$ and rotates $q_a^{*}=\frac{Q_1}{T}=\frac{2NU}{N{p}_{r}T(N+T)}$ annually. Substituting for $Q_1$ and $q_a^{*}$ into $Q_1(p-c)$ and $q(p-c+p-\frac{p}{p_r}p-(p-c))$ yields the optimal initial stockpile building profit and the annual rotation profit, respectively.
• 2.If $B<B_c$, only part of $Q_1=\frac{U}{p}=\frac{2NU}{p_r(N+T)}$ can be rotated over $T$ years. The quantity rotated annually satisfies $q(p-\frac{p}{p_r}p)+H=B$ which yields $q_b=\frac{4(B-H)N^2}{p_r(N-T)(N+T)}$. By the end of $T$, $q_{b}T$ units are rotated and the cycle of rotating them begins again which leaves $Q_1-q_{b}T=\frac{2N(2HNT+(N-T)U-2BNT)}{p_r(N-T)(N+T)}$ un-rotated units of PPEP to expire at the end of year $L$. Therefore, the GO maintains a stockpile of $Q_1$ for years 1 to $L$ and a stockpile of $q_{b}T=\frac{4(B-H)N^{2}T}{p_r(N-T)(N+T)}$ for years $L+1$ to $N$. Substituting for $Q_1$ and $q_b^{*}$ into $Q_1(p-c)$ and $q_b(p-c+p-\frac{p}{p_r}p-(p-c))$ yields the optimal initial stockpile building profit and the annual rotation profit, respectively.

 □

Proof of Corollary 2

Proof

The results are directly obtained by subtracting the corresponding expressions in Propositions 2 and 3. □

Proof of Proposition 4

Proof

Substituting $Q_j=\frac{U_j}{p_j}$ into Eq. (8) and taking the first derivative with respect to $U_j$ yields $\frac{dSL}{d{U}_j}=\frac{f_j\left(\frac{U_j}{p_j}\right){\omega }_j}{p_j}>0$, which implies that the service level is increasing in the budget allocation to PPEP $j$, $j=1,2,\dots ,m$. Suppose that for two PPEPs, $k$ and $h$, we have $\frac{f_k\left(\frac{U_k}{p_k}\right){\omega }_k}{p_k}>\frac{f_h\left(\frac{U_h}{p_h}\right){\omega }_h}{p_h}$. Then, there is a positive $ϵ$ sufficiently small for which ${\omega }_k{\int }_0^{\frac{U_k+ϵ}{p_k}}{f}_k\left(x_k\right)d{x}_k+{\omega }_h{\int }_0^{\frac{U_h-ϵ}{p_h}}{f}_h\left(x_h\right)d{x}_h>{\omega }_k{\int }_0^{\frac{U_k}{p_k}}{f}_k\left(x_k\right)d{x}_k+{\omega }_h{\int }_0^{\frac{U_h}{p_h}}{f}_h\left(x_h\right)d{x}_h$, i.e., the GO provide a higher service level with the same expenditure. Therefore, an allocation in which $\frac{f_k\left(\frac{U_k}{p_k}\right){\omega }_k}{p_k}>\frac{f_h\left(\frac{U_h}{p_h}\right){\omega }_h}{p_h}$ can’t be optimal. For the same reason, an allocation is which $\frac{f_k\left(\frac{U_k}{p_k}\right){\omega }_k}{p_k}<\frac{f_h\left(\frac{U_h}{p_h}\right){\omega }_h}{p_h}$ can’t be optimal and for a solution to be optimal $\frac{f_k\left(\frac{U_k}{p_k}\right){\omega }_k}{p_k}=\frac{f_h\left(\frac{U_h}{p_h}\right){\omega }_h}{p_h}$ must be satisfied. Therefore, because an allocation of $U_i$ to PPEP $i$, determines the allocations $U_j,j\ne i$ required to satisfy the necessary optimality condition and the allocations must satisfy Constraints (9–12), the allocation satisfying the necessary optimality condition and the constraints is a unique global optimum. □

Proof of Proposition 5

Proof

The first derivative of $S{L}_T$ with respect to $S_j$ is

$$\frac{dS{L}_T}{d{S}_j}=\frac{{\omega }_{j,2}((1-F_j\left(\frac{U_j}{p_j}\right))g_j\left(\frac{S_j}{r_j}\right)+F_j\left(\frac{U_j}{p_j}\right)g_j(F_j\left(\frac{U_j}{p_j}\right){\int }_0^{\frac{U_j}{p_j}}(\frac{U_j}{p_j}-x_j)f_j\left(x_j\right)d{x}_j+\frac{S_j}{r_j}))}{p_{h,j}}>0,$$

which implies $S{L}_T$ is increasing in the Phase II budget allocation to PPEP $j$ if there is decrease in the allocation to other PPEPs. Also, the weighted service level for PPEP $j$ for a given $U_j$ as a function of $S_j$ can be written as

$$\begin{array}{ccc}\hfill S{L}_j\left(S_j\right)& =& {\omega }_{j,2}{G}_j\left(\frac{S_j}{p_{h,j}}\right)(1-F_j\left(\frac{U_j}{p_j}\right))+F_j\left(\frac{U_j}{p_j}\right)({\omega }_{j,1}\hfill \\ & & +{\omega }_{j,2}{G}_j(\frac{S_j}{p_{h,j}}+\left({\int }_0^{\frac{U_j}{p_j}}(\frac{U_j}{p_j}-x_j)f_j\left(x_j\right)d{x}_j\right)F_j\left(\frac{U_j}{p_j}\right))).\hfill \end{array}$$

Suppose that for two PPEPs, $k$ and $h$, the total budget allocation is $A=S_h+S_k$ and $\frac{dS{L}_k}{d{S}_k}>\frac{dS{L}_h}{d{S}_h}$. Then, there is a positive $ϵ$ sufficiently small for which $S{L}_k(S_k+ϵ)-S{L}_k\left(S_k\right)>S{L}_h\left(S_h\right)-S{L}_h(S_h-ϵ)$ and $S{L}_T$ increases by the $ϵ$ change in allocation, i.e., the GO provides a higher service level with the same expenditure. Therefore, an allocation in which $\frac{dS{L}_k}{d{S}_k}>\frac{dS{L}_h}{d{S}_h}$ can’t be optimal. For the same reason, an allocation in which $\frac{dS{L}_k}{d{S}_k}<\frac{dS{L}_h}{d{S}_h}$ can’t be optimal and for a solution to be optimal Eq. (19)must be satisfied. Because an allocation of $S_i$ to PPEP $i$ determines the allocations $S_j,j\ne i$ required to satisfy the necessary optimality condition and the allocations must satisfy Constraint (18), the allocation satisfying the necessary optimality condition and the constraints is a unique global optimum. □

Proof of Proposition 6

Proof

The proof of Proposition 6 is similar to the proofs of Propositions 4 and 5. □

Proof of Proposition 7

Proof

The optimality of $p^{*}=\frac{p_r(N+T)}{2N}$ is established in Proposition 1. The service level in Phases I and II if all three supply options are utilized is

$$SL=\frac{U-a_1\ell }{p}+\frac{\Psi -V(p_r+a_2\ell )({\mu }_I+{\mu }_{II})}{p_h}+({\mu }_i+{\mu }_{II})\ell$$ (32)

Since $\frac{d^{2}SL}{d{\ell }^2}=-\frac{2a_2({\mu }_I+{\mu }_{II})}{p_h}<0$ we obtain the optimal $\ell$ by solving $\frac{dSL}{d\ell }=0$ which gives ${\ell }^{*}=\frac{(p_h-p_r)p_r{(N+T)}^2({\mu }_I+{\mu }_{II})-4a_{1}N{p}_{h}T}{2a_2{p}_r{(N+T)}^2({\mu }_I+{\mu }_{II})}$. Solving ${\ell }^{*}=0$ yields ${\overline{a}}_1=\frac{(p_h-p_r)p_r{(N+T)}^2({\mu }_I+{\mu }_{II})}{4N{p}_{h}T}$ above which investing in volume flexibility is suboptimal.

Suppose $a_1<{\overline{a}}_1$ then substituting for ${\ell }^{*}$ into the equality of Constraint (23) gives

$${\overline{Q}}_t=\frac{p_r{N}_e^2{\mu }_e(8a_{1}N{p}_h^{2}T+p_r{N}_e^2(4a_2\Psi -(p_h+p_r){\mu }_e{\rho }_h))-16a_1^2{N}^2{p}_h^2{T}^2}{4a_2{p}_h{p}_r^2{N}_e^4{\mu }_e}$$

Solving ${\overline{Q}}_t=0$ yields ${\dot{a}}_1$ in Table 7 above which $Q_t^{*}={\overline{Q}}_t$ and below which $Q_t^{*}=0$.

Suppose $a_1<{\dot{a}}_1$, then $U$ is allocated to building the maximum stockpile and investing in $\ell$. In the case of a pandemic, $\Psi$ is allocated to purchasing $\ell ({\mu }_1+{\mu }_2)$ units from additional capacity. Since by Constraint (25), at most $D_r$ units can be rotated annually, the maximum stockpiles is $T{D}_r$. Solving $a_1\ell +\ell (p_r+a_2\ell )({\mu }_1+{\mu }_2)=Y+\Psi -D_{r}Tp-NB$ in $a_1$ yields ${\ddot{a}}_1$ in Table 7. Because of our assumption that the maximum sales volume of the manufacturer is insufficient to rotate the PPEP with a budget of $Y$, $D_r$ must be such that ${\dot{a}}_1>{\ddot{a}}_1$, i.e., a region where the maximum possible stockpile is being rotated while not spending all of $Y$. Solving ${\dot{a}}_1={\ddot{a}}_1$ yields ${\overline{D}}_r$ in Table 7. For a region between ${\ddot{a}}_1$ and ${\dot{a}}_1$ to exist, $D_r<{\overline{D}}_r$ must hold. If $D_r\le {\overline{D}}_r$, then for ${\ddot{a}}_1\le a_1\le {\dot{a}}_1$, it is optimal to build the maximum stockpile of ${\overline{D}}_{r}T$ and use the left over from $Y$ to build extra capacity. As extra capacity becomes cheaper, i.e., $a_1<\ddot{a}$, more of $Y$ is invested in adding capacity and less than the maximum manufacturer’s sales volume of ${\overline{D}}_r$ is rotated annually. Solving $a_1{\ell }^{*}+{\ell }^{*}(p_r+a_2{\ell }^{*})({\mu }_1+{\mu }_2)=Y+\Psi$, yields ${\widehat{a}}_1$ in Table 7, below which, all of $Y$ is used for building capacity and no stockpile is used. □

Proof of Corollary 3

Proof

The distributor’s profit is

$$Z_D=(\frac{U}{p_{r,s}^{*}}+\frac{N(B-H)}{p_{r,s}^{*}})(p_r-w)+\frac{\left(N(\overline{u}-p_r)\kappa \right)(p_r-w)}{\overline{u}}.$$

with an optimal price to non-GO consumers of $p_r=\frac{1}{2}(\overline{u}+w)$. The manufacturer’s profit is

$$Z_m=(\frac{U}{p_{r,s}^{*}}+\frac{N(B-H)}{p_{r,s}^{*}})(w-c)+\frac{\left(N(\overline{u}-p_r)\kappa \right)(w-c)}{\overline{u}}.$$

The manufacturer’s, knowing the distributor’s optimal policy, sets the wholesale price to

$$W^{*}=\frac{1}{2}(c+\overline{u}+\frac{8(BN-HM+U)\overline{u}}{N(c+3\overline{u})\kappa }).$$

Subtracting the optimal no-GO wholesale price, retail price, manufacturer’s profit and distributor’s profit from their optimal post-GO optimal values yields the values in Corollary 3. □

Proof of Proposition 8

Proof

The distributor’s profit is:

$$Z_d=\frac{U(p-w)}{p}+\frac{NU(p-\frac{p}{p_{r,s}^{*}}p)}{pT}+\frac{N(\overline{u}-p_r)\kappa (p_r-w)}{\overline{u}}+HN(\alpha -1),$$

which is concave in $p$ with an optimal price $p^{*}=\frac{(N+T)(c+3\overline{u})}{8N}$. The manufacturer’s profit is

$$Z_m=N(\frac{\overline{u}-p_r}{\overline{u}}-\frac{U}{pT})(w-c)+\frac{U(w-c)}{p}+\frac{N{\sum }_{i=1}^T\frac{U(w-c)}{pT}}{T}.$$

Since the manufacturer is the leader and knows the distributor’s optimal policy, we substitute $p^{*}$ into $Z_m$ which yields

$$Z_m=\frac{1}{2}N(w-c)(\frac{16U}{(N+T)(c+3\overline{u})}+\kappa j-\frac{w\kappa }{\overline{u}})$$

$Z_m$ is concave with optimal solution at $w^{*}=\frac{1}{2}(c+\overline{u}+\frac{32T\overline{u}(Y-H\text{N1}\alpha )}{{(N+T)}^2(c+3\overline{u})\kappa })$. □

Supplementary material

Supplementary material associated with this article can be found, in the online version, at 10.1016/j.ejor.2022.10.004

Appendix B. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/