A biometrics-based mutual authentication and key agreement protocol for TMIS using elliptic curve cryptography

Abstract

Telecare Medicine Information System (TMIS) refers to a medical model that uses communication and information technology to realize multiple medical functions such as remote disease diagnosis, treatment, and health care. Because TMIS is carried out on an insecure public Internet, a large number of mutual authentication and key agreement protocols for TMIS have been proposed to protect the privacy of patients. Recently, Ostad-Sharif et al. proposed a novel anonymous authentication and key agreement scheme for TMIS. In this work, we will demonstrate that Ostad-Sharif et al.’s scheme exists the problems of strong authentication and inefficient password change, and it cannot resist the off-line password guessing attack. To overcome the weaknesses found in Ostad-Sharif et al.’s scheme, we propose a biometrics-based mutual authentication and key agreement protocol for TMIS, making full use of the advantages of one-way hash function and elliptic curve cryptosystem (ECC). The security of the proposed scheme is formally proved under the widely used random oracle model (ROM), and various known malicious attack resistances also are presented by the heuristic discussion. Compared with the existing related schemes, the computation cost and communication overhead of our scheme are reduced by 74.5% and 27.3% respectively.

Introduction

Telecare Medicine Information System (TMIS) uses computer, communication, medical technology and equipment to realize face-to-face consultation between experts and patients, experts and medical staff through remote transmission of data, text, voice and image data [9]. It is not only a medical or clinical problem, but also a communication network, database and other aspects’ problem, and they need to be integrated into the network system.

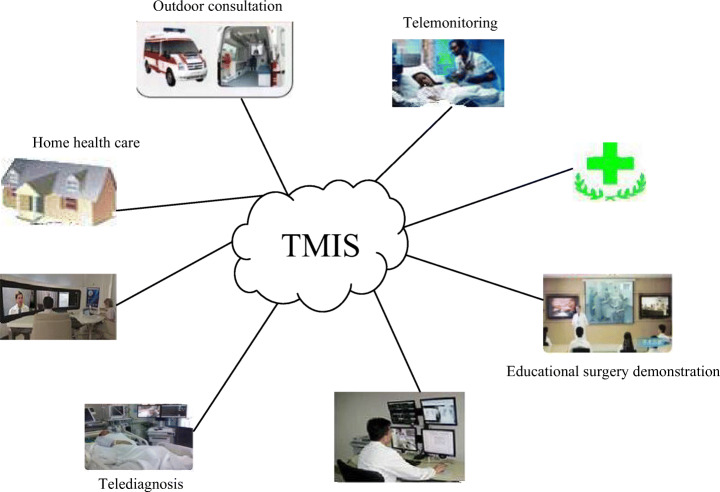
Driven by 5G technology, the application scenarios of TMIS have been expanded. The sudden COVID-19 has become an opportunity for the rapid growth of telemedicine. Telemedicine can prevent cross infection, reduce the burden of the hospital, and ensure the patients to obtain much-needed medical services. As shown in Fig. 1, the specific applications of TMIS include telediagnosis, remote consultation and nursing, educational surgery demonstration, remote surgery and treatment, telemonitoring, remote medical information service, etc.

Fig. 1.

Typical architecture of TMIS

TMIS is mainly composed of the following three parts: a) Providers of medical services. They are generally located in the medical centers of big cities and have rich medical resources and experience in diagnosis and treatment. b) Demanders of medical services. They may be local medical institutions that do not have sufficient medical capacity or conditions. Also, they may be patients in remote areas. c) The communication network and medical devices connecting provider and demander. The communication network includes ordinary telephone network, wireless communication network and communication satellite network; medical devices include computer software and hardware, diagnosis and treatment instruments, etc.

With the increasing maturity of technologies such as computers, sensors, and mobile Internet, as well as the continuous enhancement of national health awareness and the significant increase in demand for health services, TMIS shows strong application potential in the health and medical field [1, 13, 41]. It provides flexible and convenient electronic medical services for user, and gradually penetrates into people’s lives. More and more people begin to pay attention to the information security of TMIS. Since medical records are exposed to unsecured public network, they may be damaged, changed or leaked. This makes TMIS more vulnerable to various security threats and attacks. In order to protect the privacy security of users and medical data, efficient mutual authentication and key agreement schemes are urgently needed.

The authentication key agreement (AKA) protocol can realize mutual authentication between users and servers. While ensuring that only legitimate users can access the server, it can also resist server spoofing attacks. After user and server complete mutual authentication, the shared session key will be established to ensure the security of future communications. Moreover, the session key is negotiated by both parties, and they have the same contribution to the generation of the session key, which enhances the security of the session key.

In most secure communications, the communication system is required to provide confidentiality and authentication for the transmitted data [14, 33, 39]. Confidentiality means that the transmitted data can only be read by the designated receiver. Authentication means that the receiver can confirm that the received data is from the sender, and the data has never been tampered during transmission. In order to meet the requirement of secure communication, the communication participants need to share a one-time session key used to encrypt and authenticate messages. Therefore, participants need a key establishment protocol to generate and distribute the session key before communication. According to the existence of key generation center (KGC), key establishment protocols are generally divided into key transfer protocol and key agreement protocol. In the key transfer protocol, KGC will share a secret value with the user during the registration phase, and use this secret value to distribute the key. The key agreement protocol does not need the participation of KGC. Two or more participants exchange information and negotiate a common session key in an insecure channel controlled by the adversary, and nobody can determine the final session key value in advance. Key agreement protocol, encryption and digital signature are considered as the smallest three cryptographic primitives.

Related works

In order to ensure the communication security on the public channel, a large number of two-factor authentication schemes [3, 15, 21, 22, 37, 40] have been introduced in the past decades. However, researchers pointed out that these schemes were vulnerable to bypass attacks [27], and the secret parameters stored in the smart card may be exposed to the adversary. Later, researchers introduced biometrics into their authentication schemes [2, 7, 10, 17, 20, 23, 29], and the popular three-factor authentication scheme appeared. These schemes overcome the security weaknesses mentioned above.

In 2000, Hwang and Li [19] proposed a smart-card-based remote user authentication scheme using the ElGamal public key cryptosystem. Their scheme did not need to maintain a password table for verifying users’ legitimacy, and can withstand the replay attack. On the basis of Hwang and Li’s scheme, Sun [34] further proposed an efficient and practical remote user authentication scheme using smart cards. Their scheme not only provided the same advantages as Hwang and Li’s scheme, but also significantly reduced the communication and computation costs. Soon afterwards, Malasri and Wang [26] designed a novel two-tier scheme for verifying the authenticity of patient data, making full use of the advantages of ECC and symmetric encryption/decryption. And Boyen [6] pointed out that any protocol involving only two parties was vulnerable to dictionary attacks on the server. Later, Awasthi and Srivastava [4] proposed a new biometrics-based authentication scheme using the bitwise XOR operations and chaotic one-way hash function. However, Das and Goswami [11] discovered that their scheme failed to protect strong replay attack, establish a secret session key, provide the user anonymity and lacked rigorous formal security analysis. To withstand the security flaw, Das and Goswami proposed a novel and secure biometrics-based remote user authentication scheme.

In 2010, Li and Hwang [23] proposed an efficient biometrics-based remote user authentication scheme using smart cards, and its security was based on the smart card, biometrics verification and one-way hash function. However, Chang et al. [7] pointed out that applying only collision-resistant one-way hash functions would make users unable to be authenticated in Li and Hwang’s scheme, and the security of secret data cannot be ensured. Then they proposed a biometrics-based user authentication scheme to ensure uniqueness and anonymity at the same time. They claimed that only the legal user/patient himself/herself can access the remote server, and no one can trace him/her according to the transmitted data in their scheme. Their scheme is efficient due to the usage of one-way hash function and exclusive-or (XOR) operations. However, Das and Goswami [10] proved that Chang et al.’s scheme had design flaws in login and authentication phase and password change phase, failed to protect privileged insider attack, the man-in-the-middle attack, and did not provide proper authentication. Then they proposed an improved uniqueness-and-anonymity-preserving remote user authentication scheme.

In 2015, Amin et al. [2] demonstrated that Das and Goswami’s scheme lacked proper protection against several security attacks such as user anonymity, off-line password guessing attack, smart card theft attack, user impersonation attack, server impersonation attack, session key disclosure attack. To overcome these pitfalls, they proposed an anonymity preserving remote patient authentication scheme for e-health care systems. However, Ravanbakhsh and Nazari [29] proved that their scheme was vulnerable to privileged-insider attack, replay attack, session key disclosure attack, and did not provide patient untraceability and backward secrecy. Then they proposed an efficient remote mutual authentication scheme using ECC and Fuzzy Extractor. Also, Singh et al. [32] proposed an elliptic curve signcryption-based mutual authentication protocol. It greatly reduced the computing cost and communication overhead of smart card. And Shunmuganathan et al. [31] proposed a secure and efficient two factor authentication scheme for multi-server environment, and claimed that the advantage of this scheme was to protect the data stored in the smart card by increasing the dynamic attribute of identity and randomization of each session key. Experiments show that the scheme can resist various attacks, such as forgery attack, replay attack, smart card theft attack and so on. Chaudhry [8] conducted research on the multi-factor authentication and key agreement protocol for social multimedia, and at the same time verified the security of the proposed scheme with the well-known automatic security verification tool ProVerif, but the application field of the scheme is too narrow and the versatility is not strong.

In order to prevent information leakage, the secret high-entropy data can also be stored in the device (such as a smart card) carried by the user, which constitutes the Two-Factor AKA (2FAKA) protocol. For the 2FAKA protocol, the most basic security requirement is two-factor security, that is, the attacker cannot impersonate the legitimate user even if he obtains the user’s password or smart card. However, with the rapid development of the existing side-channel-attack technology, the secret information in the common smart card can be analyzed, and then the adversary can implement offline dictionary attack, which makes many schemes unable to provide two-factor security. For this, Wang et al. [38] proposed the idea of combining “fuzzy verification factor” with “honeywords” to solve the problem of offline dictionary attack caused by smart devices loss. The main function of “fuzzy verification factor” is to detect the user’s wrong input in time, which can effectively solve the delay and improve the user experience by reducing the computing and communication cost. “Honeywords” enables the protocol to identify the online guessing behavior of attackers in time, and achieve the security beyond the traditional upper limit while meeting the availability index. Moreover, the security of protocol is proved under the modified Random-Oracle-model (ROM).

In 2016, Tewari and Gupta [36] proposed an ultra-lightweight authentication protocol with very low computing and storage costs, and analysis shows that the protocol can meet most security requirements. Recently, Ostad-Sharif et al. [28] found that Ravanbakhsh and Nazari’s scheme [29] existed the problems of known session-specific temporary information attack and perfect forward secrecy. To overcome these deficiencies, they proposed a novel anonymous and unlinkable user authentication and key agreement scheme for TMIS based the elliptic curve cryptosystem (ECC). In this paper, we will point out that Ostad-Sharif et al.’s scheme still exists some problems, such as inefficient password change, off-line password guessing attack resistance, etc., then we give a new scheme. We combine elliptic curve cryptosystem with fuzzy extractor, and apply it to login and authentication phase, which solves the problem of password and biometric correctness detection. Moreover, it makes our protocol have strong authentication and password guessing attack resistance. Also, the ingenious combination of lightweight cryptographic primitives (such as hash, XOR and concatenation) further reduces the computational cost and communication overhead of the scheme.

Our contributions

The main contributions of this paper are as follows.

• The recently-proposed Ostad-Sharif et al.’s enhanced mutual authentication and key-agreement protocol for TMIS is reviewed, and we find that their scheme exists the problems of strong authentication and inefficient password change, and it cannot resist the off-line password guessing attack.

• To overcome the weaknesses in Ostad-Sharif et al.’s scheme, we propose a biometrics-based mutual authentication and key agreement protocol for TMIS.

• The security of the proposed scheme is formally proved under the widely used ROM.

• We demonstrate that the proposed scheme can provide all kinds of security by heuristic discussion.

Organization of the paper

The rest of our work is arranged as follows: Section 3 introduces some preliminaries. Section 4 reviews Ostad-Sharif et al.’s protocol. Section 5 points out the weaknesses of Ostad-Sharif et al.’s scheme. Our biometrics-based mutual authentication and key agreement protocol for TMIS is presented in Section 6. The security of the proposed scheme is formally proved under the widely used ROM in Section 7. We demonstrate that the proposed scheme can provide various security by heuristic discussion in Section 8. In Section 9, the performance of our scheme is compared with the related works. Finally, the conclusions are given in Section 10.

Preliminaries

This section introduces some basic knowledge that will be used in this paper, including some common symbols, elliptic curve defined in finite field, fuzzy extractor and so on.

Symbols guide

For simplicity, the notations and their descriptions used in the entire article are listed in Table 1.

Table 1.

Notations used in the paper

Notation	Description
Fp	a finite field
E(Fp)	an elliptic curve defined on Fp
G	a based point with a big prime order q over the E(Fp)
$Z_q^{\ast }$	the interval [1,q − 1]
IDi	the identity of the patient
PWi	the password of the patient
σ	an extracted string
𝜃	a public auxiliary string
SK	the session key
s	the server’s long-term private key
Pubs	the server’s public key
SCi	the smart card issued to every specific patient
Ek(⋅)/Dk(⋅)	symmetric encryption/decryption with key k
h(⋅)	the one-way hash function
⊕	XOR operation
∥	the concatenation operation
$\mathcal{A}$	adversary

Elliptic curve over a prime finite field F_p

The elliptic curve equation defined on the prime finite field F_p is:

$$y^2=x^3+ax+b(modp),$$ 1

where a,b ∈ F_p and △ = 4a³ + 27b² (mod p)≠ 0

The elliptic curve E(F_p) is defined as:

$$E(F_p)=\{(x,y)\mid x,y\in F_p,y^2=x^3+ax+b\}\cup \{\mathcal{O}\},$$ 2

where $\mathcal{O}$ is the infinity point.

The number of points on the elliptic curve E(F_p) is represented by ♯E(F_p), which is called the order of the elliptic curve.

Some operations on the elliptic curve are shown as follows:

1. If P = (x₁,y₁) ∈ E(F_p), and Q = (x₂,y₂) ∈ E(F_p), then P + Q = (x₃,y₃), where x₃ = λ² − x₁ − x₂ (mod p) and y₃ = λ(x₁ − x₂) − y₁ (mod p), where

$$\lambda =\left\{\begin{array}{cc}\frac{y_2-y_1}{x_2-x_1}(modp),& ifP\ne Q,\\ & \\ \frac{3x_1^2+a}{2y_1}(modp),& ifP=Q\mathrm{.}\end{array}\right)$$

2. Let P = (x,y) ∈ E(F_p), then the scalar multiplication in E(F_p) is defined as: tP = P + P + ⋯ + P(t − times).

Elliptic curve discrete logarithm problem (ECDLP): for the points P,Q ∈ E(F_p), variable α ∈ F_p, it is hard to calculate α meeting Q = α ⋅ P.

Elliptic curve computational Diffie-Hellman (ECDH) problem: for the points G,aG,bG ∈ E(F_p), it is computational impossible to calculate abG ∈ E(F_p).

Fuzzy extractor

In 2004, Dodis et al. [12] proposed the concept of fuzzy extractor. The fuzzy extractor Fe = (Gen,Rep) has two algorithms: the generation algorithm Gen and the regeneration algorithm Rep. The generation algorithm Gen outputs a string σ and a public auxiliary string 𝜃 for the input biometrics B (the first sampling of biometrics); The regeneration algorithm Rep outputs a string ${\sigma }^{\prime }$ for the input biometrics $B^{\prime }$ (the second sampling of biometrics) and the public auxiliary string 𝜃. If the distance between the two samples B and $B^{\prime }$ is close enough, then $\sigma ={\sigma }^{\prime }$. The fuzzy extractor can convert noisy biometrics into stable strings, and this good property enables the fuzzy extractor to be used in cryptographic systems.

Using fuzzy extractor, users can take their own biometrics as the input of Gen to obtain a public auxiliary string 𝜃 and an extracted random string σ. The random string σ can be used as the key of the cryptosystem; the public auxiliary string 𝜃 does not need to be kept secretly, as long as it is stored. After the cryptosystem runs, the key σ will be destroyed. When the cryptosystem needs to use the key again, the user takes his own biometrics and public auxiliary string 𝜃 as the input, and uses the regeneration algorithm Rep to reproduce the key σ. It can be seen that users do not need to store the key. When using the key, they only need to input their own biometrics, and the fuzzy extractor can recover the key safely and reliably.

Review of Ostad-Sharif et al.’s scheme

This section elaborates Ostad-Sharif et al.’s ECC-based anonymous user authentication and key agreement protocol for TMIS, which includes four phases: system setup, patient registration, login and authentication, and password change.

System setup phase

Firstly, the server selects an elliptic curve E(F_p) over a finite field F_p and a base point G with a large prime order q. Secondly, the server selects a random number $s\in Z_q^{\ast }$ as its private key. Finally, it publishes {E(F_p),G,p,q,h_i(⋅)} and keeps s secretly, where h_i(⋅)(i = 0,1,⋯ ,4) are one-way collision-resistant hash functions.

Patient registration phase

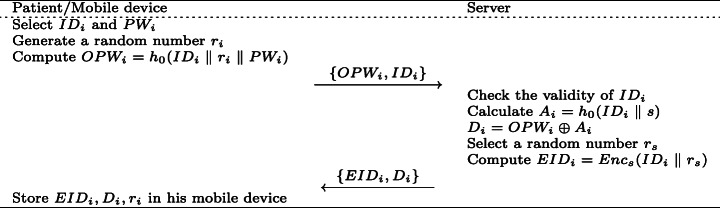
To access services from a medical server, a new user needs to register on the server through the following steps. This phase is shown in Fig. 2.

1. The patient selects an identity ID_i, password PW_i, generates a random number r_i, computes OPW_i = h₀(ID_i ∥ r_i ∥ PW_i), then sends a registration request {OPW_i,ID_i} to the server via a secure channel.

2. On receiving the request message {OPW_i,ID_i}, the server checks whether the ID_i exists in his database, and if so, the server requests the patient to choose a different identity. Otherwise, the server computes A_i = h₀(ID_i ∥ s), D_i = OPW_i ⊕ A_i, selects a random number r_s and computes EID_i = Enc_s(ID_i ∥ r_s). Finally, the server submits {EID_i,D_i} to the patient.

3. Upon reception of the response message {EID_i,D_i}, the patient stores {EID_i,D_i,r_i} into his mobile device.

Fig. 2.

Registration phase of Ostad-Sharif et al.’s scheme

Login and authentication phase

The login and authentication phase of Ostad-Sharif et al.’s scheme will be described in this subsection. When patient wants to access the service from server, he/she needs to do the following. As shown in Fig. 3.

1. The patient inputs his/her identity ID_i, password PW_i. Subsequently, the mobile device retrieves r_i and D_i from its memory, and computes OPW_i = h₀(ID_i ∥ r_i ∥ PW_i), A_i = OPW_i ⊕ D_i. Then, the mobile device generates a random number $x_i\in Z_q^{\ast }$, computes X_i = h₁(ID_i ∥ PW_i ∥ x_i)G, V_i = h₂(ID_i ∥ A_i ∥ X_i ∥ T_i), where T_i is its current time. Finally, the mobile device submits {EID_i,X_i,V_i,T_i} to the server via a public channel.

2. Upon reception of {EID_i,X_i,V_i,T_i}, the server checks the freshness of T_i, aborts if not; otherwise, the server computes (ID_i ∥ r_s) = Dec_s(EID_i), A_i = h₀(ID_i ∥ s), and verifies whether h₂(ID_i ∥ A_i ∥ X_i ∥ T_i)=?V_i. If the equation does not hold, the server aborts the session; otherwise, it generates a random number $x_s\in Z_q^{\ast }$ and computes X_s = h₁(ID_s ∥ s ∥ x_s)G, K = h₁(ID_s ∥ s ∥ x_s)X_i and SK = h₃(ID_i ∥ T_i ∥ K). Next, the server selects a random number $r_s^{new}\in Z_q^{\ast }$, and computes $EI{D}_i^{new}=En{c}_s(I{D}_i\parallel r_s^{new})$, $OEI{D}_i^{new}=EI{D}_i^{new}\oplus h_4(SK)$, $V_s=h_2(A_i\parallel X_s\parallel EI{D}_i^{new}\parallel SK)$. Finally, the server sends $\{OEI{D}_i^{new},X_s,V_s\}$ to the mobile device.

3. After receiving $\{OEI{D}_i^{new},X_s,V_s\}$, the mobile device computes K = h₁(ID_i ∥ PW_i ∥ x_i)X_s, SK = h₃(ID_i ∥ T_i ∥ K), $EI{D}_i^{new}=OEI{D}_i^{new}\oplus h_4(SK)$, verifies whether $h_2(A_i\parallel X_s\parallel EI{D}_i^{new}\parallel SK)\stackrel{?}{=}{V}_s$. If so, the mobile device substitutes EID_i with $EI{D}_i^{new}$.

Fig. 3.

Login and authentication phase of Ostad-Sharif et al.’s scheme

Password change phase

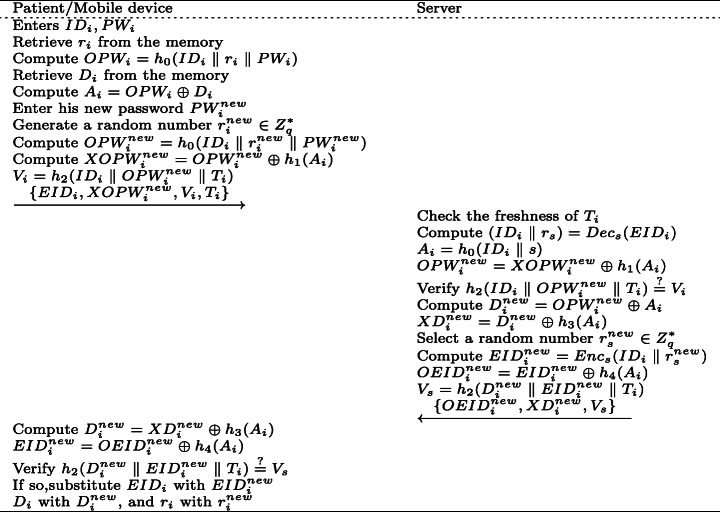
In practice, the user’s password is low entropy and easy to be leaked. At this stage, the user can change his/her password without repeating the registration process. The detailed steps are as follows. As shown in Fig. 4.

1. The patient inputs his/her identity ID_i, password PW_i, and computes OPW_i = h₀(ID_i ∥ r_i ∥ PW_i), A_i = OPW_i ⊕ D_i. Then the mobile device asks the patient to input a new password.

2. The patient enters a new password $P{W}_i^{new}$, and the mobile device generates a new random number $r_i^{new}\in Z_q^{\ast }$, computes $OP{W}_i^{new}=h_0(I{D}_i\parallel r_i^{new}\parallel P{W}_i^{new})$, $XOP{W}_i^{new}=OP{W}_i^{new}\oplus h_1(A_i)$, $V_i=h_2(I{D}_i\parallel OP{W}_i^{new}\parallel T_i)$. Then the mobile device sends $\{EI{D}_i,XOP{W}_i^{new},V_i,T_i\}$ to the server.

3. After receiving $\{EI{D}_i,XOP{W}_i^{new},V_i,T_i\}$, the server checks T_i’s freshness. If it is fresh, the server computes (ID_i ∥ r_s) = Dec_s(EID_i), A_i = h₀(ID_i ∥ s), $OP{W}_i^{new}=XOP{W}_i^{new}\oplus h_1(A_i)$, and verifies whether $h_2(I{D}_i\parallel OP{W}_i^{new}\parallel T_i)\stackrel{?}{=}{V}_i$. If not, the server aborts the session; otherwise, it computes $D_i^{new}=OP{W}_i^{new}\oplus A_i$ and $X{D}_i^{new}=D_i^{new}\oplus h_3(A_i)$. Then, the server selects a random number $r_s^{new}\in Z_q^{\ast }$ and computes $EI{D}_i^{new}=En{c}_s(I{D}_i\parallel r_s^{new})$, $OEI{D}_i^{new}=EI{D}_i^{new}\oplus h_4(A_i)$, $V_s=h_2(D_i^{new}\parallel EI{D}_i^{new}\parallel T_i)$. Finally, the server submits $\{OEI{D}_i^{new},X{D}_i^{new},V_s\}$ to the patient.

4. On receiving $\{OEI{D}_i^{new},X{D}_i^{new},V_s\}$, the mobile device computes $D_i^{new}=X{D}_i^{new}\oplus h_3(A_i)$, $EI{D}_i^{new}=OEI{D}_i^{new}\oplus h_4(A_i)$, and verifies whether $h_2(D_i^{new}\parallel EI{D}_i^{new}\parallel T_i)\stackrel{?}{=}{V}_s$. If true, the mobile device substitutes EID_i with $EI{D}_i^{new}$, D_i with $D_i^{new}$, and r_i with $r_i^{new}$.

Fig. 4.

Password change phase of Ostad-Sharif et al.’s scheme

Weaknesses of Ostad-Sharif et al.’s protocol

In the section, we will point out that Ostad-Sharif et al.’s protocol exists the problems of strong authentication, inefficient password change and the off-line password guessing attack resistance. The detailed description is as follows.

Strong authentication

In the login and authentication phase of Ostad-Sharif et al.’s protocol, after the user enters his/her identity ID_i and password PW_i, the smart card does not check their correctness and proceeds to the next step.

1. Assuming that the patient inputs the wrong password $P{W}_i^{\ast }$ instead of the correct password PW_i. Then, the smart card computes $OP{W}_i^{\ast }=h_0(I{D}_i\parallel r_i\parallel P{W}_i^{\ast })$, $A_i^{\ast }=OP{W}_i^{\ast }\oplus D_i=OP{W}_i^{\ast }\oplus OP{W}_i\oplus A_i\ne A_i$.

2. Smart card generates a random number $x_i\in Z_q^{\ast }$, computes $X_i^{\ast }=h_1(I{D}_i\parallel P{W}_i^{\ast }\parallel x_i)G$, $V_i^{\ast }=h_2(I{D}_i\parallel A_i^{\ast }\parallel X_i^{\ast }\parallel T_i)$, where T_i is its current time. Finally, the smart card submits $\{EI{D}_i,X_i^{\ast },V_i^{\ast },T_i\}$ to the server via a public channel.

3. Upon reception of $\{EI{D}_i,X_i^{\ast },V_i^{\ast },T_i\}$, the server checks the freshness of T_i, aborts if not; otherwise, the server computes (ID_i ∥ r_s) = Dec_s(EID_i), A_i = h₀(ID_i ∥ s). Then the server verifies whether $h_2(I{D}_i\parallel A_i\parallel X_i^{\ast }\parallel T_i)\stackrel{?}{=}{V}_i^{\ast }$.

It is obviously that $h_2(I{D}_i\parallel A_i\parallel X_i^{\ast }\parallel T_i)\ne V_i^{\ast }$ because $A_i^{\ast }\ne A_i$. Therefore, the server considers the patient to be illegal, refuses him/her to log in and terminates the session.

Similarly, if the patient enters an incorrect identity ID_i, the above problem will also occur during the login and authentication phase. This problem increases the communication and computing costs of the server.

Inefficient password change

In the password change phase of Ostad-Sharif et al.’s protocol, the old password is not verified for correctness, and we find some problems with the password change phase. The details are described as follows.

1. Assuming that the patient inputs the wrong password $P{W}_i^{\ast }$ instead of the correct password PW_i, and the smart card computes $OP{W}_i^{\ast }=h_0(I{D}_i\parallel r_i\parallel P{W}_i^{\ast })$, $A_i^{\ast }=OP{W}_i^{\ast }\oplus D_i=OP{W}_i^{\ast }\oplus OP{W}_i\oplus A_i\ne A_i$. Then, the smart card asks the patient to input a new password.

2. The patient enters a new password $P{W}_i^{new}$, and then the patient and the server perform mutual authentication phase. After that, the server submits $\{OEI{D}_i^{new},X{D}_i^{new},V_s\}$ to the patient.

3. On receiving $\{OEI{D}_i^{new},X{D}_i^{new},V_s\}$, the mobile device computes $D_i^{new\ast }=X{D}_i^{new}\oplus h_3(A_i^{\ast })$, $EI{D}_i^{new\ast }=OEI{D}_i^{new}\oplus h_4(A_i^{\ast })$, and verifies whether $h_2(D_i^{new\ast }\parallel EI{D}_i^{new\ast }\parallel T_i)\stackrel{?}{=}{V}_s$.

It is obviously that $h_2(D_i^{new\ast }\parallel EI{D}_i^{new\ast }\parallel T_i)\ne V_s$ because $A_i^{\ast }\ne A_i$. So the smart card refuses to update the password and terminates the session. This increases the burden on the server. If a malicious adversary sends a large number of password change requests to a specific server, it may cause the server to be paralyzed, and thus can not provide normal services for legitimate users.

Off-line password guessing attack

Messerges et al. [27] and He et al. [18] point out that all smart cards cannot resist the side channel attack and all data can be extracted from the smart cards. We assume an adversary $\mathcal{A}$ has extracted the information {EID_i,D_i,r_i} from the smart card. In this subsection, we will prove that $\mathcal{A}$ can obtain the patient’s password once he/she obtains the smart card of the patient in Ostad-Sharif et al.’s scheme. The details are as follows.

1. $\mathcal{A}$ intercepts patient’s login information {EID_i,X_i,V_i,T_i} on public channel, and guesses patient’s identity $I{D}_i^{\prime }$ and password $P{W}_i^{\prime }$ from the user identity space D_id and the password space D_pw respectively.

2. $\mathcal{A}$ computes $OP{W}_i^{\prime }=h_0(I{D}_i^{\prime }\parallel r_i\parallel P{W}_i^{\prime })$, $A_i^{\prime }=OP{W}_i^{\prime }\oplus D_i$, $V_i^{\prime }=h_2(I{D}_i^{\prime }\parallel A_i^{\prime }\parallel X_i\parallel T_i)$.

3. $\mathcal{A}$ verifies whether $V_i^{\prime }\stackrel{?}{=}{V}_i$ or not. If true, $\mathcal{A}$ gets the patient’s real identity ID_i and password PW_i. Otherwise, $\mathcal{A}$ repeats (1) and (2) until he/she finds the correct identity and password.

Therefore, Ostad-Sharif et al.’s protocol cannot resist the off-line password guessing attack.

Our proposed scheme

To overcome the security weaknesses of Ostad-Sharif et al.’s protocol and enhance the security of protocol, we give a biometrics-based mutual authentication and key agreement protocol (BBAKA) for TMIS using elliptic curve cryptography. It consists of four phases: initialization phase, patient registration phase, login and authentication phase, password change phase. Fig. 5 shows the general flow of BBAKA protocol. Firstly, the key generation center (KGC) initializes system and generates public parameters. Secondly, the user and the server interact to complete mutual authentication and establish a common session key. The details are presented as follows.

Fig. 5.

General flow of BBAKA protocol

Initialization phase

KGC initializes the system parameters as follows, then publicizes them.

1. The server chooses an elliptic curve E(F_p) and a base point G with large prime order q over E(F_p).

2. The server selects a secure one-way hash function: $h:{\{0,1\}}^{\ast }\to {\{0,1\}}^{l_h}$.

3. The server selects a random number $s\in Z_q^{\ast }$ as its long-term private key and calculates Pub_s = s ⋅ G as its public key.

4. Server keeps s secretly and publishes the system parameters {E(F_p),G,Pub_s,q,h(⋅)}.

Patient registration phase

If the patient needs to access the medical server, he/she should first register on KGC as the following steps. The details are shown in Fig. 6.

1. The patient selects an identity ID_i, password PW_i, imprints his/her biometrics B_i, generates a random number r_i, computes (σ_i,𝜃_i) = Gen(B_i), OPW_i = h(ID_i ∥ r_i ∥ PW_i). Then the patient sends a registration request {OPW_i,ID_i} to KGC via a secure channel.

2. Upon receiving the request message {OPW_i,ID_i}, KGC checks whether h(ID_i) exists in its database. If so, KGC requests the patient to choose a different identity. Otherwise, it computes A_i = h(ID_i ∥ s), D_i = OPW_i ⊕ A_i, selects a random number r_s and computes EID_i = Enc_s(ID_i ∥ r_s), C_i = h(ID_i ∥ A_i ∥ OPW_i). Then KGC stores {EID_i,D_i,C_i,h(⋅)} in a smart card SC_i and submits SC_i to the patient via a secure physical channel.

3. After receiving SC_i, the patient computes y_i = r_i ⊕ h(σ_i) and stores y_i,𝜃_i in SC_i.

Fig. 6.

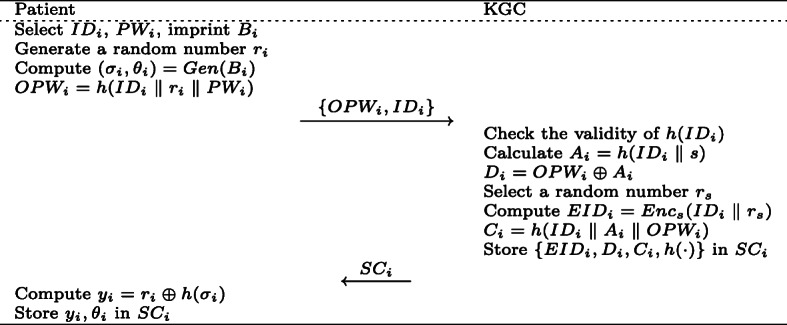
Registration phase of BBAKA protocol

Login and authentication phase

When the patient wants to login server, he and server need to authenticate each other’s legitimacy, and establish a shared session key to ensure the security of subsequent communication. The detailed description of this phase is shown in Fig. 7.

1. Patient inputs his identity ID_i, password PW_i, imprints B_i. Then the mobile device retrieves y_i and D_i from its memory, and computes σ_i = Rep(B_i,𝜃_i), r_i = y_i ⊕ h(σ_i), OPW_i = h(ID_i ∥ r_i ∥ PW_i), A_i = OPW_i ⊕ D_i. Following, the mobile device verifies whether h(ID_i ∥ A_i ∥ OPW_i)=?C_i holds. If it does not hold, the mobile device terminates this session. Otherwise, the mobile device generates a random number $\alpha \in Z_q^{\ast }$, and computes X_i = α ⋅ G, V_i = h(ID_i ∥ A_i ∥ X_i ∥ T₁), where T₁ is the current time. Finally, the mobile device submits {EID_i,X_i,V_i,T₁} to server.

2. Upon reception of {EID_i,X_i,V_i,T₁}, server checks the freshness of T₁, aborts if not; otherwise, server computes (ID_i ∥ r_s) = Dec_s(EID_i), A_i = h(ID_i ∥ s). Then server verifies whether h(ID_i ∥ A_i ∥ X_i ∥ T₁)=?V_i, if not, aborts the session; otherwise, it generates a random number $\beta \in Z_q^{\ast }$ and computes X_s = β ⋅ G, SK = h(ID_i ∥ T₁ ∥ A_i ∥ β ⋅ X_i). Next, server selects a new random number $r_s^{new}\in Z_q^{\ast }$, computes $EI{D}_i^{new}=En{c}_s(I{D}_i\parallel r_s^{new})$, $V_s=h(A_i\parallel T_2\parallel EI{D}_i^{new}\parallel SK)$, and sends $\{EI{D}_i^{new},X_s,V_s,T_2\}$ to the mobile device.

3. After receiving $\{EI{D}_i^{new},X_s,V_s,T_2\}$, the mobile device computes SK = h(ID_i ∥ T₁ ∥ A_i ∥ α ⋅ X_s), verifies whether $h(A_i\parallel T_2\parallel EI{D}_i^{new}\parallel SK)\stackrel{?}{=}{V}_s$. If so, it substitutes EID_i with $EI{D}_i^{new}$.

Fig. 7.

Login and authentication phase of BBAKA protocol

Password and biometrics change phase

At this stage, the patient can change his password and biometrics according to the following steps.

1. Patient inserts his smart card into the card reader and inputs his/her identity ID_i, password PW_i, imprints his/her biometrics B_i. Then smart card SC_i computes σ_i = Rep(B_i,𝜃_i), r_i = y_i ⊕ h(σ_i), OPW_i = h(ID_i ∥ r_i ∥ PW_i), A_i = OPW_i ⊕ D_i.

2. SC_i checks h(ID_i ∥ A_i ∥ OPW_i)=?C_i. If not, SC_i will reject the patient’s password and biometrics change request. Otherwise, patient is asked to enter a new password PW_inew and biometrics B_inew.

3. The patient enters a new password PW_inew and imprints his/her new biometrics B_inew.

4. On receiving PW_inew and B_inew, SC_i generates a new random number r_inew, and computes (σ_inew,𝜃_inew) = Gen(B_inew), OPW_inew = h(ID_i ∥ r_inew ∥ PW_inew), D_inew = OPW_inew ⊕ A_i, C_inew = h(ID_i ∥ A_i ∥ OPW_inew), y_inew = r_inew ⊕ h(σ_inew). Finally, SC_i updates {D_i,C_i,y_i,𝜃_i} with {D_inew,C_inew,y_inew,𝜃_inew}.

Unlike Ostad-Sharif et al.’s protocol, our password and biometrics change phase does not require the participation of server, and patient can complete it locally. In this way, the computing and communication costs of server are reduced, which makes our protocol more efficient.

Formal security proof

In this section, we give the formal security proof of BBAKA protocol under the random oracle model (ROM) [5].

Security model

The BPR adversary model is widely used to prove the security of authentication scheme based password. U₁ and U₂ are protocol participants. The model allows each user to execute multiple protocols with other users. A user can execute a polynomial protocol instance in parallel. ${\mathit{\pi }}_{U_i}^t$ represents the t th instance of user U_i.

The security of the protocol depends on the capability of the adversary, which is simulated by a series of queries. It is assumed that the probability polynomial time (PPT) adversary $\mathcal{A}$ completely controls the communication and can query any instance. $\mathcal{A}$ can perform the following queries.

• Execute(U₁,U₂): This query executes the protocol between users U₁ and U₂. The adversary gets all messages during the execution of the protocol.

• $Send({\mathit{\pi }}_{U_i}^t,M)$: This query allows adversary $\mathcal{A}$ to send a message M to instance ${\mathit{\pi }}_{U_i}^t$, then ${\mathit{\pi }}_{U_i}^t$ executes the protocol π honestly and returns a response message to $\mathcal{A}$.

• $Reveal({\mathit{\pi }}_{U_i}^t)$: This query returns the session key held by instance ${\mathit{\pi }}_{U_i}^t$.

• Corrupt(U_i): This query allows $\mathcal{A}$ to get the long-term private key of U_i. But $\mathcal{A}$ can’t get any intermediate data in the process of protocol execution.

• $Test({\mathit{\pi }}_{U_i}^t)$: This query attempts to simulate the adversary’s ability to distinguish between session key and random key. Test oracle randomly selects a bit b. If b = 1, the session key is returned; If b = 0, random key is returned. Suppose that $\mathcal{A}$ can only make one Test query.

Let $ID{S}_i^t$ be the session identifier of participant instance ${\mathit{\pi }}_{U_i}^t$, which is a function of all messages received and sent by ${\mathit{\pi }}_{U_i}^t$. Let $I{D}_i^t$ be the partner identifier which is used to identify the participant who is exchanging keys with the instance ${\mathit{\pi }}_{U_i}^t$.

Definition 1 (Partnership) Two instances ${\mathit{\pi }}_{U_i}^t$ and ${\mathit{\pi }}_{U_j}^m$ are partners if and only if: $ID{S}_i^t=ID{S}_j^m$ and $I{D}_i^t=I{D}_j^m$.

Definition 2 (Freshness) Instance ${\mathit{\pi }}_{U_i}^t$ is fresh. If the status of this instance is accepted after receiving the last expected message, and neither ${\mathit{\pi }}_{U_i}^t$ nor its partners have been asked for Reveal query.

Definition 4 (Semantic Security) For any $\mathcal{A}$, $Succ(\mathcal{A})$ is an event that $\mathcal{A}$ makes one Test query on some fresh instances and correctly guesses the value of b. The advantage that $\mathcal{A}$ attacks the protocol π is defined to be $Ad{v}_{\mathit{\pi }}^{AKE}(\mathcal{A})=2|Pr[Succ(\mathcal{A})]-\frac{1}{2}|$. The protocol π is called semantically secure if $Ad{v}_{\mathit{\pi }}^{AKE}(\mathcal{A})$ is negligible.

Security proof

First, we introduce the simulation of two oracles: Hash oracle and encryption/ decryption oracle.

Simulation of Hash Oracle Query

On receiving h(u) query, Hash returns v as follows.

• v = h(u) is returned if (u,v) exists in list L_H.

• Otherwise, select a constant $v\in {\{0,1\}}^{l_h}$ randomly and send it to $\mathcal{A}$, then add (u,v) into list L_H.

Simulation of encryption/decryption Oracle Queries

• When E_k(u) is queried, it returns v if the record (k,u,∗,v) exists in the list L_C. Otherwise, it returns a random number $v\in {\{0,1\}}^{l_c}$ and adds (k,u,E,v) into L_C.

• When D_k(v) is queried, it returns u if the record (k,u,∗,v) exists in the list L_C. Otherwise, it returns a random number u and adds (k,u,D,v) into L_C.

Next, we prove that the protocol is secure against the active adversary under ECDH assumption.

Theorem 1 Under ECDH assumption, BBAKA protocol can resist the attack of PPT adversary. The corresponding adversary advantage is

$$Ad{v}_{\mathit{\pi }}(\mathcal{A})\le \frac{q_h^2}{2^{l_h}}+\frac{q_c^2}{2^{l_c}}+\frac{{(q_s+q_e)}^2}{2^{l_r}}+\frac{q_s}{2^{l_h-1}}+2q_{h}Ad{v}_{\mathit{\pi }}^{ECDH}(\mathcal{A})+2q_s\cdot max\{\frac{1}{|D|},\frac{1}{2^l},{\epsilon }_b\}$$

where q_h,q_c,q_s and q_e denote the number of Hash, encryption/decryption, Send and Execute oracle queries, respectively, $Ad{v}_{\mathit{\pi }}^{ECDH}(\mathcal{A})$ denotes $\mathcal{A}$’s probability of solving the ECDH problem successfully, l_h is the output size of Hash oracle, l_c is the output size of encryption/decryption oracle and l_r is the string length of random numbers. |D| is the size of the password space, l is the length of σ, ε_b represents the probability that the biometric information of two different users satisfies the condition $d(B_i^{\prime },B_i)<\mathrm{\Delta }t$, which is obviously a negligible infinitesimal

Proof To prove that BBAKA protocol π is secure, we define five games G_i(0 ≤ i ≤ 4). Pr[Succ_i] denotes the probability which $\mathcal{A}$ success in the game G_i.

GameG₀: $\mathcal{A}$’s query is responded as the real BBAKA protocol, so the probability that $\mathcal{A}$ success in Game G₀ is equal to $\mathcal{A}$’s advantages in the original protocol. Then

$$Ad{v}_{\mathit{\pi }}(\mathcal{A})=2|Pr[Suc{c}_0]-\frac{1}{2}|$$ 3

Game G₁: Hash oracle and encryption/decryption oracles are simulated as above, and other oracles are simulated as the original protocol. Then

$$Pr[Suc{c}_1]=Pr[Suc{c}_0]$$ 4

Game G₂: This game considers the hash result conflict and the random number conflict of all communication messages. In the transmitted messages {EID_i,X_i,V_i,T₁} and $\{EI{D}_i^{new},X_s,V_s,T_2\}$, X_i and X_s contain random numbers α and β, respectively. According to the birthday paradox, the probability of collision in the Hash queries, encryption/decryption queries and transcripts are at most $\frac{q_h^2}{2^{l_h+1}}$, $\frac{q_c^2}{2^{l_c+1}}$ and $\frac{{(q_s+q_e)}^2}{2^{l_r+1}}$ respectively. Thus

$$|Pr[Suc{c}_2]-Pr[Suc{c}_1]|\le \frac{q_h^2}{2^{l_h+1}}+\frac{q_c^2}{2^{l_c+1}}+\frac{{(q_s+q_e)}^2}{2^{l_r+1}}$$ 5

Game G₃: In this game, instead of using hash oracle, $\mathcal{A}$ tries to guess the correct hash value from other oracle queries. It is indistinguishable from G₂ except that $\mathcal{A}$ maybe guess V_i and V_s. Thus, we have

$$|Pr[Suc{c}_3]-Pr[Suc{c}_2]|\le \frac{q_s}{2^{l_h}}$$ 6

Game G₄: In this terminating game, the session key is guessed without querying the hash oracle, so $\mathcal{A}$ has no advantage to guess b. It has no advantage in distinguishing between the real session key and random session key. Then we have

$$Pr[Suc{c}_4]=\frac{1}{2}$$ 7

G₄ and G₃ are indistinguishable unless $\mathcal{A}$ queries Hash oracle on < ID_i ∥ T₁ ∥ A_i ∥ β ⋅ X_i >. Suppose $\mathcal{A}$ can query Corrupt(U_i) in the following three ways.

• Corrupt(U_i) returns U_i’s biometrics B_i to $\mathcal{A}$, and the probability is at most q_s ⋅ ε_b.

• Corrupt(U_i) returns U_i’s password PW_i to $\mathcal{A}$, and the probability is at most $\frac{q_s}{|D|}$;

• Corrupt(U_i) returns parameters stored in SC_i to $\mathcal{A}$, and the probability is at most $\frac{q_s}{2^l}$;

The above three cases cannot occur at the same time, so the probability is at most $q_s\cdot max\{\frac{1}{|D|},\frac{1}{2^l},{\epsilon }_b\}$. So

$$|Pr[Suc{c}_4]-Pr[Suc{c}_3]|\le q_{h}Ad{v}_{\mathit{\pi }}^{ECDH}(\mathcal{A})+q_s\cdot max\{\frac{1}{|D|},\frac{1}{2^l},{\epsilon }_b\}$$ 8

Then, we have

$$\begin{array}{cc}Ad{v}_{\mathit{\pi }}(\mathcal{A})& =2|Pr[Suc{c}_0]-\frac{1}{2}|\\ & =2|Pr[Suc{c}_1]-Pr[Suc{c}_4]|\\ & =2|Pr[Suc{c}_1]-Pr[Suc{c}_2]+Pr[Suc{c}_2]-Pr[Suc{c}_3]+Pr[Suc{c}_3]\\ & -Pr[Suc{c}_4]|\\ & \le 2(|Pr[Suc{c}_1]-Pr[Suc{c}_2]|+|Pr[Suc{c}_2]-Pr[Suc{c}_3]|+|Pr[Suc{c}_3]\\ & -Pr[Suc{c}_4]|)\\ & \le \frac{q_h^2}{2^{l_h}}+\frac{q_c^2}{2^{l_c}}+\frac{{(q_s+q_e)}^2}{2^{l_r}}+\frac{q_s}{2^{l_h-1}}+2q_{h}Ad{v}_{\mathit{\pi }}^{ECDH}(\mathcal{A})+2q_s\cdot max\{\frac{1}{|D|},\frac{1}{2^l},{\epsilon }_b\}\end{array}$$

Finally, the theorem is proved according to formulas (3)-(8).

Other analysis

In this section, we analyze the important security features and various attack resistances of BBAKA protocol by heuristic discussion method. In addition, password guessing attack resistance has been proven in Section 7.2, so it is omitted here.

Mutual authentication and session key agreement

In the login and authentication phase of BBAKA protocol, server can authenticate the legitimacy of patient by comparing whether h(ID_i ∥ A_i ∥ X_i ∥ T₁)=?V_i, where A_i = h(ID_i ∥ s), X_i = α ⋅ G, T₁ is the current timestamp. $\mathcal{A}$ has two ways to calculate A_i. The first one is that $\mathcal{A}$ tries his best to get the user’s identity ID_i and the system master key s; the second one is that $\mathcal{A}$ calculates A_i by A_i = OPW_i ⊕ D_i, where OPW_i = h(ID_i ∥ r_i ∥ PW_i), r_i = y_i ⊕ h(σ_i). This requires $\mathcal{A}$ to get the patient’s identity ID_i, password PW_i, biometrics B_i and the smart card. Clearly, both approaches are almost impossible for any adversary. In addition, since that only legitimate server can get these secret parameters ID_i,SK,X_s and s, patients can authenticate server by checking $h(A_i\parallel T_2\parallel EI{D}_i^{new}\parallel SK)\stackrel{?}{=}{V}_s$, where SK = h(ID_i ∥ T₁ ∥ A_i ∥ α ⋅ X_s). After mutual authentication, patient and server establish a shared session key SK = h(ID_i ∥ T₁ ∥ A_i ∥ α ⋅ X_s). Therefore, our scheme can provide mutual authentication and session key agreement.

User anonymity and untraceability

User anonymity implies that adversary cannot get the user’s real identity ID_i. In our protocol, the patient’s identity is sent with a fake name EID_i = Enc_s(ID_i ∥ r_s), where s is the server’s private key. To obtain the patient’s identity ID_i, $\mathcal{A}$ needs to get the values of s and the random number r_s. For any adversary, this is almost impossible to accomplish. Furthermore, the patient’s pseudonym is updated at the end of each session without disclosing any information to the adversary. In addition, for the login request {EID_i,X_i,V_i,T₁} and response message $\{EI{D}_i^{new},X_s,V_s,T_2\}$, they are all protected by the random numbers α, β and r_s, and $\mathcal{A}$ cannot get any useful information from these messages. Therefore, users is anonymity and $\mathcal{A}$ can’t track users.

Perfect forward secrecy

In BBAKA protocol, the session key SK = h(ID_i ∥ T₁ ∥ A_i ∥ β ⋅ X_i), where A_i = h(ID_i ∥ s) and X_i = α ⋅ G. It is protected by server’s private key s and random numbers α,β. Even if $\mathcal{A}$ gets the master key s, he/she cannot get the value of β ⋅ X_i unless the ECDLP problem is solved. So the perfect forward secrecy is provided in our protocol.

User friendliness

Our protocol allows patients to freely choose and change their identities ID_i, passwords PW_i and biometrics B_i, which makes our protocol get a good user experience.

Resist the stolen-verifier attack

Our scheme does not require server to maintain a verification list to store secret parameters related to the user’s password and biometrics, and server’s database is not useful for $\mathcal{A}$ to access patients’ other private information. Therefore, it can resist the stolen-verifier attack.

Resist the privileged insider attack

In the registration phase of BBAKA protocol, patient sends {OPW_i,ID_i} to server, where OPW_i = h(ID_i ∥ r_i ∥ PW_i). Because OPW_i is protected by the random number r_i, server cannot get the patient’s password PW_i. In addition, patient does not send any biometrics information to server, so it is impossible for server to know the patient’s biometrics. Moreover, the use of random number ensures patient a different OPW_i in every session. Therefore, our protocol can resist the privileged insider attack.

Resist the user impersonation attack

To impersonate a legitimate patient, $\mathcal{A}$ must compute V_i = h(ID_i ∥ A_i ∥ X_i ∥ T₁), where A_i = h(ID_i ∥ s), X_i = α ⋅ G. Obviously, $\mathcal{A}$ cannot get A_i’s value without the system private key s. In addition, as described in the previous section, our protocol can provide user anonymity and untraceability, so $\mathcal{A}$ also cannot get the user’s identity ID_i. Thus, the user impersonation attack is powerless against our protocol.

Replay attack

Suppose the adversary intercepts a login message {EID_i,X_i,V_i,T₁} and replays it to the server, the server can quickly detect this attack by checking the freshness of T₁. Even if T₁ is modified by the adversary, the server can also detect the replay attack by verifying h(ID_i ∥ A_i ∥ X_i ∥ T₁)=?V_i. Similarly, the patient can find the replay attack by checking the freshness of T₂ and verifying $h(A_i\parallel T_2\parallel EI{D}_i^{new}\parallel SK)\stackrel{?}{=}{V}_s$. Thus, BBAKA protocol can resist the replay attack.

Man-in-the-middle attack

As discussed above, BBAKA protocol can provide mutual authentication and resist the impersonation attack. So it can successfully resist man-in-the-middle attack.

Resist the denial of service attack

In BBAKA protocol, patients can only send login requests after they are locally authenticated. The details are as follows: The patient inputs his/her identity ID_i, password PW_i, imprints B_i. Then the mobile device computes σ_i = Rep(B_i,𝜃_i), r_i = y_i ⊕ h(σ_i), OPW_i = h(ID_i ∥ r_i ∥ PW_i), A_i = OPW_i ⊕ D_i, and verifies h(ID_i ∥ A_i ∥ X_i ∥ T₁)=?V_i. If it does not hold, the mobile device will end this session. Namely, only after the patient is authenticated by the mobile device, the login request is sent to the server. Thus, our protocol is secure against the denial of service attack.

Known session-specific temporary information attack

In our protocol, the patient and the server establish the session key SK = h(ID_i ∥ T₁ ∥ A_i ∥ β ⋅ X_i), where A_i = h(ID_i ∥ s), X_i = α ⋅ G. Suppose that the temporary secrets α and β are leaked to the adversary, he still cannot calculate the session key unless he knows the system private key s. Also, only the legitimate server has the private key, $\mathcal{A}$ is impossible to get s. So in any case, the adversary cannot calculate the session key.

Smart card loss attack

In our scheme, even if the patient’s smart card/mobile device is lost, he/she still can not be impersonated by a malicious adversary $\mathcal{A}$ without his/her password. Furthermore, as mentioned above, BBAKA protocol can successfully resist the offline password guessing attack. Therefore, the smart card loss attack is powerless against BBAKA protocol.

Functionality and performance analysis

In this section, we carefully compares the functionality and performance of our protocol with the related works [24, 25, 28, 30, 35]. Comparison results are shown in Table 2.

Table 2.

Security comparison

scheme	[28]	[24]	[25]	[35]	[30]	Our
Mutual authentication and key agreement	√	√	√	√	√	√
User anonymity	√	√	√	×	√	√
User un-traceability	√	×	×	√	√	√
Perfect forward secrecy	√	√	√	√	×	√
User friendliness	×	×	√	√	√	√
Resist stolen-verifier attack	×	×	√	√	×	√
Resist off-line password guessing attack	×	√	×	×	√	√
Resist privileged insider attack	√	√	√	√	√	√
Resist the user impersonation attack	√	√	√	√	√	√
Resist the replay attack	√	×	×	√	×	√
Resist man-in-the-middle attack	√	√	√	√	√	√
Resist the denial of service attack	×	√	×	×	√	√
Resist ephemeral secret leakage attack	√	×	×	×	√	√
Resist smart card loss attack	√	√	×	√	√	√

Table 2 shows that [25, 28] and [35] cannot resist off-line password guessing attack and denial of service attack. Ostadsharif et al. [28] and [24] fail to provide the user friendliness. [24], [25] and [35] are powerless to resist the ephemeral secret leakage attack. Li et al. [24], [25] and [30] are vulnerable to the replay attack. Ostadsharif et al. [28], [24] and [30] can not resist the stolen-verifier attack. In addition, [30] and [25] exist the problems of perfect forward secrecy and smart card loss attack resistance respectively. However, our protocol can provide all these security features.

Next, we will compare the performance of BBAKA protocol with the recent existing authentication protocols [24, 25, 28, 30, 35]. We define the notations used for execution time in Table 3.

Table 3.

Notations of some operations

Notation	Meaning	Execution time (s)
Tm	One elliptic curve point multiplication operation	0.063075
Ts	One symmetric encryption/decryption operation	0.0087
Th	One-way hash function	0.0005
Te	One modular exponentiation operation	0.522
Tchao	One chebyshev chaotic map	0.066
Tpk	One public key encryption/decryption	0.522

According to He et al. [16], the executing time of elliptic curve point multiplication, symmetric encryption/decryption, one-way hash function, modular exponentiation, chebyshev chaotic map and public key encryption/decryption are 0.063075, 0.0087, 0.0005, 0.522, 0.066 and 0.522 second respectively. Since the executing time of concatenation and XOR operation are very short, we neglect them in all protocols. Furthermore, we assume that the size of random number, hash output, timestamp, chebyshev output and elliptic curve point are 64 bits, 160 bits, 32 bits, 320 bits and 320 bits respectively. In addition, the symmetric cryptographic algorithm used is AES-128 and the output size of public key encryption/decryption is 320 bits. The performance comparison results are shown in Table 4.

Table 4.

Performance comparison of our protocol with the related ones

Scheme	Execution time of U	Execution time of S	Total execution time (second)	Communication cost
[28]	7Th + 2Tm	7Th + 2Tm + 2Ts	14Th + 4Tm + 2Ts ≈ 0.2767	1184 bits
[24]	11Th + 2Tchao	8Th + 2Tchao	19Th + 4Tchao ≈ 0.2735	1760 bits
[25]	7Th + Tpk + Ts	9Th + Tpk + 2Ts	16Th + 2Tpk + 3Ts ≈ 1.0781	1344 bits
[35]	10Th + 3Tchao	3Th + 2Tchao	13Th + 5Tchao ≈ 0.3365	1184 bits
[30]	2Th + 3Tm	2Th + 3Tm	4Th + 6Tm ≈ 0.3805	1280 bits
Our	6Th + 2Tm	4Th + 2Tm + 2Ts	10Th + 4Tm + 2Ts ≈ 0.2747	1280 bits

In the login and authentication phase of BBAKA protocol, the mobile device executes six one-way hash function operations and two elliptic curve point multiplication operations. So the execution time of the mobile device is 6T_h + 2T_m. The server executes four one-way hash function operations, two elliptic curve point multiplication operations and two symmetric encryption/decryption operations. So the execution time of the server is 4T_h + 2T_m + 2T_s. Thus, the total execution time of BBAKA protocol is 10T_h + 4T_m + 2T_s ≈ 10 × 0.0005 + 4 × 0.063075 + 2 × 0.0087 ≈ 0.2747 (second).

The mobile device sends request message {EID_i,X_i,V_i,T₁} to the server, and then the server sends response message $\{EI{D}_i^{new},X_s,V_s,T_2\}$ to the mobile device. So the communication cost of BBAKA protocol is 1280 bits.

According to Fig. 8, the total execution time of BBAKA protocol is obviously the least. Compared with protocols of Lwamo et al. [25] and Salem et al. [30], the total time-consuming of BBAKA protocol is reduced by about 74.5% and 27.8% respectively. In terms of communication cost, Fig. 9 shows that our protocol is significantly superior to the protocols [24] and [25], and almost equal to protocols [28, 35] and [30]. Also, our protocol can overcome four weaknesses of Ostad-Sharif et al.’s scheme [28] and Sureshkumar et al.’s scheme [35]. Compared with Li et al’s scheme [24], the communication overhead of BBAKA protocol is reduced by 27.3%. Although the communication cost of BBAKA protocol is slightly higher than Sureshkumar et al.’s protocol [35], it can overcome four weaknesses of their scheme. In summary, BBAKA protocol has great advantages in both execution time and communication cost.

Fig. 8.

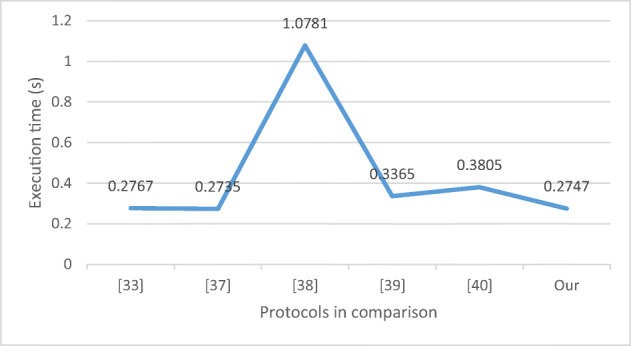
Execution time illustration of different protocols

Fig. 9.

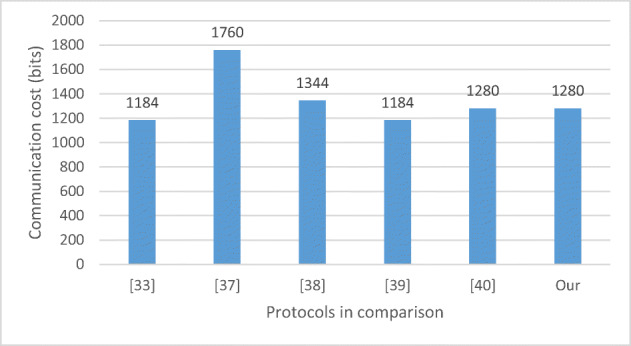
Communication cost illustration of different protocols

Conclusions

In this paper, Ostad-Sharif et al.’s scheme is reviewed, and then we point out that their scheme cannot provide the strong authentication and is vulnerable to off-line password guessing attack. Moreover, their scheme fails to update password correctly in the password change phase. To overcome these weaknesses, we propose a biometrics-based mutual authentication and key agreement protocol for TMIS. We take full advantage of lightweight cryptographic primitives such as ECC and hash functions, which makes our protocol more suitable for TMIS. Our protocol can provide not only the three security missing in Ostad-Sharif et al.’s protocol but also other security, such as user anonymity, un-traceability, perfect forward secrecy, etc. In addition, it can also resist all kinds of known attacks, such as stolen-verifier attack, privileged insider attack, replay attack, etc. Also, we prove the security of BBAKA protocol by formal method under ROM. Compared with related existing protocols, our protocol has less computation cost and communication overhead. In the future work, we will consider designing the key agreement protocol based on lattice cryptography to further improve the efficiency and security of the scheme.