Empirical assessment of prediction intervals in Cochrane meta-analyses

Introduction

Meta-analysis aims at combining and contrasting results from multiple independent studies. A critical issue is that the combined studies could be heterogeneous because of differences in study populations, designs, conducts, etc.¹ The random-effects model is used in many meta-analyses to account for between-study heterogeneity, and the point estimate of the combined result and its confidence interval (CI) are often of primary interest. However, although the CI from a random-effects meta-analysis accounts for heterogeneity, it may not reflect the treatment effect in a future study.

Most existing practices of meta-analyses have also focused on estimating certain heterogeneity measures, such as the between-study variance τ² and the I² statistic.^2,3 The I² statistic describes the amount of total variation across studies that is due to heterogeneity.² However, I² has several limitations.^4–6 For example, it may depend on the sample sizes of the combined studies.^7,8 A low value of I² could correspond to high clinical dispersion, while a high value does not necessarily suggest that the study effects are dispersed over a wide range.⁹ Moreover, I² should not be used as an absolute measure, and it could have large uncertainties.⁵

As an alternative solution to appraising heterogeneity, the prediction interval (PI) has been advocated in the meta-analysis literature over the past decade.^5,10–13 It describes the range of the true effect of a new study in the future. The CI only reflects the accuracy of the combined effect of the existing studies in a meta-analysis, while the PI incorporates both the uncertainties in the combined effect and the potential heterogeneity between the new study and the existing studies. Depending on the extents of heterogeneity, the PI is generally wider than the corresponding CI; when no heterogeneity exists, the PI is identical to the CI. Although some meta-analysis applications have begun to embrace the merits of PIs (e.g., by presenting both CIs and PIs in forest plots),¹⁴ the majority of contemporary meta-analyses still appraise heterogeneity based solely on I² and seldom report PIs.

This article empirically examines how PIs might differ from CIs in meta-analyses. We use a comprehensive collection of meta-analyses published in the Cochrane Database of Systematic Reviews (CDSR). The findings further illustrate the importance of reporting PIs in meta-analysis practice.

Methods

The CDSR provides reviews on various healthcare-related topics. It publishes issues monthly, which include reviews on new topics with formal analyses and protocols without formal analyses; it also withdraws reviews and protocols that are outdated or flawed. We searched for all reviews published from 2003 Issue 1 to 2020 Issue 1. Our study included all published reviews with statistical data in each issue and excluded all withdrawn reviews. Each Cochrane review may contain multiple meta-analyses on different outcomes and/or intervention comparisons. For meta-analyses with binary outcomes, we excluded studies with zero event counts in both intervention and control groups. We also restricted the meta-analyses to be those with at least 3 studies, because the calculation of PIs may have technical difficulty for meta-analyses with only 2 studies.

We used the restricted maximum likelihood (REML) estimation to perform the random-effects model for each selected meta-analysis. The 95% PI was calculated based on the t-distribution with k − 2 degrees of freedom as suggested by Higgins et al.,¹⁰ where k represents the number of studies in the meta-analysis. The t-distribution was used to adjust for the uncertainties in the estimated between-study variance. To be consistent with the calculation of PI, we obtained the 95% CI of each meta-analysis also based on the t-distribution.

We examined whether the CI and PI covered the null value in each meta-analysis. The CI and PI shared the same center, and the PI length was equal to or wider than the CI length. We calculated the ratio of the PI length over the CI length. If the CI covered the null, the PI must cover the null as well. If the CI did not cover the null, the PI could still cover the null, so the true effect of a future study could be in an opposite direction to the meta-analysis result; we were primarily interested in such cases. Moreover, we explored how such cases related to the number of studies and I² in a meta-analysis. All meta-analyses were performed using the R package “metafor.”¹⁵

Results

Table 1 presents the summary results. We obtained a total of 66,031 Cochrane meta-analyses with at least 3 studies. When implementing the REML estimation, computational issues occurred in 100 meta-analyses (e.g., failure of the convergence of the REML algorithm). The following results were based on the remaining 65,931 meta-analyses without computational issues. Among them, 18,549 (28.1%) meta-analyses had 95% CIs not covering the null value, indicating statistically significance, while only 10,097 (15.3%) had 95% PIs not covering the null. In other words, due to heterogeneity, 8,452 (12.8%) meta-analyses produced statistically significant overall estimates based on existing studies, but the true effects in future studies could be in opposite directions to these meta-results. Moreover, τ² was estimated as 0 in 22,862 (34.7%) meta-analyses, so their PIs were identical to CIs. The ratios of PI lengths over CI lengths were between 1.0 and 1.2 in 14,938 (22.7%) meta-analyses, while 10,484 (15.9%) meta-analyses had ratios over 3.0, indicating that their PIs were substantially wider than CIs.

Table 1.

Summary results of 95% confidence intervals (CIs) and 95% prediction intervals (PIs) among the 65,931 Cochrane meta-analyses.

Scenario	No. of meta-analyses (%)
Interval covering the null value or not
95% CI not covering the null	18,549 (28.1%)
95% CI covering the null	47,382 (71.9%)
95% PI not covering the null	10,097 (15.3%)
95% PI covering the null	55,834 (84.7%)
Future studies with true effects potentially in opposite directions to meta-results
95% CI not covering the null but 95% PI covering the null	8,452 (12.8%)
Ratio of PI length over CI length
1.0 (i.e., PI is identical to CI with no heterogeneity)	22,862 (34.7%)
1.0–1.2	14,938 (22.7%)
1.2–1.4	3,537 (5.4%)
1.4–1.6	2,882 (4.4%)
1.6–1.8	2,405 (3.6%)
1.8–2.0	2,037 (3.1%)
2.0–2.2	1,714 (2.6%)
2.2–2.4	1,514 (2.3%)
2.4–2.6	1,418 (2.2%)
2.6–2.8	1,137 (1.7%)
2.8–3.0	1,003 (1.5%)
>3.0	10,484 (15.9%)

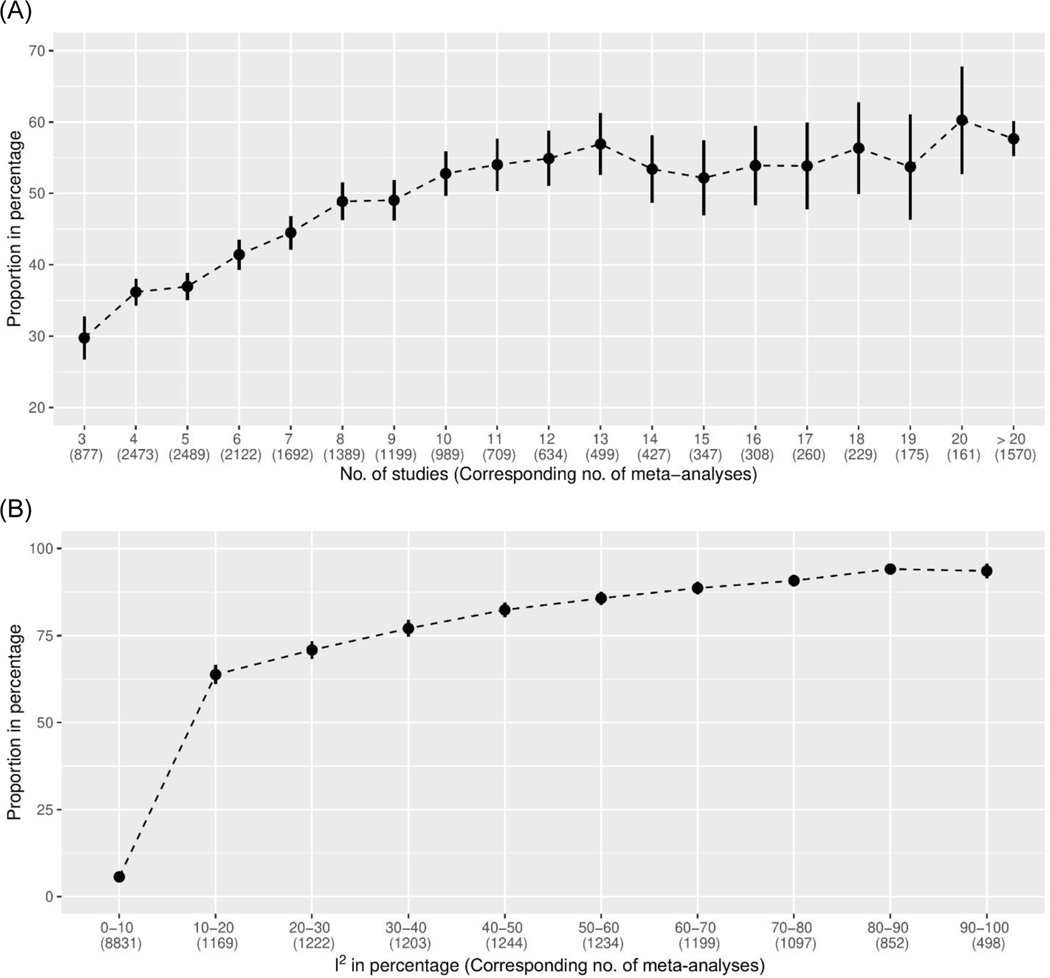
Figure 1 displays the proportions of meta-analyses with 95% CIs not covering the null value but 95% PIs covering the null, categorized by the number of studies and I². These proportions generally increased as the number of studies and I² increased; they sharply increased particularly for meta-analyses with less than 10 studies or relatively small I² values. When I²>30%, more than 75% of meta-analyses with statistically significant conclusions had 95% PIs covering the null. This phenomenon was expected because more substantial heterogeneity likely produced wider PIs. Meta-analyses with many studies were more likely to detect small effects, while they were also likely to detect heterogeneity, leading to substantial differences between their CIs and PIs.

Figure 1.

Proportions of the Cochrane meta-analyses with 95% confidence intervals not covering the null value but 95% prediction intervals covering the null, categorized by (A) the number of studies and (B) the I² statistic in a meta-analysis. The vertical bars represent the Wald-type 95% confidence intervals of the proportions.

Discussion

This study has investigated the CIs and PIs among a large collection of Cochrane meta-analyses. We illustrated that over 10% of meta-analyses could have statistically significant results but their PIs covered the null value, indicating that true effects in future studies could be potentially in opposite directions to the meta-results. We also showed that such cases more likely occurred in meta-analyses with many studies or large I² values. These findings implied that researchers should cautiously use the CI of the combined result in a meta-analysis to make clinical decisions for new patients. Although 95% PIs have been recommended to be reported along with meta-results and 95% CIs, many contemporary meta-analyses fail to comply with this recommendation. Such practice should be further promoted so that meta-results could be properly used to aid decision making in future studies.

Our study has several limitations. First, the PIs were derived based on the t-distribution under the frequentist framework. Although they accounted for uncertainties in the estimated between-study variance, they treated within-study variances as fixed, known values as in conventional meta-analysis methods. In certain cases (e.g., small sample sizes, rare events), this assumption may not be appropriate. More sophisticated models (e.g., Bayesian hierarchical models) may be preferred to produce PIs that represent full uncertainties, including those in within-study variance estimates.¹⁰ Second, our conclusions were based on the meta-analyses published in the CDSR. The number of studies was relatively small in most meta-analyses. Also, they were performed primarily to investigate healthcare interventions. Cautions are needed when our conclusions are used in other research fields.