Shape-morphing into 3D curved surfaces with nacre-like composite architectures

Abstract

Inhomogeneous in-plane deformation of soft materials or cutting and folding of inextensible flat sheets enables shape-morphing from two dimensional (2D) to three-dimensional (3D), while the resulting structures often have weakened mechanical strength. Shells like nacre are known for the superior fracture toughness due to the “brick and mortar” composite layers, enabling stress redistribution and crack stopping. Here, we report an optimal and universal cutting and stacking strategy that transforms composite plies into 3D doubly curved shapes with nacre-like architectures. The multilayered laminate exhibits staggered cut distributions, while the interlaminar shear mitigates the cut-induced mechanical weakness. The experimentally consolidated hemispherical shells exhibit, on average, 37 and 69% increases of compression peak forces, versus those with random cut distributions, when compressed in different directions. Our approach opens a previously unidentified paradigm for shape-conforming arbitrarily curved surfaces while achieving high mechanical performance.

2D composite plies are transformed into 3D curved surfaces with nacre-like architectures and superior mechanical performance.

INTRODUCTION

To realize shape-morphing and complex curvature conforming of flat sheets, two strategies have been commonly pursued. One is to introduce inhomogeneous in-plane strains in soft stretchable materials via approaches such as pneumatic inflation (1–5), swelling (6–9), application of electric fields (10, 11), and thermal activation (12, 13). The other exploits kirigami and origami strategies to program the Gaussian curvatures from inextensible flat sheets (14, 15). Both approaches, however, fail to produce 3D geometries that are both lightweight and mechanically strong as a result of the material’s intrinsic softness and/or geometric discontinuities.

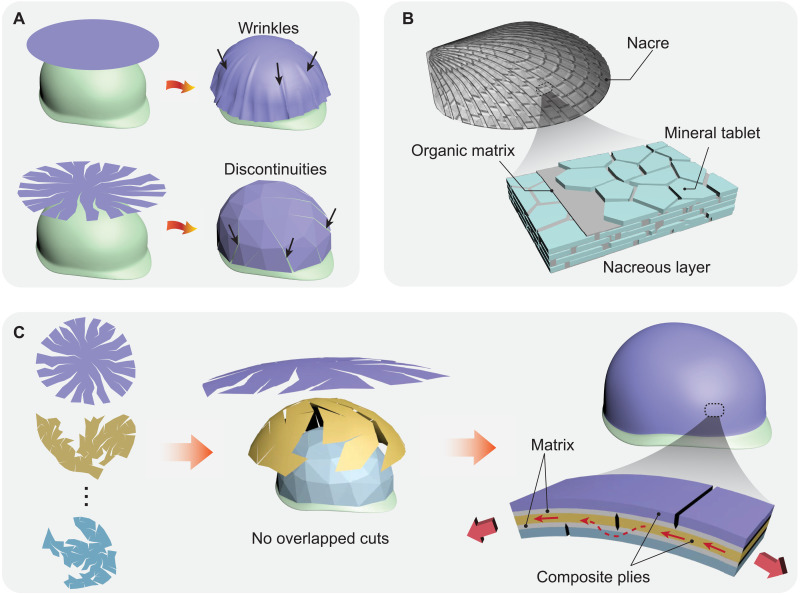
Laminated composites, which are constructed from preforms comprising layers of either high-performance fibers or minimally shear deformable films, have been extensively used in the aerospace and automotive industries (16, 17), sports products (18), and medical equipment (19), where the properties such as lightweight, high mechanical strength, and stiffness are essential. The technology for manufacturing these materials into flat and singly curved structures is well established (20). However, to achieve complex curved shapes, the inevitable local deformation in the anisotropic materials often results in shear failure, wrinkling and crumpling (see Fig. 1A), or substantial changes in local reinforcement architectures, all of which severely limit the mechanical performance of the resulting structures. Conventionally, flat plies are “cut and darted” to better conform to the desired shape. But this process has been highly empirical with little control of the layup architectures (21, 22). Thermoforming techniques have also been used to preform composite plies into the desired shapes before consolidation under heat compaction (23). This approach is restricted to shear deformable materials and will result in nonuniform thicknesses (due to shear deformation-induced local material thickening) and wrinkles in the resulting structures, where shear deformation alone is not sufficient for the material to conform to the final shape. Recent advancement in mechanical metamaterials provides new strategies, e.g., via kirigami, in programming curvatures by introducing perforated cuts into a planar sheet, enabling the deployment of nonperiodic tessellations to conform approximately to any prescribed 3D target shapes (15, 24–26). However, the small hinges and uncovered regions of these tessellations are detrimental to the mechanical properties of the entire structure. Alternatively, the computer graphics community segments a nondevelopable surface into developable polyhedral nets via algorithmically determined surface cuts (27–33), allowing for full coverage of the desired 3D surfaces without empty space. However, the cut-induced discontinuities compromise the mechanical strength of the resulting structure severely (Fig. 1A). Hence, there is an unmet demand to realize shape-morphing structures with high mechanical performance.

Fig. 1. Shape-morphing strategy inspired by the architecture of nacre.

(A) Wrapping a flat sheet around a curved surface results in wrinkles. Introducing cuts to the sheet can avoid the generation of wrinkles but induce discontinuities in the resulting structures. (B) Schematic of the nacre architectures, the staggered “brick-and-mortar” microstructures enable the nacre to exhibit extraordinary mechanical performance. (C) Optimization of the cuts in multilayered plies avoids cuts overlapping at the same position upon stacking. Upon application of a tensile stress, the composite plies carry the tensile load while the matrix transfer the load between plies via shear, ensuring the integrity and the optimized strength of the resulting structures.

Biological materials, such as bones and mollusk shells, are typically composed of limited components with plenty of flaws but exhibit extraordinary mechanical strength and toughness in comparison with their artificial counterparts due to the ordered hierarchical architectures and the abundant interfacial interactions (34–37). For instance, nacre comprising multiple mineral tablets bound by an organic matrix exhibits a generic microstructure consisting of staggered mineral bricks with minimum discontinuities overlapped at the same location (Fig. 1B). Here, we apply the same layering principle to composite thin sheets and develop a universal approach that allows for shape conforming of 2D composite plies to 3D curved laminates with surpassing mechanical properties.

For a given curved surface, we calculate multiple pathways to cut and unfold the discretized surface to a set of valid 2D nets without self-overlapping, all of which are optimized to minimize the number of overlapped cuts at the same position when the multilayered plies are stacked (Fig. 1C). After consolidation of the stacked and folded composite plies, load sharing among plies via interlaminar shear can mitigate the cut-induced weakness, providing additional strength to the 3D structures. That is, under an applied tensile stress, the composite plies carry the tensile load while the matrix transfers the load between plies via shear, ensuring the structural integrity and the optimized mechanical performance of the resulting shell-like 3D shapes.

Our approach is validated by quasi-static mechanical testing of 2D and 3D specimens with (or without) the optimized layups. The specimens with optimized layup show a notable improvement in mechanical performance in comparison to those without optimization, including more than 200% increase in the tensile strength for 2D specimens and, on average, 37 and 69% increases in the compression peak forces for hemispherical shells when compressed in different directions.

RESULTS

Unfolding and cutting pathway optimization

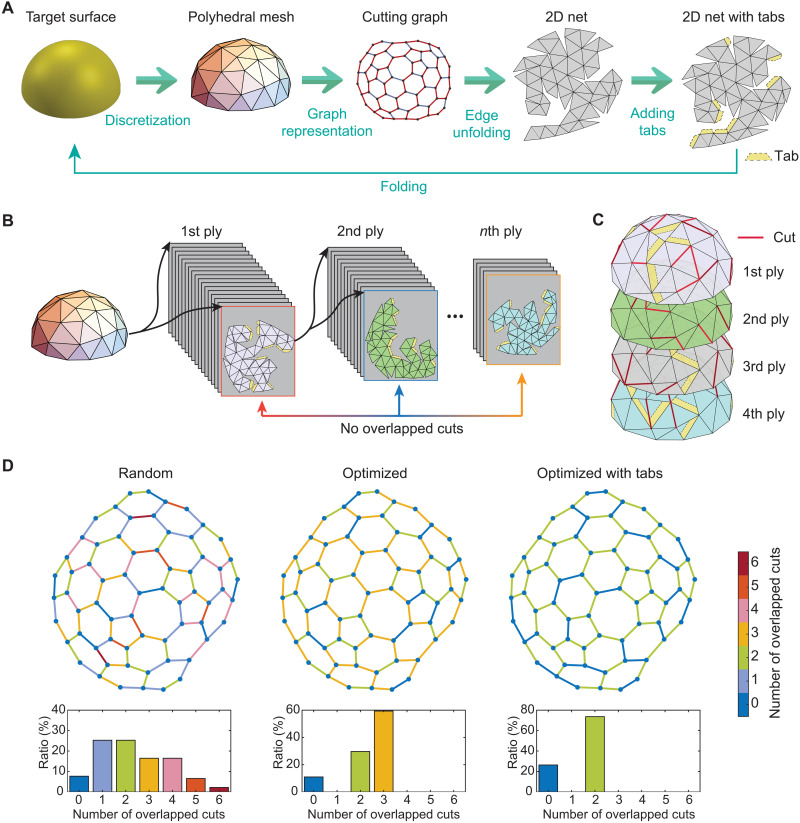
First, we unfold the curved surface to valid 2D nets without self-overlapping. For a given target surface such as a hemisphere, one of the simplest structures with nonzero curvatures, we approximate the smooth surface using a polyhedral mesh comprising triangular facets with appropriate dimensions (Fig. 2A). While discretizing the surface with finer facets results in better smoothness and conformability to the target surface, it also increases the computational expense for optimization and compromise the mechanical performance since more cuts have to be introduced. In our study, we use N ∈ [50,100] triangular facets to approximate the prescribed surface to obtain good conformability and high mechanical strength at reasonable computational cost. Then, we represent the polyhedral mesh using a cutting graph and use this graph to unfold the mesh to 2D nets by calculating its minimum spanning tree (MST) using the Prim’s algorithm (38). Since the cutting graph elucidates the connection of the facets for the polyhedral mesh (i.e., the vertices and lines of the cutting graph correspond to the facets and edges of the mesh, respectively), the partition pathway of the polyhedral mesh can be determined by the MST of the cutting graph. For instance, by assigning a set of weights to the edges of the cutting graph, we can obtain a specific MST to identify the cutting pathway, where the edges will be cut if they do not belong to the MST (see details of the unfolding procedure in section S3.2).

Fig. 2. Unfolding approach and optimization procedure of the multi-ply stacking.

(A) Schematic of unfolding a polyhedral mesh into a 2D net to conform a prescribed 3D curved surface. (B) Optimization procedure to avoid overlap of cuts at the same location. The cut edges of each ply are mutually exclusive from those of other plies by mutating the weights of the cutting graph. (C) Stacking of four optimized plies without cut overlapping. The existence of cuts is ignored where the tabs are introduced. (D) Comparison of the number of overlapped cuts from the random design and the optimized designs with and without tabs. The colors of lines in the cutting graph indicate different numbers of overlapped cuts. The bar charts illustrate the ratio of the number of overlapped cuts to the total number of edges n_edge in the mesh. Each design consists of eight plies.

However, the unfolded net is typically not a valid one since it contains multiple overlaps. To obtain a valid net without any overlap, we check whether any facet of the nets is intersected with each other (39). Moreover, to minimize the effect of cuts on the mechanical performance of the folded composite structure, we add tabs to the cut edges of the net if no new overlap is introduced by the tabs (see design of the tab in fig. S12). Hence, after the folded plies are consolidated, load transfer through the interlaminar shear stress between the additional tabs and the corresponding facets provides extra strength to the cut edges, which is known as the shear lag effect (40–43). Our experiments suggest that when the tab width is large enough (i.e., w_tab ≥ 15 mm, for the composite material considered here), the in-plane strength will not be compromised regardless of the presence of the cuts (see experimental validations in figs. S6 and S7).

To produce a 3D curved structure with high mechanical strength, multiple plies are typically stacked and consolidated (44, 45). However, wrapping several plies with the same geometry gives rise to repeated cuts at the same location, which severely reduces the strength of the resulting structure (Fig. 1A). To tackle this issue, we exploit load sharing by interlaminar shear among the consolidated plies and propose a universal optimization approach to guide the cutting pathway of each ply to minimize the number of overlapped cuts (Fig. 2B). Specifically, for a simple polyhedral mesh, we can find multiple cutting pathways producing valid 2D nets without self-overlapping. We randomly choose one from these nets as one of the optimized plies. For the next ply, we calculate the cutting pathway such that it is mutually exclusive on the cuts from the previous ply(ies) by mutating the weights of the cutting graph. We repeat this procedure until the maximum number of optimized plies n_max is achieved, where no cuts overlap at the same position (see details about the model in section S3.3). As a result, the edges of the polyhedral mesh (E_mesh) and the cut edges of the ith optimized ply (E_i) must satisfy the following constraints

$$E_1\cup E_2\cup \dots E_{n_{\text{max}}}\subseteq E_{\text{mesh}}$$ (1)

$$E_i\cap E_j=\mathrm{Ø},i,j=1,2,\dots ,n_{\text{max}} \text{and} i\ne j$$ (2)

The maximum number of optimized plies, n_max, is determined by the number of the edges of the polyhedral mesh n_edge and the number of cuts in each ply n_cut through

$$n_{\text{max}}=\lfloor n_{\text{edge}}/n_{\text{cut}}\rfloor$$ (3)

where the floor function ⌊x⌋ outputs the greatest integer less than or equal to x. For instance, the hemispherical mesh shown in Fig. 2B has 65 triangular facets, n_edge = 91 edges and 27 cycles in its cutting graph. To unfold the mesh to a 2D net, n_cut = 27 cuts are necessary. According to Eq. 3, the maximum number of optimized plies for this hemispherical mesh is n_max = 3. Namely, the optimized cuts will not repeat at the same position in a three-ply layup. For a structure comprising more than three plies, the optimized plies can be repeated until reaching the target thickness.

n_max can be increased when additional tabs are added to the cut edges to further mitigate the mechanical weakness induced by the cuts. Here, we assume that the cut can be ignored where a tab with large enough dimension is added. For the hemispherical mesh shown in Fig. 2B, the number of cuts (n_cut) can be reduced from 27 to between 17 and 23 for the design with tabs, and the specific number is determined by the geometry of the net, which affects the number of tabs that can be introduced to the net. Therefore, n_max = 4 can be achieved for the optimized design with tabs, resulting in the structure without cut overlapping at the same position in a four-ply layup. The optimized plies of the hemispherical mesh are demonstrated in Fig. 2C; the cuts and tabs are highlighted with red lines and yellow patches, respectively. We can observe that no cut overlaps at the same position among the four plies leading to the cuts homogeneously distributed in the entire structure (movie S1).

To quantify the effectiveness of our model, we compare the number of overlapped cuts at each edge of the hemispherical mesh for three different designs shown in Fig. 2D, including the random design, the optimized design, and the optimized design with tabs. Each design comprises eight plies. The bar charts in Fig. 2D illustrate the ratio of the number of overlapped cuts to the total number of edges n_edge in the mesh. In the case with random design, each ply is generated by assigning random weights to the cutting graph of the hemispherical mesh; up to six cuts are found overlapped at some edges. The maximum number of overlapped cuts is reduced to three for the optimized design. Since the optimized design with tabs repeats the cuts in every four plies, the maximum of cuts overlapped at the same position is reduced to two, clearly demonstrating the validity of our model on homogenizing the cut distribution in the shells.

Theoretical analysis and experimental validation

The principle of our approach is to optimize the cut distribution in a multi-ply stacked composite structure with minimum compromise on the mechanical performance while achieving shape-morphing to 3D curved structures. The mechanical strength of the laminated plies under various loading conditions is therefore crucial. However, it is challenging to characterize the effect of cut distribution on the in-plane properties of 3D curved structures directly. To validate the effectiveness of our approach for different structures, we develop a simplified model to investigate the impact of cut distribution on mechanical properties of the composite plies and fabricate both 2D and 3D specimens to characterize their mechanical responses under various loading conditions as the extreme loading conditions for practical applications are often unpredictable. Note that our algorithm is not used to optimize a specific mechanical property under a given loading condition; instead, it is a universal approach to design overall mechanically strong structures. By extending a biocomposite model proposed by Gao et al. (34, 46), we are able to capture the mechanical responses of composite plies with different layups. Both theoretical analysis and finite element simulations indicate that higher modulus and strength can be achieved when the cuts are more homogeneously distributed in the structures (see section S3.1 for additional details about the model).

Our experimental samples are fabricated from Tensylon HSBD30A (DuPont), a high modulus bidirectional laminate made from ultrahigh molecular weight polyethylene (UHMWPE) with two orthogonal layers of solid-state extruded films coated with adhesives (see details about the fabrication in section S1). Among the high-strength fiber-based materials, solid-state extruded films such as Tensylon have much higher in-plane shear stiffness and can only undergo a few degrees of in-plane shear before failure (47). Therefore, they cannot easily be thermoformed into a hemisphere without wrinkling or tearing.

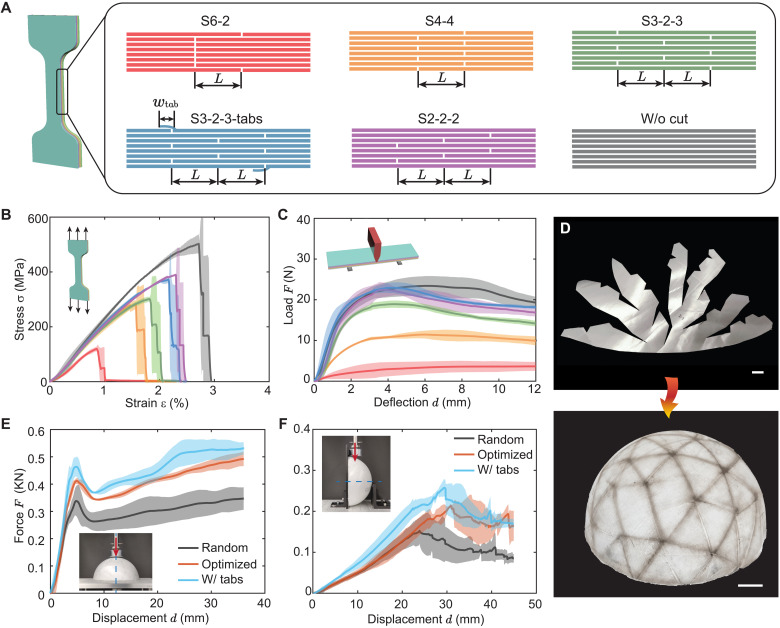
First, we conduct uniaxial tensile tests for dog bone specimens with different layups of cut (Fig. 3A). Each specimen consists of eight plies with a through-cut in each ply. By changing the position of the cuts in the plies, we can mutate the number of overlapped cuts at different positions. As seen in Fig. 3A, we design five sets of specimens. The first (denoted as S6-2) has six and two cuts overlapped at two positions with the distance of L = 25 mm between the cuts. Assuming that the 25-mm overlap is enough to recover the full strength of a single cut, we expect the tensile strength of this specimen is around a quarter of the specimen without any cuts, since the weakest position of the specimen has only two plies connected among the eight plies. To enhance the strength of the specimens, we evenly distribute the cuts between the two positions, obtaining the S4-4 specimen, which redistributes the in-plane load across each cut with 25-mm overlap between the adjacent plies and is expected to have half the tensile strength of the specimens without any cuts. Similarly, if the cuts are arranged at three positions, the resulting specimen (S3-2-3) is expected to have up to $\frac{5}{8}$ of the tensile strength of the pristine specimen without any cuts. We can further increase the strength of the specimens by introducing tabs (see S3-2-3-tabs specimen in Fig. 3A). After consolidation, the shear forces between the tabs and the adjacent plies can provide additional strength to the specimens. To evaluate the effect of the tabs on the mechanical properties of the specimens, we compare the S3-2-3-tabs specimen, which has a tab on the top ply and at the bottom ply, respectively, with the S2-2-2 specimen, which has only two cuts at each position and no cut in the top and bottom plies. When the width of the tabs is large enough, the S3-2-3-tabs and S2-2-2 samples should have similar tensile strength. The specimen without cuts is tested as a reference.

Fig. 3. Experimental validations for 2D and 3D structures with different layups.

(A) 2D specimens of different cut distributions. Each specimen consists of eight plies with varying cut positions. S6-2 denotes six and two cuts overlapped at two positions. The same notion applies to others, and the distance between cuts is L = 25 mm. (B) Experimental stress-strain curves for the dog bone specimens under uniaxial tensile tests and (C) load-deflection curves for the rectangular specimens under three-point bend tests. The color of each line corresponds to that shown in (A). (D) Experimental snapshots of a cut ply and a consolidated hemisphere with the optimized layup fabricated from Tensylon HSBD30A. Scale bars, 20 mm. (E and F) Force-displacement curves of the hemispherical samples with different layups when compressed (E) along the axial direction and (F) perpendicularly to the axial direction of the shells. Shaded areas indicate the SD of the measurements.

In Fig. 3B, the stress-strain curves of the dog bone specimens under uniaxial tensile loading is in full agreement with our assumptions, that is, the S6-2 specimens have the smallest mean strength (average strength of three specimens) with σ₆₋₂ = 119 MPa, a 76% reduction in strength compared with the specimens without a cut (σ_{w/o cut} = 503 MPa). As expected, S4-4 and S3-2-3, the specimens with more homogenized cut distributions (where cuts are not at the same location in consecutive plies) have a higher strength than the S6-2 specimens (which have cuts at the same location in six consecutive plies), exhibiting σ₄₋₄ = 281 MPa and σ₃₋₂₋₃ = 302 MPa. The strength of the specimens with tabs (σ_{3−2−3−tabs} = 372 MPa, with w_tab = 15 mm) is substantially enhanced relative to that without tabs and similar to the strength of the specimens that have no cuts in the top and bottom plies (σ₂₋₂₋₂ = 390 MPa), validating the effectiveness of tabs in our optimization model. To characterize the cut distribution on bending properties of the specimens, we then compare the load-deflection curves of the three-point bending tests for rectangular samples sharing the same cut distribution with the dog bone samples in Fig. 3C. A trend similar to that observed in the tensile tests is also seen in the bending behavior, that is, both (i) homogenizing the cut distribution and (ii) adding the tabs can enhance the mechanical strength of the structures, indicating that our optimization approach is valid for different types of loads. More details about the experimental tests can be found in section S2.

We now move to validate the optimized hemispherical structures. Three types of hemispherical specimens with different layups (i.e., the random design and the optimized design with and without tabs) are manufactured on the basis of our model. Figure 3D presents the experimental snapshots of a single cut ply and a processed hemisphere with the optimized layup, showing seamlessly conformal coverage of the multistacked plies to the entire hemisphere. It is noted that there are no wrinkles in the hemisphere, confirming that the triangular facet size selected in our experiments is appropriate. Then, we conduct the compression tests (with load applied along the axial direction of the hemisphere) and report the resultant forces as a function of the applied displacement in Fig. 3E. All curves show a linear regime followed by a load drop before further stiffening, and the average peak force of three optimized specimens F_optimized∥ is remarkably larger than that of the random cut designs, characterized by F_optimized∥ = 1.22F_random∥. The optimized specimens with tabs show an even larger peak force with F_tabs∥ = 1.37F_random∥. Clearly, including tabs in our model improves the mechanical strength of the resulting structures. To validate that our optimized designs are superior to the random designs under various loading conditions, we also compress the shells along the direction that is perpendicular to the central line of the shells and report the force-displacement curves in Fig. 3F. Despite different loading conditions, the optimized designs show better performance than the randomly designed structures, characterized by F_optimized⊥ = 1.40F_random⊥ and F_tabs⊥ = 1.69F_random⊥. Note that our algorithm can produce more than one optimized design for a given target surface, but the variation of mechanical properties for different optimized structures is negligible considering the substantial improvement of the mechanical performance resulted from the optimized designs versus that from the randomly designed structures (see validations in fig. S9). Moreover, to ensure that the results are representative for comparison, all random designs tested in our experiments are different to avoid the cases that only those with very weak mechanical performance are selected.

Generality of our model

Armed with the confidence of our optimized model in conforming hemispherical shell structures using nonshear deformable laminated plies, we extend our model to various curved surfaces to demonstrate its universality. For a convex surface with only positive Gaussian curvature, we can optimize the cutting pathways to unfold such surface into a couple of 2D nets in a single patch, which, when folded to the prescribed 3D surfaces, have minimal overlapped cuts at the same position (e.g., the hemisphere in Fig. 2, the semi-ellipsoid in fig. S14, and the helmet in fig. S15).

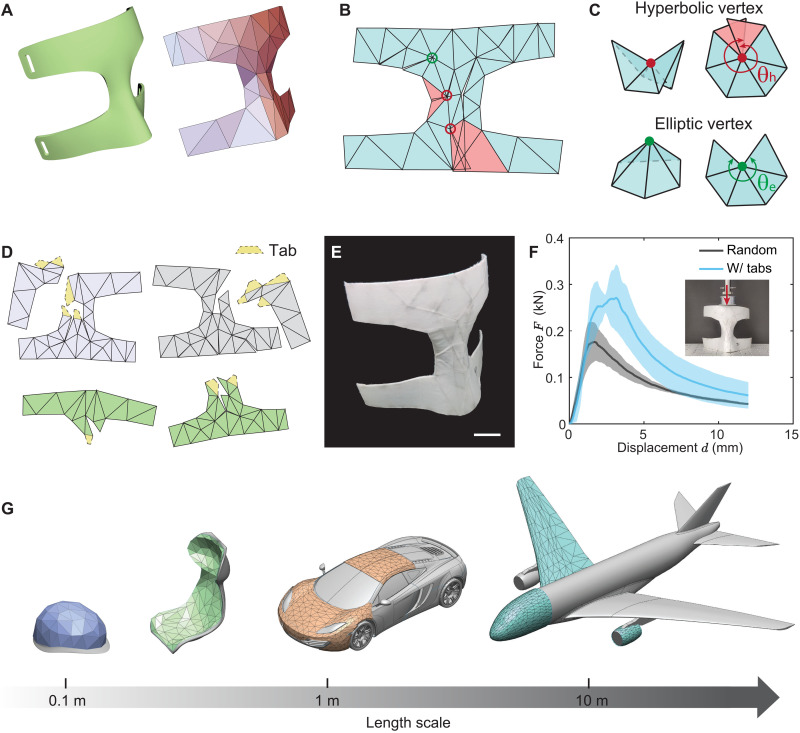
However, there are many examples of nonconvex polyhedral meshes that do not have a valid unfolding within a single patch, owing to the existence of negative Gaussian curvatures. For example, a face guard, where lightweight and high strength are essential to protecting the face from full-contact impact, has both positive and negative Gaussian curvatures (Fig. 4A). Unfolding this kind of surfaces typically results in 2D nets with local self-overlaps (see the red facets shown in Fig. 4B). This is because the surfaces with negative Gaussian curvatures contain hyperbolic vertices, and the sum of the adjacent facets’ angles for each hyperbolic vertex θ_h is larger than 2π. Therefore, at least two cuts have to be introduced for the hyperbolic vertex to avoid local overlaps, whereas for the elliptic vertex, one cut is enough to avoid local overlaps as θ_e < 2π (Fig. 4C).

Fig. 4. Generality of our model to nonconvex surfaces.

(A) A face guard with both positive and negative Gaussian curvatures. (B) Overlap cannot be avoided in a single patch of the unfolded net due to the existence of hyperbolic vertices. (C) Unfolding for the hyperbolic vertex leads to θ_h > 2π and a self-overlapped net, while unfolding for the ellipsoidal vertex results in θ_e < 2π and an overlap-free net. (D) Optimized plies for the faceguard with each ply comprising two patches. (E) Experimental snapshot of the consolidated face guard fabricated from Tensylon HSBD30A. Scale bar, 20 mm. (F) Experimental force-displacement curves for face guards with random design and optimized design with tabs. Shaded areas indicate the SD of the measurements. (G) Potential applications of our model in structures with different length scales, ranging from helmets and auto racing seats to automobiles and airplanes.

Although a few algorithms have been developed to unfold nonconvex polyhedral meshes into a single patch (29, 39) without consideration of their mechanical performance, and such algorithms can be easily integrated into our model, the constraint to minimize cut overlaps hinders us from finding valid nets in a single patch for nonconvex surfaces. To enhance the capability and efficiency of our model on handling 3D shapes with arbitrary curvatures, we introduce additional cuts for the nonconvex surfaces to avoid self-overlaps induced by the hyperbolic vertices. We note that the additional cuts will segment the 2D net into several patches, weakening the final 3D shape. To mitigate this, we minimize the number of additional cuts by using the greedy algorithm (30) and add tabs to the additional cuts (see details about the model in section S3.3). Accordingly, an optimized design for a nearly arbitrary curved structure can be realized. For the face guard shown in Fig. 4A, it yields three optimized plies with each ply comprising two patches (Fig. 4D) and without overlapped cuts. Figure 4E is a photograph of an experimentally realized face guard after folding and consolidation of 12 Tensylon HSBD30A plies, nearly perfectly representing the design seen in Fig. 4A. To further demonstrate the validity of our model for arbitrary surfaces, we conduct compression tests of the face guards with different layups and compare their force-displacement curves in Fig. 4F. The results clearly reveal that the optimized designs have much better mechanical performance than the random designs, and the average peak force of three optimized specimens with tabs is around 59% larger than that of the random designs. Moreover, our geometric approach does not contain any size variable; therefore, it is scale invariant and can be readily applied to 3D structures with different length scales, ranging from helmets and auto racing seats to automobiles and airplanes (Fig. 4G), showing great potentials in shape-morphing structures that demand high mechanical performance (see the suggested fabrication procedure for potential industrial applications in fig. S5).

DISCUSSION

We have presented a universal algorithm to morph flat composite plies toward prescribed 3D curved surfaces with optimal layup architectures. By minimizing the number of overlapped cuts at the same position and introducing additional tabs at applicable edges, we create nacre-like thin shell architecture, where the cuts are homogeneously distributed in the multi-ply stacked structures for stress redistribution and fracture stopping, enabling not only 3D curved surfaces but also high mechanical performance under various loading conditions. Our algorithm is distinguished from conventional optimization approaches as we do not have specific loads or boundary conditions in our optimization. Our goal is to achieve high strength for various loading scenarios, which is beneficial for the unpredictable conditions of practical applications.

Through 2D and 3D mechanical testing under different loading conditions, we have demonstrated the validity of our approach on improving the mechanical performance while achieving shape-morphing from 2D to 3D. Our model is universal to structures of nearly arbitrary curvatures and can accommodate all the existing algorithms for unfolding polyhedral meshes. While the results demonstrated in this work are based on a single mesh, our algorithm holds the potential to use the designs based on different meshes in future studies. For instance, one can approximate the target surface using the combination of two different meshes whose edges are mutually orthogonal with each other. By stacking the optimized designs from these meshes, the number of plies without overlapped cut can be further increased (fig. S17). However, it should be noted that the orientation of each composite ply (with orthotropic mechanical properties) has not been optimized in our model, since the cut distribution is more dominant on the mechanical performance than the orientation of the orthotropic plies. Hence, the algorithms proposed in this work have great potentials in guiding the designs of diverse composite structures with curved geometries, where lightweight and high mechanical performance are desired. It opens up a new paradigm for the design of next-generation, sustainable composite structures whose shapes can be preserved with minimal compromise on mechanical strength and stiffness while wasting less materials.

MATERIALS AND METHODS

Sample fabrications

All structures investigated in this study were fabricated from Tensylon HSBD30A plies (DuPont) with thickness t = 155 μm. The Tensylon ply is composed of cross-plied (0/90) solid-state extruded UHMWPE films with a polyolefin adhesive on one side of the film. To fabricate the 2D specimens, we first cut the plies with embedded slit patterns using a cutting table (Gerber Technology). Then, the stacked plies were consolidated in a press (Wabash 800 Ton) with a normal pressure of 20.7 MPa and a temperature of 110°C. Last, the samples were cut out of the manufactured panels using a waterjet. To fabricate 3D structures with desired shapes, we cut plies with the optimized geometries using a laser cutter (Universal Laser PLS 4.75) and stacked the cut plies into a 3D mold of the target shape. Then, we wrapped release films around the mold and the stacked plies and transferred them to a vacuum bag. The bag was vacuumed and the plies were consolidated in an autoclave under pressure of 1.38 MPa at 110°C. Last, the consolidated structure can be removed from the mold.

Experimental characterizations

All mechanical testing was performed using a universal testing machine (5564, Instron Inc., USA) equipped with a 2000-N load cell for the tensile and compression tests and with a 100-N load cell for the three-point bending tests. The tests were performed under displacement control at a rate of 0.05 mm/s for the tensile tests and 0.2 mm/s for compression and bending tests, respectively.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S17

Tables S1 to S3

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S6