Abstract
Many individuals fail to engage in sufficient physical activity (PA), despite its well-known health benefits. This paper examines Model Predictive Control (MPC) as a means to deliver optimized, personalized behavioral interventions to improve PA, as reflected by the number of steps walked per day. Using a health behavior fluid analogy model representing Social Cognitive Theory, a series of diverse strategies are evaluated in simulated scenarios that provide insights into the most effective means for implementing MPC in PA behavioral interventions. The interplay of measurement, information, and decision is explored, with the results illustrating MPC’s potential to deliver feasible, personalized, and user-friendly behavioral interventions, even under circumstances involving limited measurements. Our analysis demonstrates the effectiveness of sensibly formulated constrained MPC controllers for optimizing PA interventions, which is a preliminary though essential step to experimental evaluation of constrained MPC control strategies under real-life conditions.
I. Introduction
The benefits of physical activity to personal health, and to public health in general, are enormous. It has been established that an increase in walking from 4,000 to 8,000 steps/day reduces the risk for all-cause mortality by 51% for adults; this includes reduced risk of cancer and heart disease [1]. The prevalence of this healthy behavior in the general population is low; approximately 53% of adults in the US are sedentary [2]. Much work has been done over the years to understand best methods for behavioral interventions. To date, the implementation of large-scale effective behavioral interventions has proven to be very difficult; nonetheless there is hope for affordable real-world interventions that can improve public health. Based on recent advances in technology and the availability of PA data through smartphones and other devices, control systems engineering (CSE) has been proposed as a tool to deliver optimal mobile health (mHealth) interventions on a large scale [3], [4]; the work done in [5], [6] shows significant potential. Because of the importance of dynamic modeling to CSE, it is essential to choose an appropriate health behavior theory, and apply the proper dynamical systems framework to attain a meaningful control-oriented model.
Behavioral theories provide guidance regarding the driving forces behind behavior, and the interconnections between behavior and its influences. Such theories explain behavior through various psychological constructs, which in principle are similar to latent variables utilized in the chemical processing industry [7]. A particular variable might not be directly measured, yet its dynamics can be inferred through interrelations with measurable components. Social Cognitive Theory (SCT) has been regarded as one of the most influential theories and been incorporated in various health behavior interventions [8], [9], and is considered in this work.
MPC has been widely adopted in the chemical processes industries (and beyond) due to its versatility, simplicity, and ability to incorporate constraints [10], [11]. MPC applies a receding horizon strategy where a system model is used to predict the effect of future changes in manipulated variables on system states and outputs over a prediction horizon p. Future actions in the manipulated variables (Δu(k)) are obtained by solving the optimization problem shown in (1), over a move horizon m, subject to specified constraints. Then, only the first move is applied and the computations are repeated at each sampling instant utilizing measurements from the current state of the process [11]:
| (1) |
ur represents setpoint targets for manipulated variables. ΓY, Γu and ΓΔu represent controlled variable, manipulated variable, and move suppression weight matrices, respectively. ΓY, Γu, ΓΔu, p and m are adjustable controller parameters. MPC enables the enforcement of constraints on controlled (y), manipulated (u), and move-size (Δu) variables:
| (2) |
| (3) |
| (4) |
In the unconstrained case, the optimization problem per (1) reduces to a linear system of equations (Ax = b), which has a closed-form solution. On the other hand, when constraints are enforced, the optimization problem denoted by (1)-(4) is a quadratic objective with linear inequality constraints, which constitutes a readily solvable Quadratic Programming (QP) problem [11].
In prior work, hybrid model predictive control (HMPC) was proposed as a means for implementing PA behavioral interventions [12]. In [12], behavior (as measured by steps/day) was the sole output of importance, while the manipulated variables were restricted to a series of predetermined discrete values. In this work, a hybrid formulation is abandoned with an emphasis on exploring diverse constraint enforcement strategies to examine if these result in desired intervention outcomes. Through judicious problem formulation and constraint enforcement, the controller can be guided towards making user-friendly decisions that will maximize intervention benefits while reducing the risk of reduced participant engagement and drop outs. Furthermore, in this paper we examine MPC strategies on an enhanced SCT model description that considers the possibility of dual, competing behavioral outcomes (such as fitness and fatigue). Both the modeling of this phenomena and the suitability of MPC-based strategies under these conditions is examined.
All of the results discussed in the paper impact the design of the YourMove intervention, which is being developed by our research team as part of the activities of NIH grant R01CA244777 [13]. The paper is organized as follows: Section II describes the simulation model and intervention design, Section III presents and discusses simulation results for the various formulations, while Section IV ends with conclusions and implications for future work.
II. Simulation Model & Intervention Design
A. Social Cognitive Theory (SCT)
SCT describes the reciprocal influence between behavior, personal (cognition, confidence, and biology) and environmental factors [14], [15]. As a consequence, behavior interacts with these factors in recycle loops allowing the possibility of predicting the ability of an individual to engage in determined behavior based on endogenous and exogenous parameters. Some of the constructs are self-perceived and relative, while others can be directly measured [5], [9]. The work done in [5] proposes a fluid analogy based on the main constructs of SCT and their connections. In this paper, only the subsystem involving behavior (η4), self-efficacy (η3), and behavioral outcomes (η5) is considered, as seen in Figure 1. This subsystem consists of Operant Learning (OL) and Self-Efficacy (SE) loops [16], which is collectively referred to as OLSE system in this paper.
Fig. 1:
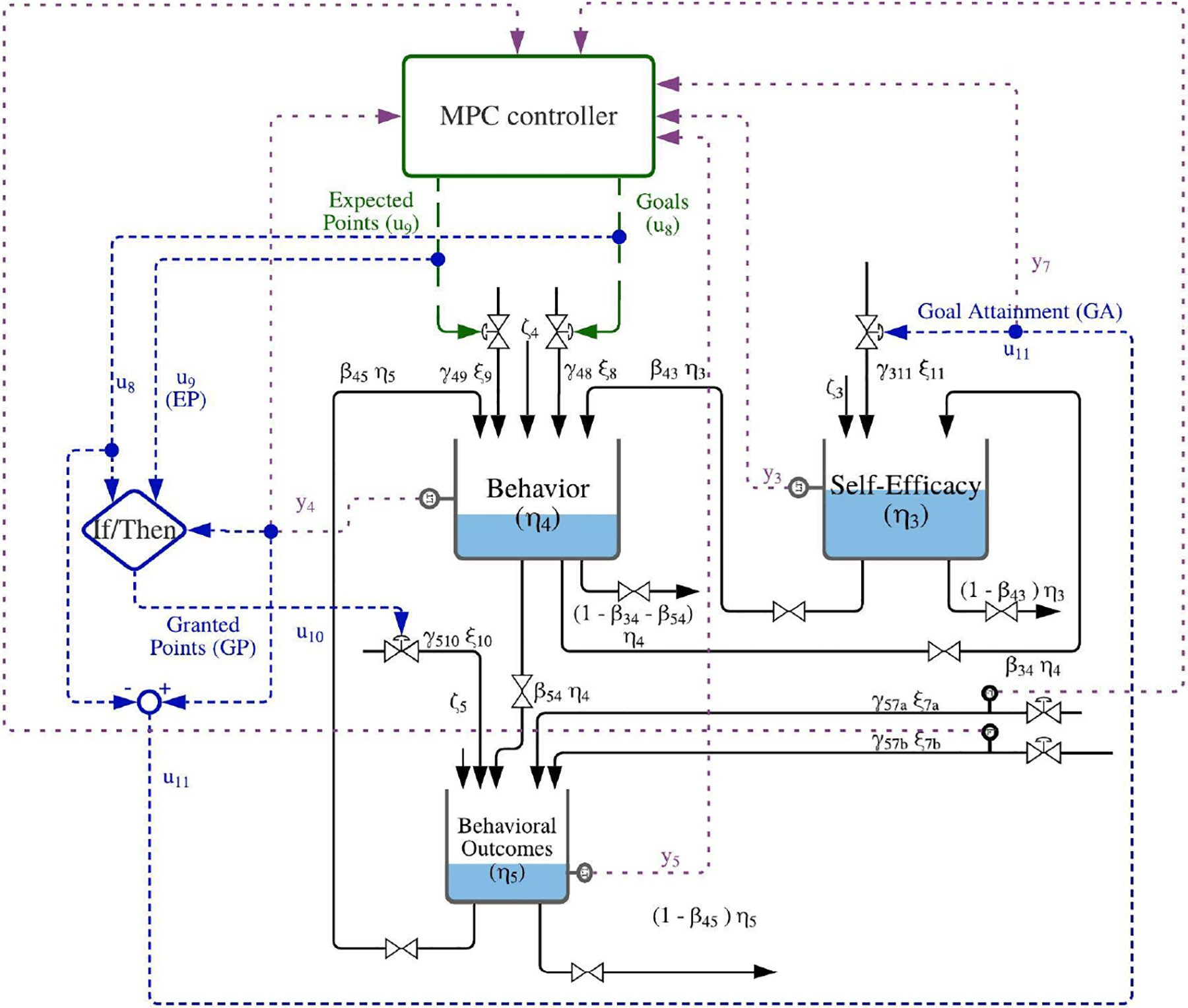
Schematic illustrating the fluid analogy of the SCT model for an Operant Learning-Self-Efficacy (OLSE) system in an intervention setting including the implementation of MPC controller. Adapted from [5], [9], [17]
B. Fluid Analogy Formulation for SCT
Fluid analogies are used to relate SCT components to each other over time. In the fluid analogy main constructs are modeled as tanks (inventories), while exogenous components are treated as inflows/outflows of the system. This provides a structure and framework to readily obtain mathematical formulas from SCT following chemical engineering principles such as mass conservation [3], [5]. By applying conservation of mass to each inventory, a system of ODEs is obtained to represent the schematic shown in Figure 1.
| (5) |
| (6) |
| (7) |
τi represents the time constant for inventory i, γij represents the gain between inventory i and the inflow/outflow j, βiz represents the gain in inventory i for changes in inventory z, and ζi represents unmeasured disturbances, where i, j, z are integers. To assure abiding by conservation of mass:
| (8) |
The primary inventory for the intervention is behavior (η4) for the daily step-count. This construct can represent different characteristics (e.g. duration, frequency, and type) and their fluctuations over time [5], [9]. The time frame used in this study is on a daily level, however, similar frameworks can be applied on a different temporal granularity (e.g. weekly level) based on the behavior of interest. Self-efficacy (SE; η3) is a core component of SCT, and represents the perceived capability of the individual to engage in behavior. Fluctuations in SE depend on other main constructs in the SCT model (like behavior) and other inflows/outflows. Another important construct in SCT is behavioral outcomes (BO; η5), which represents physical and psychological consequences (like fatigue and positive reinforcement) of engaging in a particular behavior. Some of the external factors that can influence behavioral outcomes include environmental context and the presence of financial or psychological incentives.
C. Intervention Design & Development
In an intervention setting like the one being developed in YourMove, individualized goal targets are given to participants on a daily basis [13], [18]. Those who achieve their daily goals earn points that can be transferred to various rewards chosen as part of a wellness program (e.g., water bottles, gift cards, etc). The number of expected points for each day and the daily step target are delivered through a digital user platform, such as a smartphone. To utilize the SCT model in the intervention the following input signals are included:
Goals (ξ8; u8): These represent the daily step target and directly influence behavior.
Expected Points (EP; ξ9; u9): The amount of points a participant expects to get, should they meet the daily target. A maximum of 500 points/day can be earned.
Granted Points (GP; ξ10): The amount of granted points, which is equivalent to ξ9 when a participant achieves the daily step goal.
Goal Attainment (GA; y7; ξ11): This signal represents the difference between the behavior and given goal.
| (9) |
Goals and EP are independent signals, whereas GP and GA depend on meeting the daily goal. It is important to note that GA can act both as an inflow (when behavior exceeds the given goal) and as an outflow (when the goal is not met); this significantly impacts SE. Due to the importance of GA, it is considered as a measurable system output. Environmental context (ξ7) represents environmental factors that can affect behavior. In the context of this work, outside temperature is considered as a stochastic disturbance that can impact behavior, for example by deviating from the participant’s ideal temperature to exercise.
MATLAB and Simulink are used to implement the simplified SCT model and MPC controller depicted in Figure 1. A state-space representation of the system shown in equations (5) – (7) and (9) is utilized to design the controller. All examined scenarios utilize the following parameters:
τ3 = 1, τ4 = 2, τ5 = 5.
γ311 = 1.3, γ48 = 1, γ49 = 0.3, γ57 = 4, γ510 = 5.
β34 = 0.5, β43 = 0.2, β45 = 0.2, β54 = 0.4.
The intent of the simulations in this work is to explore different MPC strategies, starting with the simplest unconstrained case on the SE loop as the system. Subsequent decisions like more sufficient problem specifications and constraint boundaries are made based on expert (behavioral scientists) judgement of the feasibility and likely limitations of the obtained responses in each scenario. Based on the experts feedback, the complexity of the system is increased and the control strategy and tuning are adjusted to reach responses that capture real-life behavior in four scenarios.
III. Results and Discussion
The results of four different scenarios are presented and discussed; these are: 1) SE loop unconstrained, 2) SE loop with constraints on SE, 3) SE loop with constraints on GA, and 4) a dual competing dynamics behavioral outcomes OLSE system with constraints on GA and stochastic disturbances. The baseline for all simulations assumes an initial goal level ξ8initial = 1, 000 steps/day. While this value may seem somewhat low, it provides insights into the performance of the control strategies at extreme initial conditions. The desired outcome of the simulated intervention is to achieve a sustained level of 10,000 steps/day for the behavior of the participants. All shown results are in terms of deviation from steady-state. The findings of each of the cases are discussed, along with their implications on future work.
A. Self-Efficacy (SE) loop: Unconstrained Case
This first case illustrates the issues resulting from an insufficient problem specification: no constraints are enforced, only behavior serves as a controlled variable (ΓY = diag(0, 1, 0)), and there is no target tracking for manipulated variables (Γu = 0). This leads to the large moves in the manipulated variables, seen in Figure 2; such moves imply setting very high goals which would not be met immediately, consequently yielding a large negative GA at the beginning of the intervention. This results in a significant drop in SE, while behavior increases rapidly to meet the given goals after day 5. This scenario demonstrates a short and very ambitious intervention which may not be a very successful way of adopting and maintaining a healthy behavior, as it is too demanding on participants. The sudden large decrease in SE can lead to participants dropping out of the intervention [18]. It is also seen that the EP signal required is very large, which suggests that this intervention may be impractical; it relies heavily on financial rewards to engage participants in PA, and exceeds the maximum amount of allowed daily points.
Fig. 2:
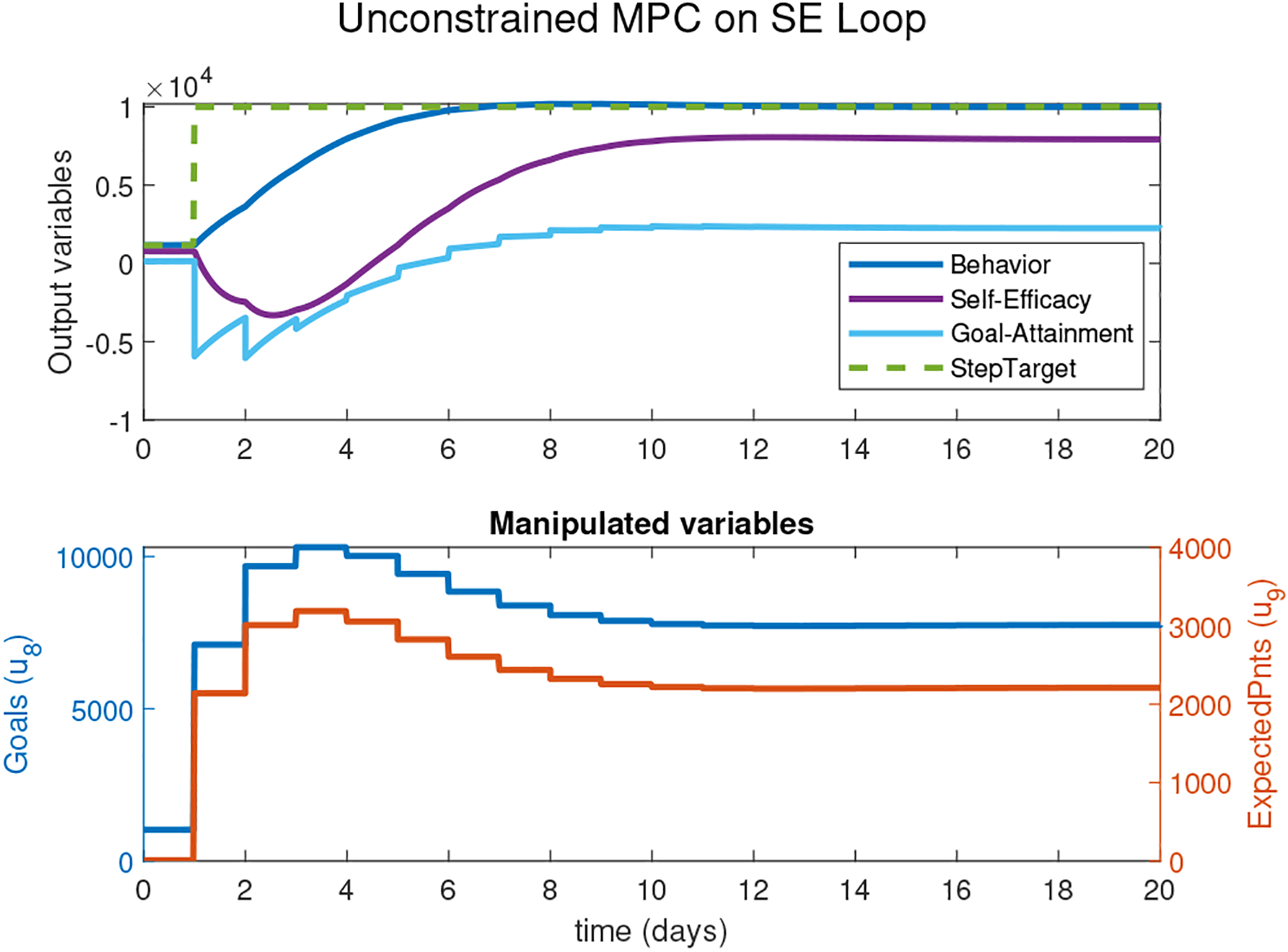
Simulation results from applying an unconstrained MPC controller on the Self-Efficacy loop. The controller parameters are: p = 100, m = 50, ΓY = diag(0, 1, 0), Γu = 0, ΓΔu = diag(1, 1).
This scenario illustrates the need for imposing sensible constraints during interventions. There are physical limitations to the manipulated variables involved: a participant can only walk a finite number of steps within a day, and there are financial limitations to EP. Such limitations are akin to the limitations in opening a valve, which can be addressed through constraints as seen in subsequent scenarios.
B. Self-Efficacy (SE) loop: Constrained Self-Efficacy
To take into account the physical and financial limitations of the system, constraints on the manipulated variables, as seen in (10), are applied to all presented constrained cases.
| (10) |
The SE output also is constrained to assure that its level does not get too low, where
| (11) |
The results seen in Figure 3 paint a very interesting picture. The intervention in this constrained case reaches steady-state in twice the time, taking close to 11 days for the response to settle. This is due to constraint enforcement, where optimal moves in the manipulated variables are obtained as a result of the QP problem; initial moves in the manipulated variables are significantly lower than the unconstrained case. Although EP is changed abruptly by the controller, the constraint is not violated and the EP signal is phased off by the end of the intervention.
Fig. 3:
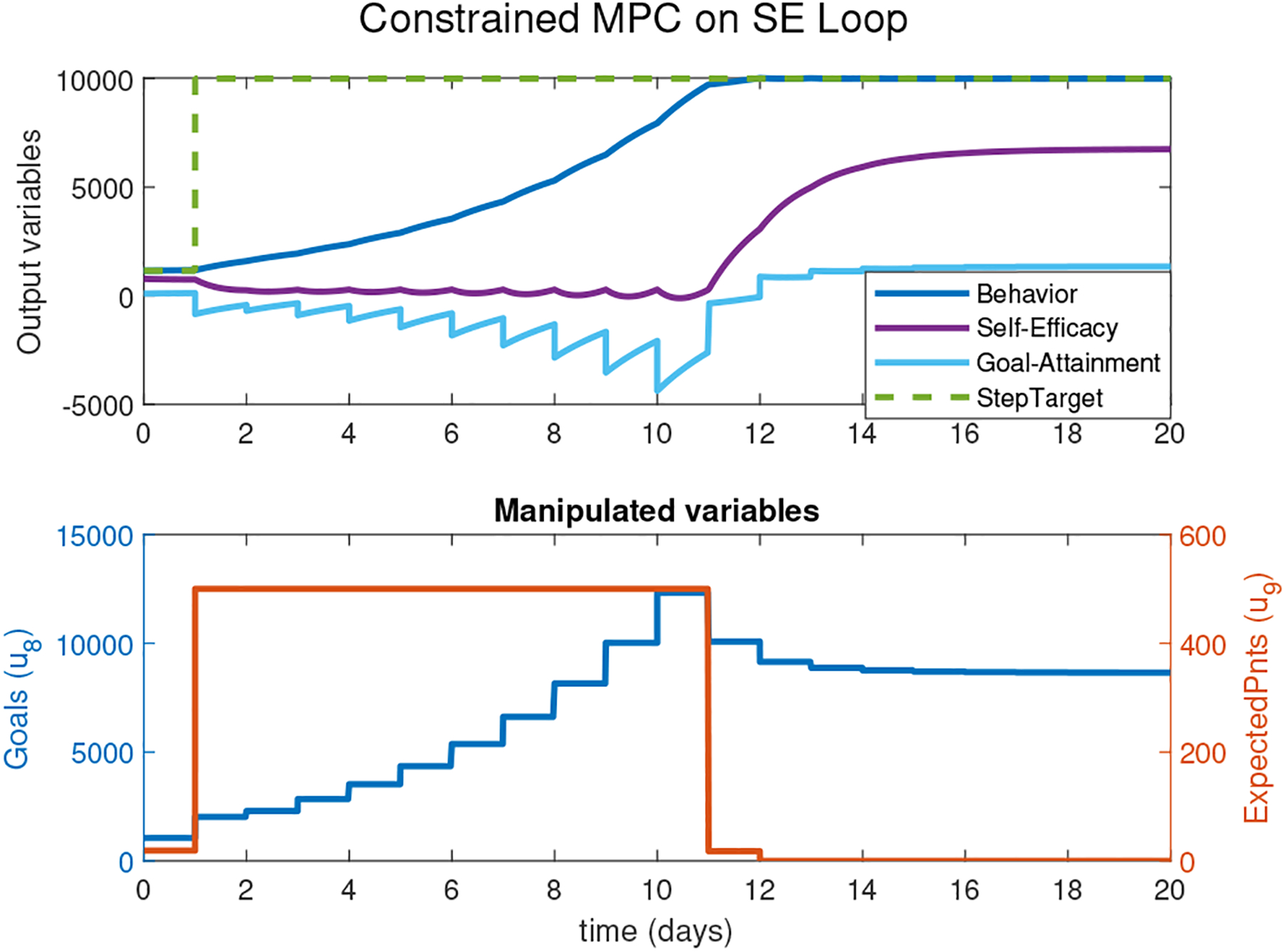
Simulation results from applying a constrained MPC controller on the Self-Efficacy loop, with a lower level constraint on the self-efficacy. The controller parameters are: p = 100, m = 50, ΓY = diag(0, 1, 0), Γu = 0, and ΓΔu = diag(0.1, 0.1).
Despite improved controller performance, this case demonstrates yet another “ambitious” intervention. This is evident in the initially negative GA values, which progressively decrease until the behavior response reaches the settling time. The observed GA dynamic response shows the shortcomings of this intervention, as participants are most likely to drop out if they do not achieve their given daily goals for long periods of time.
C. Self-Efficacy (SE) loop: Constrained Goal Attainment
The self-efficacy is a behavioral construct perceived by the participant, and cannot be easily measured. In cases of unreliable SE measurement methods, more reliable signals can be used by the controller to infer on SE levels. In this case GA is utilized as it is an inflow to the SE inventory in (5), and can be readily estimated through (9).
In this control strategy a lower constraint of −100 steps/day is placed on the GA output; to avoid dependency on financial rewards a target for EP is set at points/day with an associated weight Γu(2,2) = 1. The remaining tuning parameters and constraints are maintained the same as in Section III-B. The control strategy and tuning in this case are ideal for achieving the desired output. Figure 4 shows that the controlled variable response settles within the span of 32 days, which is slower than the previous cases. This is reached by modest and achievable moves in the goals over a longer period of time to reach steady-state, due to the constrained GA. This is evident also in the GA signal being positive throughout the simulation and not violating the applied constraints. Consequently, there is no observable large drop in SE. This is a testament to the effectiveness of applying constraints on the readily available signal of GA, to avoid significant changes in SE. Moreover, EP use does not exceed the placed upper constraint of 500 points/day and follows the 0 points/day target to avoid financial dependency on EP in maintaining healthy PA levels.
Fig. 4:
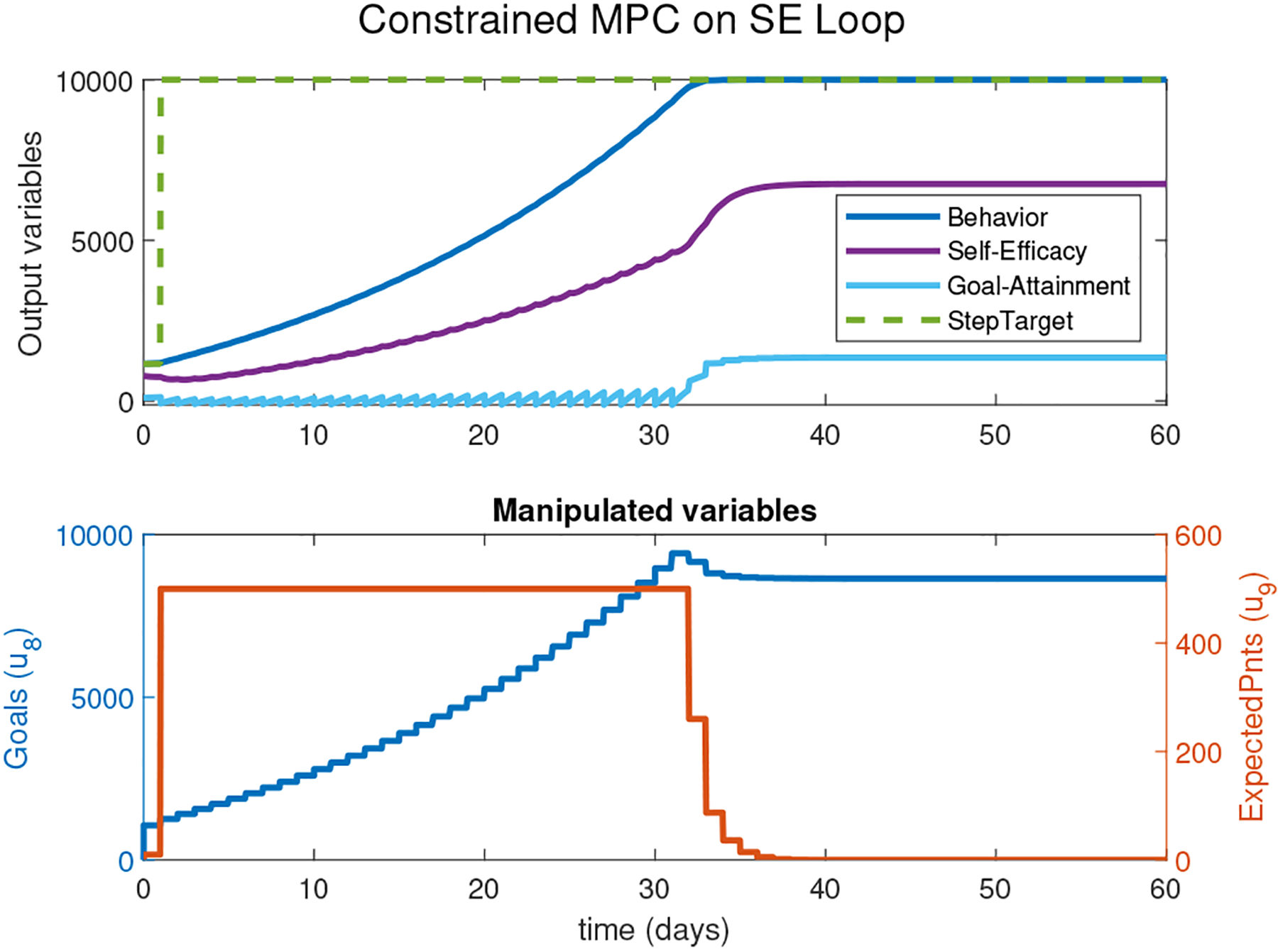
Simulation results from applying a constrained MPC controller on the Self-Efficacy loop. Low constraint is applied on goal attainment. The controller parameters are: p = 100, m = 50, ΓY = diag(0, 1, 0), Γu(2, 2) = 1, and ΓΔu = diag(0.1, 0.1). Additional enforced constraints: −100 ≤ y11 ≤∞ steps/day.
D. Dual Behavioral Outcomes Dynamics OLSE System: Constrained Goal Attainment with Disturbances
In this scenario the scope of the simulation is increased by the inclusion of OL recycle loop. In real world circumstances, distinct behavioral outcomes can vary at different speeds and have a separate impact on behavior. For instance fatigue might predominate after initially engaging in PA, however, over the long run fatigue fades away and fitness takes effect, especially if engagement in the intervention is maintained. To mimic the separate and possibly competing dynamics for behavioral outcomes an addition to the SCT model is made by including separate inventories for the mentioned expected outcomes (fatigue; , and fitness; ). Figure 5 depicts the proposed fluid analogy for the OL recycle loop in an open-loop setting. To model the dual dynamics in behavioral outcomes equation (7) is replaced with the following equations in the ODEs representing the system:
| (12) |
| (13) |
| (14) |
Assuming an instantaneous effect of fatigue and fitness on the overall behavioral outcome (i.e., performance), τ5 = 0, which simplifies the problem as follows.
| (15) |
Fig. 5:
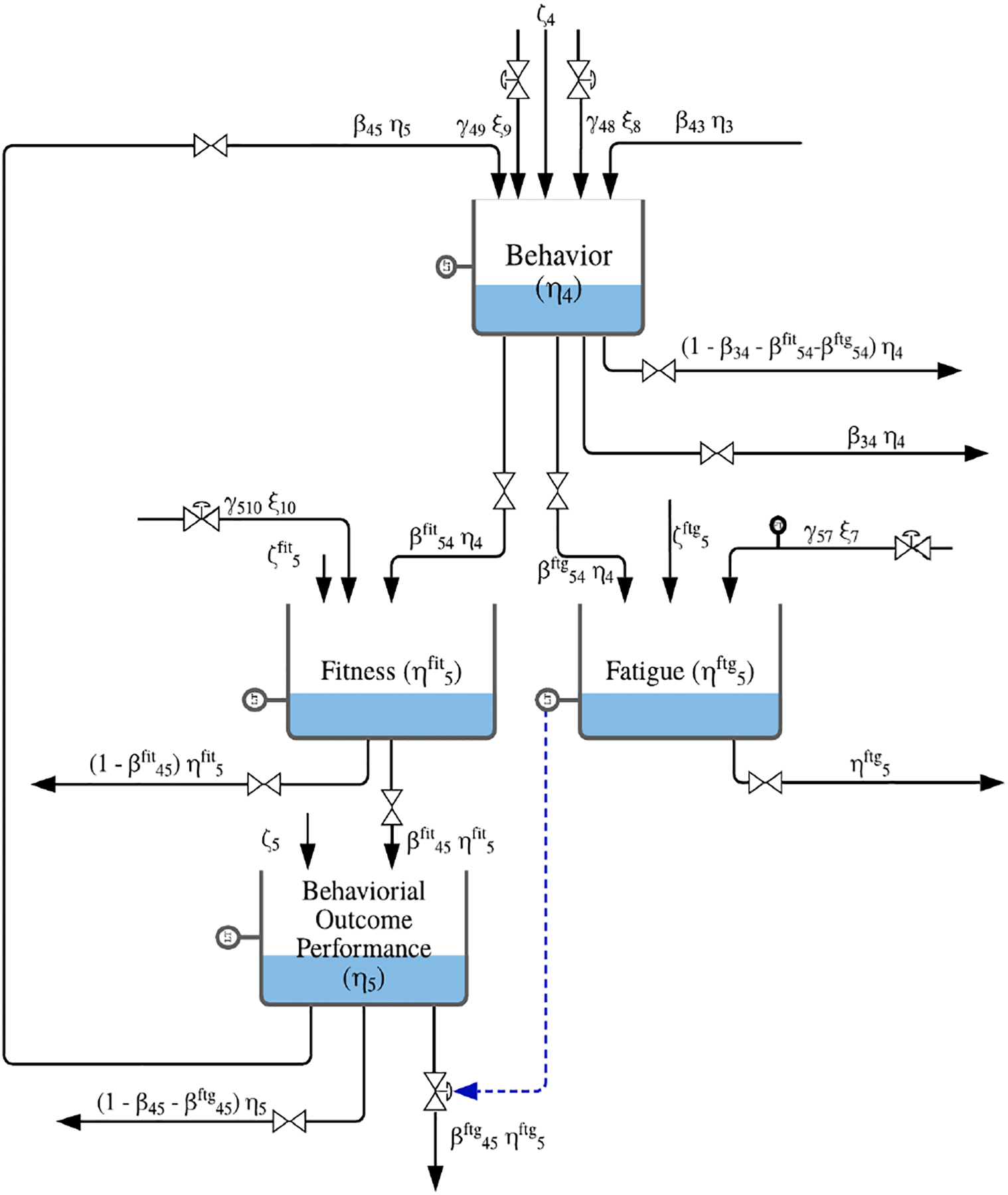
Schematic illustrating dual (and competing) behavioral outcome dynamics for the Operant Learning recycle loop.
The same analysis can be applied to any behavioral outcome or construct in the SCT model, based on the behavior of interest and whether behavioral outcomes can be separately quantified. In this scenario, only fitness and fatigue behavioral outcomes dynamics are included. This dual behavioral outcomes OL recycle loop system can model a variety of second order behavioral outcomes responses (e.g. inverse response, overshoot) based on the choice of participant parameters. The coefficients for the added system components in this simulation are as follows:
, , τ5 ≈ 0.
γ57 = 4, γ510 = 5.
, , β45 = 0.2, , .
The addition of the dual BO dynamics OL recycle loop increases problem complexity through nonlinearity resulting from the condition of granted points and the presence of higher order dynamics. The same control strategy and controller tuning from the previous case is applied in this scenario, with the main differences being the inclusion of fatigue and fitness behavioral outcomes dynamics in the internal controller model, the addition of 50 points/day as an upper move size constraint for change in EP (Δu9), and inclusion of GP as a measured disturbance. Moreover, a stochastic temperature disturbance is also introduced in this scenario on day 50. Simulation results illustrate the ability of the controller to effectively handle stochastic conditions in a complex system.
As seen in Figure 6, the controlled variable response settles within 33 days from the beginning of the intervention. Due to the negative effect of fatigue on the amount of daily steps taken at the beginning of the intervention, the participant does not meet the given goals for the first 9 days. This is evident in the slightly negative GA signal at the beginning of the intervention, and is deemed acceptable as the GA signal does not violate the −100 steps/day constraint and progressively increases along with the behavior. Furthermore, the slightly negative GA values do not lead to a significant drop in SE levels. All enforced constraints are satisfied including the constraint on the move size for EP. Moreover, EP use is within constraints and is phased off to minimal utilization after reaching the 10,000 steps/day setpoint. The inclusion of manipulated variable target on EP proves to be very effective in maintaining EP close to 0 points/day despite stochastic conditions after day 50; the controller only relies on EP when needed. This is important in terms of avoiding financial dependency as the main driver to maintain a healthy behavior, and also plays a major role in assuring that such control strategies are feasible to apply on a large scale.
Fig. 6:
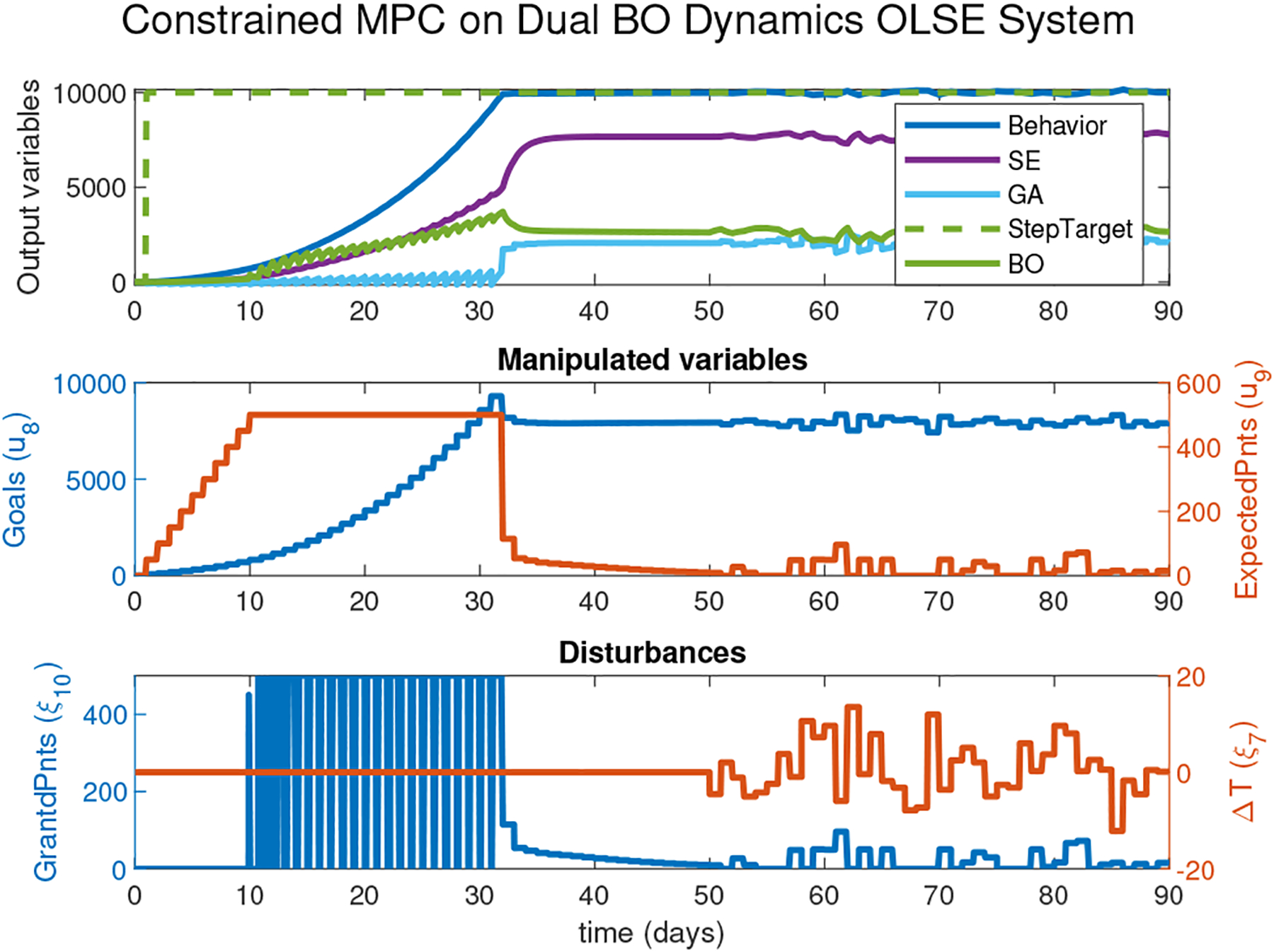
Simulation results from applying constrained MPC on dual BO dynamics OLSE system in the presence of a measured noisy disturbance. Low constraint is applied on goal attainment. The controller parameters are: p = 100, m = 50, ΓY = diag(0, 1, 0, 0, 0), Γu(2, 2) = 1, and ΓΔu = diag(0.1, 0.1). Additional constraints: −∞ ≤ Δu9 ≤ 50 points/day, and −100 ≤ y11 ≤ ∞ steps/day.
IV. Conclusions and Future Work
The results discussed in this paper show the benefits of proper problem formulation and provide a proof of concept for the use of fluid analogies and MPC in operating behavioral interventions. It has been demonstrated that MPC, with sensibly formulated objective function and constraints, can provide a reliable approach for delivering physical activity interventions, even under circumstances involving limited measurement capabilities. The full benefits of this research will be achieved by integrating system identification and control in what we refer to as a “control-optimization trial” (COT; [19]), which is part of the efforts being developed for YourMove [13]. Dynamic modeling based on system identification concepts [17], particularly input signal design, will enable estimating participant-specific coefficients for the SCT model from experimental data. Moreover, the work done in this paper focuses on deterministic conditions to reach a better understanding of the impact of different control strategies. The experimental data from our clinical trial will help identify noise and stochastic conditions, enabling simulations to further understand these diverse control strategies in more realistic conditions. Additional efforts include automating controller tuning to facilitate personalized MPC-based interventions with minimal user involvement.
ACKNOWLEDGMENT
Support for this work has been provided by the National Institutes of Health (NIH) through grant R01CA244777. The opinions expressed in this paper are the authors’ own and do not necessarily reflect the views of NIH.
References
- [1].Saint-Maurice PF, Troiano RP, Bassett J, David R, Graubard BI, Carlson SA, Shiroma EJ, Fulton JE, and Matthews CE, “Association of Daily Step Count and Step Intensity With Mortality Among US Adults,” JAMA, vol. 323, no. 12, pp. 1151–1160, 03 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].“Adult physical inactivity prevalence maps by race/ethnicity,” 2 2021.
- [3].Hekler EB, Klasnja P, Riley WT, Buman MP, Huberty J, Rivera DE, and Martin CA, “Agile science: creating useful products for behavior change in the real world,” Trans. Beh. Medicine, vol. 6, no. 2, pp. 317–328, 02 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Rivera DE, Pew MD, and Collins LM, “Using engineering control principles to inform the design of adaptive interventions: A conceptual introduction,” Drug and Alcohol Dependence, vol. 88, pp. S31–S40, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Martín CA, “A system identification and control engineering approach for optimizing mhealth behavioral interventions based on social cognitive theory,” Ph.D. dissertation, 2016. [Google Scholar]
- [6].Navarro-Barrientos J-E, Rivera DE, and Collins LM, “A dynamical model for describing behavioural interventions for weight loss and body composition change,” Mathematical and Computer Modelling of Dynamical Systems, vol. 17, no. 2, pp. 183–203, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Qin SJ, “Recursive PLS algorithms for adaptive data modeling,” Computers & Chemical Engineering, vol. 22, no. 4–5, pp. 503–514, 1998. [Google Scholar]
- [8].Lopez LM, Tolley EE, Grimes DA, and Chen-Mok M, “Theory-based interventions for contraception,” Cochrane Database of Systematic Reviews, no. 1, 2009. [DOI] [PubMed] [Google Scholar]
- [9].Martín CA, Rivera DE, Hekler EB, Riley WT, Buman MP, Adams MA, and Magann AB, “Development of a control-oriented model of social cognitive theory for optimized mhealth behavioral interventions,” IEEE Trans. on Control Systems Tech, vol. 28, no. 2, pp. 331–346, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Bordons C and Camacho EF, Model Predictive Control. Springer Verlag London Ltd, 2007. [Google Scholar]
- [11].García CE, Prett DM, and Morari M, “Model predictive control: Theory and practice—a survey,” Automatica, vol. 25, no. 3, pp. 335–348, 1989. [Google Scholar]
- [12].Martín CA, Rivera DE, and Hekler EB, “A decision framework for an adaptive behavioral intervention for physical activity using hybrid model predictive control,” in ACC, 2016, pp. 3576–3581. [Google Scholar]
- [13].“Optimizing individualized and adaptive mhealth interventions via control systems engineering methods,” R01CA244777: National Institute of Health, National Cancer Institute. [Online]. Available: https://reporter.nih.gov/search/g7QkpEP3VUS-bXgSgfT-GA/project-details/10051197 [Google Scholar]
- [14].Bandura A, “Human agency in social cognitive theory.” American Psychologist, 1989. [DOI] [PubMed] [Google Scholar]
- [15].——, “Social cognitive theory: An agentic perspective,” Annual Review of Psychology, vol. 52, no. 1, pp. 1–26, 2001. [DOI] [PubMed] [Google Scholar]
- [16].Loeber S, Croissant B, Heinz A, Mann K, and Flor H, “Cue exposure in the treatment of alcohol dependence: Effects on drinking outcome, craving and self-efficacy,” Brit. Jrnl of Clinical Psych, vol. 45, no. 4, pp. 515–529, 2006. [DOI] [PubMed] [Google Scholar]
- [17].Rivera DE, Hekler EB, Savage JS, and Symons Downs D, “Intensively adaptive interventions using control systems engineering: Two illustrative examples,” in Optimization of Behavioral, Biobehavioral, and Biomedical Interventions, Collins LM and Kugler KC, Eds. Springer, 2018, pp. 121–173. [Google Scholar]
- [18].Hekler E and Klasnja P, personal communication.
- [19].Hekler EB, Rivera DE, Martin CA, Phatak SS, Freigoun MT, Korinek E, Klasnja P, Adams MA, and Buman MP, “Tutorial for using control systems engineering to optimize adaptive mobile health interventions,” Journal of Medical Internet Research, vol. 20, no. 6, p. e8622, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]


