Abstract
Scientists and researchers are much interested in studying graphene and silver nanoparticles for the enhancement of heat transport due to their extensive variety of applications in different areas of industrial and engineering such as drug delivery, medical devices, ultra-light, excellent electrical conductivity, strong medical strength, health care, consumer, food, etc. Therefore, in the existing investigation, the MHD flow of a mixed convective hybrid nanoliquid with graphene and silver nanoparticles past a rotating disk is considered. Water and ethylene glycol (50:50) is used as a base liquid in the existing model. The mechanism for heat transport is computed with the existence of thermal radiation and thermal convective condition. Homogeneous and heterogeneous chemical reactions are assumed in the flow behavior. The mathematical formulation of the proposed problem is based on the nonlinear PDEs which are then transformed to nonlinear ODEs by manipulating the appropriate similarity transformation. The simulation of the existing problem has been performed with the help of the homotopy analysis technique. The outcomes of the different flow parameters on the velocities, temperature, concentration, skin friction coefficient, and Nusselt number of the hybrid nanofluid are attained via graphs and tables. Some significant results from the existing problem demonstrate that the rate of heat transport is greater for the thermal Biot number and nanoparticles volume fraction. Further, it is noticed that the velocity of the liquid particles becomes lower for a higher magnetic field parameter.
Subject terms: Engineering, Mathematics and computing
Introduction
In these days numerous processes at industrial level encompass of thermal energy transfer. In any industrial or engineering phenomena heat is required to be removed, added or transferred from one stream to another one, which has become a key task in industry. There are many methods used to enhance thermal performance, one of which is the spread of nano-sized particles in pure fluid as proposed by Choi and Estman1. Shah et al.2 have deliberated upon micropolar fluid flow with gold nanoparticles in the blood and have established that fluid micro-rotational velocity has amplified with growing in rotational factor while thermal flow of blood has grown up with enhancement in nanoparticles concentration. Shoaib et al.3 computed intelligently the generation of irreversibility and thermal flow rate for radiated nanoliquid flow over a sheet. Yadav et al.4 have inspected the impacts of magnetic field and sinusoidal heating on nanoparticles flow through a cavity. Khan et al.5 have deliberated radiative swirling motion of MHD Casson nanofluid over gyrating cylinder. Safwa et al.6 have used non-Fourier energy modal to discuss nanofluid flow over shrinking/stretching porous surface and have evaluated dual solution of their modeled problem. Biswas et al.7 have evaluated computationally the influence of MHD over Maxwell nanoparticles flow past a stretching sheet subject to thermally radiated chemical reactions.
The mixing of two different nanoparticles in pure fluid further supplements the thermal performance of pure fluid. Wahid et al.8 have studied Marangoni hybrid nanoparticles flow on an infinite penetrable disk and have revealed that thermal flow has accelerated with augmentation in nanoparticles volume fraction, suction and porosity factors. As depicted by Usman et al.9 the hybrid nanoparticles have superior thermal flow rate in comparison of nanofluid. Sundaeep et al.10 have deliberated influence of nonlinear thermal radiations upon MHD hybrid nanofluid flow subject to effects of heat source on a curved stretching sheet. Ashwinkumar et al.11 have deliberated convective thermal flow in MHD hybrid nanoparticles using two different geometrical views and have concluded that augmentation in thermal radiation factor and nanoparticles concentration have boosted the distributions of temperature. Chu et al.12 have scrutinized MHD time-dependent hybrid nanofluid flowing amid of infinite two plates subject to different shape of nanoparticles. Khan et al.13 discussed bioconvection hybrid nanoliquid flow upon a heated thin movable needle. Waini et al.14 have studied MHD time-dependent hybrid nanoparticles flow subject to the motion of fluid induced by rotary disk. Eid and Nafe15 have analyzed variations in thermal conductance and effects of thermal flow generation over MHD hybrid nanofluid flow on permeable surface using slip conditions.
Mixed convective flows of fluid also called combined natural and forced convective flows occur in many transportation phenomena at industrial level. These flows are very important and play a pivotal role in many industrial applications. Alghamdi16 has inspected the influences of chemically reactive activation energy upon mixed convective nanoparticles flow past a rotary disk and have concluded that thermal and mass diffusivities have upsurge with augmentation in Hartmann number. Ahmad et al.17 have evaluated mixed convection liquid flow above a curved surface subject to influences of chemical reactions. Qaiser et al.18 assisted numerically the mixed convection fluid flow past an expanding surface and have revealed that motion of fluid has retarded and heat flow has upsurge with higher values of magnetic field effects. Rasool and Wakif19 have scrutinized numerically the effects of mixed convective EMHD over nanofluid flow over Riga plate by employing modified Buongiorno nanoparticles model. Awan et al.20 have produced a scientific result for rate type fluid using the effects of mixed convection upon fluid flow system through a singular kernel. Islam et al.21 have investigated mixed convective Maxwell nanofluid flow past an extending cylinder, using different flow conditions with their impact upon flow system.
The investigation of magnetic characteristics and electrically conducting behavior of fluid is termed as magneto-hydrodynamics (MHD) included salty water, plasma and liquid metals etc. Behind MHD the focal idea is that current can be persuaded by employing magnetic effects that causes polarization of liquids as proposed by Alfven22. Many applications of these fluids comprised the fields of astrophysics, geophysics magnetic drug delivery and sensor engineering etc. Sohail et al.23 have presented MHD Casson liquid flow subject to thermal conductance past a bidirectional nonlinear stretching surface. Khan et al.24 have explored MHD nanoliquid flow with influence of chemically reactive and viscously dissipative effects past a moving needle. Kodi and Mupori25 have deliberated time-dependent Casson MHD fluid flow past a surface using chemical reactions and heat absorption influences upon flow system. Nazeer et al.26 deliberated theoretically the MHD liquid flow in a micro-channel and have revealed that velocity of fluid flow system has retarded in response of strong magnetic field. Asjad et al.27 inspected the effects of activation energy upon bioconvective MHD liquid flow through an exponentially expanding sheet.
Heat transmission is mostly boosted by applying thermal radiations to the fluid flow system. These radiations play a substantial role in heat flow problems when coefficient of convective heat transfer is pretty small. Waqas et al.28 have analyzed the significances of chemically reactive and bio-convective on MHD nanofluid flow using thermal radiation and have determined that heat flow of fluid has inflamed with magnetic effects and radiation factor. Muhammad et al.29 have inspected nonlinear thermal radiated Eyring-Powel nanoparticles flow above a Riga plate. Kumar et al.30 have discussed the thermal radiation influence upon MHD naturally convective nanofluid flow past a plate using sudden jerk. Shaw et al.31 have discussed MHD hybrid nanoliquid flow subject to the effects of quadratic thermal radiation above a stretched cylinder. Gumber et al.32 have scrutinized micropolar nanoliquid flow over a vertically placed plate with consequence of thermal radiations and suction/injection effects. Wahid et al.33 have deliberated MHD mixed convection nanoliquid flow past an absorbent flat vertical plate using thermal radiations.
Many fluid flow systems with influence of chemical reactions are incorporating both homogenous as well heterogeneous characteristics for instance biochemical reactions combustions and catalysis etc. Wang et al.34 have inspected the influence of homogenous /heterogeneous reactions upon a non-Newtonian fluid flow. Bashir et al.35 have conducted a comparative work on nanofluid flow using homogeneous and heterogeneous influence and have concluded that with augmentation in nanoparticles concentration, the thermal profiles and skin friction have upsurge. Nawaz et al.36 have reviewed numerically the effects of Darcy-Forchheimer model on micropolar fluid with homogeneous and heterogeneous reactions. Gangadhar et al.37 have deliberated MHD fluid flow with influences of autocatalyze chemical reactions and convection heat effects. Tahir et al.38 have investigated numerically the influences of heterogeneous and homogenous reactions upon Maxwell nanofluid flow over stretched surface subject to magnetic effects. Ayub et al.39 have deliberated MHD nanoliquid flow through gyratory disks subject to heterogeneous and homogenous reactions and have established that liquid motion has retarded and temperature profiles have upsurge with corresponding incrimination in the values of magnetic parameter.
From the above cited literature, it is observed that there is less work on the enhancement of heat transport of the water and ethylene glycol (50:50)-based hybrid nanofluid flow containing silver and graphene nanoparticles over a rotating disk. Therefore, in the present work for the improvement of heat transport, the graphene and silver nanoparticles are mixed in the base fluid 50%W (water) + 50%EG (ethylene glycol) over a rotating disk is considered. The role of magnetic field and thermal radiation are taken into deliberation. The catalyzed chemical reactions including the homogeneous and heterogeneous chemical reactions are evaluated in the current analysis. With the implementation of HAM scheme, the solution to the present problem is obtained. Flow behavior of various profiles of the hybrid nanoliquid versus discrete flow parameters is accomplished via graphs. The skin friction and heat transmission of the hybrid nanofluid with respect to different parameters are also discussed.
Problem formulation
Let us assume the mixed convective flow of a hybrid nanofluid over a spinning disk with magnetic field and thermal radiation effects. The flow is taken as laminar, steady, and incompressible. Simulation for mass transport is encountered with the utilization of homogeneous and heterogeneous chemical reactions. In the present study, graphene and silver nanoparticles are mixed with 50%W (Water) + 50%EG (Ethylene glycol). It is assumed that the disk rotates with the angular velocity along -axis. In a cylindrical coordinate system, the velocity components are denoted by . A magnetic field of strength is employed normal to the flow direction. The convective condition is implemented for the simulation of heat transport. The surface temperature is represented by and represents the ambient temperature. Keeping in mind the aforementioned flow assumptions, the governing equations can be written as40:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
with boundary conditions46,47:
| 7 |
The radiative heat flux is deliberated as:
| 8 |
The hybrid nanofluid thermophysical properties are defined as:
| 9 |
The correspondence variables are defined as:
| 10 |
The non-dimensional form of the Eqs. (1–6) are obtained by applying the above-mentioned similarity transformation in Eq. (10):
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
With boundary conditions:
| 17 |
Further, it is assumed that the ratio of the diffusion coefficient and are to be comparable, therefore ratio of diffusion coefficient is assumed to be 1, so and .
Therefore, Eqs. (15) and (16) are reduced as:
| 18 |
with boundary conditions:
| 19 |
After the simplification, some significant dimensionless parameters are discussed here. The magnetic field is denoted by , is the mixed convention parameter, Prandtl number is represented by , is the radiation parameter, is the Schmidt number, homogeneous chemical reaction parameter is symbolized by , heterogeneous chemical reaction is denoted by , is the thermal Biot number, and the ratio of diffusion coefficient is expressed by .
| 20 |
where , and .
In dimensionless form, and are:
| 21 |
where is the local Reynolds number.
HAM solution
The initial guesses are given as:
| 22 |
The linear operators are given as:
| 23 |
with
| 24 |
where are called the arbitrary constants.
HAM convergence
Convergence of the modeled equations is ensured through the use of HAM. The parameter is crucial to the model system of equations' convergence. Figure 1 depicts the convergence regions for the velocities, thermal, and concentration profiles at the 18th order of approximation. The convergence regions of velocities, temperature and concentration profiles respectively are , , and .
Figure 1.

-curves for , , and .
Results and discussion
This portion determined the physical aspect of several flow parameters on velocities, temperature, skin friction coefficient and Nusselt number of the hybrid nanofluid. Table 1 shows the thermophysical characteristic of the water, ethylene glycol and graphene nanoparticles. Table 2 shows the comparison of the present investigation with previous studies. Here, we have found a great agreement with previous studies. Table 3 explains the fluctuation of the skin friction coefficient of the hybrid nanofluid via magnetic field parameter , mixed convection parameter and nanoparticles volume fraction . It has noted from Table 2 that is higher when , and are rises. In Table 4, the role of the radiation parameter , thermal Biot number and nanoparticles volume fraction on the Nusselt number is deliberated. In this investigation, it is revealed that with the increase of , and , the Nusselt number is increases. Figure 2 displays the influence of mixed convection parameter on the primary velocity of the hybrid nanofluid flow. This figure determines that the nanofluid primary velocity increases with the increase in . This is due to the fact that when the buoyancy on free convection gets considerable, a mixed convection occurs. Therefore, the buoyancy will grow if the value of is enlarged. The flow velocity increased as the buoyancy force does as well. The role of the primary velocity of the hybrid nanofluid flow versus magnetic parameter is discussed in Fig. 3. It is interpreted that the enhancement in led to a decline in the primary velocity of the hybrid nanofluid. This effect is due to the reason that as we increase , so does the Lorentz force. Lorentz force is actually retarding force acting against the velocity profile. So, the increasing increases the opposing force (as shown in Table 3) to the hybrid nanofluid flow which results a reduction in the velocity profile of the hybrid nanofluid flow. Figure 4 explores the influence of the magnetic field parameter on the secondary velocity profile of the hybrid nanofluid. The decayed in secondary velocity of the hybrid nanofluid is noticed for higher estimates of the magnetic parameter. Further, it is due to the fact that the rising values of produce a Lorentz force. So, the production of the Lorentz force slows down the liquid particles motion that’s why the velocity profile is diminished. Figure 5 demonstrates the fluctuation in temperature profile of the hybrid nanoliquid due to the rising of the radiation parameter . It is eminent that an augmentation in radiation parameter upsurges the temperature of the hybrid nanoliquid. Since the radiation parameter and the mean absorption coefficient are inversely proportional, more heat is transmitted to the working liquid via the radiation phenomenon. The temperature increases as decreases with increasing values. Both the rate of thermal convection into the fluid and the deviation of radiative heat flow increase as a result. The growth of thermal boundary layers derives from the improved thermal heat transmission. The effect is a thickening of the thermal layer. The effect of the thermal Biot number on the temperature of the hybrid nanoliquid is shown in Fig. 6. Figure 6 explains that as the values of the thermal Biot number increase, the hybrid nanofluid temperature also increases. Further, on the rotating disk, the thermal Biot number is connected with the convective condition. Also, the thermal boundary layer thickness is enhancing due to the implementation of the convective condition. So, near the surface of the disk, the hybrid nanoliquid temperature increases when the thermal Biot number rises. The consequence of the homogeneous chemical reaction parameter on the hybrid nanoliquid concentration profile is discussed in Fig. 7. In this investigation, it is observed that the concentration of the hybrid nanofluid is enhanced with the rising of the homogeneous chemical reaction parameter. For different values of the heterogeneous chemical reaction parameter, the behavior of hybrid nanoliquid concentration is deliberated in Fig. 8. It is evident that the concentration of the hybrid nanofluid declines due to the increment in the heterogeneous chemical reaction parameter. In Fig. 9, the role of the Schmidt number on the concentration of the hybrid nanoliquid is identified. In this figure, it is recognized that the hybrid nanofluid concentration is lesser for higher values of . Generally, is defined as the ratio between the momentum diffusivity and mass diffusivity. So, with the increase of , the mass diffusivity of the fluid is small. Therefore the concentration of the hybrid nanofluid is lesser due to the increase in .
Table 1.
| Thermophysical properties | ||||||
|---|---|---|---|---|---|---|
| 50%W + 50%EG | 1056 | 3288 | 0.425 | 0.00509 | 0.00341 | 29.86 |
| Graphene | 2250 | 2100 | 2500 | 1 × 107 | 2.84 × 10−4 | – |
| Silver | 10,500 | 235 | 429 | 63 × 10−6 | 1.89 × 10−5 | – |
Table 2.
Comparison of with reported results when all other parameters are zero.
Table 3.
Chang in due to , and .
| 0.1 | 1.670699 | ||
| 0.3 | 1.671767 | ||
| 0.5 | 1.672835 | ||
| 0.7 | 1.673903 | ||
| 0.2 | 1.670767 | ||
| 0.4 | 1.670905 | ||
| 0.6 | 1.671042 | ||
| 0.8 | 1.671180 | ||
| 0.01 | 1.224952 | ||
| 0.02 | 1.281557 | ||
| 0.03 | 1.343170 | ||
| 0.04 | 1.409918 |
Table 4.
Chang in due to , and .
| 1.0 | 0.152344 | ||
| 1.5 | 0.152346 | ||
| 2.0 | 0.152348 | ||
| 2.5 | 0.152349 | ||
| 1.0 | 1.720965 | ||
| 2.0 | 2.183312 | ||
| 3.0 | 3.249004 | ||
| 4.0 | 3.893915 | ||
| 0.01 | 0.109616 | ||
| 0.02 | 0.118770 | ||
| 0.03 | 0.128756 | ||
| 0.04 | 0.139692 |
Figure 2.

versus .
Figure 3.
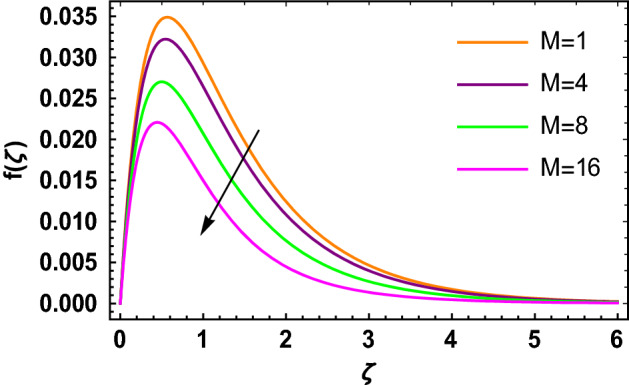
versus .
Figure 4.

versus .
Figure 5.

versus .
Figure 6.
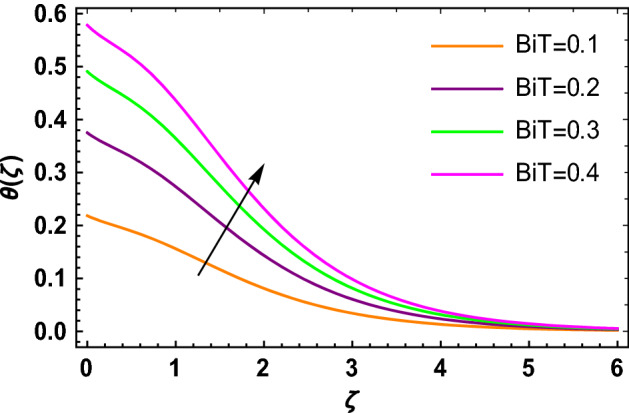
versus .
Figure 7.

versus .
Figure 8.

versus .
Figure 9.

versus .
Conclusion
In this investigation, MHD flow of hybrid nanofluid containing graphene and silver nanoparticles with water and ethylene glycol (50:50) over a rotating disk is analyzed. To explore the idea of heat transport, simulation for thermal radiation under convective condition is performed. Furthermore, the homogeneous and heterogeneous chemical reactions are discussed in the present flow phenomenon. On the basis of HAM method, solution of the modeled problem is performed. It is detected that hybrid nanofluid skin friction coefficient is enhanced due to magnetic parameter, mixed convection parameter and nanoparticles volume fraction. Intensification in Nusselt number is noticed for higher radiation parameter, thermal Biot number and nanoparticles volume fraction. Escalation in mixed convection parameter increases the velocity profile, while reduces with the increasing magnetic parameter. With the rising of radiation parameter and thermal Biot number, hybrid nanofluid temperature gets higher. Hybrid nanofluid concentration is greater for homogeneous chemical reaction parameter. Also, it is noted that the higher heterogeneous chemical reaction parameter and Schmidt number lowers the hybrid nanofluid concentration.
Acknowledgements
The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2022 under project number FRB650048/0164.
Abbreviations
- (u, v, w)
Velocity components
Cylindrical coordinate system
Magnetic field strength
Temperature
- EG
Ethylene glycol
Gravity
Mean absorption coefficient
Thermal conductivity
Radiative heat flux
- and
Chemical reaction rate
- and
Diffusion coefficient
Chemical species
- , and
Dimensionless velocities
- and
Homogeneous and heterogeneous concentration
Thermal Biot number
Homogeneous chemical reaction parameter
Heterogeneous chemical reaction parameter
Magnetic field parameter
Prandtl number
Radiation parameter
Schmidt number
Skin friction coefficient
Nusselt number
Greek letter
Temperature
Kinematic viscosity
Electrical conductivity
Density
Specific heat
Stefan-Boltzmann constant
Dynamic viscosity
Dimensionless mixed convection parameter
Non-dimensional mixed convection parameter
Ratio of diffusion coefficient
Angular velocity
Subscript
Fluid
Hybrid nanofluid
At the surface
Free stream
Author contributions
All authors equally contributed.
Data availability
All data used in this manuscript have been presented within the article.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Anwar Saeed, Email: anwarsaeed769@gmail.com.
Poom Kumam, Email: poom.kum@kmutt.ac.th.
References
- 1.Choi, S. & Eastman, J. Enhancing Thermal Conductivity of Fluids with Nanoparticles (1995). https://www.osti.gov/biblio/196525. Accessed 10 Sept 2021.
- 2.Shah Z, Khan A, Khan W, Alam MK, Islam S, Kumam P, Thounthong P. Micropolar gold blood nanofluid flow and radiative heat transfer between permeable channels. Comput. Methods Programs Biomed. 2020;186:105197. doi: 10.1016/j.cmpb.2019.105197. [DOI] [PubMed] [Google Scholar]
- 3.Shoaib Z, et al. Intelligent computing for entropy generation in Jeffrey nanofluid through radiated flow. Waves Random Complex Media. 2022 doi: 10.1080/17455030.2022.2085345. [DOI] [Google Scholar]
- 4.Yadav CK, et al. Effect of sinusoidal heating and Hartmann number on nanofluid based heat flow evolution in a cavity. Mater. Today Proc. 2022;63:157–163. doi: 10.1016/j.matpr.2022.02.434. [DOI] [Google Scholar]
- 5.Khan A, Saeed A, Gul T, Mukhtar S, Ali I, Jawad M. Radiative swirl motion of hydromagnetic Casson nanofluid flow over rotary cylinder using Joule dissipation impact. Phys. Scr. 2021;96:45206. doi: 10.1088/1402-4896/abdf83. [DOI] [Google Scholar]
- 6.Safwa Khashi’ie N, Md Arifin N, Hafidzuddin EH, Wahi N. Dual stratified nanofluid flow past a permeable shrinking/stretching sheet using a non-Fourier energy model. Appl. Sci. 2019;9:2124. doi: 10.3390/app9102124. [DOI] [Google Scholar]
- 7.Biswas R, Hossain MS, Islam R, Ahmmed SF, Mishra SR, Afikuzzaman M. Computational treatment of MHD Maxwell nanofluid flow across a stretching sheet considering higher-order chemical reaction and thermal radiation. J. Comput. Math. Data Sci. 2022;4:100048. doi: 10.1016/j.jcmds.2022.100048. [DOI] [Google Scholar]
- 8.Wahid NS, Arifin NM, Khashi’ie NS, Pop I. Marangoni hybrid nanofluid flow over a permeable infinite disk embedded in a porous medium. Int. Commun. Heat Mass Transf. 2021;126:105421. doi: 10.1016/j.icheatmasstransfer.2021.105421. [DOI] [Google Scholar]
- 9.Usman M, Gul T, Khan A, Alsubie A, Ullah MZ. Electromagnetic couple stress film flow of hybrid nanofluid over an unsteady rotating disc. Int. Commun. Heat Mass Transf. 2021;127:105562. doi: 10.1016/j.icheatmasstransfer.2021.105562. [DOI] [Google Scholar]
- 10.Sandeep N, Ranjana B, Samrat SP, Ashwinkumar GP. Impact of nonlinear radiation on magnetohydrodynamic flow of hybrid nanofluid with heat source effect. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022;236:1616–1627. doi: 10.1177/09544089211070667. [DOI] [Google Scholar]
- 11.Ashwinkumar GP, Samrat SP, Sandeep N. Convective heat transfer in MHD hybrid nanofluid flow over two different geometries. Int. Commun. Heat Mass Transf. 2021;127:105563. doi: 10.1016/j.icheatmasstransfer.2021.105563. [DOI] [Google Scholar]
- 12.Chu Y, Bashir S, Ramzan M, Malik MY. Model‐based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. 2022 doi: 10.1002/mma.8234. [DOI] [Google Scholar]
- 13.Khan A, Saeed A, Tassaddiq A, Gul T, Kumam P, Ali I, Kumam W. Bio-convective and chemically reactive hybrid nanofluid flow upon a thin stirring needle with viscous dissipation. Sci. Rep. 2021;11:1–17. doi: 10.1038/s41598-021-86968-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Waini I, Khashi’ie NS, Kasim ARM, Zainal NA, Bin Hamzah K, Md Arifin N, Pop I. Unsteady magnetohydrodynamics (MHD) flow of hybrid ferrofluid due to a rotating disk. Mathematics. 2022;10:1658. doi: 10.3390/math10101658. [DOI] [Google Scholar]
- 15.Eid MR, Nafe MA. Thermal conductivity variation and heat generation effects on magneto-hybrid nanofluid flow in a porous medium with slip condition. Waves Random Complex Media. 2022;32:1103–1127. doi: 10.1080/17455030.2020.1810365. [DOI] [Google Scholar]
- 16.Alghamdi M. Significance of Arrhenius activation energy and binary chemical reaction in mixed convection flow of nanofluid due to a rotating disk. Coatings. 2020;10:86. doi: 10.3390/coatings10010086. [DOI] [Google Scholar]
- 17.Ahmad U, Ashraf M, Abbas A, Rashad AM, Nabwey HA. Mixed convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. Sci. Rep. 2021;11:1–10. doi: 10.1038/s41598-021-92409-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Qaiser D, Zheng Z, Riaz Khan M. Numerical assessment of mixed convection flow of Walters-B nanofluid over a stretching surface with Newtonian heating and mass transfer. Therm. Sci. Eng. Prog. 2021;22:100801. doi: 10.1016/J.TSEP.2020.100801. [DOI] [Google Scholar]
- 19.Rasool G, Wakif A. Numerical spectral examination of EMHD mixed convective flow of second-grade nanofluid towards a vertical Riga plate using an advanced version of the revised Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2021;143:2379–2393. doi: 10.1007/S10973-020-09865-8/TABLES/4. [DOI] [Google Scholar]
- 20.Awan AU, Riaz S, Ashfaq M, Abro KA. A scientific report of singular kernel on the rate-type fluid subject to the mixed convection flow. Soft Comput. 2022;26:4575–4585. doi: 10.1007/s00500-022-06913-3. [DOI] [Google Scholar]
- 21.Islam S, Khan A, Kumam P, Alrabaiah H, Shah Z, Khan W, Zubair M, Jawad M. Radiative mixed convection flow of Maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Sci. Rep. 2020;10:1–18. doi: 10.1038/s41598-020-74393-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alfvén H. Existence of electromagnetic-hydrodynamic waves. Nature. 1942;150:405–406. doi: 10.1038/150405d0. [DOI] [Google Scholar]
- 23.Sohail M, Shah Z, Tassaddiq A, Kumam P, Roy P. Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over non-linear bi-directional stretching surface. Sci. Rep. 2020;10:1–16. doi: 10.1038/s41598-020-69411-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Khan A, Kumam W, Khan I, Saeed A, Gul T, Kumam P, Ali I. Chemically reactive nanofluid flow past a thin moving needle with viscous dissipation, magnetic effects and hall current. PLoS ONE. 2021;16:e0249264. doi: 10.1371/journal.pone.0249264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kodi R, Mopuri O. Unsteady MHD oscillatory Casson fluid flow past an inclined vertical porous plate in the presence of chemical reaction with heat absorption and Soret effects. Heat Transf. 2022;51:733–752. doi: 10.1002/htj.22327. [DOI] [Google Scholar]
- 26.Nazeer M, Hussain F, Khan MI, El-Zahar ER, Chu Y-M, Malik MY. Theoretical study of MHD electro-osmotically flow of third-grade fluid in micro channel. Appl. Math. Comput. 2022;420:126868. [Google Scholar]
- 27.Asjad MI, Zahid M, Inc M, Baleanu D, Almohsen B. Impact of activation energy and MHD on Williamson fluid flow in the presence of bioconvection. Alex. Eng. J. 2022;61:8715–8727. doi: 10.1016/j.aej.2022.02.013. [DOI] [Google Scholar]
- 28.Waqas H, Khan SU, Bhatti MM, Imran M. Significance of bioconvection in chemical reactive flow of magnetized Carreau–Yasuda nanofluid with thermal radiation and second-order slip. J. Therm. Anal. Calorim. 2020;140:1293–1306. doi: 10.1007/s10973-020-09462-9. [DOI] [Google Scholar]
- 29.Muhammad T, Waqas H, Khan SA, Ellahi R, Sait SM. Significance of nonlinear thermal radiation in 3D Eyring–Powell nanofluid flow with Arrhenius activation energy. J. Therm. Anal. Calorim. 2021;143:929–944. doi: 10.1007/s10973-020-09459-4. [DOI] [Google Scholar]
- 30.Kumar MA, Reddy YD, Rao VS, Goud BS. Thermal radiation impact on MHD heat transfer natural convective nano fluid flow over an impulsively started vertical plate. Case Stud. Therm. Eng. 2021;24:100826. doi: 10.1016/j.csite.2020.100826. [DOI] [Google Scholar]
- 31.Shaw S, Samantaray SS, Misra A, Nayak MK, Makinde OD. Hydromagnetic flow and thermal interpretations of Cross hybrid nanofluid influenced by linear, nonlinear and quadratic thermal radiations for any Prandtl number. Int. Commun. Heat Mass Transf. 2022;130:105816. doi: 10.1016/j.icheatmasstransfer.2021.105816. [DOI] [Google Scholar]
- 32.Gumber P, Yaseen M, Rawat SK, Kumar M. Heat transfer in micropolar hybrid nanofluid flow past a vertical plate in the presence of thermal radiation and suction/injection effects. Partial Differ. Equ. Appl. Math. 2022;5:100240. doi: 10.1016/j.padiff.2021.100240. [DOI] [Google Scholar]
- 33.Wahid NS, Arifin NM, Khashi’ie NS, Pop I, Bachok N, Hafidzuddin MEH. MHD mixed convection flow of a hybrid nanofluid past a permeable vertical flat plate with thermal radiation effect. Alex. Eng. J. 2022;61:3323–3333. doi: 10.1016/j.aej.2021.08.059. [DOI] [Google Scholar]
- 34.Wang J, Khan MI, Khan WA, Abbas SZ, Khan MI. Transportation of heat generation/absorption and radiative heat flux in homogeneous–heterogeneous catalytic reactions of non-Newtonian fluid (Oldroyd-B model) Comput. Methods Programs Biomed. 2020;189:105310. doi: 10.1016/j.cmpb.2019.105310. [DOI] [PubMed] [Google Scholar]
- 35.Bashir S, Ramzan M, Malik MY, Alotaibi H. Comparative analysis of five nanoparticles in the flow of viscous fluid with nonlinear radiation and homogeneous–heterogeneous reaction. Arab. J. Sci. Eng. 2022;47:8129–8140. doi: 10.1007/s13369-021-06094-5. [DOI] [Google Scholar]
- 36.Nawaz Y, Arif MS, Shatanawi W. A new fourth-order predictor–corrector numerical scheme for heat transfer by Darcy–Forchheimer flow of micropolar fluid with homogeneous–heterogeneous reactions. Appl. Sci. 2022;12:6072. doi: 10.3390/app12126072. [DOI] [Google Scholar]
- 37.Gangadhar K, Kumari MA, Subba Rao MV, Alnefaie K, Khan I, Andualem M. Magnetization for burgers’ fluid subject to convective heating and heterogeneous-homogeneous reactions. Math. Probl. Eng. 2022;2022:1–5. doi: 10.1155/2022/2747676. [DOI] [Google Scholar]
- 38.Tahir W, Althobaiti N, Kousar N, Alhazmi SE, Bilal S, Riaz A. Effects of homogeneous–heterogeneous reactions on Maxwell ferrofluid in the presence of magnetic dipole along a stretching surface: A numerical approach. Math. Probl. Eng. 2022;2022:1–13. [Google Scholar]
- 39.Ayub A, Sabir Z, Shah SZH, Wahab HA, Sadat R, Ali MR. Effects of homogeneous–heterogeneous and Lorentz forces on 3-D radiative magnetized cross nanofluid using two rotating disks. Int. Commun. Heat Mass Transf. 2022;130:105778. doi: 10.1016/j.icheatmasstransfer.2021.105778. [DOI] [Google Scholar]
- 40.Ming C, Zheng L, Zhang X. Steady flow and heat transfer of the power-law fluid over a rotating disk. Int. Commun. Heat Mass Transf. 2011;38:280–284. doi: 10.1016/j.icheatmasstransfer.2010.11.013. [DOI] [Google Scholar]
- 41.Lv Y-P, Gul H, Ramzan M, Chung JD, Bilal M. Bioconvective Reiner–Rivlin nanofluid flow over a rotating disk with Cattaneo–Christov flow heat flux and entropy generation analysis. Sci. Rep. 2021;11:1–18. doi: 10.1038/s41598-021-95448-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dawar A, Bonyah E, Islam S, Alshehri A, Shah Z. Theoretical analysis of Cu–H2O, Al2O3–H2O, and TiO2–H2O nanofluid flow past a rotating disk with velocity slip and convective conditions. J. Nanomater. 2021 doi: 10.1155/2021/5471813. [DOI] [Google Scholar]
- 43.Sandeep N. Effect of aligned magnetic field on liquid thin film flow of magnetic-nanofluids embedded with graphene nanoparticles. Adv. Powder Technol. 2017;28:865–875. doi: 10.1016/j.apt.2016.12.012. [DOI] [Google Scholar]
- 44.Sadiq K, Jarad F, Siddique I, Ali B. Soret and radiation effects on mixture of ethylene glycol-water (50%-50%) based Maxwell nanofluid flow in an upright channel. Complexity. 2021;2021:1–12. doi: 10.1155/2021/5927070. [DOI] [Google Scholar]
- 45.Nisar KS, Khan U, Zaib A, Khan I, Baleanu D. Numerical simulation of mixed convection squeezing flow of a hybrid nanofluid containing magnetized ferroparticles in 50%: 50% of ethylene glycol–water mixture base fluids between two disks with the presence of a non-linear thermal radiation heat flux. Front. Chem. 2020;8:792. doi: 10.3389/fchem.2020.00792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Khan U, Bilal S, Zaib A, Makinde OD, Wakif A. Numerical simulation of a nonlinear coupled differential system describing a convective flow of Casson gold–blood nanofluid through a stretched rotating rigid disk in the presence of Lorentz forces and nonlinear thermal radiation. Numer. Methods Partial Differ. Equ. 2020 doi: 10.1002/NUM.22620. [DOI] [Google Scholar]
- 47.Ragupathi P, Muhammad T, Islam S, Wakif A. Application of Arrhenius kinetics on MHD radiative Von Kármán Casson nanofluid flow occurring in a Darcy–Forchheimer porous medium in the presence of an adjustable heat source. Phys. Scr. 2021;96:125228. doi: 10.1088/1402-4896/AC297C. [DOI] [Google Scholar]
- 48.Bachok N, Ishak A, Pop I. Flow and heat transfer over a rotating porous disk in a nanofluid. Phys. B Condens. Matter. 2011;406:1767–1772. doi: 10.1016/j.physb.2011.02.024. [DOI] [Google Scholar]
- 49.Maleque KA, Sattar MA. Steady laminar convective flow with variable properties due to a porous rotating disk. J. Heat Transf. 2005;127:1406–1409. doi: 10.1115/1.2098860. [DOI] [Google Scholar]
- 50.Kelson N, Desseaux A. Note on porous rotating disk flow. ANZIAM J. 2000;42:C837–C855. doi: 10.21914/anziamj.v42i0.624. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data used in this manuscript have been presented within the article.


