Maximum SNP F_ST Outperforms Full-Window Statistics for Detecting Soft Sweeps in Local Adaptation

Abstract

Local adaptation can lead to elevated genetic differentiation at the targeted genetic variant and nearby sites. Selective sweeps come in different forms, and depending on the initial and final frequencies of a favored variant, very different patterns of genetic variation may be produced. If local selection favors an existing variant that had already recombined onto multiple genetic backgrounds, then the width of elevated genetic differentiation (high F_ST) may be too narrow to detect using a typical windowed genome scan, even if the targeted variant becomes highly differentiated. We, therefore, used a simulation approach to investigate the power of SNP-level F_ST (specifically, the maximum SNP F_ST value within a window, or F_{ST_MaxSNP}) to detect diverse scenarios of local adaptation, and compared it against whole-window F_ST and the Comparative Haplotype Identity statistic. We found that F_{ST_MaxSNP} had superior power to detect complete or mostly complete soft sweeps, but lesser power than full-window statistics to detect partial hard sweeps. Nonetheless, the power of F_{ST_MaxSNP} depended highly on sample size, and confident outliers depend on robust precautions and quality control. To investigate the relative enrichment of F_{ST_MaxSNP} outliers from real data, we applied the two F_ST statistics to a panel of Drosophila melanogaster populations. We found that F_{ST_MaxSNP} had a genome-wide enrichment of outliers compared with demographic expectations, and though it yielded a lesser enrichment than window F_ST, it detected mostly unique outlier genes and functional categories. Our results suggest that F_{ST_MaxSNP} is highly complementary to typical window-based approaches for detecting local adaptation, and merits inclusion in future genome scans and methodologies.

Significance.

Studies that use genetic variation to search for genes evolving under population-specific natural selection tend to analyze data at the level of genomic windows that may each contain hundreds of variable sites. However, some models of natural selection (e.g., favoring an existing genetic variant) may result in genetic signals of local adaptation that are too narrow to be detected by such approaches. Here, we use both simulations and empirical data analysis to show that searching for a site-specific signal of elevated genetic differentiation can find instances of local adaptation that other approaches miss, and therefore, the integration of this signal into future studies may significantly improve our understanding of adaptive evolution and its genetic targets.

Introduction

Geographically distinct populations are exposed to different selective pressures, which may result in local adaptation. The detection of genomic regions under positive selection specific to one population is essential to uncovering the genetic basis of locally adaptive trait variation. Local adaptation can exist between populations with low genome-wide genetic differentiation, and comparing genetic variation between these closely related populations can allow for much more powerful detection of positive selection than is possible from a single population. In light of that advantage, as well as the potential applicability of genetic mapping and functional approaches to locally adaptive traits, local adaptation has played a key role in our increasing understanding of adaptive evolution at the genetic level (Kawecki and Ebert 2004; Yeaman 2015; Tigano and Friesen 2016). In addition to its importance for evolutionary biology and ecology, the identification of regions under selection has implications for applied fields such as health sciences and agriculture because it can also pinpoint regions of the genome that hold functional diversity (Bamshad and Wooding 2003; Ross-Ibarra et al. 2007). There has also been increasing recognition of the importance of local adaptation for a species’ future adaptive potential, with implications for conservation genetics and adaptation to climate change (Funk et al. 2012; Aitken and Whitlock 2013; Fitzpatrick and Keller 2015).

Population genomic scans for local adaptation compare genetic variation between two or more populations, often searching for specific genomic windows that depart from genome-wide patterns of differentiation in a manner consistent with population-specific natural selection. Positive selection has traditionally been conceptualized and modeled as a selective sweep, which traditionally involves a new beneficial mutation rising to fixation, with strong effects on genetic variation at linked sites (Smith and Haigh 1974; Kaplan et al. 1989). However, there are different kinds of selective sweeps, depending on the initial and final frequencies of the favored variant, and different statistical tests for deviations from neutrality vary in their power to detect them.

First, selective sweeps can be classified as hard or soft sweeps. In a hard sweep, only a single original haplotype carrying the advantageous allele is boosted by natural selection. This situation might be expected if selection favors either a newly occurring mutation or else a variant at low enough frequency that only one copy contributes to the sweep by chance. In a soft sweep, two or more distinct haplotypes carrying the beneficial variant increase in frequency. In some cases, soft sweeps occur because the advantageous allele was present in the population, segregating neutrally, prior to the onset of selection (Hermisson and Pennings 2005). But they can also be the result of recurrent mutations or influx of new alleles through migration (Pennings and Hermisson 2006a, 2006b).

Selective sweeps can also be classified as complete or partial sweeps. In a complete sweep, the advantageous allele has reached fixation in the population. In a partial sweep, the advantageous allele is at an intermediary frequency. This may occur either because the sweep is still ongoing, because positive selection ended prior to fixation, or (in the context of local adaptation) because migration continues to supply the non-favored variant. Situations in which a sweep might terminate prematurely include an environmental change, a polygenic trait reaching its new optimum or threshold value, or an allele reaching a balanced equilibrium in a scenario such as heterozygote advantage.

Different kinds of selective sweeps leave different signatures of local adaptation and our power to detect them will differ depending on which methods we use (Lange and Pool 2016). Some common approaches to scanning the genome for population-specific selective sweeps use F_ST (or F_ST-based) statistics to quantify genetic differentiation between populations. Local adaptation is expected to create genomic regions with more extreme differentiation than what would be expected under neutrality, since allele frequencies in these regions will change faster as the beneficial allele increases in frequency (Lewontin and Krakauer 1973). Neutral expectations can be inferred either with demographic simulations or an outlier approach. Demographic simulations, based on a previously estimated model of population history, can be used to mimic the history of the populations being studied in the absence of natural selection. Outlier approaches rely on the genome-wide distribution of F_ST as a proxy for the neutral distribution, since neutral forces (including those due to demographic history) can broadly be expected to affect the whole genome similarly. Genome scans for regions under selection have typically focused on measuring F_ST or other statistics in windows of the genome of some predefined size to search for highly differentiated genomic regions.

A motivating empirical example for the present study comes from an investigation of the genetic basis of locally adaptive melanism in high altitude Drosophila melanogaster populations. Here, the authors used QTL mapping to identify genomic regions associated with derived dark pigmentation traits, and then used F_ST to scan these regions for signatures of selection (Bastide et al. 2016). One very narrow and strong QTL for highland Ethiopian melanism contained the well-known pigmentation gene ebony, which also contributed to melanic evolution in an Uganda population (Pool and Aquadro 2007; Rebeiz et al. 2009). Assessing genetic differentiation between the Ethiopia and Zambia populations for the window containing ebony, although full-window F_ST was only marginally elevated, it had an SNP with extremely high F_ST (0.85). Compared with demographic simulations, this window's maximum SNP F_ST value was among the top 1% of all windows, while its full-window F_ST was only among the 7% highest (Bastide et al. 2016). Simulated scenarios of soft sweeps from standing variation replicated this pattern of extremely high maximum SNP F_ST and only moderately high window F_ST, suggesting that some kinds of selective sweeps that may not be detected using full-window F_ST could potentially be detected with an SNP-level F_ST approach. Further potential support for the use of SNP-level F_ST signals to detect adaptive events in this same species was demonstrated by much stronger parallel signatures of selection seen at the SNP level compared with the window level in fly populations that independently adapted to cold environments (Pool et al. 2017).

Challenges of using SNP-level F_ST values to detect selection include their variability due to random sampling effects (Weir et al. 2005) and the large number of tests that need to be made against a null distribution. Therefore, larger sample sizes are needed than for window F_ST. By using the highest SNP F_ST value within a window as a summary statistic for that window, and comparing it against null simulations with demography and recombination, we may somewhat improve the multiple testing issue, since here we are not treating all tightly linked SNPs as fully independent tests. Another advantage of this approach is that the maximum value summarizes each window of the genome, making it more comparable to any other window-based metric in terms of the number of tests and units of the genome analyzed. If full-window F_ST and maximum SNP F_ST are able to detect different types of selective events, then using both metrics could result in a more comprehensive scan for signatures of local adaptation. The genome-wide distribution of these statistics in natural populations, compared with their neutral expectations, might also shed light on the contribution of different kinds of selective sweeps to local adaptation.

To understand the utility of using the highest F_ST value of any SNP within a window (hereafter F_{ST_MaxSNP}) as a local adaptation summary statistic, we performed power analyses based on extensive simulations, and then applied these results to empirical data from natural populations of D. melanogaster. We focused on comparisons between two populations and calculated the power of F_{ST_MaxSNP} to detect signatures of local adaptation under a wide range of different selective scenarios (including partial and/or soft sweeps) and demographic histories (including population bottlenecks and scenarios with ongoing migration). We performed demographic simulations and compared the power of F_{ST_MaxSNP} to both full-window F_ST based on all variable sites (herein, F_{ST_FullWin}) and a comparative haplotype-based statistic (χ_MD, Lange and Pool 2016). Then, we investigated the genome-wide distribution of F_{ST_MaxSNP} and F_{ST_FullWin} among several natural populations of D. melanogaster, to determine whether either statistic was enriched genome-wide in empirical data compared with neutral expectations. Finally, we used an outlier approach to perform a genome scan for regions potentially under local adaptation between the Ethiopia and Zambia populations mentioned above, using F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD (Lange and Pool 2016), and we determined the extent of overlap between candidate regions identified according to these different methods. These analyses allowed us to both identify the parameter space in which F_{ST_MaxSNP} outperforms other statistics, and to assess the utility and complementarity of applying these approaches to real data.

Results

Maximum SNP F_ST and Full-Window Summaries Have Complementary Power to Detect Local Adaptation

We performed power analyses of F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD using population genetic simulations with and without natural selection. We used msms (Ewing and Hermisson 2010) to simulate a two-population isolation model with positive selection in one population but not the other. With constrained initial and final allele frequencies, yielding local sweeps that could be hard or soft, and partial or complete. Beyond the simple isolation model, demographic scenarios with population size bottlenecks or migration were simulated as well (simulation commands in supplementary table S1, Supplementary material online). For each scenario, we simulated both a low effective population size (N_e) model with mutation and recombination parameters based on estimates for humans, and a high N_e model with parameters motivated by D. melanogaster (see Materials and Methods), following the design of a previous power analysis study that did not include F_{ST_MaxSNP} (Lange and Pool 2016). These low and high N_e scenarios entail very different levels of diversity and scales of linkage disequilibrium (motivating contrasting window sizes of 100 kb vs. 5 kb in most of our analyses), and they may therefore provide useful reference points for a range of taxa beyond the motivating species themselves. For the low N_e simulations, we focused on sweeps with a selection coefficient of s = 0.01. In high N_e species, many successful sweeps may have weaker advantages. Here, we focused on results with s = 0.001. High N_e results with s = 0.01 gave similar results except where noted below (supplementary table S1, Supplementary material online). F_{ST_MaxSNP}, F_{ST_Fullwin}, and χ_MD were calculated between the selected and nonselected populations at the end of the simulation. Power was defined in a locus-specific context, based on the proportion of selection simulations giving a more extreme value of the summary statistic than the 95th quantile of its distribution from neutral simulations.

Unsurprisingly, all three statistics were found to have high power for the case of complete hard sweeps (fig. 1; supplementary table S1, Supplementary material online). These simulations were conditioned on fixation of a beneficial new mutation in one population that had not occurred in the other population. In light of this fixed difference, F_{ST_MaxSNP} in all replicates had its maximum value (F_{ST_MaxSNP} = 1). In such cases, the power of F_{ST_MaxSNP} was binary, either zero or one, depending on whether or not 5% of the corresponding neutral replicates had an allele that reached fixation. In our simple isolation model, the likelihood that a neutral allele can reach fixation increases with the split time (supplementary table S1 and fig. S1, Supplementary material online). Stronger bottlenecks also boost the likelihood of having neutral alleles reach fixation (supplementary table S1 and figs. S2 and S3, Supplementary material online). Hence, power for F_{ST_MaxSNP} to detect complete hard sweeps goes from high, for recent splits and weaker bottlenecks, to zero for histories in which more than 5% of neutral replicates contain a fixed difference. Similarly, F_{ST_FullWin} and χ_MD had higher power to detect signatures of local adaptation following recent splits and in weaker bottlenecks, but their change in power was gradual and continuous instead of binary.

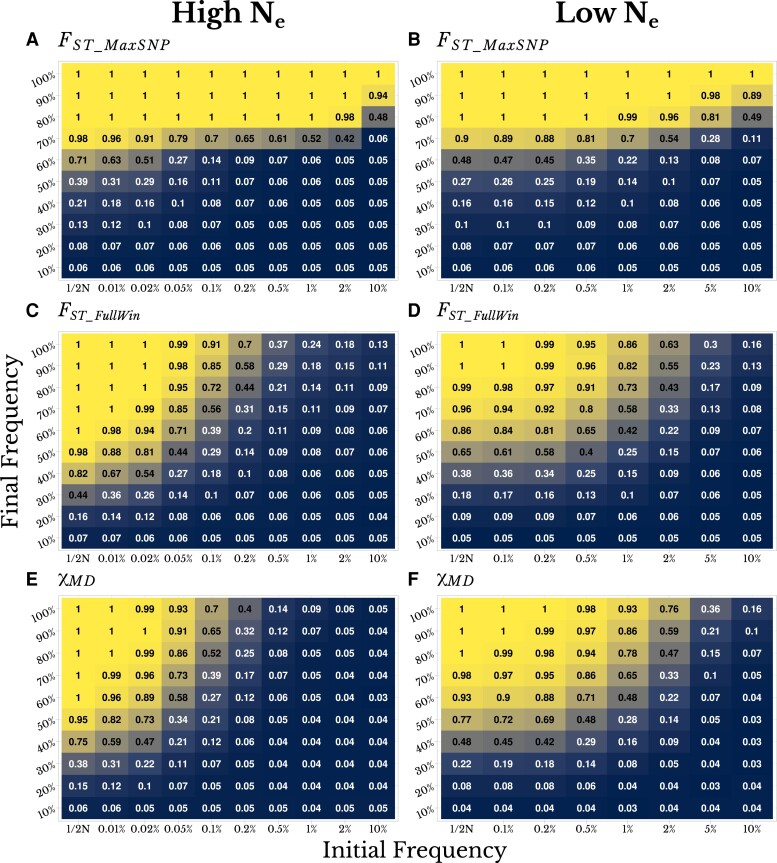
Fig. 1.

SNP-level F_ST and full-window statistics show complementary power to detect local adaptation, depending on the type of selective sweep simulated. Numbers and colors in each panel both depict statistical power to detect local adaptation, in high N_e populations (s = 0.001, left column) and low N_e populations (s = 0.01, right column). In each panel, the x-axis illustrates the pre-selection frequency of a favored variant (with the left column indicating selection on newly occurring mutations) and the y-axis illustrates the final frequency of the sweep (with the top row showing complete sweeps). Detection power is shown for (A and D) F_{ST_MaxSNP}, (B and E) F_{ST_FullWin}, and (C and F) χ_MD. These results are based on a demographic history of simple isolation between two populations without change in population size, with a split time of 0.2N_e generations.

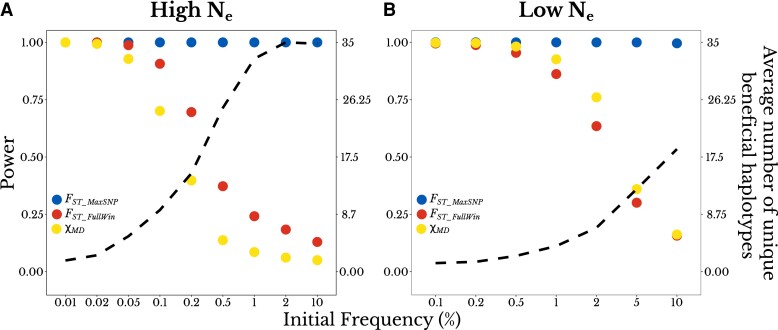
In the case of complete or nearly complete soft sweeps, F_{ST_MaxSNP} showed a clear power advantage over F_{ST_FullWin} and χ_MD. Notably, for sweeps ending between 80 and 100% frequency, F_{ST_MaxSNP} had high power to detect local adaptation, even for cases with rather high initial frequencies of the beneficial allele (e.g., 10%; figs. 1 and 2). In contrast, F_{ST_FullWin} and χ_MD showed rapidly diminishing performance as sweeps became softer (figs. 1 and 2). These results make sense, in that beneficial alleles that drift to higher pre-selection frequencies have more time to recombine onto multiple haplotypes, and recombination events will have happened closer to the selected site on average. Therefore, soft sweeps are generally narrower in width and may not substantially alter full-window statistics (Catania et al. 2004; Schlenke and Begun 2004; Hermisson and Pennings 2005). Although the two full-window statistics maintained good power for lower initial frequencies, some of the replicates of those scenarios are actually generating hard sweeps due to the chance survival of a single haplotype carrying the favored variant (Jensen 2014), as shown by an average number of beneficial haplotypes lower than two in these simulations (fig. 2). Moreover, as the average number of haplotypes carrying the favored variant increased, the power of the full-window statistics decreased (fig. 2), while the power of F_{ST_MaxSNP} was unchanged.

Fig. 2.

F_{ST_MaxSNP} shows an increasing power advantage as sweeps become softer. For complete sweeps with a range of initial frequencies (x-axis), the two y-axes show detection power for each statistic (left axis, dots) and the average number of unique beneficial haplotypes present at the end of the simulation (right axis, dashed line). Results are shown for (A) high N_e populations (s = 0.001) and (B) low N_e populations (s = 0.01), for the same demographic history as in fig. 1.

Contrasting results were obtained for partial, harder sweep scenarios. In cases where new mutations or rare standing variants were only boosted to intermediate frequencies, F_{ST_FullWin} and χ_MD had fairly strong power, whereas F_{ST_MaxSNP} declined sharply in effectiveness at around 60% final frequency for hard sweeps (fig. 1). These results are also intuitive, in that partial hard sweeps can meaningfully alter allele frequencies across a whole window and generate a class of identical haplotypes, even though no single SNP traverses an extreme range of frequencies. The broadly similar power profiles of F_{ST_FullWin} and χ_MD are somewhat surprising in light of their distinct basis (albeit consistent with Lange and Pool 2016). Less surprising is that for the challenging scenario of partial soft sweeps, none of the three statistics showed strong power in the scenarios examined (fig. 1).

Whereas the above simulations had no migration, we also wondered if F_{ST_MaxSNP} might prove useful in detecting targets of local adaptation for which genetic differentiation had been whittled down in width by recombination with migrant alleles over time (Sakamoto and Innan 2019). We, therefore, simulated scenarios with varying combinations of migration rate and population split time, while assuming symmetric migration rates and equal but opposing selective pressures. Overall, F_{ST_MaxSNP} and F_{ST_FullWin} performed very similar to each other and better than χ_MD. Particularly, in the high N_e scenarios (which feature a higher ratio of recombination to mutation events) with intermediate migration rates, there was a narrow space of parameters in which F_{ST_MaxSNP} performed slightly better than F_{ST_FullWin} (supplementary fig. S4, Supplementary material online). The split time between the populations greatly affected the power of χ_MD, which performed better on recent splits. The power of the F_ST statistics showed a small improvement for more recent splits and intermediate migration rates. Although small, the effect of split time also seemed more pronounced on F_{ST_FullWin} than F_{ST_MaxSNP} (supplementary fig. S4, Supplementary material online). Overall, these analyses provide only modest support for the notion that F_{ST_MaxSNP} could help detect peaks of genetic differentiation driven by local adaptation that have been narrowed by migration and recombination.

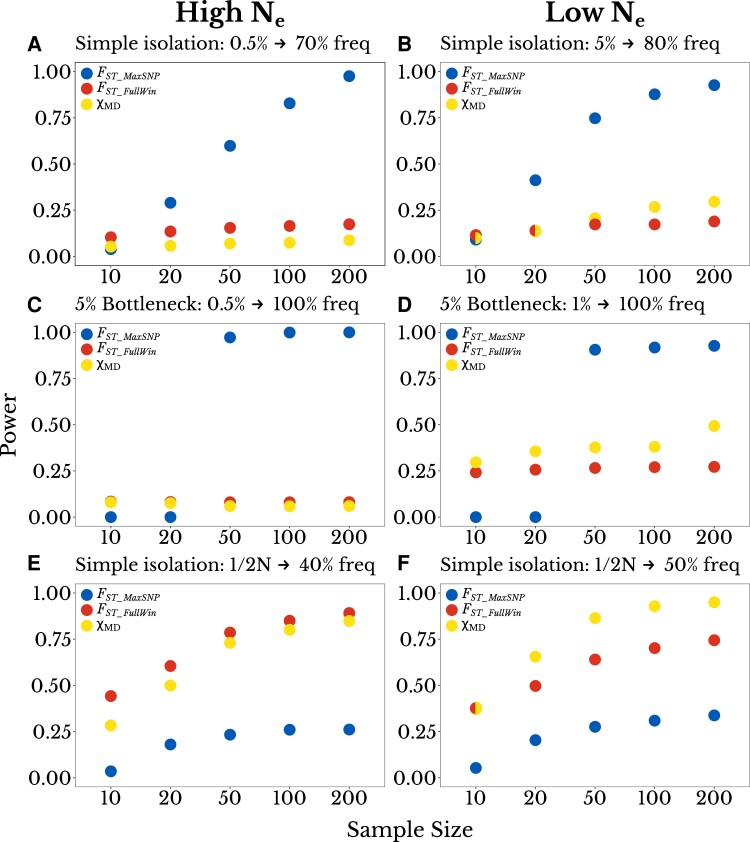
In the above simulations, we used a sample size of 50 chromosomes per population. We generally expect statistical power to be correlated with sample size and understanding the effect of sample size on the power of each statistic is relevant when designing an experiment or choosing which statistics to use. We analyzed the power of F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD in three scenarios for high N_e and three for low N_e. We chose scenarios in which F_{ST_MaxSNP} and the window-wide statistics performed differently: a mostly complete soft sweep, a complete soft sweep with a bottleneck, and a partial hard sweep. We found that sample size had a stronger effect on F_{ST_MaxSNP} than on the window-wide statistics (fig. 3). F_{ST_MaxSNP} is based on allele frequencies at a single site, so it is more sensitive to the increased sampling variance at lower sample sizes than window-wide statistics. The sampling variance in each SNP in a window should fluctuate around the mean, so when information from each SNP is combined the full-window F_ST statistic suffers less from the reduced sample size. Demographic history also affected the effect of sample size on each statistic: in scenarios with a population bottleneck, which also increases sampling variance, the power of F_{ST_MaxSNP} changed from near 1 at sample size 50 or higher to 0 at sample sizes smaller than 50 (fig. 3C and D). More generally, F_{ST_MaxSNP} was found to perform much better with 50 chromosomes than with 20, but showed relatively less improvement for sample sizes larger than 50.

Fig. 3.

The power of F_{ST_MaxSNP} is particularly sensitive to sample size. Here, the power of each statistic (y-axis) is plotted as a function of sample size (x-axis; number of chromosomes per population). We found that depending on sample size, F_{ST_MaxSNP} outperforms F_{ST_FullWin}and χ_MD for a simple isolation model, for: (A) a high N_e population with initial beneficial allele frequency of 0.005 and final frequency of 0.70, and (B) a low N_e population with initial frequency of 0.05 and final frequency of 0.80. Similar results were observed for a complete soft sweep with a population bottleneck of 0.05, except that the loss of power for F_{ST_MaxSNP} was more immediate at lower sample sizes, for: (C) a high N_e population with initial frequency of 0.05, (D) a low N_e population with initial frequency of 0.01. For partial hard sweep scenarios where F_{ST_FullWin} and χ_MD outperform F_{ST_MaxSNP}, all three statistics show more gradual sample size effects, specifically for new mutations and: (E) a final frequency of 0.40 in a high N_e population, and (F) a final frequency of 0.50 in a low N_e population.

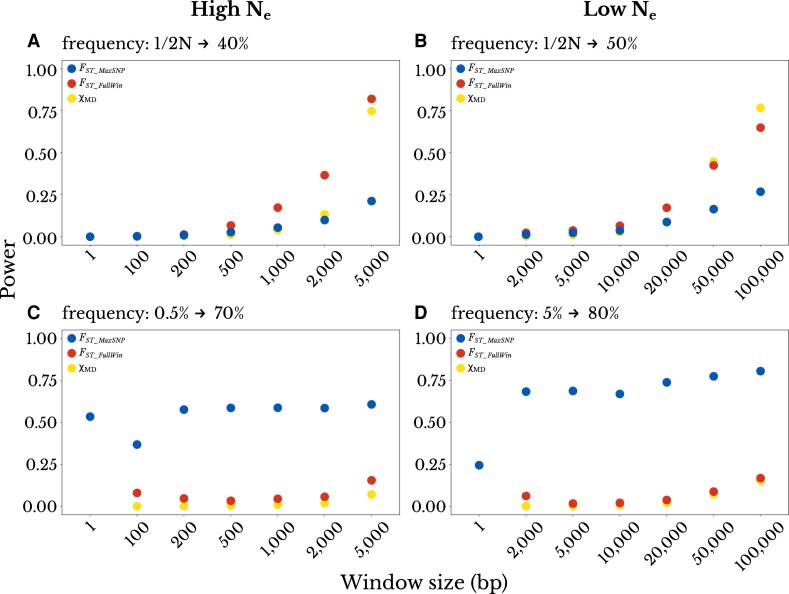
We also analyzed the effect of window size on the power of each statistic, with the aim of determining whether there would be a window size for which a single statistic would perform well in contrasting scenarios. For example, one might hope that F_{ST_FullWin} for a narrower window might retain good performance for partial hard sweeps, while also capturing the advantages of F_{ST_MaxSNP} for complete soft sweeps. We explored four scenarios of partial sweeps, two for the high N_e and two for the low N_e. For each population size, we chose one scenario in which the power of F_{ST_MaxSNP} outperformed F_{ST_FullWin} and χ_MD, and one in which it underperformed. In practice, a reduction in window size would result in an increase in the number of tests performed in a genome scan. Therefore, we applied a Bonferroni correction to the P-value proportional to the reduction in size. The correction for window size equal to one site (a single SNP) was proportional to the average number of SNPs in the largest window (the default window size used in our analyses). Our results showed that, for the two scenarios in which F_{ST_MaxSNP} outperformed F_{ST_FullWin} and χ_MD, the power of each statistic remained mostly constant (fig. 4). For the scenarios in which F_{ST_FullWin} and χ_MD had an advantage, the power of each statistic, as well as the difference among them, declined with smaller window sizes. Overall, there was no window size in which a single statistic performed well for all scenarios, and hence, it may be preferable to apply F_{ST_MaxSNP} and full-window statistics separately to empirical data.

Fig. 4.

Varying window size does not reveal a single statistic with broad detection power. The top panels show partial hard sweeps for which F_{ST_FullWin}and χ_MD outperform F_{ST_MaxSNP}: (A) a high N_e population with a final beneficial allele frequency of 0.40, and (B) a low N_e population with a final frequency of 0.50. The bottom panels show mostly complete soft sweeps for which F_{ST_MaxSNP}outperforms F_{ST_FullWin} and χ_MD: (C) a high N_e population with an initial beneficial allele frequency of 0.005 and final frequency of 0.70, and (D) a low N_e population with initial frequency of 0.05 and final frequency of 0.80. These power values reflect a Bonferroni-corrected significance threshold to reflect the relatively larger number of smaller windows needed. Results do not suggest that any statistic in a smaller window size captures the advantages of both F_{ST_MaxSNP} and the full-window statistics.

Outliers for F_{ST_MaxSNP} and F_{ST_FullWin} Are Enriched in Empirical Data

In light of the above results, we were interested in applying both F_{ST_MaxSNP} and F_{ST_FullWin} to an empirical data set, in part with an interest in quantifying the relative enrichment of outliers for each statistic and what that might hint about the modes of selection active in these populations. We chose to focus on data from the Drosophila Genome Nexus (Lack et al. 2015, 2016), because it contained several populations of D. melanogaster that were linked by an estimated model of population history (Sprengelmeyer et al. 2020) and had at least minimal sample sizes available for studying genome-wide patterns of F_ST (supplementary table S2, Supplementary material online). We included six natural populations of flies. From the ancestral range in Zambia, we included one town population (Siavonga) and one wilderness population (Kafue). We also included four additional town populations: from Rwanda, South Africa, Ethiopia, and France (the latter three having independently colonized colder environments; Pool et al. 2017).

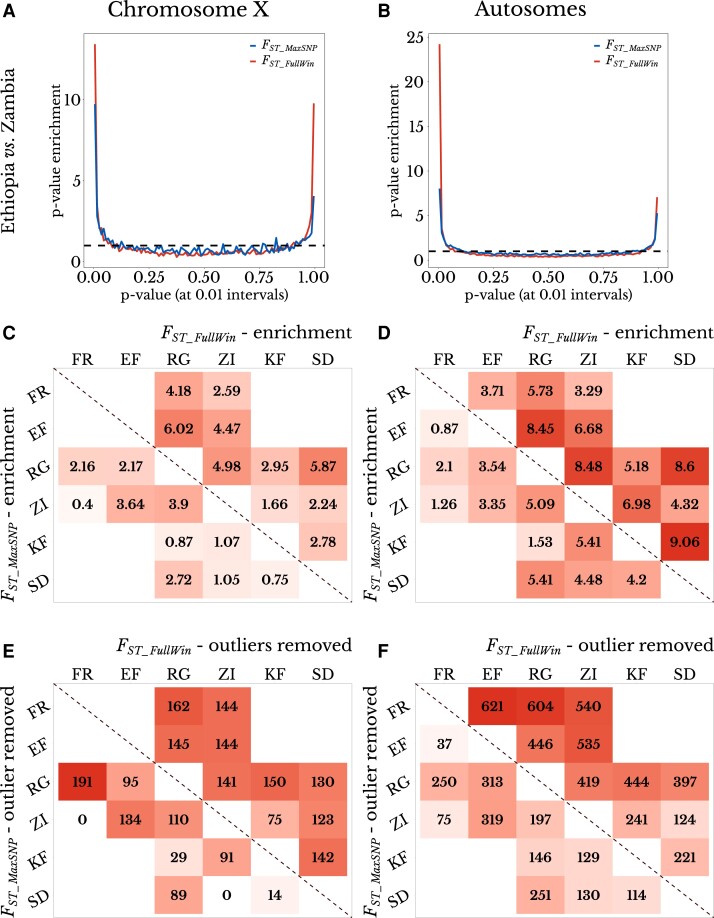
We calculated a P-value for each empirical window in each pairwise population comparison, based on neutral distributions of F_{ST_MaxSNP} or F_{ST_FullWin} generated using coalescent simulations of the estimated demographic history (Sprengelmeyer et al. 2020; simulation commands in supplementary table S2, Supplementary material online). Under neutrality, a uniform distribution of P-values is expected. In general, for most population pairs, the distribution of P-values for F_{ST_MaxSNP} and F_{ST_FullWin} showed a U-shape instead of a uniform distribution (e.g., fig. 5A and B). The deviation from the expected uniform distribution could be attributed to the action of natural selection producing windows with higher and lower F_ST than expected (e.g., by local adaptation and shared sweeps, respectively) or by a misspecification of the neutral demographic model. However, the average F_ST values of simulated data from this model were found to align well with empirical measurements (Sprengelmeyer et al. 2020), and similar results were found with other summary statistics. The enrichment of high F_ST (defined as P-values from 0 to 0.05) and low F_ST (P-values from 0.95 to 1) varied for each statistic and across the population comparisons (fig. 5C and D). Particularly for high F_{ST_FullWin}, the strongest enrichments were often observed for more geographically proximate, closely related population pairs, perhaps reflecting reduced noise from neutral genetic differentiation.

Fig. 5.

F_{ST_MaxSNP} and F_{ST_FullWin} both show outlier enrichment between natural populations of D. melanogaster. (A and B) Ethiopia–Zambia F_{ST_MaxSNP} and F_{ST_FullWin} values on (A) chromosome X and (B) autosomes show enrichment of low (right) and especially high values (left), based on the distribution of P-values obtained from neutral demographic simulations. (C and D) F_{ST_MaxSNP} (lower diagonal) and F_{ST_FullWin} (upper diagonal) both show enrichment of high outliers on (C) chromosome X and (D) combined autosome arms. F_{ST_FullWin} shows a greater enrichment in nearly all cases. (E and F) The number of outlier regions that were removed to erase the signature of enrichment for high F_{ST_MaxSNP} (lower diagonal) and F_{ST_FullWin} (upper diagonal) for each population on (E) chromosome X and (F) the combined autosome arms. F_{ST_FullWin} was associated with a greater outlier region enrichment for most population pairs, reinforcing the window-level patterns shown in (C) and (D). Populations: SD, South Africa; ZI, Zambia; KF, Kafue; RG, Rwanda; EF, Ethiopia. Population pairs that were not present in the same demographic model were not evaluated. Color scale ranges from the minimum to maximum value within each panel.

All population pair comparisons showed an enrichment for windows with high F_{ST_FullWin}. The smallest enrichment was found between the Zambia (town) and France populations, for which there were 3.29 more windows with high F_{ST_FullWin} than expected by chance. The highest enrichment was found in the comparison between the South Africa and Kafue (Zambia wilderness) populations, with an enrichment factor of 9.06. For F_{ST_MaxSNP}, eight population pairs had an enrichment value > 2, the highest being 5.41 (between the Zambian town and wilderness populations, and between South Africa and Rwanda). On the other hand, one population pair was slightly depleted of windows with high F_{ST_MaxSNP} (enrichment to 0.87 between France and Ethiopia). In nearly all comparisons, F_{ST_FullWin} showed higher enrichment than F_{ST_MaxSNP} (fig. 5). However, this difference in enrichment could be influenced by single local sweeps that generate multiple linked outlier windows. We, therefore, pursued a complementary analysis in which nearby outlier windows were merged into “outlier regions”, which were then removed one at a time until the observed enrichment was erased (see Materials and Methods). For almost every population pair, we had to remove a larger number of regions to erase the signal of enrichment of F_{ST_FullWin} than the signal of F_{ST_MaxSNP} (fig. 5E and F). Hence, the greater enrichment of F_{ST_FullWin} relative to F_{ST_MaxSNP} does not appear to be a product of broader linkage signals of F_{ST_FullWin} outliers alone. Instead, this pattern could hint that sweeps in the unique detection parameter space of F_{ST_FullWin} (i.e., partial harder sweeps) are more common among these populations than sweeps in the unique space of F_{ST_MaxSNP} (i.e., more complete softer sweeps). However, these results may be influenced by other evolutionary forces as well, and they do not offer definitive conclusions about the prevalence of different models of selection (see Discussion).

Our simulation results above suggested that high F_{ST_MaxSNP} and F_{ST_FullWin} outliers might be capturing different kinds of selective sweeps. To assess this possibility from the empirical data, we focused on high F_{ST_MaxSNP} and F_{ST_FullWin} outlier regions (as described above) from the Ethiopia versus Zambia comparison. We calculated the frequency of the most common haplotype, haplotype homozygosity, and the H2/H1 statistic (Garud et al. 2015) for the outlier regions exclusively detected with F_{ST_MaxSNP} and those exclusively detected with F_{ST_FullWin}. Congruent with F_{ST_MaxSNP} exclusive outliers mainly detecting cases of soft sweeps and F_{ST_FullWin} exclusive outliers detecting hard partial sweeps, we found that for both the Ethiopian and the Zambian populations, the frequency of the most common haplotype and haplotype homozygosity was lower in the F_{ST_MaxSNP} outliers, while H2/H1 was higher (meaning the haplotype homozygosity calculated with and without the most common haplotype was more similar to each other) in the F_{ST_MaxSNP} exclusive outliers than F_{ST_FullWin} (supplementary fig. S5, Supplementary material online).

We also performed an outlier removal analysis for windows with high P-values (low F_ST), which could reflect shared sweeps or other processes. Similar to the low P-value enrichment analysis, we found varied results for each statistic and population pair (supplementary fig. S6, Supplementary material online).

Genome Scan for Signatures of Selection

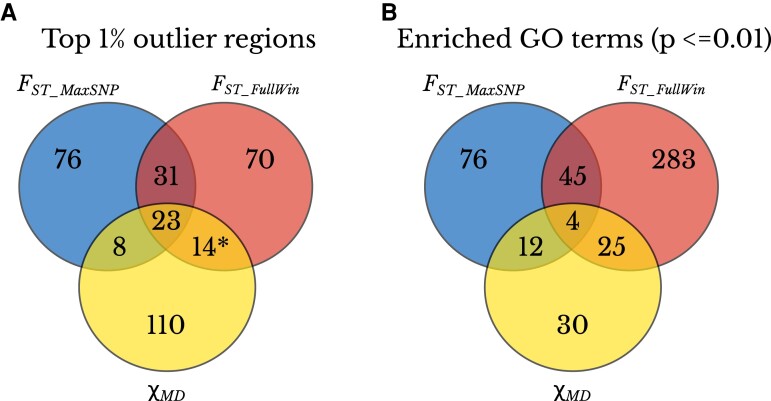
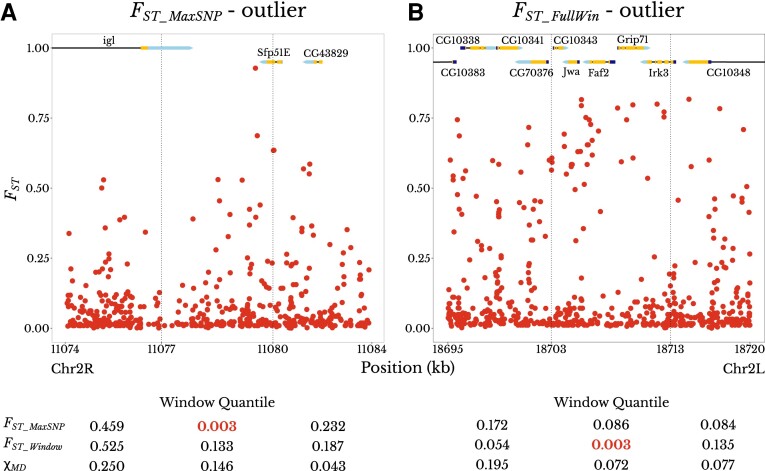
We chose to complement the above multi-population analysis of genome-wide patterns with a closer analysis of a single population pair. We chose to compare the Ethiopia and Zambia town populations because (1) their relatively large sample sizes of 129–181 and 60–76, respectively, for each chromosome arm (supplementary table S2, Supplementary material online) are more conducive to the analysis of specific F_{ST_MaxSNP} outliers; (2) these populations showed enrichments of both F_{ST_MaxSNP} and F_{ST_FullWin} (fig. 5); and (3) past results from these populations helped motivate the present study (e.g., Bastide et al. 2016). We performed genome scans for regions potentially under population-specific selection between these populations using F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD. For each statistic, we obtained a list of outlier windows (top 1%), and as above, we merged nearby outlier windows into regions (Materials and Methods). We obtained 138 outlier regions for F_{ST_MaxSNP}, 138 for F_{ST_FullWin}, and 155 for χ_MD. Our results showed an overlap of just 39% between the outlier regions detected with F_{ST_MaxSNP} and F_{ST_FullWin}. Perhaps surprisingly in light of the above power results, there was a smaller overlap of either F_ST metric with χ_MD (fig. 6A), although the overlap of the haplotype statistic with F_{ST_FullWin} was indeed slightly greater. In regions that were outliers for F_{ST_MaxSNP} but not F_{ST_FullWin}, the distribution of individual SNP F_ST values often had a narrow sharp F_ST peak, with most of the other SNPs having low F_ST values. On the contrary, in regions there were outliers for F_{ST_FullWin} but not F_{ST_MaxSNP}, often no single SNP had a large F_ST value, but there was a broad moderate F_ST plateau with many SNPs showing intermediate F_ST values (fig. 7).

Fig. 6.

The three statistics detect mostly unique genomic regions and functional categories. (A) Overlap between the top 1% outlier regions detected with F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD. * indicates the average number of outlier regions between the two statistics: 15 F_{ST_FullWin} outlier regions exclusively overlap χ_MD outliers and 13 χ_MD outlier regions exclusively overlap F_{ST_FullWin} outliers. (B) Overlap between enriched GO terms with raw P-value <= 0.01, out of a total of 47,496 GO terms, based on the outlier regions detected with F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD.

Fig. 7.

Examples of the distinct SNP-level F_ST landscapes associated with F_{ST_MaxSNP} versus F_{ST_FullWin} outliers. Each plot shows an outlier window for an Ethiopia–Zambia F_ST statistic, plus its adjacent windows. Dashed vertical lines delimit the boundaries of the windows. Numbers under each window are the empirical quantiles of that window's statistic (F_{ST_MaxSNP}, F_{ST_FullWin}, and χ_MD) in relation to the chromosome arm-wide distribution of the same statistic, with the outlier (quantile < 0.01) value in red. (A) An outlier window for F_{ST_MaxSNP} (center) shows a peak-like F_ST landscape with one particularly differentiated SNP. (B) An outlier window for F_{ST_FullWin} (center) shows a broad plateau of fairly high F_ST values. Gene names and structures are shown at the top of each plot. Protein-coding exons are in yellow, while 5′ and 3′ untranslated regions are in dark blue and light blue, respectively.

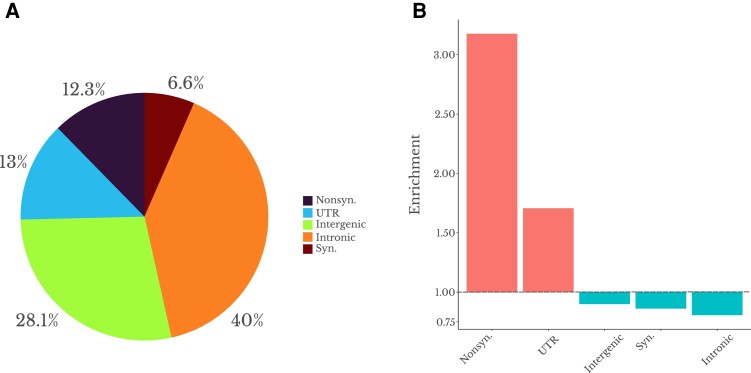
The SNP with the highest F_ST value in each outlier region for F_{ST_MaxSNP} could potentially represent the target of selection; therefore, we asked whether they were enriched for functional site annotations generally associated with greater evidence for positive and negative selection. We classified these SNPs into five different classes: nonsynonymous, synonymous, untranslated region of the mRNA (UTR), intronic, and intergenic. We then compared the proportion of “top SNPs” (i.e., having the highest SNP F_ST within a F_{ST_MaxSNP} outlier region) in each functional site category against that category's genome-wide proportion, based on SNPs with similar allele frequencies. We found the biggest enrichment among nonsynonymous (protein-altering) sites, with an enrichment of 3.2, followed by UTR sites (fig. 8). The remaining classes were not enriched, and the intronic class was the most depleted class, with an enrichment of 0.8 (fig. 8). Previous studies have found evidence of selection on noncoding sites in Drosophila, especially on UTR sites—which have shown more selective constraints and proportionally more adaptive substitutions than intronic and intergenic sites (Andolfatto 2005; Lange and Pool 2018). The enrichment of nonsynonymous and UTR sites in our analysis also mirrors results from human F_ST outliers (Barreiro et al. 2008). Overall, there is a strong tendency for our top SNPs to occur in site categories more likely to affect fitness, as we would predict if some of them are actual targets of selection. If a beneficial mutation in these sites was already present as a standing variation in the population before the onset of selection, the increase in the frequency of beneficial mutation in a single population could result in a narrow sharp F_ST peak within the genomic region (fig. 7).

Fig. 8.

The most differentiated SNPs in F_{ST_MaxSNP} top outlier regions are strongly enriched for site categories known to experience more frequent selection. (A) Proportional distribution of these top SNP among five different classes: nonsynonymous, untranslated regions (UTR), intergenic, synonymous, and intronic. (B) Enrichment analysis of each the five classes in the outlier regions for F_{ST_MaxSNP} in comparison to genome-wide distribution for all SNPs with similar minor allele frequencies.

We then performed Gene Ontology (GO) term enrichment analysis separately for each statistic's list of outlier regions. Considering only GO terms with raw P-value <0.01 from each list, we found mostly lower overlaps between enriched GO terms compared with the spatial overlap between outlier regions (fig. 6B; supplementary table S3, Supplementary material online). The three statistics differed substantially in the number of enriched GO terms by this criterion: 357 for F_{ST_FullWin}, 133 for F_{ST_MaxSNP}, and 71 for χ_MD (out of 47,496 total GO terms tested). We emphasize that enriched terms in each set are not necessarily independent and any given list of enriched GO terms will contain overlapping categories. The relative overlap between GO terms enriched for each statistic largely followed the relative numbers of enriched GO terms for each (fig. 6B). Mirroring the outlier region results, most enriched GO terms were detected for only one of the three statistics, highlighting the complementarity of each statistic described above. Different categories of genes have different mutational target sizes and may also vary in their ability to harbor potentially functional variation. Hence, the supply of standing genetic variation to generate soft (as opposed to hard) sweeps may differ between GO categories, as hinted by our results. Here, a number of the most enriched GO terms for F_{ST_FullWin} involved nucleotide/ribonucleotide binding (supplementary table S3, Supplementary material online). Whereas, many of the most enriched GO terms for F_{ST_MaxSNP} pertained to ion channels, a finding concordant with previously reported parallel signals of positive selection in cold-adapted D. melanogaster populations, based on SNP-level genetic differentiation outliers (Pool et al. 2017).

Discussion

F_{ST_MaxSNP} Complements Other Statistics by Detecting Soft Sweeps

Identifying regions under selection can help us answer further questions about the evolution of local adaptation, such as which biological functions are under selective pressure, the number of loci underlying adaptive events, the source of the adaptive variation, and the kinds of genetic changes that might be under selection. Our results underscore the importance of deploying methods capable of capturing different kinds of selective sweeps when the aim of the study is to identify as many genes potentially under local adaptation as possible.

F_{ST_MaxSNP}, in particular, seems to be especially useful to detect soft sweeps with relatively large initial and final frequencies of the beneficial allele. Instances of mostly complete soft sweeps, as simulated here, represent regions in which a beneficial allele was present in several different haplotypes that might have increased in frequency along with the beneficial allele. While the selected SNP itself changed in frequency drastically, resulting in a large F_{ST_MaxSNP}, the alleles around it must have changed in frequency to a lesser degree because many background haplotypes were hitchhiking along with the beneficial allele. Therefore, while the beneficial variant can have an extreme F_ST value, the lower allele frequency changes in the other SNPs in that window would result in a F_{ST_FullWin} that is not statistically significant, and thus a low power to detect a selective sweep under these conditions.

The full-window metrics, F_{ST_FullWin} and χ_MD, had greater power than F_{ST_MaxSNP} to detect relatively harder, partial sweeps that had intermediate final allele frequencies. In these sweeps, no individual SNP changed dramatically in frequency, so none have F_ST values higher than what could be obtained randomly in the genome. However, the increase in the frequency of one or a few haplotypes resulted in many SNPs in the same region with intermediate F_ST, producing a window-wide pattern that is too extreme to be generated by chance—even if each single marker individually did not have an extreme F_ST value.

We note that Kimura et al. (2007) also compared the power of a maximum SNP F_ST statistic against a haplotype statistic, in the context of detecting hard sweeps from SNP genotyping data. Consistent with our study, they found that the haplotype statistic performed better than maximum SNP F_ST in this hard sweep context. They also found that among simulation replicates, these two statistics were inversely correlated. These results are congruent with our general findings of complementary power between maximum SNP F_ST and either a comparative haplotype identity statistic or a full-window F_ST statistic.

The Power of Each Statistic Depends on Population History

Importantly, the relative utility of each statistic to detect local adaptation was found to vary as a function of demographic history. For example, although F_{ST_MaxSNP} is generally much better than the studied full-window statistics at detecting complete soft sweeps, this advantage can be reversed if demography, in conjunction with sample sizes, yields fixed differences in at least 5% of windows under neutrality (in which case the power of F_{ST_MaxSNP} as we have defined it becomes zero). We demonstrated this phenomenon in cases with elevated genetic drift between populations, resulting from either a more ancient population split (supplementary fig. S1, Supplementary material online) or else a strong population bottleneck in the adapting population (supplementary figs. S2 and S3, Supplementary material online). These results underscore the importance of performing simulations to test whether F_{ST_MaxSNP} is expected to be a useful metric for any given population pair of interest.

There was little difference in the power of F_{ST_MaxSNP} and F_{ST_FullWin} to detect regions under selection in scenarios with varying migration rates. We had wondered if F_{ST_MaxSNP} would outperform F_{ST_FullWin} in scenarios with older splits, as selection might only maintain a narrow window of differentiation between the two populations in the presence of long-term recombination with migrant haplotypes (Sakamoto and Innan 2019). Nonetheless, differences in the time of population divergence and local adaptation only had a small effect in a very narrow space of parameters (intermediate migration rates for high N_e populations, supplementary fig. S1, Supplementary material online), suggesting that even in scenarios with recent divergence, the populations had already reached a state of equilibrium and the balance between migration, selection, and recombination, which did not result in contrasting signatures of selection between F_{ST_MaxSNP} and F_{ST_FullWin}. However, both metrics outperformed χ_MD on the simulated scenarios, indicating that selection could not maintain long-shared haplotypes in the presence of migration.

For simplicity, we have limited our focus to the detection of local adaptation from two-population isolation models (with and without migration). Such histories may be generally relevant for many taxa, including species that have recently invaded novel ranges, comparisons between domestic organisms and wild relatives, and island-dwelling taxa. Still, it is worth keeping in mind that many species exist as geographically complex mosaics of populations connected by migration. Patterns of genetic variation prouced by positive selection (and by neutral processes) in spatially explicit contexts involve additional nuance not reflected in our study (e.g., Ralph and Coop 2015; Lee and Coop 2017). For example, a hard sweep in a subdivided population is expected to be narrower than it would otherwise be, as recombination events continue to whittle down the sweeping haplotype as it spreads from one deme to another (Santiago and Caballero 2005), which might further support the analysis of F_ST at the level of SNPs or narrower windows. However, more detailed study is needed to fully document the expected genomic scale of F_ST outliers in spatially complex population models.

Consideration Must Be Given to Window Size, Sample Size, and Multiple Testing

In this study, we have used neutral demographic simulations to estimate statistical power at the single window level, only penalizing multiple tests when comparing between window sizes. Clearly, our results do not imply the power to identify genome-wide significant loci, which is only rarely attainable for population genomic scans. Instead, most genome scans aim to identify good candidates for downstream study, and our results are best interpreted in terms of the relative utility of these summary statistics to identify local adaptation candidates. Similar interpretations should apply to genome scan outliers based on F_{ST_MaxSNP} versus other window-based summary statistics, unless it can be shown (e.g., via neutral demographic simulations) that an extreme observed value of F_{ST_MaxSNP} would not be expected anywhere in the genome.

In light of the complementary performance of F_{ST_MaxSNP} and F_{ST_FullWin} for the non-migration cases, we tested whether F_{ST_FullWin} across shorter windows could yield a balance of reasonable power to detect both complete soft sweeps and partial hard sweeps. However, the relationship between window size and the power—while accounting for the increase in the number of tests in smaller windows—did not follow this prediction. Our results suggest that applying both F_{ST_MaxSNP} and F_{ST_FullWin} to conventionally sized windows is preferable to shrinking the window size in an effort to identify narrower soft sweeps. Nevertheless, window size remains a challenging decision in genome scans including those searching for local adaptation. Importantly, the scale of elevated genetic differentiation depends on multiple factors, including the magnitudes of selection, recombination, and migration, the timing of the onset of adaptation, and as we highlight, the initial frequency of a favored variant. In general, we suggest that genetic differentiation on both SNP and broader scales should be incorporated into scans for local adaptation, whether using the specific summary statistics described here, or attempting to develop a single statistic or integrated analysis framework that encompasses the advantages of both.

An important caveat of using F_{ST_MaxSNP} is that it requires a greater sample size than F_{ST_FullWin}. With smaller samples, it is easy to get a large F_{ST_MaxSNP} at one of the many analyzed SNPs through sampling variance alone, whereas an extreme F_{ST_FullWin} value is less likely in this scenario. It is difficult to provide any universal advice regarding sample size, because the neutral variance of F_{ST_MaxSNP} also depends strongly on demographic history, as shown above. Nonetheless, we have shown that in two scenarios in which F_{ST_MaxSNP} outperformed F_{ST_FullWin}, its power declined considerably when we decreased the sample size from 50 to 20 chromosomes. Although the relationship between sample size and power will depend on the specific populations being studied, the utility of F_{ST_MaxSNP} seems most promising when sample sizes are around 100 alleles per population or more. However, it would be advisable to conduct neutral simulations based on estimated or suspected demography, in order to identify sample sizes for which it is very unlikely to get extreme single-SNP F_ST values in the absence of local adaptation.

Both F_{ST_FullWin} and F_{ST_MaxSNP} Outliers Are Enriched among Drosophila Populations

When we applied F_{ST_FullWin} and F_{ST_MaxSNP} to empirical data from D. melanogaster populations, we found that enrichment patterns of F_{ST_FullWin} and F_{ST_MaxSNP} varied among population pairs, both for high and low F_ST values. The excess of windows with high F_ST observed could be explained by local adaptation: unique selective sweeps in one population increase the differentiation between two populations in that region. Not all population pairs showed the same degree of enrichment for high F_ST. A larger enrichment could be due to a higher number of selective sweeps between two populations, stronger selective events that impacted a larger region of the genome, or a neutral history more conducive to outlier detection. The populations we studied cover a large geographical scale, most are located in sub-Saharan Africa and one in Europe. These populations are exposed to a variety of environments, ranging from warm tropical lowlands to cool high latitude and high altitude regions, in addition to commensal versus wilderness settings (Sprengelmeyer et al. 2020). Hence, they are most likely exposed to several unique selective pressures that could be underlying local adaptation and an enrichment of high F_ST values.

Alternatively, enrichment for high F_ST could also be explained by background selection, which is expected to reduce genetic diversity and therefore result in lower effective population sizes in that genomic region. Genetic drift is stronger in regions of low N_e, which could increase the differentiation between two populations and produce high F_ST (Charlesworth et al. 1993). However, a simulation study of background selection targeting stickleback exons found no evidence for background selection increasing F_ST outliers (Matthey-Doret and Whitlock 2019).

On the other extreme, the existence of enrichment for low values of F_ST suggests that many regions of the genome maintained unexpectedly similar allele frequencies between two populations. Following a population split, neutral evolutionary forces such as genetic drift are expected to increase the genetic differences between two populations. The fact that many regions seemed to have changed less than what was expected due to neutral forces could also be explained by the action of natural selection. This pattern could be the product of shared selective sweeps (i.e., similar selective pressures) taking place in both populations, instead of local adaptation. Shared balancing selection could also be acting at some loci to maintain allele frequencies constant between two populations, perhaps even from before their split time.

We should also acknowledge that the demographic models applied here are simply the best available estimates of population history, and no demographic model fully accounts for the complexity of natural populations. Demographic model misspecification could result in some enrichment of high and/or low F_ST values. One potential source of error in demographic estimation is natural selection. The demographic models were estimated based on tentatively neutral regions of the genome (Sprengelmeyer et al. 2020). However, these regions could be under the influence of linked positive and negative selection, with the potential to bias demographic estimation. For example, if the presumed neutral data was substantially affected by either local adaptation or shared sweeps, it could bias the neutral distribution of F_ST towards higher or lower values, respectively, making it more difficult to detect F_ST outliers in that direction. Nonetheless, previous work suggests that this effect might be weak on demographic inference in D. melanogaster (Lange and Pool 2018).

Having hundreds of F_ST outlier regions (high or low) between recently diverged population pairs is not unreasonable in light of previous estimates of adaptive divergence. It has been estimated that 19% of substitutions between D. melanogaster and D. simulans were driven by positive selection (Lange and Pool 2018). Individual genomes from these two species differ at about 5% of sites, although roughly 1% is expected to be driven by segregating polymorphism rather than fixed differences. Given a genome of 120 million bases, this implies an estimated 120,000,000 × (0.05–0.01) × 0.19 = 912,000 selectively driven differences between species. These species are estimated to have diverged about 13,000,000 generations ago (with some uncertainty; Obbard et al. 2012), whereas our studied populations are all estimated to have diverged within the past 195,000 generations (Sprengelmeyer et al. 2020). Crudely then, we might predict as many as 912,000 × (195,000/13,000,000) = 13,680 selectively driven differences between a population pair such as Ethiopia and Zambia D. melanogaster. Hence, although any outlier set may contain both true and false positives for local adaptation, our finding of hundreds of potential targets of adaptation between pairs of D. melanogaster populations does not exceed the potentially expected number of selection-driven differences between them.

In nearly all population pairs, F_{ST_FullWin} showed a larger enrichment than F_{ST_MaxSNP}. The greater enrichment of F_{ST_FullWin} persisted when we instead pursued an outlier region removal strategy. In light of the complementary zones of power shown in fig. 1, these results suggest that roughly speaking, there might be a larger contribution of partial hard sweeps than complete soft sweeps to local adaptation among these populations. Furthermore, the importance of partial sweeps in populations of D. melanogaster has been proposed previously, including for some of the populations studied here (Pool and Aquadro 2007; Bastide et al. 2016; Garud and Petrov 2016; Vy et al. 2017). Therefore, seeing fairly low levels of overlap between F_{ST_MaxSNP} and F_{ST_FullWin} outliers, alongside particularly strong enrichment for F_{ST_FullWin} outliers, is congruent with the suggested predominance of partial sweeps in the species.

Precautions Are Needed to Ensure High-Quality F_{ST_MaxSNP} Outliers

A critically important caveat of using F_{ST_MaxSNP} is that this statistic should be more sensitive to bioinformatic errors than a metric that uses information from all the SNPs in a window. A sequencing or mapping error could cause a single SNP in a window to have a high F_ST value, while in a full-window approach such errors are often minimized by being localized to only one or few of the SNPs being aggregated. To reduce false positives from data artifacts, particular consideration should be given to multiple aspects of data preparation and analysis when using F_{ST_MaxSNP}. Prior to population genetic analysis, it is worth considering whether enhanced genotype calling filters are called for, such as increased quality score or depth of coverage thresholds. Excluding sites within a few bp of called indels may also be helpful in reducing erroneous site calls (Lack et al. 2015). Furthermore, it is important to ensure that data from all population samples have been collected and assembled the same way. For example, Lange et al. (2022) found that a set of SNP-level genetic differentiation outliers from a comparison between individually sequenced and pool-sequenced population samples were not reliable until genomes from the individually sequenced population were reassembled using a pipeline analogous to the pool-seq data.

Precautions should also apply to the population genetic analysis itself. Given that F_{ST_MaxSNP} is very sensitive to sample size (fig. 3), variation in missing data among the sequences of each individual may result in heterogeneous sample sizes for different SNPs in a given window, and therefore using a relatively high minimum sample size threshold for each population is essential. Finally, additional quality control assessment of F_{ST_MaxSNP} outliers following population genetic analysis is desirable. For example, it may be worth confirming that outlier SNPs do not appear to be impacted by depth anomalies suggestive of cryptic structural variation, and are not associated with alignment uncertainty or suboptimal quality scores. When depth or alignment issues are present, the outlier SNP could potentially be tagging a structural variant under local selection as opposed to representing a pure false positive. In other cases, soft sweeps targeting structural variants might be missed entirely if they fail to strongly alter frequencies at linked SNPs.

The enrichment of nonsynonymous (and UTR) sites among our “top SNPs” in F_{ST_MaxSNP} outlier regions (fig. 8) offers hope that at least in our empirical analysis, many F_{ST_MaxSNP} outlier regions may represent true positives for local adaptation, and that top SNPs may sometimes even reflect causative variants. However, we emphasize that even for true cases of local adaptation, a non-causative SNP may sometimes have a slightly higher F_ST value than the causal SNP, simply by chance. And in light of the data quality concerns described above, it makes sense to interpret isolated high F_ST SNPs with caution.

Overall then, F_{ST_MaxSNP} outliers may have a wide range of potential significance, ranging from false positives to indicating strong hypotheses for specific variants under selection. Functional experiments may hold particular appeal for F_{ST_MaxSNP} outliers, both to confirm their validity and to investigate the variants they implicate. First, methods such as reciprocal hemizygosity tests (Stern 2014; Turner 2014) may confirm that the implicated genes are associated with detectable trait differences between populations, which would support the outlier F_ST signal representing a true positive. Further molecular or transgenic experiments could then assess the consequences of modifying individuals high-F_ST variants, to improve our understanding of the precise genetic changes targeted by natural selection.

Summary and Future Prospects

Here, we have shown that SNP-level F_ST (F_{ST_MaxSNP}) offers strong power to detect soft sweeps, and is highly complementary to full-window frequency and haplotype statistics for detecting local adaptation. These results stress the importance of taking into account the different signatures left by different kinds of selective sweeps in the genome when deciding how to perform a genome scan. The raw summary statistics evaluated here can either be applied in parallel, or their signals can be integrated into frameworks such as approximate Bayesian computation and machine learning. Thus far, the latter methodologies have been used more extensively to detect and classify selective sweeps within a single population (Peter et al. 2012; Schrider and Kern 2016, 2017; Sheehan and Song 2016). However, such approaches are equally applicable to the study of local adaptation (Key et al. 2014). Future work could investigate whether methods that combine multiple statistics would benefit from including F_{ST_MaxSNP}, potentially increasing their power to detect soft sweeps and their accuracy in classifying different types of sweeps. Because studies of genetic differentiation between populations inherently control for evolutionary variance in the shared ancestral population, local adaptation may offer a better “signal-to-noise ratio” regarding the types of positive selection acting in natural populations, compared with single population studies. Hence, our results may contribute toward not only an improved ability to detect local adaptation, but also a clearer understanding of adaptation in nature more generally.

Methods

Simulation Power Analysis

To generate adaptive and neutral distributions of genetic diversity, we performed simulations of demographic history scenarios with and without natural selection using msms (Ewing and Hermisson 2010). Our simulations consisted of two populations with a population split, and population-specific selective sweeps in the scenarios with natural selection. For each model, we obtained 10,000 replicates from which we calculated the statistics of interest. Power was calculated as the proportion of replicates under selection with a statistical value larger than 95% of the values obtained in its corresponding replicates without selection. We investigated the power of three different statistics: F_{ST_MaxSNP}, F_{ST_FullWin} and χ_MD (Lange and Pool 2016), which were calculated on windows of fixed size. F_{ST_MaxSNP} is based on the SNP within a window with the highest F_ST value. F_{ST_FullWin} was calculated as the ratio of the average between population variance for all SNPs in a window over the average total (between + within population) variance for all SNPs (Reynolds et al. 1983). No minor allele frequency filter was applied for SNP calling in the power analysis—but see below for criteria used to reject or accept any simulation replicates based on the allele frequency of the beneficial allele in particular. χ_MD stands for Comparative Haplotype Identity; it compares the average length of identical haplotypes in a window between two populations, and was calculated following Lange and Pool (2016). Our simulations used two general sets of parameters, following Lange and Pool (2016). One set with high effective population size (N_e = 2,500,000) was based on parameters from D. melanogaster (with a population mutation rate of 0.01 and a population recombination rate of 0.05). The other set with a low N_e was based on parameters from humans (with population mutation and recombination rates of 0.001). To maintain similar scales of diversity and linkage between these scenarios, the default window size used in our simulations was 5,000 bp for simulations of populations with high N_e and 100,000 bp for simulations of populations with low N_e. The different window sizes for each population size reflect the amount of genetic diversity in high and low N_e populations. Except where otherwise stated, the sample size was 50 chromosomes.

We initially used scenarios of constant population size and a simple population split to simulate scenarios of selective sweeps with varying initial and final allele frequencies, representing hard and soft sweeps as well as complete and partial sweeps. We also simulated scenarios of population bottlenecks and population splits for complete selective sweeps, and for scenarios with varying migration rates for hard sweeps (not constrained by ending allele frequency). For bottlenecks, the population that will experience local adaptation underwent a period of reduced population size for the first 0.01 coalescent units after the population split (which in most scenarios including these, occurred 0.05 coalescent units ago; supplementary table S1, Supplementary material online).

The simulations of populations with high N_e were done for two different selection coefficients (s = 0.01 and s = 0.001) and simulations of populations with low N_e only included s = 0.01 (supplementary table S1, Supplementary material online). Simulations of complete sweeps only used replicates in which the beneficial allele went to fixation. Simulations of partial sweeps only accepted replicates in which the beneficial allele stayed within 4% of the targeted ending frequency. Selection initiation time was adjusted in each case to maximize the proportion of accepted replicates. Moreover, in the scenarios with initial allele frequencies larger than 1/2N_e, both the selected and nonselected populations had the same initial frequency.

For models that included migration (gene flow), selection of equal magnitudes but in opposite directions was imposed on each population. Per generation migration rates varied from 0.0004 to 0.004 in simulations with high N_e populations and from 0.01 to 0.10 in simulations with low N_e populations. For each migration rate, split times varied from 0.1 to 1 coalescent unit.

We calculated the effect of sample size on the power of each statistic in six different scenarios: four models with demographic history of a simple isolation between two populations and two models with population size bottleneck. Of the simple isolation models, two models for high N_e populations were considered: one in which F_{ST_FullWin} outperformed F_{ST_MaxSNP} (initial allele frequency of 1/2N_e and final allele frequency of 0.4) and another where F_{ST_MaxSNP} outperformed F_{ST_FullWin} (initial frequency of 0.005 and final frequency of 0.7). Two scenarios for low N_e populations were also considered: one in which F_{ST_FullWin} outperformed F_{ST_MaxSNP} (initial allele frequency of 1/2N_e and final allele frequency of 0.5) and another where F_{ST_MaxSNP} outperformed F_{ST_FullWin} (initial frequency of 0.05 and final frequency of 0.8). For the bottleneck models, we used models with a bottleneck of 5% (i.e., a reduction to 5% of the prior N_e for 0.01 coalescent units in the adapting population immediately following the population split) and only models in which F_{ST_MaxSNP} outperformed the window-wide statistics were considered: one model for high N_e population (initial allele frequency from 0.5 to 100%) and one for low N_e populations (initial allele frequency from 1 to 100%). For all the six scenarios, we used sample sizes of 10, 20, 50 (original sample size), 100, and 200 chromosomes.

We calculated the effect of window sizes on the power of each statistic in four different scenarios, the same scenarios of simple isolation used to calculate the power of sample sizes above. For the high N_e scenarios, we used window sizes of 5 kb (original size), 2 kb, 1 kb, 0.5 kb, 0.2 kb, 0.1 kb, and 1 bp. For the low N_e scenarios, we used window sizes of 100 kb (original size), 50 kb, 20 kb, 10 kb, 5 kb, 1 kb, and 1 bp. For the 1 bp (one single SNP) windows, we only calculated F_ST (here F_{ST_MaxSNP} = F_{ST_FullWin}). To calculate χ_MD, we used a minimum haplotype threshold of 10% of the window size (as was used for the original analyses). For each window size smaller than the original, we applied a P-value Bonferroni multiple testing correction proportional to the reduction in size (or equivalently, the increased number of windows needed to cover a given genomic region) to calculate power. That is, while for the standard window size power is the number of replicates with a P-value of 0.05 or lower, for a window half the size of the original the P-value would need to be 0.025 or lower. Except for the window size of 1 bp, in which the correction was the average number of SNPs in the window with the largest size (the default window size used in our other analyses).

Empirical Enrichment of F_{ST_MaxSNP} and F_{ST_FullWin}: Data and Simulations

Our data set consists of individual fly strain genomes from six natural populations of D. melanogaster: one non-human commensal population from Kafue, Zambia (KF) and five human commensal populations from different countries: Zambia (ZI), South Africa (SD), Rwanda (RG), Ethiopia (EF), and France (FR), using data from Lack et al. (2016) and Sprengelmeyer et al. (2020). From each population, for each chromosome arm (ChrX, Chr2L, Chr2R, Chr3L, Chr3R), we excluded genomes from lines with a known inversion for that arm. To boost the sample size of two populations with genomes from partially inbred lines (Ethiopia and France), instead of only using homozygous regions of the genome (as in the original filtering of the published data set), we also included heterozygous regions identified by Lack et al. (2016), and therefore counted two alleles at each site from these regions. For any pair of lines with excess identity by descent (IBD) between them (defined as more than 10 megabases of IBD outside previously defined regions of low recombination; Lack et al. 2016), we excluded one member of the pair from this data set. Non-African admixture was filtered out from haploid data from African populations based on data from Lack et al. (2016). For each population sample and each chromosome arm, we chose a sample size to jointly maximize the number of analyzable sites and the sample size itself. Our resulting sample sizes are shown in supplementary table S2, Supplementary material online. For sites with more than that number of alleles called, we downsampled to match the chosen sample size.

We calculated pairwise F_{ST_FullWin} and F_{ST_MaxSNP} for all populations using diversity-scaled window sizes designed to contain 250 non-singleton SNPs in the ZI sample. F_{ST_MaxSNP} and F_{ST_FullWin} were calculated using each SNP with minor allele count larger than two, using the same approach described in the power analysis. To compare empirical and null distributions for similar recombination rates, each window was assigned to one of five recombination rates bins based on estimates from Comeron et al. (2012); the bins corresponded to recombination rates from 0.5–1, 1–1.5, 1.5–2, 2–3, and greater than 3. Windows with recombination rates lower than 0.5 were not used due to low spatial resolution for localizing signatures of selection in low recombination regions. We obtained P-values for each window using neutral demographic simulations performed using ms (Hudson 2002). Demographic simulations were performed using parameters estimated for the evolutionary history of nine populations of D. melanogaster, including all the populations we analyzed (Sprengelmeyer et al. 2020). The other three populations were lowland Ethiopia (EA), Cameroon (CO), and Egypt (EG). We did not use those three populations in our empirical analyses due to their lower sample sizes. Nonetheless, they were included in the simulations in order to accurately reflect the estimated patterns of migration.

Each demographic model had been estimated based on tentatively neutral genetic markers (short introns and 4-fold synonymous sites from regions with sex-averaged recombination rates of at least 1 cM/Mb) from inversion-free chromosome arms (Sprengelmeyer et al. 2020). A model was estimated for each of three chromosome arms that had lower inversion frequencies (X, 2R, and 3L), and the history was inferred iteratively, such that not all population samples were present in the same model. To better approximate genetic diversity in all populations, we used two sets of demographic models: Northern model (containing ZI, RG, CO, EF, FR, EG, and EA) and Southern model (containing ZI, RG, CO, SD, and KF). The Northern model for the chromosome X was subdivided into two sub-models (one with ZI, RG, CO, EF, and EA and another with ZI, RG, CO, FR, and EG). Hence, we simulated four Northern models and three Southern models (command lines in supplementary table S2, Supplementary material online). The models for the autosomal chromosome arms (2R and 3L) were simulated using the highest sample sizes for any autosomal arm of each population (supplementary table S2, Supplementary material online). Simulated sample sizes were downsampled to match the sample sizes of each specific arm when comparing empirical and simulated F_ST patterns for any given arm. A minor allele count of three or greater was also applied to the simulated data, mimicking the same filtering used on the empirical data. The window size and crossing over rate used in each replicate were based on a random sampling with replacement from the empirical windows, and the single gene conversion rate and mean tract length were based on the estimates of Comeron et al. (2012). Therefore, a null distribution was generated for each model and each recombination bin (described above). For each model and each recombination bin, 50,000 replicates were simulated.

Enrichment Calculation

F_{ST_FullWin} and F_{ST_MaxSNP} were calculated for each population pair and each chromosome arm. F_ST was calculated for the simulated data using the same sample sizes as the empirical data (supplementary table S2, Supplementary material online). For sites with more than two alleles, only the two most common alleles were kept. Sites with minor allele counts lower than two were discarded from empirical and simulated analyses.

P-values were calculated for each window based on the neutral distribution of its corresponding recombination group. Windows from chromosome X were compared with neutral distributions based on the model for chromosome X. For autosomal loci, we determined that simulations from the 3L model yielded somewhat milder outlier enrichments than the 2R model, and therefore, we conservatively focused on results from the 3L model.

We calculated P-value enrichments for F_{ST_FullWin} and F_{ST_MaxSNP} using P-value bins of width equal to 0.05, resulting in 20 bins of P-value 0 to 1. We counted how many windows had a given P-value for each bin and divided the observed number by how many windows we expected to have with a P-value in that bin based on simulated data.

Neighboring windows with low P-value could be showing the effect of a single selective sweep. Therefore, we complemented this outlier window enrichment analysis with one based on “outlier regions”. We intentionally defined outlier regions generously, preferring to falsely lump two sweeps versus splitting a single sweep into two or more regions. Formally, starting with the window containing the lowest P-values, we extended the region surrounding it until we reached a stretch of five consecutive windows with P > 0.1 to create an outlier region. We removed the outlier regions from our analysis and repeated the process until the signal of enrichment was erased (defined as the P < 0.05 bin having no more enrichment than the 0.05 < P < 0.1 bin). For each of F_{ST_MaxSNP} and F_{ST_FullWin}, we recorded the total number of outlier regions that had to be removed for a given population pair. On the other hand, since neighboring windows with high P-values (low F_ST) could be showing shared sweeps, we repeated the process described above for outlier regions based on high P-values. For high P-value windows, we defined enrichment as the P > 0.95 bin having no more windows than the 0.9 < P < 0.95 bin.

Genome Scan for Regions under Selection—Ethiopia Versus Zambia

We performed a genome scan for candidate regions under selection between the Ethiopia (EF) and Zambia (ZI) populations. We calculated F_{ST_FullWin}, F_{ST_MaxSNP}, and χ_MD for each window of the genome. We used an outlier approach and considered windows in the top 1% of each statistic to be the candidate regions under selection. Here, we combined multiple outlier windows into the same outlier region if they were separated by no more than five windows with P-value > 0.01. To investigate whether the candidate regions detected with each statistic were the same or unique, we calculated how many regions overlapped between the different statistics. We considered that two regions were overlapping if at least 50% of the smaller region overlapped the larger one.

For each list of candidate regions under selection, we performed a GO term enrichment analysis using a method initially described by Pool et al. (2012). For each gene within a candidate region, we obtained GO term annotations from FlyBase. The GO terms for each gene also included all the parents of each term. GO terms that appeared repeatedly in a candidate region were counted only once for that region. We calculated the P-values for each GO term based on 10,000 permutations of the genomic locations of the outlier regions. This procedure allows genes to have different null probabilities of being outliers, particularly based on their length. We obtained a list of enriched GO terms for each statistic defined as the GO terms with raw P-values less than or equal or to 0.01. We then determined the overlap between the three lists of enriched GO terms.

To investigate whether F_{ST_MaxSNP} and F_{ST_FullWin} outliers might be detecting different kinds of selective sweeps, we focused on the outlier regions that were exclusive to each statistic. We calculated the frequency of the most common haplotype, haplotype homozygosity, and the H2/H1 statistic (Garud et al. 2015) for the window with the most extreme statistic in each region. In case of ties, one window was chosen randomly (for F_{ST_MaxSNP}, randomizations were proportional to the number of top SNPs in each window). The expectation is for hard sweeps, a single haplotype has risen in frequency in the population, and therefore, the frequency of the most common haplotype, as well as haplotype homozygosity, should be higher following a hard sweep than a soft sweep. H2/H1 (calculated following Garud et al. 2015) calculates the ratio of the haplotype homozygosity calculated without the most common haplotype (H2) over the overall haplotype homozygosity including the most common haplotype (H1); it should be higher following soft sweeps than hard sweeps. We calculated these statistics for all windows of the genome with recombination rates above 0.5 that had a minimum sample size of 10 chromosomes from each population. For each window, we excluded haplotypes with an amount of missing data above the average for that window. We did not consider sites with singletons (only one of the haplotypes had a different allele for that site) when calculating haplotype frequencies. Ambiguous haplotypes were assigned to a matching haplotype; the assignment probability for each matching haplotype was proportional to its frequency.

To investigate whether the sites with highest F_ST values in the outlier genomic regions for F_{ST_MaxSNP} potentially were the targets of selection, we calculated their enrichment across different categories of functional sites. We classified each site into five classes: nonsynonymous, synonymous (only considering 4-fold synonymous), untranslated regions of the mRNA (UTR), intronic, and intergenic. For each outlier region, we focused on the SNP(s) with the highest F_ST value. If more than one site were tied for highest F_ST in an outlier region, instead of counting 1 for each site class we counted 1/(the number of top sites), so the total count for each region was always 1 regardless of how many SNPs were tied for highest F_ST value. We then counted how many sites in each class were present across all outlier regions. We also calculated the genome-wide proportion of each site class, restricting our analysis to sites in which the average minor allele frequency between the Ethiopia and Zambia populations were within the range of average minor allele frequency for all sites with the highest F_ST values in the outlier regions. Lastly, we calculated enrichment for each site class as the ratio between the proportion of sites in the outlier regions over the proportion of sites in the genome.

Supplementary material

Supplementary material is available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).

Funding

This research was funded by NIH grants R01 GM127480 and R35 GM13630, and by NSF grant DEB 1754745.

Data Availability Statement

No new empirical data were generated for this research. Scripts used in the analyses presented can be found at https://github.com/ribeirots/fst_maxsnp.git.