Abstract
Wire rope isolators (WRI) effectively isolate shocks and vibrations, making them an ideal choice for many industries, including military and aerospace. A sizeable experimental program was conducted to investigate the cyclic hysteretic behavior of WRIs in all possible loading directions. The test matrix included several isolators subjected to different load-displacement amplitudes at varying rates and other geometries and sizes of the WRIs themselves. This study evaluates the effective stiffness and damping characteristics of WRIs in both the tension/compression (or vertical) and shear/roll (or lateral) directions through laboratory tests and mathematical modeling. It was found that the wire rope diameter significantly influences the stiffness of the WRI more than the other geometric characteristics. Additionally, the damping characteristics of the WRI were found to be correlated to the height-to-width ratio for a given wire rope diameter. The cyclic loading tests showed that, unlike in the lateral directions, in the vertical direction, the load-displacement hysteresis loops are asymmetric. Therefore, the original Bouc-Wen model of hysteresis was used for the lateral direction. A modified version of the same model was developed to simulate the observed asymmetric hysteretic behavior in the vertical direction.
Keywords: Wire rope isolator, Vibration, Mathematical model, Bouc-Wen, Cyclic test, Stiffness, Damping
Wire rope isolator; Vibration; Mathematical model; Bouc-Wen; Cyclic test; Stiffness; Damping.
1. Introduction
Wire rope isolators have been used to protect small equipment and lightweight structures from vibrations for a long time. They are easy to install, relatively inexpensive, and do not require power to operate (i.e., passive isolation system). Wire rope isolators are used for protection against vibrations in construction, offshore drilling platforms, and other applications. The design of a wire rope isolator is currently based on catalogs provided by the manufacturers.
Wire rope isolators are the preferred isolation systems, especially in military and aerospace industries, because they are long-lasting and withstand climatic conditions. Some of the applications of wire rope isolators include protecting equipment from vibrations and protecting structures from vibrations of machines.
The hysteresis behavior of WRI has been extensively studied in the literature [1, 2, 3, 4, 5, 6]. In general, the hysteresis loop of WRI can be divided into two regions: the elastic region and the plastic region. The elastic region is the region in which the isolator behaves elastically. The plastic region is the region in which the isolator behaves plastically. The elastic region can be further divided into linear and nonlinear elastic regions. The linear elastic region is the region in which the isolator behaves linearly. The nonlinear elastic region is where the isolator behaves nonlinearly when subjected to large displacement amplitudes or when loaded in a specific direction. Many studies have observed this behavior [3, 4, 6, 7, 8, 9].
The damping or energy dissipation capability of the WRI can be studied from its hysteresis behavior under cyclic loading. This hysteresis is a natural way, available in mechanical and structural systems, to provide restoring forces against movements and dissipate energy. Previous studies [3, 4, 6, 7, 8, 9] have verified and confirmed that the WRI exhibits a hysteresis curve under cyclic loading and is due to the frictional resistance between the wire strands [10]. The studies [11, 12, 13] also shows that dry friction in the wire rope can cause energy dissipation. A WRI has inherent frictional damping from the wire rope as a typical nonlinear hysteretic damping device. Hence, the loading and unloading paths are different and result in a hysteresis curve when a cyclic load is applied. The area of the hysteresis curve explains the energy dissipation capability.
A comprehensive review of related studies is provided next. The problem statement follows this and the methodology to accomplish the objectives of this investigation. In this paper, the results of an extensive experimental program are presented to investigate the cyclic behavior of wire rope isolators to determine their effectiveness and limitations and where they can be better applied. Based on the Bouc-Wen model of hysteresis, mathematical models are then developed to simulate their hysteretic behavior in all loading directions. Identifying models’ parameters used a hybrid optimization algorithm combining the Particle Swarm Optimization (PSO) as a global optimizer and the Interior-Point algorithm as a local optimizer.
2. Review of related studies
Wire rope isolators (WRI) are devices used to reduce vibration transmission from one structure to another. They are composed of steel wires that are compressed to form an isolator. In a previous study, Leblouba et al. [4] found that Polycal Wire Rope Isolators (PWRI) exhibited asymmetric, soft-hardening, rate-independent, hysteresis behavior. This behavior was observed at small deformations (softening) and at large deformations (hardening). In a subsequent study, Lee et al. [14] found that the shear strain increased the energy dissipation but decreased the damping ratio.
In contrast, the increase in the compressive stress increased the damping ratio. Additionally, the authors of this paper developed a macro model to simulate the load-displacement response of the isolation system. The prediction results of this model were consistent with the experimental results. Finally, Cen et al. [15] used finite element analysis (FEA) to create a simplified model of a PWRI. This model was then used to study the vertical static stiffness of the PWRI. The results of the FEA showed that the vertical static stiffness of the PWRI was reduced as the degree of compression deformation increased.
Additionally, the steel wires in the PWRI exhibited significant displacement changes when subjected to axial tensile and compress loads. The findings of these papers have practical implications for the design and selection of WRI specifications. Moreover, these results may be used to predict the load capacity and energy dissipation of a WRI under various loading conditions.
Barbieri et al. [16] conducted an experimental and mathematical study of wire rope isolators. They found that the physical parameters used in a Bouc-Wen model can be adjusted using the Particle Swarm Optimization method by comparing numerical and experimental results for two different systems: wire-rope isolator and Stockbridge damper. The results showed that fine adjustments were efficient, i.e., the numerical and experimental results can be made close. The authors conclude that the Bouc-Wen model is well suited for the dynamic analysis of such systems.
Previous work on WRI in the literature has shown the effectiveness of WRI as a vibration control device in reducing the transmission of vibration from one structure to another. The results also indicate that WRIs are affected by compression and tension loads.
WRI is made up of a wire rope coiled around several turns [7, 17]. The stiffness of the isolators increases under tension and decreases under compression, making the hysteresis curve asymmetrical. The energy loss ratio decreases with increasing displacement amplitude. The effective stiffness of the isolators is strongly affected by the wire rope diameter, the number of coils, and the displacement amplitude [8].
Recently, Balaji and Selvakumar [18] reviewed the applications of non-linearity in passive vibration control devices. They found that the non-linearity introduced into the systems has more significant benefits than the linear systems. Moreover, they found that the nonlinear devices effectively have a broad frequency bandwidth and can provide better vibration isolation than linear devices.
Salvatore et al. [19] investigated experimentally and numerically the vibration isolation capability of a nonlinear wire rope spring. They concluded that the device exhibits a distinct non-symmetry under compression and tension and is suitable for vibration damping applications. Rashidi et al. [20] studied the behavior of an industrial wire rope isolator under static and dynamic loads. The authors found that the isolator exhibits hysteresis behavior under static and dynamic loads. The artificial neural network model they proposed can predict the behavior of the isolator in all loading conditions with reasonable accuracy. In the same year, Vaiana et al. [21] conducted dynamic and static tests on four-wire rope isolators to identify their mechanical characteristics. The authors found that wire rope isolators have high effective stiffness and equivalent damping ratio in small displacements, but this decreases in the relatively large displacements range. They also found that the shape of the hysteresis loops changes according to the displacement range, with a softening stiffness at small displacements and a hardening stiffness in the relatively large displacements range. These papers concluded that wire rope isolators are suitable for vibration damping applications and exhibit hysteresis behavior under static and dynamic loads. However, these studies differ in their conclusions about the applicability of wire rope isolators in different displacement ranges. Salvatore et al. found that the device is suitable for vibration damping applications in a broad frequency range.
In contrast, Vaiana et al. [21] found that the device is ideal for vibration damping applications in the small and relatively large displacement ranges. Rashidi et al. [20] did not make any specific conclusions about the applicability of wire rope isolators in different displacement ranges. In terms of experimental work, Salvatore et al. [19] conducted the most comprehensive study, investigating the vibration isolation capability of a nonlinear wire rope spring over a wide range of frequencies. They found that the device is suitable for vibration damping applications and exhibits hysteresis behavior under static and dynamic loads. Vaiana et al. [21] also conducted a series of tests on four wire rope isolators, but they only investigated the mechanical characteristics of the isolators in three displacement ranges. Rashidi et al. [20] studied the behavior of an industrial wire rope isolator under various static and dynamic loads.
It can be deduced from discussing references [19, 20, 21] that earlier work on WRIs has worked chiefly on individual or few samples [3, 10, 15] of WRI to study its characteristics and performance in the vibration reduction and for a specific application. Further earlier work also focused on polycal type WRI, and very little literature is present for the helical WRI. Hence a detailed, in-depth study on helical WRI is desirable.
3. Problem statement and research objectives
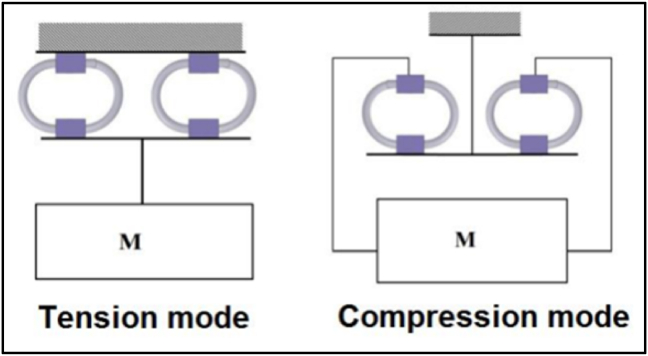
To understand the behavior of Wire Rope Isolators (WRIs) and provide researchers with a complete study of their mathematical modeling, we conducted this research. In the following sections, the hysteresis behavior of WRIs is studied under quasi-static cyclic loading conditions using laboratory tests and modeled using appropriate mathematical models. The loading modes in each direction are defined from the orientation of WRI used in the applications. The loading modes used in the applications are shown in Figure 1. The tension/compression hysteresis behavior of WRIs is achieved by subjecting the specimens to quasi-static cyclic vertical loading. Previously reviewed studies demonstrated that WRIs exhibit similar hysteresis behavior under the cyclic roll and cyclic shear loading in the lateral direction. However, this finding is verified as part of this study.
Figure 1.
(a) Wire rope isolator, (b) Orientation for different applications depending on the desired vibration direction.
The mathematical model of the hysteresis behavior, for both vertical and lateral directions, is developed using the original version of the Bouc-Wen model of hysteresis equations. The Bouc-Wen model parameters are identified using a hybrid method and cyclic loading test results. The optimization algorithm used to determine the dynamical system parameters is a hybrid of Particle Swarm Optimization (PSO) and Interior-Point (IP). The Bouc-Wen model of hysteresis is applicable to simulate symmetric hysteresis loops, which, as we will see later, in the case of the WRI when loaded in the lateral direction. However, in the vertical direction (tension/compression), the WRI exhibits asymmetric behavior, and hence a suitable modification is proposed in this study.
The mathematical models developed for vertical and lateral directions were validated with the cyclic loading tests. This validation was performed at various displacement amplitudes to verify the ability of the model parameters to predict the hysteresis behavior for ranges of displacement amplitudes. In addition, another objective set for this study is to investigate the effect of the geometric characteristics of WRI on their hysteretic behavior. This work will enhance the understanding of the WRI in terms of its behavior under various displacement amplitude and loading rates. The mathematical model presented is an easy-to-use model that can be used to predict WRI performance and characteristics. The developed mathematical model can then be readily incorporated into engineering software.
4. Experimental program
A series of quasi-static cyclic loading tests were performed to study the behavior of WRIs under different loading directions. The energy dissipation capabilities are then evaluated using the Equivalent Damping Ratio (EDR), computed from the hysteresis curve and the effective stiffness. The cyclic loading behavior is also used to study the hardening and softening effects of the WRI under various displacement amplitudes. Further, the influence of the wire rope diameter and height to width ratio (H/W) on the hysteretic behavior is evaluated.
In this section, the experimental setup, test results, and the effects of geometric characteristics of WRI on its equivalent damping and effective stiffness are discussed.
4.1. Test setup
This study tested wire rope isolators in both the vertical and lateral directions to investigate cyclic loading behavior in the tension/compression and roll/shear directions. The tests were conducted in a displacement-controlled mode assuming three displacement amplitudes (3 mm, 6 mm, 9 mm) and at an 8 mm/min rate to reduce the inertia effects. The test setup is shown in Figure 2.
Figure 2.
Test setup for each cyclic loading direction.
Additionally, the effect of loading rate on the cyclic loading behavior was studied. Nine wire rope isolators were used in the quasi-static behavior study, and the geometric characteristics of each isolator were also examined. An Instron 5982 machine of 100 kN capacity was used to run the experimental work. Table 1 shows the geometric properties of test specimens. The Instron 5982 machine is controlled using the BLUEHILL® UNIVERSAL software from the manufacturer.
Table 1.
Geometry specifications of test specimens.
| Isolator # | Wire rope diameter, (mm) | Number of coils | Width, (mm) | Length, (mm) | Height, (mm) | |
|---|---|---|---|---|---|---|
| 1 | 6.4 | 8 | 64 | 146 | 54 | 0.84 |
| 2 | 6.4 | 8 | 71 | 146 | 59 | 0.83 |
| 3 | 6.4 | 8 | 80 | 146 | 64 | 0.8 |
| 4 | 6.4 | 8 | 89 | 146 | 65 | 0.73 |
| 5 | 9.5 | 8 | 84 | 216 | 71 | 0.85 |
| 6 | 9.5 | 8 | 105 | 216 | 76 | 0.72 |
| 7 | 12.7 | 8 | 105 | 216 | 90 | 0.86 |
| 8 | 12.7 | 8 | 121 | 216 | 95 | 0.79 |
| 9 | 12.7 | 8 | 133 | 216 | 108 | 0.81 |
4.2. Test results and discussion
The study results showed that the stiffness of the WRI was different in tension and compression loading, and the hysteretic curve was asymmetrical, as demonstrated in Figure 3. In addition, the displacement amplitude had a significant impact on the hysteretic curves in the vertical direction. For small displacement amplitudes (i.e., 3 mm), the hysteresis curves were symmetrical on both sides with observed stiffness softening and quasi-linear behavior. The asymmetrical curves became more apparent when isolators were loaded to larger displacements due to the nonlinear contact between the stranded wires for higher loads.
Figure 3.
Force-Displacement hysteretic behavior of WRIs under tension/compression of isolator No. (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9.
The hardening in the tension mode and softening in the compression mode were observed for higher displacement amplitudes (6 mm and 9 mm); this is because when the isolator is under tension, the wire strands contract, which increases the number of contact points; thus, the surface of friction increases. This will imply more dry friction and eventually stiffens the isolator. In contrast, the wire strands move further apart when the isolator is compressed, leaving fewer contact points. In this case, most of the stiffness of the isolator comes from the wire strand itself.
As shown in Figure 4, the hysteresis behavior of wire rope isolators in the roll was different from tension/compression loading. In addition, the stiffness of the WRI remained the same for both positive and negative roll. This behavior is different from vertical loading, where stiffness is different in tension and compression. From Figure 5, it can be observed that the hysteresis exhibited symmetric nature in the cyclic roll direction. The symmetric nature of the hysteresis in roll can be attributed to the circular section of the coil, and the equal number of loop turns of the WRI. The negative and positive loading results in the similar displacement mode (Figure 5(a)) in both directions for roll loading. In contrast, in tension and compression loading, both loads resulted in different force-displacement shapes, as shown in Figure 5(b).
Figure 4.
Force-Displacement hysteretic behavior of WRIs under lateral (cyclic roll) of Isolator No. (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7, (h) 8, (i) 9.
Figure 5.
The shape of a loaded isolator (a) in roll, (b) in tension/compression.
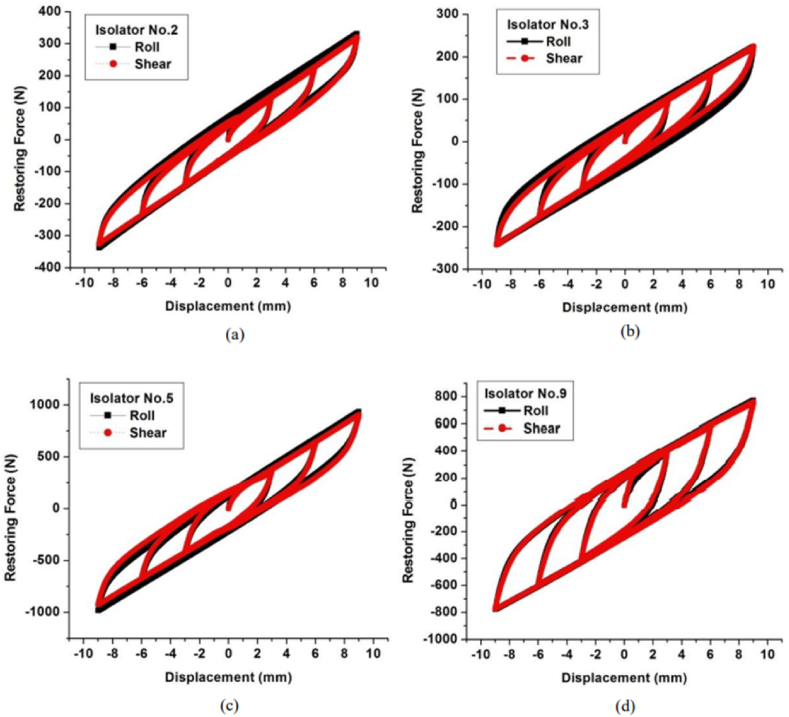
The lateral hysterics behavior under cyclic shear and cyclic roll are shown in Figure 6. The maximum average cyclic roll loadings in both positive and negative directions of the isolators #2,#3, #5 #9 are 323.3 N, 222.6 N, 934.6 N, and 766.9 N, respectively, and the maximum average shear loadings of those isolators in both positive and negative directions are 324.5 N, 221.5 N, 938.2 N and 767. 5 N respectively. It can be observed that the restoring force for both roll and shear loadings are in close approximation, showing that WRI exhibits similar behavior for both roll and shear loading. Therefore, lateral hysterics behavior can be studied either along the x-axis or the y-axis (Figure 1). In this study, cyclic behavior in the lateral direction was studied along the y-axis using a cyclic roll load. The present study also investigated the effect of rate-of-loading on WRI behavior.
Figure 6.
Hysteresis behavior under lateral cyclic loading (roll and shear) at 8 mm/min (a) Isolator No. 2, (b) Isolator No. 3, (c) Isolator No. 5, (d) Isolator No. 9.
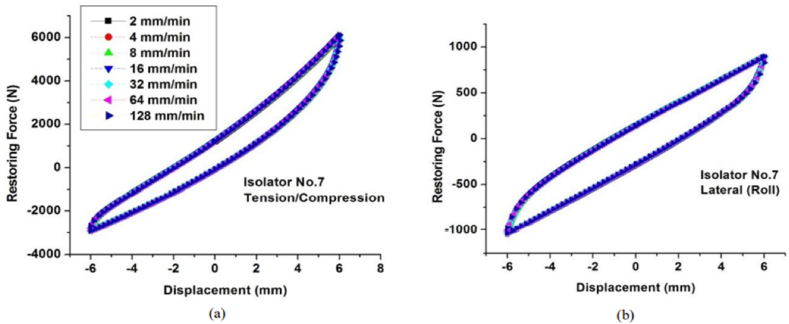
The cyclic test was carried out at 2 mm/min, 4 mm/min, 8 mm/min, 32 mm/min, 64 mm/min, and 128 mm/min in both directions at 6 mm displacement amplitude, and the results are shown in Figure 7. The maximum tension and compression loadings of isolator #7 for all loading rates are within 6390.5 ± 2N and 2775.5 ± 1.5 N, respectively. Further, for the lateral roll loading, the maximum loading is within 876.5 ± 1 N for the testing rate of loadings. Hence, the cyclic loading behavior is rate-independent over the test range due to the energy dissipation mechanism through friction contact. This rate independence enabled the dynamic characteristics of WRI to be analyzed using a quasi-static test when the inertial effects were neglected. The test was also conducted to study the effect of coil orientation, such as right-hand and left-hand coil (Figure 8), on the hysteresis behavior of WRI. The hysteresis curves resulting from both coil types were similar, suggesting that a WRI with the same geometric characteristics, except for coil orientation, will exhibit a similar hysteresis curve in both the vertical and lateral direction.
Figure 7.
Effect of loading rate on the hysteresis behavior of WRI under (a) tension/compression, (b) roll.
Figure 8.
Comparison of hysteresis behavior between right and left coil of isolator No. 7, (a) Tension/compression, (b) Roll, (c) WRI with Left hand and Right-hand Coil.
The WRI exhibited rate-independency and the memory effect in the lab test. The memory effect of the WRI is seen in Figure 9. The test was conducted in both vertical and lateral directions with increasing displacement amplitude from 1 mm to 10 mm in increments of 1 mm per cycle. The subsequent displacement input resulted in the overlapping of the behavior in both directions. This overlapping can be explained by the wire strand interaction from the input load. The frictional contact of the wire strands results in the wire strand displacing in a similar configuration and following the displacement history. This memory effect of the WRI is a significant characteristic since it can be understood that the WRI, under cyclic loading, undergoes similar displacement modes.
Figure 9.
Hardening overlap (memory effect) under cyclic loading in (a) Vertical, (b) Lateral.
The hysteresis behavior was studied using two parameters, namely the equivalent damping ratio and the effective stiffness, which were evaluated from the hysteresis curve. These parameters allow an estimation of the damping capability and stiffness characteristics.
5. Equivalent damping ratio and effective stiffness
5.1. Equivalent damping ratio
The equivalent damping ratio () measures the energy dissipated due to frictional resistance between the wire strands. It is evaluated as the equivalent viscous damping and is represented by: [6, 22].
| (1) |
| (2) |
where is the area of the hysteresis loop and and are the maximum and minimum forces, respectively. and are the maximum and minimum displacements, respectively. Both forces and displacements are obtained from the hysteresis behavior of the corresponding isolator. The equivalent damping ratio provides measurable damping achieved by WRIs. A higher value of EDR means a higher damping capacity.
At 3 mm displacement amplitude, the for all isolators was 0.13–0.23. For the 6 mm displacement amplitude, the decreased, on average, by 30%. For the 9 mm displacement amplitude, the of isolators decreased by about 28%. The of all isolators in this amplitude became closer at about 0.13 to 0.07.
As shown in Figure 10(a), the of all isolators reach their highest damping effectiveness when they are loaded under small amplitude levels (i.e., 3 mm). However, the hysteresis loops become narrower as the amplitude increases, decreasing the damping effectiveness. This can be due to the wire rope strands moving away at higher displacements, reducing the contact surface. Hence, frictional resistance and damping effectiveness are reduced. The wire rope isolators with different geometries have different damping capacities (total energy dissipation). The WRI with higher wire rope diameters was observed to have a greater capability in dissipating energy, which could be attributed to the increased frictional contact in the higher wire rope diameter. Hence, those isolators provide a larger damping capacity than isolators with smaller wire rope diameters. The hysteresis curve of the WRI with a greater wire rope diameter (Isolator #7, #8, and #9) has shown a larger hysteresis area (Figure 10(b)). This larger hysteresis area indicates that these isolators can dissipate significant energy per cycle. Thus, geometrically different isolators were found to have a similar trend in the damping effectiveness for various displacement amplitudes.
Figure 10.
(a) and (b) Hysteresis area of the WRIs under various displacement amplitudes under vertical tension/compression cyclic loading.
Figure 11(a) shows the variation of the of various isolators during the roll test as a function of the displacement amplitude. For a 3 mm displacement amplitude, the varied from 0.16 to 0.27. When the displacement amplitude was increased to higher values, the decreased as observed in the lateral direction. For a 6 mm displacement, the equivalent damping ratio decreased on average by 25 %, which was lower than the vertical direction. A similar result in the decrease of the equivalent damping ratio with respect to wire rope diameter was observed. Based on this result, it can be understood that the WRI with a greater wire rope diameter has a higher damping capability. However, the amount of damping required for the application depends on the amount of isolation required. The hysteresis area (Figure 11(b)) in the lateral direction also increased for higher displacement, as seen in the case of the vertical direction. The larger wire rope diameter of a WRI showed a higher hysteresis area which shows that they can dissipate more energy than the WRI with a smaller wire rope diameter.
Figure 11.
(a) EDR, and (b) Hysteresis area of the WRIs under various displacement amplitudes under lateral roll cyclic loading.
5.2. Effect of height to width ratio and displacement amplitude
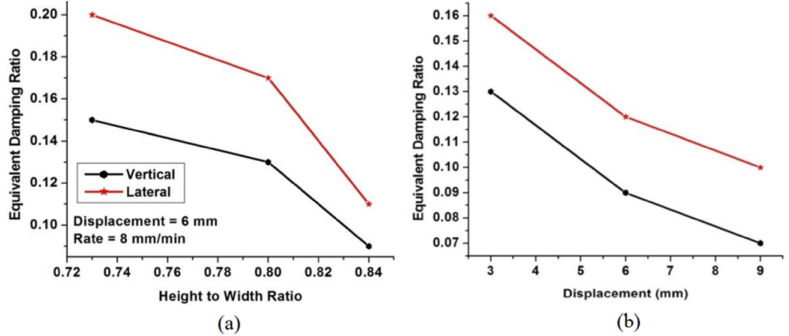
It can be observed from Figure 12 that the equivalent damping ratio decreases as the height to width ratio () increases for both the lateral and vertical directions; this is due to the increased stiffness of the isolator as the ratio increases. A similar observation was also made for all the tested isolators. Figure 12 can be used in applications that demand better isolation and, based on these curves, the WRI can be oriented to take the excitation in the lateral direction.
Figure 12.
Equivalent damping ratio versus (a) ratio, (b) Loading direction.
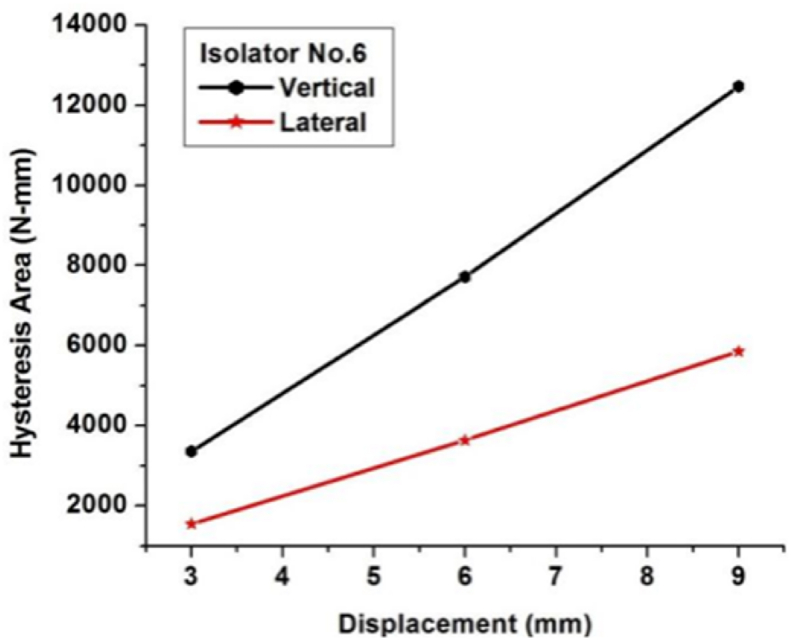
From Figure 13, it can be seen that the hysteresis area increases as the displacement amplitude increases, which can be attributed to the increased stiffness of the isolator as the displacement amplitude increases. A closer examination of Figure 10(b) and Figure 11(b) reveals the isolators with higher values of ratio have an increased hysteresis area than other isolators with the same wire rope diameter. Hence, in the application which requires high energy dissipation, WRIs with a high ratio can be preferred. Similarly, the vertical direction was found to dissipate relatively higher energy than the lateral direction in Figure 13. This fact can be used in the orientation of the WRI for this type of application.
Figure 13.
Hysteresis area versus displacement amplitude in the vertical and lateral directions.
5.3. Effective stiffness
WRI's effective stiffness is defined as the ratio of the maximum difference in force to the maximum difference in displacement, that is:
| (3) |
where and represent the force and displacement, respectively, and the subscripts max and min represent the maximum and minimum values of each parameter.
The effective stiffness of a wire rope isolator (WRI) is dynamic and calculated after one complete loading and unloading cycle. To determine the static stiffness of the WRI, a static loading is required. The effective dynamic stiffness is an indicative quantity, which helps to understand the increment or decrement of the WRI’s stiffness under cyclic loading. This effective stiffness can also be viewed as the linear interpolation of the hysteresis curve.
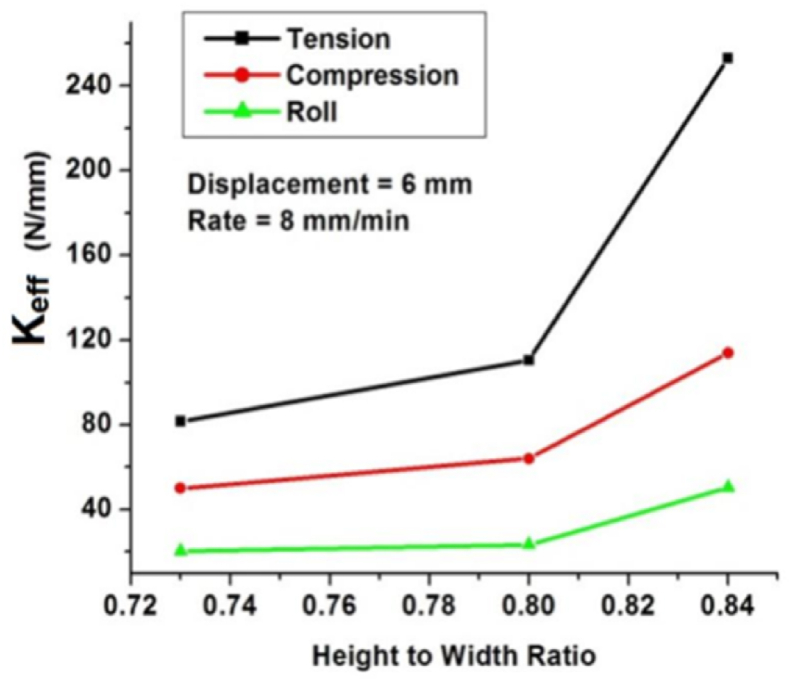
The effective stiffness decreases with higher displacements (Figure 14) due to the softening behavior of the WRI. The greater wire rope diameter has a relatively higher value of effective stiffness due to the increased wire rope diameter. However, the WRI with a lesser ratio for the same diameter has a higher value of . The significance of the ratio in the stiffness contribution can be understood in Figure 15. The isolators were compared with the same wire rope diameter and length but different height to width ratios. Figure 15 shows the effect of the ratio on the effective stiffness. The effective stiffness was obtained in each loading: tension, compression, and roll at 6 mm displacement amplitude. As can be observed, the higher ratio shows a greater stiffness. The higher value of the ratio induces greater hardening than the WRI with a similar wire rope diameter. From the isolation of the system point of view, softening is desirable since softening reduces the system’s natural frequency. Hence, better isolation at low-frequency excitations can be achieved. Therefore, any hardening can be undesirable for the low-frequency excitations. Accordingly, the lower ratio can be used for isolation against low-frequency excitation. On the other hand, the orientation of the WRI can be adjusted depending on the application.
Figure 14.
Effective stiffness under (a) Tension/Compression, (b) Roll loading directions.
Figure 15.
Effect of ratio on the effective stiffness under different loading conditions.
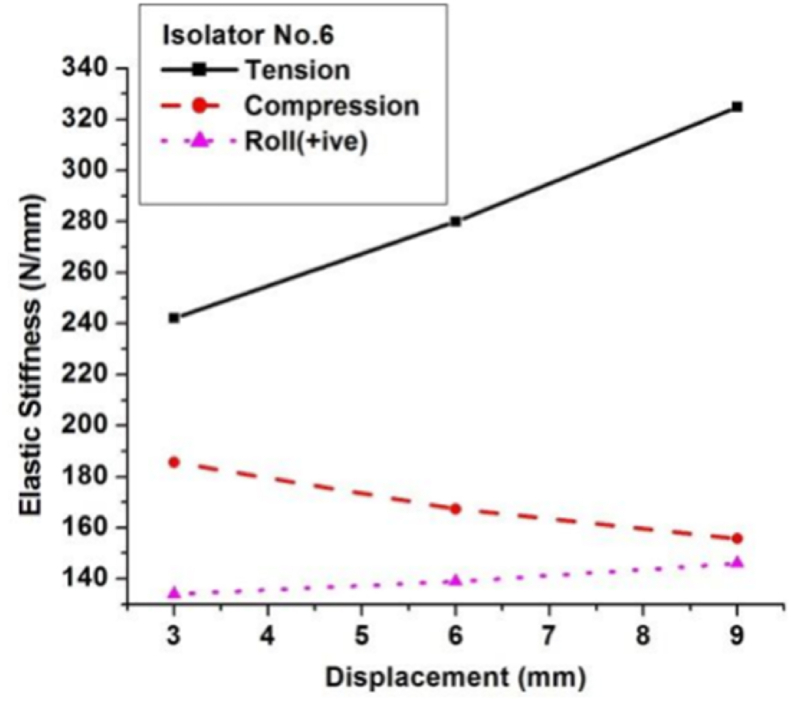
Figure 16 shows the effective stiffness against tension, compression, and roll load displacements. The effective stiffness under compression declines with higher displacement, indicating softening behavior. However, under tension, elastic stiffness increases due to the hardening. For the roll load, stiffness was constant for the tested displacement range, and hence, the hysteresis curve was symmetric. This result suggests that when a system is supported from the top, it may be subjected to compression mode rather than tension, as shown in Figure 17. This is due to the softening behavior of WRIs under compression, which improves the isolation by reducing the system's natural frequency.
Figure 16.
Effective stiffness in tension, compression, and roll loads for various displacement amplitudes.
Figure 17.
Loading modes of the WRI when supporting from the top.
6. Mathematical modeling
The hysteresis behavior of the WRI was discussed in the previous section, and it was observed that the WRI exhibits hysteresis behavior under cyclic loading due to its frictional damping phenomenon. We also showed that the geometric characteristics of the WRI significantly influence the hysteresis behavior. A natural next step is to develop analytical models to predict the hysteresis behavior of wire rope isolators. However, a closed-form solution is challenging due to the number of involved parameters and uncertainties associated with the manufacturing and material properties. Therefore, we resorted to mathematical modeling, which has the advantage of its readiness to be incorporated into larger software, such as those based on the Finite Element Method.
This section proposes mathematical models for the WRI hysteresis behavior in both vertical and lateral directions. The Bouc-Wen model of hysteresis [23, 24, 25] is used to accomplish this task. The Bouc-Wen model is a first-order nonlinear differential equation that hysterically relates input displacement with the output restoring force. The original Bouc-Wen model is limited to modeling symmetric hysteresis loops as in the case of shear and roll load behavior. However, for tension/compression, the hysteresis loop is asymmetric. Hence, a modified version of the original Bouc-Wen model of hysteresis is proposed and validated using experimental results.
6.1. Shear/roll direction
The wire rope isolators tested in the previous sections exhibited symmetric hysteretic force-displacement behavior in the shear/roll directions. Therefore, the original Bouc-Wen model of hysteresis is chosen to model the behavior of WRIs in the shear/roll loading directions.
The restoring force mobilized in the WRI in the shear/roll direction has two parts: a linear part and a nonlinear part:
| (4) |
The linear part is represented by the term , and the nonlinear part is represented by . In Eq. [4], is the restoring force, is the displacement, is the post-to-pre elastic stiffness ratio, is the yield strength, and is a dimensionless quantity that characterizes the Bouc-Wen model, the following differential equation gives it:
| (5) |
where , , , and are dimensionless quantities that control the shape of the hysteresis loop. Using the experimental data from the shear/roll loading direction tests on the WRIs, the hybrid optimization method, discussed later, was employed to identify the parameters of the Bouc-Wen model of hysteresis. As we will see in Section 6.4, the Bouc-Wen model of hysteresis is a good fit for the experimental data for the WRIs in the shear/roll loading direction and capture all features of a typical symmetric hysteresis.
6.2. Tension/compression direction
The WRI exhibits asymmetrical hysteresis behavior when loaded in the tension/compression direction due to its hardening and softening effect. In tension, the WRI undergoes hardening, while in compression, it undergoes softening. A mathematical model for the asymmetric hysteresis can be developed by understanding the terms used in the original Bouc-Wen model equation. In Eq. [4], the first term represents the elastic force, and the second term represents the history-dependent damping force. The mathematical modeling of the hysteresis behavior was developed by constructing the individual components of the Bouc-Wen model.
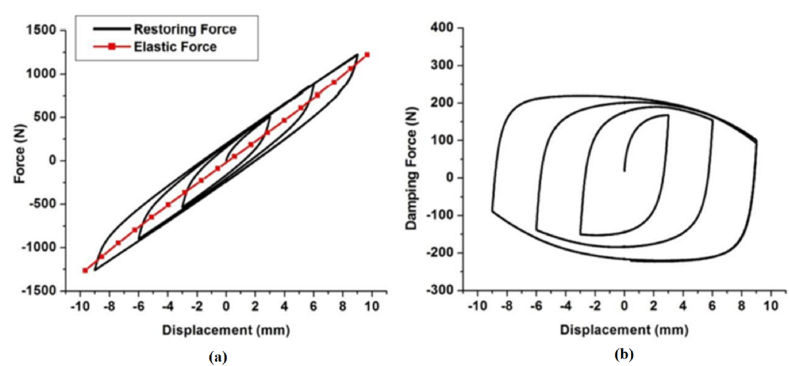
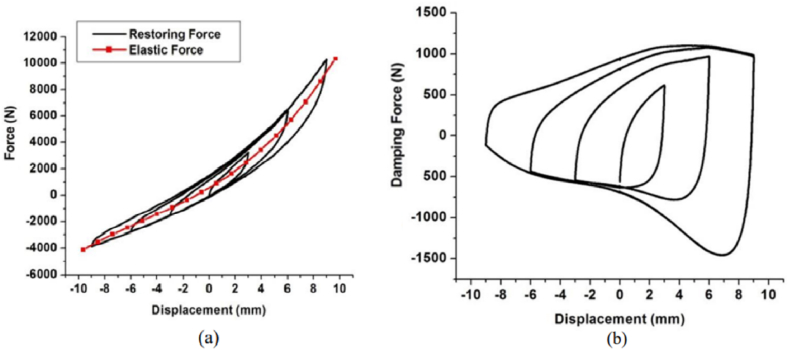
For the symmetric hysteresis curve, the elastic and damping force plots are shown in Figure 18. The elastic force and damping force for the asymmetric hysteresis curve are shown in Figure 19. As can be observed, the elastic force component of the restoring force induces the asymmetric nature and hence needs to be adjusted in the Bouc-Wen model. However, the available Bouc-Wen equation can satisfactorily model the damping force component. Therefore, a modification in the elastic force model is desired to agree with the test results.
Figure 18.
Force-displacement in roll direction divided into (a) Restoring force, (b) Damping force.
Figure 19.
Force-displacement in tension/compression direction divided into (a) Restoring force, (b) Damping force.
The non-linearity in the elastic force of a WRI isolator can be modeled using a modulating function depending on the desired level of accuracy and degree of non-linearity. In this work, the elastic term in the original Bouc-Wen model of hysteresis is changed with the following modulating function:
| (6) |
The parameters in Eq (6). are defined in Figure 20. The complete restoring force can then be written as:
| (7) |
Figure 20.
Modulating force for the modified Bouc-Wen model of hysteresis.
Note that the second term is kept as the original Bouc-Wen model. The modified Bouc-Wen mode parameter identification was carried out using the experimental results belonging to the tension/compression tests and employing the hybrid optimization method (see details in Section 6.3).
6.3. Mathematical model system identification
The two mathematical models employing the Bouc-Wen model of hysteresis have several parameters that need to be identified. The first mathematical model (Eqs. (4) and (5)), specialized for the symmetric behavior observed in the shear/roll direction, possesses seven parameters, , which can be easily identified using shear/roll test data and an adequate method, such as least-squares.
The second mathematical model (Eqs. (6) and (7)), specialized for the asymmetric behavior observed in the tension/compression direction, possesses ten parameters, , the identification of which is not an easy task as it requires a more robust optimization algorithm in addition to the test data.
The system identification of both mathematical models was made by minimizing the following objective function:
| (8) |
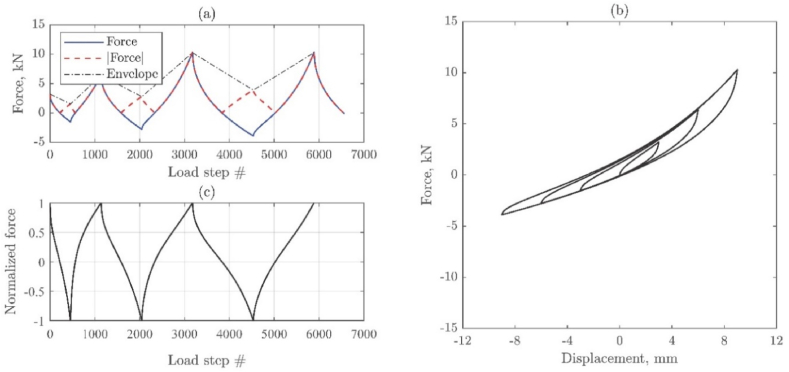
where is the recorded force, is the predicted force, is the length of the force vector, and is the envelope of the absolute force, . The envelope, as shown in Figures 21 and 22, is used to give equal importance to both small and large force-displacement hysteresis loops. The normalized force by the envelope ranges between −1 and +1. Without normalization, the identification algorithm would converge to a solution where only larger hysteresis loops are well represented.
Figure 21.
Isolator No. 7 in roll direction (a) Measured force and its envelope, (b) Measured force-displacement curve; (c) Normalized force.
Figure 22.
Isolator No. 7 in tension/compression direction (a) Measured force and its envelope, (b) Measured force-displacement curve, (c) Normalized force.
The optimization algorithm to minimize the objective function, , is a hybrid one using Particle Swarm and Interior-Point using Matlab (Mathworks, Inc.). For a detailed description of the steps involved in the system identification, the reader is referred to references [24, 25].
In the shear/roll direction, the identified model parameters are tabulated in Table 2, while in the tension/compression loading direction, the identified model parameters are tabulated in Table 3. Note that in both loading directions, the Bouc-Wen model parameters were: , for all tested isolators.
Table 2.
First mathematical model parameters for the symmetric behavior in the shear/roll direction∗.
| Isolator # | (N/mm) | (mm) | (N) | |
|---|---|---|---|---|
| 1 | 205.15 | 0.39 | 60.0 | 0.2448 |
| 2 | 151.69 | 0.4 | 47.95 | 0.2065 |
| 3 | 105.3 | 0.52 | 43.78 | 0.1966 |
| 4 | 103.37 | 0.55 | 47.69 | 0.166 |
| 5 | 300.35 | 0.38 | 93.4 | 0.1767 |
| 6 | 270.65 | 0.37 | 86.29 | 0.132 |
| 7 | 350.64 | 0.34 | 88.49 | 0.2533 |
| 8 | 310.45 | 0.34 | 90 | 0.1361 |
| 9 | 290.33 | 0.38 | 99.15 | 0.1077 |
The Bouc-Wen model parameters are for all isolators.
Table 3.
Second mathematical model parameters for the symmetric behavior in the tension/compression direction∗.
| Isolator # | (N/mm) | (N/mm) | (N/mm) | (mm) | (mm) | (mm) | (mm) | (N/mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 146.65 | 58.12 | 122.91 | -4.61 | 4.23 | 228.57 | 0.2549 | 0.0138 |
| 2 | 119.83 | 35.46 | 59.37 | -1.46 | 4.42 | 162.81 | 0.2377 | 0.0058 |
| 3 | 68.47 | 73.82 | 36.15 | -7.55 | 2.92 | 148.53 | 0.3565 | 0.1 |
| 4 | 58.84 | 12.92 | 16.13 | -1.01 | 2.91 | 131.97 | 0.345 | 0.005 |
| 5 | 552.49 | 239.8 | 746.39 | -1.03 | 5.29 | 762.19 | 0.2256 | 0.0146 |
| 6 | 180.12 | 187.38 | 71.04 | -7.52 | 3.99 | 384.15 | 0.4058 | 0.095 |
| 7 | 366 | 488.49 | 550.06 | -8.14 | 0.01 | 941.12 | 0.5621 | 0.0362 |
| 8 | 317.46 | 391.25 | 87.6 | -7.54 | 4.88 | 885.89 | 0.6378 | 0.0368 |
| 9 | 218.76 | 313.08 | 76.54 | -7.88 | 1.35 | 629.11 | 0.4111 | 0.0214 |
The Bouc-Wen model parameters are for all isolators.
6.4. Results and discussion
The proposed mathematical models are a good fit for the experimental data for the WRIs in the shear/roll and tension/compression loading direction. They could capture all features of the asymmetric hysteresis we have observed in laboratory tests. Figures 23 and 24 show the comparison between the mathematical models and test results for Isolator #3 and #6, respectively. Similar observations were made for all the isolators.
Figure 23.
Comparison between the test results and mathematical models (isolator No. 3) in (a) Vertical direction and (b) Lateral direction.
Figure 24.
Comparison between the test results and mathematical models (isolator No. 6) (a) Vertical direction, (b) Lateral direction.
The Bouc-Wen parameters identified for each isolator are shown in Tables 2 and 3 for the tension/compression and shear/roll directions, respectively. These parameters can be used to simulate the behavior of wire rope isolators for any displacement amplitude. The tested WRIs have standard sizes and are manufactured by many factories. Therefore, for many applications, the WRI required for vibration isolation applications can be selected from the lists that often come within the guides provided by the suppliers. The commonly accepted procedure to choose the suitable WRI for a given application is given in the catalog of the WRI manufacturer [26], which is based on the static stiffness of the WRIs using the linear approach. Such a linearized selection process is suitable for a linear isolator. However, it may be ideal for a nonlinear isolator to use a nonlinear model for a more accurate prediction of the isolation capability.
The results of this study are pretty comprehensive due to the number and different sizes of wire rope isolators. Therefore, the identified parameters of the mathematical models can effectively be used to predict the isolation capability of a broader range of WRIs.
The accuracy of the proposed mathematical model is shared by all mathematical models that attempt to replicate physical experiments. Any discrepancies between the physical test (“true results”) and the mathematical model can be first attributed to the inherent limitations of the mathematical model and then to the various uncertainties associated with the experiment (material, fabrication, test setup, and the actuator's accuracy).
7. Summary and conclusions
This study presented an analysis of the restoring force-displacement relation of the WRI under cyclic loading in vertical and lateral directions. The hysteresis behavior in the vertical direction was obtained from tension∖compression loading, and roll loading was used to determine the hysteresis behavior in the lateral direction.
The WRI exhibits a hysteresis behavior under cyclic loading in all loading directions, indicating that the restoring force is a function of instantaneous displacement and the history of displacement. This dependency can be described as a memory effect, which means the history of displacements also influences the response of the WRI for a given load. In general, the hysteresis behavior of the friction type damper is rate-independent. Earlier studies have suggested that the WRI exhibits rate-independent behavior. Mathematically, hysteresis is defined as the rate-independent memory effect. These memory effects in damping materials may not be purely rate-independent due to hysteresis coupling with viscous-type memory.
Quasi-static cyclic loading behavior of the WRI was studied using a series of quasi-static cyclic loading tests. The rate-independent property of the WRI was verified by subjecting the WRI to various quasi-static cyclic loadings with varying rates and comparing the results.
In the shear/roll loading direction, the wire rope isolators exhibit symmetric hysteresis, rate-independent behavior, therefore, the original Bouc-Wen model of hysteresis was adopted, and its parameters were identified to fit the experimental data accurately.
In the tension/compression loading direction, the wire rope isolators exhibit asymmetric hysteresis, rate-independent behavior. They exhibit hardening under tension and softening under compression. Consequently, a modification was introduced to the Bouc-Wen by replacing the linear part with a modulating force to simulate the observed asymmetric behavior of the isolators accurately.
An increased value of the height to width ratio () increases the hardening of the WRI. The equivalent damping ratio was significantly influenced by the size of the wire rope diameter, and an increased value of the ratio decreases the equivalent-damping ratio. The damping ratio of an isolator is affected by the height to width ratio and the displacement amplitude. The damping ratio is greater for an isolator with a high height to width ratio for a given displacement amplitude. The damping ratio also increases with increasing displacement amplitude. In applications where high levels of damping are required, an isolator can be designed to achieve smaller displacements. The hysteresis area also increases with increasing displacement amplitude. In applications where high levels of energy dissipation are required, an isolator with an increased height-to-width ratio can be preferred.
The study found that the effective stiffness and effective damping of a WRI are significantly influenced by the size of the wire rope diameter. In particular, the study found that the equivalent-damping ratio was inversely proportional to the size of the wire rope diameter. The study also found that the ratio can be used to achieve a wide variety of effective stiffness and the equivalent damping for similar wire rope diameters.
These findings suggest that the height-to-width ratio can control the hysteresis behavior and equivalent damping of a WRI. Furthermore, the study's findings indicate that the effective stiffness and damping of a WRI are significantly influenced by the size of the wire rope diameter. The hysteresis nature of the WRI in the vertical direction is asymmetric; however, at smaller displacements, the hysteresis is symmetric, and the critical displacement at which the hysteresis curve shifts from symmetric to asymmetric can be studied as the future scope of the present work.
Declarations
Author contribution statement
Moussa Leblouba; PS Balaji; Muhammad E.R: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
Moussa Leblouba was supported by the Ministry of Higher Education, Malaysia and the University of Sharjah, United Arab Emirates.
PS Balaji was supported by Curtin University, Australia.
Data availability statement
Data will be made available on request.
Declaration of interest's statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Alessandri S., Giannini R., Paolacci F., Malena M. Seismic retrofitting of an HV circuit breaker using base isolation with wire ropes. Part 1: preliminary tests and analyses. Eng. Struct. 2015;98:251–262. [Google Scholar]
- 2.Alessandri S., Giannini R., Paolacci F., Amoretti M., Freddo A. Seismic retrofitting of an HV circuit breaker using base isolation with wire ropes. Part 2: shaking-table test validation. Eng. Struct. 2015;98:263–274. [Google Scholar]
- 3.Demetriades G.F., Constantinou M.C., Reinhorn A.M. Study of wire rope systems for seismic protection of equipment in buildings. Eng. Struct. 1993;15(5):321–334. [Google Scholar]
- 4.Leblouba M., Rahman M.E., Barakat S. Behavior of polycal wire rope isolators subjected to large lateral deformations. Eng. Struct. 2019;191:117–128. [Google Scholar]
- 5.Ni Y.Q., Ko J.M., Wong C.W., Zhan S. Modelling and identification of a wire-cable vibration isolator via a cyclic loading test. Proc. IME J. Syst. Control Eng. 1999;213(3):173–182. [Google Scholar]
- 6.Balaji P.S., Moussa L., Rahman M.E., Vuia L.T. Experimental investigation on the hysteresis behavior of the wire rope isolators. J. Mech. Sci. Technol. 2015;29(4):1527–1536. [Google Scholar]
- 7.Balaji P.S., Moussa L., Khandoker N., Shyh T.Y., Rahman M.E., Ho L.H. Experimental study on vertical static stiffnesses of polycal wire rope isolators. IOP Conf. Ser. Mater. Sci. Eng. 2017;217 [Google Scholar]
- 8.Balaji P.S., Leblouba M., Rahman M.E., Ho L.H. Static lateral stiffness of wire rope isolators. Mech. Base. Des. Struct. Mach. 2016;44(4):462–475. [Google Scholar]
- 9.Balaji P.S., Rahman M.E., Moussa L., Lau H.H. Wire rope isolators for vibration isolation of equipment and structures – a review. IOP Conf. Ser. Mater. Sci. Eng. 2015;78 [Google Scholar]
- 10.Tinker M.L., Cutchins M.A. Damping phenomena in a wire rope vibration isolation system. J. Sound Vib. 1992;157(1):7–18. [Google Scholar]
- 11.Peng Y-x, Chang X-d, Sun S-s, Zhu Z-c, Gong X-s, Zou S-y, et al. The friction and wear properties of steel wire rope sliding against itself under impact load. Wear. 2018;400–401:194–206. [Google Scholar]
- 12.Chang X.-D., Peng Y.-X., Zhu Z.-C., Gong X.-S., Yu Z.-F., Mi Z.-T., et al. Experimental investigation of mechanical response and fracture failure behavior of wire rope with different given surface wear. Tribol. Int. 2018;119:208–221. [Google Scholar]
- 13.Yu-xing P., Xiang-dong C., Zhen-cai Z., Da-gang W., Xian-sheng G., Sheng-yong Z., et al. Sliding friction and wear behavior of winding hoisting rope in ultra-deep coal mine under different conditions. Wear. 2016;368–369:423–434. [Google Scholar]
- 14.Lee S.-J., Truong G.T., Lee J.-E., Park S.-H., Choi K.-K. Dynamic characteristics of combined isolation systems using rubber and wire isolators. Nucl. Eng. Technol. 2022;54(3):1071–1084. [Google Scholar]
- 15.Cen B., Lu X., Zhu X. Research of numerical simulation method on vertical stiffness of polycal wire rope isolator. J. Mech. Sci. Technol. 2018;32(6):2541–2549. [Google Scholar]
- 16.Barbieri N., Barbieri R., da Silva R.A., Mannala M.J., Barbieri LdSAV. Nonlinear dynamic analysis of wire-rope isolator and Stockbridge damper. Nonlinear Dynam. 2016;86(1):501–512. [Google Scholar]
- 17.Balaji P.S., Moussa L., Rahman M.E., Ho L.H. An analytical study on the static vertical stiffness of wire rope isolators. J. Mech. Sci. Technol. 2016;30(1):287–295. [Google Scholar]
- 18.Balaji P.S., Karthik SelvaKumar K. Applications of nonlinearity in passive vibration control: a review. J. Vibr. Eng. Technol. 2021;9(2):183–213. [Google Scholar]
- 19.Salvatore A., Carboni B., Chen L.-Q., Lacarbonara W. Nonlinear dynamic response of a wire rope isolator: experiment, identification and validation. Eng. Struct. 2021;238 [Google Scholar]
- 20.Rashidi S., Ziaei-Rad S. Experimental and numerical vibration analysis of wire rope isolators under quasi-static and dynamic loadings. Eng. Struct. 2017;148:328–339. [Google Scholar]
- 21.Vaiana N., Spizzuoco M., Serino G. Wire rope isolators for seismically base-isolated lightweight structures: experimental characterization and mathematical modeling. Eng. Struct. 2017;140:498–514. [Google Scholar]
- 22.Foss G.C. Modal damping estimates from static load-deflection curves. Shock Vib. Digest. 2006;38:535. [Google Scholar]
- 23.Bouc R. A mathematical model for hysteresis. Acta Acustica. 1971;24(1):16–25. [Google Scholar]
- 24.Wen Y.-K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976;102(2):249–263. [Google Scholar]
- 25.Wen Y.K. Equivalent linearization for hysteretic systems under random excitation. J. Appl. Mech. 1980;47(1):150–154. [Google Scholar]
- 26.INC IE Wire Rope Isolators 2014. www.enidine.com
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.