Nuclear Magnetic Resonance and Metadynamics Simulations Reveal the Atomistic Binding of l-Serine and O-Phospho-l-Serine at Disordered Calcium Phosphate Surfaces of Biocements

Abstract

Interactions between biomolecules and structurally disordered calcium phosphate (CaP) surfaces are crucial for the regulation of bone mineralization by noncollagenous proteins, the organization of complexes of casein and amorphous calcium phosphate (ACP) in milk, as well as for structure–function relationships of hybrid organic/inorganic interfaces in biomaterials. By a combination of advanced solid-state NMR experiments and metadynamics simulations, we examine the detailed binding of O-phospho-l-serine (Pser) and l-serine (Ser) with ACP in bone-adhesive CaP cements, whose capacity of gluing fractured bone together stems from the close integration of the organic molecules with ACP over a subnanometer scale. The proximity of each carboxy, aliphatic, and amino group of Pser/Ser to the Ca²⁺ and phosphate species of ACP observed from the metadynamics-derived models agreed well with results from heteronuclear solid-state NMR experiments that are sensitive to the ¹³C–³¹P and ¹⁵N–³¹P distances. The inorganic/organic contacts in Pser-doped cements are also contrasted with experimental and modeled data on the Pser binding at nanocrystalline HA particles grown from a Pser-bearing aqueous solution. The molecular adsorption is driven mainly by electrostatic interactions between the negatively charged carboxy/phosphate groups and Ca²⁺ cations of ACP, along with H bonds to either protonated or nonprotonated inorganic phosphate groups. The Pser and Ser molecules anchor at their phosphate/amino and carboxy/amino moieties, respectively, leading to an extended molecular conformation across the surface, as opposed to an “upright standing” molecule that would result from the binding of one sole functional group.

1. Introduction

Bone mineral constitutes nanoparticles of a structurally disordered and carbonate-bearing form of Ca hydroxyapatite [HA; “apatite”; Ca₁₀(PO₄)₆(OH)₂].¹⁻⁵ Vast research efforts have been spent to understand the mechanisms of bone mineralization,⁵⁻¹⁰ which remain controversial but are believed to be governed by noncollagenous proteins (NCPs) that carry a high density of negatively charged carboxy-bearing (Asp/Glu) and phosphorylated residues.^5,9−11 For decades, mainstream models for the NCP/mineral interactions involved “charge-matching” arguments assuming that the protein adopts a secondary structure with its negatively charged sidechains matching the Ca²⁺ positions at the apatite mineral surface to provide epitaxial crystal growth.^6,7 However, doubts thereof arose from the subsequently accumulating evidence that (i) the crystal-binding domains of most NCPs lack a well-defined secondary structure^10,11 and (ii) both synthetic and biogenic nanocrystalline apatite particles formed from aqueous solutions—such as body fluids—consist of a “core” of an ordered HA lattice coated by a 1–2 nm thick surface layer (“shell”) of amorphouscalcium phosphate (ACP),^4,12−16 often termed the “hydrated surface layer”.^2,3,17 These recent insights have led to a paradigm shift advocating simpler electrostatic models for which the net charge of the protein and its underlying distribution control the NCP binding at biogenic apatite.¹⁸⁻²¹

An accurate atomistic probing of biomolecular adsorption at structurally disordered inorganic calcium phosphate (CaP) surfaces by experimental techniques is hampered by the particle fragility, coupled with their structural disorder. The most detailed current insight is provided by magic-angle-spinning (MAS) nuclear magnetic resonance (NMR) experiments, often utilizing proteins with isotopic ¹³C/¹⁵N labeling at specific sites in its “crystal”-binding domain. Some MAS NMR reports targeted biomolecular binding at bone mineral,²²⁻²⁶ but adsorption on model systems of HA nanoparticles is most commonly encountered, encompassing the surface binding of small biomolecules²⁷⁻³² and various mineralization-controlling NCPs such as statherin,^33,34 osteopontin,³⁵ osteonectin,^36,37 and osteocalcin.³⁸ Here, advanced NMR techniques relying on through-space dipolar interactions, such as ¹³C{³¹P} and ¹⁵N{³¹P} rotational-echo double resonance (REDOR)³⁹ NMR experiments, have been exploited for obtaining (semi-)quantitative ¹³C–³¹P and ¹⁵N–³¹P interatomic distance-information along with 2D ¹³C–¹³C correlation NMR experiments that offer constraints on the surface-bound molecular conformation.

Considering the difficulties in experimental probing of the surface binding at atomic resolution, computer modeling by atomistic molecular dynamics (MD) and/or metadynamics simulations offers a rich source of structural information on the organic/inorganic interface.^{18−20,40−48} They may reveal the precise binding sites of the biomolecule along with its detailed surface-immobilized conformation—henceforth referred to as the binding mode of the molecule. Yet, outstanding problems in computational modeling of biomolecular adsorption at an in vitro- or in vivo-generated nanocrystalline apatite surface concern how its structural disorder and potentially pH-dependent phosphate speciation are accounted for. As discussed further in the Supporting Information, these critical aspects remain essentially ignored in all but a few very recent modeling studies.⁴⁴⁻⁴⁹

Interfaces between phosphorylated biomolecules and disordered CaP phases are not only of pivotal importance for understanding bone mineralization but also underpin casein–ACP complex-formation in milk⁵⁰⁻⁵³ and structure–function relationships of hybrid organic/inorganic (bio)materials, such as the bone-tissue-adhesive properties of CaP cements incorporating O-phospho-l-serine (Pser),⁵⁴⁻⁵⁹ which by their capacity to glue bone tissues together makes them promising for accelerating bone-fracture healing. As unveiled by an array of advanced MAS NMR techniques, we recently demonstrated that the “bone-gluing” strength of such a cement correlates well with its content of an amorphous “ACP/Pser” phase of Pser molecules intimately integrated with ACP across a sub-nm scale.⁶⁰ An analogous “ACP/Ser” component forms in l-serine (Ser) doped cements which, however, exhibit poor bone-adhesive properties,⁶⁰ as discussed and rationalized further herein.

Herein, we advance the atomic-scale insight into the organic/inorganic interface further by examining cements prepared from uniformly ¹³C/¹⁵N–enriched l-serine and O-phospho-l-serine (the latter synthesized herein for the first time), thereby enabling direct experimental probing of the proximity of each carboxy/aliphatic and amino group to the inorganic phosphate moieties of ACP by ¹³C{³¹P} and ¹⁵N{³¹P} REDOR NMR experimentation, respectively. These results are contrasted with information from heteronuclear ¹³C{³¹P} and ¹H{³¹P} correlation 2D NMR experiments that reveal the contacts between the organic functional groups of Pser/Ser and the inorganic 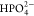/ 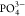phosphate moieties of ACP. We also discuss the similarities and differences between the inorganic/organic contacts in the amorphous ACP/Pser and ACP/Ser biocement components with that of nanocrystalline HA particles grown from a Pser-bearing aqueous solution, henceforth referred to as “Pser@HA”, and constituting a simplified model of a carboxy-bearing or/and phosphorylated protein residue interacting with bone mineral. Moreover, the NMR-derived ¹³C–³¹P and ¹⁵N–³¹P interatomic-distance constraints were contrasted with results from state-of-the-art well-tempered metadynamics MD simulations^61,62 employing the INTERFACE force field and the HA-surface preparation protocol of refs (45) and (49) to faithfully model the adsorption of Ser and Pser molecules at the amorphous surface of apatite nanoparticles. These structural models offer a wealth of structural details about the Ser/Pser binding modes (encompassing the surface-bound molecular conformation), as well as a quantification of the relative contribution of each functional group toward the binding via a recently introduced analysis protocol.⁴⁸

2. Materials and Methods

2.1. Preparation of ¹³C/¹⁵N-Enriched Samples

l-serine (Aldrich; 99.5%) and O-phospho-l-serine (Flamma SpA; 95%) with all isotopes at their natural abundance were used as received. [U–¹³C/¹⁵N]-l-serine enriched to 98% with respect to both ¹³C/¹⁵N was purchased from CortecNet (France). It was used to prepare [U–¹³C/¹⁵N]-O-phospho-l-serine, which was obtained as its HCl salt (Figure S1) from the corresponding BocNH-Ser-CO₂-tert-Bu analogues via phosphoramidation with tert-butyl N, N′-diisopropylcarbamimidate followed by peroxide oxidation to yield the protected phosphate ester, which was converted into the desired product by global deprotection under acidic conditions; see Section S3 for details. These isotopically labeled Ser and Pser powders are for simplicity abbreviated as Ser* and Pser*, respectively. They were used for producing a nanocrystalline HA powder with surface-immobilized Pser* molecules, as well as cements comprising N mol % of Ser* or Pser*, which are henceforth denoted by SerN and PserN, respectively.

2.1.1. Pser@HA Specimen

5.0 mL of a 500 mM aqueous solution of CaCl₂ in deionized water was pipetted in a 20 mL flask placed in a water bath at 37 ± 2 °C, whereupon Pser*·HCl was added to the solution to yield a concentration of 10 mM. 5 mL of 300 mM (NH₄)₃PO₄(aq) was added at 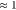mL/min with continuous magnetic stirring. The pH of the solution was subsequently raised to 7.5 by dropwise addition of 1 M NaOH(aq), leading to precipitation of floccular ACP particles. Deionized water was added to a final volume of 20 mL, and the flask was sealed. The suspension was aged for one week at 37 ± 0.2 °C, leading to a final pH value of 5.3. The as-formed Pser@HA particles were isolated by centrifugation, cleaned twice with deionized water, and then dried in a desiccator at room temperature for 4 days.

The Pser content was estimated as ≈ 5 wt % by contrasting the integrated ¹⁵N NMR intensity from the Pser@HA specimen with that of the Pser16 cement with known Pser content. The transmission electron microscopy images of Figure S2 reveal agglomerates of crystalline domains with variable sizes (from a few nm to 10–20 nm) that are fused together by ACP. The surface area was estimated to be 159 m²/g by the Brunauer–Emmett–Teller model⁶³ (N₂ uptake at relative pressures (P/P₀) of 0.05–0.15, using a Micrometrics ASAP2020 volumetric adsorption analyzer).

The Pser@HA synthesis protocol was preceded by extensive testing of optimal preparation conditions by using Pser (Flamma SpA) with concentrations in the 5–200 mM range. As verified by Figure S3, [Pser] ≥ 20 mM yielded products with little/no surface immobilization but predominantly comprised the Ca salt of Pser, Ca[O-phospho-l-serine]·H₂O,^64,65 henceforth denoted CaPser.

2.1.2. Ser/Pser-Doped Cements

The SerN and PserN cements with N = {8, 16, 30} were prepared in batches of 0.25 g by first dissolving/suspending each organic Ser* and Pser* additive in 60 μL of deionized water (see Table S1), whereupon a powder of α-Ca₃(PO₄)₂ (α-TCP) (see refs (54) and (60) for preparation details) was added at liquid-to-powder (L/P) ratio of 0.24 mL/g. The powder and liquid were mixed with a spatula for ≈30 s. The cement paste was cured at 21 °C and 30% relative humidity for 15–30 min and then transferred to a sealed plastic bag that was stored at 37 °C for 7 days at 100% humidity. All cement specimens were thereafter stored under dry conditions in a desiccator. For practical reasons, pH measurements of the cement pastes prior to their setting were performed on larger SerN/PserN batches of 3.0 g and a slightly higher L/P = 0.4 mL/g ratio. Table S1 presents the pH value associated with each cement preparation, obtained as an average over three independent preparations.

2.2. Solid-State NMR Experiments

The solid-state NMR experimentation was performed with Bruker Avance-III spectrometers operating at the magnetic fields (B₀) of 9.4 T or 14.1 T, which provided {¹H, ¹³C, ³¹P} Larmor frequencies of {−400.1, −100.6, −162.0} MHz and {−600.1, −150.9, −242.9} MHz, respectively, along with 60.4 MHz for ¹⁵N at 14.1 T. A fine powder of each specimen was packed in a ZrO₂ rotor of outer diameters of either 2.5 mm (thin-wall), 3.2, or 4 mm, as specified along with each MAS rate (ν_r) in the figure captions and in Section S1, which provides all details of each NMR experiment. Full rotors were employed throughout, except for the REDOR NMR³⁹ experiments, for which each sample was restricted to the center 1/3 volume of a 4 mm rotor. ¹H/¹³C, ³¹P, and ¹⁵N chemical shifts are quoted relative to neat tetramethylsilane (TMS), 85% H₃PO₄(aq), and solid ¹⁵NH₄Cl, respectively.

2.3. Metadynamics Simulations

The preparation of the simulated systems and the well-tempered metadynamics simulations were performed as described in ref (48). Here, we only recapitulate the most essential information and refer to Section S2 and ref (48) for details. A box with side-lengths {3.9, 4.3, 7.8} nm (periodic boundary conditions) contained the simulated system of three components (Figure 1a): one Ser or Pser molecule in a water phase (2600 H₂O molecules) that interfaced a “HA slab”, whose interior consisted of an HA lattice of the biologically relevant P6₃/m modification.⁶⁶ The “surface” segment was generated according to ref (45), which mimics a disordered surface at a nanocrystalline HA-particle by introducing acidic protons at randomly selected phosphate groups accompanied by Ca²⁺-cation removal until a charge-neutral surface is obtained, whose {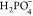, , 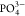} speciation matches that of phosphate ions in an aqueous solution at a given pH value; see Figure 1. The HA surface and the Pser/Ser protonation states were implemented for the experimentally relevant pH values of 4.5 for Pser and 7.4 for Ser, as explained further in Section S2.

Figure 1.

(a) Simulated three-component system, consisting of a “HA slab” with a lattice of crystalline HA and a disordered surface that interface a water phase that contains one Pser molecule (or Ser; not shown). The surface atoms are enlarged for better visualization. The box lengths along the z and x directions are indicated, along with the (approximate) lengths of the water and lattice/surface domains. (b,c) Dependence of the average number of protons per phosphate group at the as-prepared HA surface (red curve) along with the net number of protons of the molecular forms of (b) Pser and (c) Ser (black curves) plotted against the pH value of the solution. The most stable molecular form of (b) Pser and (c) Ser at a given pH value is shown on top of each graph, where the colored circles enclose the functional group(s) with altering protonation states between the pH domains marked by black vertical lines. The vertical green lines mark the simulated pH values of 4.5 and 7.4. Each number inside the graph specifies the respective pK_a values of the organic functional groups, as well as the inorganic {H₃PO₄, H₂PO₄⁻, and 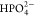} surface species (the phosphate speciation at the surface matches that of the surrounding solution⁴⁵).

The atomistic MD simulations involved NVT ensembles at the temperature T = 37 °C, utilizing the GROMACS v2018.1 platform⁶⁷ and the following force-fields: INTERFACE^45,49 for the HA slab, CHARMM36 (July 2017)⁶⁸ for the Pser/Ser molecules, and TIP3P⁶⁹ (without Lennard-Jones terms for H⁷⁰) for water. Well-tempered metadynamics^61,62 with a bias factor of γ = 5 and 32 independent “walkers”^62,71 were employed to ensure an efficient sampling of the molecular conformations and accelerate the convergence, using the variational enhanced sampling (VES) protocol⁷² implemented in the PLUMED2.4 software.⁷³ Two collective variables were exploited for locating the most stable surface-bound molecular conformation, involving the distance between the center of the HA slab and the COO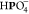^–/ atom of the respective Ser/Pser molecule along with an interaction-energy dependent function defined in Section S2. The reported modeled parameters and their uncertainties are averages over 4 independent simulations.

3. Results and Discussion

3.1. Local ³¹P Environments Probed by MAS NMR

Figure 2 displays ³¹P MAS NMR spectra recorded from the nanocrystalline Pser@HA sample and the PserN/SerN cements with N = {8, 16, 30}. The peak intensities of the single-pulse-acquired NMR spectra of the left panel quantitatively reflect the relative phase constituents of each sample, whereas those of the right panel of Figure 2 were obtained by ¹H → ³¹P CP, thereby only revealing ³¹P NMR signals from phosphate groups nearby protons. The directly excited ³¹P MAS NMR peak shapes from the cements are complex due to the contributing signals from unreacted α-TCP (Figure S4). The absence of protons in the α-TCP structure, however, renders the ¹H → ³¹P CPMAS spectra considerably simpler because they only comprise ³¹P resonances from ¹H-bearing phases, which predominantly involve the amorphous ACP/Pser or ACP/Ser components.⁶⁰ We henceforth focus on the ¹H → ³¹P CPMAS NMR spectra along with the deconvolutions into their underlying NMR-peak components and the associated best-fit parameters presented in Table S6. The NMR spectra from the cements in Figure 2 overall match those presented in ref (60) from near-identical preparations with ¹³C/¹⁵N isotopes at natural abundance.

Figure 2.

³¹P MAS NMR spectra recorded at 14.00 kHz MAS either directly by single pulses (left panel) or by ¹H → ³¹P CP (right panel) from (a,b) Pser@HA, or from the as-indicated (c–f) SerN and (g–l) PserN cements. Note that no NMR peak from remnants of the proton-free α-TCP precursor (Figure S4) appear in the CPMAS-derived spectra; the latter are shown together with the best-fit spectra (orange traces) and the deconvolutions into the as-indicated peak components given in each legend. The narrow NMR peaks at 1.4 ppm and −1.0 ppm stem from minor impurities of brushite (CaHPO₄·2H₂O) and CaPser (Ca[O-phospho-l-serine]·H₂O), respectively, while that marked by an asterisk in (d) derives from an unknown impurity. Table S6 lists the best-fit NMR parameters.

Both the directly excited and CP-derived ³¹P MAS NMR spectra of the Pser@HA specimen (Figure 2a,b) are typical for nanocrystalline HA particles, which involve a crystalline HA “core” coated by a surface layer (“shell”) of ACP.^{2−4,12−17} The “core” and “shell” components produce a narrow and broad resonance, respectively,^4,12−14 centered at the corresponding ³¹P chemical shifts δ_P ≈ 3.0 ppm and δ_P ≈ 2.2 ppm (Figure 2a,b and Table S6). The lower shift of the ACP component reflects the acidic solution (pH = 5.3) surrounding the Pser@HA particles before their isolation, which yields a surface layer of ACP enriched in protonated phosphate moieties^{4,13,14,16,74} resonating at lower ³¹P shifts than nonprotonated 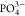groups.⁷⁵⁻⁷⁷ Moreover, the close ¹H–³¹P distances of 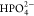/H₂PO₄⁻ groups emphasize the “ACP” contribution in the ¹H → ³¹P CPMAS NMR spectrum (Figure 2b) relative to the directly excited counterpart (Figure 2a); also see Table S6.

Cements prepared from α-TCP and water in the absence of Pser consist of disordered HA.^60,78−80 Although ACP and HA particles are unstable in acidic aqueous solutions, they become stabilized by negatively charged organic additives in weakly acidic solutions.⁴ The pH value of the precursor paste before the cement setting is reduced for increasing Pser/Ser content, while at a fixed doping level N, Pser yields a markedly lower pH value than Ser (Table S1). Hence, the highly acidic PserN cement pastes preclude HA formation, whereas the Ser8 and Ser16 samples comprise significant HA contributions (Figure 2d,f and Table S6), as proved unambiguously by the heteronuclear correlation NMR results of Section 3.2. The progressively reduced pH values for the Pser-bearing cements also manifest as ³¹P resonance displacements of the ACP/Pser phase toward lower chemical shifts for increasing N. These acidic conditions also induced a minor brushite (CaHPO₄·2H₂O) formation, as signified by the narrow resonance at δ_P = 1.4 ppm^60,81,82 (Figure 2h,j,l). It is instructive to contrast the ³¹P shifts among the ACP (≈2.2 ppm; Figure 2a,b), ACP/Ser (≈2.3 ppm; Figure 2d,f), and ACP/Pser (0.7–1.8 ppm; Figure 2h,j,l) phases with that from amorphous tricalcium phosphate of approximate stoichiometry Ca₃(PO₄)₂·nH₂O (δ_P ≈ 3 ppm)^81,83,84 and the H³¹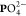 environments of amorphous CaHPO₄·nH₂O (δ_P ≈ 1.5 ppm).^4,77

3.2. Organic/Inorganic Interface Probed by ¹H–³¹P Correlation NMR

Figure 3 presents the ¹H MAS NMR spectra recorded from the Pser@HA sample along with the SerN and PserN cements. The various ¹H sites of the present specimens may be of organic {COOH, POH, NH₃, CH_n} or inorganic {OH, H_n} origin, along with H₂O molecules that may either constitute an integral component of the inorganic ACP and HA structures (“structure-bound”), associated with the inorganic/organic ACP/Pser and ACP/Ser components or being mobile physisorbed species. The latter ¹H₂O molecules typically resonate in the 4.5–5.5 ppm spectral region,^{13,14,16,74,85,86} where Figure 3 suggests that they constitute a significant fraction of the entire proton reservoir in the Pser@HA and PserN/SerN samples. Moreover, the characteristic ¹H NMR peak at δ_H ≈ 0 ppm^{12−14,16,74,85,86} from OH groups in the HA lattice is observed from several specimens. We refer to Mathew et al.(60) for discussions on the various ¹H resonance assignments made from nominally identical PserN and SerN cement compositions.

Figure 3.

¹H NMR spectra recorded at 9.4 T and 14.00 kHz MAS from the as-indicated SerN and PserN cements, as well as the Pser@HA and Pser samples. The green trace in (g) is a vertical expansion. The sharp peaks at 3.8/1.1 ppm in (f,g) stem from a minor isopropanol impurity, whereas those marked by asterisks in the NMR spectra from Pser@HA and Ser8 derive from HA-associated surface water molecules, as discussed in detail in refs (60) and (74)

The remainder of the article focuses on the probing of the organic/inorganic interface in the Pser@HA, Pser16, and Ser16 specimens, which were examined by dipolar-based MAS NMR experimentation, such as the dipolar-mediated heteronuclear multiple-quantum coherence (D-HMQC) ¹H{³¹P} NMR spectra^60,82,87,88 shown in Figure 4. They were recorded from the Pser@HA, Pser16, and Ser16 specimens using a short HMQC excitation period (τ_exc = 176 μs) to ensure detection predominantly of ¹H and ³¹P sites separated by at most a few hundreds of pm. In each D-HMQC spectrum, a 2D NMR correlation peak centered at the chemical-shift pair {δ₁, δ₂} ≡ {δ_P, δ_H} evidences close spatial proximity between ¹H and ³¹P sites resonating at the (average) chemical shifts δ_H and δ_P, respectively.

Figure 4.

¹H{³¹P} D-HMQC correlation NMR spectra acquired at 34.00 kHz MAS from the (a) Ser16, (b) Pser16, and (c) Pser@HA specimens using a short HMQC excitation period of 176 μs. The 2D NMR spectra are shown together with projections along the ¹H (horizontal) and ³¹P (vertical) dimensions at the top and to the right, respectively; the green trace in (c) is a three-fold vertical expansion of the ¹H projection. Directly excited (“single-pulse”) ¹H MAS NMR from crystalline Pser and Ser are displayed by red traces in (a,b). Most of the ¹H resonances marked along the horizontal dimension are of organic origin, whereas the peaks assigned along the ³¹P dimension originate either from HA (blue color) or the ACP/Pser or ACP/Ser cement constituents (cyan color). The 2D NMR regions {δ_P, δ_H} ≈ {1.6, 5.8} ppm and {δ_P, δ_H} ≈ {4.3, 5.0} ppm marked by the respective yellow and blue rectangles in (c) are discussed in Section 3.2).

Figure 4a offers direct and unambiguous evidence for an intimate ACP/Ser integration across a sub-nm scale, whereas the Pser16 counterpart reveals HMQC correlations stemming from both intramolecular ¹H–³¹P dipolar interactions of Pser and Pser···ACP contacts of the ACP/Pser phase (Figure 4b). The ¹H{³¹P} D-HMQC spectral signatures observed from a PserN cement in the high-δ_H region reflect correlations between acidic protons and (in)organic phosphate groups. Hence, it depends strongly on the pH value before cement setting (i.e., on the Pser content; Table S1). Indeed, the higher pH = 5.3 of the solution that immersed the Pser@HA particles renders the 2D NMR spectrum in Figure 4c closer to that reported previously from a Pser4 specimen⁶⁰ than that from Pser16. As expected from the results of Figures 2 and 3, the D-HMQC NMR spectra recorded from the Pser@HA powder (see Figure 4c) and the Ser16 cement (Figure 4a) manifest the HA-characteristic correlation at {δ_P, δ_H} = {2.9, 0} ppm.^{13,14,16,74,86}

Correlations between the organic protons of the {NH₃, CH_n} moieties and 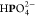/ 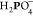groups of ACP dominate the ¹H NMR spectral range of δ_H ≲ 10 ppm, as becomes evident by contrasting the projection of the 2D NMR spectra of Figure 4a,b along the ¹H dimension with the single-pulse-acquired ¹H MAS NMR spectra from the crystalline Pser and Ser samples. The comparatively more intense 2D NMR-peak intensities of the 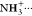PO₄ contacts with ¹H shifts ≈9 ppm relative to those of CH_n···PO₄ (4–5 ppm) ppm of either cement suggest much shorter distances between the inorganic phosphate species and the positively charged moiety than the aliphatic groups that do not bond directly to the surface, as indeed predicted by the metadynamics simulations (Section 3.3) and discussed further in Section 3.6.

Moreover, the HMQC NMR spectrum of Pser@HA reveals two broad but resolved 2D NMR peaks (marked by blue/yellow rectangles in Figure 4c) not observed from the cements. They are tentatively attributed to either aliphatic protons or water molecules nearby inorganic phosphate groups, where the 2D correlation centered at {δ_P, δ_H} ≈ {1.6, 5.8} ppm and extending toward lower ³¹P and ¹H chemical shifts likely reflects CH_n/H₂O···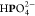 proximities. Further work is required to reach firmer assignments, particularly for the {δ_P, δ_H} ≈ {4.3, 5.0} ppm correlation, whose high ³¹P shift is atypical of (and let alone 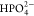) groups in CaP phases, although ¹H–³¹P correlation NMR peaks at similar shifts have been ascribed to 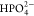species in the HA lattice.⁷⁴ As discussed further in Section S4, the signal at δ_H ≈ 7 ppm in the ¹H{³¹P} D-HMQC NMR spectra from Pser and Pser@HA is characteristic of structure-bound H₂O molecules of “ACP”, encompassing the amorphous surface of nanocrystalline HA.^16,60,89

3.3. Surface Binding of Pser and Ser Modeled by Metadynamics

3.3.1. Overview and General Considerations

Metadynamics simulations were utilized to locate the energetically most favorable molecular adsorption at a structurally disordered HA surface representative for the nanocrystalline Pser@HA particles as well as the ACP component of the Pser16/Ser16 cements. The simulations were performed for a pH-dependent HA surface representative of structurally disordered forms of its crystallographic (100) and (001) faces interfacing a water phase comprising one Ser or Pser molecule with protonation states for each of pH = {4.5, 7.4}; see Figure 1 and Section S2.

Numerous experimental studies on HA nucleation/growth in the presence of both small and large biomolecules suggest a preference for molecular adsorption at the larger (100) or (101) HA surfaces relative to their smaller (001) counterpart,^28,90−93 as also corroborated by previous modeling.^{18,40,43−45,94,95} Indeed, the consistently stronger adsorption at the “disordered” (100) surface was recently deduced by metadynamics simulations of the Pser binding at HA across a wide pH range of 4.5–14 (ref (48)): Table S3 reproduces the results for the Pser adsorption at each pH = {4.5, 7.4} value and (100)/(001) surface,⁴⁸ along with those obtained herein from Ser. Hence, we focus on the results for (100) at each experimentally relevant pH = 7.4 for Ser16 and pH = 4.5 for Pser16/Pser@HA, whose most probable/representative stable binding modes are exemplified in Figure 5. No aliphatic CH/CH₂ groups of either molecule are discussed because they do not bind directly at the HA surface.

Figure 5.

Representative examples of the most stable/probable metadynamics-derived molecular binding modes at a “disordered (100) HA surface” of (a) Ser at pH = 7.4 and (b) Pser at pH = 4.5. All red numbers mark selected distances (in pm) between directly bonded Ser/Pser···HA atoms, while those in black indicate C–P and N–P distances relating to the experimental constraints from NMR. The green numbers in (b) represent intramolecular C–P distances of Pser. For visualization purposes, only a few surface contacts are shown for each organic moiety. Notably, because none of the surface-binding modes of either Ser or Pser involve the sole anchoring of one functional group (Table 1), both molecules assume an extended conformation that “caps” the HA surface. We underscore that owing to the distributions of stable binding modes, no single graphical picture can capture all details of the molecular adsorption (Tables 1, S3, and S4).

There are two main groups of A···Bcontact modes (i.e., “bonding types”) between an organic atom site A of Ser/Pser and an inorganic surface-atom B: (i) electrostatic (“ion–ion”) interactions among negatively charged O sites of carboxy/phosphate groups and positive Ca²⁺ cations of the ACP layer at nanosized HA particles, and (ii) H bonds between an organic (inorganic) proton and an inorganic (organic) O site. Notably, although carboxy/phosphate groups of biomolecules adsorb via both interaction types, each electrostatic bond (e.g., CO···Ca²⁺) is around 2.5 times stronger than its H-bond counterpart (e.g., CO···).⁴⁸ These relative interaction strengths underlie the current consensus that ion–ion interactions dominate the energy landscape of biomolecular adsorption,¹⁸⁻²¹ notwithstanding that the H bonds (140–220 pm) are shorter than the O···Ca²⁺ distances (240–330 pm); see Figure 5.

3.3.2. Distinct Biomolecular Binding at (100) and (001) HA Faces

Our comments made in Section S2.5 about biomolecules interacting with inorganic species at an essentially amorphous HA surface might seem to preclude any preferential adsorption at a specific HA surface type. This apparent contradiction, however, may be reconciled by noting that the consistently stronger adsorption at the “(100)” surface does not stem primarily from crystallographic/structural features—where the (hkl) notation rather specifies the crystallographic origin of the disordered (100) and (001) surfaces—but merely from its higher molar ratio n_Ca/n_P ≈ 1.55 relative to that of n_Ca/n_P ≈ 1.15 for (001) across the pH-range of 3.8–7.4. Consequently, the comparatively higher Ca²⁺ abundance (and larger n_Ca/n_P ratio) at the disordered (100) surface relative to its (001) counterpart emphasizes the electrostatic CO/PO···Ca²⁺ interactions that predominantly govern the net biomolecular adsorption energy,^18−21,48 as confirmed by Table S3.

The above-quoted n_Ca/n_P values were estimated from the chemical speciations of the two outermost layers at each (100) and (001) surface at the end of the metadynamics MD simulation (≈40 ns); see Table 1 of ref (48) for the corresponding precise speciations at the outermost surface layer relevant for the pH values of the present study. Notably, due to minor ion-dissolution processes, the exact Ca²⁺/phosphate surface speciations vary slightly throughout each metadynamics simulation, thereby not necessarily being identical to those plotted in Figure 1b,c that represent the initially prepared outermost surface layer; see ref (48) for details.

Table 1. MD-Derived Surface-Adsorption Data^a.

	Pser		Ser
pH	4.5	7.4	4.5	7.4
ΔFads	–40.7	–66.4	–36.6	–37.7
Contributions to Binding Energyb
phosphate	0.72	0.70
carboxy	0.20	0.26	0.57	0.64
amino	0.08	0.04	0.30	0.16
hydroxyl			0.13	0.10
Binding Mode Statisticsc
PN	0.51	0.15
PC	0.23
PCN	0.15	0.74
CN			0.41	0.30
CNO			0.55	0.59

^aMetadynamics-derived Helmholtz free energy of adsorption (ΔF_ads) for the Pser and Ser binding at the disordered (100) surface for pH = {4.5, 7.4}; see Section S2. A more negative ΔF_ads value implies a stronger surface binding. The results representative for the Pser@HA/Pser16 (pH = 4.5) and Ser16 samples (pH = 7.4) are typeset in boldface. The data for Pser are reproduced from ref (48).

^bFractional contribution of each functional group to the net adsorption energy, as defined in Section S3. No aliphatic group is surface bound.

^cDistribution of stable binding modes, where each number reflects the probability (relative fraction/contribution) out of all stable binding modes. The capital letters P, C, N, and O represent the phosphate (Pser), carboxy, amino, and hydroxyl (Ser) group contributions, respectively. Only binding modes with probability ≥ 0.10 are listed.

3.3.3. Ser and Pser Binding Modes at HA/ACP

Figure 5a exemplifies one of the most probable/representative Ser binding modes at ACP in solutions at physiological pH = 7.4, relevant both for the ACP/Ser component of the SerN cements and the amorphous surface at HA nanoparticles, all of which involve simultaneous {COO^–, , OH} anchoring; they account for ≈60% of all stable Ser binding modes, with the remaining constituting a dual carboxy/amino binding (Table 1). The absence of any significant binding mode by one functional group alone leads to a near-parallel “capping” of the Ser molecule along the ACP surface, as illustrated in Figure 5a. Although typically all three {COO^–, , OH} moieties bind at the HA surface, Table 1 reveals strikingly different relative contributions of {64, 16, 10}% among the respective groups toward stabilizing/driving the Ser adsorption. The overwhelming carboxy-group contribution stems from its prevalent contact mode of strong electrostatic CO···Ca²⁺ interactions (Table S3), whereas the modest net contribution of ≈26% to the total adsorption energy from the and OH groups together reflect their primary (for the amino group exclusive) contact mode of weaker H bonds.

In neutral and alkaline solutions, Pser preferentially anchors at the ACP surface by all three {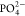, COO^–, } moieties,⁴⁸ leading to a significantly more negative adsorption energy than that for Ser (Table 1). The stronger binding originates primarily from the organic phosphate group of Pser, which is the main adsorption promoter and involved in all stable binding modes regardless of the precise pH and (100)/(001) surface type;⁴⁸ see Table S3. However, the Pser–ACP binding weakens significantly in the acidic solutions relevant for the Pser16 and Pser@HA sample preparation conditions (3.9 ≤ pH ≤ 5.3). This feature may be traced to a lower amount of Ca²⁺ cations at the CaP surface and thereby fewer CO···Ca²⁺ and PO···Ca²⁺ electrostatic contacts, where the latter are diminished further because they are superseded by weaker POH···H_nPO₄ bonds (Table S4) accompanying the onset of protonation of the organic phosphate group for pH 6.8 (Figure 1). These effects combine into a significantly weakened Pser adsorption at pH = 4.5 (Table 1), which incidentally nearly matches that of Ser at the comparatively Ca-richer HA surface at pH = 7.4 that promotes electrostatic interactions.

Relative to the Pser surface immobilization at pH = 7.4, the weaker Pser···ACP contacts in acidic solutions are reflected in a larger distribution of distinct binding modes at pH = 4.5 (Table 1), along with an overall more modest COO^– participation: roughly half of all surface-bound Pser molecules anchor by a dual binding of their phosphate and amino groups, as depicted by Figure 5b, whereas all other binding constellations occur either by the phosphate/carboxy moieties (≈23%) or by all three groups together (≈15%); see Table 1. (We remind that all binding modes not listed in Table 1 are insignificant, such as the anchoring of one functional group alone of either molecule). Yet, although the and COO^– moieties participate in ≈90% and ≈40% of all binding modes, respectively, Table S3 reveals that their corresponding net energy contributions to stabilizing the adsorption only amount to ≈8% () and ≈20% (COO^–) due to the higher CO···Ca²⁺ interaction-energy per bond relative to that of NH···PO and the overall dominant PO···Ca²⁺ interactions.

Out of all functional groups of Pser, the simulations predict the strongest binding at the ACP surface by the phosphate group. However, the broad ³¹P NMR peak from the ACP/Pser phase (Figures 2 and 4) cannot discriminate between the organic and inorganic phosphate contributions, which underscores the very intimate Pser···ACP contacts in the Pser/ACP phase across a sub-nm scale. Indeed, NMR experiments sensitive to the ³¹P–³¹P distance distributions revealed essentially equal average distances in synthetic/pristine ACP and the ACP/Pser components in PserN cements.⁶⁰

3.4. ¹³C–³¹P Correlation NMR Reveals Ser/Pser–ACP Contacts

Figure 6 presents ¹H → ¹³C CPMAS spectra observed from the polycrystalline Ser, Pser, and CaPser powders along with that of the nanocrystalline Pser@HA specimen and the PserN/SerN cements with N = {8, 16, 30} prepared from the Pser*/Ser* precursors. The strikingly different ¹³C NMR peak widths observed from the precursors relative to Pser@HA or any cement reflect the distinctly different local order of the ¹³C environments. Hence, even routine ¹³C CPMAS NMR experiments give qualitative evidence for organic/inorganic contacts. Although heteronuclear ¹⁷O–⁴³Ca NMR experiments would enable the most direct probing of the electrostatic CO/PO···Ca²⁺ interactions that dominate the molecular adsorption, such experiments are precluded for NMR-signal sensitivity reasons along with further sample preparation obstacles which require isotopic ¹⁷O and ⁴³Ca labeling.⁹⁶⁻⁹⁸ Consequently, we resorted to less challenging ¹³C–³¹P NMR experiments, which merely probe the Pser/Ser···ACP contacts via their ¹³C–³¹P distances in ¹³C–O···Ca²⁺···O–³¹P motifs.

Figure 6.

¹³C CPMAS NMR spectra obtained at 9.4 T and 9.00 kHz MAS from (a) polycrystalline Pser (black trace) and CaPser (red trace), (b) Pser@HA, and as-indicated (c–e) PserN cements, as well as (f) polycrystalline Ser along with (g,h) SerN cements. All NMR spectra were recorded from specimens prepared from ¹³C-enriched precursors, except for those shown in (a,f). The asterisk in (h) marks a minor peak from an unknown impurity.

Figure 7 displays ¹³C{³¹P} D-HMQC NMR^87,88 spectra recorded from the Pser16 and Ser16 cements, where each ¹³C–³¹P proximity is revealed by a 2D NMR cross peak centered at the shift-pair {δ_P, δ_C}. Owing to the phosphate group of Pser, however, the ¹³C{³¹P} D-HMQC spectrum observed from Pser16 primarily reflects the intramolecular ¹³C–³¹P distances, which also account for the observed NMR-intensity increase along ¹³CO ¹³CH ¹³CH₂ in Figure 7a; this is particularly evident when contrasting the various peak intensities of the HMQC projection with their counterparts of the corresponding ¹H → ¹³C CPMAS NMR spectrum (Figure S5). The 2D NMR-peak intensities reflect semiquantitatively the relative through-space ¹³C–³¹P distances. The significantly emphasized intensity and the higher ¹³C chemical-shift dispersion of the ¹³COO^–···³¹P correlations from the Ser16 cement relative to the Pser16 counterpart (as is also evident from the ¹³C CPMAS NMR spectra of Figure 6) corroborates the metadynamics predictions (Section 3.3): the carboxy group of Ser anchors directly at the ACP surface, in contrast with (a majority of) the Pser molecules. However, owing to the HMQC-signal buildup across longer distances, cross-peaks associated with all¹³C sites are detected for the present τ_exc values (Figure 7), despite that none of the CH/CH₂ groups of either Pser/Ser molecule bind directly to any species of ACP.

Figure 7.

¹³C{³¹P} D-HMQC correlation NMR spectra obtained at B₀ = 14.1 T and ν_r = 24 kHz from (a) Pser16 and (b) Ser16 cements by using a HMQC excitation period of (a) 1.75 ms and (b) 2.0 ms. The 2D NMR spectra are shown together with projections along the ¹³C (horizontal) and ³¹P (vertical) dimensions at the top and to the right, respectively, along with their ¹H → ¹³C CPMAS NMR spectra acquired under the same conditions. (c) Zoom around the carboxy-resonance region of the 2D NMR spectrum in (b). The rectangles indicate ¹³C–³¹P correlations resolved at the ¹³C chemical shifts of 184 ppm (blue), 177/174 ppm (yellow), and 170 ppm (grey).

The close COO^–···ACP contacts of the Ser molecules are reflected in emphasized 2D NMR-signal intensities in the zoom around the ¹³COO^– region of the 2D NMR spectrum of the Ser16 cement (Figure 7c): four 2D NMR ridges are resolved at the ¹³C chemical shifts {184.2, 176.8, 174.0, 170.0} ppm. Notably, none of them coincides with that of δ_C = 175.2 ppm from polycrystalline Ser (Figure 6f). As is most transparent from Figure S5, the NMR peaks around δ_C = {184, 170} ppm are markedly emphasized (the latter peak is barely discernible in the CPMAS NMR spectrum), whereas the comparatively reduced intensities between 181 ppm and 172 ppm stem from Ser molecules further away from the inorganic phosphate groups. Its significant ¹³C shift-dispersion reflects a range of similar yet distinct COO^–··· proximities of weakly bound Ser molecular configurations at the ACP surface (along with some resonances from nonbonded molecules; see Section 3.5.3 and the comments mentioned above).

We onwards focus on the two D-HMQC NMR signals centered at the {δ_P, δ_C} shift-pairs of {3.0, 184.2} ppm and {2.4, 170.0} ppm, which are tentatively assigned to COO^– moieties that are strongly surface bound predominantly/solely via electrostatic CO···Ca²⁺ interactions and CO··· H bonds, respectively. While noting that those two contact modes were predicted by modeling (Section 3.3), the NMR-peak assignments were based on the distinctly different ¹³C and ³¹P chemical shifts involved in each correlation: the high shifts of the {δ_P, δ_C} = {3.0, 184.2} ppm signal are well-aligned with COO^– moieties nearby 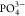groups (see Sections 3.1 and 3.2), whereas the lower chemical shifts of the {2.4, 170.0} ppm correlation are commensurate with H-bond-mediated ¹³COO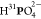^–··· contacts, whose ¹³C chemical shift incidentally matches that of the ¹³COOH group of polycrystalline Pser that manifests analogous inter molecular COOH··· motifs.^65,99,100 Notably, Figure 6 reveals a lower NMR-signal intensity at 184 ppm from the Ser16 cement relative to its Ser8 counterpart, suggesting a concurrently reduced number of CO···Ca²⁺ contacts for increasing batched Ser content, along with earlier and more qualitative findings by Mathew et al.(60) and our inferences in Section 3.7.

To our knowledge, the present study provides the first ¹H/³¹P/¹³C correlation NMR signatures of surface-bound Pser molecules at nanocrystalline HA, noting that the previous ³¹P{¹H} and ¹³C{¹H} heteronuclear correlation spectra presented by Wang et al.(32) from similar nanocrystalline HA preparations in Pser-bearing solutions gave no convincing evidence for Pser···HA contacts. For instance, the ¹³C NMR features merely suggested a prevalence of Pser in crystalline environments than surface-bound ones, which likely resulted from using a very high [Pser] = 200 mM in the solution.³² Likewise, our ¹³C CPMAS spectra recorded from various Pser@HA syntheses with increasing Pser concentrations revealed a dominance of crystalline CaPser in all preparations with [Pser] ≥ 20 mM (Figure S3).

3.5. Quantitative Probing of Ser/Pser–ACP Contacts by ¹³C{³¹P} REDOR NMR

3.5.1. NMR-Derived Dipolar Second Moments

For a quantitative probing of the relative proximities among the {¹³CO, ¹³CH, ¹³CH₂} sites of Ser/Pser and the inorganic phosphate groups at the HA/ACP surface, we collected the ¹³C{³¹P} REDOR NMR dephasing curves presented in Figure 8. Here, a rapid (slow) dephasing reflects short (long) distances of a given ¹³C_j site to the inorganic phosphate groups of ACP (with the caveat of intramolecular ¹³C_j–³¹P interactions in Pser). Table 2 collects the set of REDOR-derived dipolar second moments^101−106 {M₂(CO–P), M₂(CH–P), M₂(CH₂–P)}, extracted by fitting the respective dephasing curves of each sample (Section S1.3). The precise M₂(C_j–P) value depends on the underlying set of interatomic distances {r(C_j–P_k)} between a given ¹³C site and its nearby P atoms via a sum over [r(C_j–P_k)]⁻⁶ terms. This renders the shortest distance contributions most influential for the net M₂(C_j–P) value.

Figure 8.

¹³C{³¹P} REDOR NMR dephasing curves (ΔS/S₀) recorded at B₀ = 14.1 T and ν_r = 10 kHz and plotted for increasing dipolar recoupling/dephasing periods (τ_rec) for the ¹³CO, ¹³CH, and ¹³CH₂ functional groups of the (a,b) polycrystalline Pser and CaPser powders (¹³C at natural abundance) along with the ¹³C-enriched (c) Pser@HA, (d) Pser16, and (e) Ser16 specimens. Each curve in (a–e) corresponds to the best fit of the {τ_rec, ΔS/S₀} data to eq S2, which yielded the dipolar second moments {M₂(C_j–P)} listed in Table 2. The ¹³COO^– NMR spectral region of the Ser16 sample comprises three distinct resonances at δ_C = {184, 177, 174.5} ppm, whose associated dephasing curves are labeled by their chemical shifts in the legend in (e). Note the different horizontal scale in (e) relative to (a–d).

Table 2. Experimental and Calculated Dipolar Second Moments^a.

	15N–31P		13C–31P
	M2(NH3–P)/kHz2		M2(CO–P)/kHz2		M2(CH–P)/kHz2		M2(CH2–P)/kHz2
sample	exp.	calc.	exp.	calc.	exp.	calc.	exp.	calc.
Ser16	2.7 ± 0.4	4.9 ± 0.7	11.1b	14.0b	8.9	13.0	7.9	9.6
Pser16c	2.8 ± 0.4	5.2 (4.0)±0.7	13.1	13.8 (8.3)	18.2	25.8 (8.9)	75.4	96.8 (5.7)
Pser@HAc	4.0 ± 0.4	5.2 (4.0)±0.7	15.7	13.8 (8.3)	20.9	25.8 (8.9)	73.7	96.8 (5.7)
Pserd	3.2 ± 0.4	4.5	18.6	24.5	18.9	24.8	79.9	102.5
CaPser		4.6	15.9	20.8	27.8	38.2	71.7	93.4

^a15N–³¹P and ¹³C–³¹P dipolar second moments obtained for the as-indicated functional groups from ¹⁵N{³¹P} and ¹³C{³¹P} REDOR NMR experiments, respectively, and compared with data calculated either from metadynamics-derived structural models (for Ser16, Pser16, and Pser@HA) or from the crystal structures of Pser and CaPser.⁶⁵ The M₂(C_j–P) data uncertainties are ±1.7 kHz² (NMR) and ±2.2 kHz² (metadynamics model), with kHz² ≡ 1000 s^–2.

^bNet experimental/calculated values; the NMR analysis afforded the extraction of three M₂(CO–P) values of {23.6, 9.3, 13.3} kHz² for the ¹³CO shifts at {184, 177, 174.5} ppm, respectively.

^cValues within parentheses represent the contribution to the net M₂(N–P) and {M₂(C_j–P)} values from the Pser···HA contacts alone; the contribution from the intramolecular ¹⁵N–³¹P and ¹³C_j–³¹P dipolar interactions account for the difference.

^dThe {M₂(C_j–P)} and M₂(N–P) values were obtained from the Pser (Flamma) and isotopically enriched Pser* samples, respectively.

The NMR-derived {M₂(C_j–P)} data from the polycrystalline Pser/CaPser powders were validated against those calculated from their crystal structures.^64,65,99 As expected^103−106 and discussed further in Section S1.3, the NMR-derived dipolar second moments are consistently lower than their theoretical counterparts (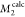). Yet, the 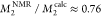ratios are essentially constant (Table S5): a very good agreement is observed for all relativeM₂(C_j–P) values within each Pser or CaPser structure, which remain well within the experimental uncertainties. For Pser, the experimental and calculated M₂(CO–P):M₂(CH–P):M₂(CH₂–P) ratios relate as 1.0:1.0:4.3 and 1.0:1.0:4.2, respectively, whereas both data sets for CaPser are 1.0:1.8:4.5.

The markedly different relative M₂(CO–P):M₂(CH–P) values among the Pser and CaPser crystal structures are noteworthy: Despite the long intramolecular ¹³CO···³¹PO₄ distances in both structures, the comparatively high M₂(CO–P) values (particularly for Pser) originate mainly from multiple intermolecular ¹³COOH···³¹PO₄ contacts via H bonds.^65,99,100 Moreover, the markedly different M₂(CH–P) values in Table 2 reflect distinctly different molecular conformations in the CaPser and Pser crystal structures, whose corresponding θ(P–O–C^β–C^α) dihedral angles of 280° and 153° translate into intramolecular ¹³CH···P distances of 341 pm and 384 pm, respectively. Notably, such widely differing Pser conformations are readily discriminated by the ¹³C{³¹P} REDOR NMR experiments. Hence, notwithstanding that each M₂(C_j–P) value is dominated by the intramolecular ¹³C_j–³¹P distance for all scenarios where intermolecular Pser···Pser contacts are negligible (thereby obscuring the herein targeted C_j···ACP contacts), the M₂(CH–P) parameter offers a valuable constraint on the conformation of the surface-bound Pser molecules, such as in the Pser@HA and Pser16 systems.

3.5.2. Validation of the Metadynamics-Derived Dipolar Second Moments

The dipolar second moment M₂(C_j–P) reflects all {¹³C_j–³¹P_k} distances of the adsorbed molecule to its adjacent inorganic phosphate groups (Section S1.3), but cannot unveil the precise underlying distance distribution. However, because the metadynamics simulations do offer such atomistic details (Figure 5), we first validated the modeled M₂(C_j–P) data against the experimental counterparts.

Considering that all REDOR-derived M₂(C_j–P) values are underestimated by (Table S5 and Section S1.3), a “perfect match” between the metadynamics-generated models and the experiments should result in 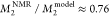for each ¹³C_j–³¹P contact. Notwithstanding a somewhat larger scatter in the ratios of Table S5 (which stems from higher data uncertainties of the simulated systems than the very accurate C/P atom coordinates of the Pser/CaPser crystal structures^64,99), it is gratifying that the data in Tables 2 and S5 confirmed our expectations for all ¹³C_j–³¹P pairs of both Ser/Pser molecules, except for the modeled M₂(CO–P) values relative to the experimental counterparts of Pser@HA and Pser16 that yielded 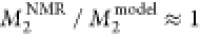. The somewhat stronger COO^–···ACP contacts in both Pser@HA and Pser16 specimens than those predicted by the metadynamics simulations imply that the carboxy group contributes more to the Pser binding than that suggested by the binding mode statistics of Table 1. However, besides noting that the phosphate/amino binding-mode population is presumably slightly overestimated at the expense of (primarily) the phosphate/carboxy/amino counterpart, more quantitative corrections cannot be made. We remind that the ¹³C{³¹P} D-HMQC NMR spectra also suggested weaker COO^–···ACP interactions of the Pser molecules than those of Ser (Section 3.4).

3.5.3. Discussion

The NMR-derived dipolar second moments of the aliphatic groups of Ser (Table 2) suggest M₂(C_j–P) kHz² as the marker of an absence of direct surface binding of any atom of a given ¹³C_j functional group at the ACP surface. We remind that regardless of the (non)adsorption of Pser at ACP, the intramolecular ¹³C_j–³¹P dipolar interactions render all M₂(C_j–P) values of the Pser@HA and Pser16 specimens markedly higher than those from Ser16, as is evident from the dephasing curves of Figure 8. However, the simulation-derived model enables a separation of the intra/intermolecular contributions to the net M₂(C_j–P) value: indeed, Table 2 confirms the expectation that both CH/CH₂ groups of Pser exhibit very low dipolar second moments once their intramolecular contributions are excluded (particularly that of M₂(CH₂–P), for which the organic phosphate group accounts for ≈95% of the net value).

It is gratifying that each of the three {M₂(CO–P), M₂(CH–P), M₂(CH₂–P)} NMR-derived data agrees mutually very well among the Pser@HA and Pser16 samples, which suggests overall (very) similar Pser contacts/distances to the inorganic phosphate moieties. Hence, despite the formally distinct nature of the ACP/Pser phase of the biomedical PserN cements and the Pser adsorption at a nanocrystalline “HA” surface (Pser@HA), the local structure of their organic/inorganic interfaces must be similar in both specimens, thereby consolidating the current consensus that nanocrystalline HA is coated by a layer of “ACP”^4,12−16 (although its precise chemical/structural nature remains unknown). This aspect also justifies that the single metadynamics simulation at pH = 4.5 mimics well the Pser···ACP interactions in both Pser@HA and Pser16 specimens, as well as supporting the physical relevance of the herein employed HA-surface preparation procedure.⁴⁵ These important issues are discussed further in Section S2.5.

We now return to the partially overlapping ¹³C NMR peaks in the carboxy domain of the NMR spectrum from the Ser16 cement (Figure 6h), which, according to their distinct ¹³COO^–···ACP contacts, were grouped into three regions in the ¹³C{³¹P} D-HMQC spectrum of Figure 7c. As expected from the δ_C = 184 ppm resonance attributed to CO···Ca²⁺ motifs (Section 3.4), its very rapid dipolar dephasing is consistent with a sizable dipolar second moment of 23.6 kHz² (Table 2). In contrast, the spectral region marked by a yellow rectangle in Figure 7c and deconvoluted into two peak components around 177/174.5 ppm reflects more weakly surface-bound COO^– groups with lower dipolar second moments of 9.3/13.3 kHz² (Figure 8 and Table 2). Although a large M₂(CO–P) value is also anticipated from COO^– moieties surface bound via H bonds and giving an NMR peak at 170 ppm, its minor NMR intensity (and thereby very small population) did not permit reliable analyses of the REDOR NMR data (e.g., see Figure S6). Altogether, the varying dipolar second moments of these COO^–···ACP contact modes/distances underlie the average value of M₂(CO–P) ≈ 11.1 kHz² (Table 2), which qualitatively corroborates the metadynamics predictions of direct COO^–···ACP bonds.

We contrasted the D-HMQC NMR-derived and modeled relative populations of the three types of surface-bound COO^– sites that produce the three spectral regions marked in Figure 7c and attributed to COO^– sites bound solely by Ca²⁺ cations (≈184 ppm), sites weakly bound by both electrostatic and H-bond interactions (181–172 ppm), and solely by H bonds (≈170 ppm). Quantitative agreements are not expected because the 2D NMR intensities depend strongly on the precise HMQC excitation/reconversion periods. Deconvolution of the ¹³C projection of the D-HMQC spectrum (results not shown) yielded fractional populations of {0.27, 0.59, 0.14} for the respective {184, 181–172, 170} ppm resonance regions, whereas the corresponding metadynamics-simulation-derived fractions are {0.68, 0.27, 0.05}. While both experimental and modeled results accorded qualitatively well for the overall most sparse contact mode of solely CO···HPO₄²⁻ interactions, the main discrepancy concerns the strong dominance of CO^–···Ca²⁺ interactions predicted by the model (68% of all direct surface contacts and consistent with the results of Table S4) compared to the much lower estimate by NMR (27%). The differences presumably stem from the difficulties by NMR to accurately quantify the contributions from the 181–172 ppm resonance-region stemming from “weakly bound” carboxy groups, which may involve non-negligible ¹³COO^– NMR signals from more distant nonbonded molecules that are not accounted for in the simulation analysis.

3.6. ¹⁵N{³¹P} REDOR NMR Reveals the Amino-Group Binding

Figure 9a,b displays the ¹H → ¹⁵N CPMAS NMR spectra of Pser, the ¹⁵N-enriched Ser* and Pser* precursor powders, together with those of Pser@HA, Pser16, and Ser16. As for the ¹³C NMR spectra (Figure 6), the Ser/Pser adsorption is mirrored by a significant ¹⁵N resonance broadening along with a minor increase in the average chemical shift of ≈2 ppm and ≈5 ppm for the Ser and Pser bearing specimens, respectively. The amino-group binding at ACP was probed by ¹⁵N{³¹P} REDOR NMR experiments on the Pser@HA, Pser16, and Ser16 cements, whose dipolar dephasing curves are displayed in Figure 9c along with that from the Pser* powder. For the latter, Table S5 reveals a ratio of 0.71 between the NMR-derived M₂(N–P) value and that calculated from the Pser crystal structure,⁹⁹ which is close to the expected ratio of 0.76 (Section 3.5.2). Moreover, the ratio of 0.77 between the experimental and modeled M₂(P–N) data for the Pser@HA sample suggests a very faithful metadynamics modeling of its ACP/HA contacts (Figure 5b).

Figure 9.

¹H → ¹⁵N CPMAS NMR spectra recorded from powders of (a) Pser (¹⁵N at natural abundance) along with the ¹³C/¹⁵N-enriched Ser* and Pser* precursors, and their (b) Pser@HA, Pser16, and Ser16 products. The NMR peaks at 32.8 ppm and 44.0 ppm observed from the Pser* specimen are attributed to the ¹⁵N sites of ¹³C/¹⁵N-enriched O-phospho-l-serine and its HCl salt, respectively. (c) ¹⁵N{³¹P} REDOR NMR dephasing curves recorded from the as-indicated samples. All NMR results were obtained at B₀ = 14.1 T and ν_r = 10 kHz.

Particularly, when recalling the very good mutual match between the {M₂(C_j–P)} sets among the Pser@HA and Pser16 specimens (Section 3.5), the significantly lower M₂(N–P) value of the Pser16 cement (as well as for Ser16) relative to Pser@HA is surprising (Table 2). It suggests much weaker ACP contacts in both Pser/ACP and Ser/ACP cement components than the counterparts of the Pser@HA particles (also see Section S1.3). Although the NMR-derived dipolar second moments from the cements also suggest longer ACP distances than the metadynamics predictions, the qualitative feature of near-equal M₂(N–P) values of the models for both Ser/Pser molecules is supported by the REDOR NMR experiments on the Pser16 and Ser16 samples.

The amino group binds to the ACP surface exclusively via H bonds to the negatively charged O atoms of the phosphate groups. Table S4 reveals that the NH··· contact mode dominates for Pser (pH = 4.5), whereas the amino group of Ser (pH = 7.4) forms an equal number of bonds to 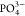and 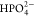moieties. For the pH conditions of the Pser16 and Ser16 cements, the binding-energy contribution from the amino group is higher for Ser than Pser (Table S3), which also accords with the dipolar second moments of Table 2: although both the experimental and modeled M₂(N–P) values for Pser16 are slightly higher than their Ser counterparts, once excluding the intramolecular ¹⁵N–³¹P Pser contribution, the expectation of a stronger surface binding of the group of Ser is confirmed by its 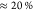higher modeled M₂(N–P) value than that of Pser.

3.7. Implications for Bone-Adhesive Properties

We recently reported a strong correlation between the amount of the amorphous ACP/Pser component and the measured shear strength of PserN cements used for gluing two cubes of either cortical bone⁵⁴ or steel⁶⁰ together across a wide composition range up to N = 87 mol %.⁶⁰ The shear strength reflects the bone-adhesive properties.⁵⁴ Notably, both parameters exhibit a nonmonotonic trend against the batched Pser content, with an initial increase up to a plateau of near-constant shear-strengths and ACP/Pser contents in cements incorporating 40–60 mol % Pser, followed by their concurrent decrease for increasing N because the bone-adhesive-promoting ACP/Pser component becomes gradually replaced by crystalline CaPser and unreacted Pser.⁶⁰ In contrast, SerN cements form an amorphous ACP/Ser phase that only develops with the batched Ser content up to N ≲ 16 mol % (which is insufficient for giving a high shear strength), whereas all remaining Ser remains unreacted.⁶⁰

Consequently, the formation of an amorphous component featuring both significant organic–organic and organic–inorganic interactions appears to be a prerequisite for favorable bone-adhesive properties of an α-TCP-derived cement. Hence, the results herein combined with those of ref (60) suggest that a significant bone-adhesion cannot stem from the adsorption strength of a given biomolecule at ACP alone, because the Pser···ACP binding energy at pH = 4.5 essentially matches with that of Ser···ACP at pH = 7.4 (Table 1), implying that both Pser16/Ser16 cements feature similar Pser···ACP and Ser···ACP net interaction strengths. Nonetheless, while both Pser and Ser molecules may enter ACP/Pser and ACP/Ser phases in the respective PserN and SerN specimens with N ≲ 16 mol %, their amounts develop very differently upon increasing organic content (vide supra). Consequently, the main distinction between the PserN and SerN cements concerns their respective degrees of Pser···Pser and Ser···Ser contacts.

Due to its low Pser content ( wt %), the Pser@HA sample is expected to involve essentially “isolated” surface-bound Pser molecules with long Pser···Pser distances. Likewise, the metadynamics modeling involved one sole Pser (or Ser) molecule. Hence, the good agreement between the M₂(C_j–P) NMR results of the Pser@HA and Pser16 samples, as well as with the modeled data, suggest that 16 mol % of either Pser or Ser may be sufficiently low to be dispersed within the ACP matrix without any significant Pser···Pser or Ser···Ser aggregation (i.e., analogously with a “monolayer” adsorption scenario). However, the substantial Pser contribution to the ACP/Pser cement component in all Pser-rich PserN cements—for which the shear strength is maximal—cannot be reconciled with a monolayer Pser adsorption at ACP, but must involve a significant Pser···Pser aggregation, yet with the molecules remaining intimately integrated also with the inorganic species of ACP (see comments in Section 3.3.3 and ref (60)). Although further work is required for a definite proof, we propose that the high bone-adhesion/shear-strength of the PserN cements with 40 ≲ N ≲ 60 mol % stems from a “stickiness” accompanying the high organic content of their ACP/Pser component, in conjunction with its dominance of the entire cement constitution. Naturally, the “stickiness” is low in cements with batched Pser contents ≲ 20 mol %, as well as for all SerN specimens⁶⁰ due to their insignificant tendency of Ser···Ser aggregation.

4. Conclusions

We have presented the first atomistic probing of the Pser and Ser binding at structurally disordered CaP surfaces by a synergistic combination of advanced solid-state NMR experimentation and metadynamics MD simulations, revealing the relative proximities of each molecular functional group and their respective underlying types of bonds, as well as the conformation of the adsorbed molecules. Our study encompassed the organic/inorganic interactions in a sample of surface-bound Pser at nanocrystalline HA particles (Pser@HA) along with two biocements prepared from α-Ca₃(PO₄)₂ doped with 16 mol % of either Pser or Ser. Notably, the very close sets of ¹³C–³¹P dipolar second moments observed from the cement and the Pser@HA sample highlight the similarities of the Pser binding at ACP and the structurally disordered surface layer of nanocrystalline HA, thereby corroborating the current consensus that it is faithfully described as “ACP”.^4,13−16

The Pser and Ser adsorption is primarily mediated by electrostatic interactions between Ca²⁺ cations and the negatively charged organic COO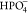^–/ groups and, to a lesser extent, by H bonds to the inorganic phosphate groups, which involves NH···PO₄ and CO/PO···HPO₄ contacts for the amino and carboxy/phosphate groups, respectively. The dominance of electrostatic interactions for driving the adsorption implies that the phosphate group of Pser and the carboxy group of Ser are mainly responsible for stabilizing their surface binding, fully consistent with earlier inferences that biomolecules bind at bone minerals mainly via ion–ion interactions.¹⁸⁻²¹

All detailed information about the number of electrostatic/H-bond interactions and the accompanying interatomic distances were extracted from the metadynamics models. They were validated against the NMR-derived interatomic-distance constraints encoded by the dipolar second moments {M₂(CO–P), M₂(CH–P), M₂(CH₂–P)} that convey the relative proximities between the ¹³C atoms of the respective {COO^–, CH, CH₂} group and the inorganic phosphate moieties of ACP, as well as the M₂(N–P) counterpart informing about the 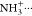ACP contacts. The overall good agreement confirmed the accuracy of our metadynamics simulations, notably the validity of the herein employed HA-surface preparation protocol of ref (45), which produces a disordered apatite surface with pH-dependent phosphate speciation. For our experimental conditions of 3.8 ≤ pH ≤ 5.3 (Pser@HA and Pser16) and pH = 7.4 (Ser16), both Pser and Ser molecules anchor at their amino groups, together with the HPO₄⁻ group of Pser and the COO^– group of Ser, which leads to an extended conformation of both surface-immobilized molecules. The OH group of Ser also participates in the binding at ACP via both electrostatic OH···Ca²⁺ interactions and H bonds to the inorganic phosphate groups, but they contribute overall little to the net adsorption energy (≈10%). The only discrepancy between the experiments and models concerned an underestimation of the metadynamics-derived COO^–···ACP proximities relative to those deduced by NMR on the Pser@HA and Pser16 specimens.

Besides rationalizing the distinction in bone-adhesive properties of Pser and Ser doped α-Ca₃(PO₄)₂-based cements (Section 3.7), our findings settle some earlier suggestions/speculations about which functional groups are involved in the molecular binding of Ser and Pser at nanocrystalline HA.^90,107−109 We stress that the binding modes discussed herein (Table 1 and Figure 5) are the most probable ones from an energetic viewpoint over a distribution of several distinct but stable modes. The nature of the comparatively weak adsorption of small biomolecules (such as amino acids and oligopeptides) at structurally disordered CaP surfaces must be analyzed/discussed in terms of “distributions” and/or “effective contacts”, as those encoded by dipolar second moments. The existence of a distribution of very similar binding modes is indeed mirrored in the broad and typically asymmetric ¹³C/¹⁵N MAS NMR peak shapes observed from each functional group which, except for the COO^– moiety of Ser16, remained unresolved. The ¹³C–³¹P correlation NMR spectrum of the latter revealed four ¹³COO^– resonances from groups with different proximities to ACP: the two COO^– environments closest to the inorganic phosphates were tentatively attributed to those solely involved in electrostatic COO^–···Ca²⁺ interactions (≈184 ppm) and H-bonded COO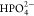^–··· moieties (≈170 ppm). However, most of the COO^– groups bind by both interaction types, as mirrored in a resonance-continuum across the 181–172 ppm spectral region.

We conclude by highlighting the power of the herein-implemented combination of advanced solid-state NMR experiments with metadynamics simulations for an enhanced probing of the detailed biomolecular binding at structurally disordered CaP surfaces, which remains essentially untapped but is potentially very rewarding. Another ubiquitous tool exploited herein concerns the recently introduced Debye–Hückel-based analysis⁴⁸ reviewed in the Supporting Information, which offers a straightforward decomposition of the net modeled biomolecular binding energy into its contributions from the various functional groups of the surface-immobilized molecule, as well as for quantifying each individual electrostatic/H-bond interaction energy.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.2c02112.

• Experimental solid-state NMR conditions; metadynamics simulation parameters, data analysis, and further discussion; synthesis and characterization of Pser*; discussion on the ¹H NMR shift of water in ACP; cement batch compositions; further data on the modeled surface binding and relative dipolar second moments; best-fit ³¹P NMR parameters; additional solid-state NMR spectra; and TEM images (PDF)

The authors declare no competing financial interest.