Skip to main content
NCBI home page
Systematic Biology logoLink to Systematic Biology
. 2022 Jan 18;71(6):1541–1548. doi: 10.1093/sysbio/syac003

Comparing Partitioned Models to Mixture Models: Do Information Criteria Apply?

Stephen M Crotty 1,2,3,✉, Barbara R Holland 4
Editor: Vincent Savolainen
PMCID: PMC9558833  PMID: 35041002

Abstract

The use of information criteria to distinguish between phylogenetic models has become ubiquitous within the field. However, the variety and complexity of available models are much greater now than when these practices were established. The literature shows an increasing trajectory of healthy skepticism with regard to the use of information theory-based model selection within phylogenetics. We add to this by analyzing the specific case of comparison between partition and mixture models. We argue from a theoretical basis that information criteria are inherently more likely to favor partition models over mixture models, and we then demonstrate this through simulation. Based on our findings, we suggest that partition and mixture models are not suitable for information-theory based model comparison. [AIC, BIC; information criteria; maximum likelihood; mixture models; partitioned model; phylogenetics.]

The rapid and ongoing advancement of modern sequencing technologies has led to a vast abundance of biological sequence data that is apt for phylogenomic analysis (Song et al. 2012; Jarvis et al. 2014; Zheng and Wiens 2016; Simion et al. 2017). It is now standard that sequence alignments used for major phylogenetic analyses comprise multiple genes or genomic regions. Simply concatenating genes and applying a single model of nucleotide substitution has long been known to introduce systematic bias (Kolaczkowski and Thornton 2004; Phillips et al. 2004).

Several modeling approaches have been put forward to deal with heterogeneity between genes, partition models and mixture models being two widely used examples. In a partition model, each site is assigned to a block, typically based on the gene and/or codon-position to which it belongs. Each block has its own model of nucleotide substitution and, optionally, its own branch lengths. In a mixture model, the likelihood for each site is calculated as a weighted average over a set of models. Partition models have thus far seen wider use, in part due to the availability of methods for doing model selection and finding a good partition (Lanfear et al. 2012), and in part, because there are fast, likelihood-based software implementations (Guindon et al. 2010; Stamatakis 2014).

There are several approaches commonly employed to partition empirical alignments. Most commonly, the first step is to partition based on some biological knowledge about the sequences. This might involve creating separate blocks for each gene in the alignment, sites in each codon position, or coding and noncoding regions. Other methods have been put forward that offer a data-driven partitioning rationale, grouping sites together based on their estimated substitution rate (Rota et al. 2018). PartitionFinder (Lanfear et al. 2012) is a widely used program that attempts to optimize a partition defined by the user. This is done by merging blocks if doing so increases the BIC score.

Many different mixture models have been proposed and implemented to date (Foster 2004; Lartillot and Philippe 2004; Pagel and Meade 2004; Le et al. 2008; Meade and Pagel 2008; Jayaswal et al. 2014). Many of these have been available only under a Bayesian framework for computational reasons. Those for which maximum-likelihood implementations are available may have other limitations imposed to simplify computation. For example, the HAL-HAS model (Jayaswal et al. 2014) allows heterogeneity both across sites and across lineages, but does not allow for tree-space search. The GHOST model of Crotty et al. (2020), available in IQ-TREE (Nguyen et al. 2015), offers a much more general mixture model in a maximum-likelihood framework. It infers tree topology, mixtures of edge lengths, and model parameters using an expectation–maximization algorithm. For a fuller exploration of partition and mixture models, see Crotty et al. (2020) and Whelan and Halanych (2017) and references therein.

Model selection in phylogenetics has been accomplished via a variety of methods, such as likelihood ratio tests, cross-validation, and Bayes factors. By far, the most common approach is information-theoretic methods, such as the Akaike information criterion (AIC), the corrected Akaike information criterion (AICc), and Bayesian information criterion (BIC). This is in large part due to the influence of Posada and Buckley (2004), which asserted that information-theoretic methods were advantageous, as they could be applied to simultaneously choose between a multitude of non-nested models. However, given the rapidly evolving landscape of computational phylogenetic methods, it may be naive to assume that long-established information-theoretic model selection approaches will maintain their validity in all situations. Indeed, there is a growing body of literature that elucidates the shortcomings of these approaches when applied to phylogenetic analyses.

It is important to clearly define the goal of model selection in the phylogenetic context. When new models of sequence evolution or methods of tree reconstruction are proposed in the literature, it is typically demonstrated with the use of simulation studies to what extent they are successful in recovering the true tree, and how accurately they estimate tree and model parameters. These are the two metrics that principally concern phylogeneticists. AIC was of course developed without these principal concerns in mind. Rather, it is more inclined to choose the best model in terms of predictive accuracy, which (outside of phylogenetics) is often the primary objective of modeling. Given a multiple sequence alignment of a gene, for example, we do not expect to ever observe new sites. All sites within the gene form part of the analysis, and so maximizing the predictive accuracy of a model is not particularly relevant to phylogeneticists. Ultimately, AIC attempts to maximize predictive accuracy by approximately minimizing the expected Kullback–Liebler divergence between the true and proposed models. However, in the phylogenetic framework, it is not a fait accompli that this corresponds directly to the most accurate reconstructions.

Shavit Grievink et al. (2010) demonstrated that in the presence of heterotachy, models with the best AIC score were not the most likely to recover the correct tree topology. Jhwueng et al. (2014) pointed out that in the context of phylogenetics, AIC is a biased estimator for the expected Kullback–Leibler divergence, due to the fact that the likelihood function is not continuously differentiable when one accounts for the discrete nature of tree space. Seo and Thorne (2018) demonstrated that in respect to partition models, AIC tended to favor clumping errors (preferring too few blocks) over splitting errors (preferring too many blocks). They argued that splitting errors were preferable to clumping errors and proposed a remedial correction factor to both AIC and BIC. Susko and Roger (2020) countered this argument, asserting that splitting errors could result in short blocks which may increase the probability of stochastic error misleading phylogenetic estimation. They also examined the theoretical underpinnings of the use of information criteria in the context of complex phylogenetic models. They concluded that a variety of factors can degrade the effectiveness of AIC, for example, parameters (edge lengths or mixture weights) approaching zero, or the presence of closely related sequences.

One question which we feel deserves particular attention, is whether or not information theoretic-based comparisons between partition models and mixture models in a maximum-likelihood framework, as done in Le and Gascuel (2010) and Wang et al. (2019), lead to optimal tree reconstruction. Thus far, such comparisons are rare in the literature; however, this can easily be explained. Due to their innate complexity, phylogenetic mixture models (particularly mixtures of branch lengths) have been predominantly implemented within a Bayesian framework. Naturally, it makes no sense to make information-theoretic-based comparisons between Bayesian-based mixture model analyses and maximum likelihood-based partition model analyses. The introduction of the GHOST model makes mixture models in a maximum likelihood framework far more accessible to phylogeneticists, and there now exists the potential for their use to become widespread. Consequently, there also exists the potential for complex mixture models to be directly compared with partition models using common information-theoretic metrics such as AIC, AICc, and BIC. We therefore think that this is the appropriate time to caution against such practices, for several reasons which we detail below.

Evidence from Simulation

To demonstrate the inherent advantage (in terms of likelihood) that the partition model enjoys over a mixture model, we conducted two simulation-based experiments. The first involved replicating the famous experiments of Kolaczkowski and Thornton (2008), in which they simulated heterotachous alignments using a 4-taxon, 2-tree partition structure, and showed that maximum parsimony outperformed maximum likelihood in recovering the true topology. We simulated 100 replicate multiple sequence alignments of 10,000 base pairs (bp) under a two-class partition model on 12 taxa. Although gene-based partitioning of sites would typically yield blocks an order of magnitude shorter than this, we deliberately simulated longer alignments in order to reduce stochastic variation, thereby demonstrating the effect more clearly. We used a JC (Jukes and Cantor 1969) model of nucleotide substitution on each class and the weight of each class was fixed at 0.5. For each class, Seq-Gen (Rambaut and Grassly 1997) was used to simulate 100 blocks of 5000 bp. Each pair of blocks were then concatenated together, to form 100 replicate sequence alignments of length 10,000 bp.

For each of the 100 alignments, we fit a GHOST model with two JC classes. We also fit several partition models, each with two equal-sized blocks, which differed from each other in the amount of allocation error introduced into each partition model. We defined the allocation error in a partition model, 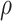Inline graphic, as the proportion of sites that were allocated to the incorrect block. 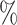For example, Inline graphic implies that Block 1 would consist of all sites simulated under Class 1, and Block 2 would consist of all sites simulated under Class 2; whereas Inline graphic would indicate that Block 1 would consist of 90Inline graphic of the sites simulated under Class 1 and 10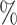Inline graphic of the sites simulated under Class 2, while Block 2 would consist of the remaining sites.

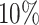The GHOST model and the correctly specified partition model both recovered the correct topology for all 100 alignments. With an allocation error of Inline graphic, the partition model recovered the correct topology for 97 of the 100 alignments. For an allocation error of Inline graphic or more, the partition model failed to recover the correct topology on any of the alignments. Figure 1 shows that partition models with an allocation error less than or equal to Inline graphic outperform the GHOST model in terms of AIC. This means that if using AIC to select between the GHOST model and a partition model, one risks selecting a model that is less likely to recover the true topology.

Figure 1.

Figure 1.

Open in a new tab

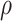Performance of the GHOST model and partition model for alignments simulated based on the Kolaczkowski and Thornton heterotachy simulations. a) The 4-taxon trees used to simulate alignments under the Jukes-Cantor (JC) model of nucleotide substitution. Branch lengths are measured in substitutions per site. b) Mean AIC for the 100 simulated alignments is shown on the y-axis. Error bars indicate Inline graphic standard errors of the mean. The x-axis displays Inline graphic, the proportion of sites in the alignment that were assigned to the incorrect block. The number above each data point is the proportion of alignments for which the correct tree topology was inferred.

For the second experiment, we investigated a scenario with more taxa, random branch lengths, and a more general model of sequence evolution. We simulated 20 replicate multiple sequence alignments of 10,000 base pairs (bp) under a two-class partition model on 12 taxa. We used a GTR model of nucleotide substitution on each class and the weight of each class was fixed at 0.5. The edge lengths for each class were randomly drawn from an exponential distribution with a rate parameter of 10. The relative substitution rates for each class were drawn randomly from a uniform distribution on the (0.5, 5) interval. The four base frequencies for each class were assigned a minimum of 0.1, with the remainder allocated proportionally by scaling a normalized set of four observations from a uniform distribution on the (0, 1) interval. For each class, Seq-Gen (Rambaut and Grassly 1997) was used to simulate 20 blocks of 5,000 bp. Each pair of blocks were then concatenated together, to form 20 replicate sequence alignments of length 10,000 bp.

For each of the 20 alignments, we fit a GHOST model with two GTR classes. As before, we also fit several partition models, each with two equal-sized blocks, which differed from each other in the amount of allocation error introduced into each partition model.

Both the GHOST model and all the partition models inferred the correct tree topology for all 20 alignments. We compared the models based on likelihood, AIC, and the Euclidean distance between the true and inferred edge lengths. The inferred blocks were matched to the true blocks such that the Euclidean distance was minimal. 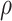Figure 2a indicates that when using AIC to distinguish between the partition model and the GHOST model, the partition model is superior for Inline graphic. However, Figure 2b suggests that in terms of the accuracy of the inferred parameters, the partition model is superior to the GHOST model only for very small values of Inline graphic. So, in this simple case at least, there is a significant window, approximately Inline graphic, for which using AIC to choose between the GHOST model and a partition model will result in the selection of a demonstrably inferior model. The simple reason is the inflated likelihood of the partition model (relative to the mixture model) that is all but guaranteed by the nature of their respective likelihood functions.

Figure 2.

Figure 2.

Open in a new tab

Performance of the GHOST model and partition model for simulated alignments, in terms of a) AIC, and b) accuracy of inferred edge lengths, as measured by the Euclidean distance between the inferred and true edge lengths. Error bars indicate Inline graphic standard errors of the mean. The x-axis displays Inline graphic, the proportion of sites in the alignment that were assigned to the incorrect block.

Comparison of the Likelihood Functions

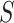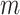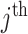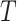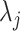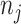Consider a multiple sequence alignment, Inline graphic, which consists of Inline graphic concatenated blocks, with the Inline graphic block having evolved homogeneously according to some model of sequence evolution, Inline graphic, on a common tree topology, Inline graphic, with edge lengths, Inline graphic. 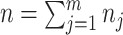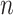Let Inline graphic be the total number of sites in the alignment, and Inline graphic be the number of sites in the Inline graphic block, such that Inline graphic.

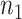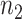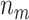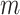We define Inline graphic to be a vector of length Inline graphic, that maps the sites in the alignment to their respective blocks. The first Inline graphic entries of Inline graphic are 1, the next Inline graphic entries of Inline graphic are 2, and so on, with the final Inline graphic entries of Inline graphic being Inline graphic. Under the partition model, we can write down the expression for the log-likelihood of Inline graphic as

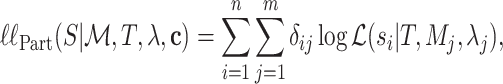graphic file with name Equation1.gif (1)

where,

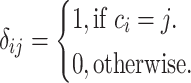graphic file with name Equation2.gif

Similarly, we can write down the likelihood of 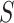Inline graphic under the mixture model as

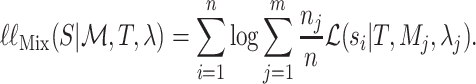graphic file with name Equation3.gif (2)

When comparing Equations 1 and 2, it is obvious that they are very similar. The fundamental difference between the two lies in the way the contributions to the site-likelihood from each class are weighted. In Equation 2, each class makes a contribution to the site-likelihood, according to the class weight, 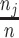Inline graphic. Thus, the overall site-likelihood under the mixture model can be considered as a weighted average of the site-likelihoods under each of the 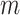Inline graphic classes. In Equation 1, we see that the site-likelihood is solely determined according to the block to which the site belongs. We can quantify the effect of this on the overall likelihood score of the two models by taking the difference between the two likelihood expressions. This difference can be simplified to the following expression, the details of the derivation are given in Appendix A:

graphic file with name Equation4.gif (3)

Equation 3 looks complex, but it can be understood intuitively. The outer sum is over the 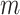Inline graphic blocks in the partition while the inner sum is over the individual sites within each block. The argument to the logarithm is essentially the sum of the weights of each block, that is, the proportion of sites within each block, scaled by the ratio of the site-likelihoods under the mixture and partition models, respectively. We now consider this expression with respect to four different types of alignment: those that are homogeneous both within and between blocks; those that are homogeneous within blocks but heterogeneous between blocks; those that are heterogeneous within blocks but homogeneous between blocks; and finally those that are heterogeneous both within and between blocks. For the purposes of the following arguments, we will consider the difference expression conditional on the true, generative tree and model parameters, and we will further assume that the sequence length of each block is long enough as to render stochastic variation in site pattern frequencies negligible. Owing to the consistency of maximum likelihood, these assumptions are sufficient to claim that for the 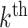Inline graphic block,

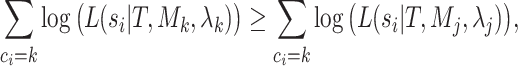graphic file with name Equation5.gif (4)

with equality if and only if 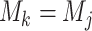Inline graphic and Inline graphic.

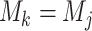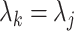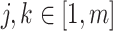  1. If the alignment is truly homogeneous both within and between blocks, then neither the partition model nor the mixture model are misspecified, but both are redundantly complex. Given we are considering the likelihood difference under the generative model parameters, it follows that Inline graphic and Inline graphic for all Inline graphic. As such, the site-likelihood ratios that scale the weights within the argument of Equation 3 are always equal to 1 by definition. This fact trivially results in the likelihood difference between the methods being 0, meaning there is no inherent advantage to either method when the alignment is homogeneous.

  2. If the alignment is homogeneous within blocks, but heterogeneous between blocks, then once again, neither the partition nor mixture models are misspecified. However, the partition model enjoys the intuitive advantage in that it is aware of precisely which sites evolved under which of the 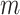Inline graphic models. While it is true that individual sites in the 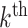Inline graphic block may exist such that 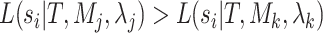Inline graphic for some 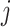Inline graphic, given Equation 4 we would expect these cases to be in the minority. Intuitively then, we would expect that with this type of alignment Equation 3 would result in a positive difference in likelihoods, that is, favoring the partition model, with the magnitude of the difference increasing proportionally with the amount of heterogeneity between blocks in the alignment. With reference to the simulations, this corresponds to the left-most point on the x-axis of Figures 1 and 2, where all sites are correctly partitioned. We observe that the partition model comprehensively outperforms the mixture model in terms of AIC, but there is no significant difference between the models with respect to the accuracy of topological inference or inferred model parameters.

  3. If the alignment is heterogeneous within blocks but homogeneous between blocks, for example when sites are incorrectly partitioned, then this is the worst scenario for the partition model. Each block is essentially generated from an identical mixture of models, so the partition model does not benefit from the ability to fit a different model to each block. It also lacks any capacity to model the heterogeneity that exists within each block. Conversely, the mixture model is not constrained by the mapping of sites to blocks, and can therefore model the heterogeneity within the alignment as effectively as it could if the sites were correctly partitioned. 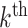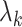Given the heterogeneity within blocks, there exists sites in the Inline graphic block that did not evolve according to Inline graphic and Inline graphic. As such, it would not be unexpected to find Inline graphic. In respect to Equation 3, this is likely to manifest in a negative difference in likelihoods, that is, favoring the mixture model. This scenario corresponds to the right-most point on the x-axis of Figures 1 and 2. 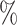Given we have two blocks of equal size, each generated under a homogeneous model, when 50Inline graphic of the sites are erroneously partitioned the result is two blocks that are identical in terms of the generating model, each being a 50–50 heterogeneous mixture of the initial alignment. We observe in the figures that the mixture model is superior in terms of AIC, as well as the accuracy of inference. This scenario is perhaps least interesting in practice, as it is difficult to envisage an empirical example of such an alignment.

  4. The space in between the two extremes of Case 2 and 3 represent the alignments that contain heterogeneity both within and between blocks. It is not possible to generalize in these cases about the direction or magnitude of the likelihood difference. With respect to our simulations, this represents all points in between the extremities of the x-axes of Figures 1 and 2. The community might benefit from a more comprehensive simulation-based study that systematically analyses different levels of within- and between-block heterogeneity, and the resulting effect on respective likelihoods of partition and mixture models.

Discussion

Surprisingly, given the wealth of literature examining the performance of partition models (Brown and Lemmon 2007; Darriba and Posada 2015; Kainer and Lanfear 2015), we found no simulation study in which the issue of incorrectly allocating sites to blocks was addressed in a general way. Many studies have looked at the effect of oversplitting, where a block of sites evolving under one model is incorrectly allocated to two blocks; or undersplitting, where two blocks evolving under different models are grouped together; but none have simulated scenarios where a group of sites evolving under one model is incorrectly allocated across several blocks of a partition. Our simulation demonstrates that partition models are effective, providing the sites are partitioned such that heterogeneity exists between but not within blocks. When this criterion is not met however, the accuracy of topological inference and parameter estimates can be quickly compromised. The strategy of partitioning empirical alignments based on gene boundaries or codon position is not without merit, but few would argue that doing so results in homogeneous blocks. One can easily imagine a set of genes that contain regions of relaxed purifying selection within each gene. Methods such as PartitionFinder do not split single genes into multiple blocks, rather they focus only on potentially merging genes. Previous studies have found that for precisely this reason mixture models are able to recover biologically relevant signals from empirical alignments, that are not recovered under a partition model. For example, Crotty et al. (2020) analyzed an individual sodium channel gene in 11 species of fish. They recovered a signal corresponding to the evolution of electric pulse control in certain species of electric fish. This signal was not recoverable by a codon position-based partition model, because the strongly contributing sites were spread across all three codon positions. In a different study, Crotty et al. (2018) used the GHOST model to identify a heterogeneous region within the P1 gene of Cassava Brown Streak Virus, consisting of approximately 100 nucleotides. Gene-based partitioning of the alignment would have constrained the entire P1 gene to be modeled homogeneously, and this region would have remained hidden. These results were obtained in spite of the fact that information theory-based model selection would overwhelmingly favor the adoption of the partition model. Were these studies to base model selection solely on information criteria, the insight proffered by the mixture model would be lost.

The current typical phylogenomic analysis consists of partitioning the alignment by gene boundaries, running PartitionFinder to merge blocks and select models, and then carrying out tree reconstruction. Given that PartitionFinder relies on information criteria to merge blocks, as Seo and Thorne (2018) show the process is susceptible to clumping errors. This suggests that blocks (genes) are often merged when they should not be, which implies heterogeneity within the resulting blocks. When this fact is coupled with the evidence presented currently, that partition models perform poorly (in terms of accuracy of topological and parameter inference) in the presence of within-block heterogeneity, the reliability of this approach must be questioned.

As discussed earlier, we are not the first to highlight potential shortcomings of the practice of using information criteria for model selection in the field of phylogenetics. The simplicity of this approach to model selection predicated its widespread adoption. But with ever-increasing complexity of models and methods of reconstruction, it may be time for the community to focus on developing alternative approaches to model discrimination.

In light of the arguments presented here, we recommend that information criteria should not be used to discriminate between partition and mixture models, as the potential exists for important biological insights to be overlooked, or erroneous conclusions to be drawn. Rather, we would recommend that partition and mixture models are applied concurrently, so that any discordance that might arise between the two can be rigorously investigated.

 

Appendix A

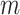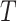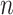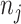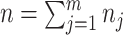Consider we have a multiple sequence alignment, Inline graphic, which consists of Inline graphic concatenated blocks, with the Inline graphic block having evolved homogeneously according to some model of sequence evolution, Inline graphic, on a common tree topology, Inline graphic. 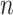Let Inline graphic be the total number of sites in the alignment, and Inline graphic be the number of sites in the Inline graphic block, such that Inline graphic.

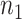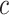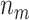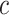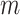We define Inline graphic to be a vector of length Inline graphic, that maps the sites in the alignment to their respective blocks. The first Inline graphic entries of Inline graphic are 1, the next Inline graphic entries of Inline graphic are 2, and so on, with the final Inline graphic entries of Inline graphic being Inline graphic. Under the partition model, we can write down the expression for the log-likelihood of 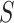Inline graphic, conditional on 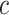Inline graphic, Inline graphic as

graphic file with name Equation6.gif (A.1)

where Inline graphic takes a value of 1 if Inline graphic, and 0 otherwise.

Similarly, we can write down the likelihood of 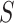Inline graphic under the mixture model, 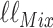Inline graphic as

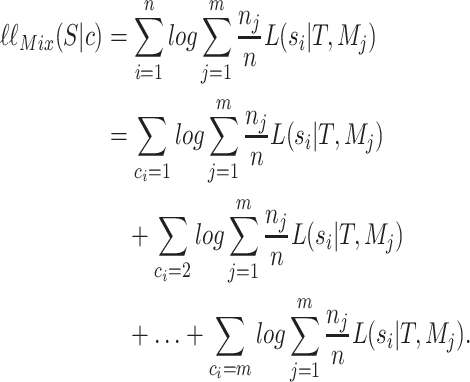graphic file with name Equation7.gif (A.2)

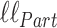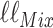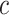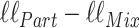Assume now that we calculate Inline graphic and Inline graphic under identical tree and model parameters, such that the only difference between the two models is the conditioning on Inline graphic for the partition model. We can quantify the difference that knowledge of Inline graphic makes to the likelihood, by evaluating the quantity Inline graphic:

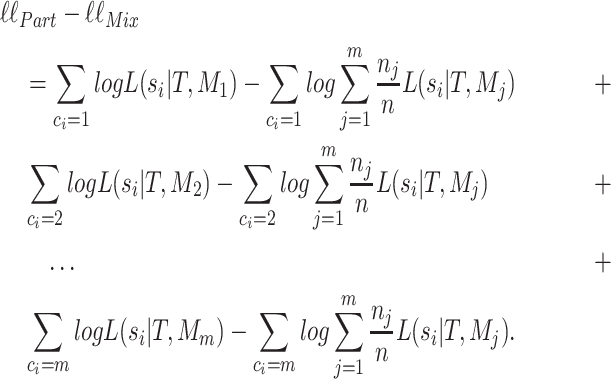graphic file with name Equation8.gif (A.3)

For simplicity we now consider the 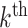Inline graphic term of this difference,

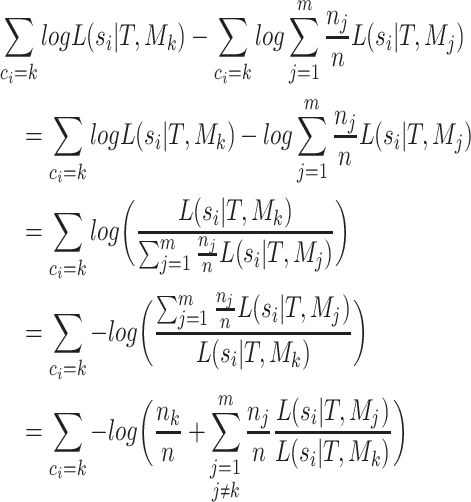graphic file with name Equation9.gif (A.4)

Substituting (4) back into each term of (3) yields:

graphic file with name Equation10.gif

Contributor Information

Stephen M Crotty, School of Mathematical Sciences, University of Adelaide, Adelaide, SA 5005, Australia; Center for Integrative Bioinformatics Vienna, Max F. Perutz Laboratories, University of Vienna and Medical University of Vienna, Vienna, Austria; ARC Centre of Excellence for Mathematical and Statistical Frontiers, The University of Adelaide, Adelaide, SA, Australia.

Barbara R Holland, School of Natural Sciences (Mathematics), University of Tasmania, Hobart, TAS 7001, Australia.

References

  1. Brown J.M., Lemmon A.R.. 2007. The importance of data partitioning and the utility of Bayes factors in Bayesian phylogenetics. Syst. Biol. 56(4):643–655. [DOI] [PubMed] [Google Scholar]
  2. Crotty S.M., Minh B.Q., Bean N.G., Holland B.R., Tuke J., Jermiin L.S., Haeseler A.V.. 2020. GHOST: recovering historical signal from heterotachously evolved sequence alignments. Syst. Biol. 69(2):249–264. [DOI] [PubMed] [Google Scholar]
  3. Crotty S.M., Rohrlach A.B., Ndunguru J., Boykin L.M.. 2018. Characterising genetic diversity in Cassava Brown Streak Virus. bioRxiv, Available from: 10.1101/455303. [DOI] [Google Scholar]
  4. Darriba D., Posada D.. 2015. The impact of partitioning on phylogenomic accuracy. bioRxiv, Available from: 10.1101/023978. [DOI] [Google Scholar]
  5. Foster P.G. 2004. Modeling compositional heterogeneity. Syst. Biol. 53(3):485–495. [DOI] [PubMed] [Google Scholar]
  6. Guindon S., Dufayard J.-F., Lefort V., Anisimova M., Hordijk W., Gascuel O.. 2010. New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0. Syst. Biol. 59(3):307–321. [DOI] [PubMed] [Google Scholar]
  7. Jarvis E.D., Mirarab S., Aberer A.J., Li B., Houde P., Li C., Ho S.Y., Faircloth B.C., Nabholz B., Howard J.T., Suh A., Weber C.C., da Fonseca R.R., Li J., Zhang F., Li H., Zhou L., Narula N., Liu L., Ganapathy G., Boussau B., Bayzid M.S., Zavidovych V., Subramanian S., Gabaldón T., Capella-Gutiérrez S., Huerta-Cepas J., Rekepalli B., Munch K., Schierup M., Lindow B., Warren W.C., Ray D., Green R.E., Bruford M.W., Zhan X., Dixon A., Li S., Li N., Huang Y., Derryberry E.P., Bertelsen M.F., Sheldon F.H., Brumfield R.T., Mello C.V., Lovell P.V., Wirthlin M., Schneider M.P., Prosdocimi F., Samaniego J.A., Vargas Velazquez A.M., Alfaro-Núñez A., Campos P.F., Petersen B., Sicheritz-Ponten T., Pas A., Bailey T., Scofield P., Bunce M., Lambert D.M., Zhou Q., Perelman P., Driskell A.C., Shapiro B., Xiong Z., Zeng Y., Liu S., Li Z., Liu B., Wu K., Xiao J., Yinqi X., Zheng Q., Zhang Y., Yang H., Wang J., Smeds L., Rheindt F.E., Braun M., Fjeldsa J., Orlando L., Barker F.K., Jønsson K.A., Johnson W., Koepfli K.P., O’Brien S., Haussler D., Ryder O.A., Rahbek C., Willerslev E., Graves G.R., Glenn T.C., McCormack J., Burt D., Ellegren H., Alström P., Edwards S.V., Stamatakis A., Mindell D.P., Cracraft J., Braun E.L., Warnow T., Jun W., Gilbert M.T., Zhang G.. 2014. Whole-genome analyses resolve early branches in the tree of life of modern birds. Science 346(6215):1320–1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Jayaswal V., Wong T.K., Robinson J., Poladian L., Jermiin L.S.. 2014. Mixture models of nucleotide sequence evolution that account for heterogeneity in the substitution process across sites and across lineages. Syst. Biol. 63(5):726–742. [DOI] [PubMed] [Google Scholar]
  9. Jhwueng D.-C., Huzurbazar S., O’Meara B.C., Liu L.. 2014. Investigating the performance of AIC in selecting phylogenetic models. Stat. Appl. Genetics Mol. Biol. 13(4):459–475. [DOI] [PubMed] [Google Scholar]
  10. Jukes T., Cantor C.. 1969. Evolution of protein molecules. In: Munro H.N., editor. Mammalian protein metabolism. New York: Academic Press. p. 21–123. [Google Scholar]
  11. Kainer D., Lanfear R.. 2015. The effects of partitioning on phylogenetic inference. Mol. Biol. Evol. 32(6):1611–1627. [DOI] [PubMed] [Google Scholar]
  12. Kolaczkowski B., Thornton J.W.. 2004. Performance of maximum parsimony and likelihood phylogenetics when evolution is heterogeneous. Nature 431(7011):980–984. [DOI] [PubMed] [Google Scholar]
  13. Kolaczkowski B., Thornton J.W.. 2008. A mixed branch length model of heterotachy improves phylogenetic accuracy. Mol. Biol. Evol. 25(6):1054–1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lanfear R., Calcott B., Ho S.Y., Guindon S.. 2012. PartitionFinder: combined selection of partitioning schemes and substitution models for phylogenetic analyses. Mol. Biol. Evol. 29(6):1695–1701. [DOI] [PubMed] [Google Scholar]
  15. Lartillot N., Philippe H.. 2004. A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol. Biol. Evol. 21(6):1095–1109. [DOI] [PubMed] [Google Scholar]
  16. Le S.Q., Gascuel O.. 2010. Accounting for solvent accessibility and secondary structure in protein phylogenetics is clearly beneficial. Syst. Biol. 59(3):277–287. [DOI] [PubMed] [Google Scholar]
  17. Le S.Q., Lartillot N., Gascuel O.. 2008. Phylogenetic mixture models for proteins. Philos. Trans. R. Soc. B 363(1512):3965–3976. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Meade A., Pagel M.. 2008. A phylogenetic mixture model for heterotachy. In: Pontarotti P., editor. Evolutionary biology from concept to application. Berlin, Heidelberg: Springer. p. 29–41. [Google Scholar]
  19. Nguyen L.-T., Schmidt H.A., von Haeseler A., Minh B.Q.. 2015. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol. Biol. Evol. 32(1):268–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pagel M., Meade A. (2004). A phylogenetic mixture model for detecting pattern-heterogeneity in gene sequence or character-state data. Systematic Biology, 53(4):571–581. [DOI] [PubMed] [Google Scholar]
  21. Phillips M.J., Delsuc F., Penny D. (2004). Genome-scale phylogeny and the detection of systematic biases. Mol. Biol. Evol. 21(7):1455–1458. [DOI] [PubMed] [Google Scholar]
  22. Posada D., Buckley T.R.. 2004. Model selection and model averaging in phylogenetics: advantages of Akaike Information Criterion and Bayesian approaches over likelihood ratio tests. Syst. Biol. 53(5):793–808. [DOI] [PubMed] [Google Scholar]
  23. Rambaut A., Grassly N.C.. 1997. Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci.: CABIOS 13(3):235–238. [DOI] [PubMed] [Google Scholar]
  24. Rota J., Malm T., Chazot N., Peña C., Wahlberg N.. 2018. A simple method for data partitioning based on relative evolutionary rates. PeerJ 6:e5498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Seo T.-K., Thorne J.L.. 2018. Information criteria for comparing partition schemes. Syst. Biol. 67(4):616–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Shavit Grievink L., Penny D., Hendy M.D., Holland B.R.. 2010. Phylogenetic tree reconstruction accuracy and model fit when proportions of variable sites change across the tree. Syst. Biol. 59(3):288–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Simion P., Philippe H., Baurain D., Jager M., Richter D.J., Di Franco A., Roure B., Satoh N., Queinnec E., Ereskovsky A., et al. (2017). A large and consistent phylogenomic dataset supports sponges as the sister group to all other animals. Curr. Biol. 27(7):958–967. [DOI] [PubMed] [Google Scholar]
  28. Song S., Liu L., Edwards S.V., Wu S.. 2012. Resolving conflict in eutherian mammal phylogeny using phylogenomics and the multispecies coalescent model. Proc. Natl. Acad. Sci. USA 109(37):14942–14947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Stamatakis A. 2014. RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30(9):1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Susko E., Roger A.J.. 2020. On the use of information criteria for model selection in phylogenetics. Mol. Biol. Evol. 37(2):549–562. [DOI] [PubMed] [Google Scholar]
  31. Wang H.-C., Susko E., Roger A.J.. 2019. The relative importance of modeling site pattern heterogeneity versus partition-wise heterotachy in phylogenomic inference. Syst. Biol. 68(6):1003–1019. [DOI] [PubMed] [Google Scholar]
  32. Whelan N.V., Halanych K.M.. 2017. Who let the CAT out of the bag? Accurately dealing with substitutional heterogeneity in phylogenomic analyses. Syst. Biol. 66(2):232–255. [DOI] [PubMed] [Google Scholar]
  33. Zheng Y., Wiens J.J.. 2016. Combining phylogenomic and supermatrix approaches, and a time-calibrated phylogeny for squamate reptiles (lizards and snakes) based on 52 genes and 4162 species. Mol. Phylogenet. Evol. 94:537–547. [DOI] [PubMed] [Google Scholar]

Articles from Systematic Biology are provided here courtesy of Oxford University Press

RESOURCES