Abstract
The Ornstein–Uhlenbeck (OU) model is widely used in comparative phylogenetic analyses to study the evolution of quantitative traits. It has been applied to various purposes, including the estimation of the strength of selection or ancestral traits, inferring the existence of several selective regimes, or accounting for phylogenetic correlation in regression analyses. Most programs implementing statistical inference under the OU model have resorted to maximum-likelihood (ML) inference until the recent advent of Bayesian methods. A series of issues have been noted for ML inference using the OU model, including parameter nonidentifiability. How these problems translate to a Bayesian framework has not been studied much to date and is the focus of the present article. In particular, I aim to assess the impact of the choice of priors on parameter estimates. I show that complex interactions between parameters may cause the priors for virtually all parameters to impact inference in sometimes unexpected ways, whatever the purpose of inference. I specifically draw attention to the difficulty of setting the prior for the selection strength parameter, a task to be undertaken with much caution. I particularly address investigators who do not have precise prior information, by highlighting the fact that the effect of the prior for one parameter is often only visible through its impact on the estimate of another parameter. Finally, I propose a new parameterization of the OU model that can be helpful when prior information about the parameters is not available. [Bayesian inference; Brownian motion; Ornstein–Uhlenbeck model; phenotypic evolution; phylogenetic comparative methods; prior distribution; quantitative trait evolution.]
Phylogenetic comparative methods (PCMs) aim to analyze data sets of species traits in a phylogenetic framework. They are used for various purposes, including detecting selection (e.g., Martins 1994; Butler and King 2004; Ingram and Mahler 2013), measuring the rate of trait evolution (e.g., O’Meara et al. 2006; Revell and Harmon 2008; Revell and Collar 2009; Eastman et al. 2011; Jones et al. 2015; Martin 2016), estimating ancestral traits (e.g., Martins and Hansen 1997; Bokma 2002; Paradis et al. 2004; Harmon et al. 2008; Lemey et al. 2010; Revell 2012; Landis et al. 2013; Elliot and Mooers 2014; Kratsch and McHardy 2014; Meseguer et al. 2018), control for the phylogenetic codependency of multispecies data (e.g., Felsenstein 1985; Grafen 1989), or estimate the impact of a covariate on a trait (e.g., Davis et al. 2012; Gohli and Voje 2016; Solbakken et al. 2017; Lattenkamp et al. 2021).
The first model to be considered in PCMs was Brownian motion (BM) (Cavalli-Sforza and Edwards 1967; Felsenstein 1973), a model assuming that traits evolve in an undirected manner, at a speed governed by a rate parameter. Then, the Ornstein–Uhlenbeck (OU) model has been used as a model of stabilizing selection and drift (Lande 1976,Hansen and Martins 1996,Felsenstein 1988). Under the OU model, traits are deterministically attracted towards a selective optimum, at a speed determined by a selection strength parameter. Stochastic variation around this selection-driven trajectory follows a Brownian model (Hansen and Martins 1996). BM is therefore a limiting case of the OU model when there is no selection. A notable difference between the OU and Brownian models is that under the OU model, the imprint of shared evolutionary history on species traits is progressively erased due to the convergent effect of selection (Hansen and Martins 1996).
The Brownian and OU models have burgeoned into a number of extensions, including models with heterogeneous evolutionary rates (e.g., O’Meara et al. 2006; Lemey et al. 2010; Eastman et al. 2011), early-burst models of adapative radiation (Harmon et al. 2010) (see also Blomberg et al. 2003; Freckleton and Harvey 2006), models of punctuated evolution (e.g., Bokma 2002; Uyeda et al. 2011; Landis et al. 2013; Elliot and Mooers 2014), or multivariate models (e.g., Hansen and Martins 1996; Revell and Harmon 2008; Revell and Collar 2009). Also, recognizing that selection is a dynamic process, the OU model has been extended to accommodate multiple selective optima. This model, known as the Hansen model (Hansen 1997), assumes various selective regimes across the phylogeny. The Hansen model has been used for testing a priori evolutionary hypotheses characterized by specific “paintings” of selective regimes on the tree (e.g., Hansen 1997; Butler and King 2004), or for estimating the location of selective regimes on the tree (e.g., Ingram and Mahler 2013; Uyeda and Harmon 2014).
A number of issues have been reported in maximum-likelihood (ML) inference with the OU model (see notably Ané 2008,Boettiger et al. 2012,Ho and Ané 2013, 2014; Cooper et al. 2016). In particular, Ho and Ané (2014) reported that the selective optimum and the ancestral trait at the root of the tree are not separately identifiable (i.e., infinitely many pairs of values for these parameters have the same likelihood, impeding their joint estimation). This situation generalizes, under some conditions, to the Hansen model with multiple selective optima. Also, when the estimated value of selection strength is close to 0, the location of the selective optimum or the number of selective regimes cannot be estimated (Ho and Ané 2014). Ho and Ané (2014) stress that these issues should not be restricted to ML inference and also concern Bayesian inference.
In recent years, a number of programs have arisen that extend statistical comparative biology to Bayesian inference, in particular, the R packages bayou (Uyeda and Harmon 2014), POUMM (Mitov and Stadler 2017), and the program RevBayes (Höhna et al. 2016). The models used in Bayesian inference are characterized by the same probabilistic models as their ML analogs, but notably differ in their ability to include subjective prior information. There is thus the potential for the prior to have a strong influence on the results in case the data are not very informative, or in case parameters are not separately identifiable, as is the case for the OU model (Ho and Ané 2013, 2014). Although it has been noticed that the prior for the number of selective regimes in the Hansen model could strongly influence the results (Uyeda and Harmon 2014), to this day, little is known about the impact of the prior when fitting the OU model.
This article studies how some of the problems identified in ML inference with the OU and Hansen models manifest themselves in Bayesian inference. Of particular interest, are the potential consequences of the nonidentifiability (or weak identifiability) of some parameters (the selective optimum and the initial state at the root on the one hand, and the selection strength and the rate of evolution on the other hand) in the case where prior information is vague. Nonidentifiability is shown to induce correlation among parameters in the posterior, so that the prior for one parameter may strongly impact the posterior of another. It is important, in that case, that investigators are aware that part of the difference between the posterior and the prior of a parameter is due to the prior of another parameter. Furthermore, the parameter for the strength of selection (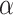 ) plays a central role, as it interacts with all other parameters. All conclusions are therefore conditional on the correct estimation of
) plays a central role, as it interacts with all other parameters. All conclusions are therefore conditional on the correct estimation of  , and the prior for
, and the prior for 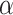 should be set with the greatest care. I emphasize that, in the absence of precise prior information about
should be set with the greatest care. I emphasize that, in the absence of precise prior information about 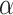 and/or the rate of evolution, setting this prior is not straightforward. A reparameterization of the OU model in terms of only identifiable parameters is proposed, which I hope makes it easier to set priors when no prior information is available.
and/or the rate of evolution, setting this prior is not straightforward. A reparameterization of the OU model in terms of only identifiable parameters is proposed, which I hope makes it easier to set priors when no prior information is available.
Overview of Models
OU Model
Consider a rooted ultrametric tree  and a set of observed tip traits
and a set of observed tip traits  (one value per species). Under the OU model,
(one value per species). Under the OU model,  is multivariate normally distributed, with the same expected trait value for all species:
is multivariate normally distributed, with the same expected trait value for all species:
 |
(1) |
where  (in unit of traits) is the selective optimum,
(in unit of traits) is the selective optimum,  is the root trait,
is the root trait, 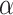 is the strength of selection (in unit of
is the strength of selection (in unit of  ), and
), and 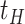 (in unit of time) is the tree height. Thus, under the OU model, expected trait values are deterministically attracted from the initial value
(in unit of time) is the tree height. Thus, under the OU model, expected trait values are deterministically attracted from the initial value  to the optimum
to the optimum  as time passes. The stronger the selection, the faster the trait values are expected to approach
as time passes. The stronger the selection, the faster the trait values are expected to approach  .
.
The variance–covariance structure of the OU distribution is given by the matrix:
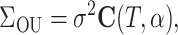 |
(2) |
where the stochastic rate  (in unit of squared trait/time) scales the amount of stochasticity about
(in unit of squared trait/time) scales the amount of stochasticity about  . The matrix
. The matrix 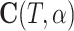 determines the expected covariation between the trait values of the different species, given the phylogeny and
determines the expected covariation between the trait values of the different species, given the phylogeny and 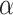 (see Hansen 1997, and Appendix 1 of the Supplementary material available on Dryad at https://doi.org/10.5061/dryad.vdncjsxrc for details). In particular,
(see Hansen 1997, and Appendix 1 of the Supplementary material available on Dryad at https://doi.org/10.5061/dryad.vdncjsxrc for details). In particular,  assumes a certain degree of phylogenetic signal, that is, the more recent the tMRCA of two species, the more similar their trait values are expected to be. The value of
assumes a certain degree of phylogenetic signal, that is, the more recent the tMRCA of two species, the more similar their trait values are expected to be. The value of 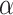 then determines how quickly the phylogenetic signal is erased by the homogenizing effect of selection: the higher
then determines how quickly the phylogenetic signal is erased by the homogenizing effect of selection: the higher 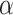 , the quicker the phylogenetic signal is lost.
, the quicker the phylogenetic signal is lost.
We now define two limiting forms of the OU model: BM, which is the OU model with  , and the white-noise (WN) model, with
, and the white-noise (WN) model, with  (see Cooper et al. 2016).
(see Cooper et al. 2016).
Under BM, without selection, the expected trait value of all current species given  stays constant as time passes:
stays constant as time passes:  . Also, the phylogenetic signal of traits reaches a maximum as compared to higher values of
. Also, the phylogenetic signal of traits reaches a maximum as compared to higher values of 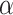 .
.
The other extreme is the WN model, with mean  : selection is so fast that all trait values are expected to be almost immediately located around the optimum. The phylogenetic signal gets down to zero, meaning that the phylogenetic relationships among species no longer influence the trait values. The trait value of a species is thus independent from the trait values of the other species and varies around
: selection is so fast that all trait values are expected to be almost immediately located around the optimum. The phylogenetic signal gets down to zero, meaning that the phylogenetic relationships among species no longer influence the trait values. The trait value of a species is thus independent from the trait values of the other species and varies around  with variance
with variance 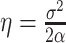 (see Appendix 1 of the Supplementary material available on Dryad).
(see Appendix 1 of the Supplementary material available on Dryad).
See Appendix 1 of the Supplementary material available on Dryad for the expression of  and more details on the OU model.
and more details on the OU model.
Hansen Model
Hansen’s model (Hansen 1997) is identical to the OU model, except that  is allowed to vary among branches, which changes the mean of trait
is allowed to vary among branches, which changes the mean of trait  of species
of species  into:
into:
 |
where  is a function of
is a function of 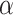 ,
,  , and the set of optima along the path in the tree from the root to species
, and the set of optima along the path in the tree from the root to species  .
.
As for the OU model, in the limit of  , the Hansen model converges to BM, with
, the Hansen model converges to BM, with  for all
for all  . In the limit of
. In the limit of  , it converges to a WN model with different means for the different regimes:
, it converges to a WN model with different means for the different regimes:  , with
, with  the optimum for species
the optimum for species  . The variance–covariance structure of the Hansen model is identical to the OU model, with the same implications about the impact of
. The variance–covariance structure of the Hansen model is identical to the OU model, with the same implications about the impact of 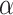 on the amount of phylogenetic signal. See Appendix 1 of the Supplementary material available on Dryad for the expression of
on the amount of phylogenetic signal. See Appendix 1 of the Supplementary material available on Dryad for the expression of  and more details on Hansen’s model.
and more details on Hansen’s model.
Measuring the Realized Effect of Selection
In the previous section, we have seen how the BM and WN models are limiting forms of the OU model that arise as  or
or  , respectively. However, these models are only extremes of a continuum along which the importance of selection in determining the observed trait values increases.
, respectively. However, these models are only extremes of a continuum along which the importance of selection in determining the observed trait values increases.
Throughout this article, I will use the metric  (slightly modified from Hansen et al. 2008) as a measure of the realized effect of selection in determining observed trait values, for a given OU process:
(slightly modified from Hansen et al. 2008) as a measure of the realized effect of selection in determining observed trait values, for a given OU process:
 |
(3) |
where  is the expected variance of the OU process at the time of sampling (i.e., at time
is the expected variance of the OU process at the time of sampling (i.e., at time 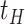 above the root) and where
above the root) and where  is the variance that would be expected under BM (i.e., if
is the variance that would be expected under BM (i.e., if 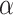 was 0). See Appendix 2 of the Supplementary material available on Dryad for details.
was 0). See Appendix 2 of the Supplementary material available on Dryad for details.
The metric  thus represents the percent decrease in trait variance caused by selection over the study period (
thus represents the percent decrease in trait variance caused by selection over the study period (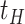 ), as compared to the variance expected under pure drift (i.e., under BM). For instance,
), as compared to the variance expected under pure drift (i.e., under BM). For instance,  means that selection has reduced the variance of traits by 25
means that selection has reduced the variance of traits by 25 over period
over period  .
.
Notice that the fact that  depends only on the product
depends only on the product  implies that it measures the realized effect of selection (Cressler et al. (2015) called
implies that it measures the realized effect of selection (Cressler et al. (2015) called  the “opportunity for selection”). In a case where
the “opportunity for selection”). In a case where 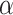 is high, but the process has run for a very small period of time (very low
is high, but the process has run for a very small period of time (very low 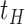 ),
),  will be low, reflecting the fact that selection (although it is strong) has not had time to substantially influence the evolution of traits. Conversely,
will be low, reflecting the fact that selection (although it is strong) has not had time to substantially influence the evolution of traits. Conversely, 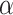 may be low and
may be low and  very high, in which case
very high, in which case  is high because the accumulation of slow selection over a large period of time did influence substantially the evolution of traits. Thus,
is high because the accumulation of slow selection over a large period of time did influence substantially the evolution of traits. Thus,  describes the net macroevolutionary effect produced by the accumulation of microevolutionary selective effects (the magnitude of which is described by
describes the net macroevolutionary effect produced by the accumulation of microevolutionary selective effects (the magnitude of which is described by 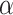 ), over a given period of time (
), over a given period of time ( ). Figure 1 shows the relationship between
). Figure 1 shows the relationship between  ,
,  and
and 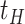 and illustrates how the value of
and illustrates how the value of  reflects the shape of trait evolutionary trajectories. Further notice that
reflects the shape of trait evolutionary trajectories. Further notice that  is a direct indicator of how close an OU model actually is from the BM and WN models, statistically, with a high (respectively low) value of
is a direct indicator of how close an OU model actually is from the BM and WN models, statistically, with a high (respectively low) value of  indicating closeness to a WN (respectively BM) model (see Appendix 2 of the Supplementary material available on Dryad for details).
indicating closeness to a WN (respectively BM) model (see Appendix 2 of the Supplementary material available on Dryad for details).
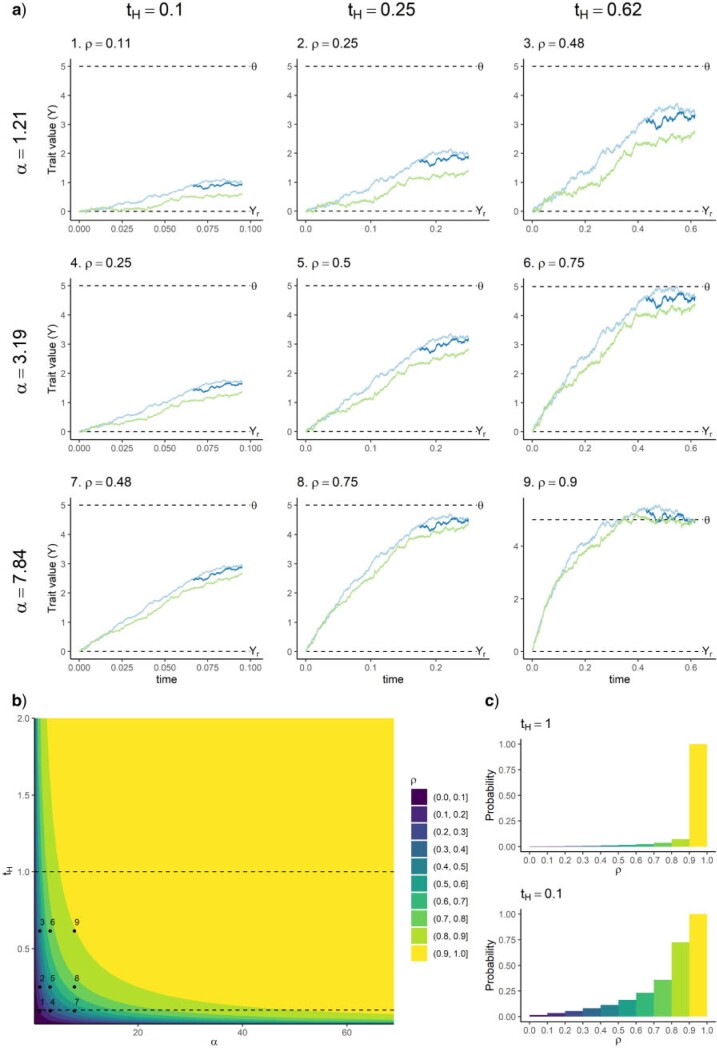
Figure 1.
a) Trait trajectories for a three-tip tree for nine different combinations of values of  and
and 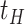 . b) Value of
. b) Value of  as a function of
as a function of 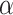 and
and  . The nine points correspond to the nine trajectories in (a). Note that the analysis of a given data set with a given
. The nine points correspond to the nine trajectories in (a). Note that the analysis of a given data set with a given 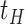 occurs along a horizontal line of this graph. c) Priors for
occurs along a horizontal line of this graph. c) Priors for  corresponding to a uniform prior for
corresponding to a uniform prior for 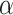 from 0 to 69, when
from 0 to 69, when  or
or  . The relative heights of the different bars match the relative distances between the
. The relative heights of the different bars match the relative distances between the  isoclines in b), along the lines
isoclines in b), along the lines  or
or  (represented by dashed lines in b).
(represented by dashed lines in b).
In sum,  measures the realized impact of selection, given the length
measures the realized impact of selection, given the length 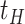 that the process has run, while
that the process has run, while 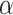 measures the absolute strength of selection, independently of
measures the absolute strength of selection, independently of 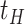 .
.
Another interesting transform of 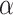 is the phylogenetic half-life
is the phylogenetic half-life  , which represents the expected time needed for a trait to cover half the distance between the initial value
, which represents the expected time needed for a trait to cover half the distance between the initial value  , and the selective optimum
, and the selective optimum  . Phylogenetic half-life, like
. Phylogenetic half-life, like 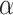 , measures the absolute magnitude of selection but is probably easier to interpret. Some authors have preferred to scale
, measures the absolute magnitude of selection but is probably easier to interpret. Some authors have preferred to scale 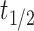 in units of tree heights (e.g., Hansen et al. 2008; Ané et al. 2017; Cooper et al. 2016), in which case, like
in units of tree heights (e.g., Hansen et al. 2008; Ané et al. 2017; Cooper et al. 2016), in which case, like  , it depends on the product
, it depends on the product  and is then a measure of the realized effect of selection over time
and is then a measure of the realized effect of selection over time 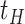 .
.
I elaborate in the discussion on the pros and cons of interpreting 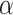 ,
, 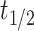 , or
, or  . Meanwhile, I use
. Meanwhile, I use  to interpret the value of
to interpret the value of 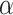 in terms of the realized impact of selection, given some
in terms of the realized impact of selection, given some 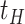 . In particular, this article aims to illustrate how the prior assigned to
. In particular, this article aims to illustrate how the prior assigned to  may translate into a very stringent prior for
may translate into a very stringent prior for  , in favor of either BM (low
, in favor of either BM (low  ) or WN (high
) or WN (high  ) processes, and how such stringent priors may impact the estimation of the other parameters, as a result of complex interactions among parameters.
) processes, and how such stringent priors may impact the estimation of the other parameters, as a result of complex interactions among parameters.
Interactions among the Parameters of the OU Model
The probability distribution of trait values (i.e., the likelihood) under the OU model is characterized by two ridges. The occurrence of a ridge in a likelihood function implies that the data are equally likely for infinitely numerous combinations of values of a set of parameters, implying that the values of the parameters cannot be separately identified.
This happens the first time for the parameters  and
and  , which cannot be separately identified under the OU model when only contemporaneous tip trait values are observed (Ho and Ané 2014). Specifically, when tips are contemporaneous, the OU likelihood is invariant along the following ridge in the
, which cannot be separately identified under the OU model when only contemporaneous tip trait values are observed (Ho and Ané 2014). Specifically, when tips are contemporaneous, the OU likelihood is invariant along the following ridge in the  plane (see Fig. 2a,b):
plane (see Fig. 2a,b):
 |
where  is any value considered for the expected value of tip traits. Indeed, there are infinitely numerous pairs of values of
is any value considered for the expected value of tip traits. Indeed, there are infinitely numerous pairs of values of  and
and 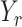 that induce the same value of
that induce the same value of  (hence not changing the value of the likelihood), for a given value of
(hence not changing the value of the likelihood), for a given value of  (hence for a given value of
(hence for a given value of  ).
).
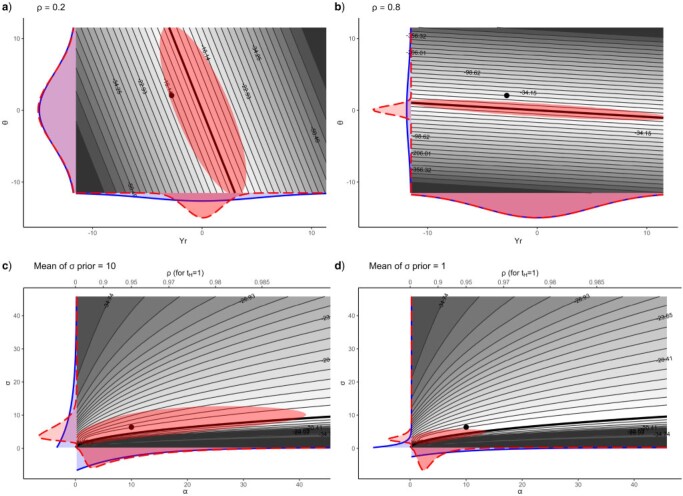
Figure 2.
Example ridges in the OU likelihood. Gray shades represent the value of the log-likelihood, for a data set simulated with  , of which the trait values were scaled to mean 0 and unit variance. Density plots with solid lines in the margins represent the priors. The darker areas superimposed on the likelihood surface represent the 95
, of which the trait values were scaled to mean 0 and unit variance. Density plots with solid lines in the margins represent the priors. The darker areas superimposed on the likelihood surface represent the 95 highest posterior density region of the joint posterior of
highest posterior density region of the joint posterior of  and
and  (in a and b) or of
(in a and b) or of  and
and 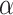 (in c and d). Density plots with dashed lines in the margins represent the marginal posteriors. The posteriors were approximated by numerical integration. Black dots represent the true values of the parameters used to simulate the data set. a) and b) represent the
(in c and d). Density plots with dashed lines in the margins represent the marginal posteriors. The posteriors were approximated by numerical integration. Black dots represent the true values of the parameters used to simulate the data set. a) and b) represent the  ridge, with
ridge, with  fixed to its true value and with
fixed to its true value and with  (a) or
(a) or  (b). In both cases, the priors for
(b). In both cases, the priors for  and
and  are centered normal distributions with sd = 5. The thick black line is the top of the ridge, of equation
are centered normal distributions with sd = 5. The thick black line is the top of the ridge, of equation  , with
, with  the ML estimator of the mean of tip trait values (equal to 0 in this example, since trait values were scaled to 0 mean). In a), because
the ML estimator of the mean of tip trait values (equal to 0 in this example, since trait values were scaled to 0 mean). In a), because  is low, the ridge has a highly negative slope. As a consequence, the plausible range of
is low, the ridge has a highly negative slope. As a consequence, the plausible range of  , as constrained by the
, as constrained by the  prior, corresponds to a narrow interval of high likelihood on the scale of
prior, corresponds to a narrow interval of high likelihood on the scale of  , inducing a marginal posterior for
, inducing a marginal posterior for  that is narrower than its prior. In b),
that is narrower than its prior. In b),  is high and the converse happens. c) and d) The
is high and the converse happens. c) and d) The 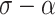 ridge, with
ridge, with  and
and  fixed to their true values is represented. The prior for
fixed to their true values is represented. The prior for 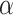 is in both cases an exponential distribution with mean 10. The prior for
is in both cases an exponential distribution with mean 10. The prior for  is an exponential distribution with mean 10 in c) and with mean 1 in d). The thick black line has equation
is an exponential distribution with mean 10 in c) and with mean 1 in d). The thick black line has equation  , with
, with 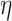 the stationary variance of the process, set to 1 (the sample variance of the tip trait values after scaling). As
the stationary variance of the process, set to 1 (the sample variance of the tip trait values after scaling). As 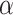 grows, this line tends to be the top of the ridge. The difference with the
grows, this line tends to be the top of the ridge. The difference with the  ridge is that the top of this ridge is not completely flat. However, as one moves towards higher
ridge is that the top of this ridge is not completely flat. However, as one moves towards higher 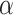 values, it gets ever flatter. In d), the prior for
values, it gets ever flatter. In d), the prior for  restricts inference to smaller values of
restricts inference to smaller values of  than in c). As a consequence, the a priori smaller plausible values of
than in c). As a consequence, the a priori smaller plausible values of  correspond to a region around the likelihood ridge that matches smaller
correspond to a region around the likelihood ridge that matches smaller 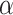 values. This has the effect of shifting the marginal posterior of
values. This has the effect of shifting the marginal posterior of 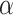 towards smaller values. In this example, the true value of
towards smaller values. In this example, the true value of  would even be excluded from the 95
would even be excluded from the 95 credible interval, because of the prior for
credible interval, because of the prior for  .
.
Nonidentifiability of parameters can be partially remedied by resorting to Bayesian inference, which allows including additional information about parameter values by specifying prior distributions, thus limiting the range of plausible values for parameters. For instance, specifying priors for  and
and  will constrain inference to remain within a given, plausible part of the ridge represented in Figure 2. Figure 2a shows that, when
will constrain inference to remain within a given, plausible part of the ridge represented in Figure 2. Figure 2a shows that, when  is low, constraining the range of
is low, constraining the range of  by way of a prior may constrain the posterior range of
by way of a prior may constrain the posterior range of  . In this case, the investigator will rightfully deduce that the posterior of
. In this case, the investigator will rightfully deduce that the posterior of  is narrower than its prior because the data carries information about
is narrower than its prior because the data carries information about  . However, this conclusion is conditional on: 1)
. However, this conclusion is conditional on: 1)  (equivalently
(equivalently  ) being correctly estimated and 2) the prior for
) being correctly estimated and 2) the prior for  . Indeed, if
. Indeed, if  is estimated to be high (e.g., because of the prior for
is estimated to be high (e.g., because of the prior for 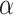 , see next section), the estimated shape of the ridge would be more like that of Figure 2b, in which case it is the prior for
, see next section), the estimated shape of the ridge would be more like that of Figure 2b, in which case it is the prior for 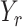 that constrains the width of the posterior of
that constrains the width of the posterior of  . Also, if one had chosen a wider prior for
. Also, if one had chosen a wider prior for  , the posterior of
, the posterior of  would have been wider. This shows how the nonidentifiability of
would have been wider. This shows how the nonidentifiability of  and
and  under the OU model makes the conclusions of Bayesian inference highly dependent on the relative widths of the prior distributions of
under the OU model makes the conclusions of Bayesian inference highly dependent on the relative widths of the prior distributions of  and
and  , and on the estimate of
, and on the estimate of 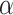 .
.
A second ridge occurs in the 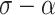 plane. The difference with the
plane. The difference with the  ridge is that the top of the
ridge is that the top of the 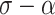 ridge is not completely flat: it seems that there is always one single pair of values of
ridge is not completely flat: it seems that there is always one single pair of values of 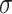 and
and 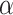 that maximizes the likelihood, for any values of the other parameters (
that maximizes the likelihood, for any values of the other parameters ( and
and  ). However, as
). However, as 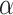 increases, the top of the ridge becomes increasingly flat, and
increases, the top of the ridge becomes increasingly flat, and  and
and  become less and less separately identifiable. Indeed, we have seen above that as
become less and less separately identifiable. Indeed, we have seen above that as 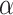 increases, the OU likelihood progressively becomes similar to the WN likelihood, where the expected value of tip traits is
increases, the OU likelihood progressively becomes similar to the WN likelihood, where the expected value of tip traits is  , and the variance of tip traits is
, and the variance of tip traits is  . Thus, if
. Thus, if 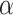 is estimated to be sufficiently high that the WN model can be substituted for the OU model, any two pairs of values of
is estimated to be sufficiently high that the WN model can be substituted for the OU model, any two pairs of values of  and
and 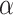 yielding the same value of
yielding the same value of 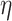 are almost equally likely. This is visible in Figure 2c,d, where we observe a ridge in the
are almost equally likely. This is visible in Figure 2c,d, where we observe a ridge in the 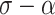 plane, of equation:
plane, of equation:
 |
The existence of this second ridge implies that the estimates of  and
and  may be correlated, which provides grounds for the priors of one of these parameters to impact the estimate of the other parameter. For instance, Figure 2c,d shows the posteriors of
may be correlated, which provides grounds for the priors of one of these parameters to impact the estimate of the other parameter. For instance, Figure 2c,d shows the posteriors of  and
and 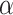 obtained with a wider prior for
obtained with a wider prior for  (with mean 10) and for a narrower prior (with mean 1). We can see that the narrower prior for
(with mean 10) and for a narrower prior (with mean 1). We can see that the narrower prior for  induces a narrower posterior, not only for
induces a narrower posterior, not only for  but also for
but also for 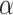 . This emphasizes that the choice of prior for
. This emphasizes that the choice of prior for  may impact the estimate of
may impact the estimate of 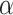 or vice versa.
or vice versa.
In summary, the mathematical structure of the OU model is such that the estimates of  ,
,  and
and  are highly conditional on the value of
are highly conditional on the value of 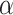 , and on their priors. If the data are very informative, the estimate of
, and on their priors. If the data are very informative, the estimate of 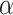 will depend little on the priors. But if the data are not so informative, or if some very stringent priors are used, the outcome of the analysis will be very dependent on the priors.
will depend little on the priors. But if the data are not so informative, or if some very stringent priors are used, the outcome of the analysis will be very dependent on the priors.
Setting a Prior for the Selection Strength
In Bayesian inference, investigators must specify prior distributions for all parameters. With the OU or Hansen models, the choice of prior for 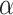 is very important, as it may influence the estimation of all other parameters (as detailed in the previous section), yet this is anything but an intuitive task.
is very important, as it may influence the estimation of all other parameters (as detailed in the previous section), yet this is anything but an intuitive task.
When an investigator undertakes the task to set a prior, they may be in one of two cases: 1) they have rather precise biological information about the value of the parameter, 2) they have rather vague information, or no information at all. The first situation is less prone to errors: the investigator will choose a narrow prior which covers the a priori credible zone adequately. In the second situation, the investigator mainly wants the prior to reflect their large uncertainty about the parameter, which is not as straightforward as it seems.
To do so, the investigator’s first instinct may be to use a flat prior that covers all the plausible values of the parameter, for any natural system similar to that under study. It is even often the case that the investigator extends the range of the prior far beyond plausible values, confident that the flatness of the prior guarantees that the prior will have no effect. This was my first instinct when I first came into contact with the OU model and I set an exponential prior for  with a very large mean.
with a very large mean.
As an example of a flat prior for 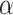 , let us consider a uniform prior distribution:
, let us consider a uniform prior distribution:
 |
Let us assume branch lengths in our phylogeny are in Ma, so that 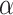 is in Ma
is in Ma . We want to decide on an upper bound
. We want to decide on an upper bound 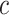 so that
so that  covers the whole range of plausible values of
covers the whole range of plausible values of  that we may expect in nature. It is hard to interpret biologically the value of
that we may expect in nature. It is hard to interpret biologically the value of 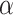 , so let us consider instead the phylogenetic half-time
, so let us consider instead the phylogenetic half-time  (see Hansen 1997; Cooper et al. 2016), which represents the time necessary for the process to cover half the way between
(see Hansen 1997; Cooper et al. 2016), which represents the time necessary for the process to cover half the way between  and
and  . We are looking for a small value
. We are looking for a small value  that represents strong-enough selection. By browsing the literature, we realize that there certainly are cases (for some specific traits and organisms) where rapid selection has been shown to change significantly the value of a trait over, say, 10,000 years. So let us choose
that represents strong-enough selection. By browsing the literature, we realize that there certainly are cases (for some specific traits and organisms) where rapid selection has been shown to change significantly the value of a trait over, say, 10,000 years. So let us choose  Ma, so that
Ma, so that 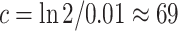 Ma
Ma represents a high-enough value of
represents a high-enough value of 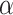 .
.
Now, if we look at this prior on the scale of  for trees of height
for trees of height  or
or  (see Fig. 1c), we see that in both cases the prior for
(see Fig. 1c), we see that in both cases the prior for  is not flat at all and favors WN-like models a lot. The difference between the shape of the prior for the two tree heights further illustrates that the same prior for
is not flat at all and favors WN-like models a lot. The difference between the shape of the prior for the two tree heights further illustrates that the same prior for 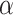 for data sets with different
for data sets with different 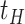 translates into different priors for
translates into different priors for  : the smaller
: the smaller 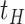 is, the more the prior favors small values of
is, the more the prior favors small values of  (i.e., more BM models).
(i.e., more BM models).
Also notice that, as shown in Appendix 3 of the Supplementary material available on Dryad, setting a flat prior on 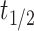 instead of
instead of 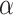 may well result in a very Brownian prior or very WN prior.
may well result in a very Brownian prior or very WN prior.
In conclusion, the interpretation of a vague prior for the strength of selection highly depends on the chosen scale (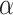 ,
, 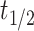 , or
, or  ). We therefore need to decide whether we are more comfortable interpreting a prior for 1) selection’s absolute strength (
). We therefore need to decide whether we are more comfortable interpreting a prior for 1) selection’s absolute strength ( ), 2) the lag time for selection to have a certain effect (
), 2) the lag time for selection to have a certain effect (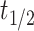 ), 3) the realized effect of selection in shaping trait values (
), 3) the realized effect of selection in shaping trait values ( ), or 4) yet another meaningful transform of
), or 4) yet another meaningful transform of 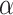 . I discuss these options in the discussion, but for now, it is important to notice that if we do not choose a prior that blends relatively evenly the different values of
. I discuss these options in the discussion, but for now, it is important to notice that if we do not choose a prior that blends relatively evenly the different values of  , we may end up with a prior that favors overwhelmingly one of the two extremes of the continuum: BM or WN processes. A nonexhaustive review of papers fitting the OU or Hansen models using Bayesian inference shows that the priors assigned to
, we may end up with a prior that favors overwhelmingly one of the two extremes of the continuum: BM or WN processes. A nonexhaustive review of papers fitting the OU or Hansen models using Bayesian inference shows that the priors assigned to  range from very BM processes to very WN processes, corresponding to very different a priori assumptions about the role of selection in shaping trait values. These priors are represented on the scale of
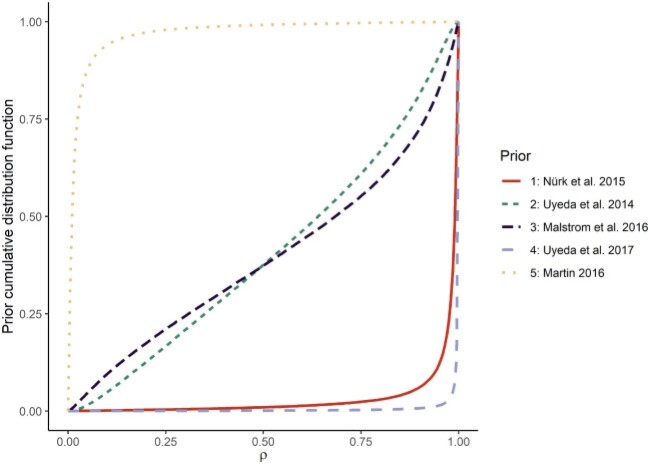
range from very BM processes to very WN processes, corresponding to very different a priori assumptions about the role of selection in shaping trait values. These priors are represented on the scale of  in Figure 3. The two most extreme priors are that of Martin (2016), very Brownian with 95
in Figure 3. The two most extreme priors are that of Martin (2016), very Brownian with 95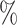 of the prior density below
of the prior density below  (hereafter the BM prior) and that of Uyeda et al. (2017), very WN with 95
(hereafter the BM prior) and that of Uyeda et al. (2017), very WN with 95 of the prior density above
of the prior density above  (hereafter the WN prior). Note that these two studies used the same prior for
(hereafter the WN prior). Note that these two studies used the same prior for 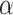 (a half-Cauchy distribution with scale 1), but for very different tree heights, which translates into very different priors for
(a half-Cauchy distribution with scale 1), but for very different tree heights, which translates into very different priors for  . Martin (2016) analyzed a tree with 42 taxa (comparable to the simulations of this study) while Uyeda et al. (2017) studied a tree with 857 taxa, which is probably much less sensitive to the choice of prior. Note that the investigators of these studies have probably based their choice of prior on sensible considerations and I only want here to point out that a wide variety of priors are used, when looking on the scale of
. Martin (2016) analyzed a tree with 42 taxa (comparable to the simulations of this study) while Uyeda et al. (2017) studied a tree with 857 taxa, which is probably much less sensitive to the choice of prior. Note that the investigators of these studies have probably based their choice of prior on sensible considerations and I only want here to point out that a wide variety of priors are used, when looking on the scale of  .
.
Figure 3.
A set of five priors for 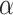 found in the literature, translated into priors for
found in the literature, translated into priors for  . These priors can be observed to range from favoring a lot low values of
. These priors can be observed to range from favoring a lot low values of  (Martin 2016) or high values of
(Martin 2016) or high values of  (e.g., Uyeda et al. 2017).
(e.g., Uyeda et al. 2017).
Simulation Study
In order to investigate the impact of the choice of prior for 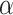 , I simulated data sets under various processes and analyzed them using one or the other of the two extreme priors for
, I simulated data sets under various processes and analyzed them using one or the other of the two extreme priors for 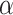 : the BM prior of Martin (2016), and the WN prior of Uyeda et al. (2017). Notice that the goal of these analyses is to see the cascading effects of the
: the BM prior of Martin (2016), and the WN prior of Uyeda et al. (2017). Notice that the goal of these analyses is to see the cascading effects of the  prior to the estimates of other parameters. To this aim, I deliberately choose the priors for the other parameters to be sufficiently wide around their known true value to show the effects of among-parameter correlations. It is understood that the priors of the present analysis are not meant to represent good practice.
prior to the estimates of other parameters. To this aim, I deliberately choose the priors for the other parameters to be sufficiently wide around their known true value to show the effects of among-parameter correlations. It is understood that the priors of the present analysis are not meant to represent good practice.
Main Analytical Setting
Trees of height 1 were simulated with  , 20, or 40 tips according to a Yule process with a speciation rate equal to
, 20, or 40 tips according to a Yule process with a speciation rate equal to  . Twenty replicate trees were simulated for each value of
. Twenty replicate trees were simulated for each value of  (60 trees in total). Continuous traits were simulated along each tree according to three processes:
(60 trees in total). Continuous traits were simulated along each tree according to three processes:
Brownian motion, with
 and
and 
a WN-like model with
 and
and  , with
, with  (i.e.,
(i.e.,  for a tree of height 1) and
for a tree of height 1) and 
a Hansen model with two selective regimes, one for each of the two descendant lineages of the root, with
 and
and  ,
,  ,
,  and
and  . So that we do not end up with selection regimes applying to a low number of lineages, the simulated trees were conditioned on having at least 3, 5, and 10 tips on either side of the root for
. So that we do not end up with selection regimes applying to a low number of lineages, the simulated trees were conditioned on having at least 3, 5, and 10 tips on either side of the root for  = 10, 20, and 40, respectively.
= 10, 20, and 40, respectively.
In total, 180 data sets were generated (3 tree sizes  3 sets of trait values
3 sets of trait values  20 replicates). Simulated ancestral trait values at internal nodes were recorded along with tip trait values and the phylogeny.
20 replicates). Simulated ancestral trait values at internal nodes were recorded along with tip trait values and the phylogeny.
The OU and Hansen models were fitted to the simulated data sets with RevBayes (Höhna et al. 2016). The RevBayes code used for these analyses is a modification of RevBayes tutorials (May 2019a,b) and is available in Appendix 4 of the Supplementary material available on Dryad. Ancestral trait values for all nodes were estimated.
Tip trait values were normalized to mean 0 and unit variance before inference, so that the same priors could be used for all analyses. The parameters in units of traits (i.e.,  and
and  ) estimated from the normalized data (scaled parameters) can be converted back to their original unit (unscaled parameters) if needed. Scaled parameters are useful for comparison with the prior, because the scaled prior was the same for all analyses. However, they cannot be compared to the true values of parameters used in simulation, since these were expressed in unscaled trait units (see Appendix 5 of the Supplementary material available on Dryad for detail). Figures show unscaled parameters, unless stated otherwise. The unit of
) estimated from the normalized data (scaled parameters) can be converted back to their original unit (unscaled parameters) if needed. Scaled parameters are useful for comparison with the prior, because the scaled prior was the same for all analyses. However, they cannot be compared to the true values of parameters used in simulation, since these were expressed in unscaled trait units (see Appendix 5 of the Supplementary material available on Dryad for detail). Figures show unscaled parameters, unless stated otherwise. The unit of 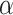 is
is  and is thus invariant to trait scaling.
and is thus invariant to trait scaling.
For each analysis, one Monte Carlo Markov Chain (MCMC) was run for 100,000 iterations after a burnin period of 10,000. A second run was made for 60 analyses, showing that different runs yielded qualitatively similar results.
The effect of the prior for  on estimated parameters was studied through two series of analyses.
on estimated parameters was studied through two series of analyses.
An OU model was fitted to each data set with the BM and the WN priors. This amounted to 360 analyses (180 data sets
 2 priors).
2 priors).I proceeded as in 1., except the Hansen model was fitted instead of the OU model.
Details on the priors can be found in Appendix 3 of the Supplementary material available on Dryad, and the R code and files for running the simulations and prepare the RevBayes scripts are given in Appendix 4 of the Supplementary material available on Dryad.
Additional Analyses
I assessed the sensitivity of the results of the OU analyses (point 1 above) with trees of 40 tips to three aspects by rerunning these analyses changing one thing at a time. Ancestral trait values were not estimated. First, trees with 300 tips were simulated instead of 40 to investigate a case where the likelihood may be very informative and dominate the prior. Second, trees were simulated under a birth–death model instead of a Yule model, with a net diversification rate  and a turnover rate
and a turnover rate  . Trees generated in this way have shorter terminal branches than Yule trees, which may preserve phylogenetic signal for higher values of
. Trees generated in this way have shorter terminal branches than Yule trees, which may preserve phylogenetic signal for higher values of  . The value of
. The value of 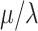 has been shown to have substantial effects in ML parameter inference (Cooper et al. 2016). Third, a flatter prior was considered for
has been shown to have substantial effects in ML parameter inference (Cooper et al. 2016). Third, a flatter prior was considered for  (with mean 100 instead of mean 10 in the main analyses), to determine if this could impact the estimation of
(with mean 100 instead of mean 10 in the main analyses), to determine if this could impact the estimation of  , as suspected above (see Fig. 2).
, as suspected above (see Fig. 2).
Results
All the results shown in the main text are for trees with 40 tips. Results for trees with 10 or 20 tips are qualitatively similar and can be found in Appendix 6 of the Supplementary material available on Dryad, along with a full report on MCMC mixing. The results of the three additional analyses are given in Appendix 7 of the Supplementary material available on Dryad, and mentioned where appropriate in the main text. The posterior distributions for ancestral trait values are qualitatively similar to those of  and can be found in Appendix 8 of the Supplementary material available on Dryad.
and can be found in Appendix 8 of the Supplementary material available on Dryad.
OU Model
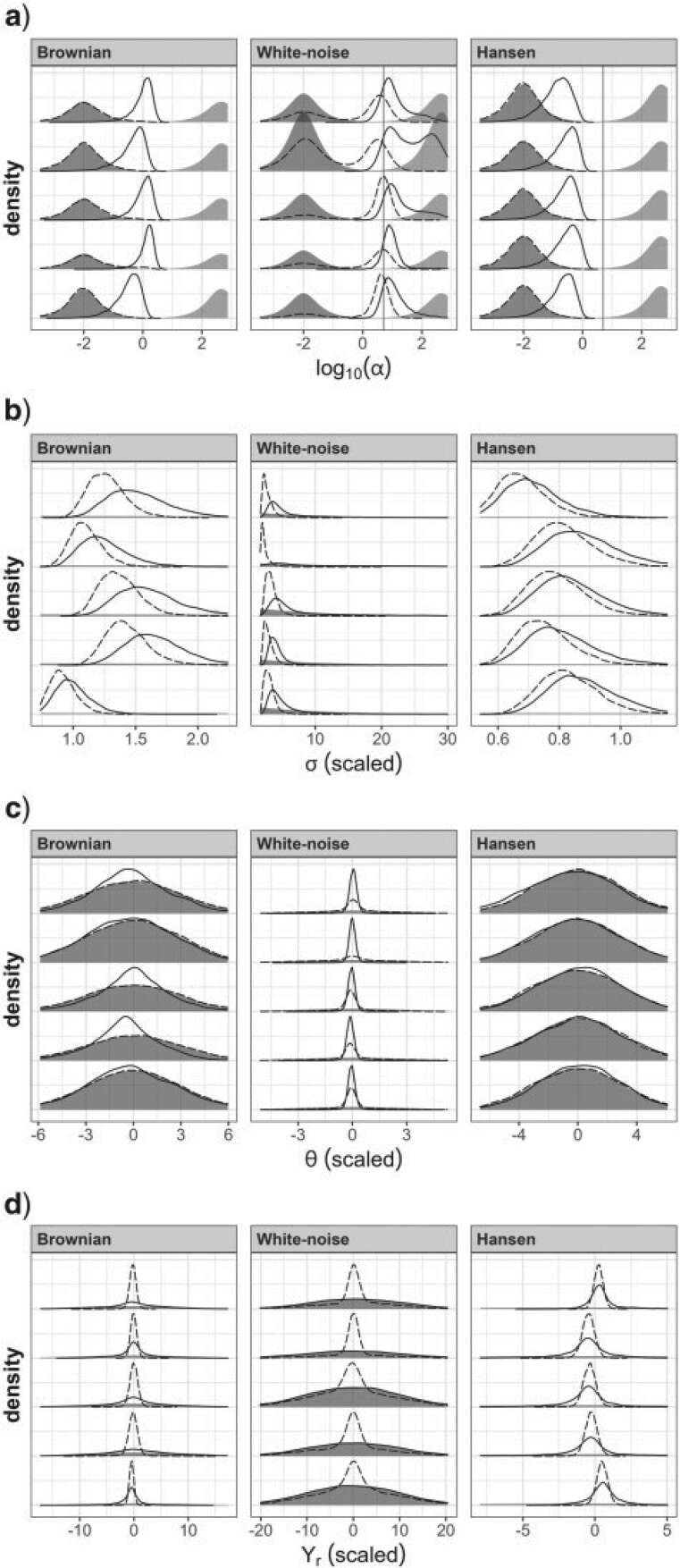
Figure 4a shows that using one or the other prior for 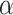 has an influence on the marginal posterior of this parameter. For BM data, the posterior of
has an influence on the marginal posterior of this parameter. For BM data, the posterior of 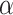 is equal to the prior when using the BM prior, as the data do not disagree with the prior. In contrast, with the WN prior, the BM data have dragged the posterior of
is equal to the prior when using the BM prior, as the data do not disagree with the prior. In contrast, with the WN prior, the BM data have dragged the posterior of 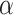 towards more Brownian values. With WN data, the marginal posterior obtained with the BM prior is bimodal, with one mode located around the true value
towards more Brownian values. With WN data, the marginal posterior obtained with the BM prior is bimodal, with one mode located around the true value  and a smaller mode located as the prior. This is indicative of a conflict between the prior and the data. A slight bimodality is also sometimes observed with the WN prior, with one mode located around the true value, and a smaller mode located as the prior. For Hansen data, the phylogenetic signal produced by the two clades having different selective optima is interpreted as evidence for low selection. Consequently, the BM prior is not contradicted by the data, producing a posterior identical to the prior, while the posterior obtained with the WN prior is located under much more Brownian values of
and a smaller mode located as the prior. This is indicative of a conflict between the prior and the data. A slight bimodality is also sometimes observed with the WN prior, with one mode located around the true value, and a smaller mode located as the prior. For Hansen data, the phylogenetic signal produced by the two clades having different selective optima is interpreted as evidence for low selection. Consequently, the BM prior is not contradicted by the data, producing a posterior identical to the prior, while the posterior obtained with the WN prior is located under much more Brownian values of 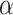 than the prior.
than the prior.
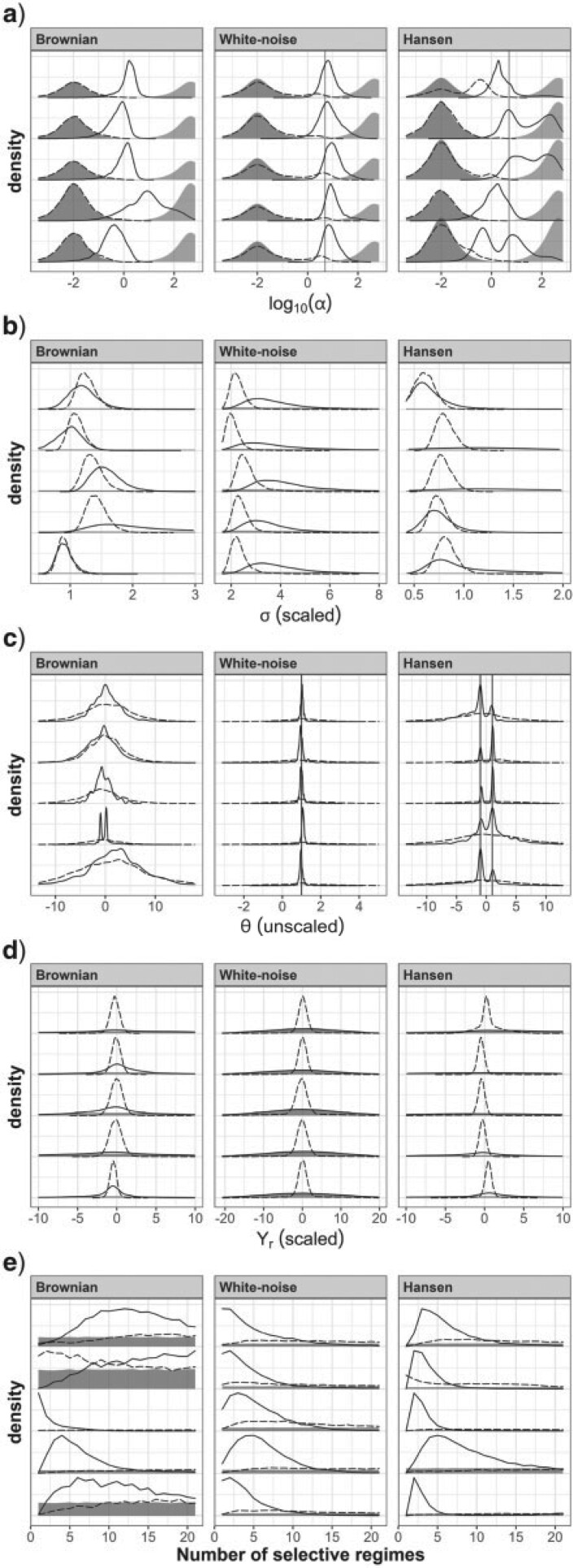
Figure 4.
Marginal posteriors for trees with 40 tips when fitting an OU model. Dashed curves, posteriors with the BM prior. Solid curves, posteriors with the WN prior. Shaded areas represent the priors. For  , the darker and lighter areas represent the BM and WN priors, respectively, and the vertical line represents the value used in simulations. The posterior densities for five of the 20 analyses are represented (see Appendix 8 of the Supplementary material available on Dryad for graphs for all analyses). Different columns correspond to different simulation models. The rows correspond to a)
, the darker and lighter areas represent the BM and WN priors, respectively, and the vertical line represents the value used in simulations. The posterior densities for five of the 20 analyses are represented (see Appendix 8 of the Supplementary material available on Dryad for graphs for all analyses). Different columns correspond to different simulation models. The rows correspond to a) 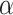 , b)
, b)  , c)
, c)  , and d)
, and d)  . Note that because the analyses were carried out on scaled trait values, both the priors and the true values cannot be represented on the same graph for parameters in unit of traits (see Appendix 5 of the Supplementary material available on Dryad). The scaled version of such parameters is plotted here for comparison with priors.
. Note that because the analyses were carried out on scaled trait values, both the priors and the true values cannot be represented on the same graph for parameters in unit of traits (see Appendix 5 of the Supplementary material available on Dryad). The scaled version of such parameters is plotted here for comparison with priors.
In summary, the chosen prior had an influence on the estimated value of 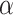 , for all types of data sets. This provides ground for the marginal posteriors of the other parameters to be influenced by the prior for
, for all types of data sets. This provides ground for the marginal posteriors of the other parameters to be influenced by the prior for 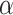 , through the interactions among the parameters outlined above.
, through the interactions among the parameters outlined above.
For BM and Hansen data, the marginal posterior distribution of  is located in a region wherein the prior appears flat, indicating that in these cases estimates of
is located in a region wherein the prior appears flat, indicating that in these cases estimates of  are likely driven by the data rather than by the prior. This was however not necessarily the case for WN data, for which we notice that the prior is more curved in the range occupied by the posterior (Fig. 4b). This should draw our attention, as it is possible that the prior for
are likely driven by the data rather than by the prior. This was however not necessarily the case for WN data, for which we notice that the prior is more curved in the range occupied by the posterior (Fig. 4b). This should draw our attention, as it is possible that the prior for  prevents the posterior from moving towards higher values. Furthermore, Figure 5a shows that the values of
prevents the posterior from moving towards higher values. Furthermore, Figure 5a shows that the values of 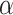 and
and  are highly positively correlated when
are highly positively correlated when  is roughly higher than 0.65 (i.e.,
is roughly higher than 0.65 (i.e.,  ), which is the manifestation of the weak identifiability of these parameters outlined above. In this context, it is possible that the prior for
), which is the manifestation of the weak identifiability of these parameters outlined above. In this context, it is possible that the prior for  , by excluding higher values, prevents
, by excluding higher values, prevents 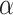 from reaching higher values. The analyses shown in Appendix 7 of the Supplementary material available on Dryad with a flatter prior for
from reaching higher values. The analyses shown in Appendix 7 of the Supplementary material available on Dryad with a flatter prior for  indicate that this happened for a number of analyses: with the WN data and the WN prior, the posterior of
indicate that this happened for a number of analyses: with the WN data and the WN prior, the posterior of  has a fatter tail, and the upper posterior mode for
has a fatter tail, and the upper posterior mode for 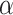 , located close to the prior, becomes dominant.
, located close to the prior, becomes dominant.
Figure 5.
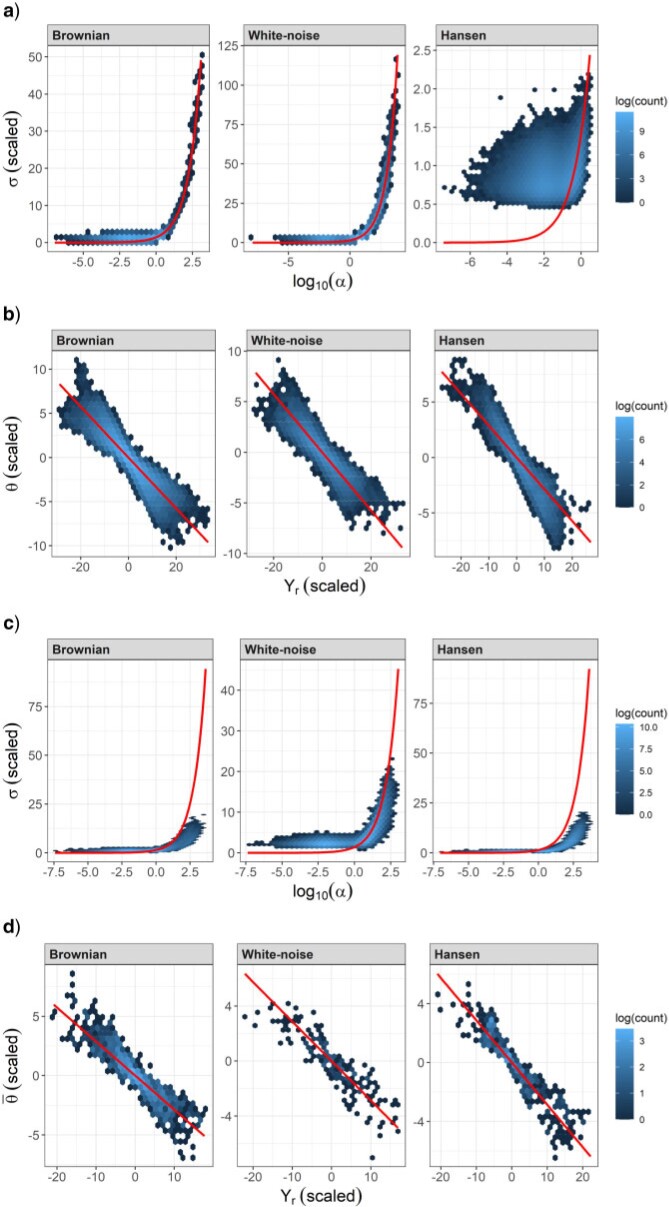
Correlation among parameters in the joint posterior. Each plot was drawn by pooling the posterior samples of all analyses conducted on data sets that were produced with the same simulation model. a) and c) Correlation of  and
and  for inference with the OU and Hansen models, respectively. The curve
for inference with the OU and Hansen models, respectively. The curve  is represented. b) Correlation of
is represented. b) Correlation of  and
and  for inference with the OU model. Only posterior samples with intermediate
for inference with the OU model. Only posterior samples with intermediate 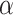 values (i.e., between 1 and 2) were included. The curve
values (i.e., between 1 and 2) were included. The curve 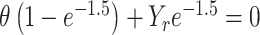 is represented. d) Correlation of
is represented. d) Correlation of  and
and  for inference with the OU model.
for inference with the OU model.  is the average of
is the average of  across branches. Only posterior samples with intermediate
across branches. Only posterior samples with intermediate 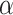 values (i.e., between 1 and 2) were included. The curve
values (i.e., between 1 and 2) were included. The curve  is represented. Note that in the Hansen model, the formula of the expected relationship between
is represented. Note that in the Hansen model, the formula of the expected relationship between  and
and  is not this curve, although in this case it comes close to it.
is not this curve, although in this case it comes close to it.
As predicted above and illustrated in Figure 2, the posterior of  is similar to the prior whenever the posterior of
is similar to the prior whenever the posterior of 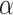 is BM-like, while it is concentrated around 0, the sample mean of tip trait values, when
is BM-like, while it is concentrated around 0, the sample mean of tip trait values, when 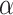 is estimated to be higher (Fig. 4c). The inverse is true for the posterior of
is estimated to be higher (Fig. 4c). The inverse is true for the posterior of  , which is estimated close to 0 when
, which is estimated close to 0 when 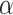 is low, and similar to its prior when
is low, and similar to its prior when  is high (Fig. 4d). This situation extends to all ancestral trait values besides
is high (Fig. 4d). This situation extends to all ancestral trait values besides  , as shown in Appendix 8 of the Supplementary material available on Dryad.
, as shown in Appendix 8 of the Supplementary material available on Dryad.
Appendix 7 of the Supplementary material available on Dryad shows that the influence of the prior for  is lesser with trees of 300 tips and for WN data sets. As these data sets are more informative than trees with 40 tips, the true value is recovered regardless of the prior for WN data. The estimates of the other parameters also became less dependent on the prior, but the correlations among parameters illustrated in Figure 5 due to nonidentifiability largely remain. For the trees simulated under the birth–death model, the results are overall similar to pure-birth trees, although we note that, for WN data and the BM prior, the upper mode located around the true value (in Fig. 4a) becomes much smaller. With the WN prior, the upper mode located around the prior altogether disappears. Both these effects are likely due to the fact that birth–death trees, through their having younger nodes, have favored the production of trait data sets with more phylogenetic structure, which is interpreted by the model as evidence for more BM processes.
is lesser with trees of 300 tips and for WN data sets. As these data sets are more informative than trees with 40 tips, the true value is recovered regardless of the prior for WN data. The estimates of the other parameters also became less dependent on the prior, but the correlations among parameters illustrated in Figure 5 due to nonidentifiability largely remain. For the trees simulated under the birth–death model, the results are overall similar to pure-birth trees, although we note that, for WN data and the BM prior, the upper mode located around the true value (in Fig. 4a) becomes much smaller. With the WN prior, the upper mode located around the prior altogether disappears. Both these effects are likely due to the fact that birth–death trees, through their having younger nodes, have favored the production of trait data sets with more phylogenetic structure, which is interpreted by the model as evidence for more BM processes.
6.2. Hansen Model
The analyses with the Hansen model yielded results that were overall similar to analyses with the OU model (Fig. 6). In particular, the prior for  had a strong influence on the results, with larger posterior values of
had a strong influence on the results, with larger posterior values of 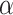 with the WN prior (Fig. 6a). The main difference between the two sets of analyses was logically observed with the Hansen data sets. While the OU model accommodated the difference in trait values between the two clades with different regimes in Hansen data sets by invoking low values of
with the WN prior (Fig. 6a). The main difference between the two sets of analyses was logically observed with the Hansen data sets. While the OU model accommodated the difference in trait values between the two clades with different regimes in Hansen data sets by invoking low values of 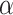 , the Hansen model yielded larger posterior values of
, the Hansen model yielded larger posterior values of 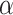 , especially with the WN prior. Such high values of
, especially with the WN prior. Such high values of  are indeed more likely under the Hansen model than under the OU model, because the former can accommodate the observed phylogenetic structure of trait values by invoking different selection regimes. This is obvious when looking at the posterior distribution of the selective optima obtained for Hansen data, which has two modes located around the two true values of
are indeed more likely under the Hansen model than under the OU model, because the former can accommodate the observed phylogenetic structure of trait values by invoking different selection regimes. This is obvious when looking at the posterior distribution of the selective optima obtained for Hansen data, which has two modes located around the two true values of  with the WN prior (Fig. 6c).
with the WN prior (Fig. 6c).
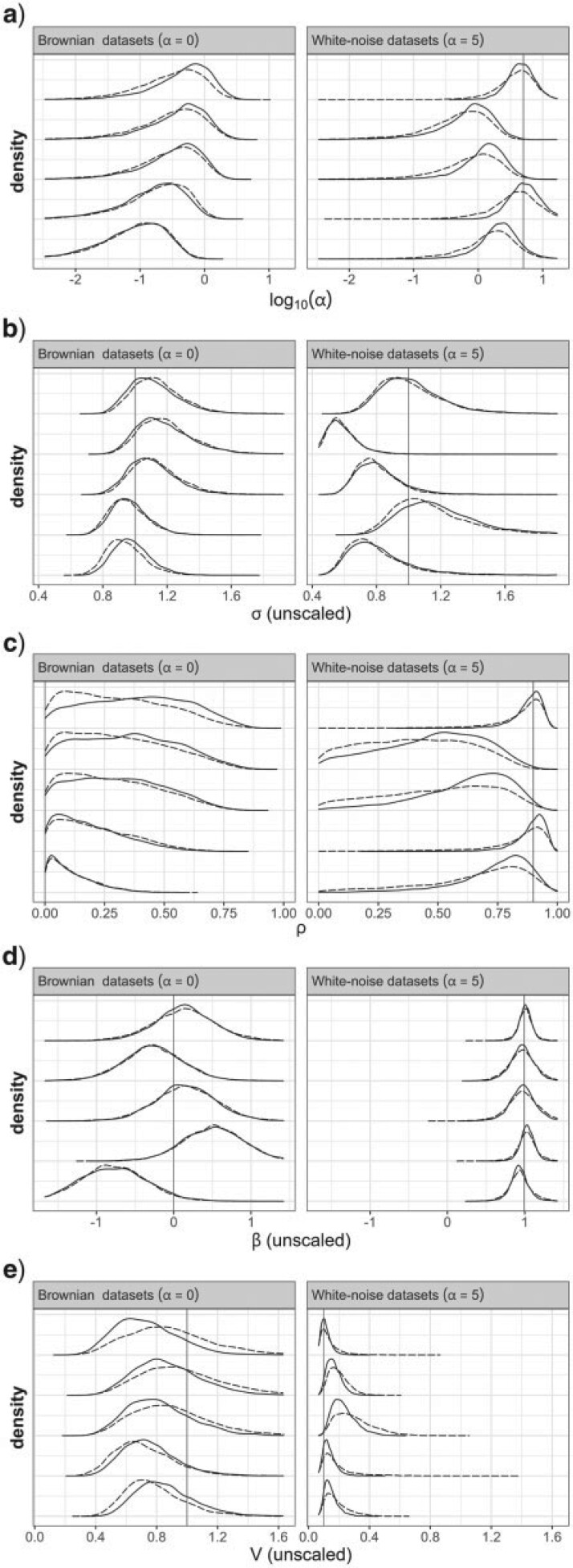
Figure 6.
Marginal posteriors for trees with 40 tips when fitting the Hansen model with multiple selective optima. The dashed and solid curves represent the posteriors obtained with the BM and WN priors, respectively. Shaded areas represent the priors. For 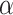 , the darker and lighter shaded areas represent the Brownian and WN priors, respectively. For
, the darker and lighter shaded areas represent the Brownian and WN priors, respectively. For 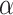 and
and  , the vertical line(s) represent(s) the value(s) used in simulations. The posterior densities of 5 of the 20 analyses are represented. Different columns correspond to different simulation models. The rows correspond to: a)
, the vertical line(s) represent(s) the value(s) used in simulations. The posterior densities of 5 of the 20 analyses are represented. Different columns correspond to different simulation models. The rows correspond to: a) 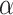 , b)
, b)  , c) the
, c) the  ’s (pooled together), d)
’s (pooled together), d)  , and e)
, and e)  (the number of selective regimes). The plots of e) are represented for
(the number of selective regimes). The plots of e) are represented for  for visibility, but the prior is flat from 0 to the number of branches (see Appendix 3 of the Supplementary material available on Dryad). The scaled version of parameters is plotted here for comparison with the priors, except for the
for visibility, but the prior is flat from 0 to the number of branches (see Appendix 3 of the Supplementary material available on Dryad). The scaled version of parameters is plotted here for comparison with the priors, except for the  ’s which have been unscaled for comparison with the true values.
’s which have been unscaled for comparison with the true values.
The interactions between parameters when fitting the Hansen model are also similar to what was observed with the OU model. In particular, the posterior of 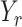 is narrow and those of the
is narrow and those of the  ’s are wide whenever
’s are wide whenever  is estimated to below, and conversely when
is estimated to below, and conversely when 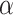 is estimated to be high, implying that the effect of the nonidentifiability of
is estimated to be high, implying that the effect of the nonidentifiability of  and the
and the  ’s remains with the Hansen model (Fig. 6). This lack of identifiability is further exemplified by the same negative correlation between the values of the
’s remains with the Hansen model (Fig. 6). This lack of identifiability is further exemplified by the same negative correlation between the values of the  ’s and
’s and  (Fig. 5d). Finally, we note the same correlation between
(Fig. 5d). Finally, we note the same correlation between  and
and  when
when  is high, with the difference that the relationship between
is high, with the difference that the relationship between  and
and 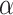 is no longer the curve
is no longer the curve 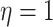 (Fig. 5c). This is expected as, in the Hansen model with strong selection, the sample variance of tip trait values (equal to 1) is expected to be made up of the variance of tip trait values around their mean (
(Fig. 5c). This is expected as, in the Hansen model with strong selection, the sample variance of tip trait values (equal to 1) is expected to be made up of the variance of tip trait values around their mean (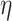 ), plus the variation of the
), plus the variation of the  ’s among selective regimes, so that
’s among selective regimes, so that 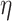 is expected to be less than 1.
is expected to be less than 1.
With the Hansen model, the prior for 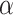 further impacts the number of selective regimes (
further impacts the number of selective regimes ( , Fig. 6e). With the BM prior, we see that the posterior of
, Fig. 6e). With the BM prior, we see that the posterior of  is rather flat (as is the prior for
is rather flat (as is the prior for  ). The standard Bayesian interpretation of observing a posterior close to the prior is that the data are not very informative about the parameter. However, in the present case, this conclusion is conditional on the estimate of
). The standard Bayesian interpretation of observing a posterior close to the prior is that the data are not very informative about the parameter. However, in the present case, this conclusion is conditional on the estimate of 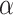 . Indeed, whenever
. Indeed, whenever 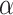 is low (as was the case here with the BM prior), the influence of selection is so low that the value of
is low (as was the case here with the BM prior), the influence of selection is so low that the value of  no longer impacts the posterior significantly. We thus observe the posterior of
no longer impacts the posterior significantly. We thus observe the posterior of  close to the prior, not because the data are uninformative, but because our choice of prior restricted inference to BM-like models. Another important aspect to consider when interpreting the estimate of
close to the prior, not because the data are uninformative, but because our choice of prior restricted inference to BM-like models. Another important aspect to consider when interpreting the estimate of  is the quantitative difference in the values of the
is the quantitative difference in the values of the  ’s for the different regimes. For instance, in Figure 6e, inspecting the posterior of
’s for the different regimes. For instance, in Figure 6e, inspecting the posterior of  for Hansen datasets and the WN prior does not generally show evidence in favor of
for Hansen datasets and the WN prior does not generally show evidence in favor of  , the true value. However, upon inspection of the posterior distributions of the
, the true value. However, upon inspection of the posterior distributions of the  ’s in Figure 6c, it is clear that whenever
’s in Figure 6c, it is clear that whenever  , the
, the  different values of
different values of  fall into only two significantly different modes. This suggests that there are only two significantly different selective regimes, which is the correct answer in this case.
fall into only two significantly different modes. This suggests that there are only two significantly different selective regimes, which is the correct answer in this case.
Summary on Parameter Estimation with the OU and Hansen Models
The previous sections have shown that choosing a prior for 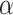 is not so straightforward and that it is easy to set a prior for
is not so straightforward and that it is easy to set a prior for 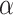 that is very stringent in favor of BM or WN models. Translating the
that is very stringent in favor of BM or WN models. Translating the 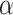 prior on the scale of
prior on the scale of  allows to have a clear sight of whether the prior favors such extreme models. If this is the case, and data are not informative enough to contradict the prior, inference may in effect be carried out with a BM or WN model, which may have consequences on the estimation of all the other parameters (
allows to have a clear sight of whether the prior favors such extreme models. If this is the case, and data are not informative enough to contradict the prior, inference may in effect be carried out with a BM or WN model, which may have consequences on the estimation of all the other parameters ( ,
,  , and
, and  ).
).
In particular, leaning on the BM side will likely induce a narrow posterior for  as compared to the prior, which is actually only indicative of the fact that the slope of the
as compared to the prior, which is actually only indicative of the fact that the slope of the  ridge is highly negative (as in Fig. 2a). In this case, conclusions about
ridge is highly negative (as in Fig. 2a). In this case, conclusions about  must be done conditional on the prior for
must be done conditional on the prior for  and are only valid if the low estimate of
and are only valid if the low estimate of  is correct and not caused by a poor prior choice. The converse happens when one leans on the WN side, with a narrow posterior for
is correct and not caused by a poor prior choice. The converse happens when one leans on the WN side, with a narrow posterior for  being the reflection of the prior for
being the reflection of the prior for  (as in Fig. 2b). The OU model shows here a rather counter-intuitive behavior, and I hope that this study can make this clearer. Most importantly, investigators must be aware that there is no way to estimate either
(as in Fig. 2b). The OU model shows here a rather counter-intuitive behavior, and I hope that this study can make this clearer. Most importantly, investigators must be aware that there is no way to estimate either  or
or  with contemporaneous data, without prior information about one of these parameters, as already emphasized in other studies (see Ho and Ané 2014).
with contemporaneous data, without prior information about one of these parameters, as already emphasized in other studies (see Ho and Ané 2014).
We have also seen that the parameters 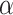 and
and  are weakly identifiable whenever
are weakly identifiable whenever 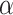 and
and  translate into a high-enough value of
translate into a high-enough value of  . This may induce a strong correlation of the estimates of
. This may induce a strong correlation of the estimates of  and
and  , which provides the opportunity for the prior of one of these parameters to impact the posterior of the other, as shown in Figure 2c,d. The priors for these two parameters may even be in conflict if they intersect away from the top of the likelihood ridge.
, which provides the opportunity for the prior of one of these parameters to impact the posterior of the other, as shown in Figure 2c,d. The priors for these two parameters may even be in conflict if they intersect away from the top of the likelihood ridge.
All these parameters are common to all types of inference with the OU model, whatever the purpose of the analysis, and the issues outlined here probably concern most types of OU analyses. For instance, if one wants to estimate ancestral trait values (e.g., Martins and Hansen 1997; Bokma 2002; Paradis et al. 2004; Harmon et al. 2008; Lemey et al. 2010; Revell 2012; Landis et al. 2013; Elliot and Mooers 2014; Kratsch and McHardy 2014; Meseguer et al. 2018), the estimates are conditional on the prior for  and the estimate of
and the estimate of  (Appendix 9 of the Supplementary material available on Dryad shows that the
(Appendix 9 of the Supplementary material available on Dryad shows that the  ridge extends to the trait values of all ancestral species). If one wants to estimate the rate of phenotypic evolution
ridge extends to the trait values of all ancestral species). If one wants to estimate the rate of phenotypic evolution  , or its variation among clades (e.g., O’Meara et al. 2006; Revell and Harmon 2008; Revell and Collar 2009; Eastman et al. 2011; Jones et al. 2015; Martin 2016), the interaction between the priors for
, or its variation among clades (e.g., O’Meara et al. 2006; Revell and Harmon 2008; Revell and Collar 2009; Eastman et al. 2011; Jones et al. 2015; Martin 2016), the interaction between the priors for  and
and  may impact the results significantly. If the investigator wants to test whether selection has had a significant impact on the evolution of traits, by comparing a BM model with an OU model (e.g., Butler and King 2004; Collar et al. 2009; Harmon et al. 2010; Beaulieu et al. 2012; Cooper et al. 2016), the prior for
may impact the results significantly. If the investigator wants to test whether selection has had a significant impact on the evolution of traits, by comparing a BM model with an OU model (e.g., Butler and King 2004; Collar et al. 2009; Harmon et al. 2010; Beaulieu et al. 2012; Cooper et al. 2016), the prior for 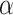 may entirely determine the results. In the case that we want to determine if the data are consistent with a Hansen model with several selective regimes (e.g., Uyeda and Harmon 2014; Cuff et al. 2015; Vining and Nunn 2016; Uyeda et al. 2017), obtaining a proper estimate of
may entirely determine the results. In the case that we want to determine if the data are consistent with a Hansen model with several selective regimes (e.g., Uyeda and Harmon 2014; Cuff et al. 2015; Vining and Nunn 2016; Uyeda et al. 2017), obtaining a proper estimate of 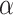 is necessary. Studies that test for the impact of a predictor trait on a response trait (e.g., Davis et al. 2012; Gohli and Voje 2016; Solbakken et al. 2017; Lattenkamp et al. 2021) are also concerned. In particular, we note that the
is necessary. Studies that test for the impact of a predictor trait on a response trait (e.g., Davis et al. 2012; Gohli and Voje 2016; Solbakken et al. 2017; Lattenkamp et al. 2021) are also concerned. In particular, we note that the  coefficient of the SLOUCH model (Hansen et al. 2008), which takes value 1 when the effect of selection is maximal, and value 0 when it is minimal, corresponds to
coefficient of the SLOUCH model (Hansen et al. 2008), which takes value 1 when the effect of selection is maximal, and value 0 when it is minimal, corresponds to  of the present study. It appears that
of the present study. It appears that  and
and  are very similar metrics, so that the extreme
are very similar metrics, so that the extreme 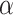 priors studied in the present article translate into stringent priors for both
priors studied in the present article translate into stringent priors for both  and
and  . Hence, if SLOUCH were used in a Bayesian context with, for instance, the BM prior for
. Hence, if SLOUCH were used in a Bayesian context with, for instance, the BM prior for 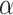 of Martin (2016), the analysis would almost deterministically conclude that phylogenetic inertia, rather than selection, affected the response variable. Note that most of the literature cited here resorted to maximum-likelihood inference, which does not use priors. However, the advent of Bayesian programs may soon allow these models to be implemented for Bayesian inference (most of them could already be implemented in RevBayes).
of Martin (2016), the analysis would almost deterministically conclude that phylogenetic inertia, rather than selection, affected the response variable. Note that most of the literature cited here resorted to maximum-likelihood inference, which does not use priors. However, the advent of Bayesian programs may soon allow these models to be implemented for Bayesian inference (most of them could already be implemented in RevBayes).
Interpretation of 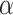 or
or 
The speed at which trait values are attracted towards the optimum, in units of  , is given by
, is given by  . The inverse of
. The inverse of  thus acts as a coefficient modulating the speed of attraction by selection. We hardly have any experience in real life of such a quantity as
thus acts as a coefficient modulating the speed of attraction by selection. We hardly have any experience in real life of such a quantity as 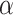 , in unit of
, in unit of  , and it is certainly not common to find estimates of selection in the biological literature in this unit. As a consequence, it may be preferable to find a transformation of
, and it is certainly not common to find estimates of selection in the biological literature in this unit. As a consequence, it may be preferable to find a transformation of 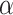 whose meaning is clearer.
whose meaning is clearer.
The meaning of the phylogenetic half-time ( ) is much clearer: it is the time necessary for a trait value to cover half the way to the optimum, whatever the starting point. An evolutionary biologist certainly has a better intuition of whether, for instance, a hundred thousand years for a trait value to climb half way up a hill in an adaptive landscape is plausible or not in their study system.
) is much clearer: it is the time necessary for a trait value to cover half the way to the optimum, whatever the starting point. An evolutionary biologist certainly has a better intuition of whether, for instance, a hundred thousand years for a trait value to climb half way up a hill in an adaptive landscape is plausible or not in their study system.
I find that the quantity  is another meaningful transform of
is another meaningful transform of 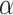 (and
(and 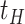 ), which renders the cumulative effect that selection has had on the traits, from the root to the tips of the particular tree being studied. It is a direct reflection of the shape of evolutionary trajectories, which should be quite meaningful to many investigators, and the same value of
), which renders the cumulative effect that selection has had on the traits, from the root to the tips of the particular tree being studied. It is a direct reflection of the shape of evolutionary trajectories, which should be quite meaningful to many investigators, and the same value of  represents the same trajectory shape in every system. In contrast, neither
represents the same trajectory shape in every system. In contrast, neither 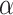 nor
nor 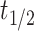 bear such a universal meaning, as the same value of any one of these quantities can translate into flat or steep trajectories, depending on the height of the tree at study. In fact, it is common place for investigators using the OU model to interpret
bear such a universal meaning, as the same value of any one of these quantities can translate into flat or steep trajectories, depending on the height of the tree at study. In fact, it is common place for investigators using the OU model to interpret  or
or  relative to tree height (e.g., Hansen et al. 2008; Ané et al. 2017; Cooper et al. 2016).
relative to tree height (e.g., Hansen et al. 2008; Ané et al. 2017; Cooper et al. 2016).
In the shoes of an investigator that has no prejudice on whether selection has been influential in determining the trait values under study, parameterizing the OU model in terms of  rather than
rather than  or
or 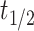 thus makes sense to me. The investigator can choose a prior distribution for
thus makes sense to me. The investigator can choose a prior distribution for  and verify graphically how this prior translates in terms of expected trajectories. It can be verified that the prior blends flat (BM-like) and steep (WN-like) trajectories, thus expressing correctly an a priori uncertainty about the relevance of selection in the study system. Also notice that many studies have used the OU model as a means for testing whether selection has had an effect at all, through the statistical comparison of a BM versus an OU model (e.g., Butler and King 2004; Collar et al. 2009; Harmon et al. 2010; Beaulieu et al. 2012; Cooper et al. 2016), concluding that selection had a significant effect when the OU model is better than the BM model. However, as shown in Appendix 2 of the Supplementary material available on Dryad, the value of
and verify graphically how this prior translates in terms of expected trajectories. It can be verified that the prior blends flat (BM-like) and steep (WN-like) trajectories, thus expressing correctly an a priori uncertainty about the relevance of selection in the study system. Also notice that many studies have used the OU model as a means for testing whether selection has had an effect at all, through the statistical comparison of a BM versus an OU model (e.g., Butler and King 2004; Collar et al. 2009; Harmon et al. 2010; Beaulieu et al. 2012; Cooper et al. 2016), concluding that selection had a significant effect when the OU model is better than the BM model. However, as shown in Appendix 2 of the Supplementary material available on Dryad, the value of  determines how close the OU model is to a BM model independently from tree height, while
determines how close the OU model is to a BM model independently from tree height, while 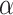 does not. Thus, setting a prior on
does not. Thus, setting a prior on 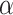 that favors extreme
that favors extreme  values may have a substantial impact on model selection. For instance, if the true model is an intermediate OU model with, say,
values may have a substantial impact on model selection. For instance, if the true model is an intermediate OU model with, say,  , and the
, and the  prior is WN (such as the prior of Uyeda et al. 2017), the comparison is actually made between BM and WN, and the rejection of the WN model is incorrectly interpreted as a rejection of the OU model. In contrast, a prior for
prior is WN (such as the prior of Uyeda et al. 2017), the comparison is actually made between BM and WN, and the rejection of the WN model is incorrectly interpreted as a rejection of the OU model. In contrast, a prior for  that includes low and high values would not favor one or the other model a priori.
that includes low and high values would not favor one or the other model a priori.
In opposition to the use of  instead of
instead of 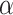 or
or 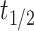 is the following argument. We note that
is the following argument. We note that  is not a parameter sensu stricto, as it is calculated from
is not a parameter sensu stricto, as it is calculated from 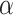 (a parameter) and
(a parameter) and 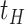 (a datum). Consider now an investigator who samples a natural process at time
(a datum). Consider now an investigator who samples a natural process at time  and assigns some prior for
and assigns some prior for  , which translates into some prior for
, which translates into some prior for 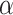 . Had this investigator sampled the process at a later time
. Had this investigator sampled the process at a later time  , by setting the same prior for
, by setting the same prior for  , they would have assumed a different prior for
, they would have assumed a different prior for 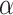 . This means that the a priori of the investigator about the absolute magnitude of selection (
. This means that the a priori of the investigator about the absolute magnitude of selection (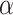 ) in one given natural system depends on the time of sampling. One could rightfully argue that the same prior should be assigned for the same natural process, independently of the time at which the process is observed. Note that the same argument would preclude scaling the tree to unit height, as recommended in other studies (e.g., Cooper et al. 2016). While I consider this argument to be valid, I think that, in practice, investigators that are unsure about how to formulate a prior about
) in one given natural system depends on the time of sampling. One could rightfully argue that the same prior should be assigned for the same natural process, independently of the time at which the process is observed. Note that the same argument would preclude scaling the tree to unit height, as recommended in other studies (e.g., Cooper et al. 2016). While I consider this argument to be valid, I think that, in practice, investigators that are unsure about how to formulate a prior about 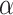 or
or 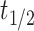 in their original unit, had better set the prior on
in their original unit, had better set the prior on  , and check the shape of evolutionary trajectories that the prior corresponds to. In fact, as we will see below, a uniform prior on
, and check the shape of evolutionary trajectories that the prior corresponds to. In fact, as we will see below, a uniform prior on  is able to correctly estimate
is able to correctly estimate  , for data sets simulated under BM or WN.
, for data sets simulated under BM or WN.
Finally, notice that, although I focused here on  , others may prefer to calculate
, others may prefer to calculate  for another reference time period. For instance, considering that most of the tree nodes are located closer to the present, using
for another reference time period. For instance, considering that most of the tree nodes are located closer to the present, using  may seem more meaningful to some. Also, if one knows approximately the generation time
may seem more meaningful to some. Also, if one knows approximately the generation time 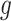 of the studied organisms, the metric
of the studied organisms, the metric  reflects the percent variance that is lost in one generation due to selection.
reflects the percent variance that is lost in one generation due to selection.
Reparameterization of the OU Model
When using models like the OU model, whose parameters are not separately identifiable, or weakly so, Bayesian inference provides a sensible means to leverage prior information to identify the parameters. Investigators that have such prior knowledge about some parameters should implement it, by expressing a prior on a scale that they feel comfortable interpreting. Therefore, this study should not be interpreted as an argument against setting a prior on 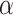 or
or 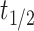 in time units, but rather addresses investigators that have vague or no prior information about the OU parameters. I particularly want to emphasize the fact that a prior that may seem uninformative on a certain scale, may appear very stringent when looked at on another scale. Furthermore, the prior for one parameter (especially
in time units, but rather addresses investigators that have vague or no prior information about the OU parameters. I particularly want to emphasize the fact that a prior that may seem uninformative on a certain scale, may appear very stringent when looked at on another scale. Furthermore, the prior for one parameter (especially 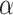 ) may have cascading effects on the other parameters, in ways that may not be immediately obvious.
) may have cascading effects on the other parameters, in ways that may not be immediately obvious.
These words of caution should not be taken to mean that the OU model cannot be used when one has no prior information, and I propose here a reparameterization of the OU model, building on that of Ho and Ané (2014), that seems to behave nicely all along the BM–WN continuum.
The OU model is reparameterized in terms of parameters that are fully identifiable, and for which I think we can easily set a meaningful prior distribution. These parameters are  , the expected tip trait value
, the expected tip trait value 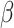 (see Ho and Ané 2014), and the variance of tip traits
(see Ho and Ané 2014), and the variance of tip traits  . Appendix 10 of the Supplementary material available on Dryad shows how these three parameters are sufficient information for calculating the OU likelihood, and how the parameters
. Appendix 10 of the Supplementary material available on Dryad shows how these three parameters are sufficient information for calculating the OU likelihood, and how the parameters 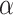 and
and  can be deduced from these new parameters. Given the nonidentifiability of
can be deduced from these new parameters. Given the nonidentifiability of  and
and  , it is necessary to further assume a value for
, it is necessary to further assume a value for  to deduce a value for
to deduce a value for 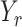 , or vice versa. But, this is only necessary for those who are specifically interested in these parameters.
, or vice versa. But, this is only necessary for those who are specifically interested in these parameters.
We have seen above the meaning of  , and a uniform prior distribution for
, and a uniform prior distribution for  between 0 and 1 blends trait trajectories ranging from flat (BM) to steep (WN), expressing our prior ignorance about the net effect of selection. Some investigators may prefer using a beta prior for
between 0 and 1 blends trait trajectories ranging from flat (BM) to steep (WN), expressing our prior ignorance about the net effect of selection. Some investigators may prefer using a beta prior for  and play around with the parameters to adjust the prior mix of trait trajectories as they see fit.
and play around with the parameters to adjust the prior mix of trait trajectories as they see fit.
Parameter  should be estimated to lie somewhere around the sample mean
should be estimated to lie somewhere around the sample mean 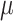 of tip trait values. It is thus logical to choose a prior for
of tip trait values. It is thus logical to choose a prior for  that is centered around
that is centered around 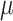 . A normal distribution with mean
. A normal distribution with mean  and a standard deviation equal to two times the sample standard deviation should do nicely, allowing the estimate of
and a standard deviation equal to two times the sample standard deviation should do nicely, allowing the estimate of  to deviate substantially from
to deviate substantially from  .
.
For high values of  , covariances of trait values among species are close to 0, so that
, covariances of trait values among species are close to 0, so that  should be estimated close to the sample variance
should be estimated close to the sample variance 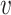 of tip traits. For low values of
of tip traits. For low values of  , due to higher covariances,
, due to higher covariances, 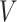 is expected to be greater than
is expected to be greater than  . Appendix 10 of the Supplementary material available on Dryad shows that values of
. Appendix 10 of the Supplementary material available on Dryad shows that values of  higher than
higher than  are highly unlikely. A log-normal prior for
are highly unlikely. A log-normal prior for  with a mode at
with a mode at  and a standard deviation on the log scale equal to 0.5 (which has most of the density between 0 and
and a standard deviation on the log scale equal to 0.5 (which has most of the density between 0 and  ) should thus be appropriate.
) should thus be appropriate.
To assess the behavior of this reparameterization, it was applied to the same simulated data sets as above (simulated under BM or WN, with a single selective optimum). Figure 7 shows an overall good coverage, for both BM- or WN-simulated data sets, suggesting that the reparameterization is a sensible way to use the OU model in the absence of prior information.
Figure 7.
Marginal posterior densities obtained with the reparameterized OU model. a) Posterior of 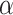 , directly comparable to Figure 4a. b) Posterior of
, directly comparable to Figure 4a. b) Posterior of 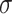 , comparable to Figure 4b, except here
, comparable to Figure 4b, except here  is unscaled for comparison with the true value. c) Posterior of
is unscaled for comparison with the true value. c) Posterior of  . d) Posterior of
. d) Posterior of  (unscaled). e) Posterior of
(unscaled). e) Posterior of  (unscaled). The data sets used here are a subset of those used for Figure 4: 5 BM (
(unscaled). The data sets used here are a subset of those used for Figure 4: 5 BM ( ) and 5 WN (
) and 5 WN ( ) data sets. The vertical lines show the true values of the parameters. The prior for
) data sets. The vertical lines show the true values of the parameters. The prior for  was a uniform distribution. The prior for
was a uniform distribution. The prior for  was a normal distribution centered around the sample mean of tip traits and SD of 2. Two priors were considered for
was a normal distribution centered around the sample mean of tip traits and SD of 2. Two priors were considered for  , consisting of log-normal distributions with a mode at the sample variance of tip traits, and with an SD on the log scale of 0.5 (solid curves) or 2 (dashed curves).
, consisting of log-normal distributions with a mode at the sample variance of tip traits, and with an SD on the log scale of 0.5 (solid curves) or 2 (dashed curves).  and
and  are not parameters of the reparameterized OU model, and their values were deduced a posteriori from the values of
are not parameters of the reparameterized OU model, and their values were deduced a posteriori from the values of  ,
, 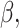 and
and  (see Appendix 10 of the Supplementary material available on Dryad).
(see Appendix 10 of the Supplementary material available on Dryad).
Appendix 11 of the Supplementary material available on Dryad provides a RevBayes script to implement this reparameterization, fully or partially: investigators can choose between setting a prior on  ,
,  or
or  ; on
; on  alone or on any combination of two parameters among
alone or on any combination of two parameters among  ,
,  and
and  ; on
; on  ,
,  or
or 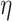 (the stationary variance). Notice that, based on Ho and Ané (2014), I suspect that the same type of reparameterization could be used for Hansen’s model for regimes applying to connected subtrees, albeit with several values of
(the stationary variance). Notice that, based on Ho and Ané (2014), I suspect that the same type of reparameterization could be used for Hansen’s model for regimes applying to connected subtrees, albeit with several values of  for the different regimes.
for the different regimes.
Conclusion
Bayesian inference with the OU model may behave in an unexpected manner due to complex interactions among parameters, caused by ridges in the likelihood function. In this context, investigators should be aware that some of their conclusions are highly dependent on the chosen priors. In particular, the value of the parameter  (related to the parameter
(related to the parameter 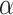 for the strength of selection and to tree height), which conveys a sense of the relevance of selection in determining trait values, largely determines the outcome of inference, whatever its purpose (i.e., estimate the strength of selection, ancestral traits, the neutral rate of evolution, compare models with or without selection, assess the impact of a trait on another, etc...). I hope that this article can entice investigators to cautiously consider the priors they use when using the OU model. I think that despite these potential pitfalls, investigators who have little prior information about the parameters should not be discouraged to carry out OU inference, for even in this situation comparative data can still provide useful insights into trait evolution. It seems that the proposed reparameterization of the OU model may help achieve this, or at least be a good tool for safety check.
for the strength of selection and to tree height), which conveys a sense of the relevance of selection in determining trait values, largely determines the outcome of inference, whatever its purpose (i.e., estimate the strength of selection, ancestral traits, the neutral rate of evolution, compare models with or without selection, assess the impact of a trait on another, etc...). I hope that this article can entice investigators to cautiously consider the priors they use when using the OU model. I think that despite these potential pitfalls, investigators who have little prior information about the parameters should not be discouraged to carry out OU inference, for even in this situation comparative data can still provide useful insights into trait evolution. It seems that the proposed reparameterization of the OU model may help achieve this, or at least be a good tool for safety check.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No. 708207. I thank Michael Landis, Michael May, Josef Uyeda, and the associate editor Sebastian Höhna for their very constructive comments on this article.
Supplementary material
Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.vdncjsxrc.
References
- Ané C. 2008. Analysis of comparative data with hierarchical autocorrelation. Ann. Appl. Stat. 2(3):1078–1102. [Google Scholar]
- Ané C., Ho L.S.T., Roch S.. 2017. Phase transition on the convergence rate of parameter estimation under an Ornstein-Uhlenbeck diffusion on a tree. J. Math. Biol. 74(1):355–385. [DOI] [PubMed] [Google Scholar]
- Beaulieu J.M., Jhwueng D.-C., Boettiger C., O’Meara B.C.. 2012. Modeling stabilizing selection: expanding the Ornstein-Uhlenbeck model of adaptive evolution. Evolution 66(8):2369–2383. [DOI] [PubMed] [Google Scholar]
- Blomberg S.P., Garland T.J., Ives A.R.. 2003. Testing for phylogenetic signal in comparative data: behavioral traits are more labile. Evolution 57(4):717–745. [DOI] [PubMed] [Google Scholar]
- Boettiger C., Coop G., Ralph P. (2012). Is your phylogeny informative? Measuring the power of comparative methods. Evolution 66(7):2240–2251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokma F. 2002. Detection of punctuated equilibrium from molecular phylogenies. J. Evol. Biol. 15(6):1048–1056. [Google Scholar]
- Butler M.A., King A.A.. 2004. Phylogenetic comparative analysis: a modeling approach for adaptive evolution. Am. Nat. 164(6):683–695. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza L.L., Edwards A.W.. 1967. Phylogenetic analysis: models and estimation procedures. Evolution 21(3):550–570. [DOI] [PubMed] [Google Scholar]
- Collar D.C., O’Meara B.C., Wainwright P.C., Near T.J.. 2009. Piscivory limits diversification of feeding morphology in centrarchid fishes. Evolution 63(6):1557–1573. [DOI] [PubMed] [Google Scholar]
- Cooper N., Thomas G.H., Venditti C., Meade A., Freckleton R.P.. 2016. A cautionary note on the use of Ornstein–Uhlenbeck models in macroevolutionary studies. Biol. J. Linnean Soc. 118(1):64–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cressler C.E., Butler M.A., King A.A.. 2015. Detecting adaptive evolution in phylogenetic comparative analysis using the Ornstein-Uhlenbeck model. Syst. Biol. 64(6):953–968. [DOI] [PubMed] [Google Scholar]
- Cuff A.R., Randau M., Head J., Hutchinson J.R., Pierce S.E., Goswami A.. 2015. Big cat, small cat: reconstructing body size evolution in living and extinct Felidae. J. Evol. Biol. 28(8):1516–1525. [DOI] [PubMed] [Google Scholar]
- Davis R., Javoiš J., Pienaar J., Õunap E., Tammaru T.. 2012. Disentangling determinants of egg size in the Geometridae (Lepidoptera) using an advanced phylogenetic comparative method. J. Evol. Biol. 25(1):210–219. [DOI] [PubMed] [Google Scholar]
- Eastman J.M., Alfaro M.E., Joyce P., Hipp A.L., Harmon L.J.. 2011. A novel comparative method for identifying shifts in the rate of character evolution on trees. Evolution 65(12):3578–3589. [DOI] [PubMed] [Google Scholar]
- Elliot M.G., Mooers A.Ø.. 2014. Inferring ancestral states without assuming neutrality or gradualism using a stable model of continuous character evolution. BMC Evol. Biol. 14:226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. 1973. Maximum-likelihood estimation of evolutionary trees from continuous characters. Am. J. Hum. Genetics 25(5):471–492. [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. 1985. Phylogenies and the comparative method. Am. Nat. 125(1):1–15. [Google Scholar]
- Felsenstein J. 1988. Phylogenies and quantitative characters. Annu. Rev. Ecol. Syst. 19(1):445–471. [Google Scholar]
- Freckleton R.P., Harvey P.H.. 2006. Detecting non-Brownian trait evolution in adaptive radiations. PLoS Biol. 4(11):e373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gohli J., Voje K.L.. 2016. An interspecific assessment of Bergmann’s rule in 22 mammalian families. BMC Evol. Biol. 16(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafen A. 1989. The phylogenetic regression. Philos. Trans. R. Soc. Lond. B 326(1233):119–157. [DOI] [PubMed] [Google Scholar]
- Hansen T.F. 1997. Stabilizing selection and the comparative analysis of adaptation. Evolution 51(5):1341–1351. [DOI] [PubMed] [Google Scholar]
- Hansen T.F., Martins E.P.. 1996. Translating between microevolutionary process and macroevolutionary patterns: the correlation structure of interspecific data. Evolution 50(4):1404–1417. [DOI] [PubMed] [Google Scholar]
- Hansen T.F., Pienaar J., Orzack S.H.. 2008. A comparative method for studying adaptation to a randomly evolving environment. Evolution 62(8):1965–1977. [DOI] [PubMed] [Google Scholar]
- Harmon L.J., Losos J.B., Davies T.J., Gillespie R.G., Gittleman J.L., Jennings W.B., Kozak K.H., McPeek M.A., Moreno-Roark F., Near T.J., Purvis A., Ricklefs R.E., Schluter D., Schulte J.A. II, Seehausen O., Sidlauskas B.L., Torres-Carvajal O., Weir J.T., Mooers A.Ø. 2010. Early bursts of body size and shape evolution are rare in comparative data. Evolution 64(8):2385–2396. [DOI] [PubMed] [Google Scholar]
- Harmon L.J., Weir J.T., Brock C.D., Glor R.E., Challenger W.. 2008. GEIGER: investigating evolutionary radiations. Bioinformatics 24(1):129–131. [DOI] [PubMed] [Google Scholar]
- Ho L.S.T., Ané C.. 2013. Asymptotic theory with hierarchical autocorrelation: Ornstein-Uhlenbeck tree models. Ann. Stat. 41(2):957–981. [Google Scholar]
- Ho L.S.T., Ané C.. 2014. Intrinsic inference difficulties for trait evolution with Ornstein-Uhlenbeck models. Methods Ecol. Evol. 5(11):1133–1146. [Google Scholar]
- Höhna S., Landis M.J., Heath T.A., Boussau B., Lartillot N., Moore B.R., Huelsenbeck J.P., Ronquist F.. 2016. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol. 65(4):726–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingram T., Mahler D.L.. 2013. SURFACE: detecting convergent evolution from comparative data by fitting Ornstein-Uhlenbeck models with stepwise Akaike Information Criterion. Methods Ecol. Evol. 4(5):416–425. [Google Scholar]
- Jones K.E., Smaers J.B., Goswami A.. 2015. Impact of the terrestrial-aquatic transition on disparity and rates of evolution in the carnivoran skull. BMC Evol. Biol. 15(1):8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kratsch C., McHardy A.C.. 2014. RidgeRace: ridge regression for continuous ancestral character estimation on phylogenetic trees. Bioinformatics 30(17):i527–i533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande R. 1976. Natural selection and random genetic drift in phenotypic evolution. Evolution 30(2):314–334. [DOI] [PubMed] [Google Scholar]
- Landis M.J., Schraiber J.G., Liang M.. 2013. Phylogenetic analysis using Lévy processes: finding jumps in the evolution of continuous traits. Syst. Biol. 62(2):193–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lattenkamp E.Z., Nagy M., Drexl M., Vernes S.C., Wiegrebe L., Knörnschild M.. 2021. Hearing sensitivity and amplitude coding in bats are differentially shaped by echolocation calls and social calls. Proc. R. Soc. B 288(1942):20202600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemey P., Rambaut A., Welch J.J., Suchard M.A.. 2010. Phylogeography takes a relaxed random walk in continuous space and time. Mol. Biol. Evol. 27(8):1877–1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin C.H. 2016. The cryptic origins of evolutionary novelty: 1000-fold faster trophic diversification rates without increased ecological opportunity or hybrid swarm. Evolution 70(11):2504–2519. [DOI] [PubMed] [Google Scholar]
- Martins E.P. 1994. Estimating the rate of phenotypic evolution from comparative data. Am. Nat. 144(2):193–209. [Google Scholar]
- Martins E.P., Hansen T.F.. 1997. Phylogenies and the comparative method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. Am. Nat. 149(4):646–667. [Google Scholar]
- May M.R. 2019a. Relaxed Ornstein-Uhlenbeck models. Available from: https://revbayes.github.io/tutorials/cont_traits/relaxed_ou.html.
- May M.R. 2019b. Simple Ornstein-Uhlenbeck models. Available from: https://revbayes.github.io/tutorials/cont_traits/simple_ou.html.
- Meseguer A.S., Lobo J.M., Cornuault J., Beerling D., Ruhfel B.R., Davis C.C., Jousselin E., Sanmartín I.. 2018. Reconstructing deep-time palaeoclimate legacies in the clusioid Malpighiales unveils their role in the evolution and extinction of the boreotropical flora. Global Ecol. Biogeogr. 27(5):616–628. [Google Scholar]
- Mitov V., Stadler T.. 2017. Fast and robust inference of phylogenetic ornstein-uhlenbeck models using parallel likelihood calculation. bioRxiv, p. 115089. 10.1101/115089. [DOI]
- O’Meara B.C., Ané C., Sanderson M.J., Wainwright P.C.. 2006. Testing for different rates of continuous trait evolution using likelihood. Evolution 60(5):922–933. [PubMed] [Google Scholar]
- Paradis E., Claude J., Strimmer K. (2004). APE: analyses of phylogenetics and evolution in R language. Bioinformatics 20(2):289–290. [DOI] [PubMed] [Google Scholar]
- Revell L.J. 2012. phytools: an R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 3(2):217–223. [Google Scholar]
- Revell L.J., Collar D.C.. 2009. Phylogenetic analysis of the evolutionary correlation using likelihood. Evolution 63(4):1090–1100. [DOI] [PubMed] [Google Scholar]
- Revell L.J., Harmon L.J.. 2008. Testing quantitative genetic hypotheses about the evolutionary rate matrix for continuous characters. Evol. Ecol. Res. 10(3):311–331. [Google Scholar]
- Solbakken M.H., Voje K.L., Jakobsen K.S., Jentoft S.. 2017. Linking species habitat and past palaeoclimatic events to evolution of the teleost innate immune system. Proc. R. Soc. B 284(1853):20162810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyeda J.C., Hansen T.F., Arnold S.J., Pienaar J.. 2011. The million-year wait for macroevolutionary bursts. Proc. Natl. Acad. Sci. USA 108(38):15908–15913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyeda J.C., Harmon L.J.. 2014. A novel Bayesian method for inferring and interpreting the dynamics of adaptive landscapes from phylogenetic comparative data. Syst. Biol. 63(6):902–918. [DOI] [PubMed] [Google Scholar]
- Uyeda J.C., Pennell M.W., Miller E.T., Maia R., McClain C.R.. 2017. The evolution of energetic scaling across the vertebrate tree of life. Am. Nat. 190(2):185–199. [DOI] [PubMed] [Google Scholar]
- Vining A.Q., Nunn C.L.. 2016. Evolutionary change in physiological phenotypes along the human lineage. Evol. Med. Public Health 2016(1):312–324. [DOI] [PMC free article] [PubMed] [Google Scholar]