The Occurrence Birth–Death Process for Combined-Evidence Analysis in Macroevolution and Epidemiology

Abstract

Phylodynamic models generally aim at jointly inferring phylogenetic relationships, model parameters, and more recently, the number of lineages through time, based on molecular sequence data. In the fields of epidemiology and macroevolution, these models can be used to estimate, respectively, the past number of infected individuals (prevalence) or the past number of species (paleodiversity) through time. Recent years have seen the development of “total-evidence” analyses, which combine molecular and morphological data from extant and past sampled individuals in a unified Bayesian inference framework. Even sampled individuals characterized only by their sampling time, that is, lacking morphological and molecular data, which we call occurrences, provide invaluable information to estimate the past number of lineages. Here, we present new methodological developments around the fossilized birth–death process enabling us to (i) incorporate occurrence data in the likelihood function; (ii) consider piecewise-constant birth, death, and sampling rates; and (iii) estimate the past number of lineages, with or without knowledge of the underlying tree. We implement our method in the RevBayes software environment, enabling its use along with a large set of models of molecular and morphological evolution, and validate the inference workflow using simulations under a wide range of conditions. We finally illustrate our new implementation using two empirical data sets stemming from the fields of epidemiology and macroevolution. In epidemiology, we infer the prevalence of the coronavirus disease 2019 outbreak on the Diamond Princess ship, by taking into account jointly the case count record (occurrences) along with viral sequences for a fraction of infected individuals. In macroevolution, we infer the diversity trajectory of cetaceans using molecular and morphological data from extant taxa, morphological data from fossils, as well as numerous fossil occurrences. The joint modeling of occurrences and trees holds the promise to further bridge the gap between traditional epidemiology and pathogen genomics, as well as paleontology and molecular phylogenetics. [Birth–death model; epidemiology; fossils; macroevolution; occurrences; phylogenetics; skyline.]

Introduction

Birth–death processes are stochastic processes used to model population dynamics with two main parameters, the birth rate and the death rate, which are respectively the rate at which new lineages appear, and the rate at which lineages are removed from the process. In macroevolution, these two rates correspond to the speciation and extinction rates, while in epidemiology they correspond to the transmission and recovery rates. These processes already enjoy a long history of applications in evolutionary biology. In the first half of the 20th century, Yule (1925) introduces them in the field with macroevolutionary applications in mind, to model the number of species within genera. Kendall (1948) then derives analytically the transition probabilities for linear birth–death processes, and discusses their use in the context of evolutionary biology, with a special focus on epidemiology. Ground-breaking work by Nee et al. (1994) followed on the probability density of the reconstructed tree in a linear birth–death process, that is, the tree obtained by pruning all extinct lineages from the full genealogical history of the process (see Fig. 1b). The linear birth–death process was then later extended to allow rates to vary in different parts of the tree (Alfaro et al. 2009), over time (Morlon et al. 2011), or depending on some character of interest (Maddison et al. 2007).

Figure 1.

Different approaches to infer past history and number of lineages. a) The full unknown history of the population. Different types of data can be used in order to infer the past history of the population. b) Genetic sequencing data and character data for present-day individuals only. c) Enriched tree with past samples with documented character data (represented as diverse ammonite morphs). d) Occurrences alone (represented as all ammonite fossils indistinctly). Finally, e) a more comprehensive total-evidence method integrates extant genetic sequences, samples with character data, and occurrences in a unified framework.

Although diversification histories inferred from extant species sometimes agree with those inferred from the fossil record (Morlon et al. 2011; Xing et al. 2014; Silvestro et al. 2018), there remains a gap between these two approaches in macroevolution (Marshall 2017). On the one hand, extant species provide invaluable information regarding the dynamics of the diversification process, especially close to the present. On the other hand, the fossil record, albeit incomplete, could much better inform extinction estimates (Quental and Marshall 2010). An extension introduced by Stadler (2010) and dubbed the Fossilized Birth–Death Process (FBDP) (Heath et al. 2014) aimed at jointly modeling extant and extinct taxa along the same tree, and thus helped bridge the gap between paleontology and molecular phylogenetics. In this model, each species can be sampled and included in the reconstructed tree throughout its lifetime at a fixed rate (see Fig. 1c). The probability density of the resulting phylogeny is derived in closed-form and has been successfully used as a prior in Bayesian phylogenetic analyses to study the diversification history of hymenopterans (Zhang et al. 2015), as well as the penguins (Gavryushkina et al. 2016). The same model has also been used in the context of epidemiology, where infected individuals can as well be sampled throughout the infectious period and be included in the reconstructed tree (Stadler et al. 2013). Finally, model extensions have been introduced to explicitly take into account stratigraphic ranges (i.e., the interval between the first and the last fossil appearance of a species) or, in the context of epidemiology, patient-specific durations of infection (Stadler et al. 2018). Although we focus here on the birth–death modeling framework, we note that an alternative line of the phylogenetic literature has evolved in parallel around the coalescent framework, following pioneering work in population genetics by Kingman (1982). Models and methods have been developed in coalescent models as well to incorporate sampling through time (Drummond et al. 2002; Parag et al. 2020).

An important feature of many standard paleontological data sets is that only a fraction of fossils have been thoroughly described and are associated with morphological data. Similarly, in standard epidemiological surveys, only a fraction of the recorded case count data is typically sequenced. In this article, we call samples with character data the subset of samples with either morphological data or molecular data, and occurrences the recorded samples without character data, which contain valuable information regarding the underlying number of lineages (see Fig. 1d). For this reason, they have long been used in paleontology to infer diversity trajectories (Raup 1972; Sepkoski et al. 1981), and even preservation, origination, and extinction rates in an alternative Bayesian setting (Silvestro et al. 2014; Silvestro et al. 2019). Some authors have analyzed occurrences in the standard FBD-based Bayesian framework, considering them as leaves in the tree with missing character data, and integrating over the unknown topology, in a paleontogogical (Heath et al. 2014; Gavryushkina et al. 2014; O’Reilly and Donoghue 2020) or epidemiological (Featherstone et al. 2021) context. Applying the standard FBD model in this case implicitly means that both samples with character data and occurrence data are assumed to have been generated under the same process, with the same rates. A second step towards integrating these occurrences was performed by Vaughan et al. (2019), who explicitly modeled an additional sampling process for occurrences, allowing for the joint analysis of the observation of a phylogeny and a record of occurrences (see Fig. 1e). Vaughan et al. (2019) additionally proposed an inference framework based on the use of a particle filter to compute the likelihood. Rasmussen et al. (2011) present another method based on a particle filtering algorithm to consider occurrences and trees in tandem, although in a coalescent framework instead of a birth-death framework. Gupta et al. (2020) then built on previous work by Vaughan et al. (2019) and described soon after a fast algorithm to compute the likelihood of the data, focusing on a special case of the model where all lineages sampled through time are removed from the process upon sampling. Finally, Manceau et al. (2021) presented a method to compute the distribution of number of lineages conditioned on a reconstructed tree and a record of occurrences.

In this article, we extend these last two methods to include piecewise-constant parameters, allowing us to explicitly incorporate known variation in birth, death, and sampling rates through time. We implement our work as a new distribution, coined the occurrence birth–death process (OBDP), available in the Bayesian phylogenetic software RevBayes (Höhna et al. 2016) to compute the joint probability density of a tree and a record of occurrences. This can readily be used to sample the posterior of trees and the number of lineages through time, given an observed record of occurrences and a list of samples with character data attached. We illustrate the versatility of the method on two empirical data sets coming from the fields of epidemiology and macroevolution. In epidemiology, we infer the prevalence through time for the coronavirus disease 2019 (COVID-19) outbreak on the Diamond Princess cruise ship, based on the joint observation of molecular sequences and case count data. In macroevolution, we infer the diversity through time in the cetacean clade, based on the joint observation of molecular data for extant species, morphological character data for some fossils and some extant species, and the record of fossil occurrences available on the Paleobiology Database.

Materials and Methods

Phylodynamic Model

We consider that a population of individuals starts at the time of origin with one lineage, and evolves through time under a birth–death process with piecewise constant birth rate, , and death rate, 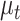. Three different sampling schemes are simultaneously applied along the process. First, individuals can be sampled through time and be included in the tree, with piecewise-constant sampling rate . Second, they can be sampled through time as raw occurrences not included in the tree, with piecewise-constant sampling rate 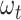. Third, lineages reaching the present time are included in the tree with a fixed probability 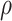. Finally, upon sampling, lineages are removed with a piecewise-constant probability of removal 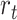. Note that time 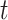is thus assumed to run backwards from 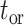to .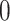

As a result of these three sampling steps, we observe a reconstructed tree , which is the tree spanning all 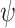-sampled and -sampled individuals, as well as a record of occurrences 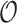, which is a timeline recording successive -sampling events. We aim at (i) computing the probability density of , which will play the role of the phylodynamic likelihood in our Bayesian framework and (ii) compute the probability distribution of the total number of lineages in the process at time , , conditioned on the observed . Note that the number of lineages in at time 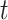, denoted 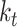, is an obvious lower bound of the total number of lineages in the process at time , 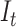. For this reason, we are targeting the probability distribution 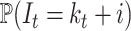, where stands for the number of hidden lineages.

In our Supplementary Appendix available on Dryad at https://doi.org/10.5061/dryad.p8cz8w9rq, we extend the method introduced by Manceau et al. (2021) to include piecewise-constant parameters in computing two quantities. First, defining 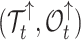as the tree and record of occurrences constrained to 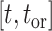, we aim at numerically computing the joint probability of the partial tree and occurrence record between time 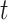and the origin, and the total number of lineages at time ,

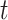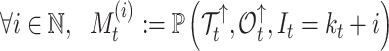(1)

which can be used to compute, upon reaching present day , .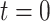

Second, defining 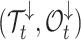as the tree and record of occurrences constrained to 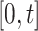, we aim at numerically computing the probability of the partial tree and occurrence record between time 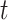and the present, conditioned on the total number of lineages at time ,

(2)

which can as well be used to compute, upon reaching the time of origin , .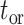

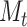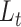We derive initializing conditions and Master equations governing the evolution of and through time and compute these quantities by numerically evaluating the system ordinary differential equations (Supplementary Appendix available on Dryad). Note that in this numerical evaluation we have to make one approximation, namely to assume a maximal number of lineages 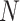(while it could in theory become arbitrarily large). In practice, 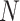must be chosen large enough to cover most of the high-density support of the and 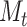probability distributions to avoid biasing calculations.

Finally, provided we know both quantities at time 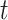, the probability distribution 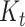of the number of hidden lineages living at time is given by,

(3)

where, in the last step, the first probability simplifies to 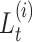thanks to the Markov property of the process. We summarize all the notation introduced above in Table 1.

Table 1.

Parameters and objects of the occurrence birth–death process

Parameter	Signification		Object	Signification
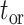
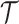
	Time of origin			Reconstructed tree
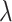
	Speciation rate			Record of occurrence times
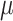
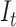
	Extinction rate			Total number of lineages
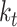
	Fossil sampling rate			Number of sampled lineages
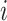
	Occurrence sampling rate			Number of hidden lineages
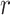
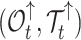
	Removal probability at sampling			Occurrences and tree before time t
	Sampling probability at present			Occurrences and subtrees after time t

Bayesian inference framework

We consider a Bayesian inference framework with additional model layers for character data evolution along the reconstructed tree 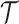. For epidemiological applications, we superimpose a model of molecular evolution, leading to the observation of a sequence alignment for both extant and extinct taxa in . For applications in macroevolution, we superimpose (i) a model of morphological evolution, leading to the observation of character data for both extant and extinct taxa in and (ii) a model of molecular evolution, leading to the observation of a sequence alignment for extant taxa only. 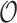We summarize all model parameters as , and all (molecular and morphological) character data as , noting that is independent of given the tree and parameters. Thus, the target posterior distribution of reconstructed trees and model parameters 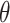can be written as the product of the phylodynamic likelihood, the likelihood of character data given and , and prior probabilities:

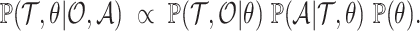(4)

First, we sample this posterior distribution using a Metropolis–Hastings Markov Chain Monte Carlo (MCMC). Second, the posterior probability distribution of the ancestral number of lineages can be written as,

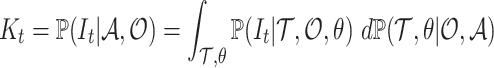(5)

and is thus numerically computed as the mean of 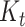over the trace of the posterior of .

Numerical Implementation

We implement our model in RevBayes (Höhna et al. 2016, 2017), an open-source software for Bayesian inference in phylogenetics. RevBayes is fully based on graphical models (Höhna et al. 2014), a unified framework for representing complex probabilistic models in the form of graphs where nodes correspond to model variables and edges to their probabilistic relationships. It allows the user to construct interactively their own phylogenetic graphical model in the Rev language, by combining hundreds of available models of nucleotide substitution, rate variation across sites and along the tree, and tree priors proposed in the literature (see Fig. 6(b) for an illustration with our model). Our three key additions consist of (i) introducing the OBDP distribution (Fig. 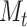6(a)) into RevBayes, so that it can be used by the community within other graphical models; (ii) implementing the core algorithms responsible for computing the quantities and through time and eventually the final log-likelihood; and (iii) including a function to generate the posterior probability distribution of the number of lineages through time.

Figure 6.

Inferred diversification history of Cetacea. a) Posterior probability distribution of the total number of genera over time. The credible intervals (2.5 and 97.5 quantiles) are indicated in dashed lines, the expected diversity with a solid green line and the inferred LTT in black. Periods of biotic or abiotic factors that are hypothesized to have driven diversification changes are adapted from Marx and Fordyce (2015) and shown for information but had no influence on the analysis. ACC = Antarctic Circumpolar Current. Black dots below represent the occurrences used in the analysis. b) Posterior means and credible intervals for extinction, origination, net diversification, and fossil sampling over time.

Figure 2 summarizes the full workflow to go from the raw data to the inferred reconstructed tree , model parameters , and diversity trajectories .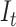

Figure 2.

Workflow for using the occurrence birth–death (OBD) model for diversity inference. One first needs to specify a graphical model with priors and provide some empirical (molecular, morphological, and occurrence) data. A MCMC chain is run to sample the posterior distribution of trees and parameters, using joint likelihood . Finally, these traces are used to compute the posterior distribution of the number of lineages through time ().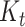

Validation of the Method

Direct likelihood comparison

We verify that the phylodynamic likelihood computed using or coincides with (i) previous RevBayes implementations (Höhna et al. 2017; Heath et al. 2019) of linear birth–death processes that are special cases of our framework, when no occurrences are included and and (ii) an earlier Python implementation of the likelihood with constant parameters (Manceau et al. 2021). We use a small fixed data set and compute the likelihood using (i), (ii), and our implementation, under a wide range of parameters which are listed in Figure 3.

Figure 3.

Validation of the likelihood calculation. Each parameter is varying a–f) while keeping the others at their baseline values h) and evaluating the likelihood of the toy data set i) where occurrences are shown on the right, and both samples at present and in the past are present on the tree. Filled dots are removed samples, unfilled are not removed. For all parameters a–f), our RevBayes implementation is compared to the Python code provided in Manceau et al. (2021) and whenever possible b, c, e, f), to earlier implementations of the FBDP available in RevBayes, fixing 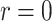, 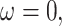and .

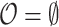Quantitative validation of the MCMC implementation

We follow a procedure called simulation-based calibration (Talts et al. 2018) for validating our MCMC implementation. It consists in the following three steps: (i) we define priors (Table 2) for all the involved parameters and simulate 1000 parameter sets in Python, trees with sampled fossils, occurrences, and genetic sequences (100 nucleotides long), conditioning on the survival of at least two lineages to the present; (ii) for each simulated data set, we use the same priors to infer the posterior distribution of reconstructed trees and parameters; and (iii) we compute the proportion of data sets for which the true (simulated) parameter values fall within a 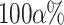credible interval of the posterior distribution, for a range of 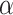values (19 evenly spaced between 0.05 and 0.95). If the MCMC is correctly sampling the posterior distribution, the proportion of posterior credible intervals recovering the truth should be close to .

Table 2.

Prior distributions of the OBDP parameters for the quantitative validation test

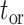
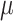
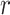
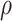
Parameter								Mutation rate
Prior or model

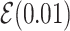
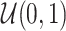
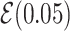
Note: for Uniform distribution with given lower and upper bound, for Exponential with given rate parameter. The model of molecular evolution is the Jukes–Cantor 1969 substitution model (JC69) with strict clock hypothesis.

For this analysis, is chosen for each simulation as the true maximum number of hidden lineages plus a margin of , to avoid unnecessary computations. In practice, this choice requires expert knowledge specific to each particular clade.

SARS-CoV-2 Data Analysis

Molecular and occurrence data set

We use the model implementation with piecewise constant rates to perform a phylodynamic analysis of the spread of SARS-CoV-2 aboard the Diamond Princess cruise ship, a well-documented outbreak from February 2020. The outbreak is an example of a closely monitored, geographically constrained closed population, and thus constitutes an ideal case study of the disease dynamics and the mitigation policies undertaken.

The sequenced data used for this analysis consists of a set of 70 full-length viral genomes collected between February 15th and February 17th, all acquired from GISAID (Shu and McCauley 2017). Acknowledgements for laboratories that contributed the genome sequences used in this analysis are given in Supplementary Appendix G available on Dryad. All available sequences were aligned to reference genome MN908947, and sites subject to low sequencing accuracy were masked. Following the standard NextStrain pipeline, sites 13402, 24389, and 24390 as well as 150 bases at the ends of the genomes were masked, thought to be sequencing artifacts that would bias the alignment (Hadfield et al. 2018).

In this example, we define occurrences as patients testing positive for SARS-CoV-2 using reverse-transcription polymerase chain-reaction (RT-PCR) viral detection methods. Daily reports of new cases and total number of samples tested were published by the Japanese Ministry of Work throughout the outbreak and later compiled in the COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (Dong et al. 2020). Out of all 712 cases detected amongst passengers, we focus on the 705 cases detected while guests were still aboard the cruise ship, from the beginning of the cruise on January 20th until February 27th. Sequencing dates and case counts were communicated as daily reports throughout the outbreak. For all report entries, exact dates were uniformly assigned to all occurrences within each day. Additionally, we shift dates by a day to account for the delay between sampling and reporting of the PCR results. The full data set, in its original and processed formats, is presented in Supplementary Figure S16 available on Dryad.

Model assumptions

The model parameterization allows us to examine two complementary aspects of the temporal change in epidemic spread. First, we estimate the effective reproductive number across all time intervals of interest. The reproductive number is the expected number of secondary cases produced by a single infected individual and is a standard epidemiological parameter, quantified in our model as , with rate parameter encompassing either patient recovery or death in this application. Second, we infer the corresponding prevalence trajectories, to bring insight into the total infectious population throughout the outbreak. This includes potentially undetected asymptomatic patients, which are thought to make up a significant proportion of the total infected population (Mizumoto et al. 2020).

To achieve these two goals, we make full use of the skyline implementation of our model by fixing independent shifts for different rate parameters. In doing so, we closely follow the exact timeline of events of the outbreak. The testing strategy was initiated by Japanese authorities after a first guest was confirmed positive for SARS-CoV-2 on February 3rd. It was then extended to asymptomatic passengers from February 11th onward. Sequencing of some of the viral samples was then performed between February 15th and February 17th. To these four sampling parameters shifts, we additionally introduce another shift for the birth rate 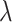before the start of mandatory cabin isolation, on February 5th, producing the full timeline of 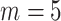intervals.

Reports of the total number of samples tested were assembled to adjust prior means for 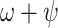on different time intervals and account for the extension of testing to asymptotic passengers. In total, testing efforts yielded 4066 samples over the entire period of interest, with 3622 of them being obtained after February 11th. All settings and priors used in this analysis are presented in detail in Supplementary Table S7 available on Dryad.

Cetacean Data Analysis

Context

Cetaceans are a group of marine mammals, represented by 89 living species, that possess a remarkable and well-studied fossil record (Fordyce 2009). Their history can be summarized by three main phases (Marx et al. 2016), (i) starting 53 Ma, a 10 myr land-to-sea transition accompanied by drastic morphological transformations in the archaeocetes (stem cetaceans), (ii) the emergence of neocetes (crown cetaceans, including filter-feeding mysticetes and echolocating odontocetes) at the Eocene–Oligocene boundary (34 Ma) and their radiation up to a Mid-Miocene peak (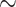12 Ma) followed by (iii) a sharp decline in diversity in the last 4–6 myr.

Several studies have already attempted to estimate the diversity trajectory of cetaceans, using the fossil record (Uhen and Pyenson 2007), molecular phylogenies (Morlon et al. 2011), or both (Marx and Fordyce 2015) but even the latter total-evidence study did not include all fossil occurrences in its analyses. Although the initial huge discrepancies between the history inferred from the fossil record and from molecular phylogenies (Quental and Marshall 2010) have been partially bridged, including occurrences may help further provide a more reliable time-calibrated tree and a robust diversity trajectory estimation.

Molecular, morphological, and occurrence data sets.

The data can be subdivided into three parts: molecular, morphological, and occurrences. Data sets were collected and analyzed separately and are stored on the Open Science Framework (https://osf.io) (Aguirre-Fernández et al. 2020). Molecular data come from Steeman et al. (2009) and comprises 6 mitochondrial and 9 nuclear genes, for 87 of the 89 accepted extant cetacean species. Morphological data were obtained from Churchill et al. (2018), the most recent version of a widely used data set first produced by Geisler and Sanders (2003). After merging 2 taxa that are now considered synonyms on the Paleobiology Database (PBDB) and removing 3 outgroups that would have violated our model’s assumptions, it now contains 327 variable morphological characters for 27 extant and 90 fossil taxa (mostly identified at the species level but 21 remain undescribed). In order to speed up the analysis, we further excluded the undescribed specimens and reduced this data set to the generic level by selecting the most complete specimen of each genus. Genus level has been the preferred unit of analysis in previous studies of cetacean diversity that include fossils (e.g., Marx and Uhen 2010; Dominici et al. 2020) since Uhen and Pyenson (2007) introduced it to counteract taxonomic inflation caused by the naming of extinct cetacean species based on fossil material of limited taxonomic value. Indeed, the computing cost increases rapidly with the maximum number of hidden lineages (see Supplementary Appendix Figure S12 available on Dryad), to the point of becoming the bottleneck in our MCMC when . Given that a mid-Miocene peak diversity between 100 and 220 species is expected (Quental and Marshall 2010), with less than 100 observed lineages in our inferred tree at that time, should therefore be about 150. Inferring instead the tree of cetacean genera allows us to reduce to 70 hidden lineages. The final data set thus contains 41 extant and 62 extinct genera.

Occurrences come from the PBDB (data archive 9, M. D. Uhen) on May 11, 2020. The data set initially consisted of all 4678 cetacean occurrences, but the cetacean fossil record is known to be subject to several biases (Uhen and Pyenson 2007; Marx and Uhen 2010; Dominici et al. 2020). A detailed exploration (see Supplementary Appendix F available on Dryad) of this occurrence data set revealed several notable biases. First, an artifactual cluster of occurrences in very recent times, combined with other expected Pleistocene biases (Dominici et al. 2020), led us to remove all Late Pleistocene and Holocene occurrences. Second, we detected substantial variations in fossil recovery per time unit across lineages (see Supplementary Fig. S13 available on Dryad) resulting from oversampling of some species and localities, possibly due to greater abundance or spatiotemporal biases (Dominici et al. 2020). This observation violates our assumption of identical fossil sampling rates among taxa during a given interval. In order to reduce this bias, we retained occurrences identified at the genus level and further aggregated all occurrences belonging to an identical genus found at the same geological formation. In the case of occurrences for which the geological formation was not specified, we used geoplate data combined with stratigraphic interval as a proxy for geological formation. This resulted in a total of 968 occurrences retained for the analysis.

Model assumptions

Each fossil comes along with a stratigraphic age uncertainty interval. Reducing this interval to either the midpoint, or a uniformly drawn point, has been shown to lead to serious biases in the divergence time estimates (Barido-Sottani et al. 2019). We instead follow the same procedure as Heath et al. (2019) and apply a uniform prior for the age of fossils with morphological characters, within the bounds of their stratigraphic age uncertainty. As a result, the age of a fossil included in the tree can slide within this interval during the MCMC.

Based on previous work showing huge discrepancies in mutation rates between odontocetes and mysticetes (Dornburg et al. 2012), and generally between nuclear and mitochondrial sequences (Allio et al. 2017) we considered a relaxed clock across the tree and partitioned between the two types of sequences. Much less biological knowledge is available about the dynamics of morphological characters (Wright 2019). We thus chose a minimal substitution model and partitioned the alignment in order to treat separately characters that are represented by a different number of states.

Moreover, we made the most of the piecewise-constant parameter framework to include 4four shifts in diversification and extinction rates at variable time points, using autocorrelated exponential priors in successive intervals. We also added shifts in fossilization rates in the Early Oligocene (Rupelian), Early Miocene (Aquitalian), and End Miocene (Messinian), in order to give more flexibility to the model during these geological periods of well-established low preservation (Marx et al. 2016). Additional flexibility could be introduced by increasing the number of rate shifts.

Finally, we added monophyly constraints on the mysticetes and odontocetes clades to further speed up the analysis.

All prior distributions are fully detailed in Supplementary Table S6 available on Dryad.

Results

Validation of the Method

Direct likelihood comparison

We illustrate in Figure 3 the perfect agreement with likelihood values computed using previous functions under a wide range of parameters, for both 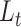and 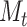traversal algorithms.

Quantitative validation of the MCMC implementation

Figure 4 shows a good correspondence between the proportion of posterior credible intervals containing the true parameter value and the width of the credible interval. This indicates that the MCMC is properly calibrated, that is, samples adequately the targeted posterior distribution (see Supplementary Appendix E available on Dryad for more details).

Figure 4.

Results of the simulation-based calibration. Each dot corresponds to the proportion of simulated parameters (y-axis) falling within its inferred posterior credible interval with a given level (x-axis). The black line corresponds to the expected perfect match.

Reproductive Number and Prevalence in the COVID Outbreak

Figure 5 shows the raw data, as well as the estimates of the total instantaneous prevalence and reproductive number through time.

Figure 5.

Analysis of the SARS-CoV-2 outbreak aboard the Diamond Princess cruise ship. a) Occurrence and sequenced data are plotted as daily new observations. We focus on infections detected while guests were still aboard, until the end of the harbor quarantine on February 27th. b) Posterior probability distribution of the instantaneous total infected population aboard the cruise ship. The credible intervals (2.5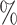 and 97.5 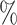quantiles) are indicated in dashed lines, the expected prevalence with a solid green line and the inferred lineages through time (LTT) in black. c) Mean estimates and 95 highest posterior density intervals (HPI) for the effective reproductive number () throughout a 38-day period starting at the beginning of the cruise.

The instantaneous prevalence is typically always slightly lower than the total number of new cases detected each day, or daily incidence. It also differs conceptually from the epidemiological prevalence in that detected cases are all assumed to be immediately removed from the infectious population upon sampling (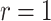) through quarantining measures. For public health applications, all patients still infected with the virus are generally counted into the prevalence.

The reproductive number is inferred with very high uncertainty in the beginning of the epidemic, when very few cases were observed, and with a much higher precision in the second part of the process. It decreases synchronously with the launching of nonpharmaceutical interventions in early February (i.e., testing effort and cabin quarantine).

Total Diversity in the Cetacean Clade

Figure 6a shows the inferred diversity of cetacean genera over the past 50 million years. The diversity curve indicates an Early-Eocene origin followed by a monotonous diversification up to a first Mid-Miocene peak (12 Ma), before reaching its maximum in the Pliocene (between 2.6 and 5.3 Ma) with more than 100 inferred genera. The last few million years correspond to a sharp decline leading to the 41 extant genera.

This diversification history is reflected in Figure 6b by a 55 myr trend of slightly decreasing genus origination rates (from 0.16 to 0.10 genera per myr) and increasing genus extinction rates (from 0.035 to 0.085 genera per myr). Then, from the Pliocene to the present, both rates increase drastically to around 0.25 genera per myr, and the diversification rate reaches a minimum (but still non-negative, as expected with a lognormal prior). In parallel, the background fossil sampling rate is estimated between 0.020 and 0.025 samples per lineage and per myr, and lower values are recovered in the three geological periods with expected lower sedimentary record (more details in the Discussion). The inferred phylogenetic timetree is shown in the Supplementary Appendix Figure S14 available on Dryad.

Discussion

Technical Achievements and Limitations

In this article, we extend the work of Gupta et al. (2020) and Manceau et al. (2021) to consider piecewise-constant rates through time, and implement the OBDP in the popular phylogenetic inference software RevBayes. This enables us to simultaneously incorporate numerous occurrences without character data, together with taxa for which we have genetic sequences and/or morphological characters. In addition to using the OBDP as a tree prior for inferring epidemiological or macroevolutionary parameters, tree topology and divergence dates, it allows users to compute the posterior probability distribution of the number of lineages through time, in a post-MCMC analysis (see workflow in Fig. 2). We validate the framework and illustrate its use in the fields of epidemiology and macroevolution.

The likelihood computation can be very fast when lineages become extinct upon sampling (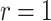), relying on the results of Gupta et al. (2020), for data sets containing relatively few occurrences (in the order of a 100). This advantage is lost when including larger numbers of occurrences but can be recovered with the ingenious approximation developed by Zarebski et al. (2022). In practice, the assumption that these implementations rely on (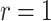) only makes sense for some epidemiological applications, when infected individuals can self-quarantine and be safely assumed to be removed from the process. For macroevolutionary applications, the 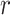parameter typically equals zero, and the likelihood computation relies on a more computationally intensive method to numerically solve Master equations (see details in Supplementary Appendix A available on Dryad). Supplementary Appendix Figure 12 available on Dryad provides an estimate of the run-time increase with N (on the order of min on a cluster) based on simulations. More work is thus needed to help speed up the likelihood computation when , on data sets for which a large number of hidden lineages is expected. This will be especially important for further applications in macroevolution and paleobiology, as many data sets feature thousands of fossils occurrences.

COVID-19 Diamond Princess Epidemic

The application of our method to the study of a thoroughly documented outbreak highlights the versatility of our model implementation. The ability to incorporate both incidence data and pathogen sequences, in combination with temporal information constitutes one of the first few instances of the use of a combined-evidence phylodynamic approach for the inference of epidemiological trajectories.

The conclusions that we draw from both our parameter estimates and the prevalence trajectory are consistent with other analyses. The basic reproductive number is inferred to be 4.01 in the absence of any intervention and detection, during the first 15 days of the cruise (see Fig. 5b), higher than most estimates for early global outbreaks (Lai et al. 2020; Nadeau et al. 2021). We then infer a decrease in reproductive number, which remains near or below 1 in the last 23 days of the time period of interest, suggesting that the epidemic was mostly contained by measures taken. These trends agree with other studies in magnitude, and although estimates ranging from 2.28 to 14.8 have been reported for the first time period, most analyses infer a reproductive number below 2 in the subsequent time periods (Hoshino et al. 2021; Zhang et al. 2020; Rocklöv et al. 2020). Interestingly, we note that in our results the decrease in reproductive number is driven by the sampling and removal of individuals from the infectious population, with the total sampling rate going up from 1.76 to 2.14 days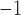, after February 11th (see Supplementary Fig. 17 available on Dryad for the detailed timeline). This extended sampling, which can be attributed to the decision to test asymptomatic passengers, results in occurrences strongly influencing the estimated instantaneous prevalence. This highlights the successful integration of both sequence and occurrence data, and the added value brought about by this new implementation.

Biases inherent to many epidemiological data sets indicate important areas for development. For instance, sampling of outbreaks is most often carried out with the aim of quickly monitoring the disease, without rigorously following a protocol. This can result in inconsistent sampling and reporting strategies, with gaps and/or missing data. We note for example that no new cases were reported between February 19th and February 22th. Although it is likely due to a delay in reporting or testing, we did not model a drop in sampling as no changes in the monitoring efforts were reported. Additionally, due to a 24 h reporting delay for this data set, the first detected case was originally placed after the start of the quarantine. We tried to meticulously remove as many such biases as possible, but our framework could also be improved in the future to explicitly account for these.

Other potential biases include the effect of population structure—the Diamond princess outbreak is likely to have spread in at least two distinct subpopulations: guests and crew members (Nishiura 2020)—and density dependence—the outbreak being in a closed, geographically constrained population (Rocklöv et al. 2020). Further developments of the method to cover these scenarios could provide even better insight into the dynamics of this outbreak.

Past Cetacean Diversity

Molecular and paleontological data come with their inherent limitations, for example, a lack of information about extinct lineages for the former and substantial spatiotemporal biases for the latter. Combining them into a single analysis may gather enough signal to mitigate these limitations, but special attention should be paid to model assumptions. We have endeavored to respect these constraints, by (i) correcting occurrence distribution sampling biases (see Supplementary Appendix E available on Dryad) and (ii) including skyline variation in diversification and preservation rates.

The emerging patterns of cetacean generic diversification in Figure 6 are consistent with previous estimates (Uhen and Pyenson 2007; Morlon et al. 2011; Marx and Fordyce 2015): (i) the “boom and bust” dynamics of prolonged diversification followed by a recent decline is recovered and (ii) estimated generic richness is higher than the incomplete raw generic counts, as expected. The diversification of cetaceans, starting in the Eocene and accelerating in the Neogene, has been associated by previous authors with the development of the Antarctic Circumpolar Current (ACC) that fueled a diatom radiation, via nutrient supply, prompting the diversification of bulk filtering cetaceans. The diversity drop in the last 4 myr has been linked to the global climate deterioration and the Northern Hemisphere glaciation, which coincides with the final establishment of modern mysticete gigantism and long-distance migration. Our inferred diversity trajectory (Fig. 6) is compatible with these hypotheses. On the other hand, the distinct second peak with maximum diversity in the Pliocene is unexpected and will require further investigation.

When it comes to the dated phylogeny, many of the deepest nodes are much older than what has been inferred previously in the literature. This observation could be explained by an unbalanced sampling of fossil genera included in the tree compared to fossil occurrences: 1–8–50 ratio of archaeocete–mysticete–odontocete specimens with character information versus a 1–2–8 ratio for occurrences (based on the PBDB taxonomy information). Indeed, the few archaeocete lineages included may then appear incoherent with the many Eocene occurrences, leading to an artificially early placement of the Neocete diversification. This pattern of differential preservation between younger and older lineages is to be expected and could be accounted for with increasing occurrence sampling rates over time. We therefore advise to account for similar sampling heterogeneity when performing similar analyses in the future. More broadly, simulations are required to examine in more detail the impact of spatiotemporal sampling biases (Close et al. 2020) on this and other approaches to estimating time tree and diversity.

New Avenues for Phylogenetics

Over the last decade, the field of phylogenetics has expanded considerably with the development of the FBDP and related extensions, of which the OBDP is the latest instance. As a result, the long-standing opposition between molecular-based and fossil-based macroevolutionary inferences is in the process of being bridged, and case count records can be analyzed jointly with sequencing data in epidemiology applications. Many extant clades with a relatively rich paleontological record—for example, turtles, sharks, and angiosperms—as well as outbreak surveillance data, could benefit from this new method to infer reliable phylogenies and diversity/prevalence trajectories.

Future progress could be made to couple birth rates with abiotic drivers, such as biogeography (see also work on multitype birth–death processes Scire et al. 2020), or biotic drivers such as density dependence (see also Etienne et al. 2012). Going even further down the mechanistic road for macroevolutionary applications, stratigraphic palaeobiology could even become an explicit part of diversification models, by considering the accumulation of sediments over finer time and spatial scales (Patzkowsky and Holland 2012). We anticipate that these approaches will all benefit from combining paleontological and molecular data.

Overall, our two empirical applications demonstrate that a phylogenetic framework can be successfully applied to recover both the past outbreak prevalence and the past paleodiversity. In contrast to alternative approaches, it maximizes the use of available evidence, since it uniquely allows us to combine genetic and morphological character data, together with occurrences. Further, our inference method relies on a generating model, incorporating explicit assumptions about the processes giving rise to our data, including sampling. We argue that it is prospectively more flexible than alternative approaches to mitigating sampling biases.

Supplementary Material

Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.p8cz8w9rq.

Funding

This work was supported by a Postdoctoral Fellowship funded by Eidgenossische Technische Hochschule Zurich to M.M.