Abstract

Integration of the sensitivity-relevant electronics of nuclear magnetic resonance (NMR) and electron spin resonance (ESR) spectrometers on a single chip is a promising approach to improve the limit of detection, especially for samples in the nanoliter and subnanoliter range. Here, we demonstrate the cointegration on a single silicon chip of the front-end electronics of NMR and ESR detectors. The excitation/detection planar spiral microcoils of the NMR and ESR detectors are concentric and interrogate the same sample volume. This combination of sensors allows one to perform dynamic nuclear polarization (DNP) experiments using a single-chip-integrated microsystem having an area of about 2 mm2. In particular, we report 1H DNP-enhanced NMR experiments on liquid samples having a volume of about 1 nL performed at 10.7 GHz(ESR)/16 MHz(NMR). NMR enhancements as large as 50 are achieved on TEMPOL/H2O solutions at room temperature. The use of state-of-the-art submicrometer integrated circuit technologies should allow the future extension of the single-chip DNP microsystem approach proposed here up the THz(ESR)/GHz(NMR) region, corresponding to the strongest static magnetic fields currently available. Particularly interesting is the possibility to create arrays of such sensors for parallel DNP-enhanced NMR spectroscopy of nanoliter and subnanoliter samples.
Nuclear magnetic resonance (NMR) spectroscopy is a powerful tool employed in research, industry, and medicine. The use of NMR methodologies in an even wider range of applications is often hindered by the relatively large minimum number of resonating spins needed to achieve a sufficiently large signal-to-noise ratio (SNR) in the available experimental time. In most of the situations studied by NMR spectroscopy the samples are concentration limited. In these conditions, the largest SNR is obtained with the largest possible sample volume compatible with the high-homogeneity region of the magnet at the strongest possible magnetic field. However, there are also situations where the sample is volume limited. For volume-limited samples, the use of an inductive detector having a sensitive volume matched to the volume of the sample under investigation results in a significant improvement of the SNR.1−12 For samples in the nanoliter and subnanoliter range, noninductive detection methods have been also proposed, such those based on nitrogen vacancies in diamond13−16 and magnetic resonance force microscopy.17−21 Another approach to increase the SNR, applicable to samples of any volume, is to increase the nuclear spin polarization, e.g., by microwave-, optical-, and chemistry-based methodologies.22−34 In the microwave DNP approach, the sample under investigation contains unpaired electron spins which are excited into electron spin resonance (ESR). The electron spin excitation allows one to enhance the nuclear magnetization of several orders of magnitude above its thermal value, improving the SNR in the NMR experiment by the same factor and reducing the required experimental time as the square of this factor.
During the last two decades, separate integration on a single chip of the front-end electronics of inductive NMR spectrometers35−49 as well as ESR spectrometers50−55 has been demonstrated. These approaches are suitable, e.g., for the miniaturization of the probe, for the reduction of the losses and complexity of the connections, and for the realization of dense arrays of detectors. In this work, we demonstrate the cointegration on a single silicon chip of the front-end electronics of NMR and ESR detectors. The excitation/detection planar spiral microcoils of the NMR and ESR detectors are concentric and interrogate the same sample volume. This combination of sensors allows one to perform dynamic nuclear polarization (DNP) experiments using a single-chip-integrated DNP microsystem having an area of about 2 mm2. In particular, we report 1H DNP experiments on liquid samples having a volume of about 1 nL performed at 10.7 GHz(ESR)/16 MHz(NMR). NMR enhancements as large as 50 are achieved on TEMPOL/H20 solutions at room temperature.
Description of the Single-Chip DNP Microsystem
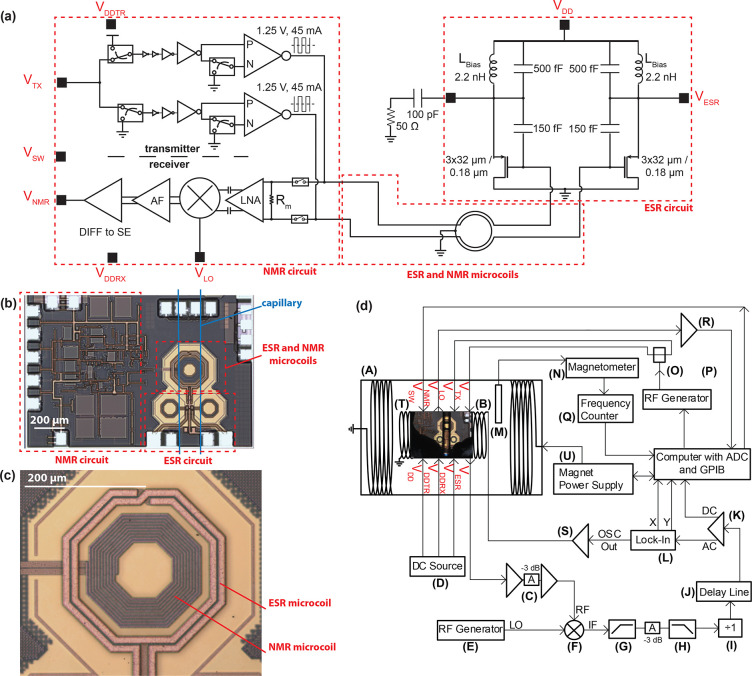
The single-chip DNP microsystem is composed of two parts: the ESR and NMR detectors (Figure 1a). The ESR- and NMR-integrated electronic circuits are very similar to those previously reported.42,54 The chip has a size of 1.1 × 1.6 mm2, and it is fabricated using a standard silicon CMOS technology (TSMC 180 nm, MS/RF). The NMR detector consists of a broadband (10 MHz to 1 GHz) transmit/receive electronic circuit directly connected (i.e., without tuning and matching capacitors) to an excitation/detection microcoil (Figure 1a). Since the NMR detector does not contain an rf source, it requires an external source to produce the 16 MHz rf signals for the local oscillator (VLO) and the transmitter (VTX). The rf signal VTX is amplified by the integrated transmitter rf electronics. When the integrated switch is in the transmit mode, a peak-to-peak rf voltage of about 2.5 V and a peak-to-peak rf current of about 90 mA is delivered to the NMR microcoil and the dissipated power in the NMR microcoil is 56 mW. When the switch is in the receive mode, the electromotive force induced in the NMR microcoil by the spin precession is amplified by an rf receiver amplifier (30 dB, from 10 MHz to 1 GHz), downconverted to the kHz range using an integrated mixer driven by the local oscillator signal, and further amplified by an additional integrated low-frequency amplifier (20 dB, dc to 1 MHz). The NMR microcoil is concentrically placed inside the ESR microcoil (Figure 1c). The two coupled concentric microcoils are simulated using a full-wave electromagnetic simulator (Advanced Design System ADS, Keysight Technologies). The obtained S-parameter files are used in an integrated circuits simulator (Cadence, Cadence Design Systems Inc.) to simulate both the ESR- and the NMR-integrated detectors. In these simulations, it is found that an NMR coil with more than 15 turns significantly reduces the quality factor of the ESR coil and quenches the oscillation of the ESR circuitry. This is qualitatively explained by the losses caused by the induced currents in the NMR coil. To keep a safety margin, the number of turns is reduced from 22 to 10 and the outer diameter is shrunk with respect to the NMR microcoil of the previous design.42 The reduction of the number of turns and the outer diameter reduces the inductance from 150 to 17 nH and the series resistance from 110 to 30 Ω. The NMR microcoil has an external diameter of 191 μm, a wire width of 3 μm, a wire thickness 2.3 μm, and a spacing of 2 μm between turns (Figure 1c). The dc power consumption of the NMR system is 170 mW in the transmit mode and 40 mW in the receive mode.
Figure 1.
Set-up for characterization of the single-chip-integrated DNP microsystem operating at 10.7 GHz(ESR)/16 MHz(NMR). (a) Schematic of the single-chip DNP microsystem. Dashed red lines indicate the NMR/ESR circuits and the concentric NMR/ESR microcoils. Black squares next to the port names represent the bonding pads. VDDTR, VDDRX, and VSW ports are connected to several nets, and their connections are not shown in the schematic for simplicity. VDDTR and VDDRX are the supply voltages of all of the blocks in the transmitter and receiver of the NMR circuit, respectively. VSW is the control signal that is connected to all of the switches in both the transmitter and the receiver of the NMR circuit. (b) Photograph of the single-chip DNP microsystem. Blue lines indicate the position of the capillary containing the sample under investigation. Dashed red lines indicate the NMR/ESR circuits and the concentric NMR/ESR microcoils as in a. (c) Photograph of the NMR and ESR microcoils. ESR microcoil has 2 turns. NMR microcoil has 10 turns. (d) Block diagram of the complete setup for characterization of the single-chip DNP microsystem: (A) electromagnet (Bruker, 0–2.2 T); (B) homemade modulation coil (0.33 mT/A); (C) rf amplification stage composed of two rf amplifiers (Analog Devices HMC-C001) and a 3 dB attenuator; (D) three dc power supplies (Keithley 2400); (E) rf generator (Rohde&Schwartz SMR-20); (F) mixer (Mini-Circuits ZX05-153-S+); (G) 100 MHz high-pass filter (Crystek CHPFL-0100); (H) 300 MHz low-pass filter (Crystek CLPFL-0300); (I) frequency divider (Valon Technology 3010); (J) homemade delay-line discriminator (200 MHz central frequency, 1 MHz detection range, 5 MHz FM bandwidth); (K) amplifier (Stanford Research Systems SR560); (L) lock-in amplifier (EG&G 7265); (M) NMR magnetometer probe (Metrolab Instruments SA 1062 probe 3); (N) NMR magnetometer main electronic unit (Metrolab Instruments SA PT2025); (O) rf splitter (Mini-Circuits ZFSC-2-11); (P) rf generator (Stanford Research Systems SG384); (Q) frequency counter (Fluke PM6681); (R) amplifier (EG&G 5113); (S) power amplifier (Rohrer PA508); (T) photograph of the single-chip DNP-NMR microsystem with the capillary containing the sample placed on the microcoils and the bonding wires protected by glob-top (black material covering the bottom part of the chip); (U) magnet power supply (Bruker, 0–150 A).
The ESR detector is a slightly modified version of the one previously reported,54 where the bonding pads are distanced to facilitate placement of a capillary containing the liquid sample under investigation (Figure 1a–c). The ESR detector is a differential Colpitts LC oscillator operating at 10.7 GHz. The excitation/detection ESR microcoil has two turns, an external diameter of 270 μm, a wire width of 12 μm, a wire thickness of 2.3 μm, and a spacing of 2 μm between turns (Figure 1c). The NMR microcoil placed inside the ESR microcoil reduces the effective inductance of the ESR microcoil from 2.8 to 2.3 nH and thus increases the operating frequency of the ESR detector from 10.1 to 10.7 GHz with respect to the ESR detector previously reported.54 The maximum microwave power dissipated into the ESR microcoil is about 17 mW with a maximum microwave field B1e of about 0.1 mT at the center of the microcoil. Since the excitation microwave field is produced by the integrated microwave LC oscillator, no external microwave sources are required to perform the ESR excitation. The ESR detection is also performed by the integrated microwave LC oscillator. The external microwave electronics are used only to measure the frequency variation of the integrated LC oscillator due to the ESR phenomenon of the sample placed in close proximity with the inductor of the oscillator (i.e., the ESR microcoil). The dc power consumption of the ESR circuit is 90 mW at the maximum supply voltage of the oscillator of 2 V and 5 mW at the minimum supply voltage of the oscillator of 0.85 V.
The complete setup for the characterization of the single-chip DNP microsystem is shown in Figure 1d. The frequency-to-voltage conversion of the ESR detector output is performed by a delay-line discriminator (DLD) whose central frequency is 200 MHz. In order to match the DLD central frequency and improve the spectral purity, the signal at the output of the detector is amplified, mixed with an external reference, filtered, and shaped through a divide by 1 frequency divider. The dc-coupled output of the DLD is amplified and digitized by an analog to digital converter (ADC). This signal is used to monitor the ESR oscillator frequency. The ac-coupled output of the DLD is amplified and sent to a lock-in amplifier for further amplification and synchronous demodulation. The lock-in amplifier also generates the reference signal which is used for magnetic field modulation. An NMR magnetometer is used to track the variations of the magnetic field produced by the electromagnet in which the DNP experiments are performed. The frequency lock with the NMR magnetometer is necessary due to the relatively large drift (about 1 ppm/h) of the electromagnet. The NMR frequency measured by the magnetometer is used to set the frequency of the rf generator connected to the integrated transmitter VTX and to the local oscillator VLO of the integrated receiver. In particular, the rf generator frequency is set 20 kHz below the frequency measured by the NMR magnetometer. This allows one to obtain an NMR signal above the 1/f-noise corner frequency of the integrated NMR receiver. A switch signal VSW determines the pulse width of the NMR excitation. The output of the integrated NMR receiver VNMR is amplified, digitized, and digitally processed. The maximum NMR signal amplitude is obtained with a rf pulse length τrf≅ 5 μs. The maximum microwave magnetic field B1e at the center of the ESR coil is about 70 μT, as estimated from measurements performed on a BDPA sample (see below).
The samples are contained in borosilicate glass capillaries (BGCT 0.2, Capillary Tube Supply Ltd.) with a 0.2 mm outer diameter (o.d.) and 0.18 mm inner diameter (i.d.). The capillaries are sealed with a torch (Microtorch, Prodont Holliger). The nondegassed solutions of pure water (H2O) (W3500, Sigma-Aldrich) and 4-hydroxy-2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPOL) (176141, Sigma-Aldrich) are obtained by dilution at room temperature in air starting from a 1 M solution. The degassed solutions are prepared as follows. The degassing of water is performed by bubbling with a nitrogen flow for about 1 h. A 200 mL glass vial, with inlet/outlet pipes for the nitrogen flow, is filled with pure water heated to 70 ◦C by a hot plate. A pipet is used to transfer the degassed water into a 2 mL glass vial containing the appropriate amount of TEMPOL molecules to produce a 100 mM solution. The 10 and 1 mM solutions are prepared in 2 mL glass vials by subsequent dilution in degassed water. The preparation of the solutions and the filling/sealing of the capillaries is performed in a few seconds to minimize the absorption of O2 in contact with air (the diffusion length of O2 in water in 1 s is about 60 μm).
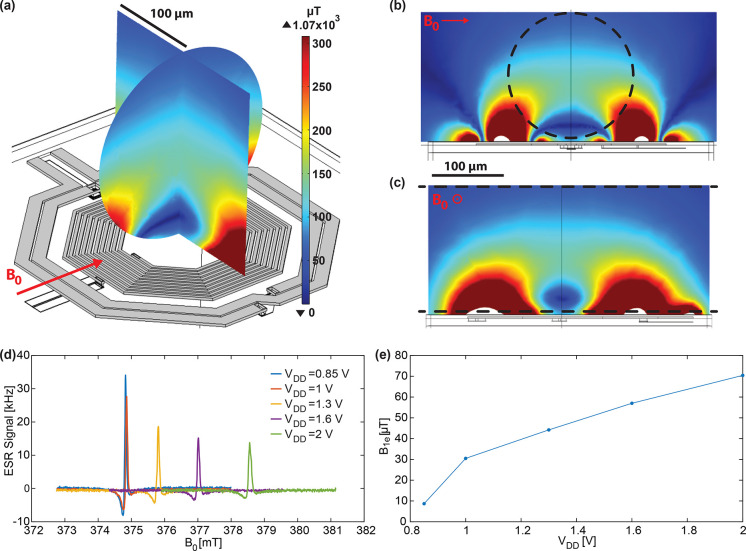
Electromagnetic and electrical simulations of the integrated microwave oscillator, performed with ADS and Cadence, show that the maximum achievable microwave current Imw in the ESR microcoil is 74 mA, obtained with an oscillator supply voltage of 2 V. Figure 2 shows the result of a COMSOL simulation performed with microwave current Imw = 74 mA in the ESR microcoil. The indicated magnetic field is one-half of the magnitude of the component of the microwave magnetic field perpendicular to the static magnetic field (i.e., B1e) in two orthogonal cross sections of the capillary where the sample is confined. The microwave magnetic field B1e in the center of the coil is about 100 μT. The obtained microwave magnetic field is the result of the superposition of the microwave magnetic field created by the ESR coil and the microwave magnetic field caused by the induced microwave currents in the NMR microcoil. Moving vertically from the chip (and coils) surface into the sample region, the total microwave magnetic field first decreases, cancels out in the dark blue region, then increases, and finally decreases again further away from the chip surface. This is the expected magnetic field produced by two concentric coils of different diameters carrying currents flowing in opposite directions. Simulations of the microwave magnetic field produced by the ESR microcoil with the NMR microcoil terminated with a high impedance (or without the NMR microcoil) show that the average microwave magnetic field in the sample region could be increased by almost 1 order of magnitude (and, as expected, in the center of the coil would be approximately given by B1e = μ0Imw/d ≅ 400 μT).
Figure 2.
Simulations and experiments for characterization of the microwave magnetic field produced by the ESR microcoil. (a) Three-dimensional representation of the ESR and NMR microcoils together with the map of the microwave magnetic field B1e, defined as one-half of the component perpendicular to the static magnetic field B0 (indicated by the red arrow) of the microwave magnetic field produced by the microwave current into the ESR microcoil. In a, the two perpendicular cross sections correspond to the region occupied by the water solution inside the capillary. (b and c) Maps of B1e in two larger regions. Black dashed lines indicate the region occupied by the water solution inside the capillary. Simulations are performed using COMSOL Multiphysics (COMSOL Inc.). Amplitude of the microwave current in the ESR microcoil is set to 74 mA, according to the combined results of simulations of the ESR/NMR-integrated electronics performed with an Advanced Design System (ADS, Keysight Technologies) and Cadence (Cadence Design Systems Inc.). (d) ESR spectra of a sample of BDPA placed in the center of the ESR microcoil for different ESR oscillator supply voltages VDD. Increase of the resonance static magnetic field is due to the increase of the oscillator frequency with the oscillator supply voltage VDD. (e) Microwave magnetic field B1e in the center of the ESR coil extracted from measurement of the line width of the ESR signals shown in d according to the equation ΔB0,zc = (2/γT2)(1 + γ2B12T1T2)1/2,56 where ΔB0,zc is the field difference between the two zero crossings of the ESR signal and corresponds to the peak-to-peak line width of the dispersion signal measurable without magnetic field modulation. Experimental conditions: fmw≅ 10.7 GHz. Modulation frequency: fm = 16.7 kHz. Modulation magnetic field: Bm = 6 μT.
To cross-check these simulation results, we performed experiments with a single crystal of 1:1 α,γ-bisdiphenylene-β-phenylallyl:benzene (BDPA/benzene, 152560, Sigma-Aldrich) having a size of about 70 × 70 × 5 μm3 placed in the center of the ESR microcoil (Figure 2d). At room temperature, BDPA has relaxation times T1≅ T2≅ 100 ns.57 Since the line width depends only on B1e and the relaxation times,56 knowledge of the relaxation times and measurement of the line width allows one to estimate the value of B1e. From the measured ESR signals reported in Figure 2d, the extracted value of B1e in the center of the ESR microcoil is about 70 μT at the maximum supply voltage of the oscillator of 2 V (Figure 2e), corresponding to the simulated maximum current in the ESR coil of 74 mA. As discussed above, the full-wave COMSOL simulation gives a B1e in the center of the ESR microcoil of about 100 μT, in good agreement with the 70 μT estimated from these BDPA measurements.
Experimental Results
The capillary-encapsulated samples of TEMPOL/H2O solutions are fixed on top of the single-chip DNP microsystem with a small drop of vacuum grease (high-vacuum grease, Dow Corning). As shown on the left side of Figure 3, at concentrations of 1 and 10 mM the ESR spectra consist of three hyperfine lines due the 15N nucleus (I = 1). At concentrations of 100 mM and 1 M a single line is observed, as also reported by Gafurov et al.58 After obtaining the ESR spectrum, the B0 magnetic field is set to one of the three maxima for concentrations of 1 and 10 mM and to the single maximum for the 100 mM and 1 M concentrations. For all NMR spectra shown on the right side of Figure 3, the rf pulse length is τrf = 5 μs, the acquisition time is Tdaq = 400 ms, and the pulse repetition time is Tr = 500 ms. The nonenhanced NMR spectra are the average of Navg = 100 000 spectra obtained in about 14 h. The DNP-enhanced NMR spectra are the average of Navg = 1000 spectra obtained in about 9 min. In the DNP-enhanced NMR measurements, the microwave excitation is present also during the NMR detection. The frequency shift between the nonenhanced and the enhanced NMR spectra is caused by the dc current flowing in the two-turn ESR microcoil. Even though the coil is designed such that the magnetic field created by the dc current running in each section is almost entirely canceled by the magnetic field created by the dc current running in the adjacent section, a small field is still created in the direction of B0 due to the nonzero distance (about 14 μm) between the two wires. The observed shift (up to 4 ppm) is much larger than that attributable to temperature effects. Since the temperature-induced frequency shift for the 1H nucleus in water is about 0.01 ppm/◦C,59 the observed shift would correspond to a temperature increase of 400 ◦C, which is obviously impossible for a liquid water sample. In a future version of the integrated ESR detector, this shift will be entirely suppressed by an ESR oscillator design in which no dc current runs through the ESR microcoil, such as the Colpitts oscillator.54
Figure 3.

ESR (left column) and NMR (right column) spectra of TEMPOL/H2O solutions for different concentrations (1 mM, 10 mM, 100 mM, and 1 M). In the NMR spectra, the red curves are the nonenhanced (B1e = 0) NMR spectra enlarged 5 times whereas the blue curves are the DNP-enhanced NMR spectra (B1e≅ 60 μT). DNP enhancement ε values for each spectra are given on the top-right corner. Enhancement is defined as the ratio of the integrals of the enhanced and nonenhanced NMR signals in the frequency domain. ESR measurements are performed in the following conditions. Modulation frequency: fm = 16.7 kHz. Modulation magnetic field: Bm ≅ 6 μT. Microwave frequency: fmw ≅ 10.7 GHz. Microwave magnetic field: B1e ≅ 60 μT. NMR measurements are performed in the following conditions. frf ≅ 16 MHz. Pulse length: τrf = 5 μs. Pulse repetition time: Tr = 500 ms. Time-domain match filter time constant: Tm = 100 ms. Acquisition time: Tdaq = 400 ms. Number of averaging: Navg = 100 000 (for the nonenhanced signal) and Navg = 1000 for the enhanced signal.
Figure 4 reports the DNP enhancements (Figure 4a) and the NMR line widths (Figure 4b) obtained with TEMPOL/H2O solutions having different concentrations. A maximum enhancement of about −50 is obtained with the largest B1e (i.e., about 70 μT) with a 10 mM degassed solution. Enhancements on the order of −100 have been previously reported at 0.3 T.60−66 In particular, Höfer et al. reported an enhancement of −100 for a 10 mM solution of TEMPOL/H2O at room temperature (i.e., with the same test sample and experimental conditions of this work).60 The lower enhancement measured in our work is probably due to the lower average B1e which, as shown in Figure 4, is insufficient to reach the saturation region. This is caused by the NMR coil inside the ESR coil, which reduces significantly the microwave magnetic field B1e produced by the ESR coil as explained in the description of the system. Figure 4 shows also that the degassing of water increases the enhancement, especially for low radical concentrations. The enhancement of the NMR signal for the 1 mM degassed solution is almost three times larger than that measured with the nondegassed solution. For the 10 mM sample, the enhancement increase caused by degassing is much lower, probably due to the negligible additional relaxation induced by the presence of the O2 molecules (0.2 mM at room temperature) with respect to the relaxation due to 10 mM TEMPOL molecules. As shown in Figure 4b, for 1 and 100 mM concentrations, the NMR line width is about 20 Hz (i.e., 1 ppm), mainly limited by the lack of shim coils in the electromagnet (a very similar chip operated in a 7 T magnet equipped with shimming coils shows spectral resolutions down to about 2 Hz46). The NMR line width of the 1 M solution is about 90 Hz, presumably due to the large concentration of TEMPOL, which significantly reduces the T2 value.60,67
Figure 4.

DNP enhancement and NMR line width. (a) Enhancement ε and (b) NMR line width of TEMPOL/H2O solutions with different concentrations (1 mM, 10 mM, 100 mM, and 1 M) at different microwave magnetic fields B1e. Enhancement is defined as the ratio of the integrals of the enhanced and nonenhanced NMR signals in the frequency domain. NMR line width is defined as the full width at half-maximum of the NMR signal in the frequency domain. At an operating frequency of 16 MHz, a line width of 20 Hz corresponds to 1.25 ppm.
Outlook
In this work we demonstrated, for the first time, the integration of a DNP microsytem consisting of an NMR transceiver and an ESR oscillator on a single silicon chip of less than 2 mm2. Measurements on TEMPOL/H2O solutions, performed at 10.7 GHz(ESR)/16 MHz(NMR), show enhancements as large as −50 on samples having an effective volume of about 1 nL. In the following, we discuss the improvements and extensions of the approach demonstrated in this work. A straightforward but rather modest increase of the SNR can be obtained by a narrowband design of the integrated NMR receiver. Despite the generally lower enhancement factors observed in liquid-state DNP at high magnetic fields, a very significant improvement of the SNR (and of the spectral separation of chemically shifted signals) can be obtained by increasing the operating frequency of the NMR/ESR subsystems.22 A moderate increase of the frequency to the 40 GHz(ESR)/60 MHz(NMR) region could allow for low-cost DNP-enhanced NMR spectrometers in permanent magnets. The use of state-of-the-art submicrometer-integrated circuit technologies should allow the extension of the single-chip DNP microsystem approach proposed here up the THz(ESR)/GHz(NMR) region,68−70 corresponding to the strongest static magnetic fields currently available. We previously reported single-chip ESR detectors operating at up to 146 GHz51 and single-chip NMR detectors operating at up to 300 MHz.42,44,47 However, the combination of single-chip NMR/ESR detectors at these frequencies (and above) has been not demonstrated yet. The main technical challenge for extension of the proposed single-chip DNP microsystem approach to higher frequencies is the coupling between the NMR and the ESR excitation/detection structures, which influence the strength of the microwave field B1e. In order to obtain a sufficiently large B1e, the NMR structure and its impedance termination should be carefully codesigned with the ESR structure with possible drawbacks in terms of NMR sensitivity. Another interesting opportunity offered by the single-chip approach is the possibility to create dense arrays of such sensors for parallel DNP-enhanced NMR spectroscopy of a large number of nanoliter and subnanoliter different samples (or a bigger volume of the same sample). In addition, preliminary measurements performed with the DNP microsystem proposed in this work show that it can be operated also at temperatures down to 4 K, at least. Hence, the single-chip DNP approach proposed here could be well suited also for the study of DNP processes other than the Overhauser effect in liquids at room temperature.
Acknowledgments
Financial support from the Swiss National Science Foundation (SNSF) is gratefully acknowledged (grant 200020-175939). We thank Giancarlo Corradini for wire bonding and bonding protection, Pierrick Clement for his help in capillary sealing, and Mohammadmahdi Kiaee for his help in degassing the samples.
The authors declare no competing financial interest.
References
- Olson D. L.; Peck T. L.; Webb A. G.; Magin R. L.; Sweedler J. V. High-resolution microcoil 1H-NMR for mass-limited, nanoliter-volume samples. Science 1995, 270, 1967–1970. 10.1126/science.270.5244.1967. [DOI] [Google Scholar]
- Webb A. G. Radiofrequency microcoils in magnetic resonance. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 1–42. 10.1016/S0079-6565(97)00004-6. [DOI] [Google Scholar]
- Lacey M. E.; Subramanian R.; Olson D. L.; Webb A. G.; Sweedler J. V. High-resolution NMR spectroscopy of sample volumes from 1 nL to 10 μL. Chem. Rev. 1999, 99, 3133–3152. 10.1021/cr980140f. [DOI] [PubMed] [Google Scholar]
- Minard K. R.; Wind R. A. Picoliter 1H NMR Spectroscopy. J. Magn. Reson. 2002, 154, 336–343. 10.1006/jmre.2001.2494. [DOI] [PubMed] [Google Scholar]
- Massin C.; Vincent F.; Homsy A.; Ehrmann K.; Boero G.; Besse P. A.; Daridon A.; Verpoorte E.; De Rooij N.; Popovic R. S. Planar microcoil-based microfluidic NMR probes. J. Magn. Reson. 2003, 164, 242–255. 10.1016/S1090-7807(03)00151-4. [DOI] [PubMed] [Google Scholar]
- Sakellariou D.; Le Goff G.; Jacquinot J. F. High-resolution, high-sensitivity NMR of nanolitre anisotropic samples by coil spinning. Nature 2007, 447, 694–697. 10.1038/nature05897. [DOI] [PubMed] [Google Scholar]
- Maguire Y.; Chuang I. L.; Zhang S.; Gershenfeld N. Ultra-small-sample molecular structure detection using microslot waveguide nuclear spin resonance. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 9198–9203. 10.1073/pnas.0703001104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krojanski H. G.; Lambert J.; Gerikalan Y.; Suter D.; Hergenröder R. Microslot NMR probe for metabolomics studies. Anal. Chem. 2008, 80, 8668–8672. 10.1021/ac801636a. [DOI] [PubMed] [Google Scholar]
- Bart J.; Kolkman A. J.; Oosthoek-de Vries A. J.; Koch K.; Nieuwland P. J.; Janssen H.; van Bentum J.; Ampt K. A.; Rutjes F. P.; Wijmenga S. S.; et al. A microfluidic high-resolution NMR flow probe. J. Am. Chem. Soc. 2009, 131, 5014–5015. 10.1021/ja900389x. [DOI] [PubMed] [Google Scholar]
- Zalesskiy S. S.; Danieli E.; Blumich B.; Ananikov V. P. Miniaturization of NMR systems: Desktop spectrometers, microcoil spectroscopy, and “NMR on a chip” for chemistry, biochemistry, and industry. Chem. Rev. 2014, 114, 5641–5694. 10.1021/cr400063g. [DOI] [PubMed] [Google Scholar]
- Finch G.; Yilmaz A.; Utz M. An optimized detector for in-situ high-resolution NMR in microfluidic devices. J. Magn. Reson. 2016, 262, 73–80. 10.1016/j.jmr.2015.11.011. [DOI] [PubMed] [Google Scholar]
- Chen Y.; Mehta H. S.; Butler M. C.; Walter E. D.; Reardon P. N.; Renslow R. S.; Mueller K. T.; Washton N. M. High-resolution microstrip NMR detectors for subnanoliter samples. Phys. Chem. Chem. Phys. 2017, 19, 28163–28174. 10.1039/C7CP03933F. [DOI] [PubMed] [Google Scholar]
- Schirhagl R.; Chang K.; Loretz M.; Degen C. L. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. 10.1146/annurev-physchem-040513-103659. [DOI] [PubMed] [Google Scholar]
- Glenn D. R.; Bucher D. B.; Lee J.; Lukin M. D.; Park H.; Walsworth R. L. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 2018, 555, 351–354. 10.1038/nature25781. [DOI] [PubMed] [Google Scholar]
- Smits J.; Damron J. T.; Kehayias P.; McDowell A. F.; Mosavian N.; Fescenko I.; Ristoff N.; Laraoui A.; Jarmola A.; Acosta V. M. Two-dimensional nuclear magnetic resonance spectroscopy with a microfluidic diamond quantum sensor. Sci. Adv. 2019, 5, eaaw7895. 10.1126/sciadv.aaw7895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D. B.; Glenn D. R.; Park H.; Lukin M. D.; Walsworth R. L. Hyperpolarization-enhanced NMR spectroscopy with femtomole sensitivity using quantum defects in diamond. Phys. Rev. X 2020, 10, 021053. 10.1103/PhysRevX.10.021053. [DOI] [Google Scholar]
- Rugar D.; Züger O.; Hoen S.; Yannoni C. S.; Vieth H. M.; Kendrick R. D. Force detection of nuclear magnetic resonance. Science 1994, 264, 1560–1563. 10.1126/science.264.5165.1560. [DOI] [PubMed] [Google Scholar]
- Degen C. L.; Poggio M.; Mamin H. J.; Rettner C. T.; Rugar D. Nanoscale magnetic resonance imaging. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 1313–1317. 10.1073/pnas.0812068106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose W.; Haas H.; Chen A. Q.; Jeon N.; Lauhon L. J.; Cory D. G.; Budakian R. High-Resolution nanoscale solid-state nuclear magnetic resonance spectroscopy. Phys. Rev. X 2018, 8, 011030. 10.1103/PhysRevX.8.011030. [DOI] [Google Scholar]
- Schnoz S.; Däpp A.; Hunkeler A.; Meier B. H. Detection of liquids by magnetic resonance force microscopy in the gradient-on-cantilever geometry. J. Magn. Reson. 2019, 298, 85–90. 10.1016/j.jmr.2018.11.009. [DOI] [PubMed] [Google Scholar]
- Grob U.; Krass M.-D.; Heritier M.; Pachlatko R.; Rhensius J.; Kosata J.; Moores B.; Takahashi H.; Eichler A.; Degen C. L. Magnetic resonance force microscopy with a one-dimensional resolution of 0.9 nm. Nano Lett. 2019, 19, 7935–7940. 10.1021/acs.nanolett.9b03048. [DOI] [PubMed] [Google Scholar]
- Griesinger C.; Bennati M.; Vieth H.-M.; Luchinat C.; Parigi G.; Höfer P.; Engelke F.; Glaser S. J.; Denysenkov V.; Prisner T. F. Dynamic nuclear polarization at high magnetic fields in liquids. Prog. Nucl. Magn. Reson. Spectrosc. 2012, 64, 4–28. 10.1016/j.pnmrs.2011.10.002. [DOI] [PubMed] [Google Scholar]
- Slichter C. P. The discovery and renaissance of dynamic nuclear polarization. Rep. Prog. Phys. 2014, 77, 072501. 10.1088/0034-4885/77/7/072501. [DOI] [PubMed] [Google Scholar]
- Liu G.; Levien M.; Karschin N.; Parigi G.; Luchinat C.; Bennati M. One-thousand-fold enhancement of high field liquid nuclear magnetic resonance signals at room temperature. Nat. Chem. 2017, 9, 676–680. 10.1038/nchem.2723. [DOI] [PubMed] [Google Scholar]
- Plainchont B.; Berruyer P.; Dumez J.-N.; Jannin S.; Giraudeau P. Dynamic nuclear polarization opens new perspectives for NMR spectroscopy in analytical chemistry. Anal. Chem. 2018, 90, 3639–3650. 10.1021/acs.analchem.7b05236. [DOI] [PubMed] [Google Scholar]
- Ardenkjær-Larsen J. H.; Fridlund B.; Gram A.; Hansson G.; Hansson L.; Lerche M. H.; Servin R.; Thaning M.; Golman K. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 10158–10163. 10.1073/pnas.1733835100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capozzi A.; Cheng T.; Boero G.; Roussel C.; Comment A. Thermal annihilation of photo-induced radicals following dynamic nuclear polarization to produce transportable frozen hyperpolarized 13C-substrates. Nat. Commun. 2017, 8, 15757. 10.1038/ncomms15757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capozzi A.; Hyacinthe J.-N.; Cheng T.; Eichhorn T. R.; Boero G.; Roussel C.; van der Klink J. J.; Comment A. Photoinduced nonpersistent radicals as polarizing agents for X-nuclei dissolution dynamic nuclear polarization. J. Phys. Chem. C 2015, 119, 22632–22639. 10.1021/acs.jpcc.5b07315. [DOI] [Google Scholar]
- Kouřil K.; Kouřilová H.; Bartram S.; Levitt M. H.; Meier B. Scalable dissolution-dynamic nuclear polarization with rapid transfer of a polarized solid. Nat. Commun. 2019, 10, 1733. 10.1038/s41467-019-09726-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mompeán M.; Sánchez-Donoso R. M.; De La Hoz A.; Saggiomo V.; Velders A. H.; Gomez M. V. Pushing nuclear magnetic resonance sensitivity limits with microfluidics and photo-chemically induced dynamic nuclear polarization. Nat. Commun. 2018, 9, 108. 10.1038/s41467-017-02575-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orlando T.; Dervişoğlu R.; Levien M.; Tkach I.; Prisner T. F.; Andreas L. B.; Denysenkov V. P.; Bennati M. Dynamic nuclear polarization of 13C nuclei in the liquid state over a 10 T field range. Angew. Chem. 2019, 131, 1416–1420. 10.1002/ange.201811892. [DOI] [PubMed] [Google Scholar]
- Eills J.; Hale W.; Sharma M.; Rossetto M.; Levitt M. H.; Utz M. High-resolution nuclear magnetic resonance spectroscopy with picomole sensitivity by hyperpolarization on a chip. J. Am. Chem. Soc. 2019, 141, 9955–9963. 10.1021/jacs.9b03507. [DOI] [PubMed] [Google Scholar]
- Griffin R. G.; Swager T. M.; Temkin R. J. High frequency dynamic nuclear polarization: New directions for the 21st century. J. Magn. Reson. 2019, 306, 128–133. 10.1016/j.jmr.2019.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisser D.; Karthikeyan G.; Lund A.; Casano G.; Karoui H.; Yulikov M.; Menzildjian G.; Pinon A. C.; Purea A.; Engelke F.; et al. BDPA-nitroxide biradicals tailored for efficient dynamic nuclear polarization enhanced solid-state NMR at magnetic fields up to 21.1 T. J. Am. Chem. Soc. 2018, 140, 13340–13349. 10.1021/jacs.8b08081. [DOI] [PubMed] [Google Scholar]
- Boero G.; Frounchi J.; Furrer B.; Besse P. A.; Popovic R. S. Fully integrated probe for proton nuclear magnetic resonance magnetometry. Rev. Sci. Instrum. 2001, 72, 2764–2768. 10.1063/1.1374599. [DOI] [Google Scholar]
- Anders J.; Chiaramonte G.; SanGiorgio P.; Boero G. A single-chip array of NMR receivers. J. Magn. Reson. 2009, 201, 239–249. 10.1016/j.jmr.2009.09.019. [DOI] [PubMed] [Google Scholar]
- Sun N.; Yoon T. J.; Lee H.; Andress W.; Weissleder R.; Ham D. Palm NMR and 1-chip NMR. IEEE J. Solid-State Circuits 2011, 46, 342–352. 10.1109/JSSC.2010.2074630. [DOI] [Google Scholar]
- Anders J.; SanGiorgio P.; Boero G. A fully integrated IQ-receiver for NMR microscopy. J. Magn. Reson. 2011, 209, 1–7. 10.1016/j.jmr.2010.12.005. [DOI] [PubMed] [Google Scholar]
- Anders J.; SanGiorgio P.; Deligianni X.; Santini F.; Scheffler K.; Boero G. Integrated active tracking detector for MRI-guided interventions. Magn. Reson. Med. 2012, 67, 290–296. 10.1002/mrm.23112. [DOI] [PubMed] [Google Scholar]
- Ha D.; Paulsen J.; Sun N.; Song Y.-Q.; Ham D. Scalable NMR spectroscopy with semiconductor chips. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 11955–11960. 10.1073/pnas.1402015111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anders J.; Handwerker J.; Ortmanns M.; Boero G. A low-power high-sensitivity single-chip receiver for NMR microscopy. J. Magn. Reson. 2016, 266, 41–50. 10.1016/j.jmr.2016.03.004. [DOI] [PubMed] [Google Scholar]
- Grisi M.; Gualco G.; Boero G. A broadband single-chip transceiver for multi-nuclear NMR probes. Rev. Sci. Instrum. 2015, 86, 044703. 10.1063/1.4916206. [DOI] [PubMed] [Google Scholar]
- Lei K.-M.; Mak P.-I.; Law M.-K.; Martins R. P. A μNMR CMOS transceiver using a butterfly-coil input for integration with a digital microfluidic device inside a portable magnet. IEEE J. Solid-State Circuits 2016, 51, 2274–2286. 10.1109/JSSC.2016.2579158. [DOI] [Google Scholar]
- Grisi M.; Vincent F.; Volpe B.; Guidetti R.; Harris N.; Beck A.; Boero G. NMR spectroscopy of single sub-nL ova with inductive ultra-compact single-chip probes. Sci. Rep. 2017, 7, 44670. 10.1038/srep44670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporrer B.; Wu L.; Bettini L.; Vogt C.; Reber J.; Marjanovic J.; Burger T.; Brunner D. O.; Pruessmann K. P.; Tröster G.; et al. A fully integrated dual-channel on-coil CMOS receiver for array coils in 1.5–10.5 T MRI. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 1245–1255. 10.1109/TBCAS.2017.2764443. [DOI] [PubMed] [Google Scholar]
- Montinaro E.; Grisi M.; Letizia M.; Pethö L.; Gijs M.; Guidetti R.; Michler J.; Brugger J.; Boero G. 3D printed microchannels for sub-nL NMR spectroscopy. PLoS One 2018, 13, e0192780 10.1371/journal.pone.0192780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grisi M.; Conley G. M.; Sommer P.; Tinembart J.; Boero G. A single-chip integrated transceiver for high field NMR magnetometry. Rev. Sci. Instrum. 2019, 90, 015001. 10.1063/1.5066436. [DOI] [PubMed] [Google Scholar]
- Handwerker J.; Pérez-Rodas M.; Beyerlein M.; Vincent F.; Beck A.; Freytag N.; Yu X.; Pohmann R.; Anders J.; Scheffler K. A CMOS NMR needle for probing brain physiology with high spatial and temporal resolution. Nat. Methods 2020, 17, 64. 10.1038/s41592-019-0640-3. [DOI] [PubMed] [Google Scholar]
- Lei K.-M.; Ha D.; Song Y.-Q.; Westervelt R. M.; Martins R.; Mak P.-I.; Ham D. Portable NMR with Parallelism. Anal. Chem. 2020, 92, 2112–2120. 10.1021/acs.analchem.9b04633. [DOI] [PubMed] [Google Scholar]
- Yalcin T.; Boero G. Single-chip detector for electron spin resonance spectroscopy. Rev. Sci. Instrum. 2008, 79, 094105. 10.1063/1.2969657. [DOI] [PubMed] [Google Scholar]
- Matheoud A. V.; Gualco G.; Jeong M.; Zivkovic I.; Brugger J.; Rønnow H.; Anders J.; Boero G. Single-chip electron spim resonance detectors operating at 50 GHz, 92 GHz, and 146 GHz. J. Magn. Reson. 2017, 278, 113–121. 10.1016/j.jmr.2017.03.013. [DOI] [PubMed] [Google Scholar]
- Anders J.; Angerhofer A.; Boero G. K-band single-chip electron spin resonance detector. J. Magn. Reson. 2012, 217, 19–26. 10.1016/j.jmr.2012.02.003. [DOI] [PubMed] [Google Scholar]
- Gualco G.; Anders J.; Sienkiewicz A.; Alberti S.; Forro L.; Boero G. Cryogenic single-chip electron spin resonance detector. J. Magn. Reson. 2014, 247, 96–103. 10.1016/j.jmr.2014.08.013. [DOI] [PubMed] [Google Scholar]
- Matheoud A. V.; Sahin N.; Boero G. A single chip electron spin resonance detector based on a single high electron mobility transistor. J. Magn. Reson. 2018, 294, 59–70. 10.1016/j.jmr.2018.07.002. [DOI] [PubMed] [Google Scholar]
- Schlecker B.; Hoffmann A.; Chu A.; Ortmanns M.; Lips K.; Anders J. Towards low-cost, high-sensitivity point-of-care diagnostics using VCO-based ESR-on-a-chip detectors. IEEE Sens. J. 2019, 19, 8995–9003. 10.1109/JSEN.2018.2875767. [DOI] [Google Scholar]
- Poole C. P.Electron spin resonance: a comprehensive treatise on experimental techniques; Dover Publications Inc.: Mineola, NY, 1996. [Google Scholar]
- Goldsborough J. P.; Mandel M.; Pake G. E. Influence of exchange interaction on paramagnetic relaxation times. Phys. Rev. Lett. 1960, 4, 13. 10.1103/PhysRevLett.4.13. [DOI] [Google Scholar]
- Gafurov M. TEMPOL as a polarizing agent for dynamic nuclear polarization of aqueous solutions. Magn. Reson. Solids 2013, 15, 13103. [Google Scholar]
- Petley B. W.; Donaldson R. W. The temperature dependence of the diamagnetic shielding correction for proton NMR in water. Metrologia 1984, 20, 81. 10.1088/0026-1394/20/3/002. [DOI] [Google Scholar]
- Höfer P.; Carl P.; Guthausen G.; Prisner T.; Reese M.; Carlomagno T.; Griesinger C.; Bennati M. Studies of dynamic nuclear polarization with nitroxides in aqueous solution. Appl. Magn. Reson. 2008, 34, 393. 10.1007/s00723-008-0118-4. [DOI] [Google Scholar]
- Höfer P.; Parigi G.; Luchinat C.; Carl P.; Guthausen G.; Reese M.; Carlomagno T.; Griesinger C.; Bennati M. Field dependent dynamic nuclear polarization with radicals in aqueous solution. J. Am. Chem. Soc. 2008, 130, 3254–3255. 10.1021/ja0783207. [DOI] [PubMed] [Google Scholar]
- McCarney E. R.; Armstrong B. D.; Lingwood M. D.; Han S. Hyperpolarized water as an authentic magnetic resonance imaging contrast agent. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 1754–1759. 10.1073/pnas.0610540104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Türke M. T.; Tkach I.; Reese M.; Höfer P.; Bennati M. Optimization of dynamic nuclear polarization experiments in aqueous solution at 15 MHz/9.7 GHz: a comparative study with DNP at 140 MHz/94 GHz. Phys. Chem. Chem. Phys. 2010, 12, 5893–5901. 10.1039/c002814m. [DOI] [PubMed] [Google Scholar]
- Enkin N.; Liu G.; Tkach I.; Bennati M. High DNP efficiency of TEMPONE radicals in liquid toluene at low concentrations. Phys. Chem. Chem. Phys. 2014, 16, 8795–8800. 10.1039/C4CP00854E. [DOI] [PubMed] [Google Scholar]
- Türke M.-T.; Parigi G.; Luchinat C.; Bennati M. Overhauser DNP with 15N labelled Frémy’s salt at 0.35 T. Phys. Chem. Chem. Phys. 2012, 14, 502–510. 10.1039/C1CP22332A. [DOI] [PubMed] [Google Scholar]
- Münnemann K.; Bauer C.; Schmiedeskamp J.; Spiess H. W.; Schreiber W. G.; Hinderberger D. A mobile DNP polarizer for clinical applications. Appl. Magn. Reson. 2008, 34, 321–330. 10.1007/s00723-008-0130-8. [DOI] [Google Scholar]
- Asakura T.; Demura M.; Ogawa H.; Matsushita K.; Imanari M. NMR imaging of diffusion of small organic molecules in silk fibroin gel. Macromolecules 1991, 24, 620–622. 10.1021/ma00002a045. [DOI] [Google Scholar]
- Razavi B. A. 300-GHz fundamental oscillator in 65-nm CMOS technology. IEEE J. Solid-State Circuits 2011, 46, 894–903. 10.1109/JSSC.2011.2108122. [DOI] [Google Scholar]
- Takahashi T.; Kawano Y.; Makiyama K.; Shiba S.; Sato M.; Nakasha Y.; Hara N. Maximum frequency of oscillation of 1.3 THz obtained by using an extended drain-side recess structure in 75-nm-gate InAlAs/InGaAs high-electron-mobility transistors. Appl. Phys. Express 2017, 10, 024102. 10.7567/APEX.10.024102. [DOI] [Google Scholar]
- Razavi B.RF microelectronics, 2nd international ed.; Pearson Education International: Upper Saddle River, NJ, 2012. [Google Scholar]