Abstract
Purpose
Enlarged lymph nodes are indicators of cancer staging, and the change in their size is a reflection of treatment response. Automatic lymph node segmentation is challenging, as the boundary can be unclear and the surrounding structures complex. This work communicates a new three‐dimensional algorithm for the segmentation of enlarged lymph nodes.
Methods
The algorithm requires a user to draw a region of interest (ROI) enclosing the lymph node. Rays are cast from the center of the ROI, and the intersections of the rays and the boundary of the lymph node form a triangle mesh. The intersection points are determined by dynamic programming. The triangle mesh initializes an active contour which evolves to low‐energy boundary. Three radiologists independently delineated the contours of 54 lesions from 48 patients. Dice coefficient was used to evaluate the algorithm's performance.
Results
The mean Dice coefficient between computer and the majority vote results was 83.2%. The mean Dice coefficients between the three radiologists’ manual segmentations were 84.6%, 86.2%, and 88.3%.
Conclusions
The performance of this segmentation algorithm suggests its potential clinical value for quantifying enlarged lymph nodes.
Keywords: active contours, computed tomography (CT), dynamic programming, lymph node segmentation, sphere subdivision
1. Introduction
Enlarged lymph nodes are important indicators of cancer staging, and their size changes contribute to therapy response assessment. The traditional unidimensional and bidimensional metrics are based on the assumption that tumors change uniformly in all directions, which is not always the case. Volume as a biomarker has been intensively studied and is believed to be a better biomarker than a unidimensional or bidimensional metric.1 Computed tomography (CT) provides high‐resolution images widely used in detecting and following up enlarged lymph nodes. However, obtaining volumes of lymph nodes by manually tracing the boundaries can be time‐consuming and subjective. Therefore, computer algorithms are needed to provide accurate, reproducible and objective volume measurements of lymph nodes.
Although it is an important task and has attracted much attention, automated lymph node segmentation remains a difficult task because the boundary is often not clear, the contrast is weak, and surrounding structures can be of high density such as vessels, low density such as fat, or similar density such as soft tissue.
Honea et al. proposed an active surface model that inflated a balloon from a point inside the lymph node of interest.2 The balloon technique had difficulty preventing the balloon from passing weak boundaries. The algorithm was evaluated on phantom data but not a real patient dataset.
Yan et al. proposed a two‐dimensional (2D) marker‐controlled watershed method and propagated the segmentation result to neighboring slices.3 The 2D segmentation and propagation technique did not take into account the three‐dimensional (3D) compact shape information.
Dornheim et al. proposed a 3D Stable Mass‐Spring Model to fit several models of different sizes to the data and select the one that fit best.4 The number of masses and springs was often small, resulting in boundaries jointed by long line segments.
Beichel and Wang proposed an approach based on optimal surface finding (OSF).5 OSF converted the segmentation problem into a graph optimization problem. The same method was used to interactively edit the results.
Some work focuses on automatic detection and segmentation of lymph nodes. Schwartz et al. proposed a method based on Hessian blob detection and marker‐controlled watershed segmentation.6 Barbu et al. proposed a marginal space learning‐based method for detection and Markov random field‐based method for segmentation.7 Feulner et al. extended Barbu et al. by employing a cascade of binary classifiers.8 Haar features and gradient‐aligned features were used to detect lymph node centers, graph cut were used to segment the candidates, and a classification stage followed to determine whether the segmentation was a lymph node.
Wang et al. proposed a spiral scanning technique for lung nodule segmentation that transformed a 3D image into a 2D image, performed segmentation on the 2D image and converted the result back to 3D.9 The intersection points of the scanning rays and the boundary formed a cloud of points that lack structure of a closed surface mesh.
Dynamic programming is a powerful tool to minimize cost that had been applied to many image segmentation problems.10 It has the advantage of finding a connected path despite lack of image feature in some region. Lalande et al. applied it to detect cardiac boundaries in MRI by maximizing the membership to the edge fuzzy set.11 Liu et al. employed it to segment breast mass in MRI images with sophisticated edge detector.12 Wang et al. applied it to segment pulmonary nodules in CT with intrinsic cost that favors smooth path and external cost that favors strong edges.9 When a circular object went through polar transformation, the start and end of rays were connected, and the problem of finding a closed curve in the original image transformed to finding a circular shortest path (CSP) in the transformed image.13, 14 Timp and Karssemeijer applied CSP to segment lesions in mammography.14 However, our path is not circular. Cost function was often designed so that the gradient along it was maximized and the discontinuity was minimized. We would like the region close to the boundary in lymph node to be homogeneous, so we designed the cost function to favor a path having the property.
In this study, we propose a two‐stage segmentation method that takes into account the prior knowledge that lymph nodes are compact in shape and homogeneous in density. The method consists of an initial segmentation by sphere subdivision and dynamic programming and a refinement by excluding nonlesion region, morphological smoothing, and active contour‐based segmentation. The algorithm is described in Section 2, the patient data and the performance of the algorithm on the dataset is presented in Section 3, and the discussions and conclusions follow in Sections 4 and 5.
2. Methods
A user initializes the segmentation by drawing an elliptical region of interest (ROI) that encompasses the lymph node on one axial slice. The 2D ROI is extended to a cylindrical volume of interest (VOI). Let the plane where the elliptical ROI was drawn be the XY plane, and the lengths of major and minor axis be L and S, the VOI extended 2L in the Z axis in both directions. Rays are cast from the center of the ROI, along which sample points are taken. Assuming the lesion was not 2L away from the center, 2L sample points were taken, with spacing between sample points the same as the spacing in XY plane. The intersections of the rays and the boundary of the lymph node form a triangle mesh. The rays are arranged in specific order to form a 2D image, one column for each ray; however, unlike other 2D images, each column is aware of the adjacent rays in 3D. A cost value is assigned to each point of the 2D image. The intersection points are determined by dynamic programming, which minimizes the cost function. The triangle mesh initializes an active contour which evolves to low‐energy boundary.
2.A. Transformation of a 3D volume to a 2D image
The surface of a solid object can be approximated by a triangle mesh. If all the surfaces are visible from a single point within the object, the triangle mesh can be determined by the distance of each vertex to the center point. By shrinking the distances to unit length, the triangle mesh can be deformed to a polyhedron that can be inscribed in a unit sphere. Figure 1 shows the approximation of a sphere by subdividing an octahedron.
Figure 1.
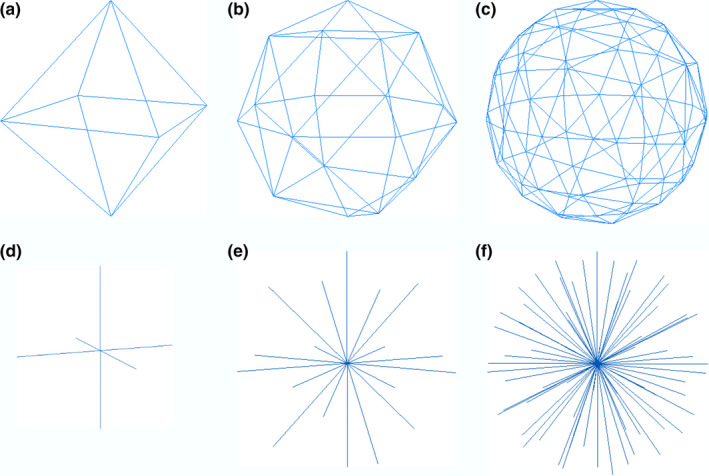
Approximate a sphere by a polyhedron. (a) a regular octahedron. (b) Subdivide each edge in (a) into two edges (n = 2). (c) Subdivide each edge in (a) into four edges (n = 4). (d)(e)(f) the rays from the center of the polyhedron and the vertex on the sphere. [Color figure can be viewed at wileyonlinelibrary.com]
Starting from an octahedron (or any regular bipyramid), the subdivision technique divides each triangle face into smaller ones. An octahedron has four points on the equator and one point on each pole. An N‐level subdivision divides each edge on the equator into N edges and adds points along N‐1 latitudes. Vertices on the same level have the same latitude, which makes it easier to determine if a voxel is inside a mesh or not. Since the southern hemisphere is symmetrical to the northern hemisphere, only the northern hemisphere is described here. Let the north pole be level 0 and the equator be level N. A level n vertex V, the center of sphere O, and the north pole P form an angle (elevation) called . There are four points (in the case of an octahedron) on the first level, forming four triangles with the north pole, and 4n points on the nth level, forming 4n triangles with points on level n‐1. There are 4N2 triangle faces on the northern hemisphere, covering an area of 2πR2, where R is the radius of the sphere. To cover the sphere with triangles of similar area, each triangle covers , and the elevation of each level can be derived as
| (1) |
The vertices of the triangle mesh can be arranged from north pole to south pole, from west to east. Figure 2 shows the arrangement of part of the northern hemisphere for Fig. 1(c) by cutting along one international dateline, where the zero vertex is the north pole, and vertices 0, 4, 12, and 24 are along the international dateline. We can define the predecessors of a vertex as the vertices that connect with the point at an edge and have smaller indices. The predecessor with the largest index is called the vertex's immediate predecessor. For example, the predecessors of vertex 14 are vertex 5, 6, and 13, and vertex 13 is the immediate predecessor. It is easy to see that vertex n‐1 is the immediate predecessor of vertex n for n>=1. The rays are ordered by the vertices they pass through.
Figure 2.
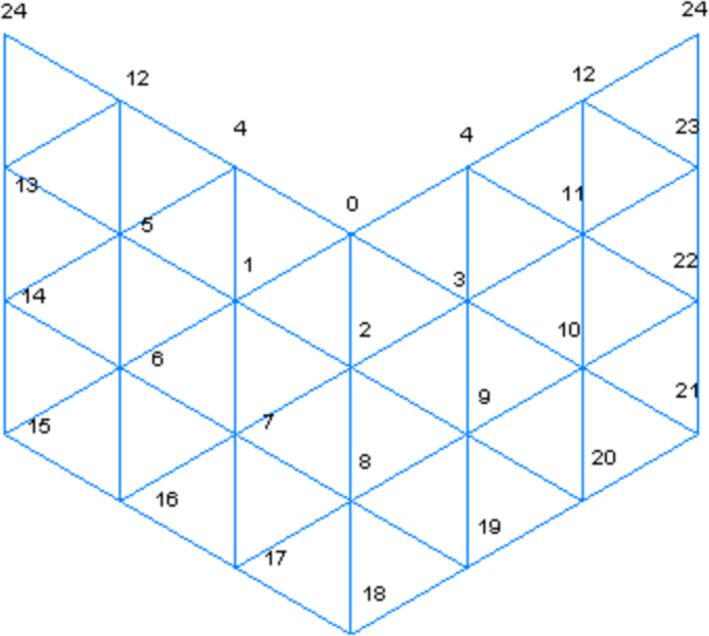
The order of vertices on a section of the northern hemisphere of the Fig 1(c). [Color figure can be viewed at wileyonlinelibrary.com]
Points along each ray are sampled and the intensities are interpolated. The length of the ray is twice the semimajor axis of the ROI. The rays are then stacked in the order from north pole to south pole, east to west to form a 2D image, as shown in Fig. 3, where pixels outside of the cylindrical VOI are set to 0.
Figure 3.

Converting 3D volume to 2D image. (a) A manually selected ROI. (b) Resample the volume to form a 2D image using the proposed method (N = 13). [Color figure can be viewed at wileyonlinelibrary.com]
Throughout the study, N was a fixed value of 13, resulting in 698 rays for each lesion.
In Fig. 3(b), let the coordinate of the bottom left corner be (0,0); assume that the x‐coordinate increases from left to right, and y increases from bottom to top. The left‐most column represents the sample points along the ray from the center to the north pole. The right‐most column represents the sample points along the ray from the center to the south pole.
2.B. Optimal path finding by dynamic programming in 2D
The tumor boundary on the resampled 2D image can be determined by dynamic programming. Observing that tumor boundary points often have large gradients, and that densities along a ray from the center of the ROI to a boundary point are homogeneous, we try to locate the boundary points by minimizing the cost of a path from the north pole to the south pole. There are three terms in the cost function: gradient cost, homogeneity cost, and discontinuity cost.
2.B.1. Gradient cost
The gradient cost Cg can be defined as the following:
| (2) |
where
The points with strong gradient have a gradient cost close to 0, and the points with weak gradient have a gradient cost close to 1. The idea of clamping the gradient is that a point with gradient 50 is as good an edge point as a point with a higher gradient value.
2.B.2. Homogeneity cost
The homogeneity cost function at a point (x,y) is defined as the weighted standard deviation along the vertical line (column) x from the bottom point (x,0) to (x,y), and the points closer to (x,y) are weighted more, particularly, the weight of (x,0) is 1, and the weight of (x,n) is γn where γ ≥ 1. The weighting makes intensity variation at a greater distance from the boundary less significant, which may assist in the segmentation of lymph nodes with central necrosis. The weighted standard deviation of intensities x0, x1,…xN with weight w0, w1,…wN can be defined as:
| (3) |
where,
A 7 × 7 window is taken from the center of the ROI, and the standard deviation of the pixel density inside the window σ0 is used to estimate the standard deviation of the lymph node of interest. The standard deviations of the closest n (n = 5 in our experiment) points to the center of the ROI are set to no less than σ0. The homogeneity cost is then defined as:
| (4) |
2.B.3. Discontinuity cost
Observing that boundary points on neighboring rays have similar lengths from the center of the ROI, the difference in y values for two neighboring rays is penalized. The larger the difference, the higher the penalty. A quadratic function of the deviation is used. Considering that a larger lymph node allows for larger deviations, the discontinuity cost is defined as:
| (5) |
The cost for the first column is the weighted sum of the gradient cost and homogeneity cost, namely,
| (6) |
The predecessor of (0,y) is set to (0,y) itself.
The accumulated cost of point (x,y) can be calculated recursively as:
| (7) |
where ray pred is a predecessor of ray x, and npred is the number of predecessors of ray x. The minimum is taken from points that are from (pred, y‐s) to (pred, y+s). The formula favors points on a boundary having similar distances to the center as their predecessors. The parent of (x,y) is set to be the point along its immediate predecessor ray such that the curly bracket part in Eq. (7) takes minimum value.
The accumulation matrix can be solved row by row from the north pole ray (leftmost column) to the south pole ray (rightmost column) quickly by dynamic programming. The minimum value along the south pole ray corresponds to the minimum cost from north pole to south pole. As the parent value of each point (x,y) recorded the position of the point to its left that leads to the minimum cost at (x,y), from right to left, for each column, the point on the minimum cost path is identified as seen in Fig. 4.
Figure 4.

Boundary points calculated by dynamic programming overlaid on the image. [Color figure can be viewed at wileyonlinelibrary.com]
When calculating the accumulation matrix for one column, the dynamic programming only uses information from its predecessors.
The 2D segmentation result can easily be converted back to 3D. Each triangle on the mesh and the center of the ROI form a tetrahedron. For a give voxel, its elevation determines its level, and its longitude determines which tetrahedron the ray passes through. The length of the line segment from the center to the voxel is used to ascertain whether it is inside or outside the triangle mesh.
2.C. Refinement by active contours
The tumor boundary identified by converting minimum cost path in 2D to surface in 3D works well in general, but may include regions whose density was beyond typical lymph node density range in some cases. Regions with density lower than 0 HU and higher than 160 HU are excluded and the result is smoothed with morphological operations. Then, geometric active contours are applied to evolve a contour to high gradient boundary while keeping the contour smooth.15
A modified geometric active contour method was used to refine the contour.16 As the initial contour was close to the true boundary, the inflation or deflation term was not used. To mitigate the problem that the contour may pass through weak boundary, we strengthened the potential well by increasing its coefficient term α in the following equation. A volume‐preserving mean curvature flow was employed to smooth the contour with coefficient β.
| (8) |
Where is a level set function that has negative values at points inside the boundary, positive values at points outside the boundary, and zero on the boundary. κ is the curvature defined as , and κ mean is the average of the curvature along the contour.
α and β were a fixed value of 10 throughout the study.
When the evolution stopped, the lesion was taken as the region with .
Figure 5 showed the final segmentation result.
Figure 5.
Computer segmentation result of the lesion in Fig 3. [Color figure can be viewed at wileyonlinelibrary.com]
3. Materials and results
3.A. Materials
A total of 48 colorectal cancer patients were scanned on CT with contrast: 14 patients were scanned with GE scanners, 14 were scanned with Siemens scanners, and 20 were scanned with Phillips scanners. The number of scans with interval between adjacent slices of 1.5, 2, 2.5, 3, 3.2, and 5 mm was 5, 7, 10, 16, 7, and 3, respectively. The pixel spacing ranged from 0.59 to 0.98 mm, with an average value of 0.736 mm.
A total of 54 lymph nodes were identified to evaluate the performance of the algorithm. Three radiologists independently delineated the contours of the nodes manually. The region on which 2 of 3 radiologists agreed was considered the gold standard. The average size of the lymph nodes was 28.0 mm in longest diameter with a standard deviation of 13.2 mm. The average sizes for mediastinum, abdomen, and pelvis nodes were 29.4, 25.6, and 27.3 mm, respectively.
3.B. Performance evaluation
The performance of a segmentation algorithm is often evaluated by comparing the segmentation results of the algorithm with some gold standard, which can be the results generated by human observers.3, 16, 17 The comparison can either be the volumetric matching based, such as Dice coefficient,17 or contour distance‐based, such as the maximum distance between computer result and gold standard, aka, Hausdorff distance, and the average distance between them.
Dice coefficient measures the similarity of two samples.18 For a lymph node, given the set of voxels R C inside the computer‐generated contour and the voxels R G inside the gold standard contour, the Dice coefficient is defined as:
| (9) |
The overlap ratio (also known as Jaccard index19 or intersection over union) is also used in evaluating the similarity of two sets, which is defined as:
| (10) |
Dice coefficient and overlap ratio are monotonically related through the following formula:
| (11) |
3.C. Results
The statistics on the performance of the algorithm is shown in Table 1 as well as inter‐reader variabilities. The average Dice coefficient (overlap ratio) of the algorithm on the 54 lymph nodes was 83.2% (71.9%) with a standard deviation of 7.8% (10.6%). The range of Dice coefficients (overlap ratios) is from 54.3% to 93.8% (37.3% to 88.4%), and first, second (median), and third quartiles of Dice coefficients (overlap ratios) were 80.5%, 83.9%, and 88.7% (67.2%, 72.3%, and 79.3%). In a study on general lesion segmentation evaluation, radiologists agreed that an overlap ratio of 70% and above was considered good, 40%–60% acceptable, and below 40% poor.20 According to these criteria, all of the segmentations could be considered good or acceptable, and 53 of 54 segmentations could be considered acceptable, and 32 of them could be considered good. Figure 6 showed some typical segmentation results. Figures 6(a) and 6(c) showed computer results at first and second quartiles (Dice coefficients 0.81 and 0.84). Figure 6(e) showed the result with Dice coefficient 0.94.
Table 1.
Statistics of the performance of the algorithm and inter‐reader variabilities
| Computer vs gold standard | R1 vs R2 | R1 vs R3 | R2 vs R3 | |
|---|---|---|---|---|
| Dice coefficient ± SD (%) | 83.2 ± 7.8 | 84.6 ± 9.8 | 88.3 ± 7.1 | 86.2 ± 7.5 |
| Hausdorff distance ± SD (mm) | 8.9 ± 8.0 | 6.8 ± 4.0 | 5.4 ± 3.0 | 5.9 ± 3.5 |
| Average distance ± SD (mm) | 1.4 ± 1.0 | 1.2 ± 0.7 | 0.9 ± 0.5 | 1.0 ± 0.5 |
Figure 6.
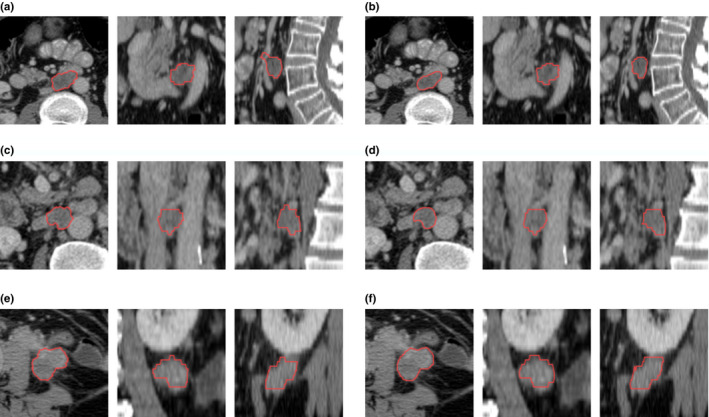
Some segmentation results. (a), (c), and (e) were the computer results in axial, coronal, and sagittal view, and (b), (d), and (f) were the majority vote of the three human observers. The Dice coefficient of (a) and (b) was at the first quartile, 0.81; the Dice coefficient of (c) and (d) was at the second quartile (median), 0.84; the Dice coefficient of (e) and (f) was 0.93. [Color figure can be viewed at wileyonlinelibrary.com]
Large Hausdorff distance was observed between computer and gold standard and among readers. The average maximum distance between computer contour and gold standard boundary is 8.9 mm with a standard deviation of 8.0 mm. Although large interobserver Hausdorff distance was also observed, for example, average of 6.8 mm between R1 and R2, the computer results deviated from gold standard more. One explanation could be that the algorithm can make mistakes that a human observer does not, for example, omit part of the lesion for some elongated or irregular lesions.
The average distance between computer and gold standard and among readers was much smaller than Hausdorff distance. The average distance of the computer results and gold standard showed an average of 1.4 mm and standard deviation of 1.0 mm, close to the average of 1.2 mm between reader 1 and reader 2.
The distribution of the comparison metrics was shown in box plots in Fig. 7. Reader 1 and reader 2 had the worst agreement in terms of Dice coefficient, and the first to third quartile range fully encompassed the same range for the agreement between computer result and the gold standard [Fig. 7(a)]. Figures 7(b) and 7(c) showed that there were more extreme cases that the computer results deviated from the gold standard, and agreement between the computer result and the gold standard, in terms of distance, was slightly worse than the agreement among readers.
Figure 7.
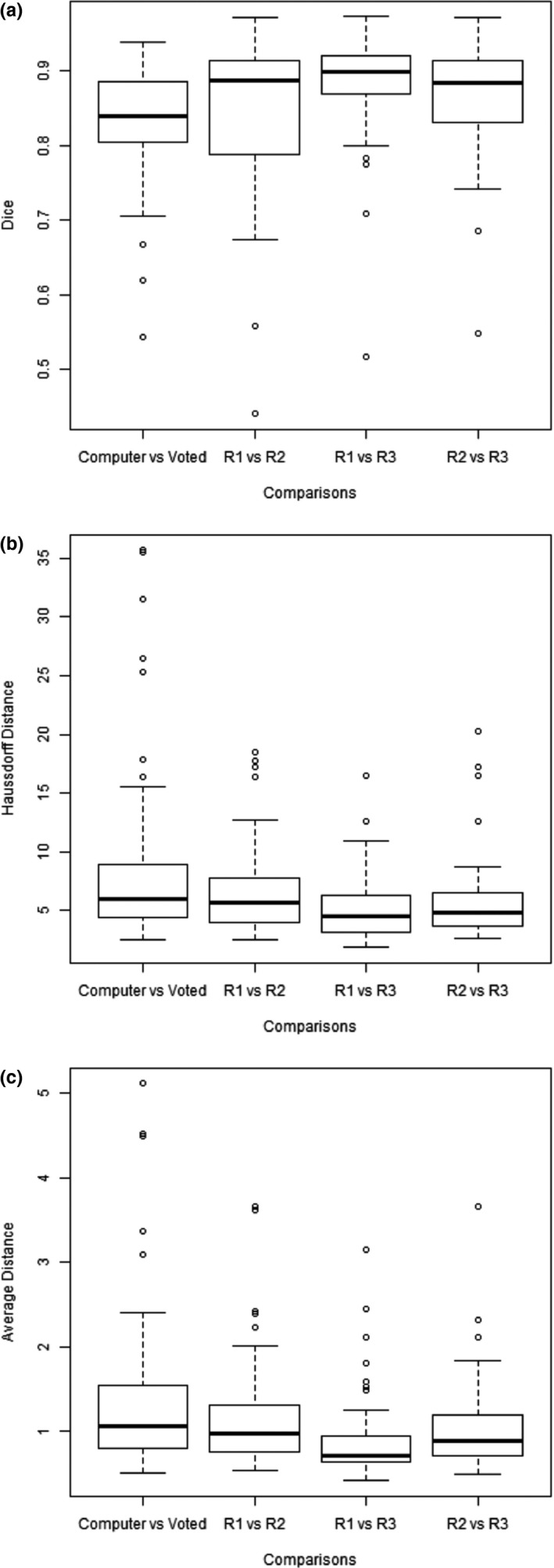
Box plots of Dice coefficients (a), Hausdorff distances (b), and average distances (c) between computer and the majority vote (gold standard) and among radiologists.
4. Discussion
The proposed method was comprised of two steps, an initial segmentation by dynamic programming (DP) and a refinement step by excluding nonlesion regions and morphological smoothing (MS) and active contours (AC). The initial segmentation step was crucial as it would be hard to refine a contour that was far off from the expected boundary.
A few experiments were conducted to evaluate the contribution of each component in the proposed method. Four variants of the proposed method, namely, a method that only used dynamic programming (DP), a method with DP and MS, a method with DP with only gradient and discontinuity cost (simple DP), and simple DP with MS and AC, were tested with the same lesions. The results were compared with the proposed method in Table 2.
Table 2.
The performance of the proposed method in comparison with four variants
| Dice (%) | Hausdorff distance (mm) | Average distance(mm) | |
|---|---|---|---|
| DP + MS + AC (proposed) | 83.2 | 8.9 | 1.4 |
| DP | 79.0 | 8.9 | 1.6 |
| DP + MS | 79.7 | 8.9 | 1.5 |
| Simple DP | 67.4 | 14.4 | 3.0 |
| Simple DP + MS + AC | 77.5 | 11.7 | 2.0 |
Bold values were indicates the best results achieved in the experiment.
Unsurprisingly, the proposed method (DP + MS + AC) showed the best results in all variants. DP alone yielded results with reasonable good Dice coefficient (average 79.0%). With MS, the average Dice coefficient increased to 79.7%, and average distance to gold standard also improved slightly. And with AC, the average Dice coefficient increased to 83.2%, and average distance to gold standard further reduced.
A good cost function was crucial to the performance of dynamic programming. The proposed method took into consideration high gradient at boundary and homogeneous inside the lesion. A DP with simple gradient cost performs poorer in terms of Dice coefficient and distance, and the refinement step could improve but the end result was worse than the proposed method.
DP has the strength in segmenting some lesions with weak boundaries. Lymph nodes can be found in many places, sometimes attached to anatomical structures of similar intensity, and the lack of edge response and the absence of contrast impose difficulty to edge‐ or region‐based segmentation methods. DP guarantees to find a continuous path with minimum cost. The cost function was designed that a path passing through the clear boundary points and bridging the gap (weak boundary) smoothly has a small cost.
To evaluate the performance of segmentation algorithm, it is often to compare the computer‐generated results with human readers. However, it is hard and time‐consuming for human observers to draw the target boundaries. Sometimes, the computer results were compared with the results of one experienced human reader,3 sometimes more than one human readers participated in the effort,17, 21 and the majority vote of the human observers, that is, the regions that the majority of the observers agreed upon, were considered the gold standard. It is known that inter‐reader variability can be large in medical imaging;22 we used the majority vote as the gold standard which mitigated the inter‐reader variability.
It is difficult to compare different algorithms directly, as different datasets and different gold standards were employed. Yan et al. segmented 29 lymphomas and achieved an overlap ratio of 83.2%.3 Beichel and Wang segmented 111 lymph nodes, after adjusting the result of 40 cases, achieved average Dice coefficients of 84.7%, 83.6%, and 80.9%, dividing the dataset into three groups.5 Our algorithm achieved an average Dice coefficient of 83.2%, which was close to inter‐reader variability, and similar to Beichel and Wang's results.
We assumed that the lymph nodes were compact; however, some lymph nodes are less compact than others. For example, elongated lymph nodes can extend much longer in Z axis than the unidimensional measure in XY plane. This posed difficulty as a compact shape could result in a smaller cost than the actual boundary. Figure 8(c) showed an elongated lesion that the computer missed a portion of the lesion.
Figure 8.
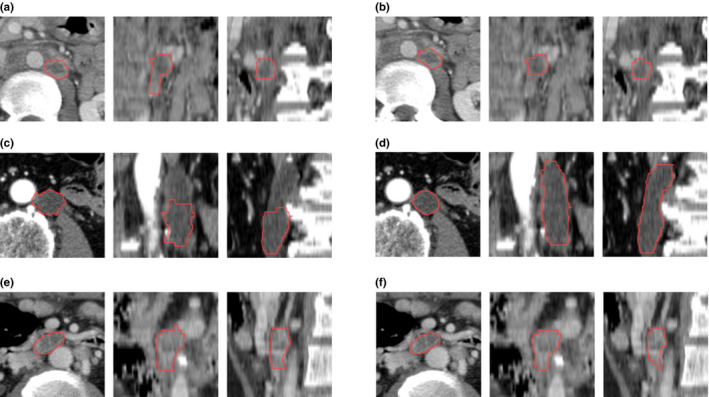
The three cases with worst Dice coefficients. (a), (c), and (e) showed computer segmentation results in axial, coronal, and sagittal view, and (b), (d), and (f) showed the majority vote of the three human observers; the Dice coefficients of which were 0.54, 0.62, and 0.67, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
Although generally lymph nodes showed homogeneous density distributions, some lymph nodes can have irregular enhancement patterns, and some may have necrosis in the center. The algorithm could perform poorer in these situations. Figure 8(a) and 8(e) showed lesions with necrosis and peripheral enhancement.
5. Conclusions
Analysis of enlarged lymph nodes is crucial in staging cancer and assessing treatment response. Automatic quantification of lymph nodes is a difficult task as the surroundings may be complex. We proposed a two‐stage method. The volume of interest was converted to 2D by ray casting. A dynamic programming procedure was used to find an optimal triangle mesh that minimized the cost function, which assumed low value when the edge was strong, the interior was homogeneous, and the shape was compact. The mesh surface was then refined by active contours. This method would be valuable for lesion contour delineation and volumetric quantification in clinical applications such as treatment planning and therapy response assessment.
Conflict of interest
The authors have no conflicts to disclose.
Acknowledgments
This work was in part supported by Grants U01 CA140207 from the National Cancer Institute (NCI). The content is solely the responsibility of the authors and does not necessarily represent the funding sources.
References
- 1. Zhao B, Oxnard GR, Moskowitz CS, et al. A pilot study of volume measurement as a method of tumor response evaluation to aid biomarker development. Clin Cancer Res. 2010;16:4647–4653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Honea DM, Ge Y, Snyder WE, Hemler PF, Vining DJ. Lymph node segmentation using active contours. Proc. SPIE. 1997;265–273.
- 3. Yan J, Zhao B, Wang L, Zelenetz A, Schwartz LH. Marker‐controlled watershed for lymphoma segmentation in sequential CT images. Med Phys. 2006;33:2452–2460. [DOI] [PubMed] [Google Scholar]
- 4. Dornheim L, Dornheim J, Rössling I. Complete fully automatic model‐based segmentation of normal and pathological lymph nodes in CT data. Int J Comput Assist Radiol Surg. 2010;5:565–581. [DOI] [PubMed] [Google Scholar]
- 5. Beichel RR, Wang Y. Computer‐aided lymph node segmentation in volumetric CT data. Med Phys. 2012;39:5419–5428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Schwartz LH, Zhao B, Yan J. Automated determination of lymph nodes in scanned images. Patent US20080317314 A1. 2008.
- 7. Barbu A, Suehling M, Xu X, Liu D, Zhou SK, Comaniciu D. Automatic detection and segmentation of axillary lymph nodes. Med Image Comput Comput Assist Interv. 2010;13:28–36. [DOI] [PubMed] [Google Scholar]
- 8. Feulner J, Zhou SK, Hammon M, Hornegger J, Comaniciu D. Lymph node detection and segmentation in chest CT data using discriminative learning and a spatial prior. Med Image Anal. 2013;17:254–270. [DOI] [PubMed] [Google Scholar]
- 9. Wang J, Engelmann R, Li Q. Segmentation of pulmonary nodules in three‐dimensional CT images by use of a spiral‐scanning technique. Med Phys. 2007;34:4678–4689. [DOI] [PubMed] [Google Scholar]
- 10. Ungru K, Jiang X. Dynamic programming based segmentation in biomedical imaging. Comput Struct Biotechnol J. 2017;15:255–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Lalande A, Legrand L, Walker PM, et al. Automatic detection of cardiac contours on MR images using fuzzy logic and dynamic programming. Proc AMIA Annu Fall Symp. 1997:474–478. [PMC free article] [PubMed]
- 12. Liu J, Ma W, Lee SY. A Segmentation Method Based on Dynamic Programming for Breast Mass in MRI Images. In International Conference on Medical BiometricsBerlin, Heidelberg: Springer; 2008:4901:307–313. [Google Scholar]
- 13. Sun C, Pallottino S. Circular shortest path in images. Pattern Recogn. 2003;36:709–719. [Google Scholar]
- 14. Timp S, Karssemeijer N. A new 2D segmentation method based on dynamic programming applied to computer aided detection in mammography. Med Phys. 2004;31:958–971. [DOI] [PubMed] [Google Scholar]
- 15. Caselles V, Kimmel R, Sapiro G. Geodesic active contours. Int J Comput Vis. 1997;22:61–79. [Google Scholar]
- 16. Tan Y, Schwartz LH, Zhao B. Segmentation of lung lesions on CT scans using watershed, active contours, and Markov random field. Med Phys. 2013;40:043502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Cui Y, Tan Y, Zhao B, et al. Malignant lesion segmentation in contrast‐enhanced breast MR images based on the marker‐controlled watershed. Med Phys. 2009;36:4359–4369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- 19. Jaccard P. The distribution of the flora in the alpine zone. New Phytol. 1912;11:37–50. [Google Scholar]
- 20. Jolly MP, Grady L. 3D general lesion segmentation in CT. 5th International Symposium on Biomedical Imaging: From Nano to Macro. 2008;796–799.
- 21. Armato SG III, McLennan G, Bidault L, et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): a completed reference database of lung nodules on CT scans. Med Phys. 2011;38:915–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Armato SG III, McNitt‐Gray MF, Reeves AP, et al. The Lung Image Database Consortium (LIDC): an evaluation of radiologist variability in the identification of lung nodules on CT scans. Acad Radiol. 2007;14:1409–1421. [DOI] [PMC free article] [PubMed] [Google Scholar]


