Report of the AAPM TG‐256 on the relative biological effectiveness of proton beams in radiation therapy

Abstract

The biological effectiveness of proton beams relative to photon beams in radiation therapy has been taken to be 1.1 throughout the history of proton therapy. While potentially appropriate as an average value, actual relative biological effectiveness (RBE) values may differ. This Task Group report outlines the basic concepts of RBE as well as the biophysical interpretation and mathematical concepts. The current knowledge on RBE variations is reviewed and discussed in the context of the current clinical use of RBE and the clinical relevance of RBE variations (with respect to physical as well as biological parameters).

The following task group aims were designed to guide the current clinical practice:

1. Assess whether the current clinical practice of using a constant RBE for protons should be revised or maintained.

2. Identifying sites and treatment strategies where variable RBE might be utilized for a clinical benefit.

3. Assess the potential clinical consequences of delivering biologically weighted proton doses based on variable RBE and/or LET models implemented in treatment planning systems.

4. Recommend experiments needed to improve our current understanding of the relationships among in vitro, in vivo, and clinical RBE, and the research required to develop models. Develop recommendations to minimize the effects of uncertainties associated with proton RBE for well‐defined tumor types and critical structures.

1.

Table of Contents
Abstract
1. INTRODUCTION
1.A. Definition of relative biological effectiveness
1.B. Rationale for the current clinical use of RBE=1.1
1.C .Advantages and disadvantages of using a constant RBE
1.D. Potential clinical significance of understanding spatial variations in RBE
1.E. Potential reasons for differences in the biological effects between protons and photons
2. PROTON RBE MODELS
2.A. The RBE as parameterized within the linear‐quadraticcell survival model
2.B. Empirical models for the effects of proton LET on α and β
2.C. Empirical models based on experimental microdosimetry
2.D. Mechanism‐inspired models for Proton RBE
2.D.1. Local effect model
2.D.2. Microdosimetric‐kinetic model
2.D.3. Repair‐misrepair‐fixation model
2.E. Clinical implications of biophysical models of proton RBE
3. REVIEW OF PUBLISHED EXPERIMENTS
3.A. Methods
3.B. Clonogenic cell survival as surrogate for the RBE for TCP
3.B.1. RBE as a function of LET
3.B.2. RBE as a function of (α/β) γ
3.B.3 .RBE as a function of dose
3.B.4. Patient variability and RBE as function of genomic heterogeneity
3.B.5. Other biological endpoints related to cell survival
3.B.6. Tumor response in vivo
3.C. Proton RBE related to normal tissue complication probability
3.D. Summary: Assessment of the deviations of RBE from 1.1
4. ASSESS WHETHER THE CURRENT PRACTICE OF A CONSTANT RBE 6;SHOULD BE REVISED
4.A. Should we use an average RBE value different from the current value of 1.1?
4.B. Should we use a constant RBE value, which may differ from tumor to tumor, organ to organ, or patient to patient?
4.C. Is there enough evidence to apply RBE values depending on dose, endpoint, and LET?
4.D. Is there a potential difference in RBE between passively scattered beams and beam scanning?
4.E. What information should be saved in treatment planning systems for outcome analysis?
5. ASSESSMENT OF CLINICAL IMPACT WHEN REVISING CURRENT PRACTICE ON RBE
5.A. Practical considerations when dealing with RBE uncertainties in current practice
5.B. Assess treatment sites for which a revision of current clinical practice would be most significant
5.C. Biological dose in treatment plan optimization
5.D. Impact on dose normalization and clinical physics
6. RECOMMENDATIONS FOR FUTURE EXPERIMENTS
6.A. Uncertainties in measured RBE values: Standardization of dosimetric reporting and experimental parameters
6.B. Novel and mechanistic biology studies to quantify and explain RBE variability
7. SUMMARY AND RECOMMENDATIONS
Abbreviations
References

Abbreviations

CSC

cancer stem cell

CT

computed tomography

CTV

clinical target volume

DICOM

Digital Imaging and Communications in Medicine

DICOM RT ION

DICOM Ion Radiation Therapy

DICOM RT

DICOM Radiation Therapy

DNA

deoxyribonucleic acid

DSB

double‐strand break

EUD

equivalent uniform dose

Gy(RBE)

prescription dose in proton therapy

IMPT

intensity modulated proton therapy

IMRT

intensity modulated photon therapy

LEM

local effect model

LET

linear energy transfer

LET_d

dose‐averaged linear energy transfer

LPL

lethal and potentially lethal (model)

LQ

linear quadratic

MKM

microdosimetric‐kinetic model

MRI

magnetic resonance imaging

MU

monitor unit

MV

megavoltage

NTCP

normal tissue complication probability

OAR

organ at risk

PET

positron emission tomography

PTV

planning target volume

RBE

relative biological effectiveness

RMF

repair‐misrepair‐fixation (Model)

RMR

repair‐misrepair (Model)

ROS

reactive oxygen species

SLD

sublethal damage

SOBP

spread‐out Bragg peak

TCD50

dose for 50% local tumor control

TCP

tumor control probability

TPS

treatment planning system

2. Introduction

1.A. Definition of relative biological effectiveness

Current treatment planning methods generally rely on dose‐based surrogates of biologic response, such as the underlying dose prescription and organ at risk (OAR) plan constraints, instead of directly optimizing clinical endpoints such as tumor control probability (TCP) and normal tissue complication probability (NTCP). However, when using treatments with nonconventional radiation modalities such as protons, this approach is insufficient as the same absorbed dose distribution may produce a very different clinical outcome due to differences in energy deposition characteristics at the microscopic (cellular and molecular) levels. These effects are quantified by the relative biological effectiveness (RBE).

The proton RBE is the ratio of the absorbed doses that produce the same biological effect or clinical endpoint X [Eq. (1)] between a reference radiation (e.g., ⁶⁰Co γ rays or MV x rays) and a proton beam irradiation under otherwise the same conditions, i.e.,

$$RBE(\text{EndpointX})=\frac{Dos{e}_{\mathit{reference}}(\text{EndpointX})}{Dos{e}_{\mathit{proton}}(\text{EndpointX})}$$ (1)

In Eq. (1), the equivalent proton and reference radiation doses are an implicit function of many physical, biological, and treatment parameters, including the fraction size, total treatment dose, dose rate, and proton beam properties. Also, it is important to note that the concept of an RBE, which is a measure of relative rather than absolute biological response, varies from endpoint to endpoint. For example, the RBE for cell survival is not necessarily equivalent to the RBE for a clinical endpoint. It is currently recommended by the International Commission on Radiation Units and Measurements (ICRU)¹) that the RBE‐weighted dose be defined as the product of absorbed dose and RBE (with the unit Gy(RBE)).

It is important to understand that this definition is clinically easiest to interpret in regions of tissue that receive a uniform absorbed dose. For example, in vitro cell survival experiments are usually conducted under uniform irradiation at the sample location, that is, the uniform absorbed dose can be used to describe the dose effect. In regions of tissue that receive a nonuniform dose of radiation, the RBE must be computed for each (uniformly irradiated) region of tissue within the larger tissue region of interest. In organs at risk, the determination of RBE values is further complicated by the interplay between dose–volume structural and functional effects and inhomogeneities in the dose distribution. The RBE for normal tissue effects due to nonuniform dose (such as spinal cord injury, lung injury, etc.) is more challenging to define. In the clinical context, RBE values should be assigned on a dose computation voxel grid (which can be the same as the CT voxel grid) as a dose‐modifying factor considering the dose in each voxel independent of other voxels. Organ effect modeling can then be based on the RBE‐weighted dose distribution.

1.B. Rationale for the current clinical use of RBE = 1.1

Proton therapy treatments are currently planned and delivered assuming a constant proton RBE relative to high‐energy photons of 1.1, meaning that a given proton absorbed dose is assumed to be equivalent to a 10% higher photon absorbed dose. This value was deduced as an average value of measured RBE values in vivo mostly done in the early days of proton therapy, that is, in the 1970s. Note that the average value of 1.1 relative to Co‐60 reference radiation was initially reported for (a) the center of the target volume, (b) a 2 Gy(RBE) fraction size, and (c) averaged over various endpoints such as skin reaction or LD₅₀.

To validate clinical practice, a review in 2002 summarized RBE values for proton therapy based on published data.² It was found that, although the RBE varied as a function of both physical and biological parameters, the estimated average RBE in the center of a spread‐out Bragg peak (SOBP) was indeed ~1.1 at 2 Gy(RBE) fraction size.² The ICRU in 2007¹ as well as the International Atomic Energy Agency (IAEA) in 2008³ judged that the continued use of a constant RBE of 1.1 in proton therapy is not unreasonable.

1.C. Advantages and disadvantages of using a constant RBE

There are obvious advantages of using a constant RBE. Converting photon doses into biologically equivalent proton doses for clinical trials is then straightforward. Furthermore, clinical dosimetry is based on the absorbed dose distributions in the target. At present, commercial treatment planning systems (TPS) do not provide an option to compute dose distributions weighted by a variable proton RBE.

On the other hand, the continued use of a constant RBE may lead to suboptimal plans that do not fully exploit the potential of proton therapy. Any opportunities to exploit spatial and dosimetric variations in RBE to further enhance proton therapy will depend on the magnitude of such variations as well as the consideration of clinical scenarios under which such deviations occur. Furthermore, the interpretation of outcome data might be misleading when tissue‐ and spatially variant RBE variations are neglected.

While the RBE deviation from 1.1 may not seem to be significant clinically today due to many other sources of uncertainty, the clinical evidence of RBE variability may become apparent as other sources of uncertainty are reduced and as more treatment response and bio‐ and imaging marker data are accumulated. Furthermore, field‐specific dose (and RBE) distributions are becoming more complex with pencil beam scanning techniques employing multifield uniform dose as compared to passive scattered beam deliveries where each field delivers a uniform SOBP distribution.

1.D. Potential clinical significance of understanding spatial variations in RBE

There is substantial evidence that the RBE of protons may be a complex function of numerous factors such as treatment technique (proton energy, scanning technique), dose, cell type, oxygenation, intrinsic radiosensitivity, and the biological or clinical endpoint of interest (local tumor control or treatment complication). Locally, in a voxel, the RBE depends on endpoint, dose, and particle energy distributions(s).

In view of the biological complexity of the RBE concept, a fresh look at the current clinical practice of a constant RBE of 1.1 is warranted, especially with regards to

1. If the goal is to incorporate RBE variations in proton therapy, it is not sufficient to confirm that the average value in the center of a treatment field is 1.1. We need to understand the spatial variations of RBE within and outside the target volume, ideally on a voxel‐by‐voxel basis. Voxel refers to a volume of a few mm³ over which averaging may occur when computing and reporting dose and other quantities. There is also a need to understand how the RBE at the cellular and voxel levels contributes to the overall RBE for an organ or larger regions of tissue and, especially, for dose‐limiting critical structures and complex functional endpoints.

2. Currently, there are no clear clinical data that would indicate the need to adopt a constant RBE value other than 1.1, which may in part be because range uncertainties may mitigate the effect of an increase in RBE at the end of range. On the other hand, there have been concerns that we may under‐ or overestimate the RBE for certain structures and that this could potentially impact the clinical efficacy of proton therapy or give rise to unexpected complications.^{4, 5, 6}

3. Uncertainties in dose calculations and delivering proton therapy treatments are being reduced based on research in many areas which will most likely result in a reduction in margins potentially increasing the significance of correcting for spatial variations in proton RBE.⁷

4. It has been suggested that the dose‐averaged linear energy transfer (LET_d) could potentially be used in biological treatment optimization even without knowing dose‐ and endpoint‐specific RBE values accurately.⁸ It has been shown that by considering spatial variations in LET_d within treatment plan optimization, it might be possible to increase the therapeutic ratio in intensity‐modulated proton therapy (IMPT).^{8, 9} There is a need to understand whether or not differences in plans optimized using (LET_d times dose) vs (RBE times dose) for relevant molecular or cellular endpoint are large enough to be clinically relevant when viewed against the uncertainties and gaps in our understanding of the underlying clinical endpoint and patient‐specific biology.

5. An increasing number of proton centers are treating patients with proton beam scanning, and it has been shown that variations in RBE might be greater in scanned beams relative to passive scattered beams.^{9, 10} IMPT delivered with scanning pencil beams holds the greatest therapeutic potential and will be employed at the majority of new proton centers.

6. Recent theoretical studies have addressed the issue of RBE spatial variations in patients^{11, 12, 13, 14, 15, 16} and have analyzed the impact of fractionation on RBE in proton therapy.^{17, 18, 19, 20} There is thus increased interest in understanding the clinical relevance of RBE spatial variations.

1.E. Potential reasons for differences in the biological effects between protons and photons

Endpoints of interest for radiation therapy are exhibited at the tumor/organ/tissue level. These clinical endpoints are early and late normal tissue toxicity and local tumor control or recurrence (local failure) that are driven by tissue architecture and effects at the cellular and subcellular levels, in particular cell survival and proliferation. There are many potential underlying biological mechanisms responsible for the enhanced biological effectiveness of protons relative to photons.²¹ Even if protons induce the same number of DNA double‐strand breaks (DSBs) per unit dose as photons, the distribution of the DSBs among cells and among the individual chromosomes or parts of a chromosome may differ. It is not only the absolute yield of DNA damage but also the local complexity and spatial distribution of DNA damage within the cell and along the DNA, for example, locations of DSBs, single‐strand breaks or base damage, as well as the properties of the intrinsic cell repair mechanisms that determines biological effect.²² Physically, an important aspect to understanding radiation effects lies in the spatial distribution of energy deposition events and the clustered energy depositions this may cause. There are several spatial levels that need to be considered: clustering of DNA lesions at the level of a few tens of base pairs (e.g., local complexity of the cluster), clustering of DNA lesions at the level of chromosomes (e.g., proximity effects and breakage and reunion theory), and the spatial distribution of damage across cells. Biologically, the complexity of clustered DNA lesions may correlate with the choice of DNA repair pathway and cells with mutations in DNA repair genes may have a differential response as a function of how complex the clustered DNA lesions are.²³

3. Proton RBE models

This subsection summarizes and compares some of the empirical and mechanism‐inspired biophysical models for proton RBE at the molecular and cellular levels. The scope of the discussion examines the relationship between proton RBE, the linear–quadratic (LQ) model radiation sensitivity parameters α and β (or α/β), and putative mechanisms of action related to the induction and biological processing of DNA DSBs into more lethal forms of damage. The presented molecular and cellular RBE models are briefly contrasted to the assumptions implicit in current clinical use of a constant RBE = 1.1 in proton therapy. The model formalisms are not necessarily consistent as empirical models are based on fit parameters, whereas mechanism‐inspired models may rely on different interpretations of biological and physical phenomena. This section is not meant to be comprehensive. Interested readers are directed to the cited literature for an in‐depth discussion of relevant concepts.

2.A. The RBE as parameterized within the linear‐quadratic cell survival model

The LQ model is a well established model that has been used successfully in radiation biology for decades.²⁴ The LQ model relates the surviving fraction S to the dose D by

$$S(D)=\text{exp}(-\alpha D-\beta G{D}^2),$$ (2)

where α (Gy⁻¹) and β (Gy⁻²) characterize the intrinsic radiation sensitivity of cells of interest in a tumor target or tissue of interest, and G is the generalized (Lea‐Catcheside) dose protraction factor.²⁵ The equation is typically used with G = 1 (single fraction), and α/β is often used to characterize the sensitivity of a cell or tissue to fraction size.

The dose protraction factor corrects the quadratic (βD ²) term in the LQ model for the effects of fraction size as well as the overall temporal pattern of radiation delivery, that is, the effects of intra‐ and interfraction sublethal damage (SLD) repair. For the special case when the time interval between daily dose fractions is large compared to the half‐time for SLD repair τ (i.e., repair is complete between fractions), the dose protraction factor with monoexponential repair kinetics as shown below is often used,²⁵ that is,

$$G(n)=\frac{2}{n{x}^2}(e^{-x}+x-1),wherex\equiv \lambda \mathrm{\Delta }t$$ (3)

here, n is the number of daily fractions (D = n × d if d = dose per fraction), λ is a repair constant λ = ln2/τ, and Δt is the total time to deliver a single fraction. For the special case when λΔt → ∞ (large fraction delivery time), G → 0. For the alternate special case where λΔt → 0 (short fraction delivery time), G≅1/n. Equation (3) is premised on the idea that the repair of SLD formed on one treatment day is complete before (and therefore unable to interact with) SLD formed on subsequent treatment days. Versions of the dose protraction factor that account for the incomplete repair^{26, 27} or a quadratic SLD repair process^{28, 29, 30, 31, 32, 33} have also been proposed. When the dose protraction factor is included in the LQ model, α and β are considered independent of the kinetics of SLD repair. That is, when a single dose of radiation is delivered at very high dose rate, the dose delivery time becomes small compared to the half‐time for SLD repair τ and G → 1. Conceptually, this scenario corresponds to a situation in which negligible SLD repair occurs during irradiation, although significant levels of SLD repair may still occur after irradiation (e.g., between treatment days).

Accordingly, using Eq. (2), the RBE can be derived as:

$$\begin{array}{cc}& RBE=\frac{{(\alpha /\beta )}_{\gamma }}{2G_{\gamma }D}\hfill \\ & \left\{-1+\sqrt{1+\frac{4G_{\gamma }D}{{(\alpha /\beta )}_{\gamma }}\left(1+\frac{G_{\gamma }D}{{(\alpha /\beta )}_{\gamma }}\frac{{(RB{E}_{\mathit{HD}})}^2}{RB{E}_{\mathit{LD}}}\right)RB{E}_{\mathit{LD}}}\right\}\hfill \end{array}$$ (4)

here, D and D _γ are the total treatment dose (D = n × d). The low‐dose (LD, D→0) and high‐dose (HD, D→∞) RBE are defined as³⁴

$$RB{E}_{\mathit{HD}}=\sqrt{\frac{\alpha \left(LE{T}_d\right)}{{\alpha }_{\gamma }}}andRB{E}_{\mathit{HD}}=\sqrt{\frac{G\beta (LE{T}_d)}{G_{\gamma }{\beta }_{\gamma }}}$$ (5)

For any combination of non‐zero (biophysically meaningful) radiosensitivity and treatment parameters, RBE _LD and RBE _HD encompass the range of RBE values possible using Eq. (5). Empirical observations indicate that RBE_LD is often larger than RBE_HD, that is, RBE_LD = RBE_max and RBE_HD = RBE_min. ^{17, 34}

Note that per Eqs. (4) and (5), it is not strictly part of the definition of an RBE that the number of fractions used for the reference treatment is (must be) equal to the number of fractions used in the proton treatment. However, clinically, if the proton prescription dose is given as Gy(RBE), it is assumed that both modalities are subject to the same fractionation schedule and that the RBE is assigned as the RBE per dose per fraction. RBE effects are thus typically separated from fractionation effects.

In this case, the RBE for cell survival is the ratio of the dose d _γ of the reference radiation to the proton dose d that produces the same cell surviving fraction, that is, we are seeking the RBE ≡ d _γ /d such that S(d _γ )=S(d). For a polyenergetic proton beam that delivers dose d, the RBE for cell survival is related to the dose‐averaged radiosensitivity parameters α _d and β _d in a region of interest. The RBE simply follows from the LQ model with G = 1. Thus, Eqs. (4) and (5) are a generalization of the more commonly used RBE formula for a single fractionation leading to Eq. (6) for the special case when n = m = 1 and the total treatment dose D is equal to the fraction size d, i.e., D = d/n:

$$RBE=\frac{\sqrt{{\alpha }_{\gamma }^2+4{\beta }_{\gamma }d\left({\alpha }_d+{\beta }_{d}d\right)}-{\alpha }_{\gamma }}{2{\beta }_{\gamma }d}$$ (6)

2.B. Empirical models for the effects of proton LET on α and β

Relative biological effectiveness models based on the LQ model, as computed using Eq. (2) (with G = 1) and (4), estimate RBE for protons based on linear energy transfer (LET), dose per fraction, and the cell‐specific parameters α and β (or α/β) for the reference radiation. The dependence of proton alpha and beta parameters on LET and cell type is defined in different variants for different models. In the Wilkens and Oelfke³⁵ proton RBE model, α = α _γ  + p ₁ LET _d and β = β _γ with α _γ  = 0.1 Gy⁻¹ and p₁ = 0.02 Gy⁻¹/(keV/μm) for V79 cells assuming a specific RBE in the center of the SOBP as reference. Several other empirical proton RBE models for α and β are of a similar form but do not require a reference RBE at the center of the SOBP. In such models,

$$\begin{array}{cc}\hfill \alpha (LE{T}_d)& ={\alpha }_{\gamma }(p_0)+p_1\frac{LE{T}_d}{{(\alpha /\beta )}_{\gamma }},\hfill \\ \hfill \beta (LE{T}_d)& ={\beta }_{\gamma }[p_2+p_{3}h(LE{T}_d)]\hfill \end{array}$$ (7)

where p ₀, p ₁, p ₂, and p ₃ are model‐specific (fitted) parameters (Table 1) and h(LET _d ) is defined as

$$h(LE{T}_d)=\left\{\begin{array}{c}\frac{LE{T}_d}{{[\alpha /\beta ]}_{\gamma }}\hfill \\ 1\hfill \\ LE{T}_d\sqrt{{(\alpha /\beta )}_{\gamma }}\hfill \end{array}\right.$$ (8)

in Refs. ^{12, 34}, Ref 36, and Ref 37, respectively. These models are based on a subset of published in vitro cell survival data. Empirical models such as these suggest a consensus on a trend toward RBE _LD ≡ α/α _γ that increases in linear fashion with increasing proton LET _d . The empirical models also imply that the slope in RBE _LD as a function of LET is larger for cells with a small (α/β) _γ than for cells with large (α/β) _γ . For large dose per fraction treatments, the RBE will approach RBE _HD ≡ (β/β _γ )^1/2 = [p ₂ + p ₃  h(LET _d )]^1/2. Values of RBE _HD increase with increasing LET in the Carabe et al.^{12, 34} and McNamara et al.³⁷ models and are independent of LET in the Wilkens and Oelfke³⁵ and Wedenberg³⁶ models. Also, RBE _HD is either (a) independent of (α/β) _γ, ^{35, 36} (b) increases with decreasing (α/β) _γ, ^{12, 34} or (c) increases with increasing (α/β) _γ .^{1/2 37}

Table 1.

Recommended parameters for selected empirical proton RBE models. The fits by Wedenberg et al. and Carabe et al. are based on a subset of the experimental cell survival data used by McNamara et al

Model	p0	p1	p2	p3
McNamara37	0.99064	0.35605	1.1012	−0.00387
Wedenberg36	1.0	0.434	1.0	0.0
Carabe12	0.843	0.413644	1.09	0.01612

2.C. Empirical models based on experimental microdosimetry

Linear energy transfer is a macroscopic quantity defined as the average energy locally transferred to the material by a charged particle per unit length of the particle track. This measure can be used as a descriptor of the radiation quality, and has been found to correlate with RBE. LET is a nonstochastic two‐dimensional quantity (energy transfer per path length of a particle). Its dose‐averaged value, LET_d, or track‐averaged value, LET_t, both neglect the shape of the LET distribution.

In a Monte Carlo environment, these quantities can be calculated in patients. For instance, the LET_d is obtained as the energy loss dE of a particle multiplied by the energy loss per particle step dx divided by the density ρ summed over all events relative to the total energy deposited as shown in Eq. (9).

$${\text{LET}}_{\mathrm{d}}=\frac{{\sum }_{\mathit{events}}dE(dE/dx)1/\rho }{{\sum }_{\mathit{events}}dE}$$ (9)

Microdosimetric quantities characterize instead the stochastic nature and spatial distribution of particle interactions in micrometer‐sized volumes. The fundamental microdosimetric quantities are the specific energy z (in Gy) and the lineal energy y (in keV/μm).³⁸ The specific energy in a volume V is defined as z=ε/ρV where ε is the energy imparted in the volume and ρ the mass density of the medium. Lineal energy is the microdosimetric counterpart of LET and is defined as y = ε ₁/$\overline{l}$ where ε ₁ is the energy imparted in the volume in a single event and $\overline{l}$ is the mean chord length of the volume. Similar to the LET quantity one can define the frequency–mean lineal energy, y_F, and the dose–mean lineal energy, y_D.

A different approach, related to microdosimetry, is the consideration of the proton track structure, that is, the stochastic spatial distribution of energy deposition events produced by the primary particle and its spatially and temporally correlated delta ray (electron) halo. Microdosimetric quantities (lineal energy spectra or event size distributions) can either be measured^{39, 40, 41} (e.g., with a tissue‐equivalent proportional counter) or determined from event‐by‐event Monte Carlo track structure simulations.^{42, 43} These spectra have been further converted into RBE using weighting functions from the literature.^{44, 45} A sharp increase in dose‐mean lineal energy for a 1 mm diameter volume (height gas pressure was set to represent a 1 μm diameter sensitive volume) was reported for 15 and 30 MeV⁴⁶ when compared to 50–200 MeV proton beams.³⁹ For smaller, 10 and 100 nm sensitive volumes, it has been reported that dose‐mean lineal energy values only slowly vary for energies between 50 and 300 MeV, followed by a sharp increase for energies below 10 MeV.⁴⁷ Microdosimetry data support small variations in RBE in the middle of an SOBP compared to the entrance region and increase in RBE for proton energies of 30 MeV or less. This predicted increase in RBE based on the conversion of the microdosimetry spectra to RBE is sensitive to empirical‐ and endpoint‐specific weighting functions.^{46, 48}

2.D. Mechanism‐inspired models for proton RBE

The microdosimetric‐kinetic model (MKM) of Hawkins,^{49, 50, 51, 52} recent versions of the local effect model (LEM)⁵³ and the repair‐misrepair‐fixation (RMF) model^{54, 55, 56} are examples of mechanism‐inspired models that explain the effects of particle characteristics such as LET on clonogenic cell survival in terms of putative mechanisms connecting the induction and biological processing of SLD (e.g., DSB) into more lethal forms of damage (e.g., chromosome aberrations). Differences in the models arise from the emphasized mechanisms of action as well as differences in the way proximity and domain‐size effects (a domain is defined as a subcellular volume) are treated.

2.D.1. Local effect model

The LEM aims to derive the biological effects of ion radiation from the response of cells or tissues to photon radiation. The LEM makes use of the concept of a local dose, which is defined as the expectation value of the energy deposition at any position in the radiation field for a given pattern of particle trajectories. The key assumption made in the LEM is that equal “local doses” produce equal local biological effects, independent of the radiation quality. The relevant local dose is derived from an amorphous track structure representation of the energy deposition as a function of the radial distance to the particle trajectory. Particle effectiveness is calculated based on the microscopic local dose distribution pattern of ion traversals within the cell nucleus, assuming the nucleus is the sensitive target for the observed radiation effects.

In the first implementation of the model (LEM I),⁵⁷ the local biological effect is derived directly from the corresponding photon dose–response curve, characterized by the parameters α, β, and threshold dose where the cell survival curve becomes log‐linear, D_t. In LEM II,⁵⁸ the increased yield of DSB, resulting from the induction of DNA single‐strand breaks in close vicinity (<25 base pairs) is taken into account, leading to a further enhancement of the biological effects at very high local doses (>1000 Gy). The LEM III⁵⁹ model extended the track structure model to include an energy dependent extension of the track core. In the latest version (LEM IV⁵³), it is assumed that the final biological response of a cell to radiation is directly linked to the initial spatial distribution and density of DSB within subnuclear targets rather than the local dose distribution itself. In line with the general concepts of the LEM formalism, similar spatial patterns of DSB induction produce the same biological response, independent of the properties of the radiation creating the spatial pattern of initial damage. The calculation of the spatial DSB distribution in LEM IV is directly derived from the (local) radial dose profiles used in earlier versions of the LEM. Assuming a homogeneous distribution of the DNA within the nucleus as a first approximation, the mean number of DSB in any small subvolume of the nucleus is determined from experimental photon data, which indicate that the yield of radiation‐induced DSB is approximately 30 DSB Gy⁻¹ cell⁻¹. Based on the local average number of DSB, spatial DSB distributions are then determined by means of Monte Carlo techniques, that is, actual DSB distributions are determined by considering the amorphous track structure pattern as the probability density distribution of DSB. A sensitivity analysis of the RBE predictions by the LEM model has been reported.⁶⁰ The structure of the LEM formalism is more complex compared to empirical models and simple functional relationships between RBE, dose, LET, and α/β cannot be given.

The LEM is used clinically to compute RBE‐weighted dose distribution for carbon ion therapy.⁶¹

2.D.2. Microdosimetric‐kinetic model

The MKM^{49, 50, 51, 52} combines a microdosimetric formalism to describe the distribution of initial damage within and among cells, as proposed in the theory of dual radiation action,⁶² with a kinetic model for the conversion of the initial radiation‐induced DSB into lethal chromosome aberrations. In the MKM, the nucleus of a mammalian cell is partitioned into p domains. As in the earlier lethal and potentially lethal (LPL)⁶³ and the repair‐misrepair model (RMR)⁶⁴ models, a system of coupled, nonlinear differential equations are used to simulate the time‐dependent conversion of initial DSB into lethal chromosome aberrations. One differential equation tracks the number of unrepaired DSB per domain and another tracks the accumulation of lethal damage per domain. In the MKM, first‐order (individual DSB) and second‐order (pairs of DSB) repair events contribute to the accumulation of lethal damage. The MKM has been developed further to include dose delivery time and their impact on repair pathways.⁶⁵

For convenience, all subnuclear domains in the MK model are assumed to have the same effective size in the sense that, if deformed into a sphere of unit density, they all have the same diameter δ. For mammalian cells, empirically determined values for p range from a few hundred to a few thousand domains per nucleus (δ ~ 0.2–1 μm).⁶⁵ The segments of the DNA within each domain are free to move around within the individual domains. It is assumed that the movement of DNA within each domain, and any damage it bears, is forever confined to the domain in which it was initially created. The confinement of sections of DNA may be due to a combination of tethering of the chromatin to the nuclear matrix or membrane and the excluded volume of other chromosomes or distant parts of the same chromosome. Although the concept of a subnuclear domain may be considered a theoretical fudge factor to account for situations in which pairs of DSB separated by large distances have a low or zero probability of combining to form a lethal chromosome interaction, experimental observation of fluoroscopically marked points on the chromosomes of eukaryotic cells indicates such points move by apparent random walk in a seemingly confined space of about the same size as the hypothesized domains.^{66, 67}

For the LET of protons, the accumulation of lethal damage among cells is well approximated by a Poisson distribution with a mean equal to the number of domains times the average number of lethal lesions per domain. By equating the dose‐dependent formulation of lethal damage to αD + βD ², the MK model can be used to develop formulas to predict the effects of particle LET on α and β consistent with equation (7), ⁵¹:

$$\begin{array}{cc}\hfill \alpha & ={\alpha }_{\gamma }\left(1+p_1\frac{LE{T}_d}{{\left(\alpha /\beta \right)}_{\gamma }}\right),where{p}_1=\frac{0.229}{\rho {\delta }^2}\hfill \\ \hfill \beta & ={\beta }_{\gamma }\left(\mathit{assumed}\right)\hfill \end{array}$$ (10)

For several mammalian cells, the inferred domain diameter from the analysis of cell survival data indicate δ = 0.70 ± 0.14 μm,^{49, 51, 52} which implies values of p ₁ on the order of 0.3–0.7 for mammalian cells. It is striking that the functional form of Eq. (7) derived from several empirical studies of particle RBE is identical to the MK model formula for α. The numerical estimate of p ₁ from 0.3 to 0.7 also encompasses the estimates of p ₁ from empirical studies (Table 1).

The MKM is used clinically to compute RBE‐weighted dose distribution for carbon ion therapy.⁶⁵

2.D.3. Repair‐misrepair‐fixation model

The RMF model⁵⁴ explicitly links the induction and biological processing of initial DSB to the formation of lethal point mutations and chromosome aberrations. In the RMF model, a coupled system of nonlinear ordinary differential equations is used to model the time‐dependent kinetics of DSB induction, rejoining, and pairwise DSB interaction to form lethal (and nonlethal) chromosomal damage. The RMF model assumes that it is the formation of lethal point mutations (e.g., misrepair or fixation of individual DSB) and chromosome damage (primarily exchanges) rather than the initial DSB that are the dominant mechanism underlying the effects of proton LET on reproductive cell survival. The RMF model postulates a first‐order repair term that gives rise to exponential rejoining kinetics for most DSB (>98%) and a second‐order (quadratic) term to account for the small subset of the initial DSB (<2%) that undergo pairwise DSB interactions to form an exchange. The earlier LPL⁶³ and RMR⁶⁴ models also postulate linear and quadratic terms for the repair of sublethal and potentially lethal damage but the RMF model treats initial DSB formation as a compound Poisson process, whereas DSB induction is effectively governed by a simple Poisson process in the LPL and RMR models. A Poisson model for DSB induction is reasonable for low‐LET radiations, but a poor approximation for intermediate and higher LET radiations.⁵⁴ The RMF model considers the entire cell nucleus as the domain for pairwise DSB interactions, whereas the LEM and MKM models treat the interactions and consequences of DSB formed in adjacent and nearby domains independent (separate) from DSB interactions within the same subcellular domain or chromatin loop. The need for explicit subnuclear domains is largely eliminated by considering pairwise DSB interactions arising from the same particle track (intra‐track pairwise DSB interactions) separate from pairwise DSB interactions arising from two or more independent particle tracks (inter‐track pairwise DSB interactions).

For low dose rates and for doses comparable to and smaller than α/β, the RMF system of differential equations is well approximated by an LQ model in which α and β are related to the RBE for DSB induction (RBE _DSB ) by

$$\begin{array}{cc}\hfill \alpha & ={\alpha }_{\gamma }·RB{E}_{\mathit{DSB}}(1+\frac{2{\overline{z}}_F}{{(\alpha /\beta )}_{\gamma }}RB{E}_{\mathit{DSB}}).\hfill \\ \hfill \beta & ={\beta }_r·RB{E}_{\mathit{DSB}}·RB{E}_{\mathit{DSB}}\hfill \end{array}$$ (11)

Note that the form of Eq. (11) is similar to the fit function to experimental data [Eq. (7)]. Here, ${\overline{z}}_F\cong LE{T}_d/\rho {\delta }^2$ is the frequency‐mean specific energy,³⁸ where δ is the diameter of the cell nucleus and ρ is the mass density of the cell nucleus. After substitution of Eq. (11) into Eq. (6), the low‐dose and high‐dose RBE for cell survival (with G = G _R  = 1) is related to RBE _DSB by

$$\begin{array}{cc}\hfill RB{E}_{\mathit{LD}}& =RB{E}_{\mathit{DSB}}(1+\frac{2{\overline{z}}_F}{{(\alpha /\beta )}_{\gamma }}RB{E}_{\mathit{DSB}})\ge RB{E}_{\mathit{DSB}}.\hfill \\ \hfill RB{E}_{\mathit{HD}}& =RB{E}_{\mathit{DSB}}\ge 1\hfill \end{array}$$ (12)

The term in Eqs. (11) and (12) proportional to ${\overline{z}}_F·RB{E}_{\mathit{DSB}}·RB{E}_{\mathit{DSB}}$ arises from the interactions of pairs of DSB formed by the same track, and the term proportional to RBE _DSB arises from the misrepair or fixation of individual DSB. Because of inter‐track DSB interactions, β increases as the square of the RBE for DSB induction.

2.E. Clinical implications of biophysical models of proton RBE

Among the published models, there is a remarkable consensus that proton RBE increases in approximately linear fashion with LET_d (slope ~ 0.03 ± 0.01 per keV/μm) over the range of LET_d values of most significance for clinical proton therapy (i.e., protons with an LET_d up to ~10–15 keV/μm). Differences among the empirical and mechanism‐inspired models primarily arise beyond the Bragg peak and/or how the relation between LET_d and RBE is affected by cell type and large doses per fraction compared to (α/β) _γ . The latter difference among proton RBE models arise from differences in the assumed or modeled effects of proton LET_d on the β radiosensitivity parameter, that is, does β increase, decrease, or remain about the same over the relevant range of proton LET_d values? Based on the models, the use of a constant clinical RBE = 1.1 that is independent of (α/β) _γ , fraction size, and the effective LET_d (or distribution of LET_d values) within tumor targets and OAR is not well justified in terms of our current understanding of the RBE for cell survival.⁶⁸

4. Review of published experiments

3.A. Methods

This section is a summary of a review on experimental data, which mostly focused on proton RBE for clonogenic cell survival, although other endpoints, for example, chromosome aberrations, micronuclei, apoptosis, and animal models, were considered and available data summarized.⁶⁹ The following parameters were extracted or estimated from each published experimental dataset: α _γ and β _γ describing dose–response to low‐LET photons, α and β describing dose–response to protons, and LET_d at the position of the biological sample. For the purpose of relating RBE values to macroscopic dosimetric parameters, LET_d is an approximation that neglects the small‐scale features of the primary particle track. In the center of an SOBP, the average LET_d is typically between ~2.8 keV/μm and ~2.1 keV/μm (decreasing with increasing depth of the SOBP center). Small regions at the distal fall‐off of the SOBP can typically show LET_d values up to 12 keV/μm.⁶⁹ This holds for typical SOBPs with ranges between 10 and 25 cm and SOBP widths between 5 and 20 cm. Note that for low‐energy beams and small SOBP widths (e.g., as used for treating ocular melanoma), LET_d values could be higher, that is, potentially up to ~5 keV/μm in the SOBP center and ~20 keV/μm in the sharp fall‐off region. The above overall characteristics hold for both passively scattered beams and active scanning beams (IMPT) provided the dose in the latter case is reasonably uniform. While primary and secondary protons (the latter caused by nuclear interactions) are the main contributor to dose in proton therapy, secondary particles heavier than protons can also impact dose and LET_d (and RBE) up to a few percent in particular in the entrance region.⁷⁰

3.B. Clonogenic cell survival as surrogate for the RBE for TCP

The most relevant cellular endpoint for an assessment of the clinical RBE for local tumor control is clonogenic cell survival, which is also the most studied endpoint in vitro. Most publications and experiments in vitro focus on the dose range between ~1 and 10 Gy. Most in vitro experiments were conducted using Chinese hamster lung fibroblast or ovary cell lines, with some studies using rat and mouse cell lines, mostly from tumors.⁶⁹ A limited amount of data is available for established cell lines from human tumors, and a few studies have used normal human fibroblasts or epithelial cells.⁶⁹

3.B.1. RBE as a function of LET

In a previous analysis of published in vitro data, two linear fits of RBE vs LET_d were performed, one using the reported error bars and the other fit giving each data point equal weight.⁶⁹ The RBE at the reference photon LET_d (⁶⁰Co; 0.31 keV/μm) was 1.02 ± 0.04 at 2 Gy (if given equal weights to the data, the value is 1.08 ± 0.06 at 2 Gy). This is in line with the common expectation that protons with a LET_d equal to the photon reference should have an RBE of 1.0. However, the RBE at the reference photon LET_d was found to be highest for α/β < 3 Gy with an RBE of ~1.24 ± 0.07 at 2 Gy (~1.15 ± 0.05 if all data are equally weighted).

If we assume the LET_d in the central region of an SOBP to be typically between ~2.0 and ~3.0 keV/μm, the average RBE value over all in vitro studies is 1.12 ± 0.05 at 2 Gy (1.18 ± 0.06 if given equal weights to the data).⁶⁹ Thus, the in vitro cell survival data do not provide compelling evidence for the use of a constant clinical RBE other than 1.1 as an average for the midpoint of an SOBP.

In addition to the RBE at the center of an SOBP, RBE values over the entire Bragg curve are of significant clinical interest. The review also reported RBE over a range of LET_d values, that is, the average RBE for LET_d values between 0 and 3 keV/μm (the entrance region of an SOBP up to the SOBP center), between 3 and 6 keV/μm (the downstream half of an SOBP), between 6 and 9 keV/μm (distal edge region), and between 9 and 15 keV/μm (SOBP dose fall‐off region).⁶⁹ Again, averaged over all published data, for the entrance region up to the center of the SOBP, the average RBE at 2 Gy was reported as 1.10 ± 0.03 (or 1.15 ± 0.04 if equal weights are assumed for all data). For the downstream half of the SOBP, the RBE value at 2 Gy increases to 1.21 ± 0.05 (or 1.38 ± 0.11 for equal weights). The distal edge region shows an average RBE value at 2 Gy of 1.35 ± 0.10 (or 1.38 ± 0.17 for equal weights). Finally, for the fall‐off one finds 1.72 ± 0.18 (or 1.74 ± 0.21 for equal weights). Thus, one can expect a significant increase in RBE as a function of depth in tissue for an SOBP proton therapy field (Fig. 1). The data shown in Fig. 1 are based on fits to experimental data but the models discussed in Section 1.D. would predict a very similar relationship. For the SOBPs with large SOBP width, the RBE in the center is below 1.1. For all scenarios, the RBE at the distal edge is ~1.35, on average. These values are average values deduced from all cell lines and experiments on cell survival in vitro published and may not necessarily reflect clinical RBE values.

Figure 1.

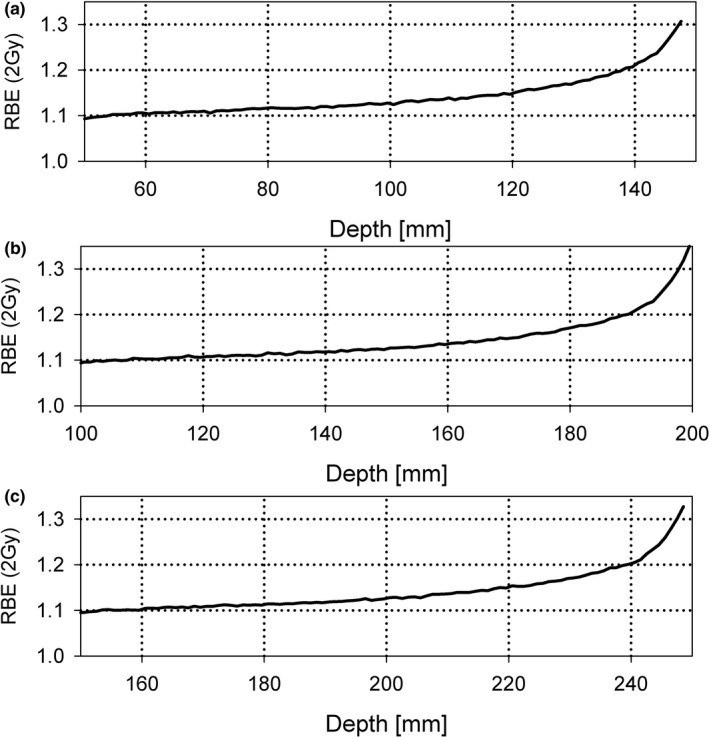
Increase in RBE for 2 Gy (relative to 6‐MV photons) across various SOBPs created by a passive scattering system.⁶⁹ (a) Range/SOBP widths: 15 cm/5 cm; (b) 20 cm/10 cm; (c) 25 cm/10 cm. The RBE values are based on a linear fit of experimental data on RBE vs LET _d in the range of LET _d < 15 keV/μm independent of α/β for all published in vitro cell survival data. Only the region >95% of the SOBP dose is included.

3.B.2. RBE as a function of (α/β) _γ

Models predict an increasing RBE with decreasing α/β. One would also expect the slope to be greater for higher LET_d values. These trends are not statistically significant when analyzing all published in vitro cell survival data simultaneously.⁶⁹ An increase in $\sqrt{(\beta /{\beta }_{\mathrm{x}})}$ as a function of LET_d is not significant and is visible only for LET_d values in excess of ~5 keV/μm⁶⁹ [see Eqs. (7) and (10)]. Others have indicated that the increasing RBE with decreasing α/β is significant only at low α/β values (<~5 Gy).^{71, 72} The combined data are too noisy to confirm this, possibly due to differences in interlaboratory experimental procedures. Uncertainties associated with the reference and proton beam dosimetry, LET_d estimates, biological assays, and nonlinear regression analysis of the measured data are also likely to contribute to the lack of a definitive trend toward increasing RBE values with decreasing α/β.

Fits of experimental data based on a Bayesian bootstrap analysis with the RMF model not only depend on the dose range of interest but may also be ambiguous in terms of α and β (see Fig. 2). This supports the comparison of model predictions directly to the experimental cell survival data, rather than comparing to “measured” α and β parameters (they are not truly measured but instead derived) or even “measured” RBE values (which are usually derived from estimates of α and β rather than truly measured).

Figure 2.

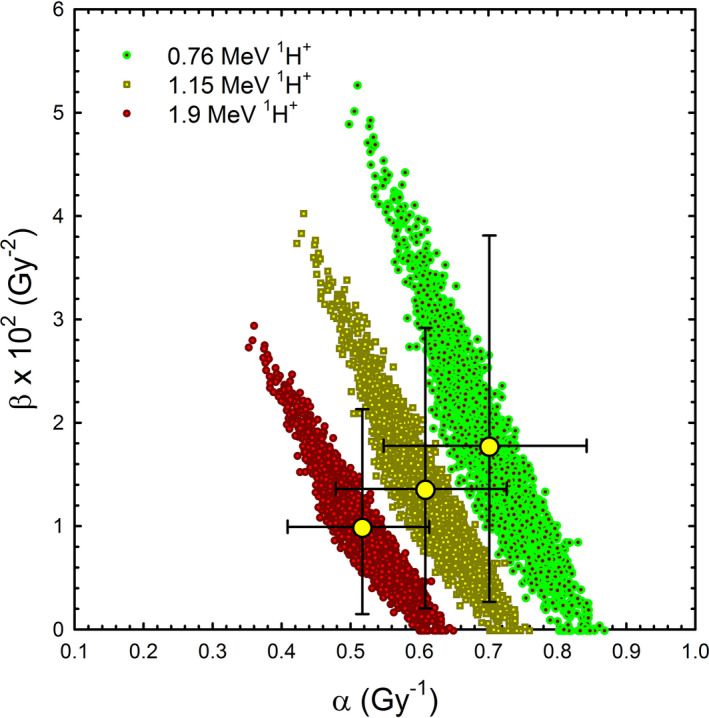
Distribution of all possible RMF parameters that fit measured data for three proton energies equally well (within few % in terms of the surviving fraction). The large dots with error bars represent the mean values (Robert Stewart; unpublished).

3.B.3. RBE as a function of dose

Relative biological effectiveness for cell survival seems in general to increase with decreasing dose, particularly for high LET_d or low α/β. For large dose per fraction, RBE might decrease toward ~1.0 because of the disappearing shoulder in the dose–response curve. The dose dependency of the RBE is difficult to assess from experimental data in the clinically relevant region also because of limitations of the available experimental cell survival assays for large doses of radiation (surviving fractions less than about 10⁻³ to 10⁻⁴ are very challenging to measure). Furthermore, most of the published studies only report cell survival data for 1 or 2 dose levels below 2 Gy, which increases uncertainties in lower dose RBE estimates. Most prescription doses currently are at ~2 Gy per fraction. Thus, critical structures in the lateral and distal fall‐offs are subject to lower doses and thus potentially higher RBE values, independent of LET_d effects. In addition, the validity of the LQ equation is unclear at doses below ~1 Gy and above ~10 Gy. The majority of the data show an increase in RBE as dose decreases, as one would expect from the LQ model.⁶⁹ For instance, experiments indicate that the RBE decreases by ~5%–10% if the dose increases from 2 to 6 Gy.⁶⁹ For low α/β, there is a more pronounced increase in RBE as dose decreases.⁶⁹ Note that fractionation effects are not incorporated in the standard definition of RBE as RBE is defined per fraction [Eq. (1)].

3.B.4. Patient variability and RBE as function of genomic heterogeneity

There is considerable RBE heterogeneity between cell lines even for the same LET.⁶⁹ We do not know much about how the genomic (and proteomic and microenvironmental) context of a cell or tissue influences sensitivity to proton‐induced RBE estimates for critical molecular and cellular endpoints. Emerging data suggest that a subset of human cancers have defects in DNA repair pathways that influence the RBE.⁷³ For example, homologous recombination is required for the repair of frank DNA DSBs occurring in late S‐ and G2‐phases of the cell cycle as well as for the repair and restart of collapsed DNA replication forks. It has been shown that in human cell lines and in CHO cells, defective homologous recombination increases the RBE for low‐LET proton radiation.^{74, 75, 76, 77} Recent data in human cancer and normal cell lines confirm these findings, and furthermore, suggest that repair pathways at replication forks are required to cope with proton‐induced clusters of DNA lesions that pose a barrier to fork progression.^{77, 78} These repair pathways, which are controlled by the BRCA1/2 breast cancer susceptibility and Fanconi anemia genes, are altered in large subsets of several cancer types implying that proton radiation may be associated with an increased RBE in the affected tumors, even at mid‐SOBP (RBE ~1.3–1.8).⁷⁸

3.B.5. Other biological endpoints related to cell survival

The intestinal crypt regeneration assay in mice is a useful surrogate for the number of surviving cells^{79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89} and has been suggested as quantitative assay for RBE intercomparisons among proton therapy centers. This assay can only be used at doses sufficiently high to deplete the number of surviving cells so that individual surviving stem cells can be counted. The dose–response curve has three regions, a plateau where according to Poisson statistics all crypts contain at least one surviving cell, a transition region, and an exponential region when most of the regenerated crypts result from the proliferation of a single surviving cell. Analysis is typically done in the dose range between 10 and 20 Gy. The data show a slight increase in RBE with LET_d and an increase in the RBE for decreasing dose. The RBE values are in general between 1.0 and 1.1. It is worth noting that, not only were these experiments conducted using large doses as indicated above, but jejune crypts have a very large α/β ratio. Even with these two combined factors, the experiments still resulted on an average RBE above 1.0.

3.B.6. Tumor response in vivo

There are methods to directly measure the response of human tumors to radiation. Perhaps, more clinically relevant are measurements of TCD₅₀, that is, the dose for 50% local control of the tumor using human tumor cells that have been implanted in immunodeficient animals. It is possible to measure tumor regrowth in these xenografts after initial shrinkage post radiation. The proton RBE for tumor growth delay of NFSa (fibrosarcoma) in mice found a proton RBE of ~0.8 (at ~30 Gy relative to 180 kVp x rays; note that relative to ⁶⁰Co the RBE would be ~1.0).⁹⁰ The study of tumor growth delay of human hypopharyngeal squamous cell carcinoma cells in mice resulted in an RBE between 1.1 and 1.2 at ~20 Gy relative to 6 MV photons using a 23‐MeV proton beam.⁹¹ A study on the recurrence of mouse mammary carcinoma in mice resulted in an RBE of ~1.1 (at ~50 Gy relative to ⁶⁰Co).⁹² Similarly, cell survival can be measured as a surrogate for tumor response by transferring tumor cells to recipient animals, for example, in the lung colony assay, or tissue culture. There have not yet been any tumor xenograft studies undertaken to confirm the recently described increased in vitro RBE values in cells with homologous recombination and other DNA repair defects.^{76, 77, 78}

3.C. Proton RBE related to normal tissue complication probability

While cell survival might be the most relevant effect for TCP considerations, other endpoints could potentially be more relevant for NTCP. Note that high LET regions at the end of range are often at the edge of the planning target volume (PTV), that is, in normal tissues. Moreover, due to various sources of uncertainties (anatomic and computational), high LET regions may extend well into normal tissues, especially in or near low‐density structures. In addition, considering typically lower α/β of healthy tissue as well as lower doses than in the target, one might expect RBE values derived directly from observed normal tissue complications to be larger than RBE values derived from clonogenic cell survival after 2 Gy or more.

Organ‐specific effects of interest are early effects such as erythema and late effects such as lung fibrosis, brain necrosis, or spinal cord injury. It is an open question as to whether or not (or to what extent) the RBE for cell survival is a useful (predictive) surrogate for OAR clinical endpoints. Several published studies have demonstrated no association between fibroblast radiosensitivity and the development of late normal tissue effects such as fibrosis.^{93, 94} The relationship between clinically observed late effects and DNA repair capacity has been discussed.⁹⁵ Surviving cells with unrepaired or misrepaired damage can transmit changes to descendent cells. Malignant transformation can thus be initiated by gene mutation or chromosome aberration.

Various endpoints have been studied with respect to differences between proton and photon response. These include the induction of reactive oxygen species (ROS) preceding DNA damage, single or double strand break induction, formation of foci of repair‐related proteins, repair proteins or gene expressions, induction of chromosome aberrations, mutations and micronuclei formations, as well as apoptosis and effects on the cell cycle. Furthermore, in vivo data on animal systems, mostly looking at whole‐body effects, have been studied. In general, RBE values for endpoints other than clonogenic cell survival are not in disagreement with a clinical RBE of 1.1 but selected endpoints did show considerable deviations from this value.⁶⁹

3.D. Summary: Assessment of the deviations of RBE from 1.1

The validity of RBE values for different cell lines of varying radiosensitivity measured mostly at high doses and mid‐SOBPs is unclear in terms of clinical applicability. There are also considerable interexperiment and interlaboratory inconsistencies for the same cell lines.

1. Although there is a large amount of data on the RBE for clinically relevant LET_d values, (α/β) _γ and doses, the proton RBE values are still associated with considerable uncertainties.

2. RBE increases with increasing LET and thus with increasing depth if an SOBP is being delivered. The RBE is significantly higher toward the distal end of an SOBP (see Fig. 1). Averaged over all published values, assuming 2 Gy per fraction and for a typical spread‐out Bragg peak delivery, the RBE relative to 6 MV photons for in vitro cell survival averaged over all (α/β) _γ does increase with depth from ˜1.1 in the entrance region, to ˜1.15 in the center, ˜1.3 at the distal edge and ˜1.7 in the distal fall‐off. For low‐energy beams and small SOBP widths, LET_d and thus RBE values can be higher. The LET_d might also be slightly increased in the penumbra as compared to the center of the beam due to scattered and secondary protons.

3. These average values consider 2 Gy at the point of interest. There is also likely an RBE increase as dose increases in the distal as well as lateral fall‐offs.

4. Despite the abundant in vitro and in vivo evidence supporting the notion that RBE may depend on many factors, the use of a constant clinical RBE of 1.1 at ˜2 Gy per day/fraction is reasonable if an average for an SOBP field is assigned conservatively (although the data seem to indicate a slightly higher average of ˜1.15⁶⁹). Caution is warranted for small SOBP widths (and tumor targets) and/or low (α/β) _γ where the average RBE could be higher.

5. There appears to be a slight trend toward an increase in RBE as (α/β) _γ decreases. The current clinical RBE of 1.1 could potentially underestimate the RBE for fraction sizes that are small compared to (α/β) _γ and overestimate the RBE for fraction sizes that are comparable to or larger than (α/β) _γ .

6. The usefulness of various reported molecular and cellular endpoints, including cell survival, for defining a clinical RBE values for use in NTCP models is unclear at this time. In general, RBE values for clonogenic cell survival and other endpoints are not in disagreement with a clinically used RBE of 1.1. On the other hand, selected endpoints do show considerable deviations from this value.

When discussing RBE, the focus is typically on the use of molecular and cellular surrogates to relate the RBE for one endpoint (e.g., DSB induction measured via γH2AX or pulsed‐field gel electrophoresis) to the RBE for cell survival (e.g., apoptosis or reproductive cell death) and not to the RBE for clinical endpoints (damage to normal tissue or local tumor control). It is unclear whether or not the numerical values and trends in RBE estimates derived from laboratory studies are sufficiently predictive of the RBE for clinical endpoints to justify a move away from a constant clinical RBE = 1.1. The RBE at the center of the SOBP (and hence elsewhere too) may be significantly higher than 1.1 if cells harbor defects in certain DNA repair pathways, such as homologous recombination and nonhomologous end‐joining, which likely are quite common in several human cancer types.

5. Assess whether the current practice of a constant RBE should be revised

4.A. Should we use an average RBE value different from the current value of 1.1?

The RBE is significantly higher toward the distal end of an SOBP. The currently used value of 1.1 seems to hold only for the entrance of an SOBP (see Figs. 1 and 3 as well as Section 2.D.3.). One has to keep in mind that this holds for cell survival in vitro and that RBE values for other endpoints are less well known. As outlined above, the use of a constant clinical RBE of 1.1 at 2 Gy in the target is not entirely unreasonable if RBE values should be chosen conservatively (smaller RBE values) to avoid underdosage of the target. Caution is warranted for small SOBP widths and/or low (α/β) _γ where the average RBE could be higher.

Figure 3.

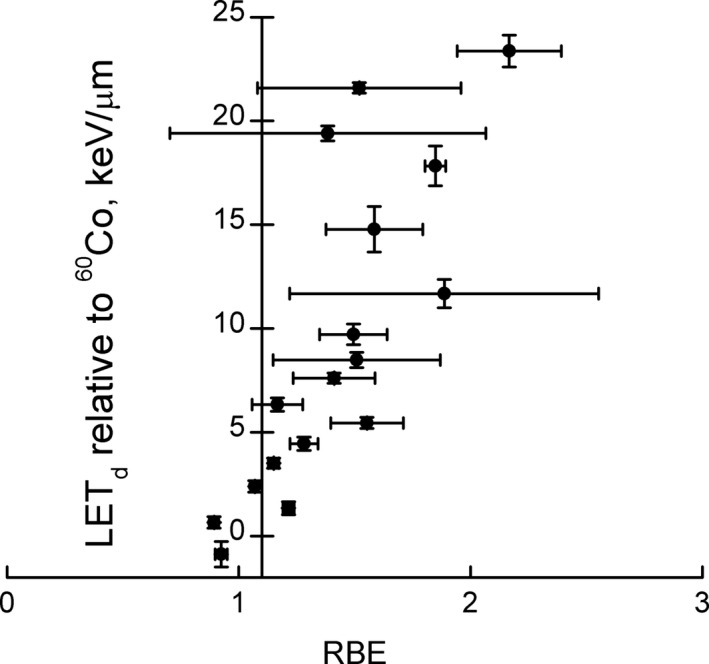
Uncertainty weighted experimental RBE data for clonogenic cell survival measured in vitro at 2 Gy for LET _d <25 keV/μm relative to ⁶⁰Co. Note that the vertical line is drawn through RBE = 1.1. All data are shown irrespective of α/β. (adopted from⁶⁹).

Figure 3 summarizes the available clonogenic cell survival data. Note that LET_d values in the entrance and center of an SOBP are typically <6 keV/μm but increase in the distal edge and dose fall‐off region. In Fig. 3, LET_d values are relative to the photon reference radiation and can thus be below zero for high‐energy protons.

Generally, in vivo data supersede in vitro observations for relevance to the clinic. However, to what extent tumor growth delay in vivo provides information superior to in vitro data remains unclear. In vitro approaches remain important for mechanistic studies, and in instances where increased RBE is clearly a cellular phenotype (such as in the setting of DNA repair defects) in vitro data are more likely to correlate closely with in vivo findings.

The relevance of RBE data for various molecular and cellular endpoints to clinical RBE values for dose‐limiting OAR is unclear at this time. The very limited RBE values for endpoints other than clonogenic cell survival are not in disagreement with a clinical RBE of 1.1. However, many late effects are certain to involve larger scale (multicellular and tissue level) biological mechanisms, including chronic inflammation, tissue remodeling, etc. It is an open question as to whether or not (or to what extent) biological mechanisms acting at the multicellular and tissue levels might impact on the selection of a nonconstant RBE value for OAR clinical endpoints. The impact and clinical significance of the very different spatial dose distributions produced in an OAR by photons and protons is also unclear, that is, dose–volume and structural effects may play out in very different ways. If equivalent spatial and temporal distributions of damaged, dead and dying cells do invoke/initiate the same higher level biological mechanisms of action, then the RBE for cell survival may be a quite reasonable surrogate for clinical RBE. Otherwise, dose–response and/or dose–volume effects may play out in quite different ways for photon vs proton irradiation. Effects such as these would imply the need for a dose–volume response parameter, n, in the Lyman–Kutcher–Burman model that differs for protons and photons. It may not be sufficient to just define a voxel‐specific RBE. The analysis of normal tissue toxicities with respect to RBE could be overshadowed by response differences between photon and proton dose distributions. Most constraints and outcome analysis are based on photon dose distributions

4.B. Should we use a constant RBE value, which may differ from tumor to tumor, organ to organ, or patient to patient?

Although there are sparse clinical data indicating that the use of a constant RBE = 1.1 gives rise to proton treatments which differ substantially in clinical effectiveness or toxicity from MV x ray treatments, concerns have been expressed that this constant RBE may be an under‐ or overestimate for certain tumors and OAR.^{4, 5, 6, 20, 96} Even though an it might be an appropriate average value for most tumors and normal tissues, some exceptions may, for example, exist with regard to small SOBP widths, tumors, or tissues with very low or very high α/β values, certain beam arrangements in scanning beams and hypofractionation. Assigning different RBE values for such tissues and geometrical locations may be advisable.

There is evidence for a trend toward an increase in RBE as α/β decreases (see Section 2.D.3.). If the effect is large, the current clinical RBE could potentially underestimate clinical RBE values at low α/β and overestimate the RBE at high α/β. Figure 4 shows RBE values for cell survival at α/β 0–3, 3–6, 6–9, and >9 Gy. The vertical line is drawn through RBE = 1.1. Only for α/ β < 3 Gy there is a clear trend as a function of LET_d in the clinically relevant range. Tumor volume might play a role as well as SOBP fields with small SOBP widths where the LET_d rise at the distal edge affects the whole volume and might require an RBE of 1.15 or even 1.2.

Figure 4.

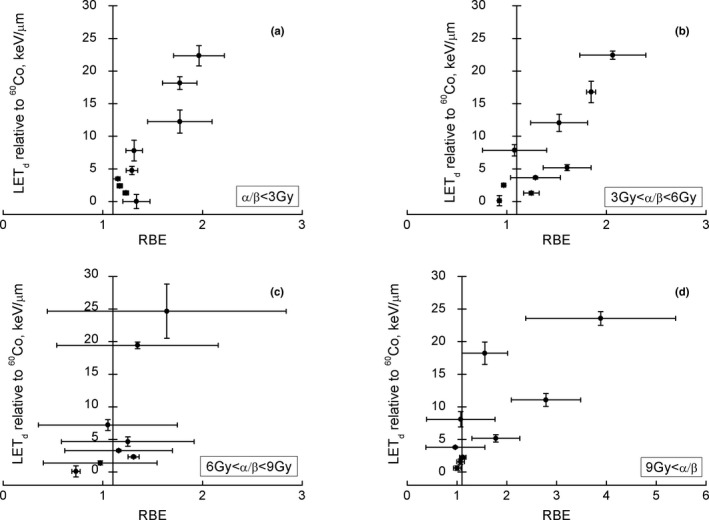
Uncertainty weighted RBE for clonogenic cell survival as a function of LET _d for different ranges of α/β and LET _d <25 keV/μm relative to ⁶⁰Co (adapted from⁶⁹). Note that the vertical lines are drawn through RBE = 1.1.

One could potentially prescribe higher RBE values for certain tumors, for example, 1.2 for prostate because of the low α/β commonly set to 1.5 Gy in clinical trial designs⁹⁷ with support from analyses of multi‐institutional datasets (0.9–2.2 Gy⁹⁸). This may also hold for other tumors such as breast. Furthermore, some DNA repair‐deficient tumors may have high RBE values.⁷⁸ While it may be welcomed to have a higher RBE‐weighted dose than planned for, it does impact the assessment of clinical trials comparing photon and proton arms. The data summarized in Section 2.D.3. indicate, however, that the LET_d dependency of RBE is most likely more significant than the RBE variation with α/β. On the other hand, low RBE values such as 1.05 could be assigned to medulloblastoma because of the presumably high α/β (~25 Gy) as has been suggested.⁵ However, for the latter, there is no clinical evidence that there is an increased rate of recurrences in proton therapy because of an overestimation of RBE.⁶

There are no comprehensive RBE studies in a sufficient number of genomically diverse cancer cell lines or human tumors. Given the genomic heterogeneity that exists in cancers, it is conceivable, even likely, that in clinical practice the RBE at mid‐SOBP varies substantially from patient to patient. A subset of tumor types or patients may exist in which the effective clinical RBE is much higher or somewhat lower than 1.1. In the absence of robust biomarkers to identify individual patients with proton‐susceptible tumors and without knowledge of what contributes to differential radiation sensitivity, the continued use of an average RBE independent of tumor type and patient is not unreasonable. Genomic or functional biomarkers to define individual radiosensitivity or at least sensitivity of patient subpopulations are thus clearly desirable.⁷⁸ If accurate biomarkers were available to provide patient‐specific information on radiosensitivity, treatment optimization based on RBE‐weighted dose estimates that incorporate this interpatient variability would be desirable.

At this time, it is not yet possible to identify individual cancers with a RBE >1.1. As molecular profiling of human cancer advances, this may be revisited. If we were able to identify tumors with increased RBE, clinical practice could be changed in a variety of ways, that is, (a) there could be the potential for dose de‐escalation to spare normal tissues, especially in settings where there is concern for toxicity such as in pediatric patients, (b) one might try to exploit a biological RBE advantage by using scanned beams to increase LET in the tumor, (c) one might combine treatments with targeted drugs that seek to exploit an increased RBE further via a synergistic effect or that convert a repair‐proficient cancer into a repair‐deficient tumor, and (d) patients may be selected for proton treatment slots that otherwise would not have been available to them.

If one were to choose a RBE different from 1.1 as an average value, one should distinguish between tumors and organs at risk, that is, choosing a conservative, higher RBE, for normal structures and a conservative, lower RBE, for tumors. While cell survival might be the most relevant cellular endpoint for TCP considerations, other endpoints could potentially be more relevant for NTCP. Thus, it is an open question as to what extent a constant clinical RBE for an OAR correlate with the RBE for clonogenic cell survival (or any other molecular endpoint). Clinical evidence to address this issue could come from an analysis of early or late effects in regions of low α/β and/or high LET. This would occur, for example, if an SOBP field ranges out in the brainstem when treating targets in the brain. Brainstem and cervical spine toxicities (e.g., necrosis) found in 4 out of 111 (3.6%) medulloblastoma patients were analyzed.⁹⁶ No clear correlation between elevated LET_d and regions of toxicity was found, however, the sample size is small.

For normal tissues with a low α/β value, below 5 Gy, for example, that are exposed to LET_d values above 6–10 keV/μm (e.g., if the beam stops in the brainstem) a more conservative constant RBE of 1.2 or 1.3 might be more appropriate. However, solutions like this might be cumbersome particularly because existing TPS might be unable to incorporate such an approach. It is more practical to adjust proton therapy dose constraints relative to photon therapy by applying RBE values different from 1.1 for certain scenarios.

Alternatively, if sufficient clinical data are available to create a dose–response curve for TCP or normal tissue complication probabilities, RBE could be defined based on clinical data and the definition of a point on the dose–response curve, for example, D₅₀ for tumors.

4.C. Is there enough evidence to apply RBE values depending on dose, endpoint, and LET?

Figures 3 and 4 demonstrate the uncertainties in the published RBE values and thus suggest that the modeling of continuous RBE values as a function of dose, LET_d, and α/β in a treatment planning system to base the optimization on biologically weighted dose instead of just physical dose might not be feasible with acceptable error. The data support the idea that RBE does depend on dose, endpoint, and LET, but they are not sufficient to allow statements on what RBE values should be used to a clinically acceptable precision. Combining many in vitro datasets from multiple laboratories into a single analysis may unnecessarily introduce noise and overestimate the RBE uncertainty. Another way to report uncertainty would be to consider the % difference in RBE‐weighted dose assuming a constant RBE of 1.1 or a spatially variant RBE (using whatever biological model).

Variable RBE values could be largely disregarded in the past because delivery techniques and conservative margins made proton therapy insensitive to them. The increase in RBE is currently considered only by avoiding the end of range, the region of highest RBE, close to critical structures, but it is not quantitatively incorporated in planning and evaluation of proton treatments. For IMPT, the spot intensities, and therefore the LET_d distributions, in the target are, in general, highly heterogeneous. Therefore, RBE may deviate significantly from 1.1 and vary considerably within an organ or tumor (e.g., see calculated LET_d distributions for two clinical scenarios in Fig. 5). Thus, variation in RBE may have to be considered in the future even though there are uncertainties, that is, the errors introduced in RBE‐weighted dose distributions using a constant RBE of 1.1 may be as large as those introduced by biological uncertainties. However, LET is based on physics properties and can be calculated quite accurately based on the treatment plan information.⁹⁹ It is possible that LET_d might be useful as a pragmatic physical surrogate for tumor and tissue RBE.

Figure 5.

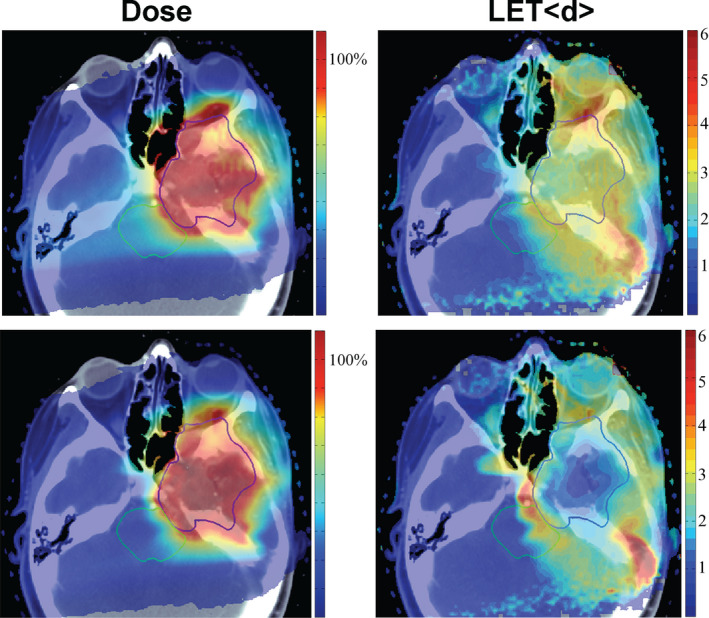
Clinically equivalent dose distributions for two IMPT plans (chordoma; dose in % of prescribed dose; GTV in blue). The right column shows the LET _d distributions in keV/μm differ significantly.⁹

4.D. Is there a potential difference in RBE between passively scattered beams and beam scanning?

An aspect that needs to be considered is the move toward scanning beams, which may result in overall slightly higher LET_d values compared to passive scattering. Whether this will impact an average RBE is unclear. In general, two more or less equivalent dose distributions could have different underlying LET distributions (as dose is given as LET times particle fluence).

Considerable differences can be expected for particular organs at risk dependent on the underlying physics of the proton beam, that is, primary or secondary protons (or even heavier secondaries), and differences in energy spectra. Figure 5 shows that LET_d distributions can be influenced in IMPT, something that is not possible with passive scattered delivery (at least not without changing beam angles or field patching). This also suggests that LET_d and RBE values could depend on the treatment plan especially outside of the target volume.

The local dose rate also differs between scanned beam delivery and passively scattered delivery. Whether ultra‐high dose rates in excess of 20 Gy/s show differential responses between murine normal and tumor tissues in vivo is controversial,^{91, 100, 101} effects of ultra‐high dose rates on biological response have not been found in vitro.

4.E. What information should be saved in treatment planning systems for outcome analysis?

If RBE is considered in treatment planning, it would be sufficient to store dose and (RBE × dose) distributions. If (RBE × dose) is not directly computed in the planning system, the only alternative is to apply reconstructed RBE estimates based on information stored in, for example, a DICOM RT ION file. However, the fully implemented DICOM RT ION standard does contain sufficient information on how the proton beam is delivered field‐by‐field for both passive scattering or active scanning proton beams to enable the reconstruction of (RBE × dose) distributions using Monte Carlo methods.⁹⁹ Archiving only the three‐dimensional (3D) dose, scaled by a constant RBE factor, is insufficient to resolve the energy and depth dependent LET_d effects. Therefore, it is important to archive the entire treatment plan with beam delivery information (including phase space of incident particles) for future outcomes analysis.

For patients that are treated today with plans that were not based on explicit biological optimization one would need Monte Carlo generated LET_d distributions in addition to the dose distribution if recurrences, toxicities or other response markers are to be retrospectively analyzed with respect to RBE. This would, however, only satisfy those bio physical models that are based on LET. Tissue‐specific characteristics, such as α and β, might be missing. Thus, the required parameters will depend on the biological model that is used, for example, whether it is an empirical function dependent on LET_d or it first calculates more fundamental yields of DNA damage based on particle energy spectra and then converts this to cell death or other endpoints.

Although one might imagine computing a clinical RBE as a ratio of the equivalent uniform dose (EUD)^{102, 103, 104} of protons and MV x rays that produces the same TCP or NTCP, it is recommended to assign RBE values on a voxel‐by‐voxel basis as a dose‐modifying factor independent of other voxels. TCP and NTCP modeling can then be based on the RBE‐weighted dose distribution or EUD.

6. Assessment of clinical impact when revising current practice on RBE

5.A. Practical considerations when dealing with RBE uncertainties in current practice

As discussed in previous sections, the RBE for a given subvolume in a target or a critical normal tissue depends on many factors. In addition, the robustness of the plan, particularly the physical range uncertainties of proton beam, is also an important consideration. Because LET (and thus the RBE at the same dose and α/β) is higher in the distal part of an SOBP and because the dose decreases sharply at the distal end of a proton beam, accompanied by an α/β in this edge which is usually lower than that in the target, the location of the distal falloff plays an important role in predicting RBE variations in a given treatment plan. The physical range uncertainties of proton beams are a complex topic, which is addressed in the AAPM Task Group Report #202. When designing a treatment plan, the strategy most often used in current practice is to minimize the risk of the end‐of‐range uncertainties in proton beam angle selections. This strategy addresses physical range uncertainties as well as RBE effects. The following methods are commonly used when designing and evaluating a treatment plan:

1. Beam angle selection to avoid proton beams ranging directly into a critical normal structure that is adjacent and distal to the target. This is particularly true if the normal tissue has a maximum tolerance dose (such as the brainstem, spinal cord, or optic pathway). The RBE dose could be higher at the distal end of the beam, resulting in significant risk for exceeding the maximum tolerance doses. This is particularly true for low α/β tissues with higher RBE and high RBE uncertainties. Note that a strategy of treating through a normal organ, instead of stopping the beam in front of a normal organ to avoid placing a high RBE in the distal end in the organ may have excessively emphasized the effects of distal RBE over a higher dose to a large volume of normal organ.

2. To use more beam angles to spread out the high RBE portion of the beam to different areas. This will minimize the potential impact of a single beam pointing toward one location (where the critical normal structure may be located). When using multiple beams, the weight of each individual beam is reduced; therefore, it reduces the impact of RBE uncertainties at the distal end for each beam.

3. To use lateral beam falloff to spare nearby normal structures. Although the lateral beam penumbra is not as sharp as in the distal penumbra of a proton beam, it provides a more reliable, lowered RBE to protect normal tissues.

4. To minimize potential range uncertainties by carefully selecting beam angles not to go through regions of day‐to‐day anatomical variations, such as bladder filling, bowel gas variations, etc. The simulation CT used for planning is a snapshot of a patient's anatomy, which may not be reproducible in day‐to‐day treatment.

5. It is also useful to avoid proton beams going through tissue heterogeneities. Dose calculation other than Monte Carlo may not be accurate after passing through complex tissue heterogeneities, such as complex bony structures or low‐density lung tissues or air cavities. Inaccurate dose calculation contributes to additional RBE uncertainties.

6. Plan robustness evaluation could be used to visualize the impact of range uncertainties. Recent TPS may have implemented plan robustness evaluation tools for both scanning and passive scatter beam plans. The treatment planning system may demonstrate what the plan will look like if the range of the proton beam is altered by a fixed percent of its water‐equivalent depth. It is expected that the heavily impacted area near the end of range for proton beams will also present a large RBE uncertainty.

7. Intensity‐modulated proton therapy allows the delivery of multiple‐field uniform dose to the target instead of single‐field uniform (SOBP) doses per field. This allows for more degrees of freedom when avoiding end‐of‐range uncertainties close to critical structures.

Treatment planning for proton therapy is evolving rapidly. Future TPS may have the option to report LET or LET‐dependent RBE‐weighted dose distributions to give planners more insight regarding the potential RBE effects or provide the ability to include RBE uncertainties as part of the robustness analysis of the plan.

5.B. Assess treatment sites for which a revision of current clinical practice would be most significant

There have been concerns that RBE may be under‐ or overestimated for certain tumors or organs at risk (see Section 4.B.). Theoretical studies have addressed the issue of RBE variations in patients^{11, 12, 13, 14, 15, 20} and have analyzed the potential impact of RBE on fractionation in proton therapy.^{17, 18, 19} In general, RBE effects will be more prominent in tumors involving low α/β tissues, which makes prostate, breast, sarcoma, and certain brain tumors sites to be cautious with. It seems that variations in RBE in the target could be on the order of 10–20%, which might be detectable in clinical trials. For example, in a randomized clinical trial on prostate cancer comparing proton therapy with IMRT, one might expect a more than 10% higher biologically effective dose in the tumor on the proton arm, at least on a population‐averaged basis, (considering a low α/β for prostate).

As the RBE depends on dose and many treatment sites are being considered for hypofractionation one has to be aware of a potential reduction in RBE, even below 1.1, due to a decrease in RBE with increasing dose depending on the endpoint.

Toxicities in proton therapy should be analyzed not only with respect to dose distributions but also with respect to potential RBE cold or hot spots. Evidence could come from early or late effects in regions of low α/β and/or high LET. This includes, for example, brainstem toxicities (e.g., necrosis) found in medulloblastoma or ependymoma patients.

The slope of the NTCP dose–response curve is generally steeper compared to TCP dose–response curves, which would indicate that RBE uncertainties are even more critical for NTCP. For normal tissues that are greatly affected by hot spots, such as the brainstem, spinal cord, or optic nerves, etc., the RBE uncertainty is a great concern during treatment planning for targets that are next to these structures. Different maximum dose constraints may be adopted for these tissues when planning proton treatments and comparing a proton plan and a photon plan due to the potential RBE uncertainties in the proton plan.

5.C. Biological dose in treatment plan optimization

Biophysical models have significant uncertainties, which arise from uncertainties associated with the measurement and interpretation of biological assays, the dosimetry of the reference radiation and proton beam, and the manner in which a model characterizes the mechanisms of action. The other critical issue is the relevance of modeled physical or biophysical endpoints (LET_d, DNA damage, cell survival) at determining the effective RBE for tumor control or for early and late OAR toxicities. Furthermore, the variation in RBE for molecular or cellular endpoints may produce sharp changes in the determination of (RBE × dose) distributions. Sharp gradients in the (RBE × dose) or (LET_d × dose) distribution make plan optimization more sensitive to small changes in beam modulation. The determination of an optimal (RBE × dose) distribution may be further complicated by the heterogeneous distribution of biological parameters within and adjacent to the treatment volume, such as a mix of tumor and healthy tissue in the margins of the PTV.

Despite the potential limitations and caveats of plan optimization based on variable RBE models or LET_d, it is not entirely unreasonable to expect a clinical advantage from incorporating such models into IMPT optimization. Note that a homogeneous dose distribution does not guarantee a homogeneous distribution of LET_d or RBE. One potential advantage of LET_d as a surrogate for RBE is that it is a pure physical quantity that can be calculated quite accurately based on the treatment plan information.⁹⁹ Although LET_d alone cannot provide actual proton RBE values, it is a correlated indicator for local increase or decrease of RBE, which increases with LET_d for a given dose and α/β (Fig. 5).

An optimization algorithm can attempt to move elevated LET_d regions away from certain areas/organs, for example, tissues with low α/β.^{8, 9, 105} As seen in Fig. 5, there are likely differences between passively scattered fields, IMPT fields using single‐field uniform dose and IMPT fields using multifield uniform dose in terms of the underlying LET_d distributions. This can be exploited in treatment optimization. It has been shown that LET_d‐based optimization is feasible with standard treatment planning system if the spot map is reoptimized after dose‐based optimization. Optimization based on LET_d allows maintaining current prescription doses and maintains the clinical practice of delivering homogeneous target doses, that is, it can in principle be validated by a clinical trial. On the other hand, optimizing based on LET_d instead of RBE only considers the component of RBE that is closely correlated with the small‐scale ionization density of individual proton tracks. For a radiation resistant tumor, one might favor placing the highest LET/biologically effective regions solely within gross residual disease. The opposite might be the case, for example, in an optic nerve glioma. Here, within the target volume there are critical normal tissues and thus the emphasis might be more on delivering a homogenous physical or RBE‐weighted dose.

5.D. Impact on dose normalization and clinical physics

Using a variable RBE in the clinic would have an impact on the dose prescription and delivery. The number of monitor units (MU) defines the beam‐on time and is set usually based on the delivered absorbed dose for the calibration condition. Traditionally, the calibration point is in the center of a uniform dose volume. Although a uniformly distributed biological dose could be generated, the absorbed dose could be heterogeneously distributed, which might introduce positional or dosimetric uncertainties during the measurement process. IMPT may offer different ways to calibrate MU, for example, using a uniform scanning pattern to calibrate near the shallow depth, rather than in an SOBP.

Using a variable RBE would result in the delivery of nonflat SOBPs, which would impact quality assurance measurements. On the other hand, this cannot be avoided in the future as most centers are moving toward IMPT with inhomogeneous dose distributions per field.

There are also considerations with respect to commissioning. Prior to incorporating a biophysical model into the treatment planning process, accurate measurements of the beam parameters need to be made. Verifying simulated LET values using, for example, nuclear track detectors^{106, 107, 108} might be warranted. Since LET may become an optimization parameter that will determine the plan quality, we may want to include LET measurements in patient‐specific QA in addition to dose.¹⁰⁹

7. Recommendations for future experiments

RBE data for clonogenic survival as a function of LET_d show substantial spread in absolute RBE values at any given LET_d (see Figs. 3 and 4 and Section 2.D.3.). Given the large amount of data included, this spread of the RBE values is remarkable. A large part of the spread in absolute RBE values may have resulted from inconsistencies in experimental design among different laboratories. In addition, uncertainties in dosimetry likely contribute significantly. It is unlikely that simply continuing to repeat such studies, employing the same or similar experimental techniques, will reduce the uncertainties. Thus, there is a critical need to understand the reasons, both biological and physical, for the large spread in values. Such understanding should be aided by standardization and reporting of experimental procedures and by the description of full dosimetric details to facilitate interlaboratory comparisons of data and to reduce uncertainties.¹¹⁰ Standardization will ultimately also contribute to future mechanistic insights and improved clinical outcomes.

6.A. Uncertainties in measured RBE values: Standardization of dosimetric reporting and experimental parameters

A workshop in 2013 held at National Institute of Standards and Technology discussed the importance of dosimetric standardization in radiobiology research and reporting of physical details in publications.¹¹⁰ In summary, it was recommended that biologists and physicists collaborate on study design and execution. Radiation physicists may help to ensure that study design is satisfactory to achieve the accuracy and precision of the independent variables (e.g., dose and LET_d or energy spectra at the points of measurements) of relevance to the biologic endpoint. Publications should include, at a minimum, specific details regarding the experimental setup and dosimetry.

Regarding experimental setup and dosimetric reporting: First, it would be helpful if experimental assessments of proton RBE applied a common photon reference radiation, ideally this would be 6‐MV (mega voltage) photons or, alternatively, ⁶⁰Co as the difference between these two modalities is assumed to be negligible. RBE values and photon dose–response curves reported in the literature use different reference photon conditions, from megavoltage to kilovoltage (kV). The use of kV x rays as a reference is also challenging because of the varying levels and types of filtration used to reduce or eliminate low‐energy (high‐LET) photons. Correcting proton RBE values deduced from these experiments based on an average RBE of the reference radiation is often not feasible because RBE values relating photon modalities are endpoint dependent.¹¹¹ A potential alternative approximation is to use proton LET_d values relative to the LET of the secondary electrons from the respective photon reference radiation when analyzing experimental data. Second, investigators are encouraged to provide detailed physics experimental design information, including LET_d values and LET spectra and how they were measured or calculated. Such data are not commonly presented in biologic publications, yet are essential for further development of biologic effect models. Furthermore, in comparison to passively scattered beams, scanned beams have narrower energy spectra. Thus, the utilization of scanned proton beams for experimental procedures would provide the highest quality LET_d data. Moreover, currently, there is a paucity of data characterizing the biologic effects of scanned proton beams. This is of particular relevance as the field increasingly adopts scanning beam technology for clinical treatments.

Regarding common biologic measures: Clonogenic survival is the most prevalent biologic endpoint in RBE studies. Different laboratories use not only different irradiation conditions but also cell handling protocols that may impact absolute clonogenic survival and hence RBE values. Cells may differ in whether they are in exponential growth or in plateau phase, corresponding with low‐ vs high‐cell densities, whether they are trypsinized and replated a day prior to irradiation or (shortly) after irradiation, or are attached vs in suspension. Such differences in experimental conditions can cause substantial differences in radiation sensitivity. Additionally, cell lines can change over time in culture, so availability of a central stock of a few selected cell lines for use in intercomparison of results from different facilities would be important.

Ideally, going forward to address the experimental needs discussed below, a list of minimum dosimetric information on experimental setups and a standard set of biology conditions could be adopted by various labs performing cell survival experiments to allow direct comparisons of data among labs. It is beyond the scope of this Task Group to recommend specifics, but experimenters in the field should consider discussion on this important issue.

Ultimately, standardization of experimental approaches and dosimetric reporting will help reduce uncertainty and quantify variability in RBE values as a function of LET, dose, dose per fraction, tissue, or cell type, etc. Once standard biological conditions and physics parameters are agreed upon, it may be worthwhile to have a “reference” RBE vs LET experimental curve, using a standard phantom, determined at a select number of facilities with a small number (<5) of authenticated human control cell lines that have demonstrated phenotypic stability. These could be used for standardization of experimental data obtained in the future. It would also be helpful to have a centralized location for storage of (raw) biological and physical data that complies with the agreed upon standards.

6.B. Novel and mechanistic biology studies to quantify and explain RBE variability

It seems clear that variability in RBE results not only from physical factors such as LET but also from underlying biological differences, including species (e.g., murine vs human), whether the tissue is normal or tumor, differences in repair of proton damage to DNA, and potentially the role of immune responses for in vivo RBE. Additionally, there are important biological questions specific to proton beams that must be addressed in order to maximize the clinical gain of proton therapy.

An increasing number of studies focus on high‐throughput screening both for therapeutic effect and toxicities of anticancer compounds. In order to reduce uncertainties associated with RBE data, it may be useful to consider such assays for studies of particle therapy.^{112, 113, 114} A high‐throughput approach, assessing response at multiple dose levels in a large number of patient‐derived cell lines, when combined with knowledge of the genomic profiles of each, might allow for a more detailed understanding of the molecular mechanisms that contribute to differential RBE values and identify potential approaches to further enhance therapeutic efficacy (e.g., selection of patients most suited for proton therapy based on tumor profiling or identification of molecular pathways for drug targeting).

At the DNA level, the biophysical modeling would be aided by further elucidation of the chemical nature of complex DNA lesions, how the spectrum of damages differs between photons and protons, and how these damages determine the cells' fate, taking into consideration the genetic profile of particular cell lines. This likely will require development of new assays. Using existing assays that permit temporal tracking of DNA damage response and repair,¹¹⁵ additional information on DNA damage response and repair kinetics induced by different proton LET_d and over a range of doses can inform some of the biophysical models (see Section 1.D.). In the absence of detailed knowledge of the chemical composition of clustered damages, a potential surrogate could be complexity of DNA repair‐related protein foci such as γH2AX. For example, it has been suggested that the size of γH2AX foci may relate to damage complexity and correlate with survival (e.g.,^{77, 78, 116}).

As discussed in Section 3.C., a recent finding that may explain at least a fraction of the variation between human tumor cell lines is that genetic differences such as alterations in certain DNA repair‐related pathways, particularly ones involving homologous recombination or the Fanconi Anemia pathway, can have a significant impact on proton RBE values.^{76, 78, 117} Not only could these findings explain some of the differences in RBE values, but the implication that proton therapy may have a biologic and clinical advantage in human tumors that harbor such defects has clinical significance, as discussed in Section 4.B. It is becoming increasingly clear that alterations in these DNA repair pathways exist in human cancers at a clinically meaningful frequency.¹¹⁸ Genomic or foci biomarkers are needed to identify tumors with increased susceptibility to proton radiation. Answering this question involves not only development of appropriate assays, but coupling the approaches with development of a large (ever increasing) database of clinical outcomes from proton therapy. Additionally, combined use of proton therapy with pharmacologic agents that exploit DNA repair pathway defects must be investigated as a way to exploit the defects in cancer cells to increase therapeutic gain further.

A pervasive issue in all discussions of quantifying RBE is the choice of experimental models and endpoints. As discussed above, most available RBE data are from studies of clonogenic survival in established cell lines. For tumors, clonogenic survival of monolayer‐cultured tumor cells historically has been considered an appropriate endpoint but it is evident that this endpoint has limitations as it does not account for effects due to tumor vasculature,^{119, 120} stimulation of immune responses,^{121, 122, 123} and more generally, the tumor microenvironment that may impact tumor response to radiation. For normal tissues, with the growing realization that late tissue damage in response to radiation is complex and can involve chronic oxidative stress and inflammation^{124, 125} as well as damage to vasculature,¹²⁶ it seems clear that additional studies are needed to determine whether or not clonogenic cell survival is a relevant endpoint for determining the RBE for early or late normal tissue response. The relevance of RBE values for clonogenic cell survival to cancer induction is also highly debatable.¹²⁷ To achieve a full understanding of appropriate RBE values to apply to tumors and normal tissues in the clinic, models and/or endpoints in addition to cell survival need to be developed.

Potentially important biological responses that have been shown to differ between protons and photons include angiogenesis and cell migration,¹²⁸ patterns of gene expression,^{128, 129} DNA methylation,¹³⁰ and production of ROS.¹³¹ Further quantification and mechanistic understanding of these processes is needed as such findings may support the suggestion that a variable RBE should be used in proton treatment planning.¹³²

There is interest in development of 3D tumor or tissue models that may provide a better approximation of the in vivo environment, prior to advancing proton studies into animal models. Tissue homeostasis is dynamically maintained by reciprocal interactions between epithelium and stroma as well as by the 3D architecture and tissue microenvironment. Evaluation of the roles of such interactions and tissue architecture in radiation response and cancer induction are needed. 3D models of normal tissues have significant advantages as surrogates for in vivo animal studies because they are more readily manipulated, and hence, more amenable to study mechanisms of intercellular signaling, more cost effective, and provide a useful bridge between two‐dimensional (2D) cell culture and animals models.^{133, 134} Compared to 2D monolayers, 3D cultures allow development of cell morphology, cell–cell and cell–extracellular matrix interactions and differentiation more characteristic of in vivo.¹³³ Published data comparing responses of normal cells irradiated with photons in 2D and 3D do not all agree; some report that cells in 3D show increased survival and DNA repair,¹³⁵ while others indicate no differences in responses.^{136, 137} Most of these studies have used detection of DNA repair protein‐related foci as the damage endpoint, so the relationship to clonogenic survival is not clear. No data with clinical energy protons appear to have been published, so there is no indication of whether RBE values would change in 3D cultures compared to 2D.⁷⁷ Nevertheless, the data with 3D tissue models support the important idea that radiation response depends on cell/tissue organization, emphasizing the potential usefulness of data from proton RBE studies using 3D normal tissue models.

3D‐in vitro constructs of breast and brain cancers, called mammospheres or neurospheres, or, more generally tumorspheres, have been described (e.g., Refs. ^{138, 139}) and used in studies of responses to photon irradiation. As with the 3D normal tissue models, little has been done using these models with proton irradiation, but the potential for use in RBE studies is clear. It is important to point out that the 3D tissue and tumor models just described are still rather simplistic compared to tissues and tumors in vivo as they lack vasculature and immune cells. A challenge is to develop ever more realistic organotypic tissue and tumor models for proton therapy studies.

Ultimately, in vivo data supersede in vitro data in terms of clinical relevance. However, in vivo studies are not only more costly, but also associated with potentially higher levels of uncertainty. For example, in calculating RBE variations as a function of depth of penetration, only a few studies have reliably documented significant findings. This in part is likely due to the need for meticulous processing of samples; preserving the relationship between in vivo proton range and dosimetry, to the postmortem processing of the biological sample. It is also in part due to the difficulty in positioning the finite target precisely in a high LET gradient region. In order to reduce the reliance on postmortem assessment, studies of biologic effect might utilize imaging‐based response parameters. For example, the use of high field strength magnetic resonance imaging in animals might provide data on spatial variations of biologic effect along the beam path. Such data would not only relate to clinical outcomes, but also provide information on normal tissues, including outcomes in which cell kill is not the only variable (radiation‐induced edema, necrosis, vascular damage, etc.).

With the increasing development of sophisticated imaging techniques using such powerful approaches as CT, MRI, PET, and bioluminescence, one can envision noninvasive, quantitative imaging approaches with sufficient spatial resolution and sensitivity to provide robust, dose‐dependent tissue, and tumor alterations that can be used after photon and proton irradiations for calculation of RBEs for normal tissues and tumors. Examples include measurement of apoptosis in tumor and normal tissues by scintigraphy, optical methods, or microPET.¹⁴⁰ Additionally, with improvements in imaging of hypoxic regions and the increasing use of scanning proton beams, the possibility to selectively target higher doses to hypoxic regions improves. In this context, therefore, development of higher resolution and more sensitive approaches to image regions of low oxygen in tumors could positively impact the use of proton therapy.

A source of heterogeneity in tumors is the presence of cancer stem‐like cells (CSCs) that appear to be resistant to therapies, including conventional photon irradiation, perhaps because of enhanced DNA repair ability and/or increased antioxidant capacity.^{138, 139, 141} In light of the discussion above about some fraction of human tumor cells having higher RBE values because of DNA repair defects, one might ask whether CSCs have lower proton RBEs. Although the published data are scarce, it has been reported that CSCs may be more effectively killed by carbon ions compared to photons in colon and pancreas cancers both in vitro and in vivo,^{142, 143, 144} and CSCs from colon and breast cancers may be more efficiently eliminated by proton irradiation than photon treatment, at least in vitro.^{145, 146, 147} These latter findings suggest a higher RBE for CSCs and, hence, a potential therapeutic gain with protons over photon irradiations in tumors where CSCs are a significant resistant population.¹⁴⁸ Additional carefully controlled studies of CSCs treated with protons versus photons are needed.

The increasing use of hypofractionation in radiotherapy with both photons and protons raises important issues for RBE determinations. There has been discussion on whether “new” biology is responsible for the greater than expected antitumor efficacy of some hypofractionation regimens.^{149, 150} Some have proposed that consideration of only the clonogenic survival of only the tumor cells is not sufficient to account for the observed responses,^{119, 120, 151} although not all agree.^{149, 152, 153} Important contributing factors might be that at high doses the relevant “target” for antitumor effects changes from the tumor cells themselves to vasculature^{119, 120, 151} or that stimulation of the immune system at high doses^{121, 122, 123} plays a role. How or if these high dose differences impact RBE values is not clear, and carefully designed experiments comparing, at the same doses and identical experimental conditions, outcomes after proton vs photon irradiations are needed. Only in vivo studies will accurately address these issues, and both tumor and relevant normal tissues need to be assessed quantitatively for a variety of fraction sizes.

8. Summary and recommendations

This Task group report outlines the basic concepts of RBE as well as the biophysical interpretation and mathematical concepts. The current knowledge on RBE variations was reviewed and discussed in the context of the current clinical use of RBE. The second part of the report focused on a critical assessment of the current practice as follows:

• 1The current clinical practice of using a constant RBE for protons should generally be maintained but specific clinical scenarios warrant a change in current practice.

Based on experimental data and models, the use of a constant clinical RBE = 1.1 that is independent of (α/β) _γ , fraction size and LET_d (or distribution of LET_d values) within tumor targets and OAR is not well justified in terms of our current understanding of the RBE for cell survival (see Sections 1.D. and 2.D.3. of this report). However, considering the uncertainties in quantifying and modeling RBE effects in various tumor and normal tissues for various end points, it is premature to adopt and recommend a variable RBE model to use clinically.^{154, 155} While it is acknowledged that RBE increases as a function of LET, the data and models to incorporate such variability need to be cross‐validated against in vivo studies and clinical outcomes. Therefore, in general, the use of a constant RBE of 1.1 should be maintained in current clinical practice (see Section 3.C. of this report). A potential exception would be the end of range being in a critical structure with known low α/β where a tapering off for SOBP fields might be considered or different physical dose constraints compared to photons may be defined, for example, by increasing the RBE to 1.2 or 1.3. Alternatively, the RBE increase may be incorporated by a decrease in tolerance dose. The latter could be safely done if it is in line with the current use of prescriptions and constraints based on an RBE of 1.1, that is, no reduction in currently defined target dose should be prescribed or increase in dose to specified volumes of normal structures.

• 2It is important to acquire clinical data to allow the reconstruction of RBE doses and correlate with clinical outcome in both prospective and retrospective studies.

Recurrences and toxicities in proton therapy should be analyzed in the context of potential RBE variations and treatment plans should be archived in a way that allows retrospective data analysis based on RBE and/or LET (see Section 3.C. of this report).

• 3There are sites and treatment strategies to be identified where variable RBE might be safely utilized for clinical benefit.

The fact that RBE varies implies that the use of a constant RBE does not necessarily reflect the best clinical practice. That the current clinical practice could have negative consequences (or suboptimal response) for some treatment sites has been speculated.⁵ Elevated LETd values corresponding to RBE >1.1 occur at the end of range and lower than average LET_d values may occur even in the center of the tumor target. Within critical structures of known low α/β, RBE adjustments outside of the CTV but potentially in the PTV might be considered (see Sections 3.C. and 4.D. of this report). This could mitigate normal tissue damage with acceptable risk of reducing tumor control. LET_d or RBE‐weighted dose optimization strategies might be able to influence the LET_d in critical structures as well as in tumors.

• 4The proton therapy community needs to assess the potential clinical consequences of delivering biologically weighted doses based on LET_d and/or RBE and as a function of dose and biological endpoints and assess the potential for harm and benefits associated with the clinical implementation of variable RBE and dose‐weighted LET_d models into TPS.

Because interpatient variability and many other factors with the potential to impact proton RBE for clinical endpoints, a conservative approach is warranted (see Section 4.D. of this report). To avoid underdosing the tumor, the RBE should not be increased beyond 1.1 in the CTV (larger RBE values imply lower physical dose to the CTV). We know that not all patients need the same dose delivered to their tumor to achieve local control. However, in clinical practice, all patients for a specific disease site (and staging, etc.) are currently treated to the same prescription dose. Ideally, a predictive assay or biomarker is needed that would allow identification of patients who are more radiosensitive vs radioresistant. This includes potential RBE variations due to patient‐ or/and tumor‐specific radiosensitivity.

Given the uncertainties in input parameters in biophysical models, a 3D modeling of biological dose (dose times RBE) in treatment optimization is currently not feasible with acceptable uncertainties. Clinical tools should be developed to allow users to visualize and optimize LET_d or RBE doses for evaluation purposes. The knowledge and potential consequences (what‐if scenarios) will inform clinicians. In particular, the use of these tools to analyze previously delivered treatment plans may help the community to establish baseline and consensus regarding what is safe and what is risky.

Vendors of TPS are encouraged to include RBE models in their software. For now, these options should be considered in the research domain and only available to users with in depth knowledge of the limitations of RBE models.

• 5Experiments are needed to improve our current understanding of the relationships among in vitro, in vivo, and clinical RBE and develop recommendations to minimize the effects of uncertainties associated with proton RBE for well‐defined tumor types and critical structures. Given the clinical practice of multimodality treatments, RBE experiments using radiation‐drug combinations are needed as well.

While more experimental data are needed, the huge variability particularly in in vitro experiments makes it doubtful that increasing the number of experiments performed in the same manner as before will significantly reduce RBE uncertainties. In part, the existing variability is likely due to inconsistent dosimetry and different biological experimental approaches, which should be addressed by standardizing experimental techniques. The latter may reduce uncertainties for cell survival experiments, which could help to define variable RBE values for certain tumors. It may also be able to determine effective tumor RBE values from the analysis of data from clinical trials. Additional studies are needed to examine if and/or to what extent RBE values for in vitro molecular and cellular endpoints are related to and predictive of the RBE for early and late damage to relevant OAR (see Section 5.C. of this report). In vivo data are very sparse. Analyzing clinical data might also help to guide and focus animal models, which are potentially costly. Future in vitro and in vivo studies should exploit as much as possible high‐throughput, high accuracy experimental approaches in order to generate large amounts of accurate and reproducible data, especially in combination with genomic analyses and mechanistic evaluations.

In conclusion, for fraction sizes small compared to α/β, the accumulated evidence from empirical studies^{37, 69} and mechanistic considerations^{54, 156, 157} suggests that proton RBE increases in approximately linear fashion as a function of LET_d up to the peak of a pristine Bragg peak (in the region from ~2 to ~12 keV/μm) and at a more rapid rate beyond the peak for molecular and cellular endpoints such as DNA DSB induction^{156, 157} and clonogenic survival.^{158, 159}

Uncertainties in RBE estimates from in vitro and in vivo studies are substantial in part due to nonstandardized experimental techniques and limited description in reporting of the reference and particle beam dosimetry techniques.¹¹⁰ There is a need for additional preclinical (in vitro and in vivo) studies to examine particle RBE in the limit of small dose per fraction (<1–2 Gy) and for doses large compared to α/β in order to differentiate among alternate models and mechanisms of action. Preclinical and retrospective clinical studies are needed to examine whether or not trends in particle RBE for key molecular and cellular endpoints are predictive of the RBE for clinical endpoints particularly considering patient variability in radiosensitivity. Preclinical studies of the effects on particle RBE of targeted chemical and immunological treatments in combination with radiation are needed. Standardized absolute dosimetry, microdosimetry and Monte Carlo track structure simulations, including the effects of secondary ions, are essential to aid in the interpretation and effective analysis of data from experimental studies. They are also critical for the establishment of correlation between measured biological responses and computed physical parameters for the development of predictive RBE models.

Preclinical and clinical studies are needed to examine and separate dose–volume effects from the effects of proton RBE in order to develop and validate biophysical models to determine equivalent tolerance dose constraints for conventional and hypofractionated proton therapy. Clinical studies are needed to examine whether or not spatial variations in proton RBE within OAR correlate with unexpected treatment effects. As toxicities are relatively rare events clinical studies should be combined with complimentary animal models because patient‐specific radiosensitivity hampers proper interpretation of clinical RBE. In addition, even without clinical evidence, LET_d distributions could be minimized in critical structures to exploit the unique biological characteristics of proton beams to improve the therapeutic ratio using IMPT.⁸