Development of an autonomous treatment planning strategy for radiation therapy with effective use of population‐based prior data

Abstract

Purpose

Current treatment planning remains a costly and labor intensive procedure and requires multiple trial‐and‐error adjustments of system parameters such as the weighting factors and prescriptions. The purpose of this work is to develop an autonomous treatment planning strategy with effective use of prior knowledge and in a clinically realistic treatment planning platform to facilitate radiation therapy workflow.

Method

Our technique consists of three major components: (i) a clinical treatment planning system (TPS); (ii) a formulation of decision‐function constructed using an assemble of prior treatment plans; (iii) a plan evaluator or decision‐function and an outer‐loop optimization independent of the clinical TPS to assess the TPS‐generated plan and to drive the search toward a solution optimizing the decision‐function. Microsoft (MS) Visual Studio Coded UI is applied to record some common planner‐TPS interactions as subroutines for querying and interacting with the TPS. These subroutines are called back in the outer‐loop optimization program to navigate the plan selection process through the solution space iteratively. The utility of the approach is demonstrated by using clinical prostate and head‐and‐neck cases.

Results

An autonomous treatment planning technique with effective use of an assemble of prior treatment plans is developed to automatically maneuver the clinical treatment planning process in the platform of a commercial TPS. The process mimics the decision‐making process of a human planner and provides a clinically sensible treatment plan automatically, thus reducing/eliminating the tedious manual trial‐and‐errors of treatment planning. It is found that the prostate and head‐and‐neck treatment plans generated using the approach compare favorably with that used for the patients’ actual treatments.

Conclusions

Clinical inverse treatment planning process can be automated effectively with the guidance of an assemble of prior treatment plans. The approach has the potential to significantly improve the radiation therapy workflow.

1. Introduction

Inverse planning derives a patient‐specific treatment plan through iterative interactions with an objective function, whose role is to mathematically rank a candidate treatment plan. While the approach has led to clinical implementation of IMRT and VMAT, the planning process routinely used in the clinics is rather tedious and labor intensive. The underlying issue responsible for this problem is the involvement of multiple model parameters (e.g., the weighting factors and prescription in the objective function) in treatment planning.^{1, 2, 3, 4} Ideally, these model parameters should be optimized before or together with the fluence map or machine parameters such as the apertures defined by multileaf collimators.^{5, 6} For computational purpose, these parameters are generally determined through manual trial‐and‐errors since their influence on the final dose distribution is not known until an optimization is done. Consequently, treatment planning remains to be one of the most labor intensive and time‐consuming tasks in current radiation therapy practice.

There have been intense research activities in treatment planning automation to improve the plan quality and workflow. Xing et al. pioneered the automation of the manual selection process of model parameters two decades ago with the use of a plan evaluation function and outer‐loop optimization.^{1, 2} Recently, it is attempted to replace the original decision‐function constructed based on empirically known DVHs or clinical experience by a prior treatment plan, which had similar anatomy to the one under planning.⁴ In reality, however, no two cases are identical and the use of DVHs of a previous patient as reference for guiding the plan selection could lead to sub‐optimal solution. Here, we propose to consider a spectrum of historical plans that share similar anatomical features in carrying out the two‐loop optimization. With effective use of an assemble of prior treatment plans, the resultant solution out of the two‐loop optimization is no longer “tightened up” to a single reference plan, thus making it possible to find better dosimetric distribution.

In practice, other options for utilizing historical treatment plans are through the use of class‐solution^{7, 8} and machine learning techniques, in which a library of prior plans are employed to train the system to provide the best model parameters. The parameters are then used as input of subsequent inverse planning. The method has recently been applied to predict the weighting factors^{9, 10, 11} and the prescription DVHs^{12, 13, 14, 15} needed for driving an inverse planning calculation. We emphasize that all these approaches only use prior knowledge‐derived parameters (i.e., either weighting or prescription or both) to “warm start” the inverse planning, instead of using them to guide the plan search throughout the optimization process. Additionally, the predicted DVHs prescription by machine learning may not always be physically realizable. For completeness, we mention that heuristic optimization^{14, 16, 17, 18, 19, 20, 21} and multiobjective optimization^{22, 23, 24} have also been developed to facilitate inverse planning process and these algorithms can, in principle, be improved with incorporation of prior knowledge, especially population‐based data.

The purpose of this work is to develop an autonomous treatment planning technique with effective use of a spectrum of prior plans that share similar anatomical features with the case under planning. Instead of using a simplified research inverse planning platform,^{25, 26, 27, 28} which often ignores some important geometric and physical factors, we proceed with an API‐like programming environment capable of interacting with a commercial treatment planning system (TPS) to implement the proposed strategy that mimics a planner's interactive planning and decision‐making process in searching for a sensible solution. The approach here enables us to leverage the sophisticated software subroutines (e.g., dose calculation, optimization, image registration, etc.) existing already in a clinical‐grade TPS to test the new algorithm. By implementing the outer‐loop optimization strategy in this programming environment, we demonstrate that IMRT/VMAT treatment planning can be readily automated.

2. Methods and materials

Our treatment planning system consisted of following components: (i) a clinical TPS; (ii) a robust formulation of plan evaluator or decision‐function; (iii) an outer‐loop optimization independent of the clinical TPS to assess a TPS‐generated plan and to drive the search toward a solution consistent with the decision‐function; and (iv) a programming method to query and interact with the TPS using Microsoft (MS) Visual Studio Coded UI, which is applied to record some common planner‐TPS interactions as subroutines. The following summarizes the details of the technique.

2.A. Software platform for autopiloted planning

Figure 1 shows the workflow of the population knowledge‐based autonomous planning. An independent C# program is written to accomplish the tasks delineated in Fig. 1. In this program, the interactions with a commercial Eclipse TPS (Varian Medical Systems, Palo Alto, CA) are realized through a series of subroutines that are prerecorded actions of a planner in operating the TPS by using Microsoft Visual Studio Coded UI.^{29, 30} For example, to perform a 3D dose calculation in Eclipse, “F5” is clicked after the beam setup is done. A subroutine for performing dose calculation can be generated by recording this action, which is called when dose distribution needs to be updated in the C# program. Coded UI provides a unique framework for us to probe and manipulate UI elements of TPS in application programming in C# or other programming environment. We have recorded more than a dozen essential actions in Eclipse operation for the work here (for example, exporting DVH to a file by pulling down the textbox “show DVH view” and selecting “export DVH in tabular form”, opening an optimization window by clicking “F10” and then starting an optimization by clicking “Optimize” button, and converting an isodose curve into a structure by right clicking “dose” on the left side menu and then selecting “convert isodose level to structure”) and saved them into a library of subroutines. The subroutines are called into our C# program to interact with the TPS for a variety of actions, for example, to assess the quality of a plan generated by the TPS and to provide updated model parameters to refine the Eclipse plan. We note that the method described here is not limited to the Eclipse TPS and this will be discussed in Section 4.

Figure 1.

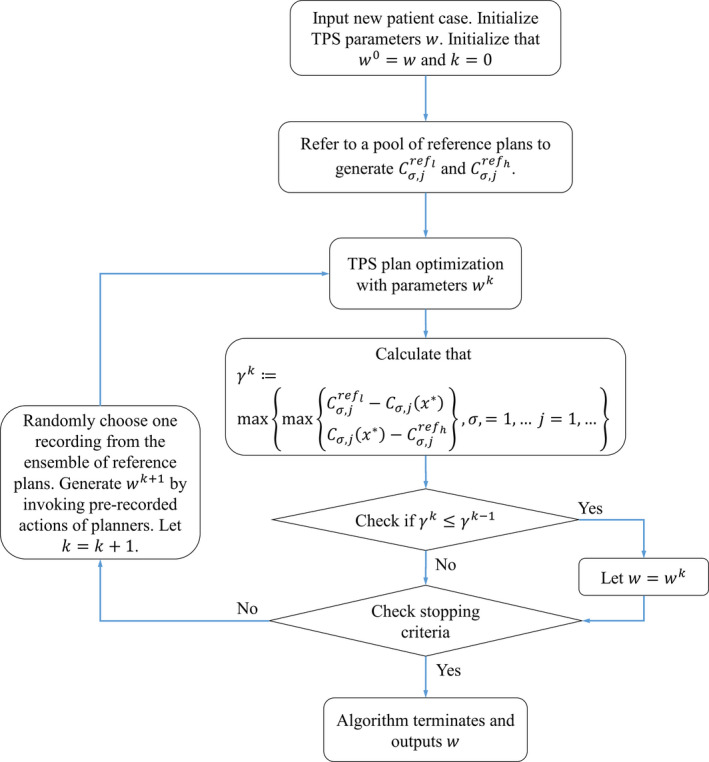
Flowchart of the autopiloted plan optimization scheme. An outer‐loop decision‐function analyzes the TPS plan and feeds the TPS optimizer with updated parameters for iterative improvement of the treatment plan. The algorithm terminates if either (i) γ ^k = 0, or (ii) no improvement has been made in consecutive iterations.

2.B. Automation of VMAT/IMRT treatment planning

2.B.1. Library of reference cases

For a given patient, a set of reference plans with similar anatomy is chosen automatically with some predefined geometric criteria.²¹ Specifically, the images of current case are overlaid with a candidate reference plan from a library of previously treated patients and the correlation between the two sets of images is examined. Only the reference cases with high correlation are selected as reference plans. For each structure, the signed difference of the contour points of the current and reference plans is computed for ray lines starting from the center of the mass of the structure.³¹ The points for a ray‐line to be in and out of the structure are recorded. The signed difference of an intercepting point is given by subtracting the radial distance of the point in the current case from that of the reference case. A plan is not considered as a good reference if the signed difference of any intercepting point in any structure is greater than 3 mm for a small structure such as the optic nerve and 5–15 mm for a large structure such as the skin contour.

2.B.2. Autopilot process

The iterative adjustment of Eclipse plan follows the flowchart delineated in Fig. 1, which involves the following key steps: (i) obtaining a candidate Eclipse plan, (ii) evaluating the Eclipse plan with the independent plan evaluator or decision‐function, (iii) deriving a new set of Eclipse planning with the new parameters, and (iv) updating the Eclipse planning parameters and obtaining the corresponding Eclipse plan. Specifically, at each step during the iterative adjustment of TPS planning parameters, the distance of the DVH curves of the involved structures to the DVHs of the best plan in the ensemble is examined. For the structure with the largest distance, a trial adjustment of the Eclipse plan is made by changing the weighting of the structure and reoptimization of the Eclipse plan. This continues until no further improvement in the DVHs with the above adjustment is noted. Using an ensemble of reference plans allows us to minimizing any potential overfitting problem caused by the use of a single reference plan. Formally, the plan selection process is to solve the following bi‐level optimization problem:

$$min\mathit{\gamma }$$

$$\mathrm{s}.\mathrm{t}.$$

$$\left\{\begin{array}{c}{x}^{\ast }\in argmin\left\{F_{TPS}\left(x;w\right):x\in X_{TPS}\left(w\right)\right\}\\ \begin{array}{c}{C}_{\mathit{\sigma },j}^{re{f}_l}-C_{\mathit{\sigma },j}\left(x^{\ast }\right)\le \mathit{\gamma },\forall \mathit{\sigma },j\\ \begin{array}{c}{C}_{\mathit{\sigma },j}\left(x^{\ast }\right)-C_{\mathit{\sigma },j}^{re{f}_h}\le \mathit{\gamma },\forall \mathit{\sigma },j\\ \mathit{\gamma }\ge 0\end{array}\end{array}\end{array}\right.$$ (1)

where $w$ is the input parameter to the TPS, $F_{TPS}\left(x;w\right)$ and $X_{TPS}\left(w\right)$ are the objective function and the feasible region of the optimization problem solved by the TPS for fixed parameter $w$, $C_{\mathit{\sigma },j}\left(x^{\ast }\right)$ is the j‐th dosimetric characteristic variable of structure $\mathit{\sigma }$ for the plan $x^{\ast }$, and $\mathit{\gamma }$ measures the infeasibility of the constraint that $C_{\mathit{\sigma },j}\left(x^{\ast }\right)$ should fall within the band $\left[C_{\mathit{\sigma },j}^{re{f}_l},C_{\mathit{\sigma },j}^{re{f}_h}\right]$. The values of $C_{\mathit{\sigma }j}^{re{f}_l}$ and $C_{\mathit{\sigma }j}^{re{f}_h}$ represent the low and high boundary values of the same dosimetric characteristic variable extracted from the library of reference plans. In this study, we divide the DVH curve of each structure into segments and the j‐th dosimetric characteristic variable of structure $\mathit{\sigma }$ is simply the j‐th DVH segment of the structure. Note that the prior knowledge or the library of reference plans sets our preferred variation range of the dosmetric quantity $C_{\mathit{\sigma }j}$, which is similar to the use of prior data to set expectations for the planning process in previous studies.^{12, 13, 14, 15, 18, 19} Also note that the first constraint in (1) requires that plan $x^{\ast }$ should be the output of the optimization problem in the TPS, which serves as a lower level minimization problem embedded within the bi‐level model framework.

Our approach of utilizing prior plans goes, however, beyond merely setting expectations as the knowledge is integrated with the optimization algorithm to guide the search for the optimal solution. In order to speed up the calculation, the beam and weighting parameters of a prior plan in the middle of the ensemble are used to “warm start” the autopiloted planning process. However, the final solution does not rely on the selection of the initial selection of starting plan. During the calculation, instead of letting the DVH segment value $C_{\mathit{\sigma }j}$ stop anywhere when its value is inside the range defined by $C_{\mathit{\sigma }j}^{re{f}_l}$ and $C_{\mathit{\sigma }j}^{re{f}_h}$, we continuously “push” the $C_{\mathit{\sigma }j}^{ref}$ value toward a lower value in the predefined range by changing the reference value.

2.C. Evaluation

The above technique is applied to plan two clinical cases: a five‐field IMRT prostate case and a VMAT head‐and‐neck (HN) case. In the prostate IMRT case, 6 MV photon energy is used and the beam angles are 0^o, 50^o, 100^o, 260^o, and 310^o, respectively. 78 Gy is prescribed to cover V₉₅ of the PTV in 39 fractions. For comparison, the resultant dose distributions of the autopilot scheme are compared with the corresponding plans used for clinical treatments. To construction of the reference plan library, 15 previously treated prostate cancer patients are selected using the procedure outlined in Section 2.B. For the HN case, two 360^o 6 MV VMAT arcs are used. Nine previously treated HN cases are selected as reference plans. We acknowledge that the database can be enlarged to better cover the variations in patient anatomy. Given that the cases selected to form the library are reasonably close to the cases under planning and considering the pilot nature of the study, the number is reasonable.

3. Results

3.A. Five‐field IMRT prostate treatment

In Fig. 2, we show the band of DVH representing the preferred range and distribution of the resultant DVH curve for the prostate case under planning. To illustrate the progressive improvement of the autopilot process, in Fig. 3 we show the DVH results of involved structures for the 1^st, 7^th, and 14^th iteration. The improvement saturate after about 14 iterations and the calculation thus terminates after the 14^th iteration. At each outer‐loop iteration, the TPS parameters are adjusted, which leads to a different dose distribution. While these plans are on the Pareto front, the autoplanning process here explores plans beyond the traditional Pareto front. For example, when a “hot spot” presents in PTV, a “tuning structure” would be created automatically by converting the corresponding isodose curve into a structure and this process would drive the plan away from the traditional Pareto surface, leading to improvements in all DVHs. Figure 4 shows the DVH comparison between the clinical and autopiloted plans for the case. Figure 5 shows the isodose distribution of the two plans. Only minor discrepancy is seen between the autopiloted plan obtained under the guidance of the population‐based library of reference plans and clinical plan generated by a human planner independently.

Figure 2.

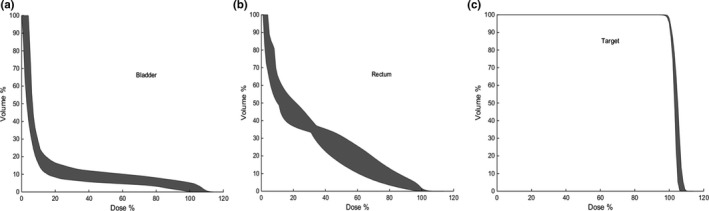
Plots of reference DVHs of bladder (a), rectum (b), and PTV (c) for the prostate case under planning. The ensemble of DVHs represents the preferred range of the resultant DVH curve.

Figure 3.

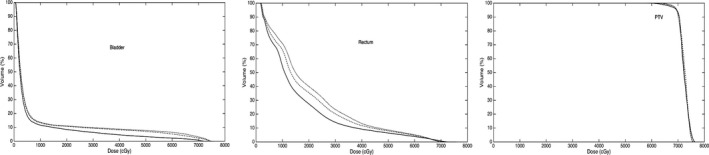
DVHs of the bladder, rectum, and prostate at iteration #1 (dotted), #7 (dashed), and #14 (solid). A systematic improvement in the DVHs is observed.

Figure 4.

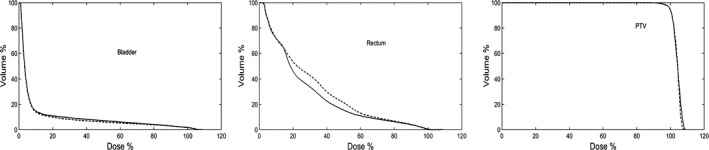
A comparison of DVHs of the clinical and autopiloted plans for the five‐field IMRT prostate case. The dashed and solid curves represent the DVHs of clinical and autopiloted plans, respectively.

Figure 5.

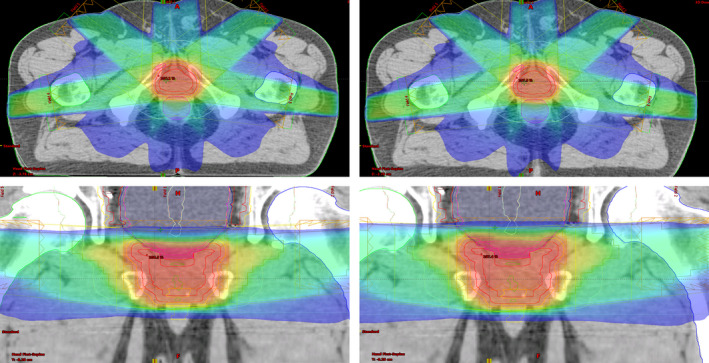
Side‐by‐side comparison of the isodose distributions of autopiloted (right) and clinical (left) plans for the prostate case.

3.B. HN VMAT case

In Fig. 6, we show the ensemble of DVHs of the spinal cord, brainstem and PTV of the reference plans obtained using the method of Section 2.B for the HN case under planning. Figure 7 shows the DVH comparison between the clinical and autopiloted planning for the case, and Fig. 8 shows the isodose distributions of the two plans. Again, only minor discrepancy is seen between the autopiloted plan obtained under the guidance of the population‐based library of reference plans and clinical plan generated by a human planner independently.

Figure 6.

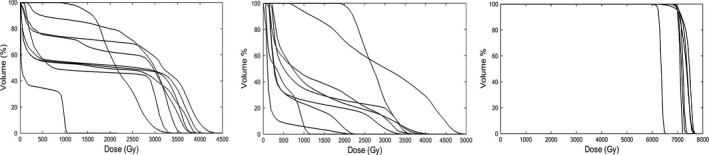
Plots of reference DVH curves of spinal cord (a), brainstem (b), and PTV (c) for the head‐and‐neck case under planning. The ensemble of DVHs presents the preferred range of the resultant DVH curve.

Figure 7.

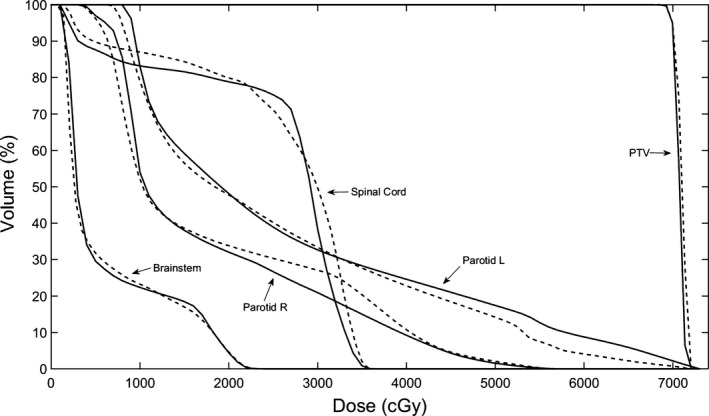
A comparison of DVHs of the clinical and autopiloted plans for the two‐arc head and neck VMAT case. The dashed and solid curves represent the DVHs of clinical and autopiloted plans, respectively.

Figure 8.

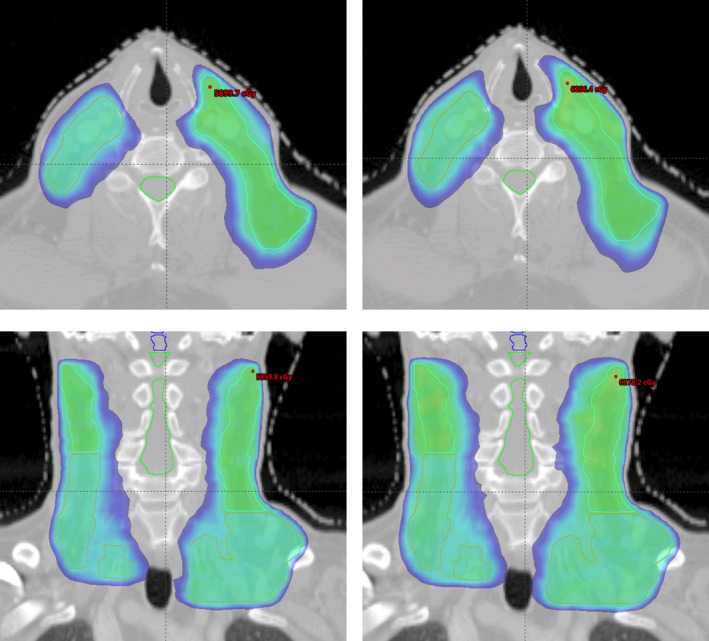
Side‐by‐side comparison of the isodose distributions of autopiloted (right) and clinical (left) plans for the head‐and‐neck case.

Computationally, depending on the complexity of the case, it takes about a few hours to complete a plan selection process, but this can be improved with improved programming, and, in the future, better integration with the commercial TPS. However, comparing with the current manual planning process, which could take days of a dosimetrist's time for clinically challenging cases, the proposed method eliminates the manual trial‐and‐error modification of the optimization parameters and facilitates the clinical workflow.

4. Discussion

In inverse planning, an optimized solution is obtained under the guidance of an objective function containing multiple model parameters.^{1, 10, 27, 32, 33, 34, 35} In the past two decades, much of the efforts in research and commercial product development have been focused on finding a better function with mathematical constraints to provide clinically sensible solution. While the formulation of objective function and the technique used to search through the solution space under the guidance of the objective function are important to the success of inverse planning, clinical IMRT/VMAT planning has been handicapped by the involvement of multiple model parameters that necessitates trial‐and‐error determination. In this paper, we proposed an effective technique to autopilot the VMAT/IMRT planning process in a clinical TPS platform. The automation is realized by combining the functionalities of the black‐box TPS and a decision‐function incorporating population‐based prior knowledge. The calculation is analogous to the planning process of a human planner, with a candidate plan assessed iteratively by the decision‐function each time after the Eclipse optimization is done.^{1, 2, 10} During the autopiloted planning, the C# program interacts with TPS continuously to extract the updated information and to instruct on what to do next until a satisfactory plan is obtained.

In addition to the effective utilization of population‐based prior data, a technical innovation of the work here is the use of Coded UI to recording the mouse clicks/keystrokes as executable subroutines for specific tasks during planning. By doing so, we can extract the updated information of treatment planning and interact with the TPS effectively to autopilot the process. In practice, because the Windows platform encompasses a large number of TPS and other clinical application software, the presented method should be valuable for future clinical research and practice. We note that, while Coded UI is designed for the Windows environment, the principles and strategies proposed here are quite broad. There are analogous software tools for other operating systems. For Unix and Linux environment, other record‐and‐playback services such as UNIX Session Recorder (Sikuli, Linux Desktop Testing Project) can be employed.³⁶

The programming environment described here is highly interactive, making it easy to principle‐testing and prototyping. Currently, the development of treatment planning algorithm(s) is often done in simplified software platforms^{25, 26, 27, 28} without considering some important geometric and physical factors. The approach here enables researchers to leverage the sophisticated software subroutines existing already in a clinical‐grade TPS to test new ideas without repeating some well‐known tasks. The approach may also facilitate the translation of research to clinical practice. Finally, we note that the implementation here represents only one of many possible applications of the proposed strategy. The approach is applicable to streamline other clinical tasks in TPS or other software tools. We also note that practical issues such as error handling, such as unexpected windows popup during the autopiloted planning process, are not discussed. In principle, a preventive action can be taken by adding some checking points in the C# program of autopiloted planning to monitor the potential popup window(s).

Conclusion

Inverse planning in modern radiation therapy involves multiple steps of manual operation and is known to be a time‐consuming process. In this work, we propose an autonomous treatment planning strategy to facilitate the inverse planning process. The research here is directly translatable to clinical practice as the backbone of the plan optimization is built upon a commercial TPS. Additionally, the approach is quite general and allows us to incorporate empirical judgment and population‐based prior knowledge into the plan selection process. The utility of the approach has been demonstrated successfully by using two clinical cases. With the increased interest in using prior knowledge in radiation oncology applications, the data analytics and decision‐making method may prove to be useful to facilitate clinical workflow.

Conflict of interest

Lei Xing is the principal investigator of a master research agreement (MRA) with Varian Medical Systems.