Abstract
Purpose
To evaluate a method for measuring breast density using photon‐counting spectral mammography. Breast density is an indicator of breast cancer risk and diagnostic accuracy in mammography, and can be used as input to personalized screening, treatment monitoring and dose estimation.
Methods
The measurement method employs the spectral difference in x‐ray attenuation between adipose and fibro‐glandular tissue, and does not rely on any a priori information. The method was evaluated using phantom measurements on tissue‐equivalent material (slabs and breast‐shaped phantoms) and using clinical data from a screening population (). A state‐of‐the‐art nonspectral method for breast‐density assessment was used for benchmarking.
Results
The precision of the spectral method was estimated to be 1.5–1.8 percentage points (pp) breast density. Expected correlations were observed in the screening population for thickness versus breast density, dense volume, breast volume, and compression height. Densities ranged between 4.5% and 99.6%, and exhibited a skewed distribution with a mode of 12.5%, a median of 18.3%, and a mean of 23.7%. The precision of the nonspectral method was estimated to be 2.7–2.8 pp. The major uncertainty of the nonspectral method originated from the thickness estimate, and in particular thin/dense breasts posed problems compared to the spectral method.
Conclusions
The spectral method yielded reasonable results in a screening population with a precision approximately two times that of the nonspectral method, which may improve or enable applications of breast‐density measurement on an individual basis such as treatment monitoring and personalized screening.
Keywords: breast density, mammography, photon counting, precision, spectral imaging
1. Introduction
It is well‐established that breast density is directly correlated to the risk of developing breast cancer,1, 2 and inversely correlated to the diagnostic accuracy of mammography.3, 4 Breast density therefore has the potential to improve risk assessments,5, 6 which in turn enables the transformation from population‐based to personalized screening in order to increase sensitivity and minimize cost of breast‐cancer screening.7, 8, 9, 10, 11 In a personalized screening approach, high‐risk women are called to mammography at an earlier age, more frequently, and/or are examined with other modalities. Breast‐cancer treatment may also benefit from using breast density as a biomarker.10, 11, 12 The administration of preventive and adjuvant chemotherapy can be related to risk, and the effect of drugs such as tamoxifen and raloxifene that simultaneously reduce the susceptibility to breast cancer and breast density, can be monitored. Further, breast density has the potential to facilitate clinical trials by working as a surrogate for breast cancer,10 and it is an important input parameter to dose calculations.13
Traditionally, breast density is estimated from the areal fraction of fibro‐glandular tissue in the mammogram. This area‐based density is most commonly determined by visual assessment and reported using the BI‐RADS breast‐density categories.14 Automated and computerized methods have been developed in order to reduce workload and address inter‐reader variability of manual assessment.15 Assessment of area‐based density is well‐established in clinical practice, but an intrinsic limitation is that the method does not have a simple relationship to the underlying quantity that is being assessed, i.e., the volume of fibro‐glandular tissue in the breast. This ambiguity may lead to dependencies on random external factors such as compression or image processing parameters.
Methods to measure the volumetric fraction of fibro‐glandular tissue in the breast (sometimes referred to as the volumetric breast density) are becoming an established alternative to the area‐based density measure.15 These methods are more consistent and can be expected to improve many applications of breast density, such as risk estimates,15, 16, 17, 18 although clinical results on this topic are, so far, not conclusive.19, 20, 21
Computed tomography (CT) and magnetic resonance imaging (MRI) provide volumetric data that can be converted to breast density either by a voxel‐wise binary segmentation of the breast,22 or by a continuous measurement of voxel contents.23 Nonetheless, in routine breast imaging or a screening setting, the only data available may be regular mammograms, but measuring tissue volumes from two‐dimensional data is challenging; two properties (the thicknesses of adipose and glandular tissue) cannot be computed from a single projection measurement without any a priori knowledge. Highnam and Brady proposed that mammograms could be normalized to represent tissue thicknesses by accurate modeling of the imaging system,24 the standard mammogram form (SMF).25 SMF has inspired a number of methods, which all require some information in addition to the mammogram, such as the height of the compression paddle,26, 27, 28, 29, 30 or an entirely fatty pixel.31 In addition, a breast model or a low‐pass filtration may be required to account for any thickness gradients.
Spectral breast‐density measurement was first considered by Breitenstein and Shaw,32 and investigated experimentally by Shepherd et al. using a device for dual x‐ray absorptiometry.33 As x‐ray attenuation is material‐specific, it is possible to extract the thicknesses (and volumes) of adipose and glandular tissue with exposures at two different x‐ray energies using so‐called material decomposition.34 Spectral breast‐density measurement is attractive because there is no need for a compression height measurement, which often only has an accuracy of several millimeters,35 or a reference fatty pixel, which may be difficult to extract from dense breasts or in the presence of artifacts (e.g., skin folds or dips), or a thickness model, which may fail at e.g., irregular thickness changes. However, the major challenge of spectral measurements is to streamline the acquisition of spectral information, so that the method can be applied for routine clinical use and screening.
One possibility for obtaining spectral information is to use two exposures with different beam qualities, investigated for breast‐density measurements by Ducote and Molloi.36, 37 The introduction of photon‐counting detectors in medical imaging has, however, enabled one‐shot spectral imaging,38, 39 i.e., photons from a single acquisition are sorted according to energy by the detector. One major advantage of this approach compared to dual‐exposure methods is that the patient and workflow are unaffected; there is no additional dose or examination time. In addition, misregistration errors are avoided and reduction of electronic noise and scatter improves the material decomposition.
Philips MicroDose SI (Philips Health Systems, Kista, Sweden) is a spectral mammography system with a photon‐counting detector. Spectral breast‐density measurement has been evaluated on prototype systems using phantom data,40, 41 and on the commercial system using clinical data.42 This study is a comprehensive evaluation of the algorithm for measuring breast density in the commercial system using phantom data and clinical data. Special attention is put on determining the precision.
2. The spectral breast‐density measurement method
2.A. Theoretical background
In a photon‐counting system, the detected signal in energy bin of a detector element is
| (1) |
where is the number of incident photons and is the incident energy spectrum. and represent the linear attenuation coefficients and thicknesses of the breast constituents, where subscripts , , and indicate fibro‐glandular, adipose, and skin tissue, respectively. With this notation, breast density is defined as and the total breast thickness is . is the detector response function, ideally a rect function, but in practice will decay with energy (quantum efficiency), have a weak nonlinear dependence on the count rate (proportional to with constant read‐out time) caused by pile‐up and chance coincidence, and have a weak nonlinear dependence on the counts in other energy bins () in case of cross talk between bins. Equation (1) assumes that scattering can be treated as absorption, i.e., a system with efficient scatter rejection.
For most natural body constituents at mammographic x‐ray energies, x‐ray attenuation is made up of only two interaction effects, namely photoelectric absorption and scattering processes.34 Assuming known system properties (), constant and known skin thickness (), and known linear attenuation coefficients (, , ), acquisitions over two different energy ranges () according to Eq. (1) yield a system of equations with a unique solution for and :
| (2) |
Measurements at more than two energies () yield an over‐determined system of equations under the assumption of only two independent interaction processes. Measuring at a single energy () corresponds to nonspectral imaging, and cannot alone be used for determining breast density as it would be the solution to a single equation in two unknowns.
2.B. Spectral mammography system
The Philips MicroDose SI mammography system comprises a tungsten‐target x‐ray tube with 0.5 mm aluminum filtration, a precollimator, and an image receptor, which is scanned across the object (Fig. 1, left). The image receptor consists of photon‐counting silicon strip detectors with corresponding slits in the precollimator (Fig. 1, center). This multislit geometry rejects virtually all scattered radiation.43
Figure 1.

Left: Photograph and schematic of Philips MicroDose SI. Center: The image receptor and electronics. Right: Transmitted spectrum through 40 mm of glandular and adipose tissue, measured and calculated from Ref. 44 (top), and (bottom) the linear attenuation of tissue‐equivalent material, measured and from Ref. 46, and of glandular and adipose tissue from Ref. 47 and calculated from Ref. 45. [Color figure can be viewed at wileyonlinelibrary.com]
Photons that interact in the detector are converted to pulses with amplitude proportional to the photon energy.39 A low‐energy threshold provides efficient rejection of electronic noise by discriminating against all pulses below approximately 5 keV. Low levels of electronic noise and scattered radiation are important factors for spectral imaging to work efficiently [implicit assumptions of Eqs. (1) and (2)]. The system allows image acquisitions at 26, 29, 32, 35, and 38 kV. A high‐energy threshold sorts the detected pulses into two bins according to energy, which are the high‐energy part of the spectrum (referred to as the high bin) and the total spectrum (the sum bin). The threshold level is set depending on kV in the range 15–25 keV.
Figure 1, right, shows measured counts in the high bin and the difference between the sum and the high bins (essentially the low bin), compared to a generic 32‐kV tungsten spectrum,44 transmitted through 40 mm of adipose and glandular tissue. It is clear that the measurement contains a larger portion of the counts in the low bin than what would be expected from the spectrum and a threshold at 19 keV, which emphasizes the fact that the threshold level is only an estimate and, furthermore, the energy resolution of the threshold is approximately 5 keV.39 This uncertainty does, however, not impact the breast density measurement as will be discussed in the following section.
2.C. Calibration and image processing
Equation (2) is preferably solved by calibration because system properties (, , and ) may be complex and partially unknown. For instance, as was seen in the previous section, the incident x‐ray spectra as well as the exact levels of the detector thresholds were not known. Nonspectral calibration was applied approximately weekly by imaging a 0–72 mm (in steps of 12 mm) polymethyl methacrylate (PMMA) step wedge. This calibration step allowed for mapping of pixel values in each energy bin to equivalent thicknesses of PMMA and accounts for nonspectral drifts of system response, e.g., caused by changes in x‐ray tube output. Figure 2 shows an overview of the calibration procedures for a case in medio‐lateral oblique (MLO) view, imaged at 32 kV and with a compression height of 51 mm.
Figure 2.

Illustration of the calibration procedure and spectral breast‐density measurement for a: Unprocessed high‐ and sum‐energy images (raw counts); nonspectral calibration on a PMMA step wedge; high‐ and sum‐energy mammograms; spectral calibration on tissue‐equivalent material and PMMA‐to‐thickness and ‐density LUTs; thickness and density maps; calculation of density and volume measures. Iso‐thickness and ‐density lines (dotted) and calibration points (circles) are indicated in the LUTs. Note that the thickness and density maps are normally not displayed to the user but are an internal part of the algorithm.
The subsequent spectral calibration allowed for mapping of equivalent thicknesses of PMMA to thicknesses of adipose and glandular tissue. Calibration data were acquired by imaging tissue‐equivalent material (CIRS Inc., Norfolk, VA, USA) in a range of thickness‐density combinations as listed in Table 1. The thickness range was determined by tube voltage (the system picks kV in response to compression height), and the density range was chosen to approximately correspond to thickness (anticorrelation between thickness and density was assumed).
Table 1.
Calibration with tissue‐equivalent material per x‐ray tube voltage. The calibration points were defined by combining the listed thicknesses and densities
| Voltage | Thicknesses | Densities |
|---|---|---|
| 26 kV | [10 20 40] mm | [50 70 100]% |
| 29 kV | [20 40] mm | [30 50 70 100]% |
| 32 kV | [20 40 60] mm | [0 30 50 70 100]% |
| 35 kV | [40 60 80] mm | [0 30 50 70 100]% |
| 38 kV | [60 80] mm | [0 30 50 70 100]% |
To ensure accurate interpolation and extrapolation, system modeling according to Ref. 39 was used to generate large PMMA‐to‐thickness and PMMA‐to‐density look‐up tables (LUTs), which were fitted to the measured calibration data by a six‐parameter affine transform. The LUTs for 32 kV are shown as example in Fig. 2. Note that the thickness and density ranges covered by the LUTs are substantially larger than the calibration ranges in Table 1, which is necessary to cover all physically possible combinations and to account for noise. Iso‐thickness and ‐density lines are shown in the LUTs (dotted). The calibration points (circles) are essentially parallel to the iso lines, which is expected from the calibration points in Table 1.
The spectral calibration was carried out only once during the study, but, to account for drifts of the spectral response, the high‐energy bin was multiplied with a factor such that the signal ratio between the two energy bins was kept constant in the open beam. In addition, the spectral response can be expected to vary systematically with detector temperature because of changes in charge collection efficiency. Small temperature variations (< ±1°C) can be expected in the water‐cooled detector, and an approximately linear dependency of the LUTs was found within this span. The detector temperature was therefore monitored, and the effect on the LUTs was compensated for by a linear function.
The linear attenuation of tissue‐equivalent material was measured in this study using a procedure described in Appendix A. The results are shown in the lower plot of Fig. 1, right, together with published attenuation data. The average difference at 20‐30 keV between our measurement and a calculation from the elemental composition of breast tissue,45 which the material is made to mimic, is small and within 0.3%, which is in line with previous studies.46 Nevertheless, as has also been noted previously,46 there is a larger (8% for adipose and 2% for glandular tissue) difference to direct attenuation measurements by Johns and Yaffe.47 A preliminary investigation of clinical data using the tissue‐equivalent material as calibration base resulted in an unreasonable distribution of densities ranging from negative values to values above 100%. The calibrated breast densities were therefore transferred to attenuation according to Johns and Yaffe (henceforth referred to as display values) using a linear transfer function derived in Appendix A.
The PMMA‐to‐thickness and ‐density LUTs yield pixel‐wise measurements of thickness and density, referred to as thickness and density maps (see examples in Fig. 2). The thickness map was used to calculate the volume element corresponding to each pixel, which in turn was used to calculate measures of breast volume, dense volume, and density for the entire breast. The procedure is described in detail in Appendix A. The mode (most common value) of the thickness map was used as a measure of the compressed breast thickness, independent of the compression paddle height. We assumed 1.5 mm of skin on each side of the breast.48 Segmentation and exclusion of the pectoralis muscle were performed for MLO views and the skin line was excluded by removing 5 mm of the periphery of the breast.
3. Analysis
3.A. Phantom measurements
Slabs of tissue‐equivalent material were used to evaluate the accuracy and precision of the spectral breast‐density measurement. Accuracy is in this study defined as the mean deviation from ground truth, and precision refers to the degree of variation between measurements.
Six sets of images, each containing 25 different phantom configurations were acquired on two different MicroDose SI units. The phantom configurations ranged from 20 mm to 110 mm thickness, from 250 cm3 to 1360 cm3 volume, and from 0% to 100% breast density in terms of the tissue‐equivalent material. In terms of display values, the density ranged from 18% to 85%. The six sets of images were acquired on each of the two systems under varying conditions corresponding to reasonable circumstances in clinical practice: Two sets under normal conditions in a stable laboratory environment, two sets with large detector temperature variations, one set with a worn‐out x‐ray tube close to the end of its expected life time, and one set after a large number of consecutive exposures corresponding approximately to the maximum number of exposures between PMMA calibrations. Additionally, one set of images containing six configurations of low thicknesses and high densities was acquired on both units. A total of 162 data points were acquired.
The average and the standard deviation of the errors were evaluated using the tissue‐equivalent material as ground truth, and taken as measures of accuracy and precision, respectively. As the same type of material was used for calibration and for the measurements, accuracy in this case should not be confused with deviations from actual breast‐density values, which is in our case defined by the measurement accuracy of the attenuation values in Ref. 47, but refers to the deviation from phantom specifications, caused by systematic uncertainties, such as in the LUT interpolation.
3.B. Clinical measurements
Clinical data were collected with one MicroDose SI unit as part of a screening program for women aged 40 to 75 yr at Södersjukhuset in Stockholm, Sweden. The data were collected with informed consent and within the Karolinska mammography project for risk prediction of breast cancer (KARMA). For an examination to be included, we required it to contain exactly one image in craniocaudal (CC) view and one image in MLO view for each laterality. This resulted in a total of 1333 examinations with four images each. The breast density was measured in these images under the following additional constraints: No implants; compression height between 20 and 100 mm; successful automatic pectoralis segmentation. The upper limit in compression height was set by technical constraints specific to the system that was used for this study and is not a limitation of the commercial system.
A measure of accuracy (mean deviation from ground truth) could not be obtained from the clinical data as there was no ground truth available, but the data were evaluated in terms of statistical properties (e.g., range and distribution) to verify that these were reasonable. The precision (the degree of variation from one examination to the next) was evaluated by the correlation between the following pairs of variables: Breast thickness and compression height (a one‐to‐one relation within the precision of the compression paddle height is expected); breast density and breast volume (a weak anti‐correlation is expected); contralateral (left‐right) breast density; and ipsilateral (CC‐MLO) breast density.
Even though measurements from the same examination (ipsilateral and contralateral) are likely to exhibit strong correlation, we expect some degree of variation. Common to both contralateral and ipsilateral measurements are variations caused by algorithm inaccuracy, differences in environmental and system conditions, and differences in positioning of the breast. For the contralateral images, there are additional biological variations between the breasts. For the ipsilateral images, a systematic error from slightly different breast volumes in the CC and MLO views and random variations caused by pectoralis‐segmentation inaccuracy can be expected. If we assume that these sources of variation are independent and normally distributed and we neglect the contribution from the pectoralis segmentation (expected to be small based on previous experience), we can estimate the contribution from biological variation () and from other sources (), given the contralateral () and ipsilateral variations ():
| (3) |
3.C. Comparison to nonspectral breast‐density assessment
A nonspectral algorithm for breast‐density assessment has been developed previously and shown to perform well on the MicroDose system.30 This nonspectral algorithm, applied on the sum of the high‐ and low‐energy bins, was used to benchmark the performance of the spectral algorithm.
In summary, calibration data were acquired by imaging a range of thickness‐density combinations of the same type of tissue‐equivalent material that was used for the spectral calibration. Using the calibration data, effective linear attenuation coefficients for adipose and glandular tissue were calculated and fitted to second degree polynomials of x‐ray tube voltage and breast thickness. To measure the density in an image, the breast thickness was estimated by a model that assumed a constant thickness equal to the compression height in the central part of the breast, and semi‐circles perpendicular to the skin line and with a diameter equal to the compression height in the peripheral part. The measurement was restricted to an area with thickness larger than half the compression height to reduce errors from model imperfections and the skin line. To ensure a meaningful comparison between the spectral and nonspectral algorithms, the following adaptions of the nonspectral algorithm were made compared to the implementation described in Ref. 30: Density values outside the range [0%, 100%] were allowed; display values were calculated as described in Appendix A; identical pectoralis segmentations were used for both algorithms.
A major difference between the spectral and nonspectral algorithms is the use of additional thickness information in the nonspectral algorithm, and a phantom experiment was designed to evaluate the effect of this difference. Two breast‐shaped phantoms were milled from tissue‐equivalent material with equal specified density using thickness maps derived from two spectral mammograms (Fig. 3). The skin model in the spectral algorithm was disabled for this investigation. Two images were acquired of each phantom with compression heights obtained by compressing the phantom. Deviations of the measured compression heights of ±1 mm were simulated by setting the compression height manually; 1 mm is the smallest step that the compression mechanics can resolve and it is also a realistic precision for compression paddles calibrated for breast‐density estimation.35 The precision for the respective algorithms was taken as the standard deviation of the difference to the specified density.
Figure 3.

The custom‐made phantoms that were used to compare the spectral and nonspectral algorithms. [Color figure can be viewed at wileyonlinelibrary.com]
The precision of the nonspectral algorithm was estimated on clinical data from the contralateral and ipsilateral correlation as described in Section 3.B.. Systematic differences between the spectral and nonspectral algorithms were investigated by comparing the measured densities on the population. A limitation of the comparison is that the nonspectral algorithm did not include a skin model.
4. Results
4.A. Phantom measurements
Figure 4 shows the measured density and volume as a function of ground truth for the 162 phantom measurements. Ground truth was given by the specifications of the tissue‐equivalent material, which were transferred to display values according to Appendix A. Linear fits and the Pearson correlation coefficients are shown in the figure. The accuracy (mean deviation from ground truth) of the density measurement was 0.2 percentage points (pp), and the precision (one standard deviation) was 1.8 pp. The accuracy of the volume measurement was 1.9%, and the precision was 1.6%. Table 2 shows a stratification of the accuracy and precision on environmental and system conditions.
Figure 4.
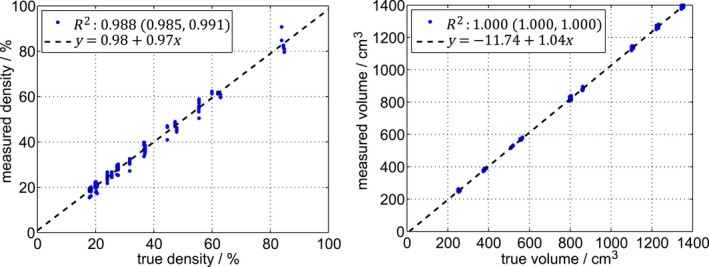
Measured density (left) and volume (right) as a function of ground truth for 162 measurements. The dashed lines are linear fits. The Pearson correlation coefficients () are given with 95% confidence intervals. [Color figure can be viewed at wileyonlinelibrary.com]
Table 2.
Accuracy (A) and precision (P) for the phantom measurements, stratified on environmental and system conditions, with the number of measurement points (n)
| n | Density | Volume | |||
|---|---|---|---|---|---|
| A [pp] | P [pp] | A [%] | P [%] | ||
| Normal conditions | 50 | 0.6 | 1.1 | 1.8 | 1.2 |
| Temperature variation | 50 | 0.5 | 1.3 | 1.8 | 1.5 |
| High load | 25 | −1.3 | 2.3 | 3.2 | 1.2 |
| Old x‐ray tube | 25 | 0.5 | 1.3 | 1.7 | 1.7 |
| High density | 12 | −0.7 | 3.3 | 0.4 | 1.8 |
| Total | 162 | 0.2 | 1.8 | 1.9 | 1.6 |
4.B. Clinical measurements
The spectral breast‐density measurement was successful (all constraints listed in Section 3.B. fulfilled) for 99.7% of all images. Specifically, pectoralis segmentation was successful for 99.6% of all MLO images. The nonspectral algorithm was successful for 99.3% of all images. For inclusion of an image, we required that both algorithms be successful, resulting in a total of 1329 examinations and a total of 5289 images (not all of the examinations contained four images with all constraints fulfilled).
Figure 5 shows measures from the spectral algorithm: Breast density, dense volume, and total breast volume (including skin). The scatter plots show the dependencies of these variables on breast thickness (including skin). Error bars indicate the spread (one standard deviation of the measurements within equal‐sized thickness intervals), and a moving average filter was applied to illustrate the trend. The data were fitted to a general power function () with coefficients and for each measure shown in Fig. 5 and listed in Table 3. The density was anticorrelated to breast thickness, whereas the dense volume and breast volume were directly correlated to thickness.
Figure 5.

Breast density (top), dense volume (middle), and breast volume (bottom) measured in 5289 mammograms with the spectral algorithm. The scatter plots show the dependencies on breast thickness smoothed with a moving average filter, with error bars (one standard deviation), and with a fitted general power function. The marginal histograms show distributions of the measures projected along the axes of the scatter plots. The mammograms represent the minimum (top), median (middle), and maximum (bottom) densities. [Color figure can be viewed at wileyonlinelibrary.com]
Table 3.
Statistics of the breast measures obtained from the screening population: The range, mode, mean, median, standard deviation (std), parameters of the distribution fits, and thickness dependencies ()
| Range | Mode | Mean | Median | Std | Fitted distribution | Thickness dependence | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Density [%] | [4.5 99.6] | 12.5 | 23.7 | 18.3 | 15.9 | ‐ |
|
|
|||
| Dense volume [cm3] | [11 564] | 90 | 119 | 106 | 60 |
|
|
|
|||
| Breast volume [cm3] | [49 2671] | 624 | 699 | 647 | 368 |
|
|
|
|||
| Thickness [mm] | [15 92] | 55 | 52 | 53 | 13 |
|
‐ | ‐ | |||
The left‐side marginal histograms in Fig. 5 show distributions, i.e., the sum over all thicknesses in the scatter plots, with statistics listed in Table 3, including the range, mode (most frequent value), mean, median, and standard deviation. As all three distributions are clearly skewed and non‐Gaussian, the mean and standard deviation are questionable descriptors of the data but are included for comparison to other studies. The bottom marginal histogram shows the breast‐thickness distribution. Mammograms in Fig. 5 show the cases with minimum, median, and maximum densities in the distribution.
Log‐normal distributions were fitted to the dense‐volume and total breast‐volume distributions, which makes sense for positively bound data describing natural growth (sometimes referred to as Gibrat's law). The breast‐thickness data were farther offset from 0 (less skewed) and a normal distribution was used for fitting. We expect the data toward larger volumes and thicknesses to be biased because the technical limitation of 100 mm maximum compression height led radiographers to disqualify women with larger breasts (note the skewness of the thickness distribution in Fig. 5, which is expected to be Gaussian). To compensate for the bias, the breast volume and breast thickness fits assumed right censored data above 1000 cm3 and 70 mm, respectively. Fitting parameters are listed in Table 3. No distribution fit is provided for the density data because a suitable distribution type was not evident.
Figure 6 shows the measured breast thickness as a function of the compression height. The correlation was strong and the linear regression coefficient was close to 1 (the Pearson correlation coefficient and a linear fit are indicated in Fig. 6). There was a constant offset close to 1 mm.
Figure 6.

Compression height as a function of measured breast thickness with a linear fit. The Pearson correlation coefficient () is given with a 95% confidence interval. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 7 shows the contralateral and ipsilateral breast‐density correlation for the spectral algorithm, with Pearson correlation coefficients (95% CL: 0.975–0.979) and (95% CL: 0.991–0.993), respectively. The ipsilateral correlation was hence significantly stronger than the contralateral correlation, indicating that the contralateral variation was substantially impacted by biological factors, whereas the ipsilateral variation was determined by the other factors as described in Section 3.B..
Figure 7.
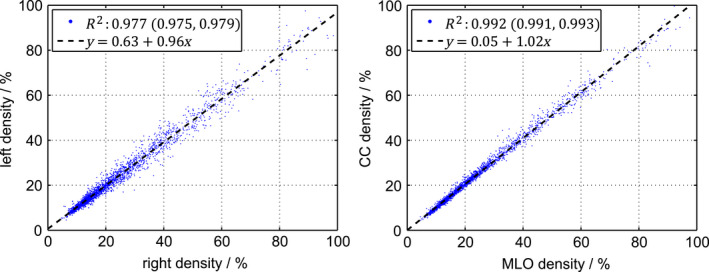
Contralateral (left) and ipsilateral (right) breast density, measured by the spectral algorithm. The Pearson correlation coefficients () are given with 95% confidence intervals. The dashed lines are linear fits. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 8 shows the distributions of contralateral and ipsilateral differences in breast density, i.e., the projections along one‐to‐one lines (lines of identity) in Fig. 7. The standard deviations were 2.4 pp and 1.5 pp, respectively. From Eq. (3), we can estimate the biological variation between contralateral breasts to 1.9 pp, and the contribution from other sources, essentially the system precision, to 1.5 pp. The ipsilateral difference distribution is skewed and exhibits a heavy left tail, which may be due to slightly different image volumes in the CC and MLO views. In particular, adipose tissue along the pectoralis muscle directed toward the axilla may be additionally included in the MLO view, resulting in an overall lower density for the MLO images compared to the CC images.
Figure 8.
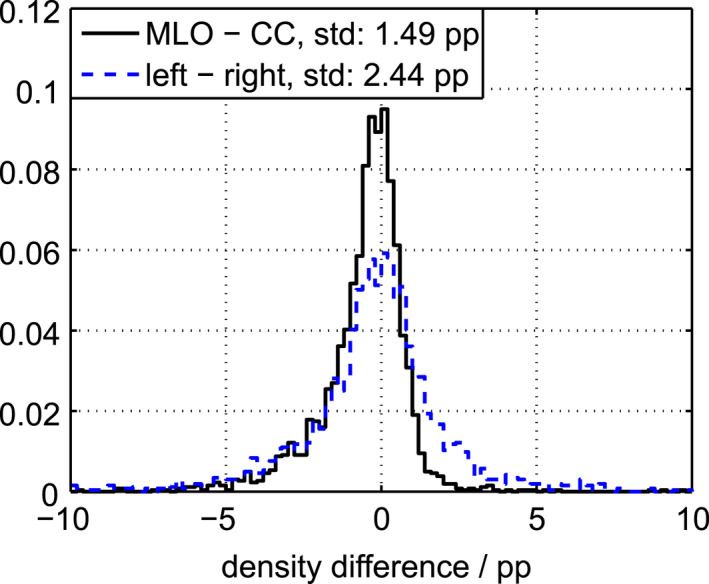
Distributions of contralateral and ipsilateral differences in density. [Color figure can be viewed at wileyonlinelibrary.com]
4.C. Comparison to nonspectral breast‐density assessment
The nonspectral algorithm measured the mode, mean, and median of the density distribution to 14.5%, 23.0%, and 19.2%, which are comparable to the results of the spectral algorithm in Table 3.
Figure 9 shows the contralateral and ipsilateral breast‐density correlation for the nonspectral algorithm, with Pearson correlation coefficients (95% CL: 0.957–0.962) and (95% CL: 0.952–0.958), respectively. The correlation was, hence, in both cases significantly weaker than for the spectral algorithm. The strength of the contralateral and the ipsilateral correlation was similar, indicating that variation due to other factors than natural variation (essentially the algorithm precision) is dominating. The standard deviations of the distributions of contralateral and ipsilateral density differences were 2.7 and 2.8 pp, respectively, which is larger than the expected natural variation between breasts and therefore gives an indication of the algorithm precision. Note that the ipsilateral spread is even higher than the contralateral density spread, which might be due to limited reproducibility of the breast‐thickness model between CC and MLO views.
Figure 9.

Contralateral (left) and ipsilateral (right) breast density measured by the nonspectral algorithm. The Pearson correlation coefficients () are given with 95% confidence intervals. The dashed lines are linear fits. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 10 shows breast density measured by the nonspectral versus the spectral algorithm. Identical results are expected from the two algorithms, but the nonspectral algorithm reported comparably lower values at high densities. A possible explanation for this systematic difference is the following: (a) Higher densities imply lower thicknesses (Fig. 5, top); (b) a fixed offset (inaccuracy) in the compression height becomes relatively larger at low thicknesses; (c) the compression height was slightly higher than the actual breast thickness (Fig. 6); (d) overestimation of the breast thickness is inherently correlated to underestimation of the density in a nonspectral algorithm. A similar trend has been observed previously for a comparison between a nonspectral algorithm and ground truth as determined by magnetic resonance imaging.49
Figure 10.
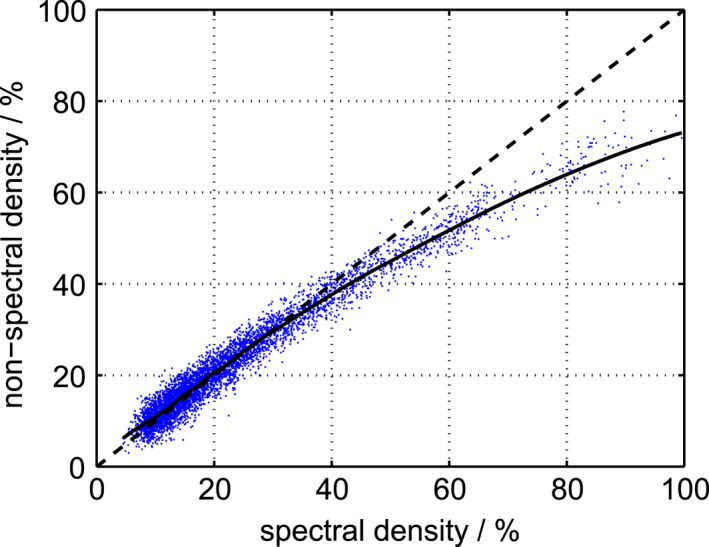
Breast density measured by the nonspectral algorithm versus the spectral algorithm. The data were smoothed with a moving average filter (solid). A one‐to‐one line (line of identity) is included for reference (dashed). [Color figure can be viewed at wileyonlinelibrary.com]
Results from the measurements on breast‐shaped phantoms are summarized in Table 4. The same compression height was reported for both acquisitions of the thick phantom (row 1–2 in Table 4). For the thin phantom, the compression height differed by 1 mm (row 3–4), which is of the same order as the simulated deviation of ±1 mm (row 5–6). The error of the spectral algorithm was 1.2 pp on average and was relatively uniform over the range of measurements with a standard deviation of 0.063 pp. The average error is within the expectations for a particular measurement condition, considering the 1.8 pp standard deviation reported in Section 4.A..
Table 4.
Spectral and nonspectral measurements of breast density for the two breast‐shaped phantoms. Row 1‐4 show results with compression heights determined by the system. Rows 5–6 show results from simulated deviations in the compression height
| Thickness | Density | |||
|---|---|---|---|---|
| True | Compression | True | Spectral | Nonspectral |
| 50 mm | 53 mm | 39.5% | 40.7% | 38.9% |
| 50 mm | 53 mm | 39.5% | 40.8% | 38.8% |
| 25 mm | 26 mm | 39.5% | 40.7% | 32.0% |
| 25 mm | 25 mm | 39.5% | 40.6% | 37.4% |
| 50 mm | (sim.) 54 mm | 39.5% | 40.7% | 36.0% |
| 50 mm | (sim.) 52 mm | 39.5% | 40.7% | 41.8% |
For the nonspectral algorithm, the error was small for the thick phantom with correct compression height, but large deviations were observed for the thinner phantom. The sensitivity to compression height was substantial with errors of about 2.9 pp/mm for the thick phantom and 5.4 pp/mm for the thin phantom. (A previous study reported 4 pp/mm for another but similar nonspectral algorithm,22 which is similar to the average of these two measurements.) The errors were substantially less uniform than for the spectral algorithm with a standard deviation of 3.3 pp.
5. Discussion
5.A. Accuracy
The accuracy (mean deviation from ground truth) of the spectral method was good (0.2 pp in density and 1.9% in volume as determined by phantom measurements), which confirms that the calibration works properly. The major factor affecting accuracy for both density and volume was a high exposure load (Table 2), whereas the other investigated conditions had no notable effect.
For the clinical images, the range of density values was within [0%, 100%], which is physically sound. The range is shown in Fig. 5 using mammograms for the maximum and minimum densities, but it should be noted that the measurement error in the boundary cases of the distribution is large. In particular for the high‐density case, the density is likely lower than 99.6% because the error distribution caused by precision is particularly broad at high densities (Table 2) and the case is at the tail of that distribution (maximum density + maximum precision error).
The strong correlation between compression height and the spectral thickness measurement (Fig. 6) indicates accurate spectral thickness measurements; the constant offset of about 1 mm is within the expected accuracy of the compression height. The measured breast density was anticorrelated to breast thickness (Table 3 and Fig. 5, top), as expected. The dense volume was only weakly correlated to breast thickness with an approximately square‐root dependence (Fig. 5, middle and Table 3). The total breast volume, on the other hand, was strongly correlated to breast thickness with a close‐to quadratic dependence (Fig. 5, bottom and Table 3).
Table 5 shows that the density measurements reported in this study fall within the range of a sample of previously published mean and median values. (Median values are generally lower than mean values because of the skewed distributions, which sets the extreme points.) The relatively large span of density distributions in the literature (Table 5) can be partly attributed to differences in the populations (age, ethnicity etc.), but also to differences in the underlying algorithms, primarily in the definitions of dense and adipose tissue. For example, had we used the tissue‐equivalent material that was used for calibration (based on Ref. 45) to define breast tissue (instead of Ref. 47), we would have ended up with a nonphysical density range of [−23%, 123%]. Also, an early investigation of several measurements of the elemental composition of glandular tissue reported a large variation,50 which, if used as basis for an x‐ray attenuation calculation, would result in a span of 29% in linear attenuation at 20 keV — substantially larger than the difference between tissue‐equivalent material and Ref. 47 (c.f. Fig. 1, right).
Table 5.
Examples of published breast data and intrapatient correlation measures in comparison to the data reported in this study. Results from spectral and nonspectral methods are cited. The correlation data are listed as the squared Pearson correlation coefficients (), which were in some cases recalculated from the published nonsquared coefficients (see footnotes for the original values). Note that median values are generally lower than mean values because of the skewed distributions and possibly a better descriptor of the distributions
| Method | n | Density [%] | Volume [cm3] | correlation | |||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | Contra. | ipsi. | ||||
| Gennaro et al54 | Nonspectral | 527 | ‐ | 11.5 | ‐ | 554 | 0.80a | 0.75a | Commercial Volpara software |
| Kontos et al52 | Nonspectral | 71 | 21.9 | ‐ | ‐ | ‐ | 0.90 | ‐ | Commercial Quantra software |
| Yaffe et al22 | Nonspectral | 191 | 14.3 | ‐ | 769 | ‐ | ‐ | ‐ | Validated using breast CT, skin excluded |
| Aitken et al21 | Nonspectral | 367 | ‐ | 26.2 | ‐ | 524 | ‐ | ‐ | |
| Gooßen et al30 | Nonspectral | 245 | 22.3 | ‐ | ‐ | ‐ | 0.85b | 0.86b | Same nonspectral algorithm as in this work |
| This work | Nonspectral | 1329 | 23.0 | 19.2 | ‐ | ‐ | 0.96 | 0.96 | |
| Machida et al42 | Spectral | 40 | ‐ | ‐ | ‐ | ‐ | ‐ | 0.98c | Same spectral algorithm as in this work |
| This work | Spectral | 1329 | 23.7 | 18.3 | 699 | 647 | 0.98 | 0.99 | |
Calculated from contralateral correlation and ipsilateral correlation.
Calculated from contralateral correlation and average ipsilateral correlation for right and left.
Calculated from .
5.B. Precision
The precision (the degree of variation between measurements) in density measurement of the spectral algorithm was shown to be 1.8 pp in phantom experiments under a range of conditions. The largest deterioration in density precision was found for high densities and high exposure loads (Table 2), whereas the precision in volume exhibited relatively small variations over the range of measurement conditions. The precision, as well as the accuracy, seems relatively independent of detector temperature and the age of the x‐ray tube, which indicates that the temperature compensation (Section 2.C.) works well and that the x‐ray spectrum does not change over time.
The precision found in the phantom measurements is in good agreement with the 1.5 pp precision determined by the ipsilateral correlation of screening mammograms. It should be noted, however, that the measures are slightly different; the phantom experiments comprised several systems and a range of conditions, so the precision refers to what can be expected from an entire installed base, whereas the clinical measurements were done on a single system, but contained variations caused by for instance positioning and pectoralis segmentation. A study of a different algorithm for spectral breast‐density measurement reported a precision of pp,40 which is in line with the present results.
The precision of the nonspectral algorithm was found to be 2.7–2.8 pp from the contralateral and ipsilateral density correlation, and the error is hence close to twice that of the spectral algorithm evaluated on the same mammograms. The investigation of the breast‐shaped phantoms indicates that the uncertainty of the thickness estimation in the nonspectral algorithm is of the order of 3.3 pp (at 40% density), which covers most, or all, of the difference between the two algorithms.
The intrapatient correlation measures of the spectral algorithm (ipsilateral and contralateral correlation) are higher than those of the nonspectral methods listed in Table 5. The nonspectral algorithm applied in this study performed substantially better than in a previous study of the same algorithm, which can be explained at least partly by the fact that a conventional non‐photon‐counting system with worse scatter and noise properties was used in the previous study. Moreover, the nonspectral algorithm used in this study performed at least on par with other nonspectral algorithms, and can hence be regarded as representative.
It is reasonable to question whether the high precision offered by the spectral algorithm has any clinical relevance or if these types of improvements are mainly technology driven. One application of density measures is risk estimates. A meta‐analysis of 42 studies on the correlation between breast density and breast cancer risk reported an increase in risk of approximately 4% per percentage point breast density.2 Risk estimates generally contain many other factors, and this relatively weak dependence makes it unlikely that a few percentage points additional precision will be a game changer to, for instance, divide women into risk categories for personalized screening.
Instead, the increased precision is more likely to be beneficial for measuring variations within the same individual. One example is given in the present study, where the natural variation between contralateral breasts was estimated — a result that could not have been obtained with lower precision. A clinically more relevant application is monitoring of treatment with drugs such as tamoxifen and raloxifene, which have been shown to reduce the susceptibility to breast cancer, and for which breast density works as a surrogate endpoint biomarker.12 In an early study, the area‐based breast density decreased by 19% (7.9 pp at an average of 41.9%) over the first 18 months of tamoxifen treatment (including an age‐related decrease).51 Assuming a linear relationship between area‐based and volumetric breast density (which is approximately the case for small variations52), this change corresponds to a yearly reduction of 1.9 pp at a volumetric density of 15% (the mode of the density distribution measured in this study). A more recent study measured the yearly reduction in volumetric breast density for treatment with tamoxifen to 1.17%–1.70% (0.30%–0.56% for the control group).53
Hence, with a precision of ≤ 2 pp, the spectral algorithm would be at the borderline of seeing the effect of tamoxifen treatment on an individual level and a yearly basis, which is necessary for efficient monitoring, and the precision advantage over the nonspectral algorithm seems relevant for these types of applications. Also, any additional increase in precision by further refinement of the algorithm would be beneficial.
6. Conclusions
The spectral method yielded reasonable results in terms of distributions of, and correlation between, breast measures in a screening population. The precision of the method was approximately two times that of the investigated nonspectral method on average, and the improvement was larger for thin/dense breasts. The nonspectral method investigated here is expected to be representative for nonspectral methods in general, and we conclude that the precision of the spectral method is superior to that of nonspectral methods, which was also corroborated by comparing to a sample of previous studies. High‐precision measurement methods may not be necessary for risk estimates, but may be an enabler for measuring changes in a single individual, such as in treatment monitoring. One example is given in the present study where high precision enabled estimation of the natural density variation between contralateral breasts.
Conflict of interest
Henrik Johansson, Miriam von Tiedemann, Klaus Erhard, Harald Heese, and Erik Fredenberg were all employed by Philips at the time of the study. Sabee Molloi has received research contracts from Philips.
Acknowledgments
The clinical data used for this study were collected within the Karolinska mammography project for risk prediction of breast cancer (KARMA), initiated by Prof. Per Hall, Karolinska Institute, Stockholm, Sweden, and funded by Märit and Hans Rausing's Initiative Against Breast Cancer. Special thanks are extended to Dr. Ann Sundbom and the staff at Södersjukhuset, Stockholm, Sweden for collecting the clinical data, and to Prof. Per Hall for providing important clinical insights. The authors are also grateful to Mr. Staffan Karlsson at the Royal Institute of Technology (KTH) for manufacturing the breast phantoms, as well as to Mr. Stefan Langemark, Mr. Håkan Langemark, Dr. Björn Cederström, Dr. Mats Lundqvist, and Mr. Jonas Rehn, all with Philips Health Systems, for invaluable discussions.
Appendix A.
Transfer of calibrated breast density to display values
Linear transfer function
We have used the breast‐tissue attenuation values from Ref. 47 together with the assumption of a constant and known skin thickness48 and skin attenuation calculated from the elemental composition45 to calculate display values for breast density. However, the system was calibrated using tissue‐equivalent material, which is made to mimic attenuation calculated from the elemental composition of breast tissue according to Ref. 45 and does not include skin. This appendix describes in detail how we transfer calibration values to display values.
With the same assumptions as preceding Eq. (2), a linear combination of any two reference materials of different and low atomic numbers, such as aluminum (Al) and polyethylene (PE), mimics the energy‐dependent attenuation of a third material of a given thickness. In other words, the normalized thicknesses of these materials ( and ) are unique descriptors of the attenuation coefficient of the third material () with thickness at all energies () given the known attenuation coefficients of the reference materials ( and ):
| (A1) |
For the case of a breast consisting of adipose, fibro‐glandular, and skin tissue (, , and ), it is convenient to convert Eq. (A1) to matrix notation:
| (A2) |
| (A3) |
The relationship between measured data () and data corrected for skin () is
| (A4) |
where holds the equivalent thicknesses of reference materials for CIRS tissue‐equivalent material. The conversion to another representation of breast‐tissue attenuation (in our case as published by Johns and Yaffe47 — subscript ) becomes:
| (A5) |
Determination of equivalent material thicknesses
The equivalent Al and PE thicknesses were derived in two ways: (a) calculations from published values on linear attenuation coefficients, and (b) measurements on samples of tissue‐equivalent material. Most of the procedure have been described in Ref. 55, but it is summarized here for clarity.
With known values of the linear attenuation coefficient, the relation to the normalized reference thicknesses and could, in principle, be found by calculating Eq. (A1) at two arbitrary energies and solving the resulting linear system of equations [similar to Eq. (2)]. However, the limited validity of the assumptions underpinning Eq. (A1) may lead to a slight dependency on the energies chosen. Therefore, we used a linear least‐squares fit over the energy bins corresponding to a typical mammography spectrum (). This procedure corresponds to the following minimization with respect to and :
| (A6) |
where and were calculated from the elemental composition using the XCOM database,56 assuming pure Al, and PE composition from Ref. 57.
For measurements of reference thickness on sample materials, a three‐level step wedge of Al foil was overlaid with a step of PE to create a six‐level calibration matrix. Images were acquired with the sample and the step wedge both visible, and x‐ray attenuation was measured by mapping the high‐ and low‐energy counts obtained from a region‐of‐interest (ROI) located on the sample against those obtained from ROIs on the calibration matrix.
Table A1 shows the measured and calculated equivalent thicknesses of Al and PE. The values of the tissue‐equivalent material are the means of two measurements at 20 mm and 50 mm of material, which differed by 1% on average, mainly because of spectrum and count rate differences. The equivalent thicknesses for published attenuation data were calculated according to Eq. (A6) on available data points in the interval 15–40 keV. Inserting the values in Table A1 into Eq. (A5) yields the linear transfer function between calibration data and display values.
Table A1.
Normalized equivalent thicknesses of aluminum (Al) and polyethylene (PE) for fibro‐glandular (g), adipose (a), and skin (s) tissue, measured on tissue‐equivalent material (CIRS) and calculated from published data.45, 47
Calculation of volume
The PMMA‐to‐density and ‐thickness LUTs yield thickness and density maps and . The volume element corresponding to each pixel was calculated as the integral of the height‐dependent area element () over the breast in the detector‐to‐source direction:
| (A7) |
where and are the detector‐strip and scan directions (Fig. 1), is the source‐to‐image distance and is the pixel side length. The source‐to‐pixel distance depends on , but, for the MicroDose system, is approximately independent of because of the rotational geometry; the breast support and compression paddle are curved to be perpendicular to the beam path. The pixel‐to‐breast distance depends on the distance between detector and patient support () and the distance between the patient support and the breast (). The breast was assumed to be at the patient support within the compressed breast region and otherwise centered between the patient support and the compression paddle. Measures of breast volume, dense volume, density, and thickness for the entire breast were calculated according to:
| (A8) |
Note that the skin thickness is included in the volume and breast thickness, but excluded from the dense volume and density measures.
References
- 1. Wolfe JN. Breast patterns as an index of risk for developing breast cancer. Am J Roentgenol. 1976;126:1130–1137. [DOI] [PubMed] [Google Scholar]
- 2. McCormack VA, dos Santos I. Silva, “Breast density and parenchymal patterns as markers of breast cancer risk: a meta‐analysis”. Cancer Epidemiol Biomarkers Prev. 2006;15:1159. [DOI] [PubMed] [Google Scholar]
- 3. Carney PA, Miglioretti DL, Yankaskas BC, et al. Individual and combined effects of age, breast density, and hormone replacement therapy use on the accuracy of screening mammography. Ann Intern Med. 2003;138:168. [DOI] [PubMed] [Google Scholar]
- 4. Boyd NF, Guo H, Martin LJ, et al. Mammographic Density and the Risk and Detection of Breast Cancer. New Engl J Med. 2007;356:227–236. [DOI] [PubMed] [Google Scholar]
- 5. Tice JA, Cummings SR, Smith‐Bindman R, Ichikawa L, Barlow WE, Kerlikowske K. Using clinical factors and mammographic breast density to estimate breast cancer risk: development and validation of a new predictive model. Ann Intern Med. 2008;148:337–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Chen J, Pee D, Ayyagari R, et al. Projecting absolute invasive breast cancer risk in white women with a model that includes mammographic density. J Natl Cancer Inst. 2006;98:1215–1226. [DOI] [PubMed] [Google Scholar]
- 7. Siu AL, U.S. Preventive Services Task Force . Screening for breast cancer: U.S. Preventive Services Task Force recommendation statement. Ann Intern Med. 2009;151:716–726. [DOI] [PubMed] [Google Scholar]
- 8. Schousboe JT, Kerlikowske K, Loh A, Cummings SR. Personalizing mammography by breast density and other risk factors for breast cancer: analysis of health benefits and cost‐effectiveness. Ann Intern Med. 2011;155:10–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Drukteinis JS, Mooney BP, Flowers CI, Gatenby RA. Beyond mammography: new frontiers in breast cancer screening. Am J Med. 2013;126:472–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Boyd NF, Martin LJ, Yaffe MJ, Minkin S. Mammographic density and breast cancer risk: current understanding and future prospects. Breast Cancer Res. 2011;13:223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Ng K‐H, Lau S. Vision 20/20: mammographic breast density and its clinical applications. Med Phys. 2015;42:7059–7077. [DOI] [PubMed] [Google Scholar]
- 12. Li J, Humphreys K, Eriksson L, Edgren G, Czene K, Hall P. Mammographic density reduction is a prognostic marker of response to adjuvant tamoxifen therapy in postmenopausal patients with breast cancer. J Clin Oncol. 2013;31:2249–2256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Dance DR, Sechopoulos I. Dosimetry in x‐ray‐based breast imaging. Phys Med Biol. 2016;61:R271–R304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. American College of Radiology . BI‐RADS Committee, Breast imaging reporting and data system. American College of Radiology; 1998.
- 15. Yaffe MJ. Mammographic density ‐ Measurement of mammographic density. Breast Cancer Res. 2008;10:209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kopans DB. Basic physics and doubts about relationship between mammographically determined tissue density and breast cancer risk. Radiology. 2008;246:348–353. [DOI] [PubMed] [Google Scholar]
- 17. Martin LJ, Boyd NF. Mammographic density. Potential mechanisms of breast cancer risk associated with mammographic density: hypotheses based on epidemiological evidence. Breast Cancer Res. 2008;10:201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Shepherd JA, Kerlikowske K, Ma L, et al. Volume of mammographic density and risk of breast cancer. Cancer Epidemiol Biomarkers Prev. 2011;20:1473–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Boyd N, Martin L, Gunasekara A, et al. Mammographic density and breast cancer risk: evaluation of a novel method of measuring breast tissue volumes. Cancer Epidemiol Biomarkers Prev. 2009;18:1754–1762. [DOI] [PubMed] [Google Scholar]
- 20. Lokate M, Kallenberg MG, Karssemeijer N, Van den Bosch MA, Peeters PH, Van Gils CH. Volumetric breast density from full‐field digital mammograms and its association with breast cancer risk factors: a comparison with a threshold method. Cancer Epidemiol Biomarkers Prev. 2010;19:3096–3105. [DOI] [PubMed] [Google Scholar]
- 21. Aitken Z, McCormack VA, Highnam RP, et al. Screen‐film mammographic density and breast cancer risk: a comparison of the volumetric standard mammogram form and the interactive threshold measurement methods. Cancer Epidemiol Biomarkers Prev. 2010;19:418–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Yaffe MJ, Boone JM, Packard N, et al. The myth of the 50‐50 breast. Med Phys. 2009;36:5437–5443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Boston RC, Schnall MD, Englander SA, Landis JR, Moate PJ. Estimation of the content of fat and parenchyma in breast tissue using MRI T1 histograms and phantoms. Magn Reson Imaging. 2005;23:591–599. [DOI] [PubMed] [Google Scholar]
- 24. Highnam R, Brady JM. Mammographic image analysis. In: Computational Imaging and Vision, Vol. 14. Dordrecht: Springer Science+Business Media Dordrecht; 1999. [Google Scholar]
- 25. Highnam R, Pan X, Warren R, Jeffreys M, Smith GD, Brady M. Breast composition measurements using retrospective standard mammogram form (SMF). Phys Med Biol. 2006;51:2695–2713. [DOI] [PubMed] [Google Scholar]
- 26. Kaufhold J, Thomas JA, Eberhard JW, Galbo CE, Trotter DEG. A calibration approach to glandular tissue composition estimation in digital mammography. Med Phys. 2002;29:1867–1880. [DOI] [PubMed] [Google Scholar]
- 27. Pawluczyk O, Augustine BJ, Yaffe MJ, et al. A volumetric method for estimation of breast density on digitized screen‐film mammograms. Med Phys. 2003;30:352–364. [DOI] [PubMed] [Google Scholar]
- 28. Diffey J, Hufton A, Astley S. A new step‐wedge for the volumetric measurement of mammographic density. In: Astley S, Brady M, Rose C, Zwiggelaar R, eds. IWDM 2006, LNCS 4046. Berlin Heidelberg: Springer; 2006:1–9. [Google Scholar]
- 29. Hartman K, Highnam R, Warren R, Jackson V. Volumetric assessment of breast tissue composition from FFDM images. In: Krupinski EA, ed. IWDM 2008, LNCS 7361. Berlin Heidelberg: Springer; 2008:33–39. [Google Scholar]
- 30. Gooßen A, Heese HS, Erhard K. Automatic volumetric glandularity assessment from full field digital mammograms. In: Maidment AA, et al., eds. IWDM 2012, LNCS 7361. Berlin Heidelberg: Springer; 2012:753–760. [Google Scholar]
- 31. van Engeland S, Snoeren PR, Huisman H, Boetes C, Karssemeijer N. Volumetric breast density estimation from full‐field digital mammograms. IEEE Trans Med Imaging. 2006;25:273–282. [DOI] [PubMed] [Google Scholar]
- 32. Breitenstein DS, Shaw CC. Comparison of three tissue composition measurement techniques using digital mammograms ‐ A signal‐to‐noise study. J Digit Imaging. 1998;11:137–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Shepherd JA, Kerlikowske KM, Smith‐Bindman R, Genant HK, Cummings SR. Measurement of breast density with dual x‐ray absorptiometry: feasibility. Radiology. 2002;223:554–557. [DOI] [PubMed] [Google Scholar]
- 34. Alvarez RE, Macovski A. Energy‐Selective Reconstructions in X‐Ray Computerized Tomography. Phys Med Biol. 1976;21:733–744. [DOI] [PubMed] [Google Scholar]
- 35. Mawdsley GE, Tyson AH, Peressotti CL, Jong RA, Yaffe MJ. Accurate estimation of compressed breast thickness in mammography. Med Phys. 2009;36:577–586. [DOI] [PubMed] [Google Scholar]
- 36. Ducote JL, Molloi S. Quantification of breast density with dual energy mammography: a simulation study. Med Phys. 2008;35:5411–5418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Ducote JL, Molloi S. Quantification of breast density with dual energy mammography: an experimental feasibility study. Med Phys. 2010;37:793–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Taguchi K, Iwanczyk JS. Vision 20/20: single photon counting x‐ray detectors in medical imaging. Med Phys. 2013;40:100901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Fredenberg E, Lundqvist M, Cederström B, Åslund M, Danielsson M. Energy resolution of a photon‐counting silicon strip detector. Nucl Instr Meth A. 2010;613:156–162. [Google Scholar]
- 40. Ding H, Molloi S. Quantification of breast density with spectral mammography based on a scanned multi‐slit photon‐counting detector: a feasibility study. Phys Med Biol. 2012;57:4719–4738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Gooßen A, Heese H, Erhard K, Norell B. Spectral Volumetric Glandularity Assessment. In: Maidment AA, et al., eds. IWDM 2012, LNCS 7361. Berlin Heidelberg: Springer; 2012:529–536. [Google Scholar]
- 42. Machida Y, Tozaki M, Yoshida T, Saita A, Yakabe M, Nii K. Feasibility study of a breast density measurement within a direct photon‐counting mammography scanner system. Jpn J Radiol. 2014;32. [DOI] [PubMed] [Google Scholar]
- 43. Åslund M, Cederström B, Lundqvist M, Danielsson M. Scatter rejection in multi‐slit digital mammography. Med Phys. 2006;33:933–940. [DOI] [PubMed] [Google Scholar]
- 44. Boone JM, Fewell TR, Jennings RJ. Molybdenum, rhodium, and tungsten anode spectral models using interpolating polynomials with application to mammography. Med Phys. 1997;24:1863–1874. [DOI] [PubMed] [Google Scholar]
- 45. Hammerstein GR, Miller DW, White DR, Masterson ME, Woodard HQ, Laughlin JS. Absorbed radiation dose in mammography. Radiology. 1979;130:485–491. [DOI] [PubMed] [Google Scholar]
- 46. Byng JW, Mainprize JG, Yaffe MJ. X‐ray characterization of breast phantom materials. Phys Med Biol. 1998;43:1367–1377. [DOI] [PubMed] [Google Scholar]
- 47. Johns PC, Yaffe MJ. X‐ray characterisation of normal and neoplastic breast tissues. Phys Med Biol. 1987;32:675–695. [DOI] [PubMed] [Google Scholar]
- 48. Huang SY, Boone JM, Yang K, Kwan ALC, Packard NJ. The effect of skin thickness determined using breast CT on mammographic dosimetry. Med Phys. 2008;35:1199–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Gubern‐Mérida A, Kallenberg M, Platel B, Mann RM, Martí R, Karssemeijer N. Volumetric Breast Density Estimation from Full‐Field Digital Mammograms: a Validation Study. PLoS ONE. 2014;9:e85952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Woodard HQ, White DR. The composition of body tissues. Br J Radiol. 1986;59:1209–1219. [DOI] [PubMed] [Google Scholar]
- 51. Cuzick J, Warwick J, Pinney E, Warren RM, Duffy SW. Tamoxifen and breast density in women at increased risk of breast cancer. J Natl Cancer Inst. 2004;96:621–628. [DOI] [PubMed] [Google Scholar]
- 52. Kontos D, Bakic PR, Acciavatti RJ, Conant EF, Maidment ADA. A comparative study of volumetric and area‐based breast density estimation digital mammography: results from a screening population. In: Martí J, et al., eds. IWDM 2010, LNCS 6136. Berlin Heidelberg: Springer; 2010:378–385. [Google Scholar]
- 53. Engmann NJ, Scott C, Jensen MR, et al. Longitudinal changes in volumetric breast density with tamoxifen and aromatase inhibitors. Cancer Epidemiol Biomarkers Prev. Available online ahead of print; 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Gennaro G, Highnam R. This is what volumetric breast density is. Poster number C‐1033 at ECR 2013, 10.1594/ecr2013/c-1033; 2013. [DOI]
- 55. Fredenberg E, Dance DR, Willsher P, et al. Measurement of breast‐tissue x‐ray attenuation by spectral mammography: first results on cyst fluid. Phys Med Biol. 2013;58:8609–8620. [DOI] [PubMed] [Google Scholar]
- 56. Berger MJ, Hubbell JH, Seltzer SM, Coursey JS, Zucker DS. XCOM: photon cross section database. National Institute of Standards and Technology, Gaithersburg, MD; 2005. http://physics.nist.gov/xcom.
- 57. Hubbell JH, Seltzer SM. Tables of x‐ray mass attenuation coefficients and mass energy‐absorption coefficients. National Institute of Standards and Technology, Gaithersburg, MD; 2004. http://www.nist.gov/pml/data/xraycoef.


