Hyperelastic continuum models for isotropic athermal fibrous networks

Abstract

Many biological materials contain fibrous protein networks as their main structural components. Understanding the mechanical properties of such networks is important for creating biomimicking materials for cell and tissue engineering, and for developing novel tools for detecting and diagnosing disease. In this work, we develop continuum models for isotropic, athermal fibrous networks by combining a single-fibre model that describes the axial response of individual fibres, with network models that assemble individual fibre properties into overall network behaviour. In particular, we consider four different network models, including the affine, three-chain, eight-chain, and micro-sphere models, which employ different assumptions about network structure and kinematics. We systematically investigate the ability of these models to describe the mechanical response of athermal collagen and fibrin networks by comparing model predictions with experimental data. We test how each model captures network behaviour under three different loading conditions: uniaxial tension, simple shear, and combined tension and shear. We find that the affine and three-chain models can accurately describe both the axial and shear behaviour, whereas the eight-chain and micro-sphere models fail to capture the shear response, leading to unphysical zero shear moduli at infinitesimal strains. Our study is the first to systematically investigate the applicability of popular network models for describing the macroscopic behaviour of athermal fibrous networks, offering insights for selecting efficient models that can be used for large-scale, finite-element simulations of athermal networks.

1. Introduction

Many biological materials consist of fibrous protein networks as their main structural components, and such networks play a critical role in determining their mechanical properties and other functions [1–6]. For instance, the extracellular matrix (ECM) of tissues contains a random network of collagen and elastin [7,8]. Changes in the structure of these networks can give rise to abnormal mechanical properties of tissues that disrupt cell mechanosensitive responses and, in turn, initiate or exacerbate pathologies [9,10]. Blood clots are composed of networks of fibrin, whose structure and mechanical properties are crucial for preventing bleeding [11–14]. Thus, understanding and quantifying the mechanical behaviour of fibrous networks is important not only for designing biomimetic materials that serve as physiologically relevant environments for cell engineering, but also for developing novel diagnostic techniques for disease [15,16]. With this as motivation, this paper is concerned with the development of continuum models for fibrous networks.

Fibrous networks can be classified into thermal and athermal networks, depending on the nature of the constituent fibres [3]. A network is said to be thermal when its fibres are subjected to significant thermal fluctuations, such that the fibre’s persistence length (i.e. the length over which the fibre appears straight in the presence of Brownian forces) is much smaller or comparable to its contour length [2]. Examples include molecularly crosslinked, flexible networks like rubbers and polyacrylamide gels, in which the fibre persistence length is far less than its contour length and the fibre appears as a random coil [17]. Another example is given by semiflexible, cytoskeletal networks like actin and intermediate filament networks, in which the fibre has a persistence length comparable to its contour length or the distance between network crosslinks [2]. In this case, the bending energy of the fibre just outcompetes the entropic tendency of the fibre to crumple into a random coil, and the fibre exhibits small but significant thermal fluctuations around a straight conformation. On the other hand, a network is said to be athermal when its fibres are large enough or rigid enough to be negligibly affected by thermal fluctuations, with the fibre’s persistence length being much larger than its contour length [3,18]. Examples of athermal networks include collagen networks in the ECMs and fibrin networks in blood clots. These athermal fibres often behave mechanically like slender elastic beams.

Continuum modelling of fibrous networks treats the network as a mechanical continuum, with the goal of developing a constitutive relation that describes the macroscopic response of the network in relation to the properties of the constituent fibres and the network structure [19]. Such modelling efforts typically comprise two steps. The first step is to derive a force–extension relation for single fibres along their axial direction (i.e. the direction connecting the two ends of the fibre). For flexible fibres, entropic models of Gaussian or Langevin type are usually used [17]. The Gaussian model assumes that the fibre is a freely jointed chain of rigid rods, being infinitely stretchable without approaching its fully extended state; this results in a linear force–extension relation. By contrast, the more realistic Langevin model accounts for the finite stretchability of the fibres yielding a strain-stiffening force–extension relation. For semiflexible fibres, different models have been proposed (e.g. [20,21]) building upon the classical worm-like chain model [22], treating fibres as continuous and smooth filaments with well-defined local curvatures. Then, fibre behaviour can be described by the free energy of bending of fibres induced by thermal fluctuations. As a fibre is stretched, the amplitude of its transverse thermal undulations decreases, causing a decrease in available fibre conformations and thus an entropic strain-stiffening of the fibre. Different from the above entropic models, models for athermal fibres are intrinsically energetic, so that the force–extension relation can be derived from the stored elastic energy of the fibres. These fibres often exhibit a linear elastic or strain-stiffening response under axial tension, but can buckle when subjected to axial compression, thus having a limited compression resistance [3,23].

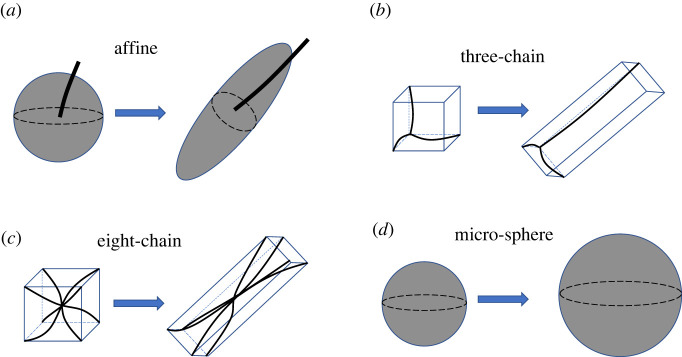
The second step of continuum modelling is to develop a network model that relates the stretch of individual fibres to the macroscopic network deformation, so that the overall response of the network can be computed by adding contributions from fibres over all orientations. Over the years, several network models have been developed for isotropic fibrous networks. These network models can be categorized into affine and non-affine models. The affine model (also called the full network model) [17,24,25] considers fibres isotropically distributed in the orientation space and assumes that the fibres deform according to the macroscopic deformation of the network (figure 1a), i.e. the axial stretch of any fibre is taken to be identical to the corresponding macro-stretch of the continuum along the fibre’s direction.

Figure 1.

Schematics for the geometry and deformation of different network models under simple shear. (a) Affine model. Each point on the spherical surface represents a unique fibre orientation, with only one representative fibre shown in the figure. (b) Three-chain model, where each fibre is aligned with one of the edges of the unit cell. (c) Eight-chain model, where each fibre connects the centre of the unit cell to one of the cell vertices. (d) Micro-sphere model. Each point on the spherical surface represents a unique fibre orientation, with all the fibres stretched to the same degree. The rotation of the fibres, however, is not well defined; thus, fibre deformation is not shown in the figure.

The development of non-affine models, however, is motivated by the fact that the true fibre deformation is usually non-affine [2,3]. One type of such non-affine models is the unit-cell model [19], which idealizes the actual structure of the network as a periodic array of unit cells, each of them containing a certain number of fibres with prescribed arrangements. The most popular unit-cell models are perhaps the three-chain model [26] and the eight-chain model [27]. In the three-chain model, the unit cell is initially cubic containing three mutually orthogonal fibres along its edges (figure 1b). Under a prescribed macroscopic deformation, the three fibres are taken to be aligned with the principal directions of the deformation, and the stretch of the fibre is determined by the corresponding principal stretch value. The eight-chain model has a setting similar to that of the three-chain model, the key difference being that the unit cell contains eight fibres connecting the centre of the cell to the eight cell vertices (figure 1c). Due to the symmetry of such a network structure, the stretch of all the eight fibres equals the root mean square of the principle stretch values. Another type of non-affine model is the so-called micro-sphere model [28], which also considers fibres isotropically distributed in the orientation space (figure 1d). In this model, however, the axial stretch of a given fibre differs from the corresponding macro-stretch of the continuum, and is obtained by minimizing the average free energy of the fibrous networks. This minimization procedure yields an effective axial stretch of all the fibres to be the p-root average of the macro-stretch over all orientations, where p is a material parameter describing the network’s non-affinity. For the special case of p = 2, the micro-sphere model recovers the eight-chain model.

These different network models, along with appropriately chosen force–extension relations for individual fibres (e.g, Langevin model for flexible fibres, and worm-like chain model for semi-flexible fibres), have been extensively used to study the overall behaviour of thermal networks, such as rubber [19,25], actin [20,29,30] and intermediate filament networks [31]. These networks are either incompressible themselves (e.g. dry rubber networks), or embedded in an incompressible fluid (e.g. actin networks in cytosol). Since these thermal networks typically have small pore sizes, fluids do not have enough time to migrate through the network on a timescale of seconds to minutes. Therefore, in these scenarios, thermal networks can be modelled as incompressible, hyperelastic materials. In particular, for the various network models described above, fairly good agreement between model predictions and experimental data was generally found. Compared with the affine and three-chain models, the eight-chain model was found to be better at simultaneously capturing the behaviour of rubber networks under different loading conditions (e.g. uniaxial tension, biaxial tension, and simple shear) [19,27]. The micro-sphere model, which includes the eight-chain model as a special case, further improves model capacity and provides better predictions for the behaviour of rubber and actin networks [28].

Despite the extensive and systematic study of network models for thermal networks, it remains unclear if these models can be extended to accurately describe the macroscopic behaviour of athermal networks, such as collagen and fibrin networks. Different from thermal networks, athermal networks often have a much more open structure with large pore sizes; consequently, fluids can flow in and out of the networks on a similar timescale, causing significant changes in the network volume [18,32]. However, in this work, we do not consider the dynamic network response induced by fluid flow; instead, we are interested in the quasi-static behaviour of the networks after fluid flow has completed and the network has reached an equilibrium state, in which case the athermal networks can be modelled as compressible, hyperelastic materials. In particular, we ask the following question: given that the affine, three-chain, eight-chain and micro-sphere models have been widely used to describe the mechanical properties of incompressible, thermal networks, can they be further generalized to capture the quasi-static behaviour of compressible, athermal networks?

To answer this question, we develop various continuum models for athermal networks by combining each of the above network models (the affine, three-chain, eight-chain and micro-sphere models) with a single-fibre model that has been found to successfully capture the axial response of athermal fibres. This single-fibre model was first developed by Steinwachs et al. [5], assuming that the fibre can stiffen under axial tension and soften under axial compression. Further, to account for the compressibility of the network, we incorporate into our models a volumetric energy term that can describe nonlinear volumetric responses of the network, following the earlier work of [33]. Thereafter, we systematically evaluate the models’ performance by assessing how well they fit available experimental data for collagen and fibrin networks subjected to various loading conditions, including uniaxial tension, simple shear, as well as combined tension (or compression) and shear. We also analyse why different models may have different capacities in capturing the true behaviour of athermal networks. Finally, we end with the conclusions of this study.

2. Continuum models for athermal fibrous networks

In this section, we develop various continuum models for isotropic, athermal fibrous networks. As already discussed in the Introduction, these models contain two parts: (i) a single-fibre model that describes the axial force–extension response of individual fibres and (ii) a network model that describes the structure and kinematics of the networks, as well as determines the overall network behaviour by adding contributions from all the fibres. Next, we discuss these two components.

2.1. Single-fibre model

There are two types of single-fibre models that are widely used to describe the axial response of athermal fibres. These include the (i) physics-based models, such as those based on the worm-like chain models [34] or the elastic beam models [35,36]; and the (ii) phenomenological models [5,37] that employ simple, empirical functions (e.g. exponential functions) to characterize fibre behaviour. Both types of models have their respective advantages and disadvantages. Specifically, the physics-based models have clear physical meanings but can have rather complex forms (e.g. [30,31]). By contrast, the phenomenological models may lack clear physical origin, but typically have simple forms and are easy to use.

In this work, we characterize the axial response of individual fibres using the phenomenological model of Steinwachs et al. [5], for simplicity. This model has been used to successfully describe the behaviour of athermal collagen fibres, capturing the asymmetric response of fibres to tension and compression. In particular, the fibre is assumed to be wavy in its unloaded state and to exhibit three distinct regimes in response to external forces. When the fibre is axially stretched, it has an initially constant stiffness, up to the point where the fibre is fully straightened. Upon further stretching, the fibre gradually stiffens with a stiffness that increases with tensile strain. On the contrary, when the fibre is axially compressed, it softens with a stiffness that decreases with compressive strain. More specifically, the fibre’s differential stiffness, κ_f, is given by

$${\kappa }_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f})={\kappa }_0\{\begin{array}{cc}{\mathrm{e}}^{({\lambda }_{\hspace{0.17em}f}-1)/d_0},\hspace{0.17em}& \text{if}\hspace{0.17em}{\lambda }_{\hspace{0.17em}f}<1,\hspace{0.17em}\\ 1,\hspace{0.17em}& \text{if }1\le {\lambda }_{\hspace{0.17em}f}<{\lambda }_s,\hspace{0.17em}\\ {\mathrm{e}}^{({\lambda }_{\hspace{0.17em}f}-{\lambda }_s)/d_s},\hspace{0.17em}& \text{if}\hspace{0.17em}{\lambda }_{\hspace{0.17em}f}\ge {\lambda }_s.\hspace{0.17em}\end{array}$$ 2.1

In the above expression, λ_f is a kinematic variable denoting the axial stretch of the fibre, as given by the ratio between the end-to-end length of the deformed fibre and that of the undeformed fibre. Moreover, κ₀ is the initial stiffness of the fibre, λ_s is the critical stretch at the onset of fibre stiffening (i.e. when the fibre is just straightened), d_s is a coefficient describing the exponential stiffening of the fibre and d₀ is a coefficient describing the exponential softening of the fibre; these material parameters define the material properties of a single fibre and are determined from experimental data. We note that d_s (or d₀) can be interpreted as the strain scale of fibre stiffening (or softening), where smaller values of d_s (or d₀) correspond to faster rate of stiffening (or softening).

For later use, we also determine the axial force, F_f, and the strain energy, w_f, associated with a single fibre. Following earlier studies, we assume that the fibre is force-free and has a zero strain energy in its unloaded state. Then, making use of the relation F′_f(λ_f) = κ_f(λ_f) and w″_f(λ_f) = κ_f(λ_f), we may compute F_f and w_f by integrating κ_f with respect to λ_f once and twice, respectively. Consequently, we have the results that

$$F_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f})={\kappa }_0\{\begin{array}{cc}{d}_0[{\mathrm{e}}^{({\lambda }_{\hspace{0.17em}f}-1)/d_0}-1],& \text{if}\hspace{0.17em}{\lambda }_{\hspace{0.17em}f}<1,\\ {\lambda }_{\hspace{0.17em}f}-1,& \text{if}\hspace{0.17em}1\le {\lambda }_{\hspace{0.17em}f}<{\lambda }_s,\\ {\lambda }_s-1+d_s[{\mathrm{e}}^{({\lambda }_{\hspace{0.17em}f}-{\lambda }_s)/d_s}-1],& \text{if}\hspace{0.17em}{\lambda }_{\hspace{0.17em}f}\ge {\lambda }_s,\end{array}$$ 2.2

and

$$w_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f})={\kappa }_0\{\begin{array}{cc}{d}_0[d_0\hspace{0.17em}{\mathrm{e}}^{({\lambda }_{\hspace{0.17em}f}-1)/d_0}-{\lambda }_{\hspace{0.17em}f}-d_0+1],& \text{if }{\lambda }_{\hspace{0.17em}f}<1,\\ {({\lambda }_{\hspace{0.17em}f}-1)}^2/2,& \text{if }1\le {\lambda }_{\hspace{0.17em}f}<{\lambda }_s,\\ {({\lambda }_s-1)}^2/2+({\lambda }_s-d_s-1)({\lambda }_{\hspace{0.17em}f}-{\lambda }_s)+d_s^2[e^{({\lambda }_{\hspace{0.17em}f}-{\lambda }_s)/d_s}-1],& \text{if }{\lambda }_{\hspace{0.17em}f}\ge {\lambda }_s.\end{array}$$ 2.3

Other phenomenological models, such as the linear model of [38,39] and the exponential model of [37,40], have also been used to describe the axial response of individual fibres. Those models typically assume that fibres cannot sustain compressive forces, as would be the case if d₀ → 0 in (2.1)–(2.3). However, we do not make such an assumption; instead, we treat d₀ as a material parameter and determine it by fitting the model to experimental data. As will be seen below, d₀ determined from experimental data is indeed very close to 0.

Finally, we note that the main objective of this paper is to explore the applicability of different network models (see the next section) to describe the network behaviour. As will be seen later, whether a given network model works or not depends largely on the underlying assumptions made in the network model, regardless of the choice of the single-fibre models (provided that the single-fibre model is reasonably good at describing the axial response of individual fibres). Thus, we expect the conclusions of our study to hold for different single-fibre models.

2.2. Network models

In this subsection, we present network models for isotropic fibrous networks. We also combine each of these network models with the above single-fibre model to develop full continuum models for athermal fibrous networks.

As already mentioned in the Introduction, we focus on the quasi-static behaviour of athermal networks, which can be modelled as compressible, hyperelastic solids. Then, the mechanical behaviour of the networks can be fully described by a strain energy density function, W [41]. Following earlier works on compressible hyperelastic solids [19], W may be written in an additive form

$$W(\mathbf{F})=W_1(\mathbf{F})+W_2(J),$$ 2.4

where F = ∂x/∂X is the deformation gradient tensor, with x and X being the positions of a material point in the deformed and undeformed configurations, respectively, J = det(F) is the Jacobian, W₁ is the strain energy density associated with a chosen network model (see below), and W₂ is the volumetric strain energy density due to volume changes. Different models for W₂ have been proposed in the literature; interested readers are referred to the excellent book of Anand & Govindjee [42] for a comprehensive review. Here, we employ the model developed by Bischoff et al. [33], which has the capacity to describe general nonlinear volumetric response of a material. In this model, W₂ is given by

$$W_2(J)=\frac{B}{{\alpha }^2}\{\cosh [\alpha (J-1)]-1\},$$ 2.5

where B determines the bulk modulus of the material, and α describes the nonlinearity of the volumetric response. Note that W₂ is empirical in nature, and both B and α are material parameters to be determined from experimental data. Also note that W₂ serves to control the material’s overall compressibility (which for protein networks comes largely from the fluid flow through the fibre mesh, and is both variable and usually unmeasured). In particular, when B → ∞, the material is incompressible, whereas when B has small values, the material is highly compressible.

W₁ in (2.4) denotes the strain energy density predicted by a chosen network model. Such models account for the network structure, first computing the stretch of individual fibres from the macroscopic network deformation, and then computing the total strain energy of the network by summing up the energy of all the fibres. In the following, we will briefly summarize various network models, including the affine, three-chain, eight-chain and micro-sphere models. As will be seen, these models differ in how they describe the isotropic network structure, as well as in how they compute the axial stretch of individual fibres from the macroscopic network deformation.

Before introducing the network models, we note that we will make the following assumptions that will apply to all models. First, although different fibres in a random network generally have different shapes (e.g. the end-to-end length and the contour length), we assume, for simplicity, that all the fibres have the same shape. This shape can be interpreted as the average shape of all the fibres, as can be described by the average end-to-end length and the average contour length of all the fibres. Second, in order to ensure that the fibrous networks are stress-free in the undeformed configuration, we assume that all the fibres are initially force free. In reality, the initial state of a fibre (i.e. force free, pre-stretched, or pre-compressed) depends sensitively on the local polymerization conditions of the network. A detailed account of these effects, however, is beyond the scope of this work.

2.2.1. Affine model

The affine model accounts for all the fibres isotropically distributed in space, and assumes that these fibres deform affinely with the continuum [17,19] (figure 1a). As a result, the axial stretch of each fibre, ${\lambda }_{\hspace{0.17em}f}^{\mathrm{aff}}$, is given by the macro-stretch of the continuum along the direction of that fibre, i.e.

$${\lambda }_f^{\mathrm{aff}}=|\mathbf{F}\mathbf{M}|,$$ 2.6

with M being the unit vector along the fibre orientation in the undeformed configuration, and | · | denoting the norm of a given quantity. Thus, the strain energy density associated with the affine model can be computed by integrating the strain energy of fibres over the entire orientation space

$$W_1^{\mathrm{aff}}(\mathbf{F})=\frac{N}{4\pi }{\int }_S{w}_f\hspace{0.17em}({\lambda }_f^{\mathrm{aff}})\hspace{0.17em}\mathrm{d}S=\frac{N}{4\pi }{\int }_0^{\pi }{\int }_0^{2\pi }{w}_f\hspace{0.17em}(|\mathbf{F}\mathbf{M}|)\sin \theta \hspace{0.17em}\mathrm{d}\varphi \hspace{0.17em}\hspace{0.17em}\mathrm{d}\theta .$$ 2.7

Here, N is the number of fibres per unit volume of the undeformed network, S is the surface of a unit sphere representing the orientation space, with each point on S denoting a unique fibre orientation, and θ and ϕ are, respectively, the polar angle and the azimuthal angle in a spherical coordinate. Note that M can be expressed in terms of θ and ϕ as M = [sinθcosϕ, sinθsinϕ, cosθ]^T.

2.2.2. Three-chain model

In the three-chain model [3,26], the network is idealized as a periodic array of initially cubic unit cells, each containing three fibres located along the edges of the cell (figure 1b). These fibres deform with the unit cell, such that the end-to-end vector of a fibre always coincides with the corresponding cell edge. For a prescribed network deformation, the unit cell deforms into a general cuboid, with the cell edges (or the fibres) always aligned with the principal directions of the deformation, and the stretches of the edges (or the fibres) equal to the corresponding principal stretch values. As such, the strain energy density associated with the three-chain model can be computed by summing up the strain energy of the three classes of fibres

$$W_1^{3\mathrm{ch}}(\mathbf{F})=\frac{N}{3}\sum _{i=1}^3{w}_{\hspace{0.17em}f}({\lambda }_i),$$ 2.8

where the λ_i (i = 1, 2, 3) denote the principal stretches associated with the deformation gradient F.

The deformation of fibres predicted by the three-chain model is generally non-affine. This can be easily seen when the network is subjected to simple shear deformation. As the shear deformation progresses, the three classes of fibres rotate simultaneously while remaining mutually orthogonal (figure 1b). This is in contrast to what would happen if these fibres deformed affinely with the continuum, in which case the angles between these fibres would change during the course of the simple shear deformation. Finally, we note that the three-chain model can be viewed as a method of sampling the rotation and stretching of fibres along the three principal directions of the deformation.

2.2.3. Eight-chain model

The eight-chain model is similar to the three-chain model, the main difference being that there are eight fibres connecting the centre of the unit cell to each of the eight cell vertices [27] (figure 1c). Due to the symmetry of this network structure, the end-to-end lengths of all the fibres equal half of the length of the unit cell’s body diagonal. Thus, the axial stretch of each fibre is given by the root mean square of the principal stretch values, i.e.

$${\lambda }_{\hspace{0.17em}f}^{8\mathrm{ch}}=\sqrt{\frac{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}{3}}=\sqrt{\frac{\mathrm{trace}(\mathbf{C})}{3}},$$ 2.9

where C =F^T F is the right Cauchy–Green deformation tensor. Consequently, the strain energy density associated with the eight-chain model is given by

$$W_1^{8\mathrm{ch}}(\mathbf{F})=N{w}_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f}^{8\mathrm{ch}}).$$ 2.10

Fibre deformation predicted by the eight-chain model is again non-affine, as can be also seen when the network undergoes simple shear deformation. If the deformation of fibres were affine, then as shear progresses some of the fibres would be stretched whereas the rest would be compressed. This scenario, however, differs from the predictions of the eight-chain model, where all the fibres are stretched to the same degree (see (2.9) and figure 1c), implying that fibre deformation is generally non-affine for this model. We also note that the eight-chain model can be viewed as a method of sampling the rotation and stretch of fibres in eight directions relative to the principal directions of the deformation.

2.2.4. Micro-sphere model

The original micro-sphere model [28] considers all the fibres isotropically distributed in space (figure 1d), with each fibre subjected to a tube constraint. This tube constraint accounts for the conformational constraints placed on a fibre by its neighbours, having important ramifications on the fibre conformational entropy. However, since in this work, we focus on athermal networks, whose mechanical response is dominated by the fibre elastic energy and is negligibly affected by its conformational entropy, we expect the tube constraint to have no significant effects on the mechanical behaviour of the network. Thus, we neglect the tube constraint. Similar simplifications have also been used in [30], where the authors found that typical parameters for the tube constraint have a minor influence (less than $4\text{\%}$) on the final result at small to intermediate strains (around $20\text{\%}$).

The micro-sphere model incorporates non-affine fibre deformations by allowing axial fibre stretches to fluctuate around the corresponding macro-stretches of the continuum. In particular, the axial stretches of fibres are determined by minimizing the network strain energy density, under the ad hoc constraint that the p-root average of axial fibre stretch equals that of the macro-stretch. Here, p is a material parameter describing the non-affinity of the network. This minimization procedure leads to the result that the axial stretches of all the fibres equal the p-root average of the macro-stretch, i.e.

$${\lambda }_{\hspace{0.17em}f}^{\mathrm{msph}}(\mathbf{F})={(\frac{1}{4\pi }{\int }_S|\mathbf{F}\mathbf{M}{|}^{\hspace{0.17em}p}\hspace{0.17em}\mathrm{d}S)}^{1/p}={(\frac{1}{4\pi }{\int }_0^{\pi }{\int }_0^{2\pi }|\mathbf{F}\mathbf{M}{|}^p\sin \theta \hspace{0.17em}\mathrm{d}\varphi \hspace{0.17em}\mathrm{d}\theta )}^{1/p}.$$ 2.11

Here, we recall that S denotes the surface of a unit sphere, where each point on S represents a unique fibre orientation, M. Thus, the strain energy density associated with the micro-sphere model is given by

$$W_1^{\mathrm{msph}}(\mathbf{F})=N{w}_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f}^{\mathrm{msph}}).$$ 2.12

Note that when p = 2, equations (2.11) and (2.12) can be shown to reduce to (2.9) and (2.10), respectively, so that the micro-sphere model recovers the eight-chain model.

In summary, the hyperelastic response of the compressible athermal networks can be characterized by the strain energy density W in (2.4), with W₂ given by (2.5), and W₁ given by (2.7), (2.8), (2.10) or (2.12), depending on the choice of the network model. Then, the first Piola–Kirchhoff stress, P, of the fibrous network is given by

$$\mathbf{P}=\frac{\mathrm{\partial }W}{\mathrm{\partial }\mathbf{F}}=\frac{\mathrm{\partial }{W}_1}{\mathrm{\partial }\mathbf{F}}+\frac{B}{\alpha }\sinh [\alpha (J-1)]\hspace{0.17em}J{\mathbf{F}}^{-\mathrm{T}}.$$ 2.13

Remarks. —

• 1. In the literature, the names ‘affine,’ ‘three-chain,’ ‘eight-chain’ and ‘micro-sphere’ have been used to describe different types of network models, which are independent of the choice of single-fibre models. However, since we have combined these network models with the single-fibre model in §2.1 to develop full continuum models, we will henceforth use these names to describe the corresponding continuum models.
• 2. Both the affine and micro-sphere continuum models require the computation of two-dimensional integrals over the surface of a unit sphere (see, e.g. (2.7) and (2.11)). These surface integrals are computed by discretizing the surface with 808 triangular elements and employing linear finite element interpolations. This number was found to be sufficient to guarantee convergence [43,44].
• 3. The affine, three-chain and eight-chain continuum models each contain a set of six material parameters, $\mathbf{c}=\{K,d_0,d_s,{\lambda }_s,B,\alpha \}$, where K = Nκ has been treated as a single material parameter (recall that κ is the stiffness of individual fibres at small strains, and N is the number density of fibres). On the other hand, the micro-sphere continuum model contains a set of seven material parameters, $\mathbf{c}=\{K,d_0,d_s,{\lambda }_s,B,\alpha ,p\}$.

3. Results and discussion

In this section, we evaluate the performance of the affine, three-chain, eight-chain and micro-sphere models in describing the mechanical properties of athermal networks, including collagen and fibrin networks. Specifically, we test how well these models capture the network behaviour under three different loading conditions, including (i) uniaxial tension, (ii) simple shear and (iii) combined tension and shear. These loading conditions are commonly used to measure the mechanical properties of fibrous networks. For each loading condition, we fit each of our models to available experimental data (for both collagen and fibrin networks), and assess the accuracy of the model by quantifying the mismatch between model predictions and experimental measurements.

3.1. Uniaxial tension

In this subsection, we examine the ability of different models to capture the response of fibrous networks under uniaxial tension. In particular, we compare model predictions with the experimental data of Roeder et al. [45] for collagen networks, and with that of Purohit et al. [46] for fibrin networks.

In standard uniaxial-tension tests, network samples are stretched along a given direction and are allowed to deform freely in directions perpendicular to the loading direction. Thus, we assume that the networks undergo a homogeneous deformation, with the deformation gradient given by

$$\mathbf{F}=\left(\begin{array}{ccc}\mu & 0& 0\\ 0& \mu & 0\\ 0& 0& \lambda \end{array}\right).$$ 3.1

Here, λ denotes the axial stretch along the loading direction, and μ denotes the corresponding lateral stretch, which is chosen in such a way that the lateral stresses predicted by a given model are zero. (Without loss of generality, we have assumed that loading is applied in the z direction.) Then, for each model, we may compute the axial stress, P_zz, as a function of the axial stretch, λ, using (2.13).

We fit the above-predicted stress–stretch (P_zz − λ) response of the network to available experimental data by solving a minimization problem, with the goal of finding the set of material parameters, c, that minimizes the cost function

$$\pi (\mathbf{c})=\sum _{i=1}^n{[P_{zz}({\hat{\lambda }}_i;\mathbf{c})-{\hat{P}}_i]}^2,$$ 3.2

where $({\hat{\lambda }}_i,{\hat{P}}_i)$ (i = 1, …, n) are the pairs of experimental data for the axial stretch and axial stress, respectively, with n denoting the total number of experimental data points. We note that under uniaxial tension, most fibres in a network are extended; thus, network behaviour is governed mostly by fibre tensile properties, and not by their compressive properties. Consequently, uniaxial-tension data alone are insufficient for determining material parameters that describe compressive responses, such as d₀ in equation (2.1). Thus, in the above minimization problem, we set d₀ = 1 × 10⁻² for all models, and solve for the rest of the material parameters. This choice of d₀ is motivated by the fact that athermal fibres typically buckle easily under compression, so that d₀ (which describes the strain scale of softening) is expected to be very close to 0.

We evaluate the ability of each model to capture the true network response by computing the relative error, which describes how closely the predicted network response matches the measured network response. In particular, we define the relative error as

$$e({\mathbf{c}}^{\ast })=\sqrt{\frac{\sum _{i=1}^n{[P_{zz}({\hat{\lambda }}_i;{\mathbf{c}}^{\ast })-{\hat{P}}_i]}^2}{\sum _{i=1}^n{\hat{P}}_i^2}},$$ 3.3

where c* is the set of optimal material parameters that minimizes the cost function (3.2).

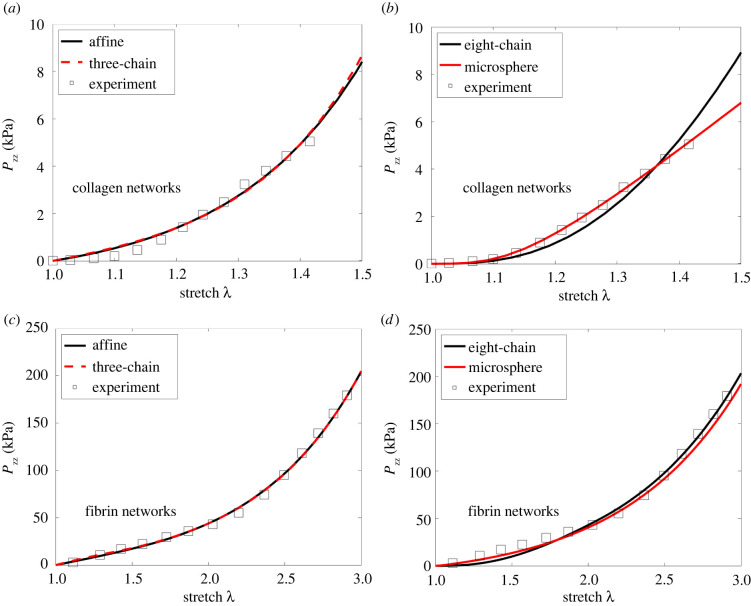
Figure 2 presents the stress–stretch curves predicted by different models when fitted to the experimental data for collagen and fibrin networks. The optimal material parameters obtained from data fitting, as well as the relative errors, are shown in tables S1 and S2 in the electronic supplementary material. We observe that for both the collagen and fibrin networks, the slope of the stress–stretch curve (i.e. the tangent modulus of the material) increases with stretch, indicating a nonlinear strain-stiffening response of these networks. This nonlinear behaviour can be captured fairly well by all the continuum models, with relative errors below $14\text{\%}$ (see electronic supplementary material, tables S1 and S2). We note, however, that the fitted parameters differ for different network models. This is because in order to obtain similar overall network behaviour (as was done in data fitting), different models would require different sets of parameters (the same set of parameters would cause different models to have rather different model predictions).

Figure 2.

Axial stress P_zz as a function of axial stretch λ. Results predicted by the (a) affine (ε_s = 4.14 × 10⁻⁶) and three-chain (ε_s = 4.53 × 10⁻⁶) models, as well as by the (b) eight-chain (ε_s = 0.5) and micro-sphere (ε_s = 0.25) models, are shown for collagen networks. The experimental data of Roeder et al. [45] are also displayed. The corresponding results are also shown for fibrin networks, including predictions of the (c) affine (ε_s = 0.506) and three-chain (ε_s = 0.514) models, as well as of the (d) eight-chain (ε_s = 0.323) and micro-sphere (ε_s = 0.248) models. The corresponding experimental data of Purohit et al. [46] are also shown. Note that ε_s = λ_s − 1 denotes the critical strain for fibre stiffening (obtained by data fitting).

There are two possible mechanisms responsible for the strain-stiffening behaviour of the network. First, as deformation progresses, fibres rotate towards the direction of the maximum principal stretch (i.e. the uniaxial loading direction), leading to realignment along that direction, and thus to strain stiffening of the network. This mechanism of fibre realignment is purely geometric, independent of the properties of individual fibres. Second, strain stiffening of individual fibres can also cause overall strain stiffening of the network. This mechanism comes into effect only after the fibres are stretched beyond the critical strain (ε_s = λ_s − 1) at which fibre stiffening occurs. How each mechanism contributes depends on the network model used to infer the experimental data. For example, for the collagen networks, ε_s = 4.15 × 10⁻⁶ for the affine model, suggesting that fibre stiffening kicks in at very small strains, thus contributing to overall stiffening of the network much earlier than fibre realignment. On the other hand, ε_s = 0.5 for the eight-chain model, suggesting that in the considered deformation range fibres are linear elastic and do not stiffen; consequently, the nonlinear network response is solely due to fibre realignment. These observations suggest that the inference of the underlying physics depends on the particular choice of models.

3.2. Simple shear

In this subsection, we test the ability of various models to describe the network behaviour under simple shear. To do this, we compare model predictions with the experimental data of Storm et al. [31] for collagen networks and that of van Oosten et al. for fibrin networks [32].

The deformation gradient for simple shear can be written as

$$\mathbf{F}=\left(\begin{array}{ccc}1& 0& \gamma \\ 0& 1& 0\\ 0& 0& 1\end{array}\right),$$ 3.4

where γ denotes the amount of shear. (Here, we have assumed, without loss of generality, that shear is applied in the x–z plane along the x-direction.) Thus, for each model we can compute the shear stress, P_xz, together with the nominal shear modulus, G = P_xz/γ, as a function of γ, using (2.13). We fit the predicted modulus–strain (G–γ) curve to the available experimental data (for both collagen and fibrin networks) by solving a minimization problem analogous to the problem in §3.1. We also evaluate the relative errors using an expression that is similar to (3.3).

Since simple shear deformation is volume conserving (J = 1), the last term in (2.13) vanishes, implying that network behaviour under simple shear is insensitive to the values of B and α (which describe how a network responds to volume changes). As a consequence, the values of B and α cannot be inferred from shear response. Motivated by this observation, when performing curve fitting, we solve for material parameters other than B and α.

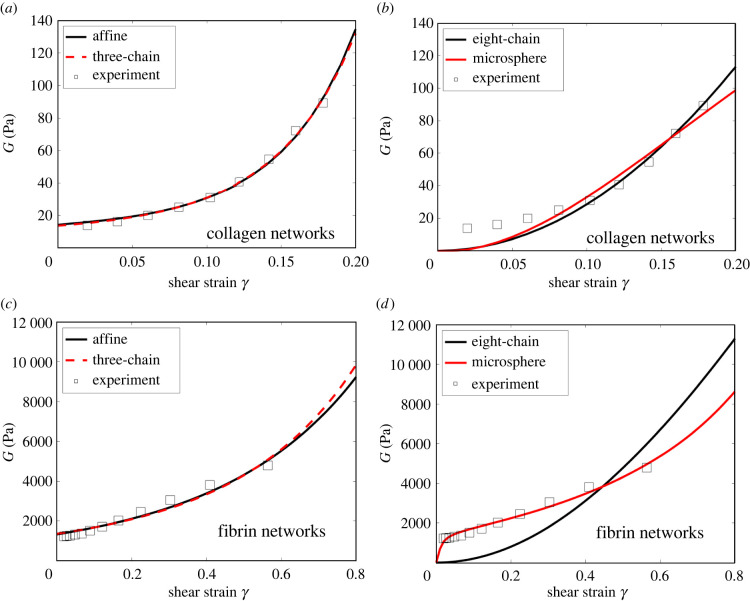
The best-fit G–γ curves, along with the corresponding experimental data, are shown in figure 3. The optimal material parameters and the associated relative errors are shown in tables S3 and S4 in the electronic supplementary material. It can be seen from figure 3 that for both the collagen and fibrin networks, the shear modulus increases with shear strain, again indicating a nonlinear strain-stiffening behaviour of the networks.

Figure 3.

Nominal shear modulus G as a function of the amount of shear γ. Results predicted by the (a) affine (ε_s = 1.2 × 10⁻⁷) and three-chain (ε_s = 4.18 × 10⁻⁸) models, as well as by the (b) eight-chain (ε_s = 0.73) and micro-sphere (ε_s = 0.49) models, are shown for collagen networks. The experimental data of Storm et al. are also displayed. The corresponding results are also shown for fibrin networks, including predictions of the (c) affine (ε_s = 6.47 × 10⁻⁸) and three-chain (ε_s = 7.87 × 10⁻¹¹) models, as well as of the (d) eight-chain (ε_s = 0.052) and micro-sphere (ε_s = 0.0083) models. The corresponding experimental data of van Oosten et al. [32] are also shown. Note that ε_s = λ_s − 1 denotes the critical strain for fibre stiffening (obtained by data fitting).

From figure 3, we observe that both the affine and three-chain continuum models accurately describe the network’s nonlinear shear responses. Moreover, since the critical strains for fibre stiffening are rather small for these models, stiffening of individual fibres contributes to the overall material nonlinearity much sooner than fibre realignment. On the other hand, the eight-chain and micro-sphere models capture network response at large strains, but significantly underestimate the shear modulus at small strains. In particular, as the shear strain tends to zero, the shear modulus predicted by both models also tends to zero, indicating that the networks are mechanically unstable at small shear strains. These predictions significantly differ from the true network properties.

Upon closer inspection, we identify two reasons that explain why the eight-chain and micro-sphere models lead to unstable network response at small strains. First, in both models, under a prescribed network deformation all the fibres are stretched to the same degree described by a single, effective stretch (see (2.9) and (2.11)). (By contrast, in the affine and three-chain models, fibres along different directions are generally stretched to different extents, as would be expected in real situations.) Second, all fibres are assumed to be force free at zero strain. It can be shown (see the appendix) that taken together, these two factors lead to a vanishing shear modulus at small strains. Also, we note that the failure of these models is due to the underlying assumptions made in describing network kinematics, independent of the choice of the single-fibre models.

In this context, we note that if all the fibres are taken to be initially pre-stretched, the eight-chain and micro-sphere models (as well as the affine and three-chain models) do give rise to stable network responses with positive shear moduli. However, it is known from more detailed, discrete fibre network simulations that pre-stress is not necessarily required for the stability of athermal networks [1,3,18,47]. Therefore, the reliance of the eight-chain and micro-sphere models on pre-stress to achieve network stability is an unwanted feature, restricting their utility in describing the mechanical behaviour of athermal networks.

Finally, we note that our results do not contradict earlier findings that the eight-chain and micro-sphere models can accurately describe the mechanical response of thermal networks like rubber. In those cases, chains within the network are always pre-stressed with an entropic, contractile tendency (unless the two ends of the chains overlap). As a result, the eight-chain and micro-sphere models are guaranteed to yield positive shear modulus and stable network behaviour.

3.3. Combined tension and shear

In this subsection, we study the performance of different models in characterizing network response under combined tension and shear. Specifically, we compare model predictions with the available experimental data of van Oosten et al. [32] for collagen and fibrin networks. In their experiments, cylindrical disc-shaped network samples were sandwiched between the two parallel plates of a shear rheometer. These samples were axially compressed or stretched in steps by changing the gap between the two plates. At each level of axial stretch, the axial stress of the sample was measured after the fluid had re-distributed and the material had reached an equilibrium state. In addition, a small amount of shear strain was superimposed by rotating one of the plates relative to the other. This was used to measure the shear modulus of the sample at that level of axial strain. Thus, both the axial stress and the shear modulus were recorded as a function of axial strain.

Given that the network samples were very thin, and that both the top and bottom surfaces of the samples were firmly attached to the rheometer plates, we assume that the lateral strain of the samples was zero. This assumption has also been used in previous studies to simulate the loading conditions in such experiments [18,48]. Thus, we may write the deformation gradient as

$$\mathbf{F}=\underset{\mathrm{shear}}{\underbrace{\left(\begin{array}{ccc}1& 0& \gamma \\ 0& 1& 0\\ 0& 0& 1\end{array}\right)}}\underset{\mathrm{stretch}}{\underbrace{\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& \lambda \end{array}\right)}}=\left(\begin{array}{ccc}1& 0& \gamma \lambda \\ 0& 1& 0\\ 0& 0& \lambda \end{array}\right),$$ 3.5

where λ is the axial stretch, and γ is the amount of superimposed shear, with $\gamma =2\text{\%}$ in the experiment.

For each model, we first set γ = 0 in (3.5) and use (2.13) to compute the axial stress, P_zz, as a function of λ. We then set $\gamma =2\text{\%}$ and repeated the above procedure to compute the nominal shear modulus, G = P_xz/γ, as a function of λ. Thereafter, we simultaneously fit the stress–stretch (P_zz–λ) relation, as well as the modulus–stretch (G–λ) relation, to the corresponding experimental data for collagen and fibrin networks. The stress data and the modulus data have rather different magnitudes. To avoid bias in data fitting, in the cost function, we use different weights for the two datasets. In particular, we choose weights that are inversely proportional to the squared magnitudes of the two datasets.

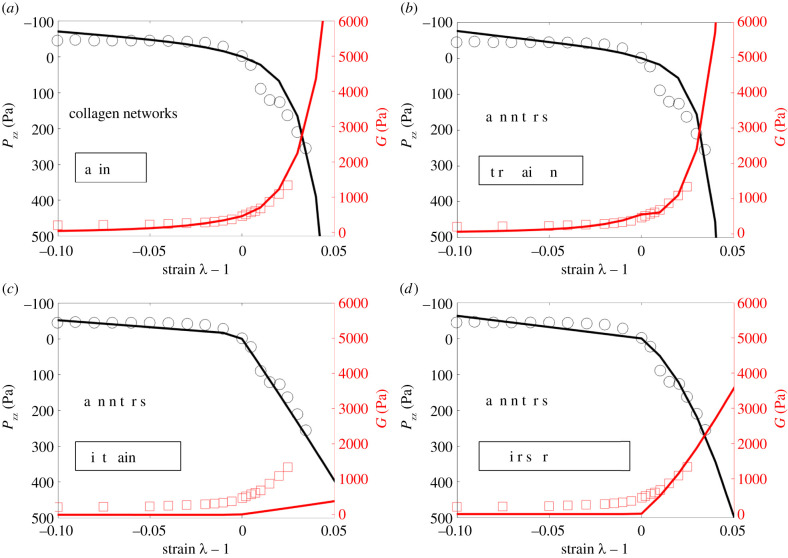
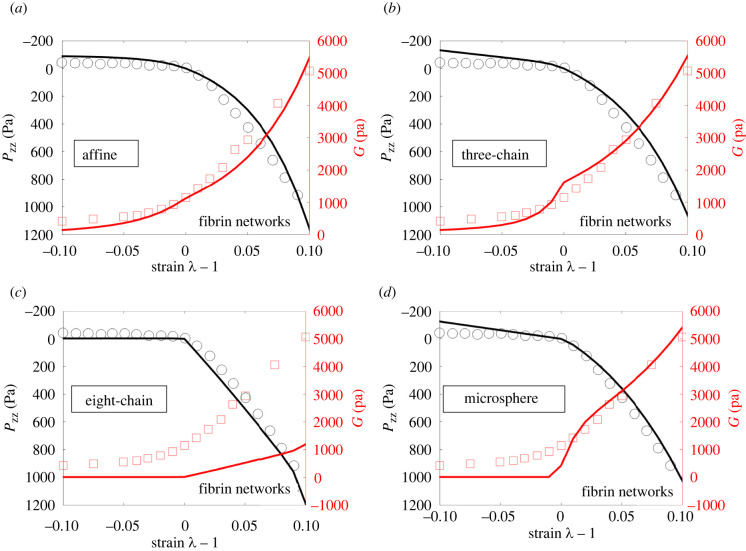
Figure 4 presents the best-fit curves and the corresponding experimental data for collagen networks, with electronic supplementary material, table S5 showing the calibrated material parameters and the associated relative errors. Figure 5 and electronic supplementary material, table S6 display the corresponding results for fibrin networks.

Figure 4.

Axial stress P_zz and nominal shear modulus G of collagen networks as a function of axial strain (ε = λ − 1). Results predicted by the (a) affine (ε_s = 0.001), (b) three-chain (ε_s = 0.0065), (c) eight-chain (ε_s = 0.53) and (d) micro-sphere models (ε_s = 0.47), as well as the corresponding experimental results of van Oosten et al. are shown. Note that ε_s = λ_s − 1 denotes the critical strain for fibre stiffening (obtained by data fitting).

Figure 5.

Axial stress P_zz and nominal shear modulus G of fibrin networks as a function of axial strain (ε = λ − 1). Results predicted by the (a) affine (ε_s = 2.92 × 10⁻¹⁴), (b) three-chain (ε_s = 2.76 × 10⁻¹⁴), (c) eight-chain (ε_s = 0.0289) and (d) micro-sphere models (ε_s = 0.0086), as well as the corresponding experimental results of van Oosten et al., are shown. Note that ε_s = λ_s − 1 denotes the critical strain for fibre stiffening (obtained by data fitting).

It can be seen from figure 4 that the stress–stretch behaviour of the collagen network displays strong tension–compression asymmetry, with network behaviour being much stronger under tension than under compression. Correspondingly, the network shear modulus increases with increasing extension, but decreases with increasing compression. The stiffening of the network in tension can be attributed, once again, to fibre realignment along the loading direction and strain stiffening of fibres, whereas softening in compression is primarily due to buckling of fibres [18,32].

Further, we observe from figure 4 that the affine and three-chain models can reasonably characterize both the axial and shear response of the network. On the other hand, the eight-chain and micro-sphere models capture the axial properties of the network, but not its shear properties. In particular, the eight-chain model significantly underestimates the networks shear modulus for all strains, and the micro-sphere model underestimates the shear modulus for small tensile and compressive strains. These discrepancies can again be attributed to the fact that these two models describe fibre deformations using a single effective stretch, which is insufficient to simultaneously capture the multi-axial response of the network. In particular, for the special case when the axial strain is zero (λ = 1), the deformation gradient in (3.5) reduces to simple shear in (3.4). In this case, the shear modulus predicted by the eight-chain and micro-sphere models will always be close to zero (as discussed in §3.2), thus failing to match the experimental data. We note that the predicted shear modulus is not exactly zero due to the finite amount of shear strain, i.e. $2\text{\%}$, applied to the network. As this shear strain tends to zero, the predicted shear modulus will tend to zero (as shown in the appendix). We also make similar observations for the fibrin networks in figure 5.

In this context, we remark that the kinematics and mechanics of random athermal networks depend strongly on the detailed structure of the network, such as the network connectivity and cross link density [1,2,47]. In particular, deformation of fibres in random networks is known to be highly non-affine [8,49–51], partially due to heterogeneities in network structure. These detailed structural features and complex fibre kinematics, are not captured by any of our continuum models, which all employ simplifying assumptions about network structure and fibre kinematics [3]. However, the affine and the three-chain models appear to have sufficient complexity that they are able to represent the macroscopic behaviour of the networks with reasonable accuracy. Thus, they can be used as efficient, reduced-order tools to describe the macroscopic responses of athermal networks. In particular, these models can be easily implemented in finite-element packages to perform large-scale, structural simulations for athermal networks.

Similar to our findings, a recent study on modelling of fibrous tissues also suggests that, although the affine model fails to describe the underlying non-affine fibre kinematics, it can capture the macroscopic response of fibrous tissues using appropriate material parameters obtained from data fitting [52]. These material parameters, however, must be interpreted with care, because they are tuned to compensate for the model errors made in describing the network structure and kinematics. Consequently, their values (obtained from data fitting) can differ significantly from those that represent the true fibre properties.

Finally, we emphasize that our results do not imply that the affine and three-chain models are better than the eight-chain and micro-sphere models per se. In fact, as already mentioned, the eight-chain and micro-sphere models do a better job in characterizing the mechanical behaviour of thermal networks like rubbers [19,28]. Apparently, the relative performance of various network models depends on specific network types. Thus, we recommend that practitioners should systematically investigate the behaviour of different models and select the ones that are best suited for the tasks at hand. Our study represents an example of one such effort.

4. Conclusion

In this work, we developed continuum models to describe the compressible, hyperelastic behaviour of isotropic athermal fibrous networks. For this purpose, we combined a single-fibre model that captures the asymmetric axial behaviour of athermal fibres, with various network models—including the affine, three-chain, eight-chain and micro-sphere models—that assemble individual fibre properties into overall network response. Then, we systematically investigated the accuracy of these models by comparing model predictions with available experimental data for collagen and fibrin networks. Specifically, we tested how well each model captures the true network behaviour under three loading conditions: uniaxial tension, simple shear, and combined tension and shear. We found that the affine and three-chain models can reasonably describe both the axial and shear response of the network. By contrast, the eight-chain and micro-sphere models accurately describe the axial behaviour, but are inadequate in capturing the shear behaviour. In particular, these models lead to zero shear modulus and thus to unstable network response at infinitesimal strains. We therefore recommended the use of the affine and three-chain models to describe the mechanical behaviours of athermal networks. These models can be implemented in finite-element codes to conduct large-scale, structural simulations for biopolymer networks like collagen and fibrin networks, serving as efficient tools to guide the design of fibrous scaffolds for cell engineering, and to understand the role of mechanics in pathologies.

Appendix A

In this appendix, we employ the eight-chain and micro-sphere models to compute the nominal shear modulus of athermal fibrous networks, which undergo simple shear deformations. In particular, we demonstrate that when all the fibres are initially force free, the shear moduli predicted by both models are zero at infinitesimal strains. We also demonstrate that when the fibres are pre-strained, those shear moduli become non-zero at infinitesimal strains.

A.1. Eight-chain model

The first Piola–Kirchhoff stress predicted by the eight-chain model is given by (2.13), with W₁ given by (2.10) and (2.9). Substituting the simple-shear deformation gradient (3.4) into (2.13), and using the definition of the nominal shear modulus, G = P_xz/γ, we arrive at

$$G=\frac{N}{3{\lambda }_{\hspace{0.17em}f}^{8\mathrm{ch}}}{F}_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f}^{8\mathrm{ch}}).(\mathrm{A}\hspace{0.17em}1)$$

Here, we recall that N is the number density of fibres, F_f = W′_f is a fibre’s axial force (see, e.g. (2.2)), and ${\lambda }_{\hspace{0.17em}f}^{8\mathrm{ch}}=\sqrt{({\gamma }^2+3)/3}$, with γ being the amount of shear in (3.4). Then, it can be easily shown that

$$\underset{\gamma \to 0}{lim}G=\frac{N}{3}{F}_{\hspace{0.17em}f}(1).(\mathrm{A}\hspace{0.17em}2)$$

If all the fibres are initially force free (i.e. F_f(1) = 0), lim_γ→0 G = 0, implying that the mechanical behaviour of fibrous networks is initially unstable.

Note that if all the fibres are pre-stretched (i.e. F_f(1) > 0), lim_γ→0 G > 0. This is indeed the case for thermal networks like rubbers, in which individual fibres are always pre-stretched with a contractile tendency (unless the two ends of a fibre coincide). On the other hand, if all the fibres are pre-compressed (i.e. F_f(1) < 0), lim_γ→0 G < 0, leading to unphysical results.

A.2. Micro-sphere model

The first Piola–Kirchhoff stress predicted by the micro-sphere model is given by (2.13), with W₁ given by (2.12) and (2.11). Substituting the simple-shear deformation gradient (3.4) into (2.13), and using G = P_xz/γ, we arrive at

$$G=\frac{N}{4\pi \gamma }{F}_{\hspace{0.17em}f}({\lambda }_{\hspace{0.17em}f}^{\mathrm{msph}}){({\lambda }_{\hspace{0.17em}f}^{\mathrm{msph}})}^{1-p}{\int }_0^{\pi }{\int }_0^{2\pi }{(1+\gamma \sin 2\theta \hspace{0.17em}\cos \varphi +{\gamma }^2{\cos }^2\theta )}^{(\hspace{0.17em}p-2)/2}(\sin \theta \hspace{0.17em}\cos \theta \cos \varphi +\gamma {\cos }^2\theta )\sin \theta \hspace{0.17em}\mathrm{d}\varphi \hspace{0.17em}\mathrm{d}\theta ,(\mathrm{A}\hspace{0.17em}3)$$

where we recall that p > 0 is a material parameter, and ${\lambda }_{\hspace{0.17em}f}^{\mathrm{msph}}$ is given by

$${\lambda }_{\hspace{0.17em}f}^{\mathrm{msph}}={(\frac{1}{4\pi }{\int }_0^{\pi }{\int }_0^{2\pi }{(1+\gamma \sin 2\theta \cos \varphi +{\gamma }^2{\cos }^2\theta )}^{\hspace{0.17em}p/2}\sin \theta \hspace{0.17em}\mathrm{d}\varphi \hspace{0.17em}\mathrm{d}\theta )}^{1/p}.(\mathrm{A}\hspace{0.17em}4)$$

Note that for the special case p = 2, equations (A 3) and (A 4) can be evaluated analytically, and (A 3) can be shown to reduce to (A 1). However, for general values of p, (A 3) and (A 4) cannot be computed analytically and numerical integration is required.

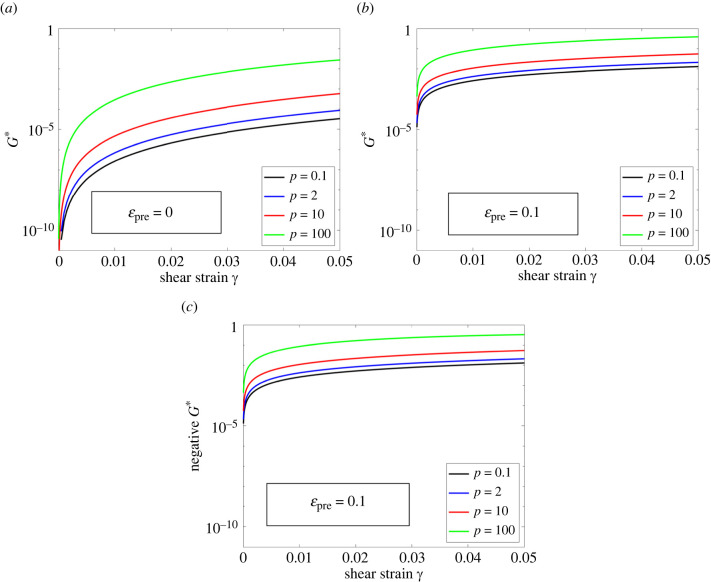
Next, we compute the normalized modulus, G* = (4πG)/(Nκ₀), as a function of γ, and study how G* behaves as γ → 0. (Recall that κ₀ is a fibre’s stiffness at infinitesimal strains, see (2.1).) To do this, we need to know the axial responses of individual fibres.

Since the value of G* at infinitesimal strains is independent of the axial responses of fibres at large strains, we assume, for simplicity, that the fibres are linear elastic. Other forms of F_f can also be used, but they will not affect the value of G* as γ → 0. In particular, we assume that F_f(λ_f) = κ₀(λ_f − 1 + ε_pre), where ε_pre denotes the pre-strain of fibres. When the fibres are initially force-free (ε_pre = 0), lim _γ→0 G* = 0 for all values of p (figure 6a), implying that the networks are initially unstable. When the fibres are pre-stretched (e.g. ε_pre = 0.1), lim _γ→0 G* > 0 for all values of p (figure 6b), indicating that the networks are stable. Finally, when the fibres are pre-compressed (e.g. ε_pre = −0.1), lim _γ→0 G* < 0 for all values of p (figure 6c), suggesting that model predictions become unphysical in this particular case.

Figure 6.

The normalized, nominal shear modulus G* predicted by the micro-sphere model for different values of p. Results are shown for (a) initially force-free fibres (ε_pre = 0), (b) pre-stretched fibres (ε_pre = 0.1) and (c) pre-compressed fibres (ε_pre = −0.1). Note that G* = (4πG)/(Nκ₀), with G given by equation (A 3).

Data accessibility

Data and codes have been uploaded to Github (https://github.com/songdawei1018/FibrousModel). The data are provided in the electronic supplementary material [53].

Authors' contributions

D.S.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, software, validation, visualization, writing—original draft; A.A.O.: conceptualization, writing—review and editing; P.A.J.: conceptualization, funding acquisition, project administration, resources, supervision, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests

Funding

This work is supported in part by the U.S. National Science Foundation (NSF) under grant nos. CMMI-1548571, NSF 16-545 and DMR 17-20530. D.S. also acknowledges the support from the Center of Engineering and Mechanobiology (CEMB) Pilot Award.