How dynamic prestress governs the shape of living systems, from the subcellular to tissue scale

Abstract

Cells and tissues change shape both to carry out their function and during pathology. In most cases, these deformations are driven from within the systems themselves. This is permitted by a range of molecular actors, such as active crosslinkers and ion pumps, whose activity is biologically controlled in space and time. The resulting stresses are propagated within complex and dynamical architectures like networks or cell aggregates. From a mechanical point of view, these effects can be seen as the generation of prestress or prestrain, resulting from either a contractile or growth activity. In this review, we present this concept of prestress and the theoretical tools available to conceptualize the statics and dynamics of living systems. We then describe a range of phenomena where prestress controls shape changes in biopolymer networks (especially the actomyosin cytoskeleton and fibrous tissues) and cellularized tissues. Despite the diversity of scale and organization, we demonstrate that these phenomena stem from a limited number of spatial distributions of prestress, which can be categorized as heterogeneous, anisotropic or differential. We suggest that in addition to growth and contraction, a third type of prestress—topological prestress—can result from active processes altering the microstructure of tissue.

1. Introduction

A peculiarity of living systems is their ability to constantly rearrange their structure in order to perform biological function. Cells, for example, transition from static to migrating while changing shape, or split in the process of cell division. At the tissue scale, specific shapes are acquired during development and are maintained at adult age to accomplish organ function, but can be lost as in the case of cancer. These rearrangements are in most cases the result of active processes taking place within the cells or tissues themselves, rather than being imposed from the exterior through boundary conditions.

Across the scales and specificities of systems, one finds a number of ways for these internal stresses to be generated, ranging from protein synthesis or pumping of ions that give rise to osmotic pressure gradients to ATP hydrolysis-fuelled changes of conformation of crosslinkers within biopolymer networks. One common point of these mechanisms is that they are controlled by biological pathways, and that they can be triggered or modulated dynamically, enabling systems to change shape or state. In this review, we aim to show how these very different force-generation mechanisms can be usefully understood with a common concept of prestress (and prestrain). While this concept has been useful in describing stable tissue shape in adult tissues [1], here we focus on how dynamic changes in prestress can alter shape. Often, prestress generation interplays with other less specific properties of living systems like their complex rheological properties, thin-sheet geometry and foam or network architecture. In some cases, it appears challenging to distinguish between phenomena stemming from dynamic prestress and those stemming from these complex material properties. An example developed below is the cell neighbour exchange (also called T1 transition) occurring in epithelia, which can have either active or passive origins.

In §2 of the review, we will present the concept of prestress and the theoretical frameworks available to describe prestress in statics and dynamics. Following on, we will briefly present in §3 the strategies available to experimentalists to identify and measure prestress in living systems. Then, in the final two sections, we will describe strategies of prestress generation in biological systems and the macroscopic effects obtained. On our way, we will show that common categories of spatial regulation of prestress (heterogeneous, anisotropic or differential) are used in systems with different compositions and scales.

Two key concepts will be used throughout this review: growth and contraction. By growth, we mean any active process that leads to increase the equilibrium size of some of the components of a system. This can be due to the addition of material within the system by some out-of-equilibrium process, e.g. the polymerization of filaments fed by monomers diffusing into it. This can also be more simply due to osmotically driven attraction of more water into the system. By contraction, we mean any active process that leads to the reduction of the equilibrium size of some of the components of a system.

In §4 of the review, we will focus on crosslinked networks of semiflexible biopolymers, either within cells—they are in this case part of the cytoskeleton—or external to them—then part of the extracellular matrix (ECM). These networks can be remodelled and crosslinked by other proteins which have out-of-equilibrium dynamics, fuelled by active processes. We will show how contraction and growth of these networks govern shapes and deformations of subcellular compartments, cells and fibrous tissue. Within the cytoskeleton, one network of particular interest is the one formed by actin and the crosslinker (and molecular motor) myosin.

Finally, in §5, we will describe how prestress affects the shape of cellularized tissue. Here, the material is formed by cells of regulated volume and mechanically connected through adhesions, molecular bonds joining their plasma membranes. The adhesions are formed of transmembrane complexes, allowing tension to be transmitted between the cytoskeletons of neighbouring cells. In this section, the elements experiencing growth and contraction interact with these other elements, making the material heterogeneous and bringing additional effects. Prestress can also be built through topological changes of the cell contours. We refer to this type of prestress as topological prestress. In particular, we suggest that, from a mechanical point of view, morphogenesis through cell proliferation is conveniently described if one distinguishes within the effect of cell division between growth prestress (increase of volume of cells) and topological prestress (due to the appearance of new cell–cell junctions following cytokinesis events).

2. Concept of prestress in living systems

In engineering, generally, ‘pre’ in ‘prestress’ refers to the fact that it is due to an operation done before establishing the system, for instance imposing boundary conditions such as tension on a structure such as wires, called tendons, before putting them in parallel with a compression-bearing material, e.g. by casting concrete. This results in a system whose reference configuration is not compatible with the reference configuration of each of its components, which are thus prestressed. In systems of linear elastic components, one can equivalently consider that they are prestrained, the prestress and prestrain being simply related by the elastic modulus.

The source of prestress is not necessarily an externally imposed force applied to a component of the system, but can also be due to an internal change in the system. Prestress can thus arise in a system which is already connected and is originally stress-free, if one of the components, which we will call the active component, changes its equilibrium configuration. As an example, a porous material (passive component) whose pores are occupied by a liquid will become prestressed if that liquid (active component) changes volume due to freezing or crystallization. In that case, ‘pre’ is not understood anymore as referring to a process in time, but rather as making reference to the fact that prestrain corresponds to the deformation between the initial configuration and a virtual configuration where the active component has assumed its new equilibrium shape. However, this stress-free configuration is virtual because the shapes of the active and passive components are not compatible anymore.

The actual configuration in the absence of external load results from the mechanical balance between the active and the passive components, neither of which will be stress-free: the observed stress field in the absence of external loads is called residual stress [1–3]. While residual stress has this narrow definition, the term prestress is somewhat broader. In the engineering community, prestress is typically due to external loads [4]. The prestressed configuration is then used as a reference configuration, from which another elastic deformation (for instance the wave propagation in the prestressed body) is studied [5]. In biophysical models, prestress can also be of active origin, for instance due to a morphogenetic event [6]. We take advantage of this relative freedom to define prestress so that it corresponds to the notion of active stress which was defined in the context of actomyosin systems [7]. Indeed, if one chooses to describe the prestressed material with respect to its original shape, that is, the configuration it would have in the absence of prestress, as a reference configuration, then one finds that there is now a stress field associated with it, which for this choice is a prestress field [8]. Since this prestress does not need to pre-exist the system, it can be adjusted at any time by non-mechanical processes, such as biological pathways, so that it can drive dynamics.

We now illustrate the concept using elementary mechanical elements. In order to describe the behaviour of individual cells within tissue, a leading approach is to use cell-based discrete models, which can capture cell–cell interactions and dynamical changes in topology. On the other hand, continuum descriptions offer the benefit of giving access to quantities such as Young’s modulus or Poisson’s ratio, and offer a vast array of tools for simplification through mathematical analysis [9]. For the sake of simplicity of presentation, we present ideas in terms of continuum models when possible, and discrete models when necessary.

2.1. Static description

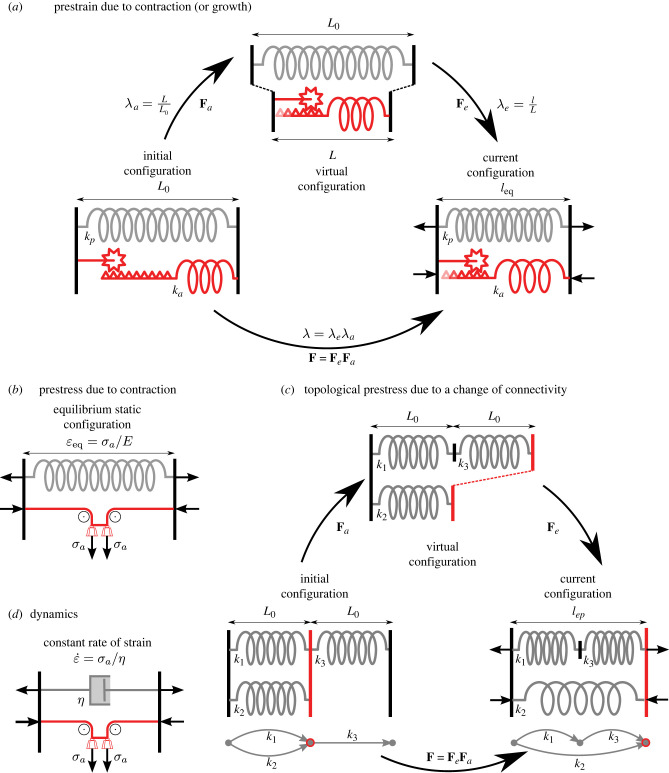
We illustrate the concept of a virtual configuration in figure 1a based on a one-dimensional example, meaning that we only consider deformations in the horizontal direction. An active element (red) is connected in parallel to a passive element (grey). The vertical black lines represent force-bearing walls. In the initial configuration, both elements have length L₀, and the system is unstressed. A contraction reduces the length of the active element to L, acting effectively like a spring that reduces its rest length through an active process. We refer to this active stretch as λ_a = L/L₀. In this example, λ_a < 1, since an active contraction occurs. In the virtual configuration, the system is still stress-free, but incompatible, since the two elements now have different rest lengths making their existing connection impossible [10]. Compatibility is restored through building stress: in the current configuration, both elements have length l, which is the new equilibrium length. The elastic stretch of the active element is λ_e = l/L. In this new equilibrium configuration, the active element is in tension (λ_e > 1), and the passive spring is in compression (its elastic stretch is l/L₀ < 1). In this framework, growth can be treated the same way, with one crucial difference: the active element increases, rather than decreases, its rest length, so that the active stretch is λ_a > 1.

Figure 1.

Prestrain and prestress in simple one-dimensional systems. (a) Illustration of deformation gradient decomposition for contractile prestrain. An active element (red) and a passive one (grey) are put in parallel in between force-bearing walls (black vertical lines). The active element is composed of a spring whose length is actively decreased (or increased) from L₀ to L, with an anelastic stretch, or prestrain, λ_a (here λ_a < 1) imposed via a crank. In the virtual configuration, both elements remain stress-free but the system’s topology (dashed line connections) is not respected. In the current configuration, even at equilibrium (no net force on the walls), the structure is under stress. Operating the crank the other way, λ_a > 1, gives the effect of growth prestrain. (b) A system equivalent to the one in a can be obtained by replacing the active crank and spring element by a stress generator element (pulleys and weight system) whose magnitude is the prestress. (c) For topological prestress, no active spring is necessary; the activity consists of disconnecting and reconnecting elements into a new network. Initially, springs k₁ and k₂ are in parallel, and the pair is connected in series with k₃. The topological change reconnects the springs, such that k₁ and k₃ are in series, this pair connected in parallel with k₂. Due to the change of topology (see directed graph insets) the initially stress-free structure becomes prestressed; spring k₂ is in tension, springs k₁ and k₃ are in compression. (d) A viscous passive element (dashpot) in parallel with a stress generator gives a permanent regime of contraction at a constant strain rate.

It is useful to understand the relationship between prestrain and prestress, since it allows a link to be made to the work on active stress in the context of contractile networks [7]. To understand this relationship, let us consider one active element in isolation, with initial length L₀, virtual length L, and current length l. The Hookean stress–strain relationship of this element is

$$\sigma =E(\frac{l}{L_0}{\lambda }_a^{-1}-1),$$ 2.1

where E is Young’s modulus. If we now deform the spring to the formerly stress-free state (l = L₀), we will be met with resisting stress σ equal to the prestress $\sigma ={\sigma }_a=E({\lambda }_a^{-1}-1)$. In this simple case, there is thus an explicit relation that can be written between the prestress field σ_a and the active stretch that characterizes prestrain λ_a = L/L₀. How can this be made sense of in the context of the stress–strain relationship of the spring, equation (2.1)? It is possible to split (2.1) as follows:

$$\sigma =\tilde{E}(\frac{l}{L_0}-1)+{\sigma }_a.$$ 2.2

This shows a Hookean behaviour near the initial, formerly stress-free state, with the modified Young’s modulus $\tilde{E}=E+{\sigma }_a$. At the formerly stress-free configuration l = L₀, we recover the prestress σ = σ_a. Up to the change of elastic modulus, we thus see the equivalence between a system in which the active element is a growing (σ_a < 0) or contracting (σ_a > 0) elastic material and a system in which the active element is a ‘stress generator’ of magnitude σ_a, see figure 1b.

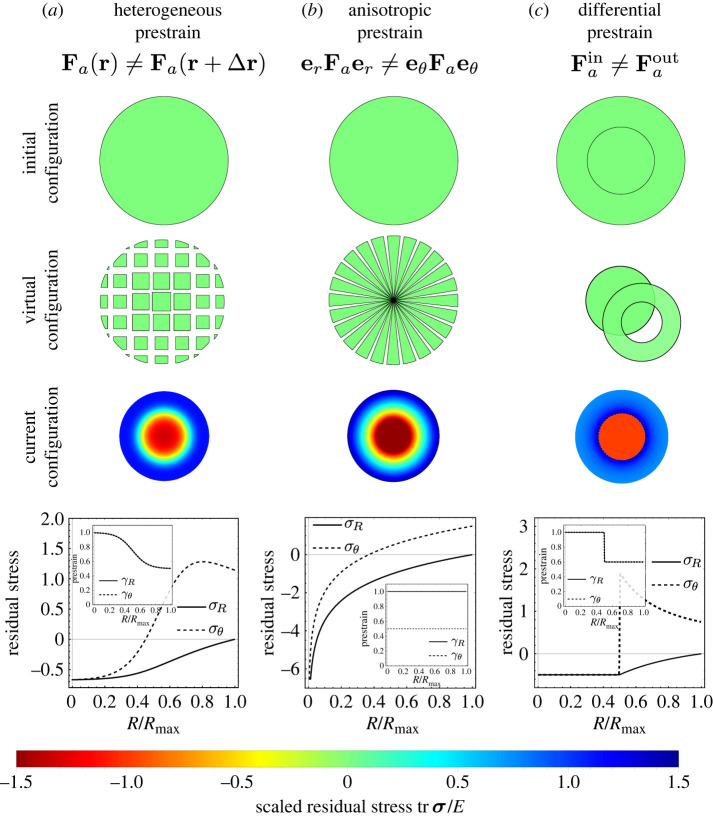
In order to describe more generally mechanical systems with prestress, and to allow the prestrain to be either due to growth or active contraction, we use a framework of anelasticity [11–13]. At its core is the decomposition of the deformation gradient as F = F_eF_a, where F is decomposed into an anelastic part F_a and an elastic part F_e, see figure 1. The elastic deformation is taken to be hyperelastic and isotropic, for example neo-Hookean, captured by a strain-energy density W = W(F_e). The anelastic deformation is associated with an irreversible process that in some way modifies the microstructure: F_a can mean active contraction, like energy-consuming contraction due to myosin, in which mass is conserved or reduced (i.e. transferred from the solid phase to an extracellular reservoir), $det{\mathbf{F}}_a\le 1$. Alternatively, it could mean growth, in which mass is added into the solid phase from an extracellular reservoir, $det{\mathbf{F}}_a\ge 1$. Cauchy stress is then defined as $\mathit{\sigma }={(det{\mathbf{F}}_e)}^{-1}(\mathrm{\partial }W/\mathrm{\partial }{\mathbf{F}}_e){\mathbf{F}}_e^{\mathsf{T}}$ and mechanical equilibrium is div σ = 0 in the absence of body forces and respecting that anelasticity (active contraction or growth) occurs at timescales much larger than elastodynamics. In this view, prestress will exist in the system due to the incompatibility [10,14–17] of the anelastic strain F_a: for instance, if the system is composed of multiple components with different incompatible reference configurations (F_a in layer 1 is different from F_a in layer 2), or anisotropy (F_a in, e.g. the radial direction does not match F_a in the hoop direction), or some heterogeneity in the anelastic strain (say, F_a(x) ≠ F_a(x + Δx)), which could capture a spatial gradient in growth or active contraction. Figure 2 illustrates how residual stress from different patterns of prestress can be created from the anelastic point of view.

Figure 2.

Creating residual stress from different patterns of prestrain in the anelastic framework for a disc. The disc is incompressible ($det{\mathbf{F}}_e=1$) and of neo-Hookean material. The boundary conditions are no traction, σe_R = 0. We denote the components of the prestrain in polar coordinates ${\mathbf{F}}_a=\text{diag}({\gamma }_R,{\gamma }_{\theta })$. Here, we illustrate contraction, γ < 1, however, equivalent situations are found for growth, γ > 1. (a) We consider spatially heterogeneous prestrain which is isotropic ($\gamma \hspace{0.17em}:={\gamma }_R={\gamma }_{\theta }$). The initial configuration shows the undeformed, uncontracted, stress-free disc. In the virtual configuration, most contraction occurs towards the periphery, leading to an incompatible body. The prestrain is explicitly shown in the inset, where γ = 1 (no prestrain) at the centre and γ = 0.5 (contraction) at the boundary of the disc. The result in the current configuration is a residually stressed body, with tensile hoop stress (${\sigma }_{\theta }>0$) at the disc boundary, and compressive stress (σ_R < 0, ${\sigma }_{\theta }<0$) at the disc centre. Due to the tensile hoop stress at the boundary, the disc would open if incised in the periphery. (b) We consider the case of anisotropic (${\gamma }_R\ne {\gamma }_{\theta }$) but spatially homogeneous ($\mathrm{d}{\gamma }_R/\mathrm{d}R=\mathrm{d}{\gamma }_{\theta }/\mathrm{d}R=0$) prestrain. This corresponds to pizza slice-shaped pieces being cut out in the virtual configuration. The resulting stress field is qualitatively the same as in the heterogeneous case. (c) We consider the case in which the outer part of the disc has a different prestrain than the inner part, prestrain being isotropic. The scenario is a discrete version of the heterogeneous case. The hoop stressis discontinuous.

A distinctly different possibility for building prestress is through changes in the microstructure due to rearrangements in the network. An example are T1 transitions, which are neighbour exchanges between cells in epithelial tissues, see §5.3. We offer to name this type of prestress topological prestress. We define it as prestress that is added to or removed from an interconnected network of mechanical elements by breaking and reconnecting network elements rather than prestressing individual elements. For instance, a passive T1 transition relaxes the stress in the system purely by exchanging which cell is connected to which, and not through modifying the reference configuration of any of the cells.

The concept of a microstructural rearrangement leading to topological prestress is illustrated in figure 1c. A network of three springs is presented in the initial configuration, but breaking and reconnecting bonds changes the network topology in the virtual configuration (topology refers to the connectivity of a network). Such changes of connectivity, which are meant to describe networks of discrete elements such as cell adhesions or polymer crosslinks, are challenging to describe with a continuum field like F_a that is meant to describe the larger tissue scale. For example, discrete deformations like slip lines in crystal plasticity have been successfully described with the continuum framework F = F_eF_a where F_a describes the macroscopic plastic deformation, F_e the elastic deformation, and F the total deformation [18,19]. But for biological tissue, which is generally amorphic and has no crystalline structure, the definition of macroscopic topological prestrain has not fully been achieved yet, although it is an active area of research [20–23].

2.2. Dynamic description

Both the active and passive elements of the system can exhibit a time-dependent behaviour. The growth rate and actomyosin contractility both depend on some non-mechanical processes, such as protein synthesis, nutrient intake, or ATP hydrolysis. All these are tightly regulated by biochemical pathways in physiological conditions, and in a large part the dynamics of the mechanical systems can be enslaved to biochemical clocks [24–27]. Active elements are also sensitive to the mechanical context. For instance, individual molecular motors are known to stall beyond some maximal load [28]. In the context of growth, the timescale is rather large, since it is the one of the cycle of cell division which takes place over hours or days. Therefore, the passive elements are considered to be always at equilibrium.

On the other hand, regimes of cell motility often rely on the dynamics of the passive component with a constant prestress. This may be required to achieve movements which are faster than the rates at which prestress can be created. This is the case e.g. for carnivorous plants [29] where an elastic instability is being used to suddenly release elastic energy that had been stored by the slow build-up of prestress.

While the full complexity of interacting timescales between the active prestress one and the passive viscoelastic ones is encountered in some cases, we will focus here on models that describe cases where they are sufficiently well separated. In the case of growth, the system is often considered to be purely elastic and the models thus focus on the timescale of the evolution of prestrain. In the case of contractile networks, viscous dissipation in the microstructure is often important for the observed dynamics and sets their timescale, whereas the active stress is often assumed to be slowly varying.

2.2.1. Dynamics governed by the active component: the example of growth laws

The timescale of elastodynamics in soft tissue (i.e. wave propagation in soft elastic media) is of the order of milliseconds, and a typical viscous timescale due to internal friction is of the order of seconds to minutes. The timescale of growth, on the other hand, varies from minutes (doubling time of Escherichia coli) to years (slow-growing tumours). Growth is thus a case where the separation of timescales is generally sufficient to consider that the passive components are instantaneously reaching their equilibrium configuration [3].

The dynamics is then governed by a law that prescribes the evolution of the active component’s prestrain as a function of the current configuration. Thermodynamic arguments based on the entropy inequality or a dissipation principle motivate appropriate forms of such a law [30–34]. By following a standard set of arguments and derivations, one arrives at a variant of the growth law

$${\dot{\mathbf{F}}}_a{\mathbf{F}}_a^{-1}=\mathbf{K}({\mathit{\sigma }}_E^{\ast }-{\mathit{\sigma }}_E),$$ 2.3

where ${\mathit{\sigma }}_E=(W\mathrm{I}-det({\mathbf{F}}_e){\mathbf{F}}_e^{\mathsf{T}}\mathit{\sigma }{\mathbf{F}}_e^{-\mathsf{T}})/{\rho }_r$ is the Eshelby stress, W is the strain-energy density, and ρ_r the density in the virtual configuration. The homeostatic Eshelby stress is σ_E* and K is a positive-definite coefficient matrix. The principle of homeostasis states that organisms have the ability to self-regulate some of their properties so as to optimize function in a physiological state, such as the ability of mammals to maintain a constant body temperature. In the context of mechanics, homeostasis can be understood as a living tissue’s ability to grow and remodel to accommodate a preferred (homeostatic) stress, i.e. to reshape itself to reduce the difference between its actual stress and the a priori known or genetically encoded homeostatic stress [31,35]. Growth laws of the type (2.3) which employ a homeostasis mechanism have been applied to morphogenesis problems, like sea urchin gastrulation [36], the formation of ribs in ammonite seashells [37], and the intestinal crypt [38], as well as other applications such as wound healing [36,39] and discrete networks such as plant cell networks [21].

2.2.2. Dynamics governed by the passive component: the example of contractile networks

On the other hand, there are systems in which the limiting rate of strain is set by the passive component. Large amplitude motion, such as muscle contraction or intracellular retrograde flow, could not take place in a purely elastic medium. Indeed, in the elastic models of figure 1a, an obvious upper bound for the amplitude of strain is the magnitude of the prestrain. However, if the passive spring is replaced by a viscous dashpot (figure 1d), then a constant rate of strain is achieved. This modelling is consistent for instance with the theory of sliding filaments for muscles, as delineated by Huxley [40], where the regime of maximum contraction speed is explained in terms of a balance between active stress and sliding friction. This compound element is thus governed by an equation of the form

$$\sigma -{\sigma }_a=\eta \dot{\epsilon }.$$ 2.4

Here, we find striking similarity with (2.3), with the difference that the strain rate of the whole system appears directly. In both cases, as long as the stress differs from a given homeostatic stress (σ*) or active stress (σ_a), an internal length, the virtual length L or a length of ‘telescoping’ of filaments, is being adjusted at a rate set by a parameter which has the dimensions of viscosity. We will come back to the molecular-scale understanding of the sliding friction in §4.1.2. In effect, this sliding friction can be likened to the fluidization of any viscoelastic liquid beyond its relaxation time. In transiently reticulated networks, such as the actomyosin network, this relaxation time is related to the residence time of crosslinkers [41] and thus the maximum speed of actomyosin contraction can be related to these crosslinker dynamics [42], yielding a Maxwell model for the passive component

$${\tau }_a{\mathit{\sigma }}^{\mathrm{\nabla }}+\mathit{\sigma }-2{\tau }_{a}E\dot{\mathit{\epsilon }}={\mathit{\sigma }}_a,$$ 2.5

where $\dot{\mathit{\epsilon }}$ is the rate of strain tensor, E the elastic modulus of the crosslinked actin network and τ_a a characteristic relaxation time. The time derivative ${\mathit{\sigma }}^{\mathrm{\nabla }}$ has to be an objective time derivative of the stress tensor σ, starting from rubber elasticity theory one obtains an upper-convected Maxwell derivative [42,43]. This can be related to the fact that the network structure is based on linear elements under stretch deformation [44]. Note that corotational derivatives are widely used in the field.

This constitutive relation is consistent with the general framework of active gels [7], which provides a thermodynamic framework relating the active prestress σ_a to the chemical potential difference associated with the myosin activity. At the molecular scale, the corresponding continuous injection of energy drives these system out of equilibrium and is at the origin of a spectacular violation of the fluctuation–dissipation relation [45], although effective equilibrium descriptions can be restored at higher scales [46].

Contrary to growing systems, contractile ones generally deform while keeping a constant mass. In order to sustain a deformation rate that will in general not be volume-preserving, the density ρ of the network needs to be actively regulated to a constant value ρ₀ by a reaction term, which in its simplest expression writes, in one dimension

$${\tau }_n(\dot{\rho }+\rho {\mathrm{\partial }}_{x}v)={\rho }_0-\rho ,$$ 2.6

where v is the velocity in x direction. Here, ${\tau }_n^{-1}$ provides another bound for the maximum rate of sustained flow. On the other hand, the reaction term in the mass balance can itself be a source of growth-related prestress. Assuming a density-dependent rheology of the material, such as σ = −E(ρ − ρ*)/ρ* in its simplest form, with ρ* an equilibrium density. When density is close to this equilibrium, ρ ≃ ρ*, we find again (2.4) with η = τ_n E and σ_a = E(ρ* − ρ₀)/ρ* [47].

Finally, one situation that is encountered in several living systems is a stationary system size emerging from an enduring permanent internal flow regime. It can be easily seen e.g. that a closed system governed by (2.6), but with different regulation densities ${\rho }_0^a<{\rho }_0^b$ in different geometrical regions a and b, will establish a flow from the region b to a. The system total size will adjust as the combination of the local growth and shrinkage, and there can be geometries and parameters for which this balances yields a constant total size. This sort of dynamic equilibrium will be exemplified below in actomyosin networks and cell spheroids.

3. Measuring prestress and prestrain in living systems

Obtaining detailed and reliable expositions of the prestresses which shape living matter has presented a great technical and conceptual challenge. A major difficulty is the large number of components which are in fact represented by the simplified components of figure 1. In every cell and tissue, numerous stress-bearing and -generating elements are mechanically coupled in complex (and often unknown) arrangements. Current techniques typically allow us to probe only small subsets of those components at once, so we are liable to overlook the many connected parts that remain invisible. On top of this, of course, the reference configuration of the components of figure 1 cannot be deduced from the reference configuration of the ensemble alone, they can only be revealed through perturbations. But living matter has a great propensity to react and adapt to the perturbations we introduce in order to measure, so that there is always a real risk of measuring artefacts.

In order to face these challenges, in recent years, a multiplicity of experimental methods has been developed by biologists and physicists to study dynamic prestress. The most commonly used approaches are

• — live imaging of molecular actors generating prestress and subsequent strain of the biological material;
• — biological perturbation of prestress generators via drugs or molecular loss of function;
• — prestress release by cutting and ablation followed by measurement of resulting strains;
• — insertion of or embedding into stress-sensing deformable elements, functioning from the tissue scale down to the subcellular scale.

These developments have been reviewed in detail elsewhere for both cell [48] and tissue scale measurements [49] and will be described when required in the sections below.

4. Prestress in biopolymer networks

4.1. Prestress in the actin cytoskeleton

The cytoskeleton is made of three categories of dynamic filaments (namely actin, microtubules and intermediate filaments) but only actin and microtubules are found to interact with molecular motors, which are major actors in prestress generation. We focus here on the actin cytoskeleton, although the framework defined above can be applied to the microtubule network, for instance to understand the force-balance within the mitotic spindle [50].

The actin cytoskeleton is made of polar semiflexible filaments composed of G-actin monomers, which turnover within filaments in timescales ranging from seconds to minutes depending on cell types and actin structures considered [51–55]. Growth rate and geometry of the actin networks are regulated by a variety of actin-binding proteins which can either nucleate, elongate or sever actin filaments, or cap their ends [56].

Actin also binds to a specific type of crosslinker, the myosin molecular motors, which walk along actin filaments by using ATP hydrolysis (figure 3b). Myosin II filaments in particular can attach to two actin filaments thanks to head domains at their two ends. Actin and myosins form together a zoology of network structures which range from the crystalline structure found in muscle sarcomeres to the less ordered actomyosin cortex, a thin actin gel lying underneath the cell membrane. Intermediate in terms of organization are linear bundles of actin enriched in myosin, such as the so-called stress fibres [57] and junctional cortex in epithelia [58]. The signalling pathways controlling the formation of these respective organizations is beyond the scope of this review and has been reviewed elsewhere [59].

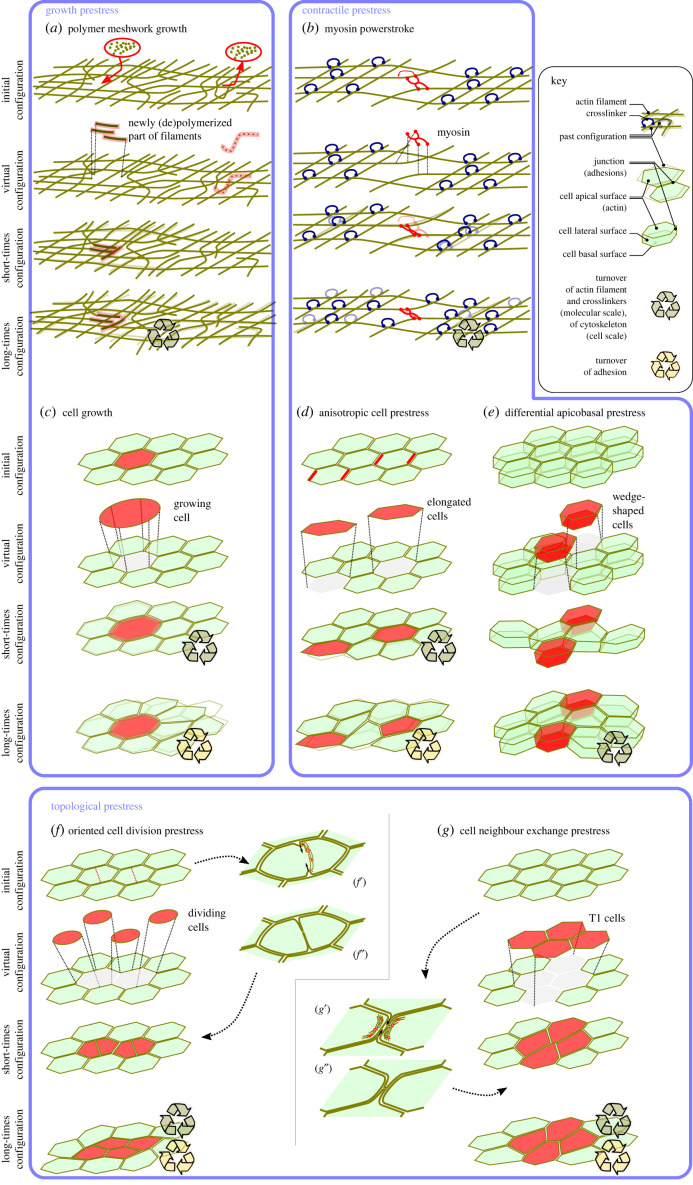
Figure 3.

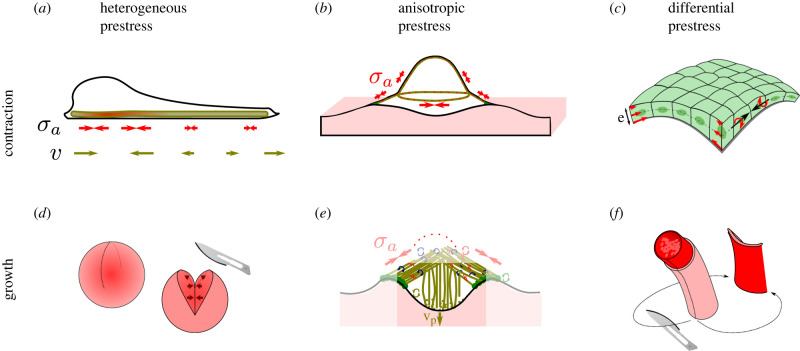
Examples of (a,b) subcellular and (c–g) tissue scale deformations due to active prestress related (a–e) to microscale rest shape change or (f,g) to a change of connectivity, which we refer to as topological prestress. (f’,f”) and (g’,g”) represent how the topological change in the tissue can be obtained by a subcellular active process, involving myosin prestress, however this level of detail can usefully be ignored when modelling tissue-scale deformations using the concept of topological prestress.

4.1.1. Mechanical balance of prestressed actomyosin

Contractile prestress. Importantly, myosin generates contractile prestress within actin networks. The contractile nature of stress fibres was demonstrated by measuring the rate and amplitude of the viscoelastic recoil of individual stress fibres after laser ablation. These two quantities were shown to be reduced when myosin II activity was inhibited by drug treatment [60]. Furthermore, dose-dependent treatments of blebbistatin (an inhibitor of myosin II contractile activity) on single cells isolated in a parallel plates traction force apparatus revealed that cell-scale traction exerted by the actomyosin cortex is proportional to myosin II ATPase activity, indicating that myosin is the main generator of contractile prestress in the cell cortex [61]. It can thus be established that the actomyosin meshwork exerts a contractile active stress, proportional to the chemical potential of myosin [7], which can be understood as a prestress.

How is it that contraction at the cell scale dominates over expansion despite the disordered nature of these networks? Various hypotheses have been proposed. The most documented one posits that because actin filaments buckle under compression, myosin activity will result only in a tensile contribution [62–64].

This contractile prestress can be balanced by the mechanical resistance of three other types of mechanical elements: the cell environment, the other cytoskeletal networks and the fluid component of the cytoplasm (or cytosol).

The tension–compression balance between tensile actomyosin and the external environment to which cells adhere was revealed thanks to the development of deformable substrates (elastomers, hydrogels or micro-posts arrays). It was shown that adherent cells seemingly ‘at rest’ apply tensile stresses radially directed towards the cell centre [65–68]. This stress is transmitted to the substrate at the sites of focal adhesions, mechano-sensitive protein aggregates connecting cells to the ECM [68,69]. Larger deformations are observed in the direction parallel to stress fibres [70]. In line with this, the recoil of the cell substrate away from the site of incision after ablation of stress fibres demonstrated the mechanical connection between those dense actomyosin fibres and the ECM [60].

Actomyosin tensile stress could also be balanced by compression of other cytoskeletal components. Among them, the microtubule network was suggested as a major mechanical actor bearing actomyosin tensile prestress, forming a biological illustration of the tensegrity model [71,72]. Depolymerizing microtubules using a drug increases traction forces on the substrate, suggesting that the compression borne by microtubules is transferred to the substrate [73]. Actomyosin pretension can however also be biochemically affected by microtubule depolymerization [74].

Finally, the tension developed within the actomyosin cortex can be balanced by the cytosol, an incompressible fluid which permeates the whole cytoplasm of the cell [75]. The cytosol is restricted from escaping by the cell plasma membrane to which the actomyosin cortex is adhered via the ERM family of proteins [76]. This mechanical balance is spectacularly broken when this cortex or its adhesion with the plasma membrane is locally ruptured: in such occasions, a high-curvature spherical protrusion, called a bleb, forms at the wounded site and inflates with cytosol from the cell body [77,78]. Reducing myosin activity, e.g. with the fittingly named drug blebbistatin, decreases the volume and rate of expansion of blebs, evidencing that the pressure driving the flow is due to the prestressed actomyosin cortex.

The actomyosin cortex and stress fibres constitute a continuous network and both contribute to cell-scale prestress [79,80], although their mechanical properties and regulatory pathways are different [79]. The spatial arrangement of these prestressed structures in equilibrium with the passive elements described above give rise, for instance, to the typical three-dimensional shape of crawling cells. In these cells, a flat compartment is formed at the cell front and an inversion of curvature of the cell profile is observed at the junction between this compartment and the dorsal cortex (figure 4b). This specific shape results from the presence of orthoradial fibres whose pretension opposes cytosol pressure. These fibres are then connected to radial stress fibres which are attached to the substrate near the cell edge via focal adhesions. Depolymerizing the orthoradial fibres via biochemical treatment restores a constant curvature along the cell profile [57].

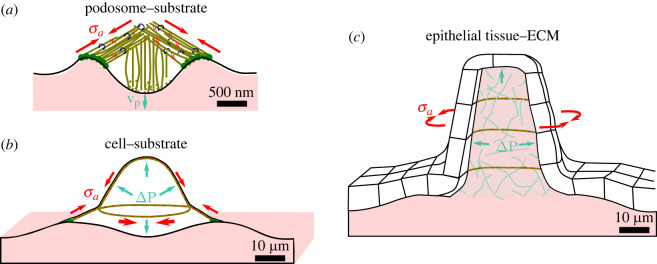
Figure 4.

Growth and/or contractile prestress governs the shape of subcellular, cellular and tissue-scale structures through mechanical connection between active and passive elements. (a) In podosomes, protruding forces applied by the actin core (growing at a rate v_p) onto the substrate are balanced by a contractile actomyosin network of prestress (σ_a), organized as a dome and attached to the substrate at the periphery via adhesion proteins [81]. (b) In adherent cells, actomyosin prestress (σ_a) is balanced by cytosol pressure (ΔP) and substrate deformation. Cell shape is further refined by anisotropic and heterogeneous actomyosin network contraction. Here, orthoradial stress fibres are connected to radial stress fibres, which are attached to the substrate via adhesion proteins at the cell periphery [57]. (c) In the zebrafish semicircular canal, pressure (ΔP) is generated within the ECM via synthesis of hyaluronan, pumping in interstitial fluid. This deforms the overlying epithelium which is further shaped by an anisotropic prestress (σ_a) generated by actin- and cadherin-rich protrusions [82].

Growth prestress. The actin cytoskeleton can also exert growth prestress. This was shown in vitro where actin networks nucleated by Arp2/3 under an AFM cantilever [83] or at the surface of spaced magnetic cylinders [84] were shown to generate compression within the network. This effect can be conceptualized as in (2.6) (also figure 3a), although the growth is often localized at the boundary. In vitro and in vivo, the mechanical activity of network growth is mechanosensitive as shown by a force–velocity relationship in line with an increase of the network density in response to load [83,85].

The generation of such growth prestress is involved in various biological functions. First, it is at the origin of the motility of the Listeria pathogen [86]. Here, like on spherical beads immersed in actin in vitro [87], growth occurs first homogeneously at the surface, which generates residual stress at the periphery of the network. The network ultimately fails via an elastic instability [88]. This symmetry breaking thus forms an anisotropic gel at the surface of the object resulting in a directional movement.

In mammalian cells, a length increase of actin filaments can increase cortical thickness and more importantly counteract tension generated by myosin in the network [89]. The best known example of a cell function in which actin network growth is involved is cell protrusivity, where actin can form a variety of structures pushing the cell membrane forward. This topic is a field of research in itself and we refer the reader to reviews treating it specifically [90].

Example: podosomes are shaped by growth and contractile prestress. An example of a prestressed structure combining growth and tensile prestress at the subcellular scale is the podosome, whose mechanics have recently been clarified (figure 4a). Podosomes are micron-scale structures present in various cell types (macrophages, cancer cells, endothelial cells) known to probe cell substrate mechanical properties and to be the site of ECM digestion. They are formed of a dense core of actin filaments, oriented normally to the substrate, and bound to a corona of radially oriented filaments which are tangential to the substrate and adhere to it thanks to focal adhesion proteins [91,92]. Protruding forces generated by actin polymerization within the podosome’s core were proposed to be a major contributor to the compression of the substrate [81]. While this growth-related prestress remains a possible player, recent findings show that the mechanical balance is dominated by the peripheral actomyosin filaments, which exert tensile forces between the tip of the core and the substrate, and hence press the core into the substrate [93]. This system shows that despite their complexity, the mechanical equilibrium of biological structures can be unravelled by combining force measurements, imaging and careful biological perturbation experiments.

4.1.2. Dynamics

As mentioned in §2.2, the dynamics of the system can come either from an evolution of the prestress or from a passive relaxation of the material. With some notable exceptions [94], the evolution of the prestress is generally slower than the relaxation of the material. Indeed, biopolymer networks are in general very dynamic as they are being constantly remodelled by processes of (de)reticulation and (de)polymerization. While the timescales of ECM proteolysis and synthesis remain largely unknown, the rapid turnover time of actin filaments entails its long times liquid-like behaviour [95]. Its effective viscosity scales like the product of the network short-times elastic modulus E and its characteristic turnover time τ_a, see (2.5). In the muscle, the only crosslinkers between actin and thick filaments are the myosin heads themselves. In order to function as sliding filaments, myosin needs to cycle from attached to detached from the actin in order to perform repeated steps [96], and the dissipation associated with maximal contraction velocity is due to an internal friction associated with the rate of detachment [40]. This is also the case in most motile and tissue cells, where the turnover time of myosin was found to be close to that of actin monomers in actin filaments and of α-actinin (one of the major actin crosslinkers) [97]. This explains persistent flows such as the retrograde flow observed in migrating and spreading cells, whose maximal rate of strain is thus set by the ratio of the prestress σ_a to the viscosity, as in (2.4) [42,95]. This is also what sets the rate at which actomyosin-rich subcellular components or tissues straighten after having been buckled by external compressive forces [98,99].

It is also of interest to consider the case in which macroscopic-scale deformation of the network is prevented by the boundary conditions. In those conditions, forces at the boundaries will need to balance the internal tension of the network. The energy input from myosin motors will then be dissipated internally by a microscopic scale creep, corresponding to the elastic energy loss incurred when elements in the network detach while under tension [40,42]. In this case, the stress measured at the boundaries will be equal to the prestress. Note that in energetic terms, there is work being continuously performed internally by the myosin in both the cases of zero external load or zero contraction of the system, the corresponding energy being respectively dissipated by internal friction and by internal creep [42]. These observations demonstrate a peculiarity of actomyosin networks where prestress and dissipation possess common molecular origins. At the microscopic scale, active processes increase the intensity of fluctuations in the medium. This has been evidenced both for the out-of-equilibrium (de)polymerization of cytoskeletal filaments [100] and for myosin activity [45], by comparing the fluctuations to those that would be expected from thermal forces only.

The actomyosin cortex and myosin contractility also participate in dynamic equilibration of prestress when substrate stiffness is varied. Cell traction assays in parallel plate geometry performed in various contractile cell types revealed that the loading rate during traction increased with substrate stiffness, with the same trend as the maximum traction force [61,101]. While the models most often evoked to explain the variations of cell tractions in response to changes in substrate stiffness over long timescales rely on mechano-transduction and subsequent changes in biochemical activity, it was found that the loading rate adapted to real-time changes in cantilever stiffness in a sub-second timescale [102,103], making purely mechanical explanations appealing [104]. Independently of the adaptation of myosin prestress to mechanical cues, a simple model such as (2.5) already predicts a biphasic behaviour with maximal traction for very large stiffness of the exterior and traction proportional to that stiffness when it is below a threshold [42]. When the actomyosin cortex continuously adhers to a deformable substrate, the interplay of this system with the elastic length scale of the substrate yields complex interactions which translate into a biphasic behaviour of the cell crawling velocity as a function of the elastic modulus of the substrate [105].

The combination of growth at the leading edge of cells and active contraction to the back is the hallmark of cell crawling on a flat substrate [95,106,107]. These two effects give rise to a dynamic equilibrium setting the size of the system [42,108].

4.2. Prestress in fibrous tissues

The ECM is a biopolymer network which is made of assemblies of filamentous proteins (the most abundant being collagen I), proteoglycans and glycosaminoglycans (GAGs). It is the main component of fibrous tissues—also called soft connective tissues—and of the basement membrane on which bidimensional epithelial tissues lie. In most tissues, the matrix content is dominated by collagen (especially type I collagen), which has the ability to self-organize into fibrils and fibres through physical bonds [109]. These fibres can measure up to dozens of microns and often form a crosslinked gel in vivo. In soft fibrous tissues, the ECM is synthesized by cells of the fibroblast family which are embedded and mechanically connected to the matrix. Here, both cells and ECM lie in an interstitial fluid. Mechanical interactions between these three phases generate a wide variety of architectures [110] and mechanical properties [111], which vary from organ to organ and according to patho-physiological conditions.

The difficulty of performing live imaging in these three-dimensional systems, combined with their physical and biological complexity, has so far impaired the understanding of their active mechanical properties. Nevertheless, recent data show how prestress can be generated in fibrous tissues and affects tissue development and pathology. Despite being largely composed of inert protein, the ECM is not mechanically passive.

4.2.1. Contractile prestress

First, contraction of the ECM can result from variation in water content within the interstitial fluid. In particular, collagen molecules, known to resist tensile stresses in fibrous tissues, change conformation with decreasing water content of the surrounding medium. This effect induces high contraction of the network, which could be important for the function of the load-bearing tendon [112,113].

But the ECM is also made contractile through the traction forces that fibroblasts exert within it. Since fibroblasts are polarized mechanically and bound to the ECM through focal adhesions, they apply force dipoles on the collagenous network, acting like active crosslinkers. Isometric contraction of fibroblast assemblies self-organizing in the collagenous matrix could be measured in between parallel cantilevers and was shown to be dependent on myosin activity [114,115]. In these systems, like in the actomyosin cortex, the nonlinear mechanical properties of collagenous networks resulting from the semiflexible nature of the fibres are thought to play a major role in the propagation and amplification of contractile stress at the tissue scale [116,117]. Because cell traction forces are sensitive to the stiffness of the extracellular environment [61,118], stiffening of the ECM fibres generated by cell traction forces triggers a positive feedback loop amplifying stiffening in fibrotic reactions [119] or during directed cell migration [120].

This mechanical activity of fibroblasts contracting the ECM influences tissue function during developement and in adulthood. First, in confirmation of a long-standing hypothesis [121], recent work shows that the patterning of multicellular aggregates in the chick dermis initiating feather follicles depends on fibroblast cell contractility, preceding differentiation of the epidermis [122]. This indicates that fibroblast contractile activity can indeed act as an organizing factor of fibrous tissues during development. Second, during lymph node physiological function, immune cells signal their arrival to the fibroblast reticular cells and tune their contractility in order to relax the tissue. This is thought to help maintain lymph node integrity while the lymph node expands [123]. Finally, cancer-associated fibroblasts, which shape the fibrous tissue of the tumour microenvironment and are more contractile than normal fibroblasts [124], could also apply active stresses at the global scale of the tumour. Along this line, it was shown that their collective contraction concomitant with an orthoradial assembly around tumour aggregates compress tumour compartments in vivo, as well as cylindrical micropillars in vitro [125].

4.2.2. Growth prestress

The interstitial fluid can generate growth prestress within the ECM. Indeed, the osmotic pressure within the ECM can be tuned in particular by the presence of GAGs and proteoglycans, thanks to their long, negatively charged chains. This property is used during developmental morphogenesis where localized synthesis of hyaluronan (a common GAG) contributes to the bulging of an epithelial monolayer laying on top of the swelling ECM [82] (figure 4c). Such water influx is then balanced by the matrix fibres under tensile load [126]. Thus, in contrast to the poro-elastic behaviour observed in the cell cortex [127], tension relaxation correlates with expelled interstitial fluid [126]. In the context of cancer, the deregulated fibrous tissue defining the mechanical properties of the tumour stroma (i.e the tumour micro-environment) is also affected by an increase in hyaluronan synthesis and subsequent elevated interstitial fluid pressure. In pancreatic adeno-carcinoma, this effect generates collapse of blood vessels, which could participate in organ loss of function and impairs delivery of therapeutic agents [128].

5. Prestress in cellularized tissue

At the tissue scale, a new structural unit becomes fundamental: the cell. From a purely mechanical view point, one crucial aspect is that cells tessellate the space occupied by a tissue into units of regulated volume, which have interactions via adhesion molecules. Being functional units, cells may have individual biochemical activity which can translate into mechanical activity, in turn giving rise to strains that can alter the tissue geometry. This biochemical activity can be patterned at the scale of single cells. For example, in epithelial tissues, which typically form thin sheets of a single cell layer, apical (cell ‘top’ surface), basal (‘bottom’) and lateral (where cells are in contact) surfaces are, to some extent, independent biological and hence mechanical units.

Since tight junctions between cells allow tissues to form impermeable layers, cells that actively and directionaly pump ions can in this way impose a pressure difference between apical and basal surfaces, which can generate and maintain a liquid-filled cavity called lumen. Lumens, like neighbouring tissues and the ECM network synthesized by cells, in turn impact tissue mechanics by boundary conditions that vary in space and time.

Cells also define a tissue topology via the neighbour relations created by cell–cell adhesion. This topology can evolve over the course of time as cell–cell junctions are assembled and disassembled, which can in turn give rise to further tissue-scale strain that can be modelled as the result of a topological prestress, as opposed to contractile or growth prestress.

With these differences in microstructure come processes with new timescales [129]. While a single actin filament may turn-over in seconds, a cell–cell junction requires at least minutes to disassemble and reassemble when a cell changes neighbour [52,130]. The creation of a new junction during cell division similarly occurs over minutes. However, the full timescale of the cell cycle, which we may consider to encompass the prestress changes associated with cell growth and cytokinesis, varies greatly between animal cell types, from minutes to years. These cell-level processes may be synchronized throughout a tissue, generating tissue-level deformations at a similar timescale, or they may be asynchronous and so add up gradually over longer timescales.

5.1. Contractile prestress

5.1.1. Supracellular scale prestressed networks in interaction with their environment

Although actomyosin is restricted to the cell cytoplasm, it can form supracellular structures by means of adhesion molecules that mechanically connect one subcellular network to that of a neighbouring cell, forming multicellular structures under tension [131,132]. The emergence of such a mechanical continuum is illustrated during the reformation of a dissociated epithelial monolayer in vitro by an increase of apparent tissue stiffness, which is coincident with the development of cell–cell junctions and dependent on actomyosin activity [133]. The tissue-level prestress generated by the continuous actomyosin network can be measured directly in vitro epithelial monolayers devoid of ECM and suspended between the arms of a force cantilever [99]. Here, a ramp of compressive strain imposed at the tissue boundary results in a linear decrease in tissue stress. As would be the case for a prestressed thin elastic plate, the tissue then buckles when it reaches a compressed state. Strikingly, the dynamics of stress recovery upon a rapidly applied compressive strain match those of an isolated actomyosin network, indicating that, in this case, the cellularized structure has little impact on the overall mechanics [99]. Such a response, consistent with a continuous model of an epithelium, has also been observed in vivo, in several Drosophila epithelia, where anisotropies of prestress were revealed by the recoil of circular regions of tissue after laser-cutting [134].

Just as epithelia can change length and generate prestress through their actomyosin networks, they can also be connected to an active element and play a passive role. Their challenge is then to bear the stress generated in order to maintain epithelial integrity [135]. This is illustrated by the blisters that epithelia form under active ion pumping directed towards their basal side. In analogy with the pressure in the cell cytoplasm, the pressure within the blister is balanced by the tension in the actomyosin network. Under increased stress, cell deformations can reach hundreds of per cents. When the actin pool is exhausted so that the filament network can no longer cover the cell surface area, the keratin network (an intermediate filament network connected through an other type of cell–cell junctions called desmosomes) takes over to resist mechanical stress [136].

While the passive response of an epithelium leads to a dome shape in the system above, an active participation of the epithelium is required to generate a tubular shape, as is the case in the zebrafish inner ear [82]. Here, anisotropic multicellular cables which are both contractile and adhesive form in the direction orthoradial to the cylinder axis, and so by breaking the symmetry of prestress allows an anisotropic shape to arise. Notably in this example, the element driving growth is an increase of osmotic pressure in the ECM actively regulated by cell synthesis of hyaluronan.

5.1.2. Spatially patterned prestress and tissue bending

The generation of anisotropic prestress, as in the zebrafish inner ear, is one example of a common strategy of spatially organizing prestress in order to control tissue shape. The most studied example is perhaps epithelial tissues where prestress, tangential to the plane of the tissue, varies along its transverse direction and drives bending via differential prestress. This aspect is particularly important during animal development and detailed reviews of this process have been made by others [137,138]. For the sake of this review, note that a variety of fine-tuned prestress regulation have been documented, including increase of prestress in the apical domain [139], increase or decrease of prestress in the basal domain [140,141], and increase in lateral prestress [142,143].

This differential prestress can be revealed by laser ablation in cultured suspended epithelia by measuring the spontaneous curvature generated orthogonal to tissue plane at a newly created free edge. This too allows for measurement of the out-of-plane forces involved by unfurling the curled tissue with a force cantilever [144].

Three-dimensional geometries other than linear folds can be produced through the same mechanism, via patterning of differential prestress throughout the plane of an epithelium. For instance in two-dimensional-cultured gut organoids, three cell types are organized within the tissue plane into concentric circular islands. Traction force microscopy and laser ablations revealed that these regions display different mechanical behaviours, with apical–basal myosin polarization in the central region leading to the doming of crypts (cup-shaped structures of the digestive tracts) [145]. In three-dimensional gut organoids, in which cells embedded in ECM form cysts, experiments revealed that crypt morphogenesis is also driven by membrane transporters which cause liquid transfer from the crypt cavity to the tissue [146]. Interestingly, the apical–basal polarization of the crypt region was found to be large enough in comparison to that outside of the crypt region for the overall morphology to be robust to organoid volume changes [146].

Recent advances in optogenetics (optical activation of engineered biomolecules) have also allowed for the experimental control of this patterned differential prestress. For example, at the stage preceding gastrulation in Drosophila, localized apical activation of RhoA, an activator of myosin contractility, was shown to be sufficient to initiate folding in a variety of directions and locations where invagination does not normally occur [147]. In vitro measurements showed that the spontaneous curvature generated by active differential prestress is so high (on the order of the inverse of tissue thickness) that competition between in-plane elastic energy and bending energy takes place. In this way, tissue folding is continuously modulated by external tension and reciprocally [148]. Nevertheless, differential prestress is not the only way to achieve folding. Recent data from the ventral furrow formation in Drosophila embryos showed the importance of the global ellipsoidal geometry of the embryo for an elongated ventral patch of myosin to achieve a fold along its long axis [131]. Indeed, heterogeneous prestress at the surface of a thin shell respecting this geometry leads to surface buckling initiating folding with the correct pattern of strain and dynamics [94].

5.2. Growth prestress

Physiological growth in living tissues often results in material added (or lost) in a non-uniform manner, forcing neighbouring tissue to accommodate the newly added material through elastic deformation. These non-uniformities, as illustrated in figure 2, include heterogeneous, anisotropic and differential prestrain F_a. As discussed in §2, this non-uniform prestrain is revealed by residual stress: an internal stress that remains when all external loads of an originally unloaded configuration are removed. Tissues actively build these internal stresses both during morphogenesis (when they rapidly change shape and add mass) and in the adult physiological state (when mass and volume changes serve the purpose of maintenance and are comparatively small).

A classic example is the residual stress in arteries, which has been theoretically and experimentally described by Fung and others [149,150]. The observation is that arteries, when radially cut, open up due to compressive stress built in the hoop (circumferential) direction. The opening angle can be used to quantify residual stress [149]. Experiments also suggest that arteries are residually stressed in the axial direction [151]. In a series of seminal studies, Fung and co-workers demonstrated residual stress in other cardiovascular systems such as the heart [152], veins [153] and the trachea [154]. Residual stress was also identified in other physiological tissues and organs such as the brain [155] and bones [156], as well as morphogenetic systems such as the optic cup [157] and the developing embryo [158]. It was also found in pathological tissue such as solid tumours [159]. Proliferation also produces compression within the core of tumours and orthoradial tension at the periphery as revealed by cutting of an excised tumour along its radius [160]. In this context, growth-related prestress is referred to as ‘solid stress’.

Apart from physiological systems, growth-induced prestress has been measured in a multitude of ways in cultured systems. Stress in growing multicellular spheroids has been measured with great precision: the growing cells were encapsulated inside permeable, elastic, hollow microspheres which deformed as the spheroids grew inside of them, allowing the traction forces to be reconstructed [161]. The external pressure applied on the spheroid by the elastic coating leads to a steady-state size of the spheroid, in which there is an equilibrium between a necrotic core and a proliferating rim. The existence of a pressure at which spheroids reach a stationary size was theoretically proposed by Basan et al. [162] and independently experimentally addressed by applying osmotic pressure to the spheroid [163].

A similar technique for measuring growth-induced stress, by the elastic deformation of the environment, was demonstrated for yeast cell colonies (which do not form cell–cell junctions) [164]. A distinctly different method was used in [165], where three-dimensional aggregates of tumour cells were co-embeded with fluorescent micro-beads in agarose gels. The displacement of the beads allows a reconstruction of the spatial stress distribution.

Prestress generated by proliferation can also be observed in two-dimensional tissues, for example during the early development of the Drosophila wing disc. In a three-dimensional finite-element simulation of the wing disc as one heterogeneous layer, the growth rate and mechanical coupling to the elastic basement membrane of the tissue provoke the formation of spatially regulated folds [166]. The doming of a part of the wing disc, the wing pouch, was recently explained through a combination of differential growth and differential growth anisotropy between tissue layers [167]. Similarly, differential growth rates between adhered tissues has been shown to regulate the looping of the chick gut [168], the formation of villi in the chick gut [169] and the gyrification of the brain [170].

Here we considered growth to be dictated by proliferation rate, but an increase of cell density can occur independently to proliferation. For instance, during the formation of the zebrafish optic cup, migration of cells from the outside of the organ is analogue to a local tissue growth. This process increases tissue curvature and is required to produce correct bending of the organ, in parallel to differential contractility [141].

Finally, the removal of cells, through cellular processes such as apoptosis, can be seen as a reverse growth and can play equally important roles during tissue morphogenesis. For example, in a transient extra-embryonic epithelial tissue named the amnioserosa, which sits between two embryonic epithelia during Drosophila embryogenesis, the gradual apoptosis of amnioserosa cells drives the final stage of dorsal closure in which those two sheets are brought together [171].

5.3. Topological prestress

The cellular microstructure of tissues offers a further mechanism through which to generate or relax prestress via changing the topology through cell–cell neighbour exchange events, termed intercalations (or T1 transitions in foam literature) [172,173]. At the subcellular scale, this process requires the coordinated action of many biomolecular players to disassemble and reassemble cell–cell junctions and has often been found to depend on the active generation of stress to shrink or expand junctions [58,174]. The resulting T1 defines an orientation, as specified by the orientation of the removed and of the added junctions. In some tissues, T1 transitions occur throughout tissues with no preferred orientation, in which case they relieve local cell packing stresses, allowing tissue ordering [175] or facilitating flow during migration [130]. The transition from such a liquid-like state to a ‘jammed’ state has been shown theoretically to relate to cell density, junctional tension and fluctuations [176]. However, the most dramatic examples occur when intercalations are globally aligned throughout a tissue, such as during Drosophila germband extension [177,178]. This results in creating neighbour relations which, in the initial configuration of the tissue, strain the cells in the transverse direction: their relaxation thus entails a tissue-scale deformation in the longitudinal direction [179], see figure 3g. Similarly, multilayered epithelia can expand (here isotropically in the plane) through ‘radial intercalation’ in which cells in lower layers intercalate into upper layers creating a precompression which is relaxed by expansion [180]. Since these are relaxation processes following out-of-equilibrium topological changes, they can be conceptualized as topological prestress. A major challenge in the analysis of such deformations is to disentangle this process from boundary stresses that may also act on the tissue [179,181,182].

Although epithelial topology is often represented as a two-dimensional network, a full three-dimensional treatment revealed different connectivity in the apical and basal domains [183]. Topological transitions were indeed observed along the apico-basal axis in a range of in vivo tissues, resulting in a three-dimensional cell shape named a scutoid. This solution is favourable when tissues are curved by different amounts with respect to their principle planar axes (i.e. tubular rather than spherical) unless the radius of curvature is large compared with the tissue thickness. It remains to be found whether these intercalations could drive bending itself, rather than simply relax stress.

A separate class of topological change which affects prestress is the introduction of a new junction into the network, which occurs during cytokinesis, see figure 3f. Again this is an oriented process, as the degree of freedom is the orientation of the new interface. Indeed, much has been discovered about the cell- and tissue-level signals read by a cell when choosing a division orientation. These signals include biochemical cues such as tissue polarization [184,185], as well as mechanical and geometrical signals such as tissue stress [186–188] and cell shape [189,190]. In turn, the choice of division orientation alters prestress. A prestrained mother cell, depending on the choice of division orientation, could be divided into two daughter cells with either an increased or reduced anisotropy in shape. In tissues, the latter choice is usually observed, so as to homeostatically regulate cell shape anisotropy [190–192]. In the zebrafish, this alignment of division with cell shape (which coincides with the principal axis of tissue stress), was shown using laser ablations to reduce the stress that builds up as a cell layer migrates over the embryo’s surface [193]. Similarly, alignment of cytokineses along a given axis can contribute to driving directional growth [194,195].

Altogether, a complete description of tissue morphogenesis can be achieved by a linear combination of the active and passive mechanical modules we have described so far (cell stretching, oriented cell division, T1 transitions), provided that one has a good knowledge of the boundary conditions, which can often be dynamic in living systems [196].

6. Conclusion and future directions

Living organisms have evolved a large number of controllable processes able to drive deformations from within the system itself. In this review, we have tentatively brought together the understanding of those systems under the generic banner of prestressed materials. Beyond the convenience of relating these working principles with a known engineering concept, this allows us to offer a classification into heterogeneous, anisotropic or differential prestress systems driven by either contractile or growth activity. Figure 5 provides an example for each of the six typologies that thus emerge.

Figure 5.

Example of biophysical systems where mechanics is governed by heterogeneous, anisotropic or differential prestress of either sign, corresponding to contraction or growth. (a) Contractile actomyosin with local accumulation, in parallel with a length-regulating element and in continuous adhesion with a substrate, generates a friction pattern that enables motility [197]. (b) Anisotropic pretension of the apical surface of cells regulates their shape [57]. (c) Differential prestress between the weakly contractile apical (top) surface and strongly contractile basal (bottom) surface causes tissue curling [148]. (d) Residual stress due to heterogeneous growth is characterized by cutting experiments in tumours, revealing tensile hoop stress at the periphery [160]. (e) The core of podosomes grows within a confined space, generating anisotropic prestress [81]. (f) Arteries change curvature if cut, this is believed to be caused by differential growth and remodelling of concentric layers [151].

Additionally, we define topological prestress as the prestress that is added to, or removed from, an interconnected network of mechanical elements not through prestressing individual elements, but purely by breaking and creating connections between the network elements. This latter type of prestress corresponds to a higher level of phenomenology, since it does not in itself describe by which (active) process the connectivity is being changed, see the examples in figure 3f,g. It also has the property that it is always providing anisotropic prestress.

From an experimental point of view, characterizing living systems as active materials is highly challenging. One difficulty is linked to the necessity to test systems while they are maintained in a state of function as close as possible to physiological conditions. For this, recent developments in organoid systems present great opportunities, since elements of tissue morphogenesis can now be recapitulated in an in vitro setting which is much simplified and much more amenable to experimental pertubations.

Observing the system simultaneously at different scales, especially combining global-scale stress and strain measurements with very local measurements could enable better characterization of how the microstructure dynamics give rise to emergent properties. For instance, tools measuring strain at the molecular scale, like Förster resonance energy transfer [198], or at the meso-scale, like micro-magnets [199], micro-droplets [200] or optical tweezers [116], could be coupled to cell-scale techniques, like parallel plate rheometry or TFM, to decipher the subcellular contributions to cell shape changes. On the other hand, cell-scale in parallel to tissue-scale mechanical testing appears necessary to understand the cellular origins of tissue flows [201].

In all cases, the interpretation of force–displacement relation measurements must be supported by careful modelling, as exemplified by the violation of the fluctuation–dissipation relation [46]. This sheds light on the vital need for combining any experimental approach with a theoretical understanding and of testing this by employing multiple modalities. Notably, extending the existing models towards geometric or material nonlinearities is a necessity given the large deformations that are commonly encountered in real systems. How the prestrain and prestress fields relate in a nonlinear context also remains to be clarified. Solving mechanical models coupling different biological structures, in relevant geometries in three dimensions also remains an important challenge: for example, a full understanding of the three-dimensional mechanical balance of single or tissue cells, or of the dynamics of fibrous tissues which is governed both by cells and ECM are still lacking.

Another challenging theoretical task is to describe topological prestrain and prestress in a continuum framework. A missing intermediate step is the linking between the cellular and tissue scales. At the scale of several cells, vertex models [202] are a highly studied family of models for biological tissue, both for their strength at capturing various tissue properties [136,203,204] and for their interesting physical behaviour [202,205,206]. However, the coarse-graining of vertex models to continuum descriptions, such as anelasticity, remains highly challenging, and is being tackled with approaches based on nearly periodic lattices [20,22,23] and discrete calculus [207,208]. These efforts may in the long term lead to the possibility of encoding topological transitions, like active or passive neighbour exchanges (T1 transitions), into a continuum field usable, for instance, in anelasticity approaches.

Seventy per cent of the total cell volume is water, and there is growing evidence in favour of a coupling between cell mechanics and osmotic gradients controlling volume [209,210]. Cells maintain a prestress inside the membrane by carefully controlling the flow of water: water mobility in and out of cells relies on the permeation of water through the plasma membrane, which can be regulated by aquaporin channels [211], as well as ion pumps which actively consume energy. Therefore, there has been recently considerable interest in the modelling of water mobility. This has been approached via a fluid phase in the framework of poroelasticity [212–214], as well as by explicitly tracking water fluxes in a vertex model [204]. In parallel, there are new developments coupling the electrochemistry of ion fluxes, mechanics of cell volume regulation, and active pumping [209,215]. Water mobility should ultimately add contributions to coarse-grained models such as anelasticity. From the experimental side, this requires the development of non-perturbative pressure sensors which is an important challenge for the future.

Data accessibility

This article has no additional data.

Authors' contributions

A.E.: conceptualization, data curation, writing—original draft, writing—review and editing; J.E.: conceptualization, data curation, writing—original draft, writing—review and editing; J.F.: conceptualization, data curation, writing—original draft, writing—review and editing; T.W.: conceptualization, data curation, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interest.

Funding

We received no funding for this study.