How do real animals account for the passage of time during associative learning?

Abstract

Animals routinely learn to associate environmental stimuli and self-generated actions with their outcomes such as rewards. One of the most popular theoretical models of such learning is the reinforcement learning (RL) framework. The simplest form of RL, model free RL, is widely applied to explain animal behavior in numerous neuroscientific studies. More complex RL versions assume that animals build and store an explicit model of the world in memory. To apply these approaches to explain animal behavior, typical neuroscientific RL models make implicit assumptions about how real animals represent the passage of time. In this perspective, I explicitly list these assumptions and show that they have several problematic implications. I hope that the explicit discussion of these problems encourages the field to seriously examine the assumptions underlying timing and reinforcement learning.

Predicting rewards is essential for the sustained fitness of animals. Since animals (including humans) experience events in their life along the continuously flowing dimension of time, predicting rewards fundamentally requires a consideration of this timeline (Fig 1). Several models have been proposed for how animals learn to predict rewards based on their experience (Balsam et al., 2010; Brandon et al., 2003; Dayan, 1993; Gallistel and Gibbon, 2000; Gallistel et al., 2019; Pearce and Hall, 1980; Rescorla and Wagner, 1972; Schultz, 2016; Sutton and Barto, 1998; Wagner, 1981). Among these, the most widely used class of models in neuroscience is reinforcement learning (RL). The core concept of RL models is that animals make an initial prediction about upcoming reward, calculate a prediction error — the difference between the experienced reward and the predicted reward, and then update their prediction based on this prediction error. The critical issue for a real animal is that it must learn not just that a reward is predicted but also when it is predicted. While RL models were inspired by psychological models such as the Rescorla-Wagner (Rescorla and Wagner, 1972) or the Pearce-Hall (Pearce and Hall, 1980) models, mathematically rigorous versions of it have borrowed extensively from concepts in computer science. The fundamental issue that makes these newer models better suited to explaining animal behavior is that they attempt to solve the question of when the reward is predicted, while Rescorla-Wagner and Pearce-Hall models punt on this issue.

Fig 1.

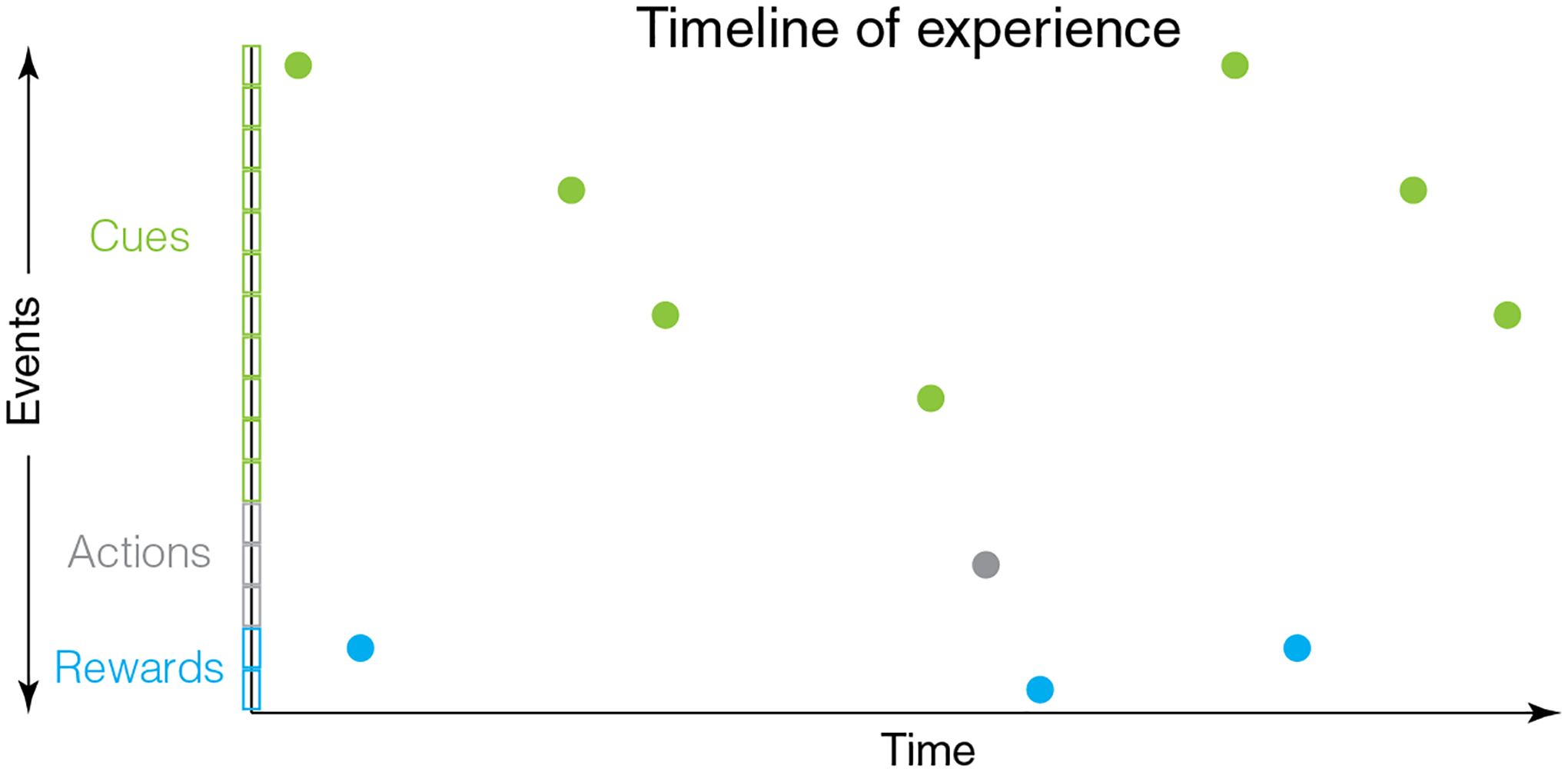
Animals experience events in their life in a timeline along the continuously flowing dimension of time. Thus, prediction of rewards requires a consideration of the flow of time. Here, external cues, internally generated actions and rewards are shown by separate colors. Distinct types of events within these groups are shown by individual boxes along the y-axis.

Explaining how these newer models account for the passage of time is the key issue considered in this perspective. Briefly, these RL models contend that the learning agent (e.g. real animals) represents the structure of their world in a “state space” that abides by simplified principles such as Markov chains (Niv, 2009; Sutton and Barto, 1998). A state is any abstract representation of observable or unobservable events in their world, and Markov chains are a special kind of state space in which transitions between states do not depend on the history of previously experienced states. Commonly used Markov chain models discretize the flow of time (Niv, 2009; Schultz et al., 1997) or assume temporal basis functions during intervals between events (Gershman et al., 2014; Ludvig et al., 2008, 2012; Petter et al., 2018). These formulations have an intrinsic mathematical simplicity to them, which makes rigorous mathematical calculations possible (e.g., the Bellman equation for value update). Here, I show that these simplifying assumptions have problematic implications when applied to learning in real animals, as they often do not naturally account for the timeline of experience of real animals. My hope is that the explicit treatment considered here stimulates serious considerations of these issues. While the solutions remain to be fully worked out, I believe there will be no progress until the problems are recognized.

Example illustrative task

Perhaps the simplest RL task for animals is cue-reward learning. Most commonly, this is studied in Pavlovian conditioning experiments in which an environmental cue is predictive of an upcoming reward (Pavlov, 1927). Often, there is a delay between when the cue turns off and the subsequent reward delivery (e.g. Bangasser et al., 2006; Beylin et al., 2001; Coddington and Dudman, 2018; Kobayashi and Schultz, 2008; Schultz et al., 1997). This variant of the task is known as trace conditioning. I will use this simple illustrative example throughout this perspective. The main reason for doing so is to show that even the simplest tasks require problematic assumptions. Indeed, the problems laid out here become more severe for tasks requiring reward predictions based on actions. Another reason is that this type of learning, i.e., cue followed by delay followed by reward, is highly ethologically relevant. For instance, for wild foragers, environmental landmarks can often act as “cues” predictive of a reward after some distance (or delay) (Chittka et al., 1995; Wystrach et al., 2019a, 2019b). Similarly, for many animals, cues reflecting the end of winter are predictive of an increased availability of food reward. It is then perhaps not surprising that even insects show evidence of such learning (Chittka et al., 1995; Dylla et al., 2013; Menzel, 2012; Toure et al., 2020; Wystrach et al., 2019a). I will first discuss the common mathematical formulation for representing state space in this task, before discussing implicit assumptions and their problematic implications.

Markov Chains

The mathematical concept of Markov chains is the building block for state space representations in RL. Briefly, a Markov chain is formed by a set of states, S = {1, 2, …, n}. An implicit assumption is that all the relevant states in the world have been specified in S. The process is assumed to start from one state and successively moves to another state (possibly itself) with a probability p_ij (where i and j are indices for the starting and ending states and can be equal). Each move is called a step. Each step results in a transition, which could be a self-transition to the same state. Crucially, the “transition probabilities” from a given state do not depend on the history of states. If we index the step number (a measure of time) by a subscript t, this means that the conditional probability p(s_t|s_t-1, s_t-2, …, s₁)=p(s_t|s_t-1). This absence of history dependence is known as the Markov property and allows some convenient mathematical representations.

The state space in RL is typically such a Markov chain. In more realistic RL formulations, the animal can also take a set of actions A={a₁, …,a_m} that transitions the agent from one state to another with a conditional probability of p(s_j | s_i, a_k). These transition probabilities can collectively be represented by a transition matrix P. The state space for an RL agent is fully described by S, A and P. This more general state space that includes an ability of agents to interact with its states using actions is the Markov Decision Process used in RL.

For simplicity, I will only consider the example illustrative task discussed above, in which a reward follows a cue after a delay. Hence, I will omit considerations of actions and the dependence of P on actions. In this task, the states can be minimally specified as the cue state and the reward state. Representing these stimuli as states allows an animal to store the sensory properties of these states in memory. For instance, the animal could learn that an auditory cue has a specific set of sensory attributes such as frequency profile, loudness, duration etc. Similarly, the sensory properties of a type of reward can be represented as a reward state. These various attributes can be stored as part of the memory of that state. Additionally, it is assumed that animals learn a representation of a scalar value for reward. In RL, the reward values are typically denoted by R(s, a), a scalar value associated with each state-action pair. For our purpose, I will denote the reward function by R(s). For the cue and reward state formalism that I adopt, R(cue)=0 and R(reward)=reward value. Thus, S, P, and R completely describe the cue-reward task of interest.

Dealing with time in Markov chains

The biggest problem with the above state space model is that there is no representation of time. The task of interest contains a delay between the cue and reward, and a delay from the reward to the next presentation of the cue (typically called the intertrial interval or ITI). However, there is no representation of these delays in the above Markov chain.

Neuroscience-related RL models solve this problem using the idea of “microstates” (Fig 2). The simplest such model assumes that the delay from cue to reward is represented by a series of states of equal duration (example 1 in Fig 2). This is known as the complete serial compound model of the state space (Moore et al., 1998; Schultz et al., 1997; Sutton and Barto, 1990). Here, the set of states is S={cue, delay¹, delay², … ,delayⁿ, reward}. This representation (with scalar reward values associated with each state) was used in early work to model temporal difference learning in tasks such as the example considered here (Schultz et al., 1997). An immediate problem with this model is that it does not represent the ITI, an interval that has been shown repeatedly to affect conditioning (Gibbon and Balsam, 1981; Holland, 2000; Kalmbach et al., 2019; Lattal, 1999). The ITI is almost always a random variable with a specified probability distribution. Since Markov chains assume that all the states must be specified, there is no obvious way to break up the ITI into a fixed set of equal duration states obeying the Markov property, unless it is exponentially distributed (K Namboodiri et al., 2021). This problem is usually avoided by only modeling the “trial period”, i.e., the delay between cue and reward. However, this is evidently an incomplete representation of the task, the stated goal of a state space. In fact, the moment at which a reward appears in the inter-cue interval can determine whether the observed conditioning to the cue is excitatory or inhibitory (Kaplan, 1984). Thus, modeling only the trial period is evidently insufficient. Nevertheless, this model has proven to be quite successful at explaining numerous aspects of conditioning and thus, has been referred to as a “useful fiction” (Ludvig et al., 2012; Sutton and Barto, 1998).

Fig 2.

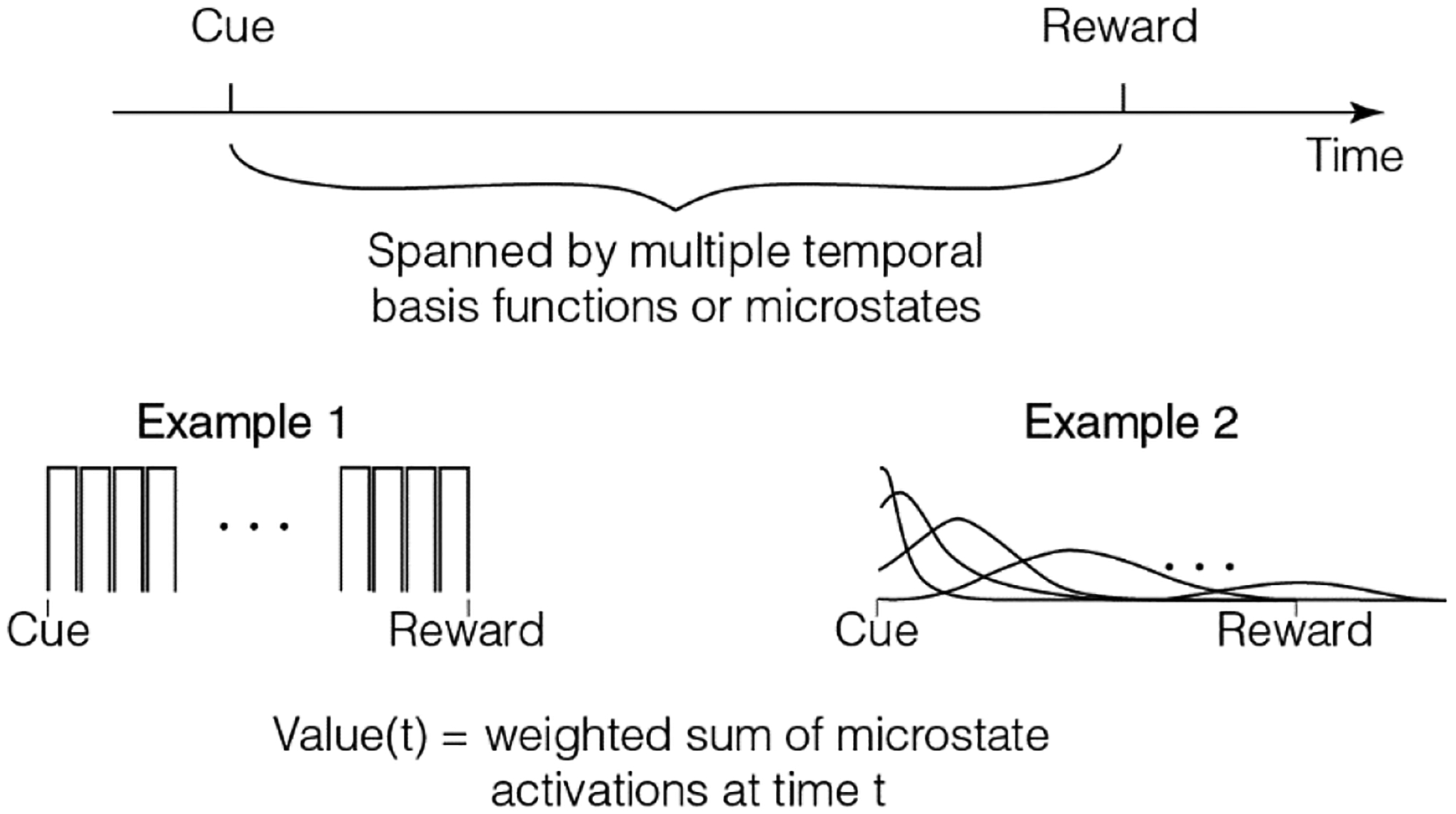
Common models for dealing with delays between cue and reward assume that such delays are spanned by multiple microstates. Two examples are shown here (see text). As can be seen, these formulations assume that the delay periods themselves are represented by many states to which an RL algorithm can attach value.

An extension of this model is to treat the states in the delay not as fixed duration states, but as a set of basis functions (also known as microstates or microstimuli) (Ludvig et al., 2008, 2012) (example 2 in Fig 2). A convenient idea is that the delay after a cue is spanned by a consecutive set of Gaussian states (Ludvig et al., 2008, 2012). In this view, each subsequent state has progressively smaller amplitude and larger width (to approximate scalar timing). This model of state space has benefits over the complete serial compound, as it allows efficient generalization and flexibility due to the non-zero value of many microstates at any given moment (Gershman et al., 2014; Ludvig et al., 2008, 2012; Petter et al., 2018). There is also some evidence for microstate-like activity patterns in brain regions such as the striatum (Mello et al., 2015), hippocampus (MacDonald et al., 2011; Pastalkova et al., 2008; Salz et al., 2016), and the prefrontal cortex (Tiganj et al., 2017). Remarkably, these neural representations can flexibly scale when the delays are altered (MacDonald et al., 2011; Mello et al., 2015). Thus, this microstate model is more consistent with neural data and is functionally advantageous over the complete serial compound. There are many variants of this general idea of a series of microstates (i.e. sequential set of delay states) following a cue (e.g., Brandon et al., 2003; Desmond and Moore, 1988; Grossberg and Schmajuk, 1989; Machado, 1997; Mondragón et al., 2014; Vogel et al., 2003; Wagner, 1981). I will not review these in detail here.

Implicit assumptions

The fundamental premise of the above models is that the delay between different environmental stimuli is a sequence of states in an animal’s state space. By breaking the flow of time into such sequences of states, these models make some implicit assumptions. These are often not immediately obvious. I will list some here.

1. Every cue has its own associated set of microstates: the idea of microstates works only if separate cues have separate sets of microstates. Thus, if the animal is learning that cue1 predicts reward1 after delay1 and cue2 predicts reward2 after delay2, the set of microstates during delay1 must be different from the set of microstates during delay2. If not, value learning will be mixed up between the two cues and cannot appropriately assign credit.

2. The microstates are specified before value learning: this may be the most important assumption. The entire idea of RL (with value updates to satisfy the Bellman equation) works only if the state space is specified. Thus, before value learning can occur, the set of sequential microstates following a cue must already exist. I will discuss the problems with this assumption in more detail in the next section.

3. Number and form of microstates are free parameters: another major assumption is that the number and form (e.g., are the basis functions Gaussian?) of microstates are treatable as free parameters for model-fitting. While the lack of principles for the formation of microstates is an obvious problem, this assumption is especially problematic as conditioning in the laboratory can occur over delays of milliseconds or even twenty-four hours (Etscorn and Stephens, 1973; Hinderliter et al., 2012; Kehoe and Macrae, 2002). Presumably, the resolution of microstates evoked over delays of milliseconds is very different from those evoked over hours. However, how does the brain know which microstates to trigger on the first experience of the cue? It is unclear what, if any, principles govern the formation of microstates in the brains of real animals over spans of five orders of magnitude.

4. The microstates during the cue to reward delay are fundamentally different from the microstates during the ITI: In the microstate framework, different delay periods that contain no external stimuli must be treated differently. Thus, the set of microstates during the cue to reward delay must be different from the set of microstates from the reward to cue delay. An explicit treatment of this formulation is found in the SOP model (Wagner, 1981).

5. Learning occurs in trials: another implicit assumption is that value learning occurs progressively by accumulation across trials. It is this trial duration that is assumed to be split into microstates. However, experiments such as the truly random control (Rescorla, 1967, 1968) throw the validity of this assumption into question. In this experiment, the rate of rewards is programmed to be the same during the presence or absence of the cue. Worse, because the events are Poisson processes, they are equally likely to occur at any moment in time. In this case, it is unclear what, if anything, can be treated as a “trial” in the animal’s brain.

6. Microstates of a cue must be reproducible across repeated presentations: for learning to occur, if cue1 evokes a set of microstates on one presentation, the same set of microstates must be evoked on the next presentation, to ascribe value to the “correct” microstate.

In the next section, I take a deeper dive into these assumptions and show that the apparent simplicity of the microstate model belies a gargantuan complexity of representation imputed in animal brains. I am by no means the first to discuss some of the problematic implications of these assumptions (Gallistel et al., 2014, 2019; Hallam et al., 1992; Hammond and Paynter Jr, 1983; Luzardo et al., 2017). Nevertheless, the following section focuses on a particularly problematic aspect of these assumptions that has not received as much discussion in the literature.

How bad is the problem really?

The problem is brought into sharp relief when considering initial learning. Remember that the whole point of the formulation of a state space is to explain reward prediction learning. Thus, I will now critically examine the implications of these assumptions for initial learning.

Imagine an animal that is first experiencing a cue that will be followed later by a reward. On this first experience, the animal knows nothing of the significance of this cue (other than its general “salience” or intensity). Indeed, cues are galore in the environments of animals. Nearly every sensory feature of the world could in principle be a cue predictive of a future reward. For instance, maybe a sound is predictive of a future reward. If an animal indeed learns to predict this reward, the above RL algorithms would require the assumption that the sound evokes microstates until the reward before first learning the relationship of the sound to reward. This is the whole point of RL: it is a model of learning after all.

What does this imply? This implies that any cue that could in principle be predictive of reward must evoke microstates during every presentation. Every sensory stimulus could in principle be such a cue. Hence, for the microstate model to work, animal brains must produce microstates for every sensory stimulus in the experience of the animal. Worse, if cue1 was experienced on two separate days, the set of microstates that were evoked by cue1 should be the same. Thus, the brain must store in memory all the microstates for the nearly infinite number of sensory stimuli, and they must all be discriminable and reliably reproducible on repeated presentations of the stimuli.

The problem is actually significantly worse. This is because the animal does not know at what delay a reward will follow a cue on the first experience of the cue. Indeed, these delays can span five orders of magnitude (Etscorn and Stephens, 1973; Hinderliter et al., 2012; Kehoe and Macrae, 2002). As mentioned above, the data that are often taken as evidence of the existence of neural microstates show that these time representations remap when the delay changes (MacDonald et al., 2011; Mello et al., 2015). How then does the brain know what exact microstates to trigger on the first presentation of the cue, much before the delay to reward is known or learned? Worse still, the brain also must trigger microstates during the delay from the reward to the next cue, for every reward and cue, to learn the distribution of intertrial intervals. How does the brain produce distinct microstates during the ITI and delay to reward on the first presentation of the cue and reward? How does the brain know that two delay periods during which no external sensory stimuli exist are fundamentally different before learning that there is a relationship between cue and reward? How also does the brain know that delays between different cue-reward-cue triplets are different?

Finally, for simplicity, we have illustrated our main point using the simplest form of RL—one in which the selection of actions to maximize future rewards is not considered. The consideration of time delays becomes even more important for action selection. For instance, real animals often perform reward-related actions after a delay from the corresponding reward-related cues. Indeed, rewards are often predicted by (cue, action) pairs only when there is a specific temporal relation between these events (Miyazaki et al., 2020; Namboodiri et al., 2015; Narayanan and Laubach, 2009). Defining microstates to span these delays worsens the combinatorial explosion of the state space, as these microstates need to then depend on both external cues and internal actions. Thus, the issues discussed here become even more vexing in this setting.

It is hopefully clear from this examination that the assumption of microstates, while seemingly simple, introduces an untenable solution for an animal brain. Solving these issues is crucial as these issues riddle application of RL to animal learning in even one of the simplest use cases considered here.

Do animals make such assumptions?

We cannot ask animals what assumptions they make during learning. Even in the case of humans where asking is possible, it is unclear if we have conscious access to the neural representations that our brains use for learning. Thus, in some sense, it is impossible to know the exact assumptions used by real animals. Hence, the best approach is likely to make the most parsimonious assumptions that solve the real-world problems faced by animals, in which the timescales of associative relationships are not known a priori.

To this end, the answer to a simple question can be illuminative. Is behavioral learning of real animals timescale-invariant or timescale-dependent? The microstate models are inherently dependent on a timescale since the shape and width of the microstates need to be specified prior to learning. In contrast, there is now considerable evidence accumulated over more than fifty years that behavioral learning is largely timescale-invariant. For instance, Fig 3 reproduces a meta-analysis of work in many labs showing that increasing the delay between a cue and outcome does not in fact increase the number of trials until acquisition if the outcome-to-outcome delays are correspondingly scaled by changing the ITI (Gallistel and Gibbon, 2000; Gibbon and Balsam, 1981). Another paper has shown that deleting 7 out of 8 trials does not reduce learning if the temporal spacing between the remaining trials is left unaltered (Gottlieb, 2008). In other words, decreasing the number of trials by a factor of 8 while increasing the ratio between outcome-outcome and cue-outcome intervals by 8 produces the same amount of conditioning. The timescale-invariance observed in these experiments makes little sense if animals make timescale-dependent assumptions about the associative structure of their environment.

Fig 3.

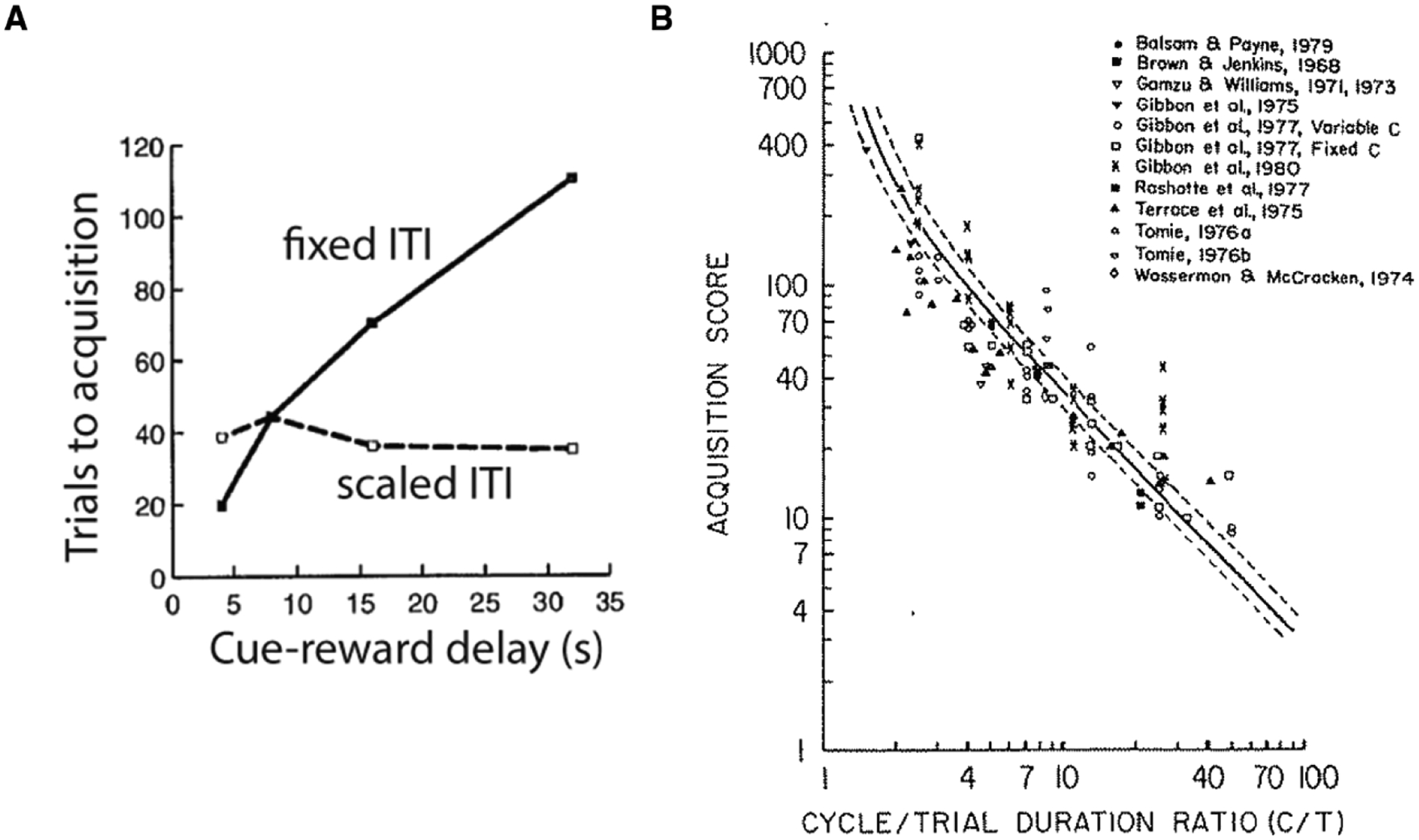
Timescale-invariance of behavioral learning. A. Reproduced from Gallistel and Gibbon, 2000. When the cue-reward delay is increased, the number of trials to acquisition increases only when the ITI is fixed. When the ITI is correspondingly scaled, the number of trials to acquisition remains largely constant. B. Reproduced from a meta-analysis published in Balsam et al. 1981. When the ratio between outcome-outcome delay (called cycle duration) and cue-outcome duration (called trial duration) is changed, the number of trials to acquisition varies in a predictable manner.

Why is the ITI so important in conditioning? Here, I will present a simple intuition for this effect. Imagine that an animal is learning the association between a cue and a reward that follows 10 s later. Now imagine two extreme values of the ITI: 100 s and 1 s. When the ITI is 100 s, the structure of the world is indeed that the cue predicts the reward, as intended by the experimenter. However, when the ITI is 1 s, the delay between a reward and the next cue is much shorter than the delay between a cue and the next reward. In this case, the reward predicts the cue rather than the other way around. Thus, what predicts what depends fundamentally on both the trial and intertrial intervals in an experiment. Once it is clear that the causal structure of a cue-reward association depends on the ITI, it is also relatively straightforward to see that this is likely timescale-invariant. For instance, say we agree that when a cue-reward delay is 10 s, a “reasonably” long ITI to interpret the experiment as cue predicting reward is 100 s. What would such a reasonably long ITI be when the cue-reward delay is 20 s instead of 10 s? A simple answer is that the corresponding ITI must be increased to 200 s for the structure to remain consistent. This is because when the ITI is scaled to 200 s when the cue-reward delay is increased to 20 s, the corresponding timeline can be perfectly superimposed after scaling on the timeline with 10 s cue-reward delay and 100 s ITI. Thus, what matters to the interpretation of the causal structure is not the absolute value of the cue-outcome delay, but the ratio between that delay and the outcome-outcome delay. This informal intuitive argument rationalizes the observations of timescale-invariance discussed in the previous paragraph.

Similarly, the notion of what constitutes a trial also depends on the ITI. For instance, in the previous examples, when the ITI is 1 s and the cue-reward delay is 10 s, the “experiment” can be thought of as backward conditioning (i.e., reward predicts cue), in which case, the “trial” is demarcated by the reward-to-cue delay instead of the cue-to-reward delay. Indeed, though Rescorla’s work was one of the earliest popularizers of the idea of a trial, he knew that the notion of a trial is unlikely to apply to his subjects, as has been discussed in detail (Gallistel, 2021).

A discussion of alternative frameworks and current limitations

At a superficial level, a major issue is that the assumption of microstates is not a realistic representation of the passage of time for real animals. This issue has been pointed out multiple times (Elman, 1990; Gershman et al., 2014; Ludvig et al., 2008) and can be addressed using more realistic models of timekeeping in the brain (e.g., Buonomano and Merzenich, 1995; Mauk and Buonomano, 2004; Namboodiri et al., 2016; Petter et al., 2018; Simen et al., 2011). However, the more important issue I raise here is regarding the assumptions needed for learning, when timescales are not specified a priori. In this light, it is useful to consider a recent highly successful model for conditioning that combines a Rescorla-Wagner rule applied to a drift diffusion model of timing (Luzardo et al., 2017). In this model, cues are postulated to initiate an accumulating timer with a fixed threshold and an adaptable slope. A learning rule adapts the slope based on the knowledge of when the reward happens, thereby adapting the slope of the accumulator to eventually time the cue-reward delay appropriately. This model explains an impressive array of phenomena. It also has a major advantage over the microstate models as it does not postulate an arbitrary number of microstates that span time delays. Nevertheless, it too suffers from similar issues as above when applied to initial learning. For it to work for initial learning, there must be a timer for every cue that could in principle be predictive of reward. As we laid out above, there are almost an infinite number of such cues, each with an infinite set of possible delays to reward. Further, when a timer is initiated at cue onset on the first time that the cue was experienced, how does the timer know that it is timing a specific upcoming reward? What if the cue does predict reward at a fixed delay but there are other intermittent cues in this delay? What if this cue was only predictive of another cue and not a reward or was not predictive of anything in particular at all? What if the reward predicted by the cue is not the immediately following reward? How does the timer get feedback about exactly which interval it is supposed to time? These issues are solvable only if the animal knows that it is timing the interval between a specific cue state and a reward state, or in other words, after learning that a specific cue and a specific reward may be related. Thus, this approach does not prescribe how an animal can initially learn the association between a cue and reward.

Another formalism within the general framework of RL is a semi-Markov/Markov renewal process model that explicitly learns the distribution of time intervals between consecutive state transitions (Bradtke and Duff, 1994; Daw et al., 2006; Namboodiri, 2021). Though very similar, there is one difference between a semi-Markov and Markov renewal process-based state space. In a simple cue-reward task, a semi-Markov state space treats the state of the world as the cue state (or the interstimulus interval state) during the delay between cue and reward (Bradtke and Duff, 1994; Daw et al., 2006). As the value of states is tied to the currently active state in a semi-Markov model, the value is stationary for the duration of this entire state. However, in a Markov renewal process, the value function can be defined in continuous time, as the states and transition times are treated separately (Namboodiri, 2021). While these models avoid any issues with breaking up the flow of time into states, they nevertheless suffer from some limitations. The key limitation is that by only learning the intervals between consecutive events in the world, such learning is very sensitive to the presence of distractors. Though existing evidence supports the prediction that distractor states impede trace conditioning (Carter et al., 2003; Clark et al., 2002; Han et al., 2003; Manns et al., 2000), it is unclear how such learning can adapt to the real world where the delay between most cues and their predicted reward is filled with other sensory stimuli. How could an animal learn to treat these intermittent sensory stimuli as distractors and not themselves predictive of subsequent outcomes? If multiple Markov chains occur simultaneously in a mixture distribution, the above learning algorithms will not be able to demix them without additional mechanisms. Hence, these algorithms still have major limitations as currently prescribed.

Another possible solution to the problem is to move completely away from RL and propose that other quantities control learning in tasks such as the one considered here. A set of models that propose that animals learn contingency (defined as normalized gain in available information) between the timing of reward predictors and rewards belongs to this class (Balsam et al., 2010; Gallistel et al., 2014, 2019; Ward et al., 2012). These models are successful at explaining numerous aspects of the learning of conditioned responses in relation to the various time intervals. Further, they can work for initial learning in a timescale invariant fashion. This model solves essentially all concerns listed above regarding initial learning by proposing that animals store their timeline of experience in memory and operate on this temporal map to uncover associations. However, whether a complicated computation such as a timescale-invariant mutual information can be calculated in an online manner by a neural network needs to be demonstrated both theoretically and experimentally. Indeed, it has been suggested that such computations can only be performed offline by intracellular molecular machinery (Gallistel, 2017) (see (Akhlaghpour, 2022; Gallistel et al., 2020; Thornquist et al., 2020) for example models of such computations). Further, this theory makes the strong prediction that cue-outcome associations with any arbitrarily long interceding delay can be learned provided the outcome-to-outcome delays are sufficiently long. This strong claim remains to be quantitatively tested in a manner that separates learning from the magnitude of performance. Currently, some evidence suggests that there may be some limitations to scale invariance. For instance, trace eyeblink conditioning has not been successfully demonstrated beyond a few seconds of trace interval (unclear if long trace interval experiments have been attempted with correspondingly long outcome-outcome delays), and recent data suggest that cue-reward associations with a 60s delay are not well-learned even when the inter-reward interval is more than 4000 s (Thrailkill et al., 2020) (though this study did show measurable behavioral learning and was not focused on analyzing the onset of acquisition). Overall, the strong prediction of this information theoretic model remains to be fully tested. Lastly, this model has not as yet been extended to sequences of stimuli that predict reward, and does not provide a clear explanation for the prediction error signals observed in midbrain dopamine neurons, which are known to drive learning in animals (Cohen et al., 2012; Kim et al., 2020; Mohebi et al., 2019; Schultz, 2016; Schultz et al., 1997).

Lastly, a recent theoretical framework proposes a solution to learn timescale-invariant predictions of the future using timescale-invariant representations of the past (Goh et al., 2021). This model uses a Laplace transform to store recent history in a timeline of events (Shankar and Howard, 2012) and uses this timeline to make a projection into the future from the present moment. This model effectively implements a neural network instantiation of the temporal map that was posited as a necessary requirement for learning (Balsam and Gallistel, 2009). Just like the contingency of timing model, this learning model also avoids the concerns raised above regarding initial learning. Since this model has been directly extended into a neural network model, it is biologically plausible based on current neuroscientific understanding. It also shows early promise in explaining dopamine dynamics (Goh et al., 2021). Despite these many appeals, it remains to be tested whether it can quantitatively fit behavioral learning and neural signals for learning such as dopamine release in the striatum.

Conclusions

Here, I explicitly list the assumptions made by well-known RL models that account for the passage of time. I show that the apparent superficial simplicity of these models belies the extraordinary complexity required to execute them. These problems are often not recognized, as researchers define a convenient state space for each experiment using free parameters. These assumptions are especially problematic when applied to initial learning, a stated goal of reinforcement learning. The fundamental issue is that breaking up the flow of time into discrete states is a problematic way to learn associations across temporal delays. This is because it is unclear prior to initial learning which intervals are worth timing. Further, learning temporal relationships only between consecutive events raises concerns as to how initial learning would be possible in the real world where many other sensory stimuli span such delays. While the solutions remain to be worked out, I hope that this perspective highlights the issues with current models. Until we acknowledge the problems, there will not be any solutions.