Highlights
-
•
High intensity ultrasound propagation generates high order harmonics.
-
•
NCG expansion and compression spread regularly and symmetrically beneath sonotrode.
-
•
Gaseous cavitation distributes asymmetrically beneath sonotrode while symmetrically far away.
-
•
Cavitation zones grow and coalescence beneath sonotrode and break away periodically.
Keywords: Acoustic cavitation, Fast Fourier Transfer, Non-linear acoustic, Acoustic spectrum
Abstract
In a sono-reactor, complex ultrasound pressure wave signal can be detected, containing multiple information related to acoustic cavitation. In this present study, acoustic cavitation in a cylinder is investigated numerically. Via Fast Fourier Transfer (FFT), the sound pressure signals from sonotrode emitting surface are separated into harmonics, sub/ultra-harmonics and cavitation white noise: (1) the appearance of harmonics proved the non-linear propagation of ultrasound, (2) at the vibratory amplitude from 5∼20μm, only harmonics exists in the frequency spectra, corresponding to expansion and compression of non-condensable gas (NCG), (3) at the vibratory amplitude range of 30∼50μm, the occurrence of sub/ultra-harmonics demonstrated gaseous cavitation occurred, and (4) at the vibratory amplitude higher than 55μm, cavitation white noise arose, pointing out the initiation of vaporous cavitation. Based on the combination of frequency spectra and cavitation zones distribution, the acoustic cavitation state in water liquid is determined.
Nomenclature
Latin letters
- A
vibratory amplitude [μm]
- C
constant
- c
sound speed [m/s]
- f
vibratory frequency [kHz]
- g
gravitational acceleration [m/s2]
- k
turbulence kinetic energy [m2/s2]
- Psound
sound power in fluid [W]
- p
gauge pressure [Pa]
- psat
saturated vapor pressure [Pa]
- psound
sound pressure [Pa]
- S
area of emitting surface [m2]
- T
numerical computation time step [s]
- t
sampling time [s]
- v
flow velocity [m/s]
- vus
emitting surface vibrating speed [m/s]
Greek letters
- α
volume fraction
- λ
sound wave length [m]
- ξ
mass fraction
- ρ
density [kg/m3]
- σ
surface tension [N/m]
Subscript
- 0
fundamental frequency
- c
condensation
- e
evaporation
- g
non-condensable gas
- l
liquid phase
- m
mixture
- v
vapor phase
1. Introduction
Ultrasound is a kind of mechanical wave, when propagating in Newtonian material, it travels in the longitudinal wave form, causing fluid particles oscillate in the propagating direction of sound wave. The vibration of particles leads to the variation of fluid density in the spreading path with intervalic distribution of rarefaction and concentration phase. Because the velocity of sound in the fluid is dependent on the momentary value of density of local fluid media, the finite volume of fluid in the positive phase of sound will oscillate quicker than those located in the negative phase. Hence, when the sound energy is high enough to transmit high amplitude pressure wave into fluid, the displacement of finite volume of fluid in the concentration phase is larger than that in the rarefaction phase [1]. This results in the non-zero displacement of particles in an oscillation period of ultrasound, which is the fundamental reason for the various frequency response except excitation frequency in the spectrum. The non-zero phenomenon introduces the investigation of linear sound propagation into non-linear acoustic problem.
Research of non-linearity during ultrasound propagation can be traced back to Nonlinear Acoustic of Hamilton and Blacks [2]. The various factors influence non-linearity finally settled by three most widely accepted equations developed by Burgers, Westervelt and the trio of Khokhlov, Zabolotskaya and Kuznetsov (KZK). The non-linearity is described by a non-linear parameter β, with its increase the fluid media is more likely to be influenced by non-linear effect. Research of Lighthill [3] evaluated the ultrasound power needed to generate non-linear phenomena is above 10-6W in liquid, which means most ultrasonic application in experiment or industry is in non-linear category. Hence the utilization of ultrasound is facing a straight forward question, how the ultrasound waves propagate and cavitation zones distribute with the increase of non-linearity caused by increasing ultrasound power.
Commonly, the working fluid imposed with ultrasound contains non-condensable gas (NCG) or gas cavities inside the defects of container surface. These gas nuclei act as the cores of cavitation bubbles, reducing the sound pressure amplitude to generate cavitation bubbles [4], [5]. Because of the existence of these gas nuclei, when the local fluid zones are covered by the rarefaction phase of ultrasound, expansion of NCG or gas cavities happens, leading to gaseous cavitation. According to the research of Briggs [6], a cylindrical crystal sound wave projector and a receiver are installed at both end of a cylinder chamber filled with impedance matching rubber and testing liquid. When testing undegassed kerosene, the open circuit voltage received is proportional to the voltage input in the projector before the occurrence of gaseous cavitation. The corresponding acoustic pressure is roughly atmospheric pressure, indicating the undegassed liquid is primarily held together by atmospheric pressure. While degassed kerosene can stand an acoustic pressure equals to the sum of cohesive pressure and the atmospheric pressure. Moreover, liquid has experienced cavitation will cavitate more easily than static liquid, and it requires some time to return to its quiet state. The experiment illustrated that the existence of cavitation nuclei will help to generate cavitation bubble. Lee et al. [7] investigated the gaseous cavitation under relatively low intensity of ultrasound through CO2 saturated water. In the rarefaction phase of ultrasound wave, dissolved CO2 becomes supersaturated, lowering the cavitation threshold, resulting in gaseous cavitation, and turbulence are induced by cavitation in fluid field.
With the increase of ultrasound intensity, the cavitation will transform into vaporous cavitation, where a series of expansion and subsequent violent collapse processes will happen. The mechanism of vaporous cavitation is different from gaseous cavitation, in the latter type, fluid media consist of homogenous mixture of NCG and liquid, hence the sound wave can propagate with slight attenuation and scattering. However, liquid vaporized and surrounded the sonotrode when vaporous cavitation occurs, this results in the sever attenuation and scattering of sound energy during propagation. Research of Briggs [6] also demonstrates that after vaporous cavitation occurred, the slope of received signal against input voltage bends off and raises slowly, meaning the cavitation bubble will attenuate and scatter the sound energy, blocking sound wave in propagation.
According to the foregoing demonstration, cavitation process has different type related to the ultrasound power level, which will affect the distribution and pattern of cavitation zones. Too weak ultrasound will not propagate far, and has no enough strength to induce vaporous cavitation. Proper intensity ultrasound can help in the cleaning process, synthetic chemistry and other resonate processing. Violent acoustic cavitation phenomenon produced by strong ultrasound will release radicals with the collapse of cavitation bubble, which is an excellent way in biotechnological applications and organic processing [8], [9], [10]. Hence the cavitation type should be treated and studied separately on the basis of utilization situation. And the experimental investigation approaches can roughly be divided into two categories, observation or signal processing. The observation ways are achieved through adding tracers or chemical additive into fluid, using high speed camera or CMOS camera to capture images respectively. Tiong et al. [11] uses Luminol solution to identify the distribution of cavitation activity zones. Bulliard-Sauret and Ferrouillat et al. [12], [13] studied the heat transfer enhancement induced by acoustic cavitation through particle image velocimetry (PIV) technology. The observation approach is very straightforward but established on the average effect or appearance of ultrasound. Therefore, the photos are usually based on a relatively larger time scale than the explosion time scale of cavitation bubble, the images are unable to identify the characteristics during transient cavitation.
In order to have a more elaborate analysis of ultrasound, and considering the ultrasound emitting source is excited by sinusoidal signal, cavitometer is fabricated to capture ultrasound pressure signal in fluid media. Treat the pressure signal with FFT, the cavitation information can be processed in the frequency domain, and extract some unique frequency response to characterize the cavitation type. The research of Frohly et al. [14] demonstrated that the frequency distribution of the oscillating signal from a ultrasonic radiated field contains harmonics and sub/ultra-harmonics of the excitation frequency, besides the complicated white noise. The harmonic is usually referred to the fundamental frequency f0 and its integer multiple frequencies, which are produced by the non-linear propagation of ultrasound wave in the medium. The sub-harmonics f0/n (n is integer) and the ultra-harmonics mf0/n (m≠n, m and n are integer) are believed to be caused by forced radial oscillation of bubbles that are resonant at the subharmonic frequencies [15], [16]. The investigation into white noise delivered that the cavitation bubbles explosion will release strong micro jet and shock waves, which are responsible to the complicated noise [17]. Based on the unique frequency response for different cavitation phenomena, Tzanakis et al. [18] uses cavitometer investigated the different frequency responses from transparent liquid (e.g. water, ethanol and glycerine) and opaque liquid (e.g. aluminium). Comparing the frequency spectra of transparent liquid with the spectrum of aluminium, the cavitation character of aluminium is determined to be similar to water. Hence the ultrasonic field in opaque liquid is considered equivalent to transparent liquids with similar frequency response. Except that, Yamamoto et al. [19] uses a different acoustic signal capture approach, which is capturing the Karman vortex street induced by ultrasound. This research also found identical feature between water and aluminium during ultrasonic waves propagation. The utilization of signal analysing approach can derive high resolution results and is capable of characterizing fluid cavitation feature.
Although utilizing signal processing approach to identify the unique frequency response occurred during cavitation is indeed a method with high resolution accuracy and convenience, but the signal capture process needs to introduce cavitometer or other pressure signal detection device, which will influence the structure of sonoreactor, interfere the propagation of ultrasound wave.
With the development of numerical simulation method and cavitation bubble dynamics, investigating ultrasound propagation process and acoustic phenomena through numerical method has attracted great attention. The numerical method is featured for observing the ultrasound propagation process, locating the distribution of cavitation zones and has great advantage in capturing pressure signal in the fluid field. With the combination of observation and signal analysing experimental approach, numerical method becomes a vital method in studying cavitation bubble behaviour and streaming. Tudela et al. has made a summary of these different approaches including linear based, non-linear based and direct transducer simulation method [20]. Initially, acoustic is studied based on the linear Helmholtz equation in frequency domain, which is a simplification of Navier-Stokes equation. With the development of fabrication and material, the sono-equipment can release higher sound energy, generating non-linear effect that attracted a group of researchers to develop a non-linear Helmholtz equation to deal with the non-linear propagation of ultrasound [21], [22]. The limitation of solving acoustic problem through Helmholtz equation is the single way of the interaction from the sound field to fluid field, the fluid field will not feed back to the sound field. Therefore, the both way coupling between sound field and fluid field should be solved directly via the N-S equation. By applying solid boundary vibration, ultrasound can be imposed to the fluid field, and generate non-linear effect. Rahimi et al. [23] using a realistic vibratory boundary condition to simulate the ultrasound propagation, investigated the acoustic streaming and acoustic cavitation phenomena. The mixing effect and velocity profile at the axis of sonotrode from the numerical simulation result is validated by PIV experiment data with good coincidence. The author has previously studied the heat transfer enhancement effect induced by ultrasound in an immersed coil heat exchanger by moving boundary, the pressure and vapor volume fraction distribution was compared with the experimental results, delivering good consistency [24].
Since the vibratory boundary condition is an appropriate and accurate approach to impose ultrasound, and transient numerical simulation has the advantage of acquiring the fluid flow field information i.e. pressure, velocity, vapor volume fraction, etc. Moreover, the propagation progress of sound wave can be observed directly. In this work, we applied the ultrasound with different intensity through varying the vibratory amplitude with an immersed sonotrode in a cylindrical vessel. The effects of ultrasound power on the intensity, pattern and distribution of acoustic cavitation are investigated. A detailed analysis of average pressure signal from the sonotrode emitting surface was conducted by observing the cavitation development and analysing the frequency spectra. The pressure signal is interpreted by FFT approach to identify the characteristic frequencies appear during different stages of cavitation. And the acoustic cavitation type is categorized by the distribution of cavitation zones and signal response. The results of this study may be useful for the selection of ultrasound parameter in a sonication process.
2. Numerical methods description
2.1. Conservation equations
The existence of cavitation nuclei is concerned as dissolved NCG in liquid. The working fluid consists of NCG, water liquid and water vapor (when vaporous cavitation happens), hence the continuity conservation should be considered in the mixture form as follow [25], [26]:
Mixture:
| (1) |
Liquid phase:
| (2) |
Vapor phase:
| (3) |
where, is the mass-average velocity and ρ is the density, αk is the volume fraction for phase k and k represents liquid, vapor or NCG. In the transport equation, the existence of NCG is evaluated by mass fraction which is a constant (1.5×10-5) in this work. The density of NCG is described as:
| (4) |
where W represents molecular weight of NCG (represented by air, 28g/mol). And the volume fraction of NCG is calculated as:
| (5) |
In this cavitation model, in order to consider the bubble radius oscillation during ambient pressure fluctuation, a physical correlation is built through the Rayleigh-Plesset (RP) equation as follow:
| (6) |
where RB is the bubble radius, psat is the saturation vapor pressure. To relate the vapor volume fraction α with bubble radius RB and bubble number density “n”, the following equation is derived as:
| (7) |
By combining Eqs. (1)∼(3) and Eqs. (6)∼(7), the phase change rate R can be derived without the second-order derivation term of bubble radius, the viscous damping and surface tension terms in Eq. (6), the final form of phase change rates Re and Rc are described as follow [27], [28], [29]:
| (8) |
The phase change rates Re and Rc respectively represent the mass transfer between vapor and liquid phases in the evaporation or condensation process. When the local pressure is lower than the saturated vapor pressure, water vapor is generated. These obtained mass source term derived from RP equation takes effects of shock waves and jets into account inherently. In the equation, Ce and Cc are constants of 0.02 and 0.01 respectively, σ is the surface tension, ξg and ξv are mass fraction of NCG and vapor respectively. represents the saturated vapor pressure corrected by simply raising the phase-change threshold with a local value of the turbulent pressure fulctuation which is described in Eq. (9):
| (9) |
Besides the above simplifications, the existence of NCG only effects density, velocity and pressure distribution, but not effect phase-change threshold due to lack of general correlation. The momentum equation for the mixture can be obtained by summing the individual momentum equations for all phases. It can be expressed as [30]:
| (10) |
where, is a body force, and μm is sum of the viscosity of the mixture. The conservation of energy for the mixture takes the following form [23]:
| (11) |
| (12) |
The first term on the right-hand side of Eq. (11) represents energy transfer due to the conduction, where Kt is the turbulent thermal conductivity. The non-linear propagation of ultrasound will generate turbulent circulation flow called acoustic streaming, the turbulence flow characteristics is simulated by the Standard k-ε turbulent model [31], [32] as follow:
| (13) |
| (14) |
2.2. Transient ultrasound simulation
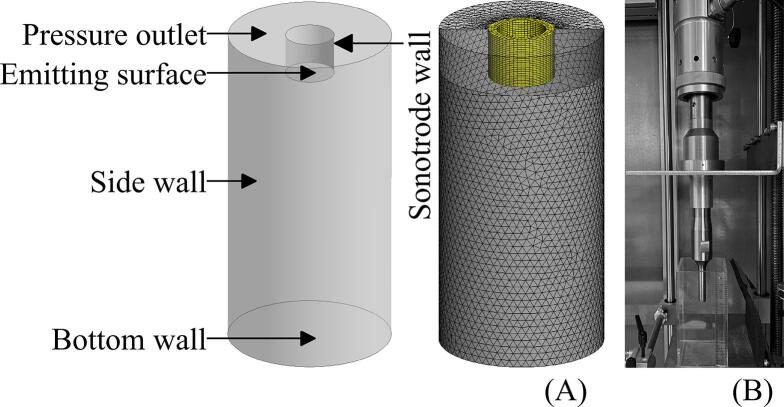
Fig. 1(A) exhibits the numerical simulation geometry in this research, which is consist of a sonotrode (as shown in Fig. 1(B)) and a cylinder. This 80mm high cylinder is 40mm in diameter and filled with water at 300K containing non-condensable gas of a mass fraction of 1.5×10-5. The emitting surface of sonotrode is 12mm in diameter and immersed 10mm under water surface. The water surface at the top of the cylinder vessel is defined as pressure outlet (gauge pressure = 0Pa); the other surfaces are applied with no-slip wall and adiabatic conditions. For the emitting surface treated as a rigid body, a detailed displacement is specified according to the excitation amplitude and frequency by equation (15):
| (15) |
where, Amax is the vibratory amplitude at maximum displacement, and vus is the vibratory velocity of sonotrode tip. The sonotrode wall is a deforming side wall elongating or shortening according to the position of emitting surface.
Fig. 1.
(A) Numerical simulation geometry and grid, (B) Sonotrode type ultrasonic device.
The computational grid is generated following three constrain conditions: 1. the largest mesh size should be small enough to resolve the sound wave length λ; 2. the high-order harmonic frequency should be resolved. To accomplish the above requirements, the mesh size Δxmax ought to be smaller than λ/20. And 3. another basic requirement is accurate to resolve the fluid field. According to the conditions above, the mesh size is constrained under 2mm in the global size (grey zone) and 1mm in the near field (yellow zone).
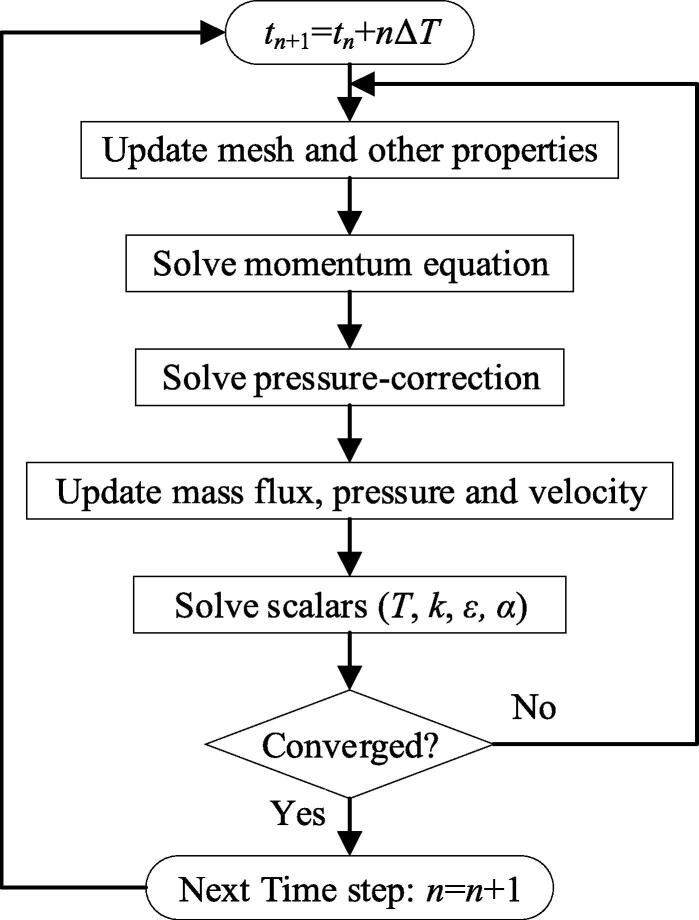
In numerical solving progress, the motion of sonotrode tip is realized by updating computation nodes at the beginning of every time step. Then, the solvation of partial differential equation for scalars is initiated with segregated solver as shown in Fig. 2. The momentum equation is solved to obtain the velocity field, where in the equation, velocity vector term is modified as -, where represents the moving velocity of nodes. In this way, the motion of sonotrode tip is implanted to generated ultrasound waves. Then using the new acquired velocity field, the pressure and velocity coupling is solved via SIMPLE algorithm. Finally, the energy equation, turbulent equation and vapor volume fraction are solved. The transient simulation is performed with a time step able to resolve the sinusoidal curve, so the vibration of sonotrode emitting surface can release actual alternating sound pressure wave. Hence, the simulation time step T is 1.25×10-6s, which corresponding to 1/40 of the excitation frequency. The numerical simulation is performed in HPC Platform of Xi’an Jiaotong University with Intel® Xeon® Processors 6258R (2.7GHz, 2×28 core and distributed shared memory of 192GB for each node). The system is running on CentOS Linux 7.7.1908, with the above settings, it takes about 7 hours to calculate 0.01s using 56 cores.
Fig. 2.
Solution procedure of fluid flow imposed with ultrasound.
3. Numerical method verification
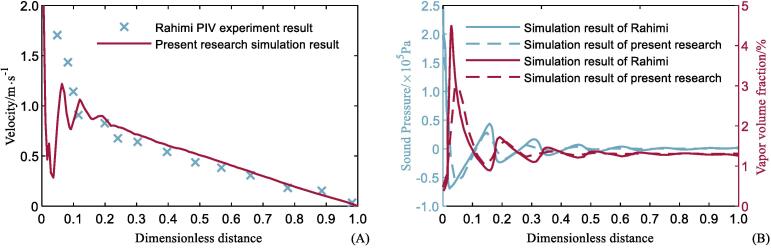
The computational geometry used in this research is identical with the geometry of Ref. [23] in vessel and sonotrode diameter, and sonotrode immersed depth, but twice deeper in vessel height. Comparing the numerical simulation results in this research with the PIV experimental results from Ref. [23] as shown in Fig. 3(A), the velocity profile against dimensionless distance from emitting surface to the bottom wall of cylinder has good agreement. Also as exhibited in Fig. 3(B), at the same depth of axis position, the pressure and vapor volume fraction distribution of the simulation results in this research is approximate to the simulation results from Ref. [23] in variation trend and magnitude. Hence the simulation approach and results in this research is validated with good accuracy in the simulation of ultrasound propagation and acoustic effects.
Fig. 3.
(A) Velocity distribution at the axis of sonotrode under emitting surface, (B) Pressure and vapor volume fraction distribution at the axis of sonotrode under emitting surface.
4. Numerical simulation results analysis
4.1. Development of cavitation zones
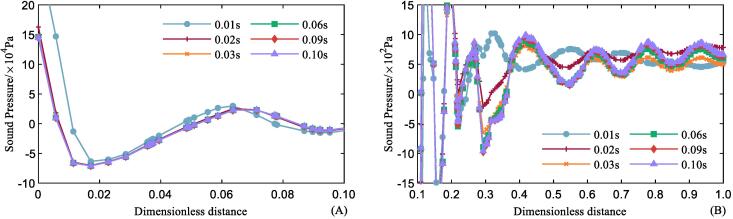
The pressure distribution along the axis of sonotrode is exhibited in Fig. 4, during the ultrasound radiation, sound waves propagated through the fluid field. Fig. 4 (A) and (B) each corresponds to the near and far field of ultrasonic radiation field respectively. In the near field, pressure fluctuation reaches a relatively steady state since 0.02s, while in the far field, it takes about 0.06s to become stable. Moreover, the powerful ultrasound wave pressure dropped about one order from 0∼5mm beneath the sonotrode, and kept almost constant oscillating amplitude to the bottom of the cylinder wall. Based on the above description, the analysis of sound pressure signal begins from 0.1s to 0.2s.
Fig. 4.
Simulation results of sound pressure distribution along the axis beneath sonotrode emitting surface at the vibratory amplitude of 30 μm, (A) near field and (B) far field.
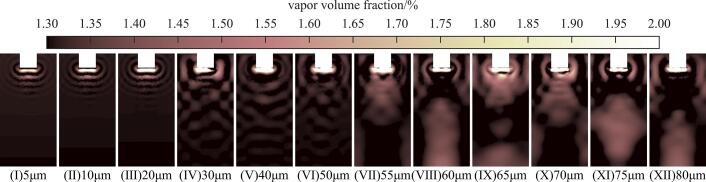
In Fig. 5 (Ⅰ)∼(XII) the cavitation zone distribution generated by each vibratory amplitude studied in this research is exhibited. From Fig. 5 (Ⅰ)∼(III) the expansion zones and compression zones regularly spreaded at interval from the emitting surface to the bottom of cylinder. And with the increase of sound power, the expansion zone in front of emitting surface grows and coalescences into larger bubbles. From Fig. 5 (Ⅳ)∼(Ⅵ), with the vibratory amplitude increasing, the non-linear propagation of ultrasound wave became more obvious, but in this progress only gaseous cavitation has happened, the cavitation zones do not have large vapor volume fraction value. The distribution of cavitation zones and compression zones become non-symmetric, the two zones pass through each other from emitting surface downward. From Fig. 5 (VII)∼(XII), water vapor is generated and the cavitation intensity continues increase, the color becomes brighter and covers larger area gradually. In this vaporous cavitation, large cavitation zones occupy the area in front of emitting surface, acting as a shield absorbs the sound energy from sonotrode. The shielding effect of cavitation bubble severely damping the sound wave energy, blocking it from propagating to the bottom of the cylinder. It is clear from Fig. 5 that when the cavitation is limited in the intensity of expansion and compression of NCG, the cavitation zones will not spread to the bottom of cylinder, forming regular stationary field in front of emitting surface. While in the region of gaseous cavitation, cavitation zones propagate far away from emitting surface, forming non-regular stationary field. Eventually, with vaporous cavitation begins, sound energy delivery is blocked, forming concentrated cavitation zone in front of emitting surface.
Fig. 5.
Simulation results of cavitation zone distribution in ultrasonic field
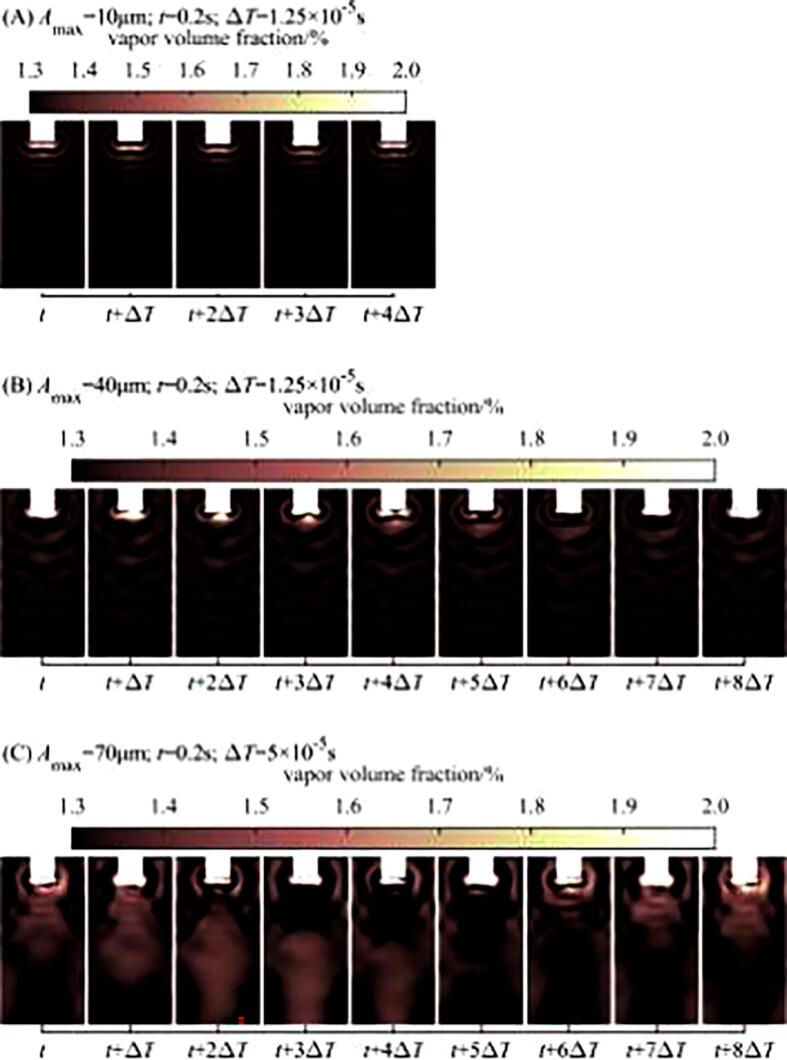
The propagation of cavitation zone at NCG expansion state is represented by the vibratory amplitude of 10μm, in Fig. 6(A) displays the progress of an ultrasound oscillation period. The cavitation zone generated and separated in front of emitting surface at the frequency of ultrasound excitation source, then moved toward the bottom of cylinder under the push of sound wave. The cavitation zone gradually faded away with the attenuation of sound energy. Fig. 6(B) exhibits the propagation progress of cavitation zones at the frequency of f/2 under the vibratory amplitude of 40μm. With the sound energy evidentally augmented, the cavitation zones are maintained to the bottom of the cylinder. Although this cavitation is in a non-linear state, it can be found deep down in the cylinder, the cavitation zones still distributed in a symmetrical pattern, which demonstrated the sound energy far away from emitting surface only able to maintain expansion and compression of NCG. The vaporous cavitation with phase transition is represented by the case at the vibratory amplitude of 70μm. With the increase of vibratory amplitude, the negative phase pressure covers larger area. The generated cavitation zone in front of emitting surface in different time contacted with each other and coalescence, showing large and concentrated cavitation zone in Fig. 6(C). And due to the existence of cavitation energy shield, the sound energy is blocked within cavitation bubble, hard to propagate to the bottom of cylinder, the bubble separation frequency is reduced to f/8. Until the cavitation zones be pushed forward and away from the emitting surface, another cavitation zone is forming in front, gradually accumulating and coalescence into large bubble. The vapor volume fraction distribution comparison between NCG expansion, gaseous cavitation and vaporous cavitation clearly explained the mechanism of non-linear propagation of ultrasound. The longitudinal propagation of high intensity ultrasound wave leads to the variation of water liquid density. Hence the ultrasound waves propagate at high and low speed in concentration and rarefaction phase respectively, exhibiting non-linearity.
Fig. 6.
Simulation results of cavitation zones propagation in (A) expansion and condensation state, starting from 0.2s with the time interval of 1.25×10-5s, (B) gaseous cavitation state, starting from 0.2s with the time interval of 1.25×10-5s, (C) vaporous cavitation state, starting from 0.2s with the time interval of 5×10-5s.
4.2. Sound pressure signal analysis
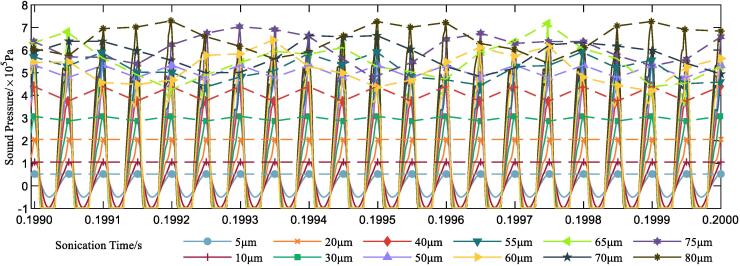
In order to clearly identify the variation trend of sound pressure against sonication time, the sound pressure signals correspond to each vibratory amplitude from 0.199s∼0.2s are exhibited in Fig. 7. It is obvious that the upper limit of sound pressure raised with the increase of vibratory amplitude and lower limit decreased accordingly, but with a minimum value at the saturation pressure corresponding to -96891.6Pa under 300K. It can be easily distinguished when the vibratory amplitude is 5∼10μm, the lower limit of sound pressure cannot reach the saturation pressure, but with the amplitude increases from 20μm to 75μm the saturation pressure is reached and the saturation state time last longer with the increase of amplitude. The upper limit of sound pressure with the amplitude of 5μm to 20μm show a consistent maximum value, meanwhile, the amplitude from30μm to 50μm have two different peak value in the interval period. Moreover, at the amplitude from 55μm to 75μm, the peak value becomes oscillating at the frequency of f/8 which corresponding to the cavitation bubble generation and separation period in Fig. 6(C), these trends are marked out with different markers and dashed lines. These different characteristics in local maximum sound pressure is caused by cavitation phenomenon, when the amplitude is 5∼20μm, the ultrasound wave is relatively gentle, the expansion of NCG is the primary acoustic effect. The further increase of amplitude from 30∼50μm leads to gaseous cavitation, NCG expands and coalesces, forming large cavitation bubbles. At this state, the cavitation threshold is reached in the negative phase of ultrasound but no water liquid evaporation has happened. With the further increase of amplitude in the range of 55∼75μm, the sound power energy is high enough and generate water liquid phase transition. The appearance of evaporation and condensation between water liquid and vapor greatly enhanced the non-linear effect created by ultrasound. In the oscillation period reaches absolute maximum sound pressure, large cavitation zone is generated in front of the emitting surface, which acted as a shielding layer blocking the propagation of ultrasound into fluid. Hence, with the augment of vibratory amplitude, in the next few periods of sound emitting, the local maximum sound pressure is relatively lower with weaker acoustic cavitation phenomenon and more sound power energy transmitted to the fluid field soon afterwards, forming an oscillation of local maximum sound pressure eventually.
Fig. 7.
Simulation results of sound pressure fluctuation with radiation time. (The peak values in each oscillation period are marked out and connected with dashed line.)
From Fig. 7, the sound pressure is evidently increasing with the increase of vibratory amplitude. Since the simulation of imposing ultrasound into fluid flow field through wall motion is employed by designating the vibratory frequency and amplitude, the actual power of ultrasound input is not a direct setup parameter. In order to determine how much sound power input will induce each cavitation state, Eq. (16) is applied first to acquire an average value of the accumulated maximum sound pressure corresponding to each vibratory amplitude from 0.1∼0.2s.
| (16) |
where psound is the average sound pressure, and pmax is the peak pressure at each oscillating period. Then using Eq. (17)∼(18) [33], the ultrasound power is delivered, and the sound pressure and power is shown in Fig. 8.
| (17) |
| (18) |
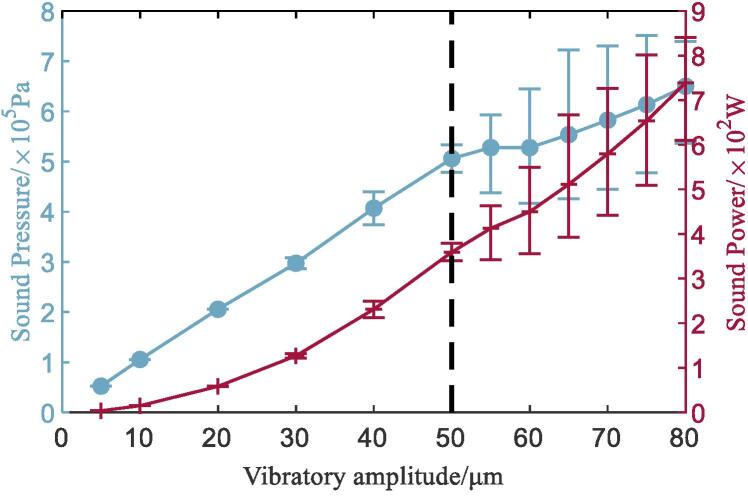
where I and Psound are sound pressure and sound power at sonotrode emitting surface respectively, and S is the surface area of sonotrode tip. Error bar is applied in each vibratory amplitude to represent the variation range of the maximal and minimal value of sound pressure and sound power. The sound wave pressure shows a relatively steady, almost linear increase against amplitude up to 50μm vibratory amplitude, while the slope of corresponding sound power keeps increasing. This trend is explained via Fig. 5(Ⅰ)∼(Ⅵ), during raising the vibratory amplitude, the cavitation zones grow into gaseous cavitation state but still distribute separately. Therefore, sound power keeps increasing quicker while slight scattering and attenuating cause the sound pressure growing linearly. As the vibratory amplitude raised higher than 50μm, the slope of sound pressure decreases and the magnitude has a drop at 60μm but continue increase until 80μm in this research. In Fig. 5(VII)∼(XII), the cavitation zones coalescence in front of emitting surface and break away periodically, which is the reason for the decrease of sound pressure slope from 50μm to 55μm. This severe damping of sound energy is called ‘cavitation shielding’, especially at high sound power output levels, an intense cloud of cavitation is produced very close to the emitting surface of sonotrode, which then through scattering and attenuation, blocking acoustic energy reaching any deeper into the medium than a few milimeter [34]. With the vibratory amplitude increases, larger cavitation zone surrounds the sonotrode, making the sound energy difficult to transmit into fluid but causing phase change (vaporous cavitation), hence the sound pressure magnitude even drops slightly at 60μm. But continue raising the vibratory amplitude, the cavitation bubbles consist of NCG and water vapor have reached the limited size, therefore the sound pressure transmitted to fluid keeps on increasing at a constant slope with the increase of vibratory amplitude.
Fig. 8.
Simulation results of ultrasound pressure and power against the amplitude of sonotrode.
4.3. Frequency spectrum analysis
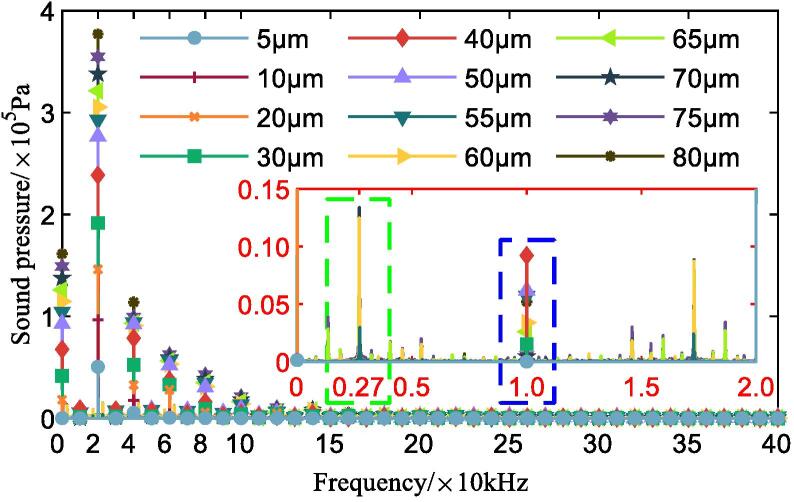
By utilizing FFT to the pressure signal, the frequency response of harmonics, sub/ultra-harmonics and cavitation white noise is separated to describe the unique characteristics in different cavitation regions as exhibited in Fig. 9. The upper limit of the spectrum is determined by the sampling frequency which is corresponding to 1/(2T), and the frequency resolution is 1/t, in this research they are 4×105Hz and 10Hz respectively. In the frequency spectrum, the linear component at f=0Hz, the fundamental harmonic frequency corresponds to the excitation frequency f0=20kHz and other harmonics of f0 at f=mf0 (m is integer) obviously have stronger magnitude than other frequency, corresponding to stronger sound energy in these frequency components [35]. Among all these harmonics, the fundamental harmonic has the highest peak value, and the magnitude of high order harmonics mf0 is decreasing with increasing m. The appearance of high order harmonics is because of non-linear propagation of ultrasound, their intensity is part of excitation source energy component, hence the magnitude decreases with increasing order m. Besides the significant frequency response in Fig. 9, the sub-harmonic frequency at f0/n (n is integer), and the ultra-harmonics beyond fundamental frequency at mf0/n except for harmonics can also be identified. These sub/ultra-harmonics have significant weaker magnitude of sound pressure compared with harmonics and linear component, but they are very important feature of acoustic cavitation frequency response [36], [37]. The sub-harmonics marked out in blue and green boxes represents for cavitation zone separation frequency, at vibratory amplitude of 30∼50μm and 55∼80μm the corresponding frequencies are decreasing and are approximately f0/2 and f0/8 respectively.
Fig. 9.
Simulation results of frequency spectrum at different amplitude from FFT. (Axes in red is zoomed sub-harmonic frequency spectra)
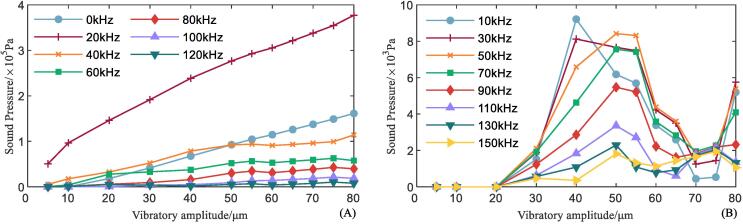
To further investigate the frequency characteristics, the linear component, harmonics and sub/ultra-harmonics are extracted from the frequency spectra and plotted against the vibratory amplitude as shown in Fig. 10. With the increase in excitation signal amplitude, the sound wave strength gradually increases and the negative phase pressure reaches the cavitation threshold at most, hence the linear component gradually became prominent among harmonics. The magnitude of linear component is positively correlated to the excitation amplitude. The fundamental harmonic is the direct reflection of excitation source intensity, hence sound pressure against amplitude at f0 is positively correlated. And the sound energy contained in fundamental harmonic part is always higher than the high order harmonics. With the increase in excitation amplitude, the propagation of ultrasound wave becomes more non-linear. The increase trend at other harmonics maintained until A=50μm, then the magnitude did not change much. Because when a in the range of 5∼50μm, there is no vaporous cavitation, so the attenuation and scattering effect of cavitation zone are not strong. After A raised up to 55μm, phase change of water liquid appeared, the existence of water vapor forming vaporous cavitation, which diminished sound energy from harmonics and stored inside the bubbles, later released by jet flow and shock wave when explode, generating white noise. The shielding effect of vaporous cavitation zone prevents the magnitude of high order harmonics from growing.
Fig. 10.
Simulation results of sound pressure magnitude (A) At part of harmonics, (B) At part of sub/ultra-harmonics.
The appearance of sub/ultra-harmonics are due to cavitation bubble oscillation, the bubbles will oscillate in their radial direction forced by the primary Bjerknes force which results from the excitation sound field, or oscillate randomly in the fluid field forced by the secondary Bjerknes force which results from the sound field from bubbles self-oscillation [38]. In Fig. 10(B) the first-harmonic and ultra-harmonics are nearly zero at amplitude from 5∼20μm, indicating the ultrasound is relatively gentle at this vibratory amplitude range, the dissolved NCG only expands or compresses in the fluid but not grows into bubbles. With the increase of vibratory amplitude to the range of 30∼50μm, NCG expands, coalescence into larger bubbles and oscillates radially, presenting an oscillating component at the f0/2 sub-harmonic, this is an indicator for identification of gaseous cavitation [14], [34]. With the amplitude increases to 55μm, the vaporous cavitation happens, the same as harmonics, the energy of sub/ultra-harmonics is taken by generated bubbles. However, the further increase of vibratory amplitude imposes higher ultrasound power into fluid field that the cavitation bubbles can no longer taking in, hence the lower order sub/ultra-harmonics (10∼70kHz) raises significantly and high order ultra-harmonics (90∼kHz) raises slightly.
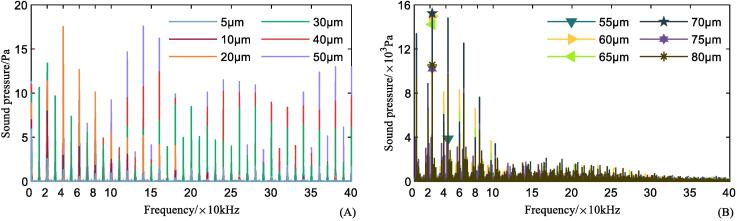
The harmonics and sub/ultra-harmonics in the frequency spectra is eliminated and delivered Fig. 11 (A) and (B), exhibiting the signal from 5∼50μm representing gaseous cavitation and 55∼80μm representing vaporous cavitation respectively. It is to be noticed that in both Fig. 11 (A) and (B) exhibits broadband signals through all frequency spectra, in gaseous cavitation these signals mostly distributed around harmonics and sub/ultra-harmonics, while in vaporous cavitation these signals densely distributed all over the frequency band. Moreover, the frequency components magnitude in vaporous cavitation is generally hundred times higher than gaseous cavitation. These broadband signals in the vibratory amplitude range of 5∼50μm is primarily caused by the non-uniform radial distribution of acoustic velocity and secondarily resulted from insufficient frequency resolution. And in the vibratory range of 55∼80μm, the broadband signal is generated by the jet flow and shock wave, which are released with the occurrence of vaporous cavitation bubble explosion, and is defined as cavitation noise in the frequency spectra. From the comparison of noise in Fig. 11 (A) and (B), the significance of phase change cavitation in white noise releasing is elucidated, and can be validated by Ref. [39] which derived similar results. However, the already made simplification of cavitation model should be noticed, which might cause the delayed appearance of white noise at flow vibratory amplitude according to Ref. [40], [41].
Fig. 11.
Simulation results of cavitation noise, (A) Gaseous cavitation noise at the amplitude range of 5∼50μm, (B) Vaporous cavitation noise at the amplitude range of 55∼80μm. (Highest peak value of white noise corresponding to each vibratory amplitude is marked out.)
5. Discussion about cavitation threshold amplitude
From the above analysis about cavitation zone distribution and frequency spectrum, cavitation first occurred at the 30μm vibratory amplitude, corresponding to 100W ultrasound power. However, it is known that an ultrasonic cleaning bath usually consumes 50W for each transducer commonly with a diameter of 30∼70mm, generating cavitation at the vibratory amplitude about 5μm[42], [43]. The following experiments were conducted to discuss the delay of cavitation in numerical simulation.
Firstly, the vibratory amplitude of two sonotrode type ultrasonic devices was measured with the apparatus shown in Fig. 12 (A) and listed in Table. 1. Sonotrode #1 has a diameter of 12mm, 1000W maximum power input (30∼100% adjustable) and works at 20kHz, and sonotrode #2 has a diameter of 22mm, 400W maximum power input (30∼100% adjustable) and works at 20kHz. Comparing the vibratory amplitude generated by 400W power input, the Φ12mm sonotrode has a 28μm displacement while the Φ22mm sonotrode generates a 19μm displacement. Moreover, sonoluminescence experiment was conducted with a luminal solution containing 0.1mol/L luminal (3-aminophthalhydrazide) and 1mol/L NaOH in distilled water. The experiment apparatus is shown in Fig. 12 (B), a Single Lens Reflex (SLR) camera was installed in a 3D-platform, a PMMA vessel filled with luminal solution of 100mm height, and sonotrode tip was immersed 10mm under solution surface. Fig. 12 (C) and (D) were both shot at ultrasound power input of 400W, it is evident that the thicker sonotrode #2 generated larger area of fluid field covered by blue light. Both vibratory amplitude measurement and sonoluminescence reflect that at the same power input, though a thicker sonotrode with larger emitting surface area generates lesser vibratory amplitude than a slender one, the cavitation effect is more extensive. This explains why a cleaning bath can easily induce large scale cavitation.
Fig. 12.
(A) Sonotrode tip vibratory amplitude measurement apparatus (sonotrode #1), (B) Sonoluminescence experiment apparatus, sonoluminescence generated with 400W power input by (C) Sonotrode #1, (D) Sonotrode #2. (Sonoluminescence photo were shot by Canon 80D equipped with an EFS 18∼135mm lens, using the settings ISO3200, f3.5 and a 60s exposure time.)
Table 1.
Experimental measurement of sonotrode tip vibratory amplitude.
| Sonotrode #1 | Sonotrode #2 | ||
|---|---|---|---|
| Power input/W | Vibratory amplitude/μm | Power input/W | Vibratory amplitude/μm |
| 1000 | 67 | 400 | 19 |
| 900 | 60 | 360 | 18 |
| 800 | 55 | 320 | 16 |
| 700 | 50 | 280 | 12 |
| 600 | 42 | 240 | 11 |
| 500 | 35 | 200 | 10 |
| 400 | 28 | 160 | 8 |
| 300 | 20 | 120 | 6 |
Also from Table. 1, the vibratory amplitude generated with minimum power input (300W) by sonotrode #1 is 20μm, while in numerical simulation, the corresponding vibratory amplitude to 300W is about 45μm by linear interpolation (in Fig. 8). This difference is ascribed to the existence of NCG, which reduces the mixture fluid density. Simply evaluating the force acting on fluid from sonotrode tip by Eq. (19):
where, Fus represents ultrasonic force acting on fluid, V represents finite volume of mixture fluid receiving momentum transmitted from sonotrode tip, and a is acceleration of sonotrode tip. From Eq. (19) we can find that with the decrease of ρm, at the same vibratory amplitude of sonotrode tip, a finite fluid volume will receive less sound power. Therefore, in numerical simulation with NCG, less ultrasound power transmits from sonotrode to fluid field at the same vibratory amplitude. This explains why in numerical simulation larger amplitude is needed to generate the same amount of ultrasound power as measured in experiment.
In addition to the above influence from ultrasound power, simplification in numerical simulation model has impact on cavitation. the mass source term described by Eqs. (8)∼(9) also give explanations. The evaporation source term Re representing phase transition of water liquid to water vapor is negatively correlated to NCG mass fraction. Therefore, the occurrence of cavitation is delayed. Furthermore, the saturated pressure should be higher with NCG existence. But due to the correlation between NCG mass fraction and saturated pressure is not described clearly yet, in this work the correction of saturated pressure by NCG mass fraction is not conducted.
6. Conclusions
In the present research, the effects of ultrasound excitation source vibratory amplitude (power level) on cavitation state is investigated through frequency spectra of sound pressure signals and distribution of cavitation zones. The characteristic signals in NCG expansion/compression, gaseous cavitation and vaporous cavitation are identified, and the cavitation zone development is visually studied with vapor volume fraction distribution. The findings of this present research are summarized as follow:
-
1.
According to the power input of sonotrode in water liquid, ultrasound power higher than 100W or 350W will generate gaseous or vaporous cavitation respectively, inducing cavitation shielding effect. The cavitation shielding is a progress of bubble generation and separation progress beneath sonotrode tip, which has a sub-harmonic frequency f0/m corresponding to the oscillation of ultrasound pressure peak value. Moreover, m is proportional to vibrating amplitude.
-
2.
Harmonics are generated due to the non-linear propagation of ultrasound, sub/ultra-harmonics are results from bubbles radial oscillation or self-oscillation in the fluid field and white noise all over the spectra is released by jet flow and shock wave from implosion of cavitation bubble.
-
3.
The sub/ultra-harmonics are indicator for gaseous cavitation, and white noise is indicator for vaporous cavitation.
-
4.
Cavitation zone development is regular at the ultrasound power below 60W (corresponding to vibratory amplitude of 20μm) with a symmetric distribution pattern but can only maintain in front of emitting surface. The power range between 120∼360W (corresponding to vibratory amplitude of 30∼50μm) generate gaseous cavitation which can spread far and show an asymmetric distribution pattern in front of emitting surface and a symmetric distribution pattern deep down the vessel. At the power range of 400∼750W (corresponding to vibratory amplitude of 55∼80μm) vaporous cavitation phenomenon is generated, causing cavitation zones coalescence with each other in front of emitting surface and break away periodically.
-
5.
A thicker sonotrode with larger emitting surface area is able to generate more extensive cavitation than a slender one, and the existence of NCG delays the occurrence of cavitation in numerical simulation.
CRediT authorship contribution statement
Weixiang Lin: Conceptualization, Methodology, Software, Formal analysis, Writing – original draft. Juan Xiao: Software, Formal analysis, Writing – review & editing, Funding acquisition. Jian Wen: Conceptualization, Writing – review & editing. Simin Wang: Conceptualization, Writing – review & editing, Supervision, Funding acquisition.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The National Natural Science Foundation of China (No. 22108216), the Fundamental Research Funds for the Central Universities (xzy012022070), Sinopec Group (2021610002001690) and HPC Platform, Xi’an Jiaotong University.
Data availability
Data will be made available on request.
References
- 1.Harvey G., Gachagan A. Simulation and measurement of nonlinear behavior in a high-power test cell. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011;58:808–819. doi: 10.1109/TUFFC.2011.1873. [DOI] [PubMed] [Google Scholar]
- 2.Hamilton M.F., Blackstock D.T., Ostrovsky L.A. Nonlinear Acoustics. J. Acoust. Soc. Am. 1974;105:578. [Google Scholar]
- 3.Lighthill S.J. Acoustic streaming. J. Sound Vib. 1978;61:391–418. [Google Scholar]
- 4.Holland C.K., Apfel R.E. Thresholds for transient cavitation produced by pulsed ultrasound in a controlled nuclei environment. J. Acoust. Soc. Am. 1990;88:2059–2069. doi: 10.1121/1.400102. [DOI] [PubMed] [Google Scholar]
- 5.Angele K. Prediction of cavitation in orifice plates—A novel and simple rule-of-thumb. Exp. Computat. Multiphase Flow. 2021;3:68–76. [Google Scholar]
- 6.Briggs H.B., Johnson J.B., Mason W.P. Properties of Liquids at High Sound Pressure. J. Acoust. Soc. Am. 1947;19:664–677. [Google Scholar]
- 7.Lee S.Y., Choi Y.D. Turbulence enhancement by ultrasonically induced gaseous cavitation in the CO2 saturated water. KSME Int. J. 2002;16:246–254. [Google Scholar]
- 8.Razavifar M., Qajar J. Experimental investigation of the ultrasonic wave effects on the viscosity and thermal behaviour of an asphaltenic crude oil. Chem. Eng. Process. - Process Intensificat. 2020;153 [Google Scholar]
- 9.Leone A., Romaniello R., Juliano P., Tamborrino A. Use of a mixing-coil heat exchanger combined with microwave and ultrasound technology in an olive oil extraction process. Innovative Food Sci. Emerg. Technol. 2018;50:66–72. [Google Scholar]
- 10.Hao F., Barbosa-Canovas G.V., Weiss J. Ultrasound Technologies for Food and Bioprocessing. Ultrasound Technol. Food Bioprocess. 2011 [Google Scholar]
- 11.Tiong T.J., Liew D.K.L., Gondipon R.C., Wong R.W., Loo Y.L., Lok M.S.T., Manickam S. Identification of active sonochemical zones in a triple frequency ultrasonic reactor via physical and chemical characterization techniques. Ultrason. Sonochem. 2017;35:569–576. doi: 10.1016/j.ultsonch.2016.04.029. [DOI] [PubMed] [Google Scholar]
- 12.Bulliard-Sauret O., Berindei J., Ferrouillat S., Vignal L., Memponteil A., Poncet C., Leveque J.M., Gondrexon N. Heat transfer intensification by low or high frequency ultrasound: Thermal and hydrodynamic phenomenological analysis. Exp. Therm Fluid Sci. 2019;104:258–271. [Google Scholar]
- 13.Poncet C., Ferrouillat S., Vignal L., Memponteil A., Bulliard-Sauret O., Gondrexon N. Enhancement of heat transfer in forced convection by using dual low-high frequency ultrasound. Ultrason. Sonochem. 2021;71 doi: 10.1016/j.ultsonch.2020.105351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Frohly J., Labouret S., Bruneel C., Looten-Baquet I., Torguet R. Ultrasonic cavitation monitoring by acoustic noise power measurement. J. Acoust. Soc. Am. 2000;108:2012–2020. doi: 10.1121/1.1312360. [DOI] [PubMed] [Google Scholar]
- 15.Neppiras E.A. Subharmonic and other low-frequency signals from sound-irradiated liquids. J. Sound Vib. 1969;10:176–186. [Google Scholar]
- 16.Ye L., Zhu X., He Y., Song T. Effect of frequency ratio and phase difference on the dynamic behavior of a cavitation bubble induced by dual-frequency ultrasound. Chem. Eng. Process. - Process Intensificat. 2021 [Google Scholar]
- 17.Song J.H., Johansen K., Prentice P. An analysis of the acoustic cavitation noise spectrum: The role of periodic shock waves. J. Acoust. Soc. Am. 2016;140:2494–2505. doi: 10.1121/1.4964633. [DOI] [PubMed] [Google Scholar]
- 18.Tzanakis I., Lebon G.S.B., Eskin D.G., Pericleous K.A. Characterisation of the ultrasonic acoustic spectrum and pressure field in aluminium melt with an advanced cavitometer. J. Mater. Process. Technol. 2016;229:582–586. [Google Scholar]
- 19.Yamamoto T., Kubo K., Komarov S.V. Characterization of acoustic streaming in water and aluminum melt during ultrasonic irradiation. Ultrason. Sonochem. 2021;71 doi: 10.1016/j.ultsonch.2020.105381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tudela I., Sáez V., Esclapez M.D., Díez-García M.I., Bonete P., González-García J. Simulation of the spatial distribution of the acoustic pressure in sonochemical reactors with numerical methods: A review. Ultrason. Sonochem. 2014;21:909–919. doi: 10.1016/j.ultsonch.2013.11.012. [DOI] [PubMed] [Google Scholar]
- 21.Trujillo F.J. A strict formulation of a nonlinear Helmholtz equation for the propagation of sound in bubbly liquids. Part I: Theory and validation at low acoustic pressure amplitudes. Ultrason. Sonochem. 2018;47:75–98. doi: 10.1016/j.ultsonch.2018.04.014. [DOI] [PubMed] [Google Scholar]
- 22.Trujillo F.J. A strict formulation of a nonlinear Helmholtz equation for the propagation of sound in bubbly liquids. Part II: Application to ultrasonic cavitation. Ultrason. Sonochem. 2020;65 doi: 10.1016/j.ultsonch.2020.105056. [DOI] [PubMed] [Google Scholar]
- 23.Rahimi M., Movahedirad S., Shahhosseini S. CFD study of the flow pattern in an ultrasonic horn reactor: Introducing a realistic vibrating boundary condition. Ultrason. Sonochem. 2017;35:359–374. doi: 10.1016/j.ultsonch.2016.10.014. [DOI] [PubMed] [Google Scholar]
- 24.Lin W., Xiao J., Su G., Wang S., Wen J. Ultrasound-assisted enhancement of heat transfer in immersed coil heat exchangers: Effects of acoustic intensity and ambient fluid properties. Int. Commun. Heat Mass Transfer. 2021;129 [Google Scholar]
- 25.Cheng H., Long X., Ji B., Peng X., Farhat M. A new Euler-Lagrangian cavitation model for tip-vortex cavitation with the effect of non-condensable gas. Int. J. Multiph. Flow. 2021;134 [Google Scholar]
- 26.Wang X., Li H., Dong J., Wu J., Tu J.-Y. Numerical study on mixing flow behavior in gas-liquid ejector. Exp. Computat. Multiphase Flow. 2021;3:108–112. [Google Scholar]
- 27.A.K. Singhal, M.M. Athavale, H. Li, Y. Jiang, Mathematical basis and validation of the full cavitation model, in: Proceedings of the ASME Fluids Engineering Division Summer Meeting, 2003, pp. 379-406.
- 28.Wang B., Liu Z., Li H., Wang Y., Liu D., Zhang L., Peng X. On the numerical simulations of vortical cavitating flows around various hydrofoils. J. Hydrodynam. Ser. B. 2017;29:926–938. [Google Scholar]
- 29.Desheng Z., Shi W., Pan D., Dubuisson M. Numerical and Experimental Investigation of Tip Leakage Vortex Cavitation Patterns and Mechanisms in an Axial Flow Pump. J. Fluids Eng. 2015;137 [Google Scholar]
- 30.Celik F., Arikan Ozden Y., Bal S. Numerical simulation of flow around two- and three-dimensional partially cavitating hydrofoils. Ocean Eng. 2014;78:22–34. [Google Scholar]
- 31.Launder B.E., Spalding D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974;3:269–289. [Google Scholar]
- 32.Thangaraj K., Kumar A., Pandit A., Joshi J. Modeling Flow Pattern Induced by Ultrasound: The Influence of Modeling Approach and Turbulence Models. Industrial & Engineering Chemistry Research - IND ENG CHEM RES. 2006;46 [Google Scholar]
- 33.F. Grieser, P.K. Choi, N. Enomoto, H. Harada, K. Okitsu, K. Yasui, Sonochemistry and the acoustic bubble, 2015.
- 34.Hodnett M., Chow R., Zeqiri B. High-frequency acoustic emissions generated by a 20 kHz sonochemical horn processor detected using a novel broadband acoustic sensor: a preliminary study. Ultrason. Sonochem. 2004;11:441–454. doi: 10.1016/j.ultsonch.2003.09.002. [DOI] [PubMed] [Google Scholar]
- 35.T. Kuroyama, Viscosity Dependence of Harmonics and Ultra-Harmonics of Acoustic Cavitation Noise, in: IEEE International Ultrasonics Symposium, IUS, 2018.
- 36.Birkin P.R., Offin D.G., Vian C.J.B., Leighton T.G. Multiple observations of cavitation cluster dynamics close to an ultrasonic horn tip. J. Acoust. Soc. Am. 2011;130:3379–3388. doi: 10.1121/1.3650536. [DOI] [PubMed] [Google Scholar]
- 37.Yusuf L., Symes M.D., Prentice P. Characterising the cavitation activity generated by an ultrasonic horn at varying tip-vibration amplitudes. Ultrason. Sonochem. 2021;70 doi: 10.1016/j.ultsonch.2020.105273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Crum L.A. Bjerknes forces on bubbles in a stationary sound field. J. Acoust. Soc. Am. 1975;57:1363–1370. [Google Scholar]
- 39.Jonnalagadda U.S., Su X., Kwan J.J. Nanostructured TiO2 cavitation agents for dual-modal sonophotocatalysis with pulsed ultrasound. Ultrason. Sonochem. 2021;73 doi: 10.1016/j.ultsonch.2021.105530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tzanakis I., Hodnett M., Lebon G.S.B., Dezhkunov N., Eskin D.G. Calibration and performance assessment of an innovative high-temperature cavitometer. Sens. Actuators, A. 2016;240:57–69. [Google Scholar]
- 41.Tzanakis I., Lebon G.S.B., Eskin D.G., Pericleous K.A. Characterizing the cavitation development and acoustic spectrum in various liquids. Ultrason. Sonochem. 2017;34:651–662. doi: 10.1016/j.ultsonch.2016.06.034. [DOI] [PubMed] [Google Scholar]
- 42.Moholkar V.S., Sable S.P., Pandit A.B. Mapping the cavitation intensity in an ultrasonic bath using the acoustic emission. AIChE J. 2000;46:684–694. [Google Scholar]
- 43.Liu L., Wen J., Yang Y., Tan W. Ultrasound field distribution and ultrasonic oxidation desulfurization efficiency. Ultrason. Sonochem. 2013;20:696–702. doi: 10.1016/j.ultsonch.2012.10.009. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.