Single-cell mutation calling and phylogenetic tree reconstruction with loss and recurrence

Abstract

Motivation

Tumours evolve as heterogeneous populations of cells, which may be distinguished by different genomic aberrations. The resulting intra-tumour heterogeneity plays an important role in cancer patient relapse and treatment failure, so that obtaining a clear understanding of each patient’s tumour composition and evolutionary history is key for personalized therapies. Single-cell sequencing (SCS) now provides the possibility to resolve tumour heterogeneity at the highest resolution of individual tumour cells, but brings with it challenges related to the particular noise profiles of the sequencing protocols as well as the complexity of the underlying evolutionary process.

Results

By modelling the noise processes and allowing mutations to be lost or to reoccur during tumour evolution, we present a method to jointly call mutations in each cell, reconstruct the phylogenetic relationship between cells, and determine the locations of mutational losses and recurrences. Our Bayesian approach allows us to accurately call mutations as well as to quantify our certainty in such predictions. We show the advantages of allowing mutational loss or recurrence with simulated data and present its application to tumour SCS data.

Availability and implementation

SCI$\Phi$N is available at https://github.com/cbg-ethz/SCIPhIN.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The development and rapid progress in single-cell DNA sequencing (Gawad et al., 2016; Navin et al., 2011; Wang and Navin, 2015) now allows the genetic profiling of individual cells. Particularly for tumours, where somatic cell evolution can lead to multiple heterogeneous cell populations and subclones (Burrell and Swanton, 2016; Greaves and Maley, 2012; Yates and Campbell, 2012), single-cell sequencing (SCS) illuminates the underlying complexity or intra-tumour heterogeneity (ITH) (Navin, 2014). Measuring and understanding ITH is central for precision medicine, given its strong links to tumour relapse and treatment failure (Burrell et al., 2013; Dagogo-Jack and Shaw, 2018; McGranahan and Swanton, 2015).

The power and resolution of SCS come with the cost of elevated error rates, due to the small amount of DNA present in each individual cell (Gawad et al., 2016; Navin et al., 2011; Wang and Navin, 2015). For whole-exome sequencing (WES), a common amplification protocol is multiple displacement amplification (MDA) (Lasken, 2009), which is efficient in creating enough DNA material for later sequencing, but suffers from uneven coverage and a high (10–20%) rate of allelic dropout whereby one allele is locally not amplified at all and cannot be later detected in the sequencing data.

If SCS data are dichotomized into mutational presence or absence per cell, a suite of phylogenetic methods were developed (Kuipers et al., 2017a; Zafar et al., 2018) to handle the high false negative rates (due to allelic dropout) particular to SCS and accurately reconstruct the evolutionary history of tumours from the genetic profiles of individual cells.

In order to obtain dichotomized data, the mutations need to be called per cell based on the raw sequencing output. Bulk callers adapted to the noise profiles of the mixed signals of many cells amplified with a different protocol are suboptimal, which has led to the development of specialized callers for single-cell data (Dong et al., 2017; Zafar et al., 2016) accounting for the noise profiles of single-cell amplification and sequencing protocols. They often share information across cells (Zafar et al., 2016), or locally across the genome (Dong et al., 2017; Lähnemann et al., 2021) to improve performance. Combining single-cell-specific read count modelling with single-cell phylogenetic modelling, we previously developed SCI$\Phi$ (Singer et al., 2018) to jointly call mutations and learn the lineage relationships between cells. As a Bayesian approach, the full posterior certainty in the mutation calls can be assessed. The tree structure allows information to be shared more effectively across cells, particularly in correcting for allelic dropout (Singer et al., 2018), leading to improved performance as compared to combining information across cells without using the phylogeny (Zafar et al., 2016).

The underlying tree model for SCI$\Phi$ contained the simplifying infinite sites assumption, which restricts mutations to only occur once in the phylogeny and to persist after occurrence, though the model did allow for homozygous mutations. Binarized single-cell data have allowed us to test such assumptions, and find that it may be often violated in real tumour samples (Kuipers et al., 2017b). More complex phylogenetic models mitigating, or entirely avoiding the infinite sites assumption, have also been developed (El-Kebir, 2018; Kozlov et al., 2020; Satas et al., 2020; Zafar et al., 2017, 2019), though there is an apparent trade-off in model complexity between too simple models that cannot capture all relevant aspects of the evolutionary process, and too complex models that are prone to over-fitting or computationally too expensive to be learned efficiently from data. The existing models rely on processed data, where the mutations have already been called. Here, we therefore bring the advances of allowing mutational recurrence and loss in tree modelling to improve mutation calling from raw SCS data. We present a novel approach to relaxing the infinite sites assumption, building on SCI$\Phi$ (Singer et al., 2018) while staying within the same computational complexity class. The new method, called SCI$\Phi$N (N can abbreviate knight in chess/crosswords so the reading SCI-finite should indicate Single-Cell mutation Identification via finite-sites Phylogenetic Inference), allows us to jointly call mutations and the phylogenetic relationship between cells under loss and recurrence, while quantifying the uncertainty in our results.

2 Materials and methods

2.1 Model overview

During tumour evolution, mutations may be accumulated by cells, but regions of the genome may also undergo copy number changes, in particular the loss of one allele (loss of heterozygosity, LOH). In our model, SCI$\Phi$N, we consider originally diploid regions of the genome which may experience somatic point mutations, monoploid regions which have already lost one allele, as well as the loss of one allele, including its mutations, during tumour evolution (Fig. 1).

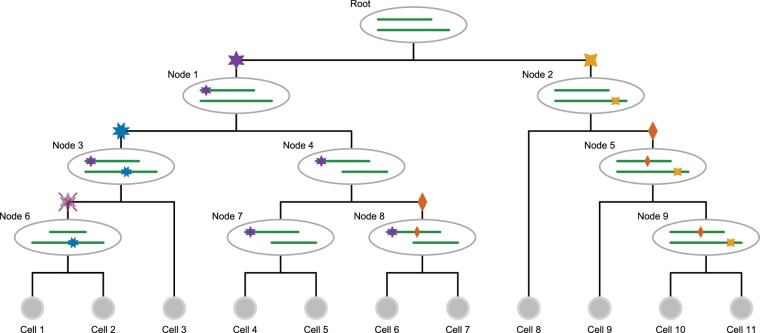
Fig. 1.

Genomic events modelled in the cell lineage tree. Starting from the tumour founder cell at the root, which has a deletion in one genomic region, different clones evolve along the different lineages. On the right-hand branch at node 2, the yellow (four-pointed star) mutation occurs as a hemizygous mutation in the remaining allele of the deleted region, later joined at node 5 by the heterozygous red (two-pointed star) mutation. This mutation reoccurs independently at node 8. There are two loss of heterozygosity events: in the left branch, the heterozygous purple (six-pointed star) mutation at node 1 becomes hemizygous in its right subtree at node 4 when the non-mutated wild type allele region is lost. At node 6 in its left subtree instead, the allele carrying the purple (six-pointed star) mutation is lost so that the mutation status returns to wild type

At each genomic position, a cell may then be wild type, or have a heterozygous or hemizygous mutation. Along with mutational losses, mutations are also allowed to reoccur independently in the phylogeny. With this space of underlying aberration events, we develop the probabilistic tree model for single-cell read and variant counts, and employ Markov chain Monte Carlo (MCMC) to perform Bayesian inference of mutation calls.

A cell lineage tree T is a binary tree with labelled leaves corresponding to the single cells. Along the branches of the tree, mutational events may occur. For each genomic locus i, we record as element τ_i of the vector τ the branch where the mutation affecting that locus occurs. For example, the blue 8-pointed star mutation in Figure 1 occurs in the branch above node 3 and is present in all descendant cells (cells 1, 2 and 3). The knowledge of the tree T, and the placement of the mutations within that tree τ, provides us with the underlying genotypes of each cell j. For each genomic locus i and cell j with v_ij variant reads (of a particular non-reference nucleotide) and coverage c_ij, we summarize the data as $D_{ij}=(v_{ij},\hspace{0.17em}{c}_{ij})$. This allows us to define the likelihood of the data

$$P(D|T,\tau ,\hspace{0.17em}{f}_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}},\hspace{0.17em}{\omega }_{\text{ht}})=\prod _{i=1}^n\prod _{j=1}^{m}P(D_{ij}|T,\hspace{0.17em}\tau ,\hspace{0.17em}{f}_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}},\hspace{0.17em}{\omega }_{\text{ht}})$$ (1)

where n is the number of genomic loci, m the number of cells, and we assume independence of the noise per cell and mutation. The parameters $f_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}}$ and ${\omega }_{\text{ht}}$ are related to the noise modelling of the amplification and sequencing protocols, which we expound in Section 2.2. For notational convenience, we drop their explicit dependence in the following.

For Bayesian inference of the tree topology and mutation calls, we first marginalize over the unknown placement of the mutations (for which we use a uniform prior over the tree branches)

$$\begin{array}{c}P(D|T)\propto \sum _{\tau }\prod _{i=1}^n\prod _{j=1}^{m}P(D_{ij}|T,\hspace{0.17em}\tau )P(\tau )\\ =\prod _{i=1}^n\sum _{{\tau }_i}P({\tau }_i)\prod _{j=1}^{m}P(D_{ij}|T,\hspace{0.17em}{\tau }_i)\end{array}$$ (2)

By rearranging the terms to treat each mutation separately, we reduce the complexity of the computation from the naïve $O(n{m}^{n+1})$ on the left of the equality to $O(n{m}^2)$ on the right. As we show below, this can be further reduced to O(nm) via tree traversals.

To compute the contribution to the likelihood from each mutation, we treat five mutation cases:

• ht: a heterozygous mutation occurs in a diploid region;

• hm: a hemizygous mutation occurs in a monoploid region which has previously lost one allele;

• wl: a wild-type allele is lost after a heterozygous mutation occurred;

• ml: a mutated allele is lost after a heterozygous mutation occurred; and

• pm: a heterozygous mutation occurs twice in the tree in parallel branches.

We consider that each possible mutation type has a fixed prior probability, namely ν for a mutation occurring in a genomic region with only one allele, ${\lambda }_{\text{wl}}$ and ${\lambda }_{\text{ml}}$ for losses of heterozygosity and κ for a parallel heterozygous mutation. We may then express the likelihood contributions as a mixture of the possibilities

$$\begin{array}{c}\sum _{{\tau }_i}P({\tau }_i)\prod _{j=1}^{m}P(D_{ij}|T,\hspace{0.17em}{\tau }_i)=:\hspace{0.17em}S(D_i|T)\\ =(1-\nu -{\lambda }_{\text{wl}}-{\lambda }_{\text{ml}}-\kappa )S_{\text{ht}}(D_i|T)+\nu S_{\text{hm}}(D_i|T)\\ +\hspace{0.17em}{\lambda }_{\text{wl}}{S}_{\text{wl}}(D_i|T)+{\lambda }_{\text{ml}}{S}_{\text{ml}}(D_i|T)+\kappa S_{\text{pm}}(D_i|T)\end{array}$$ (3)

We detail below how to compute the individual terms S in this mixture in time O(m) using tree traversals and tracking partial sums. The overall time complexity of computing the tree marginalized likelihood is O(mn), the same complexity class as in SCI$\Phi$.

Artefacts in sequencing data may mimic the effects of violations of the infinite sites assumption (Kuipers et al., 2017b), while their effect on the likelihood would scale with the number of mutations. To compensate for such effects, we introduce a regularizing prior, compounded for each lost or parallel mutation, with an exponential form as

$$P(D|T)\propto {\mathrm{e}}^{-\chi ({\lambda }_{\text{wl}}+{\lambda }_{\text{ml}}+\kappa )n}\prod _{i=1}^n\sum _{{\tau }_i}S(D_i|T)$$ (4)

where χ = 0 would correspond to no regularization, while the limit $\chi \to \infty$ would enforce the infinite sites assumption and allow no lost or parallel mutations. A fixed prior, which does not scale with the number of mutations, would roughly correspond to $\chi \approx \frac{1}{n}$.

2.2 Variant read model

The MDA process (Lasken, 2009) is akin to a Pólya urn, where successfully amplified genomic fragments are returned to the Pool to potentially be amplified in the next round. For the distribution of variant reads at a given coverage c, we therefore employ a Beta-binomial distribution with density

$$d\left(v|c,\hspace{0.17em}f,\hspace{0.17em}\omega \right)=\left(\begin{array}{c}c\\ v\end{array}\right)\frac{B(v+\alpha ,c-v+\beta )}{B(\alpha ,\beta )}$$ (5)

where B is the beta function, and we parameterize in terms of the expected frequency $f=\frac{\alpha }{\alpha +\beta }$ of the variant and the overdispersion $\omega =\alpha +\beta$. For heterozygous mutations, we expect a frequency $f\approx \frac{1}{2}$. For wild-type positions, we only expect sequencing or MDA errors, which can also be modelled with a Beta-binomial distribution with a low frequency $f_{\text{wt}}$. When the underlying state is wild type, the likelihood is

$$P_{\text{wt}}(D_{ij})=d(v_{ij}|c_{ij},\hspace{0.17em}{f}_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}})$$ (6)

Similarly, when the underlying state is hemizygous so that only a mutated allele remains, we have

$$P_{\text{hm}}(D_{ij})=d(c_{ij}-v_{ij}|c_{ij},\hspace{0.17em}3f_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}})$$ (7)

where sequencing errors may lead to any of the other three bases giving the additional factor here [which was not considered in Singer et al. (2018)].

Finally, when the underlying state is heterozygous, we explicitly include an allelic dropout parameter μ, and have the following mixture

$$\begin{array}{c}{P}_{\text{ht}}(D_{ij})=\frac{\mu }{2}{P}_{\text{wt}}(D_{ij})+\frac{\mu }{2}{P}_{\text{hm}}(D_{ij})\\ +(1-\mu )d\left(v_{ij}|c_{ij},\hspace{0.17em}\frac{1}{2}-f_{\text{wt}},\hspace{0.17em}{\omega }_{\text{ht}}\right)\end{array}$$ (8)

where the first two terms are the loss of the variant and reference allele, respectively, and the third when both alleles are amplified. In that case, we adjust the expected frequency slightly to account for errors resulting in the other bases [this is a corrected version compared to Singer et al. (2018)].

2.3 A heterozygous mutation

We compute a mixture over the different types of mutation placed upon each branch of the tree, so we start by considering, for a particular locus i, placing a heterozygous mutation everywhere in the tree T (Supplementary Fig. S1a) and wish to compute

$$S_{\text{ht}}(D_i|T)=\frac{1}{2m-1}\sum _{{\tau }_i}\prod _{\stackrel{j=1}{j\prec {\tau }_i}}^m{P}_{\text{ht}}(D_{ij})\prod _{\stackrel{j=1}{j\mathrm{\nprec }{\tau }_i}}^m{P}_{\text{wt}}(D_{ij})$$ (9)

where we divide by $(2m-1)$ to normalize over the possible placements in the tree, and where $j\prec {\tau }_i$ means that cell j is below the attachment point of the mutation and so should exhibit a heterozygous mutation at locus i, while it should be wild-type otherwise. To proceed, we factor out the contribution where every cell is wild type

$$P_{\text{wt}}(D_i)=\prod _{j=1}^m{P}_{\text{wt}}(D_{ij})$$ (10)

and define

$${\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}{\tau }_i)=\prod _{\stackrel{j=1}{j\prec {\tau }_i}}^m\frac{P_{\text{ht}}(D_{ij})}{P_{\text{wt}}(D_{ij})}$$ (11)

as the (relative) likelihood of the data when a heterozygous mutation at locus i is placed at position τ_i in the tree T. For simplicity, we will number the branches above the leaves with the number of the cell below, from 1 to m and label the inner branches from $(m+1)$ to $(2m-1)$, see Supplementary Fig. S1a. For the leaves in the tree, the computation just involves the likelihood ratio of heterozygous mutations and wild type for each cell

$${\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}j)=\frac{P_{\text{ht}}(D_{ij})}{P_{\text{wt}}(D_{ij})}\hspace{0.17em},\hspace{1em}j=1,\dots ,m$$ (12)

For the inner nodes, we can compute the probabilities using a depth-first tree traversal

$${\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}x)={\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}{x}_{\mathrm{l}}){\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}{x}_{\mathrm{r}})$$ (13)

where we denote the two children of x in the tree T as $x_{\mathrm{l}}$ and $x_{\mathrm{r}}$. This relationship is illustrated in Supplementary Fig. S1b, where having a mutation placed on the branch labelled 11 means the mutation is inherited down the tree into cells 1–3. Placing the mutation at each of the child branches (labelled 8 and 3 in Supplementary Fig. S1b) also ensures that cells 1–3 inherit the mutation. The likelihood contribution from having the mutation in cells 1 and 2 was computed when placing the mutation in the branch labelled 8, while the contribution from cell 3 was computed when placing the mutation in the branch labelled 3. By simply combining these two child contributions according to Equation (13), we obtain the likelihood contribution when placing the mutation at the parent branch. The sum

$$S_{\text{ht}}(D_i|T)=\frac{1}{2m-1}\sum _{{\tau }_i}{\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}{\tau }_i)P_{\text{wt}}(D_i)$$ (14)

can then be computed in time O(m).

2.4 A hemizygous mutation

If a mutation occurs in a region with only one allelic copy, we have the same recursion

$${\tilde{P}}_{\text{hm}}(D_i|T,\hspace{0.17em}x)={\tilde{P}}_{\text{hm}}(D_i|T,\hspace{0.17em}{x}_{\mathrm{l}}){\tilde{P}}_{\text{hm}}(D_i|T,\hspace{0.17em}{x}_{\mathrm{r}})$$ (15)

for the inner nodes and the following starting values

$${\tilde{P}}_{\text{hm}}(D_i|T,\hspace{0.17em}j)=\frac{P_{\text{hm}}(D_{ij})}{P_{\text{wt}}(D_{ij})}\hspace{0.17em},\hspace{1em}j=1,\dots ,m$$ (16)

for the leaves. For the sum, however, we exclude hemizygous mutations occurring in a single cell. The rationale is that we cannot distinguish between a hemizygous mutation in a single cell from the drop-out of the wild-type allele in the amplification process for that cell. Since drop-out occurs relatively frequently in SCS, we assume this as the simpler explanation of the data, and only consider hemizygous mutations when corroborated by at least two cells. We therefore define the sum as

$$S_{\text{hm}}(D_i|T)=\frac{1}{m-1}\sum _{{\tau }_i>m}{\tilde{P}}_{\text{hm}}(D_i|T,\hspace{0.17em}{\tau }_i)P_{\text{wt}}(D_i)$$ (17)

which we can again compute in time O(m).

2.5 Loss and parallel mutations

By tracking partial likelihood sums throughout the tree, we can include loss and parallel mutations also in linear time O(m), which we detail in Supplementary Section A.

2.6 Tree scoring complexity

The overall tree score can therefore be computed in time O(mn), since we employed tree traversals to compute the terms and partial sums needed for its computation. This is akin to the peeling algorithm of Felsenstein (1981) used to track partial likelihoods and marginalize the inner node states in leaf-labelled trees. The difference here is in the kind of biological effects we permit in our tree, and that our restrictions span generations leading to more complicated tree recursions. The restrictions we impose are such that if there is a simpler model which generates the exact same cell genotypes as the more complex one, we rule out the more complex case. For example, if two parallel mutations can be replaced by a single mutation affecting the same cells in the tree, we do not allow the parallel mutation case. Likewise, if the loss of mutation can be replaced by allelic dropout, we exclude the loss from the modelling.

2.7 Posterior mutation probabilities

With non-informative priors on the parameters and T, we obtain $P(T,\hspace{0.17em}{f}_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}},\hspace{0.17em}{\omega }_{\text{ht}}|D)\propto P(D|T,\hspace{0.17em}{f}_{\text{wt}},\hspace{0.17em}{\omega }_{\text{wt}},\hspace{0.17em}{\omega }_{\text{ht}})$. To obtain a sample from the posterior space, we employ MCMC where we may swap leaf labels or prune and reattach a subtree or perform a Gaussian random walk for the continuous parameters, as detailed in Singer et al. (2018).

From the sample of trees and parameters, we reverse the marginalization to obtain the posterior probability of each mutation occurring in each single cell. We average over the full sample of trees and parameters to obtain the posterior mutation probabilities.

From each sampled tree and parameter combination in the average, we first compute the probability of each mutation type. For heterozygous mutations, we know the relative probability of the mutation occurring at each node by normalizing ${\tilde{P}}_{\text{ht}}(D_i|T,\hspace{0.17em}x)$ by their sum. Propagating these probabilities down from the root to the leaves provides the conditional probability of mutational presence in each cell given that it is a heterozygous mutation. For hemizygous mutations and the loss of the wild-type allele, we compute the probabilities analogously.

For the posterior probabilities of loss of the mutated allele and parallel mutations, we need to track additional terms during the tree traversal, which we detail in Supplementary Section A.4.

2.8 Hill climbing

As well as using the MCMC scheme to sample trees, parameters and variant calls from the posterior, we can adapt it to find a point estimate with fewer iterations and at lower computational cost. For this, we employ hill climbing by accepting any move which increases the tree score. We terminate the search when no structure change has happened for 10 m iterations. After each termination we accept all moves for m iterations to rejig the tree before hill climbing again, and repeat the procedure 10 times.

2.9 Simulation settings

The simulated datasets were generated similarly to the process described in Singer et al. (2018). In a first step, we generated a random binary genealogical cell linage tree with 25 cells and assigned 100 mutations to the inner nodes. The mutations of node x were then propagated to the leaves in the subtree rooted at x. In addition, with probability 0.2 either the mutation or the wild-type allele was lost, simulating drop out events.

The mutations were then mapped to a 1 million base pair (bp) long random reference, with a nucleotide distribution following a Pòlya urn model as detailed in Singer et al. (2018). In addition, we also simulated sequencing errors with a frequency of ${10}^{-3}$ and polymerase chain reaction (PCR) amplification errors with a frequency of $5\times {10}^{-7}$. In contrast to Singer et al. (2018), we also simulated the loss of one allele of a mutation and the appearance of the same mutation twice independently in two distinct subtrees. With probability λ, a mutation in the subtree rooted at node x becomes wild type or homozygous alternative in the subtree rooted at node y. Here, the choice of node y is uniform in the subtree of x. With probability κ, two nodes in two distinct subtrees were chosen to be mutated to simulated the occurrence of a parallel mutation.

3 Results

3.1 Benchmarking on simulated data

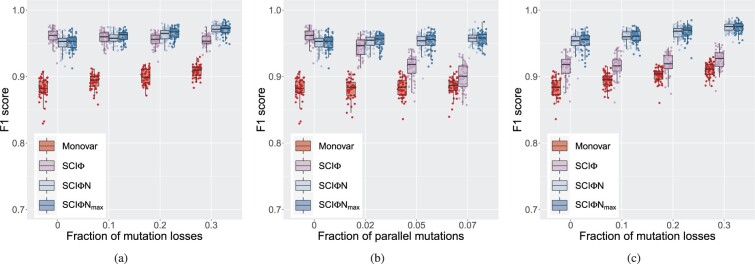
To explore the performance in calling mutations, we simulated data with various violations of the infinite sites assumption (Fig. 2). First, we added increasing amounts of losses with no parallel mutations (Fig. 2a and Supplementary Fig. S3), and we see similar F1 performance to SCI$\Phi$, with better performance at higher levels of losses, but a slight decrease in performance when there are no losses. The more complicated model of SCI$\Phi$N can explain some randomly correlated drop-out events as mutational losses, which is ruled out by the model of SCI$\Phi$ leading to a slight relative loss of recall, but better precision since actual loss events can now be properly identified by SCI$\Phi$N instead of being misclassified by SCI$\Phi$. Loss of wild-type alleles results in hemizygous mutations, which are harder to misclassify as unmutated, leading to the general increase in recall at higher rates of loss (Supplementary Fig. S3a).

Fig. 2.

Effect of infinite sites violations on single-cell mutation calling. We compare the F1 score for the mutation calls of SCI$\Phi$N to SCI$\Phi$ (Singer et al., 2018) and Monovar (Zafar et al., 2016). Also included are the results for the faster hill-climbing version of SCI$\Phi$N denoted SCI$\Phi$N${}_{\text{max}}$. (a) Losses, with no parallel mutations. (b) Parallel mutations, with no losses. (c) Losses with 5% parallel mutations

With parallel mutations (Fig. 2b and Supplementary Fig. S4), there is a clear degradation in the precision of SCI$\Phi$, while SCI$\Phi$N has near perfect precision because such events are included in the modelling. There is a slight cost of the more complex model of SCI$\Phi$N in terms of the recall, but the overall F1 score show the advantage of the SCI$\Phi$N model even at low rates of parallel mutations.

When both losses and parallel mutations are present (Fig. 2c and Supplementary Fig. S5), these effects combine to amplify the improvement of SCI$\Phi$N over the simpler infinite sites model of SCI$\Phi$. In all cases (Fig. 2), SCI$\Phi$N performs more strongly than Monovar (Zafar et al., 2016) since Monovar does not use the phylogenetic relationship between cells to help improve mutation calling.

Using hill climbing to target the highest scoring tree (Fig. 2, SCI$\Phi$N${}_{\text{max}}$) offers similar performance in mutation calling, with a slight gain in recall and slight loss in precision (Supplementary Figs S3–S5) compared to taking a sample from the posterior with SCI$\Phi$N. Finding the point estimate is however much faster, taking on average under 3 min compared to about 1 h for SCI$\Phi$N sampling in this simulation setting. (Computation times are for a single core of a cluster with Intel Xeon Gold 5118 and 6150, and AMD EPYC 7H12, 7742 and 7763 nodes.)

To benchmark the tree structure learning, we use the root mean square difference in genotype between all pairs of cells (which is their shortest path in the tree) for the inferred tree compared to the generating tree [as in Singer et al. (2018)]. SCI$\Phi$N again offers a strong improvement over SCI$\Phi$ (Supplementary Fig. S6), as soon as we leave the infinite-sites simulation setting. Although faster and with a similar performance in mutation calling, we observe a consistent slight worsening of performance in recreating the tree structure when using hill climbing to target the tree with the highest score (Supplementary Fig. S6, SCI$\Phi$N${}_{\text{max}}$) compared to the sampling approach of SCI$\Phi$N.

3.2 Mutation calling and phylogenetic reconstruction from tumour data

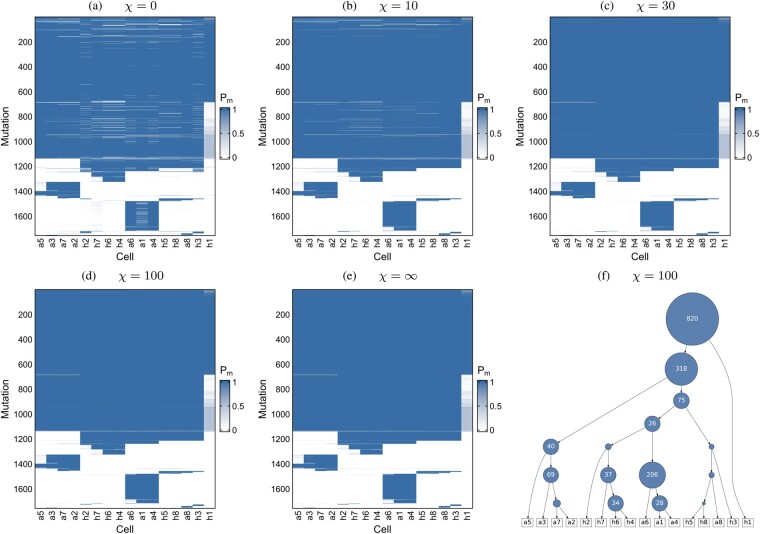
First, we applied SCI$\Phi$N to a WES dataset of 16 single cells from a breast cancer (Wang et al., 2014). For the somatic mutations previously identified by SCI$\Phi$, we examine the effect of the regularization of losses and parallel mutation (Fig. 3). This can be seen more clearly when we consider the differences to the infinite sites case (Supplementary Fig. S7), or separate out the contributions to the probability of mutation presence from the different mutation types considered in our modelling (Supplementary Fig. S8). While the majority of mutations are shared in all cells (with the possible exception of cell h1 where mutation calling is more uncertain), we observe significant amounts of loss with no penalization (χ = 0, Fig. 3a, Supplementary Fig. S8, top row). With increasing penalization, only losses and parallel mutations with stronger evidence in the sequencing data are retained, until none are allowed under the infinite sites assumption ($\chi =\infty$, Fig. 3e, Supplementary Fig. S8, bottom row).

Fig. 3.

Mutation calling on 16 breast cancer cells. (a–e) The probability of mutation presence, P_m in the single cells for different values of the regularization χ on parallel mutations and mutation losses. The ordering of the mutations and cells is determined by the tree (f) learned under moderate penalization (χ = 100)

To better interpret the penalization, we extract highly confident clonal mutations (with a posterior probability above 95% in at least 95% of cells) under the infinite sites assumption, and compute how much of their mutation probability derives from cases with mutation loss or parallel mutations (Supplementary Fig. S9a). For example, the penalization χ = 100, keeps their average contribution below 1%.

When we compare the mutation calls to Monovar (Zafar et al., 2016), SCI$\Phi$N finds many more mutations (Supplementary Fig. S10), particularly since it can correct for allelic dropout by sharing information across cells through the inferred phylogeny, in line with the simulation results. SCI$\Phi$N and SCI$\Phi$ are highly consistent across the cells. Since SCI$\Phi$ cannot model mutational loss it must call as present mutations which are supported by other cells in a subtree even without variant reads. Whereas, for neighbouring cells without variant reads, SCI$\Phi$N can identify a shared mutational loss allowing it to call a few fewer mutations than SCI$\Phi$. In terms of runtime, Monovar is notably faster than SCI$\Phi$N since it does not use or infer a phylogeny, taking around 1 h for this dataset compared to about 12 h for SCI$\Phi$N (and about 7 h for SCI$\Phi$), though the hill climbing version SCI$\Phi$N${}_{\text{max}}$ is even faster, taking around 20 min.

As a second dataset, we considered panel-based sequencing of 255 single cells on positions detected in bulk WES for a patient with acute myeloid leukaemia (Gawad et al., 2014). This dataset involves high-throughput sequencing, which may be more error and doublet (inadvertent sequencing of two cells together) prone and, with a large number of cells relative to the number of mutations profiled, is challenging for cell lineage reconstruction. With no penalization (Supplementary Fig. S11a), we observe lots of violations of the infinite sites assumption to explain the data, which are smoothed out with moderate penalization (Supplementary Fig. S11b and c). Under the infinite sites assumption (Supplementary Fig. S11d), mutations are missing which could otherwise be explained as loss or parallel mutations with more moderate penalization (Supplementary Fig. S13). The overall mutation probabilities are still highly similar across the different penalizations (Supplementary Figs S11 and S12), but the assignment of their constitute parts to different mutation types varies significantly (Supplementary Fig. S13). With no penalization, the data can be explained under the loss and parallel mutation models, while under the infinite sites model everything is explained only as mutations. Again, for high confidence clonal mutations, the penalization χ = 100, keeps the average contribution from loss and parallel mutations below 1% (Supplementary Fig. S9b).

In terms of runtime, Monovar is much faster, taking around 45 min for this second dataset compared to about 30 h for SCI$\Phi$N (and about 15 h for SCI$\Phi$ and 7 h for SCI$\Phi$N${}_{\text{max}}$), but does not benefit from sharing information across cells that we leverage with the phylogenetic modelling of SCI$\Phi$N.

4 Discussion

We developed SCI$\Phi$N, a tree inference method for cell lineage building and mutation calling from SCS data which allows for mutational losses and recurrent mutations, and which therefore better models the complex evolution of tumours. Compared to the previous, simpler model of SCI$\Phi$ which assumes the infinite sites assumption, the new method developed here offers superior mutation calling. Also, despite the strength of SCI$\Phi$N in modelling tumour evolution more realistically, we managed to constrain its computational complexity to the same class as the infinite sites model through tracking partial likelihood terms through judicious tree traversals.

SCI$\Phi$N considers the full read and variant counts for each cell at each genomic position to better distinguish mutations from sequencing and amplification noise. In addition, the tree building allows us to effectively share information across cells, especially to correct for allelic dropout, and improve mutation calling. In relaxing the infinite sites assumption, we only allowed certain types of violations including mutational losses and recurrent parallel mutations. Allelic dropout is relatively common in SCS data, so that violations like mutational losses in individual cells, that could be easily explained by allelic dropout instead, were excluded. Likewise, we also excluded violations that would recreate genotypes allowed under the infinite sites assumption. For example, a pair of parallel mutations in child branches generates the same genotypes as a single mutation in the parent branch. Our relaxation therefore only considers violations which should have an additional signal in the data beyond the infinite sites base model and typical sequencing noise. The relaxation is correspondingly more conservative than transition-based classical phylogenetic models adapted for SCS (Kozlov et al., 2020; Zafar et al., 2017).

Even with our stricter model, extra noise sources in the data can mimic infinite sites violations and create spurious signals (Kuipers et al., 2017b). For real-data analyses, we include additional penalization to reduce fitting such patterns and obtaining overly complex evolutionary histories. Though we might expect to see some violations in the infinite sites assumption during tumour evolution, we may not expect large numbers suggesting that some penalization is required. Future work which models all noise intrinsic in the generation of SCS data will be needed to remove such penalization. This will be particularly important for high-throughput sequencing with potentially higher noise, including doublet samples which combine genotypes from different phylogenetic branches, and relatively more cells than mutations.

A restriction of SCI$\Phi$N is the assumption of an underlying diploid genome which may experience LOH, and we distinguish cases where none, all or half the alleles exhibit a mutation. For non-diploid regions, we still expect the read count distributions to be quite distinct when none or all of the alleles have the mutation, compared to some, and therefore to have a degree of robustness to ploidy changes, as was the case for SCI$\Phi$ (Singer et al., 2018). However, the model of SCI$\Phi$N does not account for finer copy number changes, essentially treating all non-homozygous states as heterozygous, and so cannot resolve them or their evolutionary relationships.

For large scale datasets, the speed of MCMC schemes can become an issue. An interesting avenue has been to recode the maximum likelihood point estimate corresponding to SCI$\Phi$ as integer linear programming (ILP) constraints, which can offer significant speed-ups (Edrisi et al., 2019), as can hill-climbing in the search space (Edrisi et al., 2022), as we also explored here. Branch and bound algorithms have also been shown to offer a substantial speed-up for the binarized phylogeny problem (Sadeqi Azer et al., 2020). Interfacing these ideas may provide pathways to speed up Bayesian inference to account for model uncertainty, as well as for the more complex model developed here.

Data Availability

SCI$\Phi$N is available at https://github.com/cbg-ethz/SCIPhIN under a GNU General Public Licence v3.0 licence. The sequencing datasets were downloaded from the Sequence Read Archive with accession numbers SRA053195 and SRP044380.