Machine learning on syngeneic mouse tumor profiles to model clinical immunotherapy response

Abstract

Most patients with cancer are refractory to immune checkpoint blockade (ICB) therapy, and proper patient stratification remains an open question. Primary patient data suffer from high heterogeneity, low accessibility, and lack of proper controls. In contrast, syngeneic mouse tumor models enable controlled experiments with ICB treatments. Using transcriptomic and experimental variables from >700 ICB-treated/control syngeneic mouse tumors, we developed a machine learning framework to model tumor immunity and identify factors influencing ICB response. Projected on human immunotherapy trial data, we found that the model can predict clinical ICB response. We further applied the model to predicting ICB-responsive/resistant cancer types in The Cancer Genome Atlas, which agreed well with existing clinical reports. Last, feature analysis implicated factors associated with ICB response. In summary, our computational framework based on mouse tumor data reliably stratified patients regarding ICB response, informed resistance mechanisms, and has the potential for wide applications in disease treatment studies.

Machine learning integrating mouse transcriptome and experimental variables predicts tumor immunity and immunotherapy response.

INTRODUCTION

Immune checkpoint blockade (ICB) has been found to have clinical benefits in only a subset of patients with cancer (1–3). To optimize treatment selection and maximize the potential benefits, there is an urgent need to stratify patients for ICB treatment (4). Multiple methods to stratify patients for ICB treatment have been developed, including programmed death ligand 1 (PDL1) expression (5), microsatellite instability (5, 6), and tumor mutation burden (7). More recently, multiple integrative biomarkers derived from human samples have been reported that can better stratify patients for ICB response (8–11). However, the sensitivity of these methods is largely dependent on the size and quality of human samples, which suffer from high heterogeneity, low accessibility, and lack of proper controls.

Compared to human samples, syngeneic mouse models allow well-controlled experiments and provide a rich resource for studying tumor immunity and immunotherapy response. Syngeneic mouse models are cancer cells implanted into immunocompetent host mice of the same genetic background (12, 13) and faithfully recapitulate the complexity of cancer cells and their interactions with the immune system (14). These readily available models enable studies of in vivo ICB response in a well-controlled manner and have been widely used to investigate the mechanisms underlying immunotherapy resistance. These numerous syngeneic mouse studies have resulted in a large volume of tumor expression profiles under various immunotherapy treatments (12, 13, 15). Transcriptomic analysis on a large collection of syngeneic tumors curated from these well-controlled experiments can help elucidate mechanisms underlying ICB response and resistance in human tumors (16, 17).

Both tumor transcriptomic data and demographic information are critical factors underlying ICB response. Dimension reduction leveraging known sample experimental information could guide the decomposition of the transcriptome toward more biologically relevant results and potentially improve the performance of clustering and classification (18, 19). There has been much work in developing models that make use of available sample labels (such as therapy response) (20–24). These approaches leverage the labels to increase mutual information between computed hidden factors and the known labels (19). Meanwhile, multiple dimension reduction methods have been developed in the past. Among them, nonnegative matrix factorization (NMF) is especially applicable to transcriptomic data as gene expression is inherently nonnegative, giving NMF the added benefit of easier interpretation (25–28).

To better understand factors underlying ICB immunotherapy response, we performed a meta-analysis on the syngeneic mouse models. We present a joint NMF model using iterative updates that incorporates experimental data and ICB response data to decompose and reduce the dimensionality of tumor transcriptomic data. We provided iterative update rules for our proposed tool trained on syngeneic mouse data and validated its power in predicting human ICB response. The derived latent factors were conserved in clinical samples across a broad range of cancer types. We further explored major latent factors enriched in each cancer type and highlighted important pathways and genes for future investigation. In addition, our proposed method can be extended to predict a human sample’s likelihood to respond to a specific ICB treatment, suggesting that this framework has the potential to be a useful clinical decision support tool.

RESULTS

Overview of the joint dimension reduction framework

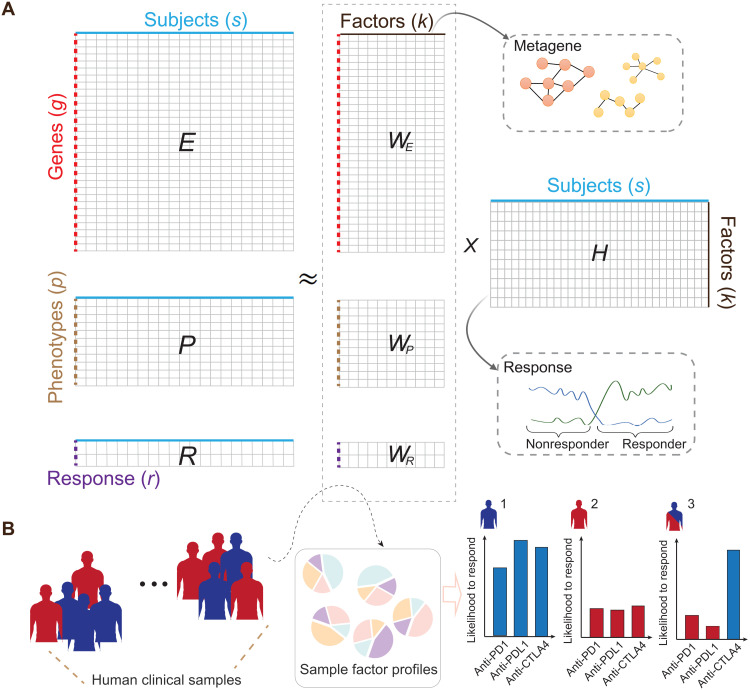
We used data from syngeneic mouse models treated with ICB to learn latent factors underlying ICB resistance and response. We curated syngeneic mouse data from a previous study (15), where we systematically collected and processed 761 syngeneic tumor RNA sequencing (RNA-seq) samples from 26 published studies (table S1). These curated in vivo RNA-seq samples were from 22 syngeneic mouse tumor models across 13 cancer types, of which 420 samples were ICB-treated (post-ICB) and 341 samples were their matched controls (treatment-naïve). Samples in the post-ICB group were treated with anti–programmed cell death protein 1 (PD1), anti-PDL1, anti-PDL2, anti–cytotoxic T lymphocyte–associated protein 4 (CTLA4), or their combinations. To ensure data consistency, gene expression levels for all samples were quantified from raw sequencing reads using a single standardized pipeline. We also manually annotated experimental variables for each sample by referring to the original article, including cancer type, cancer cell line, cell perturbation, mouse genotype, mouse strain, implantation site, mouse ICB treatment, and ICB response status (table S1). The response labels for the control group were annotated on the basis of the response status of their matched treatment group. The syngeneic mouse data were used to construct the expression matrix (E, gene*sample), experimental variable matrix (P, experimental variable*sample), and response label matrix (R, response*sample) (Fig. 1A) (Materials and Methods).

Fig. 1. Illustration of the dimension reductions to integrate transcriptomic, phenotypic, and ICB response data.

(A) The framework takes the gene expression matrix, mouse experimental variables, and ICB response data for joint dimension reduction through iterative updates. The model was trained with an extensive collection of syngeneic mouse model data with curated ICB response labels. The columns in the decomposition products W_E can be collectively interpreted as metagenes to help inform the ICB resistance and response in the syngeneic mouse models. (B) Leveraging the decomposition outputs from the model, we could simulate an individual’s likelihood to respond to anti-PD1, anti-PDL1, or anti-CTLA4 treatment with available transcriptomic data.

Measurement of the transcriptome (matrix E) is a snapshot of the sample state and reflects a mixture of various biological factors (29). To deconvolute this mixture and derive the biological signals contributing to ICB response, we developed a modified NMF model to jointly decompose E, P, and R, and find common latent factors that are manifested in these three data matrices. We formulated the problem as a joint dimension reduction to capture patterns of common variations across the E, P, and R matrices (Fig. 1A). Through iterative updates, it inferred an interpretable low-dimensional data representation, W_E, W_P, W_R,and H, that captured the major sources of variation across the E, P, and R matrices (fig. 1A) (Materials and Methods). The matrices W_E, W_P, and W_R serve as the basis for the lower-dimensional spaces, whereas the H matrix provides the coefficients for data to be projected in these spaces. The columns of the W_E matrix (gene*factor k) can be used to extract markers by selecting the top-ranked genes or to identify pathways. The rows of H (factor*sample) can be used for sample clustering and classification. Hereafter, we denote columns of the matrix W_E as metagenes, defined as a positive linear combination of a set of genes. With the model trained, the decomposition outputs were further extended to predict a human sample’s ICB treatment–specific response (Fig. 1B) (Materials and Methods).

Training and validation of the framework on syngeneic mouse tumors

We trained the joint dimension reduction framework separately using the post-ICB and control syngeneic model data. For both training processes, we split the data into training, validation, and testing sets in the ratio of 6:2:2. The training data were used to optimize the matrix reconstruction errors, and the validation set was used to tune the hyperparameters, including penalty terms for the phenotype and response matrix reconstruction errors and the number of latent factors k (Materials and Methods). In brief, the framework takes the gene expression matrix, mouse experimental variables, and ICB response as inputs and seeks lower-dimensional representations through iterative updates. The model quickly converged monotonically on the training data for treatment and control tumors (fig. S1, A and C). We repeated the experiment 10 times with random initial seeds. The penalty terms for the phenotype matrix and response matrix govern their relative importance in matrix reconstruction and are tuned in the validation set based on prediction accuracy. We noted that this balance between optimizing reconstruction error and prediction accuracy could prevent model overfitting (fig. S1, B and D) (Materials and Methods). Of the 10 replicates, the model with the best performance in the testing dataset was used for downstream analyses (table S2 and fig. S1, B and D).

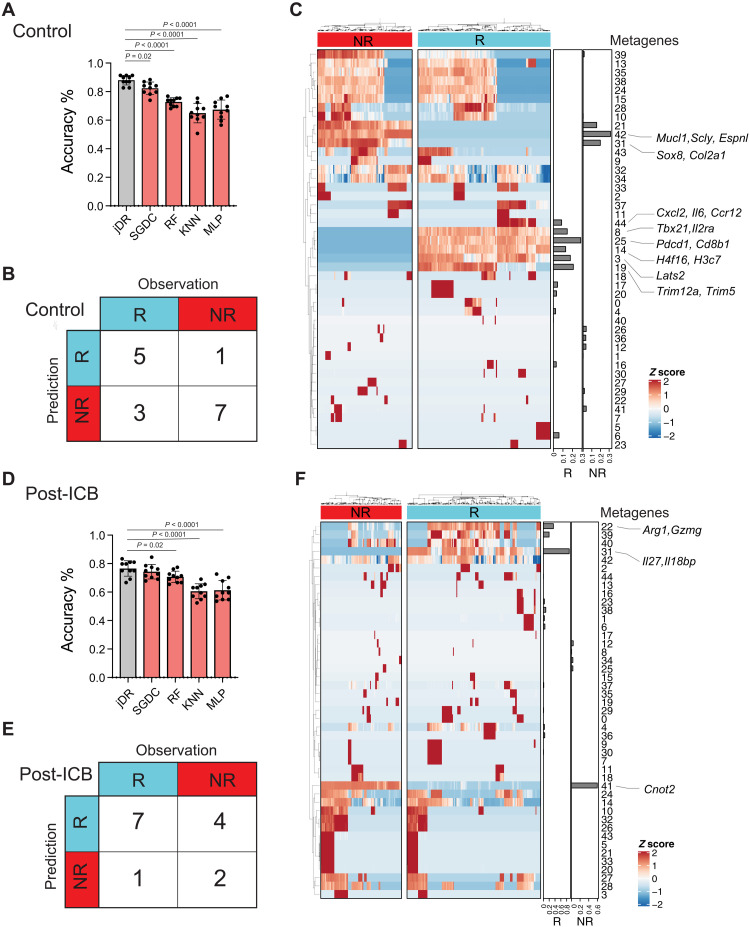
When evaluated on the testing datasets, our model accurately predicted ICB response labels for the syngeneic mouse models in both the treatment (76.5%, SE = 1.7%) and control (88.0%; SE = 1.1%) tumors (Materials and Methods). To benchmark these results, we compared our model to linear and nonlinear supervised machine learning models, including a stochastic gradient descent (SGD) classifier that contains linear models of logistic regression (LR), support vector machine (SVM) and perceptron, random forest classifier (RFC), k-nearest neighbor algorithm (K-NN), and multilayer perceptron (MLP). For these benchmarking methods, grid search was implemented by Scikit-learn to tune the model parameters (Materials and Methods). In the control group, compared to the SGD classifier (82.3%, SE = 1.4%), RF (72.8%, SE = 0.9%), KNN (64.9%, SE = 2.2%), and MLP (67.4%, SE = 2.1%) (Fig. 2A), our model achieved the best mean prediction accuracy (88.0%, SE = 1.1%). In the treatment group, our model (76.5%, SE = 1.7%) significantly outperformed the RF (70.7%, SE = 1.3%), KNN (60.6%, SE = 1.7%), and MLP (61.3%, SE = 2.2%) models as well (Fig. 2D). To further validate our model, we curated 30 additional syngeneic samples from two public studies not used in the training. This external syngeneic validation set was collected in the same manner as the training data (Materials and Methods) and was composed of 14 post-ICB and 16 control samples. In this validation, our model achieved a prediction accuracy of 64.3 and 75.0%, respectively (Fig. 2, B and E).

Fig. 2. Validity evaluation of dimension reduction framework using advanced machine learning approaches and external syngeneic mouse models.

(A to C) Results from control samples. (A) Prediction accuracy of testing data over 10 replicates. Performance of our model was benchmarked by both linear and nonlinear supervised models, SGD classifier (SGDC), RFC, K-NN, and MLP. For the baseline methods, grid search was applied to tune each model’s parameters on the training set (60%). Model performance was measured on the testing data (20%). The difference in accuracy between methods was examined by the Mann-Whitney U test. (B) Contingency table summarizing ICB response predictions on 16 external control syngeneic mouse samples collected from two public studies used for validation. (C) Heatmap of the coefficient matrix of decomposition products. Bars on the right panel were derived from the basis matrix corresponding to the ICB response labels. (D to F) Results from post-ICB samples. (E) An additional 14 external post-ICB syngeneic mouse samples were collected from two studies for validation. Responder, R; nonresponder, NR.

After decomposition, the output matrices were expected to capture the sources of variation that underlie the heterogeneity of ICB resistance and response. We identified 45 metagenes each for the control (table S3) and treatment samples (table S4). These metagenes were differentially enriched between the responder and nonresponder samples (Fig. 2, C and F). When trained on control samples, our model identified metagene_25, metagene_19, metagene_3, metagene_8, metagene_14, and metagene_44 as collective contributors to ICB response (Fig. 2C and table S5). In contrast, metagene_42, metagene_31, and metagene_21 were collective contributors to ICB resistance (Fig. 2C and table S5). Each metagene’s underlying molecular representations could be inferred by its top-ranked genes. The derived metagenes implicated different molecular or functional pathways. We reasoned that capturing these various metagenes, which collectively contribute to the ICB resistance and response, was key to our model’s good prediction performance (tables S5 and S6). Examining some of the metagenes identified as contributors to ICB response more closely, the top-ranked genes in metagene_25 included Pdcd1, Cd8b1, and Cd3g, suggesting a high level of infiltrating cytotoxic T lymphocytes (CTLs) in response tumors (30, 31), and the top-ranked gene in metagene_3 was Lats2, a tumor suppressor gene, which has been shown to suppress Yes associated protein (YAP) activity and cell proliferation (32–34). Together, these data suggest that the framework was able to deconvolute data variations in the expression profiles to derive potentially biologically meaningful signals contributing to ICB response.

Predictive power of the framework on clinical ICB response

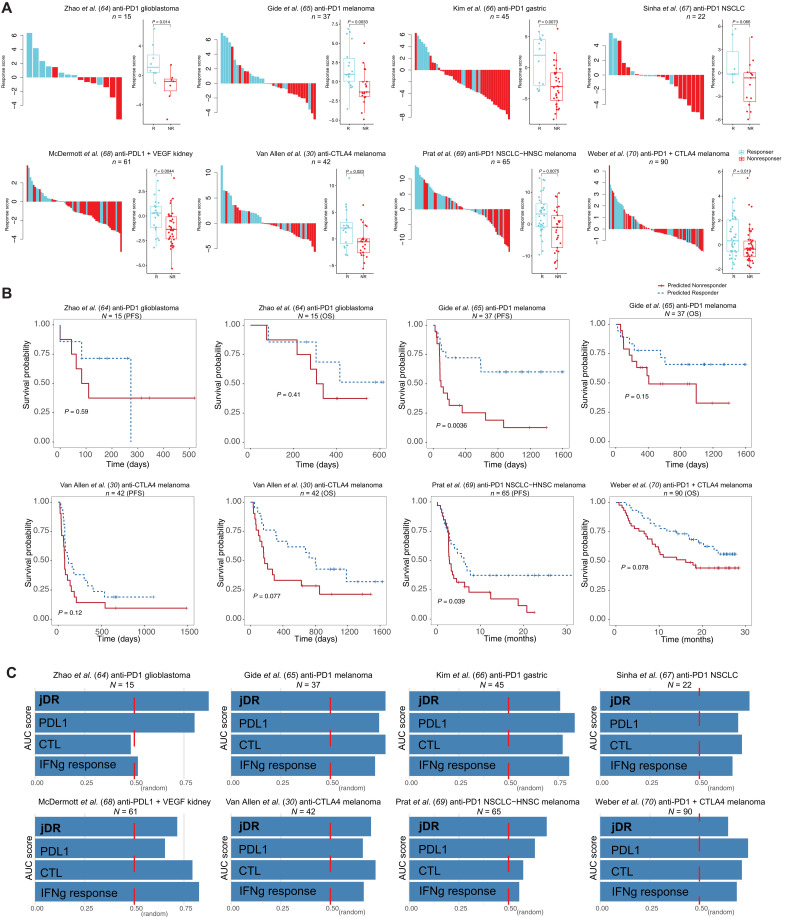
Trained on the syngeneic mouse data, the model was then extended to predict ICB response in human clinical samples with the assumption that latent factors learned from syngeneic mouse data could inform the ICB response in human clinical samples. To evaluate the effectiveness of our derived latent factors, we projected these latent factors to patient clinical samples to evaluate its ICB response prediction. We systematically collected pre-ICB samples from clinical trials for which we had matched cancer types in the syngeneic models. Transcriptome data profiled by RNA-seq were obtained from these samples before patients underwent ICB therapy. On the basis of the patients’ reported clinical prognosis, these samples were labeled as either responders or nonresponders. In total, we curated 764 human pre-ICB clinical samples from 15 clinical ICB trials to evaluate our prediction performance (Materials and Methods). We also applied our model on the tumor expression datasets containing only a few hundred genes profiled by the NanoString assay to evaluate its predictive power on a limited subset of genes. The predicted likelihood of response was defined as a continuous number computed across the human genes, cancer types, and treatment types. We also dichotomized the likelihood of response to a binary variable (responder or nonresponder) (Materials and Methods) to aid visualization. Last, all tumors were ranked by their predicted ICB response scores (Fig. 3A and fig. S2). We found that a higher tumor response prediction score was associated with better ICB response (Fig. 3A) and better posttreatment survival (Fig. 3B), demonstrating the response prediction score’s prognostic value. We noted that our model achieved a lower prediction performance in the ipilimumab (anti-CTLA4)–progressed samples compared to treatment-naïve samples (fig. S2 versus Fig. 3A). A possible explanation is that our model was trained on data from control tumors and thus not powered to model the tumors that progressed after a first-line ICB (35). The major goal of our study is to model tumor immunity and identify factoring influencing ICB response from syngeneic mouse tumor data. Although our model is different from the approaches that were trained and tested on human samples, we still found that the model can predict clinical ICB responses well. Overall, our approach achieved comparable or better average prediction accuracy [mean area under the receiver operating characteristic curve (AUC) = 0.74] than other expression-based biomarkers such as CTL (mean AUC = 0.69), PDL1 level (mean AUC = 0.72), and interferon-γ response (mean AUC = 0.68) (Fig. 3C). Together, we demonstrated that the framework has predictive power on clinical ICB response.

Fig. 3. The prediction accuracy on the human clinical trial samples and its association with patient prognosis.

(A) Waterfall plot of predicted response scores for ICB clinical trial samples. The model trained on the syngeneic mouse model data was applied to predict ICB response in human clinical samples from different cohorts. The true label was obtained from the original articles. Boxplots group the predicted scores for each sample by patient response. The score difference between the two response groups was examined by the Mann-Whitney U test. ICB treatment, cancer type, and the sample size are specified in the cohort title. (B) Kaplan-Meier overall survival curves for predicted responders versus nonresponders. Cox proportional hazards regression analysis was used to test the significance of the association. Progression-free survival, PFS; overall survival, OS; non–small cell lung cancer, NSCLC; head-neck squamous cell carcinoma, HNSC. (C) The area under the receiver operating characteristic curve (AUC) score for our joint dimension reduction (jDR) approach and other commonly used biomarkers in predicting ICB response in multiple clinical trial cohorts. IFNg, interferon-γ.

Prediction of cancer types that could benefit from ICB

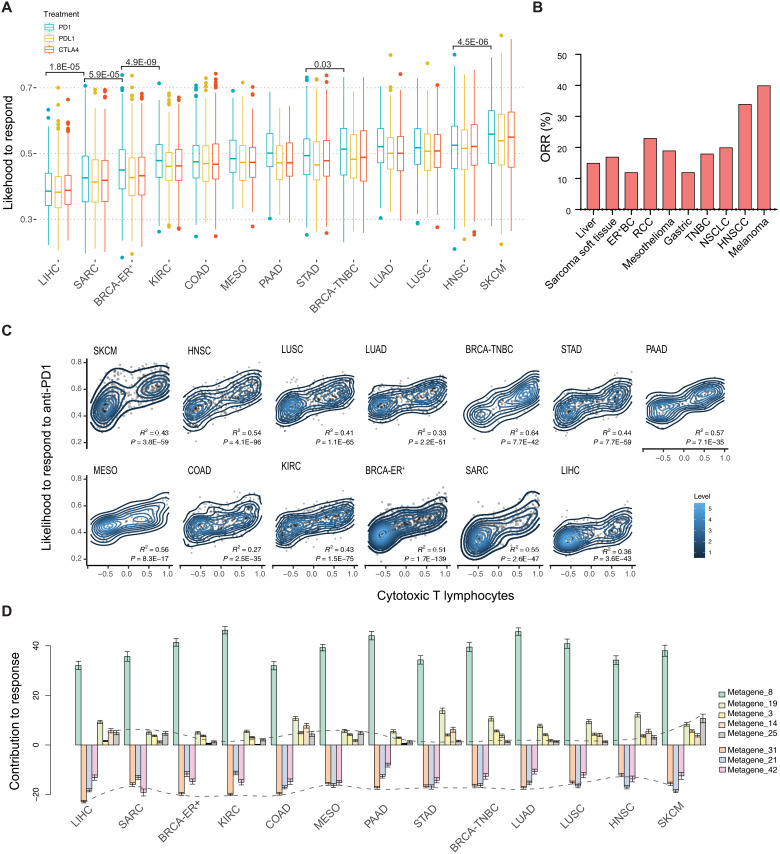
To more rigorously test our model’s performance in predicting ICB response, we applied it to samples from The Cancer Genome Atlas (TCGA) and predicted the ICB sensitivity for each cancer type. We sought to test whether our predictions of ICB-sensitive or ICB-resistant cancer types match clinical observations. Among TCGA cancer types, 13 had corresponding syngeneic mouse models in the training data. We predicted the likelihood of each sample’s response to ICB treatment with anti-PD1, anti-PDL1, and anti-CTLA4. This predicted likelihood of ICB response differed primarily by cancer type and less by the type of ICB treatment (Fig. 4A). Among the 13 cancer types, skin cutaneous melanoma (SKCM) and head and neck squamous carcinoma (HNSC) were predicted to have the highest median likelihood of response, whereas liver hepatocellular carcinoma (LIHC), sarcoma (SARC), and estrogen receptor–positive breast cancer (BRCA-ER⁺) were predicted to have the lowest median likelihood of response to ICB treatment (Fig. 4A). These predictions are consistent with the clinical trial reports assessing anti-PD1 or anti-PDL1 monotherapy on the same cancer types (Fig. 4B) (Spearman’s rank correlation, P = 0.03) (36). In addition, our model consistently predicted the likelihood of response to anti-PDL1 to be lower than anti-PD1 within each cancer type, which was also shown in the reported clinical findings (36).

Fig. 4. Profiling of predicted ICB response on human clinical samples from TCGA.

(A) The simulated results of an individual’s predicted likelihood to respond to anti-PD1, anti-PDL1, and anti-CTLA4 treatment. The predicted scores are grouped by cancer type. Only TCGA cancer types with matched syngeneic mouse models were included. The difference between treatment groups was examined by the Mann-Whitney U test and only cancer types adjacent to each other were compared. (B) Objective response rates (ORR) per cancer upon anti-PD(L)1 monotherapy from reported studies. (C) The correlation between the predicted likelihood of anti-PD1 response and inferred CTL infiltration level. The R² score and P values were derived from linear regressions. (D) Profiling of each factor’s enrichment across different cancer types. Positive scores indicate the factor positively contributed to the ICB response. Negative scores indicate resistance to ICB treatment. Scores for metagene_25 and metagene_31 were connected.

To avoid prediction bias driven by the input feature of cancer type, we masked cancer type in the input matrix and reevaluated the ICB response for all TCGA samples. This enabled us to predict ICB response for cancer types not included in the syngeneic mouse training data. With cancer type masked, our model predictions remained consistent with reported clinical trial outcomes under anti-PD(L)1 treatment (fig. S3A and table S8) (36). Specifically, the lymphoid neoplasm diffuse large B cell lymphoma was predicted to have the highest median likelihood of response among all cancer types. In contrast, glioblastoma multiforme (GBM) and LIHC were predicted to have the lowest median likelihood of responding to anti-PD1. These predictions are again highly consistent with clinical observations (37). Last, we predicted that the same individual could respond differently to each of the ICB regimens (fig. S3B), raising the possibility to use our framework to prioritize ICB treatment for patients with cancer.

We further examined whether the likelihood of response was associated with reported biomarkers and found a positive correlation with inferred CTL infiltration level (Fig. 4C and fig. S4, A and B). CTL infiltration has been shown to be a predictive marker of ICB response in several cancer types (38, 39), particularly for SKCM (40). Furthermore, the association between CTL infiltration and anti-PD1 response tends to be higher than that between CTL infiltration and anti-CTLA4 response (compare Fig. 4C and fig. S4B; P = 0.001, paired t test), suggesting that the inferred CTL infiltration level can be used as a potential biomarker to prioritize anti-PD1 regimen.

Metagenes implicate potential mechanisms of ICB response

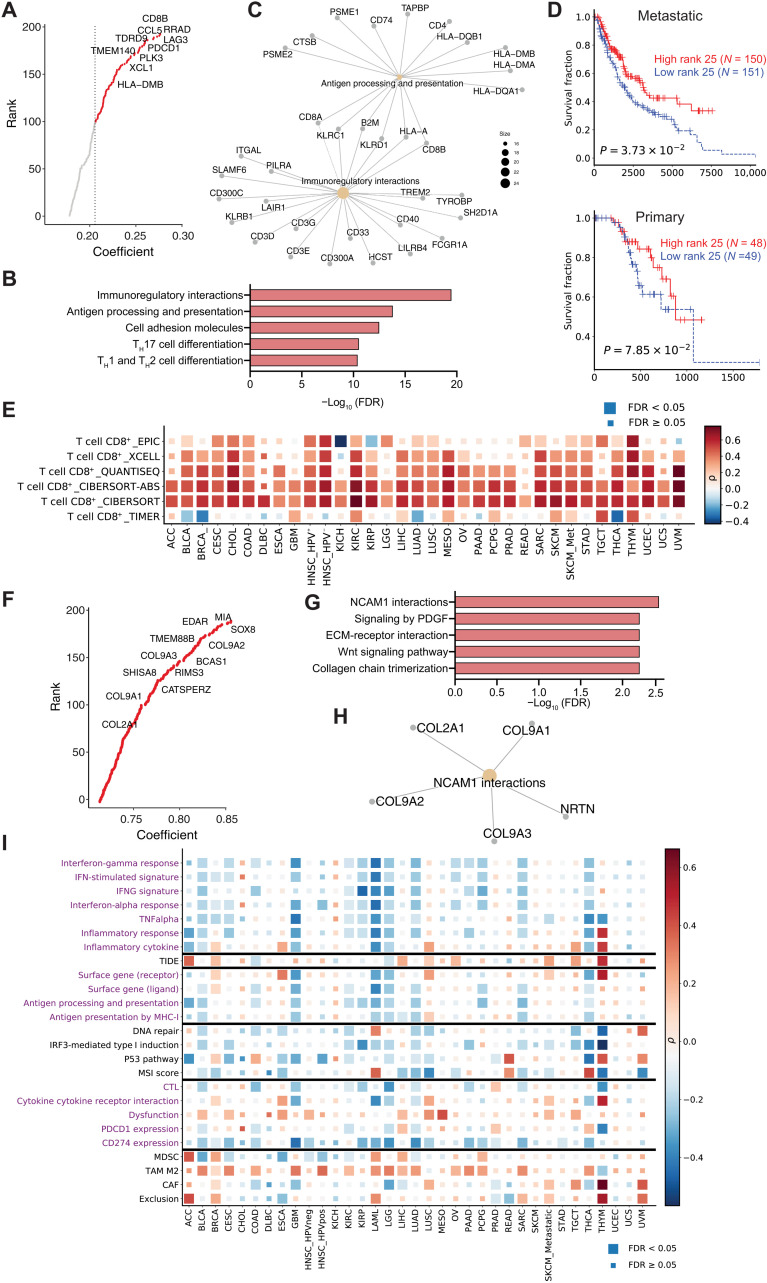
To examine the genetic features that underlie differential ICB response, we further evaluated the enrichment of metagenes in different cancer types. Specifically, metagene_25 is enriched in SKCM, which has a high response rate to anti-PD1 (Fig. 4D). The top-ranked genes in metagene_25 were Pdcd1, Cd8b1, and Cd3g (Fig. 5A), representative of CTL infiltration. Gene set enrichment analysis of genes in metagene_25 identified pathways of immunoregulatory interactions and antigen processing and presentation (Fig. 5, B and C). Metagene_25 also shows a positive correlation with improved patient survival and increased CD8⁺ T cell infiltration (Fig. 5, D and E). This is consistent with existing knowledge that higher antigen presentation and T cell infiltration in melanoma underlie its superior immune response and that higher intratumoral immune activity correlates with a better prognosis.

Fig. 5. Profiling of the metagenes derived from the dimension reductions.

(A) Top genes for metagene_25. (B) Pathway enrichment for the top 200 genes in metagene_25. (C) Gene symbols for the top two enriched pathways in metagene_25. (D) Kaplan-Meier overall survival curves for samples with high metagene_25 levels versus samples with low metagene_25 levels. The cohorts were split into high and low groups by the median score. Cox proportional hazards regression analysis was used to test the significance of the association. (E) The association between metagene_25 level and CTL infiltration level in TCGA samples. The significance of association was determined by Spearman correlation with adjustment for tumor purity. Multiple-hypothesis testing was adjusted by false discovery rate (FDR). (F) Top genes for metagene_31. (G) Pathway enrichment for the top 200 genes in metagene_31. (H) Gene symbols for the top two enriched pathways in metagene_31. (I) The association between metagene_31 level and different pathways and biomarkers (y axis) in TCGA samples. The associations between molecular phenotypes and pathways were computed for each cancer using Spearman’s partial correlation with tumor purity adjusted. The pathway expression was inferred by averaging the expression level of genes within that pathway. Color indicates the correlation coefficient (positive correlations are red and negative correlations are blue) and box size indicates the significance level (large box, FDR < 0.05; small box, not significant).

Metagene_31 is enriched in LIHC, which has a low response rate to ICB treatment (Fig. 4D). We noted that metagene_31 is also highly enriched in the syngeneic mouse models that are resistant to ICB treatment (Fig. 2C). The top genes in metagene_31 include Col2a1, Col9a1/2, and Sox8 (Fig. 5F and table S5), and enriched pathways include extracellular matrix (ECM)–receptor interactions and collagens (Fig. 5, G and H). Sox8 is a transcription factor involved in embryogenesis and is highly expressed in most hepatocellular carcinomas, where it has been shown to promote tumor cell proliferation (41). Tumor Immune Dysfunction and Exclusion (TIDE) (8) analysis suggested that Sox8 is highly expressed in alternatively activated M2 tumor-associated macrophages (TAMs), which restrict intratumoral CTL infiltration. Col2a1 encodes the alpha-1 chain of type II collagen, a component of the ECM. Collagen induction has also been reported to confer immune evasion by physically impeding CTL infiltration (42). Moreover, metagene_31 level was positively correlated with the gene signature of alternatively activated M2 TAMs (Fig. 5I), which suppress CTL response (43).

We also found that metagene_19 is highly enriched in acute myeloid leukemia (LAML), which is highly responsive to anti-PD1, and depleted in GBM (table S10), a cancer type that is resistant to anti-PD1 (37, 44). Pathway enrichment using the top genes in metagene_19 (table S5) showed regulation of the inflammatory response and myeloid cell differentiation. This is consistent with previous studies reporting that GBM is an immune-cold cancer and harbors little proinflammatory immune infiltration (45), whereas LAML inherently harbors mainly myeloid cells. Furthermore, the top-ranked genes in this metagene include Trim12a and Trim5, which encode ubiquitin E3 ligases involved in autophagy. Our results suggest further experimental investigation into these genes regarding their roles in the proinflammatory immune response. Together, these results suggest that metagenes derived from our computational framework can reflect biological features, highlight informative pathways, and suggest potential immunomodulatory targets.

DISCUSSION

In this study, we developed a joint dimension reduction framework to decompose expression and experimental variables from syngeneic mouse data to better understand tumor immunity and reveal factors influencing immunotherapy response. We found that the model trained on mouse tumors has predictive power on clinical ICB response. Leveraging the trained model, we systematically predicted the cancer types that are more likely to benefit from ICB based on TCGA data and achieved results consistent with reported clinical studies of anti-PD1 or anti-PDL1. The framework not only allows more specific prediction of ICB response in different cancer types but also reveals cancer type–specific features associated with ICB response. Our feature analysis demonstrated that our model could provide informative biological insights underlying the differential response to ICB treatment in a range of cancer types by suggesting potential immunomodulatory genes. To the best of our knowledge, this is the first and most comprehensive meta-analysis of syngeneic mouse tumors and ICB treatment data.

We have systematically predicted the likelihood of response for each TCGA sample (table S8). LAML was predicted to have a high response rate to anti-PD1, whereas GBM was predicted to have a low response rate. Metagene_19 is among the most differentially enriched metagene in these two cancer types. We reasoned that metagene_19 might be one of the major factors underlying the response in LAML and resistance in GBM. Closer examination of top-ranked genes in metagene_19 identified Trim12a and Trim5, two ortholog ubiquitin E3 ligases involved in autophagy. Autophagy has been reported to regulate antigen presentation in cancer cells (46) and phagocytosis in antigen-presenting cells (47), which collectively coordinate antitumor immune responses. Moreover, our recent work using in vivo CRISPR screens identified multiple ubiquitin E3 ligases as potential regulators of ICB response through their modulation of the myeloid composition in the tumor microenvironment (48). Therefore, our study raises the possibility that Trim12a and Trim5 might also be involved in the proinflammatory immune responses. Further studies are needed to verify their involvement in modulating the tumor microenvironment and cancer immune response.

One caveat of applying our model on the syngeneic mouse model data is the potential batch effect from samples generated by different groups across sequencing platforms. To address this, in our initial data preprocessing (15), we downloaded the raw sequencing reads from each study and processed the data through a single standardized pipeline. We further normalized the transcriptome by quantile normalization to calibrate the scaling and distribution differences across samples for each syngeneic model. We then performed batch effect correction between studies using ComBat within each syngeneic model (49). Notably, the combination of quantile normalization and ComBat was reported to most effectively remove batch effects (50). Another caveat is the uneven sample size in different models. Some models were underrepresented, whereas others were overrepresented. This representation distribution reflects the popularity of these models among researchers and the public availability of data. It may be improved in the future as more data become available. Another caveat is the criteria for determining the response to ICB, which can vary by study. These caveats limit the predictive power of our framework and can potentially be improved with more data available. Nonetheless, with the large data cohort that we collected, we derived informative biological features underlying the differences in ICB response and identified potential immunomodulatory targets for future study.

In summary, our model trained on syngeneic mouse tumor data has predictive power on clinical ICB response, implicating that analysis of syngeneic mouse tumors could help understand human tumor immunity and immunotherapy response. We perceive that this predictive power is attributable to the metagenes jointly trained from transcriptomic, experimental data, and ICB response data. Furthermore, the model was trained using a large collection of syngeneic mouse tumors from well-controlled experiments. Analyses of data from syngeneic mouse models, human clinical trials, and TCGA samples across diverse cancer types demonstrated the wide applicability of our model. Therefore, this method has the potential to be easily adapted and applied to other study domains. In addition, potential future applications of our model not covered in this study include outlier identification, feature imputation, and semi-supervised learning. In the future, we anticipate that more ICB-treated single-cell data will become available, which can further improve the resolution of our framework in modeling single-cell–level metagene features.

MATERIALS AND METHODS

Experimental design—Structure of the dimension reduction framework

Our proposed model is a modification of NMF to jointly decompose multiple matrices, including a gene expression matrix $E\in R_{\ge 0}^{n_e\times n_s}$, experimental variable matrix $P\in R_{\ge 0}^{n_p\times n_s}$, and response matrix $R\in R_{\ge 0}^{n_r\times n_s}$. Experimental variables included cancer type, cancer cell line, cell perturbation, cell genotype, mouse genotype, mouse strain, implantation type, implantation site, mouse ICB treatment, and response status for each syngeneic tumor sample. We let n_e, n_p, and n_s denote the number of genes, number of experimental variable data points, and number of samples, respectively. One-hot encoding was applied to the categorical phenotypic and response data. The model seeks lower-dimensional representations, $W_E\in R_{\ge 0}^{n_e\times k}$, $W_P\in R_{\ge 0}^{n_p\times k}$, $W_R\in R_{\ge 0}^{n_r\times k}$, and $H\in R_{\ge 0}^{k\times n_s}$ to jointly factorize the E, P, and R matrices and can be formulated as E~W_EH, P~W_PH, and R~W_RH

$$\left[\begin{array}{c}E\\ P\\ R\end{array}\right]~\left[\begin{array}{c}{W}_E\\ W_P\\ W_R\end{array}\right]H$$ (1)

We let k denote the latent factor number and let i (1 ≤ i ≤ k) be the ith column vector of the matrix E. E_i can be approximated by matrix W_E and ith column of H, which is formulated as E_i~W_EH_i. The matrices W_E, W_P, and W_R serve as the basis for the lower-dimensional spaces, whereas the H matrix provides the coefficients for data to be projected in these spaces. We require the decomposition products to be nonnegative so that the model results can be additively interpreted with ease. Given the input matrices, our model seeks a solution to the following minimization problem

$$\text{argmin} L(E,W_{E}S)+\mathrm{\lambda }L(P,W_{P}S)+\mathrm{\gamma }L(R,W_{R}S)$$ (2)

λ and γ are nonnegative regularization hyperparameters that govern the relative importance of the reconstruction terms, and L is the error function for the matrix reconstruction. Frobenius norm and the information divergence (I divergence) are the most often used discrepancy measures, and both measurements correspond to the maximum likelihood estimation given an assumed latent generative model (20). With nonnegative matrices X and Y, I divergence measures their discrepancies by

$$D(X\mid \mid Y)=\sum _{i,j}{X}_{i,j}\text{log}{X}_{\mathrm{i},j}/Y_{i,j}-X_{i,j}+Y_{i,j}$$ (3)

We note that I divergence is a generalized Kullback-Leibler (KL) divergence and could reduce to KL divergence if X and Y matrices are representations of probabilities (20, 51–53). In this application, we assume that expression data E is Gaussian-distributed and that phenotype data P and response labels R are Poisson-distributed

$$E_{\mathrm{\nu },\mathrm{\tau }}=\sum _{i=1}^k{e}_{\mathrm{\nu },i,\mathrm{\tau }} \text{and} e_{\mathrm{\nu },i,\mathrm{\tau }}~\mathrm{N}(e_{\mathrm{\nu },i,\mathrm{\tau }}\mid {W_E}_{\mathrm{\nu },i}{H}_{i,\mathrm{\tau }},\mathrm{\sigma })$$

$$P_{\mathrm{\gamma },\mathrm{\tau }}=\sum _{i=1}^k{p}_{\mathrm{\gamma },i,\mathrm{\tau }} \text{and} p_{\mathrm{\gamma },i,\mathrm{\tau }}~\mathrm{P}\mathrm{O}(p_{\mathrm{\gamma },i,\mathrm{\tau }}\mid {W_P}_{\mathrm{\gamma },i}{H}_{i,\mathrm{\tau }})$$

$$R_{\mathrm{\phi },\mathrm{\tau }}=\sum _{i=1}^k{r}_{\mathrm{\phi },i,\mathrm{\tau }} \text{and} r_{\mathrm{\phi },i,\mathrm{\tau }}~\mathrm{P}\mathrm{O}(r_{\mathrm{\phi },i,\mathrm{\tau }}\mid {W_R}_{\mathrm{\phi },i}{H}_{i,\mathrm{\tau }})$$ (4)

Although we have assumed Gaussian and Poisson distributions in this application, because of the summable property of Gaussian and Poisson random variables (54), the underlying assumptions could be changed to accommodate the uncertainty observations in the input data. Given these underlying assumptions, for this application, we denote our model as

$$\text{argmin}\parallel \widehat{W_E}\circ (E-W_{E}H){\parallel }_F^2+\lambda \mathrm{D}(\widehat{W_P}\circ P\parallel \widehat{W_P}\circ W_{P}H)+\mathrm{}\gamma \mathrm{D}(R\parallel W_{R}H)$$ (5)

We let XY denote standard matrix multiplication and let X ∘ Y denote element-wise matrix multiplication. $\widehat{W_E}$ and $\widehat{W_P}$ are feature-weight matrices empirically learned from the training data as prior information to guide the model toward biologically relevant results (55). When our model is extended from syngeneic mouse data to human sample prediction, $\widehat{W_E}$ and $\widehat{W_P}$ can be used to mask data not applicable to human samples, such as the cancer cell line.

Maximum likelihood estimation

Assuming that E_ν,τ, P_γ,τ, and R_ψ,τ are statistically independent conditional on W_E, W_P, W_R, and H, the likelihood of p(E, P, R∣W_E, W_P, W_R, H) can be denoted as

$$\prod _{\mathrm{\nu },\mathrm{\tau }}\mathrm{N}(E_{\mathrm{\nu },\mathrm{\tau }}\mid \sum _{i=1}^k{W_E}_{\mathrm{\nu },i}{H}_{i,\mathrm{\tau }},k\mathrm{\sigma })\prod _{\mathrm{\gamma },\mathrm{\tau }}\mathrm{P}\mathrm{O}(P_{\mathrm{\gamma },\mathrm{\tau }}\mid \sum _{i=1}^k{W_P}_{\mathrm{\gamma },i}{H}_{i,\mathrm{\tau }})\prod _{\mathrm{\phi },\mathrm{\tau }}\mathrm{P}\mathrm{O}\mathrm{}(R_{\mathrm{\phi },\mathrm{\tau }}\mid \sum _{i=1}^k{W_R}_{\mathrm{\phi },i}{H}_{i,\mathrm{\tau }})$$ (6)

The log-likelihood function of (6) is

$$\text{ln}p(E,P,R\mid W_E,W_P,W_R,H)=-\frac{n}{2}\text{ln}(2\mathrm{\pi })-\frac{n}{2}\text{ln}(k\mathrm{\sigma })-\frac{1}{2k\mathrm{\sigma }}\mathrm{}\mathrm{}\sum _{\mathrm{\nu },\mathrm{\tau }}{(E_{\mathrm{\nu },\mathrm{\tau }}-\sum _{i=1}^k{W_E}_{\mathrm{\nu },i}{H}_{i,\mathrm{\tau }})}^2$$

$$-\sum _{\mathrm{\gamma },\mathrm{\tau }}{(W_{P}H)}_{\mathrm{\gamma },\mathrm{\tau }}-P_{\mathrm{\gamma },\mathrm{\tau }}\text{log}{(W_{P}H)}_{\mathrm{\gamma },\mathrm{\tau }}+\text{log}\mathrm{\Gamma }(P_{\mathrm{\gamma },\mathrm{\tau }}+1)$$

$$-\sum _{\mathrm{\phi },\mathrm{\tau }}{(W_{R}H)}_{\mathrm{\phi },\mathrm{\tau }}-R_{\mathrm{\phi },\mathrm{\tau }}\text{log}{(W_{R}H)}_{\mathrm{\phi },\mathrm{\tau }}+\text{log}\mathrm{\Gamma }(R_{\mathrm{\phi },\mathrm{\tau }}+1)$$

$${=}^{+}\frac{1}{2k\mathrm{\sigma }}\parallel E-W_{E}H{\parallel }_F^2+D(P\parallel W_{P}H)+D(R\parallel W_{R}H)$$ (7)

Here =⁺ denotes the equal function after removing irrelevant constant terms that do not depend on W_E, W_P, W_R, and H. We see that this function (7) is equal to the objective function (5) after removing the additive or constant terms, demonstrating that our model is a maximum likelihood estimator with the given assumptions of uncertainty in the data matrices E, P, and H

Multiplicative updates

Our model seeks lower-dimensional representations W_E, W_P, W_R, and H to optimize the objective function (5). Multiplicative update rules are applied through the gradient of the objective function with respect to W_E, W_P, W_R, and H (56). The iterative algorithms to update W_E, W_P, W_R, and H are

$$W_E=W_E-{\mathrm{\eta }}_{W_E}{\circ \nabla }_{W_E}f(W,H)$$

$$W_P=W_P-{\mathrm{\eta }}_{W_P}{\circ \nabla }_{W_P}f(W,H)$$

$$W_R=W_R-{\mathrm{\eta }}_{W_R}{\circ \nabla }_{W_R}f(W,H)$$

$$H=H-{\mathrm{\eta }}_H{\circ \nabla }_{H}f(W,H)$$ (8)

η are parameters to control the stepwise learning rate. The derivatives of the objective function with respect to W_E, W_P, W_R, and H are derived as

$${\nabla }_{W_E}f(W,H)=-2(\widehat{W_E}\circ (E-W_{E}H))H^T$$

$${\nabla }_{W_P}f(W,H)=\widehat{W_P}{H}^T-(\frac{\widehat{W_P}\circ P}{\widehat{W_P}\circ W_{P}H}\circ \widehat{W_P})H^T$$

$${\nabla }_{W_R}f(W,H)=H^T-\left(\frac{R}{W_{R}H}\right)H^T$$

$${\nabla }_{H}f(W,H)=-2W_E^T(\widehat{W_E}\circ (E-W_{E}H))+\mathrm{\lambda }{W_P}^T\widehat{W_P}-\mathrm{\lambda }{W_P}^T(\frac{\widehat{W_P}\circ P}{\widehat{W_P}\circ W_{P}H}\circ \widehat{W_P})+\mathrm{\gamma }{W}_R^T-\mathrm{\gamma }{W_R}^T\left(\frac{R}{W_{R}H}\right)$$ (9)

The subtraction terms in the derivatives can lead to negative elements. To address this, Lee and Seung (56) proposed to adapt the learning rate η to avoid generation of negative elements. After integrating the learning rate η, the negative terms in the update rules are cancelled out and the subtraction in the update rules is avoided. Upon the derivatives, η for each basis matrix is denoted as

$$\begin{array}{c}{\mathrm{\eta }}_{W_E}=\frac{W_E}{2(\widehat{W_E}\circ W_{E}H)H^T}\\ {\mathrm{\eta }}_{W_P}=\frac{W_P}{\widehat{W_P}{H}^T} \text{and} {\mathrm{\eta }}_{W_R}=\frac{W_R}{H^T}\\ {\mathrm{\eta }}_H=\frac{H}{2{W_E}^T(\widehat{W_E}\circ W_{E}H)+\mathrm{\lambda }{W}_P^T\widehat{W_P}+\mathrm{\gamma }{W}_R^T}\end{array}$$ (10)

Using the above derivatives, we obtain the following update rules for W_E, W_P, W_R, and H. Block coordinate descent scheme is applied, in which we optimize with respect to only one rule while we keep others fixed, and then vice versa. Notably, to increase interpretability and further extend our model to human clinical response prediction, we implement the decompositions using hand-solving equations instead of the SGD optimizer (57)

$$\begin{array}{c}{W}_E\leftarrow W_E\circ \frac{(\widehat{W_E}\circ E)H^T}{(\widehat{W_E}\circ \mathit{AH})H^T}\\ W_P\leftarrow \frac{W_P}{\widehat{W_P}{H}^T}\circ (\frac{\widehat{W_P}\circ P}{\widehat{W_P}\circ W_{P}H}\circ \widehat{W_P})H^T\\ W_R\leftarrow \frac{W_R}{H^T}\circ \left(\frac{R}{W_{R}H}\right)H^T\\ H\leftarrow H\circ \frac{2W_E^T(\widehat{W_E}\circ E)+\mathrm{\lambda }{W_P}^T(\frac{\widehat{W_P}\circ P}{\widehat{W_P}\circ W_{P}H}\circ \widehat{W_P})+\mathrm{\gamma }{W_R}^T\left(\frac{R}{W_{R}H}\right)}{2{W_E}^T(\widehat{W_E}\circ W_{E}H)+\mathrm{\lambda }{W_P}^T\widehat{W_P}+\mathrm{\gamma }{W_R}^T}\end{array}$$ (11)

Immunotherapy response prediction on external data

After training our model on the syngeneic tumor data, decomposition products W_E, W_P, and W_R can be used for downstream immunotherapy response prediction on external data. We let E_et and P_et denote the external expression matrix and phenotype data, respectively. When applying the model to human ICB response prediction, as human clinical samples do not have mouse genotype or other mouse-specific information, we accommodate these feature discrepancies by masking the feature weight matrix $\widehat{W_P}$ as zeros, so that these features are not involved in the iterative updates. Similarly, we use the feature weight matrix $\widehat{W_E}$ to accommodate the gene discrepancies between mouse and human gene symbols. After obtaining W_E, W_P, W_R, $\widehat{W_P}$, and $\widehat{W_E}$ and external data E_et and P_et, we aim to solve the function

$$\text{argmin}\parallel \widehat{W_E}\circ (E_{\text{et}}-W_E{H}_{\text{et}}){\parallel }_F^2+\lambda \mathrm{D}(\widehat{W_P}\circ P_{\text{et}}\parallel \widehat{W_P}\circ W_p{H}_{\text{et}})$$ (12)

to derive coefficient matrix H_et through iterative updates as

$$H_{\text{et}}=H_{\text{et}}-{\mathrm{\eta }}_{H_{\text{et}}}{\circ \nabla }_{H_{\text{et}}}f(W,H)$$ (13)

The derivative of the objective function with respect to H is

$${\nabla }_{H_{\text{et}}}f(W,H)=-2{W_E}^T[\widehat{W_E}⨀(E-W_E{H}_{\text{et}})]+\mathrm{\lambda }{W_P}^T\widehat{W_P}-\mathrm{\lambda }{W_P}^T[\frac{\widehat{W_P}\circ P_{\text{et}}}{\widehat{W_P}\circ W_P{H}_{\text{et}}}\circ \widehat{W_P}]$$ (14)

The η_Het is specified as

$${\mathrm{\eta }}_{H_{\text{et}}}=\frac{H_{\text{et}}}{2{W_E}^T(\widehat{W_E}\circ W_E{H}_{\text{et}})+\mathrm{\lambda }{W_P}^T\widehat{W_P}}$$ (15)

to remove the negative subtraction terms. Last, we could obtain H_et through iterative updates with

$$H_{\text{et}}\leftarrow H_{\text{et}}\circ \frac{2{W_E}^T(\widehat{W_E}\circ E_{\text{et}})+\mathrm{\lambda }{W_P}^T[\frac{\widehat{W_P}\circ P_{\text{et}}}{\widehat{W_P}\circ W_P{H}_{\text{et}}}\circ \widehat{W_P}]}{2{W_E}^T(\widehat{W_E}\circ W_E{H}_{\text{et}})+\mathrm{\lambda }{W_P}^T\widehat{W_P}}$$ (16)

With coefficient matrix H_et obtained, we could further use the W_R to reconstruct the response matrix R_et for the external data using the formula R_et = W_RH_et. The number of columns in R_et corresponds to the number of samples in the external data. In the R_et matrix, the response rate is predicted as a range of values instead of a binary outcome. As we have noted, the type of ICB treatment is specified in the P_et matrix. Therefore, we could change the ICB treatment in the P_et matrix to simulate an individual’s likelihood to respond to different ICB treatments. In this scenario, our model is extended to simulate the likelihood of ICB response based on an individual’s gene expression and phenotype data.

Experiment setting and benchmarking

We split the collection of syngeneic datasets into training (60%), validation (20%), and testing (20%) sets. The split was repeated 10 times with random initial seeds. The training data are used to optimize the matrix decomposition based on the reconstruction errors, while the validation set is used to tune the hyperparameters λ and γ and the number of factors k based on the ICB response prediction accuracy. During training, the maximum number of iterations for the multiplicative updates was set to be n = 500. Early stopping criterion was specified as relative error below tolerance δ = 0.01 within 10 runs. Feature weight matrices $\widehat{W_E}$ and $\widehat{W_P}$ were empirically learned from the training dataset through correlation studies between the feature value and sample ICB response. The feature weights can serve as prior information to guide the decomposition toward biologically relevant results and greatly improve the consistency between runs (55). Before modeling, we selected a subset of representative genes (n = 5000) with highest feature weights in $\widehat{W_E}$ to achieve a more balanced sample-to-feature ratio and to reduce noise.

We apply advanced machine learning methods to benchmark the performance of our proposed model. Both linear and nonlinear models were used, including LR, SVM, RFC, K-NN, and MLP. For the evaluated models, grid search was applied to tune each model’s parameters using fivefold cross-validation on the training set (60%). Model performance was measured on the testing dataset (20%). Specifically, the search parameters include loss options (“hinge,” “log,” “squared hinge,” and “perceptron”) and penalty options (“l2” and “elasticnet”) for the linear models; criterions (“gini” and entropy) and max depth (range from 5 to 50 with interval spacing equal to 5) for the RFC; number of neighbors (range from 5 to 50 with interval spacing equal to 5) for the K-NN, learning rate (“invscaling” and “adaptive”), and activation function (“relu” and “logistic”); and a selection of number of hidden layers for the MLP. Prediction accuracy is used as selection criteria for parameter tuning and model selection. Once the model was tuned, it was applied to the testing set to evaluate prediction accuracy. Mean and SE of the prediction accuracy were reported for the trained models. Let $R_i \text{and} \widehat{R_i}$ denote true and predicted labels; prediction accuracy was defined as ${\sum }_{i=1}^s\mathrm{\delta }(R_i,\widehat{R_i})/s$, $\mathrm{\delta }(R_i,\widehat{R_i})=1 \text{if} R_i$ and $\widehat{R_i}$ belong to the same class, where s is the number of samples to be tested.

When evaluating our model on the human clinical trial samples, we used Cox proportional hazards regression analysis to test the association between the predicted likelihood of ICB response and patient survival. The predicted score difference between responders and nonresponders was examined by the Mann-Whitney U test. Gene set enrichment was performed using the enrichAnalyze function in the MAGeCKFlute R package (58), and the enriched pathways were visualized using functions from MAGeCKFlute (58). In the analysis of TCGA data, the CTL level is estimated through the bulk-tumor expression average of CD8A, CD8B, GZMA, GZMB, and PRF1.

Syngeneic data collection and preprocessing

We queried datasets deposited in the Gene Expression Omnibus (59) that matched a manually curated list of syngeneic mouse models or syngeneic cancer cell lines (table S10). For studies involving ICB treatment of anti-PD1, anti-PDL1, anti-PDL2, and anti-CTLA4, we manually annotated the experimental characteristics of each sample. The response status for each sample was curated from the original published studies. For the samples that do not have response information annotated, we labeled samples’ response statuses based on their diameter (size) change after treatment. Following a consensus (60), we used a 30% reduction as the cutoff to call a sample’s response status. To keep data consistent between human and mouse and different datasets, we dichotomized the responses to a binary label. In total, we collected 761 syngeneic tumor RNA-seq samples from 26 published studies (table S1). To ensure consistency, raw sequencing reads were downloaded from each study and processed through a standardized pipeline called RNA-seq IMmune Analysis Pipeline (RIMA) (https://liulab-dfci.github.io/RIMA/). RIMA is an automated Snakemake pipeline developed by our group to streamline RNA-seq data processing, including but not limited to read alignment, quality control (QC), expression quantification, and batch effect removal. Read alignments were performed with STAR (v.2.4.2a) (61) on FASTQ files against the mm10 reference genome assembly (mm10, Genome Reference Consortium Mouse Build 38) from the National Cancer Institute Genomic Data Commons (GDC). RNA-seq QC was performed on the aligned BAM files using RSeQC (v2.4) (62). With the reads appropriately aligned, expression levels were quantified by SALMON (v.0.14.0) (63) on the BAM files. We normalized and batch-controlled the transcripts per million data by quantile normalization and ComBat (49) within each syngeneic mouse model.

External data for validation

To evaluate the accuracy of the model’s ICB response prediction, we downloaded and processed the additional datasets GSE109485 and GSE137818 that consisted of 12 and 18 syngeneic mouse samples, respectively. A total of 16 pre-ICB samples and 14 post-ICB samples were included in these external datasets. The ICB response and mouse experimental variables were annotated from the original articles (table S2). Furthermore, we applied our model to patient clinical samples to evaluate its ICB response prediction on human samples. To evaluate the effectiveness of prediction, we systematically profiled expression data from clinical trial samples that underwent anti-CTLA4, anti-PD1, or anti-PDL1 treatments. Transcriptome data profiled by RNA-seq were obtained from these samples before patients underwent ICB therapy. On the basis of the patients’ reported clinical prognosis, these samples were labeled as either responders or nonresponders. For each dataset, we standardized the transcriptomic data across patients by quantile normalization. In total, we collected cancer patient cohorts with available RNA-seq data and immunotherapy response from 764 ICB-treated tumors spanning 16 clinical trials (9, 30, 64–76). We also collected available patient overall survival and progression-free survival information from these studies. Furthermore, we extended the model to predict the likelihood of ICB response using the clinical samples from TCGA. In this evaluation, we only included samples that matched the cancer type in the mouse training data. A total of 12 cancer types [liver hepatocellular carcinoma (LIHC), sarcoma (SARC), breast cancer (BRCA), kidney renal clear cell carcinoma (KIRC), colon adenocarcinoma (COAD), mesothelioma (MESO), pancreatic adenocarcinoma (PAAD), stomach adenocarcinoma (STAD), lung adenocarcinoma (LUAD), lung squamous cell carcinoma (LUSC), head-neck squamous cell carcinoma (HNSC), and skin cutaneous melanoma (SKCM)] from TCGA were included. For TCGS breast cancer tumors, we split tumors according to the Prediction Analysis of Microarray 50 (PAM50) subtypes (luminal A, luminal B, HER2, basal, and triple negative).

Supplementary Materials

This PDF file includes:

Figs. S1 to S4

Other Supplementary Material for this manuscript includes the following:

Tables S1 to S10

View/request a protocol for this paper from Bio-protocol.