Ensemble-function relationships to dissect mechanisms of enzyme catalysis

Abstract

Decades of structure-function studies have established our current extensive understanding of enzymes. However, traditional structural models are snapshots of broader conformational ensembles of interchanging states. We demonstrate the need for conformational ensembles to understand function, using the enzyme ketosteroid isomerase (KSI) as an example. Comparison of prior KSI cryogenic x-ray structures suggested deleterious mutational effects from a misaligned oxyanion hole catalytic residue. However, ensemble information from room-temperature x-ray crystallography, combined with functional studies, excluded this model. Ensemble-function analyses can deconvolute effects from altering the probability of occupying a state (P-effects) and changing the reactivity of each state (k-effects); our ensemble-function analyses revealed functional effects arising from weakened oxyanion hole hydrogen bonding and substrate repositioning within the active site. Ensemble-function studies will have an integral role in understanding enzymes and in meeting the future goals of a predictive understanding of enzyme catalysis and engineering new enzymes.

Structure–function has been central to understanding enzymes; ensemble–function analyses provide previously unattainable insights.

INTRODUCTION

Decades of structure-function studies have provided the foundation for our understanding of macromolecular function and enzyme catalysis [e.g., (1, 2)]. For enzymes, thousands of crystal structures from cryogenic (cryo; ~100 K) x-ray diffraction data have shown that catalytic and reactant groups are positioned in enzyme active sites to interact with substrates and transition state analogs and facilitate reactions. Supporting the importance of positioning, mispositioning of catalytic groups caused by sequence changes in enzyme variants are often associated with reduced catalysis [e.g., (3–5)], and it is now routine to obtain x-ray structures of new enzyme variants to accompany functional studies.

Nevertheless, despite enormous advances, our understanding of enzyme function is far from complete, as most simply demonstrated by our limited ability to design new enzymes that rival those from nature in catalysis and specificity and to predict catalytic efficiency of designed enzymes (6, 7). These limitations raise the question of what is missing from our current approaches and understanding. One fundamental limitation of the traditional structure-function approach is the consideration of enzymes largely in terms of individual structures. While often depicted as static cartoons, proteins do not exist in a single conformational state. Instead, they form an ensemble of conformational states that is defined by an energy landscape (8–13). Traditional cryo–x-ray structures provide snapshots of this larger ensemble, typically representing a structure or narrowed set of structures from the conformational landscape that is trapped upon freezing (14–16).

Many current proposals for enzyme function invoke conformational dynamics (11, 17–19), and there has been a corresponding interest in applying experimental approaches that provide valuable information about dynamics (20–23). Among these, x-ray crystallographic approaches provide quantitative information about the extent and direction of motion for all or nearly all the atoms of a complex. So-called pseudo-ensembles combine cryo–x-ray structural snapshots from multiple related structures under the premise that these together provide a reasonable approximation of the most accessible conformational states. That is, each cryo-structure is not representative of the complete conformational properties of an enzyme and rather represents a point or narrowed region of a broader conformational landscape that is explored by the enzyme at room temperature (RT) or ambient temperature (14, 16, 23). Another way to capture the ensemble of accessible conformational states is RT or ambient temperature x-ray crystallography, which operates at temperatures above the glass transition (~180 to 220 K) so that motions similar to those in solution remain. The extent and direction of the conformational excursions at RTs can be determined by obtaining ensemble models from high-resolution RT diffraction data and using new modeling approaches (20, 21, 24–27).

Pseudo-ensembles and ensemble information from RT x-ray crystallography have complimentary advantages, and a recent study of the enzyme ketosteroid isomerase (KSI) comparing ensembles obtained by each approach indicated that the same general conformational behaviors were captured by both (23). Information about coupled motions between atoms can be obtained by comparing the individual structures in pseudo-ensembles but is lost in ensemble models from RT x-ray crystallography. On the other hand, information for new protein variants and complexes, as highlighted here, is more readily obtained via RT x-ray crystallography, as ensemble information can be gleaned from individual crystals without the need for the tens of cryo–x-ray structures that are required to build a pseudo-ensemble.

Here, we have tested conclusions from structure-function analysis and obtained previously inaccessible mechanistic insights by taking advantage of RT x-ray crystallography to combine ensemble information for new KSI variants with functional data. We investigated two KSI variants with impaired catalytic efficiency [relative to wild-type (WT) KSI] for which a change in the position of a key active site residue was observed from comparisons of individual cryo–x-ray structures. In both cases, “ensemble-function” analysis revealed a far more complex relationship between structure and function than could be gleaned from traditional static structures. Our ensemble-function information revealed that the conformational landscape of the first variant is unaltered and thus not responsible for its compromised function; instead, its reactivity is decreased because it forms a weaker oxyanion hole hydrogen bond due to a reduced inductive effect. The second enzyme variant does have an altered ensemble of states, relative to WT KSI, but functional studies indicated that this alteration is not responsible for the observed rate effects; rather, weakened hydrogen bonding again lowers its reactivity, and, for one substrate, the altered positioning enhances reactivity, due to more favorable positioning for proton abstraction from that substrate. Most fundamentally, ensemble-function analysis allows structure to be related to energetics and catalysis in ways not possible from static structures alone. In this way, ensemble-function analysis allows previously untestable models to be distinguished and provides mechanistic insights that may be needed to predict enzyme rate enhancements and design new enzymes.

RESULTS

KSI structure function and the need for ensemble function

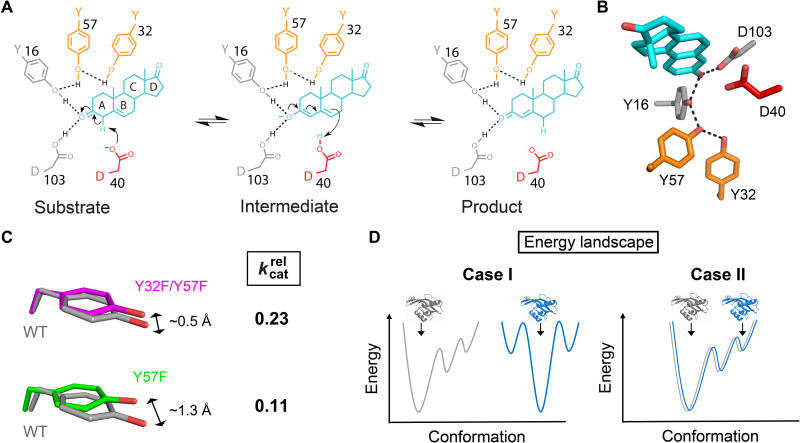
KSI binds its steroid substrates in a hydrophobic pocket and, for catalysis, uses an oxyanion hole, consisting of hydrogen bond donors Y16 and D103, and a general base, D40, that shuffles protons in steroid substrates (Fig. 1, A and B) (28, 29). Site-directed mutagenesis studies reveal large deleterious rate effects from removal of these side chains and effects from mutations of groups interacting with them (30–33).

Fig. 1. KSI reaction mechanism, active site, and structure-function results.

(A) KSI catalyzes double-bond isomerization of steroid substrates (shown for the substrate 5-androstene-3,17-dione) using a general acid/base D40 (which we refer to here as a general base) and an oxyanion hole composed of the side chains of Y16 and D103 (protonated). (A and B) Y16 is embedded within a hydrogen bond network with two other tyrosine residues, Y57 and Y32. The general base, oxyanion hole, and hydrogen bond network residues are colored in red, gray, and orange, respectively. Structural model 1OH0 from the Protein Data Bank (PDB) (28). (C) In Y32F/Y57F KSI (PDB 1DMN) (3) and Y57F KSI (PDB 1DMN) (3), Y16 (magenta and green, respectively) is misaligned with respect to its position in WT KSI (gray; PDB 3VSY) (35) [see table S1 and Materials and Methods for alignment root mean square deviations (RMSDs) and procedures, respectively; also see fig. S1]. The k_cat values for Y32F/Y57F and Y57F KSI are shown relative to WT [(3); also see table S2]. (D) An observed difference in traditional single conformation structures between WT and an enzyme variant can arise either because the underlying conformational ensembles of the molecules are different (case I) or because conditions trapped different states in the cryo–cooled structures from a common ensemble (case II). In case I, the gray (left) and blue (right) conformational landscapes are different, and the crystal structures have captured distinct states from each ensemble (indicated by arrows). In case II, the gray and blue conformational landscapes are the same, but the crystal structures have captured distinct states (indicated by arrows); in the traditional structure-function perspective, these structures are compared, and differences between them are correlated with functional effects potentially leading to incorrect mechanistic insights. Most generally, whenever a conclusion is based on a change in structure, then ensemble information is required.

Prior structure-function studies based on x-ray crystal structures suggested that changes in the KSI Y16 hydrogen bond network result in ~0.5-Å (Y57F/Y32F KSI) and ~1.3-Å (Y57F KSI) displacements of Y16 from its WT position (3), displacements larger than typical coordinate errors in crystal structures (Fig. 1C and fig. S1) (34). As Y16 donates a hydrogen bond that stabilizes the anionic transition state (Fig. 1A), the simplest interpretation of these results is that these displacements are responsible for the observed four- and ninefold decreases in catalysis, with the larger displacement resulting in the larger rate decrease (Fig. 1C and table S2). However, as elaborated and demonstrated below, ensemble information and deeper functional analyses are needed to evaluate these effects and uncover their physical origins.

There are fundamental limitations to the traditional structure-function approach taken above. As noted in Introduction, individual x-ray structures do not provide conformational ensembles (9, 35). Instead, individual x-ray structures obtained at cryo-temperatures can capture different states within an ensemble (14–16); multiple cryo–x-ray structures can be combined to provide pseudo-ensembles because each structure varies and provides snapshots of states on a protein’s conformational landscape (14, 16, 23). In addition, cryo-temperatures can alter the ensemble of states and thus not accurately capture the states occupied or predominant in the ensemble present at physiological temperature (20, 36–38). While crystallographic B-factors provide some information that could be related to ensemble properties, B-factors include model uncertainties and errors, are incomplete models for heterogeneity, and cannot be used to determine the ensemble of conformational states present from a single cryo–x-ray structure (39, 40). Further, as different conformational states can be observed in individual cryo–cooled crystals of the same protein (15, 16), differences between cryo–x-ray structures of WT KSI and KSI variants can arise either because the underlying conformational ensembles of the molecules are different or because different conditions trap different states in the cryo–cooled structures from a common ensemble, as shown schematically in Fig. 1D. Ensemble information is required to distinguish between these cases and to draw conclusions about the presence and extent of conformational changes.

The second important limitation of traditional structure-function correlations is that even if an observed conformational difference truly reflects different ensembles for the enzymes under comparison, this conformational difference may or may not be responsible for the observed rate effect. Thus, additional functional studies are also required; these are needed to test whether the change is causative or simply correlative and to determine the origin of the observed rate effects.

Structure-function to ensemble-function analysis of Y32F/Y57F KSI

We first consider Y32F/Y57F KSI, which exhibits a fourfold rate decrease relative to WT KSI (Fig. 1C and table S2). In the simplest scenario, one-fourth of the Y16 variant ensemble are reactive WT conformations, and three-fourth are alternative nonreactive conformations, as depicted by the free energy profile in Fig. 2A (left). A second possibility is that the WT configuration is even less populated, and the reaction is fourfold slower in the alternative conformational state, as depicted by the free energy profile in Fig. 2A (right). Both models (and models between these extremes) presuppose a difference in the WT and variant conformational ensembles.

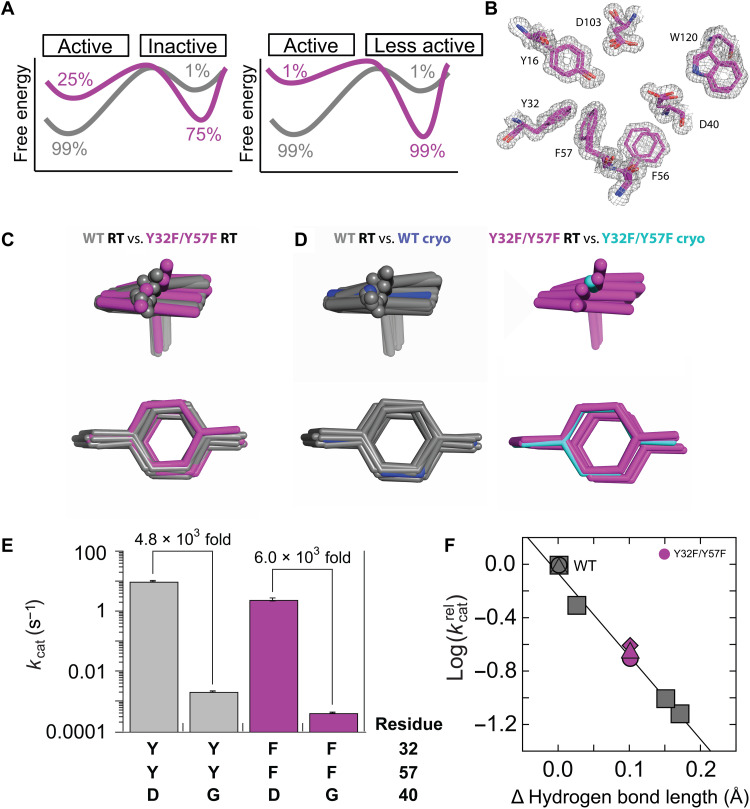
Fig. 2. Ensemble and functional data for Y32F/Y57F and WT KSI.

(A) Ensemble models for the fourfold effect in Y32F/Y57F variant. Left: In Y32F/Y57F KSI, Y16 are in reactive WT conformations 25% of the time and in alternative nonreactive conformations 75% of the time, whereas WT KSI is predominantly in reactive conformations (99%). Right: In Y32F/Y57F KSI, reactive WT conformations are populated by Y16 less than one-fourth of the time (1% in this schematic), and Y16 predominantly populates less reactive alternative conformations that are responsible for the observed reaction. (B) Electron density (gray mesh, contoured at 1 σ) and multiconformer modeling (magenta sticks) for the Y32F/Y57F KSI active site. (C) Overlay of the WT (gray sticks) (23) and Y32F/Y57F ensembles. (D) Superposition of the cryo–crystal structures and RT ensemble models. Left: WT RT ensemble (gray) (23) and the WT cryo-structure (PDB 3VSY) (94). Right: Y32F/Y57F ensemble (magenta) and the Y32F/Y57F cryo-structure (PDB 1DMN) (3). (E) The same rate effect is observed from ablating the general base D40 in WT (gray) and in Y32F/Y57F (magenta) for reaction of 5(10)-estrene-3,17-dione. (F) Catalytic effects in KSI variants versus changes in the hydrogen bond length with a bound TSA for KSI variants. Gray squares reproduce data from Pinney et al. (44) (R² = 0.99). The change in hydrogen bond distance for Y32F/Y57F KSI was obtained with the transition state analog dinitrophenol (44). Y32F/Y57F KSI kinetics relative to WT with the substrates 5(10)-estrene-3,17-dione (magenta triangle) and 5-androstene-3,17-dione (magenta diamond); Y32F/Y57F/D40G KSI relative to D40G with the substrate 5(10)-estrene-3,17-dione (magenta circle).

To test whether there is an altered conformational ensemble for Y32F/Y57F KSI, we collected RT x-ray diffraction data. x-ray data for crystals obtained at temperatures above the glass transition (~180 to 220 K) provide information about conformational heterogeneity, which is the experimental manifestation of conformational ensembles (20, 25, 26, 41–43). We used the 1.10-Å RT x-ray data to obtain Y32F/Y57F KSI multiconformer models that capture the conformational heterogeneity in the crystal (Fig. 2B, table S3, and see Materials and Methods). We then compared the Y32F/Y57F with the WT ensemble obtained previously (23) and observed that the Y16 states extend in the same directions and span the same range (Fig. 2C). Comparison to the cryo–x-ray models suggests that the different cryo-structures for WT and Y32F/Y57F KSI represent individual states within a common ensemble (Fig. 2D).

Given the highly similar ensemble of Y16 states in WT and Y32F/Y57F KSI, we needed to consider alternative models for the rate difference between these variants. These models fall into two classes: a direct effect on the Y16 hydrogen bond or indirect effects on other catalytic elements. There was no notable change in the ensemble of the other oxyanion hole hydrogen bond donor, D103 (fig. S2), in substrate binding (table S2), and mutational ablation of the general base (D40G) gave the same rate reduction for WT and Y32F/Y57F KSI (Fig. 2E and table S2), providing no indication of effects on other catalytic features. We therefore turned to consideration of energetic effects within the oxyanion hole.

Prior results established a linear free energy relationship (LFER) between the length of KSI oxyanion hydrogen bond donors and the amount of catalysis [Fig. 2F, gray points (44)]. Specifically, mutations that alter the partial positive charge on the oxyanion hole hydrogen bond donors, such as D103N, weaken the oxyanion hole hydrogen bond, resulting in its lengthening and less stabilization of the oxyanionic transition state (relative to the carbonyl ground state). The bond lengths and energetic effects in KSI follow a systematic and linear relationship that allows us to predict the energetic consequences of new mutations based on changes in hydrogen bond lengths (Fig. 2F) (45). This relationship is distinct from proposals of special energetic contributions from short or symmetrical hydrogen bonds (see text S1).

¹H nuclear magnetic resonance (NMR) chemical shifts have been shown to report on changes in hydrogen bond length (45–48). We used ¹H NMR to assess changes in hydrogen bond lengths between KSI variants because changes in hydrogen bond lengths are on the scale of <0.1 Å, near the error limits of even very high-resolution structures, and because it is generally not possible to ascribe interatomic distances for individual conformers from a RT x-ray multiconformer model; ¹H NMR chemical shifts are highly sensitive to hydrogen bond distances and, thus, provide conformational information that is complementary to that from x-ray data (46–48). In Y32F/Y57F KSI, we observed that the ¹H NMR chemical shift of the Y16-oxyanion hydrogen bond proton shifted upfield. This change indicates a lengthening of the Y16 hydrogen bond by 0.1 Å, relative to WT KSI (table S5) (44). Applying this lengthening to the above-noted LFER predicts the observed fourfold rate effect (Fig. 2F, magenta points). This lengthening is expected on chemical grounds for the Y32F/Y57F mutation, as removal of the neighboring hydrogen bond donor will lessen polarization of the Y16 hydroxyl group and thereby yield a longer and weaker hydrogen bond (Fig. 3, A and B, and text S2) (49, 50). In addition, prior work indicated that the KSI hydrogen bond donors and acceptors have sufficient conformational freedom to provide optimal hydrogen bond lengths from different orientations (23).

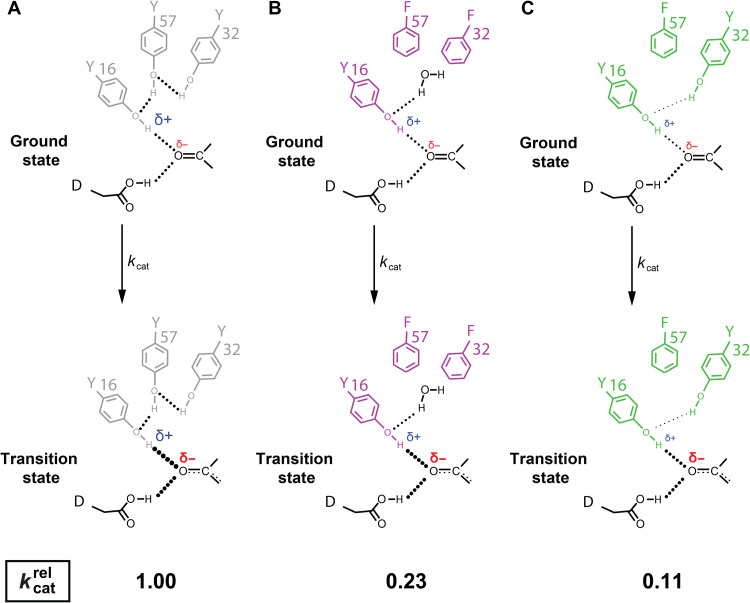
Fig. 3. KSI oxyanion hole catalytic model.

During the KSI reaction, the amount of negative charge on the substrate carbonyl increases and this negative charge accumulation is stabilized by hydrogen bonds (reflected in the size of the red δ−). Analogously, hydrogen bonds become stronger as the charge density on the hydrogen bond donating hydrogen increases (reflected in the size of the blue δ+) (45, 52, 53, 96). Thus, WT (grey, A), Y32F/Y57F (magenta, B), and Y57F (green, C) have decreasing hydrogen charge densities, respectively, and provide lesser extent of transition state stabilization (hydrogen bond strength is depicted by the size of the dots representing the hydrogen bonds). In all cases, hydrogen bonds shorten and strengthen in the transition state (indicated with thicker doted lines in the TS compared to GS), but the shortening and strengthening in the TS decreases in the following order: WT, Y32F/Y57F, Y57F.

In summary, the initial comparison of individual cryo–x-ray structures of WT and Y32F/Y57F KSI was misleading, as it reflected single structures randomly selected from the ensemble of each variant. Multiconformer models from RT x-ray data revealed highly similar ensembles of conformational states between WT and Y32F/Y57F; further analysis of the Y16 oxyanion hole hydrogen bond by NMR revealed a lengthening and weakening, presumably due to loss of the Y57/Y32 hydrogen bond network that polarizes Y16 (Fig. 3, A and B). The weakened hydrogen bond is predicted to decrease catalysis by fourfold, as is observed. A combination of ensemble, NMR, and functional data (Fig. 2, C to F; ensemble-function analysis) allowed us to evaluate and distinguish catalytic models.

Ensemble-function analysis of Y57F KSI

We now turn to Y57F KSI, where analogous ensemble and functional experiments revealed a more complex scenario than that for Y32F/Y57F KSI but one that could nevertheless be disentangled through ensemble-function studies. Given the ninefold rate decrease relative to WT KSI, in the simplest scenario, Y16 in this enzyme variant would sample reactive WT conformations about 10% of the time and would spend the remaining 90% of the time in alternative, nonreactive conformations, as depicted by the free energy profile in Fig. 4A (left). The other ensemble model, as above, is that Y16 in Y57F KSI samples alternative, less reactive conformations and reacts from those while sampling WT conformations less than 10% of the time, as depicted in the free energy profiles on the right in Fig. 4A.

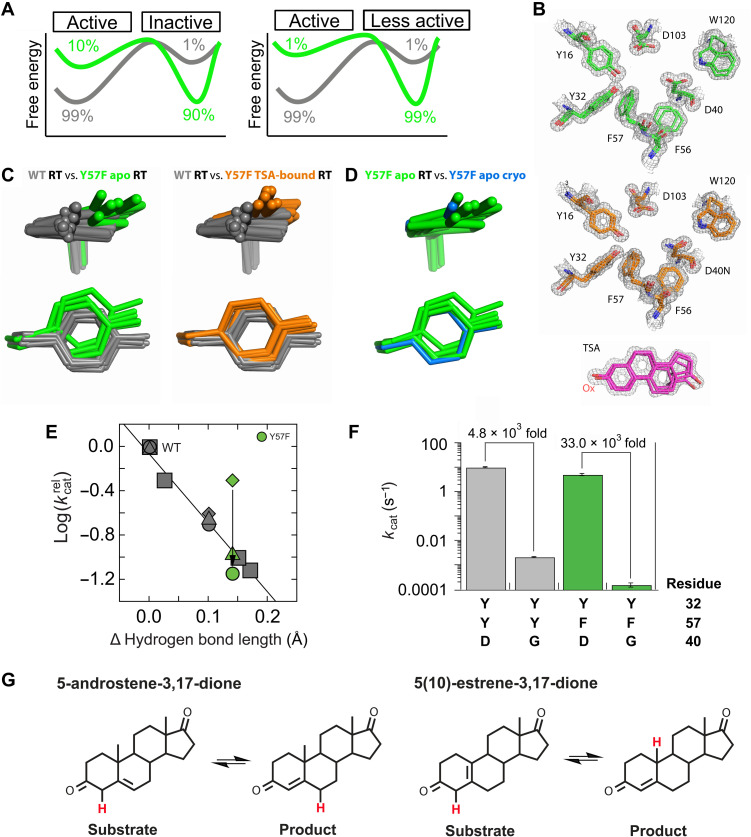
Fig. 4. Ensemble and functional data for Y57F and WT KSI.

(A) Ensemble models for the 9-fold effect in Y57F KSI. Left: in Y57F KSI, Y16 samples reactive WT conformations ~10% of the time, while spending ~90% of the time in alternative, non-reactive conformations. Right: in Y57F KSI, reactive Y16 WT conformations are not sufficiently populated, which instead reacts (less efficiently) from its alternative conformation(s). (B) Representative electron density (gray mesh) and multiconformer models for the KSI Y57F apo (top, green sticks) and Y57F (D40N) TSA-bound (bottom, orange sticks) active site. Also shown are stick model (pink) and electron density (gray mesh) of the bound TSA. D40N was present to mimic the protonated general base and increase TSA affinity (67, 95). Electron density contoured at 1 σ. (C) KSI ensemble overlays, color-coded as noted in figure; WT from (23) and Y57F ensembles from this study. (D) Y57F KSI cryo–crystal structure (PDB 1DMM) (3) and RT ensemble overlays. (E) Catalytic effects in KSI variants versus changes in the hydrogen bond length from Fig. 2A (gray symbols), now including Y32F/Y57F data points. Y57F KSI kinetics with the substrate 5-androstene-3,17-dione relative to WT (green triangle), Y57F kinetics relative to WT with the substrate 5(10)-estrene-3,17-dione (green diamond), and Y57F/D40G relative to D40G (green circle) with the substrate 5(10)-estrene-3,17-dione. (F) Different rate effects from ablating the general base D40 in WT (gray) and in Y57F (green) for reaction of the substrate 5(10)-estrene-3,17-dione (table S2). (G) KSI reaction with the steroid substrates 5-androstene-3,17-dione (left) and 5(10)-estrene-3,17-dione (right). The shuffled proton is red.

We examined the conformational ensemble for Y57F KSI with 1.16-Å RT x-ray data and multiconformer modeling (Fig. 4B and table S3). The Y16 ensemble for this enzyme variant is largely distinct from WT KSI with no observed overlap (Fig. 4C, left, and fig. S2). This observation is not consistent with the simplest model of fractional occupancy of the WT state (Fig. 4A, left). Additional evidence counter to this model comes from the set of conformations for Y57F KSI with a bound oxyanion transition state analog, obtained from RT x-ray data at 1.11-Å resolution (Fig. 4B, bottom, and table S3). With the bound transition state analog, the positions of Y16 overlap with those for apo Y57F KSI conformational states and remain distinct from those for WT KSI (Fig. 4C, right, and fig. S2). These data support a model in which the Y57 KSI reaction occurs predominantly via a distinct set of oxyanion Y16 hole conformational states.

Without additional functional data, we might draw the conclusion that misalignment of the Y16 ensemble causes the ninefold catalytic effect from Y57F mutation (Fig. 4A, right). However, we would not know the mechanistic origin of the effect—why the alternatively aligned states are less reactive—or even if the misalignment is correlated or causative. Possible models involve altered substrate binding, weakened oxyanion hole hydrogen bonding, and altered general base catalysis. Recognizing these possibilities, we tested each model via functional experiments.

The ninefold rate effect observed for reaction of Y57F KSI with the substrate 5-androstene-3,17-dione is predicted from the increased length of the Y16 oxyanion hole hydrogen bond (Fig. 4E, green triangle), similar to the fourfold effect for Y32F/Y57F KSI (Fig. 2F, magenta triangle). The loss of the neighboring Y57 hydrogen bond would be expected to lessen polarization of the Y16 hydroxyl group and thereby weaken its oxyanion hole hydrogen bond, as described above (Fig. 3, A and C, and texts S1 and S2). We speculate that the longer hydrogen bond and larger effect for Y57F KSI than for Y32F/Y57F KSI arise because solvent access is greater for Y32F/Y57F KSI and interactions with solvent water molecules are more effective at polarizing Y16 than the distorted Y16/Y32 hydrogen bond in Y57F KSI (table S2).

These results suggest that the reaction is slower because the Y16 hydrogen bond is weaker and not because the altered Y16 conformational states in Y57F KSI give slower reactions (Fig. 3). A range of conformational states are present within WT KSI’s active site that appear to allow proton transfer at sites that are several angstroms apart, as needed in the KSI reaction (Figs. 1A and 4G and fig. S4) (23). This range of conformations also appear to allow reaction from the altered conformational poses present in Y57F KSI without further sacrificing catalysis.

In contrast to the ninefold effect for Y57F KSI with the substrate 5-androstene-3,17-dione, as described above, a rate decrease of only twofold was observed for this variant when reacting with the substrate 5(10)-estrene-3,17-dione [Fig. 4, E (green diamond) and G]. As the catalytic effect was less than predicted, we reasoned that there might be a second, compensating effect, such as an increased catalytic contribution from the general base in Y57F KSI. This model predicts that Y57F KSI will have a larger catalytic effect with the general base ablated—i.e., in a D40G background—and that the effect would match the ninefold effect predicted from the LFER in Fig. 4E. Both predictions are met. The D40G mutation gives a 33 × 10³–fold effect in the Y57F background but only a 5 × 10³–fold effect in WT KSI (Fig. 4F), and in the D40G background, the Y57F mutation causes a 14-fold rate decrease, within twofold of the ninefold effect predicted by the LFER (Fig. 4E and table S2). The altered Y16 ensemble in Y57F KSI presumably differentially alters the reactivity of the two substrates, which have different geometries and protons that are shuffled between different positions (Fig. 4G and fig. S4). The ensemble of states for the general base (D40) shows no apparent change in the Y57 variant compared to WT, so that the reactivity difference may arise from differential placement of the substrate (fig. S5).

In contrast, the similar substrate affinities for WT and Y57F KSI (table S2) and prior observation that the B, C, and D rings of steroid substrates contribute solely to binding, but not catalysis, once bound provide no indication of effects coupled to the substrate binding site (51).

In summary, substituting the tyrosine at position 57 with phenylalanine in KSI results in a change in the bound and likely in the reactive ensemble. Nevertheless, our observations suggest that the observed ninefold rate decrease does not arise from these altered states but rather arises from a weakened hydrogen bond (Fig. 3, A and C). With a different substrate, the reactivity is higher than predicted on the basis of the active site hydrogen bond, and double mutant cycle analyses trace this effect to a fortuitous increase in reactive alignment with general base for this substrate in Y57F KSI.

DISCUSSION

The ensemble-function analyses carried out in this study revealed a different, and far richer, mechanistic landscape than accessible via traditional structure-function analyses. Consider the hypothetical observation of a mutation that leads to a deleterious rate effect and structural change. The simplest and most common interpretation would be that the observed change in structure causes the change in catalysis. However, multiple models are possible, as we describe for two KSI variant case studies here; we distinguished between models by integrating structural data that report on conformational ensembles, rather than static structures, with synergistic functional studies. Given the complexity of enzymes and their conformational landscapes and the various ways to alter function, there is a general need for synergistic ensemble-function studies, as illustrated here for KSI and two of its variants.

The observation of an altered residue conformation from comparison of cryo–x-ray structures for a WT and protein variant does not indicate that the mutation changes the protein’s conformational landscape; experimental ensemble information is needed. This need arises because cryo-freezing of crystals traps a protein in different conformational poses that correspond to states on a conformational landscape; thus, different structures can arise when WT and variant landscapes are identical or different (but overlapping) (Fig. 1D) (15, 16). We observed an apparent change for Y32F/Y57F KSI based on individual cryo–x-ray structures, but RT x-ray data revealed indistinguishable conformational ensembles for this variant and WT KSI (Fig. 2).

Functional effects can arise from alterations in the occupancy of states that differ in reactivity or from changes in the reactivity of the individual states, as was the case here from a weakened KSI oxyanion hole hydrogen bond. Our ¹H NMR results support the model of KSI oxyanion hole catalysis arising because the oxyanion hydrogen bonds are stronger than those to water, due to the presence of intrinsically stronger hydrogen bond donors, and not because KSI catalysis is highly sensitive to small changes in oxyanion hole positioning (Fig. 3) (45, 49, 52, 53).

Ensembles are necessary but not sufficient to provide deep mechanistic insights. Here, we combined ensemble analysis with ¹H NMR chemical shifts to obtain information about hydrogen bond lengths, and we used a previously established linear free-energy relationship between hydrogen bond length and energetics in the KSI active site to relate these lengths to energetic effects. We also used double-mutant cycles, which, for different KSI variants and different substrates, tested whether each variant’s conformational alterations affected catalytic contributions from KSI’s general base (D40). Unexpectedly, we uncovered enhanced general base catalysis for one KSI substrate apparently from a fortuitous increase in positioning in reactive conformers. These differences underscore the need for robust ensemble-function analysis and reveal the potential to exploit conformational landscapes to evolve enzymes that use new substrates and catalyze new reactions (54–57).

While different functional analyses will be needed to distinguish different mechanistic models, the need for ensemble information is universal because ensembles and the corresponding conformational landscape perspective connects structure to function [e.g., (7, 11, 12, 60, 61)]. This perspective follows from the fundamental formalism of statistical mechanics in which free-energy landscapes relate the atomic level properties of molecules to the macroscopic behavior of a population of molecules (9, 12, 13, 64, 65). Considering this relationship from a practical perspective, the rate of an enzyme-catalyzed reaction is a function of the occupancy of each state on a multidimensional energy landscape and the probability of reacting from that state (Fig. 5). Thus, observed functional changes can arise through “k-effects,” which themselves can be effects on the binding affinity or reaction rate of each state (Fig. 6, A and B), or through “P-effects” that change the probability distribution of states (Fig. 6, C and D). P-effects can occur in two subtypes, lessening the amount of the most active state but maintaining reaction predominantly through that state (Fig. 6C) or reacting predominantly through an alternative state that becomes more prevalent (Fig. 6D).

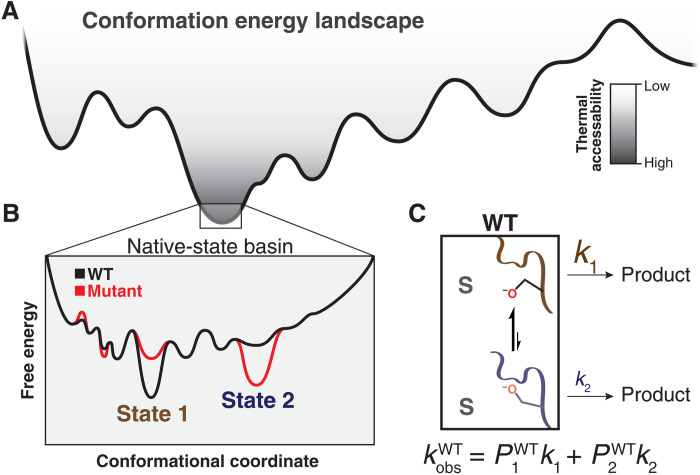
Fig. 5. Catalysis from an ensemble perspective.

(A) Enzymes form a set of states specified by energy wells on a free energy landscape, with dimensionality defined by the thousands of degrees of freedom from each rotatable bond of each residue, depicted here schematically in a single dimension. (B) An example ensemble of near-energy substates in which state 1 (brown) and state 2 (blue) lie within the lowest-energy basin (“native-state basin”). These substates have different intrinsic reactivities, reflecting different barrier heights along their individual reaction coordinates (see Fig. 6). (C) Mathematically, the observed rate constant of the WT (k_obs^WT) with substrate S is the probability-weighted (occupancy-weighted) sum of the intrinsic rate constants of each microscopic substate. Here, we show a simplified example with two states; this example can be generalized across all states with sufficient occupancy and reactivity to contribute appreciably to the observed reaction rate: $k_{\text{obs}}={\sum }_i{P}_i\times k_i$, where P is the probability of occupying state i and k is the rate of reacting from that state. Modified from (97).

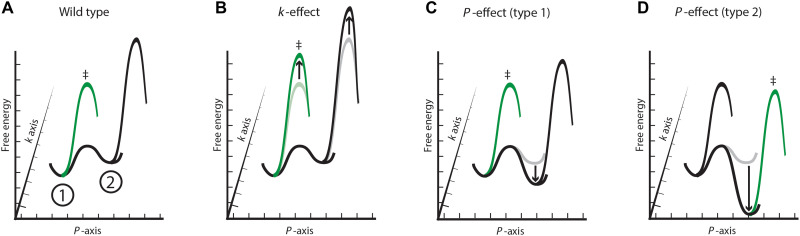
Fig. 6. The effects of functional (k-effects) and occupancy changes (P-effects) to reactivity from an enzyme ensemble.

In all panels, the k-axis is the reaction coordinate, the P-axis is the conformational coordinate, here simplified to two conformational states, and the Z axis is free energy. Profiles for enzyme variants are in gray and light green, and the green profiles (with ≠) represent the preferred reaction path; the corresponding WT profiles are in black and dark green. (A) A simplified ensemble reaction coordinate for a WT enzyme that reacts preferentially from the most active and most probable state (green). A less reactive and less probable state is also depicted (black). (B) Depiction of a k-effect, which increases the barrier to reaction uniformly in both states and reactions, occur via the most populated state (≠; green). (C) Depiction of a P-effect that changes the occupancy of states, but not the most reactive conformation. Reduced reactivity results from decreased occupancy of the more-reactive state. (D) Depiction of a P-effect that results in the enzyme reacting from a more probable but less reactive conformation (≠; green).

We describe the observed KSI mutational effects according to this framework in fig. S6. For our KSI variants, ensemble information from multiconformer models was needed to capture conformational effects (P-effects); double mutant cycles and alternative substrates were needed to identify functional interconnections; and NMR chemical shifts were needed to elucidate changes in active site hydrogen bonds that result in k-effects. Different types of functional data will be valuable for different systems and different mechanistic questions. Nevertheless, ensemble data will be valuable for all analyses, as any local, distal, or global changes in the conformational ensemble (upon ligand binding or mutation) reflects a change in the energy landscape that is part of the overall energy balance of the system and may have functional consequences.

Discussions of dynamics have become nearly inseparable from considerations of protein function and enzyme catalysis. Multiple conformational states, often involving lid or domain closures, occur in the reaction cycles of many enzymes and for enzymes with allosteric control (e.g., 8, 17, 60–65), and the need to consider multiple conformational states to understand enzyme catalysis even in the absence of these features was demonstrated in work on tunneling temperature-dependent isotope effects (62). We have illustrated the need for ensemble data, even for an enzyme lacking conformational changes and allostery, and the power of RT x-ray crystallography to rapidly provide information about the extent and direction of motions at the atomic level. Ensemble-function analysis, as carried out here by combining RT x-ray crystallography, NMR, and double mutant cycles, allowed us to relate structure to energetics and catalysis and allowed us to distinguish previously untestable models.

We anticipate synergy between ensemble-function and computational approaches. Molecular dynamics has the ability to describe the behavior of all atoms in a protein, and quantum mechanics/molecular mechanics approaches can link structure to catalytic function. Experimental ensemble-function approaches will allow, and are needed for, incisive and robust tests of predictions from these and other computational approaches and will ultimately lead to computational approaches with established accuracy and reliability that can be broadly and confidently used.

Most broadly, we expect that future ensemble-function studies will provide previously inaccessible mechanistic insights and that these insights will be indispensable in developing a predictive understanding of enzyme function, will improve our ability to develop highly specific inhibitors, and ultimately may lead to an ability to design enzymes that rival those found in nature.

MATERIALS AND METHODS

KSI expression and purification

The KSI enzymes from Pseudomonas putida (referred to herein as KSI, UniProt P07445) was expressed and purified as previously described with minor modifications (66). Briefly, BL21 cells transformed with plasmid carrying the desired KSI construct were grown at 37°C to an optical density of 0.5 to 0.6 in LB media (EMD Millipore Corp., Billerica, MA, USA) containing carbenicillin (50 μg/ml; GoldBio, St. Louis, MO, USA), and protein expression was induced with 1 mM isopropyl-β-d-1-thiogalactopyranoside (GoldBio, St. Louis, MO, USA). After induction, cultures were grown for 10 to 12 hours at 37°C. Cells were harvested by centrifugation at 5000g for 30 min at 4°C and lysed using sonication. Lysed cells were centrifuged at 48,000g for 30 min at 4°C. Enzymes were purified from the soluble fraction, first using an affinity column (deoxycholate resin), followed by a size exclusion chromatography (SEC) column Superdex 200. Before the purification of each enzyme, the affinity column, fast protein liquid chromatography loops, and SEC column were washed with 40 mM potassium phosphate (J.T.Baker, Omaha, NE, USA), 6 M guanidine (J.T.Baker, Omaha, NE, USA), and pH 7.2 buffer and then equilibrated with 40 mM potassium phosphate, 1 mM sodium EDTA, 2 mM dithiothreitol (DTT: GoldBio, St. Louis, MO, USA), and pH 7.2 buffer.

KSI solution kinetics

KSI Michaelis-Menten parameters were obtained by monitoring the 5(10)-estrene-3,17-dione and 5-androstene-3,17-dione (Steraloids, Newport, RI, USA) reaction at 248 nm (extinction coefficient, 14,800 M⁻¹ cm⁻¹) in a PerkinElmer Lambda 25 spectrophotometer (66). Reactions were measured at 25°C in 4 mM sodium phosphate and pH 7.2 buffer with 2% dimethyl sulfoxide (DMSO; J.T.Baker, Omaha, NE, USA) added for substrate solubility. Low buffer concentrations were used to minimize the background reaction rate. Values of k_cat and K_M were determined by fitting the initial rates as a function of substrate concentration to the Michaelis-Menten equation. Typically, five to seven substrate concentrations, varying from 2 to 300 μM, were used for each enzyme variant. Averaged values and errors representing the SDs are given in table S2.

KSI ¹H solution NMR

The ¹H NMR spectrum of KSI Y57F/D40N bound to (9β,13α)-3-hydroxyestra-1,3,5(10)-trien-17-one was acquired at the Stanford Magnetic Resonance Laboratory using an 800-MHz Varian ^UNITYINOVA spectrometer running VNMRJ 3.1A and equipped with a Varian 5-mm triple resonance, pulsed field gradient ¹H[¹³C,¹⁵N] cold probe, as previously described (67). The sample contained 1 mM KSI and 2 mM equilenin (Steraloids, Newport, RI, USA) in 40 mM potassium phosphate (pH 7.2), 1 mM sodium·EDTA, 2 mM DTT, and 10% DMSO-d₆ (v/v) (Cambridge Isotope Laboratories, Tewksbury, MA, USA). DMSO-d₆ served as the deuterium lock solvent and prevented freezing at low temperatures. The spectrum was obtained in a 5-mm Shigemi symmetrical microtube at −3.5°C, following temperature calibration with a 100% methanol standard. The 1331 binomial pulse sequence was used to suppress the water signal with a spectral width of 35 parts per million (ppm) (carrier frequency set on the water resonance) and an excitation maximum between 14 and 18 ppm (68). The data were processed using 10-Hz line broadening and baseline correction applied over the peaks of interest. Chemical shifts were referenced internally to the water resonance.

Protein crystallization and x-ray data collection

All enzymes were crystallized as previously described (49). Briefly, enzyme were crystallized by mixing 1 to 2 μl of enzyme at 1 mM [for the transition state analog (TSA)-bound KSI, preincubated with 2 mM of the TSA (9β,13α)-3-hydroxyestra-1,3,5(10)-trien-17-one] and 1 to 2 μl, respectively, of crystallization solution [17 to 23% polyethylene glycol 3350 (Hampton Research, Aliso Viejo, CA, USA) and 0.2 M MgCl₂ (J.T.Baker, Omaha, NE, USA)] in a vapor diffusion hanging drop setup at RT. Crystals typically appeared after 24 to 72 hours. Before data collection, crystals were transferred from the crystallization solution to paratone N oil (Hampton Research, Aliso Viejo, CA, USA) where excess crystallization solution was stripped, and crystals then were directly mounted on the goniometer for data collection. Because a large body of work identified the 180- to 220-K temperature range as an inflection point above which both harmonic and anharmonic protein motions are activated, providing strong evidence that protein behavior at 250 K approximates behavior at RT (25, 42, 43, 69, 70) and because we previously observed that data collected at 250 K were of slightly higher resolution (~0.1 to 0.2 Å) compared to data at 280 K (23), we collected data at 250 K. Data collection temperature was controlled using a N₂ cooler/heater. Single-crystal diffraction data were collected at Stanford Synchrotron Radiation Lightsource, beamline 9-2, using wavelengths of 0.886 Å. See table S3 for diffraction data statistics.

Crystallographic data processing and model building

Data processing was carried out with in-house scripts: http://smb.slac.stanford.edu/facilities/software/xds/#autoxds_script. Briefly, data reduction was done using the XDS package (71), scaling and merging was done using Aimless (72, 73), and structure factor amplitudes were obtained using Truncate (72, 74). Initial phases were obtained via molecular replacement using PHASER (75) and the Protein Data Bank (PDB) entry 3VSY as a search model. Model building was carried out with the program ARP/wARP (76) and manually in Coot (77). Traditional, single conformation models, in which major alternative side chain and backbone conformations were modeled, were refined manually after visual inspection with Coot and using phenix.refine (78). Torsion-angle simulated annealing (as implemented in phenix.refine) was used during the initial stages of refinement. Ligand restraints were generated using the GRADE server (http://grade.globalphasing.org/cgi-bin/grade/server.cgi). These models were used as input for multiconformer molding (see below).

Multiconformer models were obtained using the program qFit and previously described methods (24, 27). Subsequent to the automated multiconformer model building, ill-defined water molecules were deleted, and alternative protein side and main chain conformations were manually adjusted after visual inspection in Coot (79) and based on the fit to the electron density. Both alternative side chain rotameric states and alternative orientations within the same rotameric state were modeled. Models were subsequently refined with phenix.refine (78). Riding hydrogen atoms were added in the late stages of refinement, and their scattering contribution was accounted for in the refinement. Final multiconformer model quality was checked by MolProbity (80) and via the PDB Validation server (https://validate-rcsb-2.wwpdb.org/) and deposited on the PDB. See table S3 for refinement statistics.

Ensembles versus multiconformer models

Because mutations refer to changes in DNA sequence and variants refer to substitutions of residues on the protein level, we use the term “enzyme variants” to indicate changes on the residue level in proteins. The term “enzyme variant” is equivalent in meaning to the term “enzyme mutant” often used in the literature. For both WT and enzyme variants, each KSI state is a dimer, and each state is composed of the multiconformer models for each monomer from the KSI dimer. Thus, the WT ensemble is composed of two multiconformer models for each of the apo, ground state analog-bound, and TSA-bound states, and we refer to this ensemble of six multiconformer models as the WT ensemble (23). For Y32F/Y57F, we obtained multiconformer models for each of the monomers from the dimer in the apo state. Thus, the comparisons in Fig. 2 and figs. S2 and S5 are made between the WT ensemble made of six KSI WT multiconformer models and the Y32F/Y57F ensemble made of two Y32F/Y57F multiconformer models. For Y57F, we obtained multiconformer models for each of the monomers from the dimer of both the apo and a TSA-bound states. Thus, the comparisons in Fig. 2 and figs. S2 and S5 are made between the WT ensemble and the apo Y57F ensemble made of two multiconformer models (Fig. 2), the TSA-bound ensemble made of two multiconformer models (Fig. 2), or an ensemble made of all four multiconformer models of Y57F apo and TSA-bound states (figs. S2 and S5).

Structural alignments

KSI structures and multiconformer models were aligned on backbone atoms N, CA, C, and O of residues 5 to 125 using PyMOL and standard commands (81). The Y32F/Y57F and Y57F multiconformer models were aligned on the 250-K multiconformer model of WT apo KSI (PDB 6UCW) as previously described (23). The comparison of KSI ensemble or multiconformer models with traditional single conformation cryo–structural models from the PDB (Figs. 2 and 4) was achieved by aligning the cryo-models on the single conformation model of WT apo KSI that was used to obtain the associated 250-K multiconformer model in PyMOL and using standard commands.

Comparing crystal structures

One measure of the coordinate error is the diffraction precision index (DPI), which is an estimate of the precision of coordinates obtained by structural refinement of protein diffraction data (34, 82). For example, using the Online_DPI server (83) to calculate the average DPI value for the 1.5-Å resolution structure of apo KSI (PDB code 3VSY) returns a value of 0.075 Å, which is about 5% of the resolution. Thus, when comparing high-resolution traditional single conformation crystal structures, changes in the order of 0.5 to 1.0 Å will be significant. With respect to reproducibility between crystals, Liebschner et al. (84) compared five atomic resolution crystal structures of trypsin and found that, overall, the structures are largely identical with root mean square deviations (RMSDs) of less than 0.1 Å between the five crystal structures. With respect to the reproducibility of ensemble properties for the same protein in different crystals, our recent work showed that lysozyme side chain disorder parameters are highly similar in two different crystals at RT; these and additional analyses indicate that range of conformations (or ensembles) from different crystals are highly similar (85).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S6

Tables S1 to S7

References

View/request a protocol for this paper from Bio-protocol.