Rapid 3D roll-up of gas-phase planar gold clusters and affinity and alienation for Mg and Ge: A theoretical study of MgGeAu_n (n=1–12) clusters

Summary

A cluster is a special matter level above a single atom and between macroscopic and microscopic matter, and it is an important bridge to understanding the relationship between the structure and function of matter. Here, we perform a comprehensive theoretical study of 2D planar Au_n (n = 1–12) clusters doped with both magnesium and germanium. Two interesting results are found, namely the rapid 3D "roll-up" structural growth of the GeMgAu_n (n = 1–12) cluster ground state isomers, and the relative "alienation" of the different sizes of the Au_n (n = 1–12) cluster framework towards the Ge atom, and the relative "affinity" towards the Mg atom. This study will not only enrich the data on gold-based clusters but will also provide a simple and clear theoretical guide for the 3D structuring of planar clusters, i.e. the doping of different classes of "affinition" and "alienatation" atoms.

Graphical abstract

Highlights

• •The global minima of MgGeAu_n (n = 3–12) clusters are searched using the CALYPSO program
• •Mg and Ge doping of Au_n (n = 2–12) clusters results in rapid structural 3D "roll-up"
• •MgGeAu_n (n = 3–12) clusters exhibit relative affinity for Mg and alienation to Ge atoms
• •MgGeAu₄ cluster is the most stable one than others

Density functional theory; molecular clusters.

Introduction

As one of the well-known "stars" in the field of cluster science, gold nanoclusters have been eagerly sought after by academics for the past 20 years (Jin, 2010; Jin et al., 2016; Qian et al., 2012). This is owing in part to nanoclusters' enormous practical potential. Because the size of gold nanoclusters is typically comparable to the electron Fermi wavelength, the density of states that are continuously distributed in the macroscopic state is discrete in the cluster state, resulting in gold nanoclusters having a wide range of optical (Jin, 2015), catalytic (Liu and Corma, 2018), chiral (Pelayo et al., 2018), bio-detection and bio-imaging (Shang et al., 2011), and other properties. The properties of gold nanoclusters are derived from their size-dependent structures, although it is not easy to determine them experimentally (Gruene et al., 2008; Jin, 2010, 2015; Jin et al., 2016; Kang et al., 2020; Li et al., 2003; Shang et al., 2011; Yan et al., 2018). Fortunately, predicting the structures of gold nanoclusters theoretically is not so difficult, especially for computational searches of gas-phase Au_n clusters at the quantum-chemical level based on density functional theory (DFT). Taking small-size gold nanoclusters as an example, Wang et al. (Wang et al., 2002) and Häkkinen et al. (Häkkinen and Landman, 2000) used DFT to investigate gold clusters, and they found that the ground state structure of gold nanoclusters can remain planar at Au₆ and Au₇ size, respectively. Then, Zhao et al. (Zhao et al., 2003) and Serapian et al. (Serapian et al., 2013), Hansen et al. (Hansen et al., 2013) and Olson et al. (Olson et al., 2005) also used DFT and demonstrated that the ground state of the Au₈ cluster is also planar in structure. In addition, Götz et al. (Götz et al., 2013) employed DFT to study gold clusters and found that Au₁₀ cluster possesses the 2D structure, while Johansson et al. (Johansson et al., 2014) used the revTPSS functional and the random phase approximation to predict the neutral gold clusters to become 3D at a size of 11 gold atoms. Idrobo et al. (Idrobo et al., 2007) and Deka et al. (Deka and Deka, 2008) theoretically confirmed that up to the Au₁₃ cluster ground-state structure is planar by DFT. Li et al. (Xiao and Wang, 2004) further found that the structures of the 15 Au atomic clusters are all planar in the ground state. The conclusion that small-sized gold nanoclusters (Au_3-12) have kinds of planar structures is also supported by many other reports, like Ramiro (Ramos et al., 1987) and Arratia-Perez et al.(Arratia-Perez et al., 1989), Zhao et al. (Zhao et al., 2012a), Shao et al. (Shao et al., 2012), and Sui et al. (Sui et al., 2014), and also confirmed by Goldsmith et al. (Goldsmith et al., 2019). It is necessary to explain why, for the same theoretical prediction of small-sized nanoclusters, the conclusions obtained by different researchers at different times. This is because DFT methods rely on the choice of functionals and basis sets, which are still being developed now. Unfortunately, for theoretical chemists, there is no one-size-fits-all functional and basis set that can be applied to all atoms.

At least for now, based on the above studies, we are confident enough to believe that the ground state of the nanoclusters in the Au_3-12-sized clusters is most likely to be planar. Therefore, one interesting research scientific issue is whether the size-dependent property of the structure of small-sized gold-based alloy nanoclusters changes the planar structure of gold nanoclusters. In other words, doping gold-based nanoclusters can be thought of as changing the 2D gold nanocluster structure, and there will always be a critical size from 2D to 3D transition, or a kind of 3D “roll-up” effect. It is shown that different doping atom types and different atomic numbers have different effects on the planar structure of small-sized gold clusters. Our previous work on bromine-atom-doped gold clusters confirmed that, for the ground state clusters, the transition from 2D to 3D structures starts with Au₅Br (Zhu et al., 2021), while other studies have shown that Au₁₀Re (Sui et al., 2014), Au₈Be (Chen et al., 2011), Au₄La (Zhao et al., 2010), Au₃Bi (Zhang et al., 2019), Au₃C (Yan et al., 2013), Au₉Mn (Zhang et al., 2012), Au₈V (Nhat and Nguyen, 2011), Au₁₁Sc (Ge et al., 2010), Au₃Ti, Au₅Ti and Au₇Ti (Toprek and Koteski, 2016) are the critical sizes for such 3D "roll-up." The study of doped gold clusters with two same atoms has also been studied, for example, Ca₂Au_n, Be₂Au_n, Cu₂Au_n, Ag₂Au_n, Si₂Au_n, P₂Au_n, Na₂Au_n, Mg₂Au_n. and Al₂Au_n showing that the ground state structures from Ca₂Au₃ (Zhao et al., 2012a), Be₂Au₅ (Zhao et al., 2012b), Cu₂Au₆ and Ag₂Au₆ (Zhao et al., 2011), Si₂Au₂, P₂Au₃, (Li et al., 2012), Na₂Au₂, Mg₂Au₄ and Al₂Au₂ (Li et al., 2013) are no longer planar. Moreover, the effect of such two same kinds of atom doping on the planar structure is sometimes discontinuous, i.e., Be₂Au₅, Cu₂Au₆, and Ag₂Au₆ are 3D structures, but Be₂Au₆, Cu₂Au₇, Ag₂Au₇ revert to planar geometry. So, it is interesting to gain insight into whether different types of two atoms will break this 3D "roll-up" discontinuity, and, what will be the relative affinity and distancing differences of gold nanoclusters for different atoms after doping.

Based on the above motivation, in this work, we will theoretically investigate the 3D "roll-up" of small-size Au_n nanoclusters doped with both Ge and Mg atoms. At the same time, whether gold nanoclusters exhibit relatively different affinities and distances for Mg and Ge atoms will be also investigated together. In principle, any two different atom-doped gold nanoclusters are worth studying, but Mg and Ge were chosen for this work because they are both common materials in alloy materials. Specifically, the geometry, relative stability, electronic structure, bonding properties, and spectroscopic properties of MgAu_nGe (n = 1–12) nanoclusters will be systematically investigated.

Results and discussions

The structures of MgGeAu_n clusters

The three lowest energy isomers structures of MgGeAu_n-(i) (i = 1–3; n = 1–12) clusters are presented in Figures 1 and 2, as well as the symmetry, electron state, and the energy difference from the ground state (in eV). For all MgGeAu_n-(1) represents the ground state isomer, while MgGeAu_n-(2) is the isomer with the 2nd lowest energy. As the ground state isomers are very important (their properties will be discussed specifically in the following section), we also put their relevant calculations in Table 1, where we also present the range of the calculated vibrational frequencies. As can be seen in Table 1, the lowest vibrational frequencies of all the ground state isomers are positive, so they meet the requirement that the imaginary frequencies cannot exist in introduction. For cluster, structure-dependent size growth, isomer MgGeAu₁-(1) (C_s, ²A'') shows a triangular structure where the distances of Mg-Ge, Ge-Au. and Mg-Au are 2.63 Å, 2.65 Å, and 2.72 Å, respectively. Isomers MgGeAu₁-(2) (C_2v, ²Σ_g) and MgGeAu₁-(3) (C_2v, ⁴Σ_g) are 0.69 eV and 1.37 eV higher than the energy of the ground state isomer, respectively, and both have a linear structure, where the Mg atoms are in the middle. The ground state isomer MgGeAu₂-(1) (C_s, ¹A') possesses an irregular tetrahedral structure, while the isomers MgGeAu₂-(2) (C_2v, ¹A₁) and MgGeAu₂-(3) (C_2v, ¹A₁) exhibit triangular and tetragonal planar structures. The energies of MgGeAu₂-(2) and MgGeAu₂-(3) show 0.42 eV and 0.93 eV higher than that of MgGeAu₂-(1). It is easy to find that when the isomer MgGeAu₂-(1) is used as the core and an Au atom is captured in different directions, the isomers MgGeAu₃-(1) (C_s, ²A') and MgGeAu₃-(2) (C_s, ²A') can be formed, both of which exhibit tetrahedral and the hexahedral geometry composed of double tetrahedra geometries. Isomer MgGeAu₃-(3) (C₁, ²A) displays a 2D planar structure and can be formed through isomer MgGeAu₂-(3) by attracting an Au atom. In addition, the second- and third-lowest energy isomers of the MgGeAu₃ cluster are 0.90 eV and 1.80 eV higher than the energy of their ground state isomer. For MgGeAu₄, the structure of its ground state isomer, MgGeAu₄-(1) (C₁, ¹A), is based on the structure of the isomer MgGeAu₃-(2) by attracting an Au atom on the outer side of the Mg atom. The isomers MgGeAu₄-(2) (C_s, ¹A') and MgGeAu₄-(3) (C₁, ¹A), which have energies 1.71 eV and 1.74 eV higher than the ground state, exhibit a kind of tetrahedral-based deformation structure. For the MgGeAu₅ cluster, the energy of its ground state isomer is 0.43 eV and 0.71 eV lower than that of the second- and third-lowest energy isomers, respectively. In addition, the isomers MgGeAu₅-(1) (C₁, ²A) and MgGeAu₅-(2) (C₁, ²A) are constructed by attracting an Au atom in different directions with the isomer MgGeAu₄-(1) as their "core." The isomer MgGeAu₅-(3) (C₁, ²A), on the other hand, shows a 3D mesh-like structure. The structures of the ground state and the second-lowest energy isomer of the MgGeAu₆ cluster are also easily obtained by the deformation of the isomeric MgGeAu₅-(1) by the adsorption of an Au atom. The third lowest energy isomer of the MgGeAu₆ cluster is then an expanded 3D mesh-like with one more Au atom of the isomer MgGeAu₅-(3) structure. Furthermore, isomers MgGeAu₆-(2) (C_s, ¹A') and MgGeAu₆-(2) (C_s, ¹A') have energies 0.13 eV and 0.31 eV higher than isomer MgGeAu₆-(1) (C₁, ¹A).

Figure 1.

The three lowest energy isomers structures of MgGeAu_n-(i) (i = 1–3; n = 1–6) clusters, and the energy difference (eV) to the lowest energy isomer

Figure 2.

The three lowest energy isomers structures of MgGeAu_n-(i) (i = 1–3; n = 7–12) clusters, and the energy difference (eV) to the lowest energy isomer

Table 1.

Symmetry, electronic state, average bonding energy (E_b), the second order difference energy (Δ₂E), fragmentation energy (E_f), HOMO-LUMO energy gap (E_gap) for α- electrons, and vibrational frequency in the ground state of MgGeAu_n (n = 1–12) clusters

Cluster	Symmetry	State	Eb (eV)	Δ2E (eV)	Ef (eV)	Egap-α (eV)	Highest Freq. (ω−1)	Lowest Freq. (ω−1)
MgGeAu1	Cs	2A"	2.13	–	–	1.68	264	140
MgGeAu2	C1	1A	2.64	4.14	0.55	1.78	280	47
MgGeAu3	Cs	2Aʹ	2.82	3.58	−0.5	3.11	381	30
MgGeAu4	C1	1A	3.03	4.08	1.35	3.32	371	24
MgGeAu5	C1	2A	2.99	2.74	−0.92	2.57	333	17
MgGeAu6	C1	1A	3.07	3.65	1.22	2.58	331	15
MgGeAu7	C1	2A	3.00	2.43	−1.01	1.10	294	16
MgGeAu8	C1	1A	3.05	3.44	0.41	0.54	313	10
MgGeAu9	C1	2A	3.05	3.03	−0.47	1.33	288	12
MgGeAu10	C1	1A	3.08	3.50	0.57	0.97	270	8
MgGeAu11	C1	2A	3.07	2.94	−0.93	1.74	291	9
MgGeAu12	C1	1A	3.13	–	–	2.04	301	14

As displayed in Figure 2, for the ground state isomers MgGeAu_n-(1) (n = 7–12), their structures are based on the deformation of smaller size clusters by attracting an Au atom in different orientations, while the "core" is the geometry of the isomer MgGeAu₃-(2). In other words, this double-tetrahedral structure with Mg and Ge atoms at two vertices plays the role of the "seed" for the growth of the ground state of MgGeAu_n (n = 4–12) clusters. As for the isomers MgGeAu_n-(2) and MgGeAu_n-(3) (n = 7–12), their structures show some diversity and are not entirely grown from the "seed" of MgGeAu₃-(2). The structures of these isomers have larger size 3D mesh-like structures, such as MgGeAu₈-(2) and MgGeAu₈-(3), and another complex 3D structure in which the Mg and Ge atoms are far apart, such as the isomers MgGeAu₉-(2), MgGeAu₁₀-(2), MgGeAu₁₀-(3), MgGeAu₁₁-(2) and MgGeAu₁₁-(3). Except for the isomers MgGeAu₈-(3) (C_s, ¹A'), MgGeAu₁₀-(3) (C_s, ¹A'), MgGeAu₁₁-(2) (C_s, ²A') and MgGeAu₁₁-(3) (C_s, ²A'), all other isomers MgGeAu_n-(i) (i = 1–3; n = 7–12) exhibit C₁ symmetry and their corresponding ¹A and ²A electronic states. As shown in Figure 2, the energy differences of the isomers MgGeAu_n-(i) (i = 2–3; n = 7–12) with respect to their respective ground states are 0.55eV, 0.63eV, 0.46eV, 0.59eV, 0.11eV, 0.77eV, 0.26eV, 0.39eV, 0.31eV, 0.58eV, 0.20eV and 0.33eV.

The above analysis leads to the following important conclusion: the structure of MgGeAu_n (n = 1–12) nanoclusters will fast "roll up" into a 3D structure. For the ground state clusters, all the ground state nanoclusters are 3D except for MgGeAu₁ which must be planar. In addition, a double tetrahedral geometry as the "core" or "seed" for the growth of MgGeAu_n (n = 1–12) nanocluster structure has been found and confirmed by our study. In order to better discuss below-the-ground state nanoclusters, which are relatively more stable and more likely to be experimentally synthesized because of their relatively lowest energy, atomic coordinate information is provided in Table S1 of the Supplementary Materials. In addition, in order to make the structures of these isomers more readily available to the reader, their MOL format files are named Data S1 in the Supplementary Materials, relating to the MgGeAu_n-(i) isomers, respectively.

The relative stabilities

The relative stability of clusters is an important study in cluster research because it is size-dependent. By studying the relative stability of clusters, we can find the local most stable clusters, which is an important tool to define the "magic" clusters. The "magic" clusters can be thought of as sizes with a high probability of occurrence when atoms are aggregated into clusters under experimental conditions. Here, the ground state of MgGeAu_n (n = 1–12) nanoclusters will be investigated by the following four energies, which are binding energy per atom (E_b), second-order energy difference (Δ₂E), fragmentation energy (E_f), and LUMO-HOMO energy gap (E_gap), as displayed in the following Equations 1, 2, 3, and 4.

$$E_b\left({\text{MgAu}}_n\text{Ge}\right)=\frac{nE\left(\text{Au}\right)+E\left(\text{Ge}\right)+E\left(\text{Mg}\right)-E\left({\text{MgGeAu}}_n\right)}{n+2}$$ (Equation 1)

$${\Delta }_{2}E\left({\text{MgGeAu}}_n\right)=E\left({\text{MgGeAu}}_{n+1}\right)+E\left({\text{MgGeAu}}_{n-1}\right)-2E\left({\text{MgGeAu}}_n\right)$$ (Equation 2)

$$E_{\text{f}}\left({\text{MgGeAu}}_n\right)=E\left({\text{MgGeAu}}_{n-1}\right)+E\left(\text{Au}\right)-E\left({\text{MgGeAu}}_n\right)$$ (Equation 3)

$$E_{\text{gap}}\left({\text{MgGeAu}}_{\text{n}}\right)=E_{\text{LUMO}}\left({\text{MgGeAu}}_{\text{n}}\right)-E_{\text{HOMO}}\left({\text{MgGeAu}}_{\text{n}}\right)$$ (Equation 4)

In Equations 1, 2, and 3, the energy corresponding to the atom or cluster is denoted by E. In Equation 4, E_gap is the energy difference between the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO). The calculated results are presented in Table 1 and the curves with cluster size are plotted in Figure 3.

Figure 3.

Relative stability parameters for α-electrons in the ground state of MgGeAu_n (n = 1–12) clusters

(A) E_b, (B) Δ₂E, (C) E_f, (D) E_gap.

As displayed in Table 1 and Figure 3A, the E_b values of the MgGeAu_1-4 clusters are rapidly increasing, while the E_b curve of the MgGeAu_4-12 clusters is oscillating and increasing in smaller magnitudes. Overall, the clusters are more stable with the increase in the number of Au atoms and the interatomic bonding. Specifically, the largest E_b value, 3.07 eV, occurs at MgGeAu₆, followed by the MgGeAu₄ cluster with the second-largest E_b value of 3.03 eV, indicating that they both have the strongest local stability. Δ₂E is a typical local stability parameter that characterizes the energy relations of X_n cluster with respect to X_n-1 and X_n+1 (X_n means an arbitrary cluster and n is the size). Figure 3B shows that Δ₂E curve of MgGeAu_n (n = 1–12) nanoclusters has a distinct odd-even oscillatory trend, and even-size clusters have higher stability than odd-size ones. Specifically, the first and second strongest peaks of the Δ₂E curve occur at MgGeAu₄ and MgGeAu₆ with 4.08 eV and 3.65 eV, respectively, indicating that they are much more stable than their neighbors. The fragmentation energy E_f is the energy required to split the MgGeAu_n cluster into the MgGeAu_n-1 cluster and an Au atom, so the larger the value of E_f, the more stable its corresponding cluster is. As Figure 3C displayed, the E_f curve of the MgGeAu_n (n = 1–12) clusters is like the Δ₂E curve and exhibits odd-even oscillatory behavior. The E_f of the even-size clusters is significantly larger than that of the odd-size ones, MgGeAu₄ and MgGeAu₆ possess the largest and second-largest E_f values, 1.35 eV and 1.22 eV, respectively, indicating that both are more stable than the other clusters. Interestingly, this odd-even oscillation stability pattern of doped gold clusters has been confirmed in all similar works, even in the pure gold clusters studies (Assadollahzadeh and Schwerdtfeger, 2009; Bonačić-Koutecký et al., 2002; Chen et al., 2011; Fernández et al., 2006; Häberlen et al., 1997; Häkkinen and Landman, 2000; Wang et al., 2002; Zhang et al., 2019; Zhao et al., 2003, 2010; 2012a; 2012b; 2011; Zhu et al., 2021). This phenomenon is mainly derived from the difference in the stability of open-shell and closed-shell structures. E_gap can be used to characterize the chemical stability of the clusters, and a higher E_gap value means less susceptibility to chemical reactions. Quantum mechanics tells us that there are only two possible spin quantum numbers for a single electron, so in quantum chemical calculations, we usually distinguish between two different spin quantum numbers of electrons as α-electrons (spin up) and β-electrons (spin down). For any closed-shell system, because each α-electron has a β-electron paired with it (determined by the Pauli exclusion principle), there is no need to distinguish between them. Although for the open-shell system, when the system itself carries an odd number of electrons, there must be an unpaired α-electron, so the behavior of α- and β-electrons needs to be discussed separately. As the odd-sized MgGeAu_n (n is an odd number) clusters are open-shell systems, which have unequal α and β electrons, Table 1 and Figure 3D show the E_gap of α electrons, while the E_gap curve of β electrons is plotted in Figure S1 of the Supplementary Materials. For both α- and β-electrons, MgGeAu₄ has the largest E_gap value and thus possesses the highest chemical stability, while the cluster of MgGeAu₆ has the third and second largest values and thus possesses considerable high chemical stability.

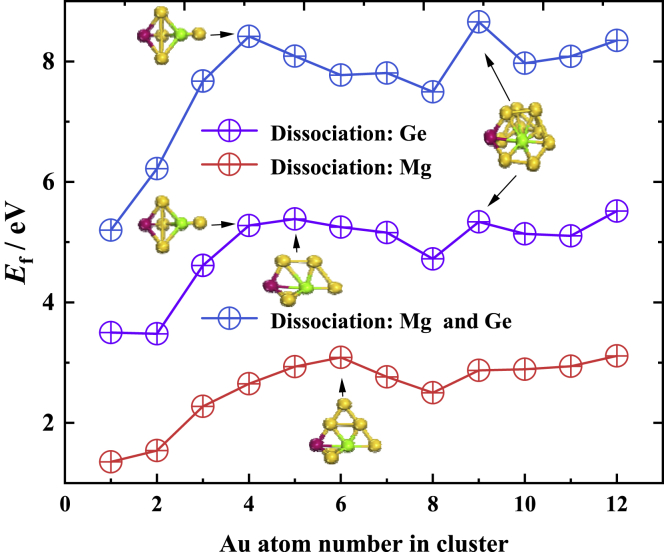
Furthermore, Equation 3 studies only one channel of dissociation of the GeMgAu_n cluster, i.e., the dissociation of GeMgAu_n into GeMgAu_n-1 and an Au. It is necessary to further investigate other possible dissociation channels corresponding to the dissociation energy. Equations 5, 6, and 7 show three other possible dissociation channels for the GeMgAu_n cluster

$$E_{\text{f}}^{\prime }\left({\text{MgGeAu}}_n\right)=E\left({\text{GeAu}}_n\right)+E\left(\text{Mg}\right)-E\left({\text{MgGeAu}}_n\right)$$ (Equation 5)

$$E_{\text{f}}^{″}\left({\text{MgGeAu}}_n\right)=E\left({\text{MgAu}}_n\right)+E\left(\text{Ge}\right)-E\left({\text{MgGeAu}}_n\right)$$ (Equation 6)

$$E_{\text{f}}^{‴}\left({\text{MgGeAu}}_n\right)=E\left({\text{Au}}_n\right)+E\left(\text{Mg}\right)+E\left(\text{Ge}\right)-E\left({\text{MgGeAu}}_n\right)$$ (Equation 7)

After structural optimization and frequency calculations of MgAu_n, GeAu_n, and Au_n (n = 2–13) clusters at the same computational level, the dissociation energy results for these different channels are presented in Table S3 of the Supplementary Materials and plotted in Figure 4. As the calculated results show, the GeMgAu_n cluster has the largest dissociation energy for the simultaneous dissociation of Ge and Mg, and the lowest dissociation energy for the dissociation of Mg alone. Compared to the dissociation Au atoms in Figure 3C, the dissociation energies of the three different channels in Figure 4 do not show significant odd-even oscillations with cluster size, but the MgGeAu₄ and MgGeAu₉ clusters are relatively stable than others for the Ge and Mg simultaneous dissociation channels. For the Ge dissociation channel, MgGeAu₅ and MgGeAu₉ have the local maximum dissociation energy, while the dissociation energies of MgGeAu₄ and MgGeAu₆ are extremely close to that of MgGeAu₅, indicating that these four clusters are relatively stable. For the Mg atom dissociation channel, the dissociation energy of MgGeAu₆ has a local maximum, implying that it has the strongest relative stability. Obviously, different dissociation channels yield different local most stable clusters, but regardless of the channels, the three MgGeAu₄, MgGeAu₆, and MgGeAu₉ always possess very high stability.

Figure 4.

Dissociation energies for Mg, Ge, and both Mg and Ge three channels from the lowest-energy states MgGeAu_n (n = 1–12) clusters

In summary, the above study can be concluded that the ground state of MgGeAu₄ and MgGeAu₆ clusters have robust stability, and thus are candidates for the "magic" clusters.

Charge transfer property

The charge transfer properties and electronic configuration of the cluster can be analyzed by NCP and NEC in NBO calculations, which can help us to understand the mechanism of cluster formation. The NCP and NEC calculations for each atom of the ground state MgGeAun (n = 1–12) cluster are shown in Tables 2, S4, and S5 in the Supplementary Materials, and their size dependence is plotted in Figure 5. The results show the following facts, (i). All Mg atoms lose electrons and play the role of electron donors in all clusters, (ii). All Ge atoms, on the other hand, are electron acceptors and thus positively charged, (iii). There are 78 Au atoms in total, while 70 of them are electron gainers and negatively charged, and the remaining 8 are electron losers and positively charged. In Figure 5A, the different atoms are colored red and blue, respectively, after charge transfer, and it can be clearly seen that there is a distinct red atom in each cluster, which corresponds to the Mg atom. Numerically, all Mg atoms lose electrons in the range from 0.73e to 1.52e, while all Ge atoms gain electrons in the range of [-0.46e, −0.01e], a few Au atoms are positively charged even though they are distributed in a small range of [0.01e, 0.15e], and most Au atoms are negatively charged from −0.43e to −0.01e. The charge transfer property of the ground state of MgGeAu_n (n = 2–12) clusters originates from the fact that Mg (1.2), Ge (1.8), Au (2.4) have different electronegativities. The electronegativity values of both Mg and Ge are smaller than that of Au, so Au is more likely to get electrons from Mg and Ge atoms when all three of them are aggregated and as the number of Au atoms increases.

Table 2.

Natural Charge Population and Natural Electron Configuration on Mg and Ge atoms in the ground state of MgGeAu_n (n = 1–12) clusters

Cluster	Natural Charge Population on Mg (in |e|)	Natural Charge Population on Ge (in |e|)	Natural Electron Configuration on Mg (in |e|)	Natural Electron Configuration on Mg (in |e|)
MgGeAu1	0.73	−0.39	[core]3S1.183p0.06	[core]4S1.914p2.41
MgGeAu2	0.90	−0.38	[core]3S1.043p0.05	[core]4S1.844p2.50
MgGeAu3	1.15	−0.21	[core]3S0.753p0.09	[core]4S1.864p2.31
MgGeAu4	1.15	−0.20	[core]3S0.763p0.09	[core]4S1.814p2.34
MgGeAu5	1.26	−0.19	[core]3S0.743p0.09	[core]4S1.804p2.35
MgGeAu6	1.28	−0.24	[core]3S0.633p0.08	[core]4S1.784p2.42
MgGeAu7	1.39	−0.46	[core]3S0.513p0.09	[core]4S1.694p2.73
MgGeAu8	1.38	−0.15	[core]3S0.533p0.08	[core]4S1.754p2.37
MgGeAu9	1.46	−0.18	[core]3S0.453p0.07	[core]4S1.714p2.44
MgGeAu10	1.44	−0.15	[core]3S0.473p0.08	[core]4S1.704p2.42
MgGeAu11	1.52	−0.01	[core]3S0.413p0.06	[core]4S1.744p2.25
MgGeAu12	1.44	−0.08	[core]3S0.483p0.07	[core]4S1.694p2.36

Figure 5.

Natural charge population (NCP) and natural electron configuration (NEC) on Mg and Ge atoms for the ground state of MgGeAu_n (n = 2–12) clusters

(A). NCP on Mg and Ge, (B) NEC on Mg, (C) NEC on Ge, and (D) NEC on Au.

Figures 5B–5D show the NEC distributions of Mg, Ge, and Au atoms, respectively, with the horizontal, dashed lines showing the valence electron configurations of the corresponding bare atoms. It can be found that the valence 3s orbital of the Mg atom always loses electrons while the 3p orbital gains electrons, similarly, the 4s orbital of the Ge atom loses electrons while the 4p orbital gains electrons. This indicates that Mg is 3s3p orbitals hybridized in the cluster, while Ge is 4s4p orbitals hybridized. For the Au atoms, their 5d orbitals lose electrons, while the 6p orbitals are all gaining electrons, and the complexity comes from the 6s orbitals of Au, which are mostly gaining electrons, but a few are also losing them. Thus, the Au atoms in the cluster are 5d6s6p orbitals hybridized.

The topology analysis of the chemical bond property of MgGeAu_n clusters

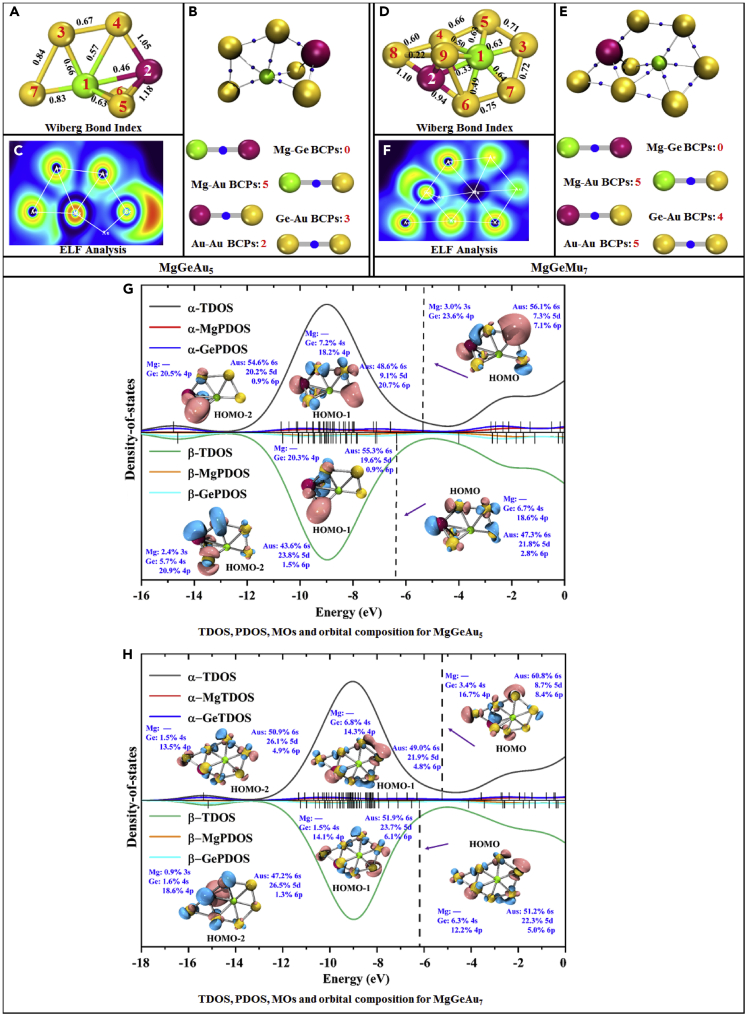
During cluster formation, the following scientific questions are often raised. Is a chemical bond formed between two atoms in a cluster? what type of bond is it? Is there a cluster size-dependent property of chemical bond strength? In the atom-in-molecule (AIM) theory, the interatomic bond critical point (BCP) calculation and found were proposed to solve the above problems. This is because if a BCP is searched between two atoms, it indicates that they are bonded, and then the nature of the bond can be determined through the Laplacian function of electron density (▿²ρ) and ELF values at this point. Specifically, ▿²ρ(BCP) < 0 and ELF(BCP) > 0.5 mean a covalent bond, while ▿²ρ(BCP) > 0 and ELF(BCP) < 0.5 suggests a non-covalent bond. Such calculations for the ground state of MgGeAu_n (n = 1–12) clusters were conducted and they are shown in Table S6 in the Supplementary Materials, and even more, the interatomic Wiberg bond index and their distances were also investigated for a more comprehensive study of the chemical bond properties. In addition, the total density of states (TDOS), the partial density of states (PDOS of Mg and Ge atoms), molecular orbitals (MOs), and the three highest occupied molecular orbitals (HOMO, HOMO-1, and HOMO-2) were also studied in order to further investigate the chemical bond in the clusters. These results are plotted in Figures 6, 7, and S4 in the Supplementary Materials.

Figure 6.

Wiberg bond index (WBI), BCPs, ELF, MOs, composition, TDOS, and PDOS for α-electrons and β-electrons of the most unstable MgGeAu₅ and MgGeAu₇ clusters

(A and D). WBI, (B and E). BCPs, (C and F). ELF, (G and H). MOs, composition, TDOS, and PDOS.

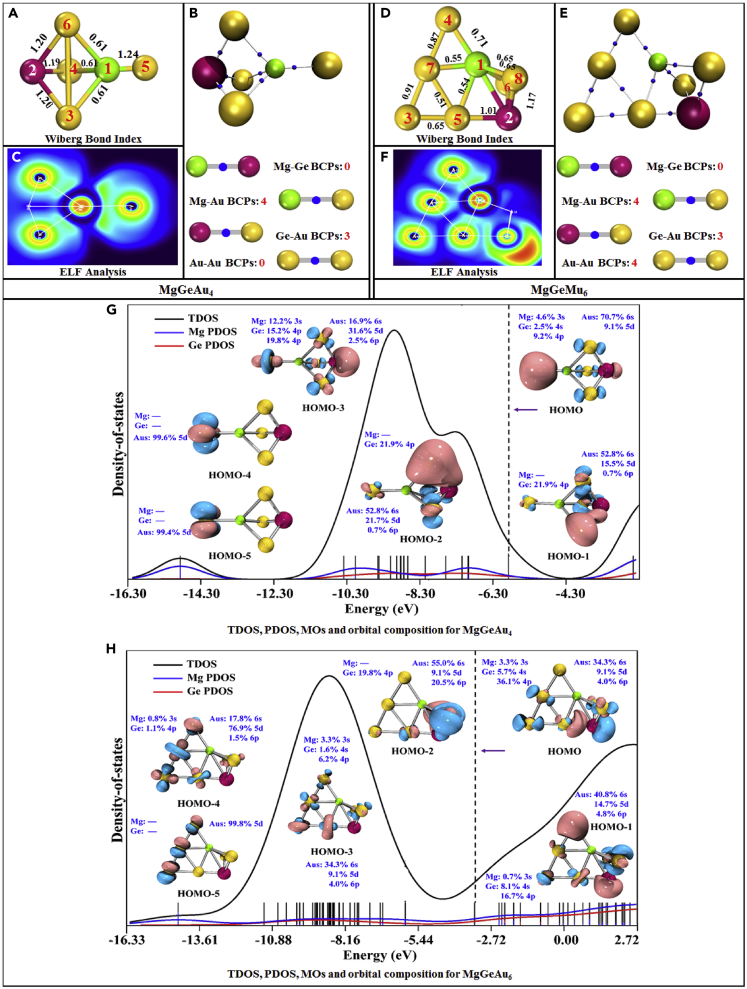
Figure 7.

Wiberg bond index (WBI), BCPs, ELF, MOs, composition, TDOS, and PDOS for α-electrons and β-electrons of the most stable MgGeAu₄ and MgGeAu₆ clusters

(A and D). WBI, (B and E). BCPs, (C and F). ELF, (G and H). MOs, composition, TDOS, and PDOS.

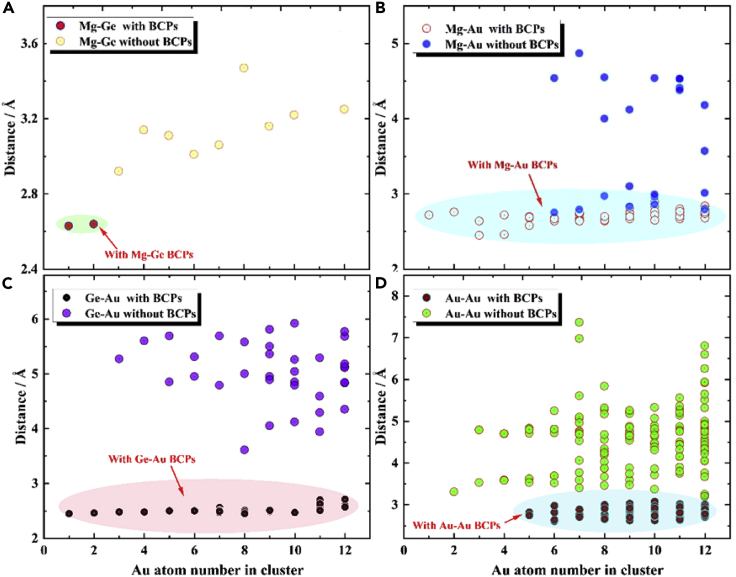
For the study of the number of atomic bonds, Figure S2 in the Supplementary Material counts the search of BCP for each cluster, and it can be easily found that Mg-Ge bonds exist only in MgGeAu₁ and MgGeAu₂, while Au-Au bonds start to appear in clusters larger than the size of MgGeAu₄ (i.e., starting from MgGeAu₅), and the number of Mg-Au bond is always excess to Ge-Au, in addition, Au -Au BCPs increase in proportion to the cluster size. Interestingly, Mg atoms can bond with up to 8 surrounding Au atoms, while Ge atoms can only form bonds with up to 4 Au atoms. Figure 8 analyzes the relationship between interatomic distances and the presence of BCPs, as shown in Figures 8A, 8C, and 8D, which show that the distances of Mg-Ge, Ge-Au, and Au-Au can determine the presence of BCPs between them, i.e., there is a clear boundary between the region with and without BCPs. In contrast, Figure 8B shows that the distance and bonding relationship of Mg-Au is more complex, and the intuitive perception that chemical bonds are formed at closer distances does not apply here. However, when we fit the Wiberg bond index against the interatomic distance, as shown in Figure S3 in the Supplementary Materials, the closer the atoms are to each other for the same type of chemical bond, the stronger the Wiberg bond index will be. In addition, combining the geometries in Figures 1 and 2, one interesting conclusion is that Mg atoms tend to "immerse" inside the Au_n (n = 1–12) clusters, while Ge atoms tend to be "crowded" to the edges! This means that small-sized Au_n (n = 1–12) clusters exhibit relative affinity for Mg atom and alienation from Ge atom. It is known from the charge transfer study in charge transfer property that Mg atoms tend to lose electrons while Au tends to gain electrons, so they can easily form ionic bonds, but both Ge and Au tend to gain electrons and it is relatively difficult for them to form bonds.

Figure 8.

The atom distance (in Å) between two atoms for each ground state of MgGeAu_n (n = 2–12) clusters, with atom1-atom2 BCPs means that in this distance, BCPs were found between these two atoms in such distances, while those distributions that were not circled meant that BCPs were not found at these distances

(A) Mg-Ge, (B) Mg-Au, (C) Ge-Au, (D) Au-Au atoms.

Figures 6 and 7 show the results for the two relatively locally most unstable and two most stable clusters, MgGeAu_5,7 and MgGeAu_4,6, in terms of bond type (through ELF), the density of states, molecular orbitals, and orbital composition. Similar results for the other clusters, MgGeAu_1-3, and MgGeAu _8-12, are presented separately in Figures S4–S11 and Table S7 of the Supplementary Materials. Obviously, ▿²ρ > 0 and ELF <0.5 hold in all BCPs, suggesting that Mg-Ge, Mg-Au, Ge-Au, and Au-Au bonds are all non-covalent bonds. The total density of states plots and partial density of states curves, such as those displayed in Figures 6G, 6H, 7G, and 7H, show that the contributions of both Mg and Ge atoms are relatively small in each molecular orbital (except for MgGeAu₁). For example, for the locally most unstable open-shell cluster, MgGeAu₇, its α- and β-electrons HOMO, HOMO-1, and HOMO-2 orbitals contain no Mg atomic orbital contributions (except for the β-electron HOMO-2 orbital which has 0.9% Mg atomic 3s orbital contributions), while there come some Ge atomic 4s (greater than 10%) and 4p (less than 10%) orbital contributions, and about 50% of the contributions are from the 6s orbitals of Au atoms, as well as a small amount of 5d and 6p orbital contributions. A similar situation occurs for the most locally stable closed-shell cluster, MgGeAu₄, where 70.7% and 9.1% of the HOMO orbitals come from the 6s and 5d orbitals of the Au atoms, while the Mg atom contributes 4.6% of the 3s orbital, while 2.5% and 9.2% of the contributions come from the 4s and 4p orbitals of the Ge atom. Therefore, we can quantify the electronic configuration of the clusters revealed by the NEC conclusion in charge transfer property in terms of orbital composition. First, although the Mg atom is 3s3p orbital hybridized, its contribution to the MOs is extremely small and can be neglected in many cases. Second, the contribution of the 4s4p orbital hybridization of the Ge atom to the MOs cannot be neglected, but it mainly comes from its 4p orbitals. Finally, the dominant contribution of the 6s5d6p orbital hybridization of the Au atom to the MOs is the 6s orbital.

Conclusions

In summary, this work investigates the structure, stability, charge transfer, and bonding properties of small-sized Au_n (n up to12) clusters possessing 2D planar structures when they are doped with Mg and Ge atoms. Interestingly, the geometries of the MgGeAu_n (n = 2–12) clusters rapidly "roll up" into 3D structures. The "seed" of cluster growth is a double-tetrahedral structure with Mg and Ge at the two vertices and three Au atoms forming a triangular base, on which almost all MgGeAu_n (n = 3–12) clusters were found to grow. Stability calculations for the ground state isomers reveal that even-size MgGeAu_n (n = 1–12) clusters are more stable than odd-size ones, with the two most stable clusters being MgGeAu₄ and MgGeAu₆. Charge transfers and electron configuration studies indicate that electrons are transferred from Mg atoms to Ge and most Au atoms, and Mg and Ge atoms are 3s3p orbitals and 4s4p orbitals hybridized, while Au is 5d6s6p orbitals hybridized. ELF and ▿²ρ calculations of BCPs based on AIM theory show that, as shown in Figure 9, Mg-Ge bonds exist only in MgGeAu₁ and MgGeAu₂, while Au-Au bonds start to appear in clusters larger than the size of MgGeAu₄, and Mg-Ge, Mg-Au, Ge-Au, and Au-Au bonds are all non-covalent bonds. Interestingly, Mg atoms tend to "immerse" inside the Au_n (n = 3–12) clusters, while Ge atoms tend to be "crowded" to the edges, suggesting that small-sized Au_n (n = 3–12) clusters exhibit relative affinity for Mg atom and alienation from Ge atom. Finally, the studies on the density of states and orbital composition confirm that the 3s of Mg, 4p of Ge, and 6s of Au atom orbitals are the main contributors to clusters MOs.

Figure 9.

The appearance of Mg-Ge, Mg-Au, Ge-Au, and Au-Au bonds in the ground state of MgGeAu_n (n = 2–12) clusters

Limitations of the study

The present work is a standard theoretical study on Au-based clusters, although the structures of numerous isomers are predicted, the corresponding energies, electronic properties, and spectral properties are calculated, as well as some interesting phenomena in the formation of ground state isomers of various sizes are found. It must be acknowledged, however, that the absolute values of these calculations are dependent on the functional and basis set of the DFT. In addition, as the spectra calculated in this work are only for the ground states isomers, they are always not directly usable in spectroscopic experiments at specific temperatures and require the consideration of the weighted population of the Boltzmann distribution of several low-energy isomers at this temperature.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
CALYPSO	Wang et al., 2012	http://www.calypso.cn
SPAP	Lv et al., 2012	http://www.calypso.cn
Gaussian09	Frish et al., 2016	https://gaussian.com
Multiwfn	Lu and Chen, 2012	http://sobereva.com/multiwfn/
VMD	Humphrey et al., 1996	http://www.ks.uiuc.edu/Research/vmd/

Resource availability

Lead contact

Any further information and requests should be directed to and will be fulfilled by the lead contact, Ben-Chao Zhu (benchao_zhu@126.com).

Materials availability

This study did not generate new materials.

Experimental model and subject details

This work does not use any experimental models.

Method details

The initial guess structures of MgAu_nGe (n = 1–12) nanoclusters were constructed by CALYPSO software (Wang et al., 2010, 2012), which is based on the particle swarm optimization (PSO) algorithm. CALYPSO structure prediction software has been successfully used for clusters (Lv et al., 2012; Zhang et al., 2020; Zhao et al., 2021; 2019), crystals (Lu et al., 2020; Lu and Chen, 2020, 2021) and materials under high pressure (Chen et al., 2021; Sun et al., 2020). For each size of MgAu_nGe nanocluster, 1000 structures will be generated (50 generations in total, 20 structures/generation), 80% of which will be generated by PSO, while the remaining 20% will be generated randomly. These generated structures will then be calculated in Gaussian 09 software (Frisch et al., 2016) for structural optimization with the low-level Hartree-Fock method. Not all the 1000 isomers obtained from the MgAu_nGe search of each size are useful, most of them can be removed by SPAP software (Wang et al., 2012) based on energy and structural similarity to select candidates for the next step of high-level structural optimization and frequency calculations with DFT in Gaussian09. The functional in the DFT calculation is chosen to be b3pw91 (Becke, 1992), the all-electron basis set 6-311g(d) (Krishnan et al., 1980) for Mg and Ge, and the pseudopotential basis set lanl2dz for Au atoms (Pritchard et al., 2019). In order to explain the rationality of this functional and basis set selection, we compared the theoretical calculation values of geometries (atomic distance in Å), vibration frequency (ω/cm⁻¹), average binding energy (E_b in eV), vertical ionization potential (VIP) and vertical electron affinity (VEA) energy of Au₂, Ge₂ and Mg₂ dimers at different level with the corresponding experimental data. Here we totally used five functionals, b3pw91, b3lyp, pbepbe, tpsstpss, wb97xd, and five base sets, lanl2dz, lanl2mb, sdd, 6-311g(d), 6-31g to test. The results are shown in the Table S2 of the Supplementary Materials, and one can find that Compared with the experimental data, b3pw91/lanl2dz and b3lyp/lanl2dz are reasonable choices for Au₂ dimer (Barnett et al., 1999; K. Huber and Herzberg, 1979a; Perdew et al., 1992), but for Mg₂ dimer, the average binding energy calculated by b3pw91/6-311g(d) is closer to the experimental value (K. P. Huber and Herzberg, 1979b; Ruette et al., 2005), and the error between the vibration frequency calculated by b3lyp/6-311g(d) and the experimental data is smaller. Finally, for Ge₂ dimer, the calculated results of b3pw91/6-311g(d) are closer to the experimental data (Amadoruge and Weinert, 2008; Kingcade et al., 1986; Miller et al., 1986; Yoshida and Fuke, 1999) than b3lyp/6-311g(d) overall, except the VEA value. Therefore, we can confirm that the selection of b3pw91/lanl2dz for Au and b3pw91/6-311g(d) for Ge and Mg is reasonable. In addition, for each candidate isomer, the calculation also considered their different spin multiplicity, i.e., 1, 3, 5, 7 for the closed-shell layer and 2, 4, 6, 8 spin multiplicity for the open-shell layer. The goal of the frequency calculation is to ensure that the optimized isomers are not transition states, so if imaginary frequencies appear in the results, they need to be eliminated and reoptimized until all frequencies are positive.

Natural bond orbital (NBO) (Reed et al., 1988) was used to analyze the nature of charge distribution and orbital composition in clusters, including natural charge population (NCP), natural electron configuration (NEC), as well as natural atom orbital (NAO) composition. Wiberg bond index analysis (Wiberg, 1968) was performed to compare the Mg-Ge, Mg-Au, and Au-Au chemical bond in the ground state of MgAu_nGe (n = 1–12) nanoclusters. The study of chemical bonding between cluster atoms started with the search of bond critical points (BCPs) by Atom-in-Molecular (AIM) theory (Bader, 1985), and then the Laplacian function of electron density (▿²ρ (BCPs)) (Lu and Chen, 2013), electron localization function values (ELFs) (Becke and Edgecombe, 1990) of these BCPs was used to determine the nature of chemical bonds. AIM theory is a useful technique for the topological analysis of chemical bonding properties. Because in this theory, the architecture is composed of its electron-density standing points and the gradient paths of electron density starting and ending at these points. Thus, the atoms within any system and the chemical bonds between atoms are natural expressions of the observable electron density distribution function of the system. In addition, the molecular orbitals (MOs), the total density of states (TDOS) and partial density of states (PDOS) of Mg, Ge, and Au atoms were analyzed by Multiwfn software (Lu and Chen, 2012) for all the ground states of MgAu_nGe (n = 1–12) nanoclusters. The molecular orbital (MOs) diagram of each ground state isomer is drawn by VMD software (Humphrey et al., 1996).

Quantification and statistical analysis

The initial enthalpies of each size MgGeAu_n cluster isomer were counted and sorted by the cak.py package of the CALYPSO software. The structural simplification states were counted and removed according to the SPAP auxiliary program of the CALYPSO software.

Published: October 21, 2022

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •This paper does not report original code.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.