Abstract
This paper introduces a new human-based metaheuristic algorithm called Sewing Training-Based Optimization (STBO), which has applications in handling optimization tasks. The fundamental inspiration of STBO is teaching the process of sewing to beginner tailors. The theory of the proposed STBO approach is described and then mathematically modeled in three phases: (i) training, (ii) imitation of the instructor’s skills, and (iii) practice. STBO performance is evaluated on fifty-two benchmark functions consisting of unimodal, high-dimensional multimodal, fixed-dimensional multimodal, and the CEC 2017 test suite. The optimization results show that STBO, with its high power of exploration and exploitation, has provided suitable solutions for benchmark functions. The performance of STBO is compared with eleven well-known metaheuristic algorithms. The simulation results show that STBO, with its high ability to balance exploration and exploitation, has provided far more competitive performance in solving benchmark functions than competitor algorithms. Finally, the implementation of STBO in solving four engineering design problems demonstrates the capability of the proposed STBO in dealing with real-world applications.
Subject terms: Engineering, Mathematics and computing
Introduction
Optimization problems represent challenges with several possible solutions, one of which is the best choice. Accordingly, optimization is the process of achieving the best solution to the optimization problem. An optimization problem has three main parts: decision variables, objective function, and constraints1. Optimization aims to determine the values of the decision variables by considering the constraints so that the objective function is optimized2. Optimization problem-solving methods fall into two groups, deterministic and random approaches. Deterministic approaches deal well with linear, continuous, differentiable, and convex optimization problems. However, the disadvantage of these approaches is that their ability is lost in solving nonlinear, non-convex, non-differentiable, high-dimensional, NP-hard problems and discrete search spaces. These items, which have led to the inability of deterministic approaches, are among the features of real-world optimization problems. Stochastic algorithms, especially metaheuristic algorithms, have been introduced to meet this challenge. Metaheuristic algorithms can provide suitable solutions to optimization problems by using random search in problem-solving space and relying on random operators3. The critical thing about metaheuristic algorithms is that there is no guarantee that the solution obtained from these methods will be the best or global optimal. This fact has led researchers to develop numerous metaheuristic algorithms to achieve better solutions.
Metaheuristic algorithms are designed based on modeling ideas that exist in nature. Among the most famous metaheuristic algorithms can be mentioned Genetic Algorithm (GA)4, Particle Swarm Optimization (PSO)5, Ant Colony Optimization (ACO)6, and Artificial Bee Colony (ABC)7. GA is based on modeling the reproductive process. PSO is developed based on modeling the swarm movement of birds and fish in nature. ACO is designed based on simulating the natural behaviors of ants, and ABC is introduced based on modeling the activities of bee colonies in search of food.
Metaheuristic algorithms must have an acceptable ability for exploration and exploitation to deliver suitable optimization performance. Exploration is the concept of global search in different parts of the problem-solving space to find the main optimal area. Exploitation means a local search around candidate solutions to find better possible solutions that may be near them. In addition to having a high quality in exploration and exploitation, balancing these two indicators is the key to the success of metaheuristic algorithms8.
The main research question is, despite the large number of metaheuristic algorithms introduced so far, is there still a need to introduce newer methods? The answer to this question lies in the concept of the No Free Lunch (NFL) theorem9. According to the NFL, the excellent performance of an algorithm in solving a set of optimization problems does not guarantee the same performance of that algorithm in other optimization problems. This result is due to the random nature of metaheuristic algorithms in achieving the solution. In other words, the NFL states that it is impossible to claim that a particular algorithm is the best optimizer for dealing with all optimization issues. As a result, the NFL theorem has encouraged researchers to design new algorithms to provide more appropriate solutions closer to global optimization problems. The NFL has also motivated the authors of this study to be able to solve optimization problems more effectively by designing a new metaheuristic algorithm.
The novelty and innovation of this paper are in designing a new algorithm called Sewing Training-Based Optimization (STBO) for optimization applications. The main contributions of this article are as follows:
A new human-based metaheuristic algorithm based on sewing training modeling is introduced.
STBO is modeled in three phases: (i) training, (ii) imitation of the instructor's skills, and (iii) practice.
STBO performance is tested on fifty-two benchmark functions of unimodal, high-dimensional, fixed-dimensional multimodal types and from the CEC 2017 test suite.
STBO results are compared with the performance of eleven well-known metaheuristic algorithms.
STBO's performance in solving real-world applications is evaluated on four engineering design issues.
The rest of the paper is organized so that a literature review is presented in the section “Literature review”. Next, the proposed algorithm is introduced and modeled in the section “Sewing Training-Based Optimization”. Simulations and analysis of their results are presented in the section “Simulation Studies and Results”. The STBO's performance in solving real-world problems is shown in the section “STBO for real-world applications.” Finally, conclusions and several study proposals are provided in the section “Conclusion and future works”.
Literature review
Metaheuristic algorithms have been developed based on mathematical simulations of various natural phenomena, animal behaviors, biological sciences, physics concepts, game rules, human behaviors, and other evolution-based processes. Based on the source of inspiration used in the design, metaheuristic algorithms fall into five groups: swarm-based, evolutionary-based, physics-based, game-based, and human-based.
Swarm-based algorithms are derived from the mathematical modeling of natural swarming phenomena, the behavior of animals, birds, aquatic animals, insects, and other living organisms. For example, ant colonies can find an optimal path to supply the required food resources. Simulating this behavioral feature of ants forms the basis of ACO. Fireflies' feature of emitting flashing light and the light communication between them has been a source of inspiration in the design of the Firefly Algorithm (FA)10. Swarming activities such as foraging and hunting among animals are intelligence processes that are employed in the design of various algorithms such as PSO, ABC, Grey Wolf Optimizer (GWO)11, Whale Optimization Algorithm (WOA)12, Marine Predator Algorithm (MPA)13, Cat and Mouse based Optimizer (CMBO)14, Tunicate Swarm Algorithm (TSA)15,16, Reptile Search Algorithm (RSA)17, and Orca Predation Algorithm (OPA)18. Other swarm-based methods are Farmland Fertility19, African Vultures Optimization Algorithm (AVOA)20, Artificial Gorilla Troops Optimizer (GTO)21, Tree Seed Algorithm (TSA)22, Spotted Hyena Optimizer (SHO)23, and Pelican Optimization Algorithm (POA)24.
Evolutionary-based algorithms are inspired by the biological sciences, the concept of natural selection, and random operators. For example, Differential Evolution (DE)25 and GA are two of the most significant evolutionary algorithms developed based on the mathematization of the reproductive process, concepts of Darwin's theory of evolution, and random operators of selection, mutation, and crossover. Some other Evolutionary-based algorithms are Genetic Programming (GP)26, Memetic Algorithm (MA)27, Evolution Strategy (ES)28, Evolutionary Programming (EP)29, and Cultural Algorithm (CA)30.
Physics-based algorithms have been developed by simulating various laws, concepts, forces, and phenomena in physics. For example, the physical phenomenon of the water cycle has been the main idea in designing Water Cycle Algorithm (WCA)31. The employment of physical forces to design metaheuristic algorithms has been successful in designing algorithms such as Gravitational Search Algorithm (GSA)32, Spring Search Algorithm (SSA)33, and Momentum Search Algorithm (MSA)34. GSA is based on modeling the gravitational force that exists between masses at different distances from each other. SSA is inspired by the simulation of the spring tensile force and the Hook law between the weights connected by springs. MSA is developed based on the mathematization of the force of bullets' momentum that moves toward the optimal solution. Simulated Annealing (SA)35, Flow Regime Algorithm (FRA)36, Equilibrium Optimizer (EO)37, and Multi-Verse Optimizer (MVO)38 belong, e.g., among some other physics-based metaheuristic algorithms.
Game-based algorithms are formed by mathematical modeling of various game rules. For example, Volleyball Premier League (VPL) algorithm39 and Football Game-Based Optimization (FGBO)40 are game-based algorithms designed based on the simulation of club competitions in volleyball and football games, respectively. Likewise, the players' attempt in the tug-of-war game has been the main inspiration for the Tug of War Optimization (TWO)41 design. Likewise, the skill and strategy of the players in completing the puzzle pieces have been the idea behind the Puzzle Optimization Algorithm (POA)42 design.
Human-based algorithms have emerged inspired by human behaviors and interactions. This group's most widely used and well-known algorithm is Teaching–Learning-Based Optimization (TLBO). TLBO is introduced based on the mathematization of educational interactions between teachers and students43. The treatment process that the doctor uses to treat patients has been a central idea in the design of the Doctor and Patients Optimization (DPO)44. The relationships and collaboration of team members to perform teamwork and achieve the planned goal have been the source of inspiration for the Teamwork Optimization Algorithm (TOA) design45. Some other human-based metaheuristic algorithms are Society Civilization Algorithm (SCA)1, Seeker Optimization Algorithm (SOA)46, Imperialist Competitive Algorithm (ICA)47, Human-Inspired Algorithm (HIA)48, Social Emotional Optimization Algorithm (SEOA)49, Brain Storm Optimization (BSO)50, Anarchic Society Optimization (ASO)51, Human Mental Search (HMS)52, Gaining Sharing Knowledge based Algorithm (GSK)53, Coronavirus Herd Immunity Optimizer (CHIO)54, Ali Baba and the Forty Thieves (AFT)55, Human Mental Search (HMS)52, Multi-Leader Optimizer (MLO), Poor and Rich Optimization (PRO)56, Following Optimization Algorithm (FOA)57, and Election-Based Optimization Algorithm (EBOA)58.
Scientists' research in metaheuristic algorithm studies also includes improving existing algorithms59–63, extending hybrid algorithms by combining different algorithms to increase their efficiency64, developing binary versions of optimization algorithms65–68, and comprehensive survey studies69–71.
Several more recent or well-known metaheuristic algorithms published by researchers are listed in Table 1. In addition, this table specifies these algorithms' categories and sources of inspiration.
Table 1.
A brief review of metaheuristic algorithms.
| Category | Algorithm | Inspiration |
|---|---|---|
| Swarm-based | Particle Swarm Optimization (PSO)5 | Searching flocks of birds and fish for food |
| Ant Colony Optimization (ACO)6 | Ant colony behavior in identifying the shortest path | |
| Artificial Bee Colony (ABC)7 | Colony behavior of honey bees in holding food resources | |
| Firefly Algorithm (FA)10 | Social behavior of fireflies | |
| Grey Wolf Optimizer (GWO)11 | Hierarchical behavior of gray wolves during hunting | |
| Whale Optimization Algorithm (WOA)12 | Social behavior of humpback whales | |
| Marine Predator Algorithm (MPA)13 | The strategy of marine predators in hunting | |
| Cat and Mouse based Optimizer (CMBO)14 | The process of chasing mice by cats | |
| Tunicate Swarm Algorithm (TSA)15,16 | Jet propulsion and swarm intelligence of tunicate swarm during the searching for a food source | |
| Reptile Search Algorithm (RSA)17 | Hunting behavior of Reptiles | |
| Orca Predation Algorithm (OPA)18 | Predatory behavior of orcas | |
| Farmland Fertility19 | Farmland fertility in nature | |
| African Vultures Optimization Algorithm (AVOA)20 | African vultures’ lifestyle | |
| Artificial Gorilla Troops Optimizer (GTO)21 | Gorilla troops' social intelligence in nature | |
| Tree Seed Algorithm (TSA)22, | Relations between trees and their seeds | |
| Spotted Hyena Optimizer (SHO)23 | Social behavior of spotted hyenas | |
| Pelican Optimization Algorithm (POA)24 | The strategy of pelicans when hunting prey | |
| Evolutionary-based | Genetic Algorithm (GA)4 | Evolutionary concepts |
| Differential Evolution (DE)25 | Darwin’s theory of evolution | |
| Genetic Programming (GP)26 | Biological evolution | |
| Memetic Algorithm (MA)27 | Darwinian principles and Dawkins’s notion of a meme | |
| Evolution Strategy (ES)28 | Biological evolution | |
| Evolutionary Programming (EP)29 | Finite state machine | |
| Cultural Algorithm (CA)30 | Human cultural evolution process | |
| Physics-based | Water Cycle Algorithm (WCA)31 | The natural cycle of water |
| Gravitational Search Algorithm (GSA)32 | Gravitational attraction force | |
| Spring Search Algorithm (SSA)33 | The tensile force of spring and Hooke's law | |
| Momentum Search Algorithm (MSA)34 | The momentum of the impact of the bullets | |
| Simulated Annealing (SA)35 | Metal annealing process | |
| Flow Regime Algorithm (FRA)36 | Classical fluid mechanics and flow regimes | |
| Equilibrium Optimizer (EO)37 | Mass balance models | |
| Multi-Verse Optimizer (MVO)38 | Multi-verse theory | |
| Game-based | Volleyball Premier League (VPL)39 | Competition among volleyball teams during a season and coaching process during a volleyball match |
| Football Game-Based Optimization (FGBO)40 | Holding football league matches | |
| Tug of War Optimization (TWO)41 | Game tug of war | |
| Puzzle Optimization Algorithm (POA)42 | The effort of the players in completing the puzzle | |
| Ring Toss Game Based Optimizer (RTGBO)72 | The effort of the players in throwing the ring towards the score rings | |
| Orientation Search Algorithm (OSA)73 | Changing the direction of movement of players on the playground to the direction determined by the referee | |
| Dice Game Optimizer (DGO)74 | Rules of the dice game | |
| Darts Game Optimizer (DGO)75 | The effort of the players to earn points in the darts game | |
| Human-based | Teaching–Learning-Based Optimization (TLBO)43 | Teaching and learning in a classroom |
| Society Civilization Algorithm (SCA)1 | Leadership phenomena of humans | |
| Seeker Optimization Algorithm (SOA)46 | The action of human randomized search | |
| Imperialist Competitive Algorithm (ICA)47 | Imperialistic competition | |
| Human-Inspired Algorithm (HIA)48 | People’s intelligence | |
| Social Emotional Optimization Algorithm (SEOA)49 | Human social behaviors | |
| Brain Storm Optimization (BSO)50 | Brainstorming process | |
| Anarchic Society Optimization (ASO)51 | A social group behaving in a chaotic way to improve its situation | |
| Human Mental Search (HMS)52 | Exploration strategies of the bid space in online auctions | |
| Gaining Sharing Knowledge based Algorithm (GSK)53 | Acquisition and exchange of knowledge during a person’s lifespan | |
| Coronavirus Herd Immunity Optimizer (CHIO)54 | Herd immunity concept to respond to COVID-19 | |
| Ali Baba and the Forty Thieves (AFT)55 | The tale of Ali Baba and the forty thieves | |
| Doctor and Patients Optimization (DPO)44 | Interactions between doctor and patient | |
| Teamwork Optimization Algorithm (TOA)45 | Teamwork of individuals in presenting their work | |
| Multi-Leader Optimizer (MLO)76 | The presence of several leaders to guide the society | |
| Poor and Rich Optimization (PRO)56 | Efforts of the two groups of the poor and the rich to achieve wealth and improve their economic situation | |
| Following Optimization Algorithm (FOA)57 | Society people follow the successful person of the society | |
| Election-Based Optimization Algorithm (EBOA)58 | The process of holding elections in society |
Based on the best knowledge from the literature review, modeling the sewing training process has not been applied to designing any metaheuristic algorithm. However, sewing training by a training instructor to beginner tailors is an intelligent human activity that has the potential to simulate an optimizer. Therefore, a new human-based metaheuristic algorithm based on mathematical modeling of sewing training is designed in this paper to address this research gap. The design of this algorithm will be discussed in the next section.
Sewing training-based optimization
This section introduces the proposed Sewing Training-Based Optimization (STBO) algorithm and presents its mathematical model.
Inspiration and main idea of STBO
The activity of teaching sewing skills by a training instructor to beginner tailors is an intelligent process. The first step for a beginner is to choose a training instructor. Selecting the training instructor is essential in improving a beginner's sewing skills. Next, the instructor teaches sewing techniques to the beginner tailor. The second step in this process is the beginner tailor's efforts to mimic the skills of the training instructor. The beginner tailor tries to bring his skills to the level of the instructor as much as possible. The third step in the sewing training process is practice. The beginner tailors try to improve their skills in sewing by practicing. The interactions between beginner tailors and training instructors indicate the high potential of the sewing training process to be considered for designing an optimizer. Mathematical modeling of these intelligent interactions is the fundamental inspiration in the design of STBO.
Mathematical model of STBO
The proposed STBO algorithm is a population-based metaheuristic algorithm whose members are beginner tailors and training instructors. Each member of the STBO population refers to a candidate solution to the problem that represents the proposed values for the decision variables. As a result, each STBO member can be mathematically modeled with a vector and the STBO population using a matrix. The STBO population is specified by a matrix representation in Eq. (1).
| 1 |
where is the STBO population matrix, is the ith STBO’s member, is the number of STBO population members, and is the number of problem variables. At the beginning of the STBO implementation, all population members are randomly initialized using Eq. (2).
| 2 |
where is the value of the jth variable determined by the ith STBO’s member , is a random number in the interval , and are the lower and upper bound of the jth problem variable, respectively.
Each STBO member represents a candidate solution to the given problem. Therefore, the problem's objective function can be evaluated based on the values specified by each candidate solution. Based on the placement of candidate solutions in the problem variables, the values calculated for the objective function can be modeled using a vector by Eq. (3).
| 3 |
where is the objective function vector and is the objective function value for the ith candidate solution.
The values of the objective function are the main criterion for comparing candidate solutions with each other. The solution with the best value for the objective function is identified as the best candidate solution or the best member of the population . Updating the algorithm's population in each iteration leads to finding new objective function values. Accordingly, in each iteration, the best candidate solution must be updated. The design of the algorithm guarantees that the best candidate solution at the end of each iteration is also the best candidate solution from all previous iterations.
The process of updating candidate solutions in STBO is performed in three phases: (i) training, (ii) imitation of the instructor’s skills, and (iii) practice.
Phase 1: Training (exploration)
The first phase of updating STBO members is based on simulating the process of selecting a training instructor and acquiring sewing skills by beginner tailors. For each STBO member as a beginner tailor, all other members with a better value for the objective function are considered training instructors for that member. The set of all candidate members as the group of possible training instructors for each STBO member is defined using the following identity
| 4 |
where is the set of all possible candidate training instructors for the ith STBO member. In the case the only possible candidate training instructor is itself, i. e., Then, for each , a member from the set is randomly selected as the training instructor of the ith member of STBO, and it is denoted as . This selected instructor teaches the ith STBO member to sewing skills. Guiding members of the population under the guidance of instructors allows the STBO population to scan different areas of the search space to identify the main optimal area. This STBO update phase demonstrates the proposed approach's exploration ability in global search. At first, a new position for each population member is generated using Eq. (5) to update population members based on this phase of the STBO.
| 5 |
where is its dth dimension, is its objective function value, are numbers that are selected randomly from the set , and are random numbers from the interval .
Then, if this new position improves the objective function value, it replaces that population member's previous position. This update condition is modeled using Eq. (6).
| 6 |
where is the new position of the ith STBO member based on the first phase of STBO.
Phase 2: Imitation of the instructor skills (exploration)
The second phase of updating STBO members is based on simulating beginner tailors trying to mimic the skills of instructors. In the design of STBO, it is assumed that the beginner tailor tries to bring his sewing skills to the level of the instructor as much as possible. Given that each STBO member is a vector of the dimension and each component represents a decision variable thus, in this phase of STBO, it is assumed that each decision variable represents a sewing skill. Each STBO member imitates skills of the chosen instructor, This process moves the population of the algorithm to different areas in the search space, which indicates the STBO exploration ability. The set of variables that each STBO member imitates (i.e., the set of skills of the training instructor) is specified in Eq. (7).
| 7 |
where is an combination of the set , which represents the set of the indexes of decision variables (i.e., skills) identified to imitate by the ith member from the instructor and is the number of skills selected to mimic, is the iteration counter, and is the total number of iterations.
The new position for each STBO member is calculated based on the simulation of imitating these instructor skills, using the following identity
| 8 |
where is the newly generated position for the ith STBO member based on the second phase of STBO, is the dth dimension of This new position replaces the previous position of the corresponding member if it improves the value of the objective function
| 9 |
where is the objective function value of .
Phase 3: Practice (exploitation)
The third phase of updating STBO members is based on simulating beginner tailoring practices to improve sewing skills. In fact, in this phase of STBO design, a local search is performed around candidate solutions with the goal to find the best possible solutions near these candidate solutions. This phase of the STBO represents the exploitation capability of the proposed algorithm in local search. In order to mathematically model this STBO phase (with a correction to stay the all newly computed population members in the given search space), a new position around each member of the STBO is first generated using Eq. (10).
| 10 |
where and is a random number from the interval Then, if the value of the objective function improves, it replaces the previous position of the STBO member according to Eq. (11).
| 11 |
where is the new generated position for the ith STBO member based on second phase of STBO, is its dth dimension, and is its objective function value.
Repetition process and pseudo-code of STBO
The first STBO iteration is completed after updating all candidate solutions based on the first to third phases. Then the update process is repeated until the last iteration of the algorithm, based on Eqs. (4) to (11). After the full implementation of the STBO on the given problem, the best candidate solution recorded during the algorithm iteration is introduced as the solution. Finally, STBO implementation steps are presented as pseudo-code in Algorithm 1.
Computational complexity of STBO
In this subsection, the computational complexity of STBO is investigated. Since the most time-consuming step in the entire algorithm is calculating the values of the objective function, which are very complicated in most real applications, the computational complexity of STBO can be estimated based on the number of population members generated in the algorithm. STBO initialization has a computational complexity equal to where is the number of STBO members and is the number of problem variables. In each STBO iteration, the candidate solution is updated in three phases. Thus, the computational complexity of the STBO update process is equal to where is the number of iterations of the algorithm. As a result, the total computational complexity of STBO is equal to .
Simulation Studies and Results
In this section, the ability of the proposed STBO algorithm in optimization applications and solution presentation is evaluated. In this regard, fifty-two standard benchmark functions consisting of twenty-three objective functions of unimodal, high-dimensional multimodal, fixed-dimensional multimodal types and twenty-nine benchmark functions from the CEC 2017 test suite77 are employed to test the STBO optimization capability29. The performance of DTBO is compared with the performance of eleven well-known metaheuristic algorithms GA, PSO, GSA, MPA, WOA, TLBO, RSA, MVO, GWO, AVOA, and TSA. Each of the competing metaheuristic algorithms and STBO is used in twenty independent runs, where each run contains 1000 iterations. The implementation results of metaheuristic algorithms are reported using six statistical indicators: mean, standard deviation (std), best, worst, median, and rank. The mean of rank is considered a ranking criterion of the performance of optimization algorithms for each objective function. The values of the control parameters of competitor metaheuristic algorithms are listed in Table 2.
Table 2.
Assigned values to the control parameters of competitor algorithms.
| Algorithm | Parameter | Value |
|---|---|---|
| AVOA | L1, L2 | 0.8, 0.2 |
| W | 2.5 | |
| P1, P2, P3 | 0.6, 0.4, 0.6 | |
| RSA | Sensitive parameter | β = 0.01 |
| Sensitive parameter | α = 0.1 | |
| Evolutionary Sense (ES) | ES: randomly decreasing values between 2 and − 2 | |
| MPA | Binary vector | U = 0 or 1 |
| Random vector | R is a vector of uniform random numbers in [0, 1] | |
| Constant number | P = 0.5 | |
| Fish Aggregating Devices (FADs) | FADs = 0.2 | |
| TSA | c1, c2, c3 | Random numbers lie in the interval [0,1] |
| Pmin | 1 | |
| Pmax | 4 | |
| WOA | l is a random number in [− 1,1] | |
| r is a random vector in [0, 1] | ||
| Convergence parameter (a) | a: Linear reduction from 2 to 0 | |
| GWO | Convergence parameter (a) | a: Linear reduction from 2 to 0 |
| Wormhole existence probability (WEP) | Min(WEP) = 0.2 and Max(WEP) = 1 | |
| MVO | Exploitation accuracy over the iterations (p) | p = 1 |
| TLBO | random number | rand is a random number from interval [0,1] |
| TF: teaching factor | TF = round [(1 + rand)] | |
| GSA | Alpha | 20 |
| G0 | 100 | |
| Rnorm | 2 | |
| Rnorm | 1 | |
| PSO | Velocity limit | 10% of dimension range |
| Topology | Fully connected | |
| Inertia weight | Linear reduction from 0.9 to 0.1 | |
| Cognitive and social constant | (C1, C2) = (2, 2) | |
| GA | Type | Real coded |
| Mutation | Gaussian (Probability = 0.05) | |
| Crossover | Whole arithmetic (Probability = 0.8) | |
| Selection | Roulette wheel (Proportionate) |
Evaluation of unimodal benchmark functions
The results of optimization of unimodal functions F1 to F7 using STBO and competitor algorithms are reported in Table 3. The optimization results show that STBO provides the exact optimal solution for functions F1 to F6. For optimization of function F7, STBO is the best optimizer compared to competing algorithms. The simulation results show that STBO has outperformed competitor algorithms in handling the F1 to F7 unimodal functions and has been ranked first among the compared algorithms.
Table 3.
Evaluation results on unimodal functions.
| GA | PSO | GSA | TLBO | MVO | GWO | WOA | TSA | MPA | RSA | AVOA | STBO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 33.35136 | 0.181599 | 1.09E−16 | 9.67E−74 | 0.160829 | 7.38E−59 | 1.50E−154 | 2.30E−47 | 8.66E−50 | 0 | 0 | 0 |
| Best | 19.78438 | 3.14E−05 | 5.38E−17 | 4.45E−77 | 0.092366 | 4.54E−61 | 2.90E−169 | 4.07E−50 | 3.59E−52 | 0 | 0 | 0 | |
| Worst | 56.28509 | 3.274664 | 2.92E−16 | 1.07E−72 | 0.252881 | 5.46E−58 | 2.60E−153 | 1.26E−46 | 5.74E−49 | 0 | 0 | 0 | |
| Std | 8.395292 | 0.729657 | 5.21E−17 | 2.84E−73 | 0.040725 | 1.36E−58 | 5.80E−154 | 4.15E−47 | 1.43E−49 | 0 | 0 | 0 | |
| Median | 33.26899 | 0.007379 | 1.02E−16 | 2.37E−75 | 0.160607 | 1.43E−59 | 1.80E−161 | 3.45E−48 | 2.18E−50 | 0 | 0 | 0 | |
| Rank | 10 | 9 | 7 | 3 | 8 | 4 | 2 | 6 | 5 | 1 | 1 | 1 | |
| F2 | Mean | 3.188112 | 1.419726 | 5.33E−08 | 1.11E−38 | 0.252866 | 7.55E−35 | 7.60E−104 | 2.32E−28 | 5.72E−28 | 0 | 1.85E−267 | 0 |
| Best | 1.869152 | 0.080876 | 3.98E−08 | 1.43E−39 | 0.150256 | 7.14E−36 | 7.70E−113 | 1.68E−30 | 3.30E−30 | 0 | 0 | 0 | |
| Worst | 4.515361 | 13.77933 | 8.14E−08 | 6.19E−38 | 0.471703 | 2.23E−34 | 5.80E−103 | 3.62E−27 | 3.98E−27 | 0 | 3.71E−266 | 0 | |
| Std | 0.693334 | 3.034488 | 1.02E−08 | 1.58E−38 | 0.069403 | 7.49E−35 | 1.60E−103 | 8.02E−28 | 9.79E−28 | 0 | 0 | 0 | |
| Med | 3.32271 | 0.434611 | 5.30E−08 | 4.37E−39 | 0.239383 | 3.76E−35 | 6.30E−107 | 2.23E−29 | 2.02E−28 | 0 | 1.61E−289 | 0 | |
| Rank | 11 | 10 | 8 | 4 | 9 | 5 | 3 | 6 | 7 | 1 | 2 | 1 | |
| F3 | Mean | 2125.752 | 1094.128 | 480.8968 | 2.60E−24 | 12.60085 | 9.67E−14 | 22,774.89 | 2.13E−11 | 8.45E−13 | 0 | 0 | 0 |
| Best | 1111.139 | 29.63701 | 218.105 | 3.17E−28 | 4.866897 | 2.26E−19 | 8159.212 | 8.49E−20 | 1.16E−19 | 0 | 0 | 0 | |
| Worst | 2997.68 | 5273.106 | 804.0185 | 2.31E−23 | 20.88111 | 1.92E−12 | 37,690.63 | 2.08E−10 | 7.29E−12 | 0 | 0 | 0 | |
| Std | 495.7954 | 1618.416 | 149.9243 | 5.49E−24 | 4.434706 | 4.29E−13 | 8502.149 | 6.29E−11 | 1.75E−12 | 0 | 0 | 0 | |
| Median | 2238.566 | 428.5796 | 458.5233 | 2.42E−25 | 13.20446 | 3.96E−17 | 21,453.44 | 2.66E−14 | 3.20E−14 | 0 | 0 | 0 | |
| Rank | 9 | 8 | 7 | 2 | 6 | 3 | 10 | 5 | 4 | 1 | 1 | 1 | |
| F4 | Mean | 3.210794 | 6.507623 | 0.993225 | 1.93E−30 | 0.611151 | 2.22E−14 | 37.28855 | 0.003514 | 2.71E−19 | 0 | 1.29E−264 | 0 |
| Best | 2.113563 | 3.511675 | 1.27E−08 | 1.32E−31 | 0.284853 | 6.78E−16 | 1.331001 | 1.18E−05 | 7.45E−20 | 0 | 6.83E−306 | 0 | |
| Worst | 4.712766 | 10.14096 | 4.183409 | 5.42E−30 | 1.408459 | 1.06E−13 | 80.18979 | 0.016565 | 6.16E−19 | 0 | 2.09E−263 | 0 | |
| Std | 0.64983 | 1.970793 | 1.230111 | 1.65E−30 | 0.293951 | 3.30E−14 | 29.04785 | 0.004762 | 1.37E−19 | 0 | 0 | 0 | |
| Med | 3.135406 | 6.130021 | 0.579869 | 1.67E−30 | 0.563237 | 7.57E−15 | 26.40247 | 0.001683 | 2.83E−19 | 0 | 3.21E−286 | 0 | |
| Rank | 9 | 10 | 8 | 3 | 7 | 5 | 11 | 6 | 4 | 1 | 2 | 1 | |
| F5 | Mean | 420.6 | 112.2916 | 43.52647 | 26.53115 | 308.8081 | 26.83281 | 27.0278 | 28.46818 | 23.58215 | 10.13576 | 1.667E−05 | 0 |
| Best | 227.4906 | 30.07967 | 25.05162 | 26.03302 | 27.29038 | 25.32729 | 26.49484 | 27.13541 | 23.00782 | 1.72E−28 | 3.862E−07 | 0 | |
| Worst | 688.7775 | 400.1077 | 177.7903 | 28.75063 | 2557.854 | 28.5481 | 27.97937 | 29.2537 | 24.95884 | 28.99011 | 6.931E−05 | 0 | |
| Std | 122.0165 | 85.2441 | 39.12394 | 0.592674 | 622.6938 | 0.947923 | 0.328332 | 0.570757 | 0.516114 | 14.17161 | 1.81E−05 | 0 | |
| Median | 386.0621 | 84.06704 | 26.38317 | 26.35271 | 31.67272 | 26.5829 | 26.96864 | 28.6545 | 23.39152 | 5.80E−26 | 9.586E−06 | 0 | |
| Rank | 12 | 10 | 9 | 5 | 11 | 6 | 7 | 8 | 4 | 3 | 2 | 1 | |
| F6 | Mean | 34.0323 | 0.028587 | 1.13E−16 | 1.18022 | 0.159222 | 0.640991 | 0.119577 | 3.83522 | 2.08E−09 | 6.617444 | 4.418E−08 | 0 |
| Best | 14.51884 | 9.98E−06 | 4.11E−17 | 0.572861 | 0.084059 | 1.14E−05 | 0.011797 | 2.823119 | 9.15E−10 | 3.624796 | 4.244E−09 | 0 | |
| Worst | 71.07024 | 0.324785 | 2.43E−16 | 1.754355 | 0.247305 | 1.7184 | 0.366934 | 4.774542 | 6.27E−09 | 7.498843 | 1.142E−07 | 0 | |
| Std | 15.19874 | 0.074692 | 4.95E−17 | 0.316997 | 0.046291 | 0.371946 | 0.110996 | 0.566697 | 1.13E−09 | 1.018988 | 2.515E−08 | 0 | |
| Med | 29.14039 | 0.00087 | 1.02E−16 | 1.223701 | 0.16068 | 0.748235 | 0.082192 | 3.934263 | 1.91E−09 | 7.154133 | 4.048E−08 | 0 | |
| Rank | 12 | 5 | 2 | 9 | 7 | 8 | 6 | 10 | 3 | 11 | 4 | 1 | |
| F7 | Mean | 0.009847 | 0.166943 | 0.067112 | 0.001589 | 0.00965 | 0.00083 | 0.001159 | 0.004861 | 0.000518 | 0.000103 | 6.378E−05 | 1.24E−05 |
| Best | 0.006283 | 0.082498 | 0.019988 | 0.000338 | 0.004902 | 0.000262 | 2.80E−06 | 0.002251 | 0.000114 | 1.21E−05 | 2.674E−06 | 2.33E−06 | |
| Worst | 0.01905 | 0.289493 | 0.255451 | 0.004146 | 0.020283 | 0.002168 | 0.005668 | 0.010801 | 0.001654 | 0.000304 | 0.000242 | 3.79E−05 | |
| Std | 0.003084 | 0.052796 | 0.050227 | 0.000938 | 0.003826 | 0.00054 | 0.001539 | 0.002418 | 0.000365 | 8.26E−05 | 6.295E−05 | 9.87E−06 | |
| Median | 0.009485 | 0.159235 | 0.05478 | 0.001583 | 0.008695 | 0.000638 | 0.000632 | 0.004281 | 0.00041 | 9.22E−05 | 4.037E−05 | 8.63E−06 | |
| Rank | 10 | 12 | 11 | 7 | 9 | 5 | 6 | 8 | 4 | 3 | 2 | 1 | |
| Sum rank | 73 | 64 | 52 | 33 | 57 | 36 | 45 | 49 | 31 | 21 | 14 | 7 | |
| Mean rank | 10.428571 | 9.1428571 | 7.4285714 | 4.7142857 | 8.1428571 | 5.1428571 | 6.4285714 | 7 | 4.4285714 | 3 | 2 | 1 | |
| Total rank | 12 | 11 | 9 | 5 | 10 | 6 | 7 | 8 | 4 | 3 | 2 | 1 | |
Evaluation of high dimensional multimodal benchmark functions
The results obtained using STBO and competitor algorithms in optimizing high-dimensional multimodal functions F8 to F13 are presented in Table 4. Based on the results, STBO has provided the exact optimal solution for optimizing functions F9 and F11. Furthermore, in solving the functions F8, F10, F12, and F13, the STBO has performed better than all competitor algorithms. Analysis of the simulation results indicates the superiority of STBO over competing algorithms in handling the high-dimensional multimodal functions of F8 to F13.
Table 4.
Evaluation results on high-dimensional multimodal functions.
| GA | PSO | GSA | TLBO | MVO | GWO | WOA | TSA | MPA | RSA | AVOA | STBO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F8 | Mean | − 8551.34 | − 6891.6 | − 2463.53 | − 5320.45 | − 7820.6 | − 6233.81 | − 11,107.1 | − 5989.44 | − 9641.09 | − 5392.18 | − 12,027.8769 | − 12,269.7 |
| Best | − 9693.59 | − 8047.43 | − 3421.12 | − 6267.63 | − 9486.17 | − 7747.76 | − 12,569.3 | − 6812.45 | − 10,493.2 | − 5729.76 | − 12,566.471 | − 12,569.3 | |
| Worst | − 7299.22 | − 5394.56 | − 1914.24 | − 4471.98 | − 6625.33 | − 4899.26 | − 8492.23 | − 4918.97 | − 8788.53 | − 4359.71 | − 10,717.161 | − 11,262.6 | |
| Std | 761.0887 | 874.6514 | 363.8174 | 473.6453 | 741.5584 | 812.3497 | 1587.459 | 638.8189 | 434.3437 | 350.8895 | 499.0349695 | 362.218 | |
| Median | − 8611.96 | − 6843.87 | − 2484.38 | − 5243.46 | − 7737.48 | − 6303.59 | − 11,928.6 | − 6010.79 | − 9651.7 | − 5542.27 | − 12,232.4668 | − 12,395.1 | |
| Rank | 4 | 6 | 11 | 10 | 5 | 7 | 2 | 8 | 3 | 9 | 2 | 1 | |
| F9 | Mean | 58.68141 | 69.57591 | 26.01816 | 0 | 108.683 | 0.464705 | 0 | 170.1913 | 0 | 0 | 0 | 0 |
| Best | 32.80754 | 32.85466 | 13.92943 | 0 | 75.69692 | 0 | 0 | 98.82944 | 0 | 0 | 0 | 0 | |
| Worst | 79.7012 | 114.4199 | 40.79327 | 0 | 166.2595 | 5.02123 | 0 | 249.7671 | 0 | 0 | 0 | 0 | |
| Std | 12.70118 | 20.94823 | 6.554449 | 0 | 24.78061 | 1.310176 | 0 | 44.86406 | 0 | 0 | 0 | 0 | |
| Med | 56.30895 | 65.84376 | 25.37144 | 0 | 100.1247 | 0 | 0 | 169.0233 | 0 | 0 | 0 | 0 | |
| Rank | 4 | 5 | 3 | 1 | 6 | 2 | 1 | 7 | 1 | 1 | 1 | 1 | |
| F10 | Mean | 3.659085 | 2.869241 | 8.55E−09 | 4.26E−15 | 0.940669 | 1.72E−14 | 4.09E−15 | 1.520055 | 4.26E−15 | 8.88E−16 | 8.88178E−16 | 8.88E−16 |
| Best | 3.045616 | 0.978948 | 6.02E−09 | 8.88E−16 | 0.087874 | 1.15E−14 | 8.88E−16 | 1.51E−14 | 8.88E−16 | 8.88E−16 | 8.88178E−16 | 8.88E−16 | |
| Worst | 4.366778 | 4.121509 | 1.33E−08 | 4.44E−15 | 2.915234 | 2.22E−14 | 7.99E−15 | 3.500347 | 4.44E−15 | 8.88E−16 | 8.88178E−16 | 8.88E−16 | |
| Std | 0.411662 | 0.78912 | 1.91E−09 | 7.94E−16 | 0.938497 | 3.53E−15 | 2.55E−15 | 1.572911 | 7.94E−16 | 0 | 0 | 0 | |
| Median | 3.720395 | 3.025406 | 8.15E−09 | 4.44E−15 | 0.703059 | 1.51E−14 | 4.44E−15 | 1.270002 | 4.44E−15 | 8.88E−16 | 8.88178E−16 | 8.88E−16 | |
| Rank | 9 | 8 | 5 | 3 | 6 | 4 | 2 | 7 | 3 | 1 | 1 | 1 | |
| F11 | Mean | 1.524898 | 0.308563 | 8.934676 | 0 | 0.407293 | 0.00097 | 0.003062 | 0.008866 | 0 | 0 | 0 | 0 |
| Best | 1.251305 | 0.012446 | 5.463953 | 0 | 0.259112 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Worst | 1.791288 | 4.090669 | 17.88423 | 0 | 0.603916 | 0.019408 | 0.06124 | 0.017366 | 0 | 0 | 0 | 0 | |
| Std | 0.143664 | 0.899622 | 3.180256 | 0 | 0.07769 | 0.00434 | 0.013694 | 0.005776 | 0 | 0 | 0 | 0 | |
| Med | 1.488223 | 0.071877 | 7.923337 | 0 | 0.415251 | 0 | 0 | 0.00982 | 0 | 0 | 0 | 0 | |
| Rank | 7 | 5 | 8 | 1 | 6 | 2 | 3 | 4 | 1 | 1 | 1 | 1 | |
| F12 | Mean | 0.155349 | 1.391328 | 0.21731 | 0.081032 | 0.807735 | 0.038726 | 0.024389 | 6.409807 | 1.64E−10 | 1.408487 | 3.3717E−09 | 1.57E−32 |
| Best | 0.042239 | 0.000558 | 4.30E−19 | 0.040371 | 0.001623 | 0.012946 | 0.000813 | 0.333781 | 7.55E−11 | 0.940108 | 6.677E−10 | 1.57E−32 | |
| Worst | 0.345347 | 3.204317 | 1.494657 | 0.138141 | 3.001919 | 0.105321 | 0.330719 | 13.96328 | 3.53E−10 | 1.629701 | 1.12808E−08 | 1.57E−32 | |
| Std | 0.075924 | 1.03366 | 0.392116 | 0.025574 | 0.822807 | 0.027369 | 0.072623 | 3.761599 | 8.51E−11 | 0.24139 | 2.36553E−09 | 2.81E−48 | |
| Median | 0.1459 | 1.500485 | 0.057647 | 0.0787 | 0.440093 | 0.029434 | 0.006351 | 5.533201 | 1.38E−10 | 1.51496 | 2.84526E−09 | 1.57E−32 | |
| Rank | 7 | 10 | 8 | 6 | 9 | 5 | 4 | 12 | 2 | 11 | 3 | 1 | |
| F13 | Mean | 2.160287 | 3.08976 | 0.015448 | 0.905929 | 0.031928 | 0.593907 | 0.227661 | 3.0785 | 0.001674 | 0.26 | 2.1597E−08 | 1.35E−32 |
| Best | 0.993663 | 0.056865 | 6.03E−18 | 0.539664 | 0.010281 | 0.274715 | 0.039034 | 1.872547 | 1.24E−09 | 1.73E−31 | 2.0205E−09 | 1.35E−32 | |
| Worst | 4.186692 | 12.9562 | 0.254017 | 1.577393 | 0.13647 | 1.105615 | 0.458168 | 3.93204 | 0.010987 | 2.9 | 1.07149E−07 | 1.35E−32 | |
| Std | 0.701865 | 3.228647 | 0.057034 | 0.230028 | 0.026955 | 0.225443 | 0.143038 | 0.558013 | 0.004015 | 0.80616 | 2.57234E−08 | 2.81E−48 | |
| Med | 2.194029 | 2.146609 | 1.23E−17 | 0.886316 | 0.026003 | 0.58815 | 0.239423 | 3.052745 | 3.12E−09 | 1.46E−30 | 1.02427E−08 | 1.35E−32 | |
| Rank | 10 | 12 | 4 | 9 | 5 | 8 | 6 | 11 | 3 | 7 | 2 | 1 | |
| Sum rank | 42 | 47 | 40 | 31 | 38 | 29 | 19 | 50 | 14 | 31 | 10 | 6 | |
| Mean rank | 7 | 7.8334 | 6.6667 | 5.1666 | 6.3333 | 4.8333 | 3.1667 | 8.3333 | 2.3333 | 5.1666 | 1.6667 | 1 | |
| Total rank | 9 | 10 | 8 | 6 | 7 | 5 | 4 | 11 | 3 | 6 | 2 | 1 | |
Evaluation of fixed dimensional multimodal benchmark functions
The results of the implementation of STBO and competitor algorithms on fixed-dimensional multimodal functions F14 to F23 are released in Table 5. Compared to competitor algorithms, the optimization results show that STBO is the best optimizer in optimizing benchmark functions F14, F15, and F18. In optimizing functions F16, F17, and F19 to F23, the proposed STBO, and some competitor algorithms have a similar value in the "mean" index. However, STBO provides more efficient performance in these functions by providing better values of the "std" index. The simulation results show that STBO performs better than competitor algorithms in solving fixed-dimensional functions F14 to F23.
Table 5.
Evaluation results on fixed-dimensional multimodal functions.
| GA | PSO | GSA | TLBO | MVO | GWO | WOA | TSA | MPA | RSA | AVOA | STBO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F14 | Mean | 0.998102 | 3.212919 | 3.564456 | 0.998007 | 0.998004 | 4.221422 | 3.88582 | 6.56528 | 0.998004 | 4.469522 | 1.14691 | 0.998004 |
| Best | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 1.002309 | 0.998004 | 0.998004 | |
| Worst | 0.998721 | 10.76318 | 8.840836 | 0.998034 | 0.998004 | 12.67051 | 10.76318 | 12.67051 | 0.998004 | 10.76318 | 2.982105 | 0.998004 | |
| Std | 0.000213 | 2.88548 | 2.189673 | 6.96E−06 | 7.30E−12 | 4.652866 | 4.146898 | 4.89171 | 1.82E−10 | 3.084637 | 0.485651 | 0 | |
| Median | 0.998004 | 2.487068 | 2.806896 | 0.998004 | 0.998004 | 1.990054 | 1.495017 | 4.948548 | 0.998004 | 2.982105 | 0.998004 | 0.998004 | |
| Rank | 5 | 7 | 8 | 4 | 2 | 10 | 9 | 12 | 3 | 11 | 6 | 1 | |
| F15 | Mean | 0.01273 | 0.001638 | 0.002156 | 0.003375 | 0.007576 | 0.001357 | 0.000693 | 0.008509 | 0.000307 | 0.001305 | 0.000429 | 0.000307 |
| Best | 0.000767 | 0.000307 | 0.000923 | 0.000309 | 0.000336 | 0.000307 | 0.000308 | 0.000308 | 0.000307 | 0.000727 | 0.000308 | 0.000307 | |
| Worst | 0.026092 | 0.020363 | 0.00352 | 0.020364 | 0.020363 | 0.020363 | 0.002252 | 0.020942 | 0.000307 | 0.002601 | 0.001223 | 0.000307 | |
| Std | 0.010579 | 0.004442 | 0.000483 | 0.007325 | 0.009629 | 0.004478 | 0.000523 | 0.010056 | 2.92E−19 | 0.000536 | 0.000231 | 2.99E−19 | |
| Med | 0.012594 | 0.000307 | 0.002076 | 0.00032 | 0.000755 | 0.000308 | 0.000475 | 0.000779 | 0.000307 | 0.001149 | 0.000322 | 0.000307 | |
| Rank | 12 | 7 | 8 | 9 | 10 | 6 | 4 | 11 | 2 | 5 | 3 | 1 | |
| F16 | Mean | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.02846 | − 1.03163 | − 1.02844 | − 1.03163 | − 1.03163 |
| Best | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03162 | − 1.03163 | − 1.03163 | |
| Worst | − 1.03161 | − 1.03163 | − 1.03163 | − 1.03162 | − 1.03163 | − 1.03163 | − 1.03163 | − 1 | − 1.03163 | − 1 | − 1.03163 | − 1.03163 | |
| Std | 4.37E−06 | 1.14E−16 | 1.25E−16 | 2.49E−06 | 4.97E−08 | 3.27E−09 | 5.93E−11 | 0.009735 | 2.10E−10 | 0.007256 | 7.20E−15 | 7.75E−16 | |
| Median | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03163 | − 1.03067 | − 1.03163 | − 1.03163 | |
| Rank | 6 | 1 | 1 | 7 | 5 | 4 | 2 | 8 | 3 | 9 | 1 | 1 | |
| F17 | Mean | 0.524411 | 0.539013 | 0.397887 | 0.422207 | 0.397887 | 0.397888 | 0.397888 | 0.397906 | 0.397887 | 0.638307 | 0.397887 | 0.397887 |
| Best | 0.397887 | 0.397887 | 0.397887 | 0.39789 | 0.397887 | 0.397887 | 0.397887 | 0.397888 | 0.397887 | 0.397901 | 0.397887 | 0.397887 | |
| Worst | 2.791186 | 2.791184 | 0.397887 | 0.882291 | 0.397888 | 0.397894 | 0.397891 | 0.397971 | 0.397887 | 5.040108 | 0.397887 | 0.397887 | |
| Std | 0.534343 | 0.538701 | 0 | 0.108293 | 6.52E−08 | 1.63E−06 | 8.40E−07 | 2.48E−05 | 2.71E−09 | 1.036187 | 0 | 0 | |
| Med | 0.397892 | 0.397887 | 0.397887 | 0.397972 | 0.397887 | 0.397888 | 0.397887 | 0.397894 | 0.397887 | 0.402551 | 0.397887 | 0.397887 | |
| Rank | 8 | 9 | 1 | 7 | 3 | 5 | 4 | 6 | 2 | 10 | 1 | 1 | |
| F18 | Mean | 5.729191 | 3 | 3 | 3.000001 | 3 | 3.000011 | 3.000005 | 15.15005 | 3 | 6.169642 | 3.000002 | 3 |
| Best | 3.000044 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| Worst | 30.53809 | 3 | 3 | 3.000003 | 3.000001 | 3.000033 | 3.000032 | 84.00069 | 3 | 39.23578 | 3.000012 | 3 | |
| Std | 8.39291 | 2.76E−15 | 2.92E−15 | 8.96E−07 | 2.54E−07 | 9.56E−06 | 8.89E−06 | 29.67426 | 5.39E−14 | 9.865771 | 3.08E−06 | 1.81E−16 | |
| Median | 3.001628 | 3 | 3 | 3 | 3 | 3.000009 | 3.000001 | 3.000008 | 3 | 3.000086 | 3.000001 | 3 | |
| Rank | 10 | 2 | 3 | 6 | 5 | 9 | 8 | 12 | 4 | 11 | 7 | 1 | |
| F19 | Mean | − 3.86228 | − 3.86278 | − 3.86278 | − 3.86203 | − 3.86278 | − 3.86096 | − 3.8602 | − 3.86273 | − 3.86278 | − 3.80846 | − 3.86278 | − 3.86278 |
| Best | − 3.86278 | − 3.86278 | − 3.86278 | − 3.8627 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.86278 | − 3.85487 | − 3.86278 | − 3.86278 | |
| Worst | − 3.85745 | − 3.86278 | − 3.86278 | − 3.8548 | − 3.86278 | − 3.8549 | − 3.85378 | − 3.86256 | − 3.86278 | − 3.68429 | − 3.86278 | − 3.86278 | |
| Std | 0.001431 | 2.09E−15 | 1.87E−15 | 0.001716 | 7.41E−08 | 0.002948 | 0.002953 | 5.09E−05 | 2.28E−15 | 0.04789 | 3.22E−13 | 2.78E−15 | |
| Med | − 3.86277 | − 3.86278 | − 3.86278 | − 3.86249 | − 3.86278 | − 3.86246 | − 3.86139 | − 3.86275 | − 3.86278 | − 3.82667 | − 3.86278 | − 3.86278 | |
| Rank | 5 | 1 | 1 | 6 | 3 | 7 | 8 | 4 | 1 | 9 | 2 | 1 | |
| F20 | Mean | − 3.19552 | − 3.29822 | − 3.322 | − 3.23822 | − 3.2446 | − 3.23965 | − 3.2753 | − 3.23237 | − 3.322 | − 2.63831 | − 3.28617 | − 3.322 |
| Best | − 3.3214 | − 3.322 | − 3.322 | − 3.31043 | − 3.32199 | − 3.32199 | − 3.32198 | − 3.32137 | − 3.322 | − 3.15625 | − 3.322 | − 3.322 | |
| Worst | − 2.99692 | − 3.2031 | − 3.322 | − 3.08169 | − 3.20259 | − 3.02064 | − 3.10782 | − 2.84 | − 3.322 | − 1.30322 | − 3.19994 | − 3.322 | |
| Std | 0.093531 | 0.048793 | 3.95E−16 | 0.065246 | 0.058264 | 0.095719 | 0.074262 | 0.146905 | 4.20E−16 | 0.417228 | 0.056151 | 2.49E−16 | |
| Median | − 3.18946 | − 3.322 | − 3.322 | − 3.1998 | − 3.20302 | − 3.26252 | − 3.32127 | − 3.31998 | − 3.322 | − 2.73165 | − 3.322 | − 3.322 | |
| Rank | 9 | 2 | 1 | 7 | 5 | 6 | 4 | 8 | 1 | 10 | 3 | 1 | |
| F21 | Mean | − 5.89083 | − 5.77879 | − 6.17737 | − 5.84595 | − 8.51163 | − 9.64743 | − 8.36636 | − 6.52198 | − 10.1532 | − 5.0552 | − 10.1532 | − 10.1532 |
| Best | − 9.0381 | − 10.1532 | − 10.1532 | − 9.44872 | − 10.1532 | − 10.1531 | − 10.1529 | − 10.138 | − 10.1532 | − 5.0552 | − 10.1532 | − 10.1532 | |
| Worst | − 2.34247 | − 2.63047 | − 2.63047 | − 3.80037 | − 2.63047 | − 5.10034 | − 5.05374 | − 2.60298 | − 10.1532 | − 5.0552 | − 10.1532 | − 10.1532 | |
| Std | 2.512564 | 3.703566 | 3.699126 | 1.769566 | 2.623726 | 1.55506 | 2.493026 | 3.337297 | 1.95E−15 | 2.48E−07 | 6.57E−15 | 3.65E−15 | |
| Med | − 6.83679 | − 2.68286 | − 3.51696 | − 5.02319 | − 10.1531 | − 10.1527 | − 10.1469 | − 5.04462 | − 10.1532 | − 5.0552 | − 10.1532 | − 10.1532 | |
| Rank | 8 | 10 | 7 | 9 | 4 | 3 | 5 | 6 | 1 | 11 | 2 | 1 | |
| F22 | Mean | − 7.21825 | − 6.31807 | − 10.4029 | − 8.09591 | − 9.6056 | − 10.4024 | − 8.0395 | − 7.53629 | − 10.4029 | − 5.08767 | − 10.4029 | − 10.4029 |
| Best | − 10.1952 | − 10.4029 | − 10.4029 | − 9.92173 | − 10.4029 | − 10.4028 | − 10.4028 | − 10.3998 | − 10.4029 | − 5.08767 | − 10.4029 | − 10.4029 | |
| Worst | − 2.62184 | − 1.83759 | − 10.4029 | − 4.21215 | − 5.08765 | − 10.4018 | − 2.76572 | − 1.82822 | − 10.4029 | − 5.08767 | − 10.4029 | − 10.4029 | |
| Std | 2.472441 | 3.837031 | 2.97E−15 | 1.699295 | 1.947221 | 0.00028 | 3.034341 | 3.483042 | 3.65E−15 | 5.80E−07 | 2.41E−14 | 2.88E−15 | |
| Median | − 7.89012 | − 4.40599 | − 10.4029 | − 8.81648 | − 10.4029 | − 10.4025 | − 10.3974 | − 10.1566 | − 10.4029 | − 5.08767 | − 10.4029 | − 10.4029 | |
| Rank | 9 | 10 | 2 | 6 | 5 | 4 | 7 | 8 | 1 | 11 | 3 | 1 | |
| F23 | Mean | − 5.78525 | − 5.62285 | − 10.5364 | − 8.30576 | − 9.99556 | − 9.72457 | − 8.77684 | − 5.46265 | − 10.5364 | − 5.12847 | − 10.5364 | − 10.5364 |
| Best | − 10.417 | − 10.5364 | − 10.5364 | − 9.98248 | − 10.5364 | − 10.5364 | − 10.5364 | − 10.4691 | − 10.5364 | − 5.12848 | − 10.5364 | − 10.5364 | |
| Worst | − 2.38428 | − 2.42173 | − 10.5364 | − 4.06348 | − 5.12846 | − 2.42172 | − 2.42169 | − 1.67573 | − 10.5364 | − 5.12847 | − 10.5364 | − 10.5364 | |
| Std | 2.966829 | 3.755817 | 1.73E−15 | 1.491856 | 1.664511 | 2.497522 | 3.196353 | 3.753624 | 2.51E−15 | 1.29E−06 | 7.08E−15 | 6.93E−16 | |
| Med | − 6.05259 | − 3.35328 | − 10.5364 | − 8.76487 | − 10.5364 | − 10.536 | − 10.5338 | − 2.84687 | − 10.5364 | − 5.12847 | − 10.5364 | − 10.5364 | |
| Rank | 8 | 9 | 1 | 7 | 4 | 5 | 6 | 10 | 3 | 11 | 2 | 1 | |
| Sum rank | 80 | 58 | 33 | 68 | 46 | 59 | 57 | 85 | 21 | 98 | 30 | 10 | |
| Mean rank | 8 | 5.8 | 3.3 | 6.8 | 4.6 | 5.9 | 5.7 | 8.5 | 2.1 | 9.8 | 3 | 1 | |
| Total rank | 10 | 7 | 4 | 9 | 5 | 8 | 6 | 11 | 2 | 12 | 3 | 1 | |
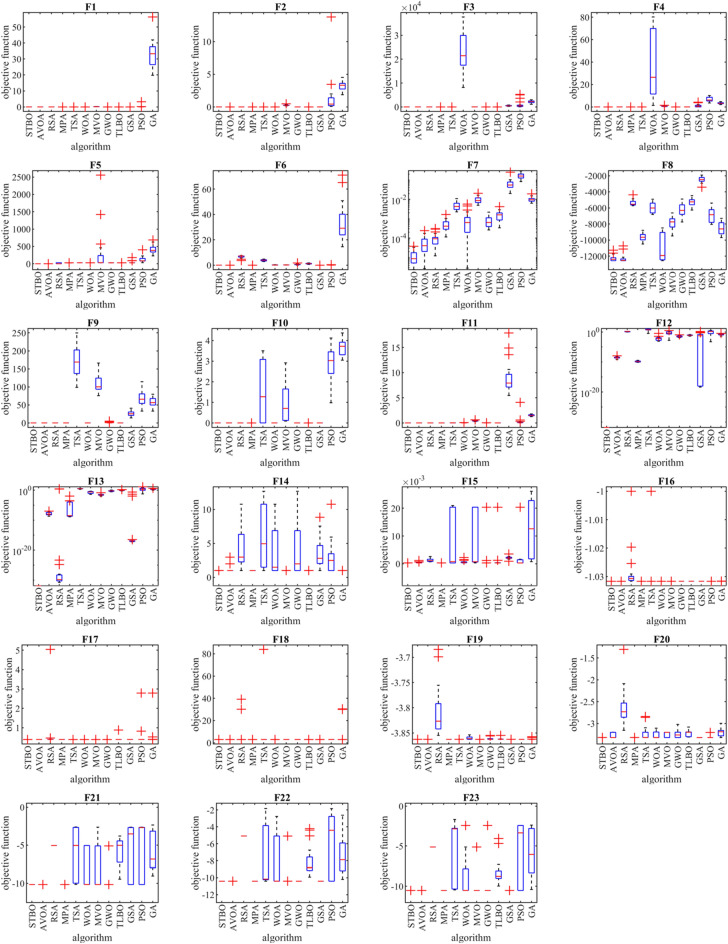
The performance of STBO and competitor algorithms in optimizing F1 to F23 functions is presented as a boxplot in Fig. 1. Intuitive analysis of these boxplots shows that the proposed STBO approach has provided superior and more effective performance compared to competing algorithms by providing better results in statistical indicators in most of the benchmark functions.
Figure 1.
Boxplot of performance of STBO and competitor algorithms in solving F1 to F23.
Statistical analysis
In this subsection, statistical analysis is presented to further evaluate the performance of the STBO compared to competitor algorithms. Wilcoxon sum rank test78 has been employed to determine whether there is a statistically significant difference between the results obtained from STBO and competing algorithms. In the Wilcoxon sum rank test, the p-value index determines the significant difference between the two data samples. The results of the Wilcoxon sum rank test on the performance of STBO and competitor algorithms are reported in Table 6. Based on these results, in cases where the -value is calculated as less than 0.05, STBO has a statistically significant superiority over the competitor algorithm.
Table 6.
Wilcoxon sum rank test results.
| Compared Algorithms | Test function type | ||
|---|---|---|---|
| Unimodal | High-multimodal | Fixed-multimodal | |
| STBO vs. AVOA | 1.01E−24 | 1.96E−21 | 0.000145 |
| STBO vs. RSA | 1.01E−24 | 1.97E−21 | 0.001816 |
| STBO vs. MPA | 1.01E−24 | 1.97E−21 | 3.29E−11 |
| STBO vs. TSA | 1.01E−24 | 1.97E−21 | 0.000299 |
| STBO vs. WOA | 1.01E−24 | 1.04E−14 | 7.98E−21 |
| STBO vs. MVO | 1.01E−24 | 1.97E−21 | 4.09E−13 |
| STBO vs. GWO | 1.01E−24 | 7.8E−16 | 5.01E−07 |
| STBO vs. TLBO | 2.44E−24 | 9.08E−09 | 0.358845 |
| STBO vs. GSA | 1.01E−24 | 1.31E−20 | 1.44E−34 |
| STBO vs. PSO | 1.01E−24 | 1.04E−14 | 6.4E−10 |
| STBO vs. GA | 3.64E−11 | 1.63E−11 | 1.78E−12 |
Convergence analysis
In this subsection, the convergence analysis of the proposed STBO is presented in comparison with competitor algorithms. The convergence curves of STBO and competitor algorithms during the optimization of F1 to F23 functions are drawn in Fig. 2. In the optimization of unimodal functions F1 to F7, which lack local optima, it can be seen that STBO has converged towards better solutions with its high ability in local search and exploitation after identifying the position of the optimal solution. Especially in solving functions F1 to F6, STBO has converged to the global optimal of these functions.
Figure 2.
Convergence curves of STBO and competitor algorithms in solving F1 to F23.
In the optimization of high-dimensional multimodal functions F8 to F13, which have a large number of local optima, it can be seen that STBO with high capability in global search and exploration has been able to identify the optimal global position well without getting stuck in local areas. With increasing iterations of the algorithm, it can be seen that STBO has converged towards better solutions. Especially in optimizing F9 and F11 functions, the proposed approach, with high ability in exploration and exploitation, has converged to the global optima. In the optimization of fixed-dimension multimodal functions F14 to F23, which have a smaller number of local optima (in comparison to F8 to F13 functions), it can be seen that STBO with high ability in balancing exploration and exploitation has provided a good performance in handling these functions. STBO first identified the main optimal area in solving these functions by providing an optimal global search. Then, by increasing the number of iterations of the algorithm, using local search, it converged towards suitable solutions. Convergence analysis shows that the proposed STBO approach, with its high ability to explore and exploit and balance during algorithm iterations, has better performance in handling functions F1 to F23 compared to competitor algorithms.
Scalability analysis
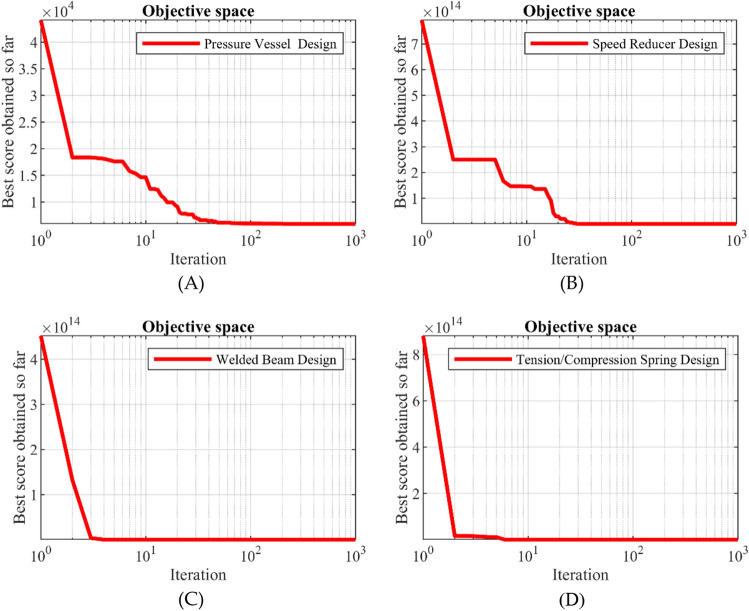
In this subsection, scalability analysis is presented to evaluate the proposed STBO approach and competitor algorithms in solving optimization problems under changes in the dimensions of the problem. In this analysis, the proposed STBO and each competing algorithm are used in optimizing the functions F1 to F13 for different dimensions equal to 50, 100, 250, and 500. The results of the scalability analysis are reported in Table 7. These found simulation results show that the efficiency of the STBO's performance does not decrease much with the increase in the dimensions of the problem. Furthermore, the scalability analysis reveals that the performance of the proposed STBO is least affected by the increase in the dimensionality of search space in comparison to competitor algorithms. This superiority is due to the proposed STBO approach's better ability to balance exploitation and exploration during the search process than competing algorithms.
Table 7.
The results of the scalability analysis of STBO.
| Index | GA | PSO | GSA | TLBO | MVO | GWO | WOA | TSA | MPA | RSA | AVOA | STBO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 50 | Mean | 285.0043 | 34.26946 | 6.91E−16 | 5.57E−68 | 1.171019 | 8.13E−44 | 1.80E−151 | 9.37E−36 | 1.87E−46 | 0 | 0 | 0 |
| Std | 71.44383 | 53.81518 | 4.58E−16 | 7.14E−68 | 0.247724 | 1.43E−43 | 5.50E−151 | 2.08E−35 | 4.78E−46 | 0 | 0 | 0 | ||
| 100 | Mean | 2782.496 | 2511.523 | 673.4191 | 8.95E−62 | 18.86453 | 2.57E−29 | 3.10E−150 | 2.63E−25 | 3.16E−43 | 0 | 0 | 0 | |
| Std | 322.4319 | 1007.265 | 358.3897 | 1.83E−61 | 2.305294 | 2.84E−29 | 9.10E−150 | 3.68E−25 | 5.78E−43 | 0 | 0 | 0 | ||
| 250 | Mean | 21,206.3 | 39,344.94 | 13,078.49 | 3.85E−58 | 798.4678 | 5.56E−18 | 2.00E−148 | 1.69E−15 | 1.31E−40 | 0 | 0 | 0 | |
| Std | 2180.106 | 8289.222 | 1581.329 | 6.19E−58 | 80.70753 | 3.34E−18 | 8.80E−148 | 1.96E−15 | 2.05E−40 | 0 | 0 | 0 | ||
| 500 | Mean | 69,817.39 | 165,845 | 40,569.3 | 6.55E−56 | 12,935.45 | 1.39E−12 | 1.80E−145 | 1.00E−10 | 4.64E−39 | 0 | 0 | 0 | |
| Std | 3479.445 | 12,186.53 | 2491.612 | 1.55E−55 | 846.7481 | 6.09E−13 | 5.50E−145 | 1.08E−10 | 4.39E−39 | 0 | 0 | 0 | ||
| F2 | 50 | Mean | 12.2036 | 8.359858 | 0.152633 | 3.04E−35 | 35.12252 | 4.52E−26 | 2.10E−104 | 2.23E−22 | 2.14E−26 | 0 | 1.10E−202 | 0 |
| Std | 1.384519 | 4.660024 | 0.465052 | 3.51E−35 | 69.37835 | 3.78E−26 | 4.00E−104 | 6.44E−22 | 2.59E−26 | 0 | 0 | 0 | ||
| 100 | Mean | 46.20699 | 123.1423 | 6.597008 | 2.04E−32 | 5.90E+15 | 4.70E−18 | 1.10E−101 | 1.53E−16 | 5.52E−25 | 0 | 1.50E−208 | 0 | |
| Std | 4.244573 | 88.20233 | 2.718062 | 1.38E−32 | 2.49E+16 | 2.32E−18 | 3.00E−101 | 1.72E−16 | 9.87E−25 | 0 | 0 | 0 | ||
| 250 | Mean | 190.8026 | 544.4599 | 77.08794 | 4.03E−30 | 6.06E+85 | 3.31E−11 | 1.07E−98 | 2.21E−11 | 1.03E−23 | 0 | 7.90E−211 | 0 | |
| Std | 9.96777 | 20.69241 | 9.352065 | 2.34E−30 | 2.63E+86 | 1.12E−11 | 4.63E−98 | 1.84E−11 | 2.51E−23 | 0 | 0 | 0 | ||
| 500 | Mean | 485.2498 | 1112.286 | 3.50E+268 | 3.60E−29 | 3.10E+211 | 5.96E−08 | 1.30E−99 | 2.02E−08 | 6.87E−21 | 0 | 3.30E−206 | 0 | |
| Std | 17.08654 | 42.27506 | 65,535 | 2.37E−29 | 65,535 | 1.15E−08 | 5.90E−99 | 2.31E−08 | 3.02E−20 | 0 | 0 | 0 | ||
| F3 | 50 | Mean | 5048.588 | 6169.914 | 1821.115 | 1.29E−19 | 650.7283 | 6.38E−06 | 124,414.6 | 0.072352 | 2.50E−07 | 0 | 0 | 0 |
| Std | 1078.129 | 4769.136 | 448.1044 | 4.71E−19 | 154.0739 | 2.16E−05 | 29,498.35 | 0.125204 | 6.11E−07 | 0 | 0 | 0 | ||
| 100 | Mean | 18,325.05 | 50,954.41 | 7927.23 | 3.10E−15 | 29,633.47 | 11.04603 | 853,493.7 | 2220.555 | 0.004078 | 0 | 1.60E−280 | 0 | |
| Std | 3075.166 | 21,471.28 | 1361.341 | 5.06E−15 | 4515.672 | 19.81332 | 168,872.8 | 1432.756 | 0.011144 | 0 | 0 | 0 | ||
| 250 | Mean | 136,756.2 | 336,528 | 57,829.84 | 3.66E−10 | 322,673.6 | 9257.031 | 6,878,229 | 206,030.5 | 107.5336 | 0 | 3.20E−241 | 0 | |
| Std | 23,655.14 | 75,834.61 | 8985.585 | 1.56E−09 | 21,061.8 | 5349.661 | 1,098,416 | 53,625.46 | 202.0424 | 0 | 0 | 0 | ||
| 500 | Mean | 668,892.5 | 1,223,667 | 275,481.2 | 1.47E−08 | 1,317,906 | 116,541.8 | 28,062,441 | 1,035,782 | 1525.209 | 0 | 1.10E−192 | 0 | |
| Std | 106,978.1 | 359,536.2 | 68,207.09 | 5.34E−08 | 103,418.5 | 59,137.88 | 9,301,240 | 165,807.8 | 1673.877 | 0 | 0 | 0 | ||
| F4 | 50 | Mean | 5.963966 | 19.53837 | 8.777958 | 1.06E−27 | 4.066982 | 1.82E−09 | 66.50783 | 2.731684 | 1.24E−17 | 0 | 6.70E−196 | 0 |
| Std | 0.978908 | 3.071924 | 1.928206 | 7.94E−28 | 1.385832 | 2.88E−09 | 27.76152 | 2.912462 | 8.45E−18 | 0 | 0 | 0 | ||
| 100 | Mean | 13.80378 | 37.51555 | 16.06594 | 1.35E−25 | 41.92272 | 0.003378 | 77.59964 | 34.24477 | 4.35E−16 | 0 | 9.20E−193 | 0 | |
| Std | 1.359287 | 3.83295 | 1.503749 | 1.33E−25 | 6.774704 | 0.003706 | 23.46463 | 12.32771 | 2.17E−16 | 0 | 0 | 0 | ||
| 250 | Mean | 26.5063 | 53.88201 | 22.08527 | 6.02E−24 | 80.66538 | 21.2961 | 77.16777 | 96.01481 | 3.04E−14 | 0 | 1.80E−204 | 0 | |
| Std | 1.60905 | 5.368787 | 1.848865 | 1.18E−23 | 3.341441 | 7.816487 | 22.70411 | 3.384094 | 2.07E−14 | 0 | 0 | 0 | ||
| 500 | Mean | 36.97724 | 67.43914 | 26.76013 | 3.20E−23 | 92.43218 | 57.82163 | 78.34497 | 99.24345 | 5.46E−13 | 0 | 1.80E−201 | 0 | |
| Std | 1.911597 | 4.690484 | 1.645312 | 2.84E−23 | 1.646392 | 6.138673 | 20.24963 | 0.22398 | 8.70E−13 | 0 | 0 | 0 | ||
| F5 | 50 | Mean | 2713.719 | 1085.306 | 131.5463 | 47.42296 | 603.6723 | 47.40183 | 47.43972 | 48.32421 | 44.03808 | 46.49249 | 0.000162 | 0 |
| Std | 1305.112 | 1169.986 | 73.26552 | 0.9332 | 920.3005 | 0.79805 | 0.54216 | 0.656619 | 0.590632 | 10.94366 | 0.000166 | 0 | ||
| 100 | Mean | 125,110.4 | 287,904.9 | 17,204.66 | 97.81196 | 1237.219 | 97.63697 | 97.80163 | 98.29339 | 95.135 | 98.96354 | 0.00046 | 0 | |
| Std | 43,089.33 | 264,617.7 | 10,886.6 | 0.677834 | 844.555 | 0.636675 | 0.37934 | 0.488629 | 0.843997 | 0.066664 | 0.000509 | 0 | ||
| 250 | Mean | 4,083,468 | 21,300,786 | 1,044,548 | 248.0782 | 35,979.2 | 247.8359 | 247.1009 | 247.9578 | 245.7841 | 248.9852 | 0.007509 | 0 | |
| Std | 1,041,684 | 5,177,053 | 294,478.5 | 0.299102 | 14,532.75 | 0.42663 | 0.319189 | 0.561326 | 0.706112 | 0.015649 | 0.018946 | 0 | ||
| 500 | Mean | 21,818,155 | 1.66E+08 | 5,695,001 | 498.0625 | 3,316,483 | 497.6689 | 495.7569 | 498.2494 | 495.6662 | 498.9886 | 0.005212 | 0 | |
| Std | 2,517,887 | 25,976,011 | 825,086.1 | 0.269248 | 471,390.8 | 0.173736 | 0.442375 | 0.48665 | 0.528731 | 0.003021 | 0.006083 | 0 | ||
| F6 | 50 | Mean | 305.615 | 42.04067 | 0.003316 | 3.660992 | 1.073896 | 2.243901 | 0.378736 | 6.441274 | 0.003395 | 11.46592 | 4.58E−05 | 0 |
| Std | 77.1288 | 53.90269 | 0.014831 | 0.597425 | 0.212681 | 0.481915 | 0.230127 | 0.957914 | 0.015141 | 1.656754 | 2.24E−05 | 0 | ||
| 100 | Mean | 2716.183 | 3158.425 | 649.5424 | 12.34831 | 18.44157 | 9.286886 | 1.937719 | 13.80242 | 0.815919 | 24.70658 | 0.014634 | 0 | |
| Std | 493.7557 | 2883.38 | 352.0708 | 0.75096 | 2.245434 | 0.787782 | 0.928162 | 1.00861 | 0.362987 | 0.166974 | 0.055799 | 0 | ||
| 250 | Mean | 21,479.14 | 40,123.4 | 12,867.19 | 44.38734 | 782.2298 | 38.47129 | 8.908795 | 41.33491 | 13.65313 | 62.19509 | 0.101121 | 0 | |
| Std | 1771.678 | 6381.723 | 1821.69 | 1.271032 | 65.41419 | 1.275285 | 2.236528 | 1.601417 | 1.08496 | 0.120169 | 0.183189 | 0 | ||
| 500 | Mean | 68,512.54 | 166,510.4 | 40,708.14 | 102.2647 | 13,141.71 | 92.61489 | 18.32255 | 95.38288 | 52.989 | 124.7206 | 0.11678 | 0 | |
| Std | 4438.758 | 14,455.79 | 3093.243 | 1.840089 | 725.7806 | 1.57135 | 5.184106 | 1.850498 | 1.997287 | 0.06375 | 0.234366 | 0 | ||
| F7 | 50 | Mean | 0.029469 | 0.563845 | 0.192132 | 0.002251 | 0.039289 | 0.001623 | 0.003268 | 0.009127 | 0.000786 | 8.80E−05 | 0.00012 | 1.21E−05 |
| Std | 0.006066 | 0.245682 | 0.070887 | 0.001521 | 0.012198 | 0.00081 | 0.004275 | 0.004542 | 0.000395 | 9.50E−05 | 0.000122 | 1.39E−05 | ||
| 100 | Mean | 0.277241 | 6.359927 | 2.081773 | 0.002365 | 0.197949 | 0.002509 | 0.001804 | 0.022533 | 0.00069 | 4.95E−05 | 0.000128 | 1.04E−05 | |
| Std | 0.109251 | 6.051414 | 0.959512 | 0.001368 | 0.028032 | 0.001204 | 0.001604 | 0.008074 | 0.000271 | 7.53E−05 | 0.000109 | 1.01E−05 | ||
| 250 | Mean | 14.51263 | 127.255 | 69.68376 | 0.003042 | 2.268139 | 0.00645 | 0.003257 | 0.093088 | 0.000885 | 8.38E−05 | 0.000157 | 1.36E−05 | |
| Std | 2.095997 | 48.34713 | 15.68223 | 0.001392 | 0.343546 | 0.00241 | 0.003305 | 0.035296 | 0.000421 | 7.11E−05 | 0.000179 | 1.18E−05 | ||
| 500 | Mean | 152.9307 | 1238.266 | 685.4945 | 0.003431 | 41.51178 | 0.010719 | 0.002206 | 0.535833 | 0.000924 | 7.47E−05 | 0.000171 | 1.67E−05 | |
| Std | 26.25327 | 198.34 | 99.68845 | 0.002319 | 6.351142 | 0.003335 | 0.002982 | 0.122946 | 0.000412 | 7.07E−05 | 0.00015 | 1.53E−05 | ||
| F8 | 50 | Mean | − 12,272.8 | − 10,802.7 | − 3403.91 | − 7204.86 | − 12,793.7 | − 9338.85 | − 19,090.3 | − 8745.76 | − 14,938.1 | − 9022.4 | − 20,353.6 | − 20,413 |
| Std | 1103.911 | 1130.198 | 507.9481 | 852.2193 | 1008.764 | 1287.406 | 2667.391 | 807.3113 | 715.9989 | 202.8098 | 524.94 | 1176.142 | ||
| 100 | Mean | − 18,876.3 | − 18,284.3 | − 4539.53 | − 9438.36 | − 24,721 | − 16,403.4 | − 38,730.4 | − 14,103.8 | − 28,018.7 | − 17,227.2 | − 40,235 | − 41,150 | |
| Std | 1754.896 | 2043.847 | 746.9655 | 961.5354 | 1632.216 | 2974.611 | 4599.436 | 889.5166 | 861.137 | 1182.774 | 1140.119 | 1847.596 | ||
| 250 | Mean | − 31,100.3 | − 36,587.6 | − 7604.78 | − 15,364.1 | − 55,415.3 | − 35,384.6 | − 87,802.5 | − 23,017.4 | − 57,688.4 | − 37,088.8 | − 96,183.8 | − 100,730 | |
| Std | 3266.845 | 2315.238 | 1353.598 | 1984.653 | 2685.69 | 2404.494 | 14,060.16 | 1501.685 | 1813.612 | 2064.086 | 6413.815 | 4650.807 | ||
| 500 | Mean | − 45,608.7 | − 55,847.5 | − 10,442.3 | − 22,573 | − 96,126.1 | − 61,887.1 | − 188,510 | − 32,328.1 | − 96,995.4 | − 66,008.1 | − 176,969 | − 201,718 | |
| Std | 3441.277 | 3362.234 | 2117.996 | 2518.76 | 2539.443 | 5243.808 | 26,903.39 | 1972.414 | 2350.496 | 4893.541 | 14,449.97 | 7420.386 | ||
| F9 | 50 | Mean | 187.09 | 116.6431 | 54.67295 | 0 | 242.2961 | 0.49703 | 0 | 359.0799 | 0 | 0 | 0 | 0 |
| Std | 25.47509 | 30.12197 | 9.988632 | 0 | 49.28747 | 1.530593 | 0 | 59.85311 | 0 | 0 | 0 | 0 | ||
| 100 | Mean | 591.5714 | 340.1137 | 133.9363 | 0 | 572.9428 | 0.189209 | 0 | 897.1359 | 0 | 0 | 0 | 0 | |
| Std | 39.8328 | 40.68969 | 18.74462 | 0 | 96.95193 | 0.84617 | 0 | 115.5391 | 0 | 0 | 0 | 0 | ||
| 250 | Mean | 2086.163 | 1457.558 | 693.863 | 0 | 2156.602 | 1.952586 | 2.27E−14 | 2711.363 | 0 | 0 | 0 | 0 | |
| Std | 64.22998 | 85.31377 | 76.61462 | 0 | 112.0258 | 3.110418 | 1.02E−13 | 271.96 | 0 | 0 | 0 | 0 | ||
| 500 | Mean | 4646.933 | 3828.066 | 2231.817 | 0 | 5422.097 | 3.544948 | 0 | 5356.486 | 0 | 0 | 0 | 0 | |
| Std | 112.9087 | 150.4184 | 112.0155 | 0 | 163.6803 | 4.402665 | 0 | 486.9464 | 0 | 0 | 0 | 0 | ||
| F10 | 50 | Mean | 5.389597 | 5.507252 | 0.286075 | 4.44E−15 | 1.754842 | 3.27E−14 | 3.91E−15 | 1.013365 | 4.44E−15 | 8.88E−16 | 8.88E−16 | 8.88E−16 |
| Std | 0.379123 | 0.949512 | 0.449919 | 0 | 0.479574 | 3.15E−15 | 2.09E−15 | 1.424865 | 0 | 0 | 0 | 0 | ||
| 100 | Mean | 7.96934 | 10.84341 | 3.155674 | 4.44E−15 | 5.028315 | 1.11E−13 | 4.62E−15 | 7.55E−10 | 4.44E−15 | 8.88E−16 | 8.88E−16 | 8.88E−16 | |
| Std | 0.3831 | 1.36695 | 0.870762 | 0 | 4.973398 | 6.71E−15 | 2.15E−15 | 3.37E−09 | 0 | 0 | 0 | 0 | ||
| 250 | Mean | 10.74289 | 15.85386 | 7.168624 | 4.44E−15 | 18.97748 | 1.40E−10 | 4.62E−15 | 4.47E−09 | 4.44E−15 | 8.88E−16 | 8.88E−16 | 8.88E−16 | |
| Std | 0.334866 | 0.676188 | 0.371374 | 0 | 4.076866 | 5.24E−11 | 2.44E−15 | 3.19E−09 | 0 | 0 | 0 | 0 | ||
| 500 | Mean | 12.25589 | 17.35226 | 9.145829 | 4.44E−15 | 20.70852 | 5.21E−08 | 3.38E−15 | 5.11E−07 | 4.44E−15 | 8.88E−16 | 8.88E−16 | 8.88E−16 | |
| Std | 0.174913 | 0.215727 | 0.303231 | 0 | 0.070891 | 1.22E−08 | 2.33E−15 | 3.81E−07 | 0 | 0 | 0 | 0 | ||
| F11 | 50 | Mean | 4.052498 | 1.457349 | 30.33821 | 0 | 0.761331 | 0.000976 | 0 | 0.00581 | 0 | 0 | 0 | 0 |
| Std | 0.803584 | 0.648617 | 7.427283 | 0 | 0.061095 | 0.004365 | 0 | 0.007483 | 0 | 0 | 0 | 0 | ||
| 100 | Mean | 26.35897 | 21.79932 | 97.63246 | 0 | 1.169893 | 0.001514 | 0 | 0.004743 | 0 | 0 | 0 | 0 | |
| Std | 4.094358 | 9.647885 | 10.20711 | 0 | 0.024039 | 0.004755 | 0 | 0.007544 | 0 | 0 | 0 | 0 | ||
| 250 | Mean | 193.6629 | 353.5776 | 1104.15 | 0 | 7.894967 | 0.001375 | 5.55E−18 | 0.012257 | 0 | 0 | 0 | 0 | |
| Std | 12.63072 | 43.8592 | 47.3678 | 0 | 0.713036 | 0.006151 | 2.48E−17 | 0.017872 | 0 | 0 | 0 | 0 | ||
| 500 | Mean | 627.7852 | 1540.037 | 4647.865 | 0 | 121.6026 | 0.001047 | 0 | 0.010433 | 0 | 0 | 0 | 0 | |
| Std | 32.5443 | 104.1384 | 113.7393 | 0 | 9.110349 | 0.004683 | 0 | 0.02146 | 0 | 0 | 0 | 0 | ||
| F12 | 50 | Mean | 1.794942 | 7.930916 | 1.742268 | 0.147094 | 2.719225 | 0.082447 | 0.013583 | 6.888216 | 8.49E−09 | 1.254882 | 5.36E−07 | 9.42E−33 |
| Std | 0.711264 | 3.528295 | 0.894647 | 0.036661 | 0.841177 | 0.031664 | 0.014297 | 4.282754 | 1.17E−08 | 0.229805 | 3.80E−07 | 2.81E−48 | ||
| 100 | Mean | 8.188648 | 32.71512 | 5.133908 | 0.36174 | 8.276208 | 0.24133 | 0.021398 | 10.24539 | 0.009444 | 1.258981 | 0.000198 | 4.71E−33 | |
| Std | 1.640979 | 24.67439 | 1.363192 | 0.040864 | 1.843543 | 0.04763 | 0.022961 | 4.540495 | 0.0039 | 0.103201 | 0.000879 | 1.40E−48 | ||
| 250 | Mean | 47,652.44 | 4,716,917 | 21.88649 | 0.633515 | 42.14883 | 0.542416 | 0.027522 | 65.1672 | 0.072691 | 1.225052 | 9.41E−05 | 1.88E−33 | |
| Std | 65,626.15 | 2,935,210 | 6.096715 | 0.040427 | 7.225588 | 0.04906 | 0.010868 | 115.8512 | 0.011464 | 0.007345 | 0.000284 | 3.51E−49 | ||
| 500 | Mean | 2,535,944 | 90,916,183 | 884.6464 | 0.824569 | 116,501.9 | 0.747753 | 0.039326 | 46,754 | 0.203489 | 1.20229 | 9.54E−05 | 9.42E−34 | |
| Std | 1,052,760 | 25,963,807 | 986.5159 | 0.016698 | 67,940.08 | 0.033203 | 0.018023 | 54,125.95 | 0.019065 | 0.002856 | 0.000205 | 1.76E−49 | ||
| F13 | 50 | Mean | 12.08077 | 39.25416 | 14.53883 | 3.017419 | 0.184215 | 1.774649 | 0.585467 | 5.23522 | 0.083563 | 1.693285 | 1.48E−07 | 1.35E−32 |
| Std | 3.219958 | 8.195503 | 11.08645 | 0.444856 | 0.054379 | 0.335202 | 0.263984 | 0.716397 | 0.068924 | 1.979402 | 2.09E−07 | 2.81E−48 | ||
| 100 | Mean | 199.7021 | 29,222.48 | 125.1532 | 8.164988 | 80.09712 | 6.324213 | 1.986033 | 12.01446 | 6.040318 | 9.890124 | 2.54E−07 | 1.35E−32 | |
| Std | 225.0718 | 43,015.76 | 44.23044 | 0.381571 | 34.61998 | 0.424363 | 0.960595 | 1.093216 | 2.587355 | 0.03041 | 2.16E−07 | 2.81E−48 | ||
| 250 | Mean | 1,881,794 | 29,219,357 | 98,379.96 | 24.24311 | 546.7537 | 21.06385 | 5.335894 | 137.2253 | 22.9728 | 24.90092 | 0.005026 | 1.35E−32 | |
| Std | 1,046,952 | 8,331,513 | 103,971.4 | 0.375005 | 71.90737 | 0.419527 | 1.264721 | 102.9533 | 0.398369 | 0.029412 | 0.022476 | 2.81E−48 | ||
| 500 | Mean | 24,409,101 | 4.10E+08 | 1,078,726 | 49.81733 | 2,251,206 | 45.92283 | 11.08914 | 3764.666 | 47.63375 | 49.89766 | 0.018481 | 1.35E−32 | |
| Std | 5,989,248 | 1.06E+08 | 392,617.9 | 0.067117 | 781,787.8 | 0.540198 | 3.486242 | 3208.632 | 0.475035 | 0.011192 | 0.046167 | 2.81E−48 |
Evaluation of the CEC 2017 test suite benchmark functions
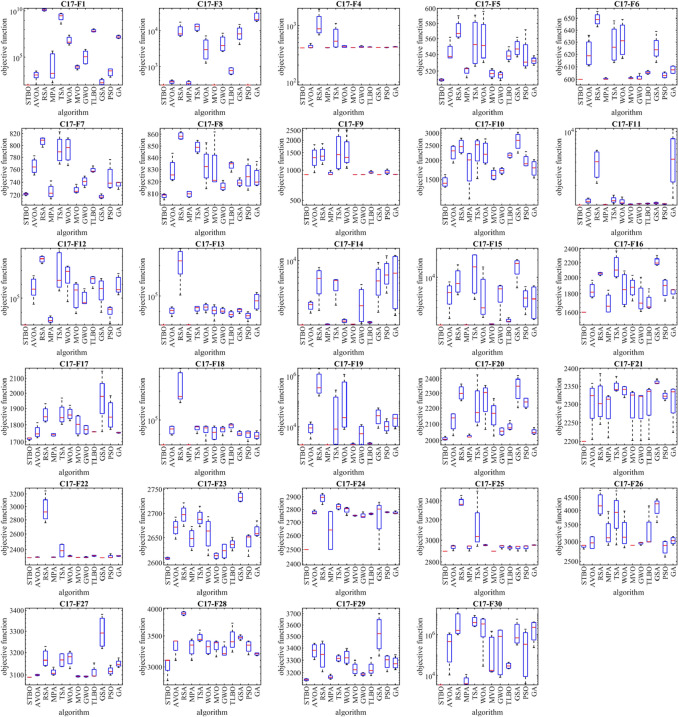
In this subsection, the performance of STBO in solving complex optimization problems of the CEC 2017 test suite is evaluated. This test suite has thirty standard benchmark functions consisting of three unimodal functions, C17-F1 to C17-F3, seven multimodal functions, C17-F4 to C17-F10, ten hybrid functions, C17-F11 to C17-F20, and ten composition functions C17- F21 to C17-F30. The C17-F2 function has been removed from this test suite due to unstable behavior. Full descriptions and details of the CEC 2017 test suite are available in the report78. The optimization results of the CEC 2017 test suite using the proposed STBO approach and competitor algorithms are reported in Table 8. Based on the optimization results, STBO is the first best optimizer in solving functions C17-F1, C17-F4 to C17-F6, C17-F8, C17-F10 to C17-F21, C17-F23 to C17-F25, and C17-F27 to C17-F30. The analysis of the simulation results found shows that the proposed STBO approach gives better results for most of the CEC 2017 test set features. It can be concluded that it performs better in solving this feature test set than the competing algorithms. Also, the results obtained from the Wilcoxon sum rank test show that the superiority of STBO against competitor algorithms in handling the CEC 2017 test suite is significant from a statistical point of view. The performance of STBO and competitor algorithms in solving the CEC 2017 test suite is presented as boxplot diagrams in Fig. 3. These diagrams intuitively show that STBO has performed more effectively in solving most of the benchmark functions of the CEC 2017 test suite by providing better results compared to competitor algorithms.
Table 8.
Evaluation results on the CEC 2017 test suite functions.
| GA | PSO | GSA | TLBO | MVO | GWO | WOA | TSA | MPA | RSA | AVOA | STBO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C17-F1 | Mean | 1.00E+02 | 1.48E+03 | 1.32E+10 | 1.14E+05 | 2.87E+09 | 8.69E+06 | 9.43E+03 | 2.30E+05 | 7.67E+07 | 2.45E+02 | 3.33E+03 | 1.65E+07 |
| Best | 1.00E+02 | 1.05E+02 | 9.16E+09 | 1.76E+02 | 3.93E+08 | 2.04E+06 | 4.43E+03 | 1.93E+04 | 5.38E+07 | 1.00E+02 | 7.03E+02 | 1.05E+07 | |
| Worst | 1.00E+02 | 3.34E+03 | 1.82E+10 | 4.52E+05 | 5.36E+09 | 2.43E+07 | 1.48E+04 | 6.81E+05 | 1.19E+08 | 5.29E+02 | 5.63E+03 | 2.48E+07 | |
| Std | 1.02E−05 | 1.38E+03 | 3.95E+09 | 2.30E+05 | 2.21E+09 | 1.07E+07 | 4.47E+03 | 3.18E+05 | 3.04E+07 | 2.03E+02 | 2.73E+03 | 6.38E+06 | |
| Median | 1.00E+02 | 1.24E+03 | 1.27E+10 | 1.82E+03 | 2.87E+09 | 4.22E+06 | 9.23E+03 | 1.11E+05 | 6.69E+07 | 1.76E+02 | 3.49E+03 | 1.53E+07 | |
| Rank | 1 | 3 | 12 | 6 | 11 | 8 | 5 | 7 | 10 | 2 | 4 | 9 | |
| C17-F3 | Mean | 3.00E+02 | 3.65E+02 | 1.01E+04 | 3.39E+02 | 1.27E+04 | 3.54E+03 | 3.00E+02 | 4.66E+03 | 7.63E+02 | 8.81E+03 | 3.00E+02 | 2.48E+04 |
| Best | 3.00E+02 | 3.00E+02 | 6.88E+03 | 3.00E+02 | 9.43E+03 | 1.24E+03 | 3.00E+02 | 2.58E+03 | 5.86E+02 | 4.05E+03 | 3.00E+02 | 1.80E+04 | |
| Worst | 3.00E+02 | 4.17E+02 | 1.74E+04 | 3.95E+02 | 1.54E+04 | 7.10E+03 | 3.00E+02 | 8.46E+03 | 9.28E+02 | 1.50E+04 | 3.00E+02 | 4.00E+04 | |
| Std | 1.57E−10 | 4.91E+01 | 4.98E+03 | 4.48E+01 | 3.04E+03 | 2.66E+03 | 5.88E−02 | 2.76E+03 | 1.80E+02 | 4.65E+03 | 2.49E−12 | 1.04E+04 | |
| Med | 3.00E+02 | 3.72E+02 | 8.11E+03 | 3.30E+02 | 1.31E+04 | 2.91E+03 | 3.00E+02 | 3.80E+03 | 7.69E+02 | 8.11E+03 | 3.00E+02 | 2.06E+04 | |
| Rank | 2 | 5 | 10 | 4 | 11 | 7 | 3 | 8 | 6 | 9 | 1 | 12 | |
| C17-F4 | Mean | 4.00E+02 | 4.23E+02 | 1.09E+03 | 4.04E+02 | 6.38E+02 | 4.24E+02 | 4.05E+02 | 4.18E+02 | 4.13E+02 | 4.07E+02 | 4.07E+02 | 4.16E+02 |
| Best | 4.00E+02 | 4.00E+02 | 6.81E+02 | 4.00E+02 | 4.08E+02 | 4.08E+02 | 4.04E+02 | 4.07E+02 | 4.10E+02 | 4.07E+02 | 4.01E+02 | 4.13E+02 | |
| Worst | 4.00E+02 | 4.79E+02 | 1.92E+03 | 4.06E+02 | 1.09E+03 | 4.41E+02 | 4.06E+02 | 4.39E+02 | 4.20E+02 | 4.07E+02 | 4.11E+02 | 4.24E+02 | |
| Std | 7.08E−09 | 3.83E+01 | 5.78E+02 | 2.78E+00 | 3.25E+02 | 1.83E+01 | 9.96E−01 | 1.52E+01 | 5.12E+00 | 1.79E−01 | 4.35E+00 | 5.41E+00 | |
| Median | 4.00E+02 | 4.06E+02 | 8.77E+02 | 4.05E+02 | 5.26E+02 | 4.22E+02 | 4.05E+02 | 4.12E+02 | 4.11E+02 | 4.07E+02 | 4.08E+02 | 4.14E+02 | |
| Rank | 1 | 9 | 12 | 2 | 11 | 10 | 3 | 8 | 6 | 4 | 5 | 7 | |
| C17-F5 | Mean | 5.09E+02 | 5.43E+02 | 5.71E+02 | 5.20E+02 | 5.55E+02 | 5.57E+02 | 5.17E+02 | 5.15E+02 | 5.39E+02 | 5.48E+02 | 5.39E+02 | 5.32E+02 |
| Best | 5.08E+02 | 5.36E+02 | 5.61E+02 | 5.12E+02 | 5.26E+02 | 5.30E+02 | 5.11E+02 | 5.09E+02 | 5.31E+02 | 5.37E+02 | 5.24E+02 | 5.27E+02 | |
| Worst | 5.11E+02 | 5.62E+02 | 5.90E+02 | 5.24E+02 | 5.91E+02 | 5.96E+02 | 5.23E+02 | 5.20E+02 | 5.50E+02 | 5.62E+02 | 5.72E+02 | 5.38E+02 | |
| Std | 1.31E+00 | 1.28E+01 | 1.34E+01 | 5.77E+00 | 3.20E+01 | 2.94E+01 | 5.24E+00 | 4.78E+00 | 7.78E+00 | 1.10E+01 | 2.24E+01 | 4.70E+00 | |
| Med | 5.09E+02 | 5.37E+02 | 5.67E+02 | 5.23E+02 | 5.52E+02 | 5.51E+02 | 5.17E+02 | 5.16E+02 | 5.38E+02 | 5.47E+02 | 5.31E+02 | 5.32E+02 | |
| Rank | 1 | 8 | 12 | 4 | 10 | 11 | 3 | 2 | 6 | 9 | 7 | 5 | |
| C17-F6 | Mean | 6.00E+02 | 6.21E+02 | 6.49E+02 | 6.00E+02 | 6.28E+02 | 6.32E+02 | 6.01E+02 | 6.01E+02 | 6.05E+02 | 6.25E+02 | 6.03E+02 | 6.08E+02 |
| Best | 6.00E+02 | 6.11E+02 | 6.43E+02 | 6.00E+02 | 6.13E+02 | 6.17E+02 | 6.00E+02 | 6.00E+02 | 6.04E+02 | 6.14E+02 | 6.01E+02 | 6.05E+02 | |
| Worst | 6.00E+02 | 6.36E+02 | 6.56E+02 | 6.01E+02 | 6.48E+02 | 6.49E+02 | 6.02E+02 | 6.05E+02 | 6.07E+02 | 6.39E+02 | 6.06E+02 | 6.11E+02 | |
| Std | 3.09E−04 | 1.17E+01 | 5.42E+00 | 6.82E−01 | 1.61E+01 | 1.52E+01 | 7.69E−01 | 2.33E+00 | 1.33E+00 | 1.07E+01 | 2.33E+00 | 3.41E+00 | |
| Median | 6.00E+02 | 6.19E+02 | 6.49E+02 | 6.00E+02 | 6.26E+02 | 6.31E+02 | 6.01E+02 | 6.00E+02 | 6.05E+02 | 6.24E+02 | 6.03E+02 | 6.08E+02 | |
| Rank | 1 | 8 | 12 | 2 | 10 | 11 | 3 | 4 | 6 | 9 | 5 | 7 | |
| C17-F7 | Mean | 7.22E+02 | 7.65E+02 | 8.07E+02 | 7.26E+02 | 7.92E+02 | 7.93E+02 | 7.28E+02 | 7.41E+02 | 7.59E+02 | 7.18E+02 | 7.46E+02 | 7.37E+02 |
| Best | 7.19E+02 | 7.51E+02 | 7.97E+02 | 7.14E+02 | 7.69E+02 | 7.66E+02 | 7.23E+02 | 7.32E+02 | 7.55E+02 | 7.14E+02 | 7.31E+02 | 7.29E+02 | |
| Worst | 7.24E+02 | 7.82E+02 | 8.12E+02 | 7.42E+02 | 8.23E+02 | 8.12E+02 | 7.37E+02 | 7.49E+02 | 7.66E+02 | 7.22E+02 | 7.76E+02 | 7.40E+02 | |
| Std | 2.01E+00 | 1.37E+01 | 7.26E+00 | 1.22E+01 | 2.42E+01 | 2.18E+01 | 6.17E+00 | 7.53E+00 | 4.73E+00 | 3.18E+00 | 2.14E+01 | 5.52E+00 | |
| Med | 7.22E+02 | 7.64E+02 | 8.09E+02 | 7.23E+02 | 7.89E+02 | 7.96E+02 | 7.26E+02 | 7.41E+02 | 7.57E+02 | 7.17E+02 | 7.39E+02 | 7.39E+02 | |
| Rank | 2 | 9 | 12 | 3 | 10 | 11 | 4 | 6 | 8 | 1 | 7 | 5 | |
| C17-F8 | Mean | 8.08E+02 | 8.29E+02 | 8.59E+02 | 8.10E+02 | 8.49E+02 | 8.33E+02 | 8.31E+02 | 8.16E+02 | 8.33E+02 | 8.19E+02 | 8.25E+02 | 8.23E+02 |
| Best | 8.05E+02 | 8.21E+02 | 8.56E+02 | 8.07E+02 | 8.44E+02 | 8.14E+02 | 8.20E+02 | 8.13E+02 | 8.28E+02 | 8.16E+02 | 8.13E+02 | 8.17E+02 | |
| Worst | 8.10E+02 | 8.44E+02 | 8.62E+02 | 8.12E+02 | 8.55E+02 | 8.53E+02 | 8.62E+02 | 8.21E+02 | 8.37E+02 | 8.23E+02 | 8.39E+02 | 8.37E+02 | |
| Std | 2.25E+00 | 1.06E+01 | 3.14E+00 | 2.67E+00 | 5.22E+00 | 1.61E+01 | 2.11E+01 | 3.76E+00 | 4.03E+00 | 3.03E+00 | 1.13E+01 | 9.46E+00 | |
| Median | 8.09E+02 | 8.25E+02 | 8.58E+02 | 8.10E+02 | 8.49E+02 | 8.32E+02 | 8.21E+02 | 8.15E+02 | 8.35E+02 | 8.19E+02 | 8.24E+02 | 8.20E+02 | |
| Rank | 1 | 7 | 12 | 2 | 11 | 9 | 8 | 3 | 10 | 4 | 6 | 5 | |
| C17-F9 | Mean | 9.00E+02 | 1.35E+03 | 1.44E+03 | 9.26E+02 | 1.60E+03 | 1.56E+03 | 9.00E+02 | 9.01E+02 | 9.49E+02 | 9.00E+02 | 9.59E+02 | 9.05E+02 |
| Best | 9.00E+02 | 9.42E+02 | 1.14E+03 | 9.01E+02 | 1.01E+03 | 1.04E+03 | 9.00E+02 | 9.00E+02 | 9.28E+02 | 9.00E+02 | 9.02E+02 | 9.02E+02 | |
| Worst | 9.00E+02 | 1.80E+03 | 1.85E+03 | 9.93E+02 | 2.52E+03 | 2.51E+03 | 9.01E+02 | 9.03E+02 | 9.89E+02 | 9.00E+02 | 1.03E+03 | 9.07E+02 | |
| Std | 2.65E−08 | 3.61E+02 | 3.04E+02 | 4.53E+01 | 7.29E+02 | 6.63E+02 | 4.44E−01 | 1.34E+00 | 2.76E+01 | 0.00E+00 | 5.22E+01 | 2.20E+00 | |
| Med | 9.00E+02 | 1.34E+03 | 1.38E+03 | 9.05E+02 | 1.43E+03 | 1.35E+03 | 9.00E+02 | 9.00E+02 | 9.39E+02 | 9.00E+02 | 9.54E+02 | 9.06E+02 | |
| Rank | 2 | 9 | 10 | 6 | 12 | 11 | 3 | 4 | 7 | 1 | 8 | 5 | |
| C17-F10 | Mean | 1.45E+03 | 2.25E+03 | 2.47E+03 | 1.84E+03 | 2.33E+03 | 2.25E+03 | 1.61E+03 | 1.71E+03 | 2.16E+03 | 2.67E+03 | 1.98E+03 | 1.78E+03 |
| Best | 1.34E+03 | 1.92E+03 | 2.20E+03 | 1.12E+03 | 1.52E+03 | 1.89E+03 | 1.50E+03 | 1.61E+03 | 2.07E+03 | 2.23E+03 | 1.84E+03 | 1.53E+03 | |
| Worst | 1.61E+03 | 2.49E+03 | 2.78E+03 | 2.22E+03 | 2.74E+03 | 2.75E+03 | 1.78E+03 | 1.79E+03 | 2.23E+03 | 3.04E+03 | 2.28E+03 | 2.02E+03 | |
| Std | 1.22E+02 | 2.73E+02 | 2.78E+02 | 5.23E+02 | 5.64E+02 | 4.17E+02 | 1.34E+02 | 7.88E+01 | 8.62E+01 | 3.58E+02 | 2.11E+02 | 2.25E+02 | |
| Median | 1.42E+03 | 2.31E+03 | 2.46E+03 | 2.01E+03 | 2.53E+03 | 2.19E+03 | 1.59E+03 | 1.71E+03 | 2.16E+03 | 2.70E+03 | 1.90E+03 | 1.78E+03 | |
| Rank | 1 | 9 | 11 | 5 | 10 | 8 | 2 | 3 | 7 | 12 | 6 | 4 | |
| C17-F11 | Mean | 1.10E+03 | 1.25E+03 | 3.99E+03 | 1.12E+03 | 1.29E+03 | 1.22E+03 | 1.13E+03 | 1.14E+03 | 1.15E+03 | 1.17E+03 | 1.14E+03 | 5.16E+03 |
| Best | 1.10E+03 | 1.17E+03 | 2.13E+03 | 1.11E+03 | 1.15E+03 | 1.12E+03 | 1.11E+03 | 1.13E+03 | 1.13E+03 | 1.13E+03 | 1.11E+03 | 1.36E+03 | |
| Worst | 1.10E+03 | 1.36E+03 | 5.72E+03 | 1.12E+03 | 1.49E+03 | 1.41E+03 | 1.14E+03 | 1.16E+03 | 1.17E+03 | 1.20E+03 | 1.15E+03 | 1.05E+04 | |
| Std | 1.11E+00 | 8.99E+01 | 1.76E+03 | 4.12E+00 | 1.44E+02 | 1.28E+02 | 1.49E+01 | 1.01E+01 | 1.77E+01 | 3.22E+01 | 1.71E+01 | 4.07E+03 | |
| Med | 1.10E+03 | 1.23E+03 | 4.05E+03 | 1.11E+03 | 1.26E+03 | 1.18E+03 | 1.12E+03 | 1.14E+03 | 1.15E+03 | 1.17E+03 | 1.14E+03 | 4.38E+03 | |
| Rank | 1 | 9 | 11 | 2 | 10 | 8 | 3 | 5 | 6 | 7 | 4 | 12 | |
| C17-F12 | Mean | 1.21E+03 | 1.24E+06 | 6.77E+07 | 3.04E+03 | 8.96E+07 | 9.35E+06 | 5.18E+05 | 1.52E+05 | 2.30E+06 | 8.96E+05 | 1.47E+04 | 1.69E+06 |
| Best | 1.20E+03 | 3.82E+04 | 3.05E+07 | 1.67E+03 | 3.30E+05 | 5.80E+04 | 8.01E+03 | 4.19E+04 | 4.93E+05 | 9.83E+03 | 1.56E+03 | 1.72E+05 | |
| Worst | 1.24E+03 | 4.05E+06 | 1.04E+08 | 5.43E+03 | 3.54E+08 | 2.04E+07 | 1.29E+06 | 4.67E+05 | 3.64E+06 | 2.59E+06 | 2.45E+04 | 5.80E+06 | |
| Std | 1.84E+01 | 1.92E+06 | 3.39E+07 | 1.70E+03 | 1.80E+08 | 9.95E+06 | 6.30E+05 | 2.15E+05 | 1.45E+06 | 1.21E+06 | 1.02E+04 | 2.79E+06 | |
| Median | 1.20E+03 | 4.39E+05 | 6.79E+07 | 2.53E+03 | 1.92E+06 | 8.48E+06 | 3.84E+05 | 4.93E+04 | 2.53E+06 | 4.92E+05 | 1.64E+04 | 4.01E+05 | |
| Rank | 1 | 7 | 11 | 2 | 12 | 10 | 5 | 4 | 9 | 6 | 3 | 8 | |
| C17-F13 | Mean | 1.31E+03 | 1.22E+04 | 4.09E+07 | 1.34E+03 | 1.62E+04 | 2.04E+04 | 1.35E+04 | 1.18E+04 | 7.10E+03 | 1.25E+04 | 5.58E+03 | 7.05E+04 |
| Best | 1.30E+03 | 4.63E+03 | 1.15E+05 | 1.31E+03 | 7.21E+03 | 8.27E+03 | 2.36E+03 | 7.43E+03 | 4.00E+03 | 7.36E+03 | 2.15E+03 | 1.22E+04 | |
| Worst | 1.31E+03 | 2.02E+04 | 1.23E+08 | 1.36E+03 | 2.19E+04 | 3.46E+04 | 2.77E+04 | 1.87E+04 | 1.17E+04 | 1.60E+04 | 9.59E+03 | 1.69E+05 | |
| Std | 3.93E+00 | 6.58E+03 | 5.78E+07 | 2.26E+01 | 7.12E+03 | 1.12E+04 | 1.07E+04 | 5.14E+03 | 3.46E+03 | 3.86E+03 | 3.12E+03 | 7.46E+04 | |
| Med | 1.31E+03 | 1.19E+04 | 2.05E+07 | 1.35E+03 | 1.79E+04 | 1.95E+04 | 1.20E+04 | 1.05E+04 | 6.35E+03 | 1.33E+04 | 5.29E+03 | 5.06E+04 | |
| Rank | 1 | 6 | 12 | 2 | 9 | 10 | 8 | 5 | 4 | 7 | 3 | 11 | |
| C17-F14 | Mean | 1.40E+03 | 2.55E+03 | 5.47E+03 | 1.43E+03 | 4.77E+03 | 1.58E+03 | 1.44E+03 | 2.83E+03 | 1.52E+03 | 5.57E+03 | 7.00E+03 | 6.76E+03 |
| Best | 1.40E+03 | 2.01E+03 | 2.19E+03 | 1.40E+03 | 2.57E+03 | 1.50E+03 | 1.43E+03 | 1.48E+03 | 1.48E+03 | 2.07E+03 | 3.68E+03 | 1.87E+03 | |
| Worst | 1.40E+03 | 2.91E+03 | 8.08E+03 | 1.45E+03 | 5.60E+03 | 1.69E+03 | 1.44E+03 | 4.80E+03 | 1.56E+03 | 9.48E+03 | 1.15E+04 | 1.16E+04 | |
| Std | 1.92E+00 | 3.95E+02 | 2.57E+03 | 2.26E+01 | 1.49E+03 | 8.89E+01 | 5.16E+00 | 1.61E+03 | 3.77E+01 | 3.12E+03 | 3.32E+03 | 5.26E+03 | |
| Median | 1.40E+03 | 2.63E+03 | 5.80E+03 | 1.43E+03 | 5.44E+03 | 1.58E+03 | 1.44E+03 | 2.53E+03 | 1.53E+03 | 5.36E+03 | 6.43E+03 | 6.80E+03 | |
| Rank | 1 | 6 | 9 | 2 | 8 | 5 | 3 | 7 | 4 | 10 | 12 | 11 | |
| C17-F15 | Mean | 1.50E+03 | 5.27E+03 | 9.25E+03 | 1.51E+03 | 1.47E+04 | 5.77E+03 | 1.56E+03 | 5.41E+03 | 1.79E+03 | 1.54E+04 | 4.46E+03 | 4.36E+03 |
| Best | 1.50E+03 | 1.95E+03 | 4.96E+03 | 1.50E+03 | 4.16E+03 | 2.03E+03 | 1.54E+03 | 1.81E+03 | 1.69E+03 | 6.55E+03 | 2.27E+03 | 1.87E+03 | |
| Worst | 1.50E+03 | 8.28E+03 | 1.65E+04 | 1.52E+03 | 2.43E+04 | 1.51E+04 | 1.58E+03 | 7.23E+03 | 2.01E+03 | 2.03E+04 | 6.87E+03 | 7.09E+03 | |
| Std | 6.65E−02 | 2.67E+03 | 5.30E+03 | 7.02E+00 | 1.11E+04 | 6.36E+03 | 1.87E+01 | 2.54E+03 | 1.51E+02 | 6.25E+03 | 1.95E+03 | 2.87E+03 | |
| Med | 1.50E+03 | 5.43E+03 | 7.77E+03 | 1.51E+03 | 1.52E+04 | 2.98E+03 | 1.56E+03 | 6.30E+03 | 1.73E+03 | 1.74E+04 | 4.35E+03 | 4.23E+03 | |
| Rank | 1 | 7 | 10 | 2 | 11 | 9 | 3 | 8 | 4 | 12 | 6 | 5 | |
| C17-F16 | Mean | 1.60E+03 | 1.84E+03 | 2.05E+03 | 1.69E+03 | 2.14E+03 | 1.86E+03 | 1.88E+03 | 1.75E+03 | 1.70E+03 | 2.21E+03 | 1.87E+03 | 1.82E+03 |
| Best | 1.60E+03 | 1.75E+03 | 2.02E+03 | 1.60E+03 | 1.99E+03 | 1.66E+03 | 1.72E+03 | 1.61E+03 | 1.64E+03 | 2.16E+03 | 1.72E+03 | 1.75E+03 | |
| Worst | 1.60E+03 | 1.96E+03 | 2.07E+03 | 1.84E+03 | 2.37E+03 | 2.09E+03 | 2.03E+03 | 2.00E+03 | 1.86E+03 | 2.30E+03 | 1.97E+03 | 1.85E+03 | |
| Std | 2.75E−01 | 9.69E+01 | 2.05E+01 | 1.17E+02 | 1.74E+02 | 2.12E+02 | 1.28E+02 | 1.78E+02 | 1.05E+02 | 6.08E+01 | 1.20E+02 | 4.95E+01 | |
| Median | 1.60E+03 | 1.82E+03 | 2.05E+03 | 1.66E+03 | 2.10E+03 | 1.85E+03 | 1.88E+03 | 1.70E+03 | 1.66E+03 | 2.19E+03 | 1.90E+03 | 1.85E+03 | |
| Rank | 1 | 6 | 10 | 2 | 11 | 7 | 9 | 4 | 3 | 12 | 8 | 5 | |
| C17-F17 | Mean | 1.72E+03 | 1.76E+03 | 1.86E+03 | 1.74E+03 | 1.86E+03 | 1.87E+03 | 1.80E+03 | 1.77E+03 | 1.76E+03 | 1.97E+03 | 1.86E+03 | 1.75E+03 |
| Best | 1.71E+03 | 1.72E+03 | 1.82E+03 | 1.73E+03 | 1.80E+03 | 1.82E+03 | 1.73E+03 | 1.74E+03 | 1.76E+03 | 1.76E+03 | 1.77E+03 | 1.75E+03 | |
| Worst | 1.72E+03 | 1.81E+03 | 1.93E+03 | 1.75E+03 | 1.97E+03 | 1.92E+03 | 1.86E+03 | 1.80E+03 | 1.76E+03 | 2.15E+03 | 1.98E+03 | 1.76E+03 | |
| Std | 7.86E+00 | 4.00E+01 | 5.17E+01 | 8.37E+00 | 7.34E+01 | 4.15E+01 | 6.32E+01 | 2.90E+01 | 1.03E+00 | 1.64E+02 | 9.71E+01 | 2.51E+00 | |
| Med | 1.72E+03 | 1.75E+03 | 1.85E+03 | 1.74E+03 | 1.84E+03 | 1.86E+03 | 1.80E+03 | 1.77E+03 | 1.76E+03 | 1.98E+03 | 1.85E+03 | 1.75E+03 | |
| Rank | 1 | 4 | 8 | 2 | 10 | 11 | 7 | 6 | 5 | 12 | 9 | 3 | |
| C17-F18 | Mean | 1.80E+03 | 2.35E+04 | 9.48E+07 | 1.83E+03 | 2.89E+04 | 2.46E+04 | 1.74E+04 | 2.31E+04 | 4.03E+04 | 1.20E+04 | 1.13E+04 | 9.29E+03 |
| Best | 1.80E+03 | 8.83E+03 | 1.57E+06 | 1.81E+03 | 1.13E+04 | 3.35E+03 | 4.18E+03 | 7.85E+03 | 1.54E+04 | 8.16E+03 | 3.07E+03 | 4.53E+03 | |
| Worst | 1.80E+03 | 3.76E+04 | 3.69E+08 | 1.85E+03 | 3.77E+04 | 3.86E+04 | 3.82E+04 | 3.58E+04 | 5.63E+04 | 1.85E+04 | 1.74E+04 | 1.76E+04 | |
| Std | 5.82E−01 | 1.52E+04 | 1.87E+08 | 1.77E+01 | 1.25E+04 | 1.59E+04 | 1.66E+04 | 1.19E+04 | 1.80E+04 | 4.91E+03 | 6.76E+03 | 6.04E+03 | |
| Median | 1.80E+03 | 2.37E+04 | 4.22E+06 | 1.84E+03 | 3.34E+04 | 2.82E+04 | 1.36E+04 | 2.43E+04 | 4.48E+04 | 1.06E+04 | 1.24E+04 | 7.52E+03 | |
| Rank | 1 | 8 | 12 | 2 | 10 | 9 | 6 | 7 | 11 | 5 | 4 | 3 | |
| C17-F19 | Mean | 1.90E+03 | 9.13E+03 | 6.79E+05 | 1.91E+03 | 7.35E+04 | 2.93E+05 | 2.02E+03 | 6.14E+03 | 2.16E+03 | 2.89E+04 | 1.14E+04 | 2.01E+04 |
| Best | 1.90E+03 | 3.26E+03 | 1.61E+05 | 1.90E+03 | 2.01E+03 | 7.90E+03 | 1.93E+03 | 1.93E+03 | 2.04E+03 | 8.74E+03 | 5.50E+03 | 8.22E+03 | |
| Worst | 1.90E+03 | 1.53E+04 | 1.87E+06 | 1.92E+03 | 2.76E+05 | 1.12E+06 | 2.27E+03 | 1.20E+04 | 2.36E+03 | 5.38E+04 | 2.00E+04 | 2.99E+04 | |
| Std | 6.62E−02 | 5.07E+03 | 8.20E+05 | 6.11E+00 | 1.38E+05 | 5.62E+05 | 1.71E+02 | 5.14E+03 | 1.46E+02 | 2.03E+04 | 6.42E+03 | 1.15E+04 | |
| Med | 1.90E+03 | 8.96E+03 | 3.41E+05 | 1.91E+03 | 8.08E+03 | 2.23E+04 | 1.95E+03 | 5.29E+03 | 2.11E+03 | 2.66E+04 | 1.01E+04 | 2.11E+04 | |
| Rank | 1 | 6 | 12 | 2 | 10 | 11 | 3 | 5 | 4 | 9 | 7 | 8 | |
| C17-F20 | Mean | 2.01E+03 | 2.12E+03 | 2.30E+03 | 2.02E+03 | 2.21E+03 | 2.26E+03 | 2.16E+03 | 2.05E+03 | 2.08E+03 | 2.33E+03 | 2.24E+03 | 2.05E+03 |
| Best | 2.00E+03 | 2.03E+03 | 2.25E+03 | 2.02E+03 | 2.09E+03 | 2.07E+03 | 2.03E+03 | 2.03E+03 | 2.06E+03 | 2.20E+03 | 2.20E+03 | 2.04E+03 | |
| Worst | 2.02E+03 | 2.16E+03 | 2.36E+03 | 2.04E+03 | 2.43E+03 | 2.35E+03 | 2.26E+03 | 2.08E+03 | 2.12E+03 | 2.42E+03 | 2.27E+03 | 2.08E+03 | |
| Std | 1.04E+01 | 6.44E+01 | 5.25E+01 | 9.05E+00 | 1.52E+02 | 1.32E+02 | 9.92E+01 | 2.46E+01 | 2.61E+01 | 9.56E+01 | 3.57E+01 | 1.88E+01 | |
| Median | 2.01E+03 | 2.14E+03 | 2.30E+03 | 2.02E+03 | 2.17E+03 | 2.30E+03 | 2.17E+03 | 2.06E+03 | 2.08E+03 | 2.35E+03 | 2.24E+03 | 2.05E+03 | |
| Rank | 1 | 6 | 11 | 2 | 8 | 10 | 7 | 4 | 5 | 12 | 9 | 3 | |
| C17-F21 | Mean | 2.20E+03 | 2.30E+03 | 2.31E+03 | 2.29E+03 | 2.35E+03 | 2.34E+03 | 2.30E+03 | 2.29E+03 | 2.30E+03 | 2.36E+03 | 2.32E+03 | 2.31E+03 |
| Best | 2.20E+03 | 2.20E+03 | 2.25E+03 | 2.21E+03 | 2.34E+03 | 2.32E+03 | 2.20E+03 | 2.20E+03 | 2.21E+03 | 2.36E+03 | 2.31E+03 | 2.22E+03 | |
| Worst | 2.20E+03 | 2.36E+03 | 2.39E+03 | 2.32E+03 | 2.38E+03 | 2.35E+03 | 2.34E+03 | 2.32E+03 | 2.34E+03 | 2.37E+03 | 2.34E+03 | 2.34E+03 | |
| Std | 1.24E−05 | 6.89E+01 | 6.02E+01 | 5.53E+01 | 1.93E+01 | 1.50E+01 | 6.49E+01 | 6.17E+01 | 6.81E+01 | 5.99E+00 | 1.16E+01 | 5.84E+01 | |
| Med | 2.20E+03 | 2.32E+03 | 2.30E+03 | 2.31E+03 | 2.34E+03 | 2.34E+03 | 2.33E+03 | 2.32E+03 | 2.34E+03 | 2.36E+03 | 2.32E+03 | 2.33E+03 | |
| Rank | 1 | 5 | 7 | 2 | 11 | 10 | 4 | 3 | 6 | 12 | 9 | 8 | |
| C17-F22 | Mean | 2.30E+03 | 2.31E+03 | 2.96E+03 | 2.31E+03 | 2.39E+03 | 2.32E+03 | 2.30E+03 | 2.31E+03 | 2.32E+03 | 2.30E+03 | 2.31E+03 | 2.32E+03 |
| Best | 2.30E+03 | 2.30E+03 | 2.76E+03 | 2.30E+03 | 2.31E+03 | 2.31E+03 | 2.30E+03 | 2.30E+03 | 2.32E+03 | 2.30E+03 | 2.30E+03 | 2.32E+03 | |
| Worst | 2.30E+03 | 2.31E+03 | 3.25E+03 | 2.31E+03 | 2.47E+03 | 2.33E+03 | 2.30E+03 | 2.32E+03 | 2.33E+03 | 2.30E+03 | 2.35E+03 | 2.33E+03 | |
| Std | 4.86E−01 | 3.68E+00 | 2.15E+02 | 3.55E+00 | 9.17E+01 | 7.91E+00 | 9.78E−01 | 6.71E+00 | 7.38E+00 | 1.81E−01 | 2.38E+01 | 5.84E+00 | |
| Median | 2.30E+03 | 2.31E+03 | 2.92E+03 | 2.31E+03 | 2.39E+03 | 2.32E+03 | 2.30E+03 | 2.30E+03 | 2.33E+03 | 2.30E+03 | 2.30E+03 | 2.32E+03 | |
| Rank | 2 | 6 | 12 | 5 | 11 | 8 | 3 | 4 | 10 | 1 | 7 | 9 | |
| C17-F23 | Mean | 2.61E+03 | 2.67E+03 | 2.70E+03 | 2.65E+03 | 2.69E+03 | 2.66E+03 | 2.61E+03 | 2.62E+03 | 2.64E+03 | 2.73E+03 | 2.64E+03 | 2.66E+03 |
| Best | 2.61E+03 | 2.65E+03 | 2.67E+03 | 2.62E+03 | 2.67E+03 | 2.61E+03 | 2.61E+03 | 2.61E+03 | 2.62E+03 | 2.72E+03 | 2.61E+03 | 2.65E+03 | |
| Worst | 2.61E+03 | 2.69E+03 | 2.72E+03 | 2.67E+03 | 2.72E+03 | 2.69E+03 | 2.62E+03 | 2.64E+03 | 2.65E+03 | 2.75E+03 | 2.66E+03 | 2.68E+03 | |
| Std | 2.10E+00 | 1.90E+01 | 2.05E+01 | 2.11E+01 | 1.81E+01 | 3.45E+01 | 6.24E+00 | 1.63E+01 | 1.11E+01 | 1.00E+01 | 2.06E+01 | 1.47E+01 | |
| Med | 2.61E+03 | 2.67E+03 | 2.70E+03 | 2.65E+03 | 2.69E+03 | 2.66E+03 | 2.61E+03 | 2.62E+03 | 2.64E+03 | 2.73E+03 | 2.65E+03 | 2.66E+03 | |
| Rank | 1 | 9 | 11 | 6 | 10 | 7 | 2 | 3 | 4 | 12 | 5 | 8 | |
| C17-F24 | Mean | 2.50E+03 | 2.78E+03 | 2.89E+03 | 2.64E+03 | 2.82E+03 | 2.80E+03 | 2.75E+03 | 2.75E+03 | 2.77E+03 | 2.74E+03 | 2.78E+03 | 2.77E+03 |
| Best | 2.50E+03 | 2.76E+03 | 2.84E+03 | 2.50E+03 | 2.80E+03 | 2.75E+03 | 2.75E+03 | 2.74E+03 | 2.76E+03 | 2.50E+03 | 2.77E+03 | 2.77E+03 | |
| Worst | 2.50E+03 | 2.80E+03 | 2.93E+03 | 2.78E+03 | 2.85E+03 | 2.82E+03 | 2.76E+03 | 2.78E+03 | 2.77E+03 | 2.86E+03 | 2.78E+03 | 2.79E+03 | |
| Std | 4.88E−05 | 1.46E+01 | 3.77E+01 | 1.66E+02 | 2.29E+01 | 3.01E+01 | 4.03E+00 | 2.06E+01 | 5.94E+00 | 1.66E+02 | 3.92E+00 | 1.05E+01 | |
| Median | 2.50E+03 | 2.77E+03 | 2.90E+03 | 2.64E+03 | 2.82E+03 | 2.81E+03 | 2.75E+03 | 2.74E+03 | 2.77E+03 | 2.80E+03 | 2.78E+03 | 2.77E+03 | |
| Rank | 1 | 8 | 12 | 2 | 11 | 10 | 5 | 4 | 6 | 3 | 9 | 7 | |
| C17-F25 | Mean | 2.90E+03 | 2.94E+03 | 3.38E+03 | 2.93E+03 | 3.13E+03 | 2.95E+03 | 2.90E+03 | 2.94E+03 | 2.93E+03 | 2.93E+03 | 2.93E+03 | 2.95E+03 |
| Best | 2.90E+03 | 2.90E+03 | 3.35E+03 | 2.90E+03 | 2.94E+03 | 2.95E+03 | 2.90E+03 | 2.92E+03 | 2.91E+03 | 2.90E+03 | 2.90E+03 | 2.95E+03 | |
| Worst | 2.90E+03 | 2.95E+03 | 3.46E+03 | 2.95E+03 | 3.50E+03 | 2.96E+03 | 2.90E+03 | 2.95E+03 | 2.95E+03 | 2.94E+03 | 2.95E+03 | 2.96E+03 | |
| Std | 3.10E−07 | 2.38E+01 | 5.00E+01 | 2.38E+01 | 2.59E+02 | 5.22E+00 | 2.51E−01 | 1.57E+01 | 1.63E+01 | 2.24E+01 | 2.41E+01 | 2.74E+00 | |
| Med | 2.90E+03 | 2.95E+03 | 3.36E+03 | 2.95E+03 | 3.03E+03 | 2.95E+03 | 2.90E+03 | 2.95E+03 | 2.93E+03 | 2.94E+03 | 2.95E+03 | 2.95E+03 | |
| Rank | 1 | 7 | 12 | 5 | 11 | 9 | 2 | 8 | 3 | 4 | 6 | 10 | |
| C17-F26 | Mean | 2.88E+03 | 2.97E+03 | 4.24E+03 | 3.26E+03 | 3.88E+03 | 3.26E+03 | 2.90E+03 | 2.96E+03 | 3.29E+03 | 4.13E+03 | 2.85E+03 | 3.02E+03 |
| Best | 2.80E+03 | 2.82E+03 | 3.82E+03 | 2.90E+03 | 2.91E+03 | 2.83E+03 | 2.90E+03 | 2.90E+03 | 2.99E+03 | 3.57E+03 | 2.60E+03 | 2.91E+03 | |
| Worst | 2.90E+03 | 3.14E+03 | 4.79E+03 | 3.96E+03 | 4.77E+03 | 3.97E+03 | 2.90E+03 | 2.98E+03 | 4.17E+03 | 4.43E+03 | 3.02E+03 | 3.13E+03 | |
| Std | 5.10E+01 | 1.84E+02 | 4.62E+02 | 4.81E+02 | 7.79E+02 | 5.06E+02 | 4.02E−02 | 3.84E+01 | 5.98E+02 | 3.89E+02 | 1.98E+02 | 1.01E+02 | |
| Median | 2.90E+03 | 2.97E+03 | 4.17E+03 | 3.10E+03 | 3.93E+03 | 3.12E+03 | 2.90E+03 | 2.97E+03 | 3.00E+03 | 4.25E+03 | 2.89E+03 | 3.03E+03 | |
| Rank | 2 | 5 | 12 | 8 | 10 | 7 | 3 | 4 | 9 | 11 | 1 | 6 | |
| C17-F27 | Mean | 3.09E+03 | 3.10E+03 | 3.17E+03 | 3.11E+03 | 3.17E+03 | 3.17E+03 | 3.09E+03 | 3.09E+03 | 3.11E+03 | 3.30E+03 | 3.12E+03 | 3.15E+03 |
| Best | 3.09E+03 | 3.10E+03 | 3.14E+03 | 3.10E+03 | 3.14E+03 | 3.13E+03 | 3.09E+03 | 3.09E+03 | 3.09E+03 | 3.22E+03 | 3.10E+03 | 3.13E+03 | |
| Worst | 3.09E+03 | 3.10E+03 | 3.23E+03 | 3.13E+03 | 3.20E+03 | 3.21E+03 | 3.10E+03 | 3.09E+03 | 3.15E+03 | 3.38E+03 | 3.14E+03 | 3.18E+03 | |
| Std | 2.28E−01 | 3.21E+00 | 4.20E+01 | 1.62E+01 | 3.29E+01 | 3.43E+01 | 3.14E+00 | 2.68E+00 | 3.02E+01 | 7.96E+01 | 1.92E+01 | 1.79E+01 | |
| Med | 3.09E+03 | 3.10E+03 | 3.17E+03 | 3.11E+03 | 3.17E+03 | 3.18E+03 | 3.09E+03 | 3.09E+03 | 3.10E+03 | 3.29E+03 | 3.11E+03 | 3.15E+03 | |
| Rank | 1 | 4 | 11 | 6 | 9 | 10 | 3 | 2 | 5 | 12 | 7 | 8 | |
| C17-F28 | Mean | 3.03E+03 | 3.33E+03 | 3.91E+03 | 3.31E+03 | 3.47E+03 | 3.31E+03 | 3.33E+03 | 3.24E+03 | 3.44E+03 | 3.47E+03 | 3.32E+03 | 3.20E+03 |
| Best | 2.80E+03 | 3.10E+03 | 3.87E+03 | 3.10E+03 | 3.40E+03 | 3.19E+03 | 3.15E+03 | 3.18E+03 | 3.23E+03 | 3.42E+03 | 3.18E+03 | 3.17E+03 | |
| Worst | 3.10E+03 | 3.41E+03 | 3.95E+03 | 3.44E+03 | 3.60E+03 | 3.41E+03 | 3.41E+03 | 3.40E+03 | 3.73E+03 | 3.52E+03 | 3.41E+03 | 3.21E+03 | |
| Std | 1.53E+02 | 1.59E+02 | 3.76E+01 | 1.54E+02 | 9.20E+01 | 1.23E+02 | 1.25E+02 | 1.07E+02 | 2.16E+02 | 4.14E+01 | 1.05E+02 | 2.22E+01 | |
| Median | 3.10E+03 | 3.41E+03 | 3.91E+03 | 3.34E+03 | 3.44E+03 | 3.32E+03 | 3.38E+03 | 3.20E+03 | 3.40E+03 | 3.47E+03 | 3.34E+03 | 3.20E+03 | |
| Rank | 1 | 8 | 12 | 4 | 11 | 5 | 7 | 3 | 9 | 10 | 6 | 2 | |
| C17-F29 | Mean | 3.14E+03 | 3.38E+03 | 3.34E+03 | 3.17E+03 | 3.31E+03 | 3.32E+03 | 3.23E+03 | 3.19E+03 | 3.23E+03 | 3.52E+03 | 3.29E+03 | 3.28E+03 |
| Best | 3.13E+03 | 3.30E+03 | 3.21E+03 | 3.15E+03 | 3.29E+03 | 3.26E+03 | 3.18E+03 | 3.17E+03 | 3.18E+03 | 3.33E+03 | 3.21E+03 | 3.22E+03 | |
| Worst | 3.15E+03 | 3.44E+03 | 3.46E+03 | 3.19E+03 | 3.34E+03 | 3.40E+03 | 3.30E+03 | 3.20E+03 | 3.32E+03 | 3.70E+03 | 3.34E+03 | 3.34E+03 | |
| Std | 8.71E+00 | 6.37E+01 | 1.17E+02 | 1.68E+01 | 2.48E+01 | 6.04E+01 | 5.29E+01 | 1.18E+01 | 6.16E+01 | 1.64E+02 | 6.07E+01 | 5.18E+01 | |
| Med | 3.15E+03 | 3.38E+03 | 3.35E+03 | 3.16E+03 | 3.31E+03 | 3.32E+03 | 3.22E+03 | 3.19E+03 | 3.22E+03 | 3.52E+03 | 3.30E+03 | 3.27E+03 | |
| Rank | 1 | 11 | 10 | 2 | 8 | 9 | 4 | 3 | 5 | 12 | 7 | 6 | |
| C17-F30 | Mean | 3.41E+03 | 5.29E+05 | 5.68E+06 | 5.60E+03 | 4.72E+06 | 3.20E+06 | 3.79E+05 | 8.36E+05 | 3.11E+04 | 1.81E+06 | 6.31E+05 | 2.25E+06 |
| Best | 3.40E+03 | 1.05E+04 | 9.84E+05 | 3.64E+03 | 2.49E+06 | 2.86E+04 | 1.47E+04 | 8.10E+03 | 2.12E+04 | 3.06E+05 | 3.87E+03 | 2.28E+05 | |
| Worst | 3.43E+03 | 1.20E+06 | 1.85E+07 | 1.10E+04 | 8.48E+06 | 6.05E+06 | 1.47E+06 | 1.70E+06 | 4.45E+04 | 5.57E+06 | 1.85E+06 | 4.21E+06 | |
| Std | 1.83E+01 | 5.90E+05 | 8.71E+06 | 3.70E+03 | 2.79E+06 | 2.95E+06 | 7.39E+05 | 9.73E+05 | 1.09E+04 | 2.57E+06 | 8.87E+05 | 2.04E+06 | |
| Median | 3.40E+03 | 4.52E+05 | 1.63E+06 | 3.87E+03 | 3.95E+06 | 3.37E+06 | 1.77E+04 | 8.19E+05 | 2.94E+04 | 6.93E+05 | 3.34E+05 | 2.29E+06 | |
| Rank | 1 | 5 | 12 | 2 | 11 | 10 | 4 | 7 | 3 | 8 | 6 | 9 | |
| Sum rank | 34 | 200 | 320 | 96 | 298 | 261 | 125 | 141 | 181 | 228 | 177 | 201 | |
| Mean rank | 1.1724 | 6.8965 | 11.0344 | 3.3103 | 10.2758 | 9 | 4.3103 | 4.8620 | 6.2413 | 7.8620 | 6.1034 | 6.9310 | |
| Total rank | 1 | 7 | 12 | 2 | 11 | 10 | 3 | 4 | 6 | 9 | 5 | 8 | |
| P-value | 6.882E−21 | 1.972E−21 | 1.289E−19 | 1.972E−21 | 1.972E−21 | 3.406E−20 | 3.881E−21 | 1.972E−21 | 1.803E−20 | 7.408E−20 | 1.972E−21 | ||
Figure 3.
Boxplot of performance of STBO and competitor algorithms in solving the CEC 2017 test suite.
STBO for real-world applications
STBO's ability to optimize optimization problems in real-world applications is evaluated in this section. To this end, STBO and competitor algorithms have been implemented on four engineering optimization challenges. These engineering challenges are pressure vessel design (PVD)79, speed reducer design (SRD)80, welded beam design (WBD)12, and tension/compression spring design (TCSD)12. Schematics of these problems are presented in Fig. 4.
Figure 4.
Schematics of four real-world applications: (A) PVD, (B) SRD, (C) WBD, (D) TCSD.
The optimization results of the four mentioned challenges are reported in Table 9. The simulation results show that STBO performs superior to competitor algorithms in optimizing all four studied engineering challenges. What is clear from the analysis of the simulation results is that STBO has an effective capability in dealing with real-world optimization applications. The convergence curves of STBO while optimizing the mentioned optimization challenges are presented in Fig. 5. The convergence curves show that STBO has identified the main optimal area in the initial iterations by providing a desirable global search. Then, by increasing the iterations of the algorithm based on the local search, it tries to get better solutions. Intuitive analysis of convergence curves shows that STBO has converged to suitable solutions with a high ability to balance exploration and exploitation.
Table 9.
Evaluation results of four real-world applications.
| GA | PSO | GSA | TLBO | MVO | GWO | WOA | TSA | MPA | RSA | AVOA | STBO | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PVD | Mean | 6645.562 | 6265.49 | 6842.164 | 6328.261 | 6478.841 | 6066.455 | 5892.921 | 5888.84 | 6117.763 | 6038.652 | 5963.405 | 5888.170 |
| Best | 6581.043 | 5918.224 | 11,605 | 6166.438 | 6039.984 | 5919.289 | 5917.261 | 5913.451 | 6109.88 | 6031.364 | 5958.117 | 5884.882 | |
| Worst | 8007.337 | 7007.411 | 7160.988 | 6513.898 | 7252.635 | 7396.34 | 5896.021 | 5893.718 | 6129.069 | 6042.513 | 5968.94 | 5895.379 | |
| Std | 657.679 | 496.2457 | 5791.998 | 126.639 | 327.0846 | 66.63439 | 13.91331 | 28.93686 | 38.24161 | 31.18698 | 27.451658 | 23.71639 | |
| Median | 7587.808 | 6114.139 | 6839.254 | 6319.815 | 6398.997 | 6417.635 | 5892.046 | 5887.624 | 6115.578 | 6036.744 | 5962.3195 | 5887.907 | |
| Rank | 11 | 8 | 12 | 9 | 10 | 6 | 3 | 2 | 7 | 5 | 4 | 1 | |
| SRD | Mean | 3190.666 | 3174.457 | 3069.904 | 3032.78 | 3109.29 | 3009.754 | 3003.541 | 3011.73 | 3001.864 | 3000.171 | 3000.197 | 3000.029 |
| Best | 3070.629 | 3054.173 | 3033.594 | 3005.931 | 3008.769 | 3004.291 | 3001.55 | 3004.837 | 2996.216 | 2996.171 | 2995.7775 | 2995.39 | |
| Worst | 3317.508 | 3368.247 | 3108.816 | 3064.938 | 3215.349 | 3012.665 | 3007.795 | 3027.316 | 3007.093 | 3002.173 | 3001.897 | 3001.627 | |
| Std | 17.14086 | 92.69298 | 18.0977 | 13.03553 | 79.74166 | 5.845531 | 1.934443 | 10.36808 | 5.219098 | 2.015032 | 1.8193737 | 1.623719 | |
| Med | 3202.346 | 3160.857 | 3069.595 | 3030.968 | 3109.29 | 3008.426 | 3003.087 | 3010.34 | 3000.431 | 2999.836 | 2999.4455 | 2999.061 | |
| Rank | 12 | 11 | 9 | 8 | 10 | 6 | 5 | 7 | 4 | 2 | 3 | 1 | |
| WBD | Mean | 1.96595 | 2.123005 | 2.54876 | 1.820886 | 1.732754 | 2.234273 | 1.730198 | 1.728896 | 1.892096 | 1.725025 | 1.7248133 | 1.724605 |
| Best | 1.83841 | 1.876176 | 2.175414 | 1.761242 | 1.727502 | 1.822536 | 1.729027 | 1.727691 | 1.866157 | 1.727296 | 1.7252098 | 1.723127 | |
| Worst | 2.038864 | 2.324247 | 3.008994 | 1.876738 | 1.744746 | 3.053648 | 1.730634 | 1.729132 | 2.016418 | 1.727726 | 1.7272073 | 1.726692 | |
| Std | 0.139733 | 0.034882 | 0.256314 | 0.027592 | 0.004875 | 0.325102 | 0.001159 | 0.000287 | 0.00796 | 0.005124 | 0.004724 | 0.004324 | |
| Median | 1.939188 | 2.100775 | 2.499548 | 1.823362 | 1.73049 | 2.248652 | 1.730157 | 1.728855 | 1.883578 | 1.725997 | 1.7249368 | 1.72388 | |
| Rank | 9 | 10 | 12 | 7 | 6 | 11 | 5 | 4 | 8 | 3 | 2 | 1 | |
| TCSD | Mean | 0.013192 | 0.014166 | 0.013564 | 0.01296 | 0.014599 | 0.014956 | 0.012816 | 0.012803 | 0.013898 | 0.0128 | 0.012737 | 0.012674 |
| Best | 0.012889 | 0.013151 | 0.012987 | 0.012822 | 0.01293 | 0.013309 | 0.01279 | 0.012786 | 0.013218 | 0.012768 | 0.01271 | 0.012652 | |
| Worst | 0.015356 | 0.016403 | 0.014345 | 0.01312 | 0.018006 | 0.018029 | 0.01284 | 0.012834 | 0.01583 | 0.012812 | 0.0127475 | 0.012683 | |
| Std | 0.000378 | 0.002092 | 0.000289 | 0.007831 | 0.001637 | 0.002293 | 0.004193 | 0.005671 | 0.006141 | 0.007417 | 0.004219 | 0.001021 | |
| Med | 0.013073 | 0.013123 | 0.013492 | 0.012965 | 0.014151 | 0.013316 | 0.012819 | 0.012806 | 0.013776 | 0.01279 | 0.0127305 | 0.012671 | |
| Rank | 7 | 10 | 8 | 6 | 11 | 12 | 5 | 4 | 9 | 3 | 2 | 1 | |
| Sum rank | 39 | 39 | 41 | 30 | 37 | 35 | 18 | 17 | 28 | 13 | 11 | 4 | |
| Mean rank | 9.75 | 9.75 | 10.25 | 7.5 | 9.25 | 8.75 | 4.5 | 4.25 | 7 | 3.25 | 2.75 | 1 | |
| Total rank | 8 | 11 | 12 | 7 | 10 | 9 | 5 | 4 | 6 | 3 | 2 | 1 | |
Figure 5.
Convergence curves of STBO on four real-world applications.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was not required as no human or animals were involved.
Conclusion and future works
This paper introduced a new metaheuristic algorithm called Sewing Training-Based Optimization (STBO) to solve optimization problems. The interactions between the training instructor and the beginner tailors are the main inspiration in the design of STBO. The proposed STBO was modeled and designed in three phases: (i) training, (ii) imitation of the instructor's skills, and (iii) practice. The STBO’s performance was tested on fifty-two objective functions of unimodal, high-dimensional multimodal, fixed-dimensional multimodal, and the CEC 2017 test suite. The optimization results of the benchmark functions showed that the proposed STBO approach has a good ability in exploration, exploitation, and balancing their proportion during the search process in the problem-solving space. Eleven well-known metaheuristic algorithms were employed to compare the performance of STBO in optimization. The simulation results showed that STBO has superior and competitive performance compared to some well-known metaheuristic algorithms, providing better results in most of the objective functions studied in this paper. STBO implementation on four engineering design challenges demonstrated the capability of the proposed algorithm in real-world applications.
Although the proposed STBO has provided good performance in most of the benchmark functions studied in this article, the proposed algorithm has some limitations. The first limitation of STBO is that it is always possible to devise newer algorithms that perform better than the proposed approach. The second limitation of STBO is that there is a possibility that the implementation of the proposed algorithm will fail in some optimization applications. Finally, the third limitation of STBO is that there is no guarantee that STBO can always provide a globally optimal solution since the proposed algorithm is based on a random search. Also, based on the concept of the NFL theorem, it is not claimed that STBO is the best optimizer for all optimization applications.
Introducing the STBO activates several research tasks for future studies. Developing binary and multimodal versions is a possible specific STBO research proposal. Employing STBO in various applications of optimization in science as well as in real-world applications are other suggestions for further studies.
Author contributions
Conceptualization, E.T.; methodology, M.D.; software, M.D.; validation, E.T. and T.Z.; formal analysis, M.D. and T.Z.; investigation, E.T.; resources, E.T.; data curation, E.T. and M.D.; writing—original draft preparation, T.Z. and M.D.; writing—review and editing, E.T. and T.Z.; visualization, E.T.; supervision, E.T..; project administration, M.D.; funding acquisition, E.T.
Funding
This work was supported by the Project of Specific Research, Faculty of Science, University of Hradec Králové, No. 2104/2022.
Data availability
All data generated or analyzed during this study are included directly in the text of this submitted manuscript. There are no additional external files with datasets.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Ray T, Liew K-M. Society and civilization: An optimization algorithm based on the simulation of social behavior. IEEE Trans. Evol. Comput. 2003;7:386–396. doi: 10.1109/TEVC.2003.814902. [DOI] [Google Scholar]
- 2.Kaidi W, Khishe M, Mohammadi M. Dynamic Levy flight chimp optimization. Knowl.-Based Syst. 2022;235:107625. doi: 10.1016/j.knosys.2021.107625. [DOI] [Google Scholar]
- 3.Sergeyev YD, Kvasov D, Mukhametzhanov M. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018;8:1–9. doi: 10.1038/s41598-017-18940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goldberg DE, Holland JH. Genetic algorithms and machine learning. Mach. Learn. 1988;3:95–99. doi: 10.1023/A:1022602019183. [DOI] [Google Scholar]
- 5.Kennedy, J. & Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95—International Conference on Neural Networks, 1942–1948 (IEEE, 1995).
- 6.Dorigo, M. & Stützle, T. Handbook of Metaheuristics, chap. Ant Colony Optimization: Overview and Recent Advances, 311–351 (Cham: Springer International Publishing, 2019).
- 7.Karaboga, D. & Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In Foundations of Fuzzy Logic and Soft Computing. IFSA 2007. Lecture Notes in Computer Science, 789–798 (Springer, 2007).
- 8.Wang J-S, Li S-X. An improved grey wolf optimizer based on differential evolution and elimination mechanism. Sci. Rep. 2019;9:1–21. doi: 10.1038/s41598-019-43546-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1:67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]
- 10.Yang, X.-S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications. SAGA 2009, 169–178 (Springer, 2009).
- 11.Mirjalili S, Mirjalili SM, Lewis A. Grey Wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 12.Mirjalili S, Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. doi: 10.1016/j.advengsoft.2016.01.008. [DOI] [Google Scholar]
- 13.Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020;152:113377. doi: 10.1016/j.eswa.2020.113377. [DOI] [Google Scholar]
- 14.Dehghani M, Hubálovský Š, Trojovský P. Cat and mouse based optimizer: A new nature-inspired optimization algorithm. Sensors. 2021;21:5214. doi: 10.3390/s21155214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kaur S, Awasthi LK, Sangal AL, Dhiman G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020;90:103541. doi: 10.1016/j.engappai.2020.103541. [DOI] [Google Scholar]
- 16.Gharehchopogh FS. An improved tunicate swarm algorithm with best-random mutation strategy for global optimization problems. J. Bionic Eng. 2022;2:1–26. [Google Scholar]
- 17.Abualigah L, Abd Elaziz M, Sumari P, Geem ZW, Gandomi AH. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022;191:116158. doi: 10.1016/j.eswa.2021.116158. [DOI] [Google Scholar]
- 18.Jiang Y, Wu Q, Zhu S, Zhang L. Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Syst. Appl. 2022;188:116026. doi: 10.1016/j.eswa.2021.116026. [DOI] [Google Scholar]
- 19.Shayanfar H, Gharehchopogh FS. Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems. Appl. Soft Comput. 2018;71:728–746. doi: 10.1016/j.asoc.2018.07.033. [DOI] [Google Scholar]
- 20.Abdollahzadeh B, Gharehchopogh FS, Mirjalili S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021;158:107408. doi: 10.1016/j.cie.2021.107408. [DOI] [Google Scholar]
- 21.Abdollahzadeh B, Soleimanian GF, Mirjalili S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021;36:5887–5958. doi: 10.1002/int.22535. [DOI] [Google Scholar]
- 22.Gharehchopogh FS. Advances in tree seed algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2022;29:3281–3304. doi: 10.1007/s11831-021-09698-0. [DOI] [Google Scholar]
- 23.Ghafori S, Gharehchopogh FS. Advances in spotted hyena optimizer: A comprehensive survey. Arch. Comput. Methods Eng. 2021;29:1569–1590. doi: 10.1007/s11831-021-09624-4. [DOI] [Google Scholar]
- 24.Trojovský P, Dehghani M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors. 2022;22:855. doi: 10.3390/s22030855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 26.Koza, J. R. & Koza, J. R. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Vol. 1 (MIT press, 1992).
- 27.Moscato, P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech Concurrent Computation Program, C3P Report826, 1989 (1989).
- 28.Rechenberg I. Evolution strategy: Optimization of technical systems by means of biological evolution. Fromman-Holzboog Stuttgart. 1973;104:15–16. [Google Scholar]
- 29.Yao X, Liu Y, Lin G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999;3:82–102. doi: 10.1109/4235.771163. [DOI] [Google Scholar]
- 30.Reynolds, R. G. An introduction to cultural algorithms. In Proceedings of the Third Annual Conference on Evolutionary Programming. 131–139 (World Scientific, 1994).
- 31.Eskandar H, Sadollah A, Bahreininejad A, Hamdi M. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012;110:151–166. doi: 10.1016/j.compstruc.2012.07.010. [DOI] [Google Scholar]
- 32.Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: A gravitational search algorithm. Inf. Sci. 2009;179:2232–2248. doi: 10.1016/j.ins.2009.03.004. [DOI] [Google Scholar]
- 33.Dehghani M, et al. A spring search algorithm applied to engineering optimization problems. Appl. Sci. 2020;10:6173. doi: 10.3390/app10186173. [DOI] [Google Scholar]
- 34.Dehghani M, Samet H. Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Appl. Sci. 2020;2:1–15. doi: 10.1007/s42452-020-03511-6. [DOI] [Google Scholar]
- 35.Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 36.Tahani M, Babayan N. Flow Regime Algorithm (FRA): A physics-based meta-heuristics algorithm. Knowl. Inf. Syst. 2019;60:1001–1038. doi: 10.1007/s10115-018-1253-3. [DOI] [Google Scholar]
- 37.Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020;191:105190. doi: 10.1016/j.knosys.2019.105190. [DOI] [Google Scholar]
- 38.Mirjalili S, Mirjalili SM, Hatamlou A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016;27:495–513. doi: 10.1007/s00521-015-1870-7. [DOI] [Google Scholar]
- 39.Moghdani R, Salimifard K. Volleyball premier league algorithm. Appl. Soft Comput. 2018;64:161–185. doi: 10.1016/j.asoc.2017.11.043. [DOI] [Google Scholar]
- 40.Dehghani M, Mardaneh M, Guerrero JM, Malik O, Kumar V. Football game based optimization: An application to solve energy commitment problem. Int. J. Intell. Eng. Syst. 2020;13:514–523. [Google Scholar]
- 41.Kaveh A, Zolghadr A. A novel meta-heuristic algorithm: Tug of war optimization. Iran Univ. Sci. Technol. 2016;6:469–492. [Google Scholar]
- 42.Zeidabadi FA, Dehghani M. POA: Puzzle optimization algorithm. Int. J. Intell. Eng. Syst. 2022;15:273–281. [Google Scholar]
- 43.Rao RV, Savsani VJ, Vakharia D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011;43:303–315. doi: 10.1016/j.cad.2010.12.015. [DOI] [Google Scholar]
- 44.Dehghani M, et al. A new “Doctor and Patient” optimization algorithm: An application to energy commitment problem. Appl. Sci. 2020;10:5791. doi: 10.3390/app10175791. [DOI] [Google Scholar]
- 45.Dehghani M, Trojovský P. Teamwork optimization algorithm: A new optimization approach for function minimization/maximization. Sensors. 2021;21:4567. doi: 10.3390/s21134567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dai, C., Zhu, Y. & Chen, W. Seeker optimization algorithm. In International Conference on Computational and Information Science. 167–176 (Springer, 2006).
- 47.Atashpaz-Gargari, E. & Lucas, C. Integrated radiation optimization: inspired by the gravitational radiation in the curvature of space-time. In 2007 IEEE Congress on Evolutionary Computation. 4661–4667 (IEEE, 2007).
- 48.Zhang, L. M., Dahlmann, C. & Zhang, Y. Human-inspired algorithms for continuous function optimization. in 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems. 318–321 (IEEE, 2009).
- 49.Xu Y, Cui Z, Zeng J. Social Emotional Optimization Algorithm for Nonlinear Constrained Optimization Problems. In: Bijaya KP, Swagatam D, Ponnuthurai NS, Subhransu SD, editors. Swarm, Evolutionary, and Memetic Computing. Springer; 2010. pp. 583–590. [Google Scholar]
- 50.Shi, Y. Brain storm optimization algorithm. In International conference in swarm intelligence. 303–309 (Springer, 2011).
- 51.Shayeghi H, Dadashpour J. Anarchic society optimization based PID control of an automatic voltage regulator (AVR) system. Electr. Electron. Eng. 2012;2:199–207. doi: 10.5923/j.eee.20120204.05. [DOI] [Google Scholar]
- 52.Mousavirad SJ, Ebrahimpour-Komleh H. Human mental search: A new population-based metaheuristic optimization algorithm. Appl. Intell. 2017;47:850–887. doi: 10.1007/s10489-017-0903-6. [DOI] [Google Scholar]
- 53.Mohamed AW, Hadi AA, Mohamed AK. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020;11:1501–1529. doi: 10.1007/s13042-019-01053-x. [DOI] [Google Scholar]
- 54.Al-Betar MA, Alyasseri ZAA, Awadallah MA, Abu DI. Coronavirus herd immunity optimizer (CHIO) Neural Comput. Appl. 2021;33:5011–5042. doi: 10.1007/s00521-020-05296-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Braik M, Ryalat MH, Al-Zoubi H. A novel meta-heuristic algorithm for solving numerical optimization problems: Ali Baba and the forty thieves. Neural Comput. Appl. 2022;34:409–455. doi: 10.1007/s00521-021-06392-x. [DOI] [Google Scholar]
- 56.Moosavi SHS, Bardsiri VK. Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Eng. Appl. Artif. Intell. 2019;86:165–181. doi: 10.1016/j.engappai.2019.08.025. [DOI] [Google Scholar]
- 57.Dehghani M, Mardaneh M, Malik O. FOA: ‘Following’ optimization algorithm for solving power engineering optimization problems. J. Oper. Autom. Power Eng. 2020;8:57–64. [Google Scholar]
- 58.Zeidabadi F-A, et al. Archery algorithm: A novel Stochastic optimization algorithm for solving optimization problems. Comput. Mater. Continua. 2022;72:399–416. doi: 10.32604/cmc.2022.024736. [DOI] [Google Scholar]
- 59.Zaman HRR, Gharehchopogh FS. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2021;2021:1–35. [Google Scholar]
- 60.Gharehchopogh FS, Farnad B, Alizadeh A. A modified farmland fertility algorithm for solving constrained engineering problems. Concurr. Comput. Pract. Exp. 2021;33:e6310. doi: 10.1002/cpe.6310. [DOI] [Google Scholar]
- 61.Gharehchopogh FS, Abdollahzadeh B. An efficient harris hawk optimization algorithm for solving the travelling salesman problem. Clust. Comput. 2021;25:1981–2005. doi: 10.1007/s10586-021-03304-5. [DOI] [Google Scholar]
- 62.Mohammadzadeh H, Gharehchopogh FS. A multi-agent system based for solving high-dimensional optimization problems: A case study on email spam detection. Int. J. Commun. Syst. 2021;34:e4670. doi: 10.1002/dac.4670. [DOI] [Google Scholar]
- 63.Goldanloo MJ, Gharehchopogh FS. A hybrid OBL-based firefly algorithm with symbiotic organisms search algorithm for solving continuous optimization problems. J. Supercomput. 2021;78:3998–4031. doi: 10.1007/s11227-021-04015-9. [DOI] [Google Scholar]
- 64.Mohammadzadeh H, Gharehchopogh FS. A novel hybrid whale optimization algorithm with flower pollination algorithm for feature selection: Case study Email spam detection. Comput. Intell. 2021;37:176–209. doi: 10.1111/coin.12397. [DOI] [Google Scholar]
- 65.Abdollahzadeh B, Gharehchopogh FS. A multi-objective optimization algorithm for feature selection problems. Eng. Comput. 2021;2:1–19. [Google Scholar]
- 66.Benyamin A, Farhad SG, Saeid B. Discrete farmland fertility optimization algorithm with metropolis acceptance criterion for traveling salesman problems. Int. J. Intell. Syst. 2021;36:1270–1303. doi: 10.1002/int.22342. [DOI] [Google Scholar]
- 67.Mohmmadzadeh H, Gharehchopogh FS. An efficient binary chaotic symbiotic organisms search algorithm approaches for feature selection problems. J. Supercomput. 2021;77:9102–9144. doi: 10.1007/s11227-021-03626-6. [DOI] [Google Scholar]
- 68.Mohammadzadeh H, Gharehchopogh FS. Feature selection with binary symbiotic organisms search algorithm for email spam detection. Int. J. Inf. Technol. Decis. Mak. 2021;20:469–515. doi: 10.1142/S0219622020500546. [DOI] [Google Scholar]
- 69.Gharehchopogh FS, Namazi M, Ebrahimi L, Abdollahzadeh B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2022;2022:1–29. doi: 10.1007/s11831-022-09804-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Gharehchopogh FS, Gholizadeh H. A comprehensive survey: Whale optimization algorithm and its applications. Swarm Evol. Comput. 2019;48:1–24. doi: 10.1016/j.swevo.2019.03.004. [DOI] [Google Scholar]
- 71.Gharehchopogh FS, Shayanfar H, Gholizadeh H. A comprehensive survey on symbiotic organisms search algorithms. Artif. Intell. Rev. 2020;53:2265–2312. doi: 10.1007/s10462-019-09733-4. [DOI] [Google Scholar]
- 72.Doumari SA, Givi H, Dehghani M, Malik OP. Ring toss game-based optimization algorithm for solving various optimization problems. Int. J. Intell. Eng. Syst. 2021;14:545–554. [Google Scholar]
- 73.Dehghani M, Montazeri Z, Malik OP, Ehsanifar A, Dehghani A. OSA: Orientation search algorithm. Int. J. Ind. Electron. Control Optim. 2019;2:99–112. [Google Scholar]
- 74.Dehghani M, Montazeri Z, Malik OP. DGO: Dice game optimizer. Gazi Univ. J. Sci. 2019;32:871–882. doi: 10.35378/gujs.484643. [DOI] [Google Scholar]
- 75.Dehghani M, Montazeri Z, Givi H, Guerrero JM, Dhiman G. Darts game optimizer: A new optimization technique based on darts game. Int. J. Intell. Eng. Syst. 2020;13:286–294. [Google Scholar]
- 76.Dehghani M, et al. MLO: Multi leader optimizer. Int. J. Intell. Eng. Syst. 2020;13:364–373. [Google Scholar]
- 77.Awad, N. et al. Evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. Technology Report (2016).
- 78.Wilcoxon F. Individual comparisons by ranking methods. Biometr. Bull. 1945;1:80–83. doi: 10.2307/3001968. [DOI] [Google Scholar]
- 79.Kannan B, Kramer SN. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 1994;116:405–411. doi: 10.1115/1.2919393. [DOI] [Google Scholar]
- 80.Mezura-Montes, E. & Coello, C.A.C. Useful infeasible solutions in engineering optimization with evolutionary algorithms. In Advances in Artificial Intelligence (MICAI 2005). Lecture Notes in Computer Science, 652–662 (Springer, 2005).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analyzed during this study are included directly in the text of this submitted manuscript. There are no additional external files with datasets.