Effect of Hyaluronic Acid on Microscale Deformations of Collagen Gels

Abstract

As fibrous collagen is the most abundant protein in mammalian tissues, gels of collagen fibers have been extensively used as an extracellular matrix scaffold to study how cells sense and respond to cues from their microenvironment. Other components of native tissues, such as glycosaminoglycans like hyaluronic acid, can affect cell behavior in part by changing the mechanical properties of the collagen gel. Prior studies have quantified the effects of hyaluronic acid on the mechanical properties of collagen gels in experiments of uniform shear or compression at the macroscale. However, there remains a lack of experimental studies of how hyaluronic acid changes the mechanical properties of collagen gels at the scale of a cell. Here, we studied how addition of hyaluronic acid to gels of collagen fibers affects the local field of displacements in response to contractile loads applied on length scales similar to those of a contracting cell. Using spherical poly(N-isopropylacrylamide) particles, which contract when heated, we induced displacement in gels of collagen and collagen with hyaluronic acid. Displacement fields were quantified using a combination of confocal microscopy and digital image correlation. Results showed that hyaluronic acid suppressed the distance over which displacements propagated, suggesting that it caused the network to become more linear. Additionally, hyaluronic acid had no statistical effect on heterogeneity of the displacement fields, but it did make the gels more elastic by substantially reducing the magnitude of permanent deformations. Lastly, we examined the effect of hyaluronic acid on fiber remodeling due to localized forces and found that hyaluronic acid partially—but not fully—inhibited remodeling. This result is consistent with prior studies suggesting that fiber remodeling is associated with a phase transition resulting from an instability caused by nonlinearity of the collagen gel.

Introduction

In biological tissues, the extracellular matrix (ECM) is a composite composed of proteins having fibrous structure with glycosaminoglycans filling the intrafibrillar space [1]. Cells sense and respond to properties of the surrounding ECM, which motivates experimental testing of how changes in ECM structure or composition affect cell response. With collagen I being the most abundant type of protein found in the ECM [1, 2], gels made of collagen fibers are a common model system to investigate cell-matrix interactions and to design scaffolds for tissue engineering. Essential for these applications is an understanding of the mechanics of these collagen gels. It is now well established that gels of fibrous proteins are nonlinear, exhibiting strain stiffening and compression softening [3–8]. Due to the random structure of the fibers, these materials are also heterogeneous, with spatial variation in both stiffness [9–12] and displacements [13–16]. Upon removing an applied load, permanent deformations remain [15, 17–22].

Many prior studies focused on the mechanics of gels made of fibers of a single protein, but cells sense and respond to cues from multiple constituents within the ECM. Hyaluronic acid (HA), for example, affects cell signaling related to proliferation, migration, and matrix remodeling [23], and its concentration is altered in disease, such as an increase in concentration occurring in the tumor microenvironment [24, 25]. There is also interest in using composite gels of collagen and HA as scaffolds for tissue engineering [23, 26, 27]. As an interstitial component between the collagen fibers, HA also can affect the mechanical properties of the collagen gel. At the scale of the bulk gel, addition of uncrosslinked HA has a relatively small effect on the small strain shear modulus, with some reports indicating an increase and others indicating a decrease in modulus [28–30]. Crosslinking of HA, however, produces a clear increase in the modulus of the composite gel [31, 32]. Interestingly, it is possible for such composite gels to exhibit synergistic effects, wherein the modulus of the composite gel is larger than the sum of the moduli of its two constituents [32, 33].

The prior experiments studying the mechanics of composite gels of HA and collagen have focused on the macroscopic scale of the bulk material, but cells sense their surroundings and produce displacements over length scales comparable to the size of the fibers. At these scales and under these magnitudes of deformation, the mechanics of fibrous materials are highly nonlinear [34–37] and heterogeneous [9–16] with notable permanent deformations [15, 17, 19, 21, 22]. Although some models have studied how adding an interstitial material like HA to a network of fibers affects the mechanics at the scale of a cell [38–40], experimental data testing model predictions are limited and have focused on qualitative observations of cell response [40], rather than on quantitative mechanical measurements.

Here, we study the mechanics of composite gels made of HA and fibrous collagen I using experiments that produce large displacements at length scales similar to those of a contracting cell. The experimental method uses spherical particles made of an active hydrogel, poly(N-isopropylacrylamide) (PNIPAAm), which contract when heated, mimicking cell-induced displacements of the extracellular matrix [37]. Our experiments quantified the full field of displacements surrounding each contracting particle, which enabled us to quantify how different concentrations of HA affected nonlinearity, heterogeneity, and permanent deformations. We also applied our method to study effects of nonlinearity and permanent deformations on mechanical remodeling of the collagen fibers due to localized forces, like those of a contracting cell.

Materials and Methods

Preparation of Gels of Collagen and Collagen-Hyaluronic Acid

Particles of PNIPAAm were created as in our prior work [37]. The average particle diameter was 80 μm. The PNIPAAm particles were treated so that they would covalently bond to the collagen fibers so as to induce displacements in the collagen gel upon contraction. To create the covalent bonding, PNIPAAm particles were treated with sulfo-SANPAH (1 mg/mL, Proteochem) and exposed to ultraviolet light for 10 min. After exposure, the treated particles were washed with 0.05 M HEPES and 1 × phosphate-buffered saline (PBS). The particles were embedded in gels of collagen or collagen with HA. All gels (both collagen only and collagen with HA) had the same final collagen concentration of 2.5 mg/mL. The collagen used was rat tail collagen I (Corning, Inc.), mixed at a 4:1 ratio with collagen I labeled fluorescently by AlexaFluor 488, as in our prior studies [15, 37]. For gels with HA, the HA (Glycosil, Advanced BioMatrix) was mixed with the collagen according to manufacturer instructions to final concentrations of 1.5, 3, or 5 mg/mL of HA. Next, the SANPAH-treated PNIPAAm particles were added to the collagen and collagen–HA mixtures. To crosslink the HA, Polyethylene Glycol Diacrylate (PEGDA, Advanced BioMatrix) in 1 × PBS was added such that the ratio of HA to PEGDA was equal to 4:1. The collagen and collagen–HA gels were polymerized at 26°C for 1.5 hr. After polymerization, 1× PBS was added to the samples to prevent dehydration.

Microscopy

Images of PNIPAAm particles in gels of collagen and collagen–HA were collected using a spinning disk confocal microscope with a Yokogawa CSU-X1 scanner on a Nikon Ti-E base using an Andor Zyla sCMOS camera, and Andor IQ3 software. The objectives used were a 20× with numerical aperture of 0.75 and 10 × with numerical aperture of 0.45. Image stacks were collected with a step size of 0.5 μm.

Temperature Control

To induce contraction of the PNIPAAm particles we controlled temperature by using a H301 stage top incubator with a UNO controller (Okolab). The temperature was changed from 26°C to 34°C to 38°C and back to 26°C. To verify the temperature of the system was equilibrated prior to imaging, we used a digital thermometer (Fisherbrand Traceable) with its probe placed in a dish filled with water within the incubator.

Image Correlation, Analysis of Displacement Fields, and Analysis of Fluorescent Intensity

Displacement fields of the collagen fibers were measured by applying Fast Iterative Digital Image Correlation [41] to the images of fluorescently labeled collagen as described previously [15, 16, 37, 42]. For experiments with no PNIPAAm particles or single particles, the correlation was applied to 20× images and used subsets of size 64 × 64 pix (20.8 × 20.8 μm) and spacing 16 pix (5.2 μm); for experiments with pairs of particles, the correlation was applied to 10× images and used subsets of size 96 × 96 pix (62.4 × 62.4 μm) and spacing 24 pix (15.6 μm). The image correlation sometimes produced erroneous displacements at locations of poor image contrast; these locations were identified based on the magnitude of the gradient of the displacement, and they were excluded from the analysis as described in our prior study [15].

To analyze the displacement field $\overrightarrow{u}$, the radial component of displacement u_r was fit to the function u_r = Ar⁻ⁿ, where r was the radial distance from the center of the contracting particle and A and n were fitting parameters with n quantifying the rate of decay of displacements over distance [15, 16, 36, 37, 42, 43]. Heterogeneous displacements ${\overrightarrow{u}}^{\prime }$ were defined as the deviation from average behavior and calculated using the equation used in our previous work [15], ${\overrightarrow{u}}^{\prime }=\overrightarrow{u}-{\overrightarrow{u}}_f$, where $\overrightarrow{u}$ was the experimentally measured full displacement field and ${\overrightarrow{u}}_f=u_f{\widehat{e}}_r$ with uf defined as u_f = Ar⁻ⁿ with A and n being the fitting parameters defined above and ${\widehat{e}}_r$ being the unit vector in the outward radial direction. We also calculated the permanent displacement field ${\overrightarrow{u}}_p$, which was defined as the displacement that remained upon restoring the temperature to the initial 26°C, hence removing the applied loading.

Strains were computed by taking the numerical gradient of the displacement field. As numerical differentiation amplifies noise, the data were first smoothed with a 3 × 3 averaging filter. The gradient was then taken by convolution with the optimal 5-tap kernel reported by [44], and the principal strains were computed.

In one set of experiments, we quantified the intensity of the images of fluorescently labeled collagen near to the contracting particles as an indicator of the local fiber density. Intensity was quantified in a region of interest shaped like a dumbbell surrounding a pair of particles. The boundary of the region of interest was composed of two circles, one surrounding each particle with radius equal to 1.4 times the encircled particle’s radius, along with an ellipse with major axis connecting the two PNIPAAm particles and minor axis length equal to the average diameter of the two particles. Regions inside the particles were excluded. The average intensity in the region of interest was computed and normalized by the average intensity in a corner of the image far from any particles. Representative images of the dumbbell-shaped region of interest and the corner regions used for normalization are shown in Fig. A.1 (Appendix).

Effects of Temperature Change on Bulk Properties

To determine whether the use of temperature change to induce contraction of the PNIPAAm particles had an effect on the bulk properties of the gels, two tests were performed. Firstly, the small strain shear modulus of collagen gels (2.5 mg/mL) was measured at different temperatures in a commercial rheometer (Kinexus Ultra+, Malvern Panalytical). A conical upper geometry having a diameter of 40 mm and angle of 4° was used. The gels were polymerized between the rheometer’s flat bottom plate and the conical upper geometry at 25°C for 90 min. Shear strains were induced by twisting the gel about its axis. The maximum shear strain applied was 0.5% to remain in the linear regime of deformation. We ensured quasi-static loading by keeping the maximum strain rate below 0.05% /s. The angular acceleration was kept below 1.17 × 10⁻⁵ rad/s² to ensure that inertial loads would be negligible. Shear modulus was calculated by fitting a line to the data of torque versus angle and applying the standard equation for torsion. The shear modulus of the gel was measured first at 25°C, then at 39°C, and finally after returning to the initial temperature of 25°C, which is a range slightly larger than used for other experiments in this study. Between each temperature change, we waited for at least 30 min for temperature equilibration. Results from two separate gels (Fig. A.2a, Appendix) showed no clear effects of the temperature change on the shear modulus of the gels.

Secondly, as HA has been observed to deswell (i.e., contract) in response to a temperature increase in the range used here [45, 46], we performed control experiments in gels of 2.5 mg/mL collagen and 5 mg/mL HA (the maximum concentration used in this study) and no contracting PNIPAAm particles. After imaging the fibers at 26°C and 38°C, we computed displacements and strains as described above. Representative results showed displacements were typically < 1 μm and strains were typically < 1% (Fig. A.2b–c, Appendix). As an indicator for deswelling, we computed the trace of the in-plane strain tensor, which was equal to −0.49%, −0.24%, and 1.34% in three independent experiments. As these displacements and strains were small compared to those produced by contracting PNIPAAm particles, swelling or deswelling of the HA likely had minimal effects on the results. These findings are consistent with our prior study showing no consistent effects of the temperature change on displacement fields in gels of collagen only [37].

Statistical Analysis

Statistical comparisons were made using one-way analysis of variance (ANOVA). As the experiments were interested in comparing how different concentrations of HA affected the mechanics of the collagen gel, comparisons were made to control gels of collagen only, for which Dunnett’s test was used to correct for multiple comparisons. The symbols * and *** are used to indicate statistical differences with p < 0.05 and p < 0.001, respectively, in comparison to collagen-only control gels.

Results and Discussion

Displacement Fields due to Localized Loading in Gels of Collagen with Hyaluronic Acid

We began by preparing gels of pure collagen and composite gels of collagen with different concentrations of HA. All experiments used a collagen concentration of 2.5 mg/mL, and for gels with HA, the concentration of HA ranged from 1.5 to 5 mg/mL. Representative images of pure collagen and collagen with 5 mg/mL HA are shown in Fig. 1. As shown by the figure, the addition of HA did not appear to change the collagen fiber length or width, although sometimes the addition of HA created pores in the fiber network with diameters of tens of μm. Such pores have been observed in prior studies and are thought to be caused by HA molecules restricting collagen fiber entanglements [47–50].

Figure 1:

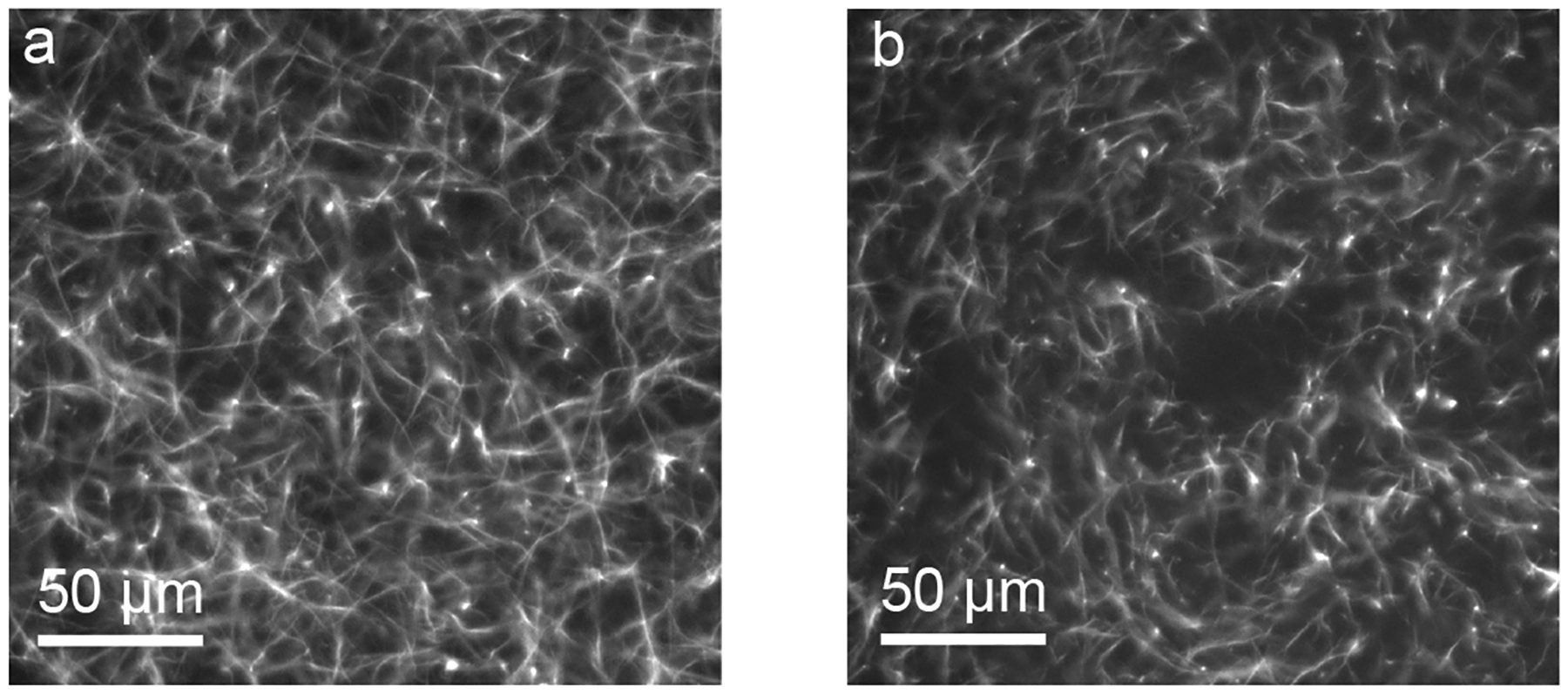
Images of gels of (a) 2.5 mg/mL collagen and (b) 2.5 mg/mL collagen with 5 mg/mL HA.

Next, we fully embedded particles made of PNIPAAm into the gels, enabling us to produce localized, well-controlled forces upon changing the temperature. Images of the collagen fibers surrounding the particles showed that the collagen fibers had similar structure to gels with no particles (Fig. 2a, b). Digital image correlation was then used to compute the full field of displacements surrounding each particle. As described in our prior work [15], the image correlation sometimes computed erroneous displacements at locations having low fiber density or contrast. Hence, we filtered out those locations (described in Methods) to exclude them from the analysis and plotted the filtered locations with white spots. Representative displacement fields showed predominantly inward displacement, consistent with the contractile boundary condition applied by the particles, though there was also heterogeneity over space (Fig. 2c, d).

Figure 2:

Displacement fields induced by contracting PNIPAAm particles. (a, b) Representative images of a PNIPAAm particle (center) within a gel of pure collagen (a) or collagen with 5 mg/mL HA (b). (c, d) Corresponding full-field displacements induced by the particles in pure collagen (c) and collagen with 5 mg/mL HA (d). Colors indicate magnitude of displacement; arrows indicate direction.

Propagation of Displacements over Distance

We next analyzed the displacement fields in further detail, beginning with the prior experimental observation that displacements in fibrous networks propagate over a long range [34–37, 51], longer than predicted by classical linear elasticity [36, 37]. Experiments and models have shown that this long range of displacement propagation results from the fact that the fiber network has a far smaller stiffness in compression as compared to tension [36, 37, 43, 52, 53], and some recent models have predicted that addition of HA would reduce the range of displacement propagation [39, 40]. To test these model predictions, we studied the decay of displacements over distance. Qualitative inspection of the displacement fields appears to show that for gels of collagen and HA, the displacements decayed to zero (dark blue) over a shorter distance than for gels of pure collagen (Fig. 2c, d). To quantify this observation, we fit the radial component of displacement to the function u_r = Ar⁻ⁿ along lines drawn in different directions outward from the center of each contracting particle [36, 37, 42], and we focused on the decay rate n, which would be equal to 2 in a linear elastic medium and < 2 in a medium in which displacements propagate over a long range [36, 37]. The decay rate n was plotted for the different paths in representative gels of pure collagen and collagen with 5 mg/mL HA with color corresponding to the value of n (Fig. 3a, b). The colors in the plots are notably different, with typical values of n in pure collagen close to 1 and typical values of n in gels of collagen and HA typically close to 2 with some paths having n > 2. As a second visualization of the results, the radial component of displacements was plotted against radial distance from the center of the particle on logarithmic axes with inward displacement being defined as positive. The slope of the data set corresponding to pure collagen (Fig. 3c) was typically less steep than that corresponding to collagen with 5 mg/mL HA (Fig. 3d), also suggesting a longer range of displacements in gels of pure collagen.

Figure 3:

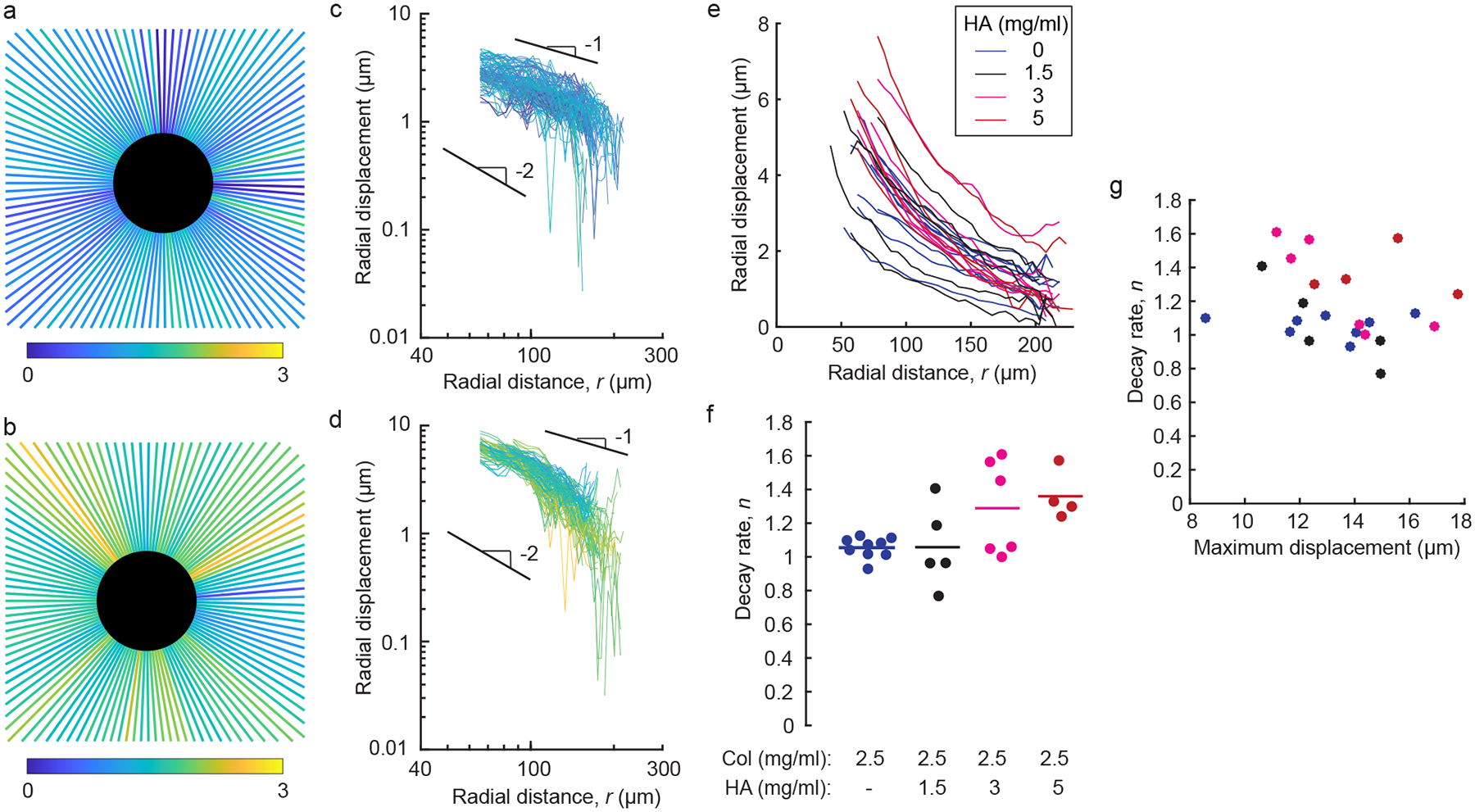
Decay of displacements over distance in gels of collagen and collagen–HA. (a, b) For the data set shown in Fig. 2, radial paths were drawn outward from the center of each contracting particle, and radial displacements were fit to u_r = Ar⁻ⁿr. Decay rates n are shown for each path (colors) in gels of pure collagen (a) and collagen with 5 mg/mL HA (b). (c, d) Inward radial component of displacement plotted on logarithmic axes against radial distance r from the center of the particles in pure collagen (c) and collagen with 5 mg/mL HA (d). In these plots, positive indicates contractile (inward) displacement. Each line corresponds to a path shown in panels a and b. Lines with slopes of 1 and 2 are shown for reference. (e) Average of inward radial displacement plotted against radial position r for contracting particles in gels of collagen (2.5 mg/ml) with varying concentrations of HA. Each line corresponds to a different particle. (f) Decay rate n in gels of pure collagen and collagen with different concentrations of HA. Each dot represents a different particle; horizontal lines indicate means over all dots in each group. (g) Decay rate n plotted against maximum displacement produced by each particle in gels of pure collagen (blue), collagen with 1.5 mg/mL HA (black), collagen with 3 mg/mL HA (magenta), and collagen with 5 mg/mL HA (red). Correlation coefficient: −0.20.

These experiments were repeated for numerous particles in gels having different concentrations of HA. We first plotted the radial component of displacement against radial distance for all particles (Fig. 3e) and then computed the average value of n for each particle. In gels of pure collagen, the mean value of decay rate n was 1.06, which is a similar value to prior results [37] and smaller than the classical linear elastic solution of 2, indicating long range propagation of displacements over space. For the collagen–HA gels, the means of the decay rate n were 1.06, 1.29, and 1.36 for HA concentrations of 1.5, 3, and 5 mg/mL, respectively, and the data set corresponding to 5 mg/mL HA was statistically larger than the data set corresponding to pure collagen (Fig. 3f). Hence, although the addition of small concentrations of HA had no effect on the decay rate n, higher concentrations caused displacements to decay over space at a statistically faster rate as compared to pure collagen.

The differences in n are caused by a tension-compression nonlinearity that is more severe under larger magnitudes of deformation [43]. Contracting particles having larger initial diameter produce larger displacements in the collagen network and, hence, smaller values of n [37]. This effect of particle size on n brings up the possibility that the differences observed in Fig. 3f were caused by systematic differences in particle size between experiments. To rule out this possibility, we manually measured the change in each particle’s radius, which was equal to the maximum displacement induced by that particle. A plot of the decay rate n against the maximum displacement (Fig. 3g) showed a modest correlation, with a correlation coefficient of −0.20, suggesting that the magnitude of displacement affected the value of n here as well, but only to a small extent. Importantly, there was no statistical difference in maximum displacement between particles in gels having different concentrations of collagen (p = 0.24, ANOVA), indicating that particle size did not cause the trends observed in Fig. 3f. Hence, the alternative explanation that trends in Fig. 3f were caused by systematic differences in particle size can be ruled out, which strengthens the conclusion that addition of HA decreases the distances over which displacements propagate.

As described above, a decay rate n smaller than 2 is caused by nonlinearity, namely a difference in stiffness in tension as compared to compression. The nonlinearity was initially attributed to strain stiffening, associated with fibers under tension aligning and, hence, stiffening [54, 55], but it was also shown that strain stiffening alone was unable to fully explain the long range of displacement propagation [35]. Another explanation comes from the fact that fibers under compression buckle [18, 37, 56], meaning the fiber network has a small stiffness in compression as compared to tension. Subsequent experiments and models have shown that softening in compression strongly increases the distance over which displacements propagate [36, 37, 43, 52], and, given that a loss in stiffness due to buckling is a severe nonlinearity, it is reasonable to conclude that compression softening is the primary cause of decay rates n smaller than 2. With this in mind, our observation that addition of HA reduced the range of displacement propagation suggests that the HA may have reduced the amount of fiber buckling present. To describe the underlying mechanism, we turn to a prior study, which showed that addition of HA causes swelling of the gel, which creates a state of tensile stress in the collagen fibers [57]. Hence the HA puts the fibers under a state of pretension, which would suppress buckling and make the composite gel more linear. While it is important to note that our experimental methodology cannot quantify the pretension directly, meaning that it is possible that the temperature change used to induce contraction of the PNPIAAm particles also affected the magnitude of pretension, our data, nevertheless, indicate a slower decay of displacements over distance caused by the HA, which would suggest suppression of buckling and, hence, notable pretension at all temperatures used in this study. These findings are also consistent with a recent mechanics model for HA-collagen composite gels, which also observed a state of pretension in the collagen fibers and predicted an associated reduction of the distance over which displacements decay [40]. Our data give the first quantitative verification of this model prediction, and, together with the prior studies [40, 57], indicate that addition of HA adds pretension to the network of collagen fibers, thereby suppressing fiber buckling, and decreasing the range over which displacements propagate.

Heterogeneity of Displacement Fields

The random structure of the fibers causes displacements at local length scales within fibrous materials to be highly heterogeneous, deviating from average behavior and fluctuating over space [13–15, 51]. Randomness in fiber structure can be observed qualitatively in Figs. 1 and 2a, b with the resulting heterogeneity of displacements appearing in Fig. 2c, d. An initial quantification of the heterogeneity can be achieved by considering that the decay rate n depends on direction outward from the center of the contracting particle. The data in Fig. 3a, b had coefficients of variation (ratio of standard deviation to mean) of 0.32 and 0.28 for, respectively, pure collagen and collagen with 5 mg/mL HA, indicating that in the representative experiments, the decay rate varied by approximately 30%.

Motivated by these initial observations, we quantified the heterogeneous displacement ${\overrightarrow{u}}^{\prime }$, which quantifies the deviation from average behavior and is defined in the Methods section. Representative maps of ${\overrightarrow{u}}^{\prime }$ are shown for gels of pure collagen and collagen with 5 mg/mL HA (Fig. 4a, b). In both cases the heterogeneous displacements were large, with the maximum magnitude ${\overrightarrow{u}}^{\prime }$ being ≈2 and ≈3 μm (for pure collagen and collagen with HA, respectively), which is of the same order as the maximum magnitudes of displacement in the same gels (namely, 5 and 10 μm, Fig. 2c, d).

Figure 4:

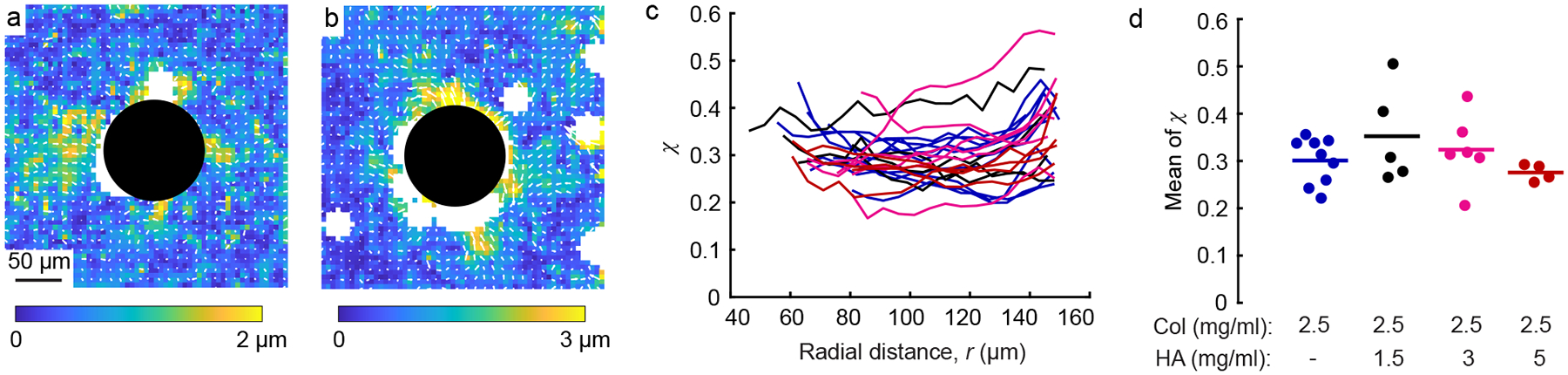
Heterogeneity of displacement fields. (a, b) Images showing representative heterogeneous displacements ${\overrightarrow{u}}^{\prime }$ induced by the same contracting particles as in Fig. 2 in gels of pure collagen (a) and collagen with 5 mg/mL HA (b). (c) Dimensionless heterogeneous displacement $\chi =\left|{\overrightarrow{u}}^{\prime }\right|/|\overrightarrow{u}|$ averaged circumferentially around each contracting particle plotted against radial distance, r. line represents χ for a different particle in gels of pure collagen (blue), collagen with 1.5 mg/mL HA (black), collagen with 3 mg/mL HA (magenta), and collagen with 5 mg/mL HA (red). (d) Mean of each line shown in panel c. Each dot represents a different particle; horizontal lines indicate means over all dots in each group. Heterogeneity χ was not statistically different between the different groups (p = 0.18, ANOVA).

To account for the fact that ${\overrightarrow{u}}^{\prime }$ would be expected to be proportional to the magnitude of displacement, we normalize ${\overrightarrow{u}}^{\prime }$ by the magnitude of displacement to compute a dimensionless heterogeneity, χ, for the displacement field produced by each contracting particle [15, 43]. We then calculated the average of χ over angle and plotted it over radial distance from the center of the particle (Fig. 4c). Data are plotted for all the gels tested, including pure collagen and collagen with 1.5, 3, and 5 mg/mL HA. Typical values of χ were in the range of 0.2 to 0.4, which is similar to our prior study [15]. As no clear dependence on radial distance was observed in Fig. 4c, we then computed the mean of χ for all radial positions (Fig. 4d). Average values of χ across all contracting particles were 0.30, 0.35, 0.32, and 0.28 for gels of pure collagen and gels with 1.5, 3, and 5 mg/mL HA, respectively. The data were not statistically different, indicating no effect of HA on heterogeneity in the displacement field.

The observation of no effect of HA on heterogeneity is at first surprising, given that the pore size of the HA is ≈17 nm (as reported by the manufacturer), meaning that the HA is essentially a homogeneous continuum on the length scale of our experiments. One would expect that adding a homogeneous continuum to the network of collagen fibers would reduce local variations in stiffness, and, since variations in stiffness cause heterogeneities in the displacement field [58], it would be expected that adding HA would reduce heterogeneity. Indeed, such an expectation is confirmed by a model of a composite of fibers connected to a continuous neo-Hookean matrix, which showed reduced heterogeneity caused by the continuous matrix [38]. This apparent conflict would be resolved if forces were supported and transmitted primarily by the fibers and not the HA. Such a case would occur if the modulus of the HA were far smaller than that of the collagen network, but the HA has a small strain shear modulus of ≈150 Pa (reported by the manufacturer) and gels of only collagen (2.5 mg/mL) have small strain shear moduli in the range of 100–200 Pa [59, 60].For an alternative explanation, we reason that the apparent modulus of the collagen fiber network may have been far greater in the presence of HA, which could occur as a result of the fact that swelling of the HA puts the collagen fibers in a state of pretension [57]. Applying uniaxial pretension to a collagen network dramatically increases its shear modulus, by more than an order of magnitude [7, 8]. Hence, the addition of HA would be expected to greatly stiffen the fiber network within the composite gel, which is consistent with experiments and modeling in composite gels showing a large increase in modulus caused by swelling of HA [32, 40]. In summary, the picture that results is that addition of HA to a gel of collagen causes swelling [57], which puts the fibers under a state of pretension, in turn leading to dramatic stiffening, wherein the effective modulus of the fiber network is far larger than that of a gel of only collagen [7, 8, 32, 40]. Therefore, in both the collagen-only gels and the composite gels, forces are supported primarily by the fibers, whose random structure causes highly heterogeneous displacement fields (Fig. 4).

Permanent Displacements

Next, we studied permanent displacements that remained after allowing the contracting particles to recover to their initial size. Previous studies have observed permanent displacements caused by various types of loading in fibrous gels [15, 17–22], but the effects of HA on permanent displacements at local length scales have not yet been quantified. Our experimental procedure began with an image of each particle at its initial reference state (26°C), followed by imaging at a contracted state (38°C) and subsequent imaging at the recovered state (26°C). We verified previously that after this increase and decrease in temperature, the particles fully recovered to their initial size [37]. The permanent displacements ${\overrightarrow{u}}_p$, defined as the displacements that remained after returning the temperature back to the initial 26°C, were computed by applying digital image correlation to the images corresponding to the reference and recovered states. Representative images showing the permanent displacement field ${\overrightarrow{u}}_p$ in pure collagen and collagen with 5 mg/mL HA (Fig. 5a, b) show similar distributions with the largest ${\overrightarrow{u}}_p$ located near the contracting particle, which follows from the fact that the displacement field in the contracted state was largest near the particle. Importantly, the magnitude of ${\overrightarrow{u}}_p$ was notably different, being a factor of approximately 3 smaller in collagen with HA as compared to pure collagen.

Figure 5:

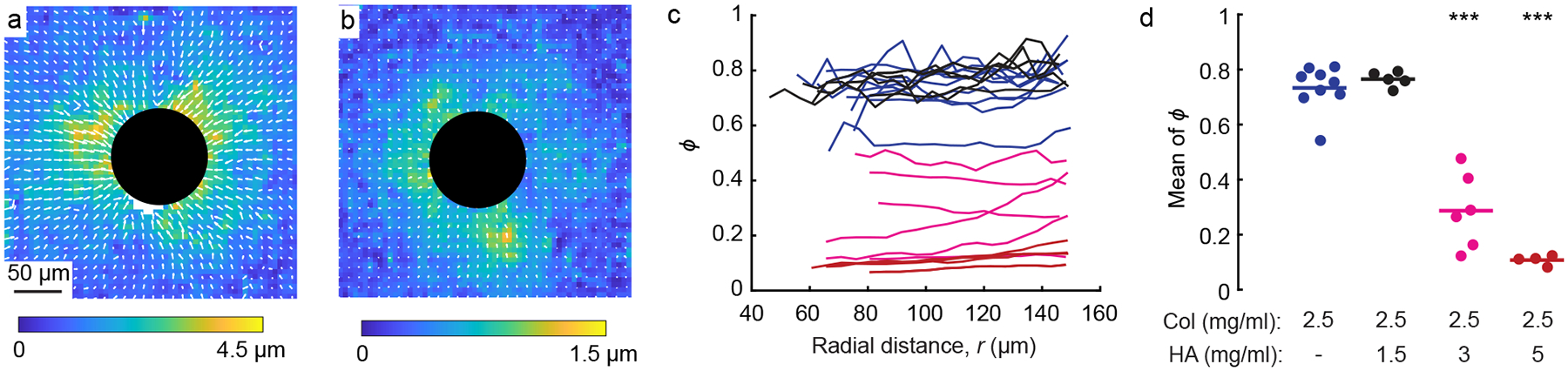
Permanent displacements. (a, b) Images showing representative fields of permanent displacements ${\overrightarrow{u}}_p$ induced by the same contracting particles as in Fig. 2 in gels of pure collagen (a) and collagen with 5 mg/mL HA (b). (c) Dimensionless permanent displacement $\varphi =\left|{\overrightarrow{u}}_p\right|/\left|\overrightarrow{u}\right|$ averaged circumferentially around each contracting particle plotted against radial distance, r. Each line represents ϕ for a different particle in gels of pure collagen (blue), collagen with 1.5 mg/mL HA (black), collagen with 3 mg/mL HA (magenta), and collagen with 5 mg/mL HA (red). (d) Mean of each line shown in panel c. Each dot represents a different particle; horizontal lines indicate means over all dots in each group.

As with the heterogeneous displacements, it would be expected that the magnitude of permanent displacements ${\overrightarrow{u}}_p$ would depend on the magnitude of displacement in the contracted state. Therefore, we normalized ${\overrightarrow{u}}_p$ by the displacement in the contracted state. The normalized permanent displacement, $\varphi =\left|{\overrightarrow{u}}_p\right|/|\overrightarrow{u}|$, was averaged in the circumferential direction and plotted against distance from the center of each particle (Fig. 5c). Gels of pure collagen or with 1.5 mg/mL HA had large permanent displacements, with values of ϕ typically in the range of 70–80%. By contrast, gels of collagen with 3 or 5 mg/mL HA had strikingly lower normalized permanent displacement ϕ, with the greatest concentration of HA causing ϕ to be only ≈10%. As there was no observed dependence of ϕ on radial position, we averaged ϕ over space for each particle. The means of the averaged values of ϕ for pure collagen and collagen with 1.5 mg/mL HA were 0.73 and 0.77, whereas for collagen gels with 3 and 5 mg/mL HA, they were far lower, 0.29 and 0.11, respectively, indicating that the higher concentration of HA dramatically reduced the permanent deformations.

These findings on effects of HA on permanent deformations are relevant for cell biology. The ability and the degree to which cells can permanently deform the surrounding ECM has implications for important cellular processes, such as migration and mechanotransduction, and also for maintaining tissue homeostasis or promoting disease progression. At the cellular level, migrating cancer cells deform the matrix as they migrate, and under these circumstances, permanent deformations can increase migration speed and efficiency as less energy is put into deforming the cell or its surroundings, meaning more energy is directed into motion [61–63]. In pathological conditions, permanent deformations are a step in a positive feedback loop that promotes further remodeling of the ECM that is supportive of collective cell invasion [64]. Therefore, preventing permanent deformations through the deposition of glycoaminoglycans like HA may play a role in building resiliency in the ECM.

Mechanical Remodeling of Fiber Structure and Density

With our observation that HA affects nonlinearity and permanent deformations of collagen gels, we next applied these findings to study mechanical remodeling of the fibers due to localized forces. We focused on the observation that localized forces applied to fiber networks can cause the fibers to align and compact into dense band-like structures [17, 36, 65–70]. Such bands can have important biological effects, as cells migrate along the aligned fibers [68, 71, 72].

Recent studies have proposed two different mechanisms that could cause these bands. The first is permanent deformations, wherein new crosslinks are formed between fibers and cause permanent deformations that remain after loads are removed [20, 21]. The second mechanism is nonlinearity, specifically the tension-compression nonlinearity associated with compression softening due to fiber buckling. Such compression softening is well-known in foams, and it creates a non-monotonic relationship between stress and strain at the scale of the foam’s microstructure, which in turn causes an instability leading to highly densified phases of bands to form when foams are compressed [73]. Uniaxial compression causes densification in fibrous materials as well [74, 75], and recently Grekas et al. developed a continuum model to predict the densification phase transition in more complicated, general stress states, such as would be produced by mechanical interactions between contracting cells [22]. The model demonstrated that densified bands of fibers can result from the phase transition caused by compression softening, with no need for permanent deformations. Hence, there are two proposed mechanisms for fiber densification and band formation—the first suggests permanent deformations are essential, and the second suggests they are not. As the presence of HA affects both nonlinearity and permanent deformations of collagen gels, we reasoned that it may be possible to use HA to give insight into the roles of these two proposed mechanisms on band formation.

We designed experiments with pairs of contracting particles in gels of pure collagen (Fig. 6a) and collagen with 5 mg/mL HA (Fig. 6b). Upon an increase in temperature, the particles contracted, producing two notable changes in the fiber structure. The first was large densification and alignment occurring between the two particles (Fig. 6a, b), similar to the bands of fibers that occur between contracting cells [17, 36, 65–70]. The second was local regions of densified fibers proceeding outward from the boundary of a particle, which were referred to as “hairs” in a prior study [22]. Although bands and hairs were more profound in the gel of pure collagen, they were still evident in the gel containing both collagen and HA. Decreasing the temperature back to 26°C allowed the particles to recover to their initial size. In the recovered state in the gel of only collagen, bands remained (Fig. 6a), consistent with prior observations [22]. By contrast, in gels of collagen and HA, the image in the recovered state appeared nearly identical to the reference state (Fig. 6b), suggesting no permanent deformation, consistent with the effects of HA shown in Fig. 5.

Figure 6:

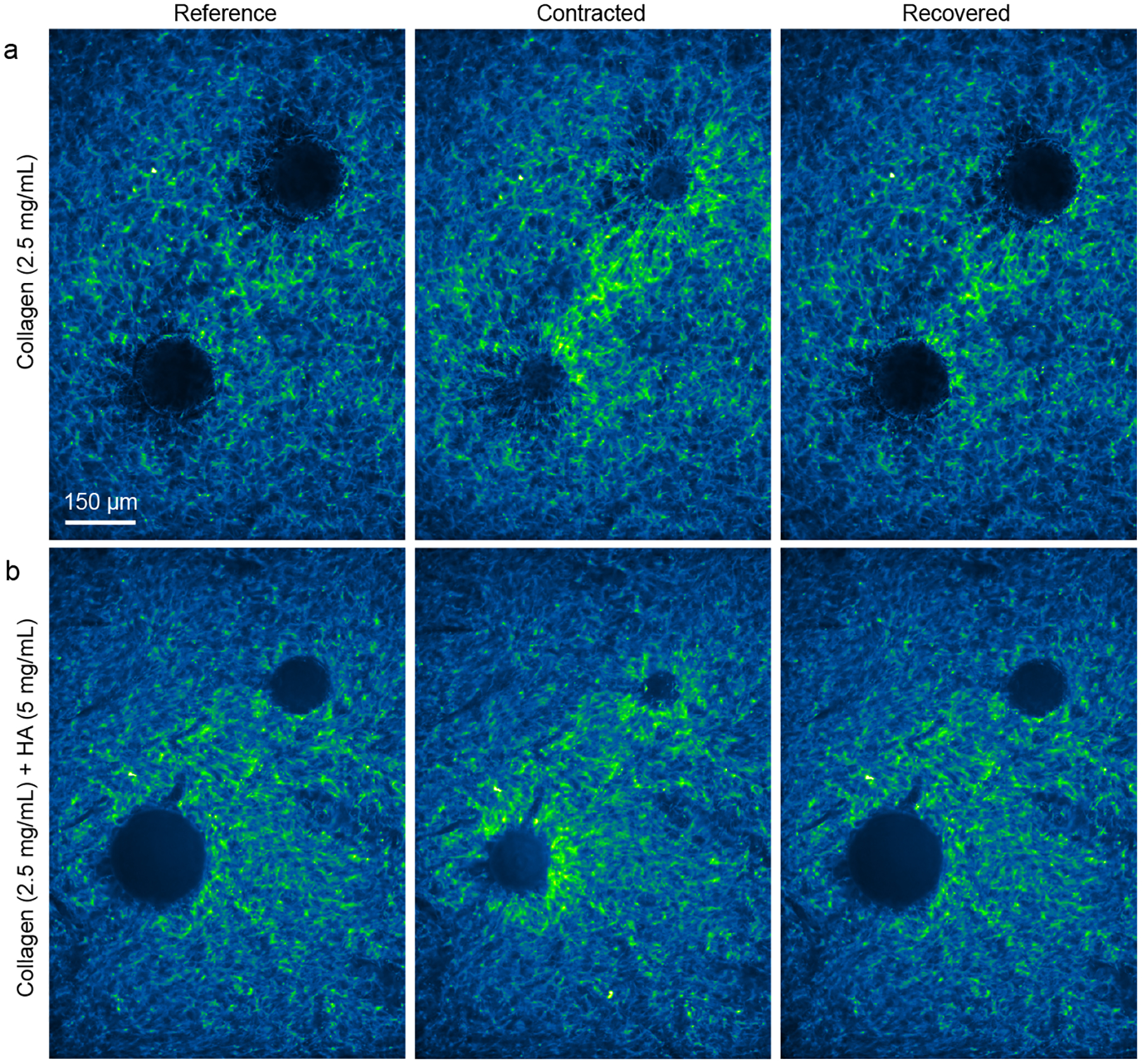
Fiber alignment and densification near pairs of contracting particles. (a, b) Images from representative experiments with pairs of contracting particles in gels of 2.5 mg/mL collagen (a) and 2.5 mg/mL collagen with 5 mg/mL HA (b). The images labeled “Reference” were collected at 26°C; “Contracted” were collected at 38°C; and “Recovered” were collected upon returning the temperature to 26°C. Images are pseudocolored such that green shows locations of greater fluorescent intensity, and, hence, densification of collagen fibers.

To quantify these observations, we computed displacements with digital image correlation, comparing the images of the contracted and recovered states to the reference state. Next we computed the displacement gradient, enabling us to compute the two in-plane principal strains, ε₁ and ε₂. Although the strain data exhibited some noise, the data clearly showed that ε₁ was typically positive indicating extension, whereas ε₂ was typically negative, indicating contraction (Fig. 7a–d). The magnitudes of principal strains were largest between the two particles, with the first principal strains oriented on the axis connecting the particles and the second oriented perpendicular to that axis. Between the contracting particles, the magnitude of ε₂ was typically notably larger than that of ε₁, often by a factor > 4. Given that ε₂ was negative, the sum of the principal strains was also negative, indicating local densification of fibers occurring between the two contracting particles. Consistent with the qualitative observations in Fig. 6, the sum of principal strains was negative for gels of both collagen and collagen with HA (Fig. 7a,b), indicating densification and band formation in both cases. Upon recovery, strains of magnitude as large as 10% remained in the gels of pure collagen, but strains were an approximately an order of magnitude smaller in gels of collagen with HA (Fig. 7c,d), consistent with the qualitative observations in Fig. 6 and the factor of 10 reduction in permanent displacements due to HA observed in Fig. 5.

Figure 7:

Strains and densification near pairs of contracting particles. (a–d) Principal strains ε₁ and ε₂ induced by pairs of particles in gels of 2.5 mg/mL collagen and 2.5 mg/mL collagen with 5 mg/mL HA in the contracted and recovered states. Black lines indicate the orientation of principal strains at locations where the magnitude of principal strain is large (exceeding the 75th percentile). These data correspond to the same particles shown in Fig. 6. Note the factor of 10 difference in color bar in panel d. (e, f) The average fluorescent intensity was quantified in a dumbbell-shaped region of interest surrounding each pair of particles and normalized by the average fluorescent intensity in a region having no particles and nominally random fiber organization. The normalized intensity is shown for three pairs of particles in gels of 2.5 mg/mL collagen (e) and 2.5 mg/mL collagen with 5 mg/mL HA (f). Each color in panels e and f represents image intensity near a different pair of particles; data points in black correspond to the particles shown in Fig. 6.

To verify these observations were consistent for multiple particles, we repeated these experiments with three pairs of particles in each type of gel. Given that the strain data exhibited some noise, we used a different indicator for densification, namely the average fluorescent intensity as in prior studies [19, 70]. To quantify densification near the edges of each particle and between each pair of contracting particles, we quantified the average fluorescent intensity in a dumbbell-shaped region surrounding the particles, and normalized the intensity by the average intensity in a corner of each image having no particles (see the Methods section and Fig. A.1, Appendix). For particles in collagen, contraction increased the average intensity by a factor of ≈2 (Fig. 7e). When the particles were allowed to recover to their initial size, the fluorescent intensity decreased, but to a value that was ≈50% greater than the initial value (Fig. 7e), indicating permanent deformations. Consistent with the images in Fig. 6b, particle contraction also increased the fluorescent intensity in gels of collagen with HA, though to a lesser extent than gels of only collagen, ≈50% (Fig. 7f). For collagen–HA gels in the recovered state, the fluorescent intensities were approximately equal to the starting values (Fig. 7f), again indicating no permanent deformations.

As gels of collagen with HA exhibited no permanent deformations, yet densified bands of fibers still occurred, there must exist a mechanism other than permanent deformations that contributes to band formation. Given the prior modeling that demonstrated how an instability caused by compression weakening can cause band formation [22], it is logical to suspect that the instability associated with compression weakening has a major effect on fiber densification and band formation. In the gels of collagen only, permanent deformations were present, suggesting the instability caused by compression weakening and permanent deformations can occur concurrently. This observation is consistent with the model by Grekas et al. [22], which accounted for this possibility by including a term in the model that produced permanent deformations. In the model of Grekas et al., inclusion of permanent deformations changed the energy landscape, and allowed dense bands to remain after removing the applied load, similar to the recovered state in Figs. 6a, 7c, and 7e. Importantly, the model of Grekas et al. showed that with or without permanent deformations, the dense bands formed as a result of a phase transition. Hence, informed by Grekas et al. and our new experimental data (Figs. 6 and 7), we conclude that the mechanism for band formation is a phase transition associated with a compression weakening instability.

Conclusions

Our objective was to quantify the effect of HA on local displacement fields in gels of fibrous collagen in response to localized loading. We designed experiments using contracting particles that generate localized displacements mimicking the displacements induced by contracting cells. We found that the addition of HA in sufficiently high concentrations caused the displacements to decay at a faster rate over distance, closer to what would be predicted by linear elasticity, indicating a gel that was more linear with less compression softening. The heterogeneity of displacements was not affected by the addition of HA. These two observations can be explained by prior studies that have shown that HA causes swelling of the gel, which puts the fibers under a state of pretension [40, 57]. The state of pretension would both suppress buckling and make the fiber network stiffer. Next, experiments that measured displacements upon removing the applied loading, showed that addition of HA almost completely suppressed permanent displacements. By applying these findings to study fiber remodeling due to localized forces, we found that HA partially—but not fully—inhibited fiber densification and alignment between pairs of contracting particles. Given that HA suppressed permanent displacements, these findings are evidence that there must be another mechanism for force-induced fiber densification and alignment, which is consistent with a recent theoretical model that treated densification and alignment as a phase transition resulting from an instability caused by compression softening [22]. We expect these findings to stimulate future research on how other glycosaminoglycans affect mechanical properties of collagen networks and to be useful for prediction and experimental design in studies of cell-matrix interactions.

Appendix

The appendix contains Fig. A.1, describing methods used for analyzing the image intensity for Fig. 7e–f, and Fig. A.2, showing analyses of effects of the temperature change on properties of gels of 2.5 mg/mL collagen and 2.5 mg/mL collagen with 5 mg/mL HA.

Figure A.1:

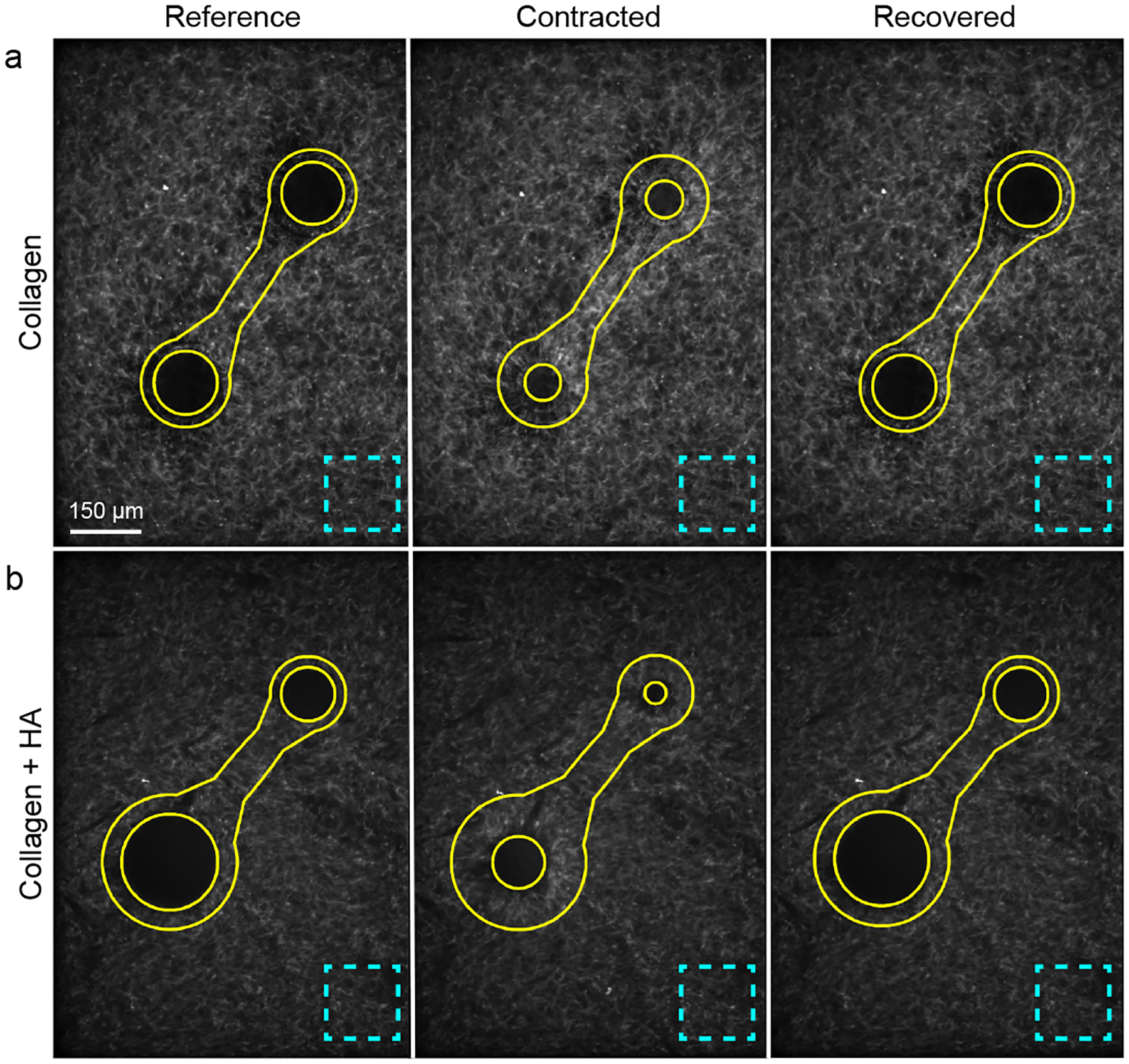
Regions of interest used to compute changes in image intensity as an indicator of fiber densification. (a, b) Representative images are shown for particles in gels of 2.5 mg/mL collagen (a) and 2.5 mg/mL collagen with 5 mg/mL HA (b) in the reference, contracted, and recovered states. Solid lines show the dumbbell-shaped regions used to compute average fluorescent intensity; dashed lines show regions in the corner of the image used to normalize the average fluorescent intensity.

Figure A.2:

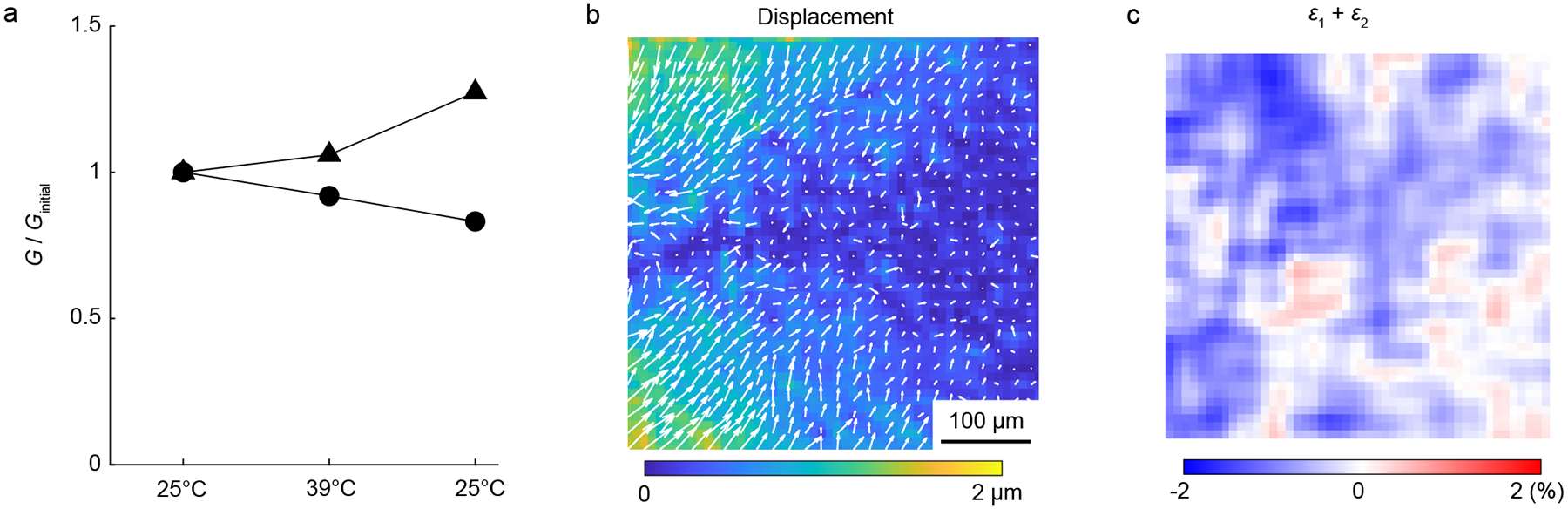
Effects of temperature change. (a) Shear modulus G of two 2.5 mg/mL collagen gels, which were tested at 25°C, 39°C, and then again at 25°C. The data were normalized by the value measured at the initial temperature G_initial. No consistent trend is apparent, meaning the temperature change was unlikely to affect the experimental results. (b, c) Magnitude of displacement (b) and trace of in-plane strain tensor (ε₁ + ε₂, c) in a representative gel of 2.5 mg/mL collagen with 5 mg/mL HA and no contracting particles, computed by correlating images collected at 38°C to those collected at 25°C. Although the trace of the strain tensor was on average negative in this field of view (−0.49%), other independent experiments gave values of −0.24% and 1.34%, indicating no consistent effects of temperature change on swelling or deswelling of the collagen–HA gels.