The impact factors of the risk index and diffusive dynamics of a SIS free boundary model

Abstract

To discuss the impact factors on the spread of infectious diseases, we study a free boundary problem describing a SIS (susceptible-infected-susceptible) model in a heterogeneous environment. Firstly, the existence and uniqueness of the global solution are given. Then the basic reproduction number related to time is defined, and a spreading-vanishing dichotomy of infectious diseases is obtained. The impacts of the diffusion rate of infected individuals, expanding capability, and the scope and scale of initial infection on the spreading and vanishing of infectious disease are analyzed. Numerical simulations are given to show that the large expanding capability is unfavorable to the prevention and control of the disease.

1. Introduction

Infectious diseases are still the major causes of suffering and death in developing countries and developed countries (Hethcote, 2000), and usually have a significant impact on population size and historical events (McNeill, 1976). For example, the West Nile virus caused an encephalitis outbreak in New York City in 1999 (Center for Disease Control and Prevention (CDC), 1999). According to the latest real-time statistics from the World Health Organization (WHO), COVID-19, as of May 2022, has infected more than 516 million individuals, and at least 6.2 million people have died worldwide. However, it is impracticable to study the spreading of infectious diseases by experiments. To understand the spread and control of infectious diseases, mathematical models as an important tool have been attracting much attention (Abdelrazec, Belair, Shan, & Zhu, 2016; Hethcote, 2000; Keeling & Rohani, 2008; Martcheva, 2015; Thomas & Urena, 2001).

To discuss the impact of spatial heterogeneity of environment and movement of individuals on infectious diseases, an SIS epidemic reaction-diffusion system was proposed by Allen et al. in (Allen, Bolker, Lou, & Nevai, 2008), and the giving system is

$$\left\{\begin{array}{ll}{S}_t-d_S\mathrm{\Delta }S=-\frac{\beta (x)SI}{S+I}+\gamma (x)I,& x\in \mathrm{\Omega },t>0,\\ I_t-d_I\mathrm{\Delta }I=\frac{\beta (x)SI}{S+I}-\gamma (x)I,& x\in \mathrm{\Omega },t>0,\\ \frac{\partial S}{\partial \eta }=\frac{\partial I}{\partial \eta }=0,& x\in \partial \mathrm{\Omega },t>0,\end{array}\right)$$ (1.1)

where S(x, t) and I(x, t) denote the density of susceptible and infected individuals at location x and time t, respectively. The positive constants d_S and d_I account for the diffusion rates of susceptible and infected individuals, the positive bounded H$\ddot{o}$lder continuous functions β(x) and γ(x) can be interpreted as rates of disease transmission and recovery for x ∈ Ω, respectively.

The authors in (Allen et al., 2008) characterized the risk of the region by the basic reproduction number ${\mathcal{R}}_0$. The DFE (disease-free equilibrium) is always unstable and there exists a unique EE (endemic equilibrium) in the high-risk domain $({\mathcal{R}}_0>1)$, and the DFE is stable if and only if infected individuals have mobility above a threshold value for the low-risk domain $({\mathcal{R}}_0<1)$. In addition, letting N = S + I, adding two equations in (1.1) and then integrating over Ω conclude that for t > 0, $\frac{\partial }{\partial t}{\int }_{\mathrm{\Omega }}(S+I)dx=0$, which implies that the total population size remains unchanged. More work on system (1.1) with constant total population size can be found in the literature (Cui & Lou, 2016; Peng, 2009; Peng & Liu, 2009; Peng & Zhao, 2012).

Considering changeable total population size, Li, Peng and Wang (Li, Peng, & Wang, 2017) studied the following SIS epidemic with a linear external source

$$\left\{\begin{array}{ll}{S}_t-d_S\mathrm{\Delta }S=\mathrm{\Lambda }(x)-S-\frac{\beta (x)SI}{S+I}+\gamma (x)I,& x\in \mathrm{\Omega },t>0,\\ I_t-d_I\mathrm{\Delta }I=\frac{\beta (x)SI}{S+I}-\gamma (x)I,& x\in \mathrm{\Omega },t>0,\\ \frac{\partial S}{\partial \nu }=\frac{\partial I}{\partial \nu }=0,& x\in \partial \mathrm{\Omega },t>0,\\ S(x,0)=S_0(x),I(x,0)=I_0(x),& x\in \mathrm{\Omega },\end{array}\right)$$ (1.2)

where d_S, d_I, β, γ, S and I have the same epidemiological interpretations as in (1.1). The linear function Λ − S represents the external source (or supply) for the susceptible population, for more explanation, please refer to literature (Gao & Ruan, 2011; Hethcote, 2000). The authors in (Li et al., 2017) mainly discussed the global stability of the unique endemic equilibrium when spatial environment is homogeneous, and the asymptotic profile of endemic equilibria if the diffusion rate of the susceptible or infected population is small or large.

Previous studies have focused on SIS epidemic models in a fixed domain. In the real world, the change of biological habitat is caused by the movement of species, which can be described mathematically by free boundary. In fact, the free boundary is widely used in many fields; for example, a single population model with a free boundary for invasive species was proposed by Du and Lin in (Du & Lin, 2010), which was extended to the competition model in (Cao, Li, Wang, & zhao, 2021; Du, Wang, & Zhou, 2017; Du & Lin, 2014; Wang & Zhao, 2014), the predator-prey model in (Lin, 2007; Takhirov & Norov, 2019; Wang & Zhao, 2017; Yousefnezhad, Mohammadi, & Bozorgnia, 2018), and a mutualistic model with advection in (Li & Lin, 2015). In recent years, a free boundary has also been introduced into epidemic models. For example, an SIR epidemic model with free boundary was discussed in (Huang & Wang, 2015; Kim, Lin, & Zhang, 2013; Zhu, Guo, & Lin, 2017), and a SIRS model with free boundary was considered in (Cao et al., 2017a). Ge et al. in (Ge, Kim, Lin, & Zhu, 2015) studied a simplified SIS model with advection and free boundary and gave the spreading speeds when spreading happens; a diffusion-advection simplified SIS epidemic model in a heterogeneous time-periodic environment was studied in (Ge, Lei, & Lin, 2017); a SIS reaction-diffusion model with free boundary and mass action mechanism was discussed in (Wang & Guo, 2019); recently an SIS epidemic reaction-diffusion model with mass-action incidence incorporating spontaneous infection in a spatially heterogeneous environment was examined (Tong, Ahn, & Lin, 2021); a SIS model risk-induced dispersal of infected individuals has been studied (Choi, Lin, & Ahn, 2022); the spreading or vanishing of an SIS epidemic model with free boundary and nonlocal incidence rate was analyzed in (Cao et al., 2017b; Huang & Wang, 2019).

Based on above discussion, in this paper, we will consider the following SIS reaction-diffusion problem

$$\left\{\begin{array}{ll}{S}_t-d\mathrm{\Delta }S=\mathrm{\Lambda }(x)-S-\frac{\beta (x)SI}{S+I}+\gamma (x)I,& x\in \mathbb{R},t>0,\\ I_t-d\mathrm{\Delta }I=\frac{\beta (x)SI}{S+I}-\gamma (x)I,& x\in (g(t),h(t)),t>0,\\ I(x,t)=0,& x\in \mathbb{R}/(g(t),h(t)),t>0,\\ g^{\prime }(t)=-\mu I_x(g(t),t),g(0)=-h_0,& t\ge 0,\\ h^{\prime }(t)=-\mu I_x(h(t),t),h(0)=h_0,& t\ge 0,\\ S(x,0)=S_0(x),I(x,0)=I_0(x),& x\in \mathbb{R},\end{array}\right)$$ (1.3)

where the interval (g(t), h(t)) is unknown and will be given with (S, I). g′(t) = −μI_x(g(t), t) (or h′(t) = −μI_x(h(t), t)) is a special case of the well-known Stefan condition, which has been established in (Lin, 2007). Biologically, this system implies that outside of the free boundaries, there is no infectious, only susceptible individuals. The interval (g(t), h(t)), which depends on time t, is the habitat for the infectious individuals. Moreover, we suppose that initial functions S₀ and I₀ satisfy

$$\left\{\begin{array}{l}{S}_0(x)\in C^2(\mathbb{R})\bigcap L^{\infty }(\mathbb{R})\text{and}{S}_0(x)>c_0\text{for}x\in \mathbb{R},\text{where}{c}_0\text{is a positive constant},\\ I_0(x)\in C^2([-h_0,h_0]),I_0(x)>0\text{for}x\in (-h_0,h_0),\\ I_0(x)=0\text{for}x\in \mathbb{R}/[-h_0,h_0].\end{array}\right)$$ (1.4)

Further, we assume that

$$(H)\underset{x\to \pm \infty }{\lim }\beta (x)={\beta }_{\pm \infty },\underset{x\to \pm \infty }{\lim }\gamma (x)={\gamma }_{\pm \infty }\mathrm{a}\mathrm{n}\mathrm{d}{\beta }_{\pm \infty }>{\gamma }_{\pm \infty },$$

which implies that the contact rate (β) and the recovery rate (γ) are similar at the faraway places, and the faraway is high-risk.

It is worth mentioning that in the fixed domain, the authors in (Li et al., 2017) primarily discussed the asymptotic profile of endemic equilibria when the diffusion rate is small or large. However, we discuss how the diffusion coefficient affects the spreading and vanishing of disease described mathematically by the free boundary problem in this paper.

The organization of this article is as below. The existence and uniqueness of the global solution are obtained in Section 2. Section 3 is devoted to the definition and properties of the basic reproduction number. Section 4 establishes a spreading-vanishing dichotomy for problem (1.3). Some sufficient conditions for the disease to spread or vanish are given in Section 5. Finally, we explain our theoretical results by numerical simulations.

2. Global existence and uniqueness

At first, we discuss the existence and uniqueness of the local solution of problem (1.3), and then we show that the solution is global by suitable estimates.

Theorem 2.1

For any given initial value (S₀, I₀) satisfying (1.4), and any ν ∈ (0, 1), there exists a T > 0 such that problem (1.3) admits a unique solution (S, I; g, h) satisfying

$$S\in C^{1+\nu ,\frac{1+\nu }{2}}(\mathbb{R}\times [0,T]),I\in C^{1+\nu ,\frac{1+\nu }{2}}([g(t),h(t)]\times [0,T]),$$ (2.1)

and

$$(g(t),h(t))\in C^{1+\frac{\nu }{2}}([0,T])\times C^{1+\frac{\nu }{2}}([0,T]).$$ (2.2)

Furthermore,

$$\Vert S{\Vert }_{C^{1+\nu ,\frac{1+\nu }{2}}(\mathbb{R}\times [0,T])}+\Vert I{\Vert }_{C^{1+\nu ,\frac{1+\nu }{2}}([g(t),h(t)]\times [0,T])}+\Vert g{\Vert }_{C^{1+\frac{\nu }{2}}([0,T])}+\Vert h{\Vert }_{C^{1+\frac{\nu }{2}}([0,T])}\le C,$$ (2.3)

where C and T only depend on $h_0,\nu ,\mu ,\Vert S_0{\Vert }_{C^2(\mathbb{R})}$, $\Vert S_0{\Vert }_{L^{\infty }(\mathbb{R})}$ and $\Vert I_0{\Vert }_{C^2([-h_0,h_0])}$.

Proof: Applying similar methods as in (Cao et al., 2017b; Chen & Friedman, 2000; Du & Lin, 2010), for system (1.3), we first straighten the free boundaries. Let ξ be a function in C³([0, ∞)) satisfying

$$\xi (y)=1\text{if}|y-h_0|<\frac{h_0}{8},\xi (y)=0\mathrm{i}\mathrm{f}|y-h_0|>\frac{h_0}{2},|{\xi }^{\prime }(y)|<\frac{5}{h_0}\text{for all}y.$$

Consider the transformation (y, t) → (x, t) such that

$$x=y+\xi (y)(h(t)-h_0)+\xi (-y)(g(t)+h_0),-\infty <y<+\infty .$$

It is obvious to know that the above transformation x → y is a diffeomorphism from (−∞, + ∞) onto (−∞, + ∞) while $|h(t)-h_0|\le \frac{h_0}{8}$ and $|g(t)+h_0|\le \frac{h_0}{8}$. Hence, it translates the left free boundary x = g(t) to the fixed line y = −h₀ and the right free boundary x = h(t) to the fixed line y = h₀. Directing calculations give

$$\frac{\partial y}{\partial x}=\frac{1}{1+{\xi }^{\prime }(y)(h(t)-h_0)-{\xi }^{\prime }(-y)(g(t)+h_0)}\triangleq A(g(t),h(t),y),$$

$$\frac{\partial y}{\partial t}=\frac{-\xi (y)h^{\prime }(t)-\xi (-y)g^{\prime }(t)}{1+{\xi }^{\prime }(y)(h(t)-h_0)-{\xi }^{\prime }(-y)(g(t)+h_0)}\triangleq B(g(t),h(t),y),$$

$$\frac{{\partial }^{2}y}{\partial x^2}=\frac{{\xi }^{\prime \prime }(y)(h(t)-h_0)+{\xi }^{\prime }(-y)(g(t)+h_0)}{{[1+{\xi }^{\prime }(y)(h(t)-h_0)-{\xi }^{\prime }(-y)(g(t)+h_0)]}^3}\triangleq C(g(t),h(t),y).$$

Let

$$S(x,t)=S(y+\xi (y)(h(t)-h_0)+\xi (-y)(g(t)+h_0),t)\triangleq u(y,t),$$

$$I(x,t)=I(y+\xi (y)(h(t)-h_0)+\xi (-y)(g(t)+h_0),t)\triangleq v(y,t),$$

$$\beta (x)=\beta (y+\xi (y)(h(t)-h_0)+\xi (-y)(g(t)+h_0))\triangleq \tilde{\beta }(y),$$

$$\gamma (x)=\beta (y+\xi (y)(h(t)-h_0)+\xi (-y)(g(t)+h_0))\triangleq \tilde{\gamma }(y),$$

$$\mathrm{\Lambda }(x)=\beta (y+\xi (y)(h(t)-h_0)+\xi (-y)(g(t)+h_0))\triangleq \tilde{\mathrm{\Lambda }}(y),$$

then the free boundary problem (1.3) can be rewritten as

$$\left\{\begin{array}{ll}{u}_t-A^{2}d\mathrm{\Delta }u-(Cd-B)u_y=\tilde{\mathrm{\Lambda }}(y)-u-\frac{\tilde{\beta }(y)uv}{u+v}+\tilde{\gamma }(y)v,& y\in \mathbb{R},t>0,\\ v_t-A^{2}d\mathrm{\Delta }v-(Cd-B)v_y=\frac{\tilde{\beta }(y)uv}{u+v}-\tilde{\gamma }(y)v,& y\in (-h_0,h_0),t>0,\\ v(y,t)=0,& y\in \mathbb{R}/(-h_0,h_0),t>0,\\ g^{\prime }(t)=-\mu v_y(-h_0,t),g(0)=-h_0,& t\ge 0,\\ h^{\prime }(t)=-\mu v_y(h_0,t),h(0)=h_0,& t\ge 0,\\ u(y,0)=u_0(y),v(x,0)=v_0(y),& y\in \mathbb{R},\end{array}\right)$$ (2.4)

where A = A(g(t), h(t), y), B = B(g(t), h(t), y) and C = C(g(t), h(t), y). The following proof first finds a suitable complete metric space, and then uses the contraction mapping theorem together with standard L^p theory and the Sobolev imbedding theorem (Ladyzenskaja, Solonnikov, & Ural’ceva, 1968) to obtain the existence and uniqueness of the solution for system (2.4). We are going to omit it here, see Theorem 2.1 in (Du & Lin, 2014) or (Li & Lin, 2015) for more details. □

Theorem 2.2

Let (S, I; g, h) be a bounded solution of problem (1.3) for t ∈ [0, T] with some T ∈ (0, + ∞), then there exist positive constants C₁ and C₂ independent of T such that

$$0<S(x,t)\le C_1\mathrm{f}\mathrm{o}\mathrm{r}x\in \mathbb{R},t\in (0,T],$$

$$0<I(x,t)\le C_1\mathrm{f}\mathrm{o}\mathrm{r}x\in (g(t),h(t)),t\in (0,T],$$

$$0<-g^{\prime }(t)\le C_2,0<h^{\prime }(t)\le C_2\mathrm{f}\mathrm{o}\mathrm{r}t\in (0,T].$$

Proof: For any bounded solution (S, I; g, h) of problem (1.3) for t ∈ [0, T], using the initial value condition together with the strong maximum principle yields

$$S(x,t)>0\mathrm{f}\mathrm{o}\mathrm{r}x\in \mathbb{R},t\in (0,T]$$

and

$$I(x,t)>0\mathrm{f}\mathrm{o}\mathrm{r}x\in (g(t),h(t)),t\in (0,T].$$

Applying the Hopf's boundary lemma to the equation of I gives that

$$I_x(g(t),t)>0,I_x(h(t),t)<0\mathrm{f}\mathrm{o}\mathrm{r}t\in (0,T].$$

Therefore g′(t) < 0 and h′(t) > 0 for t ∈ (0, T] by the free boundary condition.

Let N = S + (1 + ϵ₀)I with $1-{ϵ}_0\underset{x\in \mathbb{R}}{\sup }\beta (x)>0$, direct computation yields

$$\begin{array}{cc}{N}_t-d\mathrm{\Delta }N& =\mathrm{\Lambda }(x)-S+{ϵ}_0\beta (x)\frac{SI}{S+I}-{ϵ}_0\gamma (x)I\\ & \le \mathrm{\Lambda }(x)-S+{ϵ}_0\underset{x\in \mathbb{R}}{\sup }\beta (x)S-{ϵ}_0\underset{x\in \mathbb{R}}{\inf }\gamma (x)I\\ & =\mathrm{\Lambda }(x)-(1-{ϵ}_0\underset{x\in \mathbb{R}}{\sup }\beta (x))S-\frac{{ϵ}_0\underset{x\in \mathbb{R}}{\inf }\gamma (x)}{1+{ϵ}_0}(1+{ϵ}_0)I\\ & \le \mathrm{\Lambda }(x)-mN,\end{array}$$

where $m=\min \{1-{ϵ}_0\underset{x\in \mathbb{R}}{\sup }\beta (x),\frac{{ϵ}_0}{1+{ϵ}_0}\underset{x\in \mathbb{R}}{\inf }\gamma (x)\}$.

Recalling that I_x(h(t)⁻, t) < 0 = I_x(h(t)⁺, t) and I_x(g(t)⁻, t) = 0 < I_x(g(t)⁺, t) for 0 < t ≤ T, we have

$$\left\{\begin{array}{ll}{N}_t-d\mathrm{\Delta }N\le \mathrm{\Lambda }(x)-mN,& x\in \mathbb{R},x\ne \{g(t),h(t)\},0<t\le T,\\ N(x,0)=N_0(x)≔S_0(x)+(1+{ϵ}_0)I_0(x),& x\in \mathbb{R}/(-h_0,h_0),\\ N_x(h{(t)}^{-},t)<N_x(h{(t)}^{+},t),& 0<t\le T,\\ N_x(g{(t)}^{-},t)<N_x(g{(t)}^{+},t),& 0<t\le T.\end{array}\right)$$ (2.5)

Consider the following auxiliary problem

$$\left\{\begin{array}{ll}{N}_t^{\ast }={\mathrm{\Lambda }}^{\ast }-m{N}^{\ast },& 0<t\le T,\\ N^{\ast }(0)=\Vert N_0(x){\Vert }_{L^{\infty }(\mathbb{R})},\end{array}\right)$$ (2.6)

where ${\mathrm{\Lambda }}^{\ast }=\underset{x\in \mathbb{R}}{\sup }\mathrm{\Lambda }(x)$. For l > max{h(T), − g(T)}, taking $W_l(x,t)=N^{\ast }-N+\frac{k}{l^2}(x^2+2dt)$ for x ∈ [ − l, l] and t ∈ [0, T], $k=\underset{(x,t)\in (\mathbb{R}\times [0,T])}{\sup }N(x,t)$, which satisfies

$W_{lt}-d\mathrm{\Delta }{W}_l\ge ({\mathrm{\Lambda }}^{\ast }-\mathrm{\Lambda })-m(N^{\ast }-N).$

We claim that

$$W_l(x,t)\ge 0,(x,t)\in [-l,l]\times [0,T].$$ (2.7)

Otherwise, we suppose that $\underset{(x,t)\in (-l,l)\times [0,T]}{\min }{W}_l(x,t)<0$, there exists a point (x₀, t₀) ∈ [ − l, l] × [0, T] so that min W_l = W_l(x₀, t₀) < 0. Due to $N^{\ast }(0)=\Vert N_0{\Vert }_{L^{\infty }(\mathbb{R})}\ge N_0(x)>0$, we know that t₀ ≠ 0. Moreover, W_l(±l, t) > 0 for t ∈ [0, T], so x₀ ≠ ± l. Therefore we have (x₀, t₀) ∈ (−l, l) × (0, T]. If (x₀, t₀) ∈ (−l, l) × (0, T] with x₀ ≠ g(t₀) and x₀ ≠ h(t₀), we have

$$W_{lt}(x_0,t_0)\le 0,-d\mathrm{\Delta }{W}_l(x_0,t_0)\le 0,$$

which is a contradiction with (Λ∗ − Λ) − m(N∗ − N) > 0.

Assume that x₀ = g(t₀) or h(t₀), without loss of generality, we suppose that x₀ = g(t₀). Due to I > 0 in (g(t₀), h(t₀)), and I = 0 in $\mathbb{R}/(g(t_0),h(t_0))$, we derive

$$W_{lx}(g{(t)}^{-},t)\le 0,W_{lx}(g{(t)}^{+},t)\ge 0,$$

that is

$$W_{lx}(g{(t)}^{+},t)\ge W_{lx}(g{(t)}^{-},t),$$

which immediately gives

$$N_x(g{(t)}^{+},t)\le N_x(g{(t)}^{-},t),$$

it is a contradiction by N_x(g(t)⁺, t) > N_x(g(t)⁻, t). Hence, (2.7) holds. Let l → +∞, we have

$$N^{\ast }\ge N\mathrm{i}\mathrm{n}\mathbb{R}\times [0,T].$$

Therefore

$$S(x,t)\le N(x,t)\le N^{\ast }(t)\le \max \left\{\frac{{\mathrm{\Lambda }}^{\ast }}{m},\Vert N_0{\Vert }_{L^{\infty }(\mathbb{R})}\right\}\triangleq C_1\mathrm{f}\mathrm{o}\mathrm{r}x\in \mathbb{R},t\in [0,T],$$

it follows from I(x, t) ≤ N(x, t) that I(x, t) ≤ C₁ for x ∈ (g(t), h(t)) and t ∈ [0, T].

Finally, we show that − g′(t) ≤ C₂ and h′(t) ≤ C₂ for t ∈ (0, T]. The proof is analogous to that of Lemma 2.2 in (Du & Lin, 2010) with C₂ = 2MμC₁ and

$$M=\max \left\{\sqrt{\frac{{\sup }_{x\in \mathbb{R}}\beta (x)}{2d}},\frac{4\Vert I_0{\Vert }_{C^1([-h_0,h_0])}}{3C_1}\right\}.$$

So we omit it here. □

Theorem 2.3

System (1.3) admits a unique solution (S, I; g, h) for all t ∈ (0, + ∞).

Proof: Combining all estimates in Theorem 2.2 with the standard continuous extension method, we can prove that the unique solution (S, I; g, h) of system (1.3) exists for all t ∈ (0, + ∞). The proof is similar to Theorem 2.4 in (Cao et al., 2017b) or Theorem 2.3 in (Du & Lin, 2010), we omit it here. □

3. The basic reproduction number

In general, the basic reproduction number can be used to describe the dynamics of the temporal and spatial spread of the disease. We firstly discuss the basic reproduction number and its properties for the following problem

$$\left\{\begin{array}{ll}{I}_t-d\mathrm{\Delta }I=\beta (x)I-\gamma (x)I,& x\in \mathrm{\Omega },t>0,\\ I(x,t)=0,& x\in \partial \mathrm{\Omega },t>0,\end{array}\right)$$ (3.1)

which is given by linearizing the corresponding system of (1.3) in a bounded domain Ω at the disease-free equilibrium.

It is well-known (Allen et al., 2008; Ge et al., 2015) that the basic reproduction number $R_0^D$ for (3.1) is given by the variational formula

$$R_0^D=R_0^D(\mathrm{\Omega },d)={\sup }_{\phi \in H_0^1(\mathrm{\Omega }),\phi \ne 0}\left\{\frac{{\int }_{\mathrm{\Omega }}\beta (x){\phi }^{2}dx}{{\int }_{\mathrm{\Omega }}(d|\nabla \phi {|}^2+\gamma (x){\phi }^2)dx}\right\}.$$

Due to above definition of the basic reproduction number, the following result was given in (Allen et al., 2008; Ge et al., 2015) and (Huang, Han, & Liu, 2010).

Proposition 3.1

((Ge et al., 2015)) Letλ₀is the principal eigenvalue of the principle problem

$$\left\{\begin{array}{ll}-d\mathrm{\Delta }\psi =\beta (x)\psi -\gamma (x)\psi +\lambda \psi ,& x\in \mathrm{\Omega },\\ \psi =0,& x\in \partial \mathrm{\Omega },\end{array}\right)$$

then $1-R_0^D$ has the same sign as λ₀.

Proposition 3.2

((Ge et al., 2015)) The following assertions hold:

• $(i)R_0^D$is a positive and monotone decreasing function ofd;

• $(ii)R_0^D\to \underset{x\in \mathrm{\Omega }}{\max }\frac{\beta (x)}{\gamma (x)}$asd → 0;

• $(iii)R_0^D\to 0$asd → ∞;

• (iv) There exists a threshold value d∗ ∈ [0, + ∞) such that $R_0^D>1$ for d < d∗ and $R_0^D<1$ for d > d∗. If all sites in the domain are lower-risk (β(x) < γ(x) for x ∈ Ω), then $R_0^D<1$ for all d > 0;

• (v) Let B_h be a ball in ${\mathbb{R}}^n$ with the radius h. The $R_0^D(B_h)$ is strictly monotone increasing function of h, that is if h₁ < h₂, then $R_0^D(B_{h_1})<R_0^D(B_{h_2})$. Moreover, $\underset{h\to \infty }{\lim }{R}_0^D(B_h)=\frac{{\beta }_{\infty }}{{\gamma }_{\infty }}$ provided that (H) holds;

• (vi) Assume that β∗ and γ∗ are positive constants. If Ω = (−h₀, h₀), β(x) ≡ β∗ and γ(x) ≡ γ∗, then

$$R_0^D=\frac{{\beta }^{\ast }}{d{\left(\frac{\pi }{2h_0}\right)}^2+{\gamma }^{\ast }}.$$

Pay attention to the interval (g(t), h(t)) of the free boundary problem (1.3) is changing with t, so the basic reproduction number is not a constant, and it varies with time t. Now we define the basic reproduction number $R_0^F(t)$ for the free boundary problem (1.3) by

$$R_0^F(t)=R_0^D((g(t),h(t)),d)={\sup }_{\psi \in H_0^1((g(t),h(t))),\psi \ne 0}\left\{\frac{{\int }_{g(t)}^{h(t)}\beta (x){\psi }^{2}dx}{{\int }_{g(t)}^{h(t)}(d|\nabla \psi {|}^2+\gamma (x){\psi }^2)dx}\right\},$$ (3.2)

which is called the spatial-temporal risk index in (Lin & Zhu, 2017) or the spatial-temporal basic reproduction number in (Zhu, Ren, & Zhu, 2018). We can define $R_0^F(\infty )=\underset{t\to +\infty }{\lim }{R}_0^F(t)$ by the monotonicity in Theorem 3.3.

It follows from that Propositions 3.1 and 3.2, we have

Theorem 3.3

$(a)R_0^F(t)$is strictly monotone increasing function oft, in other words,$R_0^F(t_1)<R_0^F(t_2)$ift₁ < t₂;

• (b) If g(t) → g_∞ > −∞ and h(t) → h_∞ < ∞ as t → +∞, we have that $R_0^F(\infty )=R_0^D(g_{\infty },h_{\infty })$;

• (c) If h(t) − g(t) → ∞ as t → +∞, then $\underset{t\to +\infty }{\lim }{R}_0^F(t)\ge \min \{\frac{{\beta }_{-\infty }}{{\gamma }_{-\infty }},\frac{{\beta }_{+\infty }}{{\gamma }_{+\infty }}\}$ provided (H) holds.

Proof: (a) − g′(t) > 0 and h′(t) > 0 for t ∈ (0, + ∞) in Theorem 2.2 imply that − g(t) and h(t) are strictly increasing functions. It is easy to see that $R_0^F(t)$ is strictly monotone increasing function of t by (v) of Proposition 3.2.

(b) According to g_∞ > −∞ and h_∞ < ∞, we consider the problem

$$\left\{\begin{array}{ll}{\phi }_t-d\mathrm{\Delta }\phi =\beta (x)\phi -\gamma (x)\phi ,& x\in (g_{\infty },h_{\infty }),t>0,\\ \phi (x,t)=0,& x=\{g_{\infty },h_{\infty }\},t>0.\end{array}\right)$$

So the basic reproduction number $R_0^D((g_{\infty },h_{\infty }))$ for above problem is given by the variational formula

$$R_0^D((g_{\infty },h_{\infty }))={\sup }_{\phi \in H_0^1((g_{\infty },h_{\infty })),\phi \ne 0}\left\{\frac{{\int }_{g_{\infty }}^{h_{\infty }}\beta (x){\phi }^{2}dx}{{\int }_{g_{\infty }}^{h_{\infty }}(d|\nabla \phi {|}^2+\gamma (x){\phi }^2)dx}\right\}.$$

From (v) of Proposition 3.2 and monotonicity of g(t) and h(t), then $R_0^D((g(t),h(t)))\le R_0^D((g_{\infty },h_{\infty }))$ holds for any t > 0, i.e.,

$$R_0^F(t)\le R_0^D((g_{\infty },h_{\infty })).$$

It follows that

$$\underset{t\to +\infty }{\mathrm{lim\; sup}}{R}_0^F(t)\le R_0^D((g_{\infty },h_{\infty })).$$ (3.3)

On the other hand, duo to the definition of $R_0^D((g_{\infty },h_{\infty }))$, for any given ε > 0, there exists a function $\phi \in H_0^1((g_{\infty },h_{\infty }))$ such that $\Vert \phi {\Vert }_{H_0^1}\le 1$ and

$$R_0^D((g_{\infty },h_{\infty }))\le \frac{{\int }_{g_{\infty }}^{h_{\infty }}\beta (x){\phi }^{2}dx}{{\int }_{g_{\infty }}^{h_{\infty }}(d|\nabla \phi {|}^2+\gamma (x){\phi }^2)dx}+\epsilon .$$

By definition of $H_0^1((g_{\infty },h_{\infty }))$, for given ε > 0, there exists a function $\psi \in C_0^{\infty }((g_{\infty },h_{\infty }))$ such that $\Vert \psi -\phi {\Vert }_{H_0^1}<\epsilon$.

Note that

$$\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\psi =\overline{\{x\in (g_{\infty },h_{\infty })|\psi (x)\ne 0\}}⫋(g_{\infty },h_{\infty }).$$

Let h_ε = dist(suppψ, ∂(g_∞, h_∞)), which means that ψ(x) = 0 in (g_∞, g_∞ + h_ε) and (h_∞ − h_ε, h_∞). In view of g(t) → g_∞ and h(t) → h_∞ as t → +∞, there exists a large T > 0 such that for t > T,

$$g_{\infty }<g(t)<g_{\infty }+h_{\epsilon }/2<h_{\infty }-h_{\epsilon }/2<h(t)<h_{\infty }$$

and

$$\frac{{\int }_{g_{\infty }+h_{\epsilon }/2}^{h_{\infty }-h_{\epsilon }/2}\beta (x){\psi }^{2}dx}{{\int }_{g_{\infty }+h_{\epsilon }/2}^{h_{\infty }-h_{\epsilon }/2}(d|\nabla \psi {|}^2+\gamma (x){\psi }^2)dx}=\frac{\left({\int }_{g_{\infty }}^{h_{\infty }}-{\int }_{g_{\infty }}^{g_{\infty }+h_{\epsilon }/2}-{\int }_{h_{\infty }-h_{\epsilon }/2}^{h_{\infty }}\right)\beta (x){\psi }^{2}dx}{\left({\int }_{g_{\infty }}^{h_{\infty }}-{\int }_{g_{\infty }}^{g_{\infty }+h_{\epsilon }/2}-{\int }_{h_{\infty }-h_{\epsilon }/2}^{h_{\infty }}\right)(d|\nabla \psi {|}^2+\gamma (x){\psi }^2)dx}=\frac{{\int }_{g_{\infty }}^{h_{\infty }}\beta (x){\psi }^{2}dx}{{\int }_{g_{\infty }}^{h_{\infty }}(d|\nabla \psi {|}^2+\gamma (x){\psi }^2)dx}\ge \frac{{\int }_{g_{\infty }}^{h_{\infty }}\beta (x){\phi }^{2}dx-{(\underset{x\in \mathbb{R}}{\sup }\beta (x))}^{3/2}\epsilon (2+\epsilon )}{{\int }_{g_{\infty }}^{h_{\infty }}(d|\nabla \phi {|}^2+\gamma (x){\phi }^2)dx+\epsilon (2+\epsilon )({(\underset{x\in \mathbb{R}}{\sup }\gamma (x))}^{3/2}+d^{3/2})}\ge \frac{{\int }_{g_{\infty }}^{h_{\infty }}\beta (x){\phi }^{2}dx}{{\int }_{g_{\infty }}^{h_{\infty }}(d|\nabla \phi {|}^2+\gamma (x){\phi }^2)dx}-M\epsilon \ge R_0^D((g_{\infty },h_{\infty }))-(M+1)\epsilon ,$$

where positive constant M only depends on $d,\underset{x\in \mathbb{R}}{\sup }\beta$ and $\underset{x\in \mathbb{R}}{\sup }\gamma$. According to the monotonicity of g(t) and h(t) yields

$$R_0^F(t)\ge R_0^D((g_{\infty }+h_{\epsilon }/2,h_{\infty }-h_{\epsilon }/2))\ge R_0^D((g_{\infty },h_{\infty }))-(M+1)\epsilon \text{for}t>T.$$

Hence,

$$\underset{t\to \infty }{\mathrm{lim\; inf}}{R}_0^F(t)\ge R_0^D((g_{\infty },h_{\infty }))-(M+1)\epsilon .$$

In light of the arbitrariness of ε, we can obtain

$$\underset{t\to \infty }{\mathrm{lim\; inf}}{R}_0^F(t)\ge R_0^D((g_{\infty },h_{\infty })),$$ (3.4)

which together with (3.3) gives that (b) holds.

(c) Suppose that h(t) → +∞ as t → +∞. For any given ε > 0, there exists a large and positive constant l such that

$$\beta (x)>{\beta }_{+\infty }-\epsilon ,\gamma (x)<{\gamma }_{+\infty }+\epsilon$$

for x > l provided that (H) holds. Moreover, there exists T₀ > 0 such that h(t) > l for all t ≥ T₀. For each fixed t ∈ [T₀, ∞), let Φ(x) ∈ C²(g(t), h(t)) satisfy

$$\mathrm{\Phi }(x)=1\mathrm{f}\mathrm{o}\mathrm{r}x\in \left[0+\frac{3}{4},h(t)-\frac{3}{4}\right],$$

$$\mathrm{\Phi }(x)=0\mathrm{f}\mathrm{o}\mathrm{r}x\in \left[g(t),0+\frac{1}{4}\right]\cup \left[h(t)-\frac{1}{4},h(t)\right],$$

$$|{\mathrm{\Phi }}^{\prime }(x)|\le 4\mathrm{f}\mathrm{o}\mathrm{r}x\in [0,0+1]\cup [h(t)-1,h(t)].$$

Due to the definition of $R_0^F(t)$, for t ∈ [T₀, + ∞), we have

$$R_0^F(t)=\underset{\psi \in H_0^1((g(t),h(t))),\psi \ne 0}{\sup }\left\{\frac{{\int }_{g(t)}^{h(t)}\beta (x){\psi }^{2}dx}{{\int }_{g(t)}^{h(t)}(d|\nabla \psi {|}^2+\gamma (x){\psi }^2)dx}\right\}\ge \frac{{\int }_{g(t)}^{h(t)}\beta (x){\mathrm{\Phi }}^{2}dx}{{\int }_{g(t)}^{h(t)}(d|\nabla \mathrm{\Phi }{|}^2+\gamma (x){\mathrm{\Phi }}^2)dx}=\frac{{\int }_{g(t)}^0\beta {\mathrm{\Phi }}^{2}dx+{\int }_0^1\beta {\mathrm{\Phi }}^{2}dx+{\int }_1^l\beta {\mathrm{\Phi }}^{2}dx+{\int }_l^{h(t)-1}\beta {\mathrm{\Phi }}^{2}dx+{\int }_{h(t)-1}^{h(t)}\beta {\mathrm{\Phi }}^{2}dx}{\left({\int }_{g(t)}^0+{\int }_0^1+{\int }_1^l+{\int }_l^{h(t)-1}+{\int }_{h(t)-1}^{h(t)}\right)(d|\nabla \mathrm{\Phi }{|}^2+\gamma {\mathrm{\Phi }}^2)dx}=\frac{\left({\int }_0^1+{\int }_{h(t)-1}^{h(t)}\right)\beta {\mathrm{\Phi }}^{2}dx+\left({\int }_1^l+{\int }_l^{h(t)-1}\right)\beta (x)dx}{\left({\int }_0^1+{\int }_{h(t)-1}^{h(t)}\right)d|\nabla \mathrm{\Phi }{|}^{2}dx+\left({\int }_{g(t)}^l+{\int }_l^{h(t)-1}+{\int }_{h(t)-1}^{h(t)}\right)\gamma {\mathrm{\Phi }}^{2}dx}\ge \frac{\left({\int }_1^l+{\int }_l^{h(t)-1}\right)\beta (x)dx}{\left({\int }_0^1+{\int }_{h(t)-1}^{h(t)}\right)d|\nabla \mathrm{\Phi }{|}^{2}dx+\left({\int }_{g(t)}^l+{\int }_l^{h(t)-1}+{\int }_{h(t)-1}^{h(t)}\right)\gamma (x)dx}\ge \frac{(h(t)-2)({\beta }_{+\infty }-\epsilon )}{32d+(h(t)-l)({\gamma }_{+\infty }+\epsilon )+(l-g(t)){\max }_{x\in [g(t),l]}\gamma (x)}.$$

Hence

$$\underset{t\to +\infty }{\mathrm{lim\; inf}}{R}_0^F(t)\ge \underset{t\to +\infty }{\mathrm{lim\; inf}}\frac{(h(t)-2)({\beta }_{+\infty }-\epsilon )}{32d+(h(t)-l)({\gamma }_{+\infty }+\epsilon )+(l-g(t)){\max }_{x\in [g(t),l]}\gamma (x)}=\frac{{\beta }_{+\infty }-\epsilon }{{\gamma }_{+\infty }+\epsilon }.$$

In view of the arbitrariness of ε, we can obtain

$$\underset{t\to +\infty }{\lim }{R}_0^F(t)\ge \frac{{\beta }_{+\infty }}{{\gamma }_{+\infty }}.$$

If g(t) → −∞ as t → +∞, we can draw a conclusion that $\underset{t\to +\infty }{\lim }{R}_0^F(t)\ge \frac{{\beta }_{-\infty }}{{\gamma }_{-\infty }}$ from the above discussion.

Hence, $\underset{t\to +\infty }{\lim }{R}_0^F(t)\ge \min \{\frac{{\beta }_{+\infty }}{{\gamma }_{+\infty }},\frac{{\beta }_{-\infty }}{{\gamma }_{-\infty }}\}$ holds provided that (H) holds and h(t) − g(t) → +∞ as t → +∞.

□

Remark 3.1

If g(t) → −∞ or h(t) → +∞ as t → +∞, then $\underset{t\to +\infty }{\lim }{R}_0^F(t)>1$ provided that (H) holds.

4. Spreading-vanishing dichotomy

In this section, we are going to establish a spreading-vanishing dichotomy for the free boundary problem (1.3). We will prove that if the interval (g(t), h(t)) is finite in the end, then I → 0 uniformly as t → +∞. Rather, for each solution (S, I) of problem (1.3), $\underset{t\to +\infty }{\mathrm{lim\; sup}}\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}>0$ if the infected individuals spread to the whole area, that is, (g(t), h(t)) → (−∞, + ∞) as t → +∞.

From Theorem 2.2, we obtain that g′(t) < 0 and h′(t) > 0 for t ∈ (0, + ∞). Hence g(t) is monotonically decreasing and h(t) is monotonically increasing with t. So their limits exist, i.e.,

$$\underset{t\to +\infty }{\lim }g(t)=g_{\infty },\underset{t\to +\infty }{\lim }h(t)=h_{\infty },$$

where g_∞ ∈ [ − ∞, − h₀) and h_∞ ∈ (h₀, + ∞].

Theorem 4.1

If − ∞ < g_∞ < h_∞ < + ∞, then $\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$, and $\underset{t\to +\infty }{\lim }S(x,t)=S^{\ast }(x)$ locally uniformly for $x\in \mathbb{R}$, where $S^{\ast }(x)=\frac{1}{{(4d\pi )}^{1/2}}{\int }_0^{\infty }{\int }_{-\infty }^{+\infty }{t}^{-1/2}{\mathrm{e}}^{-t-\frac{|x-y{|}^2}{4dt}}\mathrm{\Lambda }(y)dydt$ satisfies

$$-d\mathrm{\Delta }{S}^{\ast }=\mathrm{\Lambda }(x)-S^{\ast },x\in \mathbb{R}.$$ (4.1)

Proof: At first, we show that $\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$. We argue indirectly, and assume that

$$\underset{t\to +\infty }{\mathrm{lim\; sup}}\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=\delta >0.$$

Then there exits a sequence {(x_k, t_k)} with t_k ∈ (0, ∞) and x_k ∈ [g(t_k), h(t_k)] such that

$$I(x_k,t_k)>\frac{\delta }{2}$$

for all $k\in \mathbb{N}$, and t_k → +∞ as k → +∞.

Due to − ∞ < g_∞ < h_∞ < + ∞, then x_k ∈ [g(t), h(t)] ⊆ [g_∞, h_∞], there exists a subsequence $\left\{\left(x_{k_i},t_{k_i}\right)\right\}$ of {(x_k, t_k)}, denoted by {(x_k, t_k)}, such that x_k → x₀ as k → +∞, where x₀ ∈ [g_∞, h_∞].

Define

$$I_k(x,t)=I(x,t+t_k),S_k(x,t)=S(x,t+t_k)$$

for x ∈ [g(t + t_k), h(t + t_k)] and t ∈ [ − t_k, + ∞). Using Theorem 2.1 and the standard parabolic regularity, there exists a subsequence $\{(S_{k_i},I_{k_i})\}$ of {(S_k, I_k)} such that

$$(S_{k_i},I_{k_i})\to (\widehat{S},\widehat{I})\mathrm{a}\mathrm{s}{k}_i\to +\infty ,$$

where $(\widehat{S},\widehat{I})$ satisfies

$$\left\{\begin{array}{ll}{S}_t-d\mathrm{\Delta }S=\mathrm{\Lambda }(x)-S-\frac{\beta (x)SI}{S+I}+\gamma (x)I,& x\in (g_{\infty },h_{\infty }),t\in (0,+\infty ),\\ I_t-d\mathrm{\Delta }I=\frac{\beta (x)SI}{S+I}-\gamma (x)I,& x\in (g_{\infty },h_{\infty }),t\in (0,+\infty ).\end{array}\right)$$

In view of $\widehat{I}(x_0,0)=\underset{k_i\to \infty }{\lim }{I}_k(x_{k_i},0)=\underset{k_i\to \infty }{\lim }I(x_{k_i},t_{k_i})\ge \frac{\delta }{2}$, then $\widehat{I}>0$ in (g_∞, h_∞) × (0, + ∞) by the maximum principle.

Note that $\widehat{I}(g_{\infty },0)=\widehat{I}(h_{\infty },0)=0$, it follows from the Hopf's boundary lemma that

$${\widehat{I}}_x(g_{\infty },0)>0,{\widehat{I}}_x(h_{\infty },0)<0.$$

Hence for all large enough k_i, we have

$$I_x(g(t_{k_i}),t_{k_i})=\frac{\partial I_{k_i}(g(t_{k_i}),0)}{\partial x}>0,I_x(h(t_{k_i}),t_{k_i})=\frac{\partial I_{k_i}(h(t_{k_i}),0)}{\partial x}<0$$

and

$$h^{\prime }(t_{k_i})=-\mu I_x(h(t_{k_i}),t_{k_i})>0,g^{\prime }(t_{k_i})=-\mu I_x(g(t_{k_i}),t_{k_i})<0.$$

On the other hand, in view of − ∞ < g_∞ < h_∞ < + ∞, we have obtain

$$\underset{t\to +\infty }{\lim }{h}^{\prime }(t)=\underset{t\to +\infty }{\lim }{g}^{\prime }(t)=0,$$

which is a contradiction. Therefore $\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$.

Since $\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$, for any ε > 0, there exists a sufficiently large T > 0 such that

$$0\le I(x,t)\le \epsilon ,(x,t)\in (-\infty ,+\infty )\times [T,+\infty ).$$ (4.2)

Now, for any given 0 < L < + ∞, in view of (4.2), we have $\underset{\_}{S}(x,t)\le S(x,t)\le \overline{S}(x,t)$ for (x, t) ∈ [ − L, L] × [T, + ∞), where $\overline{S}(x,t)$ satisfies

$$\left\{\begin{array}{ll}{\overline{S}}_t-d\mathrm{\Delta }\overline{S}=\mathrm{\Lambda }(x)-\overline{S}+\gamma (x)\epsilon ,& x\in (-L,L),t>T,\\ \overline{S}(x,T)=S(x,T),& x\in [-L,L],\end{array}\right)$$ (4.3)

and $\underset{\_}{S}(x,t)$ satisfies

$$\left\{\begin{array}{ll}{\underset{\_}{S}}_t-d\mathrm{\Delta }\underset{\_}{S}=\mathrm{\Lambda }(x)-\underset{\_}{S}-\beta (x)\epsilon ,& x\in (-L,L),t>T,\\ \underset{\_}{S}(x,T)=S(x,T),& x\in [-L,L].\end{array}\right)$$ (4.4)

It is well-known that

$$\underset{\_}{S}(x,t)\to {\underset{\_}{S}}^{\ast }(x,\epsilon )\mathrm{a}\mathrm{n}\mathrm{d}\overline{S}\to {\overline{S}}^{\ast }(x,\epsilon )\text{uniformly for}[-L,L]\mathrm{a}\mathrm{s}t\to +\infty ,$$

where ${\underset{\_}{S}}^{\ast }(x,\epsilon )$ and ${\overline{S}}^{\ast }(x,\epsilon )$ are unique positive steady state of problems (4.4) and (4.3), respectively. It is easily seen that

$${\underset{\_}{S}}^{\ast }(x,\epsilon )\to S^{\ast }(x)\mathrm{a}\mathrm{n}\mathrm{d}{\overline{S}}^{\ast }(x,\epsilon )\to S^{\ast }(x)\text{uniformly for}x\in [-L,L]\mathrm{a}\mathrm{s}\epsilon \to 0$$ (4.5)

by the standard parabolic regularity, where S∗(x) is the unique solution to problem (4.1).

Therefore, we obtain that

$${\underset{\_}{S}}^{\ast }(x,\epsilon )=\underset{t\to +\infty }{\lim }\underset{\_}{S}(x,t)\le \underset{t\to +\infty }{\mathrm{lim\; inf}}S(x,t)\le \underset{t\to +\infty }{\lim }S(x,t)\le \underset{t\to +\infty }{\mathrm{lim\; sup}}S(x,t)\le \underset{t\to +\infty }{\lim }\overline{S}(x,t)={\overline{S}}^{\ast }(x,\epsilon )$$

uniformly for x ∈ [ − L, L]. According to (4.5), we have

$$\underset{t\to +\infty }{\lim }S(x,t)=S^{\ast }(x)\text{uniformly for}x\in [-L,L].$$

The arbitrariness of L implies that

$$\underset{t\to +\infty }{\lim }S(x,t)=S^{\ast }(x)\text{uniformly in any bounded subset of}\mathbb{R}.$$

Theorem 4.2

Ifh_∞ − g_∞ = +∞, then $\underset{t\to +\infty }{\mathrm{lim\; sup}}\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}>0$.

Proof: Assume that $\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$ by contradiction. It follows from the proof of Theorem 4.1 that

$$\underset{t\to +\infty }{\lim }S(x,t)=S^{\ast }(x)\text{uniformly locally for}x\in \mathbb{R}.$$ (4.6)

Since h_∞ − g_∞ = +∞, from the Remark 3.1, there exists a large enough T∗ > 0 such that

$$R_0^F(t)=R_0^D((g(t),h(t)))>1\mathrm{f}\mathrm{o}\mathrm{r}t\ge T^{\ast }.$$

In view of (4.6), for any $0<\epsilon <\underset{x\in [g(T^{\ast }),h(T^{\ast })]}{\min }{S}^{\ast }(x)$, there exists a T∗∗ > T∗ such that

$$S(x,t)>S^{\ast }(x)-\epsilon ,x\in [g(T^{\ast }),h(T^{\ast })],t\ge T^{\ast \ast }.$$

Following, we consider the eigenvalue problem

$$\left\{\begin{array}{ll}-d\mathrm{\Delta }\psi =\beta (x)\psi -\gamma (x)\psi +\lambda \psi ,& x\in (g(T^{\ast }),h(T^{\ast })),\\ \psi (x)=0,& x=\{g(T^{\ast }),h(T^{\ast })\},\end{array}\right)$$

it has the principal eigenvalue λ₀ < 0 by Proposition 3.1 and the corresponding eigenvalue function ψ(x) with $\Vert \psi {\Vert }_{L^{\infty }((g(T^{\ast }),h(T^{\ast })))}=1$.

Obviously, I(x, t) satisfies

$$\left\{\begin{array}{ll}{I}_t-d\mathrm{\Delta }I\ge \frac{\beta (x)(S^{\ast }(x)-\epsilon )I}{S^{\ast }(x)-\epsilon +I}-\gamma (x)I,& x\in (g(T^{\ast }),h(T^{\ast })),t>T^{\ast \ast },\\ I(g(T^{\ast }),t)>0,I(h(T^{\ast }),t)>0,& t>T^{\ast \ast },\\ I(x,T^{\ast \ast })>0,& g(T^{\ast })\le x\le h(T^{\ast }).\end{array}\right)$$

We consider following auxiliary problem

$$\left\{\begin{array}{ll}{W}_t-d\mathrm{\Delta }W=\frac{\beta (x)(S^{\ast }(x)-\epsilon )W}{S^{\ast }(x)-\epsilon +W}-\gamma (x)W,& x\in (g(T^{\ast }),h(T^{\ast })),t>T^{\ast \ast },\\ W(g(T^{\ast }),t)=W(h(T^{\ast }),t)=0,& t>T^{\ast \ast },\\ W(x,T^{\ast \ast })=I(x,T^{\ast \ast }),& g(T^{\ast })\le x\le h(T^{\ast }),\end{array}\right)$$ (4.7)

and construct a suitable lower solution for problem (4.7).

Define

$$\underset{\_}{W}(x,t)=\delta \psi (x),g(T^{\ast })\le x\le h(T^{\ast }),t>T^{\ast \ast },$$

where δ > 0 is small enough such that δψ(x) ≤ I(x, T∗∗) for x ∈ [g(T∗), h(T∗)].

For t > T∗∗ and g(T∗) < x < h(T∗), direct computation yields

$${\underset{\_}{W}}_t-d\mathrm{\Delta }\underset{\_}{W}-\frac{\beta (x)(S^{\ast }(x)-\epsilon )\underset{\_}{W}}{S^{\ast }(x)-\epsilon +\underset{\_}{W}}+\gamma (x)\underset{\_}{W}=\beta (x)\delta \psi (x)-\gamma (x)\delta \psi (x)+{\lambda }_0\delta \psi (x)+\gamma (x)\delta \psi (x)-\frac{\beta (x)(S^{\ast }(x)-\epsilon )\delta \psi (x)}{S^{\ast }(x)-\epsilon +\delta \psi (x)}=\beta (x)\delta \psi (x)+{\lambda }_0\delta \psi (x)-\frac{\beta (x)(S^{\ast }(x)-\epsilon )\delta \psi (x)}{S^{\ast }(x)-\epsilon +\delta \psi (x)}=\frac{\delta \psi (x)}{S^{\ast }(x)-\epsilon +\delta \psi (x)}[\beta (x)\delta \psi (x)+{\lambda }_0(S^{\ast }(x)-\epsilon )+{\lambda }_0\delta \psi (x)]\le \frac{\delta \psi (x)}{S^{\ast }(x)-\epsilon +\delta \psi (x)}\left[-\frac{\beta (x){\lambda }_0({\min }_{x\in [g(T^{\ast }),h(T^{\ast })]}{S}^{\ast }(x)-\epsilon )}{{\max }_{x\in [g(T^{\ast }),h(T^{\ast })]}\beta (x)}+{\lambda }_0(S^{\ast }(x)-\epsilon )+{\lambda }_0\delta \psi (x)\right]<0$$

provided that $0<\delta <\frac{-{\lambda }_0({\min }_{x\in [g(T^{\ast }),h(T^{\ast })]}{S}^{\ast }(x)-\epsilon )}{{\max }_{x\in [g(T^{\ast }),h(T^{\ast })]}\beta (x)}$.

Due to the upper and lower solutions method and comparison principle, we obtain

$$I(x,t)\ge W(x,t)\ge \underset{\_}{W}(x,t)=\delta \psi (x)\mathrm{i}\mathrm{n}(g(T^{\ast }),h(T^{\ast }))\times [T^{\ast \ast },+\infty ).$$

Hence we have that $\underset{t\to +\infty }{\mathrm{lim\; inf}}I(x,t)\ge \underset{t\to +\infty }{\mathrm{lim\; inf}}W(x,t)\ge \delta \psi (0)>0$, which is a contradiction.

Next, we show that the left and right of free boundary are finite or infinite simultaneously in the case where β and γ are positive constants.

Theorem 4.3

Assume thatβandγare positive constants. Ifg_∞ > −∞ or h_∞ < + ∞, then − ∞ < g_∞ < h_∞ < + ∞.

Proof: Without loss of generality, we suppose that h_∞ < + ∞. Assume that g_∞ = −∞ by a contradiction, then it follows from Theorem 3.1 and (H) that $\frac{\beta }{\gamma }>1$ and there exists a large T₁ > 0 such that $R_0^F(T_1)>1$. So $R_0^F(t)>R_0^F(T_1)>1$ for t > T₁. In view of Proposition 3.1, we have λ₁ < 0, where λ₁ is a principal eigenvalue of the following problem

$$\left\{\begin{array}{ll}-d\mathrm{\Delta }\phi =\beta \phi -\gamma \phi +\lambda \phi ,& x\in (g(T_1),h(T_1)),\\ \phi (g(T_1))=\phi (h(T_1))=0\end{array}\right)$$

and φ₁(x) is corresponding eigenfunction. Hence, there exists a ε > 0 such that

$$\left\{\begin{array}{ll}-d\mathrm{\Delta }\psi -\epsilon {\psi }^{\prime }=\beta \psi -\gamma \psi +\lambda \psi ,& x\in (g(T_1),h(T_1)),\\ \psi (g(T_1))=\psi (h(T_1))=0\end{array}\right)$$

has principal eigenvalue ${\lambda }_1^{\epsilon }<0$ and eigenfunction ψ₁(x) > 0 with $\Vert {\psi }_1{\Vert }_{L^{\infty }(g(T_1),h(T_1))}=1$ in (g(T₁), h(T₁)). In addition,

$$S_t-d\mathrm{\Delta }S=\mathrm{\Lambda }(x)-S-\frac{\beta SI}{S+I}+\gamma I\ge \mathrm{\Lambda }(x)-S-\beta S,x\in \mathbb{R},t>0.$$

Obviously, using parabolic comparison principle we have S(x, t) ≥ S_m for $(x,t)\in \mathbb{R}\times (0,+\infty )$, where $S_m=\min \{{(\beta +1)}^{-1}{\inf }_{x\in \mathbb{R}}\mathrm{\Lambda }(x),{\inf }_{x\in \mathbb{R}}{S}_0(x)\}$.

From above result, it is easy to see that

$$I_t-d\mathrm{\Delta }I=\frac{\beta SI}{S+I}-\gamma I\ge \frac{\beta S_{m}I}{S_m+I}-\gamma I,x\in (g(T_1),h(T_1)),t>T_1.$$

And the following problem

$$\left\{\begin{array}{ll}-d\mathrm{\Delta }\omega -\epsilon {\omega }^{\prime }=\frac{\beta S_m\omega }{S_m+\omega }-\gamma \omega ,& x\in (g(T_1),h(T_1)),\\ \omega (g(T_1))=\omega (h(T_1))=0\end{array}\right)$$ (4.8)

admits a unique positive solution satisfying $0<\omega <S_m(\frac{\beta }{\gamma }-1)$ in (g(T₁), h(T₁)). Using the Hopf's boundary lemma yields ω′(g(T₁)) > 0 > ω′(h(T₁)). So ω′(x) has at least one zero point in (g(T₁), h(T₁)). Let the largest zero of ω′(x) in (g(T₁), h(T₁)) be x₀. Then

$${\omega }^{\prime }(x)<0\mathrm{i}\mathrm{n}(x_0,h(T_1)).$$

Next, we consider the following auxiliary problem

$$\left\{\begin{array}{ll}{\underset{\_}{I}}_t-d\mathrm{\Delta }\underset{\_}{I}=\frac{\beta S_m\underset{\_}{I}}{S_m+\underset{\_}{I}}-\gamma \underset{\_}{I},& x\in (g(T_1),h(T_1)),t>T_1,\\ \underset{\_}{I}(g(T_1),t)=\underset{\_}{I}(h(T_1),t)=0,& t>T_1,\\ \underset{\_}{I}(x,T_1)=I(x,T_1),& g(T_1)\le x\le h(T_1).\end{array}\right)$$ (4.9)

In order to obtain $0<{\epsilon }_1{\phi }_1(x_0)\le \underset{\_}{I}(x_0,t)$ for t ≥ T₁, we will show that ε₁φ₁(x) is a lower solution of problem (4.9) in (g(T₁), h(T₁)) × (T₁, + ∞). Direct calculation gives

$$\begin{array}{ccc}& & {\epsilon }_1{\phi }_{1t}-d{\epsilon }_1\mathrm{\Delta }{\phi }_1-\frac{\beta S_m{\epsilon }_1{\phi }_1}{S_m+{\epsilon }_1{\phi }_1}+\gamma {\epsilon }_1{\phi }_1\\ & =-d{\epsilon }_1\mathrm{\Delta }{\phi }_1-\frac{\beta S_m{\epsilon }_1{\phi }_1}{S_m+{\epsilon }_1{\phi }_1}+\gamma {\epsilon }_1{\phi }_1\\ & ={\epsilon }_1(\beta -\gamma ){\phi }_1+{\lambda }_0{\epsilon }_1{\phi }_1-\frac{\beta S_m{\epsilon }_1{\phi }_1}{S_m+{\epsilon }_1{\phi }_1}+\gamma (x){\epsilon }_1{\phi }_1\\ & ={\lambda }_0{\epsilon }_1{\phi }_1+\beta {\epsilon }_1{\phi }_1-\frac{\beta S_m{\epsilon }_1{\phi }_1}{S_m+{\epsilon }_1{\phi }_1}\\ & ={\epsilon }_1{\phi }_1\left({\lambda }_0+\beta -\frac{\beta S_m}{S_m+{\epsilon }_1{\phi }_1}\right)\\ & <0\end{array}$$

provided that ${\epsilon }_1<\frac{-{\lambda }_0{S}_m}{\beta }$. Meanwhile, ${\epsilon }_1{\phi }_1(g(T_1))=\underset{\_}{I}(g(T_1),t)=0$, ${\epsilon }_1{\phi }_1(h(T_1))=\underset{\_}{I}(h(T_1),t)=0$. If ε₁ is sufficiently small, then

$${\epsilon }_1{\phi }_1(x)\le \underset{\_}{I}(x,T_1),x\in [g(T_1),h(T_1)].$$

Hence, we can apply the comparison principle to conclude that

$${\epsilon }_1{\phi }_1(x)\le \underset{\_}{I}(x,t),x\in [g(T_1),h(T_1)],t>T_1$$

if ε₁ is sufficiently small with ${\epsilon }_1<\frac{-{\lambda }_0{S}_m}{\beta }$. Therefore,

$$0<{\epsilon }_1{\phi }_1(x_0)\le \underset{\_}{I}(x_0,t)\mathrm{f}\mathrm{o}\mathrm{r}t\ge T_1,$$

which implies that $\underset{\_}{I}(x_0,t)$ has a positive lower bound for t ≥ T₁.

Finally, based on the above results, we construct a suitable lower solution of I(x, t) in (x₀, h(t)) × (T₁, + ∞).

Set

$$Z={\epsilon }_2\omega \left(x_0+\frac{h(T_1)-x_0}{h(t)-x_0}(x-x_0)\right),x_0\le x\le h(t),t\ge T_1,$$

and calculate

$$\begin{array}{ccc}& & Z_t-d\mathrm{\Delta }Z\\ & ={\epsilon }_2{\omega }^{\prime }\left[\frac{h(T_1)-x_0}{{(h(t)-x_0)}^2}(x_0-x)h^{\prime }(t)\right]-d{\epsilon }_2\mathrm{\Delta }\omega {\left(\frac{h(T_1)-x_0}{h(t)-x_0}\right)}^2\\ & ={\epsilon }_2{\left(\frac{h(T_1)-x_0}{h(t)-x_0}\right)}^2\left[-d\mathrm{\Delta }\omega -\frac{x-x_0}{h(T_1)-x_0}{h}^{\prime }(t){\omega }^{\prime }\right].\end{array}$$

Using the fact that h′(t) → 0 and h(t) → h_∞ < + ∞ as t → +∞, we can find T₂ > T₁ such that $h^{\prime }(t)<\frac{\epsilon (h(T_1)-x_0)}{h_{\infty }-x_0}$ and then

$$Z_t-d\mathrm{\Delta }Z\le {\epsilon }_2{\left(\frac{h(T_1)-x_0}{h(t)-x_0}\right)}^2[-d\mathrm{\Delta }\omega -\epsilon {\omega }^{\prime }]$$

since that ω′ ≤ 0 and $\frac{x-x_0}{h_{\infty }-x_0}\le 1$ for (x, t) ∈ [x₀, h(t)] × [T₂, + ∞]. Since $-d\mathrm{\Delta }\omega -\epsilon {\omega }^{\prime }=\frac{\beta S_m\omega }{S_m+\omega }-\gamma \omega \ge 0$ and $\frac{h(T_1)-x_0}{h(t)-x_0}\le 1$, we have

$$Z_t-d\mathrm{\Delta }Z\le {\epsilon }_2\left[\frac{\beta S_m\omega }{S_m+\omega }-\gamma \omega \right]\le \frac{\beta S_{m}Z}{S_m+Z}-\gamma Z$$

for (x, t) ∈ [x₀, h(t)] × [T₂, + ∞].

In addition, we choose ε₂ small such that ε₂ω(x₀) ≤ ε₁φ₁(x₀) and

$${\epsilon }_2\omega \left(x_0+\frac{h(T_1)-x_0}{h(T_2)-x_0}(x-x_0)\right)\le I(x,T_2)\mathrm{i}\mathrm{n}[x_0,h(T_2)].$$

Applying the comparison principle yields

$$Z(x,t)={\epsilon }_2\omega \left(x_0+\frac{h(T_1)-x_0}{h(t)-x_0}(x-x_0)\right)\le I(x,t)\mathrm{f}\mathrm{o}\mathrm{r}(x,t)\in [x_0,h(t))\times [T_2,+\infty ).$$

It follows that

$$I_x(h(t),t)\le Z_x(h(t),t)=\frac{h(T_1)-x_0}{h(t)-x_0}{\epsilon }_2{\omega }_x(h(T_1))\to \frac{h(T_1)-x_0}{h_{\infty }-x_0}{\epsilon }_2{\omega }_x(h(T_1))<0$$

as t → +∞. By the free boundary condition, we have

$$h^{\prime }(t)=-\mu I_x(h(t),t)\ge -\mu Z_x(h(t),t)\to -\mu \frac{h(T_1)-x_0}{h_{\infty }-x_0}{\epsilon }_2{\omega }_x(h(T_1))>0$$

as t → +∞, which contradicts with the assumption h_∞ < + ∞. Hence, − ∞ < g_∞ < h_∞ < + ∞ holds.

According to Theorems 4.1 and 4.2, we can obtain the following spreading-vanishing dichotomy:

Theorem 4.4

Let (S, I; g, h) be the solution to problem (1.3). Then, the following alternatives hold:

• (i) Spreading: h_∞ − g_∞ = +∞ and then $\underset{t\to +\infty }{\mathrm{lim\; sup}}\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}>0$; or

• (ii) Vanishing: h_∞ − g_∞ < + ∞ and then $\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$, and $\underset{t\to +\infty }{\lim }S(x,t)=S^{\ast }(x)$ locally uniformly for $x\in \mathbb{R}$, where S∗(x) satisfies problem (4.1).

Remark 4.1

Theorem 4.3 implies that h_∞ = −g_∞ = ∞ when spreading happens if β and γ are positive constants.

5. Sufficient condition for vanishing or spreading

First, recalling the definition of $R_0^F(t)$, we have the following result from the proof of Theorem 4.2.

Theorem 5.1

Ifh_∞ − g_∞ < + ∞, then $\underset{t\to +\infty }{\lim }{R}_0^F(t)=R_0^D((g_{\infty },h_{\infty }),d)\le 1$. Moreover, if $R_0^F(t_0)\ge 1$ for any t₀ ≥ 0, then − g_∞ = h_∞ = +∞.

It is well-known in (Allen et al., 2008; Li et al., 2017; Peng, 2009; Peng & Liu, 2009; Peng & Zhao, 2012) that $R_0^D$ can be used as a threshold to describe the spreading or vanishing of infectious diseases on fixed boundary, that is, if $R_0^D((-h_0,h_0))>1$, then infectious diseases is spreading; rather, the infectious diseases is vanishing. For the free boundary problem (1.3), we will show that spreading happens when $R_0^F(0)=R_0^D((-h_0,h_0))>1$; the condition $R_0^F(0)=R_0^D((-h_0,h_0))<1$ can not ensure $R_0^F(t)<1$ for any t > 0. We will show that the spreading and vanishing of infectious disease are possible when $R_0^F(0)=R_0^D((-h_0,h_0))<1$, which mainly depends on the variables μ and I₀.

Theorem 5.2

Suppose$R_0^F(0)<1$, then

$$\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$$

if $\Vert I_0(x){\Vert }_{C([-h_0,h_0])}$ is small enough.

Proof: We prove it by constructing a suitable upper solution for I(x, t), which is similar to that of Lemma 5.3 in (Du & Lin, 2010) or (Ge et al., 2015). Due to $R_0^F(0)=R_0^D((-h_0,h_0))<1$, we consider the following eigenvalue problem

$$\left\{\begin{array}{ll}-d\mathrm{\Delta }\psi =\beta (x)\psi -\gamma (x)\psi +\lambda \psi ,& x\in (-h_0,h_0),\\ \psi (-h_0)=\psi (h_0)=0,\end{array}\right)$$

which has a positive solution ψ(x) with $\Vert \psi {\Vert }_{L^{\infty }((-h_0,h_0))}=1$, and principal eigenvalue λ₀ > 0. In view of Theorem 2.2, we know that S(x, t) ≤ C₁ for $(x,t)\in \mathbb{R}\times (0,+\infty )$. Hence,

$$I_t-d\mathrm{\Delta }I=\frac{\beta (x)SI}{S+I}-\gamma (x)I\le \frac{\beta (x)C_{1}I}{C_1+I}-\gamma (x)I,x\in (g(t),h(t)),t>0.$$

Set

$$\eta (t)=h_0\left(1+\delta -\frac{\delta }{2}{e}^{-\delta t}\right),t\ge 0,$$

and

$$W(x,t)=\epsilon e^{-\delta t}\psi \left(\frac{x{h}_0}{\eta (t)}\right),-\eta (t)\le x\le \eta (t),t\ge 0.$$

Clearly W(−η(t), t) = 0 and W(η(t), t) = 0. Direct computations yield that

$${\eta }^{\prime }(t)=h_0\frac{{\delta }^2}{2}{e}^{-\delta t},$$

$$-\mu W_x(-\eta (t),t)=-\frac{\mu \epsilon }{1+\delta -\frac{\delta }{2}{e}^{-\delta t}}{e}^{-\delta t}{\psi }^{\prime }(-h_0)<0,$$

and

$$-\mu W_x(\eta (t),t)=-\frac{\mu \epsilon }{1+\delta -\frac{\delta }{2}{e}^{-\delta t}}{e}^{-\delta t}{\psi }^{\prime }(h_0)>0.$$

Hence − η′(t) ≤ −μW_x(−η(t), t) and η′(t) ≥−μW_x(η(t), t) hold if ε is sufficiently small. And then, from the definition of η(t) we know that − η(0) < g(0) = −h₀ < h(0) = h₀ < η(0). On the other hand, by direct calculations, for t > 0 and x ∈ (−η(t), η(t)), we obtain

$$\begin{array}{cc}& W_t-d\mathrm{\Delta }W-\frac{\beta (x)C_{1}W}{C_1+W}+\gamma (x)W\\ & =-\epsilon \delta e^{-\delta t}\psi -\epsilon e^{-\delta t}{\psi }^{\prime }\frac{x{h}_0{\eta }^{\prime }(t)}{{\eta }^2(t)}-d\epsilon e^{-\delta t}\mathrm{\Delta }\psi {\left(\frac{h_0}{\eta (t)}\right)}^2-\frac{\beta (x)C_1\epsilon e^{-\delta t}\psi }{C_1+\epsilon e^{-\delta t}\psi }+\gamma (x)\epsilon e^{-\delta t}\psi \\ & =-\epsilon e^{-\delta t}{\psi }^{\prime }\frac{x{h}_0{\eta }^{\prime }(t)}{{\eta }^2(t)}+\varpi \left[\gamma (x)\left(1-{\left(\frac{h_0}{\eta (t)}\right)}^2\right)\right]+\varpi \left[-\delta +\beta (x){\left(\frac{h_0}{\eta (t)}\right)}^2-\frac{C_1\beta (x)}{C_1+\epsilon e^{-\delta t}\psi }+{\lambda }_0{\left(\frac{h_0}{\eta (t)}\right)}^2\right]\\ & \ge -\epsilon e^{-\delta t}{\psi }^{\prime }\frac{x{h}_0{\eta }^{\prime }(t)}{{\eta }^2(t)}+\varpi \left[\gamma (x)\left(1-{\left(\frac{h_0}{\eta (t)}\right)}^2\right)\right]+\varpi \left[-\delta +\beta (x)\frac{1}{{(1+\delta )}^2}-\beta +{\lambda }_0\frac{1}{{(1+\delta )}^2}\right]\\ & \ge 0\end{array}$$

provided that δ is sufficiently small and satisfies $\delta (1+{\delta }^2)+[{(1+\delta )}^2-1]\underset{x\in \mathbb{R}}{\sup }\beta (x)\le {\lambda }_0$.

Finally, we choose $\Vert I_0{\Vert }_{C([-h_0,h_0])}$ small enough such that $\Vert I_0{\Vert }_{L^{\infty }([-h_0,h_0])}\le \epsilon \psi (\frac{h_0}{1+\frac{\delta }{2}})$. Applying the comparison principle ((Du & Lin, 2010)) for free boundary problem yields

$$I(x,t)\le W(x,t),g(t)<x<h(t),t\ge 0.$$

That is

$$|I(x,t)|\le \epsilon e^{-\delta t}.$$

So

$$\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$$

if $\Vert I_0(x){\Vert }_{C([-h_0,h_0])}$ is sufficiently small.

From the above proof, taking $\eta (t)=h_0(1+\delta -\frac{\delta }{2}{e}^{-\delta t})$ and $\omega (x,t)=M{e}^{-\delta t}\psi (\frac{x{h}_0}{\eta (t)})$, we can prove similarly that ω(x, t) is still the upper solution of I(x, t) for (x, t) ∈ (g(t), h(t)) × [0, + ∞) if positive constant M is sufficiently large and μ is small enough. Therefore, the following result holds.

Theorem 5.3

Suppose$R_0^F(0)=R_0^D((-h_0,h_0),d)<1$, then

$$\underset{t\to +\infty }{\lim }\Vert I(\cdot ,t){\Vert }_{C([g(t),h(t)])}=0$$

if μ is sufficiently small.

When $R_0^F(0)<1$, Theorem 5.3 indicates that vanishing happens for small expanding capability μ, the following result shows that spreading occurs for large expanding capability μ.

Theorem 5.4

Assume$R_0^F(0)<1$, thenh_∞ − g_∞ = +∞ if μ is sufficiently large and (H) holds.

Proof: According to (v) of Proposition 3.2, we have

$$\underset{h\to \infty }{\lim }{R}_0^D\left(((-h,h),d)\right)=\frac{{\beta }_{\infty }}{{\gamma }_{\infty }}>1$$

if (H) holds, and then there exists a sufficiently large positive constant M > 0 so that $R_0^D((-M,M),d)>1$. Set

$$f_1(x,t,I)=\frac{\beta (x)SI}{S+I},x\in \mathbb{R},t>0,$$

$$f_2(x,t)=\gamma (x),x\in \mathbb{R},t>0.$$

Using the Lemma 2.5 in (Zhu & Lin, 2018) we can conclude that there exists a μ_M > 0 such that

$$\underset{t\to +\infty }{\mathrm{lim\; sup}}{g}^{\mu }(t)<-M\text{and}\underset{t\to +\infty }{\mathrm{lim\; inf}}{h}^{\mu }(t)>M$$

for μ > μ_M.

On the other hand, due to the monotonicity of g^μ(t) and h^μ(t), there exists a T₀ > 0 such that

$$g^{\mu }(T_0)<-M\text{and}{h}^{\mu }(T_0)>M.$$

Moreover,

$$R_0^F(T_0)=R_0^D((g^{\mu }(T_0),h^{\mu }(T_0)),d)>R_0^D((-M,M),d)>1.$$

Hence, if μ > μ_M, then h_∞ − g_∞ = +∞ holds by Theorem 5.1. □

Due to Theorems 5.3 and 5.4, the following result holds, see details in Theorem 5.5 in (Ge et al., 2015).

Theorem 5.5

Fixh₀andI₀, there existsμ∗ ∈ [0, + ∞) such that if μ > μ∗, then spreading happens; and if 0 < μ ≤ μ∗, then vanishing happens.

Finally, we will discuss how the diffusion coefficient d affects the vanishing and spreading of the disease.

Theorem 5.6

If the setG = {x ∈ [ − h₀, h₀], β(x) > γ(x)} ≠ ∅, then there exists d∗ > 0 such that − g_∞ = h_∞ = +∞ for d ≤ d∗ or d > d∗ and μ is large enough.

Proof: Due to Proposition 3.2 (ii) and G ≠ ∅ we conclude that

$$R_0^D((-h_0,h_0),d)\to \underset{x\in [-h_0,h_0]}{\max }\frac{\beta (x)}{\gamma (x)}>1\text{as}d\to 0.$$

There is a positive constant d∗ such that $R_0^D((-h_0,h_0),d^{\ast })=1$, and $R_0^D((-h_0,h_0),d)\ge 1$ for d ≤ d∗ by Proposition 3.2 (i) − (iii). Theorem 5.1 implies that − g_∞ = h_∞ = +∞ for d ≤ d∗, while if d > d∗, then Theorem 5.4 gives that − g_∞ = h_∞ = +∞ provided μ is large enough. □

Similarly, based on Proposition 3.2 (ii) and (iii), and Theorems 5.2 and 5.3, the following result for vanishing holds.

Theorem 5.7

Fixh₀ > 0, β(x) and γ(x). There exists a nonnegative constant $\widehat{d}$ such that − ∞ < g_∞ < h_∞ < + ∞ for $d>\widehat{d}$ provided that μ or $\Vert I_0(x){\Vert }_{C([-h_0,h_0])}$ is small enough. If β(x) < γ(x) in [ − h₀, h₀], then $\widehat{d}=0$, that is, vanishing happens if μ or $\Vert I_0(x){\Vert }_{C([-h_0,h_0])}$ is small enough.

Proof: It is easily seen that there is a constant $\widehat{d}\ge 0$ so that $R_0^D((-h_0,h_0),d)<1$ for $d>\widehat{d}$ by Proposition 3.2 (i) and (iii). If β(x) < γ(x) in [ − h₀, h₀], then $\widehat{d}=0$ by Proposition 3.2 (i) and (ii).

Since $R_0^D((-h_0,h_0),d)<1$, then vanishing happens if μ or $\Vert I_0(x){\Vert }_{C([-h_0,h_0])}$ is small enough by Theorems 5.2 and 5.3. □

6. Simulation and discussion

At first, we use numerical simulations to explain impact expanding of the capability μ on spreading of infectious diseases. Taking some functions as follows:

$$\begin{array}{c}d=1,h_0=1,S_0(x)=0.5+0.2\sin \left(\frac{\pi }{2}x\right),\\ I_0(x)=0.9\cos \left(\frac{\pi }{2}x\right),\mathrm{\Lambda }(x)=35(\cos (x)+1.05),\\ \beta (x)=3.6+0.4/(2+x^2)\sin x,\gamma (x)=3.55+1/(1+x^2)\cos x,\end{array}$$

we can know that β_±∞ = 3.6, γ_±∞ = 3.55 and (H) holds. Moreover, according to (3.2), we have

$$R_0^F(0)\le \frac{{\int }_{-1}^1\beta (x){\psi }^{2}dx}{{\int }_{-1}^1(d|\nabla \psi {|}^2+\gamma (x){\psi }^2)dx}\le \frac{\underset{x\in [-1,1]}{\max }\beta (x){\int }_{-1}^1{\psi }^{2}dx}{\underset{x\in [-1,1]}{\min }\gamma (x){\int }_{-1}^1{\psi }^{2}dx}\le \frac{3.8}{3.8202}<1.$$

Next, we discuss the asymptotic behaviors of the solution to problem (1.3) and the changing of free boundaries by choosing different expanding capabilities.

Example 6.1

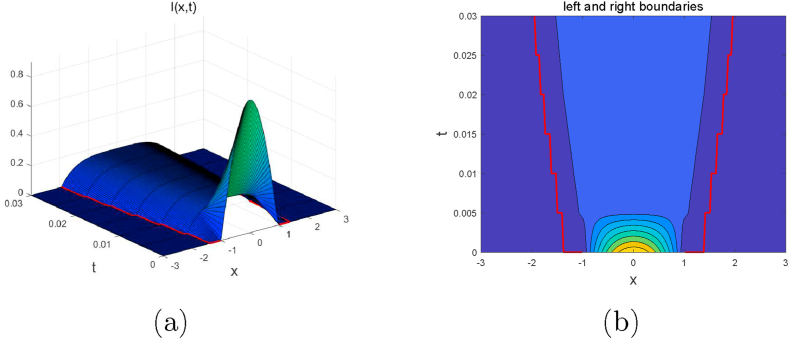
Taking μ = 50. Theorems 5.3 and 5.5 show that the solution I decays to zero if μ is small. It is easy Fig. 1 that the disease tends to extinction quickly, and the free boundaries expand slowly.

Example 6.2

Letting μ = 60. It follows from Theorems 5.4 and 5.5 that the spreading of the disease happens for large μ. It is easily seen that a spatially inhomogeneous stationary endemic state appears for large μ. The free boundaries expand quickly.

Fig. 1.

μ = 50. The left graph shows that the solution I decays to zero quickly. The right graph is the corresponding planar graph, which shows the free boundaries expand slowly and will be limited in a long run.

In this paper, we mainly discuss a SIS model with a linear source and variable total population, and the free boundaries are used to describe the spreading left and right fronts. Firstly, we present the local existence and uniqueness of solution for problem (1.3) by the contraction mapping theorem together with standard L^p theory and the Sobolev embedding theorem (see Theorem 2.1), and then we prove that the solution is global solution by some estimates (see Theorems 2.2 and 2.3). Next, the basic reproduction number $R_0^F(t)$ is defined for the SIS diffusion-reaction system with a free boundary. And then, a spreading-vanishing dichotomy for problem (1.3) is given (see Theorem 4.4). We then prove that $R_0^F(t)$ is used as the threshold to describe the spreading or vanishing of the disease. If $R_0^F(t_0)>1$ for any t₀ ≥ 0, then the disease is spreading (see Theorems 4.2 and 5.1). When $R_0^F(0)<1$, whether the disease is spreading or vanishing depends on the initial value of the infected individuals I₀ and the expanding capability μ. That is to say, if $R_0^F(0)=R_0^D((-h_0,h_0))<1$, the disease is vanishing when initial value of the infected individuals I₀ is small enough (Theorem 5.2) or the expanding capability μ is small enough (Theorem 5.3); the disease is spreading when the expanding capability μ is large enough and (H) holds (Theorem 5.4). Finally, we deal with the impact of the coefficient d for the disease. There exists a d∗ > 0, for d ≤ d∗ or d > d∗ and μ is sufficiently large, then the disease spreads (Theorem 5.6). On the other hand, there exists a $\widehat{d}\ge 0$, the disease vanishing provided $d>\widehat{d}$ if μ or I₀ are sufficiently small (Theorem 5.7). If the diffusion rates d_S and d_I are different, we believe that complicated dynamical behaviors would appear (Cui & Lou, 2016; Peng, 2009; Peng & Zhao, 2012).

In addition, our simulations indicate that expanding capability μ plays an important role in the spreading and vanishing of disease. If $R_0^F(0)<1$, the disease will vanish when the expanding capability μ is comparatively small (Fig. 1), and the disease will spread when the expanding capability μ is comparatively large (Fig. 2).

Fig. 2.

μ = 60. The solution I stabilizes to an equilibrium in the left graph. The right planar graph shows that the free boundaries expand fast.

When spreading occurs, the spreading speed for the simplified SIS model was given in (Ge et al., 2015). Owing to the coupled system for our reaction-diffusion model, some technical and mathematical difficulties for the spreading speed deserve further study.

Declaration of competing interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work, there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in, or the review of, the manuscript entitled, “The impact factors of the risk index and diffusive dynamics of a SIS free boundary model”.

Handling Editor: Dr HE DAIHAI HE