Abstract
Visual-based social group detection aims to cluster pedestrians in crowd scenes according to social interactions and spatio-temporal position relations by using surveillance video data. It is a basic technique for crowd behaviour analysis and group-based activity understanding. According to the theory of proxemics study, the interpersonal relationship between individuals determines the scope of their self-space, while the spatial distance can reflect the closeness degree of their interpersonal relationship. In this paper, we proposed a new unsupervised approach to address the issues of interaction recognition and social group detection in public spaces, which remits the need to intensely label time-consuming training data. First, based on pedestrians' spatio-temporal trajectories, the interpersonal distances among individuals were measured from static and dynamic perspectives. Combined with proxemics' theory, a social interaction recognition scheme was designed to judge whether there is a social interaction between pedestrians. On this basis, the pedestrians are clustered to identify if they form a social group. Extensive experiments on our pedestrian dataset “SCU-VSD-Social” annotated with multi-group labels demonstrated that the proposed method has outstanding performance in both accuracy and complexity.
Keywords: Social group detection, Social interaction, Spatio-temporal trajectory, Interpersonal distance measurement, Proxemics
Social group detection; Social interaction; Spatio-temporal trajectory; Interpersonal distance measurement; Proxemics
1. Introduction
In recent years, with the high development of information technology and artificial intelligence, the coverage and mining granularity of new data environment in time and space have been greatly improved, which creates conditions for the accurate perception of crowd activity information. At the same time, with the development of digitization and smart city construction [1], the video data obtained from public space is increasing explosively. Compared with other non-visual data (e.g., Wifi, GPS etc), video data contains rich spatio-temporal information about people, and is a powerful supplement to non-visual data. In this context, combined with video data and artificial intelligence technology, around the concept of “people-centred” [2], it is of great significance to deeply analyse and understand the activity information of people in urban public space, so as to build and develop a livable city that reflects the wishes of citizens and accelerate the current urbanization process.
In the study of public life, understanding the dynamic characteristics of the crowd becomes a critical study field, with the applications in potentially identifying suspicious behaviour within large number of people or the identification of moving dense areas of traffic in surveillance systems. Recently, groups have been recognised as the basic elements which compose the crowd, leading to comprehending group attributes and activities becoming the fundamental of the crowd analysis. Consequently, in order to handle the issue of understanding the crowds, we need to decompose the entire crowd into smaller groups first, which is defined as group detection task.
As the critical fundamental of crowd analysis, group detection has become a hot research topic in the computer vision area, increasing attentions in recent years. This task aims to divide pedestrians into small parts according to their social relations or interactions for further applications of analysing human attributes or behaviours at a group level. Here, the term “group” refers specifically to “social group”. In other words, we do not consider groups as those people who coincidentally move together for a short time. On the contrary, we regard social groups as groups of people that know each other (have social relations) and move together, possibly while socially interacting according to [3]. In addition, we also assume social interaction as latent interaction (i.e., conversations) between individuals.
Recently, researches on groups have attracted extensive attentions. Some of them are based on proxemics entering in the pedestrian dynamics/pedestrian psychology sphere [3], [4], [5], [6], and some focus on studying group characteristics [3], [4], [5]. In particular, it has been shown that pedestrian groups in themselves present variations in locomotion depending on various traits (e.g., age, gender, relation, height) and states (e.g., engagement in interaction) [3], [4], [5] especially the dyads (two people groups) or triads (three people groups). In addition, as an effective information, trajectory data is widely used in related field and we can obtain the trajectory directly from GPS or through tracking. Researches on person tracking have a long history with different input data: Pellegrini et al. introduced a Linear Trajectory Avoidance (LTA) model for walking people accounting for social interactions as well as scene knowledge with video data [7], whereas 3-D range sensors are exploited to person tracking in public spaces which are mounted above human height to have less occlusion between persons [8]. Once we gain trajectories of pedestrians, we can further analyse group related characteristics. For the methods not based on machine learning, trajectory data is applied to automatically discover moving clusters from a long history of recorded trajectories [9], consider the discovery of flock patterns among the moving objects [10], and identify family-group relying on mutual proximity and its time-consistency [11]. As for the methods based on machine learning, some studies focus on the relationship between group properties and social relations [12], while others localize pedestrians in small groups by modelling the relevant attributes of groups, such as interpersonal distance, motion direction and so on [13], [14].
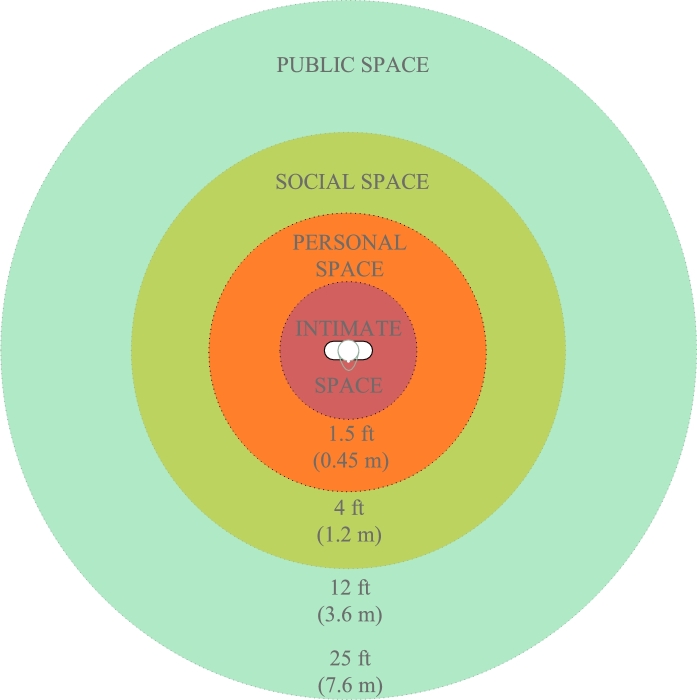
Members of social groups prefer keeping a reasonably short distance between themselves, and they are characterised by a specific group “proxemics” (a term that refers to the manner in which individuals behave or interact with each other in terms of their personal space and interpersonal distances [15]). In proxemics theory, people have a certain space distance from each other for any kind of social communication, and the category and closeness degree of social relations can be inferred from spatial distance. According to the nature of social communication, it can generally be divided into: friendship communication, colleague communication, business communication and public communication. Generally speaking, the interpersonal relationship and situation of both side of people determine the scope of self space between each other. Based on this concept, Edward T. Hall divided four kinds of spatial distances [15], [16], all of which are commensurate with the relationship between the two sides, as shown in Fig. 1. However, the spatial distance of interpersonal contact is not fixed all the time, but depends on the specific situation, the relationship between the two sides and other factors. Understanding the self space and appropriate distance required for communication can help people choose the optimal distance to contact with others, while the relationship between the two sides can also be inferred through spatial distance so as to better carry out social communication.
Figure 1.
Schematic diagram of four kinds of spatial distance division [15], [16].
Therefore, according to proxemics theory, the spatio-temporal relationship between individuals is a critical measurement basis for inferring social relation in the group clustering process. Based on the spatio-temporal trajectories of pedestrians, measuring the interpersonal distance properly can reflect the relationships between pedestrians, and finally provide theoretical and technical support for subsequent social group detection task.
So, in this paper, we propose a new unsupervised social group detection approach based on spatio-temporal interpersonal distance measurement [17] with no training parameters. The contributions of our work are summarised as follows:
-
1.
A new social interaction and social group clustering scheme based on the spatio-temporal interpersonal distance measurement [17] was proposed, which can identify the social interaction between pedestrian pairs, construct the social interaction matrix and graph in the whole scene, and finally carry out social group detection according to the constructed graph.
-
2.
A new dataset named “SCU-VSD-Social” was proposed, which was further annotated in our pedestrian dataset “SCU-VSD” [17] with multi-group labels.
-
3.
Except the conservative metrics (, and F1-), two new evaluation metrics, namely Group Clustering Accuracy (GC-Acc) and mean Group Clustering Intersection over Union (mGC-IoU) were proposed, which evaluated the performance of group clustering from the perspective of recognition rate and average intersection union ratio.
The rest of the paper is organised as follows. Section 2 introduces the related work of proxemics and group detection methods. Section 3 describes the detail contents of proposed approaches. The experimental results and discussion are analysed in Section 4. Finally, Section 5 presents the conclusion of this paper.
2. Related work
In this section, basic theories of proxemics and group detection methods are briefly introduced.
2.1. Proxemics
Proxemics [15], [16] is a discipline that studies human use of space and the impact of population density on behaviour, communication and social interaction. It is closely related to interpersonal distance. In addition, the interpersonal relationships and the situation they are in both determine the mutual self-spatial range, and the spatial distance of interpersonal also reflect the intimacy degree of interpersonal relationship between both sides [18], [19], [20], [21], [22].
In recent years, the use of various big data and newly developing technology has made significant progress in the research of interpersonal distance and proxemics [23], [24], [25], [26]. For example, based on interaction geometry, Groh et al. [23] used infrared tracking technology to make geometric representation and quantitative measurement of social interaction in a small space-time scale, and then identified whether there is a social situation between people. Cristani et al. [24] took advantage of visual information of human position and head orientation to detect social interaction in crowed scene. They also analysed social distance by computer vision technology, so as to infer social relationships [25]. Experiments showed that social distance and physical distance often match each other. The closer the relationships between people, the nearer it will be. Kroczek et al. [26] explored the impact of interpersonal distance and social anxiety on individual subjective experience, physiology and behaviour in real-time social interaction of virtual reality (VR). These existed methods have made contributions in inferring social relationships or interactions by considering the knowledge of proxemics, interpersonal distance and other useful information. Different from these approaches, this paper utilises a novel method to measure interpersonal distance by applying both Euclidean distance and Fréchet distance of trajectories between people with both static and dynamic perspectives [17]. At the same time, combined with relevant theories of proxemics, this paper further infers the social relations or interactions between pedestrians and clusters social groups based on the method of interpersonal distance measurement [17].
2.2. Group detection methods
Group detection aims to cluster pedestrians into small parts for further applications. According to different purposes of group detection, the existing work can be divided into two categories as follows:
One category clusters pedestrians based on different motion patterns of crowds [27], [28], [29], [30], [31], [32], with wide applications in medium and high-density crowd scenes, such as crowd flow monitoring and crowd behaviour analysis. For example, Shao et al. [27] adopted a robust group detection algorithm and a rich set of group-property visual descriptors through learning the collective transition prior; they then utilised visual descriptors to quantify group-level properties for crowd understanding [28]. Chen et al. [29] proposed an anchor-based manifold ranking (AMR) method to classify individuals into local clusters according to topological relationship to the anchors, and exploited a coherent merging strategy to recognise global consistency in crowed scenes. Wang et al. [30] designed a multi-view clustering method for group detection by combining the orientation and context similarities of feature points, whereas Han et al. [31] developed a crowd activity discovery algorithm to explore latent action patterns among crowd activities and clustering them. Considering that scene context can promote clustering, Zhang et al. [32] incorporated scene information to present a scene perception-guided clustering strategy, and they fully utilised various attributes of the pedestrians to make the clustering process more reasonable.
Another category focuses on clustering people to form small or social groups through capturing social interactions among individuals [33], [34], [35] with applications in low/medium density scenes, which is the premise study of group-based activity understanding and the proposed method belongs to this category. In such studies, they often adopted pairwise proximity [33], velocity information [33], trajectory data [34], [35] or interaction characteristics [35] to measure inter-group closeness for group detection. As for deep learning-based approaches [36], [37], [38], [39], they utilised various deep network frameworks to process extracted features so as to handle group detection task, such as GAN based method [36], DNN based method [37], GCN based method [38] and graph attention networks (GAT) based method [39]. Specifically, Fernando et al. [36] used generative adversarial networks (GAN) [40] to extract the relevant attributes describing the pedestrians' social identities to perform unsupervised social grouping detection. Akbari et al. [37] applied deep neural networks (DNN) to integrate various features, such as Euclidean distance, proximity distance, motion causality and trajectory shape, between pedestrian pairs to detect social groups. Sun et al. [38] presented a group-based social interaction model to explore the relationship among persons by constructing a Recursive Social Behavior Graph (RSBG). Ehsanpour et al. [39] utilised graph attention networks (GAT) [41] to capture potential interaction relationships among individuals to cluster social groups and recognise multi-group activities.
Most of the existing approaches need to spend a lot of time on data labelling and network training. In addition, they only take the Euclidean distance into consideration in a static view. Hence, we proposed a new unsupervised social group detection approach based on spatio-temporal interpersonal distance measurement [17] with no training parameters. Besides, we collected a new dataset named “SCU-VSD-Social” to better illustrate the performance of our social group detection method.
3. The proposed approaches
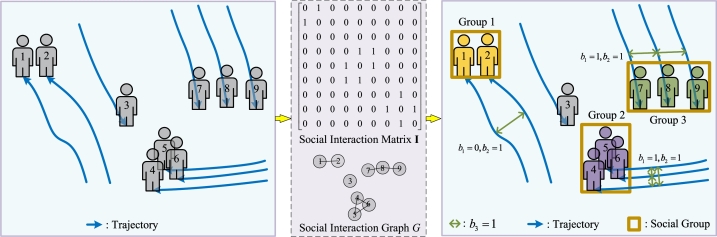
We propose an unsupervised social group detection approach based on spatio-temporal interpersonal distance measurement. Firstly, based on our previous work [17], we adopt spatio-temporal interpersonal distance measurement approach to measure interpersonal distances between pedestrians according to the trajectories of them which uses Euclidean distance and Fréchet distance [42]. Then, the social interaction recognition scheme is presented to identify whether there is a social interaction between pedestrians according to the distance between them, so as to obtain social interaction matrix. In addition, taking pedestrians as nodes and social interaction matrix as an adjacent matrix, a social interaction graph can be drawn, so the final results of social group detection can be derived. The whole process is shown in Fig. 2, and we will introduce the details in the following paragraphs.
Figure 2.
The process of clustering and social group detection.
3.1. Trajectory transformation and distance measurement
The foundation of social group detection is to speculate the social relation and interaction between people. According to proxemics theory, the interaction between people is closely related to interpersonal distance. Therefore, we need to measure interpersonal distance properly.
Based on our own previous work [17], we adopt spatio-temporal interpersonal distance measurement approach to measure interpersonal distances between trajectory pairs, which utilise Euclidean distance and Fréchet distance [42] to measure distances in both static and dynamic perspectives. In this case, we only compute distances between all pedestrians appearing in the same frame one by one. If one of them is out of the sight, we do not measure the distances between them anymore. In other words, when we see pedestrian P in a certain frame but pedestrian Q does not appear in this frame, or pedestrian P has left a frame but pedestrian Q still stays in this frame, we will not calculate the distance between them.
The Euclidean distance is used to measure the real distance between two points in m-dimensional space, while the Fréchet distance is the maximum value of the two spatio-temporal trajectory curves. And the Fréchet distance diagram is shown in Fig. 3. In this paper, we calculate the discrete Fréchet distance instead of the continuous one, which is an approximation of continuous Fréchet distance.
Figure 3.
Fréchet distance diagram (the dotted line represents the distance between spatial positions P and Q at the same time, and the longest dotted line is the Fréchet distance).
Because the surveillance video is taken at any angle, we first calibrate them by performing the perspective transformation to map the original video into the bird's eye view [17]. After calibration, the two trajectory curves P and Q are expressed discretely as p and q sampling points in the bird's eye view, also written as and respectively. represents a series of trajectory P's discrete coordinates like , while represents a series of trajectory Q's discrete coordinates like . And the coupling L between P and Q is composed of a series of sampling point pairs from and , presented as Eq. (1):
| (1) |
where and , and , and for all , we have or , or . However, in such cases, each sampling points are derived at the same moment (in the same frame) in spatio-temporal coordinate system, so the number of these points are equal, namely , so we do not use the equations ( or , or ) as an approximation in this case.
Then, we take the maximum value of sampling points in L as the discrete Fréchet distance, presented as Eq. (2):
| (2) |
where we utilise the Euclidean distance as the distance metric function . Because the Fréchet distance is the maximum value in a long time between pedestrian pairs, so it can better measure the spatio-temporal distance between pedestrians to reflect the similarity of their trajectories, which is of importance to determine whether there are social interactions between them.
By multiplying the distance with the scaling factor s, the social distance in the real world can be estimated. On the one hand, the Euclidean distance is used to measure the distance between each sampling point pair of trajectories from a local perspective, presented as Eq. (3).
| (3) |
On the other hand, from a holistic view, the discrete Fréchet distance is exploited to measure the distance between trajectory pairs, presented as Eq. (4)
| (4) |
3.2. Social interaction recognition
According to the theory of proxemics, the interpersonal distance can reflect the closeness of social relations. Usually, there are some situations that indicate there is an interaction between people. To better illustrate the idea of our proposed method, we take an example as follows: if two pedestrians have the same or highly similar trajectories, we can conclude that there is a social interaction relationship between them (we choose to represent this situation below, and here ); if two pedestrians have very close distance most of the time, even though they might be far from each other in a specific moment for some reasons (e.g., one of them wants to get the purse on the ground, and catches up with the other one immediately), they can also be considered as interactive pairs (we opt to show this situation in the following paragraphs, and here ). As shown in Fig. 2, person 1 and 2 are interactive pairs so as to form Group 1, because they are highly close most of the time although they are a little far from each other during the walking process; pedestrians in Group 2 or Group 3 have very similar trajectories and the spatial distance is very close, so they belong to the same group respectively. In addition, the distance between person 3 and any other person is quite large, so person 3 is isolated from others.
On the basis of the spatio-temporal interpersonal distance measurement method mentioned in Section 3.1, a social interaction recognition scheme is designed to identify whether there is a social interaction relationship between pedestrian pairs, and then the pedestrians are clustered according to the recognition results to address social group detection task. The proposed social interaction recognition scheme includes the following two judgement conditions. As long as any one of them is true, it is considered that there is a social interaction relationship between the pedestrian pairs:
(1) Using Fréchet distance to measure pedestrians' spatio-temporal trajectories is essentially a measurement of the similarity of the trajectories. For a pair of pedestrians, the sampling point pairs of their trajectories can be presented as a set , N is the total number of the elements in this set. Setting an interaction distance threshold , if the discrete Fréchet distance of the trajectory pair is not above the , the distances between all sample pairs of the two trajectories during the entire measurement process is not greater than the threshold. That is to say this trajectory pair is highly similar, and the spatial distance is always close. According to this scenario, it can be determined that there exists a social interaction between this pedestrian pair. The judgement condition can be formulated as Eq. (5)
| (5) |
where P and Q are corresponding projected trajectories in the bird's eye view, is the discrete Fréchet distance, s is the scaling factor, is the interaction distance threshold. Setting a quantity threshold , is used to prevent the total number of sampling point pairs of two trajectories from being too less. denotes the indicator function (if the condition in is true, the value of is 1, otherwise it is 0), the binary variable indicates whether the pedestrian pair has a social interaction or not (1 means yes, and 0 represents no). But for this judgement condition, there is a limitation. If a pair of pedestrians have a social interaction, the spatial distance between them is very close during the most of the measurement time, and the distance is relatively far (greater than the threshold) only at a few moments. In this scenario, if using the discrete Fréchet distance between these two trajectories as the evidence to recognise the interaction, the misjudgement will occur. Also, this condition is vulnerable and sensitive to noise. Therefore, another judgement condition is introduced to deal with this issue.
(2) The distances between the trajectory sampling pairs are measured one by one in the entire period, and the number of the pairs with distance no greater than can be written as Eq. (6)
| (6) |
where is the trajectory sampling pairs in the bird's eye view, is the Euclidean distance, is the indicator function. Setting a ratio threshold and a quantity threshold , if the ratio of n and N, namely , is greater than or equal to , and n is greater than or equal to , it is deemed that there is a social interaction between the two pedestrians, presented as Eq. (7)
| (7) |
where is a binary variable which denotes if the pedestrian pair has a social interaction (1 means yes, and 0 represents no). avoids the situation that the number n is too less. It indicates that in the entire measurement process, as long as the spatial distance between two pedestrians is relatively close most of the time (not less than the ), the existence of social interaction between the two persons can also be determined. This condition is a favourable supplement to the above condition.
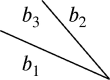
Combining the above two criteria and , the comprehensive judgement condition to recognise whether there exists a social interaction between two pedestrians, with logical expression as Eq. (8)
| (8) |
where “+” denotes logical OR, as long as any of and is equal to 1, the binary variable is 1, which means the results of the social interaction recognition between the pedestrian pairs is yes. Only when the values of and both are 0, is 0, indicating the recognition result is no. As shown in Table 1, with in rows and in columns, we present the relations of the input variable and , and the output variable .
Table 1.
The relations in b1, b2 and b3.
 |
0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
3.3. Clustering for social group detection
Based on the spatio-temporal interpersonal distance measurement method, exploiting the proposed social interaction recognition scheme, the value of between each pedestrian pair can be derived. A social interaction matrix, referred as I, can then be obtained where the elements are the corresponding (0 or 1) between pedestrian i and j. Taking pedestrians as nodes and matrix I as an adjacent matrix, a social interaction graph G can be drawn, with edges connecting node pairs whose is 1.
According to graph G, the pedestrians are clustered to form different social groups. Individuals in one social group have social interactions () with one or more people in the same group, whereas the value of between any two individuals in different social groups is 0. Thus, social groups with at least 2 members in the video sequence can be detected. If there is no social interaction between one people and every other pedestrian in the video, this person does not belong to any social group. The process of clustering and social group detection is shown in Fig. 2.
3.4. Social group detection analysis scheme
In this paper, we adopt traditional metrics to evaluate the performance of our proposed method. At the same time, we also designed new evaluation metrics so as to improve the analysis scheme. The evaluation metrics [34], [36] commonly used in the social group detection task are selected to evaluate the performance of the proposed method: , and F1-. Formally, consider two clustering solutions x, y and a representative of their spanning forests X and Y. The components of X and Y are identified by a set of trees and . We also consider the number of elements in is , and need links so as to create a spanning tree. In addition, we define as the partition of a tree with respect to the forest Y, which is a set of subtrees obtained by considering the membership relations in found in Y. If Y partitions in subtrees then links are adequate to restore the original tree. Given that all trees the global recall of X (the precision of Y) is shown as Eq. (9)
| (9) |
The precision of X (recall of Y) can be calculated by exchanging X and Y, presented in Eq. (10). Besides, the F1- comprehensively considers the precision and recall, presented as Eq. (11):
| (10) |
| (11) |
The calculation process of P, R and F1- is as Algorithm 1. In Algorithm 1, we employ disjoint-set arrays as inputs. UNION and FIND are the standard functions defined over the disjoint-set arrays. UNION represents the operation to merge two clusters, while FIND operation is to find a specific element. In the pseudo-code we utilise the notation to denote that this algorithm first applied to x and then on y analogously.
Algorithm 1.
The computation process of P, R and F1-Score.
In Fig. 4, we give a toy example of how to compute the value of P, R and F1-. The left column shows group clustering prediction results and the right one presents group ground truth labels. The circles stand for pedestrians and the number in the circle is the unique person ID belonging to different pedestrians. Besides, the line connected to different pedestrians indicates that they are in the same group. So, according to the top row in Fig. 4, we can obtain group clustering result sets and the ground truth group sets respectively. Secondly, we can get disjoint-set arrays and from CR and GT which denote the index (i.e., the ID number of pedestrians) corresponding to the location of the same number belongs to the same group. And then, x and y will be calculated through line 3-7 in Algorithm 1 to add the person who is not belong to any groups to x and y written as and respectively. Finally, P, R and F1- can be obtained according to Eq. (12)-(14) and Algorithm 1, which is shown as follows:
| (12) |
| (13) |
| (14) |
Figure 4.
A graphic example of calculating P, R and F1-Score between group clustering results and group ground truth.
In order to evaluate the experimental results of group detection from different views, we also designed new metrics from the perspective of group recognition rate and average intersection union ratio, including Group Clustering Accuracy (GC-Acc) and mean Group Clustering Intersection over Union (mGC-IoU). These two evaluation metrics need to be based on the optimal matching between the prediction results and the ground truth of group detection. Therefore, the optimal matching process between group clustering results and group ground truth are introduced in the following paragraphs, and the whole process is shown in Fig. 5.
Figure 5.
The optimal matching process between group clustering results and group ground truth.
The left column is a set of group ground truth labels in green box, and a set of numbers in red box beside group ground truth labels are group clustering results. The goal of the optimal matching process is to find the best match between the two sets of labels, which refers to allocation problem.
Allocation problem is a basic problem in the field of combinatorial optimization. It aims to determine the optimal allocation scheme in order to minimize the total cost or maximize the total efficiency. For example, assign n tasks to n objects, each task can only be assigned to one object, and each object can only be assigned to one task. There is a cost in the allocation of each task and we want to minimize the total cost. Therefore, we construct a cost matrix C, the element is the cost of assigning the i-th task to the j-th object. The problem is transformed into the need to select n elements in different rows and columns from matrix C to minimize the sum of elements, which needs to use Hungarian algorithm [43].
Therefore, in order to find the optimal match between group ground truth and group clustering results, firstly, the IoU matrix of them is constructed, and the order of is the larger value in the category of clustering results and ground truth. According to Eq. (15), IoU is the ratio of the intersection and union number of two sets. The between each clustering results sets and real group sets is calculated one by one as the element of . In addition, the elements in row i and column j indicate the IoU value of the i-th clustering results and the j-th ground truth. If the number of categories is not equal, we need to supplement 0 on the row or column according to the order to make a square matrix. For example, the clustering result sets is and the real group sets is . The intersection set of the 3-rd clustering result sets and the 2-nd real group sets is and the union set of them is . Therefore, the value of IoU is 2/3 and the value of the third row and second column of is 2/3 in Fig. 5 according to Eq. (15). Then, by subtracting each element of from the maximum value of the elements in one by one, the cost matrix C of the same order can be obtained. According to the cost matrix C, the optimal matching between group clustering results and group ground truth can be derived through the Hungarian algorithm [43]. If the number of the two categories is not equal, there will be redundant group matching failures.
| (15) |
Based on the optimal matching between group clustering results and group ground truth, two evaluation metrics are presented in the following paragraphs:
Group Clustering Accuracy (GC-Acc): In order to evaluate the performance of clustering, the accuracy of clustering is evaluated with reference to the idea of unsupervised clustering accuracy (UC-Acc) [44]. UC-Acc shows that under the condition of optimal matching between the cluster prediction results and the ground truth, the ratio of the correct number of individuals to the total number of individuals is predicted, as shown in Eq. (16)
| (16) |
where, is the individual ground truth, is the clustering prediction result of the algorithm, and m is all possible one-to-one mapping matching between the clustering prediction result and the ground truth. is the indicator function, and is the total number of individual samples. Based on the above ideas, the optimal match between the clustering prediction result and the ground truth (as shown in Fig. 5) should be found first. This process allows the number of clustering result categories to be more or less than the number of ground truth categories. On this basis, GC-Acc is equal to the ratio of the total number of intersections between each pair of matching groups to the total number of individual targets, presented as Eq. (17).
| (17) |
where is the max number of small groups after clustering, and is the number of people in each subgroup. For example, after the optimal matching process between group ground truth and group clustering results, we can calculate GC- according to Eq. (17).
Mean Group Clustering Intersection over Union (mGC-IoU): The key evaluation basis to measure the clustering effect is the coincidence degree between the number of categories of clustering prediction results and the number of ground truth categories, and the coincidence degree of each pair of matching group members. GC-Acc can reflect the latter, but it cannot directly reflect the coincidence of the number of categories. Therefore, mGC-IoU is designed to evaluate the above coincidence degree by calculating the mean value of group cluster IoU. Based on the clustering prediction results and optimal matching of ground truth, mGC-IoU calculates the mean value of intersection and union ratio of each pair of matching groups, as presented in Eq. (18)
| (18) |
where, is the intersection and union ratio of the j-th pair of matching groups, and is the number of categories of clustering results. If is greater than the number of ground truth categories, the group that fails to match is equivalent to matching an empty set. For example, after the best match process, we can obtain the value of mGC- according to Eq. (18).
4. Experiments and discussions
4.1. Comparative experiments under two trajectory acquisition methods
In order to evaluate the tolerance of the proposed method to trajectory errors, two sets of comparative experiments were conducted on the SCU-VSD-social dataset (Please refer to appendix for datasets and labelling work). The first set of experiments exploits the detector + tracking algorithms to obtain pedestrian trajectories, while the counterpart is based on the ground truth of pedestrians' trajectories. The trajectories obtained from the former one may exist detection errors and the method based on the detector + tracking algorithms is closer to the real situations. On the basic of the spatio-temporal interpersonal distance measurement method, the proposed social grouping detection method is utilised to perform group clustering and detect social groups in the video sequences. The parameter settings of the experiments are listed in the Table 2. Although the parameters there have threshold, we also regard the proposed method as an unsupervised method because it does no need for data labelling and parameter training.
Table 2.
The parameter settings of the experiments.
| Parameters | Value |
|---|---|
| interaction distance threshold τi | 1.5 |
| ratio threshold τp | 55% |
| quantity threshold τ1 | 75 |
| quantity threshold τ2 | 125 |
Due to the ID switch problem of the detector + tracking algorithms, some IDs that do not exist in the labels of social group detection may be generated. When performing testing, these redundant IDs need to be removed first. The performance results of the two sets of comparative experiments on the SCU-VSD-Social dataset are shown in Table 3.
Table 3.
The performance results of the two sets of comparative experiments on the SCU-VSD-Social dataset when the frame rate is 25 fps. (①: YOLOv5 detector + tracking method proposed in [17]; ②: The ground truth of pedestrians' trajectories).
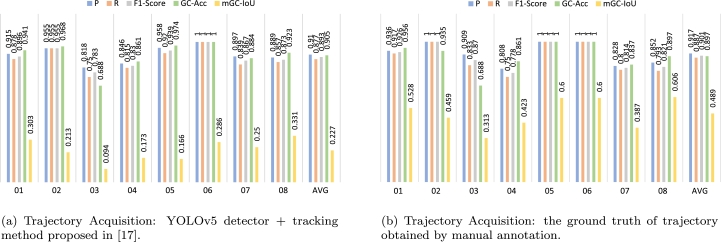
According to Table 3, the histograms of the two sets of comparative experimental results are drawn in Fig. 6, to visually compare the performance of the proposed social group detection method under the two trajectory acquisition ways. As shown in Table 3 and Fig. 6, it can be seen that in Sequence 01, 03 and 05 of SCU-VSD-Social, the performance results based on ground truth are better than those based on the detector + tracking algorithms. In Sequence 02, 05 and 06, the three evaluation metrics (, and F1-) based on the ground truth all reach 100%. In addition, GC-Acc metric based on the ground truth reaches 100% in Sequence 05 and 06. However, although in most cases the performance based on ground truth labels is better than those based on detector + tracking method, the results based on detector + tracking method of sequence 04, 07 and 08 indeed perform higher than those based on ground truth labels. The reason is that: for example, assuming that pedestrians whose ID is 1 and 2 belong to the same group, due to the ID switch problem caused by tracking, the ID is changed from 1 to 3. Therefore, the result of clustering is that ID 1, 2, 3 is a group. However, when calculating the evaluation metrics, if the distance between the trajectory whose ID is 1 to 3 and trajectory 2 is long (that is, it does not meet the clustering situation set in section 3.2), if there is no ID switch problem, 1 and 2 will not be clustered into one class; However, if we just delete the redundant track whose ID does not belong to the ground truth label (trajectory with ID 3), we can make ID 1 and ID 2 come together, which leads to the improvement of accuracy.
Figure 6.
The histograms of the two sets of comparative experimental results on SCU-VSD-Social. (a) reveals the performance on the five evaluation metrics based on the YOLOv5 detector + tracking method in [17], while (b) provides the performance on the same evaluation metrics based on the ground truth labels.
From the perspective of average performance in , , F1- and mGC-IoU, the performance results based on the ground truth (91.7%, 88.7%, 90.1% and 48.9%) exceed those based on detector + tracking algorithms respectively (91.0%, 87.7%, 89.3% and 22.7%). In GC-Acc metric, the results based on detector + tracking algorithms (90.5%) are slightly higher than those based on the ground truth (89.7%). This is because the pedestrian trajectory obtained by detector + tracking algorithms cannot completely avoid the trajectory fragment problem caused by ID switch. In the testing stage, the redundant ID is removed, which is equivalent to keeping the longest trajectory of the person for interpersonal distance measurement and social group detection. In addition, the ID confusion of pedestrians will also introduce errors. As for the perspective of the absolute value of the evaluation metrics, the reason why the average performance in mGC-IoU is pretty much lower than those in other metrics is that more social groups are detected, so the denominator is large, resulting in a lower final result.
However, in practical applications, the trajectories of pedestrians in the surveillance video are obtained by detection and tracking algorithms rather than by manual annotating. The four performance indicators in metrics (, , F1- and mGC-IoU) based on the detector + tracking approaches are 0.7%, 1.0%, 0.8% and 26.2% lower than those based on the ground truth of trajectories. And the performance based on the detector + tracking approaches is 0.8% higher than those based on the ground truth of trajectories in GC-Acc metrics. The reason for the great difference in the results of the experiment on mGC-IoU between the ground truth of trajectories and the detector + tracking algorithms is that the number of group clustering is closely related to the final performance. It also reflects the robustness ability and tolerance capacity of the proposed method for trajectory errors, which has good practical application value.
4.2. Parameter analysis
The proposed social group detection method involves several key threshold parameters, including interaction distance threshold , ratio threshold and quantity threshold . In order to verify the influence of the threshold parameters on the performance of the algorithm, based on the ground truth of trajectories, a set of experiments is conducted on SCU-VSD-Social to determine the optimal value settings of the threshold parameters. Setting the value range of the from 1.3 to 1.7 with an interval of 0.1, is from 55% to 65% with an interval of 5%, and is from 75 to 150 with an interval of 25. Under different settings of the threshold parameters, on the 8 videos of the SCU-VSD-Social dataset, the average performance result of the proposed method is shown in Table 4.
Table 4.
Under different settings of the threshold parameters (τi, τp, τ2), the average performance results of the proposed method on the SCU-VSD-Social dataset.
It can be observed from Table 4(a) to Table 4(c) that when the threshold parameters , and are set to 1.5, 55% and 125, respectively, the proposed social group detection method has achieved the best average performance on the SCU-VSD-Social dataset, with evaluation results 91.7%, 88.7%, 90.1%, 89.7% and 48.9% respectively. However, due to differences in scenes, angles, crowd density, calibration scaling factors and frame rate, when applying the proposed social group detection method on other datasets, it is necessary to properly adjust the settings of several threshold parameters.
4.3. Comparative experiments under different frame rate
In order to verify the effect of lowering the frame rate on the experimental results and inference time, we conduct the supplementary experiments when the frame rate is 12fps and 8fps respectively. The performance results of the two sets of comparative experiments on the SCU-VSD-Social dataset are shown in Table 5 and Table 6. In Table 5, before “/” indicates the experimental results of retaining odd frames and removing even frames, while after “/” indicates the results of retaining even frames and removing odd frames. In Table 6, we take “A/B/C” as an example. “A” represents results of retaining the first frame in every three frames and removing the other two frames, “B” represents results of retaining the middle frame in every three frames and removing the other two frames, and “C” represents results of retaining the last frame in every three frames and removing the other two frames. In addition, we calculate the average value of different frame extraction methods in each sequence, and then calculate the average value of all sequences to the final average result, presented in Table 5 and Table 6.
Table 5.
The performance results of the two sets of comparative experiments on the SCU-VSD-Social dataset when the frame rate is 12 fps. (①: YOLOv5 detector + tracking method proposed in [17]; ②: The ground truth of pedestrians' trajectories. In “A/B”, A represents the results of removing even frames, and B represents the results of removing odd frames.)
Table 6.
The performance results of the two sets of comparative experiments on the SCU-VSD-Social dataset when the frame rate is 8 fps. (①: YOLOv5 detector + tracking method proposed in [17]; ②: The ground truth of pedestrians' trajectories. In “A/B/C”, A represents the result of retaining the first frame in every three frames, B represents the result of retaining the middle frame in every three frames, and C represents the result of retaining the last frame in every three frames.)
We also present the histograms of the two sets of comparative experimental average results and the table of the inference time under different frame rate (25fps, 12fps and 8fps) to compare the results more clearly. In this case, we set the quantity threshold and to half and one third of the original when frame rate is 12fps and 8fps. According to Fig. 7 and Table 7, we can observe that the inference time decreases (1.65 s, 0.89 s and 0.62 s, respectively) by reducing frame rate. In the view of experiments' performance, based on the YOLOv5 detector + tracking method, the average performance under 12fps is little higher than others on four evaluation metrics (%, %, F1-% and GC-%), and the best result appears in mGC-IoU metrics (23.3%) when the frame rate is 8fps. This is because the time when the distance between pedestrians in the same group is greater than the threshold may be exactly deleted when the frame rate decreases, so they can easily be judged as the same group, leading to a better performance. But if we decrease frame rate too much, we will lose some crucial information of trajectory, which will make the results even worse. As for the ground truth based trajectory, the experimental results with frame rates of 25fps and 12fps are equally high in P, R, F1- and GC-Acc (91.7%, 88.7%, 90.1% and 89.7%, respectively), but the performance in mGC-IoU metrics (50.0%) is greatest among other experiments when the frame rate is 8fps. So, we can choose a frame rate of 12fps to reduce time complexity and ensure the accuracy of group detection. In conclusion, lowering the frame rate can indeed increase the speed of inference, but it may affect the performance of experiments to a certain degree. For example, when the frame rate is reduced too much (e.g., 8fps), although the reasoning time is reduced, the experimental results will be affected to some extent.
Figure 7.
The histograms of the two sets of comparative experimental average results on SCU-VSD-Social under different frame rates. (a) shows the results on the evaluation metrics under different frame rates based on the YOLOv5 detector + tracking method in [17], while (b) presents the results on the same evaluation metrics based on the ground truth labels.
Table 7.
The inference time in different frame rates on the SCU-VSD-Social dataset.
| 25 | 12 | 8 | |
|---|---|---|---|
| 01 | 5.20 | 2.93 | 1.77 |
| 02 | 1.54 | 0.78 | 0.51 |
| 03 | 0.68 | 0.31 | 0.23 |
| 04 | 1.18 | 0.59 | 0.47 |
| 05 | 1.57 | 0.83 | 0.67 |
| 06 | 0.50 | 0.28 | 0.19 |
| 07 | 1.60 | 0.91 | 0.68 |
| 08 | 0.95 | 0.49 | 0.41 |
| Average | 1.65 | 0.89 | 0.62 |
4.4. Illustration of the experimental results
On the SCU-VSD-Social dataset, the experimental results of the social group detection method based on interpersonal distance are displayed in Fig. 8.
Figure 8.
Visualization of social group detection based on interpersonal distance on SCU-VSD dataset.
As shown from Fig. 8(a) to Fig. 8(h), the social groups in the 8 scenarios of the SCU-VSD-Social dataset are effectively detected and marked. Specifically, different social groups are marked with different colour bounding boxes, and are assigned their group ID numbers. The group bounding box contains pedestrians who have social interactions with each other, and when an individual does not have a social interaction with everyone else in the scene, it is not belong to any social group.
Fig. 9 provides some cases of group detection errors caused by incorrect detections or by interaction inference errors. There are group detection mistakes caused by detection errors in Fig. 9(a): Group 3 has been wrongly detected because of the mistakes of incorrect recognition in person's reflection (Person ID 5) in the mirror of the left picture, while Group 1 has been detected by mistake due to the wrong identification of models in the hall as pedestrians on the right side. In addition, Fig. 9(b) shows the cases of interaction inference errors: the pedestrians with ID 55, 66, and 72 have been clustered erroneously to Group 1 on account of the close distances between them in the left image. Besides, the pedestrian with ID 26 is detected not to belong to Group 4 on the right side due to the far distance between them. However, we can observe the pedestrian with ID 26 is obviously part of Group 4 owing to the social relation among them may be “family”. So, it is considerable to merge the social relations and interpersonal distances into group detection task to enhance the performance of this task.
Figure 9.
Some cases of failing to identify groups. (a) provides group detection errors due to incorrect detections (Group 3 in the left column and Group 1 in the right column), while (b) presents error cases due to interaction inference errors (Group 1 in the left column and Group 4 in the right column).
4.5. Comparison with other social group detection approaches on GVEII dataset
In order to further verify the effectiveness of the proposed social group detection method based on interpersonal distance, it is applied to a public dataset GVEII [34] for social group detection, and the performance is compared with other existing mainstream methods.
The pedestrian trajectory information provided by this dataset are given in the form of the world coordinate system, so there is no need to calibrate the video during the experimental process. The GVEII dataset is shown in Fig. 10, which is a densely crowded scene. On the GVEII dataset, the experimental results and the comparison with other social group detection approaches is shown in Table 8.
Figure 10.

The scene of the GVEII dataset.
Table 8.
Comparison with other social group detection approaches on the GVEII dataset.
As shown in Table 8, on the GVEII dataset, the , , F1-, GC-Acc and mGC-IoU of the proposed social group detection method based on interpersonal distance are 88.4%, 84.8%, 86.6%, 87.1%, and 87.8% respectively. Besides, the three conservative metrics (, and F1-) results are better than those of compared methods. Among the algorithms for comparison, the method proposed by Solera et al. [34] is a machine learning method based on correlation clustering, while the methods proposed by Fernando et al. [36] and Akbari et al. [37] are GAN-based and DNN-based deep learning frameworks respectively. These methods are all supervised learning methods, while our unsupervised method avoids the need for labelling training data that is very time-consuming.
5. Conclusion
In this paper, a new unsupervised approach for social group detection based on spatio-temporal interpersonal distance measurement was proposed, which can identify the social interaction between pedestrian pairs, construct the social interaction matrix and graph in the whole scene, and finally carry out group detection according to the constructed graph. The proposed method needs no training parameters and does not require to label the training data. In practical application scenarios, the source of the video data is not manually labelled. Therefore, the proposed method can be effectively applied to real-life applications without considering issues such as data labelling, parameter training and model generalization. In addition, considering we only use YOLOv5 detector + tracking method [17] in this paper, we will utilise other detection and tracking algorithms to analyse the influence on the performance of group detection method on future works.
Declarations
Author contribution statement
Jie Su: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Jianglan Huang: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Linbo Qing: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Xiaohai He and Honggang Chen: Contributed reagents, materials, analysis tools or data.
Funding statement
Linbo Qing was supported by National Natural Science Foundation of China [61871278].
Honggang Chen was supported by Fundamental Research Funds for the Central Universities [2021SCU12061].
Data availability statement
The authors are unable or have chosen not to specify which data has been used.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Appendix A. Datasets and labelling work
In the pedestrian dataset SCU-VSD [17], we collected 8 video sequences with different scenes and perspective views. For each video sequence, the resolution of each sequence is , the duration is 60 seconds, and the original frame rate is 25 fps. Based on the original frames, we extract one frame every two frames (extract odd frames or even frames respectively) and make the data with frame rate of 12fps. In addition, one frame is extracted every three frames (extract the first frame, the middle one or the last frame respectively) to produce data with a frame rate of 8fps.
A rectangular reference area is selected in shooting, and the real length and width of the reference area is measured for calibration. Fig. A.11 gives an example of SCU-VSD, marking the selected rectangular areas with red boxes. The information of the selected rectangular reference areas and the perspective transformation matrix for SCU-VSD is listed in the literature [17].
Figure A.11.
Examples of the SCU-VSD dataset. (The red rectangular areas are a reference for video calibration).
In order to evaluate the proposed social group detection method, the multi-group labelling work and the pedestrians' trajectories annotation work were further carried out on SCU-VSD to obtain a new dataset named SCU-VSD-Social. For each video, we first obtain the trajectory and ID information of the pedestrians based on the YOLOv5 detector [45] and the online tracking approach proposed in [17] (hereinafter referred to as the detector + tracking algorithm). Due to the limitation of algorithm performance, it is impossible to completely avoid errors such as ID switch. Then, by manual labelling, the IDs of pedestrians with social interaction relationships in the video are labelled as the same social group, and the IDs of individual pedestrians that do not belong to any social group are recorded simultaneously. During the labelling process, each pedestrian can only have one unique ID. If the ID switch occurs in one person, the ID of the longest trajectory will be used as the standard for labelling.
In order to obtain the ground truth of pedestrians' trajectories, based on the detector + tracking algorithm, we manually correct all the ID switch and ID confusion situations of pedestrians' trajectories, and delete the false trajectories information due to misdetection by the detector. For occasional miss detection, the method of drawing a bounding box is used to manually add the position and ID information of the pedestrian in the frame.
In the process of trajectory correction, it needs to correspond with the labels of social group detection one by one to ensure that there will be no redundant IDs. After completing the annotation work, the total number of people, the number of social groups, and the number of group members in each video sequence of the SCU-VSD-social dataset are counted, with detailed information shown in Table A.9.
Table A.9.
The detailed information of social groups of SCU-VSD-Social dataset.
| Dataset∖Group information | Total number of pedestrians | The number of social groups | 2 people | 3 people | 4 people | More than 5 people |
|---|---|---|---|---|---|---|
| SCU-VSD-01 | 68 | 21 | 19 | 1 | 0 | 1 |
| SCU-VSD-02 | 31 | 9 | 7 | 1 | 1 | 0 |
| SCU-VSD-03 | 16 | 4 | 3 | 1 | 0 | 0 |
| SCU-VSD-04 | 36 | 10 | 6 | 2 | 1 | 1 |
| SCU-VSD-05 | 39 | 15 | 12 | 3 | 0 | 0 |
| SCU-VSD-06 | 18 | 4 | 3 | 0 | 1 | 0 |
| SCU-VSD-07 | 43 | 14 | 9 | 3 | 2 | 0 |
| SCU-VSD-08 | 39 | 12 | 9 | 2 | 0 | 1 |
| SCU-VSD Total | 290 | 89 | 68 | 13 | 5 | 3 |
References
- 1.Silva B.N., Khan M., Han K. Towards sustainable smart cities: a review of trends, architectures, components, and open challenges in smart cities. Sustain. Cities Soc. 2018;38:697–713. [Google Scholar]
- 2.Ji T., Chen J.-H., Wei H.-H., Su Y.-C. Towards people-centric smart city development: investigating the citizens' preferences and perceptions about smart-city services in Taiwan. Sustain. Cities Soc. 2021;67 [Google Scholar]
- 3.Zanlungo F., Yücel Z., Brščić D., Kanda T., Hagita N. Intrinsic group behaviour: dependence of pedestrian dyad dynamics on principal social and personal features. PLoS ONE. 2017;12(11) doi: 10.1371/journal.pone.0187253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zanlungo F., Yücel Z., Kanda T. Intrinsic group behaviour II: on the dependence of triad spatial dynamics on social and personal features and on the effect of social interaction on small group dynamics. PLoS ONE. 2019;14(12) doi: 10.1371/journal.pone.0225704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yücel Z., Zanlungo F., Shiomi M. Modeling the impact of interaction on pedestrian group motion. Adv. Robot. 2018;32(3):137–147. [Google Scholar]
- 6.Templeton A., Drury J., Philippides A. From mindless masses to small groups: conceptualizing collective behavior in crowd modeling. Rev. Gen. Psychol. 2015;19(3):215–229. doi: 10.1037/gpr0000032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pellegrini S., Ess A., Schindler K., Van Gool L. 2009 IEEE 12th International Conference on Computer Vision. IEEE; 2009. You'll never walk alone: modeling social behavior for multi-target tracking; pp. 261–268. [Google Scholar]
- 8.Brščić D., Kanda T., Ikeda T., Miyashita T. Person tracking in large public spaces using 3-d range sensors. IEEE Trans. Human-Mach. Syst. 2013;43(6):522–534. [Google Scholar]
- 9.Kalnis P., Mamoulis N., Bakiras S. International Symposium on Spatial and Temporal Databases. Springer; 2005. On discovering moving clusters in spatio-temporal data; pp. 364–381. [Google Scholar]
- 10.Vieira M.R., Bakalov P., Tsotras V.J. Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. 2009. On-line discovery of flock patterns in spatio-temporal data; pp. 286–295. [Google Scholar]
- 11.Pouw C.A., Toschi F., van Schadewijk F., Corbetta A. Monitoring physical distancing for crowd management: real-time trajectory and group analysis. PLoS ONE. 2020;15(10) doi: 10.1371/journal.pone.0240963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yucel Z., Zanlungo F., Feliciani C., Gregorj A., Kanda T. Identification of social relation within pedestrian dyads. PLoS ONE. 2019;14(10) doi: 10.1371/journal.pone.0223656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yücel Z., Zanlungo F., Ikeda T., Miyashita T., Hagita N. Deciphering the crowd: modeling and identification of pedestrian group motion. Sensors. 2013;13(1):875–897. doi: 10.3390/s130100875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zaki M.H., Sayed T. Automated analysis of pedestrian group behavior in urban settings. IEEE Trans. Intell. Transp. Syst. 2017;19(6):1880–1889. [Google Scholar]
- 15.Hall E.T. Doubleday; Garden City, NY: 1966. The Hidden Dimension, vol. 609. [Google Scholar]
- 16.Hall E.T. A system for the notation of proxemic behavior 1. Am. Anthropol. 1963;65(5):1003–1026. [Google Scholar]
- 17.Su J., He X., Qing L., Niu T., Cheng Y., Peng Y. A novel social distancing analysis in urban public space: a new online spatio-temporal trajectory approach. Sustain. Cities Soc. 2021;68 doi: 10.1016/j.scs.2021.102765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Perry A., Rubinsten O., Peled L., Shamay-Tsoory S.G. Don't stand so close to me: a behavioral and erp study of preferred interpersonal distance. NeuroImage. 2013;83:761–769. doi: 10.1016/j.neuroimage.2013.07.042. [DOI] [PubMed] [Google Scholar]
- 19.Abdevali M., Zabihzadeh A. Self-concept and regulation of interpersonal distance in close relationships: a study with comfortable interpersonal distance test. Q. Appl. Psychol. 2021;15(2):207–225. [Google Scholar]
- 20.Wakslak C., Joshi P. Expansive and contractive communication scope: a construal level perspective on the relationship between interpersonal distance and communicative abstraction. Soc. Personal. Psychol. Compass. 2020;14(5):271–284. [Google Scholar]
- 21.Gifford R. Projected interpersonal distance and orientation choices: personality, sex, and social situation. Soc. Psychol. Q. 1982:145–152. [Google Scholar]
- 22.Sundstrom E., Altman I. Interpersonal relationships and personal space: research review and theoretical model. Hum. Ecol. 1976;4(1):47–67. [Google Scholar]
- 23.Groh G., Lehmann A., Reimers J., Frieß M.R., Schwarz L. 2010 IEEE Second International Conference on Social Computing. IEEE; 2010. Detecting social situations from interaction geometry; pp. 1–8. [Google Scholar]
- 24.Cristani M., Bazzani L., Paggetti G., Fossati A., Tosato D., Del Bue A., Menegaz G., Murino V. BMVC. vol. 2. Citeseer; 2011. Social interaction discovery by statistical analysis of f-formations; p. 4. [Google Scholar]
- 25.Cristani M., Paggetti G., Vinciarelli A., Bazzani L., Menegaz G., Murino V. 2011 IEEE Third International Conference on Privacy, Security, Risk and Trust and 2011 IEEE Third International Conference on Social Computing. IEEE; 2011. Towards computational proxemics: inferring social relations from interpersonal distances; pp. 290–297. [Google Scholar]
- 26.Kroczek L.O., Pfaller M., Lange B., Müller M., Mühlberger A. Interpersonal distance during real-time social interaction: insights from subjective experience, behavior, and physiology. Front. Psychol. 2020;11:561. doi: 10.3389/fpsyt.2020.00561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shao J., Loy C.C., Wang X. Learning scene-independent group descriptors for crowd understanding. IEEE Trans. Circuits Syst. Video Technol. 2016;27(6):1290–1303. [Google Scholar]
- 28.Shao J., Loy C.C., Wang X. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2014. Scene-independent group profiling in crowd; pp. 2219–2226. [Google Scholar]
- 29.Chen M., Wang Q., Li X. Anchor-based group detection in crowd scenes. 2017 IEEE International Conference on Acoustics, Speech and Signal Processing; ICASSP; IEEE; 2017. pp. 1378–1382. [Google Scholar]
- 30.Wang Q., Chen M., Nie F., Li X. Detecting coherent groups in crowd scenes by multiview clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018;42(1):46–58. doi: 10.1109/TPAMI.2018.2875002. [DOI] [PubMed] [Google Scholar]
- 31.Han T., Yao H., Sun X., Zhao S., Zhang Y. Unsupervised discovery of crowd activities by saliency-based clustering. Neurocomputing. 2016;171:347–361. [Google Scholar]
- 32.Zhang X., Ma D., Yu H., Huang Y., Howell P., Stevens B. Scene perception guided crowd anomaly detection. Neurocomputing. 2020;414:291–302. [Google Scholar]
- 33.Ge W., Collins R.T., Ruback R.B. Vision-based analysis of small groups in pedestrian crowds. IEEE Trans. Pattern Anal. Mach. Intell. 2012;34(5):1003–1016. doi: 10.1109/TPAMI.2011.176. [DOI] [PubMed] [Google Scholar]
- 34.Solera F., Calderara S., Cucchiara R. Socially constrained structural learning for groups detection in crowd. IEEE Trans. Pattern Anal. Mach. Intell. 2015;38(5):995–1008. doi: 10.1109/TPAMI.2015.2470658. [DOI] [PubMed] [Google Scholar]
- 35.Tan K., Xu L., Liu Y., Luo B. Small group detection in crowds using interaction information. IEICE Trans. Inf. Syst. 2017;100(7):1542–1545. [Google Scholar]
- 36.Fernando T., Denman S., Sridharan S., Fookes Gd-gan C. Asian Conference on Computer Vision. Springer; 2018. Generative adversarial networks for trajectory prediction and group detection in crowds; pp. 314–330. [Google Scholar]
- 37.Akbari A., Farsi H., Mohamadzadeh S. Deep neural network with extracted features for social group detection. J. Electr. Comput. Eng. Innov. 2021;9(1):47–56. [Google Scholar]
- 38.Sun J., Jiang Q., Lu C. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020. Recursive social behavior graph for trajectory prediction; pp. 660–669. [Google Scholar]
- 39.Ehsanpour M., Abedin A., Saleh F., Shi J., Reid I., Rezatofighi H. Joint learning of social groups, individuals action and sub-group activities in videos. Computer Vision–ECCV 2020: 16th European Conference, Proceedings, Part IX 16; Glasgow, UK, August 23–28, 2020; Springer; 2020. pp. 177–195. [Google Scholar]
- 40.Gupta A., Johnson J., Fei-Fei L., Savarese S., Alahi A. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018. Social gan: socially acceptable trajectories with generative adversarial networks; pp. 2255–2264. [Google Scholar]
- 41.Veličković P., Cucurull G., Casanova A., Romero A., Lio P., Bengio Y. Graph attention networks. arXiv:1710.10903 arXiv preprint.
- 42.Eiter T., Mannila H. 1994. Computing discrete Fréchet distance. Tech. Rep., Citeseer. [Google Scholar]
- 43.Kuhn H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955;2(1–2):83–97. [Google Scholar]
- 44.Xie J., Girshick R., Farhadi A. International Conference on Machine Learning, PMLR. 2016. Unsupervised deep embedding for clustering analysis; pp. 478–487. [Google Scholar]
- 45.Jocher G., Stoken A., Borovec J. 2020. https://zenodo.org/record/3983579#.YUWeQSviuM8 NanoCode012, ChristopherSTAN, C. Liu, Laughing, A. Hogan, lorenzomammana, tkianai, yxNONG, AlexWang1900, L. Diaconu, Marc, wanghaoyang0106, ml5ah, Doug, Hatovix, J. Poznanski, L. Yu, changyu98, P. Rai, R. Ferriday, T. Sullivan, X. Wang, YuriRibeiro, E. R. Claramunt, hopesala, pritul dave, yzchen, ultralytics/yolov5: v3.0.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors are unable or have chosen not to specify which data has been used.