Impact of scanner variability on lymph node segmentation in computational pathology

Abstract

Computer-aided diagnostics in histopathology are based on the digitization of glass slides. However, heterogeneity between the images generated by different slide scanners can unfavorably affect the performance of computational algorithms. Here, we evaluate the impact of scanner variability on lymph node segmentation due to its clinical importance in colorectal cancer diagnosis. 100 slides containing 276 lymph nodes were digitized using 4 different slide scanners, and 50 of the lymph nodes containing metastatic cancer cells. These 400 scans were subsequently annotated by 2 experienced pathologists to precisely label lymph node boundary. Three different segmentation methods were then applied and compared: Hematoxylin-channel-based thresholding (HCT), Hematoxylin-based active contours (HAC), and a convolution neural network (U-Net). Evaluation of U-Net trained from both a single scanner and an ensemble of all scanners was completed. Mosaic images based on representative tiles from a scanner were used as a reference image to normalize the new data from different test scanners to evaluate the performance of a pre-trained model. Fine-tuning was carried out by using weights of a model trained on one scanner to initialize model weights for other scanners. To evaluate the domain generalization, domain adversarial learning and stain mix-up augmentation were also implemented. Results show that fine-tuning and domain adversarial learning decreased the impact of scanner variability and greatly improved segmentation across scanners. Overall, U-Net with stain mix-up (Matthews correlation coefficient (MCC) = 0.87), domain adversarial learning (MCC = 0.86), and HAC (MCC = 0.87) were shown to outperform HCT (MCC = 0.81) for segmentation of lymph nodes when compared against the ground truth. The findings of this study should be considered for future algorithms applied in diagnostic routines.

Introduction

Development of algorithms to assist pathologists in their daily diagnostic routine is an active and thriving area of research.^1,2,3,4,5 Slide scanners are used to digitize tissue slides from glass to whole slide images (WSI). However, each scanner has its own set of parameters and properties (i.e. camera sensors, illumination sources, software etc.). This diversity leads to scanner induced heterogeneity issues in WSI data that contributes to differences in stain presentation and contrast distributions, shown to affect downstream image analytics.^6,7,8,9

Various approaches have been proposed on how to generalize machine learning algorithms to WSI data from multiple sources. For instance, Lafarge et al¹⁰ demonstrated that a combination of domain adversarial and color augmentation improved cross-scanner mitosis detection on both internal and external cohorts. In Ciompi et al,¹¹ they found that the stain normalization is an important step in training and evaluation of colorectal cancer (CRC) classification to minimize source variability.

Similarly, Tellez et al¹² showed that the convolutional neural network (CNN) classifiers performed better with the combination of color augmentation and stain color normalization. In Zheng et al,¹³ an adaptive color deconvolution technique is proposed to normalize the WSI, showing improvement in the performance of sentinel lymph node metastasis detection. These prior works all compare slides generated from multiple sources. As a result, these slides have not only stain and contrast heterogeneity, but also suffer from inter-patient differences. Therefore, it is difficult to disentangle the various sources of heterogeneity imparted on the images.

To the best of our knowledge, the effects of heterogeneity caused by the slide scanners on the performance of image analysis algorithms in computational pathology has not yet been systematically evaluated. This study attempts to fill this niche via the lymph node segmentation across 3 different algorithms under various experiments: Hematoxylin-channel-based thresholding (HCT), Hematoxylin-based active contours (HAC), and a convolution network (U-Net). Identifying the precise boundaries of lymph nodes are critical to assist downstream efforts in CRC diagnosis.^14,15 Knowledge of positive lymph nodes for metastatic cancer is critical for guiding adjuvant chemotherapy planning.^16,17 According to clinical guidelines a minimum of 12 lymph nodes should be histologically assessed. For lymph node metastasis diagnosis, a single tumor cell counts, therefore, a precise lymph node segmentation is a critical factor for proper metastasis detection. Here, the impact of scanner variability on determining the precise localization of lymph nodes on WSI was evaluated.

Materials and methods

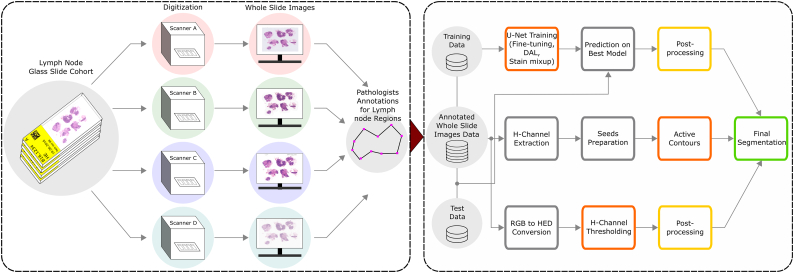
The overall workflow adopted in this study is shown in Fig. 1. Briefly, the same lymph node glass slide cohort is digitized using 4 different scanners. Each WSI was subsequently annotated by the pathologists for lymph node boundaries. After dividing into training and testing set, 3 different segmentation methods were applied (see Segmentation methods). Results were compared to the ground truth using two different evaluation metrics (Matthews correlation coefficient and Hausdorff Distance, see Evaluation measures). The following subsections describe each step of the workflow in more detail.

Fig. 1.

The workflow to assess the impact of scanner variability on lymph node segmentation. Same lymph node glass slide cohort is digitized using 4 different scanners and given to expert pathologists for lymph node annotations. The annotated WSI are then distributed into test and train sets to evaluate the scanner variability with the help of 3 different segmentation methods (i.e. core method in orange color): Hematoxylin-channel-based thresholding (HCT), Hematoxylin-based active contours (HAC), and a convolution network (U-Net). In order to minimize scanner variability, the segmentation methods are evaluated with normalization, fine-tuning, domain adversarial learning, and stain mix-up experiments. Upon application of segmentation methods, the post-processing (i.e in yellow color) is used for HCT and U-Net to achieve final segmented nodes (i.e in green color) by eliminating the undesired pixels around the region of interests. The HAC method uses an iterative smoothing operator and does not require final post-processing step.

Dataset

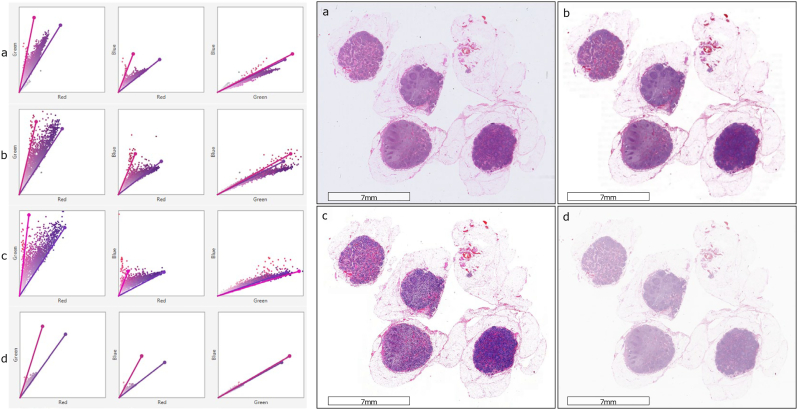
From n = 69 patients (metastatically positive cases: 28, negative cases: 41) at the Institute of Pathology, University of Bern, 100 glass slides of lymph node tissues were stained with Hematoxylin and Eosin (H&E). These slides contained 276 lymph nodes (metastatically positive: 50, negative: 226). The glass slides were scanned using 4 scanners: 3Dhistech P250, 3Dhistech P1000, Aperio GT450, and Hamamatsu S360. Due to proprietary issues, all scanners are anonymized as Scanner A, B, C, and D. The magnification and resolution varied depending on the scanner type: (a) Scanner A and B have 20× objective magnification and a pixel resolution of 0.460 μm and 0.243 μm respectively, and (b) Scanners C and D have 40× magnification (with 20× objective magnification and a 2× aperture boost) with 0.243 μm and 0.262 μm pixel resolution respectively. Fig. 2 shows the stain variability between the same slide scanned with the 4 different scanners. A detailed visual representation of stain vectors for all the data from four different scanners can be seen in Fig. A.2. In addition, the structural similarities (based on luminance, contrast, and structure) across the images from all the scanners can be observed in Fig. A.1.

Fig. 2.

A sample slide scanned with 4 different scanners. The whole slide images (right) and corresponding stain vectors (left) show the stain color and contrast differences when digitized with (a) Scanner A, (b) Scanner B, (c) Scanner C, and (d) Scanner D.

Lymph node annotations and observer variability

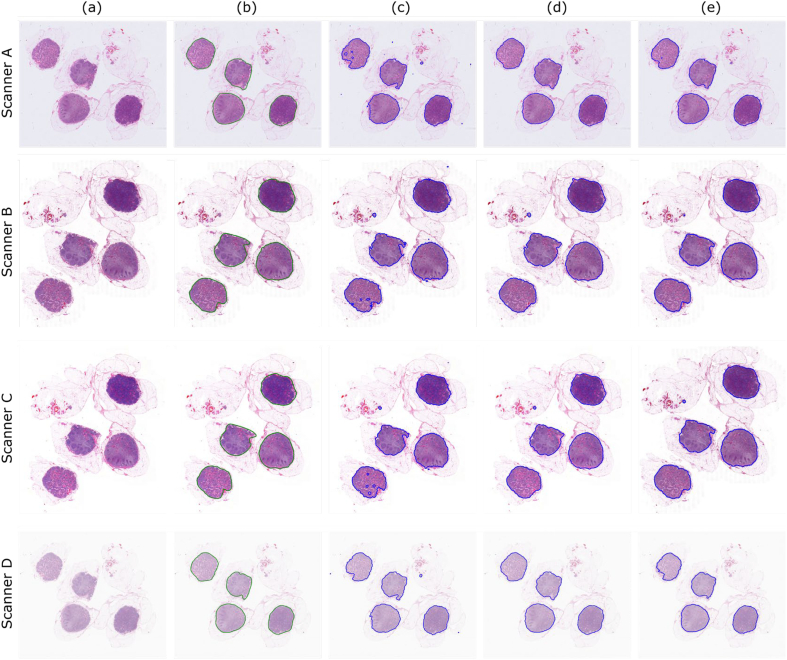
Upon scanning the slides, the acquired WSI from each scanner were visually inspected. Apart from variations in stain color and contrast, tissue detection (e.g. missing tissue) related issues differed by scanner, likely due to differences in hardware and software. As a result, digital images from the same glass slide cannot be perfectly registered across scanners. Particularly, Scanner B has mechanical limitations in scanning the full tissue region of the glass slide, and as such lymph node areas at the borders and corners of the glass slide were not scanned and thus missing from the WSI. To compensate for these issues, lymph nodes were independently annotated per WSI. Two experienced pathologists at the Institute of Pathology, University of Bern traced each lymph node (capsule and subcapsular sinus region) using the polygon tool of the Automated Slide Analysis Platform (ASAP)¹⁸ (see Fig. 4 column (b)).

Fig. 4.

A few qualitative examples of segmentation results by 3 methods across 4 scanners, column (a) re-scaled WSI, (b) ground truth, (c) HCT, (d) HAC, and (e) U-Net results. Particularly, U-Net and HAC shown a better performance detecting the boundaries. HCT method slightly failed to fully segment the lymph nodes, which most likely is due to the fact that the thresholding could not adapt to the intensity variations.

In order to evaluate the inter and intra-observer variability, the 100 WSI from Scanner A were employed. This scanner was selected due to its existing validation on diagnostic workflows at the institute. WSI are divided equally into 2 sets of 50 and provided to both pathologists who were also asked to re-annotate them again after an approximate 3 months washout period.

Segmentation methods

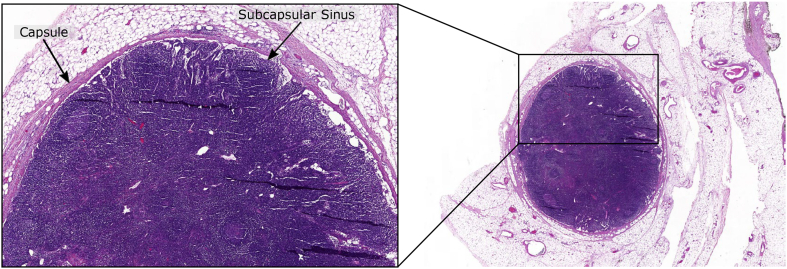
An especially challenging lymph node is shown in Fig. 3 that tends to confound segmentation methods. The undesired tissue regions around lymph nodes are similar in stain color and morphology to the capsule or small blood vessels inside a lymph node. Differentiating between these regions is thus fraught with difficulties. Image segmentation tasks are typically performed via intensity, morphology, or deep learning-based methods, so one approach of each is introduced below and employed in this study for comparison.

Fig. 3.

An exemplary whole slide image explains the morphology of the lymph node, where the region dense with nuclei is packed within a capsule and the inner area is called the subcapsular sinus. From the diagnostic point of view, the quantification of positive lymph nodes (i.e. visual identification of tumor cells) in TNM (Tumor , Lymph Nodes , Metastases ) staging is an important prognostic-marker and this visual search for tumor cells starts at the capsular region. The outer region (outward from the capsule) mostly contains fatty tissue, blood vessels, and muscle tissue; and is similar in stain color and morphology to the capsule.

Hematoxylin-channel-based thresholding

The selection of Hematoxylin-channel-based thresholding (HCT) was motivated by Lee and Paeng,¹⁹ where tissue regions of sentinel breast lymph nodes were successfully segmented for cancer stage classification.⁷ In HCT ,the Otsu threshold²⁰ is applied to the Hematoxylin-channel of each image after conversion from RGB to HED color vectors.^21,22 Upon thresholding, the local median was calculated with a disk structural element of 2 pixels and all holes were then filled in the binary mask, In order to obtain the final segmented lymph nodes, local binary morphological operations, dilation, and erosion with 6×6 and 3×3 filters respectively were used to remove spurious objects.

Hematoxylin-based active contours

Hematoxylin-based active contours (HAC) uses the morphological active contours method^23,24 where the lymph nodes were segmented using initial seeds. Down-sampled WSI were first deconvolved to separate Hematoxylin from Eosin stain^21,22 and Otsu threshold²⁰ was then applied to the separated Hematoxylin channel to get the seeds (as performed in HCT). These seeds correspond to Hematoxylin rich areas, likely candidates for lymph node presence. The seeds then grow to the boundaries of the lymph node capsule. The number of iterations and number of times the smoothing operator is applied per iteration were empirically chosen.

Convolution network: U-Net

The U-Net architecture with a small modifications was selected.²⁵ The network is consisting of 23 convolution layers and around 7.5 millions of parameters. The network summary is attached with the supplementary material.

Experimental design

All WSI were first down-scaled to 20× to ensure fair comparison regardless of base magnification, and then subsequently down-scaled again by a factor of 64, allowing them to fit into memory. The corresponding ground-truth annotations were similarly down-scaled.

HCT and HAC experiments

In both HCT and HAC, neither method requires a supervised training set and therefore could be applied to all WSI. As a pre-processing step, a Gaussian filter with a kernel size of 3×3 was applied to smooth the input image, helping to reduce noise. In HAC, the parameters such as number of iterations and number of times the smoothing operator is applied per iteration were empirically chosen as 150 and 10, respectively.

U-Net experiments

To train the U-Net, the down-scaled WSI were re-scaled further to 512×512 pixels to fit to the network. To evaluate the method across all the samples, the WSI from each scanner were divided into training (n = 80) and test (n = 20) sets by using 5-fold cross-validation. To compare the performance across all the scanners, same indices were used in each corresponding fold from all scanners to split data into training and test sets. The weights of the network were optimized using binary cross-entropy loss function, minimized with the Adam optimizer.²⁶ The learning rate was explicitly reduced upon plateau by a factor of 0.1. In order to minimize over-fitting, training samples were augmented by flipping, color, and brightness augmentations. For color augmentation, the image was converted from RGB to HED and stain vectors were then modified with linear contrast having alpha range of [0.5, 0.2], whereas brightness was randomly modified by multiplying and adding the factor of 0.75 and 15, respectively.^27,12 In the post-processing step, the final binary mask was obtained by considering the pixels with a higher probability than 50%. Five sets of experiments were executed: Single scanner versus all scanners training, stain color normalization, fine-tuning using inter-scanner weights, domain adversarial learning, and stain mix-up augmentation.

Single versus all scanners training. In single versus all scanners training, the U-Net was trained using data from one scanner and the best performing model on its associated cross-validation set was applied to the test sets from all other scanners. Training sets from all scanners were then merged and used to train a singular U-Net which was again applied on the held-out testing folds. In both cases, the network was trained for 200 epochs with a learning rate of 1e-3.

Stain color normalization. The literature suggests that color normalization improves U-Net resilience to stain and scanner variability.^28,29 Here, normalization was performed by creating a reference mosaic image that contained a balanced set of representative tiles from background and foreground regions (lymph node tissues) of the WSI belonging to a scanner. This reference mosaic image is then used to normalize all the WSI from test scanners successively by using 3 different image normalization methods, Macenko, Vahadane, and Reinhard.^21,30,31 The first 2 methods use stain deconvolution to adjust the specific hematoxylin and eosin stain vectors and the latter is based on color distribution in the Lab color space. A few example mosaic images created from WSI of different scanners are presented in Fig. A.5.

Fine-tuninginter-scanner weights. To test the hypothesis that the pre-existing model of one scanner could achieve similar performance on the target scanner in a computationally cost-effective way, fine-tuning was employed. Fine-tuning sees the initialization of a new model with weights from a previously trained model. For example, after the U-Net for Scanner A converges, these weights are employed to initialize a new model for training on Scanner B. One can then measure the performance difference from applying Scanner A to Scanner B data directly versus via the fine-tuned model. The fine-tuning process is performed for 25 epochs at a low learning rate of 1e-5, by unfreezing first 3 and last 3 convolutional layers of contraction and expansion paths of the proposed U-Net model respectively.

Domain adversarial learning. Domain adversarial learning (DAL) is a method for domain adaptation where additional unlabeled data from multiple known domains is used to train a domain discriminator using the initial model’s output embedding. However, gradients from the domain discriminator are reversed thereby training the main model to focus on domain invariant features rather than overfitting to domain-specific ones. In this experiment, we simultaneously trained a U-Net for lymph node segmentation and an additional CNN to discriminate between the input domains using activations of the U-Net.³² An adversarial training step through a gradient reversal layer is introduced to optimize segmentation and domain discriminator networks while decreasing the amount of domain-specific information in the U-Net output activations. The domain discriminator CNN consists of 4 convolutional layers, each with ReLu activations, batch normalization, and a max-pooling, then 3 fully connected layers with ReLu activations.³² In this experiment, each scanner is considered a domain and assigned an integer label. To train the DAL network over all the scanners, each time, a scanner is considered as a training domain and the rest of the 3 scanners as unseen domains. In the training domain, the samples contain annotated lymph node masks and domain labels, whereas, in the unseen domains, the samples contain only domain labels without any annotated mask. The training of the DAL network was performed in three steps using a similar schedule as Scannell et al.,³² but for 200 epochs. In the first step, the U-Net network was trained on the domain scanner for 50 epochs with a learning rate of 1e-3. In the second step, the domain discriminator was trained for the next 50 epochs with a learning rate of 1e-4. In the third step, both U-Net segmentation and domain discriminator CNN were trained together with adversarial update. After 50 epochs, the adversarial update was increased with a linear factor from 0 to 1. Each training cycle was performed with a 5-fold cross-validation, data augmentation, optimizer, and loss function (except the domain discriminator was trained by using Categorical Cross-entropy loss function) similar to the baseline experiments (i.e. Single versus all scanners training). The DAL model was evaluated by comparing the results of training and unseen domains on their respective test samples.

Stain mix-up augmentation. The stain mix-up augmentation shows unseen color domain generalization in pathological images by encouraging the model during the training to learn variations in the stain colors.³³ In the training step, the stain mix incorporates the stain colors of unseen domains to generalize the model. In this experiment, we employed the stain mix-up technique to train the U-Net for the segmentation of lymph nodes. Each training cycle consisted of a pair of 2 scanners, where 1 scanner was considered a training domain and the other a test domain. Two mosaic images were created from the background and foreground samples of each training set of training and test domains. Their stain vectors were then estimated and during the training of the segmentation model a random stain color augmentation was applied by mixing the 2 estimated stains. Each training cycle was performed with a 5-fold cross-validation, data augmentation, optimizer, loss function, number of epochs, and learning rate the same as the baseline experiments (i.e. Single versus all scanners training). The final model was evaluated to compare the results on the corresponding test sets of training and test domains. This technique was repeated for all possible combinations of scanners by considering them as training and test domains.

Evaluation measures

The segmentation methods are quantitatively evaluated using 2 metrics. Pixel-level differences are measured using the Matthews correlation coefficient (MCC).^34,35 The MCC between ground truth and segmented labels are calculated as given in Eq.(1).

$$\mathit{MCC}=\frac{\mathit{TP}\times \mathit{TN}-\mathit{FP}\times \mathit{FN}}{\sqrt{\left(\mathit{TP}+\mathit{FP}\right)\left(\mathit{TP}+\mathit{FN}\right)\left(\mathit{TN}+\mathit{FP}\right)\left(\mathit{TN}+\mathit{FN}\right)}}$$ (1)

where TP is the number of true positives, TN the number of true negatives, FP the number false positives, and FN the number of false negatives. MCC ranges between -1 and +1 where +1 represents a perfect prediction, 0 an average random prediction, and -1 inverse prediction when comparing with the ground truth. Boundary differences are measured using the Hausdorff Distance (HD).³⁶ HD calculates the maximum Euclidean distance from all the minimum distances between boundaries of ground truth (A) and boundaries of segmentation region (B) as given in Eq.(2).

$$\mathit{HD}\left(A,B\right)=max\left(h\left(A,B\right),h\left(B,A\right)\right)$$ (2)

where h(A,B) is the directed Hausdorff distance based on Equation (3)

$$h\left(A,B\right)=\underset{a\in A}{max}\underset{b\in B}{min}‖a-b‖$$ (3)

where ‖a − b‖ represents the Euclidean distance. HD between 2 perfectly overlapped boundaries is equal to zero. Expected ranges of HD for good, acceptable, and bad scores could be less than 100 μm, between 100 μm and 150 μm and higher than 150 μm, respectively. Statistical significance between different experiments on MCC accross different scanners is determined with the Wilcoxon, Friedman test and Nemenyi post-hoc test.^37,38, 39

Results

Observer variability

The mean MCC values for inter- and intra-observer variability are shown in Table 1. These results suggest that inter- and intra-observer variability is small, and the minimal differences that are present were not deemed to be clinically relevant.

Table 1.

The outcome of observer variability across the lymph node annotations (ground truth) carried out by 2 pathologists, average scores on the scale MCC and HD.

	MCC	HD (μm)
Inter-observer (n=50)	0.94±0.07	80.51±41.48
Intra-observer (n=50)	0.95±0.06	76.00±43.84

HCT and HAC experiments

The results from HCT and HAC lymph node segmentation without and with normalization using Macenko, Vahadane, and Reinhard methods are presented in Table 2. In case of no normalization, the HCT showed a performance in the range of 0.76 and 0.81 on MCC score by Scanner D and A, respectively. The higher boundary losses (HD) were observed, especially on Scanner C. Comparatively, HAC showed better performance than HCT for 3 out of 4 scanners, where Scanner A has scored 0.87 on MCC and Scanner B outperformed on HD with a score of 120.58 μm. In the case of normalization methods, the overall performance variability increased on both HCT and HAC methods. After normalizing with Macenko, both the methods showed drop in the performance in all test scanners except Scanner C in HAC. Similar trend is noticed in the Vahadane and Reinhard normalization-based results. However, in comparison with other 2 normalization methods, the Reinhard technique was able to minimize the variability with an overall drop in performance in HAC. The post-hoc analyses on both HCT and HAC with and without normalization (see Fig. A.3 and Table A.1) suggested that the performance of the HAC method was consistent for both pre- and post-normalization, whereas HCT showed variability in performance when normalization was introduced.

Table 2.

Mean MCC and HD scores on HCT and HAC lymph node segmentation methods without and with normalization using Macenko, Vahadane, and Reinhard methods. In case of normalization methods, the mean MCC and HD scores of the test scanners are upon normalizing with best performing scanners (e.g. Scanner B and A in HCT and HAC, respectively). P-values are based on MCC scores from all scanners.

Methods		Test scanner	MCC	HD (μm)	P-value
No normalization	HCT	A	0.80 ± 0.21	185.43 ± 126.12	6.09E − 08
		B	0.81 ± 0.26	123.52 ± 54.36
		C	0.80 ± 0.25	214.94 ± 184.80
		D	0.76 ± 0.29	185.48 ± 91.44
	HAC	A	0.87 ± 0.21	165.76 ± 98.53	5.78E − 08
		B	0.82 ± 0.27	120.58 ± 49.43
		C	0.85 ± 0.26	171.63 ± 96.46
		D	0.81 ± 0.29	177.58 ± 82.63
Macenko	HCT	A	0.77 ± 0.24	189.20 ± 106.38	2.29E − 11
		B	0.81 ± 0.26	123.52 ± 54.36
		C	0.79 ± 0.25	175.36 ± 76.02
		D	0.69 ± 0.34	206.14 ± 116.46
	HAC	A	0.87 ± 0.21	165.76 ± 98.53	1.27E − 09
		B	0.79 ± 0.29	124.27 ± 49.31
		C	0.85 ± 0.25	153.31 ± 62.57
		D	0.75 ± 0.35	193.25 ± 107.46
Vahadane	HCT	A	0.67 ± 0.35	243.07 ± 196.36	4.25E − 09
		B	0.81 ± 0.26	123.52 ± 54.36
		C	0.79 ± 0.25	176.36 ± 78.40
		D	0.58 ± 0.43	253.35 ± 171.29
	HAC	A	0.87 ± 0.21	165.76 ± 98.53	3.72E-09
		B	0.77 ± 0.30	126.44 ± 47.76
		C	0.85 ± 0.23	155.72 ± 64.58
		D	0.62 ± 0.43	241.99 ± 158.82
Reinhard	HCT	A	0.74 ± 0.30	222.00 ± 192.50	1.29E − 10
		B	0.81 ± 0.26	123.52 ± 54.36
		C	0.64 ± 0.32	237.24 ± 129.03
		D	0.71 ± 0.31	226.80 ± 166.68
	HAC	A	0.87 ± 0.21	165.76 ± 98.53	1.53E − 05
		B	0.76 ± 0.35	159.10 ± 110.34
		C	0.75 ± 0.35	197.78 ± 103.86
		D	0.76 ± 0.35	212.37 ± 176.00

U-Net experiments

Single versus all scanners training

There are several findings when comparing single versus all training (see Table 3). The model outperformed (MCC = 0.87) when it was trained by Scanner D and tested on C. When U-Net was trained on the data from Scanner A, B, and C, and tested on Scanner D, then the model showed slightly poor performance on the MCC metric, likely, due to the low-contrasted WSI. By considering the training and test set from the same scanner, the network outperformed on Scanner B and C with a mean MCC of 0.81 and the boundary losses reduced to a mean HD of 87.52 μm by Scanner B. In addition, when the network was trained on the samples from all 4 scanners, the mean MCC and HD in each scanner were even improved to what we have achieved on the single scanner training and testing except Scanner D that shown slight drop in performance (see Table 3). The network achieved the highest mean MCC value of 0.85 and mean HD reduced to 80 μm on Scanner B. In the single scanner training experiment, the performance variability was increased in all test scanners when compared to the outcome with the training scanner. When Scanner D was used as training scanner than variations were less compared to other 3 experiments where Scanners A, B, and C were used as training scanners. In all scanners training-based experiments, a similar trend was noticed where the U-Net performed worse on the Scanner D as compared to other scanners. Nonetheless, all scanners training have shown less variance in performance compared to the first 3 combinations of experiments in single scanner training.

Table 3.

Mean MCC and HD scores using U-Net for lymph node segmentation with single versus all scanners training strategy. P-values are based on MCC scores between train and test scanners when the U-Net is applied.

Train scanner		Test scanner	MCC	HD (μm)	P-value
Single scanner	A	A	0.80 ± 0.22	141.95 ± 82.36	2.72E − 25
		B	0.76 ± 0.23	85.03 ± 41.89
		C	0.81 ± 0.20	150.91 ± 79.45
		D	0.38 ± 0.40	248.79 ± 132.49
	B	A	0.78 ± 0.20	149.63 ± 83.08	3.74E − 29
		B	0.81 ± 0.20	87.52 ± 46.23
		C	0.79 ± 0.20	159.13 ± 78.71
		D	0.22 ± 0.27	284.86 ± 122.38
	C	A	0.78 ± 0.20	154.20 ± 91.41	1.02E − 44
		B	0.79 ± 0.20	90.81 ± 47.93
		C	0.81 ± 0.19	156.70 ± 79.84
		D	0.18 ± 0.22	292.53 ± 119.52
	D	A	0.69 ± 0.29	170.25 ± 100.26	2.52E − 16
		B	0.84 ± 0.18	74.77 ± 41.86
		C	0.87 ± 0.15	132.36 ± 71.71
		D	0.83 ± 0.19	149.67 ± 83.95
All scanners		A	0.82 ± 0.21	133.74 ± 76.78	1.03E − 19
		B	0.85 ± 0.21	80.00 ± 42.21
		C	0.82 ± 0.20	146.01 ± 71.24
		D	0.76 ± 0.25	162.67 ± 82.14

Stain color normalization

In stain normalization experiments, a mosaic from the test set of each fold of the training scanner was created and then each WSI from the corresponding fold of the test scanner was normalized to that mosaic by using Macenko, Vahadane, and Reinhard normalization methods. Same models trained in the single scanner training experiments on the corresponding training scanners were used to segment the lymph nodes on the normalized images of the each test scanner. The results of the mosaic reference image normalization approaches are tabulated in Table 4. In all 3 normalization methods, the overall performance was dropped, however, Scanner D has shown improved performance of around 54% as compared to single training experiments when tested on the model trained on Scanners A, B, and C. The Macenko and Reinhard normalization approaches have shown better performance as compared to Vahadane to minimize the variability of outcome. Overall, Reinhard has shown better resilience to performance variances in all experiments compared to its counterparts. Such performance by these normalization methods can also be observed from the post-hoc analyses presented in Fig. A.4, Table A.2, and Table A.3.

Table 4.

Mean MCC and HD values using U-Net-based lymph node segmentation by stain color normalizing WSI of test scanner to train scanner (mosaic-based normalization) by using using Macenko, Vahadane, and Reinhard methods. P-values are based on MCC scores between train and normalized scanners.

Methods	Train scanner	Normalized scanner	MCC	HD (μm)	P-value
Macenko	A	A	0.80 ± 0.22	141.95 ± 82.36	0.190
		B	0.74 ± 0.27	84.98 ± 44.72
		C	0.73 ± 0.27	150.04 ± 74.95
		D	0.73 ± 0.29	149.56 ± 80.04
	B	A	0.60 ± 0.39	175.15 ± 102.93	0.002
		B	0.81 ± 0.20	87.52 ± 46.23
		C	0.73 ± 0.27	149.89 ± 66.38
		D	0.65 ± 0.35	161.21 ± 84.03
	C	A	0.52 ± 0.41	176.48 ± 83.22	5.37E − 18
		B	0.76 ± 0.27	86.29 ± 42.75
		C	0.81 ± 0.19	156.70 ± 79.84
		D	0.62 ± 0.37	167.56 ± 90.85
	D	A	0.55 ± 0.30	203.10 ± 119	3.58E − 19
		B	0.78 ± 0.25	87.64 ± 50.55
		C	0.77 ± 0.25	144.48 ± 76.96
		D	0.83 ± 0.19	149.67 ± 83.95
Vahadane	A	A	0.80 ± 0.22	141.95 ± 82.36	1.83E − 04
		B	0.73 ± 0.27	84.86 ± 43.82
		C	0.70 ± 0.28	153.00 ± 75.57
		D	0.58 ± 0.36	177.73 ± 98.97
	B	A	0.46 ± 0.49	190.18 ± 118.82	1.81E − 07
		B	0.81 ± 0.20	87.52 ± 46.23
		C	0.72 ± 0.27	157.17 ± 74.03
		D	0.49 ± 0.49	190.49 ± 106.54
	C	A	0.40 ± 0.52	188.89 ± 99.36	5.61E − 17
		B	0.75 ± 0.28	87.33 ± 44.97
		C	0.81 ± 0.19	156.70 ± 79.84
		D	0.47 ± 0.50	197.69 ± 116.63
	D	A	0.49 ± 0.39	202.32 ± 112.66	1.81E − 23
		B	0.77 ± 0.26	88.21 ± 51.92
		C	0.76 ± 0.26	148.11 ± 82.23
		D	0.83 ± 0.19	149.67 ± 83.95
Reinhard	A	A	0.80 ± 0.22	141.95 ± 82.36	0.44
		B	0.76 ± 0.26	85.08 ± 52.23
		C	0.78 ± 0.23	143.79 ± 73.66
		D	0.77 ± 0.26	145.12 ± 84.41
	B	A	0.74 ± 0.24	140.53 ± 82.76	0.11
		B	0.81 ± 0.20	87.52 ± 46.23
		C	0.76 ± 0.25	139.67 ± 66.05
		D	0.75 ± 0.25	145.39 ± 81.53
	C	A	0.71 ± 0.25	149.52 ± 92.46	1.13E − 05
		B	0.71 ± 0.25	91.69 ± 54.42
		C	0.81 ± 0.19	156.70 ± 79.84
		D	0.72 ± 0.25	156.30 ± 92.03
	D	A	0.76 ± 0.22	149.22 ± 98.30	6.02E − 07
		B	0.75 ± 0.23	93.85 ± 55.99
		C	0.78 ± 0.22	154.53 ± 90.29
		D	0.83 ± 0.19	149.67 ± 83.95

Fine-tuninginter-scanner weights

A significant improvement can be seen in all metrics when fine-tuning was employed (see Table 5). In comparison with the single scanner training and stain color normalization approaches, the fine-tuning showed promising improvement to reduce scanner variabilities (see Table 3, Table 4). Specifically, both MCC and HD variances were significantly reduced in contrast with the mosaic image-based normalization approaches. The performance on Scanner D has improved most evidently up to 10% on MCC when a pre-trained model was fine-tuned for other scanners. The model has outperformed when trained on Scanner D and fine-tuned with Scanner C (MCC 0.87). These results reflect fine-tuning as an effective approach that requires a smaller number of epochs to achieve consistent results on the data from another scanner.

Table 5.

Mean MCC and HD values using U-Net-based lymph node segmentation by fine-tuning test scanner to pre-trained weights of train scanner. P-values are based on MCC scores between train and fine-tuned scanners.

Train scanner	Fine-tuned scanner	MCC	HD (μm)	P-value
A	–	0.80 ± 0.22	141.95 ± 82.36	4.55E − 05
	B	0.81 ± 0.21	82.17 ± 40.96
	C	0.85 ± 0.18	137.51 ± 68.12
	D	0.77 ± 0.25	151.87 ± 78.28
B	A	0.80 ± 0.20	141.27 ± 84.15	3.31E − 05
	–	0.81 ± 0.20	87.52 ± 46.23
	C	0.82 ± 0.18	149.71 ± 75.07
	D	0.73 ± 0.26	173.04 ± 92.99
C	A	0.78 ± 0.20	154.43 ± 91.76	1.52E − 14
	B	0.82 ± 0.19	84.59 ± 45.32
	–	0.81 ± 0.19	156.70 ± 79.84
	D	0.75 ± 0.25	169.19 ± 97.35
D	A	0.86 ± 0.17	123.87 ± 74.08	8.71E − 05
	B	0.85 ± 0.19	77.58 ± 42.05
	C	0.87 ± 0.16	130.02 ± 67.91
	–	0.83 ± 0.19	149.67 ± 83.95

Domain adversarial learning

In this set of experiments, all the training domains (scanners) have shown similar outcomes when tested on their respective test sets (i.e. Scanner A, B, and C scored MCC=0.86 and Scanner D scored MCC = 0.85, see Table 6). Overall, all metrics improve when comparing with single scanner training, stain normalization and fine-tuning approaches. Scanner B outperformed all previous experiments in this study with a very low boundary losses (HD = 72.79 μm). However, the DAL-trained model still performed poorly on Scanners D and A when trained on Scanners A, B, C, and D, respectively and having D and A as unlabeled target scanners. Nevertheless, the DAL has shown to be an effective technique to train the segmentation model on the unseen domains without any additional annotation required to cope with performance variances.

Table 6.

Mean MCC and HD values using domain adversarial learning-based lymph node segmentation. P-values are based on MCC scores between training and unseen domains (scanners).

Training domain	Unseen domain	MCC	HD (μm)	P-value
A	–	0.86 ± 0.17	120.54 ± 61.25	7.39E − 31
	B	0.86 ± 0.18	72.79 ± 36.79
	C	0.86 ± 0.16	138.77 ± 67.04
	D	0.59 ± 0.32	201.67 ± 102.97
B	A	0.54 ± 0.34	179.34 ± 96.06	7.01E − 27
	–	0.86 ± 0.16	74.87 ± 39.61
	C	0.80 ± 0.19	152.30 ± 75.45
	D	0.67 ± 0.28	176.16 ± 102.91
C	A	0.84 ± 0.15	127.59 ± 72.42	1.59E − 29
	B	0.81 ± 0.20	77.69 ± 39.12
	–	0.86 ± 0.15	135.59 ± 72.14
	D	0.52 ± 0.31	221.54 ± 109.77
D	A	0.64 ± 0.35	179.04 ± 109.84	6.09E − 08
	B	0.84 ± 0.20	83.32 ± 49.29
	C	0.83 ± 0.20	153.92 ± 82.13
	–	0.85 ± 0.18	135.02 ± 74.26

Stain mix-up augmentation

In stain mix-up augmentation-based experiments, the U-Net performed differently in each training and test domain combination (see Table 7). However, the Scanners B and C maintained performance on their test sets when combined with other scanners and outperformed most of the previous techniques in this study (i.e. Scanner B scored MCC = 0.87 and Scanner C scored MCC = 0.85). Nonetheless, in the same experiments, their counterpart scanners have shown higher variances in the performance. Similarly, Scanner B also achieved even better performance in the boundary loss reduction compared to the DAL method (HD = 71.94 μm) when stain mix-up was performed with Scanner C. Scanners A and D were the worse domains when combined with other domains to train on stain mix-up-based augmentation. Scanners A and C in a few cases have presented fewer variances when combined with Scanner B, C, and B, respectively.

Table 7.

Mean MCC and HD values using U-Net-based lymph node segmentation stain mix-up augmentation method. P-values are based on MCC scores between training and test domains (scanners) using Wilcoxon.³⁹

Training domain	Test domain	MCC	HD (μm)	P-value
A	A	0.73 ± 0.28	115.30 ± 95.00	0.61
	B	0.76 ± 0.24	81.85 ± 42.58
	A	0.76 ± 0.25	145.95 ± 84.14	0.52
	C	0.83 ± 0.20	143.07 ± 67.13
	A	0.85 ± 0.19	143.07 ± 63.43	3.24E − 14
	D	0.66 ± 0.31	183.79 ± 91.54
B	B	0.87 ± 0.19	73.24 ± 38.21	3.9E − 18
	A	0.10 ± 0.14	274.07 ± 95.99
	B	0.87 ± 0.14	71.94 ± 36.34	1.16E − 07
	C	0.82 ± 0.19	140.86 ± 68.00
	B	0.87 ± 0.15	73.84 ± 39.51	1.68E − 15
	D	0.73 ± 0.25	165.55 ± 83.49
C	C	0.85 ± 0.18	133.43 ± 70.55	6.09E − 09
	A	0.59 ± 0.33	169.90 ± 89.55
	C	0.85 ± 0.18	133.18 ± 71.81	0.45
	B	0.83 ± 0.20	73.21 ± 37.79
	C	0.85 ± 0.16	139.40 ± 73.80	5.33E − 15
	D	0.67 ± 0.28	182.90 ± 96.47
D	D	0.76 ± 0.26	160.33 ± 89.42	4.67E − 18
	A	0.07 ± 0.07	318.31 ± 132.31
	D	0.79 ± 0.24	150.97 ± 84.22	4.67E − 18
	B	0.77 ± 0.22	78.75 ± 34.81
	D	0.76 ± 0.23	158.65 ± 83.22	4.51E − 03
	C	0.82 ± 0.17	139.91 ± 65.55

Discussion

Due to the growing demand for digitization at institutes of pathology, it is very likely that multiple different scanners will be in use. In such a situation, the integration of computational algorithms into downstream diagnostics can become challenging, since the stain variability arising from different scanners can directly impact the outcome of machine learning-based trained models, as we have shown in this study. A change in the scanner can therefore lead to unexpected and poor outcomes in a diagnostic task, which was previously performing well. Furthermore, the techniques proposed in the literature such as normalization^40,13,41,42 of data to a single domain to overcome such variability are more focused on data acquired from different patients. Hence, it is difficult to disentangle the various sources of heterogeneity imparted on the whole slide images.

In order to systematically evaluate the impact of scanner variability, we have conducted several experiments. Firstly, our study highlights how such effects impact the outcome of 3 different lymph node segmentation methods, which is an important upstream task for diagnostics. Secondly, the study focuses on already available techniques such as normalization to reduce the heterogeneity in the data. Thirdly, we presented how inter-scanner weights based on fine-tuning can help to overcome the effect of scanner variability in a deep learning-based pipeline. Lastly, we investigated, how domain generalization methods such as domain adversarial learning and stain mix-up augmentation can be useful besides normalization and fine-tuning to minimize the performance variances.

The lymph node segmentation results have shown that the thresholding-based method (HCT) is more affected by scanner variability in contrast to the morphology-based (HAC) and deep learning-based techniques (U-Net). In the case of HCT, the intra-scanner intensity differences directly impact the performance, whereas the U-Net and HAC were able to overcome those differences. HAC stands out by U-Net in both pre- and post-normalization when comparing the variance of the outcome. Since the same tissue slides were used to acquire imaging data from all scanners, one could expect similar performance on all scanners with a model trained on one scanner. However, there are noticeable differences due to scanner variability in the results from the single scanner training experiment. In fact, due to a large number of training samples, an improvement was observed when combined training samples from all scanners were used to train the U-Net, but there is still statistically significant variance in the outcome.

In spite of stain color normalization, performance variance has increased in most cases of mosaic image-based normalization. Among the normalization methods, Reinhard has shown fewer variances in the performance as compared to Macenko and Vahadane. In contrast, the fine-tuning inter-scanner weights experiments have shown significant improvement to reduce the performance variance. With only a small difference in MCC on Scanner D when fine-tuned with Scanners A, B, and C. Interestingly, the fine-tuning approach also showed improved performance on Scanners A, B, and C when the model was trained on the lower contrast Scanner D. The results reflect fine-tuning as an effective approach that requires a smaller number of epochs to achieve consistent results on the data from another scanner. Hence, the generalizability through fine-tuning have shown to be helpful to reduce the scanner variability. Similarly, domain adversarial learning has shown to be a very effective technique to learn domain-independent features to have similar performance curve on new or unseen domains without any additional annotation requirements compared to the seen domains. However, Scanners A and D have remained challenging in all experiments indicating that further work is required to investigate these specific image differences. Likewise, the stain mix-up augmentation-based U-Net model has outperformed the single scanner versus all scanners training, fine-tuning, and domain adversarial learning on Scanner B with better MCC and HD scores. Nevertheless, the counterpart paired scanners could not maintain performance in most of the cases. Again, Scanners A and D benefitted less from such domain adaptation technique.

In an overall inter-scanner comparison, Scanners B and C have been shown to have suitable contrast and brightness combinations for lymph node segmentation methods (see Fig. 4). Particularly, Scanner B has achieved a better segmentation performance on the sinus boundary regions and the HD was in a good range. Scanner D has been depicted as a poor-performing scanner due to its low contrast and brightness distribution in WSI compared to other scanners. Similarly, Scanner A has shown to be challenging in many experiments to achieve better segmentation performance. Based on our analysis, it is suggested that the thresholding based method should not always be used for batch processing where the higher variance of intensity could lead to false detection of lymph nodes.

Before scanning the cohort for this study, each scanner was calibrated using internal software based on certain parametric criteria. However, this study also suggests that pre-calibration of all scanners within an institute to a reference glass slide before data acquisition could be beneficial. However, the choice of such a reference slide would still be challenging due to tissue morphology and stain variance originating from pre-analytical factors such as tissue thickness. One possibility would be to calibrate all scanners to the same slide printed with a color scheme according to the International Color Consortium (ICC) standards. A comparative analysis of current results using fine-tuning and domain adversarial learning with pre-calibrated data would be helpful to understand the differences. This will further help to choose a scanner and machine-learning-based pipeline for the computational tasks that are downstream used for pathological diagnostics.

Conclusions

In this paper, we have presented a systematic study to assess the impact of scanner variability on lymph node segmentation. By employing the same glass slides scanned across different scanners, we are able to remove all non-scanner variabilities from downstream consideration. Our results demonstrate that solely these scanner variabilities can severely negatively affect both traditional and deep learning algorithms. That said, modern deep learning approaches, such as U-Nets, may be more robust to these differences. Stain color normalization appears to have further improved upon these metrics but was impacted by increased performance variability. This is in line with other studies which have shown similar trends. Fine-tuning a pre-trained U-Net model using a specific scanner’s images shows potential in minimizing the effects of WSI heterogeneity on lymph node segmentation with a minimal training time of a few epochs. However, domain adversarial learning and combinations of stain mix-up augmentation could also help to develop more generalized models with less or no additional annotations required on new unseen scanners.

The study is limited to the use of H&E and that of a single task of lymph node segmentation. Future studies will investigate fine-tuning and domain adversarial learning on different stains as well as other tasks in computational pathology. In conclusion, this study provides insights into the effects of scanner variability on segmentation methods and shows several approaches on how to deal with this challenge. Fine-tuning of pre-trained models and domain adversarial learning particularly for unseen data provide a promising solution to mitigate scanner imparted variabilities. These techniques may be valuable for institutes of pathology with large-scale heterogeneous digital repositories arising from scanner and slide preparation.

Declaration of Competing Interest

None.

Appendix B. Statistical analysis across different experiments

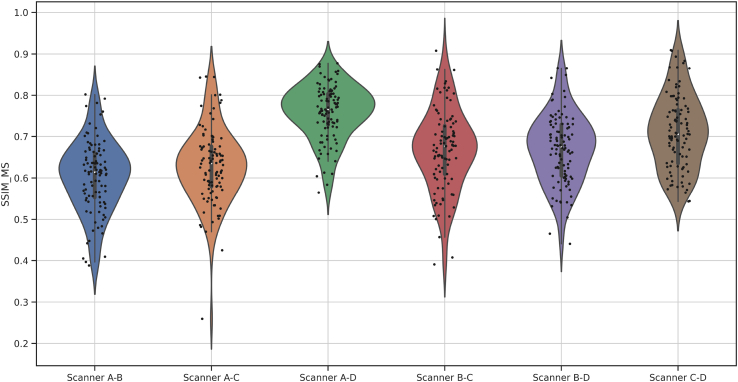
Fig. A.1.

The multiscale structural similarity index (SSIM)⁴³ measure to visualize the comparison in the images from 4 scanners on luminance, contrast, and structural difference.

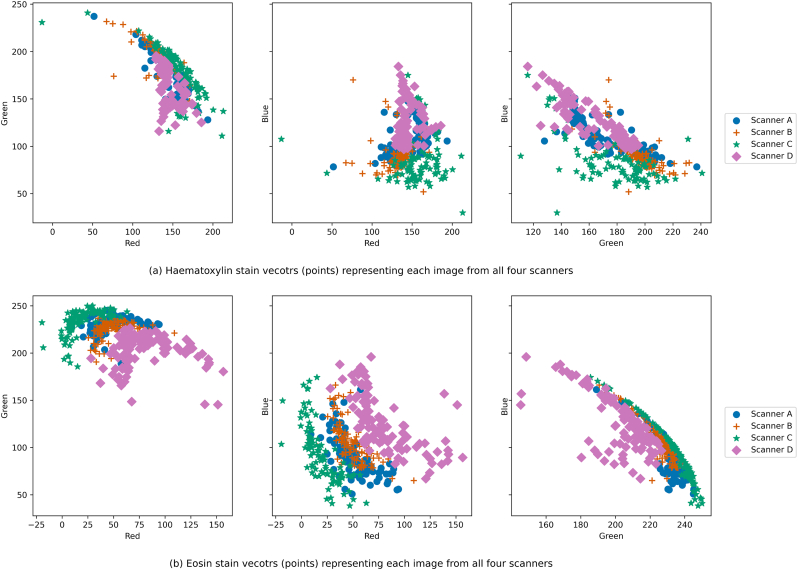
Fig. A.2.

The plots (a) and (b) contain the Hematoxylin and Eosin stain vectors (points) respectively of the images from all 4 scanners. The variability of stain color can be visually observed.

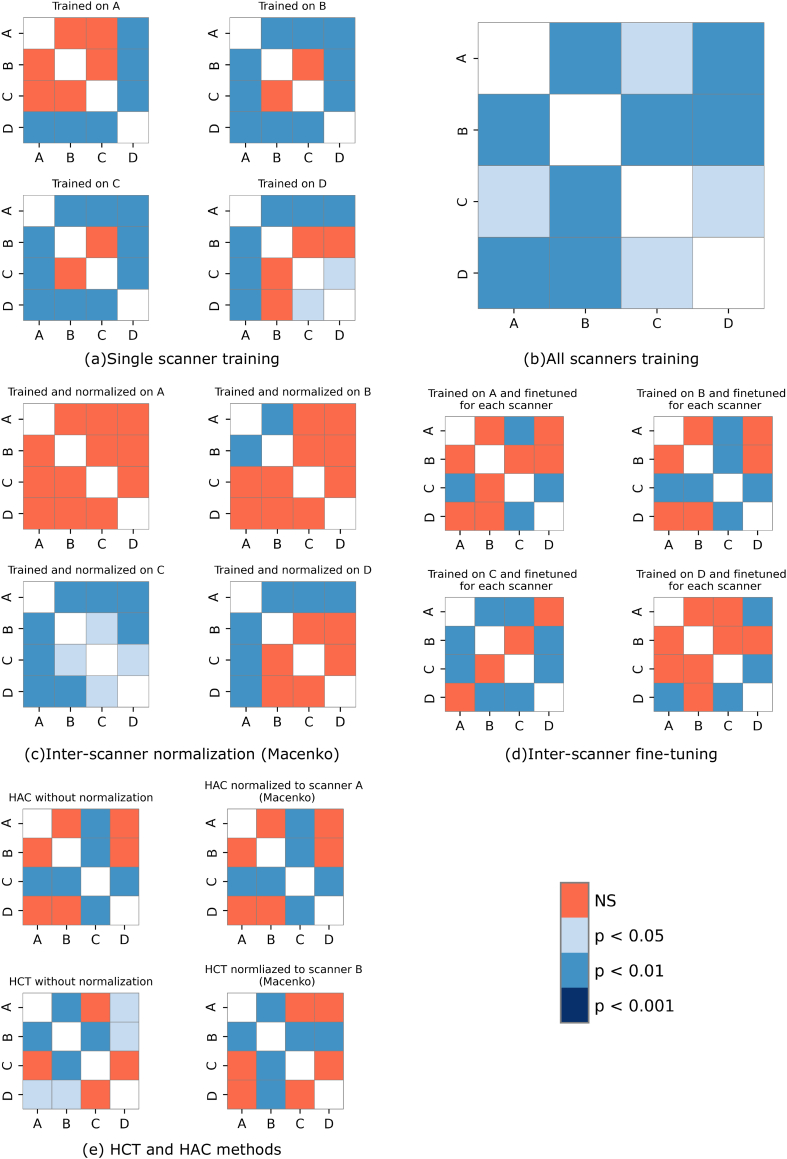
Fig. A.3.

The plots from (a) to (e) contains the P-values of Nemenyi posthoc test from all the comparisons across all the scanners, when evaluated by (a) single scanner training, (b) all scanners training, (c) inter-scanner normalization (Macenko), (d) inter-scanner fine tuning, and (e) HCT and HAC methods or experiments. The corresponding P-values are presented in Table A.1 for a detail overview.

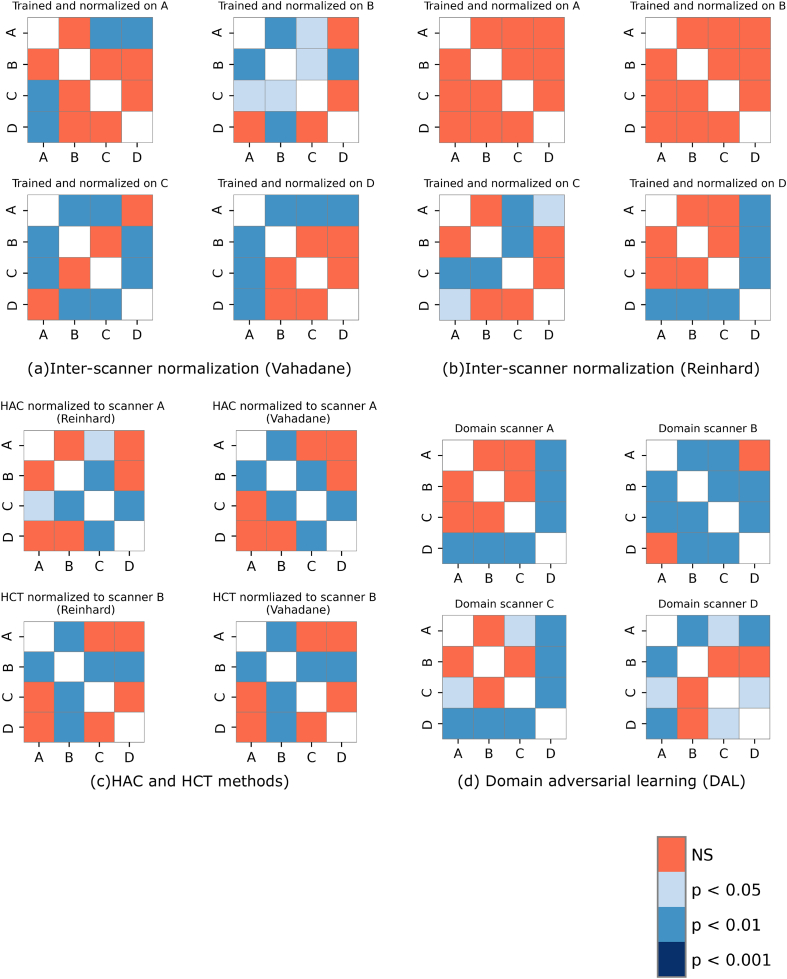
Fig. A.4.

The plots from (a) to (e) contains the P-values of Nemenyi post-hoc test from all the comparisons across all the scanners, when evaluated by (a) inter-scanner normalization by Vahadane, (b) Reinhard, (c) HAC, and HCT methods with Vahadane and Reinhard, (d) Domain adversarial learning experiments. The corresponding P-values are presented in Table A.2, Table A.3, Table A.4, Table A.5 for a detail overview.

Fig. A.5.

A few example mosaic images build of a balanced set of representative background and foreground (lymph node tissue region) tiles of whole slide images from one scanner to normalize the data of other scanners.

Table A.1.

The tables from (a) to (e) contains the P-values of Nemenyi post-hoc test from all the comparisons across all the scanners, when evaluated by (a) single scanner training, (b) all scanners training, (c) inter-scanner normalization (Macenko), (d) inter-scanner fine tuning, and (e) HCT and HAC methods or experiments. The overall results with help of plots are presented in Fig. A.3 for a prompt overview.

Trained on A						Trained on B
	A	B	C	D			A	B	C	D
A	1	0.532	0.900	0.001		A	1	0.001	0.002	0.001
B	0.532	1	0.199	0.001		B	0.001	1	0.900	0.001
C	0.900	0.199	1	0.001		C	0.002	0.900	1	0.001
D	0.001	0.001	0.001	1		D	0.001	0.001	0.001	1
Trained on C						Trained on D
	A	B	C	D			A	B	C	D
A	1	0.001	0.001	0.001		A	1	0.001	0.001	0.001
B	0.001	1	0.297	0.001		B	0.001	1	0.732	0.340
C	0.001	0.297	1	0.001		C	0.001	0.732	1	0.039
D	0.001	0.001	0.001	1		D	0.001	0.340	0.039	1
			(a) Single scanner training
			Trained on combined set (A, B, C, D)
				A	B	C	D
			A	1	0.002	0.046	0.001
			B	0.002	1	0.001	0.001
			C	0.046	0.001	1	0.013
			D	0.001	0.001	0.013	1
			(b) All scanners training
Trained and normalized on A						Trained and normalized on B
	A	B	C	D			A	B	C	D
A	1	0.311	0.270	0.257		A	1	0.001	0.057	0.244
B	0.311	1	0.900	0.900		B	0.001	1	0.609	0.244
C	0.270	0.900	1	0.900		C	0.057	0.609	1	0.900
D	0.257	0.900	0.900	1		D	0.244	0.244	0.900	1
Trained and normalized on C						Trained and normalized on D
	A	B	C	D			A	B	C	D
A	1	0.001	0.001	0.008		A	1	0.001	0.001	0.001
B	0.001	1	0.037	0.001		B	0.001	1	0.900	0.111
C	0.001	0.037	1	0.025		C	0.001	0.900	1	0.244
D	0.008	0.001	0.025	1		D	0.001	0.111	0.244	1
			(c) Inter-scanner normalization
Trained on A and fine-tuned for each scanner						Trained on B and fine-tuned for each scanner
	A	B	C	D			A	B	C	D
A	1	0.900	0.007	0.468		A	1	0.900	0.001	0.900
B	0.900	1	0.053	0.150		B	0.900	1	0.001	0.900
C	0.007	0.053	1	0.001		C	0.001	0.001	1	0.001
D	0.468	0.150	0.001	1		D	0.900	0.900	0.001	1
Trained on C and fine-tuned for each scanner						Trained on D and fine-tuned for each scanner
	A	B	C	D			A	B	C	D
A	1	0.001	0.001	0.900		A	1	0.283	0.900	0.001
B	0.001	1	0.066	0.001		B	0.283	1	0.593	0.066
C	0.001	0.066	1	0.001		C	0.900	0.593	1	0.001
D	0.900	0.001	0.001	1		D	0.001	0.066	0.001	1
			(d) Inter-scanner fine-tuning
HAC without normalization						HAC normalized to scanner A
	A	B	C	D			A	B	C	D
A	1	0.563	0.002	0.233		A	1	0.092	0.001	0.870
B	0.563	1	0.001	0.900		B	0.092	1	0.001	0.386
C	0.002	0.001	1	0.001		C	0.001	0.001	1	0.001
D	0.233	0.900	0.001	1		D	0.870	0.386	0.001	1
HCT without normalization						HCT with normalization to B
	A	B	C	D			A	B	C	D
A	1	0.001	0.578	0.013		A	1	0.001	0.402	0.419
B	0.001	1	0.001	0.043		B	0.001	1	0.001	0.001
C	0.578	0.001	1	0.283		C	0.402	0.001	1	0.900
D	0.013	0.043	0.283	1		D	0.419	0.001	0.900	1
			(e) HCT and HAC methods

Table A.2.

Inter-scannernormalization(Vahadane).

Trained and normalized on A					Trained and normalized on B
	A	B	C	D		A	B	C	D
A	1	0.092	0.005	0.001	A	1	0.001	0.014	0.355
B	0.092	1	0.732	0.233	B	0.001	1	0.043	0.001
C	0.005	0.732	1	0.778	C	0.014	0.043	1	0.517
D	0.001	0.233	0.778	1	D	0.355	0.001	0.517	1
Trained and normalized on C					Trained and normalized on D
	A	B	C	D		A	B	C	D
A	1	0.001	0.001	0.111	A	1	0.001	0.001	0.001
B	0.001	1	0.111	0.001	B	0.001	1	0.9	0.485
C	0.001	0.111	1	0.002	C	0.001	0.9	1	0.355
D	0.111	0.001	0.002	1	D	0.001	0.485	0.355	1

Table A.3.

Inter-scanner normalization (Reinhard).

Trained and normalized on A					Trained and normalized on B
	A	B	C	D		A	B	C	D
A	1	0.386	0.9	0.9	A	1	0.126	0.885	0.9
B	0.386	1	0.67	0.7	B	0.126	1	0.452	0.178
C	0.9	0.67	1	0.9	C	0.885	0.452	1	0.9
D	0.9	0.7	0.9	1	D	0.9	0.178	0.9	1
Trained and normalized on C					Trained and normalized on D
	A	B	C	D		A	B	C	D
A	1	0.793	0.001	0.015	A	1	0.468	0.9	0.001
B	0.793	1	0.001	0.15	B	0.468	1	0.188	0.001
C	0.001	0.001	1	0.386	C	0.9	0.188	1	0.003
D	0.015	0.15	0.386	1	D	0.001	0.001	0.003	1

Table A.4.

HAC and HCT with Reinhard and Vahadane normalizations.

HAC (Reinhard)					HAC (Vahadane)
	A	B	C	D		A	B	C	D
A	1	0.452	0.023	0.452	A	1	0.001	0.126	0.111
B	0.452	1	0.001	0.9	B	0.001	1	0.001	0.355
C	0.023	0.001	1	0.001	C	0.126	0.001	1	0.001
D	0.452	0.9	0.001	1	D	0.111	0.355	0.001	1
HCT (Reinhard)					HCT (Vahadane)
	A	B	C	D		A	B	C	D
A	1	0.001	0.142	0.9	A	1	0.001	0.169	0.809
B	0.001	1	0.001	0.001	B	0.001	1	0.001	0.001
C	0.142	0.001	1	0.37	C	0.169	0.001	1	0.609
D	0.9	0.001	0.37	1	D	0.809	0.001	0.609	1

Table A.5.

Domain adversarial learning.

Domain Scanner A					Domain Scanner B
	A	B	C	D		A	B	C	D
A	1	0.547	0.9	0.001	A	1	0.001	0.001	0.111
B	0.547	1	0.232	0.001	B	0.001	1	0.007	0.001
C	0.9	0.232	1	0.001	C	0.001	0.007	1	0.001
D	0.001	0.001	0.001	1	D	0.111	0.001	0.001	1
Domain Scanner C					Domain Scanner D
	A	B	C	D		A	B	C	D
A	1	0.9	0.0426	0.001	A	1	0.001	0.043	0.001
B	0.9	1	0.111	0.001	B	0.001	1	0.081	0.9
C	0.0426	0.111	1	0.001	C	0.043	0.081	1	0.039
D	0.001	0.001	0.001	1	D	0.001	0.9	0.039	1

Appendix A. Supplementary data

Supplementary material