Determining Thermodynamic and Material Properties of Biomolecular Condensates by Confocal Microscopy and Optical Tweezers

Abstract

While the roles of biomolecular condensates in health and disease are being intensely studied, it is equally important that their physical properties are characterized in order to achieve mechanistic understanding. Here we share some of the protocols developed in our lab for measuring thermodynamic and materials properties of condensates. These include a simple method for determining the droplet-phase concentrations of condensate components on a confocal microscope, and a method for determining the viscoelasticity of condensates by optical tweezers. These protocols are either generally applicable to biomolecular condensates or are unique for their characterization.

1. Introduction

Biomolecular condensates mediate a myriad of cellular functions, from transcription to sequestration of mRNA under stress [1,2], and are linked with neurodegeneration and cancer [3]. Condensates are formed via phase separation, and are sometimes called membraneless organelles; an example of the latter is stress granules. Under a microscope, condensates, especially in-vitro reconstitutions using one or two main components, often appear as μm-sized droplets. While the roles of biomolecular condensates in health and disease are being intensely studied, it is equally important that their physical properties are characterized in order to achieve mechanistic understanding. In our lab, we have extensively used confocal microscopy and optical tweezers to measure thermodynamic and materials properties of condensates [4–7]. Here we share some of the protocols developed in our lab.

A confocal microscope uses a narrow laser beam to illuminate a small spot in the sample, and thus fluorescence labeling is required to produce detectable signals. In addition, a pinhole in front of the detector eliminates out-of-focus signals. The observed “confocal” volume typically is only ~0.5 μm in diameter in the X-Y plane and ~1 μm in the Z direction. By scanning in the X-Y plane (yielding a Z slice), one can obtain a 2D image of the sample; by additionally scanning along the Z direction (yielding a Z stack), one can construct a 3D image of the sample. The fluorescence intensities in a given region can be quantified to obtain the concentrations of labeled species. This quantitative capability of confocal microscopy is well-suited for studying biomolecular condensates, as it allows for the determination of the equilibrium concentrations of different components in both the bulk phase and the droplet phase. Finally, by scanning a Z slice or Z stack over and over at different times, one can also determine dynamic properties of condensates. For example, a Z-stack time series may reveal the evolution in morphology or material state [5]. Two important methods are also implemented by such time series: fluorescence recovery after photobleaching (FRAP) is measured through a Z-slice time series, whereas particle tracking can be done via a Z-stack time series. The fluorescence recovery time can be used to deduce the diffusion constant of the fluorescently labeled species inside condensates and the nanoviscosity of the condensates [7–9]. Likewise, particle tracking data can be analyzed to obtain the mean-square displacement of particles as a function of time, which in turn yields the diffusion constant of particles inside condensates and the microviscosity of the condensates [10]. However, the time resolution of confocal scanning is typically of the order of 1 s. The viscosity determined by both FRAP and particle tracking is likely the value at low shear rate (i.e., zero-shear viscosity) [7,11]. Biomolecular condensates are not purely viscous but viscoelastic, where shear stress relaxes not instantaneously but at a finite rate. Shear relaxation times ranging from ms to s have been observed for various condensates [7,11–14]. For dynamic processes such as droplet fusion that occur on the same or longer timescale compared to shear relaxation, the effective viscosity of condensates may well be higher (shear thickening) or lower (shear thinning) than the zero-shear viscosity [7].

Optical tweezers use a focused laser beam to trap dielectric spherical objects, which most often are polystyrene beads with diameter around 1 μm. As a bead moves away from the center of the optical trap, it experiences a force that is well approximated as Hookean. Inside a purely viscous liquid, the trapped bead can be modeled as a Brownian harmonic oscillator. For complex fluids such as biomolecular condensates, the model can be extended to account for both viscous and elastic forces exerted by the environment [15,16]. Optical tweezers are well-suited to characterize material properties of biomolecular condensates. In particular, polystyrene beads trapped inside biomolecular condensates can report on the viscoelasticity of condensates (passive microrheology) [11], or can be driven on an oscillatory motion in order to characterize the viscoelasticity (active microrheology) [7]. Moreover, beads trapped at the inter-phase interface of condensates can report on the interfacial tension [7,12,17] as well as on the viscoelasticity [12,13,17]. Lastly, dual-trap optical tweezers can directly trap two droplets and bring them together for fusion (active fusion), allowing the monitoring of fusion dynamics [6,18–20].

2. Materials

All media and buffers were prepared in deionized (DI) water with a resistivity of ~18 MΩ-cm at 25 °C. All media were sterilized by autoclaving at 121 °C and 15 psi for 20 minutes. All buffers and sample solutions were filtered using 0.22 μm or 0.45 μm polyvinylidene fluoride membranes. All buffers contained 0.01% (w/v) NaN₃ to discourage microbial growth and spoilage.

2.1. Culture preparation

• 2.1.1.Miller LB (Fisher Scientific catalog# DF0446-17-3) (note 1)
• 2.1.2.Fernbach and 50 ml culture flasks
• 2.1.3.100 mg/ml ampicillin stocks prepared in DI water as 1 ml aliquots stored at −20 °C.
• 2.1.4.1 M IPTG stocks prepared in DI water as 1 ml aliquots stored at −20 °C.

2.2. Chromatography columns

• 2.2.1.Nickel-based immobilized metal affinity chromatography (Ni²⁺-IMAC) column: HisTrap FF crude (GE Healthcare catalog# GE17-5286-01)
• 2.2.2.Anion exchange column: HiTrap Q High Performance (GE Healthcare catalog# GE17-1154-01)
• 2.2.3.Cation exchange column: HiTrap SP High Performance (GE Healthcare catalog# GE17-1152-01)
• 2.2.4.Maltose binding protein (MBP) affinity column: amylose resin (New England Biolabs catalog# E8021S)

2.3. Cell lysis

• 2.3.1.DNase I stock containing: 75 mM NaCl, 250 mM MgCl₂, 0.02 mg/ml DNase I (Sigma-Aldrich catalog# DN25-100mg; Note 2), 20% (v/v) glycerol
• 2.3.2.NP40 cell lysis buffer (Thermo Fisher Scientific catalog# FNN0021)

2.4. Buffers

• 2.4.1.For Ni²⁺-IMAC column: buffer A = 50 mM imidazole, 300 mM KCl, pH 7; buffer B = 300 mM Imidazole, 100 mM KCl, pH 7.
• 2.4.2.For ion exchange columns: buffer A = 20 mM Imidazole, pH 7; buffer B = buffer A + 1 M NaCl.
• 2.4.3.For MBP affinity column: buffer A = 20 mM imidazole, 200 mM KCl, pH 7; buffer B = buffer A + 10 mM maltose.
• 2.4.4.For TEV protease reaction: 20 mM imidazole, 500 mM NaCl, pH 7.
• 2.4.5.Final experimental buffer: 10 mM Imidazole, 150 mM KCl, pH 7.

2.5. Macromolecules, dyes, and polystyrene beads

• 2.5.1.Lysozyme (VWR International catalog# 97062-138)
• 2.5.2.TEV protease (Sigma-Aldrich catalog# T4455-10KU)
• 2.5.3.Poly-L-lysine (Sigma-Aldrich catalog# P2658-25mg)
• 2.5.4.Heparin (Alfa Aesar catalog# A16198)
• 2.5.5.Ficoll70 (GE Healthcare catalog# GE17-0310-10)
• 2.5.6.FITC-Heparin (Nanocs, Inc. catalog# HRN1-FC-1)
• 2.5.7.FITC-Ficoll70 (Sigma-Aldrich catalog# 51731-1G)
• 2.5.8.FITC-Lysozyme (Nanocs, Inc. catalog# LS1-FC-1)
• 2.5.9.Alexa-Fluor 594 N-hydroxysuccinimide (NHS) ester (Fisher Scientific catalog# A20004)
• 2.5.10.

  Thioflavin T (VWR International catalog # TCT0558-025G)

• 2.5.11.

  Beads: 2 μm-diameter carboxylate-coated polystyrene beads (Polysciences, Inc. catalog# 18327-10)

3. Protein Purification

All purification steps were carried out at 4 °C unless otherwise stated. All final products were stored in a refrigerator. All inoculation steps were carried out in a sanitized environment and in front of a Bunsen flame. Initially an SDS-PAGE gel was run following each chromatography step to assure proper purification. After the protocol is standardized in a particular laboratory, only the final product may be ascertained using SDS-PAGE. A summary is given in Figure 1.

Figure 1.

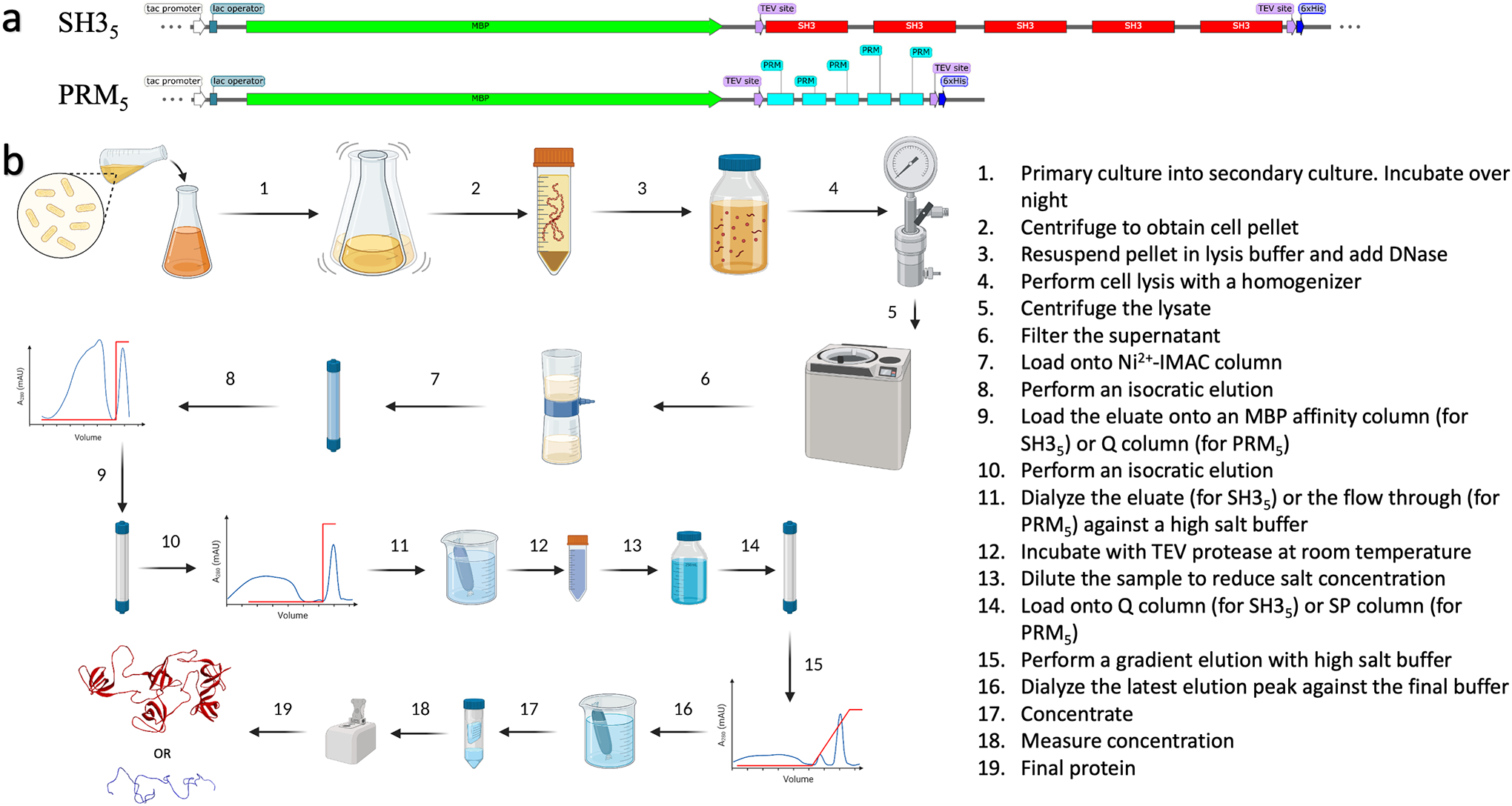
Expression and purification protocols for SH3₅ and PRM₅ proteins. (a) Plasmid maps for fusion protein constructs. (b) Purification steps.

3.1. Purification of SH3₅

• 3.1.1.Autoclave 4 × 1 L LB media in Fernbach flasks and 2 × 50 ml in culture flasks.
• 3.1.2.After the 50 ml aliquots have sufficiently cooled, add 50 μl from the ampicillin stock and inoculate from a glycerol stock containing BL21(DE3) cells transfected with a plasmid that contains the SH3₅ sequence (Figure 1a, top) as described in Li et al. [21]. Incubate for 16–18 hours overnight at 37 °C in a shaker incubator. This is the primary culture that serves to acclimate the cells to an LB environment.
• 3.1.3.Add 1 ml of the ampicillin stock to each of the 1 L LB media in the Fernbach flasks. Thereafter, add 25 ml of the primary cultures to each of the flasks. Incubate the 4 L of this secondary culture at 37 °C until OD_{λ=600 nm} reaches 0.6–0.8. At this point, induce each 1 L culture with 1 ml of the 1 M IPTG stock. Following this, reduce the temperature to 20 °C and incubate overnight for 16 hours. The SH3₅ protein can be toxic to the growth of a cells and therefore a slower growth at lower temperature achieves better yields.
• 3.1.4.Pellet the cells by centrifuging the four 1 L cultures at 4000 ×g and 4 °C for 20 minutes.
• 3.1.5.Resuspend the pellet in 100–200 ml Ni²⁺-IMAC buffer A. Add 4 ml of the DNase I stock and 1–2 ml NP40 and stir until the solution is free from clumps. Addition of DNase I is of particular importance because DNA interferes with the purification and precipitates the proteins pretty aggressively, especially the poly-cationic, disordered proline-rich motif pentamer (PRM₅).
• 3.1.6.Lyse the cells in the resuspension using a homogenizer or a sonicator. Centrifuge the lysate using 50 mL Oak Ridge tubes at 50,000 ×g and 4 °C for 40 minutes.
• 3.1.7.Filter the supernatant using 0.45 μm filters and load onto a Ni²⁺-IMAC column preequilibrated with Ni²⁺-IMAC buffer A. Wash and elute with an isocratic elution profile at 100% Ni²⁺-IMAC buffer B. The C-terminal 6×His tag of the fusion construct here binds to the column. Collect the peak.
• 3.1.8.Load the eluate directly on an MBP affinity column preequilibrated with MBP affinity buffer A. Wash and elute with an isocratic elution profile again at 100% MBP affinity buffer B. The N-terminal MBP of the construct here binds to the column. Collect the peak.
• 3.1.9.Dialyze the eluate in 4 L of TEV protease reaction buffer overnight at room temperature.
• 3.1.10.

  Add TEV protease at a molar ratio of 1:20–50 to the fusion construct in the dialysate for 2–3 days. Incubate longer or add more of the enzyme if cleavage is not complete in this time period. A relatively high amount of TEV is required due to the large amount of salt present in the reaction buffer, which hinders enzyme activity. This salt is necessary, however, to prevent aggregation during cleavage of the fusion construct.

• 3.1.11.

  Following complete cleavage, dilute the sample five times using the ion exchange buffer A to bring the NaCl concentration down to about 100 mM. Filter and load onto an anion exchange column preequilibrated with ion exchange buffer A. Run a gradient elution profile from 0 to 100% ion exchange buffer B over 200 ml. Two peaks should be observed because both MBP and SH3₅ are negatively charged at pH 7. The first peak is MBP and second peak is the SH3₅ product.

• 3.1.12.

  Ascertain the purity of the second peak using an SDS-PAGE gel and dialyze in 4 L of the final experimental buffer.

• 3.1.13.

  Concentrate to a stock at about 100–200 μM (ε_λ=280nm = 112300 M⁻¹cm⁻¹) using a 3 kD molecular-weight cutoff (MWCO) centrifugal concentrator. Test for phase separation by mixing with purified PRM₅ at a 20 μM final concentration for each. The solution should turn visibly cloudy; droplets should be observed under a widefield microscope with an objective at micron order resolution.

3.2. Purification of PRM₅

• 3.2.1.Follow steps 3.1.1 through 3.1.7 with the two exceptions. In 3.1.2, the plasmid contains the PRM₅ sequence (Figure 1a, bottom); in 3.1.3, set the post-induction incubation temperature to 18 °C.
• 3.2.2.Dilute the eluate from the Ni²⁺-IMAC column five times and load onto an anion exchange column preequilibrated with ion exchange buffer A. PRM₅ is especially prone to aggregation with DNA so this extra step is to remove DNA and any other negatively charged components that may have carried over from the lysate. Collect the flow through and concentrate it down to 15–30 ml using a 3 kD MWCO centrifugal concentrator at room temperature.
• 3.2.3.Dialyze the concentrate in 4 L of the TEV protease reaction buffer overnight at room temperature. Dialyzing in lower temperatures has been seen to encourage aggregation.
• 3.2.4.Follow step 3.1.10.
• 3.2.5.Dilute the sample five times using the ion exchange buffer A. Some aggregates may appear at this point. Filter and load quickly onto a cation exchange column preequilibrated with ion exchange buffer A. Run a gradient elution profile from 0 to 100% ion exchange buffer B over 100 ml. There should be two peaks because both TEV protease and PRM₅ are positively charged at pH 7. The second peak is PRM₅.
• 3.2.6.Follow step 3.1.12.
• 3.2.7.Concentrate to a stock at about 100–200 μM (ε_λ=280nm = 6990 M⁻¹cm⁻¹) using a 1 kD MWCO centrifugal concentrator. Test for phase separation just like in step 3.1.13 by mixing with purified SH3₅ at a 20 μM final concentration for each.

4. Labeling of proteins with Alexa-Fluor 594 NHS ester

4.1. Preparation of reaction mixture

• 4.1.1.Prepare an 8–10 mM stock solution of the Alexa dye in dimethyl sulfoxide (DMSO). Weigh the dye directly in a microcentrifuge tube and add the necessary volume of DMSO to make the desired concentration.
• 4.1.2.Prepare a stock solution of the protein that contains primary amines (in particular, Lys residues) for conjugation. Using the purified stock in imidazole buffer is acceptable because imidazole does not contain any competing primary amines. Any buffer containing primary amines should be avoided (Note 3).
• 4.1.3.Mix the protein, Alexa dye stock, and buffer such that the final concentration is about 20 μM protein and 400 μM dye in a total reaction volume of 500 μL. Incubate overnight at room temperature. This and subsequent steps are illustrated in Figure 2 (Note 4).

Figure 2.

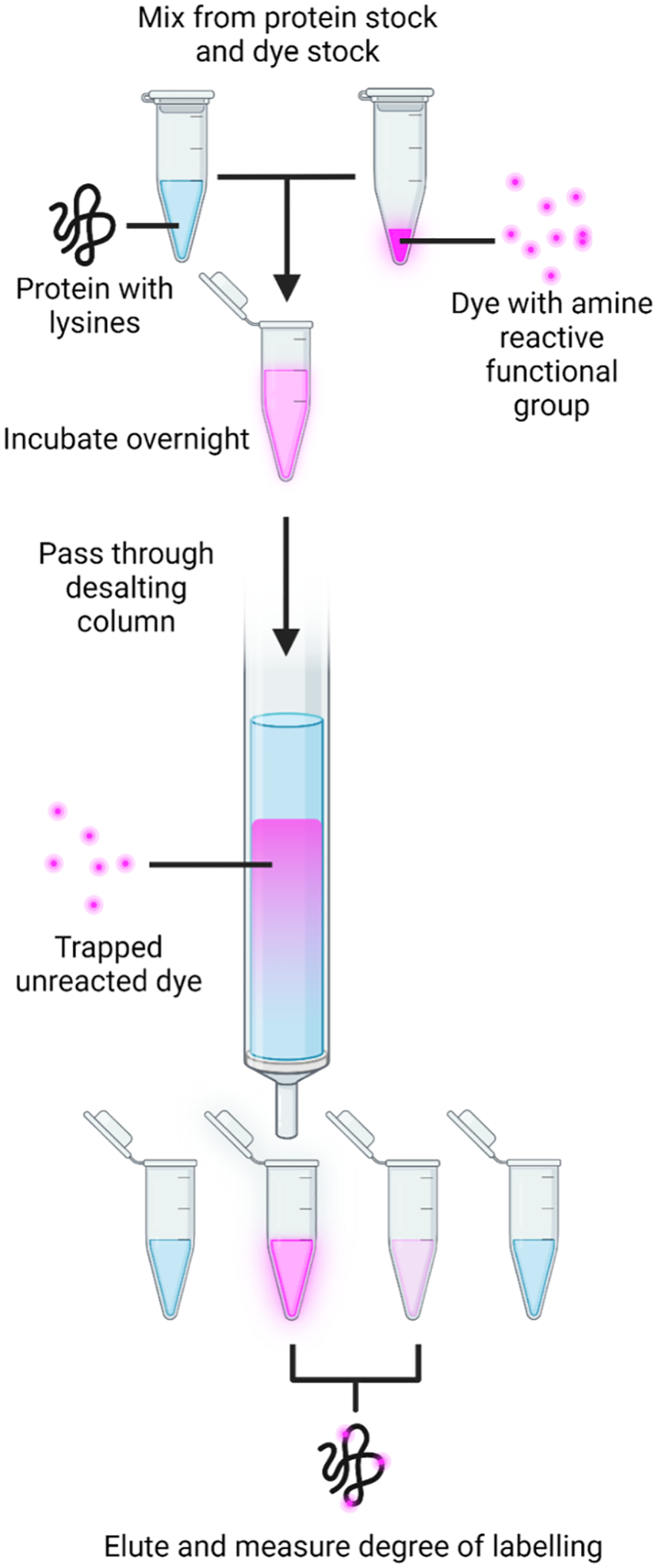
Illustration of the procedure for labeling a condensate component with a functionalized Alexa dye (Alexa-Fluor 594 NHS ester).

4.2. Elution

• 4.2.1.Equilibrate a PD MiniTrap G-25 column (GE Healthcare catalog # 28918007) with the final experimental buffer.
• 4.2.2.Load the 500 μL reaction mixture and collect the flow through and eluate at 20–30 μL fractions (2–3 drops each).
• 4.2.3.Pool the fractions that show the highest absorbance at λ = 280 nm and the λ_max (~ 590 nm for Alexa 594-SH3₅) of the labeled dye.

4.3. Calculation of degree of labeling

For a dye with absorbance maximum at λ = λ_max, obtain the degree of labeling (DOL) for the sample using the following equation:

$$\text{DOL}= \frac{A_{\lambda ={\lambda }_{\text{max}}}\times {\epsilon }_{\lambda =280}}{{\epsilon }_{\lambda ={\lambda }_{\text{max}}}^{\prime }\times \left(A_{\lambda =280}-A_{\lambda ={\lambda }_{\text{max}}}\times \text{C}.\text{F}.\right)}$$

where $A_{\lambda ={\lambda }_{\text{max}}}$ and A_λ=280 are the absorbance readings of the sample at λ = λ_max and 280 nm, respectively; ${\epsilon }_{\lambda ={\lambda }_{\text{max}}}^{\prime }$ (90000 M⁻¹cm⁻¹ for Alexa-Fluor 594 NHS ester at 590 nm) and ε_λ=280 are the molar extinction coefficients of the free dye and unlabeled protein, respectively, at the specified wavelength; and C.F. (0.56 for Alexa-Fluor 594 NHS ester with λ_max = 590 nm) is the ratio of absorbance of the free dye at 280 nm to that at λ_max.

5. Confocal microscopy

All confocal microscopy experiments can be conducted on a laser scanning or a spinning disk system with at least a 40× water objective. A typical system is the inverted Zeiss LSM 710 (and higher models), with a C-Apochromat 40× objective and a 1.2 numerical aperture (calculated for the refractive index of water). The settings suggested here are for macromolecules labeled with FITC. Depending on the dye, the correct laser and emission filter should be chosen.

5.1. Sample preparation and observation

• 5.1.1.Prepare an approximately 10 × 10 mm² square well on a clean 1.0-mm thick glass slide using double-sided tape (Scotch catalog # 3136). Aliquot 1.5 μl of your sample and seal it in using a 0.17-mm thick glass coverslip of 22 mm × 22 mm dimensions. (Always choose a coverslip that is relevant to the objective being used or adjust the objective to correct for the coverslip thickness). The aliquot should form a column of liquid sandwiched between the glass slide and the coverslip. Mount the slide in the configuration relevant to the microscope (coverslip down for inverted microscope). See Figure 3 for illustration.
• 5.1.2.For a FITC labeled sample, an Argon laser with 488 nm excitation beam is typically used. Limit the laser power to 0.2–1% to avoid bleaching. However, the power levels are laser specific and have to be tweaked to obtain sufficient emission for a typical doping concentration of labeled droplet proteins or partitioning regulators at a concentration of 1–10% of the unlabeled component [4]. Select the detection wavelength range to cover as much of the emission of the dye as possible with a minimum 5–10 nm separation from the excitation wavelength. If other dyes are present, limit the detection range such that no overlap occurs between two dyes. At least a 5 nm separation of detection ranges between different dyes is ideal. Use separate tracks for dyes that have excitation wavelengths near each other.
• 5.1.3.For imaging spherical droplets that are settling under gravity or are suspended, it is essential to run quick Z scans with minimal Z slice increment to increase the chance of obtaining Z slices that cut through the largest cross sections of droplets. Ideally, the pinhole should be kept at 1 airy unit and the slice increment minimal. To enhance speed without compromising image quality, the scan area should be cropped sufficiently. For a 105 μm × 105 μm scan area, a frame size of 512 × 512 or 1024 × 1024 pixels is optimal with a bit depth of 12 and bidirectional line scanning. Adjust the averaging number to 1 or 2 depending on how fast the scans can capture floating droplets and how grainy the image appears. Ideally, a single scan should take less than a second. A spinning disk system achieves the best results for this kind of experiment.
• 5.1.4.For imaging settled droplets the necessity for high speed is removed. The necessity for minimal Z slice increment still holds. This is because if the Z stack is to be rendered into a 3D image for droplet volume estimation then having a good resolution is necessary along the Z axis as much as it is in the X-Y plane. Hence, the pinhole should still be kept at 1 airy unit and the slice increment minimal. The averaging number may be increased to 4 – 12. The frame size may also be increased. For a qualitative determination of surface tension of settled droplets, only the height of the droplets is necessary so the Z stack can be conducted from the coverslip to just above the tallest droplet. For volume ratio determination the Z stack has to be conducted from the coverslip to the glass slide, i.e., covering the entire column of the sandwiched sample.

Figure 3.

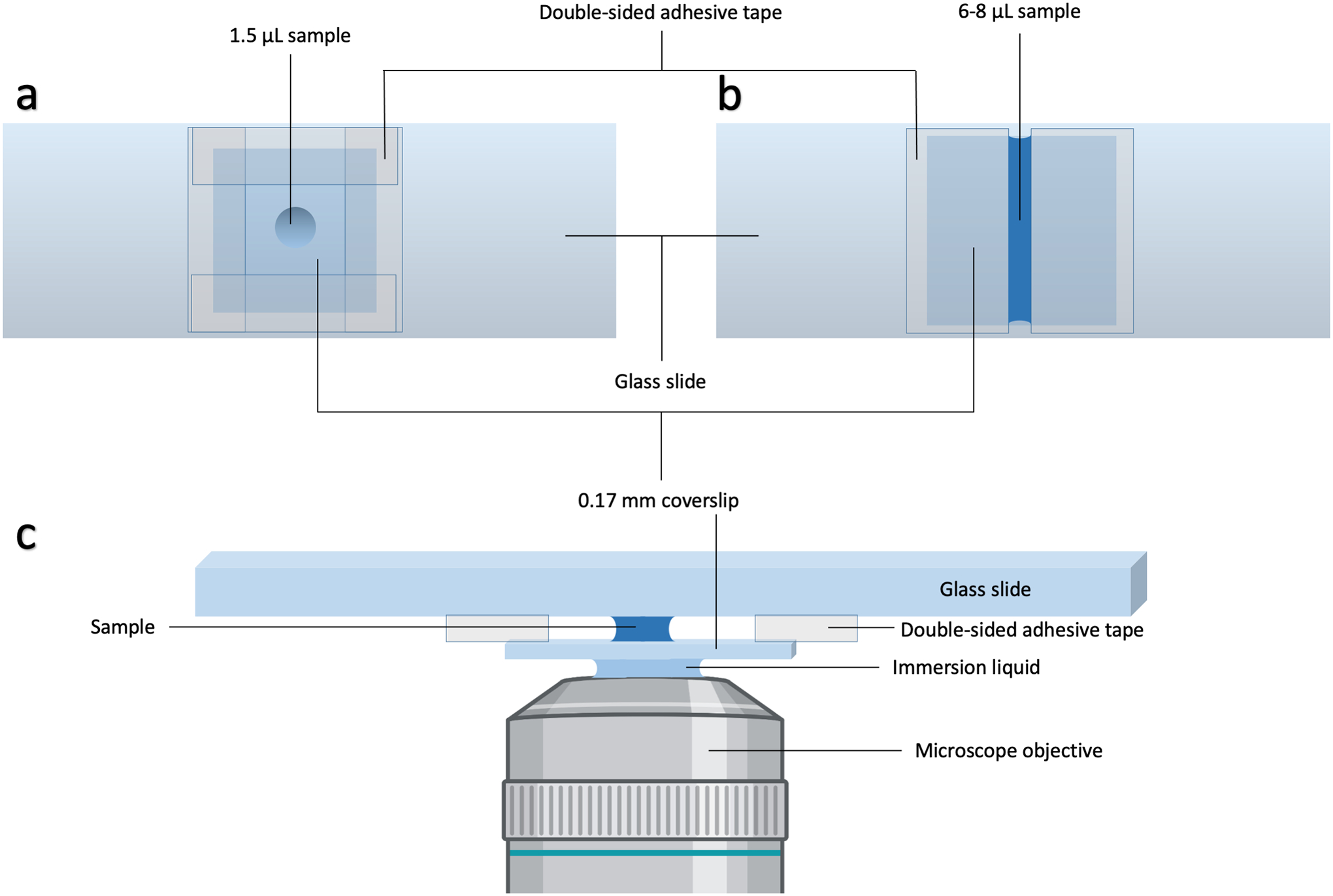
Slide preparation and mounting. (a) Slide for confocal microscopy based experiments. (b) Slide for C-Trap based experiments. (c) Side view of the slide in (a) after mounting atop an objective. For the slide in (b), the two pieces of adhesive tape would be closer to each other and in contact with the column of liquid sample.

5.2. Partition coefficient determination by fluorescence intensity

There are more elegant methods for the determination of partition coefficients [9,22] but the method described below is the easiest.

• 5.2.1.Obtain several images of droplets at different Z positions as described in 5.1.3. For the purposes of this experiment, the 2D image of a droplet at its midplane is necessary. One can obtain this by imaging suspended or settling droplets or settled droplets that remain spherical on PEG passivated slides.
• 5.2.2.Using a software like ImageJ or the ZEN Blue 2.5 (which reads Zeiss-based *.czi files), find regions of interest (ROIs) within several droplets by searching through X-Y positions and Z slices; always work with the slice that cuts the largest cross section of a droplet. Obtain the average intensities in all of these ROIs and take the mean (I_droplet) and standard deviation. Then select ROIs free of droplets. To avoid artifactual fluorescence contribution from neighboring droplets, ROIs for the intensity outside droplets should be drawn at higher Z slices where the probability of finding droplets is lower due to gravity. Similarly obtain the average intensities of all these ROIs and take the mean (I_bulk) and standard deviation.
• 5.2.3.Prepare a standard curve with known concentrations of the labeled species; cover a wide enough concentration range to encompass the fluorescence intensity outside and the fluorescence intensity inside the droplets. When possible, a relevant error reducing measure is to generate standard curves using samples containing both the labeled and unlabeled versions of the molecule at a constant ratio equal to that used in the droplet-forming sample. It is often so that the standard curves will be nonlinear due to environmental effects on the dye, in which case fit the data to a polynomial. The concentrations inside and outside the droplet can thus be obtained by solving the polynomial at the relevant intensity values inside and outside. The concentration ratio is the partition coefficient.

5.3. Determination of droplet-phase concentration by volume measurement

The preceding method might be applied to measure the concentrations, C_bulk and C_droplet, of a droplet-forming species in the bulk and droplet phases. However, C_droplet is often orders of magnitude higher than C_bulk. Therefore, generating a standard curve that extends beyond C_droplet may not be practical. Hence an alternative approach for determining C_droplet is needed.

In addition to fluorescence intensity (calibrated by a standard curve), C_bulk can simply be determined as the threshold concentration for phase separation, i.e., the minimum concentration at which phase separation is observed. The bulk-phase concentration can also be determined by centrifuging a droplet-forming sample and obtain the concentration in the supernatant by spectrophotometry. However, centrifugation to obtain the “pure” droplet phase requires a significant sample volume [21]. Here we describe a method dubbed confocal imaging of gravity-based separation (CIGraBS) [4]. See Figure 4 for a schematic.

Figure 4.

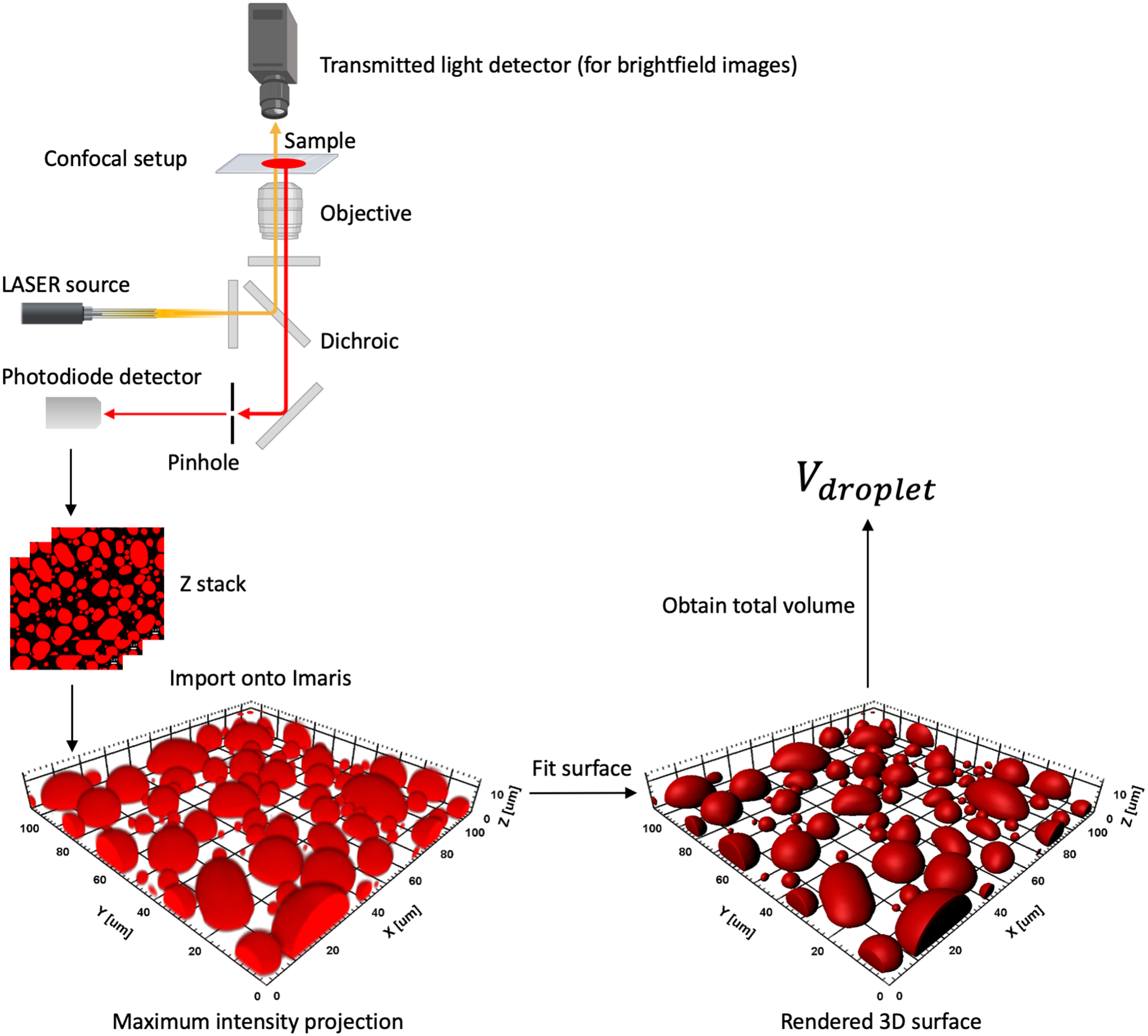
A schematic for the CIGraBS method for estimating the volume fraction of the droplet phase.

Prepare sample and obtain a Z stack as described in 5.1.4. With the laser turned off, wait for long enough till all the droplets settle on the coverslip. Following this, obtain a Z stack from below the surface of the coverslip to just above the surface of the glass slide. The surfaces can be recognized by a sharp attenuation of fluorescence intensity in the scanned region. Save the image file and import onto Imaris. Use the surpass function to generate a 3D surface fit of all the settled droplets with grain size set to 0.415 μm or lower. Make sure to match the boundary of the surface fit as best as possible to the maximum intensity projection of the Z stack. The volumes inside all the fit surfaces can now be summed to obtain the total volume, V_droplet, of the droplet phase in the scanned region. The total volume, V_sample, of the sample in the scanned region is the cuboid between the glass slide and the coverslip, and can be obtained by multiplying the scan area (A) and the distance (h) between the top and bottom surfaces. If C_initial is the initial concentration of the droplet-forming species and C_bulk is the bulk-phase concentration determined as outlined above, mass conservation yields the following equation:

$$\left(C_{\text{initial}}-C_{\text{bulk}}\right)V_{\text{sample}}=\left(C_{\text{droplet}}-C_{\text{bulk}}\right)V_{\text{droplet}}$$

which can be solved to obtain the droplet-phase concentration C_droplet.

5.4. Qualitative indication of surface tension

The height of droplets settled on a coverslip can give the rank order of interfacial tension when different condensates are compared [6]. To determine the height, simply render surfaces from 3D Z stacks of settled droplets as described in 5.3 and obtain the distance between the top and bottom of the droplets in Imaris.

6. Microrheology of biomolecular condensates using a LUMICKS^™ dual-trap optical tweezer system

6.1. Sample preparation and loading

• 6.1.1.Prepare a channel of 2–3 mm width on a clean glass slide using two strips of double-sided tape (Figure 2). Affix a coverslip on top making sure to press out any air trapped between the coverslip and the double-sided tape. Load the sample from one end of the channel until it is filled completely. Seal off both ends using vacuum grease. Mount the slide in an inverted position into the sample chamber.

6.2. Active fusion of droplets

• 6.2.1.After adjusting the objective and the condenser to the correct trapping positions, set the trapping laser to 100% and the overall power to a value just enough to trap a droplet in each of the two optical traps. For this experiment, the trap1 split should be at 50%.
• 6.2.2.Allow the two trapped droplets to grow by scavenging nearby droplets while letting other droplets settle.
• 6.2.3.If one trapped droplet is larger than the other, favor the growth of the smaller droplet by adjusting the trap1 split such that the trap hosting the smaller droplet receives 10–20 more percentage points in power. Remember to bring the trap1 split back to 50% once the droplets reach similar sizes.
• 6.2.4.Before the droplets are allowed to fuse, make sure all other nearby droplets have settled and the field is clear.
• 6.2.5.Obtain a snapshot of the two droplets when they are in separation.
• 6.2.6.Bring the two droplets as close to each other as possible using the joystick. Once they are about a few microns apart, turn on the video recording and move one of the droplets to toward the other in steps of 0.2 μm until they touch.
• 6.2.7.Allow the droplets to fuse unperturbed and terminate the video recording once the fusion is complete (Figure 5a and 5b).
• 6.2.8.Export the force progress curve of the stationary droplet as an h5 file (Figure 5c, red trace).
• 6.2.9.Release the droplets by pressing the shutter for both traps and moving the stage.
• 6.2.10.

  Trap droplets of different sizes and repeat steps 6.2.2 to 6.2.9. Variations in the size of the droplets can be obtained by truncating the time allowed for the droplet to grow in step 6.2.2. However, it is important to keep the sizes of both droplets as equal as possible.

• 6.2.11.

  Obtain the radii of the two droplets by inscribing a circle around the perimeter of the droplets in imageJ using the snapshot obtained in 6.2.5. Convert the radii from number of pixels to microns by multiplying it with the conversion factor for the brightfield camera. Average the two radii.

• 6.2.12.
  Fit the force progress curve using the following stretched exponential function (Figure 5c, black trace) [6]:

  $$\mathit{\text{Force}}=A+B\left\{1-e^{-{\left[\left(t-t_0\right)/{\tau }_{\text{fu}}\right]}^{1.5}}\right\}H\left(t-t_0\right)$$

  Where A and A + B are the pre-fusion baseline and post-fusion plateau, respectively; t₀ is the start time of the fusion process; H(t − t₀) is a Heaviside step function introduced to ensure that the stretched exponential function was fit on the data only from time t₀ onwards; and τ_fu is a parameter that provides a measure for the fusion time. A MATLAB script that imports the h5 file and does the fitting can be obtained at: https://harbor.lumicks.com/single-script/49988cc6-4ba5-4659-8ffa-7498ebc702ce.
• 6.2.13.
  Plot the fusion time parameter τ_fu vs the droplet radius for each fusion event conducted over a set of droplets of various sizes. Fit the data to a scaling relation. If the condensates are purely viscous fluids, the scaling relation is [6]:

  $${\tau }_{\text{fu}}=1.97\left(\eta /\gamma \right)R$$

  where the slope, or inverse capillary velocity, is given by the viscocapillary ratio, i.e., viscosity (η) over interfacial tension (γ).
• 6.2.14.

  The fusion time parameter can also be obtained by analyzing the video obtained in 6.2.7 as demonstrated by Ghosh and Zhou [6]. Crop the video and select the frames to just include the fusing droplets from the moment the droplets are in contact with each other. Enhance the contrast if necessary.

• 6.2.15.
  Export as a tiff series and to obtain the edge-to-edge distance (L) of the fusing droplets (Figure 5c, green trace) and fit it to the following equation:

  $$L_0-L=\left(L_0-L_{\infty }\right)\left[1-e^{-{\left(t/{\tau }_{\text{fu}}\right)}^{1.5}}\right]$$

  where L₀ and L_∞ denote the values of L at the start of the fusion process and after the fusion is complete, respectively. The MATLAB script is found at: https://harbor.lumicks.com/single-script/3798a052-4a5d-4f39-9509-f25ec152142a.

Figure 5.

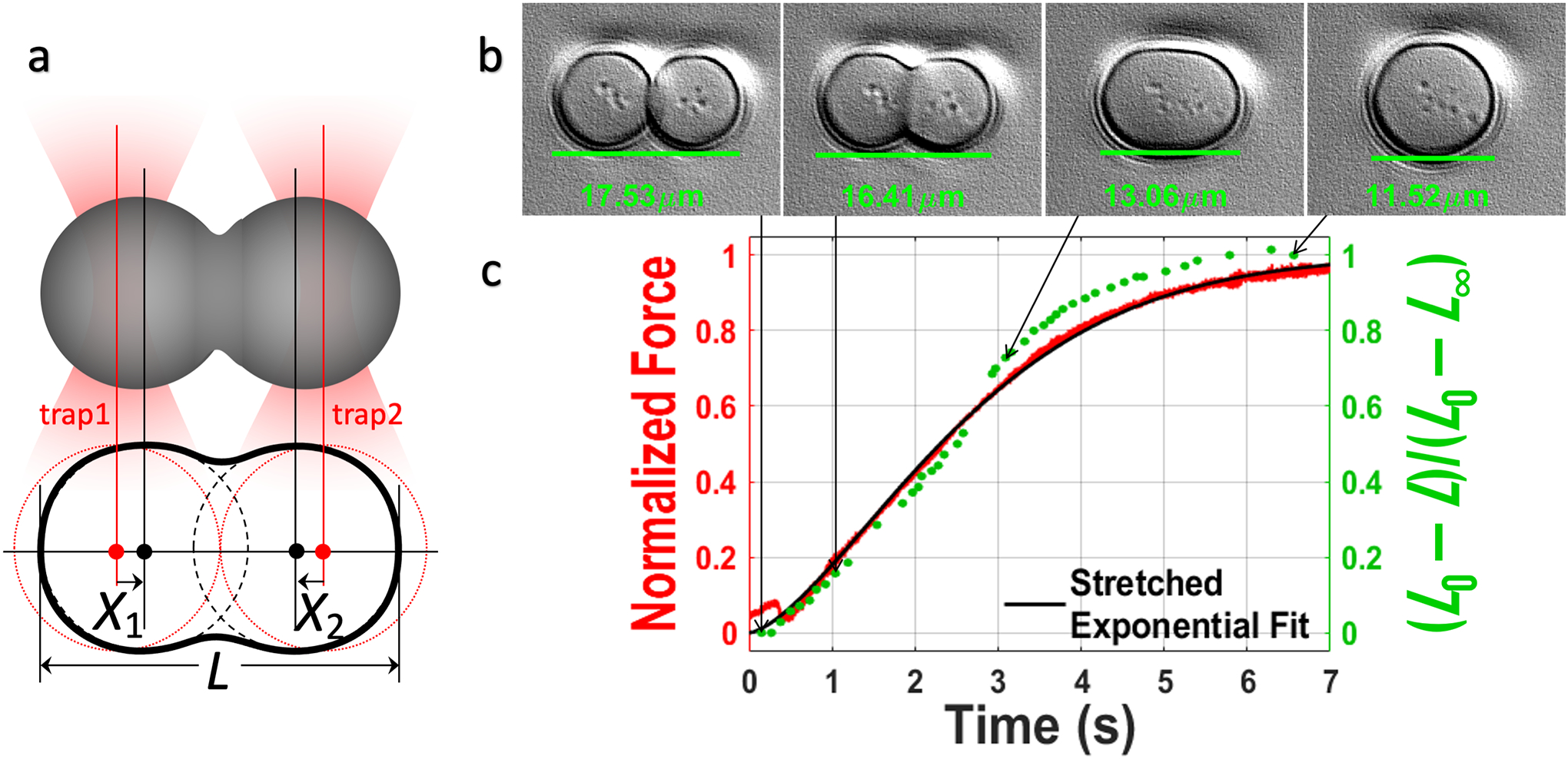
Active fusion of droplets monitored by optical tweezers and brightfield camera. (a) After being brought together by optical traps, two droplets fuse while being suspended by the traps, leading to changes in the edge-to-edge distance (L) and the forces sensed by the two optical traps. The overall power of optical traps is set to a very low level as to not impede the droplet fusion. (b) Brightfield snapshots of fusing droplets. (c) Red: normalized force signal from the stationary trap (trap2); black: fit to a stretched exponential function; green: edge-to-edge distance of the fusing droplets. The brightfield camera has a much lower time resolution than the force signal (compare the red and green traces) and thus its use for quantitative analysis is limited to droplets that fuse relatively slowly.

6.3. Determination of condensate viscoelasticity by oscillating a trapped bead inside settled droplets

• 6.3.1.Prepare a droplet sample doped with ~0.01% (w/v) 1 or 2 μm polystyrene beads (typically functionalized with a charged group like carboxylate when working with droplets made of charged components). Add beads to the buffer before the droplet-forming components. This will encourage droplets to form around beads, allowing beads to be already inside droplets when the sample is loaded onto the instrument.
• 6.3.2.Set up the sample chamber as in 6.1.1. Load the sample and allow all droplets to settle to the bottom. Note that the trap1 split is required to be set to 50% while adjusting the condenser position but should be brought back to 100% when doing this experiment. While waiting for droplets to settle, keep the trapping laser to 0%.
• 6.3.3.Once all the droplets have settled, adjust the Z position of trap1 to be just above the coverslip. Set the trapping laser to 100% and adjust the overall power to a value that is just enough to allow the maneuvering of a trapped bead inside a settled droplet. Note down this value of the overall power for the subsequent experiment. Remove the sample.
• 6.3.4.Prepare a sample containing 0.01% (w/v) or less beads in DI water. The bead concentration is determined by trial and error: it must be sufficiently high so beads can be easily found for trapping, but sufficiently low to avoid collision between beads or having multiple beads fall into the trap.
• 6.3.5.Load the bead sample and set trap1 split to 100%. Perform a calibration of trap stiffness on a single trapped bead with the trapping laser set to 100% and the overall power set to the value noted in 6.3.3. Input the diameter of the bead, the viscosity of DI water at the temperature of the sample stage, and the temperature itself. The viscosity of water is 8.9 × 10⁻⁴ Pa.s at 25 °C and typically beads of 1 or 2 μm diameters should be used. The instrument should produce a power spectrum of the trapped bead’s position and a fit to a Brownian harmonic oscillator. Repeat the calibration several times to ensure a consistent value of the trap stiffness. Note the trap stiffness given in pN/μm for the X component of trap1 and apply the calibration. Remove the bead sample.
• 6.3.6.Load the sample prepared in 6.3.1. Pipette the sample up and down multiple times before loading to ensure the resuspension of any settled beads. Alternatively, a fresh sample may be prepared.
• 6.3.7.After droplets have settled on the coverslip, adjust the Z position of trap1 to be just above the coverslip, and move the sample stage to place the X-Y position of the trap within a sufficiently large, settled droplet with a bead inside. Trap the bead with the overall power noted in 6.3.3.
• 6.3.8.
  Use the following python script (Note 5) to sinusoidally oscillate the trap1 X position at a frequency (ω/2π) of 0.5 Hz and amplitude of 1 μm:

  import bluelake as bl
  from bluelake import mirror1, pause
  bl.mirror1.start_oscillation(axis=‘X’, amplitude=1.0, frequency=0.5)
  pause(10.0)
  bl.mirror1.stop()
  

• 6.3.9.Adjust the bead position along the Z axis such that it oscillates near the center of the droplet. If it is too high (i.e., close to the top of the droplet), the force probed has a significant contribution from the interfacial tension of the droplet, leading to a large elastic component evidenced by a near zero phase difference between the X components of the force signal (F_t) and the position signal (X_t) from trap1. If it is too low (i.e., close to the coverslip), the phase difference again can be small, and the force signal can be erratic. The ideal scenario is when the phase difference is greater than π/4 at 0.5 Hz for viscoelastic biomolecular condensates. See Figure 6 for illustration.
• 6.3.10.

  By adjusting the frequency in the python script from a low to high value, obtain several oscillation profiles for F_t and X_t at different frequencies. Note that the X_t amplitude should be small enough at higher frequencies to ensure that the bead is kept being trapped during oscillation (Note 6). This is helped by the fact that the force amplitude increases at higher frequencies. In all cases the X_t amplitude should be limited so the bead does not approach the lateral surface of the droplet too closely. We recommend 0.5 – 2 μm as the range for the X_t amplitude and 0.1 to 100 Hz as the range for the frequency.

• 6.3.11.

  Export the oscillation events over all the different frequencies into separate h5 files. Repeat the experiment with different beads inside different droplets settled over different areas of the coverslip.

• 6.3.12.
  Fit X_t and F_t at each frequency to the following functions:

  $$X_t=X_{t0}\text{\hspace{0.17em}cos}\left(\omega t+{\varphi }_1\right)+B_1$$

  $$F_t=F_{t0}\text{\hspace{0.17em}cos}\left(\omega t+{\varphi }_2\right)+B_2$$

  A MATLAB script that imports the h5 file and does the fitting can be found here: https://harbor.lumicks.com/single-script/19365d16-fd02-448b-b95a-15790a49b737.
• 6.3.13.
  The force amplitude F_t0 and phase difference Δ = ϕ₂ − ϕ₁ is used to calculate the elastic and viscous moduli at each frequency using the following equation [7]:

  $$G^{\prime }\left(\omega \right)=\frac{F_{\text{t}0}}{6\pi a{X}_{\text{t}0}}\frac{\text{cos\hspace{0.17em}}\Delta -{\rm Y}}{{\left(\text{cos\hspace{0.17em}}\Delta -{\rm Y}\right)}^2+{\text{sin\hspace{0.17em}}}^2\Delta }$$

  $$G^{″}\left(\omega \right)=\frac{F_{\text{t}0}}{6\pi a{X}_{\text{t}0}}\frac{\text{sin\hspace{0.17em}}\Delta }{{\left(\text{cos\hspace{0.17em}}\Delta -{\rm Y}\right)}^2+{\text{sin\hspace{0.17em}}}^2\Delta }$$

  where ϒ = F_t0/κ_tX_t0; a is the radius of the bead; and κ_t is the trap stiffness noted in 6.3.5.
• 6.3.14.

  The frequency dependence of the complex shear modulus can be further fit to a viscoelasticity model such as the Maxwell, Jeffreys, or Burgers models [7,13,14,17]. The code for fitting to a Burgers model can be obtained here: https://harbor.lumicks.com/single-script/10cb3e3d-a1a4-409b-8921-930acdd5f026.

Figure 6.

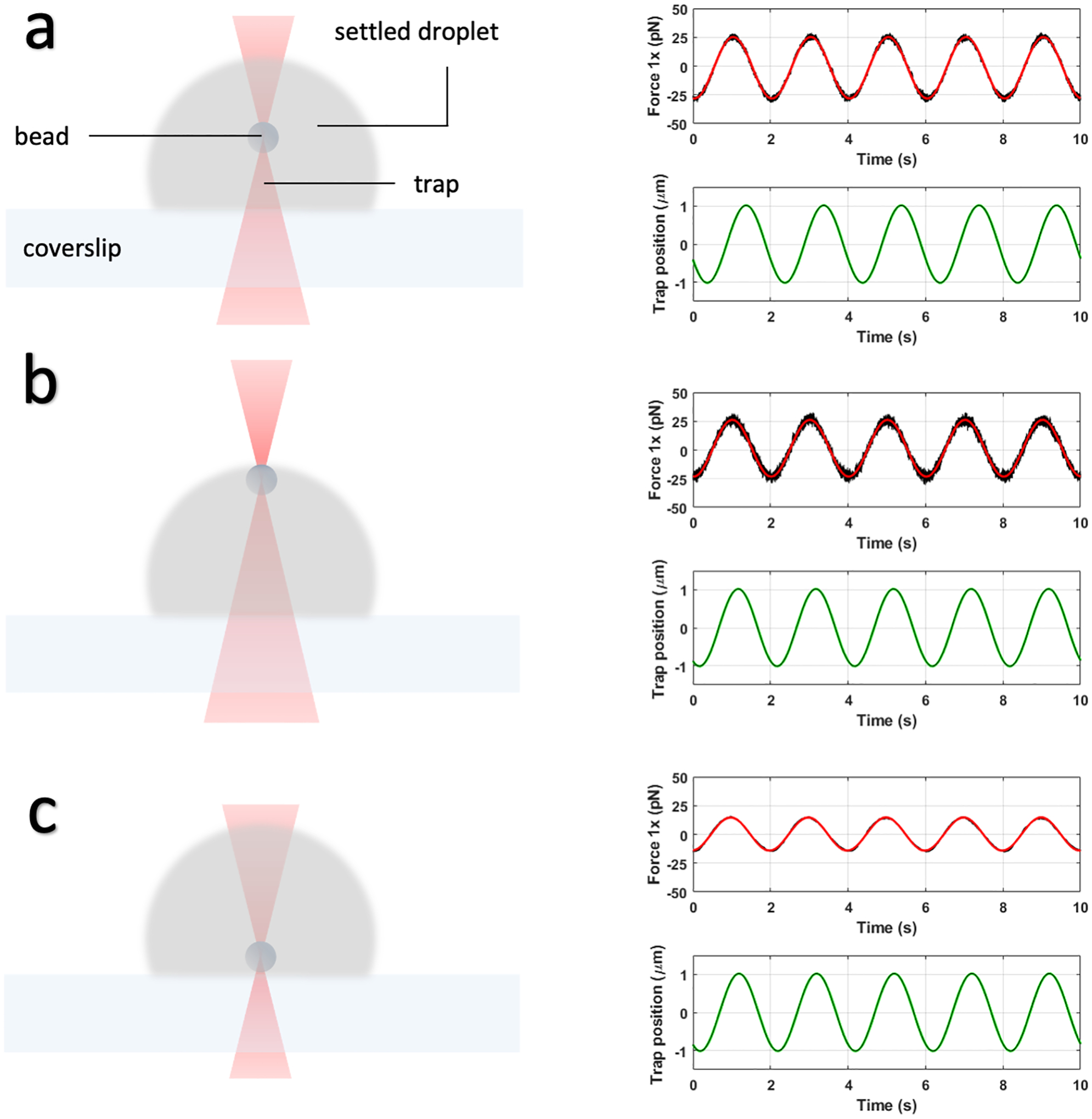
Optimal Z position for oscillating an optically trapped bead within a settled droplet. (a) The trapped bead is correctly positioned near the center of the droplet. The trap1 force trace correctly shows a phase shift of approximately π/4 ahead of the trap1 position trace. (b) The bead is too close to the surface, as indicated by a near zero phase difference between the force trace and trap position trace. (c) The bead is too close to the coverslip, as indicated by an erratic force trace with a very small amplitude.

6.4. Determination of interfacial tension by stretching a droplet suspended between two trapped beads

• 6.4.1.Load a sample containing droplets doped with beads as in 6.3.1 and 6.3.2. This time keep the trap1 split at 50%.
• 6.4.2.Let most of the droplets and beads settle with trapping laser set to 0%. Adjust the Z position of the trap to just above the coverslip. Set the trapping laser to 100% and increase the overall power gradually to a high enough level to be able to trap and lift two settled beads atop the coverslip. Once lifted, immediately lower the overall power to a low enough level such that the beads remain trapped. Droplets should begin to coalesce around both beads. Once the droplets encapsulating the beads have grown to sufficient size, move one bead toward the other to fuse the two droplets as described in 6.2.6, this time with a bead at the center of each droplet. The fusion spontaneously results in a “pre-stretch” configuration where the two trapped beads are located at opposite poles of the fused droplet [7,12] (Figure 7). Adjust the overall power to a value that allows for stretching of the droplet by trap1 without losing the bead. Remove the sample.
• 6.4.3.Load a bead sample as described in 6.3.4. Obtain the trap stiffnesses of both traps by performing a calibration as in 6.3.5 but this time with the trap1 split set to 50%. Set the trapping laser to 100% and the overall power to the value determined in 6.4.2. Repeat the calibration for consistency. Note down the trap stiffnesses for the x components of trap1 and trap2 in pN/μm, and apply the calibration. Remove the sample.
• 6.4.4.Load the same or a sample similar to the one prepared in 6.4.1. Achieve the pre-stretch configuration described in 6.4.2 with trapping laser set to 100% and overall power set to the value determined in 6.4.2 and used in 6.4.3. Let all neighboring droplets fuse with this trapped droplet or settle until the field is clear. Obtain a snapshot of this configuration.
• 6.4.5.Stretch the droplet by moving trap1 slowly till the beads are just about sticking out of the droplet surface.
• 6.4.6.Set a speed of 0.05 μm/s and let trap1 extend the droplet along the X direction for 0.5 μm. Following this, retract at the same speed in the -X direction for 0.5 μm. Repeat several times with the same and different droplets. Export the X component of the trap1 position (X_t) and X components of the trap1 and trap2 force signals (F_t1 and F_t2) as an h5 file.
• 6.4.7.
  Fit X_t, F_t1 and F_t2 to straight lines and obtain the slopes ν, f₁, and f₂. A MATLAB script that imports and fits the h5 file can be obtained here: https://harbor.lumicks.com/single-script/5686cfaf-2a7c-465d-b5cb-db4e2d223efa. Obtain the static spring constant χ_sys0 of the system comprising of the droplet and the two traps using the following relation [7]:

  $${\chi }_{\text{sys}0}=\frac{\left(f_2-f_1\right)/2}{-v}$$

  The static spring constant χ₀ of the droplet is then found as

  $$\frac{1}{{\chi }_0}=\frac{1}{{\chi }_{\text{sys}0}}-\frac{1}{{\kappa }_{\text{t}1}}-\frac{1}{{\kappa }_{\text{t}2}}$$

  where κ_t1 and κ_t2 are trap stiffnesses obtained in 6.4.3.
• 6.4.8.Estimate the diameter (2R) of the suspended droplet from the snapshot obtained in 6.4.4 using imageJ. Convert to μm.
• 6.4.9.
  The surface tension is obtained using the following relation [17]:

  $$\gamma =\frac{1}{\pi }\left[\text{ln}\left(\frac{R}{a}-1\right)+0.68\right]{\chi }_0$$

  where a is the radius of the trapped bead, R is the radius of the droplet obtained in 6.4.8, and χ₀ is the static spring constant of the droplet determined in 6.4.7.

Figure 7.

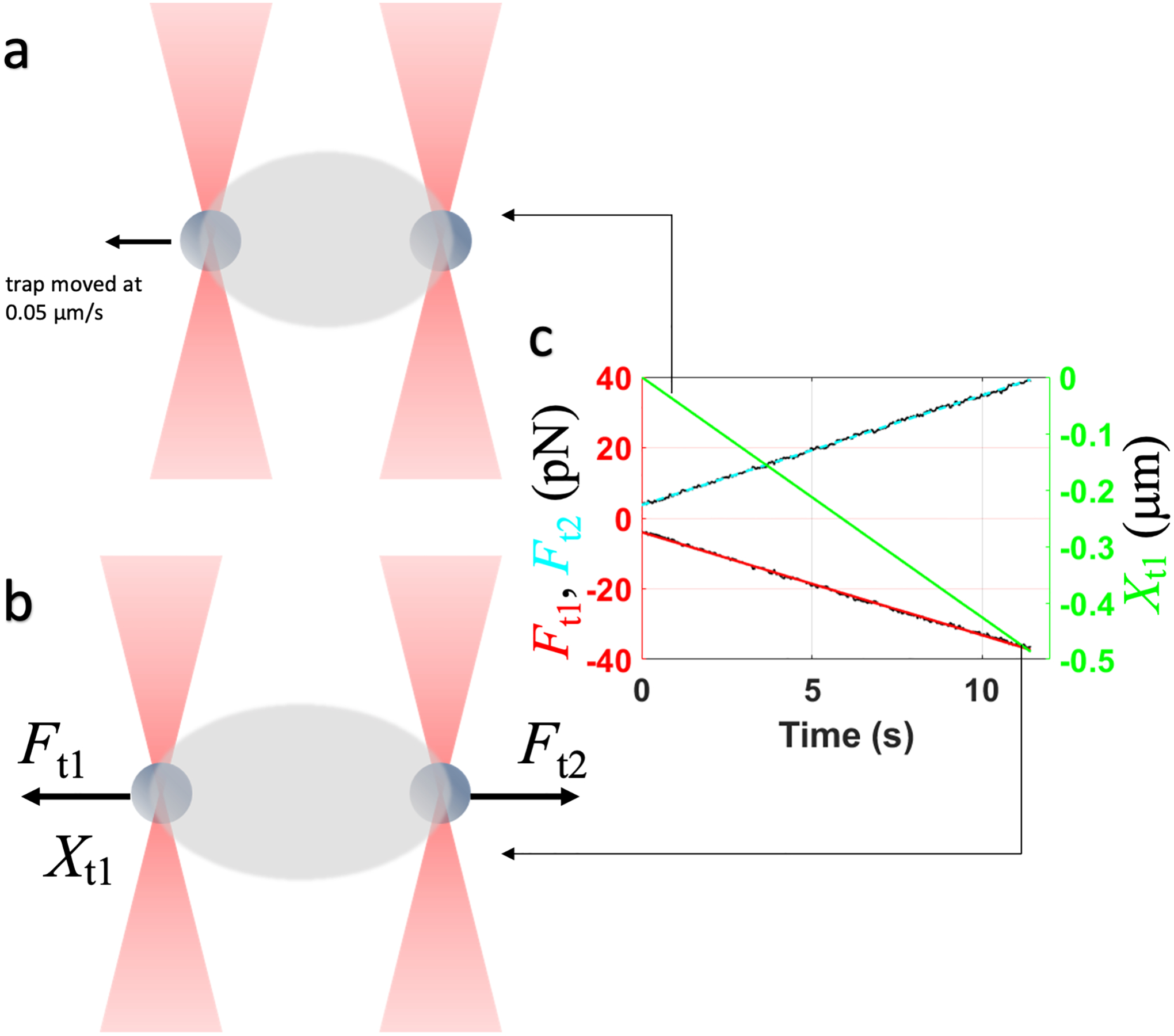
Schematic for the droplet stretching experiment. (a) Configuration when trap1 starts to pull the droplet. (b) Configuration when the pulling is complete. (c) Traces of the trap1 position and the trap1 and trap2 forces.

6.5. Determination of interfacial tension by rupturing the surface of a settled droplet using a trapped bead

• 6.5.1.Load a sample containing droplets doped with beads as in 6.3.1 and 6.3.2 with trap1 split set to 100%.
• 6.5.2.Lift a bead inside a settled droplet until it is near the top of the droplet.
• 6.5.3.Pull the bead at a low constant speed (0.1 μm/s) until it ruptures the droplet surface (Figure 8).
• 6.5.4.Export the force profile of the rupture event as an h5 file. Analyze the file using the following code to obtain the maximum rupture force and the surface tension: https://harbor.lumicks.com/single-script/d890428b-1ca6-4f98-a27e-24aeb9f65dd6.
• 6.5.5.
  The maximum rupture force, F_rup, is the difference between the force value at the beginning of the experiment and that just before the rupture event occurs. The interfacial tension is given by [7]:

  $$\gamma = \frac{F_{rup}}{2\pi af}$$

  where a is the bead radius and f is a correction factor empirically observed to be around 1.1 when compared to the interfacial tension determination by droplet stretching.

Figure 8.

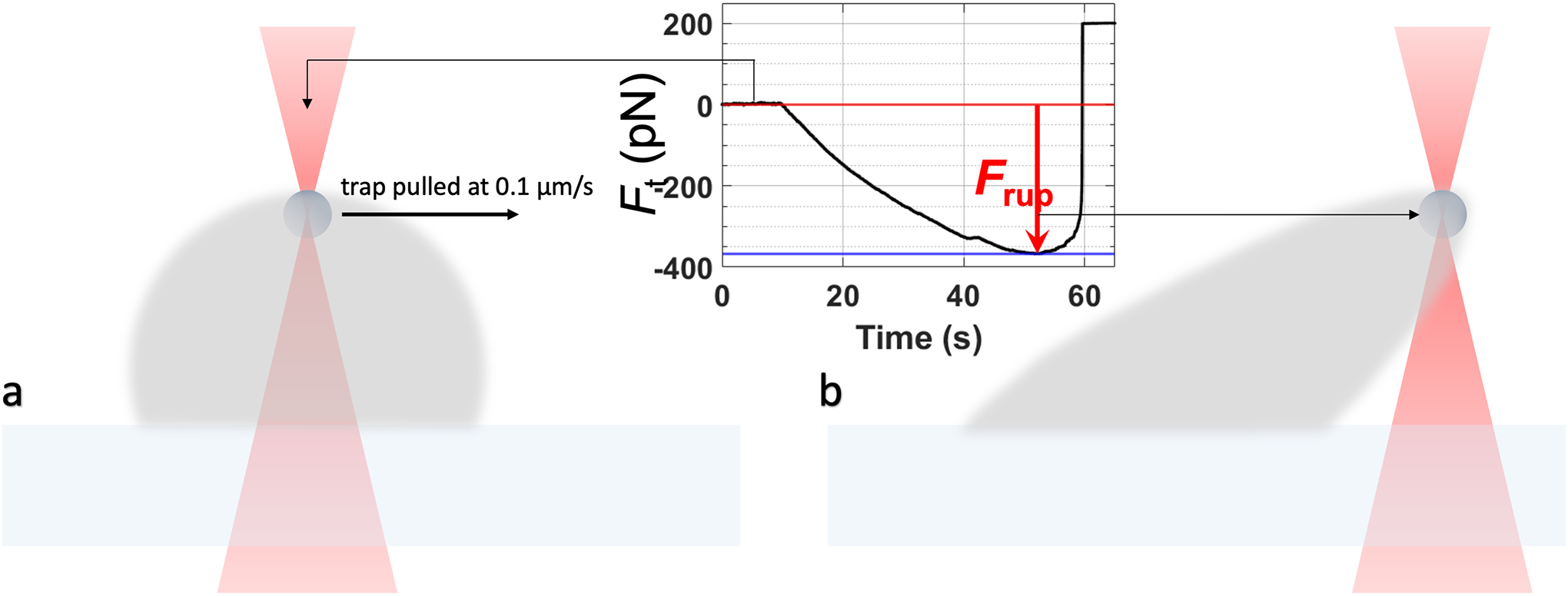
Schematic for the droplet rupture experiment. (a) Configuration before trap1 is pulled at a low constant velocity. (b) At the point of droplet rupture.

7. Concluding remarks

We have described several protocols that are either generally applicable to biomolecular condensates or are unique for their characterization. In particular, (1) the fusion constructs similar to those used for SH3₅ and PRM₅ (Figure 1a) are very commonly used for purifying intrinsically disordered proteins (IDPs), which are often the main components of biomolecular condensates. (2) The cautionary steps added in the purification protocols are well advised for other condensate-forming proteins -- adding DNase I prevents endogenous DNA from interfering with the purification process and precipitating the protein under purification; working under high salt as much as possible minimizes the chance of protein aggregation. (3) The CIGraBS method [4] for determining the concentration of a component in the droplet phase consumes very little sample and relies on a very commonly accessible instrument, i.e., a confocal microscope. (4) Microrheology by optical tweezers is so far the only approach that allows for the determination of the viscoelasticity of biomolecular condensates, especially for those in which shear relaxation occurs on the ms or faster timescales [7,11–13]. The fact that optical tweezers can also measure interfacial tension, droplet fusion speed, and other properties is a bonus, but accessibility is a limitation for most labs.

It is always prudent to compare results obtained by different methods. Whereas confocal microscopy quantifies the concentrations of condensate components via fluorescence intensity, the quantitative phase microscopy proposed by McCall et al. [22] relies on the difference in refractive index between the droplet phase and bulk phase, which can be measured on a holographic microscope. Quantification by confocal microscopy is prone to artifacts related to fluorescence quenching. To minimize these artifacts, instead of simply equating the partition coefficient to the ratio of fluorescence intensities inside and outside droplets, our protocol [4] calls for the generation of standard curves over a wide range of concentrations of the labeled species, so to cover the observed fluorescence intensities in both the bulk and droplet phase. Moreover, when generating standard curves, we add the unlabeled version of the labeled species at the same ratio as used in the droplet-forming sample. If fluorescence quenching by other components is suspected, one should add those components as well when generating standard curves.

Optical tweezers use the trapping force to balance and thus measure interfacial tension [7,12,17]. The shape of droplets resting on a coverslip is due to the balance between interfacial tension and gravity and can also be used to measure interfacial tension [23,24]. We used the height of resting droplets to give a qualitative indication of interfacial tension [6], but it should be possible to analyze the shapes of the resting droplets to quantify interfacial tension. Though the human eyes perceive the inter-phase interface as smooth, in reality the interface undergoes thermal fluctuations, which can be captured by a confocal microscope. The amplitude of the thermal fluctuations is related to the interfacial tension [12,25], but the theory has yet to be fully developed for precise quantification. Recently, micropipette aspiration, which relies on pressure suction for force balance, has been used to determine the interfacial tension of biomolecular condensates [26]. In many studies, the inverse capillary velocity (as determined by monitoring droplet fusion) has been combined with zero-shear viscosity to deduce interfacial tension. We raise a strong warning that this approach is only valid for purely viscous liquids, and can lead to serious errors, given the viscoelastic nature of biomolecular condensates and shear thickening and shear thinning that have exhibited [7].

Notes

1. Vendor and catalog# are provided only as examples for sourcing, and do not imply endorsement.

2. Other endonucleases like Benzonase may also be used.

3. Optionally, a freshly prepared solution of sodium bicarbonate may be added at a final concentration of 100 mM to the reaction mixture. This brings up the pH to ~8 which favors the reaction.

4. This protocol should work with any functionalized dye targeting selected amino acids for conjugation. Care should be taken to ascertain buffer compatibility with the conjugation reaction.

5. Details on python scripts that control different components of the LUMICKS^™ optical tweezer system can be found at https://lumicks.github.io/bluelake-api/2.0.0/examples/components/index.html.

6. Besides the potential loss of the bead from the trap, another possible complication at high frequencies is that the trap position may not reach the specified amplitude, due to device response time and inertia. Reducing the trap position amplitude may also lessen this complication.