Ramachandran Conformational Energy Maps for Disaccharide Linkages found in Burkholderia multivorans Biofilm Polysaccharides

Abstract

Ramachandran conformational energy maps have been prepared for all of the glycosidic linkages found in the C1576 exopolysaccharide that constitutes the biofilms of the bacterial species Burkholderia multivorans, a member of the Burkholderia cepacian complex that was isolated from a cystic fibrosis patient. This polysaccharide is a rhamnomannan with a tetrasaccharide repeat unit containing two mannose residues and two rhamnose residues, –[3-α-D-Man-(1→2)-α-D-Man-(1→2)-α-D-Rha-(1→3)-α-D-Rha-(1→]_n–, where approximately 50% of the rhamnoses are randomly methylated on their O3 hydroxyl groups, further increasing the overall hydrophobicity of the chains. Because of the methylation, the tetrasaccharide repeat unit actually contains six possible linkages. The conformational energy maps are fully adiabatic relaxed maps in which the energy for each (ϕ,ψ) grid point on the map represents the lowest possible energy for the molecule in that conformation, considering all the combinations of the other degrees of freedom, such as hydroxyl orientations. Molecular dynamics simulations were used to verify that these maps indeed describe the conformational dynamics of these linkages. All six linkages were found to be quite restricted in possible ϕ angles, but to exhibit several possible low-energy ψ angles, suggesting that these chains could be quite flexible.

Introduction

Bacterial biofilms are important in a number of animal and human diseases, ranging from cystic fibrosis to illnesses associated with medical devices and implants. Disrupting such biofilms offers a strategy for dealing with bacterial infections without using antibiotics and the corresponding danger of promoting antibiotic resistance. Thus, understanding the structural characteristics of bacterial biofilms could be of considerable practical importance for a number of medical applications. Particularly interesting examples of such biofilms are those produced by the various bacterial species that make up the Burkholderia cepacian complex. One of these species, the B. multivorans strain C1576 isolated clinically from a cystic fibrosis patient, produces biofilms based on a recentlyidentified rhamnomannan exopolysaccharide (Epol), designated as EpolC1576, with a hydrophobic character due to a high degree of methylation of its rhamnose residues.¹ The basic repeat unit for EpolC1576 is –[3-α-D-Man-(1→2)-α-D-Man-(1→2)-α-D-Rha-(1→3)-α-D-Rha-(1→]_n–,¹ where Man refers to mannopyranose and Rha refers to rhamnopyranose, and where half of the central rhamnose residues are randomly methylated on the O3 hydroxyl group.¹ These biofilms might be thought of as thin layers of biological gels, and while they also contain other molecules besides EpolC1576, including proteins and various small molecules, it is likely that the polysaccharide forms the principal “scaffold” of the biofilm, as in other types of gels. Experimental atomic force microscopy studies of this polysaccharide have found unusual conformational behavior suggesting significant self-association into compact globules,² which raises questions about how exactly these polymers interact in constituting the biofilms. As part of a larger project to construct a computational model for the EpolC1576 biofilm, it would be of considerable utility to be able to model the conformational behavior of this polysaccharide and its interactions with other Epol chains, both in isolation and in an aqueous environment, since water is usually the most abundant single component in biological gels. Thus, we report here a detailed analysis of the mechanical energy of these polymers and of their interactions with water.

As with any polymer, the first step in understanding the EpolC1576 polysaccharide is to construct Ramachandran-like conformational energy maps^3,4 of the variation of the molecular energy with the glycosidic torsion angles ϕ and ψ for every glycosidic linkage in the polysaccharide. Since these linkages have not previously been mapped as fully-relaxed, or adiabatic, Ramachandran maps, we have undertaken to calculate such maps for each linkage using the CHARMM36 general force field for carbohydrates.^5,6 In an adiabatic energy map, the approximation is made that the conformational behavior of the polymer can be reduced to a two dimensional problem; that is, that the energy depends only on the linkage dihedral angles in the case of polysaccharides, and that all other degrees of freedom either relax very rapidly as a function of those angles, or so very slowly that they play no role in the conformational problem. Thus, in preparing such maps, the lowest energy corresponding to each combination of ϕ and ψ is plotted, taking account of all possible combinations of all other degrees of freedom which might affect the conformational energy, such as orientations of the hydroxyl groups and the exocyclic primary alcohol in the case of the mannose residues, and in principle, the various possible ring conformations (chairs, boats, skew boats).^3,4 The conformational energy described in such maps can be affected by environment, most notably by aqueous solvation in the case of some saccharides, particularly in cases where hydrogen bonds might exist between successive sugar residues, since such hydrogen bonds might exchange for hydrogen bonds to water, substantially affecting the conformation.^7,8 In cases where this is possible, it is desirable to prepare potential of mean force maps, which plot the free energy rather than just the mechanical energy, and include entropic effects as well as the interactions (both enthalpic and entropic) with environmental water molecules whose many degrees of freedom are included only in an average manner.^7,9 Such maps for these linkages are being prepared, but their interpretation will require the vacuum maps reported here in order to fully understand the effects of solvation.

The specific disaccharide linkages modeled here are α-D-mannopyranose-(1→2)-α-D-mannopyranose; α-D-mannopyranose-(1→2)-α-D-rhamnopyranose; α-D-mannopyranose-(1→2)-3-methyl-α-D-rhamnopyranose; α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose; 3-methyl-α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose; and α-D-rhamnopyranose-(1→3)-α-D-mannopyranose. In the lowest-energy ⁴C₁ pyranose ring conformations for D-mannopyranose and D-rhamnopyranose, the C2 hydroxyl groups are in axial positions, so all three of the 1→2 disaccharide linkages are of the axial-to-axial type, which means that in their broadest outlines, governed by van der Waals repulsions as in the original such maps prepared by Ramachandran and co-workers,^10,11 these energy maps will be topologically similar. All three of the 1→3 linkages are of the axial-to-equatorial type, and so should also be similar to one another.

In order to be truly useful in modeling disaccharide, and thus polysaccharide, conformational behavior, it is necessary for these Ramachandran maps to be fully relaxed, in the sense that for every (ϕ,ψ) pair in the Ramachandran space, all other accessible conformations for all other degrees of freedom in the molecule have been minimized and the conformation with the lowest overall energy identified. When prepared in this fashion, molecular dynamics simulations of such molecules will be closely confined within the low energy portions of the maps. This can be taken as a consistency check of the validity of the mapping; if an MD trajectory strays outside of the low energy contours of the map at thermal temperatures, then something is wrong. We report here fully adiabatic vacuum conformational energy maps for each linkage in the EpolC1576 polysaccharide and demonstrate their validity with vacuum molecular dynamics (MD) simulations of the same linkage in a corresponding disaccharide. Very long timescale molecular dynamics simulations of each of these disaccharides in aqueous solution were also conducted to determine whether there are any significant solvation effects that perturb the conformation and thus might warrant the much greater effort of preparing solution potential of mean force (free energy) maps.

Procedures

Conformational Energy Mapping

Adiabatic conformational energy maps were calculated in vacuum for each of the 6 types of disaccharides which are found in the repeating units of EpolC1576. The maps were calculated using the general molecular mechanics program CHARMM^12,13 (versions c42 and c43) and the CHARMM36 force field for carbohydrates.^5,6 This force field was specifically developed for carbohydrates from extensive ab initio calculations and has been extensively tested on a range of such molecules. It contains terms for bond stretching and bond angle bending, with Urey-Bradley corrections for anharmonicity; 6–12 Lennard-Jones terms for van der Waals interactions; and Coulombic interactions between atomic partial charges located on individual atoms. Torsional energies are represented by a sum of one-, two-, and three-fold periodic terms for each set of four sequentially-bound atoms.

For these maps, the lowest energy possible for each selected (ϕ,ψ) conformation was found by conventional energy minimization, consistent with the assumption that both of the pyranose rings in each disaccharide remain in the generally lowest-energy ⁴C₁ ring conformation.¹⁴ This assumption dramatically reduces the number of conformations that must be examined. While this assumption is true for most sugars, it was checked here for the D-rhamnose case to ensure its validity for this nontypical saccharide. The alternate ¹C₄ chair form for D-rhamnose was indeed found to be higher in energy than the standard ⁴C₁ conformation, as were all of the stable skew boats; several of the skew boat conformations are not stable minima (Table S1, Supplementary Material). Extensive very long timescale MD simulations at elevated temperatures confirmed that there was no tendency for any of the sugar rings of either type to deviate from the ⁴C₁ chair conformation, either in disaccharides or in longer 8 residue oligomers, and either in vacuum or aqueous solution (see Figure S1 in the Supplementary material). Thus, in practice, the mapping only involved finding the lowest energy conformation for each of the other degrees of freedom in both disaccharide sugar rings, such as the torsional angles specifying the orientation of each hydroxyl group and the exocyclic hydroxymethyl groups, as well as optimizing bond lengths and angles. Because conventional energy minimization algorithms cannot move systems over energy barriers, such as the barriers to rotation about these torsion angles, minimizations must be carried out starting from all possible staggered combinations of the torsion angles that might plausibly correspond to energy wells for each torsional degree of freedom, apart from those of the ring, to ensure that the lowest possible minimized energy for each (ϕ,ψ) combination has been found.

For each linkage, the ϕ and ψ angles, defined as O5-C1-O3’-C3’ and C1-O3’-C3’-C2’, respectively, for the (1→3) linkages and as O5-C1-O2’-C2’ and C1-O2’-C2’-C1’ for the (1→2) linkages, were set to integral values at 20° intervals in the range from −180° to 180°. Each (ϕ,ψ) pair, representing a point in Ramachandran space for the disaccharide, was then exhaustively minimized for all possible combinations of all three staggered conformations of all hydroxyl and exocyclic primary alcohol groups to find the lowest energy associated with that point on the Ramachandran surface. For each minimization sequence, an initial 5 steps of steepest descent minimization were followed by conjugate gradient minimization until convergence was reached, defined by an energy change between steps of less than 0.001 kcal/mol or a gradient change between steps of less than 0.01 kcal/Å·mol. Rather than rigidly constraining the glycosidic linkage angles to remain fixed at the integral grid point values, a strong restraining force of 1000 kcal/Å·mol was applied during the minimizations; thus, the values of ϕ and ψ might deviate by small amounts in the range of >0.01° from the specified grid points. Nonetheless, in the subsequent energy mapping, the minimized energies were assigned to the integral positions. During the minimizations, no electrostatic or van der Waals cutoffs were employed.

As with all such Ramachandran conformational energy maps, large regions of the energy map correspond to conformations with significant atomic overlaps. In such cases, if ϕ and ψ are strongly restrained to remain at the selected values, the molecule will distort substantially, often in very unphysical ways, to relieve the enormous forces resulting from the atomic overlaps imposed by the artificial constraints. At a minimum, these changes might involve ring “flips” to alternate conformations such as higher energy twist boats, or badly distorted bond lengths or angles, or both, might result. It is even possible that under such large unnatural forces, an aliphatic proton might be forced to move through the plane of the other three substituents of the carbon to which it is attached, actually inverting the stereochemistry of that carbon atom and changing the sugar into another. Obviously all such artifacts of the constraints are of no physical interest, so great care must be taken to avoid any such occurrences. Thus, all minimized conformations were checked using the Cremer-Pople pucker parameters for both rings^15,16 to ensure that they did not change ring conformation and the stereochemistry of all chiral centers was also verified. To avoid many such problems and increase the efficiency of the calculation by avoiding extensive minimizations unlikely to produce any useful result, if after 5 steps of initial steepest descent minimization the molecular energy remained above 1000 kcal/mol, the energy for that point was arbitrarily assigned the value of 300 kcal/mol and the algorithm moved on to the next grid point. This expedient also helped to avoid representational artifacts when simple cubic spline routines were subsequently used to prepare contour maps of the surface, since such simple functions would have difficulty representing the very rapid rise to the extremely high, often effectively infinite, energy values that correspond to atomic overlaps.

The glycosidic torsion angles were defined using heavy (ring) atoms rather than the protons favored in NMR because with molecular mechanics force fields the positions of the protons displace more readily than heavier atoms, thus raising the possibility that under strong repulsive forces arising from applied artificial constraints on the glycosidic torsions, their bond angles might more easily distort to an unphysical extent. The present definitions for ϕ and ψ can be readily converted approximately to the proton-based definitions favored by carbohydrate workers by subtracting 120°.

It is of course highly unlikely that the global minimum energy conformation would correspond exactly to one of the arbitrarily-spaced integral grid points. Thus, once the minimized energy grid was calculated, preliminary contour maps of the topology were prepared using cubic spline routines in the MatLab package.¹⁷ From this preliminary map, the approximate splined global minimum position was identified. Next, the geometries corresponding to each of the four grid points on the map that bracket the apparent minimum were subjected to unconstrained minimization to verify that all four converge to the same absolute global minimum. This energy was then taken as the global minimum energy conformation for the disaccharide, and the map was recontoured at uniform intervals above this absolute minimum.

MD Simulation Protocols

For each of the disaccharide linkages studied, MD simulations were performed for a single disaccharide molecule in vacuum to test the validity of the relaxed energy maps. Langevin simulations at room temperature were carried out using the CHARMM molecular mechanics program,^12,13 with the same CHARMM36 energy parameters used in the conformational mapping. The starting atomic coordinates for each disaccharide were generated as ideal structures at glycosidic torsion starting values of (75°, −131°). The lengths of the covalent bonds involving hydrogen atoms were kept fixed using the general constraint algorithm SHAKE.^18,19 Initial velocities were assigned from a Boltzmann distribution and the initial structures were heated from 0 to 300K over 100 ps, equilibrated for an additional 100 ps, and then simulated for 1 $\mu$s using a Leapfrog Verlet integrator with a step size of 1 fs and a friction coefficient set at 2.0 ps⁻¹. As in the energy mapping, electrostatic interactions were not truncated.

Each simulation was then repeated for the disaccharide in aqueous (TIP4P)²⁰ solution. Each of these simulations was carried out for a single disaccharide molecule in the center of a cubic box with an initial box length of 37.81 Å containing 1728 water molecules in the NPT ensemble at a temperature of 300 K and a pressure of 1 atm. All van der Waals interactions were smoothly truncated on an atom-by-atom basis using switching functions¹² from 9.0 to 11.0 Å, while electrostatic interactions were treated using the Particle Mesh Ewald method^21,22 with a real space cutoff of 12.0 Å and κ = 0.454 Å⁻¹. The simulations were equilibrated for 100 ps and then integrated for an additional 1 µs using a Hoover constant pressure/temperature algorithm, at a constant pressure of 1 atm, maintained using a Hoover piston with a mass of 2000 amu and a timestep of 2 fs.²³

Results and Discussion

Figure 1 displays the calculated vacuum adiabatic conformational energy maps for all six of the disaccharide linkages. In each map, contours are shown at uniform 1 kcal/mol intervals above the calculated global energy minimum, indicated by an “X”, up to the 4 kcal/mol level, and subsequently at 2 kcal/mol intervals up to 10 kcal/mol. Under thermal equilibrium conditions the Boltzmann distribution of energies means that on a practical MD simulation timescale, excursions outside the 4 kcal/mol contour on the conformational energy map will be rare, and conformations outside the 10 kcal/mol contour will not occur. As noted above, the axial-axial character of the (1→2) linkages means that all three such maps should exhibit similar overall topologies, and that all three of the (1→3) linkage maps will also be similar. This was indeed found to be the case, with nearly all those conformations having ϕ values between −150° and 0° disallowed by steric clashes, regardless of the ψ value. All of the maps, regardless of linkage type, exhibit a broad trough running through a full cycle of 360° in ψ, between ϕ values of ∼0°and ∼180°, with several local minima located along this trough and separated by barriers of varying heights.

Figure 1.

Relaxed, or adiabatic, conformational energy maps for each of the 6 possible linkages in the EpolC1576 polysaccharide. On each map the global minimum is indicated by a red “X”. Contour levels are indicated in kcal/mol above the global minima.

Among the six maps displayed in Figure 1, it will be noted that the one that differs the most from the others is the α-D-mannopyranose-(1→2)-α-D-mannopyranose case. The global minimum on this map is at (79.7°, −51.3°). While each of the other maps has a minimum at approximately the same conformation, which for three of these is also the global minimum, in the mannose disaccharide this well is particularly deep and narrow, with steeply rising walls. This indicates that small changes in the glycosidic angles result in large changes in the total energy. Such a situation usually indicates the disruption of an intramolecular hydrogen bond between the rings of the disaccharide, and indeed this is the case for this disaccharide, where the global minimum energy conformation is stabilized by a hydrogen bond between the primary alcohol groups of the two monomers of the disaccharide, as can be seen in Figure 2, with the O6 hydroxyl of the non-reducing residue donating a proton to the corresponding group of the reducing end. In rhamnose, of course, the primary alcohol is replaced by a non-hydrogen-bonding methyl group, which is why only this mannose disaccharide is able to make this type of stabilizing interaction. Nevertheless, this conformation is favorable in all of these disaccharides, being least favored in the α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose case.

Figure 2.

The global vacuum minimum energy structure for the α-D-mannopyranose-(1→2)-α-D-mannopyranose disaccharide linkage, indicating the hydrogen bond between the exocyclic primary alcohol groups.

No other hydroxyl-hydroxyl hydrogen bonds between rings are possible for any of the other disaccharide linkages studied here. However, weaker hydroxyl to O5 ring oxygen interactions are possible for the other linkages. For example, in the 3-methyl-α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose case, the O2 hydroxyl group of the reducing end of the molecule makes a stabilizing interaction with the ring oxygen of the non-reducing sugar of the dimer in the global minimum energy conformation at (89.3°, −49.1°), as can be seen in Figure 3. Because of the lower charge assigned to the ether-like ring oxygen atoms, this type of interaction is weaker than a typical hydrogen bond, but is nonetheless favorable. This type of interaction is also possible for the non-methylated rhamnose dimer, α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose, but in that case the conformation at (76.4°, −134.2°), which does not allow this close interaction, is slightly more favorable.

Figure 3.

The global vacuum minimum energy structure for the 3-methyl-α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose disaccharide, indicating the interaction between the O2 hydroxyl group of the reducing sugar and the ring oxygen atom of the non-reducing end sugar.

An interesting feature of all of these maps is a shallow valley extending to the “southeast” (higher ϕ, lower ψ) from the minima generally located around (∼80°,∼−60°). In several of these maps with axial-equatorial linkages this extension lies within the 4 kcal/mol contour above the global minimum, so it might be expected to be populated to a reasonable extent in MD simulations of sufficient length. This was indeed found to be the case (Figure 4). As already observed, for properly-prepared relaxed, or adiabatic, conformational energy maps, MD simulations should closely follow the energy surface. This point is illustrated in Figure 4, which superimposes the vacuum MD trajectory in (ϕ,ψ) Ramachandran space at room temperature for the α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose disaccharide onto the calculated map for the disaccharide. As can be seen, the trajectory is well-contained within the 4 kcal/mol contour, with infrequent and very short excursions outside this envelope that very rarely cross the 6 kcal/mol contour. Transitions between the three wells follow low energy paths over the intervening barriers, as might be expected, and as is also shown in Figure 4 for a short portion of the simulation that sampled all three wells. The trajectories for all of the other disaccharides were similarly well described by their relaxed surfaces.

Figure 4.

Left: A 100 ns room temperature vacuum MD trajectory for α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose, sampled at 100 fs intervals, superimposed on the adiabatic energy map for the disaccharide. Right: A short 16 ps sequence from the trajectory at right, illustrating transitions between wells.

The type of representation shown in Figure 4 obscures the amount of time spent in each conformation. Figure 5, which illustrates the population density at each point, shows that while the trajectory explored the valley extending to (∼140°,∼−100°) as well as the well at (∼60°,∼100°), it spent little cumulative time there. The trajectory primarily populated the three almost equal-energy main minima on the vacuum surface, with the global minimum being most populated not only because it is slightly lower in energy, but also because it is favored by entropy since it is a broad, open valley.

Figure 5.

A probability density map for conformations arising during the 1 µs room temperature vacuum MD trajectory for α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose.

Intramolecular hydrogen bonds in biological polymers such as proteins and carbohydrates can in principle be exchanged in aqueous environments for hydrogen bonds to water molecules. Entropy usually favors such an exchange, while the hydrogen bond exchange enthalpy is usually approximately zero (one intramolecular hydrogen bond plus one water-water hydrogen bond usually approximately equaling two solute-water hydrogen bonds). Thus, the intramolecular conformational energy cost for the glycosidic conformational transition necessary to allow such a hydrogen bond exchange generally determines whether such an exchange will take place. The first potentials of mean force calculated for disaccharides in aqueous solution exhibited just such exchanges.^7,8 In the case of the α-(1→4)-linked disaccharide of D-xylopyranose, used as a model for the maltose repeat unit of amylose, the global minimum energy conformation on the vacuum Ramachandran conformational energy map disappeared and was replaced by a new global minimum that was not a minimum at all on the vacuum surface.⁷ Such an exchange was also observed in the case of the vacuum versus solution energy maps for neocarrabiose.⁸ On the other hand, for the case of cellooligomers, which are stabilized by two hydrogen bonds between successive glucose monomers, such an exchange does not occur in aqueous solution, which is the principal reason that cellooligomers have such limited solubility in water and that cellulose is completely insoluble.²⁴

In the case of the present α-D-mannopyranose-(1→2)-α-D-mannopyranose disaccharide, the MD simulations in solution exhibit a deviation in conformation (Figure 6) from the average dynamical structure in vacuum and the global energy minimum on the vacuum surface (Figure 3). As can be seen from Figure 6, the molecule in solution has its greatest density at a ψ angle between the two vacuum conformational minima, at −82.7°. This conformation has lost the hydrogen bond between the two primary alcohol groups shown in Figure 2, which has been replaced by a bridging water molecule making hydrogen bonds to both primary alcohol groups (Figure 7).

Figure 6.

Probability density computed from 1 µs MD trajectories for α-D-mannopyranose-(1→2)-α-D-mannopyranose; Left: in vacuum; Right: in aqueous solution. Note that the maximum probability density has shifted away from the two minima on the vacuum surface to a conformation centered around a ψ value of −82.7°.

Figure 7.

Left: an example of an instantaneous configuration from the trajectory for the α-D-mannopyranose-(1→2)-α-D-mannopyranose disaccharide in aqueous solution, showing the replacement of the intramolecular hydrogen bond seen in Figure 2 by two intermolecular hydrogen bonds to a single bridging water molecule. Right: an instantaneous configuration for the 3-methyl-α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose disaccharide in aqueous solution; the solvent water has induced a conformational shift, but in this case no water molecules bridge between the two rings in this most probable conformation, which thus has greater conformational flexibility, which is favored by entropy.

A solvation-induced conformational shift also occurs for the 3-methyl-α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose disaccharide (Figure 8). In this case, however, the intramolecular inter-ring hydrogen bond seen in Figure 3 is again lost, but no bridging water molecules span between the two rings (Figure 7). The hydrogen bonds of the O5 and O2’ groups to separate water molecules are more favorable than the weak intramolecular, inter-ring interaction, and do not constrain the conformation, so that the shift to a conformation centered around (72.7°,−130.8°) is favored by entropy. In contrast to these two cases, the average conformation in solution for the α-D-mannopyranose-(1→2)-3-methyl-α-D-rhamnopyranose linkage was almost completely unaffected by solvation (Figure 9). The trajectory-averaged population density maps for the α-D-mannopyranose-(1→2)-α-D-rhamnopyranose linkage are displayed in Figure S2 of the Supplementary Material.

Figure 8.

Probability density computed from 1 µs MD trajectories for the 3-methyl-α-D-rhamnopyranose-(1→3)-α-D-rhamnopyranose disaccharide; Left: in vacuum; Right: in aqueous solution. Note the strong shift in solution away from the global vacuum minimum energy conformation at (89.3°, −49.1°), which is barely populated at all in water, to conformations centered around (72.7°, −130.8°).

Figure 9.

Probability density computed from 1 µs MD trajectories for the α-D-mannopyranose-(1→2)-3-methyl-α-D-rhamnopyranose disaccharide; Left: in vacuum; Right: in aqueous TIP4P solution.

While the probability density maps in Figures 6, 8, 9, and S2 could be used to prepare crude solution conformational free energy maps for these disaccharides, much longer simulations employing umbrella potential functions would be needed to calculate reliable conformational potential of mean force Ramachandran maps for these linkages in solution that properly sampled all accessible space. Such calculations are underway and will be reported in a subsequent communication for each linkage in this oligosaccharide.

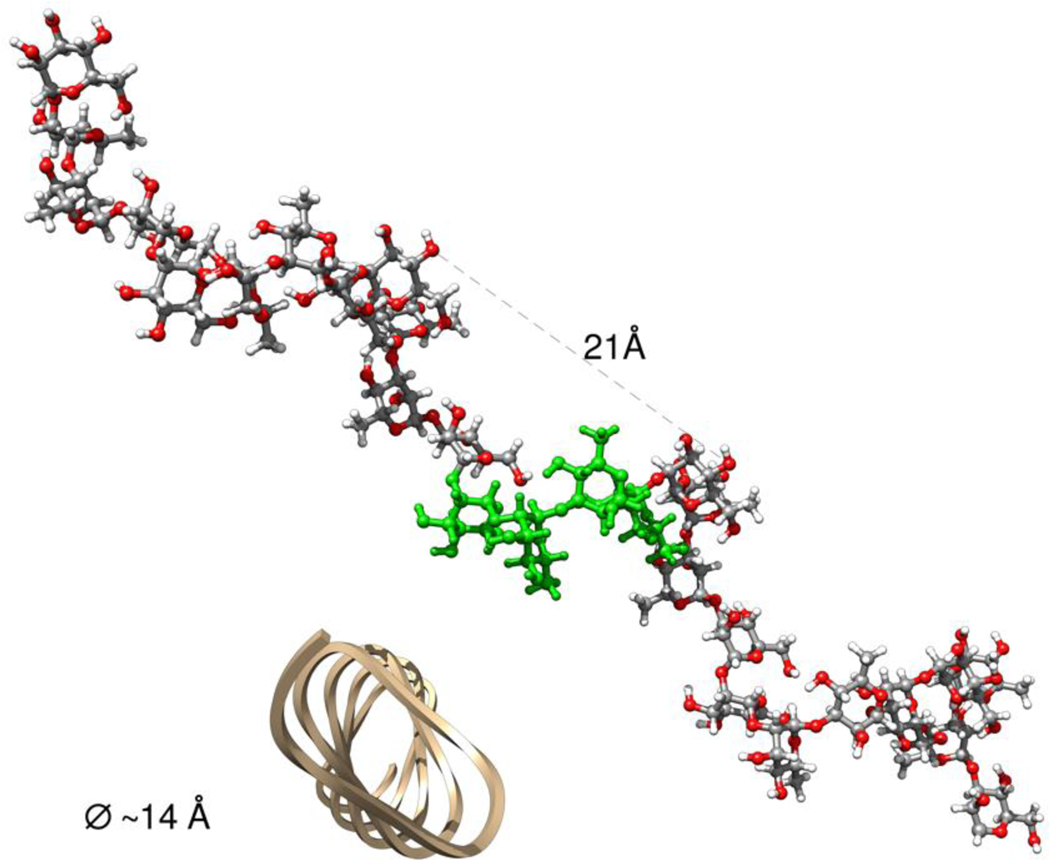
In some homopolymers such as amylose, interactions between monomers one helical turn away clash and prevent certain (ϕ,ψ) values from being allowed, altering the overall Ramachandran energy surface.²⁵ In the present extended heteropolymer no such longer-range clashes occur. A polymer constructed from repeats of the unmethylated sequence, with every glycosidic linkage set to the global minimum energy conformation for its linkage type, produces a slightly irregular helix, with approximately 9 sugar residues per turn, in ∼2.25 tetrasaccharide repeat units, and with a diameter of ∼14 Å, and an advance of ∼21 Å per turn. An example of such a helix is shown in Figure 10. As can be seen, the extended “regular” helix formed in this way exhibits no steric clashes or direct interactions between rings one turn apart like those in amylose.²⁵ From the energy maps, it can be seen that such this helix might exhibit an intermediate degree of flexibility. While the ψ angles for all of these linkages can adopt one of several values corresponding to local minima on the maps, there is very little flexibility in the ϕ angles, which are essentially confined to remain within an approximately 50° range, since most values of ϕ lead to steric clashes. However, due to the possible flexibility in ψ, actual EpolC1576 polysaccharides in biofilms may well be random coil-like rather than helices as in Figure 9.

Figure 10.

A hypothetical helical segment of the EpolC1576 polysaccharide constructed using, for each glycosidic linkage, the (ϕ,ψ) values corresponding to the global energy minimum for that linkage. One tetrasaccharide repeat unit in the center of the chain is colored green to illustrate its extent. A cartoon trace of this helix is shown in gold, based on the C3 carbon atoms of each ring to illustrate the irregular character of this helix.

Conclusions

The adiabatic conformational energy maps prepared here will make possible the construction of reasonable conformations for the Epol C1576 polysaccharides found in the biofilms produced by B. multivorans bacteria in cystic fibrosis patients. Due to the flexibility exhibited by the linkages in their ψ angles, these polysaccharides may well be fairly flexible and adopt conformations quite different from the helix shown in Figure 9, and may even behave as random coils. It must also be remembered that these are vacuum energy maps. It is entirely possible that aqueous solvation might perturb these energy surfaces, particularly in the case of the α-D-mannopyranose-(1→2)-α-D-mannopyranose disaccharide, since the hydrogen bond that stabilizes the global minimum energy conformation might exchange for hydrogen bonds to solute molecules, as has been observed in other cases,^7,8 thus shifting the conformation away from the vacuum minimum energy structure. Potential of mean force, or conformational free energy, Ramachandran maps of these linkages in aqueous solution are under preparation.