Abstract

The mixed ionic–electronic nature of lead halide perovskites makes their performance in solar cells complex in nature. Ion migration is often associated with negative impacts—such as hysteresis or device degradation—leading to significant efforts to suppress ionic movement in perovskite solar cells. In this work, we demonstrate that ion trapping at the perovskite/electron transport layer interface induces band bending, thus increasing the built-in potential and open-circuit voltage of the device. Quantum chemical calculations reveal that iodine interstitials are stabilized at that interface, effectively trapping them at a remarkably high density of ∼1021 cm–3 which causes the band bending. Despite the presence of this high density of ionic defects, the electronic structure calculations show no sub-band-gap states (electronic traps) are formed due to a pronounced perovskite lattice reorganization. Our work demonstrates that ionic traps can have a positive impact on device performance of perovskite solar cells.
Lead halide perovskites have attracted great attention in recent years due to their remarkable performance in solar cell devices, with power conversion efficiencies comparable to those of inorganic silicon devices.1,2 Contributing to the high performance of perovskite photovoltaics are several factors, including a strong optical absorption,3 low exciton binding energies,4 high conductivity5 and charge carrier diffusion lengths,6 low degree of energetic disorder,7 and defect tolerance.8 Additionally, the ease of fabrication9 and the relatively low temperature required for their processing10 make perovskite photovoltaics particularly attractive for future applications, like building integration and smart windows.11
Certain challenges, however, remain to be addressed prior to the integration of perovskite solar cells into industrial applications. These include the issues of scalability,12 sustainability,13 and stability.14 The latter has attracted significant attention, in particular in the context of achieving long-term stability by preventing the degradation of perovskite solar cells. However, often short-term instabilities are also observed in perovskite solar cells. For example, it is commonly observed that perovskite solar cells undergo an increase in the device performance—especially in the open-circuit voltage—upon subsequent current density–voltage (J–V) measurements under 1 sun illumination. This instability of device characteristics is commonly ascribed to the phenomenon of light-soaking.15 The concept of light-soaking is very general, and many different interpretations of the underlying physical mechanics have been proposed. Several research groups assigned the improvement in device performance to light-induced filling or annihilation of sub-band-gap trap states.16,17According to another study, light-soaking is dominated by electron trap states located at the grain boundaries, such that the microstructure of the active layer will significantly impact on the extent of light-soaking.18 Another fundamentally different approach assigns light-soaking effects to ion migration. For example, an early work by Huang and colleagues proposed that ion migration leads to doping of the perovskite layer near the interfaces with charge extraction layers.19 Early works by Gottesman et al. and Tao et al. proposed that the energy alignment at the TiO2/perovskite interface is modified upon illumination or biasing due to ion and/or charge accumulation,20,21 with the latter suggesting that this can be avoided by introducing a thin layer of fullerenes at the TiO2/perovskite interface. Similarly, in a more recent work, it was proposed that ion migration-induced charge accumulation at the perovskite layer interface with a metal oxide can lead to a band bending and an increase in the device photovoltage; however, such a band bending was not observed experimentally.22
The possible contribution of ion-redistribution to the improvement of photovoltaic performance of perovskite solar cells stands in stark contrast to the generally negative view on ion migration in perovskite photovoltaics. Indeed, ion migration is typically associated with undesired phenomena such as hysteresis23,24 and degradation.25,26 Ion migration in perovskite films has been the focus of many experimental and theoretical studies. The most likely mobile defects in the most commonly studied perovskite, namely, methylammonium lead triiodide (MAPbI3), are vacancies Vi+ and VMA– and interstitials Ii– and MAi+. While there exists some disagreement regarding their activation energies, which range from ∼0.1 to ∼0.6 eV,27 it is commonly accepted that the halides, in this case iodine, are the most mobile species in perovskite materials.28 There have been numerous reports of light-induced ion migration,29−31 but the underlying mechanism is still under debate. In terms of influence on the device performance, it is generally agreed upon that the changes in the ionic gradient throughout the device during a forward bias sweep result in a decrease in current and are one of the main explanations for hysteresis.32 These negative impacts, and the fact that ion migration has been identified to be one of the main internal factors responsible for degradation of perovskite photovoltaics, have led to considerable efforts dedicated to find mitigation strategies.33,34
Importantly, ion migration and redistribution across the device are typically considered to be a temporary phenomenon; i.e., once the bias is removed, the ions migrate back, and the device is assumed to resume its previous state. In this study we demonstrate that ion migration and its accumulation at the interface are driven by thermal equilibrium, thus leading to permanent ion trapping at the perovskite/extraction layer interface. Such ion trapping induces a band bending at the interface to the extraction layers, which we directly probe experimentally by employing a novel ultraviolet photoelectron spectroscopy (UPS) depth profiling method. This band bending at the interface to the extraction layers results in an increase in the built-in potential of the device and, consequently, the measured open-circuit voltage (VOC). We show that such an enhancement can occur without the presence of light and is impacted by the initial density of ions at that interface, thus revealing that it is the ion redistribution, regardless of light-soaking, that is responsible for the observed enhancement in VOC. The experimental results are supported by density functional theory (DFT) calculations, demonstrating that the iodine interstitial is stabilized at the interface with PCBM relative to the bulk, thus providing a significant driving force toward the interface. Detailed device simulations show that, by including this driving force, the ion-redistribution results in band bending that is in excellent agreement with the measured band profile. Lastly, the DFT calculations show that, despite the ionic “traps” at the interface, the defects considered here (iodine interstitials) do not generate sub-gap electronic trap states. The soft nature of the perovskite lattice and the associated lattice relaxation prevents the formation of electronic traps even at extremely high (∼1021 cm–3) ionic densities at the interface.
The device structure investigated in this work is depicted in Figure 1a and utilizes poly(3,4-ethylenedioxythiophene) polystyrenesulfonate (PEDOT:PSS) and phenyl-C61-butyric acid methyl ester (PCBM) as hole and electron extraction layers, respectively. This structure is commonly employed in inverted architecture MAPbI3 solar cells and leads to a reasonably high power conversion efficiency (PCE) of up to 20%.35−37Figure 1b shows the current–voltage characteristics of the first three sequent measurements performed directly after the fabrication of the device. It can be seen that while the short-circuit current (JSC) and the fill factor (FF) remain almost unchanged, there is a significant enhancement in the device VOC.
Figure 1.
(a) Schematic structure of the MAPbI3 photovoltaic device used in this work. (b) Current–voltage characteristic of several subsequent measurements performed directly after fabrication. The photovoltaic parameters are summarized in Table S1.
It is important to remember that, during a dual-scan current density–voltage (J–V) characterization, the device is exposed to both electrical bias and illumination, so the measurement itself does not allow the distinguishing of the contribution from these two stimuli on the observed VOC. To investigate the impact of these factors separately, we fabricated a series of identical devices which were either measured directly (reference) or exposed to solar simulator light or bias (in the dark) prior to photovoltaic characterization (Figure 2a). Figure 2b shows the impact of prebias and preillumination on the initial VOC of MAPbI3 solar cells. As expected, preillumination leads to an increase in the VOC of the device upon first measurement, with subsequent measurements leading to similar values as the reference device. Such improvement was suggested to be associated with light-induced trap filling which suppresses recombination and increases the VOC.38 Biasing the device in the dark, however, also leads to a VOC enhancement, which is even slightly higher than that introduced by illumination. Furthermore, it has to be noted that the VOC of prebiased samples shows no further improvement upon subsequent measurements under illumination, thus suggesting that biasing is the dominant factor in terms of its impact on the VOC.
Figure 2.
(a) Schematic of the standard measurement process in this study. (b) Comparison of the VOC evolution during first four subsequent measurements for reference, prebiased, and preilluminated samples, measured directly after fabrication. (c) VOC comparison of devices measured directly after fabrication to devices measured after 1 and 3 days of storage in a dark inert atmosphere. (d) VOC difference between the initial measurement of prebiased samples to unbiased reference samples.
The positive impact of electric field on the VOC of the device is intriguing considering the fact that an internal field is always present in the device simply based on the device structure. To explore if the internal field leads to a similar enhancement in the VOC, we monitored the performance of unbiased and prebiased devices directly after fabrication and upon storage under inert conditions in the dark for either 1 or 3 days (Figure 2c). The initial performance of the solar cells increases significantly with increasing storage time, while the influence of prebiasing becomes less and less significant for longer storage times. These results confirm that the presence of the internal electric field alone is sufficient to induce and maintain the same effect as that induced by externally applying a voltage.
This evolution in the open-circuit voltage parallels similar findings in the literature. The general consensus is nowadays to address those features to ionic motion and in particular to the accumulation of ions at the interface between the perovskite active layer and the extraction layers. To test this theory, we performed XPS depth profiling experiments in which we etched a freshly prepared pristine and prebiased device and monitored the I/Pb ratio (Figure S1). The experiment showed that the I/Pb ratio is significantly increased in prebiased devices, reaching >3.5 at the interface to the PCBM layer. To confirm that the change in VOC is directly related to the density of ions at that interface, we applied an additional methodology, which allows to intentionally change the density of ions at the surface of the perovskite layer during fabrication. By fractionally changing the perovskite precursor solution stoichiometry,34 it is possible to gradually increase the concentration of iodine interstitial ionic defects at that surface of the perovskite layer, thus increasing the built-in potential of the device.39 Indeed, when monitoring the increase in VOC observed for solar cells fabricated from different precursor stoichiometries (Figure 2d), it is evident that samples with high density of iodine ions at the surface (i.e., overstoichiometric samples) show nearly no change in VOC upon biasing. These results confirm that the improvement in VOC is fundamentally related to the ionic landscape in the device.
A redistribution of ions in perovskite solar cells is known to be caused by electric field or tilted energy levels, resulting in a flattening of the bands. Thus, it is not clear how ionic redistribution could improve the VOC. Ultraviolet photoemission spectroscopy (UPS) is a powerful method to probe the energy levels of materials, but its probing depth of roughly 1–2 nm makes it unsuitable for the study of energetic alignment at buried interfaces, especially in complete perovskite solar cells. In this study, we apply gas cluster ion beam (GCIB) etching on full perovskite photovoltaic devices in order to directly probe the changes in the energetics of freshly made and prebiased photovoltaic devices. Here we focus mainly on the interface between the electron transport layer (PCBM) and the perovskite active layer and monitor the valence band structure measured via UPS for different etching depths as is shown in Figure 3a,b.
Figure 3.
UPS depth profiles measured on perovskite photovoltaic devices (a) prior to and (b) after applying bias in the dark. (c, d) Corresponding device energetics at the PCBM/MAPbI3 interface.
We analyze the UPS depth profile data by fitting them with the reference spectra collected on PCBM and MAPbI3, following the method published by Lami et al. (Figure S2).40 The method allows an extraction of both the evolution of the energetics (Figure 3c,d) as well as the corresponding compositional depth profiles (Figure S3).
A comparison of the energetic alignment at the PCBM/MAPbI3 interface of freshly prepared pristine devices and devices that have been prebiased reveals stark differences. Devices measured directly after fabrication exhibit relatively flat bands with the Fermi level lying approximately in the midgap of the perovskite layer. On the other hand, after biasing, the energetic structure of the perovskite layer is markedly changed and stays the same after the removal of the bias and the transfer to the depth profiling apparatus. At the interface to PCBM, a significant band bending of the MAPbI3 energy levels is observed, also accompanied by a change in the work function across the interface, suggesting the accumulation of iodine at that interface. In the bulk of the perovskite layer, the Fermi level is very close to the conduction band, signifying that the perovskite layer is no longer intrinsic, but rather is n-type. This change agrees with previous observations that the presence of iodine vacancies leads to n-type self-doping in perovskite materials,41 suggesting that iodine ion migration not only results in band bending but also changes the bulk of the perovskite layer by leaving behind a significant density of vacancies.
We highlight that the significant differences in the energetic alignment at the perovskite/PCBM interface cannot be explained by etching-induced artifacts. First of all, XPS measurements on etched perovskite samples (Figure S4) show that no additional species (such as metallic lead, for example) are formed by the gentle cluster etching used in these experiments. Furthermore, the methodology has been recently applied by us to study the energetic alignment at 2D/3D perovskite interfaces, and no etching-induced artifacts or compositional changes were observed there either.42 Finally, to confirm the reliability of these results, we repeated the experiments on devices fabricated using a PC71BM extraction layer (Figure S5), which demonstrated that an upward band bending is observed only in biased devices, in the same way as is shown in Figure 3. The band bending also cannot be a consequence of photovoltage induced by the UPS measurements, since if formed, such photovoltage would impact similarly both pristine and biased devices.
To calculate the energy band diagram, we performed a device simulation where we accounted for the motion of iodides in the perovskite layer and assumed that the ions have not penetrated the blocking layers.43,44 The material parameters are collated in Table S2 in the Supporting Information. Figure 4a–c shows the calculated energy band diagram, and Figure 4d–f shows the corresponding iodide distribution. The simulation is run under short-circuit conditions and in the dark. Examining the results in Figure 4a–c we note that the bands of the perovskite layer are flat and that there is no evidence for the band bending reported in Figure 3. Figure 4d–f shows that at short circuit there is an accumulation of iodide ions at the PCBM interface, but the excess density is of the order 1018 cm–3. Additional simulations, performed with different dielectric constants of the perovskite layer, led to a similar result (Figure S6). The exact iodide distributions, which are shown in Figure 4d–f, are a result of a balance between drift, due to the built-in potential that pushes the ions toward accumulation at the PCBM interface, and diffusion that broadens the distribution. Such density distributions are not capable of creating a significant voltage drop. Moreover, within the device model of drift and diffusion, the iodide ions would redistribute to screen any internal field and thus would flatten the bands and not bend them. Namely, the excess iodide and band bending measured at the interface must be driven by a mechanism not included in the device model.
Figure 4.
Energy level diagrams (a–c) and iodide density distribution (d–f) obtained for ion densities of (a, d) 1017 cm–3, (b, e) 1018 cm–3, and (c, f) 1019 cm–3 obtained by numerical device simulations with a dielectric constant of 50 (more info can be found in the Supporting Information).
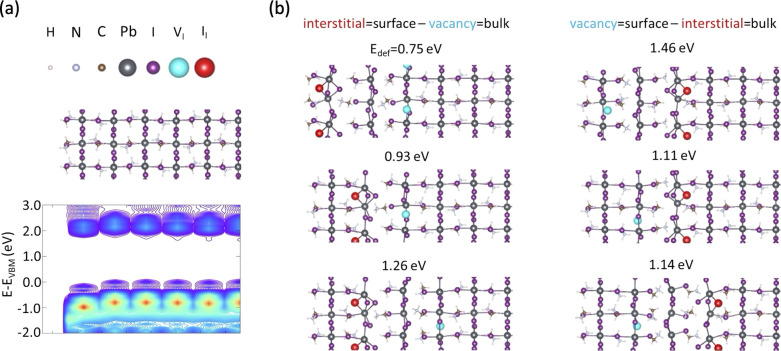
With that in mind we turn to atomistic, DFT-based simulations which may reveal the ionic energy landscape near the surface. We therefore designed periodic perovskite slab models similarly to our previous work.45 These are based on the tetragonal phase of MAPbI3, with the [001] plane exposed to the surface (that is, with an MAI-rich surface). The final slab thickness corresponds to 11 PbI6 octahedra, with a mirror plane passing through the central octahedron, to avoid spurious effects associated due to periodic boundaries.46−48 Details on the model and computational parameters are reported in the Experimental Methods section in the SI. The atomistic structure for a reference, pristine slab model, obtained after full DFT relaxation of the atomic positions, is depicted in Figure 5a, showing overall modest reorganization at the surface, in line with literature data.49,50 The corresponding layered-resolved PBE electronic density-of-states (LDOS) in Figure 5a shows (expectedly) flat valence and conduction bands along the slab thickness. Considering now the potential role of defects, we first wonder if there is a thermodynamic contribution to the accumulation of interstitial iodides at the surface, explaining the result of the XPS profiling measurement in Figure S1. To clarify this, we designed defective models containing an iodine-related Frenkel pair, with different distribution of the interstitial and vacancy with respect to the slab thickness (namely, two Frenkel pairs are added in symmetric positions with respect to the central layer, to avoid formation of polar slabs). We then proceeded to relax the atomic positions of these models and to determine the corresponding formation energy for the Frenkel pair via total energy difference, the pristine model taken as reference, finding that the most stable defective model corresponds to the case where the interstitial lies at the surface, while the vacancy locates deeper in the bulk, as shown in Figure 5b. Corresponding defect formation energy is 0.75 eV per Frenkel defect pair, which is considerably smaller than the inverse situation where the vacancy lies at the interface, and the interstitial is trapped in the bulk (1.46 eV). When considering the other configurations, we find that those with interstitial closer to the surface and vacancy trapped in the bulk are generally more stable than when the defects are swapped (except in one case, which is also the one with the smallest energy difference). The second most stable defective model also presents an interstitial iodine in the layer beneath the surface and vacancy in the bulk. These results are in line with the general consensus on a larger thermodynamical stability of interstitial defects at the surface than in the bulk,51−53 likely related to the reduced steric hindrance imposed to the lattice. Such a thermodynamic stabilization explains why iodine accumulation at the interface is irreversible. Once the iodine interstitials are driven to the perovskite/PCBM interface, they remain there, which is why they could be probed by UPS depth profiling.
Figure 5.
(a) Atomistic slab model and corresponding layered-resolved density-of-states for pristine MAPbI3. Only half of the slab model is depicted due to symmetry with respect to the central plane. (b) Atomistic slab models of MAPbI3 containing iodide-related Frenkel pairs with different location of the interstitial and vacancy. The formation energies for the Frenkel pair is reported (Edef).
We may then wonder if an ionic redistribution with accumulation of interstitial iodines at the surface would lead to a band bending similar to that observed in Figure 3. To explore this, we designed an additional supercell defective slab model (∼1000 atoms), with all iodines accumulating at the surface and vacancies distributed within the bulk. The corresponding I/Pb ratio for the outmost layer is 3.5, in line with the results of the XPS depth profiling. The resulting structure in Figure 6a shows strong lattice reorganization around the defects, compared to the pristine material. In particular, the interstitial iodine is incorporated into an irregular PbI6 octahedron, similarly to previous literature reports for negatively charged iodine interstitial defects,54 and the distance between the outmost leads and the apical iodines in the underlying layer is significantly increased. The corresponding LDOS exhibits a strong band bending effect, with valence and conduction band edges destabilizing when going from the bulk to the surface. The direction and magnitude of the predicted band bending effect match well the experimental data in Figure 3d, supporting the view that it is prompted by ion migration. We note that the corresponding density of ionic defects in Figure 3d amounts to one iodine per two chemical units, that is, an iodine density of ca. 1021 cm–3, to be compared later on with modified drift-diffusion simulations. The observed band bending is consistent with a pure electrostatic effect associated with the dipolar field imposed by charged interstitials and vacancies. Indeed, the comparison of the DOS calculated for different PbI2 layers stacked along the slab shows that, except for the outmost layer, the 2D DOS can be superimposed by applying a simple rigid shift along the energy axis (see Figure S7). We note that similar results are obtained (for smaller models) when including spin–orbit coupling in the DFT calculations (see Figure S8). An important point to mention is the lack of defect-related intragap trap states in Figure 6a. While this could be affected by the level of theory used (here, PBE),53 a recent work where a hybrid PBE0 functional (out of reach for the large models considered here) is applied to the same surface termination also highlights that interstitial iodine defects do not introduce intragap states, hence confirming our GGA results.55 The absence of intragap trap states is related to the unusual nature of the perovskite lattice that is soft enough to self-heal against the formation of deep trap states. We tested this by recalculating the electronic structure for a defective model in which the perovskite crystal structure is frozen to its pristine phase (Figure S9). The corresponding LDOS shows both bending of the valence and conduction bands and the emergence of a trap state related to the interstitial, therefore confirming the complex interplay between lattice reorganization and electrostatics. Importantly, the absence of these electronic deep trap states, even in the presence of an extremely high density of ionic defects at the surface of the perovskite, explains how high open-circuit voltages can be achieved in these systems upon the permanent ion accumulation at the interfaces of the active layer.
Figure 6.
(a) Atomistic slab model and corresponding layered-resolved density-of-states for a defective surface of MAPbI3; defective model contains four Frenkel iodine defects, with interstitials (II, red) accumulating at the surface and vacancies (VI, cyan) distributed in the bulk (vide infra). The threshold for the visualization of the Pb–I bond length is set to 3.7 Å. (b) Iodine standard potential as a function of position within the perovskite layer. (c) Measured (symbols) and simulated (full line) energy level diagram.
To make a link between atomistic and device simulations and to further confirm that the effect is stationary, we performed additional device simulations in which we introduce the iodide stabilization predicted by the DFT calculations in the form of reduced ionic standard potential that effectively creates an ionic trap at the interface to PCBM. In short, we solve the same drift-diffusion equations, but with the iodide standard potential being lowered by 0.55 eV (i.e., iodide-trap) at the perovskite/PCBM interface (Figure 6b). Figure 6c shows excellent agreement with the measured band diagram in Figure 3 and is in stark contrast to the band diagrams obtained for device models that do not include an ionic interfacial stabilization (Figure 4). We note that, based on the ion trap containing numerical device simulations, the density of ions at the interface with the PCBM layer is ∼5 × 1020 cm–3, in excellent agreement with the ca. 1021 cm–3 predicted by the DFT simulations.
To conclude, we have shown that ion trapping in perovskite solar cells may lead to a positive impact on their photovoltaic performance. Specifically, we show that the energetic landscape of the devices can be beneficially altered by ionic redistribution, leading to an overall higher built-in potential and, consequently, open-circuit voltage (Figure S10). The increase in the built-in potential additionally leads to an increase in the fill factor (Table S1), in agreement with previous theoretical predictions.56 The effect is not transient, but rather stationary, and can be measured long after the bias has been removed. The soft nature of the perovskite crystal allows an accommodation of incredible local defect densities of ∼1021 cm–3 without introducing the formation of sub-band-gap electronic trap states. Considering that the accumulation of iodine interstitials at the surface of the perovskite layer is thermodynamically favorable, it is likely to occur with time even without an application of bias and impact the device performance of perovskite solar cells regardless of their architecture. While the improvement in device performance due to ion-induced band bending would be beneficial to different types of devices, it is noteworthy that the magnitude of the improvement will be larger in devices with an initially less optimized built-in potential. This is in agreement with our previous investigations in which increasing the built-in potential by the introduction of dipoles in the device structure was more impactful for devices with a lower initial built-in potential.57,58 Nevertheless, the increase in VOC is reported in the literature also for well-optimized solar cells with passivated interfaces59 and is observed for different compositions and device structures,60 suggesting ion-redistribution plays a role in improving device performance also in state-of-the-art devices.
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC Grant Agreement 714067, ENERGYMAPS) and the Deutsche Forschungsgemeinschaft (DFG) within the framework of SPP 2196, project PERFECT PVs (project 424216076). Computational resources were provided by the Consortium des Équipements de Calcul Intensif (CÉCI) funded by the Belgian National Fund for Scientific Research (F.R.S.-FNRS) under Grant 2.5020.11 and by Tier-1 supercomputer of the Fédération Wallonie–Bruxelles, infrastructure funded by the Walloon Region under the Grant Agreement 1117545. C.Q. is an FNRS research associate, and D.B. is an FNRS research director. N.T. acknowledges the support by the Ministry of Science & Technology, Israel; and the Technion Ollendorff Minerva Center.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsenergylett.2c01636.
Photovoltaic performance parameters, XPS and UPS depth profiles and analysis, device modeling parameters and results, density of states calculations for pristine and defective perovskite slabs, and experimental details (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Cell Efficiency Chart—National Renewable Energy Laboratory. https://www.nrel.gov/pv/cell-efficiency.html (accessed on August 9, 2022).
- Schmidt-Mende L.; Dyakonov V.; Olthof S.; Ünlü F.; Lê K. M. T.; Mathur S.; Karabanov A. D.; Lupascu D. C.; Herz L. M.; Hinderhofer A.; et al. Roadmap on organic–inorganic hybrid perovskite semiconductors and devices. APL Materials 2021, 9, 109202. 10.1063/5.0047616. [DOI] [Google Scholar]
- Green M. A.; Ho-Baillie A.; Snaith H. J. The emergence of perovskite solar cells. Nat. Photonics 2014, 8, 506. 10.1038/nphoton.2014.134. [DOI] [Google Scholar]
- Goetz K. P.; Taylor A. D.; Paulus F.; Vaynzof Y. Shining Light on the Photoluminescence Properties of Metal Halide Perovskites. Adv. Funct. Mater. 2020, 30 (23), 1910004. 10.1002/adfm.201910004. [DOI] [Google Scholar]
- Paulus F.; Tyznik C.; Jurchescu O. D.; Vaynzof Y. Switched-On: Progress, Challenges, and Opportunities in Metal Halide Perovskite Transistors. Adv. Funct. Mater. 2021, 31, 2101029. 10.1002/adfm.202101029. [DOI] [Google Scholar]
- Stranks S. D.; Eperon G. E.; Grancini G.; Menelaou C.; Alcocer M. J. P.; Leijtens T.; Herz L. M.; Petrozza A.; Snaith H. J. Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber. Science 2013, 342 (6156), 341–344. 10.1126/science.1243982. [DOI] [PubMed] [Google Scholar]
- Ledinsky M.; Schönfeldová T.; Holovský J.; Aydin E.; Hájková Z.; Landová L.; Neyková N.; Fejfar A.; De Wolf S. Temperature Dependence of the Urbach Energy in Lead Iodide Perovskites. J. Phys. Chem. Lett. 2019, 10 (6), 1368–1373. 10.1021/acs.jpclett.9b00138. [DOI] [PubMed] [Google Scholar]
- Kim G.-W.; Petrozza A. Defect Tolerance and Intolerance in Metal-Halide Perovskites. Adv. Energy Mater. 2020, 10 (37), 2001959. 10.1002/aenm.202001959. [DOI] [Google Scholar]
- Vaynzof Y. The Future of Perovskite Photovoltaics – Thermal Evaporation or Solution Processing?. Adv. Energy Mater. 2020, 10 (48), 2003073. 10.1002/aenm.202003073. [DOI] [Google Scholar]
- Petrus M. L.; Schlipf J.; Li C.; Gujar T. P.; Giesbrecht N.; Müller-Buschbaum P.; Thelakkat M.; Bein T.; Hüttner S.; Docampo P. Capturing the Sun: A Review of the Challenges and Perspectives of Perovskite Solar Cells. Adv. Energy Mater. 2017, 7, 1700264. 10.1002/aenm.201700264. [DOI] [Google Scholar]
- Liu Y.; Wang J.; Wang F.; Cheng Z.; Fang Y.; Chang Q.; Zhu J.; Wang L.; Wang J.; Huang W.; Qin T. Full-frame and high-contrast smart windows from halide-exchanged perovskites. Nat. Commun. 2021, 12, 3360. 10.1038/s41467-021-23701-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swartwout R.; Hoerantner M.; Bulovic V. Scalable Deposition Methods for Large-area Production of Perovskite Thin Films. Energy Environ. Mater. 2019, 2, 119. 10.1002/eem2.12043. [DOI] [Google Scholar]
- Goetz K. P.; Taylor A. D.; Hofstetter Y. J.; Vaynzof Y. Sustainability in Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2021, 13 (1), 1–17. 10.1021/acsami.0c17269. [DOI] [PubMed] [Google Scholar]
- Wang R.; Mujahid M.; Duan Y.; Wang Z.-K.; Xue J.; Yang Y. A Review of Perovskites Solar Cell Stability. Adv. Funct. Mater. 2019, 29 (47), 1808843. 10.1002/adfm.201808843. [DOI] [Google Scholar]
- Yang C.; Hu Z.; Gao C.; Wang Y.; Zhang H.; Wang J.; Zhang J.; Zhou X.; Zhu Y. Elimination of Light-Soaking Effect in Hysteresis-Free Perovskite Solar Cells by Interfacial Modification. J. Phys. Chem. C 2020, 124 (3), 1851–1860. 10.1021/acs.jpcc.9b10022. [DOI] [Google Scholar]
- Zhao C.; Chen B.; Qiao X.; Luan L.; Lu K.; Hu B. (2015). Revealing Underlying Processes Involved in Light Soaking Effects and Hysteresis Phenomena in Perovskite Solar Cells. Adv. Energy Mater. 2015, 5, 1500279. 10.1002/aenm.201500279. [DOI] [Google Scholar]
- Shao S.; Abdu-Aguye M.; Qiu L.; Lai L.-H.; Liu J.; Adjokatse S.; Jahani F.; Kamminga M. E.; ten Brink G. H.; Palstra T. T. M. Elimination of the Light Soaking Effect and Performance Enhancement in Perovskite Solar Cells Using a Fullerene Derivative. Energy Environ. Sci. 2016, 9, 2444–2452. 10.1039/C6EE01337F. [DOI] [Google Scholar]
- Shao S.; Abdu-Aguye M.; Sherkar T. S.; Fang H.-H.; Adjokatse S.; ten Brink G.; Kooi B. J.; Koster L. J. A.; Loi M. A. The Effect of the Microstructure on Trap-Assisted Recombination and Light Soaking Phenomenon in Hybrid Perovskite Solar Cells. Adv. Funct. Mater. 2016, 26 (44), 8094–8102. 10.1002/adfm.201602519. [DOI] [Google Scholar]
- Deng Y.; Xiao Z.; Huang J. Light-Induced Self-Poling Effect on Organometal Trihalide Perovskite Solar Cells for Increased Device Efficiency and Stability. Adv. Energy Mater. 2015, 5 (20), 1500721. 10.1002/aenm.201500721. [DOI] [Google Scholar]
- Tao C.; Neutzner S.; Colella L.; Marras S.; Kandada A. R. S.; Gandini M.; De Bastiani M.; Pace G.; Manna L.; Caironi M.; Bertarelli C.; Petrozza A. 17.6% stabilized efficiency in low-temperature processed planar perovskite solar cells. Energy Environ. Sci. 2015, 8, 2365–2370. 10.1039/C5EE01720C. [DOI] [Google Scholar]
- Gottesman R.; Lopez-Varo P.; Gouda L.; Jimenez-Tejada J. A.; Hu J.; Tirosh S.; Zaban A.; Bisquert J. Dynamic phenomena at perovskite/electron-selective contact interface as interpreted from photovoltage decays. Chem. 2016, 1, 776–789. 10.1016/j.chempr.2016.10.002. [DOI] [Google Scholar]
- Hu J.; Gottesman R.; Gouda L.; Kama A.; Priel M.; Tirosh S.; Bisquert J.; Zaban A. Photovoltage Behavior in Perovskite Solar Cells under Light-Soaking Showing Photoinduced Interfacial Changes. ACS Energy Lett. 2017, 2, 950–956. 10.1021/acsenergylett.7b00212. [DOI] [Google Scholar]
- Snaith H. J.; Abate A.; Ball J. M.; Eperon G. E.; Leijtens T.; Noel N. K.; Stranks S. D.; Wang J. T.-W.; Wojciechowski K.; Zhang W. Anomalous Hysteresis in Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 1511–1515. 10.1021/jz500113x. [DOI] [PubMed] [Google Scholar]
- Li C.; Tscheuschner S.; Paulus F.; Hopkinson P. E.; Kießling J.; Köhler A.; Vaynzof Y.; Huettner S. Iodine Migration and its Effect on Hysteresis in Perovskite Solar Cells. Adv. Mater. 2016, 28, 2446–2454. 10.1002/adma.201503832. [DOI] [PubMed] [Google Scholar]
- Kim S.; Bae S.; Lee S.-W.; Cho K.; Lee K. D.; Kim H.; Park S.; Kwon G.; Ahn S.-W.; Lee H.-M.; et al. Relationship between ion migration and interfacial degradation of CH3NH3PbI3 perovskite solar cells under thermal conditions. Sci. Rep. 2017, 7, 1200. 10.1038/s41598-017-00866-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivkin B.; Fassl P.; Sun Q.; Taylor A. D.; Chen Z.; Vaynzof Y. Effect of Ion Migration-Induced Electrode Degradation on the Operational Stability of Perovskite Solar Cells. ACS Omega 2018, 3 (8), 10042–10047. 10.1021/acsomega.8b01626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferdani D. W.; Pering S. R.; Ghosh D.; Kubiak P.; Walker A. B.; Lewis S. E.; Johnson A. L.; Baker P. J.; Islam M. S.; Cameron P. J. Partial cation substitution reduces iodide ion transport in lead iodide perovskite solar cells. Energy Environ. Sci. 2019, 12, 2264–2272. 10.1039/C9EE00476A. [DOI] [Google Scholar]
- Lee J.-W.; Kim S.-G.; Yang J.-M.; Yang Y.; Park J.-M. Verification and mitigation of ion migration in perovskite solar cells. APL Materials 2019, 7, 041111. 10.1063/1.5085643. [DOI] [Google Scholar]
- deQuilettes D. W.; Zhang W.; Burlakov V. M.; Graham D. J.; Leijtens T.; Osherov A.; Bulović V.; Snaith H. J.; Ginger D. S.; Stranks S. D. Photo-induced halide redistribution in organic–inorganic perovskite films. Nat. Commun. 2016, 7, 11683. 10.1038/ncomms11683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y.-C.; Zhou W.-K.; Zhou X.; Liu K.-H.; Yu D.-P.; Zhao Q. Quantification of light-enhanced ionic transport in lead iodide perovskite thin films and its solar cell applications. Light: Science & Applications 2017, 6, e16243 10.1038/lsa.2016.243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J.; Yan H.; Zhou D.; Zhang J.; Deng S.; Xu P.; Chen R.; Kwok H.-S.; Li G. Introducing Ion Migration and Light-Induced Secondary Ion Redistribution for Phase-Stable and High-Efficiency Inorganic Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2020, 12 (36), 40364–40371. 10.1021/acsami.0c12068. [DOI] [PubMed] [Google Scholar]
- Unger E. L.; Hoke E. T.; Bailie C. D.; Nguyen W. H.; Bowring A. R.; Heumüller T.; Christoforo M. G.; McGehee M. D. Hysteresis and transient behavior in current–voltage measurements of hybrid-perovskite absorber solar cells. Energy Environ. Sci. 2014, 7, 3690–3698. 10.1039/C4EE02465F. [DOI] [Google Scholar]
- Zhao Y.; Zhou W.; Han Z.; Yu D.; Zhao Q. Effects of ion migration and improvement strategies for the operational stability of perovskite solar cells. Phys. Chem. Chem. Phys. 2021, 23, 94–106. 10.1039/D0CP04418K. [DOI] [PubMed] [Google Scholar]
- Bi E.; Song Z.; Li C.; Wu Z.; Yan Y. Mitigating ion migration in perovskite solar cells. Trends in Chemistry 2021, 3 (7), 575–588. 10.1016/j.trechm.2021.04.004. [DOI] [Google Scholar]
- Fassl P.; Lami V.; Bausch A.; Wang Z.; Klug M. T.; Snaith H. J.; Vaynzof Y. Fractional deviations in precursor stoichiometry dictate the properties, performance and stability of perovskite photovoltaic devices. Energy Environ. Sci. 2018, 11 (12), 3380–3391. 10.1039/C8EE01136B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- An Q.; Paulus F.; Becker-Koch D.; Cho C.; Sun Q.; Weu A.; Bitton S.; Tessler N.; Vaynzof Y. Small grains as recombination hot spots in perovskite solar cells. Matter 2021, 4 (5), 1683–1701. 10.1016/j.matt.2021.02.020. [DOI] [Google Scholar]
- An Q.; Paulus F.; Vaynzof Y. Controlling the Microstructure and Porosity of Perovskite Films by Additive Engineering. ACS Appl. Energy Mater. 2021, 4 (4), 2990–2998. 10.1021/acsaem.0c01550. [DOI] [Google Scholar]
- Brenes R.; Guo D.; Osherov A.; Noel N. K.; Eames C.; Hutter E. M.; Pathak S. K.; Niroui F.; Friend R. H.; Islam M. S.; Snaith H. J.; Bulović V.; Savenije T. J.; Stranks S. D. Metal Halide Perovskite Polycrystalline Films Exhibiting Properties of Single Crystals. Joule 2017, 1 (1), 155–167. 10.1016/j.joule.2017.08.006. [DOI] [Google Scholar]
- Reichert S.; An Q.; Woo Y.-W.; Walsh A.; Vaynzof Y.; Deibel C. Probing the ionic defect landscape in halide perovskite solar cells. Nat. Commun. 2020, 11, 6098. 10.1038/s41467-020-19769-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lami V.; Weu A.; Zhang J.; Chen Y.; Fei Z.; Heeney M.; Friend R. H.; Vaynzof Y. Visualising the Vertical Energetic Landscape in Organic Photovoltaics. Joule 2019, 3 (10), 2513. 10.1016/j.joule.2019.06.018. [DOI] [Google Scholar]
- Wang Q.; Shao Y.; Xie H.; Lyu L.; Liu X.; Gao Y.; Huang J. Qualifying composition dependent p and n self-doping in CH3NH3PbI3. Appl. Phys. Lett. 2014, 105, 163508. 10.1063/1.4899051. [DOI] [Google Scholar]
- Sutanto A. A.; Caprioglio P.; Drigo N.; Hofstetter Y. J.; Garcia-Benito I.; Queloz V. I. E.; Neher D.; Khaja Nazeeruddin M.; Stolterfoht M.; Vaynzof Y.; Grancini G. 2D/3D perovskite engineering eliminates interfacial recombination losses in hybrid perovskite solar cells. Chem. 2021, 7 (7), 1903–1916. 10.1016/j.chempr.2021.04.002. [DOI] [Google Scholar]
- Bitton S.; Tessler N. Electronic-ionic coupling in perovskite based solar cells: Implications for device stability. Appl. Phys. Lett. 2020, 117 (13), 133904. 10.1063/5.0023902. [DOI] [Google Scholar]
- Bitton S.; Tessler N. Electron/hole blocking layers as ionic blocking layers in perovskite solar cells. J. Mater. Chem. C 2021, 9, 1888–1894. 10.1039/D0TC04697C. [DOI] [Google Scholar]
- Quarti C.; De Angelis F.; Beljonne D. Influence of Surface Termination on the Energy Level Alignment at the CH3NH3PbI3 Perovskite/C60 Interface. Chem. Mater. 2017, 29, 958–968. 10.1021/acs.chemmater.6b03259. [DOI] [Google Scholar]
- Persson P.; Gebhardt J. C. M.; Lunell S. The Smallest Possible Nanocrystals of Semiionic Oxides. J. Phys. Chem. B 2003, 107, 3336–3339. 10.1021/jp022036e. [DOI] [Google Scholar]
- Lundqvist M. J.; Nilsing M.; Persson P.; Lunell S. DFT study of bare and dye-sensitized TiO2 clusters and nanocrystals. Int. J. Quantum Chem. 2006, 106, 3214–3234. 10.1002/qua.21088. [DOI] [Google Scholar]
- De Angelis F.; Di Valentin C.; Fantacci S.; Vittadini A.; Selloni A. Theoretical Studies on Anatase and Less Common TiO2 Phases: Bulk, Surfaces, and Nanomaterials. Chem. Rev. 2014, 114, 9708–9753. 10.1021/cr500055q. [DOI] [PubMed] [Google Scholar]
- She L.; Liu M.; Zhong D. Atomic structures of CH3NH3PbI3(001) surfaces. ACS Nano 2016, 10, 1126–1131. 10.1021/acsnano.5b06420. [DOI] [PubMed] [Google Scholar]
- Ohmann R.; Ono L. K.; Kim H.-S.; Lin H.; Lee M. V.; Li Y.; Park N.-G.; Qi Y. Real-space imaging of the atomic structure of organic-inorganic perovskite. J. Am. Chem. Soc. 2015, 137, 16049–16054. 10.1021/jacs.5b08227. [DOI] [PubMed] [Google Scholar]
- Meggiolaro D.; Mosconi E.; De Angelis F. Formation of Surface Defects Dominates Ion Migration in Lead-Halide Perovskites. ACS Energy Lett. 2019, 4 (3), 779–785. 10.1021/acsenergylett.9b00247. [DOI] [Google Scholar]
- Haruyama J.; Sodeyama K.; Han L.; Tateyama Y. Termination Dependence of Tetragonal CH3NH3PbI3 Surfaces for Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 2903–2909. 10.1021/jz501510v. [DOI] [PubMed] [Google Scholar]
- Uratani H.; Yamashita K. Charge Carrier Trapping at Surface Defects of Perovskite Solar Cell Absorbers: A First-Principles Study. J. Phys. Chem. Lett. 2017, 8 (4), 742–746. 10.1021/acs.jpclett.7b00055. [DOI] [PubMed] [Google Scholar]
- Meggiolaro D.; Motti S. G.; Mosconi E.; Barker A. J.; Ball J.; Perini C. A. R.; Deschler F.; Petrozza A.; De Angelis F. Iodine chemistry determines the defect tolerance of lead-halide perovskites. Energy Environ. Sci. 2018, 11, 702–713. 10.1039/C8EE00124C. [DOI] [Google Scholar]
- Ambrosio F.; Mosconi E.; Alasmari A. A.; Alasmary F.; Meggiolaro D.; De Angelis F. Formation of Color Centers in Lead Iodide Perovskites: Self Trapping and Defects in the Bulk and Surfaces. Chem. Mater. 2020, 32, 6916–6924. 10.1021/acs.chemmater.0c02005. [DOI] [Google Scholar]
- Tessler N. Adding 0.2 V to the Open Circuit Voltage of Organic Solar Cells by Enhancing the Built-In Potential. J. Appl. Phys. 2015, 118, 215501. 10.1063/1.4936367. [DOI] [Google Scholar]
- An Q.; Sun Q.; Weu A.; Becker-Koch D.; Paulus F.; Arndt S.; Stuck F.; Hashmi A. S. K.; Tessler N.; Vaynzof Y. Enhancing the Open-Circuit Voltage of perovskite solar cells by up to 120 mV using π-extended phosphoniumfluorene electrolytes as hole blocking layers. Adv. Energy Mater. 2019, 9 (33), 1901257. 10.1002/aenm.201901257. [DOI] [Google Scholar]
- Butscher J. F.; Intorp S.; Kress J.; An Q.; Hofstetter Y. J.; Hippchen N.; Paulus F.; Bunz U. H. F.; Tessler N.; Vaynzof Y. Enhancing the Open-Circuit Voltage of Perovskite Solar Cells by Embedding Molecular Dipoles within Their Hole-Blocking Layer. ACS Appl. Mater. Interfaces 2020, 12 (3), 3572–3579. 10.1021/acsami.9b18757. [DOI] [PubMed] [Google Scholar]
- Cho Y.; Bing J.; Kim H. D.; Li Y.; Zheng J.; Tang S.; Green M. A.; Wakamiya A.; Huang S.; Ohkita H.; Ho-Baillie A. W. Y. Immediate and Temporal Enhancement of Power Conversion Efficiency in Surface-Passivated Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2021, 13 (33), 39178–39185. 10.1021/acsami.1c06878. [DOI] [PubMed] [Google Scholar]
- Moghadamzadeh S.; Hossain I. M.; Jakoby M.; Nejand B. A.; Rueda-Delgado D.; Schwenzer J. A.; Gharibzadeh S.; Abzieher T.; Khan M. R.; Haghighirad A. A.; Howard I. A.; Richards B. S.; Lemmer U.; Paetzold U. W. Spontaneous enhancement of the stable power conversion efficiency in perovskite solar cells. J. Mater. Chem. A 2020, 8, 670–682. 10.1039/C9TA09584E. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.