Solar energy assisted thermal treatment model to decontaminate airborne viruses in hospital

Graphical abstract

Abstract

The evolution of airborne viruses across the globe has caused many deaths in recent decades. Currently, the world is witnessing the terrible behavior of SARS-CoV-2. The airborne viruses attached to the suspended air particles for a long time and spread rapidly. The dispersal of airborne viruses in the indoor air increases the risk of diseases. The present study endorses a solar-assisted heat treatment model to decontaminate airborne viruses and provide hospitals with disinfected air. A simplified model comprises the heating and cooling sections to abolish airborne viruses and cool the treated air. The heating section includes a solar parabolic trough collector (PTC)/electrical heater, porous domain, and decontamination chamber, while the cooling unit comprises storage tanks and an air cooler. A heat exchanger exchanges energy between hot and cold air streams. A solar PTC offers air heating during day time; however, the porous domain with the electrical heaters acts during the night and intermediate time. The airborne viruses can be abolished by passing through a porous domain and decontaminating chamber at 105 °C upholding an exposure period of 5 mins. The cooling section cools the disinfected air to comfortable conditions. A numerical analysis finds the optimal porosity of 0.9, owing to an exit temperature of 105 °C and a minimal pressure drop of 5.16 kPa. The high-temperature disinfected air leaving the storage tank (ST-2) further cools in an air cooler. Besides, the system’s energy efficiency is noted at 37.4 % and 91.1 % during daytime and nighttime operations, respectively.

Nomenclature

Variables

A

Area (m²)

Be

Bejan number

$c_p$

Specific heat (J/Kg K)

D

Diameter (m)

$d_p$

Particle diameter (m)

$d_s$

Sphere diameter (m)

d

Tube diameter (m)

$\dot{E}$

Energy (W)

H

Height

h

Convective coefficient (W/m² K)

$\overline{\mathrm{I}}$

Solar radiant energy (W/m²)

L

Length (m)

N_T

Number of tubes

N_P

Number of passes

P

Pressure (bar)

R

Thermal resistance (K/W)

T

Temperature (°C)

U

Overall heat transfer coefficient (W/m² K)

R

Thermal resistance (K/W)

$R_f$

Correction factor

r

Radius (m)

u

Velocity (m/s)

V

Volume (m³)

$\dot{V}$

Volume flow rate (m³/s)

Greek symbols

$\xi$

Porosity

$\epsilon$

Emissivity

λ^'

Thermal conductivity (W/mK)

$\eta$

Efficiency

$\mu$

Dynamic viscosity (Pa s)

$\nu$

Kinematic viscosity (m²/s)

$\rho$

Density (kg/m³)

$\tau$

Time (s)

Subscripts/Superscript

a

Air

ap

Aperture

b

Buffles

eq

Equivalent

o

Outer

p

Particle

Re

Required

s

Sphere

SS

Shell side

TS

Tube side

t

Tube

o

Outlet

Acronyms

ACH

Air change per hour

AIV

Avian influenza A virus

AG

Air gap

CV

Control volume

MHV

Mouse hepatitis virus

PD

Porous domain

PM

Porous media

PTC

Parabolic trough collector

SARS

Severe Acute Respiratory Syndrome

SiC

Silicon carbide

SS

Stainless steel

ST

Storage tank

TGEV

Transmissible gastroenteritis virus

WHO

World health organization

Introduction

Indoor air is an effective carrier to spread human pathogen airborne viruses in residential and commercial built environments [1]. The airborne virus spreads rapidly and intensifies the risk of diseases in the less ventilated indoor built environment [2]. Coronavirus is a single standard RNA (Ribonucleic acid) virus from the coronaviridae group, spread through airborne routes [3]. The evolution of airborne viruses shown in Fig. 1 and are as follows: Avian influenza A virus (AIV), Severe Acute Respiratory Syndrome Coronavirus (SARS-CoV-1 and SARS-CoV-2), Middle East Respiratory Syndrome Coronavirus (MERS-CoV), Mouse Hepatitis Virus (MHV), and Transmissible gastroenteritis virus (TGEV) [4], [5], [6]. An outbreak of the novel H7N9 influenza virus began in eastern China in March 2013 and affected humans severely [6].

Fig. 1.

Evolution of Airborne viruses over the decades.

The Avian influenza A virus has infected 134 people, resulting in 45 fatalities. The cases of SARS-CoV-1 were first found in Hong Kong and China in 2003 and infected thousands of people worldwide, along with 800 causalities [3], [7]. However, the MERS-CoV was first identified in an infected patient hospitalized in Saudi Arabia in 2012. MERS-CoV is a beta-coronavirus and is from the same family as SARS-CoV-1 [3]. Mouse Hepatitis Virus (MHV), a coronavirus particular to mice, was first isolated in 1949 and found to be an exceedingly contagious disease. MHV, a coronaviruses family virus, is highly infectious and transmits via aerosols, fomites, and direct contact. [8], [9]. Likewise, the Transmissible gastroenteritis virus (TGEV) belongs to a coronaviridea family similar to MHV. TGEV was noticed in 1946 in the United States and spread in swine-rich countries like England, Japan, China, Belgium, Africa, and Australia [10]. In fact, a lot of cases of transmissible gastroenteritis virus infection were recently reported in China [11], [12].

As of now, >200 countries have critically undergone medicinal and economic crises during the COVID-19 pandemic [13]. Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) diseased 518 million people and caused 6.26 million causalities worldwide [WHO, 2022]. The possible routes of pathogen SARS-CoV-2 spread in humans are witnessed direct contact (people to people), indirect contact (through fomites), and airborne transmission (virus suspended with air particles) [14], [15], [16]. Predominantly, the airborne route of virus transmission augmented the spread of COVID-19 disease as it is found in particulate matter with aerosol [17]. Morawska and Milton [18] identify the SARS-CoV-2 virus moving with microdroplets at small to medium distances (up to certain meters). They appealed to the medical community to suppress airborne virus transmission by implementing essential preventive measures. The flow dynamics of saliva droplets moving in an open atmosphere were studied by Dbouk and Drikakis [19] and found that the saliva droplets can move up to 6 m at wind speeds of 4 to 15 kmph. The number of aerosol droplets propagated by an infected individual via sneezing, coughing, and talking can be as high as 10,000 at 20 m/s, 100–1000 at 10 m/s, and 50 at 5 m/s, respectively. [20]. As a result, infections by airborne viruses are more likely to occur in hospital wards, nursing homes, and similar places since infected patients are frequently present.

Researchers have developed a consensus to destroy the airborne pathogen viruses [4], [5], [21], [22], [23], [24], [25], [26]. Several physicochemical and biochemical techniques have been evolved to disinfect the air. The spread of disease through airborne pathogens and bacteria depends on aerosol transport and aerosol infectivity. In order to address the aerosol infectivity and aerosol transport, the UV radiation and particle filtration techniques are often found suitable, respectively [27]. Despite this, high-temperature, short-time (HTST) thermal treatment is the most effective, safe, and environmentally friendly method to mitigate the aerosol infectivity and aerosol transport together [28]. The inactivation of airborne viruses in a heated environment is found to be an effective method of decontaminating infected air. However, it significantly depends on the exposure period of the virus in such an environment [4], [29]. The requisite temperature and exposure time to decontaminate various airborne viruses in Table 1 .

Table 1.

Temperature and exposure period for the inactivation of various airborne viruses.

Airborne virus	Temperature (°C)	Time (min)	References
Avian influenza A	65	10	Vlaskin [6]
	$>$ 70	1	Vlaskin [6]
MERS-CoV	56	0.5	Leclercq et al. [21]
	56	15	Leclercq et al. [21]
	65	0.5	Darnell et al. [22]
MHV	60	1	Saknimit et al. [23]
	60	5	Saknimit et al. [23]
	80	1	Saknimit et al. [23]
SARS-CoV-1	70	1.1	Yap et al. [4]
	80	<1	Kushan et al. [24]
	90	<1	Burton et al. [25]
SARS-CoV-2	70	2.5	Yap et al. [4]
	80	<1	Kushan et al. [24]
	90	<1	Burton et al. [25]
	92	15	Kushan et al. [24]
	95	1	Burton et al. [25]
	95	5	Burton et al. [25]
	100	< 5	Kampf et al. [5]
TGEV	51	5	Laude [26]
	51	2	Laude [26]

The experimental and theoretical studies [21], [22], [23], [24], [25], [26] have established inactivation temperatures and exposure times for airborne viruses AIV, MERS-CoV, MHV, SARS-CoV-1, SARS-CoV-2, and TGEV. Although, at the temperatures and exposure times listed in Table 1, the virus infectivity is significantly reduced by at least 3-log10 or 4-log10. The above observations suggest that airborne viruses are susceptible to the exposure temperature and time, while their survival period decreases as the temperature increases. [30], [24].

In this regard, Zou et al. [31] investigated a 50 μl stock solution of avian influenza H7N9 virus at 56 to 75 °C for 5 to 60 min and 70 to 100 °C for 1 to 2 min. Based on the obtained results, a virus was subsequently proved inactive at temperatures above 56 °C. Leclercq et al. [21] investigated a sample culture contaminated with MERS-CoV virus at different temperatures and exposure times and observed the reduction of viral infectivity by 4-log10 at 56 and 60 °C for 25 and 1 min, respectively. Sow et al. [32] observed the mitigation of hepatitis A and murine norovirus at 90 °C for 180 to 300 s by 4-log10 reduction. In continuation of airborne virus disinfection, specific techniques have been proposed to incapacitate or abolish the novel Coronavirus (SARS-CoV-2) [4], [25]. Yap et al. [4] have used the dry heating process to decontaminate all kinds of viruses, including SARS-CoV-2, with temperatures >70 °C. Burton et al. [25] used an unlidded dry, hot block to heat treat SARS-CoV-2 in a tissue culture medium at 56 to 95 °C and found that the virus is entirely deactivated at 80 °C (90 min) and 95 °C (5 min). Morawska et al. [33] have suggested certain preventive measures to suppress the transmission by maximizing ventilation, avoiding air recirculation, and utilizing air filters. However, such preventative measures can fail to eliminate indoor airborne viruses. Despite that, among the existing methods, there exists a massive scope to develop adaptable, enduring, and eco-friendly techniques for the inactivation of airborne viruses in ample ventilated spaces like hospital wards and medical facilities.

Plenty of experimental and analytical studies advocate the implication of solar energy, owing to its pragmatic significance in air heating applications [34], [35], [36], [37]. Notably, the solar parabolic trough collectors (PTC) proved to be the most accessible means of air heating in the built environment. India's geographic condition makes it ideal for using solar energy since it receives >5000 trillion kWh of solar radiation yearly [34]. The average annual solar insolation in almost 58 % of the country is 5 kWh/m²/day [37]. Lingayat et al. [34] studied the implication viability of solar energy for air heating in a wide range of drying applications. Pandey et al. [38] have utilized the solar PTC to heat air at a variable mass flow rate. At a lesser mass flow rate, they found elevated exit temperatures.

In the present study, a solar energy-assisted thermal treatment model is endorsed to abolish the airborne viruses and avail the disinfected air for a hospital ward. Virus-infected air passes through a heating and cooling system. The heating section comprises solar PTC/electrical heaters, a porous domain, and a decontamination chamber; however, the cooling unit includes storage tanks and an air cooler. A distributed heat exchanger enables the exchange of energy between hot and cold air streams. The infected air passes through a heating section to abolish the airborne pathogen virus at 105 °C, ensuring a mandatory exposure time of 5 mins. The high-temperature air further cools in a cooling section to avail the disinfected air in comfortable conditions ($\approx$ 30 °C) in the hospital ward.

The entire model is sized in accordance with the ventilation air requirements for a 12-bed hospital ward. The solar PTC is proposed for air heating during the sunshine hours; however, the electrical heaters wrapped around the porous domain act in the absence of solar energy. The porous materials (PMs) have been employed in different heating applications to enhance the fluid’s thermal properties as they offer appropriate mixing due to a higher surface-to-volume ratio [39], [40], [41]. This study investigates the effect of variable porosity on the temperature and pressure drop of air passing through a porous domain. An explicit numerical analysis aims to establish the optimum porosity illustrating enhanced air heating corresponding to minimum pressure drop. In addition, the thermal characterization of storage tanks determines the steady-state air outflow temperature at the mass flow rates of 0.44 kg/sec (peak load) and 0.22 kg/sec (partial load).

Model description

Fig. 2 presents a schematic of the heat treatment model, split into two major sections: heating and cooling. The heating section comprises solar PTC, electrical heaters (EH-1 and EH-2), porous domain, and a decontamination chamber (DC), while the cooling unit includes storage tanks (ST-1 and ST-2) and an air cooler (AC). However, a distributed heat exchanger (HE) is incorporated to exchange the heat between hot and cold air streams. Solar PTC aims to achieve the requisite decontamination temperature > 105 °C during sunshine. However, the electrical heater wrapped over the porous domain act for air heating during the inaccessibility of solar energy. A porous domain ensures uniform air temperature in both cases by offering enhanced air mixing.

Fig. 2.

Schematic layout of solar-energy assisted thermal treatment model.

A decontamination chamber upholds an exposure period of 5 mins to abolish the virus. Besides, a couple of storage tank is provisioned to achieve air’s natural convection cooling and to maintain a buffer of treated air for uninterrupted supply. However, an air cooler delivers the disinfected air to the hospital ward at ${30}^{°}C$ and 1 atm using forced or natural convection cooling depending on the weather conditions.

In the layout, $T_1$, $T_2$, $T_3$, $T_4$, $T_5$, $T_6$, and $T^{\ast }$ represent air temperature at the ambient, shell side exit, solar PTC exit, tube side exit, ST-1 exit, and ST-2 exit, and the inactivation temperature, respectively. The necessary ventilation air is calculated by ${\dot{V}}_a(m^3/h)=V_s\ast ACH$, considering ACH = 9 [42] for a 12-bed hospital ward of 245 m³ volume with two partitions. Each section with six patients will be ventilated with a treated airflow of 360 CFM.

Process pathway

The heat-based thermal treatment of airborne viruses follows a process pathway shown in Fig. 3 .

Fig. 3.

Pathway for thermal inactivation of airborne viruses.

Infected air is directed towards the air heating section through a surge tank and heat exchanger. A surge tank ascertains the requisite air pressure > 6 bar; however, the heat exchanger (HE) preheats the air before passing it to the porous air heater. An air filter is aligned at the entrance to eliminate the dust particles and moisture content [43]. Preheated air attains the necessary decontamination temperature of 105 °C, passing through a solar PTC or porous domain wrapped with electrical heaters, depending on the availability of solar irradiations. The porous insulated domain provides optimal surface-to-volume ratios to acquire an even temperature at the exit. The heated air at elevated pressure (>5 bar) passes through a decontamination chamber, ensuring 5 mins exposure period. Furthermore, the disinfected air moves towards the cooling section to cool at ambient conditions. The disinfected air arrives in storage tanks passing through a heat exchanger for natural convection cooling. A finned air cooler further cools the disinfected air through natural or forced convection, depending on the air outflow temperature ($T_6$).

In particular, the air heating takes place in three different modes, based on the day-round availability of solar radiant energy.

Case-1: Day-time operation, $T_2<T_3>T^{\ast }$: (HE_SS-PTC-PD-DC- HE_TS-ST-AC).

The model follows the above process loop during the sunshine hours in the daytime when there is sufficient solar radiant energy to achieve the requisite temperature rise of air ($T_2$ to $T_3$). The heated air passed through a porous domain and decontamination chamber to abolish the airborne virus by establishing appropriate mixing and requisite air residence time ($\tau$ = 5 mins). However, the electrical heaters remain inactive during daytime operation.

Case-2: Night-time operation, $T_2=T_3<$$T^{\ast }$: (HE_SS-EH-PD-DC-HE_TS-ST-AC).

The above process loop exists at night with no solar radiant energy. Air leaving the heat exchanger achieves the requisite temperature rise in the porous domain wrapped with electrical heaters. EH-1 and EH-2 function depending on the air mass flow rate.

Case-3: Intermediate operation, $T_2<T_3<T^{\ast }$: (HE_SS-PTC-EH-PD-DC- HE_TS-ST-AC).

An intermediate operation of the system indicates insufficient solar energy to achieve desired temperature increases, where $T_3<T^{\ast }$. Accordingly, the system follows the above process loop, where electrical heaters partially operate to accomplish the necessary temperature rise. A temperature control unit regulates the operation of the electrical heater. The remaining processes for all the three cases, however, follow the same path as shown in Fig. 3.

Specifications

The specifications and operations characteristics of solar PTC, porous domain, decontamination chamber, heat exchanger, storage tanks, and air cooler are illustrated, respectively. A solar PTC's aperture area required to heat the air is calculated based on its operating characteristics, as shown in Table 2 . The porous insulated domain comprises two circular stainless-steel pipes of L/D ratio 12 (L, D: 1.25 m, 0.15 m) with silicon carbide (Si-C) porous material. The incoming air splits equally between porous pipes at peak load (${\dot{m}}_{a,out}=0$. 44 kg/s); however, only one will be active at partial load (${\dot{m}}_{a,out}=0$. 22 kg/s). Such an arrangement of porous domains aims to optimize energy usage and augment air heating.

Table 2.

Specifications of major components in the schematic layout.

Solar PTC
	Location			Kolkata (22–38-59 N, 88–27-00E)
	Air heating load (kW)			18.65
	Mean solar radiant energy (W/m2)			600
	Collector aperture
		Width, length (m)		5.77 [37], 22.18
		Aperture area (m2)		128.1
	Absorber tube:
		Diameter, length (m)		0.066, 22.18
	Optical efficiency			0.71 [37]
	Thermal efficiency			0.41 [35]
Heat exchanger
	Arrangement			Counter-flow
	Air mass flow (kg/s)			0.22
	Overall heat coefficient, U (W/m2K)			296.5
	Tube side
		Heat convection constant (W/m2K)		1264.1
		$T_1$, $T_2$ (°C)		30, 75
		Tube diameter, length (m)		0.0158, 1.2
		Number of tube/passes		30
	Shell side
		Heat convection constant (W/m2K)		387
		$T_3$, $T_4$ (°C)		105, 60
		Diameter, length (m)		0.6, 1.58
		Internal volume (m3)		0.378
		Number of baffles, spacing (m)		8, 0.12
Air cooler
		Tube: surface area (m2)		4.22
		Diameter, length (m)		0.016, 84
		Fins: surface area (m2)		1.80

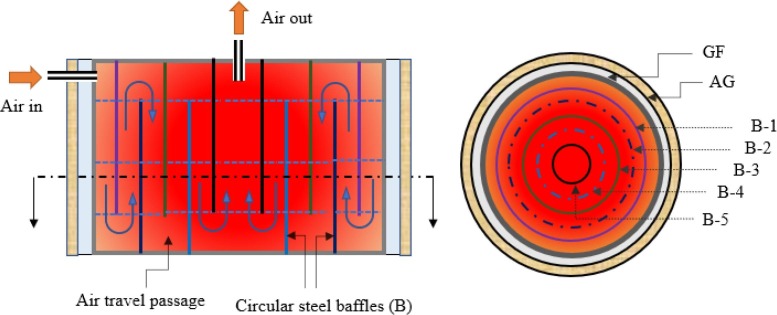
An insulated decontamination chamber of height and diameter 2.5 m and 2.94 m ascertains the requisite exposure period ($\approx$ 5 min) to abolish airborne viruses at 105 °C, as shown in Fig. 4 . Five round baffles (w, H: 0.002 m, 2.3 m) are incorporated alternatively at the top and bottom of the chamber to avoid the direct flow of treated air towards the outlet. The travel passage between the baffles or chamber’s internal volume is calculated as:

$$V_T={\dot{V}}_a{\tau }_R$$ (1)

Fig. 4.

Cross-sectional view of decontamination chamber.

In Eq (1), ${\dot{V}}_a$ and ${\tau }_R$ are volume flow rate (ρ.${\dot{m}}_{a,out}$) and passing time (exposure time). Hence the internal volume of the chamber is calculated as 16.92 m³ considering 5 min exposure period.

Further, the specifications of a shell and tube heat exchanger are listed in Table 2. In the cooling section, two stainless steel storage tanks with a height and diameter of 2.2 m and 1.5 m are incorporated to cool the disinfected air. The round baffle with a diameter and height of 1.2 m and 2.05 m is integrated at the top to prevent the straight flow of high-temperature air towards the air cooler. The internal volume of each storage tank is 3.871 m³.

Mathematical formulation

The governing equations leading to the model's numerical and analytical formulation are described. The assumptions made in the mathematical formulation are as follows:

• Candidate materials (solid and fluid) are isotropic and homogeneous.

• Fluid flow in the porous domain is steady and fully developed.

• Invariable heat coefficient adjacent to the storage tank.

• Porous domain is perfectly insulated.

Governing equations

Porous heating domain.

The fluid’s motion in a porous domain is characterized by mass, momentum, and energy conservation equations, as stated in Eq. (2–5).

Continuity Equation:

$$\frac{\partial \left({\rho }_a\xi \right)}{\partial \tau }+\mathrm{\nabla }.\left(\xi \rho u\right)=0$$ (2)

Momentum equation:

$$\frac{\partial \left(\xi {\rho }_{a}uu\right)}{\partial \tau }+\mathrm{\nabla }.\left(\xi \rho uu\right)=-\xi p+\mathrm{\nabla }.\left(\xi {\sigma }^{″}\right)+\mathrm{\Gamma }$$ (3)

In Eq. (2), ${\rho }_a$ and $\xi$ are the density and porosity of the air. $u$ represents the velocity vector. In Eq. (3), $p$, and ${\sigma }^{″}$ represent pressure and stress tensor; however, $\mathrm{\Gamma }$ implies the flow resistance in the porous domain due to the fluid’s viscosity and shape effect of the PM.

Energy Equation:

The solid phase energy equation is as follows:

$$\frac{\partial \left[\left(1-\xi \right){\rho }_s{C}_{p,s}{T}_s\right]}{\partial \tau }=\mathrm{\nabla }.\left[{\mathrm{\lambda }\prime }_{\mathit{eff}}\mathrm{\nabla }{T}_s\right]+h_v\left(T_a-T_s\right)-\mathrm{\nabla }.Q_r$$ (4)

The fluid phase energy equation is as follows:

$$\frac{\partial \left(\xi {\rho }_a{C}_{p,a}{T}_a\right)}{\partial \tau }+\mathrm{\nabla }.\left(\xi u\left({\rho }_a{C}_{p,a}{T}_a+p\right)\right)=h_v\left(T_s-T_a\right)+\mathrm{\nabla }.\left[\xi \left({\mathrm{\lambda }\prime }_f+{\rho }_a{C}_{p,a}\right)\mathrm{\nabla }{T}_a+\xi \left({\sigma }^{″}u\right)\right]$$ (5)

In Eq. (4), ${\mathrm{\lambda }\prime }_{\mathit{eff}}$ = $\xi {\mathrm{\lambda }\prime }_f+(1-\xi ){\mathrm{\lambda }\prime }_s$ represents effective thermal conductivity, where ${\mathrm{\lambda }\prime }_f$ and ${\mathrm{\lambda }\prime }_s$ are the fluid and solid phase thermal conductivities. In addition, $Q_r$ represents the solid radiation heat transfer in the radial direction calculated as $Q_r=-\left(16\sigma T_s^3/3{\sigma }_s\right)\frac{d{T}_s}{\mathit{dx}}$, where $\sigma$ ($5.67\times 10^{-8}$ Wm^-2K⁻⁴): Stefan-Boltzmann’s constant and ${\sigma }_s$: PM’s extinction coefficient. In Eq. (4) and (5), ρ, $C_p$, and $T$ represent the density, specific heat, and temperature, where the subscripts “s” and “a” denotes the solid and fluid phases.

$h_v=\frac{\mathit{Nu}{\mathrm{\lambda }\prime }_f}{d^2}$ is the volumetric heat transfer coefficient [41], [44].

Dimensionless numbers

$$\mathit{Be}=\frac{\mathrm{\Delta }P{L}^2}{\mu \nu }$$ (6)

$$\mathit{Nu}=\frac{\mathit{hD}}{{\mathrm{\lambda }\prime }_f}=0.052\frac{{(1-\xi )}^{0.14}}{\xi }{\mathit{Re}}_p^{0.86}{\mathit{Pr}}^{1/3}$$ (7)

Eq. (6) estimates the Bezan number ($\mathit{Be}$) based on the fluid’s thermophysical properties, pressure drop ($\mathrm{\Delta }P$), and length (L) of the porous domain [45]. Eq. (7) calculates the average Nu in the porous field based on the $\mathit{Re}=\frac{u{d}_P}{\nu }$, where $d_p$ is the pore diameter.

Energy efficiency

The energy balance of porous domain’s control volume is stated in Eq. (8).

$${\dot{Q}}_{\mathit{EH}/PTC}={\dot{Q}}_{\mathit{air}}+{\dot{Q}}_{\mathit{loss}}$$ (8)

$${\eta }_{\mathit{PD}}=\frac{{\dot{Q}}_{\mathit{air}}}{{\dot{Q}}_{\mathit{EH}/PTC}}$$ (9)

Eq. (9) calculates the energy efficiency of the porous domain (PD) during the day-time operation (Case-1) and intermediate or night-time operation (Case-2 and 3), assuming no radiation losses. ${\dot{Q}}_{\mathit{EH}/PTC}$ denotes the electrical power consumption or heat added by solar PTC. However, the energy required to rise the air temperature can be calculated as ${\dot{Q}}_{\mathit{air}}$ = ${\dot{m}}_a{C}_{{\mathrm{p}}_{\mathrm{a}}}\mathrm{\Delta }\mathrm{T}$, at $\mathrm{\Delta }\mathrm{T}$ = 45 °C. The heat losses from the porous domain insulated with glass fiber (GF) of a thickness ($w_{\mathit{GF}}$) 0.025 m is calculated as $\frac{{\dot{Q}}_{\mathit{loss}}}{L}={\int }_{T_1}^{T^{\ast }}\frac{\mathit{dT}}{R_{\mathit{th}}}$, where $R_{\mathit{th}}$ = $\frac{\mathit{ln}\frac{r_{\mathrm{o}}}{r_{\mathrm{i}}}}{2\pi {\mathrm{\lambda }\prime }_{\mathit{GF}}}$. $T^{\ast }$ and $T_1$ are the decontamination temperature (105 °C) and ambient temperature (27 °C).

Storage tank

The mass and energy balance of the storage tank’s control volume is stated in Eq. (10) and (11) [46]. The energy balance comprises energy in (${\dot{E}}_{\mathit{in}}$), energy out (${\dot{E}}_{\mathit{out}}$), and energy accumulated in the tank’s control volume (${\dot{E}}_{\mathit{CV}}$) in watts [35].

$$\sum {\dot{m}}_{a,in}-\sum {\dot{m}}_{a,out}=0$$ (10)

$$\sum {\dot{E}}_{\mathit{in}}-\sum {\dot{E}}_{\mathit{out}}=\sum {\dot{E}}_{\mathit{CV}}$$ (11)

$$\sum {\dot{E}}_{\mathit{in}}={\dot{Q}}_{\mathit{air},in}={\int }_{T_1}^{{\mathrm{T}}_{\mathit{air},in}}{\dot{m}}_{a,in}{C}_{{\mathrm{p}}_{\mathrm{a}}}dT$$ (12)

$$\sum {\dot{E}}_{\mathit{out}}={\dot{Q}}_{\mathit{air},out}+{\dot{Q}}_{\mathit{loss}}$$ (13)

$${\dot{Q}}_{\mathit{air},out}={\int }_{T_1}^{{\mathrm{T}}_{\mathit{air},out}}{\dot{m}}_{a,out}{C}_{{\mathrm{p}}_{\mathrm{a}}}dT$$ (14)

$${\dot{Q}}_{\mathit{loss}}=\left({\dot{Q}}_{\mathit{Convection}}+{\dot{Q}}_{\mathit{Radiation}}\right)=({\mathrm{T}}_s-{\mathrm{T}}_1)\int hd{A}_s+\mathrm{∊}\mathrm{\sigma }\left(T_S^4-T_1^4\right)A_S$$ (15)

$${\dot{E}}_{\mathit{CV}}=\frac{\partial }{\partial \tau }{Q}_{\mathit{CV}}$$ (16)

$$Q_{\mathit{CV}}={\int }_{T_1}^{\overline{T}}{m}_{a_{\mathit{net}}}{C}_{{\mathrm{p}}_{\mathrm{a}}}dT$$ (17)

In Eq. (12–15), $T_{\mathit{air},in}$, $T_{\mathit{air},out}$, and $T_s$, are the temperature of the incoming air, leaving air, ambient, and tank’s exterior wall, (°C), respectively. However, ${\mathrm{T}}_1$ indicates ambient temperature, which remains constant throughout the analysis at 27 °C. ${\dot{E}}_{\mathit{out}}$ is the sum of the air exit energy and heat lost from the tank's exterior ($A_S=2\pi rh+2\pi r^2$). In addition, $\mathrm{\sigma }$, $\mathrm{∊}$ and h designate the Stefan Boltzmann constant (5.67 × 10⁻⁸ W m⁻² K⁻⁴), surface emissivity, and convection constant (W m⁻² K⁻¹), respectively. Eq. (16) and (17) estimate the accumulated energy in the tank’s control volume, where $\overline{T}$ implies the mean temperature of net air mass accumulated ($m_{a_{\mathit{net}}}$) in the storage tank.

Churchill and Chu [42] have established a correlation for the ${\overline{\mathit{Nu}}}_d$ at ${\overline{\mathit{Ra}}}_D\le {10}^{12}$ to calculate the natural convection coefficient ($\overline{h}=\frac{\mathrm{\lambda }}{D}{\overline{\mathit{Nu}}}_D)$.

$${\overline{\mathit{Nu}}}_D={\left[0.60+\frac{0.387{\mathit{Ra}}_d^{0.16}}{{\left\{1+{(0.559/Pr)}^{0.562}\right\}}^{0.296}}\right]}^2$$ (18)

$${\overline{\mathit{Ra}}}_D=\frac{\beta g({\mathrm{T}}_S-{\mathrm{T}}_1)d^3}{\alpha \nu }$$ (19)

In Eq. (18–19), ${\overline{\mathit{Ra}}}_d$, $\mathit{Pr}$, $\nu$ , $\alpha$ , and $\beta$ are Rayleigh number, Prandtl number, kinematic viscosity (m²/s), thermal diffusivity (m²/s) and expansion constant (K⁻¹), respectively.

The MATLAB codes have been used to size the solar PTC, decontamination chamber, shell and tube heat exchanger, and the air cooler using the governing equations as follows:

Solar parabolic trough collector.

PTC's aperture area is intended according to the energy required to heat the air leaving the heat exchanger, as stated in Eq. (20).

$${\dot{Q}}_{\mathit{Req}}={\int }_{T_2}^{T_3}{\dot{m}}_{\mathit{air}}{C}_{{\mathrm{p}}_{\mathrm{a}}}dT$$ (20)

$${\dot{Q}}_{\mathit{Solar}}=A_{\mathit{ap}}{\overline{I}}_R$$ (21)

$${\dot{Q}}_{\mathit{abs}}={\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},Opt}{A}_{\mathit{ap}}{\overline{I}}_R$$ (22)

$${\dot{Q}}_{\mathit{Use}}={\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},th}{\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},Opt}{A}_{\mathit{ap}}{\overline{I}}_R=Q_{\mathit{Req}}$$ (23)

$$A_{\mathit{ap}}=\frac{{\dot{Q}}_{\mathit{gain}}}{{\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},th}{\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},Opt}{\overline{I}}_R}$$ (24)

The gross aperture area ($A_{\mathit{ap}}$ = $w_{\mathit{ap}}{L}_{\mathit{ap}}$) is estimated using Eq. (21–24), considering constant optical (${\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},Opt}$) and thermal efficiency (${\eta }_{\mathrm{P}\mathrm{T}\mathrm{C},th}$) [35], [37]. ${\overline{I}}_R$ and ${\dot{Q}}_{\mathit{abs}}$ are the mean solar radiant energy and energy absorbed by PTC’s absorber tube. However, ${\dot{Q}}_{\mathit{Use}}$ is the useful solar energy available for air heating equivalent to the required heat gain. The aperture length ($L_{\mathit{ap}}$) is calculated based on the aperture width ($w_{\mathit{ap}}$) of 5.77 m suggested by Reddy et.al [37].

$${\mathrm{\Delta }P}_{\mathit{TS}}={\int }_{X=0}^L{f}_t\left(\frac{\rho {{\overline{u}}^{2}d}_i}{2}\right)dx$$ (25)

Eq. (25) calculates the pressure drop of air passing through an absorber tube based on the friction factor $f_t={(0.790\ln {\mathrm{R}\mathrm{e}}_{\mathrm{D}}-1.64)}^{-2}$, at ${\mathrm{R}\mathrm{e}}_{\mathrm{D}}\le 5\times {10}^6$.

Decontamination chamber

The energy balance of the DC’s control volume is stated in Eq. (26).

$${\dot{Q}}_{\mathit{air},in}={\dot{Q}}_{\mathit{air}.out}+{\dot{Q}}_{\mathit{loss}}$$ (26)

Energy efficiency

$${\eta }_{\mathit{DC}}=\frac{{\dot{Q}}_{\mathit{air},in}-{\dot{Q}}_{\mathit{loss}}}{{\dot{Q}}_{\mathit{air},in}}$$ (27)

In Eq. (27), ${\dot{Q}}_{\mathit{air},in}$ and ${\dot{Q}}_{\mathit{air}.out}$ are the energy of incoming and leaving air of the decontamination chamber. It is worth noting that the heat losses are minimized by incorporating insulation layers of the air gap (AG) and glass fiber (GF). However, supplementary heaters (SH) in the chamber compensate for the existing losses, assuring ${\dot{Q}}_{\mathit{air},in}\approx {\dot{Q}}_{\mathit{air}.out}$. The existing heat losses are as follows:

$$\frac{{\dot{Q}}_{\mathit{loss}}}{\mathrm{H}}={\int }_{T_0}^{T_s}\frac{\mathit{dT}}{{\sum }_{j=1}^3{R}_j}$$ (28)

In Eq. (28), ${{\sum }_{j=1}^{3}R}_j$ = $R_1$+$R_2$+$R_3$, where $R_1$= $\frac{\mathit{ln}\frac{r_2}{r_1}}{\left(2\pi {\mathrm{\lambda }\prime }_{\mathit{AG}}\right)},R_2$= $\frac{\mathit{ln}\frac{r_3}{r_2}}{\left(2\pi {\mathrm{\lambda }\prime }_{\mathit{SS}}\right)}$ and $R_3=\frac{\mathit{ln}\frac{r_4}{r_3}}{\left(2\pi {\mathrm{\lambda }\prime }_{\mathit{GF}}\right)}$ are the thermal resistance offered by air gap ($w_{\mathit{AG}}$ = 0.05 m), stainless-steel (SS) sleeve ($w_{\mathit{SS}}$ = 0.002 m), and glass fiber ($w_{\mathit{GF}}$ = 0.1 m), respectively. $\mathrm{\lambda }\prime$ and w are the thermal conductivity (W/mk) and thickness of insulating materials.

Heat exchanger.

The optimal sizing of a shell and tube heat exchanger aims to achieve the necessary temperature drop ($\mathrm{\Delta }$ T = 45). The log mean temperature difference (LMTD) method determines the suitable dimensions of the heat exchanger, as stated in Eq. (29–37).

The energy exchange between hot and cold airstreams, as stated in Eq. (29), determines the cold air exit temperature $(t_{c.o})$ to achieve the requisite temperature drop of the treated air before the storage tank. Initially, the heat losses from the heat exchanger are disserted to size the heat exchanger; however, based on the intended dimensions, the actual cold air exit temperature ($t_{c.o})$ is calculated and considered to find the energy efficiency. The heat capacities ($\dot{m_a}{C}_{{\mathrm{p}}_{\mathrm{a}}})$ of both air streams are identical in each case, where $\dot{m_a}$ = 0.22 kg/s [47].

$$Q={\int }_{t_{c.o}}^{t_{c,i}}{(\dot{m_a}{C}_{{\mathrm{p}}_{\mathrm{a}}})}_c{\mathit{dT}}_c=-{\int }_{t_{h.o}}^{t_{h,i}}{(\dot{m_a}{C}_{{\mathrm{p}}_{\mathrm{a}}})}_h{\mathit{dT}}_h$$ (29)

The area of a heat exchanger $\left(A_{\mathit{HE}}=\pi d_{o}L{N}_t\right)$ is estimated using LMTD (${\theta }_m)$ of hot and cold airstreams in a counterflow arrangement, overall heat transfer coefficient (U), and correction factor (F).

$$A_{\mathit{HE}}=\frac{Q}{U{\mathit{FA}}_{\mathit{HE}}{\theta }_m}$$ (30)

$${\theta }_m=\frac{\left(t_3-t_2\right)-\left(t_4-t_1\right)}{\ln \frac{\left(t_3-t_2\right)}{\left(t_4-t_1\right)}}$$ (31)

$$U={\left[\frac{1}{h_{\mathit{sh}}}+R_{f,sh}+\frac{d_o}{d_i}\left(R_{f,t}+\frac{1}{h_t}\right)\right]}^{-1}$$ (32)

The correction factor (F) is calculated through non-dimensional constants R $\left\{\frac{\left(t_3-t_4\right)}{\left(t_2-t_1\right)}\right\}$ and S $\left\{\frac{\left(t_2-t_1\right)}{\left(t_3-t_1\right)}\right\}$. The coefficient U is calculated based on the convection coefficient of the tube side ($h_t$) and shell side ($h_{\mathit{sh}}$), considering the fouling factors ($R_f$) [48], [49].

The formulation of convection coefficient for tube side and shell side are as follows:

Tube side

$$h_t=0.027\left(\frac{{\mathrm{\lambda }\prime }_t}{d_o}\right){\mathit{Re}}_t^{0.8}{\mathit{Pr}}_t^{1/3}{\left(\frac{{\mu }_t}{{\mu }_{\mathit{sh}}}\right)}^{0.14}$$ (33)

Eq. (33) finds the tube side convection coefficient based on the Reynolds number (${\mathit{Re}}_t>10000)$ and Prandtl number (${\mathit{Pr}}_t$). The fluid’s mean velocity inside the tube is ${\overline{u}}_t=\frac{{(\dot{m_a})}_{\mathit{tube}}}{\rho \frac{N_T}{N_P}{(A_{\mathit{cs}})}_{\mathit{tube}}}$, where $\frac{N_T}{N_P}$ is the number of tubes per pass.

Shell side

$$h_{\mathit{sh}}=0.36\left(\frac{{\mathrm{\lambda }\prime }_t}{d_{\mathit{eq}}}\right){\mathit{Re}}_{\mathit{sh}}^{0.55}{\mathit{Pr}}_{\mathit{sh}}^{1/3}{\left(\frac{{\mu }_t}{{\mu }_{\mathit{sh}}}\right)}^{0.14}$$ (34)

Eq. (34) estimates the shell side convection coefficient based on the ${\mathit{Re}}_{\mathit{sh}}$ $\left(\frac{{\rho }_a{\overline{u}}_{\mathit{sh}}{d}_{\mathit{eq}}}{{\mu }_a}\right)$ and ${\mathit{Pr}}_{\mathit{sh}}$, where the shell side fluid’s velocity is ${\overline{u}}_{\mathit{sh}}=\frac{{(\dot{m_a})}_{\mathit{shell}}}{{\rho }_a{(A_{\mathit{cs}})}_{\mathit{shell}}}$. The shell’s cross-section area is calculated as ${(A_{\mathit{cs}})}_{\mathit{shell}}=\frac{(P_T-d_o)D_{\mathit{sh}}{L}_b}{P_T}$, where, $P_T$ is the tube pitch $\ge 1.25d_o$ and $L_b$ is the baffle spacing $\approx$ 1/5 $D_{\mathit{sh}}$. The shell diameter is ${D_{\mathit{sh}}=D}_b+c^l$, where $c^l$ is the bundle diameter clearance $\ge 0.25d_o$. The tube bundle diameter is calculated as $D_b$= $d_o{\left(\frac{N_T}{k_1}\right)}^{{1/n}_1}$, where the constants $k_1$ and $n_1$ are 0.21 and 2.20, respectively, for a square pitch tube arrangement.

The equivalent shell diameter ($d_{\mathit{eq}}$) of a square pitch tube arrangement is calculated as:

$$d_{\mathit{eq}}=4\left(\frac{P_T^2-\frac{\pi }{4}{d}_o^2}{{\pi d}_o}\right)$$ (35)

The shell side and tube side pressure losses are calculated based on the friction factor; however, on the tube side, $\mathrm{\Delta }P$ in the tube bend is also considered [47], [48].

$${\mathrm{\Delta }P}_{\mathit{SS}}=f_{\mathit{sh}}\left(\frac{\rho {\overline{u}}_{\mathit{sh}}^2}{2}\right)\left(\frac{L}{L_b}\right)\left(\frac{D_{\mathit{sh}}}{d_{\mathit{eq}}}\right)$$ (36)

$${\mathrm{\Delta }P}_{\mathit{TS}}={\int }_{X=0}^L{f}_t\left(\frac{\rho {{\overline{u}}^{2}d}_i}{2}\right)dx+\frac{1}{2}{k}_b\rho {\overline{u}}^2$$ (37)

The shell side pressure drop is calculated by Eq. (36), where the friction factor is $f_{\mathit{sh}}={2b^{\prime }{\mathit{Re}}_{\mathit{sh}}}^{-0.15}$, at ${\mathit{Re}}_{\mathit{sh}}<40000$ and $b^{\prime }=0.72$. However, Eq. (37) calculates the tube side pressure drop based on the friction factor $f_t={(0.790\ln {\mathrm{R}\mathrm{e}}_{\mathrm{D}}-1.64)}^{-2}$, at ${\mathrm{R}\mathrm{e}}_{\mathrm{D}}\le 5\times {10}^6$, and pressure drop at the tube band. The bend coefficient, $k_b$= 0.29 [49] and $\rho$ is the tube-side air density at elevated pressure.

Energy efficiency

The energy balance between hot and cold air streams passing through HE's control volume is illustrated in Eq. (38), considering the heat losses from the shell's outer perimeter.

$${\dot{Q}}_{\mathit{air},h}={\dot{Q}}_{\mathit{air},c}+{\dot{Q}}_{\mathit{loss}}$$ (38)

$${\eta }_{\mathit{DC}}=\frac{{\dot{Q}}_{\mathit{air},h}-{\dot{Q}}_{\mathit{loss}}}{{\dot{Q}}_{\mathit{air},h}}$$ (39)

The energy lost by the hot air stream {${\dot{Q}}_{\mathit{air},h}={(\dot{m_a}{C}_{{\mathrm{p}}_{\mathrm{a}}})}_h\mathrm{\Delta }{T}_h$} splits into energy recovered by cold air {${\dot{Q}}_{\mathit{air},c}={(\dot{m_a}{C}_{{\mathrm{p}}_{\mathrm{a}}})}_c\mathrm{\Delta }{T}_c$} and heat losses from the shell’s exterior. Eq. (39) evaluates the energy recovery efficacy of the HE's cold air stream. However, the heat losses are subsided by incorporating the insulation ($w_{\mathit{GF}}=0.025m$) and can be calculated using Eq. (28), where $R_j$ = $R_1$. Here, $R_1$ represents the thermal resistance offered by GF.

Air cooler.

The air cooler with an extended surface area is recommended to cool the treated air at $\approx$ 30 °C. An air cooler is intended using the NTU method considering the forced convection cooling by ambient air. However, the necessary surface area is calculated following the explicit methodologies discussed in the previous study [41]. In addition, the external convection coefficient ($h_{o,t}$) is calculated as:

$${\overline{\mathit{Nu}}}_D=C^{\prime }\left(\frac{{\mathrm{\lambda }\prime }_t}{d_o}\right){\mathit{Re}}_D^m{\mathit{Pr}}^{0.36}{\left(\frac{P_r}{{\mathit{Pr}}_s}\right)}^{1/4}$$ (40)

Eq. (40) finds the external convection coefficient ${(h}_{o,t}={\overline{\mathit{Nu}}}_D\frac{k}{d_t}$) for the staggered tube arrangement based on the ${\mathit{Re}}_D$ and $u_{\mathit{max}}=\frac{S_T}{S_T-D}u$, where the transverse clearance ($S_T$) and longitudinal clearance ($S_L$) are considered 30 mm and 35 m. The constants $C^{\prime }$ = $0.35{\left(\frac{S_T}{S_L}\right)}^{1/5}$ and m (at $\frac{S_T}{S_L}<2$) are calculated 0.33 and 0.60, respectively [47].

Computational section

A cylindrical porous domain and storage tanks (ST-1 and ST-2) are modeled and numerically investigated using a commercial version of ANSYS 19.2. A comprehensive thermodynamic characterization is carried out by adopting the prescribed numerical methodology and boundary conditions, as listed in Table 3 .

Table 3.

Specified boundary conditions for the porous domain and storage tank.

Boundary		Specifications		Credentials
Porous domain
Inlet:	Air	Boundary type: Mass flow inlet
			Mass flow rate (kg/s)	0.22
			Temperature (°C)	70
Outlet:	Air	Boundary type: Pressure outlet
			Gauge pressure (Pa)	600,000
Pipe wall:		Boundary type: Wall
			Material	Stainless steel
			Outer wall	Isothermal
			Temperature (°C)	148
Storage tank
Inlet:	Air	Boundary type: Mass flow inlet
	Mass flow rate (kg/s)		0.44	0.22
			ST-1	ST-2
	Temperature (°C)		60	$T_{\mathit{air},out}$(ST-1)
Outlet:	Air	Boundary type: Pressure outlet
Gauge pressure (Pa)			500,000
Outer wall:		Boundary type: Wall
		Material	Stainless steel
		Outer wall	Mixed
			Convective coefficient (W/m2K)	2.12
			External emissivity	0.9
			Free stream temperature (°C)	27

The porous domain of L/D ratio = 12 is investigated at altered porosities ξ $:$ 0.5, 0.6, 0.7, 0.8, and 0.9. A steady-state approach is established for a porous air heater by accepting estimated boundary conditions using a multigrid solver on a high-performance computational facility. A set of Favre mean differential equations of mass, momentum, and energy, as stated in Eq. (2–5), are solved by integrating inside a control volume to generate a set of algebraic equations. The algebraic equations are then solved iteratively using specified boundary conditions through the finite volume method. However, a porous zone is preferred in the cell zone conditions considering altered viscous and inertial resistance at respective porosities. A realizable k-ε turbulence model is preferred by amending an empirical constant C_ε,2 = 1.9. The SIMPLE method is favored as a solution method, while the second-order upwind scheme spatially discretizes convective terms.

Inclusive computational analysis of storage tanks (ST-1 and ST-2) is carried out through a time-dependent and steady-state approach at two different flow rates of 0.44 kg/s and 0.22 kg/s. The mass, momentum, and energy equations, stated in Eq. (2–5), are solved by integrating ST’s control volume to find a set of algebraic equations considering ξ = 1. The algebraic equations are further solved iteratively, accepting estimated boundary conditions through the finite volume method. A realizable k-ε turbulence model is used for turbulence modeling. The SIMPLE method is favored as a solution method, while the second-order upwind scheme spatially discretizes convective terms. However, a Second-Order Implicit (SOI) scheme is preferred for transient formulation adopting fixed time step sizes of 0.05.

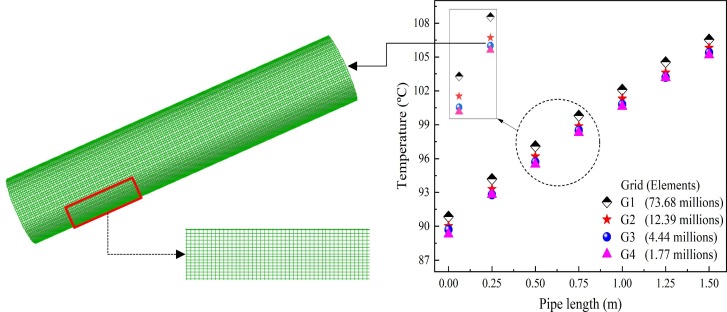
Grid independence

Fig. 5 illustrates the porous domain's optimized or structured tetrahedral mesh at the L/D ratio and porosity of 12 and 0.90. The porous domain's dissimilar meshes (G1-G4) of element sizes 1, 2, 3, and 4 mm are considered for grid independence test, at ${\dot{m}}_{\mathit{air}}$ and $T_{\mathit{air},in}$ of 0.22 kg/s and 75 °C. The axial temperature of the porous pipe domain is noted for different meshes, and the temperature attained by G3 and G4 are observed with a maximum deviation of 0.44 %. Therefore, G3, with 4.44 million elements and 3 mm element size, found an optimum mesh for further simulation.

Fig. 5.

Featured mesh with grid resolution and grid independence analysis of the porous domain.

Likewise, an optimal unstructured mesh of ST-1 with grid resolution is presented in Fig. 6 . The grid independence analysis compares the average tank temperature of unlike meshes G1 to G4 of element sizes 12, 8, 6, and 4 mm, respectively. Consequently, the optimal grid G3 with 6 mm element size and 83.56 million elements is considered for the numerical simulation with a maximum average error of 1.75 %.

Fig. 6.

Featured mesh with grid resolution and grid independence analysis of the storage tank.

Model validation

The numerical model is well validated with the experimental and analytical results of Hassan et al. [45] and the correlation of Vafai et al. [50], respectively. Hassan et al. conducted a set of experiments in a cylindrical porous test section (L = 0.5 m, $d_i$ = 0.047 m) for a fully developed region. Test section consists of the steel balls of different sphere diameters ($d_s$) 6 to 14 mm, at the porosities ($\mathrm{\xi }$) 0.554 to 0.602. Experimental outcomes of the pressure drop ($\mathrm{\Delta }$ P/L) and the temperature rise (${\mathrm{\Delta }T}_{\mathit{air}}$) of the air stream passing through a porous test section of $d_s$ = 6 mm validate the present model under the prescribed assumptions. Furthermore, the analytical data of $\mathrm{\Delta }$ P/L calculated using the correlation suggested by Vafai et al. [50] are also considered for model validation at different Reynolds numbers (${\mathit{Re}}_p=\frac{\rho u{d}_s}{\mu })$ and as follows:

$${\int }_{P_1}^{P_2}-\mathrm{d}\mathrm{P}={\int }_{\left(X=O\right)}^L\left[{\alpha }_1\frac{{\left(1-\xi \right)}^2\mu }{{\xi }^3{d}_s^2}\left(u\right)+{\alpha }_2\frac{\left(1-\xi \right)\rho }{{\xi }^3{d}_s}\left(u^2\right)\right]dx$$ (41)

Pressure loss ($\mathrm{\Delta }$ P) of the fluid passing through the porous domain is estimated using Eq. (41), where the viscus coefficient (${\alpha }_1$) and form drag coefficient (${\alpha }_2$) are 120 and 2.3, respectively. Fig. 7 (a) compares the numerical results of $\mathrm{\Delta }\mathrm{P}/\mathrm{L}$ with the experimental and analytical data at the Reynolds number ranging from 490 to 1100 for $\mathrm{\xi }$ = 0.502. The mean deviations of the numerical results for $\mathrm{\Delta }\mathrm{P}/\mathrm{L}$ from the experimental and analytical data are 13.78 and 16.24 %, respectively. In addition, Fig. 7 (b) illustrates the variation of experimental and numerical ${\mathrm{\Delta }T}_{\mathit{air}}$ with increasing heat generation per unit volume (67044 to 1957688 W/m³), at a constant${\mathit{Re}}_p$ = 1450 and $\mathrm{\xi }$ = 0.58. The mean deviation of the numerical results for ${\mathrm{\Delta }T}_{\mathit{air}}$ from the experimental data is noticed as 3.6 %. Consequently, the numerical results of the proposed model agreed well with both experimental and analytical data; therefore, the proposed model fits appropriately for the current study.

Fig. 7.

Validation of the present model with the experimental and analytical results: (a) variation of $\mathrm{\Delta }$ P/L with the ${\mathit{Re}}_p$, at $\mathrm{\xi }$ = 0.502, (b) increase in ${\mathrm{\Delta }T}_{\mathit{air}}$ with $q_v$ at the constant${\mathit{Re}}_p$ = 1450 and $\mathrm{\xi }$ = 0.58.

Results and discussion

Thermal decontamination of the infected air with airborne viruses is most commonly accomplished by heating and cooling sections. During the infected air's thermal decontamination and cooling phases, the porous heating domain and storage tanks play an essential role. The numerical analysis of a porous domain (L/D = 12) aims to establish optimal porosity, ensuring minimum pressure drop for Cases 1, 2, and 3. However, the temperature analysis confirms a suitable porosity that will allow infected air to disperse nicely and mitigate airborne viruses in Case-3.

Further, an inclusive computational analysis (transient and steady-state) reveals the thermal characterization of consecutive storage tanks ST-1 and ST-2, at ${\dot{m}}_{\mathit{air}}$ = 0.44 and 0.22 kg/s, respectively. However, an analytical design of the decontamination chamber, heat exchanger, and air cooler is based on the mathematical formulation mentioned in section 3.

Characterization of the porous domain

Effect of variable porosity on pressure drop

Fig. 8 reveals the effect of porosity on fluid’s pressure drop and the Bejan number ($\mathit{Be}$) across the porous domain corresponding to Cases 1, 2, and 3. A maximum pressure drop of 213.7 kPa is noticed at lower porosity (0.5) for the L/D ratios of 12; however, a minimum of 5.16 kPa is observed at a higher porosity (0.9). The pressure loss along the domain length ($\mathrm{\Delta }\mathrm{p}/\mathrm{L}$) exhibits an exponential trend with porosity, $\mathrm{\Delta }\mathrm{p}/\mathrm{L}=C_1{e}^{C_2\mathrm{\xi }}$, with a correlation coefficient, R² = 0.99. The parametric constants ‘$C_1$’ and ‘$C_2$’ are 14,604 and −9.173. The above relation is valid for SiC-based cylindrical porous domain at the L/D = 12 and ${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s at 6 bar. The Bejan number is often used to specify a dimensionless pressure drop across the extent of the flow field depending on fluid thermal characteristics. Consequently, the trends of the Bejan number are quite analogous to the $\mathrm{\Delta }\mathrm{p}/\mathrm{L}$.

Fig. 8.

Effect of altered porosities, $\mathrm{\xi }$: 0.5, 0.6, 0.7, 0.8 and 0.9 on $\mathrm{\Delta }\mathrm{p}$ and Bejan number (${\mathit{Be}}_L$).

Effect of porosity on temperature rise, ${\mathit{Nu}}_a$, and Re.

It is customary to visualize the thermal dispersion of the air in the porous domain wrapped with electric heaters for Case-3. Fig. 9 shows the cross-sectional temperature contours across the length of porous domain of L/D = 12, at $\mathrm{\xi }$: 0.5, 0.6, 0.7, 0.8, and 0.9, respectively. The preheated air leaving the heat exchanger at 75 °C passes into the porous domain at ${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s at 6 bar. The illustrated contours witness a significant temperature rise in the porous field at each porosity case. The visuals reveal the gradual temperature upsurge from inlet to exit at $\mathrm{\xi }$: 0.5, 0.6, 0.7, 0.8, and 0.9. It is worth noting that the lateral temperature gradient is relatively higher adjacent to the pipe inlet. However, it moderates at the trailing end of the porous domain. The uniform temperature profile indicates the presence of porous media in the heating domain, which delays the air's residence time.

Fig. 9.

Cross-sectional temperature contours of porous domain for L/D 12 at pipe length 0 to 1.25 m.

Fig. 10 (a) shows the temperature increase across the pipe length, at 0 m (inlet), 0.25 m, 0.50 m, 0.75 m, 1 m, 1.25, and 1.50 m (outlet) for the porosities, $\mathrm{\xi }$= 0.5, 0.6, 0.7, 0.8, and 0.9. Maximum temperature appears at the exit of the porous domain as 103.4, 103.9, 104.7, 105.6, and 105.4 °C; at the porosities, $\mathrm{\xi }$ = 0.5, 0.6, 0.7, 0.8, and 0.9, respectively. A polynomial fit is found to be effective for the temperature with porosity of SiC ranging from 0.5 to 0.9, while the correlation coefficient is R² = 0.99. The Eq. (42) is valid for L/D = 12 and ${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s at 6 bar, where × is the domain’s axial length. The constants of corrilation are listed in Table 4 .

$$T_{\mathit{air}}=\alpha x^2+\beta x+\gamma ,$$ (42)

Fig. 10.

Effect of porosity on; (a) temperature variations across the porous domain, (b) average ${\mathit{Nu}}_a$ and Re across the porous domain (for Case 3).

Table 4.

Constants of the correlation $T_{\mathit{air}}=\alpha x^2+\beta x+\gamma ,$ at the variable porosities.

Constants	$\mathrm{\xi }=0.5$	0.6	0.7	0.8	0.9
$\alpha$	−1.440	−1.448	−1.265	−1.373	−1.554
$\beta$	11.84	11.92	11.66	12.43	12.91
$\gamma$	88.86	89.21	90.01	90.07	89.49

The effect of porosity on ${\mathit{Nu}}_a$ and Re is shown in Fig. 10 (b). Re dominates at the higher porosity due to increased superficial velocity of the fluid in the porous domain; however, it moderates towards low porosity. The maximum Re observed at $\mathrm{\xi }$ = 0.9 is 283.5, and the minimum is 157.5 at $\mathrm{\xi }$ = 0.5. Besides, the ${\mathit{Nu}}_a$ establishes heat transfer between the fluid and solid phases in a porous domain as a function of Re and Pr, as stated in Eq. (7). The present study illustrates the surface-averaged ${\mathit{Nu}}_a$ and finds it relatively analogous to the Re.

Thermal characterization of storage tanks

The computational analysis of ST-1 and ST-2 is pursued with transient and steady-state approaches to characterize the tank’s cooling through natural convection under ambient conditions. A pair of two storage tanks accomplishes significant cooling of the treated air and uphold uninterrupted supply by storing the air at 5 bar. Thermal analysis of the ST-1 and ST-2 reveals air outflow temperature $(T_{\mathit{air},out})$, exterior wall temperature $(T_{\mathit{outerwall}})$, and average temperature $(T_{\mathit{avg}})$, at the air mass flow of 0.44 and 0.22 kg/s, respectively. However, the simulations were initiated considering the storage tanks at P ₂ $\approx$ 5 bar and 27 °C.

Transient analysis

The time-dependent analysis aims to determine the minimum time lag for establishing the steady state of ST-1. Fig. 11, Fig. 12 exhibit the sliced temperature contours of ST-1 at 0.44 and 0.22 kg/s, respectively. The temperature graphics reveal a time-depend temperature escalation of ST-1, where the instantaneous $T_{\mathit{avg}}$ can be witnessed at progressive flow time (sec). It is observed that the treated air initially disperses in the inner annular region and avoids direct flow towards the tank’s outlet due to the separation by a baffle plate. However, it moves towards the separated passage after a certain period. The critical time to occur the steady-state of ST-1 is noticed 820 sec at peak load (${\dot{m}}_{\mathit{air}}$ = 0.44 kg/sec); however, it is 1145 sec at partial load (${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s).

Fig. 11.

Time-dependent temperature contours of ST-1 at peak load (${\dot{m}}_{\mathit{air}}=$0.44 kg/s).

Fig. 12.

Time-dependent temperature contours of ST-1 at partial load $({\dot{m}}_{\mathit{air}}=$0.22 kg/s).

Fig. 13 (a) and (b) show the escalation of the $T_{\mathit{avg}}$, $T_{\mathit{air},out}$, and $T_{\mathit{outerwall}}$ with increasing flow time (sec) at a variable mass flow rate. Initially, the temperature rise is more rapid due to the substantial temperature difference between the incoming and stored air in ST-1. However, it moderates with time as the tank’s temperature increases. The maximum $T_{\mathit{avg}}$, $T_{\mathit{air},out}$, and $T_{\mathit{outerwall}}$ are observed 56.78, 54.5, and 41.5 °C, at ${\dot{m}}_{\mathit{air}}=$ 0.44 kg/s and 54.7, 51.7, and 38.6 °C, at ${\dot{m}}_{\mathit{air}}=$ 0.22 kg/s, respectively.

Fig. 13.

A time-dependent temperature escalation in a primary storage tank (ST-1) at; (a) peak load (${\dot{m}}_{\mathit{air}}=$0.44 kg/s), (b) partial load (${\dot{m}}_{\mathit{air}}=$0.22 kg/s).

Steady-state analysis

The steady-state analysis presents the treated air's flow pattern and thermal dispersion inside ST-1 and ST-2 during the continual system operation. Fig. 14, Fig. 15 reveal the steady-state temperature contours of the storage tanks at variable air mass flow. The study found that ST-2 exit air temperature is firmly stable at 47.8 °C and 45.2 °C, respectively, at peak and partial load. It can be noted that doubling the air mass flow rate does not result in a significant difference in exit temperature.

Fig. 14.

Steady-state temperature contours of ST-1 and ST-2 at the peak load $({\dot{m}}_{\mathit{air}}=$0.44 kg/s).

Fig. 15.

Steady-state temperature contours of ST-1 and ST-2 at the partial load $({\dot{m}}_{\mathit{air}}=$0.22 kg/s).

In addition, Fig. 16 shows the thermal stability of the storage tanks in terms of constant $T_{\mathit{avg}}$, $T_{\mathit{air},out}$, and $T_{\mathit{outerwall}}$ at different load conditions. The illustrated temperatures indicate the energy balance of incoming and outgoing air in the tank's control volume. Interestingly, the inferior $T_{\mathit{outerwall}}$ signifies the excellent cooling performance of the storage tanks due to the exaggerated heat transfer to the surroundings through natural convection.

Fig. 16.

Steady-state temperature of ST-1 and ST-2 at; (a) peak load (${\dot{\mathbf{m}}}_{\mathbf{a}\mathbf{i}\mathbf{r}}=$ 0.44 kg/s), (b) partial load (${\dot{\mathbf{m}}}_{\mathbf{a}\mathbf{i}\mathbf{r}}=$ 0.22 kg/s).

Inclusive system performance

Conclusively, Fig. 17 states the comprehensive thermal characteristics of the proposed model, illustrating the temperature, pressure drop, and passing time of infected air through each stage of the disinfection process. Fig. 17 (a) illustrates the steady-state temperature variation in each stage of the heating and cooling section at variable ${\dot{m}}_{\mathit{air}}$. As can be observed, the air temperature does not appear to be affected much by the change in air mass flow. Accordingly, Fig. 17 (b) presents the cumulative and instantaneous air's pressure drop and passing time (calculated by Eq. (1)) in each component of the system at a constant mass flow of 0.44 kg/s. However, the air pressure remains constant (P C) in the decontamination chamber and storage tanks as they act as a reservoir of a fixed air mass.

Fig. 17.

Characteristics of air during the entire disinfection process (a) Variation of air temperature, (b) pressure drop and passing time.

The energy efficiency of the proposed system is evaluated based on individual component efficiency under different operational conditions, as shown in Fig. 18 . The efficiency of each relevant component is determined at the peak load (${\dot{\mathrm{m}}}_{\mathrm{a}\mathrm{i}\mathrm{r}}=$ 0.44 kg/s), considering a steady-state operation. The proposed system’s efficiency can be predicted by Eq. (42), where × signifies the fraction of utilized solar energy for air heating. The system's energy efficiency is noted at 37.4 % during the Day time operation (x = 1) for Case-1. However, for Case-2, the system's efficiency appears to be 91.1 % during the Night time operation (x = 0), where the electrical resistance heaters are entirely active with an electrical efficiency of 98 % [51]. However, during the intermediate time (Case-3), solar PTC and electrical heater will be active. Hence the energy efficiency exits between 37.4 and 91.1 % as × varies from 0 to 1.

$${\eta }_{\mathit{System}}={x\eta }_{\mathit{PTC}}\ast {(1-x)\eta }_{\mathit{EH}}\ast {\eta }_{\mathit{PD}}\ast {\eta }_{\mathit{DC}}\ast {\eta }_{\mathit{HE}}$$ (42)

Fig. 18.

Energy efficiency of the proposed system; (a) Case-1 (Day time operation) (b) Case-2 (Night time operation).

It is worth noting that the ${\eta }_{\mathit{System}}$ dominates in Case-2, while it is much less in Case-1. Despite this, the solar collector benefits the system with minimal running costs except for pumping power. However, the system’s running cost exists at a peak in Case-2. Besides, the space heating can be profited from the present model due to its ability to regulate temperature and airflow in the absence of airborne viruses. Instantaneous.

In the present study, an extended computational analysis is carried out at a constant ambient temperature of 27 °C. However, in actual perspective, the ambient temperature may exist higher or lower than the proposed temperature, depending on the weather conditions. Therefore, the air-cooler may remain non-operational in the deep winter at $T_{\mathit{amb}}$ $\approx$ 5–10 °C to ensure a comfortable temperature 30 °C. However, during the summer at $T_{\mathit{amb}}$ > 27 °C, the air cooler with forced convection cooling and hospital’s cooling arrangements can take care of additional cooling.

Conclusions

A porous-based heat treatment model is intended to abolish the airborne viruses in the air and deliver the treated air to a hospital ward at $30$°C and 1 bar. A simplified model comprises the heating and cooling sections to decontaminate airborne viruses and cool the high-temperature treated air. The heating section includes a solar PTC or electrical heaters and a decontamination chamber, while the cooling unit comprises storage tanks and an air cooler. A heat exchanger is incorporated to exchange the heat between hot and cold air streams.

A solar PTC is modeled to heat the air leaving HE during the sunny hours. The insulated porous domain provides an even temperature at the exit by offering a more excellent surface-to-volume ratio. However, the porous domain wrapped with the electrical heaters acts as an air heater during the night and intermediate operation.

The numerical analysis of the porous domain (L/D = 12) aims to establish optimal porosity, ensuring minimum pressure drop for Cases 1, 2, and 3. The pressure loss along the domain length ($\mathrm{\Delta }\mathrm{p}/\mathrm{L}$) exhibits an exponential trend with porosity and follows, $\mathrm{\Delta }\mathrm{p}/\mathrm{L}=C_1{e}^{C_2\mathrm{\xi }}$, with a correlation coefficient, R² = 0.99. Hence, the overhead observations find the porous domain’s optimal porosity of 0.9, owing to exit temperature > 105 °C with a minimal pressure drop of 5.16 kPa. The porous domain’s temperature analysis aims to establish optimum porosity, ensuring admirable thermal dispersion of infected air to mitigate airborne viruses. Temperatures across the pipe length from 0 to 1.5 m are noted for the porosities, $\mathrm{\xi }$= 0.5, 0.6, 0.7, 0.8, and 0.9, at ${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s. The computational outcomes reveal a polynomial fit for the temperature with porosity of SiC ranging from 0.5 to 0.9 for ${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s at 6 bar. The trends follow $T_{\mathit{air}}=\alpha x^2+\beta x+\gamma$ with the correlation coefficient is R² = 0.99.

The computational analysis of ST-1 and ST-2 is pursued with transient and steady-state approaches to characterize the tank’s cooling through natural convection under ambient conditions. A pair of two storage tanks aim to acquire significant cooling of the treated air and uphold uninterrupted supply by storing the air at 5 bar. The time-dependent analysis aims to determine the minimum time lag for establishing the steady-state natural cooling of ST-1. The critical time to occur the steady-state of ST-1 is noticed 820 sec at peak load (${\dot{m}}_{\mathit{air}}$ = 0.44 kg/s) and 1145 sec at partial load (${\dot{m}}_{\mathit{air}}$ = 0.22 kg/s).

The steady-state analysis presents the flow pattern and thermal dispersion of the treated air in ST-1 and ST-2 during the continual system operation. ST-2 exit air temperature is firmly stable at 47.8 °C and 45.2 °C, respectively, at peak and partial load. As noted, doubling the air mass flow rate does not result in a significant difference in exit temperature. Interestingly, the lower $T_{\mathit{outerwall}}$ signifies the excellent cooling performance of the storage tanks due to the exaggerated heat transfer to the surroundings through natural convection. A finned air-cooler of 6.02 m² surface area further cools the ST-2 exit air. Although, in deep winter ($T_{\mathit{amb}}$ $\approx$ 5–10 °C), the treated air will avoid the air-cooler. The system’s energy efficiency is noted 37.4 % and 91.1 % during the Day time (x = 1) and night time (x = 0) operation, respectively. However, during the intermediate time, the energy efficiency exits between 37.4 and 91.1 % as × varies from 0 to 1.

Besides, a massive scope exists to incorporate thermal energy storage systems to optimize the solar energy uses. A further analysis can be initiated to assess the effect of variable atmospheric temperature on the system performance.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.