Abstract
High-resolution functional MRI (fMRI) is largely hindered by random thermal noise. Random matrix theory (RMT)-based principal component analysis (PCA) is promising to reduce such noise in fMRI data. However, there is no consensus about the optimal strategy and practice in implementation. In this work, we propose a comprehensive RMT-based denoising method that consists of 1) rank and noise estimation based on a set of newly derived multiple criteria, and 2) optimal singular value shrinkage, with each module explained and implemented based on the RMT. By incorporating the variance stabilizing approach, the denoising method can deal with low signal-to-noise ratio (SNR) (such as <5) magnitude fMRI data with favorable performance compared to other state-of-the-art methods. Results from both simulation and in-vivo high-resolution fMRI data show that the proposed denoising method dramatically improves image restoration quality, promoting functional sensitivity at the same level of functional mapping blurring compared to existing denoising methods. Moreover, the denoising method can serve as a drop-in step in data preprocessing pipelines along with other procedures aimed at removal of structured physiological noises. We expect that the proposed denoising method will play an important role in leveraging high-quality, high-resolution task fMRI, which is desirable in many neuroscience and clinical applications.
Keywords: Functional magnetic resonance imaging (fMRI), image denoising, principal component analysis (PCA), random matrix theory (RMT), variance stabilizing transformation
I. Introduction
FUNCTIONAL magnetic resonance (MR) imaging (fMRI), an essential non-invasive neuroimaging tool for large field of view or whole brain functional studies, has been gaining a growing amount of interest since its inception [1]-[3]. Constant efforts have been made to conduct fMRI at submillimeter resolution to image fine-scale neural organizations of the brain. This has been mostly done at ultrahigh magnetic field (≥7 Tesla) to capitalize on the increased intrinsic signal-to-noise ratio (SNR) [4]. At ultrahigh magnetic field, submillimeter fMRI mapping is achievable, enabling studies on neural circuits at laminar and columnar scales [5]-[12]. However, at such high resolutions, SNR is substantially reduced in large part due to the reduced MR signal arising from the decreased image voxel size. This reduction in SNR in turn leads to a decrease in temporal SNR (tSNR), lowering the sensitivity for detecting the small signal change associated with neuronal activation.
One strategy to tackle the problem of low SNR is to reduce the dominating unstructured random thermal noise [13] by capitalizing on spatiotemporal redundancy embedded in high-resolution fMRI timeseries using the principal component analysis (PCA) [14]-[19]. The typical implementation of PCA is to identify the principal components that are associated with the signal and nullify the leftover noise components in the image reconstruction. The identification of noise components can be done by estimating the rank of the underlying noise-free signal matrix [20] and heuristic methods for rank estimation have been proposed in the context of fMRI denoising [16], [18]. More recently, rank estimation based on the random matrix theory (RMT) has also been presented and has drawn much attention.
RMT describes the behavior of noise and signal components in a sample matrix (assumed to be low rank) that can be approximated by the additive Gaussian model [21]. The covariance matrix of the sample matrix is shown to have eigenvalues that follow a distribution characterized by several signal spikes along with a noise bulk. Asymptotically, the noise bulk approaches a limiting distribution, the so called universal Marcenko-Pastur (MP) distribution [22], with its upper edge automatically setting a boundary between signal carrying components and noise components [23]. It is also shown that probabilistic bounds for the largest noise eigenvalue can be established for an arbitrary finite matrix size using a matrix perturbation approach [24]. Experimentally, Monte Carlo simulation can be performed to obtain the largest noise eigenvalue which can serve as a cutoff threshold for denoising measured data [25], [26]. However, these methods need extra noise measurements and intense computation. In contrast, Veraart et al. [27] developed a data-driven approach to estimate rank and noise based on the property of MP distribution. However, this approach is based on a single criterion that could sometimes underestimate the matrix rank and noise.
In addition to rank estimation, another critical problem regarding signal recovery from a noisy matrix is that the signal carrying eigenvalues and the corresponding eigenvectors are also corrupted by noise [21]. Two strategies have been proposed to address this problem: one aims to directly correct the leading eigenvectors associated with the signal carrying components [28]; the other attempts to shrink the leading eigenvalues to minimize the bias [29], with the shrinkage nonlinearity determined by the chosen loss function [30]. It has been shown that optimal shrinkage nonlinearities can be developed for various noise models other than the independent and identically distributed (i.i.d.) Gaussian noise [31].
Therefore, based on RMT, the optimal PCA-based denoising practice can be achieved by 1) accurately estimating the matrix rank, and 2) further reducing the bias in the signal components. In addition, an ideal algorithm could avoid extra noise measurement and associated computation. In this work, we propose such a well-grounded PCA-based denoising algorithm by 1) deriving a set of data-driven criteria based on the finite moment property of the generalized quarter circle law [32] for robust rank and noise estimation, and 2) shrinking the signal components with estimated rank and noise based on an optimal nonlinearity for the mean square error (MSE) loss function [30].
Note that the proposed PCA-based denoising algorithm assumes that the noisy images are Gaussian distributed, which applies to complex fMRI data. However, most fMRI data are stored in magnitude format, following a Rician distribution [33]. When SNR is low (e.g., SNR < 5), the magnitude fMRI data cannot be well approximated as Gaussian distribution. To deal with magnitude images, one possible solution is to convert Rician data to Gaussian-like data to minimize Rician bias, which can be achieved by the variance-stabilizing transformation (VST) [34]. The efficacy of VST has been demonstrated in denoising magnitude diffusion images [35].
In this work, we investigate how the proposed denoising algorithm can be used to improve image quality for high-resolution fMRI data and how VST can benefit low-SNR magnitude fMRI data. The effectiveness of the proposed denoising method is evaluated and demonstrated for both simulation data and in-vivo cat brain task fMRI data with the blood oxygenation level dependent (BOLD) contrast and with the cerebral blood volume (CBV) contrast. Our results for simulation data show that the proposed denoising method can achieve a performance comparable to and in some cases better than the denoising methods requiring extra noise measurement and calculation. The in-vivo results show that the proposed denoising method holds promise in replacing conventional Gaussian smoothing owing to its ability to enhance functional sensitivity and preserve sharpness in local activations at the same level of functional mapping blurring.
II. Theory
A. Random Matrix Theory (RMT)
Assume a sampled noisy m × n matrix Y formed by n samples or measurement of m observations (assume m ≤ n) can be modeled as Y = X + σN , where X is the underlying noise-free matrix with rank r ≪ m, N is the noise matrix with i.i.d. entries with zero mean, unit variance, and finite moments, and σ is the standard deviation of the noise. Matrix Y can be decomposed to a linear combination of singular values and singular vectors,
| (1) |
where si (for i = 1, 2,…, m) are individual singular values satisfying s1 > s2 > ⋯ > sm, ui and vi are the corresponding left and right singular vectors with a size of m × 1 and n × 1, respectively. Note that si in Eq. (1) has been scaled by for convenience [30]. According to RMT, three main phenomena related to the behavior of noise and signal components can be observed [21] and briefly described below:
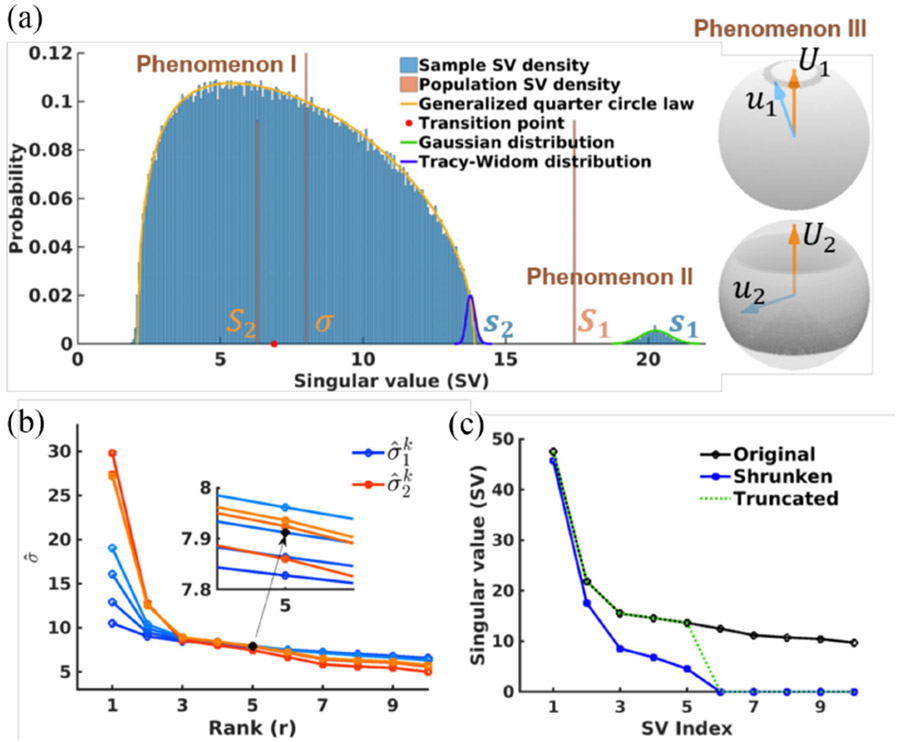
1). Noise Singular Value Dispersion (Phenomenon I):
The noise singular values si (for i = r + 1,…, m) are dispersed from σ in a certain range and their spectral measure almost surely converges to the generalized quarter circle distribution (as indicated by the yellow curve in Fig. 1(a)) as m, n → ∞ with :
| (2) |
where β is the asymptotic aspect ratio of the matrix, 1[s−, s+] is the indicator function when s is on the interval [s−, s+], and
| (3) |
are the bulk edges to which the extreme sample singular values converge. Note that in a finite condition (where m and n are finite), the largest noise singular value sr+1 fluctuates near the upper edge s+ as described by
| (4) |
where , and TWα (α = 1 for real and 2 for complex data) is the Tracy-Widom distribution [32] (as indicated by the blue curve in Fig. 1(a)).
Fig. 1.
(a) Random matrix theory in a nutshell. Three main phenomena can be observed: I. noise singular value (SV) dispersion (noise SVs asymptotically converge to the generalized quarter circle law); II. Signal SV bias (S1 v.s. s1 and S2 v.s. s2); III. Signal singular vector inconsistency (U1 v.s. u1 and U2 v.s. u2). Simulation details: matrix size = 300x165, rank = 2, additive Gaussian noise, 1000 trials. (b) Multiple criteria for effective rank and noise estimation. The true matrix rank is 5 and the estimated rank by multiple criteria is 5 whereas the estimated rank by single criteria may be smaller. Herein only k = 1, …, 4 are shown (in color changing from dark to light). (c) Optimal SV shrinkage for the mean square error (MSE) loss function. The original and truncated SV curves are also shown for comparison.
2). Signal Singular Value Bias (Phenomenon II):
The signal singular values are upward biased from their true values due to noise. Like the behavior of the largest noise singular value in the finite condition, signal singular values also fluctuate. Along appears a phase transition behavior depending on the relative strength of signal singular values to the noise standard deviation. Let Si, i ≤ r denote the noise-free singular values and define the transition point as St = β1/4 σ. For Si < St, the corresponding noise corrupted singular value si follows the same limiting Tracy-Widom distribution according to Eq. (4). For Si ≥ St [36], si follows a Gaussian distribution:
| (5) |
where stands for the normal distribution, sρ is the asymptotic location of si
| (6) |
and with α = 1 for a real and 2 for a complex matrix and , and with δ0 being the Dirac measure at s = 0. The green curve shown in Fig. 1(a) demonstrates this distribution that fits well with the sampled largest singular value as an example.
3). Signal Singular Vector Inconsistency (Phenomenon III):
In addition to the singular value bias, the noise corrupted signal singular vectors ui and vi deviate from their respective noise-free counterparts Ui and Vi (e.g., the right panel in Fig. 1(a)). Asymptotically, for Si > St the inner products between noise corrupted and noise free singular vectors are [36]
| (7) |
The smaller the noise-free singular value, the larger the angle between the noise corrupted and true singular vectors, and the less information about the true singular vector that can be decoded from the noise corrupted singular vector.
Therefore, to recover the noise-free matrix X from the noisy measurement Y, two important operations should be considered. First operation is to distinguish the signal singular values from the noise ones according to the dispersed but compact density distribution for noise described in Phenomenon I. Second operation is to nullify the recognized noise singular values and reduce the bias introduced to signal singular values and vectors as described by Phenomena II and III. Note that due to the phase transition behavior for signal components described in Phenomenon II, signal singular values that are smaller than the transition point cannot be distinguished from noise and thus will be removed together with noise. Next, we propose a well-grounded denoising algorithm incorporating the two operations described below.
B. RMT-Based Denoising Algorithm
The proposed algorithm includes the estimation of (effective) rank for the noise-free matrix and the reduction of bias for the signal components.
1). Rank Estimation:
According to RMT, the fluctuation of the signal singular values and the largest noise singular value poses a challenge to finding a fixed threshold to distinguish between signal and noise components. Ideally, the threshold should be set based on the relative strengths of the signal and noise singular values around the bulk edge. Veraart et al. provides such a way to determine the threshold based on a single criterion [27]. In this work, we will further show a series of criteria exist. The usage of multiple criteria to determine rank and the noise standard deviation can be more robust.
The criteria can be derived by appreciating the fact that the k-th moment of the generalized quarter circle distribution as described by Eq. (2) is bounded [37], i.e.,
| (8) |
where Ck is constant for given β and k with a complicated analytic form but can also be calculated numerically by letting σ = 1. Discretizing the left side of Eq. (8) and representing f(s) with the empirical singular value distribution (i.e., the probability measure) , where δsi is the Dirac measure at si, we have:
Therefore, the noise standard deviation can be estimated by
| (9) |
According to Eq. (3), σ can also be estimated by
| (10) |
Although both noise estimates converge at the true rank, they differ when rank estimation starts to deviate from the true value (Fig. 1(b)). Particularly, turns out to be more sensitive to rank estimation than , increasing more when the rank is underestimated and decreasing more when the rank is overestimated. Therefore, we can obtain the following multiple criteria for rank estimation:
| (11) |
Now, the rank estimation becomes a search of turnover points that first violate the above inequalities. The turnover point or the effective rank is found at R = max(r(k)), k = 1, 2, …, K, . Meanwhile, the standard deviation of the noise can also be estimated by taking the maximum of , i.e., . A similar strategy of rank estimation using two noise estimates is used in Veraart et al. [27].
2). Singular Value Shrinkage:
As the estimated effective rank R determines the cutoff between signal components and noise components (including signal that cannot be distinguished from noise), we can use it to identify and nullify the noise components. However, based on Phenomenon II and III in RMT, both signal singular values and vectors are biased from noise. Therefore, an optimal estimator for noise-free matrix X is the one with reduced bias in the signal components. Assume such an optimal estimator exists and can be written as
| (12) |
where η : [0, ∞) → [0, ∞) is the singular value shrinkage (SVS) nonlinearity. We need to find η so that the mean square error (MSE) between X and is minimum, i.e., . To achieve that goal, we can write the MSE explicitly as
When j ≠ i, the angle between uj(vj) and Ui(Vi) is asymptotically close to 90 degrees. Thus ⟨uj, Ui⟩ ≈ 0, ⟨vj, Vi⟩ ≈ 0, and
| (13) |
By differentiating the above function with respect to η and setting the derivative to 0 for each i = 1, …, R, we can get
In asymptotic conditions, replacing ⟨ui, Ui⟩ and ⟨vi, Vi⟩ with Eq. (7), and replacing Si by si → sρ from Eq. (6), we 2 have
| (14) |
where . By replacing η(si) in Eq. (12) with nopt(si), we can reconstruct the noise-free matrix X. Note that the derivation of Eq. (14) is simplified. A strict mathematical proof can be found in the literature [30]. Fig. 1(c) shows an example plot of Eq. (14) in a simulation with the true matrix rank being 5.
C. Rician Bias and Variance Stabilization Transformation
The proposed RMT-based denoising algorithm assumes that the noisy data are Gaussian distributed. In the context of fMRI, it can be applied directly to complex data. However, many fMRI data are in magnitude. A magnitude image can be modeled as:
| (15) |
where Y is the observed noisy image, X is the noise-free magnitude image, Nr, Ni are random variables with a normal distribution, i.e., Nr, , and σ is the standard deviation of the noise. Images with this mathematical form follow a Rician distribution [33]. Note that when the SNR , Ni, Y ≈ X + σNr, approximately following an additive Gaussian distribution. When SNR is low (such as ), however, the Gaussian approximation is no longer applicable and the variance of Y becomes strongly dependent on the unknown magnitude image X and its expectation deviates from X by a nonlinear function. These Rician biases render the denoising algorithms tailored for Gaussian data unsuitable for denoising Rician data.
One way to minimize the Rician bias is by using the variance-stabilization approach [34]. The general procedure of this approach includes: 1) noise estimation, 2) forward variance-stabilizing transformation (VST) that attempts to convert Rician data to Gaussian-like data, 3) denoising, and 4) exact unbiased inverse transformation (EUIVST) of the denoised data to estimate the noise-free signal. Two variance stabilizers, namely, “VST A” and “VST B”, are available that can be used to map a Rician random variable to new values. Both stabilizers are obtained by solving an optimization problem formulated to have a main term ensuring accuracy of variance stabilization together with a few penalty terms enabling properties needed for practical use of the stabilizer. The calculations of the “VST A” and “VST B” stabilizers differ in how those penalty terms are incorporated in the optimization (see more details in [34]). According to the behavior of the two stabilizers, “VST B” can be used in noise estimation and “VST A” can be used in the forward and inverse VST. The efficacy of the VST-based denoising framework has been demonstrated for denoising magnitude diffusion images [35]. In this work, we will further examine the performance and benefit of VST with the proposed RMT-based denoising algorithm on magnitude fMRI data.
III. Method
The proposed RMT-based denoising algorithm was tested on a simulation dataset and the in-vivo cat high-resolution fMRI data.
A. Simulation Experiment
Simulation data were generated from a 13 × 9 Shepp-Logan phantom with 212 repetitions to mimic a small fMRI data patch. Depending on the image intensity, voxels were assigned to time courses with varied signal changes and delays. Specifically, for areas with voxel intensity equal to 100, 40, 30, 20, the signal changes were 5%, 6%, 1%, 2%, respectively, and the response delays were 0, 1, 2, 4 time points, respectively. By flattening 27 the 3D data to a 2D matrix, we obtained the ground truth signal matrix with dimension 117 × 212 as shown in Fig. 2(a). After singular value decomposition, this matrix had a rank of four with singular values [355.98, 3.22, 1.17, 0.24]. The Gaussian data were created by adding Gaussian noise with std = 1, leading to tSNR ~5. Following Eq. (15), Rician data were also created.
Fig. 2.
(a) Simulation data generation based on a 13x9 Shepp-Logan phantom and time courses with varied signal changes and delays for each voxel intensity. The flattened 2D noise-free matrix has dimension 117x212 with a rank of 4. Noisy Gaussian data and Rician data were constructed to test denoising. (b) Implementation comparison between proposed method and three other RMT-based PCA denoising methods: MPPCA [27], SVS-Cordero [25], and NORDIC [26].
The proposed RMT-based denoising algorithm was then applied to the noisy data to restore the noise-free matrix. The 35 performance of the proposed method was compared with those of three existing RMT-based PCA denoising methods: MPPCA [27], SVS-Cordero [25], and NORDIC [26]. The differences in implementation between these methods are listed in Fig. 2(b). Three indices were used for quantitative comparison after 1000 40 trials: the estimated rank, the estimated noise std, and the MSE 141 between denoised matrix and ground truth matrix.
B. In-Vivo Cat Experiment
1). FMRI Data Acquisition:
In-vivo cat task Fmri data were acquired on a 9.4T, 31-cm-bore-sized animal scanner (Varian/VNMRJ, California), equipped with a gradient system capable of a maximum gradient strength of 400 mT/m and a maximum slew rate of 3000 T/m/s. A female cat (1.8 kg in weight) was scanned with a protocol approved by the University of Minnesota Institutional Animal Care and Use Committee (IACUC). The cat was initially anesthetized with ketamine and Xylazine cocktail (intramuscular injection), followed by administration of 0.8–1.1% isoflurane during the experiment. The cat was mechanically ventilated (Harvard Apparatus Inspira ASV) with a mixture gas comprising nitrous oxide and oxygen at a volume ratio of 6 to 4 (i.e., N2O:O2 = 6:4). The cat’s physiology including body temperature, respiration rate, and heart rate was monitored and controlled with care throughout the study. A surface RF loop coil of 1.5 cm in diameter was placed on the skull in the vicinity of the visual cortex to acquire fMRI data.
A block design paradigm was adopted to present a binocular full-field visual stimulation to the cat during the scan, with stimulation on for 15 seconds followed by stimulation off for 25 seconds and with a 20-second period inserted at the very beginning for baseline acquisition (20s-15s-25s-15s-25s). The visual stimulation was designed to present black and white square-wave gratings moving bi-directionally in 2D space with the gratings at 0 or 90 degrees (0.15 cycles/degree and 2 cycles/s).
The fMRI signals based on two types of imaging contrasts (BOLD; and CBV weighted CBVw) in response to the visual stimulation were collected using a 2D segmented GE-EPI sequence with the imaging parameters: repetition time (TR) = 2000 ms, echo time (TE) = 20 ms and 10 ms for BOLD and CBVw contrast, respectively, field of view (FOV) = 2.0 × 2.0 cm2, nominal RF pulse flip angle = 40°, in-plane resolution = 0.156 mm, slice thickness = 0.5 mm, 6 slices (coronal orientation), 4 segments, centric-out phase-encoding acquisition [38], bandwidth = 1953 Hz/pixel, and echo spacing = 0.74 ms. A total of 20 runs, each comprising 51 image volumes, were obtained for each fMRI contrast, leading to a total acquisition time of 77 min 20 sec. SNR on average was estimated to be ~8 for BOLD and ~5 for CBVw fMRI data, while tSNR on average was estimated to be ~6 for BOLD and ~3 for CBVw fMRI data.
2). FMRI Data Processing Pipeline:
The fMRI data processing pipeline utilized in the current study involved minimum successive processing modules (Fig. 3): 1) volume removal, 2) image denoising, 3) motion correction, and 4) general linear model (GLM) fitting. Four scenarios were considered in the image denoising module (second module): (a) no denoising when this module was skipped, (b) conventional Gaussian spatial smoothing, (c) MPPCA + Rician bias correction (MPPCA-RC) [38], [39] (not VST), and (d) VST + proposed denoising algorithm (VSTSVS). Note that due to the requirement of extra noise measurement, SVS-Cordero and NORDIC were not included for in-vivo comparison.
Fig. 3.
Flowchart for processing fMRI data including minimum preprocessing modules. The proposed VSTSVS denoising method consists of four steps: 1) noise estimation, 2) VST, 3) RMT-based PCA denoising (highlighted with 3 green boxes), and 4) exact unbiased inverse VST (EUIVST), all implemented using a patch process. Also shown are the corresponding image output for each step (right column).
In the third module of motion correction, rigid motion with six degrees of freedom (three translations and three rotations) was estimated and corrected. For improving correction accuracy, motion estimates obtained based on the denoised images with the VSTSVS method were utilized to correct for head motion in all cases.
In the final module of GLM fitting, the preprocessed data were used to fit a GLM [39] to obtain statistical estimates for generating BOLD and CBVw fMRI maps. The GLM utilized herein modeled the timeseries data at each voxel using the design matrix (representing the stimulation paradigm) and the two lowest-order polynomial regressors (accounting for low frequency drifting). For each contrast, all 20 fMRI runs were processed by denoising each run separately. The GLM fitting was applied to single run and to concatenated 20 runs.
The proposed VSTSVS method consisted of four steps as introduced in the previous session, all implemented using patch processing for improved performance [40]. Patch averaged data were used in VST whereas the central voxel of a denoised patch was kept after the proposed denoising method. The patch or window size was set to [11 11 3] voxels in VST and varied from 3 to 11 in steps of 2 for in-plane size for the proposed denoising method to study how denoising performance would change with patch sizes (the corresponding matrix dimension in denoising ranges from 27x51 to 363x51). For each patch size, the in-vivo fMRI data were also denoised on a run-by-run basis using both Gaussian smoothing and the MPPCA-RC approach for comparison.
In this work, the proposed VSTSVS method was implemented using MATLAB (The Mathworks Inc., Natick, MA). The source code can be found at https://github.com/zw1989/fmriDenoisingUsingRMT. The MPPCA denoising was fulfilled using the “dwidenoise” of MRtrix3 and specifying the option of a modified noise estimator [25]. Motion estimation was performed via SPM [41], and GLM fitting was conducted using GLMdenoise [42].
3). Denoising Performance Evaluation:
Two main metrics were utilized to quantify the functional sensitivity and functional specificity of the denoised timeseries with various window sizes. The functional sensitivity was measured by the functional contrast-to-noise ratio (fCNR), which was evaluated at each voxel by
| (16) |
where ΔS is the stimulus or task induced BOLD or CBVw signal change, and σt is the baseline std of the fMRI time course. fCNR then was averaged across an activation mask manually drawn on areas 17 and 18 of the cat visual cortex.
The functional specificity was characterized by the full width at half maximum (FWHM), i.e., the point spread function of the residual images after GLM. The overall FWHM values along three dimensions were evaluated by examining the autocorrelation of noise time courses across space. This was done by running the function “3dFWHMx” of AFNI [43], [44] upon the residual images (i.e., differences between the denoised timeseries and the GLM predicted timeseries). Note that as salt-and-pepper artifacts were observed in the residual images obtained from MPPCA-RC, the residual map were median filtered prior to FWHM evaluation to reduce the bias.
Finally, functional response maps (BOLD or CBVw percent change maps) were qualitatively evaluated with different denoising methods for single fMRI run and concatenated 20 runs. In either case, the percent change maps were displayed by setting a threshold at 1% with p-value < 0.05 (uncorrected).
IV. Results
A. Simulation Experiment
Fig. 4 reports the denoising performance comparison on the simulation data shown in Fig. 2(a) for the proposed RMT-based PCA denoising method (SVS-proposed) versus MPPCA, SVS-Cordero, NORDIC for data with additive Gaussian noise, data corrupted by Rician noise, and Rician noise corrupted data after variance stabilizing, respectively.
Fig. 4.
Denoising performance comparison among various RMT-based PCA denoising methods for (a) Gaussian data, (b) Rician data, (c) Rician data after variance stabilizing. Three indices are used for comparison: estimated rank (left panels), estimated noise (middle panels), and MSE between denoised matrix and noise-free matrix (right panels). Boxplots are used to show the statistics for 1000 trials with the black dot representing the mean value and red star representing the outliers. The dashed lines in the left and middle panels indicate the ground-truth matrix rank of 4 and the ground-truth noise std of 1, respectively.
In the case of Gaussian noise (Fig. 4(a)), the median of the estimated rank was 3 for all methods. This was reasonable because the fourth singular value of the noise-free matrix was 0.24, which was smaller than the transition point β1/4σ = 0.86. Therefore, the fourth component could not be distinguished from noise at asymptotic condition. However, this was not always true in the finite dimension case because of the fluctuation of the signal components and the largest noise component according to the RMT. Therefore, the mean values of the estimated rank were not identical for different methods, with 3.08, 3.03, 2.99, 3.16 for SVS-proposed (i.e., VSTSVS), MPPCA, SVS-Cordero, NORDIC, respectively. This result indicates the use of proposed multiple criteria for rank estimation led to more accurate results in some trials compared to the single criterion used in MPPCA, and close to or better than the performance of methods relying on the measured noise. As to noise estimation, except SVS-Cordero and NORDIC which measured noise, the five-number summary (the minimum value, the first quartile, the median, the third quartile, and the maximum value) was (0.979, 0.990, 0.993, 0.997, 1.008) for the proposed method, and (0.938, 0.962, 0.971, 0.980, 1.005) for MPPCA. The mean value for each case was close to the median. This indicates that the proposed method could estimate the noise std more accurately than that from MPPCA. When comparing MSE, two methods with singular value shrinkage (SVS-proposed and SVS-Cordero) led to smaller MSEs compared to the other two methods using singular value truncation.
In the case of Rician noise (Fig. 4(b)), the estimated ranks for data-driven methods (proposed VSTSVS and MPPCA) were generally larger than 4, indicating an overestimation of matrix rank, whereas for the other two methods, the median of the estimated rank was still 3. The average of the estimated noise for the proposed method was 0.92 whereas it was 0.87 for MPPCA. The measured MSEs were approximately 12 times larger than those in the case of Gaussian noise. Methods with singular value shrinkage still led to the smallest MSE.
When the Rician data was converted to be more Gaussian-like (Fig. 4(c)), the rank and noise estimation was improved for the proposed method and MPPCA. Compared to Rician results without VST, the MSEs were reduced by ~8-fold, reaching the same order of magnitude as those in the Gaussian noise case (although still ~50% larger).
B. In-Vivo Cat Experiment
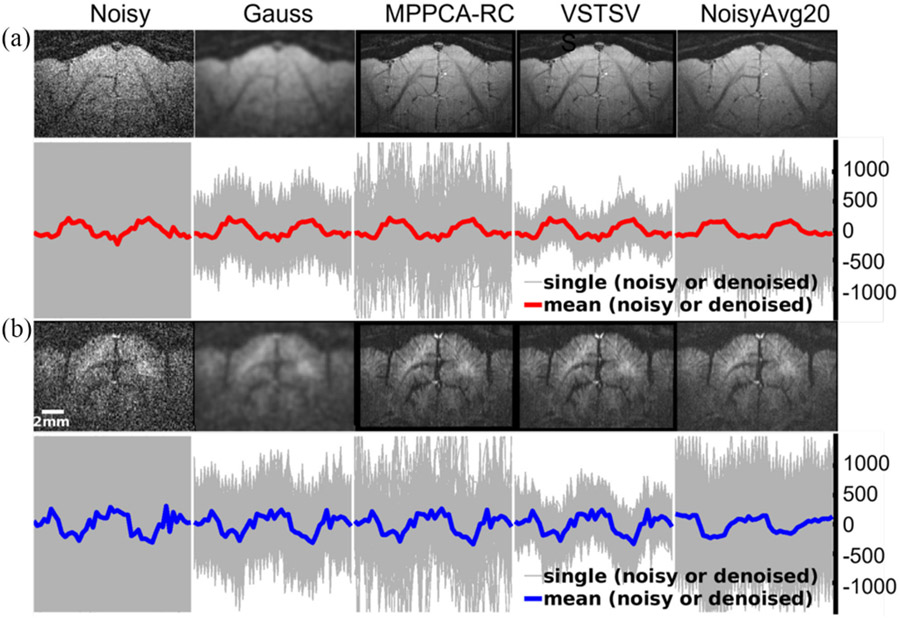
Fig. 5 shows that the use of VSTSVS to denoise high resolution low-SNR cat fMRI data substantially enhanced the image SNR, improving the image quality of a single run to a level visually comparable to that of 20 runs (or 20 averages) without denoising. Meanwhile, the use of VSTSVS improved the temporal characteristics of the time courses, leading to minimal variances between the voxel time courses of BOLD and CBVw signals across the visual cortex and enhanced tSNR. Although the image quality also improves dramatically by using the MPPCA-RC approach, the variance of single-run time courses was much larger compared to the use of VSTSVS. Specifically, the VSTSVS method reduced the variance of single-run time courses by ~49% relative to Gaussian smoothing and by ~33% relative to the MPPCA-RC approach. The reduced variance was found to be even substantially smaller than that of 20 runs without denoising (Fig. 5 right column). As no ground truth existed in the in-vivo data, high-resolution cat BOLD fMRI simulation experiment was further conducted to compare the performances of different denoising methods in terms of image recovery (see Supplementary Materials). The simulation results showed that the proposed VSTSVS method outperformed the Gaussian smoothing and MPPCA-RC approaches with increased peak signal-to-noise (PSNR) values across the entire range of noise levels and different window sizes under consideration (Fig. S3).
Fig. 5.
Denoising performance comparison for the proposed VSTSVS vs. Gaussian smoothing (Gauss) vs. MPPCA plus Rician bias correction (MPPCA-RC) in terms of image recovery and time course. Shown are images in a representative slice and time courses from voxels in the cat visual cortex with single run (first 4 columns) and averaged 20 runs (last column) for BOLD (a) and CBVw (b) based fMRI in vivo data. All three denoising methods in comparison were applied with a window size of 7 × 7 × 3. Note how the use of the proposed VSTSVS to denoise a single run resulted in image quality visually comparable to that of 20 averages without denoising, while leading to lower intensity variation in the voxel signal time courses than MPPCA-RC.
The proposed VSTSVS method outperformed Gaussian smoothing or the MPPCA-RC approach in enhancing functional sensitivity for BOLD (Fig. 6(a)) and CBVw contrast (Fig. 6(b)), increasing fCNR across the entire range of in-plane window sizes under consideration. At window size 7, for example, the averaged fCNR for BOLD was increased by about 73% relative to Gaussian smoothing, and by about 14% relative to MPPCA-RC. The numbers for CBVw were 64% and 14%, respectively. Visual examination of a representative fCNR map at window size 7 further confirmed that the proposed VSTSVS method gave rise to best fCNR inside the prescribed activation regions.
Fig. 6.
Denoising performance comparison in terms of functional contrast to noise ratio (fCNR) for (a) BOLD and (b) CBVw contrast averaged across the activation mask as a function of window size in voxel in the left panel and the comparison of BOLD fCNR vs CBVw fCNR maps in a representative slice at in-plane window size 7 in the right panel. The white contour indicates the activation mask in the slice. Note that for both BOLD and CBVw contrasts, the use of the proposed VSTSVS to denoise data yielded the highest fCNR values.
However, the proposed VSTSVS resulted in a larger FWHM or more blurring compared to Gaussian smoothing, about 29% at window size 7 for BOLD (Fig. 7(a)) and 37% for CBVw (Fig. 7(b)). This could be visually evaluated by examining the residual maps used for FWHM estimation. Note that MPPCA-RC was supposed to have a similar FWHM as VSTSVS based on the residual maps. Due to the “salt and pepper”-like patterns, a median filter was applied to the residual fMRI data processed using MPPCA-RC after GLM to reduce the bias otherwise they would introduce in FWHM estimation.
Fig. 7.
Denoising performance comparison in terms of full width at half maximum (FWHM) for (a) BOLD and (b) CBVw contrast as a function of window size in the left panel and comparison of residual maps in a representative slice used for FWHM estimation at in-plane window size 7. The green contour indicates the brain ROI with high SNR. For MPPCA-RC, the salt-and-pepper artifacts observed in the residual map were median filtered prior to FWHM evaluation to reduce the bias that they would otherwise introduce.
By drawing the fCNR as a function of FWHM, the fCNR gain for the VSTSVS method compared to other methods was apparent when the blurring degree (i.e., FHWM) was the same (Fig. 8). Quantitatively, the averaged fCNR was increased by about 20% for BOLD contrast and 12% for CBVw contrast compared to Gaussian smoothing. These numbers became larger when compared to MPPCA-RC (Fig. 8).
Fig. 8.
Denoising performance comparison in terms of fCNR as a function of FWHM for (a) BOLD and (b) CBVw contrast. Note that the use of the proposed VSTSVS gave rise to fCNR gains relative to other methods for the same level of blurring effect.
With matched blurring for Gaussian smoothing to that for RMT-based PCA methods at in-plane window size 7, functional percent change maps were further evaluated for single run and concatenated 20 runs (Fig. 9). Without denoising, percent change maps only showed meaningful information referring to brain activations with 20-run data. After denoising, the increase in functional sensitivity brought in higher activation detection rate even for single run but introduced blurring. However, for RMT-based PCA denoising, some local activation sharpness seemed to be preserved though the averaged blurring is the same as Gaussian smoothing. In addition, VSTSVS outperformed MPPCA-RC in keeping the fidelity of functional activity area without bringing in artifical activiations especially for single runs as indicated by the white arrows in Fig. 9. Further tests on the simulated high-resolution fMRI results also showed VSTSVS led to the highest PSNR of BOLD maps compared to Gaussian smoothing and MPPCA-RC (Fig. S4).
Fig. 9.
Denoising performance comparison in terms of functional percent change. Shown are BOLD (left) and CBVw (right) percent change maps for a representative slice overlaid on 20-run averaged EPI images. Percent change maps for Gaussian smoothing was chosen to have similar averaged FWHM as that for VSTSVS with window size [7 7 3]. RMT-based PCA denoising appeared to preserve sharpness at some local regions. Note that functional percent change maps using the MPPCA-RC introduced artifacts as indicated by the white arrows, especially for when using single runs.
To investigate how the use of a smaller window size may alleviate blurring, we denoised the data using a window size of [3 3 3]. The results (Fig. 10) showed that the activation patterns became sharper than when using a larger window size (Fig. 9).
Fig. 10.
BOLD (1st and 2nd rows) and CBVw (3rd and 4th rows) percent change maps for 3 representative slices obtained from 20-run noisy data (1st and 3rd rows). Denoised data (2nd and 4th rows) was obtained with the proposed VSTSVS using a smaller window size of [3 3 3] than Fig. 9.
V. Discussion
RMT-based PCA denoising has drawn much attention due to its robustness in removing non-structured noise. Several state-of-art algorithms have been proposed and applied to diffusion MRI [25]-[27], [35] and fMRI [45], [46]. However, there is still a lack of consensus about the optimal strategy and practice in implementation. In this work, we propose a multi-module PCA denoising algorithm specific to fMRI processing, with each module grounded on RMT. Meanwhile, this method is data-driven without requirement of extra noise measurement or large computation. We have demonstrated the effectiveness of the proposed method in denoising data corrupted by additive Gaussian noise (Fig. 4(a)). By synergistically combining the variance stabilizing approach [34], [35], we have also come up with a solution for denoising magnitude fMRI data with a low SNR (such as SNR<5) (Fig. 4(c), Figs. 5-9, S3, S4). Our results for in-vivo high-resolution cat fMRI data show that the proposed denoising methods holds promise in replacing conventional Gaussian smoothing due to the enhancement in functional sensitivity and the preservation in local activations.
Compared to existing RMT-based PCA denoising methods for rank and noise estimation, a data-driven noise and (effective) rank estimation algorithm is developed herein by incorporating a set of multiple criteria derived from the generalized quarter circle law (Eq. (2)) and its finite (all) moment property (Eq. (8)). We found that the use of multiple criteria (e.g., using moments up to 10) for rank and noise estimation can provide more accurate results (Fig. 4(a)) than the use of a single criterion as applied in the MPPCA approach in which only the second moment is used. For rank estimation of our data and results (Fig. S11) also suggest that the proposed method can outperform heuristic methods such as those based on Stein Unbiased Risk Estimators (SURE) [47]. The estimated rank and noise further facilitate bias reduction in signal singular values and vectors via the optimal singular value shrinkage function (Eq. (14)). The effectiveness of optimal singular value shrinkage can be appreciated by inspecting the fCNR and residual images (Figs. 6 and 7) where it helps eliminate the “salt and pepper” artifacts observed with the MPPCA approach in which singular value truncation is used. Note that the optimal shrinkage non-linearity is derived for additive i.i.d. Gaussian noise which is a special case among many other additive noise models [36]. For other possible noise models in MRI data [25], a more general yet complex algorithm other than the simple and explicit shrinkage nonlinearity used in this work should be adopted [31]. Extra tests of this algorithm on simulated and in-vivo fMRI data show comparable results in our case.
Our method is built based on asymptotic results assuming infinite matrix sizes. However, in reality the data matrix always has a finite size. To study the convergence to asymptotics, we conducted additional simulations, in which we explored how the empirical loss would approach the asymptotic loss when the matrix size increases. Our results (Fig. S7) show that the empirical loss overall appeared to approach the asymptotic loss as the matrix size increased. These results agree with what is reported in a previous study [30] showing that the empirical loss for a finite small matrix was close to the asymptotic loss.
The simulation presented in this study utilized data that were generated to reflect the typical range of signal changes in a real fMRI acquisition. The rank of 4 was obtained based on this simulation scenario. To investigate how our method would compare against other existing PCA based approaches for a different rank, we have conducted additional simulation by introducing 10 more ranks to the original Casorati matrix. Our results (Fig. S8) show that our method gave rise to 1) most accurate rank estimation, 2) estimated noise estimation close to the known noise standard deviation, and 3) smallest mean square error.
When dealing with magnitude fMRI data especially with low SNR as in the CBVw fMRI data collected in the cat experiment, variance stabilizing approach could improve the accuracy in terms of image recovery. It has been shown that VST could effectively remove the SNR dependence of the variance of the Rician data [34] by constructing a pair of forward and inverse stabilizers. However, potential artifacts could be introduced when the noise std in a voxel is overestimated so much that the intensity could be set to 0 during the inverse VST, causing false activations to occur if functional signal change from adjacent activated voxels leaks into that voxel after denoising. This false activation usually happens outside of the brain and can be masked out.
Like other PCA-based denoising approaches (e.g., MPPCA [27]), our denoising method is implemented to process patches rather than the whole brain. This is mainly because the neuronal response to the stimulation is localized and the fMRI data carrying redundant information about the functional response are locally low rank. Since our denoising method assumes that the noise-free data matrix is low rank, it makes more sense to apply our method to local patches than to the whole brain.
One may also perform patch processing in the time dimension by selecting a time window. However, this may not be favorable. Based on the random matrix theory, the singular values follow the Gaussian distribution or the Tracy-Widom distribution. The width of both distributions is inversely proportional to measurement number n. If a time window is selected, n decreases, and the fluctuation of the signal and noise components increases, leading to less accurate results. This is further confirmed by an additional simulation aimed at examining how the selection of a time window would impact the denoising performance of our method. Our results (Fig. S9) show that using a time window (to divide the entire timeseries into two data segments corresponding to resting state and activated state) appeared to reduce the denoising performance, leading to less accurate rank estimation and larger MSE than without using a time window.
Another important finding in this study is that PCA-based denoising itself may also introduce blurring (Figs. 7-9). However, the mechanism of this blurring is different from that of Gaussian smoothing. Gaussian smoothing is in fact a sliding Gaussian weighted window technique operated in spatial domain. Every voxel estimate is a weighted sum of the surrounding voxels, enhancing SNR but introducing blurring (Fig. 5). This spatial blurring then propagates to temporal domain and gives rise to time course correlation among adjacent voxels, which in turn leads to a blurred functional activation map. The blurriness depends on the window size or the FWHM of the Gaussian weighting function.
In contrast, PCA-based denoising can maintain the image sharpness in spatial domain (Fig. 5) but may introduce correlation in temporal domain, leading to an expansion of activation area or a smearing of activation signals. This is because PCA attempts to project data from a high-dimensional feature space to a low-dimensional subspace spanned by a few top principal components that account for most variances of the data. In fMRI data, those top principal components could represent the large transition patterns of the 1D structure profile flattened from the 3D structure image and/or the functional activation pattern across many voxels. In reality, the 3D structure image usually is stable and dominates the low rankness whereas the functional activation pattern is variable. Therefore, for a patch including both non-activation and activation voxels with various amplitudes, the number of noise-free singular values is large because the information is rich. However, the small singular values representing the small variations on the functional activation patterns among voxels could be buried in noise (such as the 4th singular values in the simulation data in Fig. 2(a) vs. the transition point β1/4σ). This information loss could lead to false voxel activation with small intensity change and/or activation amplitude smearing, resulting in a blurred activation map.
Due to the different blurring mechanism between Gaussian smoothing and PCA-based denoising, the use of the same window size would not lead to a similar level of blurring as evaluated by the FWHM estimated from the GLM residuals (Fig. 7). Assuming that FWHM values can be used to measure the neural activation extent, it is more straightforward to compare the denoising performances of the Gaussian smoothing against the proposed VSTSVS methods at the same FWHM. Our results (Fig. 8) reveal that the VSTSVS gives rise to higher functional sensitivity than Gaussian smoothing at a comparable level of blurring.
Is there a way to alleviate the blurring? The simplest solution is to use a window size as small as possible if the sensitivity permits (Fig. 10). The rationale of using a small window size fulfills the assumption hidden behind the PCA-based denoising methods: all voxels in the selected window or brain area have the same functional response. This assumption apparently is easier to be fulfilled when the window size is small. In addition, two other benefits follow when a small window size is used. First, the small window size drops the aspect ratio of the noisy matrix for denoising, reducing the fluctuation of the largest noise singular value (Eq. (4)) and the signal singular values (Eq. (6)). This could facilitate distinguishing signal components from noise ones. Second, the use of small window size also seems to alleviate the effect of Rician bias. Another solution for alleviating blurring from PCA-based methods is to perform denoising on voxels with similar functional activity patterns and amplitudes. This requires a prior knowledge or estimation of the nonlocal spatiotemporal characteristics of neural responses. This might be achieved by adopting the idea of non-local means [48] along the temporal dimension or by Gaussian process regress-based methods [49].
To study how our denoising method would compare to a non-PCA-based alternative, we devised another denoising approach based on the non-local means (NLM) filtering [48]. Specifically, the NLM filtering was applied to denoise two runs of cat fMRI data (one for BOLD and the other for CBV contrast). The results were compared to those obtained with the proposed method. The results (Fig. S10) show that the proposed method outperformed the NLM filtering, preserving fine brain structures (such as small vessels) in both BOLD and CBV weighted fMRI. This is in agreement with previous studies [27], [50], showing that a PCA-based method can yield better denoising performances than other non-PCA-based methods including the NLM filtering.
To study how the denoising performance of our method would be influenced by the misalignment of the fMRI volumes due to subject (or head) motion, we conducted additional simulation. Briefly, we synthesized a series of noisy fMRI data corrupted by various levels of motion, applied our pipelines to process the data, and evaluated how the denoising performance would change as a function of head motion. Our results (Fig. S6) show that the denoising performances decreased with increasing motion, leading to increased blurring in the image recovery and elevated error in BOLD activation estimation. Quantitatively, both image and BOLD PSNR values (in reference to noise-free motion-free data) decreased with increasing motion, the image PSNR being decreased by 18% and BOLD PSNR by 95% when motion increased by 120%. These results suggest that the motion should be kept as small as possible during data acquisition.
Although motion may pose a challenge to VSTSVS, we found VSTSVS can retain better image sharpness than Gaussian smoothing in the denoised images (Fig. 5), which can facilitate motion estimation and correction. We have performed further tests on motion parameter estimation based on data denoised with Gaussian smoothing and found that the use of the VSTSVS method provides the highest accuracy of motion estimation and correction, which in turn can facilitate GLM analysis and enhance the activation detection accuracy. The functional sensitivity gain for the proposed method permits less data repetitions or averaging and allows catching the dynamic changes of functional responses between fMRI runs (Fig. S5). Finally, the SVS denoising method as described in this article can be also applied to complex fMRI data.
When denoising magnitude fMRI data with the proposed method (i.e., VSTSVS), the image data should be Rician distributed. When performing parallel imaging using multiple RF coils for accelerated data acquisition, we recommend that the final magnitude image be obtained by taking the magnitude of a single composite complex-valued Gaussian image such that it is Rician distributed. The single composite complex-valued image can be reconstructed by using a SENSE-type algorithm [51] or by combining a GRAPPA-type interpolation [52] with an intelligent multi-channel combination method (e.g., spatial matched filtering [53] or SENSE-1 reconstruction [54]).
VI. Conclusion
We have proposed a multi-module PCA denoising algorithm with each module (rank and noise estimation, singular value shrinkage) explained and implemented based on the RMT. This method is data-driven without requirement of extra noise measurement or intensive computation. When synergistically combined with variance stabilizing approach, this method can deal with low SNR magnitude fMRI data with favorable performance. We have demonstrated the effectiveness of the proposed method in denoising both simulation data and in-vivo high-resolution cat fMRI data. The results show that the proposed denoising method (SVS for Gaussian data and VSTSVS for Rician data) offers several merits over other state of the art methods due to the enhanced functional sensitivity and the preserved sharpness in local activations.
Supplementary Material
Acknowledgment
The authors would like to thank Steen Moeller and Mehmet Akçakaya for their stimulating discussions on imaging denoising, Kendrick Kay for his valuable comments on fMRI analysis, and John Strupp and Brian Hanna for their assistance in setting up computation resources.
This work was supported by the NIH under Grants R01 MH111413, R01 NS118330, U01 EB026978, U01 EB025144, P41 EB027061, and P30 NS076408.
Contributor Information
Wei Zhu, Center for Magnetic Resonance Research (CMRR), Department of Radiology, University of Minnesota, USA..
Xiaodong Ma, Center for Magnetic Resonance Research (CMRR), Department of Radiology, University of Minnesota, USA..
Xiao-Hong Zhu, Center for Magnetic Resonance Research (CMRR), Department of Radiology, University of Minnesota, USA..
Kamil Ugurbil, Center for Magnetic Resonance Research (CMRR), Department of Radiology, University of Minnesota, USA..
Wei Chen, Center for Magnetic Resonance Research (CMRR), Department of Radiology, University of Minnesota, Minneapolis, MN 55455 USA.
Xiaoping Wu, Center for Magnetic Resonance Research (CMRR), Department of Radiology, University of Minnesota, USA..
References
- [1].Belliveau JW et al. , “Functional mapping of the human visual cortex by magnetic resonance imaging,” Science, vol. 254, no. 5032, pp. 716–719, Nov. 1991. [DOI] [PubMed] [Google Scholar]
- [2].Kwong KK et al. , “Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation,” Proc. Natl. Acad. Sci. USA, vol. 89, no. 12, pp. 5675–5679, Jun. 1992, doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Ogawa S et al. , “Intrinsic signal changes accompanying sensory stimulation: Functional brain mapping with magnetic resonance imaging,” Proc. Natl. Acad. Sci. USA, vol. 89, no. 13, pp. 5951–5955, Jul. 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Edelstein WA et al. , “The intrinsic signal-to-noise ratio in NMR imaging,” Magn. Reson. Med, vol. 3, no. 4, pp. 604–618, Aug. 1986, doi: 10.1002/mrm.1910030413. [DOI] [PubMed] [Google Scholar]
- [5].Menon RS et al. , “Ocular dominance in human V1 demonstrated by functional magnetic resonance imaging,” J. Neurophysiol, vol. 77, no. 5, pp. 2780–2787, May 1997. [DOI] [PubMed] [Google Scholar]
- [6].Yacoub E et al. , “Robust detection of ocular dominance columns in humans using hahn spin echo BOLD functional MRI at 7 tesla,” Neuroimage, vol. 37, no. 4, pp. 1161–1177, Oct. 2007, doi: 10.1016/j.neuroimage.2007.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Yacoub E, Harel N, and Ugurbil K, “High-field fMRI unveils orientation columns in humans,” Proc. Natl. Acad. Sci. USA, vol. 105, no. 30, pp. 10607–10612, Jul. 2008, doi: 10.1073/pnas.0804110105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Zhang NY et al. , “Functional MRI mapping neuronal inhibition and excitation at columnar level in human visual cortex,” Exp. Brain Res, vol. 204, no. 4,pp. 515–524, Aug. 2010, doi: 10.1007/s00221-010-2318-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Zhang N et al. , “High-resolution fMRI mapping of ocular dominance layers in cat lateral geniculate nucleus,” Neuroimage, vol. 50, no. 4, pp. 1456–1463, May 2010, doi: 10.1016/j.neuroimage.2010.01.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Goense J, Bohraus Y, and Logothetis NK, “fMRI at high spatial resolution: Implications for BOLD-models,” Front. Comput. Neurosci, vol. 10, p. 66, Jun. 2016, doi: ARTN66 10.3389/fncom.2016.00066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Vu AT et al. , “Tradeoffs in pushing the spatial resolution of fMRI for the 7T human connectome project,” Neuroimage, vol. 154, pp. 23–32, Jul. 2017, doi: 10.1016/j.neuroimage.2016.11.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Polimeni JR et al. , “Analysis strategies for high-resolution UHF-fMRI data,” Neuroimage, vol. 168, pp. 296–320, Mar. 2018, doi: 10.1016/j.neuroimage.2017.04.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Liu TT, “Noise contributions to the fMRI signal: An overview,” Neuroimage, vol. 143, pp. 141–151, Dec. 2016, doi: 10.1016/j.neuroimage.2016.09.008. [DOI] [PubMed] [Google Scholar]
- [14].Mitra PP et al. , “The nature of spatiotemporal changes in cerebral hemodynamics as manifested in functional magnetic resonance imaging,” Magn. Reson. Med, vol. 37, no. 4, pp. 511–518, Apr. 1997, doi: 10.1002/mrm.1910370407. [DOI] [PubMed] [Google Scholar]
- [15].Hansen LK et al. , “Generalizable patterns in neuroimaging: How many principal components?,” Neuroimage, vol. 9, no. 5, pp. 534–544, May 1999, doi: 10.1006/nimg.1998.0425. [DOI] [PubMed] [Google Scholar]
- [16].Thomas CG, Harshman RA, and Menon RS, “Noise reduction in BOLD-based fMRI using component analysis,” Neuroimage, vol. 17, no. 3, pp. 1521–1537, Nov. 2002, doi: 10.1006/nimg.2002.1200. [DOI] [PubMed] [Google Scholar]
- [17].T. A. Calhoun VD et al. , “ICA of functional mri data: An overview,” in Proc. 4th Int. Symp. Independent Compon. Anal. Blind Signal Separation, 2003, pp. 281–188. [Google Scholar]
- [18].Soltysik DA et al. , “Improving the use of principal component analysis to reduce physiological noise and motion artifacts to increase the sensitivity of task-based fMRI,” J. Neurosci. Methods, vol. 241, pp. 18–29, Feb. 2015, doi: 10.1016/j.jneumeth.2014.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Jolliffe IT and Cadima J, “Principal component analysis: A review and recent developments,” Philos. Trans. Roy. Soc. A, vol. 374, no. 2065, Apr. 2016, doi: 10.1098/rsta.2015.0202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Ulfarsson MO and Solo V, “Dimension estimation in noisy PCA with SURE and random matrix theory,” IEEE Trans. Signal Process, vol. 56, no. 12, pp. 5804–5816, Dec. 2008, doi: 10.1109/Tsp.2008.2005865. [DOI] [Google Scholar]
- [21].Johnstone IM and Paul D, “PCA in high dimensions: An orientation,” in Proc. IEEE Inst. Elect. Electron. Eng, Aug. 2018, vol. 106, no. 8, pp. 1277–1292, doi: 10.1109/JPROC.2018.2846730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Marchenko VA and Pastur LA, “Distribution of eigenvalues for some sets of random matrices,” Matematicheskii Sbornik, vol. 114, no. 4, pp. 507–536, 1967. [Google Scholar]
- [23].Johnstone IM, “On the distribution of the largest eigenvalue in principal components analysis,” Ann. Statist, vol. 29, no. 2, pp. 295–327, Apr. 2001, doi: 10.1214/aos/1009210544. [DOI] [Google Scholar]
- [24].Nadler B, “Finite sample approximation results for principal component analysis: A matrix perturbation approach,” Ann. Statist, vol. 36, no. 6, pp. 2791–2817, Dec. 2008, doi: 10.1214/08-Aos618. [DOI] [Google Scholar]
- [25].Cordero-Grande L et al. , “Complex diffusion-weighted image estimation via matrix recovery under general noise models,” Neuroimage, vol. 200, pp. 391–404, Oct. 2019, doi: 10.1016/j.neuroimage.2019.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Moeller S et al. , “NOise reduction with DIstribution corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing,” Neuroimage, Nov. 2020, Art. no. 117539, doi: 10.1016/j.neuroimage.2020.117539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Veraart J et al. , “Denoising of diffusion MRI using random matrix theory,” Neuroimage, vol. 142, pp. 384–396, Nov. 2016, doi: 10.1016/j.neuroimage.2016.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Johnstone IM and Lu AY, “On consistency and sparsity for principal components analysis in high dimensions rejoinder,” J. Amer. Stat. Assoc, vol. 104, no. 486, pp. 701–703, Jun. 2009, doi: 10.1198/jasa.2009.0158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Donoho DL, Gavish M, and Johnstone IM, “Optimal shrinkage of eigenvalues in the spiked covariance model,” Ann. Statist, vol. 46, no. 4, pp. 1742–1778, Aug. 2018, doi: 10.1214/17-AOS1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Gavish M and Donoho DL, “Optimal shrinkage of singular values,” IEEE Trans. Inform. Theory, vol. 63, no. 4, pp. 2137–2152, Apr. 2017, doi: 10.1109/Tit.2017.2653801. [DOI] [Google Scholar]
- [31].Nadakuditi RR, “OptShrink: An algorithm for improved low-rank signal matrix denoising by optimal, data-driven singular value shrinkage,” IEEE Trans. Inform. Theory, vol. 60, no. 5, pp. 3002–3018, May 2014, doi: 10.1109/Tit.2014.2311661. [DOI] [Google Scholar]
- [32].Edelman A, Sutton BD, and Wang YY, “Random matrix theory, numerical computation and applications,” in Proc. Symp. Appl, 2014, vol. 72, pp. 53–82, doi: 10.1090/psapm/072/00614. [DOI] [Google Scholar]
- [33].Gudbjartsson H and Patz S, “The rician distribution of noisy MRI data,” Magn. Reson. Med, vol. 34, no. 6, pp. 910–914, Dec. 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Foi A, “Noise estimation and removal in mr imaging: The variance-stabilization approach,” in Proc. 8th IEEE Int. Symp. Biomed. Imag.: From Nano Macro, 2011, pp. 1809–1814. [Online]. Available: <Go to ISI>: //WOS:000298849400413 [Google Scholar]
- [35].Ma X, Ugurbil K, and Wu X, “Denoise magnitude diffusion magnetic resonance images via variance-stabilizing transformation and optimal singular-value manipulation,” Neuroimage, vol. 215, Apr. 2020, Art. no. 116852, doi: 10.1016/j.neuroimage.2020.116852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Benaych-Georges F and Nadakuditi RR, “The singular values and vectors of low rank perturbations of large rectangular random matrices,” J. Multivariate Anal, vol. 111, pp. 120–135, Oct. 2012, doi: 10.1016/j.jmva.2012.04.019. [DOI] [Google Scholar]
- [37].Capitaine M and Casalis M, “Asymptotic freeness by generalized moments for gaussian and wishart matrices. Application to beta random matrices,” Indiana Univ. Math. J, vol. 53, no. 2, pp. 397–431, 2004, doi: 10.1512/iumj.2004.53.2325. [DOI] [Google Scholar]
- [38].Ades-Aron B et al. , “Evaluation of the accuracy and precision of the diffusion parameter EStImation with gibbs and NoisE removal pipeline,” Neuroimage, vol. 183, pp. 532–543, Dec. 2018, doi: 10.1016/j.neuroimage.2018.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Koay CG and Basser PJ, “Analytically exact correction scheme for signal extraction from noisy magnitude MR signals,” J. Magn. Reson, vol. 179, no. 2, pp. 317–322, Apr. 2006, doi: 10.1016/j.jmr.2006.01.016. [DOI] [PubMed] [Google Scholar]
- [40].Katkovnik V et al. , “From local kernel to nonlocal multiple-model image denoising,” Int. J. Comput. Vis, vol. 86, no. 1, pp. 1–32, 2009, doi: 10.1007/s11263-009-0272-7. [DOI] [Google Scholar]
- [41].Friston KJ et al. , “Movement-related effects in fMRI timeseries,” Magn. Reson. Med, vol. 35, no. 3, pp. 346–355, Mar. 1996, doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- [42].Kay KN et al. , “GLMdenoise: A fast, automated technique for denoising task-based fMRI data,” Front. Neurosci, vol. 7, 2013, Art. no. 247, doi: 10.3389/fnins.2013.00247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Cox RW et al. , “fMRI clustering and false-positive rates,” Proc. Natl. Acad. Sci. USA, vol. 114, no. 17, pp.E3370–E3371, Apr. 2017, doi: 10.1073/pnas.1614961114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Cox RW et al. , “FMRI clustering in AFNI: False-positive rates redux,” Brain Connect, vol. 7, no. 3, pp. 152–171, Apr. 2017, doi: 10.1089/brain.2016.0475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Adhikari BM et al. , “A resting state fMRI analysis pipeline for pooling inference across diverse cohorts: An ENIGMA rs-fMRI protocol,” Brain Imag. Behav, vol. 13, no. 5, pp. 1453–1467, Oct. 2019, doi: 10.1007/s11682-018-9941-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Ades-Aron B et al. , “Improved task-based functional MRI language mapping in patients with brain tumors through Marchenko-Pastur principal component analysis denoising,” Radiology, vol. 298, no. 2, pp. 365–373, Feb. 2021, doi: 10.1148/radiol.2020200822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Ramani S, Blu T, and Unser M, “Monte-Carlo sure: A black-box optimization of regularization parameters for general denoising algorithms,” IEEE Trans. Image Process, vol. 17, no. 9, pp. 1540–1554, Sep. 2008, doi: 10.1109/Tip.2008.2001404. [DOI] [PubMed] [Google Scholar]
- [48].Buades A, Coll B, and Morel JM, “A non-local algorithm for image denoising,” in Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit, 2005, pp. 60–65. [Google Scholar]
- [49].Strappini F et al. , “Adaptive smoothing based on gaussian processes regression increases the sensitivity and specificity of fMRI data,” Hum. Brain Mapp, vol. 38, no. 3, pp. 1438–1459, Mar. 2017, doi: 10.1002/hbm.23464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Manjon JV et al. , “Diffusion weighted image denoising using over-complete local PCA,” Plos One, vol. 8, no. 9, Sep. 2013, doi: ARTNe73021 10.1371/journal.pone.0073021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Pruessmann KP et al. , “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med, vol. 42, no. 5, pp. 952–962, Nov. 1999. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/10542355 [PubMed] [Google Scholar]
- [52].Griswold MA et al. , “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn. Reson. Med, vol. 47, no. 6, pp. 1202–1210, Jun. 2002, doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- [53].Roemer PB et al. , “The NMR phased array,” Magn. Reson. Med, vol. 16, no. 2, pp. 192–225, Nov. 1990, doi: 10.1002/mrm.1910160203. [DOI] [PubMed] [Google Scholar]
- [54].Sotiropoulos SN et al. , “Effects of image reconstruction on fiber orientation mapping from multichannel diffusion MRI: Reducing the noise floor using SENSE,” Magn. Reson. Med, vol. 70, no. 6, pp. 1682–1689, Dec. 2013, doi: 10.1002/mrm.24623. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.