Dynamic finite element analyses to compare the influences of customised total talar replacement and total ankle arthroplasty on foot biomechanics during gait

Abstract

Objective, Total talar replacement (TTR) using a customised talus prosthesis is an emerging surgical alternative to conventional total ankle arthroplasty (TAA) for treating ankle problems. Upon satisfying clinical reports in the literature, this study explored the advantages of TTR in restoring foot biomechanics during walking compared with TAA through computational simulations.

Methods, A dynamic finite element foot model was built from the MRIs of a healthy participant and modified into two implanted counterparts (TTR and TAA) by incorporating the corresponding prosthetic components into the ankle joint. Twenty bony parts, thirty-nine ligament/tendon units, nine muscle contractors, and bulk soft tissue were included in the intact foot model. The TTR prosthesis was reconstructed from the mirror image data of the participant's contralateral talus and the TAA prosthesis was modelled by reproducing the Scandinavian ankle replacement procedure in the model assembly. The model was meshed with explicit deformable elements and validated against existing experimental studies that have assessed specific walking scenarios. Simulations were performed using the boundary conditions (time-variant matrix of muscle forces, segment orientation, and ground reaction forces) derived from motion capture analyses and musculoskeletal modelling of the participant's walking gait. Outcome variables, including foot kinematics, joint loading, and plantar pressure were reported and compared among the three model conditions.

Results

Linear regression indicated a better agreement between the TTR model and intact foot model in plots of joint motions and foot segment movements during walking (R² ​= ​0.721–0.993) than between the TAA and intact foot (R² ​= ​0.623–0.990). TAA reduced talocrural excursion by 21.36%–31.92% and increased (MTP) dorsiflexion by 3.03%. Compared with the intact foot, TTR and TAA increased the midtarsal joint contact force by 17.92% and 10.73% respectively. The proximal-to-distal force transmission within the midfoot was shifted to the lateral column in TTR (94.52% or 210.54 ​N higher) while concentrated on the medial column in TAA (41.58% or 27.55 ​N higher). The TTR produced a plantar pressure map similar to that of the intact foot. TAA caused the plantar pressure centre to drift medially and increased the peak forefoot pressure by 7.36% in the late stance.

Conclusion

The TTR better reproduced the foot joint motions, segment movements, and plantar pressure map of an intact foot during walking. TAA reduced ankle mobility while increasing movement of the adjacent joints and forefoot plantar pressure. Both implant methods changed force transmission within the midfoot during gait progression.

The translational potential of this article Our work is one of the few to report foot segment movements and the internal loading status of implanted ankles during a dynamic locomotion task. These outcomes partially support the conjecture that TTR is a prospective surgical alternative for pathological ankles from a biomechanical perspective. This study paves the way for further clinical investigations and systematic statistics to confirm the effects of TTR on functional joint recovery.

1. Introduction

The ankle joint is uniquely complex in anatomy because it is formed by compound articulations of the talocrural, distal tibiofibular, and subtalar joints [1]. The talar surface of the ankle joint is the essential part of the fibro-osseous connection between the lower leg and foot, which underpins ankle stability and mobility [1]. Owing to its precarious arterial infiltration [2], the ankle joint is susceptible to degenerative pathologies secondary to trauma, such as osteoarthritis and avascular osteonecrosis [3,4]. Treatments for advanced ankle pathologies are mainly surgical and remain challenging because optimal surgical protocols are still debatable.

Total ankle arthroplasty (TAA) is widely considered one of the standard treatment methods for late-stage ankle diseases [5]. Conventional TAA resurfaces both sides of the articulation with metals, which slide on a layer of weight-bearing polyethylene to enable joint motions. Despite its positive effects on gait improvements [6,7], TAA is frequently associated with postoperative complications such as size mismatch and implant loosening [8]. A key explanation for this problem is that TAA components are usually prefabricated with fixed-size stratification and built-in motion axes [9], which do not tally with the individualised joint anatomies and complex ankle movements.

Along with the increasing application of 3D printing techniques in clinics, total talar replacement (TTR) using customised prostheses has resurged as the next treatment option for many ankle diseases, such as talus osteonecrosis and ankle arthritis [4,10]. A customised talus prosthesis accounts for individual-specific anatomies in its geometries and is, therefore, more likely to articulate with the adjacent joint surface, which is anticipated to better consolidate the joint structure and fulfil ankle function [11]. Recently, a growing body of clinical studies has reported positive outcomes for TTR treatment [[10], [11], [12], [13], [14], [15], [16], [17], [18]]. Despite the varying design, TTR exhibited consistent performance in regaining ankle mobility [10,11,15,17], easing pain [10,13,15], and improving life quality [10,15]. Plausibly, TTR has certain advantages over conventional TAA.

Currently, there is a scarcity of studies comparing the clinical outcomes of TTR and TAA. Differences between the two surgical approaches stem from foot biomechanics during locomotion. This explains the motion-force linkage underlying ankle function but is not well documented for TTR. Previous studies have shown that computational simulation is robust in assessing the internal foot deformation/stress during gait, which is normally less accessible using conventional measurement methods without invasive procedures [19]. Therefore, we established finite element models of an intact foot and two implanted feet to compare the effects of customised TTR and TAA on foot biomechanics during walking. The outcome variables included the ankle/MTP joint angle, foot arch deformation, joint contact force, plantar fascia tensile force, and plantar pressure. The TAA condition was represented by creating a set of prefabricated Scandinavian TAA components [20] in the foot model assembly. The TTR customisation procedure was mimicked by reconstructing a model part of the talar prosthesis from the mirror image data of the contralateral ankle site, which is a common practice in clinical studies in the related field [12,14,21]. Because a growing body of evidence indicated that a prosthesis design with a higher approximation to the native ankle anatomy facilitates the restoration of ankle functions [[21], [22], [23]], we hypothesised that TTR would better reproduce the foot kinematics and force distribution of an intact foot than would TAA. TTR improved ankle motions and reduced foot arch deformation/loadings to the foot segments compared to TAA.

2. Materials and methods

2.1. Participant

A healthy male (age: 33 years old, height: 171 ​cm, weight: 65 ​kg) volunteered for this study. He reported no lower limb injuries or cardiopulmonary conditions that would affect walking performance at the time of entry. The participant had normal foot morphology, with a foot arch index of 0.277 [24], a foot posture index of 2 [25], and a first intermetatarsal angle of 9.8°. The participant underwent two data collection sessions: MRI scanning of his feet to produce the foot model geometries and a walking trial to acquire his gait data. The latter were processed to generate boundary conditions for the finite element analyses. This study was approved by the University Human Subject Ethics Committee (reference number: HSEARS20201223001). The participant was fully informed of the experimental procedures and signed an informed consent form.

2.2. Experiments and motion data reduction

To facilitate the tracking of body movements, a set of retroreflective markers was attached to the participant at selected anatomic landmarks using an established protocol [26]. After ample warm-up and familiarisation with the experimental environment, the participant performed walking trials along a walkway where two force platforms (OR6, AMTI, Watertown, NY, USA) were mounted to measure the ground reaction force at a frequency of 1000 ​Hz. Walking speed was self-selected (1.25 ​m/s) by the participant and monitored using two photocells placed at the two ends of the walkway. The walking trials were repeated several times until a set of valid gait data was acquired. The gait data were valid when the participant's actual walking speed was within 5% variation of the selected value and his footsteps fell within the region of the force platforms. The marker trajectories were captured by eight optical cameras (T20, Vicon Motion Systems Ltd., Oxford, UK) sampling at 200 ​Hz.

A general OpenSim 2392 model (version 4.1, National Center for Simulation in Rehabilitation Research, Stanford, USA) was used to process gait data [27]. Model scaling was performed to accommodate subject-specific anthropometries (Fig. 1A). Inverse kinematics and dynamics were then solved sequentially on the walking data to generate a solution of joint coordinates and joint moments that best reproduced the movement patterns. The best solution was defined as the minimum sum errors between the experimental coordinate values and coordinate values computed by simulation [27]. The algorithm was built in OpenSim and executed along with the simulation steps. Forward dynamics were then implemented to calculate muscle activation. The time series of segment kinematics, lower leg muscle forces, and ground reaction forces were prepared after this session for the subsequent finite element analyses.

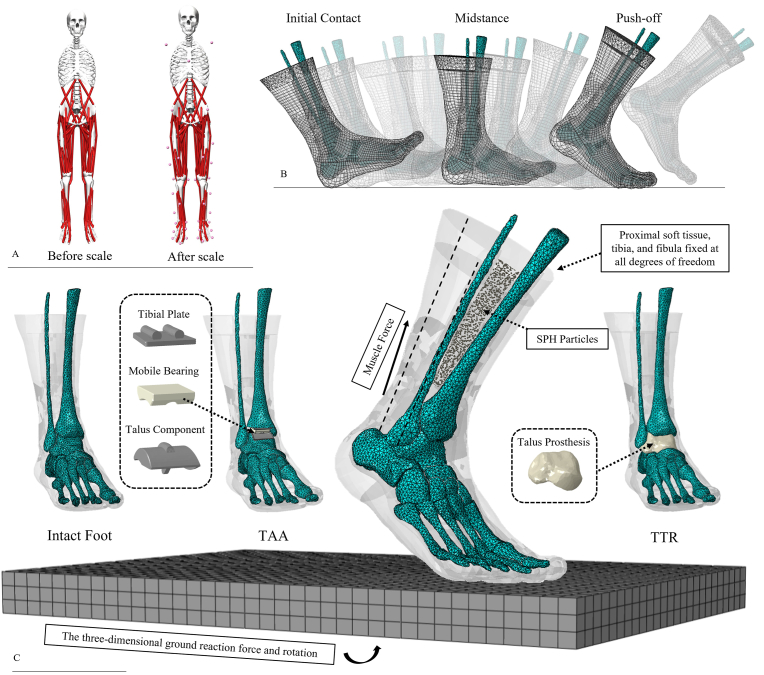
Fig. 1.

A) Subject-specific scaling of the musculoskeletal model; B) Simulation of the walking gait; C) Configurations of the three models and loading/boundary conditions for the finite element analyses. SPH: smoothed-particle hydrodynamics; TTR: total talus replacement; TAA: total ankle arthroplasty.

2.3. Finite element modelling

2.3.1. Geometry reconstruction (the intact foot)

MRI scanning (3.0T Trio TIM, SIEMENS, München, Germany) of the participant's feet was performed based on an established protocol [26]. In this study, the participant's right foot was selected for modelling. In total, 20 bones (inter-phalangeal joints of the second to fifth digits were merged for a simplification purpose) and the encapsulated bulk soft tissue were segmented and reconstructed using Mimics and 3-Matic (version 19.0, Materialise, Leuven, Belgium). Bulk soft tissue was modelled as smoothed-particle hydrodynamics (SPH) particles encapsulated in a shell unit of the skin based on an established method [26]. The SPH method was adopted owing to its robustness in solving high-impact problems and large structural deformation during foot-ground contact. Ligaments, plantar fascia, and extrinsic and intrinsic foot muscles were built using one-dimensional truss or slip-ring connectors. Their paths and attachments were determined based on MRIs and the human anatomy atlas [26]. The effects of the cartilage were mimicked by frictionless and nonlinear contact behaviour [26]. The coefficient of friction between the foot and ground plate was 0.6 [28].

2.4. Geometry reconstruction (TAA and TTR conditions)

A three-component ankle prosthesis (STAR ankle, Scandinavian Total Ankle Replacement) was selected to represent the TAA condition (Fig. 1C). The configuration and installation of the prosthesis were based on a study by Wang et al. [20]. The sizes of the prosthesis components (tibial plate: 32 ​mm ​× ​30 ​mm, talar component: 30 ​mm ​× ​31 ​mm) were selected according to the manufacturer's guidelines [29].

The TTR condition was simulated by replacing the talus with a prosthesis reconstructed from the mirror image data of the participant's left talus [12,14]. The talus prosthesis was assigned with the material property of cobalt-chromium and slightly polished to mimic the 3D printing texture (Fig. 1C). The major ligaments connecting the talus to adjacent segments on the anterior aspect were detached to represent the effects of surgical dissection [12,17]. A “surface-to-surface” contact property with a friction coefficient of 0.06 was assigned to the contacts between TAA components and contacts between the TTR prosthesis and adjacent bones [20].

2.5. Meshing

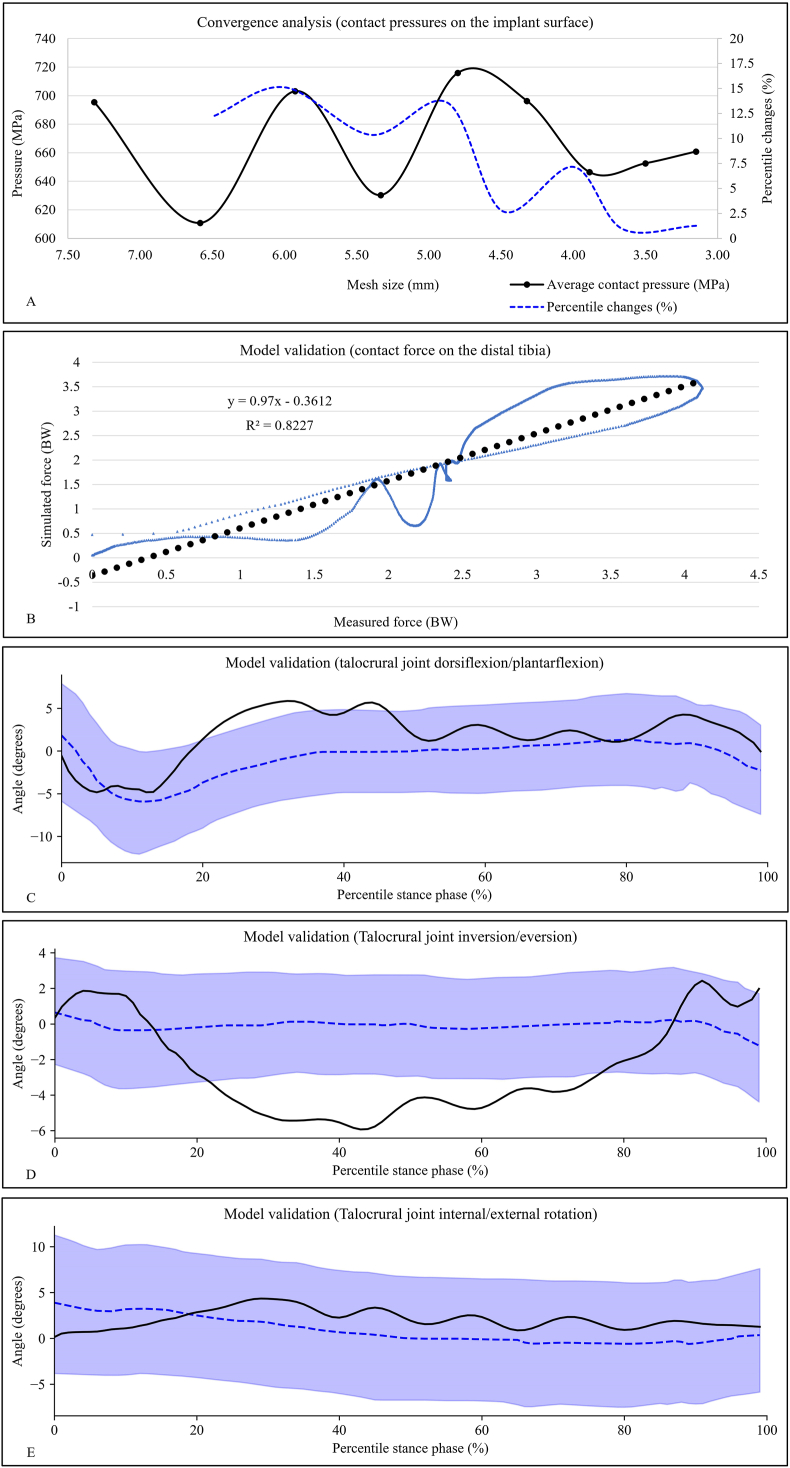
Table 1 summarises the information of the element type, element count, and material property for each model component. The global element size was 3.5 ​mm for the musculoskeletal structures and 5 ​mm for the ground plate. A localised mesh refinement was performed in regions with small and complex geometries. A mesh convergence analysis was conducted based on the results of average contact pressures on the implant surface by iterating the loading condition of the second peak of the ground reaction force during walking. The global mesh size was reduced by 10% for each simulation repetition until the deviations of the outcome parameters were less than 5% [30]. At the level of mesh size of 3.5 ​mm, changes in the pressure value were 0.94% and 1.27% respectively compared to those of the previous and next mesh size modification (Fig. 2A), indicating that the current mesh size was able to produce results with acceptable accuracy.

Table 1.

Element type, mesh count, and material property of the model components.

Model component	Element type	Material property	Density	Poisson's ratio	Mesh count
Skin	Linear triangular shell (S3R)	Hyper-elastic (first-order Ogden model, μ ​= ​0.122 ​MPa, α ​= ​18) Thickness: 2.0 ​mm	950 ​kg/m3	N/A	3062
Bulk soft tissue	SPH particle (PC3D)	Linearly elastic (Young's modulus: 0.83 ​MPa for the plantar heel, 0.70 ​MPa for the plantar forefoot/toe, 0.67 ​MPa for the plantar midfoot, and 0.20 ​MPa for the rest)	950 ​kg/m3	0.4	124778
Periosteum	Linear triangular shell (S3R)	Linearly elastic (Young's modulus: 0.9 ​MPa) Thickness: 1.5 ​mm	1000 ​kg/m3	0.4	19979
Bone	Linear tetrahedral solid (C3D4)	Linearly elastic (Young's modulus: 17000 ​MPa)	1990 ​kg/m3	0.3	18965
Extrinsic foot muscles	Slip ring connector	Linearly elastic (stiffness: 157.4 ​N/mm)	1000 ​kg/m3	N/A	N/A
Intrinsic foot muscles	Two-node truss (T3D2)	Linearly elastic (Young's modulus: 264.8 ​MPa) Cross-section area: 10 ​mm2	1000 ​kg/m3	0.4	24
Rearfoot ligaments	Two-node truss (T3D2)	Linearly elastic (Young's modulus: 100–320 ​MPa) Cross-section area: 7.1–256 ​mm2	1000 ​kg/m3	0.4	20
Other ligaments	Two-node truss (T3D2)	Linearly elastic (Young's modulus: 264.8 ​MPa) Cross-section area: 10 ​mm2	1000 ​kg/m3	0.4	67
Ground plate	Linear tetrahedral solid (C3D4)	Linearly elastic (Young's modulus: 17000 ​MPa)	1000 ​kg/m3	0.3	2850
Plantar fascia	Slip ring connector	Linearly elastic (stiffness: 182.4–232.5 ​N/mm)	1000 ​kg/m3	N/A	N/A
TAA metal components	Linear quadrilateral shell (S4R)	Linearly elastic (cobalt chromnium: 210000 ​MPa)	10000 ​kg/m3	0.29	18239
TAA bearing component	Linear quadrilateral shell (S4R)	Linearly elastic (polyethylene: 475 ​MPa)	900 ​kg/m3	0.38	5982
TTR talus prosthesis	Linear tetrahedral solid (C3D4)	Linearly elastic (cobalt chromnium: stiffness: 210000 ​MPa)	10000 ​kg/m3	0.29	8453

SPH: smoothed-particle hydrodynamics. The equations and parameters were extracted from the same references in two previous studies [26,45].

Fig. 2.

A) Convergence analysis of the mesh size. The black solid line denotes the average contact pressures on the implant surface and the blue dotted line indicates the percentile changes of the pressure value compared to that of the last mesh size modification; B) Model validation: a linear regression model examines the agreement in distal tibial force between simulation prediction and experimental measurements by Sharkey et al. The equation for the regression line is displayed; C–E) Model validation: graphic comparisons of the three-dimensional ankle motions between model predictions and fluoroscopic measures by Yang et al. The absolute joint angle values of Yang's study were offset by corresponding angle values at the neutral standing position to create consistent angle definitions. The solid line represents the simulation results of the current study. The dotted line and blue-shaded region represent the mean and one standard deviation of the results of Yang's study. TTR: total talus replacement; TAA: total ankle arthroplasty.

2.6. Boundary and loading conditions

The proximal ends of the tibia, fibula, and bulk soft tissue were fixed at degrees of freedom. The foot-ground contact during walking was driven by applying the time series of three-dimensional ground reaction forces and tri-axial rotations to the ground plate. The rotation degree of the ground plate was the reversal of the changes in the tibial orientation referring to the global coordinate system. The foot muscle forces were applied through slip-ring connectors in the models. The slip-ring connector is a polyline wire that passes through several anchor points, defining the path of a muscle, and connects two attachments on the bony surface. A slip ring allows force flow along the predefined path to enable contractile force applied between the two attachments, which mimics the effects of muscle contraction during locomotion. Likewise, muscle forces were assigned to the model as a time-variant matrix [26]. The foot and ground plate were positioned and oriented at the instant of foot-drop to initiate the simulation (Fig. 1C). All data for the boundary and loading conditions were direct outputs from OpenSim modelling.

2.7. Simulation solver, outcome variables, and comparisons

Finite element analyses of the walking trials were performed using the Abaqus (version 2016, Simulia, Dassault Systèmes, Johnston, RI, USA) dynamic explicit solver (Fig. 1B). The motions of the talocrural joint/first MTP joint, foot-ground angle, foot arch deformation, contact force on the midtarsal joint/Lisfranc joint, plantar fascia tensile force, and plantar pressure were reported and plotted as functions of the percentile stance phase. The foot-ground angle was defined as the angle between the ground plane surface and the line connecting the calcaneus tubercle and second metatarsal head [31]. Foot arch deformation was represented by midfoot movements and medial longitudinal arch angle (MLAA). Midfoot movements were quantified by measuring the angle created by the long axis of the talus and the long axis of the first ray. MLAA was defined as the angle between the vectors pointing from the navicular tubercle to the first metatarsal head and posterior calcaneus [32]. The Lisfranc joint was divided into three columns: the medial, central, and lateral columns, based on an established method [33]. The proximity of the curves of joint motions and segment movements produced by the two implant conditions to those of the intact foot condition was examined using linear regressions. The peak values of the outcome variables during the stance phase were quantitatively compared among the three conditions.

2.8. Model validation

The foot model was validated by setting up a finite element analysis using the loading and boundary conditions of a cadaveric experiment [34]. The foot model was positioned and assigned with a set of ground forces/muscular forces corresponding to the loading status of selected instants of a walking stance [34]. The primary outcome—contact forces on the distal tibia bone, was compared between the model predictions and experimental measures using linear regression analysis. Because the study applied a dynamic simulation approach, we also validated the model by comparing three-dimensional ankle joint motions with those measured using dynamic biplane fluoroscopy—a measurement modality that is normally considered the gold standard method for tracking bone movements. A radiographic study [35] on hindfoot kinematics during gait was selected as the source of fluoroscopic results because the study recruited healthy adults with average anthropometrics and walking speeds similar to those of our participant.

3. Results

All three models reported successful completion of the analysis tasks. A high-performance workstation (CPU: Intel Xeon Gold 5218R 2.10 ​GHz processor 40 cores, RAM: Micron DDR4 2666 ​MHz 128 ​GB, OS: Windows 10 Enterprise) performed the simulations and the total run times were approximately 5426, 4166, and 5967 ​minutes for the intact foot, TTR, and TAA conditions respectively.

3.1. Validation

The linear regression model indicated good agreement between the simulation predictions and cadaveric measurements of the tibial contact force values. The model reported a coefficient of determination (R²) of 0.82, a slop of 0.97, and an intercept of −0.36 (Fig. 2B). Fig. 2C–E shows that the ankle angles calculated by our intact foot model during gait mostly fell within the range of one standard deviation around the mean values measured by fluoroscopy. A major discrepancy between simulations and fluoroscopy existed in the results of talocrural inversion/eversion, where the model predicted a larger talocrural excursion on the coronal plane than fluoroscopy. A possible explanation is that the small angularity of the X-ray projectors and image matching techniques utilised in the radiological study [35] might not capture the rearfoot motions on the coronal planes as sufficiently as on the sagittal plane. Meanwhile, our foot model with structural and material simplifications in the ankle joint tended to overestimate the ankle motions.

3.2. Joint motion and segment movements

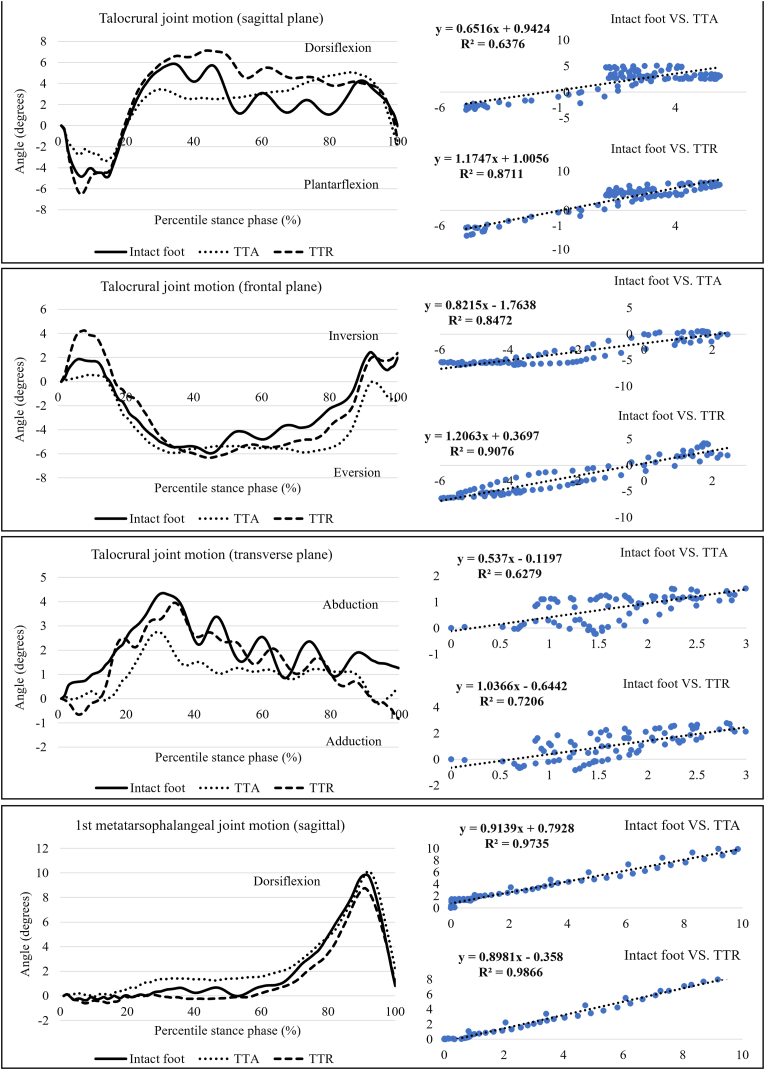
Linear regressions analysis (Fig. 3) showed that the curves of joint motions and segment movements produced by TTR had a greater degree of fit to those of the intact foot (R² ​= ​0.721–0.993) than to those of TAA (R² ​= ​0.623–0.990). Compared to those of the intact foot, the sagittal, frontal, and transverse talocrural ranges of motion were increased by 27.06%, 25.69%, and 9.95% in TTR but decreased by 21.36%, 22.98%, and 31.92%, respectively, in TAA (Table 2). A reverse trend of joint movement changes was observed in the MTP joint. The sagittal MTP range of motion and peak dorsiflexion were slightly reduced (8.26% and 11.11%, respectively) in TTR, whereas TAA increased the two angular values by 0.34% and 3.03%, respectively, compared to the intact foot.

Fig. 3.

Results of the talocrural joint motion and first MTP joint motion during walking. TTR: total talus replacement; TAA: total ankle arthroplasty.

Table 2.

Results of finite element analyses of the three models.

Outcome variable	Intact foot	TAA	TTR
Talocrural joint motion (degrees)
Sagittal RoM	10.75	8.45	13.66
Frontal RoM	8.40	6.47	10.56
Transverse RoM	4.34	2.96	4.78
Peak dorsiflexion	5.87	5.07	7.13
Peak eversion	5.95	5.91	6.33
Peak abduction	4.35	2.75	3.95
MTP joint motion (degrees)
Sagittal RoM	10.19	10.22	9.34
Peak dorsiflexion	9.84	10.14	8.75
Segment kinematics (degrees)
Peak midfoot movement	11.26	11.11	10.01
Peak MLLA	134.18	135.37	134.01
Peak joint contact force (N)
Midtarsal joint	832.20	921.51	981.35
Lisfranc joint (medial column)	66.26	93.81	89.59
Lisfranc joint (central column)	279.97	184.22	223.32
Lisfranc joint (lateral column)	222.73	352.42	433.27
Peak plantar pressure (MPa)
Rearfoot	187.10	191.93	183.27
Midfoot	124.93	109.45	99.67
Forefoot	781.87	839.43	777.47

TAA: total ankle arthroplasty; TTR: total talus replacement.

The differences in the foot-ground angles among the three conditions were not distinctive across the walking stance (Fig. 4). Likewise, the curves of midfoot deformation and MLLA produced by TTR (R² ​= ​0.973–0.990) were more similar to those of the intact foot than those of TAA (R² ​= ​0.969–0.987). The peak values of midfoot deformation and MLLA in TTR were 9.89% and 1.01% lower, respectively, than those of TAA (Table 2).

Fig. 4.

Results of the foot-ground angle, midfoot movement, and medial longitudinal arch angle during walking. TTR: total talus replacement; TAA: total ankle arthroplasty.

3.3. Joint contact force

Compared with the intact foot, TTR and TAA increased the midtarsal joint contact force by 17.92% and 10.73% respectively (Fig. 5). The two implant conditions applied less force (20.23%–34.20% lower) to the central Lisfranc column but increased force generation on the medial/lateral sides of the midfoot (Table 2). TTR produced larger contact forces on the lateral Lisfranc column (22.94% higher than TAA), whereas TAA increased the loading on the medial column (4.71% higher than TTR).

Fig. 5.

Joint contact forces are applied to the midfoot joints of interest. The foot skeleton diagram in the upper left corner shows the joint regions. The rest of the figures are plots of the contact forces as a function of percentile walking stance. TTR: total talus replacement; TAA: total ankle arthroplasty.

3.4. Plantar fascia tensile force

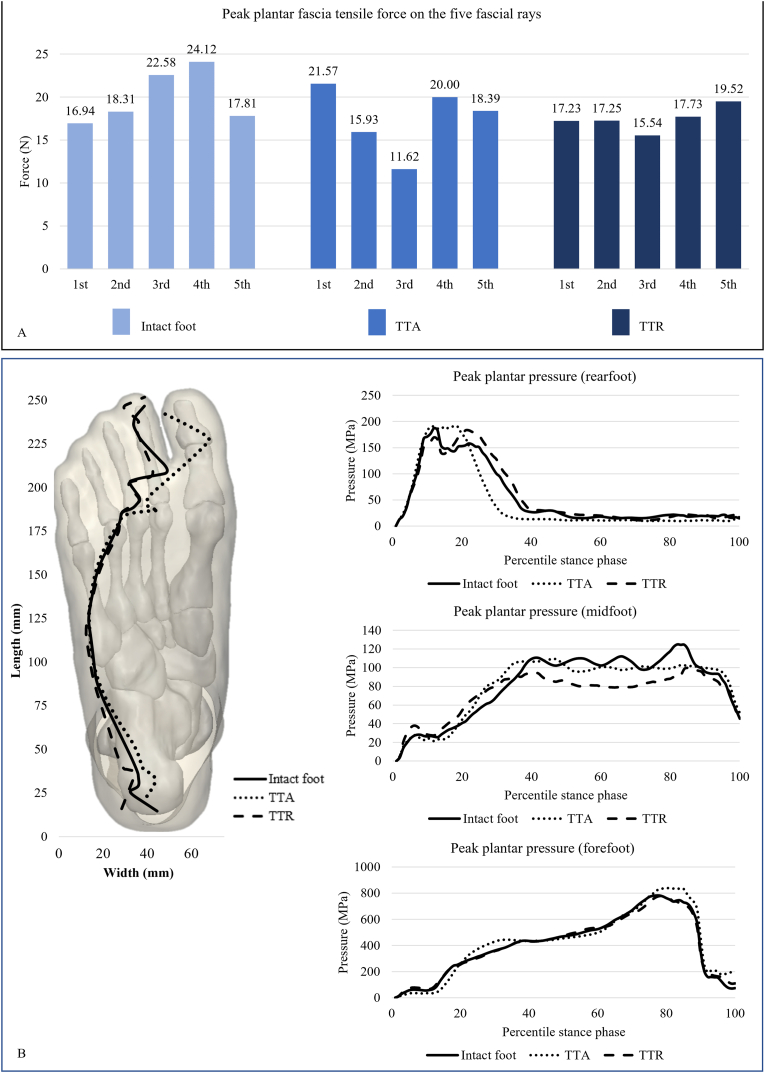
The peak tensile force on the first ray of the plantar fascia was the lowest in TTR (17.23 ​N) and highest in TAA (21.57 ​N). The intact foot produced the highest second-, third-, and fourth-ray peak tensile forces of the three conditions (18.31–42.12 ​N). Fig. 6A shows that the fascial tensile force was evenly distributed in TTR, more centrally concentrated in the intact foot, and shifted to the first ray in TAA.

Fig. 6.

A) Tensile forces on the five rays of the plantar fascia in the three models; B) Measures of plantar foot pressures of the three model conditions. The plantar foot diagram shows the trajectories of the plantar pressure centre during gait. TTR: total talus replacement; TAA: total ankle arthroplasty.

3.5. Plantar pressure

Fig. 6B shows the trajectories of the plantar pressure centre during walking. The trajectories of the three conditions roughly overlapped during the early half of the walking stance. In the late stance, the locations of the pressure centres were similar between the TTR and intact foot, whereas the pressure centre of TAA shifted medially by approximately 1.43–1.48 ​cm compared to the other two conditions. TTR produced the lowest peak pressure values across the three plantar regions. The peak forefoot pressures in TAA were 7.97% and 7.36% higher than those in TTR and intact foot respectively (Table 2).

4. Discussion

This study utilised computational simulation to examine and compare foot kinematics/force development between the two implanted feet (TTR and TAA). The results demonstrated that TTR was superior in reproducing the joint motions and segment movements of the intact foot compared to TAA. Both implants increased loadings on the midtarsal joint and reduced loadings on the central Lisfranc column. The proximal-to-distal force transmission within the midfoot was shifted to the two flanks of the midfoot under the two implant conditions. TTR retained the plantar pressure distribution of the intact foot during walking. TAA increased midfoot deformation and peak plantar pressure on the forefoot, probably because of the constrained ankle motions.

The purpose of customising a talus prosthesis is to satisfy articular congruency and maximally preserve talocrural joint motions. Previous clinical studies assessing customised talar prostheses reported standard-meeting results of dorsiflexion (5.4°–20.0°), plantarflexion (30.0°–42.5°), and total range of motion of the implanted ankle in static joint motion tests [11,12,[15], [16], [17]]. However, mobility of the implanted ankle during dynamic tasks has seldom been addressed. Our results showed that the sagittal- and frontal-plane talocrural motions of the TTR-implanted foot were in good agreement with the measured values of a healthy gait [36]. Conversely, talocrural joint motions in the TAA condition appeared to fall short of the physical range, which is consistent with the findings that the TAA-implanted foot also underperformed in the static joint motion tests (33.3°–52.3°) [37,38]. Although often analogous to a mortised hinge, the talocrural joint incorporates compound movements on multiple planes during walking, which is achieved through the sliding of the three-facet malleoli on the cylindrical surface of the talar body [39]. Compared with a conventional TAA that features a single orbit, TTR rebuilds patient-specific geometries on the articular surface that is more likely to facilitate natural joint motions.

The kinematics of the foot segments are tightly sequenced during the progression of the gait cycle [40]. Therefore, inadequate ankle motion during walking is frequently associated with increased angulation of neighbouring joints [41]. Our study demonstrated that the MTP joint was more dorsiflexed in the late stance to compensate for the constrained motion of the TAA-implanted ankle. The reduced ankle compliance in TAA may also result in hyper-mobility at the adjacent foot arch articulation [42], causing larger midfoot movements than TTR. From this perspective, the advantages of TTR over TAA in improving joint motion are beyond the implanted site and extended to interconnected components of the foot kinematic chain, which is the key to unlocking the ankle–subtalar complex during foot drop for navigating force transmission from the rearfoot to midfoot [40].

Our results of the joint contact force and plantar fascia force supported the findings that the central Lisfranc column is the dominant midfoot portion for force transmission during walking [43]. The two implant conditions had the midfoot force flow deviated from the central column. Specifically, a greater majority of the joint contact forces were applied to the medial Lisfranc column in TAA and applied to the lateral Lisfranc column in TTR. Talus dorsiflexion is coupled with calcaneus eversion/abduction and midfoot dorsiflexion to disperse forces through the midfoot [44]. Therefore, limited talus motions in TAA impeded the force flow and caused force concentration on the rearfoot [45], leading to an increased magnitude and duration of rearfoot plantar pressures in TAA at approximately 10%–30% of the stance phase. In the meantime, an opposite trend was seen in TTR where excessive talus motions navigated force flow to the lateral column of the midfoot. We speculated that the altered talus motions, either decreased or increased, would transfer loadings on the unconditioned articular surface against bony prominence [46] and redirect the force flow, which also explained the elevated midtarsal contact forces in the two implant conditions. The plantar fascia, on the other hand, is less tolerant to forces applied to its two flanks because it is histologically structured to withstand tensions on its central bundle [47]. Previous studies have frequently reported a correlation between increased risk of plantar fasciitis and reduced ankle motions in pathological feet [48]. However, the rate of plantar fascia complications after ankle joint replacement has rarely been documented. More conclusive evidence from longitudinal observations is needed to substantiate the trend shown in our results.

Plantar pressure is a common measure in clinics because it is an external manifestation of the internal foot loading and underlying pathologies. In accordance with previous studies [49,50], TAA increased the forefoot plantar pressure and moved the pressure centre medially in the late stance. Delayed ankle dorsiflexion during early and mid-stance aggravates arch collapse and forefoot abduction [40], which interferes with the initiation of foot supination at late stance and causes pressure concentration on the hallux in TAA. Similar to TAA, TTR modified the midfoot force flow, whereas this alteration seemed to be attenuated internally as it propagated to influence the pressure on the plantar foot. The footpad was made of resilient material to distribute plantar pressures [51] unless substantial changes occurred to the loading on the above foot structures. Pressure concentration was a frequent factor contradicting TAA [49] owing to possible complications, which in turn highlighted the improvements imparted by TTR in restoring the normal pressure profile.

Due to the improved proximity to the original talar geometries, TTR was demonstrated to greatly reproduce the joint motions and segment movements of a healthy foot. However, foot kinetics were not restored to an equivalent level. It is likely that a small mismatch between the prosthesis and the local anatomy can influence, to a larger extent, force transmission and soft tissue loadings. The design protocol for TTR prostheses can be improved to address this shortfall. We propose that the injury-site geometries, despite degenerative changes, can be considered in the prosthesis design process through an approach of pre-matching and predictive simulations. In addition, the surgical details of TTR, such as ligament repairment after implant installation, need to be unified across different studies [14,18]. Without ligament constraints, the implanted joint loses a portion of its stability and exceeds the normal motion range. Confined to the biomechanical scope, the current study supports the clinical application of TTR. However, it is premature to conclude its effects on ankle joint function recovery unless further studies can be conducted with summative statistics performed on a patient cohort.

Resembling other finite element analyses, our study has the limitation of adopting a single-case design, which hinders generalisation and external validation of the research outcomes to the target population. Batch modelling of multiple samples can be considered a solution to this problem. However, this approach can be performed at the cost of reduced complexities of foot geometries and boundary conditions in the model, which subsequently weakens the internal validation of the outcomes to the subject that the model represents. The strength of our model prediction was assured by the sophisticated structures and load application strategies [26]. In this study, we derived the boundary conditions for the simulation setup from a healthy gait and assumed that they were unchanged across the three model conditions. Despite the fact that an implanted foot usually produces different gait patterns, we kept the boundary condition consistent to create a comparable baseline simulation environment so that changes in the outcomes can be explicitly attributed to the influences of the implants. Using different boundary conditions would introduce confounding factors in the analyses. A full understanding of these assumptions and premises is necessary for the proper interpretation of the simulation results. Another limitation of the study was related to the prosthesis design. There are currently no design standards for prostheses, and the available models in the market vary fairly in components and configuration. We selected a model that was most commonly used in the literature. However, any element or modification added to the design influences its performance, and the results should be interpreted in a different context.

5. Conclusion

Compared with TAA, TTR better reproduced the foot joint motions, segment movements, and plantar pressure profile of an intact foot. However, TTR exerted increased contact forces on the midtarsal joint and the lateral column of the midfoot. TAA restricted talocrural motions, which was likely associated with excessive angulations of the distal foot segments and force concentration on the medial column of the midfoot. TTR appeared to generate foot kinematics that were more similar to those of a healthy gait; however, this approximation did not convert to a full restoration of the internal loading status of the foot. Clinicians are suggested to consider the limitations of the current TTR design process and the premises for application decision, though further studies are needed for a more conclusive statement on the effects of TTR on ankle joint function recovery.

Funding

This work was supported by the National Natural Science Foundation of China (NFSC) [grant numbers: 11732015 and 11972315].

Declaration of competing interest

The author(s) have no conflicts of interest relevant to this article.