Abstract
Objective:
Traditional radiotherapy (RT) treatment planning of non-small cell lung cancer (NSCLC) relies on population-wide estimates of organ tolerance to minimize excess toxicity. The goal of this study is to develop a personalized treatment planning based on patient-specific lung radiosensitivity, by combining machine learning and optimization.
Approach:
Sixty-nine non-small cell lung cancer patients with baseline and mid-treatment [18]F-fluorodeoxyglucose (FDG)-PET images were retrospectively analyzed. A probabilistic Bayesian Networks (BN) model was developed to predict the risk of radiation pneumonitis (RP) at three months post-RT using pre- and mid-treatment FDG information. A patient-specific dose modifying factor (DMF), as a surrogate for lung radiosensitivity, was estimated to personalize the normal tissue toxicity probability (NTCP) model. This personalized NTCP was then integrated into a NTCP-based optimization model for RT adaptation, ensuring tumor coverage and respecting patient-specific lung radiosensitivity. The methodology was employed to adapt the treatment planning of fifteen NSCLC patients.
Main results:
The magnitude of the BN predicted risks corresponded with the RP severity. Average predicted risk for grade 1–4 RP were 0.18, 0.42, 0.63, and 0.76, respectively (p < 0.001). The proposed model yielded an average area under the receiver-operating characteristic curve (AUROC) of 0.84, outperforming the AUROCs of LKB-NTCP (0.77), and pre-treatment BN (0.79). Average DMF for the radio-tolerant (RP grade = 1) and radiosensitive (RP grade ≥ 2) groups were 0.8 and 1.63, p < 0.01. RT personalization resulted in five dose escalation strategies (average mean tumor dose increase = 6.47 Gy, range = [2.67–17.5]), and ten dose de-escalation (average mean lung dose reduction = 2.98 Gy [0.8–5.4]), corresponding to average NTCP reduction of 15% [4–27].
Significance:
Personalized FDG-PET-based mid-treatment adaptation of NSCLC RT could significantly lower the RP risk without compromising tumor control. The proposed methodology could help the design of personalized clinical trials for NSCLC patients.
1. Introduction
Non-small cell lung cancer (NSCLC) is the most common type of lung cancer, accounting for approximately 84% of all lung cancer diagnoses. Although radiation therapy (RT) is the most common treatment option for unresectable NSCLC patients, its effectiveness in advanced-stage patients remains limited, with roughly 30% local failure rate at 2 years post chemo-RT [1]. Many studies have reported the positive impact of higher tumor (biologically effective) dose in improving (chemo-)RT outcome; consequently, dose escalation strategies have been adopted as a means to improve tumor control [2, 3, 4, 5, 6, 7, 8]. However, more aggressive treatments are typically constrained by higher risks of toxicity, including radiation pneumonitis (RP) [9], esophagitis [1], and cardiac toxicity [10].
To improve the efficacy of these “one-size-fits-all” approaches, the field of radiation oncology has recently experienced a surge in positron emission tomography (PET)-based dose escalation trials [11, 12, 13, 14, 15, 16]. However, therapeutic impact of such PET-based approaches is limited by four main factors: (i) the assumption, either implicit or explicit, that PET tracer uptake is directly (linearly) related to radiosensitivity (e.g., the higher the uptake, the higher the dose boost), (ii) relying on pre-specified (subjective) dose boost (or reduction) levels without taking into account “optimal” dose level for individual patients, (iii) adopting a tumor-centric approach with secondary emphasis on normal tissue response, and (iv) reliance on pre-treatment images for assessing response, thereby treating patient response as static.
Considering these limitations, a more nuanced, personalized approach wherein the patient selection and dose (de)escalation is performed by accounting for patient-specific radiosensitivity during the RT course might prove more effective in terms of overall treatment-induced toxicity and tumor control.
In this work, we propose a novel mathematical framework for mid-treatment (dynamic) adaptation of RT treatment course using patient-specific prediction of normal tissue toxicity. We focus on the risk of symptomatic RP (grade ≥ 2), denoted by RP2+, as the main toxicity endpoint to guide the adaptation. 18F-fluorodeoxyglucose (FDG) PET images acquired at baseline and during the course of treatment are used as imaging biomarkers to predict the risk of RP at 3-months post-RT. A Bayesian predictive model is employed to synthesize patient-specific PET imaging, clinicopathological, and dosimetric data into a predicted risk of symptomatic RP. These biomarker-informed predictions are then integrated into treatment planning via a patient-specific NTCP model to select individualized dose (de)escalation levels during the treatment course and biologically adapt the treatment plan to minimize the patient-specific risk of RP and/or maximize tumor control while keeping the patient-specific NTCP within a pre-specified threshold. Briefly, the contributions of this study are as follows:
A framework for assessing patient-specific RP risk based on pre- and mid-treatment imaging data.
A method for updating patient-specific NTCP based on this estimated risk.
A methodology for incorporating the updated NTCP into the treatment plan optimization and adaptation.
The proposed methodology addresses the aforementioned gaps in PET-based dose (de)escalation strategies: (i) it foregoes the linear assumption for estimating radiosensitivity, (ii) through a novel NTCP-based treatment planning, it yields biologically-optimal plans, (iii) it takes into account patient-specific risk of radiation toxicity, and (iv) by taking advantage of mid-treatment images, it treats the RT treatment and patient response as a dynamic (rather than static) problem.
The current study should be regarded as a proof-of-concept towards a truly personalized treatment planning. It successfully combines biomarker information, machine learning-based risk prediction, and treatment plan optimization. The overall methodology is modality-agnostic (could be used in photon or proton RT delivery), and is designed flexible enough to adapt to other treatment sites beyond lung cancer, provided that a reliable predictive model could be developed for the chosen toxicity endpoint. To the best of our knowledge, this is the first instance of combing machine learning and treatment plan optimization for personalized treatment at clinical scale.
2. Methods
Our methodology consists of three primary modules: the Risk Prediction module predicts the patient-specific risk (probability) of RP2+, P(RP), using baseline and mid-treatment patient-specific information. This prediction will then be used as input to the NTCP Update module, wherein a patient-specific NTCP will be calculated using the concept of dose modifying factor (DMF) [17]. Finally, the Plan Adaptation module adapts the RT treatment plan based on this patient-specific NTCP estimate to minimize the risk of RP2+, within the constraints imposed by tumor control. A detailed flowchart of the proposed framework is given at the end of § 2.5.3.
2.1. Dataset
The data for our study comes from a recent Phase II clinical trial of photon (intensity modulated RT, IMRT) versus passive scattered proton RT (PSPT) for stage IIB-IIIA NSCLC patients (NCT00915005). All patients with available pre- (week 0) and mid-treatment FDG-PET/CT (weeks 2–7) scans in the original trial were selected for this retrospective study. After the exclusion of ineligible patients (due to poor image quality or missing information), 69 patients (PSPT = 24, IMRT = 45) were selected for the final study. The mean dose to gross tumor volume (GTV) was 66–82 Gy-RBE (median = 74 Gy-RBE) delivered over 30–37 fractions (median = 37). Grade 2+ RP was observed in 18 patients (26%, 7 (29%) in the PSPT arm and 11 (24.4%) in the IMRT arm, p > 0.05). Further details on patients’ characteristics and RT delivery is given in Table S1 of the Supplementary Material. We refer to the original trial publication [18] for more extensive discussion of the trial results.
2.2. Mid-treatment biomarker
Following prior reports on the potential role of 18F-fluorodeoxyglucose (FDG) PET scan as an imaging biomarker for RP risk [19, 20, 21, 22], we focus on the FDG-PET as our imaging biomarker. Voxel-level FDG PET standard uptake value (SUV) obtained from pre- and mid-RT images were extracted. Pre-treatment scans were acquired 1–3 months prior to the RT initiation, and mid-treatment PET scans were acquired during weeks 4–5 of the treatment. All PET image acquisitions followed the same protocol and were consistent across all patients and time-points; specifically, patients had fasted for a minimum of 6 hours and had a blood glucose level of 80–120 mg/dL before intravenous administration of 18F-FDG (555–740 MBq [15–20 mCi]) and the data was acquired 60 minutes after injection using a GE Discovery ST PET/CT scanner (resolution: 5 × 5 × 3mm). To calculate the FDG uptake between pre- and mid-treatment scans, the accompanying CT in both PET/CT images were first registered to the manually contoured planning CT (drawn by a qualified radiation oncologist) using a rigid followed by B-spline deformable image registration. The resulting vector fields were then used to propagate the binary label maps and the planning dose onto the PET images (Figure 1). In calculating SUV metrics, the region of interest was limited to the contours of normal lung (volume of both lung minus GTV). Further, to account for cardiac and respiratory motion artifacts, all voxels in close proximity (within 5mm) to the heart were discarded from the calculations. Conventional SUV-based FDG metrics (SUVmean, SUV5%–95%) along with the slope of the linear regression line relating the delivered dose to SUV change, denoted by SUVslope [23] were calculated using an in-house script and checked against the automatic calculations performed in MIM Vista (MIM Software Inc., Cleveland, OH). Finally, pre-, mid-, and Δ-SUV metrics (SUV2/SUV1) were used as specific imaging features in our predictive model.
Figure 1:
Workflow for the PET-PET image registration process. DIR: deformable image registration.
2.3. Risk Prediction module: Predicting RP using Bayesian Networks
2.3.1. Bayesian networks background
The diverse patient-specific information collected at baseline and during RT should be synthesized into an estimate for the RP risk post-RT. In this work, a Bayesian Network (BN) model is trained for predicting the probability of toxicity based on several dosimetric, clinical, and imaging features. BNs are direct acyclical graphs (DAG) [24] which encode a joint probability distribution among the set of variables X in the dataset [24, 25]. Given a dataset X = {X1, X2, . . . , Xp}, the joint probability distribution can be decomposed into a product form of conditional probability relationships among the variables:
| (2.1) |
where Π(Xi) denotes the set of parents (i.e., conditional dependencies) for the node Xi. The underlying assumption is that the probability of Xi is (conditionally) independent of all other variables Xj ∈ {X \ {Xi, Π(Xi)}}.
The reason for choosing BN over other ML-based predictive models (e.g., random forests, support vector machines, deep networks, etc.) are three-fold: (i) Unlike other score or vote-based classification methods, BN provides a concise representation of the probabilistic dependencies between the set of random variables in the dataset, which can be used for direct probabilistic inference; (ii) Unlike the “black-box” nature of the other models, the graphical architecture of BNs offers transparencies and can increase trust in its predictions, an important feature in sensitive medical decision makings; (iii) through modeling inter-variables dependencies, BNs are capable of handling missing data by inferring their values from their dependencies (i.e., parents).
2.3.2. Data pre-processing
The features included in the BN were a collection of aforementioned imaging biomarker information, dosimetric information (e.g. mean lung dose (MLD), V5-V60, D2%, D98%, etc.), clinopathological information (e.g., age, sex, performance status, lung functionality (FEV1/FVC), etc.), tumor-related information (staging, nodal involvement, tumor location, GTV volume, etc.), and PET-derived imaging features (SUV5–95%, SUVmean, and SUVslope). It should be noted that although in calculating SUV metrics, we obtain voxel-level information, in building the predictive model only aggregate SUV metrics are used. The reason is two-fold: (i) to reduce the number of possible features to include during model training, and (ii) to reduce the impact of voxel-level uncertainty on model predictions caused by intrinsic PET information noise and image registration. Among the selected features (94 in total), the continuous ones were then binned into two or three disjointed intervals according to Hartemink algorithm [26].
2.3.3. Model training
Training a Bayesian Network involves finding the structure (arcs) and parameters (conditional probabilities) of the network. For the structural learning, a hill-climbing algorithm combined with Bayesian information criterion (BIC) score was used to select the best model structure:
| (2.2) |
where M is the BN structure (a set of conditional dependencies, i.e., arcs) and d is the number of parameters of the global distribution (here, the assumption is multinomial distribution). Model averaging using bootstrapping (R=1000) was used to find the most stable arcs (i.e., those which appeared in over 50% of the structures). Once a final structure was found, the network parameters were estimated using maximum likelihood algorithm.
2.3.4. Model assessment
Although the output of interest is the probability of developing toxicity, it is hard (if not impossible) to assess patient-specific probability in practice. Therefore, in order to assess the model’s predictive performance, the patient-specific RP class C* was assigned using the Bayes’ theorem on the probabilities estimated from the final network M* [24]:
| (2.3) |
where δ denotes the patient-specific information, a realization of X. Subsequently, the classification performance was (internally) assessed using area under the curve (AUC) of the receiver-operating characteristics curve (ROC).To test the predictive performance, we use a Cross Validation (CV) scheme. Specifically, in each loop, the dataset was randomly divided into training-validation subsets using a 80–20 split. Within each split, the best model structure was found using the bootstrapping technique mentioned in §2.3.3, the optimal structure was then used to optimize the model parameters (still using the same 80% of the subset), and finally, the parameterized network was used to test the prediction accuracy on the remaining 20%. The entire process was repeated 10 times, and the average performance was reported.
The output of the BN model is the predicted RP risk P(RP), based on the baseline and mid-treatment information. This risk will be used in the next steps to guide the treatment planning. In order to integrate the BN-based risk predictions with treatment plan optimization, an intermediate step is required to translate this risk into a parameter in the treatment planning optimization problem. This is the focus of the next section.
2.4. NTCP Update module: Towards a patient-specific NTCP
Using the traditional Lyman-Kutcher-Burman (LKB) NTCP model, the risk of developing toxicity from a dose D delivered to the lung is given by:
| (2.4) |
where
| (2.5) |
and , TD50 and m are the population-wide estimates denoting the dose leading to toxicity in 50% of the population and the dose-slope at TD50, respectively, n is the volume parameter, and Di the dose to relative sub-volume vi.
Using the concept of dose modifying factors (DMFs), Tucker et al. [27, 17] extended the LKB model to incorporate non-dosimetric features such as clinical risk factors (e.g., smoking status [27]) and/or biological information (e.g., single-nucleotide polymorphisms, SNPs [17]). Using their proposed concept, including k non-dosimetric features will lead to the linear adjustment of gEUD in Eq. (2.4):
| (2.6) |
In order to integrate the BN-predicted RP risks with conventional treatment planning to determine how (and how much) the dose should be adopted to account for this patient-specific risks, we borrow the concept of DMF but treat it not as the modifying effect of one single covariate (e.g., smoking or gene mutation), but a synthesis of all patient-specific information as predicted by our BN predictive module; that is, a patient-specific DMF can be estimated based on the BN predictions:
| (2.7) |
In this view, the role of the predictive module is transformed from assessing patient-specific probability P(RP) which is a hard-to-grasp concept that cannot readily be integrated with treatment planning, to estimating patient-specific DMF (denoted as ), which not only can be viewed as a surrogate for the radiosensitivity of the lung tissue, but as we shall see, can also be integrated within treatment planning to personalize the treatment plan.
| (2.8) |
where Φ−1 is the inverse of Φ. The fact that Φ−1(z) is only defined for z ∈ (0, 1) implies that PBN(RP) ≠ 0, 1. Note that this is not, in practice, restrictive, since, from a prospective angle, no event has truly a probability of 0 or 1. Figure 2 illustrates the relationship between and the predicted risk PBN(RP). Generally, the lower the PBN(RP), the lower the , and the shallower the NTCP curve (indicating less radiosensitive lung tissue).
Figure 2:
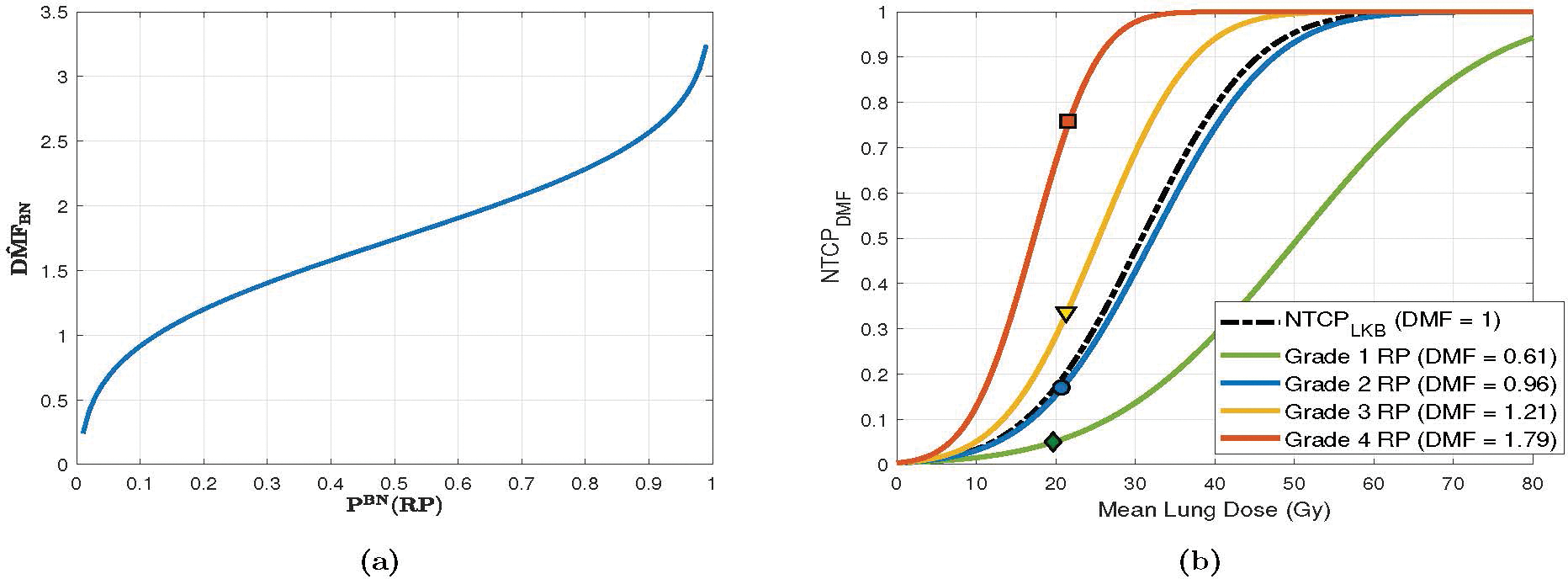
Relationship between BN-predicted RP risk PBN(RP), and NTCPDMF. (a) changes in as a function of (BN-) predicted risk for a representative case with mean lung dose of 17.49 Gy. (b) NTCP curves for four exemplary cases with varying radiosensitivity, as estimated by DMF. The points symbolized by diamond, circle, triangle, and square symbols denote the calculated risk at the mean lung dose for each case. NTCP parameters were set to their population-wide estimates: TD50 = 30.8 Gy, m = 0.37, and n = 0.99.
2.5. Plan Adaptation module: NTCP-based RT personalization
If we are agnostic about patient radiosensitivity due to insufficient information (as is often the case before the start of the treatment), we can do no better than to assess the risk assuming that the patient is similar to the “average” population, and set (note that in this case, NTCPBN = NTCPLKB). However, once more information becomes available during the treatment course (in the form of PET scan images or other relevant biological information), the RP risk can be estimated using the predictive model, and a patient-specific DMF can be derived via Eq. (2.8). This will lead to a personalized NTCP model, which in turn could be used to adapt the treatment course.
2.5.1. Mathematical modeling
In the remainder of this section, we will use and to refer to the set of voxels in the target and normal lung, respectively, and use to refer to all other regions of interest (ROIs). Assuming that the new information, i.e., FDG PET images, and hence, new estimate for are revealed just before fraction T ∈ (1, N], where N is the total number of fractions (we treat N as fixed). This gives Nrem = N − T + 1 remaining fractions for delivering the adapted dose. Further, we assume during the first T − 1 fractions, a total dose of , had been delivered to the ROIs. We set an upper bound on the maximum tolerable (projected) NTCP and a lower bound δ on the projected TCP. Further, to avoid target hot/cold-spots, we impose a minimum and maximum dose constraints on the tumor dose (respectively ζ and ). The goal of the optimization is to find the optimal post-adaptation dose distribution during the adaptation period [T, N] so as to ensure maximum overall TCP while minimizing predicted NTCP.
We model TCP using the linear-quadratic (LQ) Poisson model [28]:
| (2.9) |
where is the survival fraction of cells in tumor voxel i after delivery of a total dose Di to a target with radiosensitvity parameters αT and βT (assumed to hold for all voxels within the target). We denote by N0 and the total initial number of clonogenic cells and the total number of tumor voxels in the target volume. The NTCP formulation has to be adjusted to account for fractionation effect. This can be accomplished by using the fractionation-corrected version of NTCP in Eq. (2.7), as proposed in [29]. To avoid overcrowding the notations, we refer to Appendix A for more details on how to incorporate fractionation effect in the NTCP formulation. In order to be more consistent with current clinical practice and ensure higher quality clinical plans, we use the physical dose model and penalize the squared deviation from a prescribed tumor dose .
Putting all these together, in order to biologically adapt the treatment, the following fluence-map optimization (FMO) problem should be solved:
| (2.10) |
| (2.11) |
| (2.12) |
| (2.13) |
| (2.14) |
| (2.15) |
| (2.16) |
| (2.17) |
| (2.18) |
| (2.19) |
where Am is the dose deposition matrix for the voxels in , u1 and u2 are the vectors of beamlet weights (fluence maps) for the pre- and post-adaptation periods, ∥.∥2 is the Euclidean norm, and f(x) represents all other dosimetric constraints (e.g., mean/min/max dose or dose-volume histogram constraint). Note that since u1 is already known at the time of adaptation (from the original plan), the only decision variable here is u2.
The above formulation is noncovex and, as such, prone to suboptimal solutions. In the next section, we will give a convex reformulation of the problem.
2.5.2. Convex reformulation
Assuming the non-convex DVH-based constraints are handled (using approximate techniques such as constraint generation [30], conditional value-at-risk [31], etc.), the only sources of non-convexity in arise from the TCP and NTCP constraint (2.12)–(2.13). Fortunately, as proven in Appendix B, it can be shown that can be reformulated into a convex function using the following log-transformation:
| (2.20) |
Similarly, it has been shown that log TCPLQ(D) is strictly concave as long as we have , for every tumor voxel k [29]. Given that this assumption holds for clinically meaningful values for αT ≃ 0.35 Gy−1 , (αT/βT) ≃ 10 Gy, and N ≃ 35 for lung tumors1, a simple log-transformation h(TCPLQ) = log TCPLQ will take care of the convexity of (2.13)2. Therefore, by replacing (2.12) and (2.13) by their convex counterparts, we reach the following convex formulation, which can then be solved to global optimality by conventional convex optimization algorithms:
| (2.21) |
| (2.22) |
| (2.23) |
| (2.24) |
The output of this step is the adapted beamlet weights (and hence, the adapted dose distribution ) that respects individual patient’s risk of toxicity PBN(RP). By ensuring that the patient-specific NTCP will remain below a user-defined prescribed threshold and the predicted TCP remain high, the algorithm automatically chooses the plan which is tailored towards the biological characteristic of a given patient, thus resulting in a (NTCP-wise) personalized RT treatment plan. This plan will then be delivered until the next update point or the end of treatment course. In the next section, we discuss some details pertaining to the adaptation strategy.
2.5.3. Adaptation strategies
Based on the estimated radiosensitivity, one of two adaptation strategies could be pursued:
-
De-escalation: For radiosensitive patients (those projected to develop RP2+ under the original plan), we minimize NTCP (i.e., reduce mean lung dose) as much as possible, within TCP boundaries. We need to distinguish between two cases that might arise under this scenario. In the first case, the NTCP constraint (2.23) can still be satisfied if the integral dose to the lung is reduced (without violating tumor-based constraints (2.13)–(2.14). In other words, a feasible solution for exists and will be found by solving to derive the optimal de-escalation strategy. This is termed Type 1.a Adaptation.
In the second case, there is no feasible solution for which will simultaneously satisfy the tumor and NTCP constraints; in other words, too much dose has already been delivered to the lung. In this case, the goal of adaptation is to minimize the NTCP as much as possible, without jeopardizing tumor coverage. To achieve that, instead of , the Adaptation Module relaxes the hard NTCP constraint (2.23) and solves the following optimization problem instead:(2.25) (2.26)
where , and and are priority weights assigned to tumor coverage and NTCP minimization, respectively, and will be determined by the planner. We refer to this type of optimization as Type 1.b Adaptation.3It would significantly improve the adaptation speed if the feasibility of can be determined in advance, before solving the problem. This can be easily achieved by setting u2 = 0 and verifying whether constraints (2.12)–(2.14) hold.
- Escalation: For radio-tolerant patients (those unlikely to develop RP2+ under the original plan), we maximize TCP (i.e., increase target dose) without violating NTCP constraints. This can be achieved simply by setting in (2.27) to its upper bound and solving the following optimization problem to optimality (this is referred to as Type 2 adaptation):
(2.27) (2.28)
Figure 3 shows the methodology flowchart.(2.29)
Figure 3:
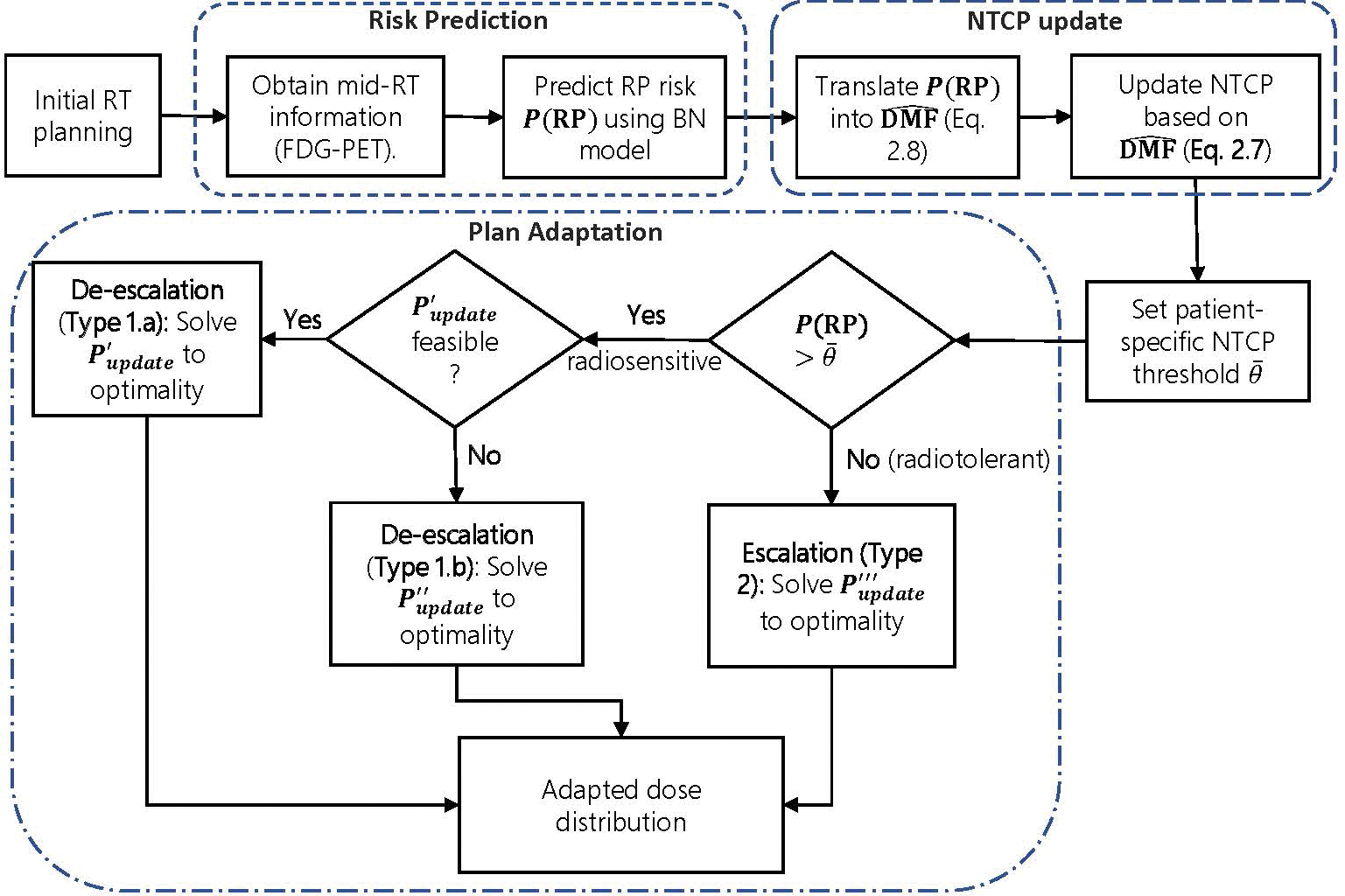
The schematics of the biological RT adaptation framework.
3. Numerical results
Image registration was performed in open-source imaging platform SlicerRT (Slicer.org) and Plastimatch (plastimatch.org). The image registration uncertainty was estimated to be within 5mm. All 69 patients were used during training and validation of the BN model. Parameter and structural learning were performed using bnlearn [35] package in R v3.5.1. The classification performance was evaluated via AUC based on a cut-off points derived from the ROC curve. Dose calculation and visualization were performed using matRad toolbox [36] in MATLAB R2019a. Photon and proton dose calculations were respectively based on the methods proposed by Bortfeld et al. [37] and Hong et al. [38]. To ease up the computational burden, the ROIs were limited to four volumes: GTV, normal lung (total lung excluding GTV), spinal cord, and heart. Voxel size was upsampled to 5 × 5 × 5mm to reduce memory requirements. Max-dose constraint of 54 Gy-RBE was imposed on spinal cord. For heart and normal lung, mean dose constraints of, respectively, 26 and 24 Gy(RBE) were imposed. Additionally, in line with the accepted level of toxicity for grade 2 RP, as reported in QUANTEC 2013 [39], an upper bound was set for the RP NTCP constraint (2.12). Minimum acceptable TCP was set to δ = 90%, and minimum and maximum target dose (to GTV) were set to ζ = 66 and Gy(RBE), respectively. Population-wide NTCP parameters were set to TD50 = 30.8 Gy, m = 0.37, n = 0.99, and α/β for tumor and normal lung were set to 10 and 3 Gy, respectively. All plans were first optimized with the same beam arrangements and dosimetric constraints of the original plan to recreate the original (delivered) dose distribution. The quality of the re-optimized plan was tested both visually and using dosimetric criteria extracted from the delivered dose. Once verified, the re-optimized plan was used as the basis of comparison between the baseline and adapted plans. For optimization, MATLAB implementation of the interior-point optimization algorithm, IPOPT [40] was used. All computations were performed on a desktop computer with 3.70 GHz Intel(R) Core(TM) i7–8700K CPU with 32 GB of RAM.
3.1. Experimental setup
We ran the Predictive Module on the data acquired before (Pre) and during the RT (Mid) data. The impact of adding mid-treatment information (additional FDG PET images) on model’s predictive performance was assessed via the difference in the ROC-AUC. Both models were benchmarked against the LKB NTCP model of Eq. (2.4). The mid-treatment BN was used to predict patients’ updated risk in the Adaptation Module. Fifteen patients were selected to evaluate the performance of the Adaptation Module: 5 patients who did not develop RP (RP2+ = 0) and 10 who did (RP2+ = 1). The correct adaptation strategy (Type 1.a, 1.b, or 2) was automatically selected according to § 2.5.3. The adapted plans were compared to the original plans based on DVH metrics and the change in the projected RP risk.
3.2. RP risk prediction
The pre-treatment and mid-treatment BN models for predicting RP2+ yielded AUCs of 0.79 (95% confidence interval, CI = [0.59–0.89]) and 0.84 (95%CI = [0.73–0.96]), respectively, as demonstrated in Figure 4. Both models improve upon the predictive performance of LKB NTCP models (AUC = 0.77, 95% CI = [0.55–0.87]), which solely rely on dosimetric information extracted from RT plans to predict the toxicity risk. The final mid-treatment BN model is depicted in Figure 5. According to the model, the risk of developing grade 2+ RP is affected by three major factors: (i) RT-specific factors, including the dose delivered to normal lung (e.g., V5, V20, MLD) and longer treatment length; (ii) clinical factor, including sex, breathing function, performance status, and smoking status; and (iii) underlying biological factors captured by FDG SUV metrics, specifically those extracted from mid-treatment images.
Figure 4:
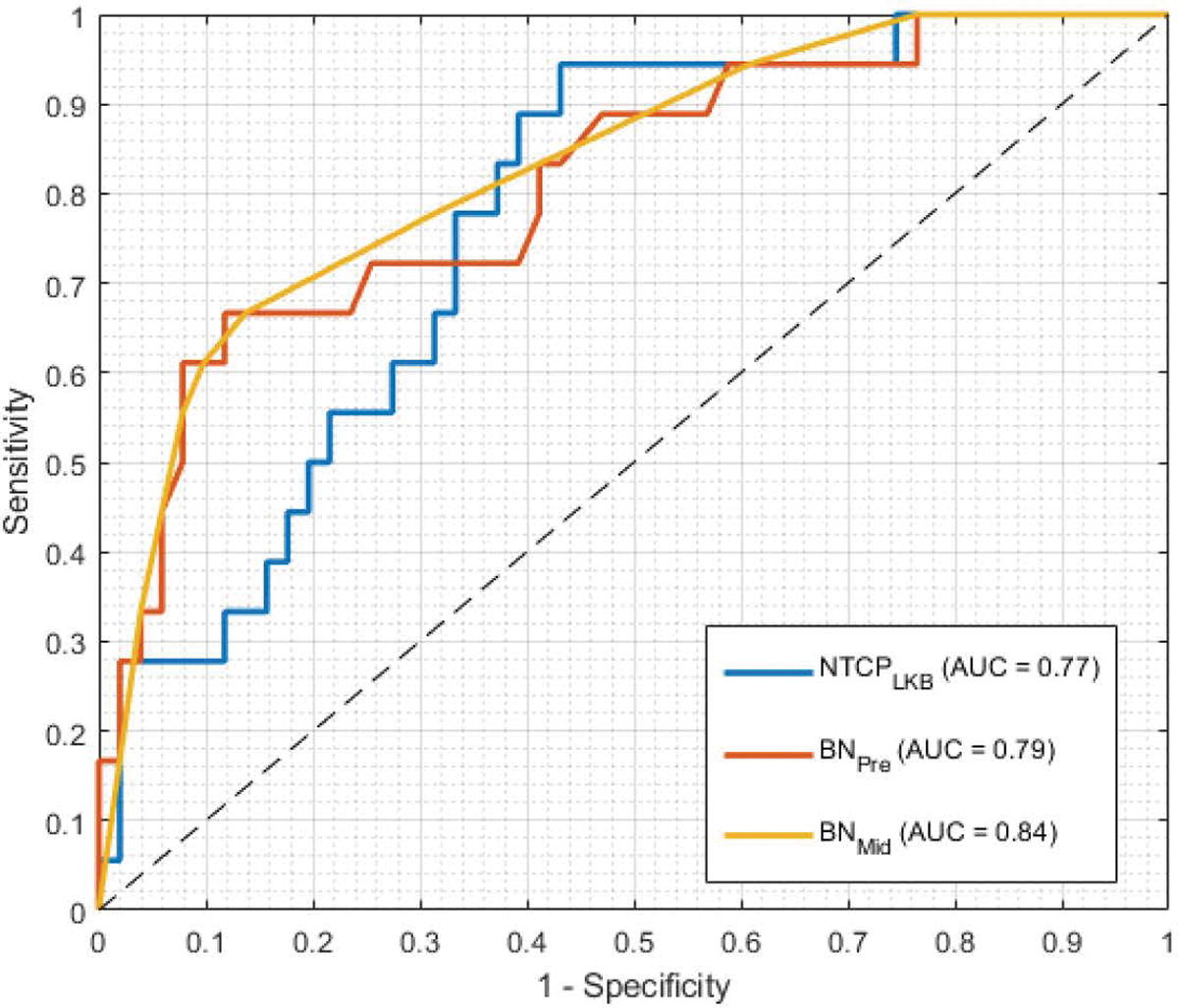
Receiver-operating characteristic (ROC) curves for predicting the risk of Grade 2+ radiation pneumonitis (RP) at 3 months post-RT. Three depicting models are the LKB NTCP model of Eq. (2.4), and the BN models trained on pre- and mid-treatment data. The dashed line represent the chance line (AUC = 0.50). Optimal cut-off values used for the classifiers were 0.22, 0.50, and 0.54 for the predictions of NTCPLKB, BNPre and BNMid models.
Figure 5:
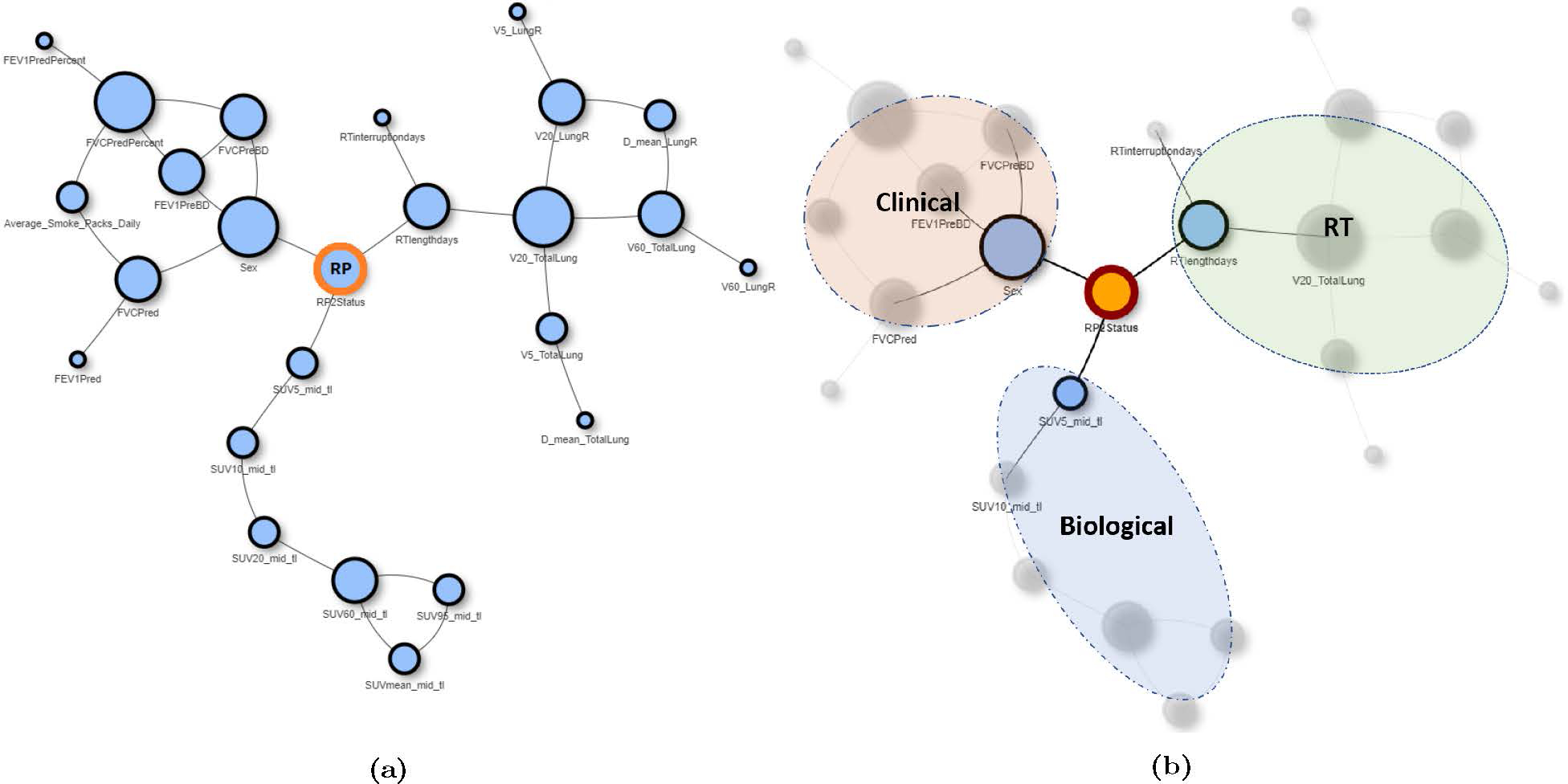
The structure of the final mid-treatment BN model for predicting the RP risk PBN(RP): (a) Full BN structure, (b) BN structure with feature classification according to feature type.
Figure 6a shows the waterfall plot of the RP risks predicted by the final BN. On average, patients who did not develop RP2+ had significantly lower predicted risk than those who did (0.17 vs. 0.49, Wilcoxon’s p < 0.0001, 95%CI for difference between groups = [−0.55, −0.15]). Further, the magnitude of the predicted risks corresponded with the severity of the radiation toxicity (i.e., RP grade), as depicted in Figure 6b. Specifically, the average predicted risk for grade 1–4 RP were 0.18, 0.42, 0.63, and 0.76, respectively (Kruskal-Wallis’ χ2 = 17.93, p = 0.0004).
Figure 6:

BN-predicted RP riskss: (a) waterfall plot for patients predicted risk, grouped by the (actual) post-RT RP status, where RP2+ = 0 (1) denotes patients who did not (did) develop RP; (b) Box and Whisker plot for patient’s BN-predicted risk according to RP grade, scored based on CTCAE v3, with corresponding Wilcoxon’s p-values for group comparison.
3.3. Plan adaptation
For those patients (n = 10) who were classified as high-risk (hereon after denoted by RP2+ = 1) and whose predicted risk was above the maximum NTCP threshold of , a dose de-escalation strategy (Type 1.a or 1.b) was performed. Dose escalation strategy (Type 2) was applied to the patients who were predicted not to develop grade ≥ 2 RP (classified as low-risk, RP2+ = 0), and whose predicted risk was below 0.20. Before presenting the full results, we first investigate four representative cases in more details.
3.3.1. Case 1: Minor de-escalation
Case 1 was a 75 years old non-smoker male, treated with proton RT to an originally-planned dose of 76 Gy-RBE in 37 fractions. LKB NTCP model predicted a risk of 0.12. The patient eventually developed grade 2 RP (RP2+ = 1). BN-predicted risk for this patient was 0.26 (corresponding to ). The Adaptation Module was used to de-escalate the dose to bring the projected risk below the maximum NTCP threshold of 0.20 (Type 1.a adaptation). Figure 7a shows the DVH plots for the original vs. adapted plans. The DVH plot for the target (GTV) shows is lowered to spare the dose to the entire normal lung (depicted in the DVH plot of the normal lung). This drop in the mean tumor dose resulted in the mean lung dose reduction (MLDorig = 19.2 vs. MLDadapt = 17.2 Gy-RBE), which in turn were predicted to result in an NTCP reduction of 0.06 (Figure 7b). It appears from Figure 7e that this reduction in NTCP has been achieved by shifting a partial region of high dose (> 60 Gy-RBE) outside the normal lung (V60orig = 15% vs. V60adapt = 11%). This has come at the expense of dose increase in the area denoted by the white arrows (note that no constraint was imposed to regulate the dose in these areas).
Figure 7:
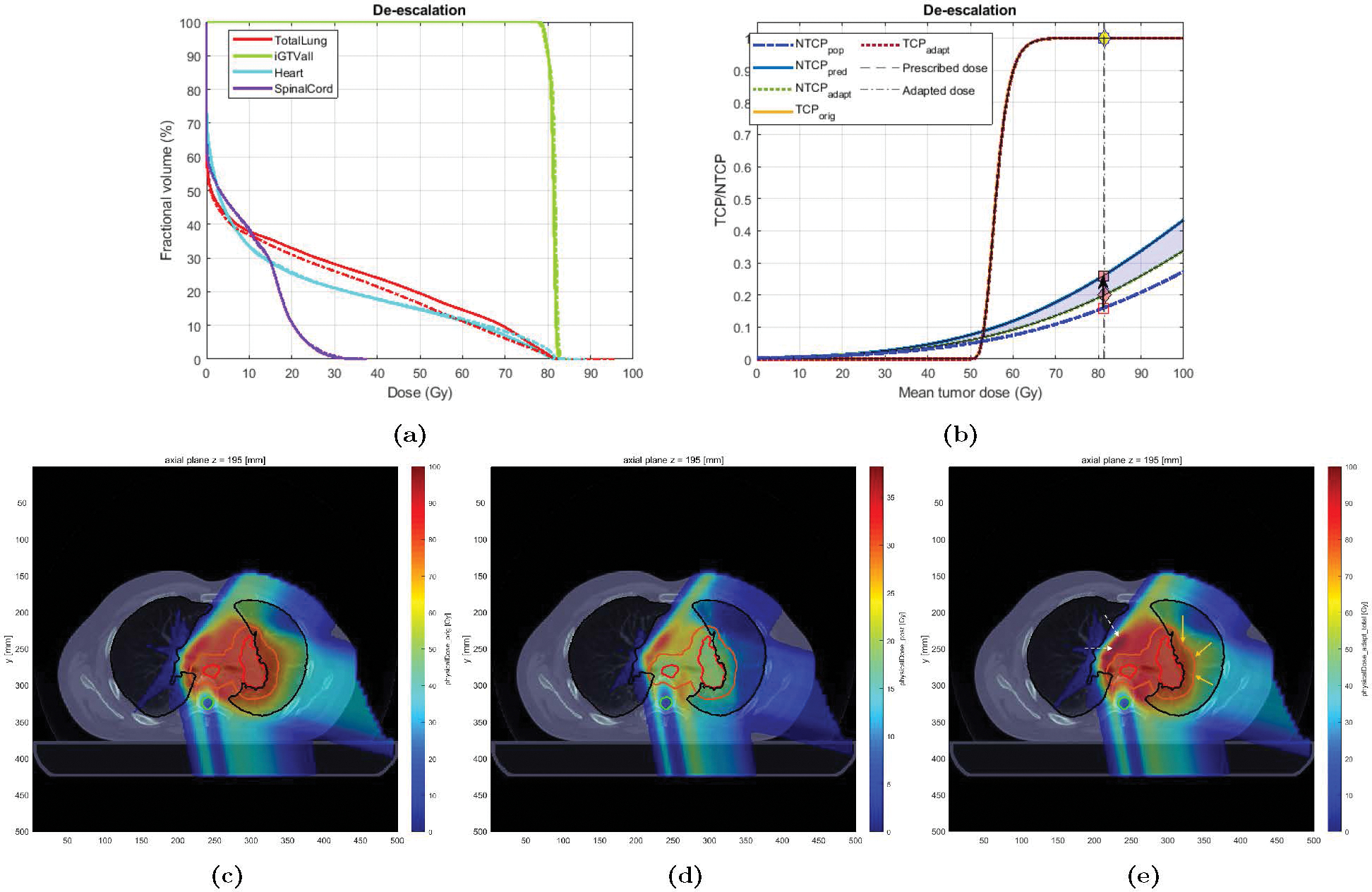
Original vs. Adapted plans for Case 1: (a) Dose volume histogram (DVH) for the original (solid) and adapted (dashed) plans; (b) TCP-NTCP curves for both plans. The black arrow denotes the change in NTCP from the initial expectation (0.12) to the projected risk (0.26). The pink diamond denotes the adapted risk (0.20); (c)-(e): Dose distribution for Case 1; (c) original plan (37 fx), (d) adapted plan (for the remaining 10 fractions), and (e) new plan (27 fx of original + 10 fx adapted). The contours for GTV, PTV, total lung, and spinal cord are colored in red, orange, black, and cyan, respectively. The yellow (white) arrows denote the areas where the dose has been decreased (increased) in the adapted plan compared to the original one. The blue shaded area denotes the change in NTCP due to adaptation.
3.3.2. Case 2: Moderate de-escalation
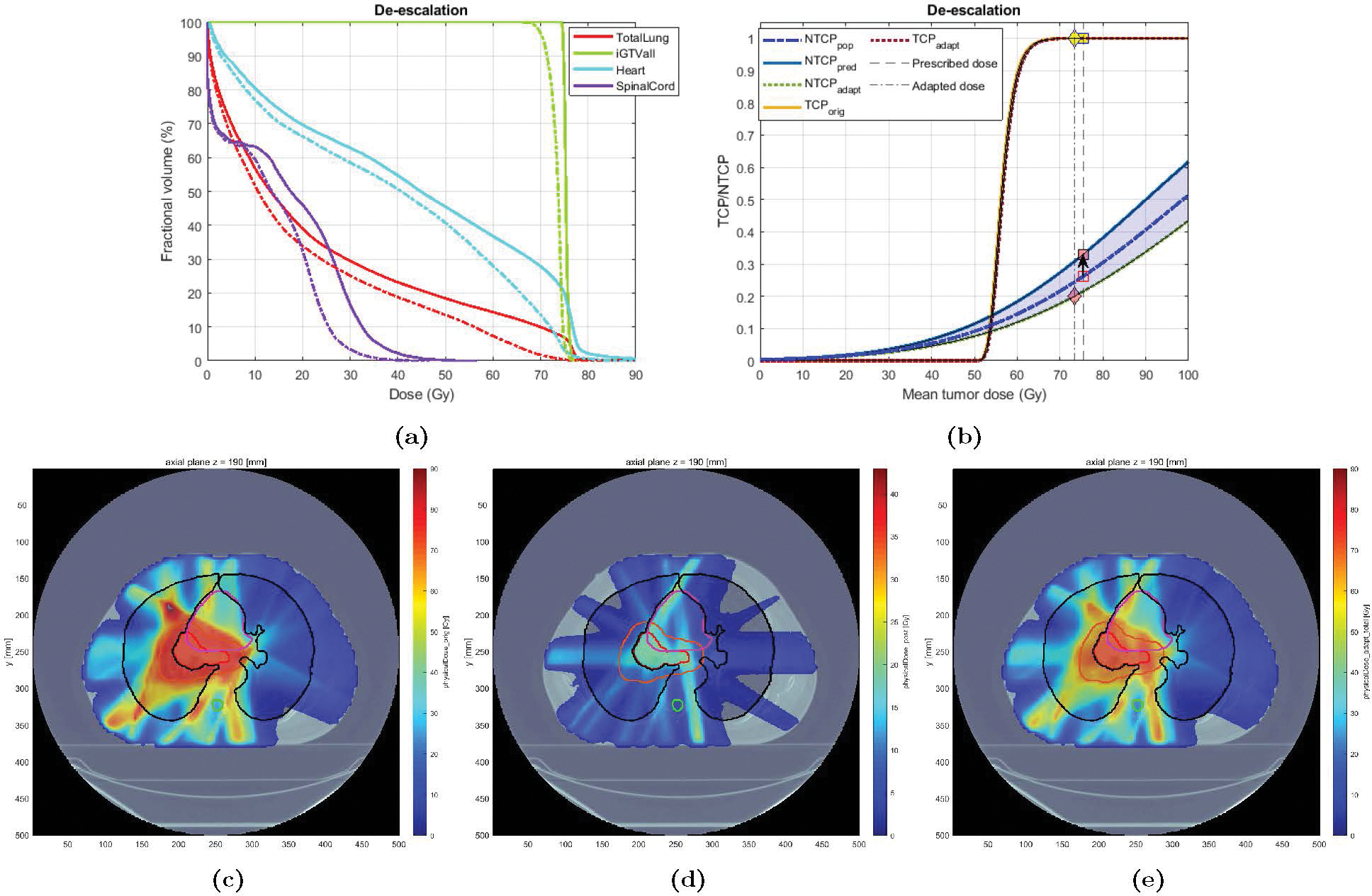
Case 2 was an 80 years old male with a history of heavy smoking, treated with IMRT to an originally planned dose of 74 Gy in 33 fractions. The patient eventually developed grade 3 RP (RP2+ = 1). Based on the planned dose, LKB NTCP was estimated at 0.20. The BN model projected the RP risk to be 0.33 (). Therefore, the Adaptation Module seeks to de-escalate the dose (using Type 1.a adaptation) in order to lower the risk below the pre-specified threshold of . Figure 8 shows the DVH and NTCP-TCP plots for the original and the adapted plan. In this case, the NTCP goal of 0.20 (down from the original 0.33) was achieved after a 2-Gy mean tumor dose reduction (from 75.4 to 73.4 Gy) - corresponding to MLD reduction from 23.4 to 19.2 Gy. Note that, as depicted in Figure 8b, this has been achieved without compromising TCP (close to 100%). Also, tumor coverage remains high (D98adapt = 76.5 Gy). Figure 8e better illustrates this significant dose reduction.
Figure 8:
Original vs. Adapted plans for Case 3: (a) DVH plots for the original (solid) and adapted (dashed) plans; (b) TCP-NTCP curves for the original and the adapted plan. (c)-(e): Dose distribution for Case 3: (c) original plan (37), (d) adapted plan (for the remaining 13 fx), and (e) new plan (24 fx of original + 13 fx adapted). The contour for GTV, PTV, total lung, heart, and spinal cord are colored in red, orange, black, purple, and cyan, respectively.
3.3.3. Case 3: Major de-escalation
Case 3 was a 48 years old heavy smoker female treated with IMRT who eventually developed grade 3 RP. The original plan delivered a mean GTV dose of 82 Gy and the LKB NTCP was estimated at 0.24, while the mid-treatment BN-projected risk based on patient-specific information (acquired at fx 25), was 0.67 (), indicating a patient with higher-than-average lung radiosensitivity. Accordingly, a de-escalation strategy was chosen for plan adaptation. Based on the high predicted radiosensitivity of this case, the NTCP goal of 0.20 could not be achieved given the already delivered dose and the constraints on the minimum TCP and tumor dose (respectively set at 90% and 66 Gy); that is, the amount of dose delivered in the first 24 fractions (MLDpre = 17 Gy, ) was deemed “too much”. Therefore, Type 1.b adaptation was chosen wherein the goal was set to minimize the NTCP risk as much as possible, within the given constraints (i.e., solve in (2.25), with and ). Figure 10 shows the results. After tumor dose reduction of 16.8 Gy (from 82.7 down to 65.9 Gy), corresponding to an MLD reduction from 25.2 to 19.8 Gy, the minimum NTCP of 0.41 was achieved (down from 0.67 using the original plan). Note that even after this significant tumor dose reduction, the estimated TCP remained very high (Figure 9b). Also note that only a dose of about 10 Gy was found optimal to deliver over the remaining 13 fraction; i.e., the adapted plan called for a ultra-hyperfractionation scheme of ≈ 0.77 Gy/fx to preserve lung functionality. This can be verified in Figure 9d.
Figure 10:

Original vs. Adapted plans for Case 4: (a) DVH plots for the original (solid) and adapted (dashed) plans; (b) TCP-NTCP curves for the original and the adapted plan. (c)-(e): Dose distribution for Case 4: (c) original plan (30), (d) adapted plan (for the remaining 11 fx), and (e) new plan (19 fx of original + 11 fx adapted).
Figure 9:
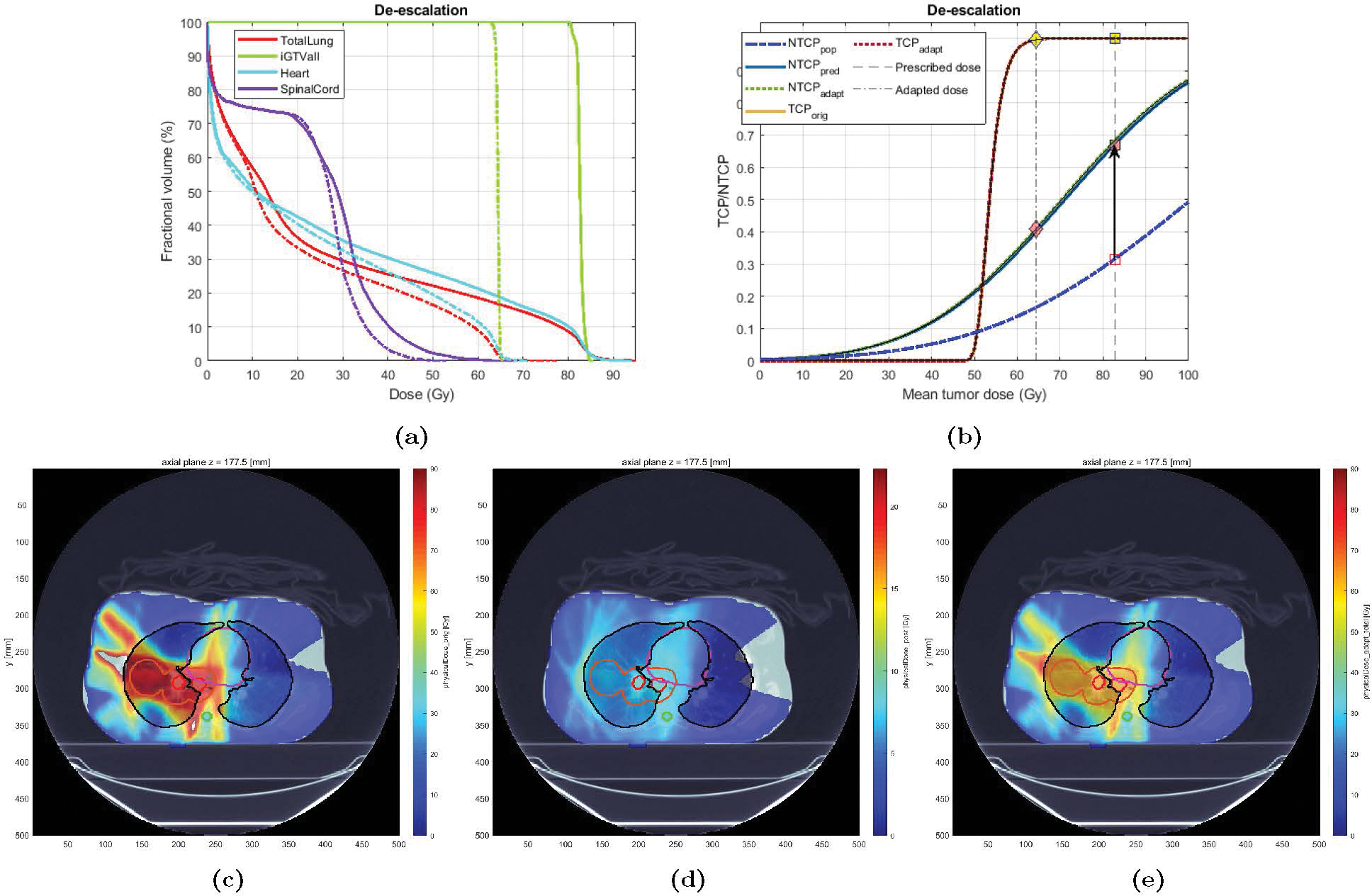
Original vs. Adapted plans for Case 2: (a) DVH plots for the original (solid) and adapted (dashed) plans; (b) TCP-NTCP curves for the original and the adapted plan. (c)-(e): Dose distribution for Case 2; (c) original plan (33 fx), (d) adapted plan (for the remaining 10 fx), and (e) new plan (23 fx of original + 10 fx adapted).
3.3.4. Case 4: Dose escalation
Case 4 was a 66 years old male with moderate history of smoking, treated with IMRT to a mean tumor dose of 65.8 Gy in 30 fractions. The treatment was well-tolerated (RP grade = 1). The mid-treatment FDG-PET was taken at fraction 20. The estimated LKB NTCP was 0.17 and the predicted BN-based risk was 0.09 (), indicating a radio-tolerant patient (in terms of normal lung radiosensitivity). Since the predicted NTCP is lower than the NTCP threshold of 0.20, an escalation adaptation strategy was pursued (Type 2). Figure 10a shows the results of the adaptation strategy. The mean tumor dose was increased from 65.8 in the original plan to 78.9 Gy, resulting in an increase in the projected NTCP to 0.17 (which was still lower than the maximum tolerable level of 0.20), while respecting the constraints on heart and spinal cord.
Table 1 summarizes the results of the plan adaptation for all fifteen tested patients. All patients who were predicted in the RP2+ = 0 class (n = 5) and whose predicted risk was projected to be lower than 0.20, received dose escalation (Type 2). On average, dose escalation resulted in an increase in mean tumor dose (MTD) of about 6.47 Gy(RBE) (range = [2.67–17.5], standard deviation, σ = 6.25). This came at the expense of an average increase in MLD of 0.12 Gy(RBE) [2.57–7.05] (σ = 1.46). Consequently, the average increase in projected NTCP was 0.02 [0–0.08] (σ = 0.03). The projected NTCP after adaptation was successfully kept below 0.20 in all cases. Among the remaining patients (n = 10) who were candidates for de-escalation (predicted in the RP2+ = 1 with predicted NTCP > 0.20), two underwent Type 1.a adaptation (reaching an acceptable adapted NTCP ≤ 0.20), and eight were adapted via Type 1.b adaptation (NTCP was minimized as much as possible, but could not be reduced below 0.20). On average, for de-escalation candidates, MTD was reduced by 7.98 Gy(RBE) [0.15–19] (σ = 6.40), resulting in an average MLD and NTCP reduction of 2.98 Gy(RBE) [0.8–5.4] (σ = 1.33) and 0.15 [0.04–0.27] (σ = 0.07), respectively. Average for the radio-tolerant (RP2+ = 0) and radiosensitive (RP2+ = 1) groups were 0.8 and 1.63.
Table 1:
Summary of the adaptation results.
| No. | RP grade | Update fx | P(RP) | Adapt | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| 1 | 76.70 | 11.30 | 0.06 | 1 | 36/37 | 0.01 | 0.38 | 2 | 79.5 | 11.7 | 0.01 |
| 2 | 61.40 | 19.66 | 0.17 | 1 | 20/30 | 0.09 | 0.61 | 2 | 78.9 | 17.2 | 0.17 |
| 3 | 74.99 | 18.05 | 0.13 | 1 | 31/37 | 0.12 | 0.96 | 2 | 79.49 | 18.79 | 0.13 |
| 4 | 74.70 | 16.60 | 0.11 | 1 | 31/37 | 0.15 | 1.13 | 2 | 79.7 | 17.4 | 0.17 |
| 5 | 77.20 | 15.78 | 0.10 | 1 | 12/37 | 0.19 | 0.94 | 2 | 79.77 | 16.89 | 0.20 |
| 6 | 76.27 | 19.20 | 0.12 | 2 | 28/37 | 0.26 | 1.15 | 1.a | 76.12 | 17.2 | 0.20 |
| 7 | 75.40 | 23.40 | 0.20 | 3 | 29/33 | 0.34 | 1.21 | 1.a | 73.4 | 19.2 | 0.20 |
| 8 | 71.82 | 24.48 | 0.22 | 2 | 23/33 | 0.54 | 1.30 | 1.b | 64.82 | 20.51 | 0.36 |
| 9 | 73.40 | 16.86 | 0.19 | 2 | 30/35 | 0.64 | 2.04 | 1.b | 54.4 | 14.68 | 0.48 |
| 10 | 65.98 | 24.26 | 0.22 | 3 | 28/30 | 0.67 | 1.63 | 1.b | 65.43 | 23.46 | 0.63 |
| 11 | 82.20 | 25.20 | 0.24 | 3 | 25/37 | 0.68 | 1.58 | 1.b | 65.9 | 19.8 | 0.41 |
| 12 | 75.70 | 15.98 | 0.11 | 2 | 28/33 | 0.68 | 2.14 | 1.b | 65.14 | 13.64 | 0.50 |
| 13 | 71.98 | 22.12 | 0.19 | 3 | 25/30 | 0.73 | 1.82 | 1.b | 65.68 | 18.86 | 0.53 |
| 14 | 77.68 | 24.10 | 0.28 | 3 | 28/30 | 0.76 | 1.60 | 1.b | 66.12 | 20.71 | 0.62 |
| 15 | 72.05 | 23.91 | 0.21 | 4 | 28/30 | 0.76 | 1.79 | 1.b | 65.72 | 21.66 | 0.64 |
|
| |||||||||||
| Mean/Median*/Mode† | |||||||||||
|
| |||||||||||
| All | 73.83 | 20.06 | 0.17 | 2* | 28*/33* | 0.44 | 1.35 | 1.b† | 70.67 | 18.11 | 0.35 |
| RP2+=0 | 73.00 | 16.28 | 0.11 | 1* | 31*/37* | 0.11 | 0.80 | 2† | 79.47 | 16.40 | 0.14 |
| RP2+ = 1 | 74.25 | 21.95 | 0.20 | 3* | 28*/33* | 0.61 | 1.63 | 1.b† | 66.27 | 18.97 | 0.46 |
MTD = mean tumor dose; MLD = mean lung dose; fx: fraction; P(RP): BN-predicted risk; : pat ient-specific dose modifying factor; Adapt: Adaptation type: (1.a) dose de-escalation, (1.b) minimizing NTCP, (2) dose escalation; : Original plan; : Adapted plan. MLD and MTD are given in Gy(RBE).
3.4. Impact of biomarker acquisition timing
To investigate the impact of biomarker acquisition timing, we varied the update point for a representative the cases (Case 3 in § 3.3) and re-ran the Adaptation Module for each instance. In keeping with the actual range of the image acquisition timeline in the entire dataset, we simulated the experiments by varying the timing of the PET acquisition between fractions 10–37 (out of a total 37 fractions). We assumed the same FDG image was taken on each timepoint. Similarly, all the other parameters, including the predicted risk of 0.66, dosimetric criteria, and total number of fractions, remained unchanged; that is, the difference in the reported adapted NTCP value is solely the result of varying the update point (and thus the adaptation “room”). The result, given in Figure 11, point to the large impact of the timing on the overall performance of the adaptation scheme (NTCPadapt = 0.20 vs. 0.43, when the update point was at fx 20/37 vs. 30/37).
Figure 11:
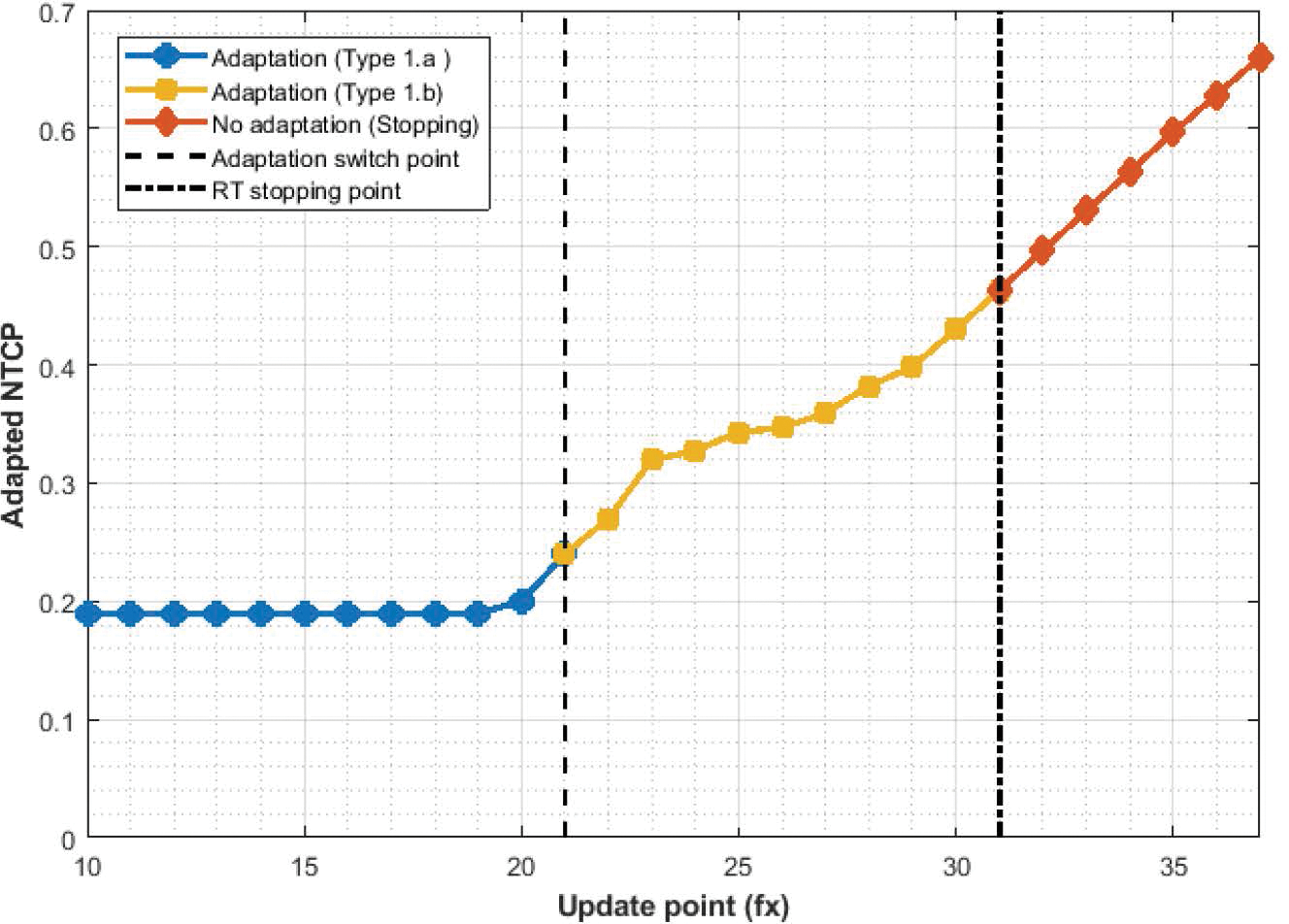
Impact of the change in update point on overall adaptation performance, in terms of adapted NTCP. The adaptation switches from Type 1.a to Type 1.b when the update point changes from fraction 20 to 21. There is no use in updating after fraction 31/37, as the dose delivered to tumor already exceeds the minimum tumor dose of 66 Gy(RBE), rendering the adaptation problem infeasible. The reported NTCP is for the case where the RT is stopped at the corresponding fractions.
4. Discussion
In this paper, we have presented an end-to-end methodology for personalizing the radiation treatment of NSCLC patients using patient-specific information collected from pre- and mid-treatment FDG PET images. The proposed methodology synthesizes the imaging data with other clinicopathological information using an interpretable Bayesian Networks machine learning model, predict the probability of developing radiation toxicity (grade 2+ RP), and uses that prediction to automatically adapt the treatment course based on a novel NTCP-based plan optimization. We had previously proposed a TCP-based adaptive approach [41] to integrate imaging (PET) information regarding tumor response into treatment planning. There, we assumed that the change in PET SUV signal between pre- and mid-treatment scans can be directly translated into patient-wise radiosensitivity parameter α. The methodology proposed here can be seen both as complimenting our previous approach, insofar as it focuses on NTCP instead, and extending it, since it embeds the imaging information within a response prediction model before estimating patient-specific radiosensitivity. The methodology improves upon other pre-treatment classification methods by including mid-treatment information to update the initial risks. Further, instead of a simple binary classification which is not amenable to plan adaptation, it estimates the probability of developing RP risk, which is not only closer to the concept of NTCP and can be implemented during treatment planning, but is capable of distinguishing between patients in the same RP class and advises a more nuanced adaptation strategy, thus helping to move from a stratified approach towards a more personalized one. Finally, the method is capable of automatically finding the optimal adaptation strategy for each patient, given their predicted risk and the desired levels of TCP and NTCP set by physician/planner.
The effectiveness of Bayesian Networks for predicting RP risks has been investigated by a number of authors [42, 43, 44, 45]. Our model extends their results to include mid-treatment imaging information alongside clinicopathological data. Despite the relatively smaller sample size in our dataset, the predictive performance (AUC ≃ 0.84) was on par with the previous results. In the final model, RP was shown to be simultaneously impacted by three main classes of factors: dosimetric factors extracted from the delivered plan, clinicopathological factors evident at presentation, and radiobiological factors indicated by the mid-treatment FDG PET information (SUV features). It is interesting that in the latter class, in addition to the well-known mean SUV, both lower SUV percentiles (5–20%), and higher percentiles (60,95%) were also picked by the model as potential predictors of the outcome (Figure 5), indicating that, despite being highly correlated with one another (Pearson’s r ∈ [0.63, 0.99]), they nevertheless provide somewhat complimentary information with regards to RP risk. Further, the results of bootstrapping showed that the frequency with which each class appeared in the final model was roughly equal, indicating a balanced contribution across the classes, which is more or less in line with common wisdom, and thus can provide a qualitative validation for our predictive model and enhance physicians’ trust in its predictions.
The results showed that the addition of mid-treatment FDG-PET images improved the predictive performance of the BN model, resulting in an AUC increase from 0.79 to 0.84. Specifically, this corresponded to reclassification of 3 patients in our cohort (all from RP2+ = 0 to 1, denoting an increase in sensitivity). Although the impact of post-treatment FDG uptake on RP had been previously reported [23, 46], such information cannot be used for plan adaptation purposes, as the treatment is already over by the time the RP prediction is made. The effect of mid-treatment FDG information in predicting RP has not, to the best of our knowledge, been reported (except for our previous findings on a subpopulation of the current dataset [47]). It is noteworthy that despite using far fewer features, a simple LKB NTCP risks yielded a descent AUC of 0.77, indicating the relative adequacy of such models for comparing the relative risks between two plans.
The correspondence between predicted risk and RP severity, as depicted in Figure 6b, is very important. Unlike many (binary) classification scores which are solely used to stratify patients between two groups (responders vs. non-responders) and are often noninformative with regards to severity, the BN-predicted risks showed an association with the RP grade (the higher the grade, the higher the predicted risk). Although this trend is very promising, the small sample size in the higher RP grades (grade 3, n=5, and grade 4, n=1) made it impossible to fully investigate this association. Nevertheless, this is a crucial feature in our adaptation approach, as the magnitude of the predicted risk is used to determine the intensity of dose (de)escalation; i.e., patients with a higher risk (hence, likely to develop more severe RP) underwent more intense dose de-escalation.
The results of the adaptation showed that the methodology is capable of automatically adapting the treatment course for a wide range of patient risks and original plans. During the optimization of the de-escalation cases (especially in Type 1.b optimization), the minimum tumor dose constraint was often the binding constraint, preventing from further improving NTCP. For a number cases in Type 1.b, it would have been possibly to further improve NTCP by lowering the minimum tumor dose constraint to, say, 60 Gy(RBE), if deemed permissible by the treating physician. Similarly, during dose escalation, the restricting constraint was often the maximum tumor dose of 80 Gy(RBE). Given the precedence of delivering up to 86 Gy(RBE) to NSCLC patients [21], one could increase the upper bound for a more aggressive plan. However, it is impossible to evaluate the impact of such dose (de)escalation strategies on tumor control without an equivalent patient-specific TCP model. In our numerical results, the adopted plan was usually an approximately linearly scaled version of the original plan. This can be explained by the (roughly) linear relationship between predicted risk and DMF in Figure 2 when the predicted risk is between around 0.2 and 0.8. Knowing this, the adapted plan can be simply obtained by a linear dose (de)escalation that results in the fulfilment of the NTCP constraint, thus saving computational time by foregoing a full-on optimization. Nevertheless, the optimization model is capable of delivering the optimal adapted plan for cases when the predicted risk is outside the linear range.
One important factor in determining the quality of the adapted plans (and how likely it is to respect NTCP constraints) is the timing of the image acquisition (i.e., update point). Unfortunately, there does not appear to be consensus for the optimal acquisition timing of FDG PET images for NSCLC patients [48, 19, 49]. In our experiments, as can be deduced from Table 1, in cases where the update point was towards the end of the treatment and only a few fractions were available for plan adaptation, the Adaptation Module did relatively worse. This is intuitive, since the later the information arrives, the less “room” there is for adaptation. This results were confirmed by the experiments in § 3.4. However, the benefit of earlier image acquisition is somewhat mitigated by the fact that images taken earlier during the treatment might not have the same level of biological information present at later fractions, mainly due to the time and the dose threshold needed for biological changes to manifest in radiological images. The latter can impose some challenges in translating the results of this work in treatments with small number of fractions such as stereotactic body radiation therapy, which are current gaining momentum for treatment of early stage lung cancers [50, 51]. In such cases, dispersing the dose over multiple stages or “pulses” could give the biological effect time to be manifested in biomarkers and subsequently be used in RT adaptation, similar to the newly-proposed PULSAR paradigm [52].
Our methodology follows a modular design, wherein each of the three modules (risk prediction, NTCP penalization, and plan adaptation), could be modified to account for alternative approaches. For instance, one can use a different model for the risk prediction phase, as long as the model is probabilistic (i.e., provides probability of outcome instead of class) and there is at least some level of association between these probabilities and RP severity. Similarly, instead of DMF to link the model’s prediction to NTCP parameter, one can simply update the population-wide TD50 and use the update TD50 to arrive at a patient-specific NTCP. Further, other (faster) optimization algorithms such as conic optimization [53] or lexicographic optimization [54] can be used in the Adaptation Module, as long as the method is capable of handling TCP and NTCP constraints.
Consistent with the result of the original trial [18], we could not detect any differences between the proton and photon arm in our secondary study in terms of incidence of Grade 2+ RP. Further, no significant difference was observed between the two arms in terms of mid-course FDG uptake pattern (Supplementary Material, Figures S2–3). Although it has been hypothesized that proton therapy could lower the incidence of RP by reducing the volume of lung tissue exposed to low-dose bath (i.e., V5–10Gy), this could not be confirmed in the original trial, potentially due to the higher volume of lung exposed to higher doses (V20–80Gy). In a subsequent study of PSPT vs. Intensity Modulated Proton Therapy (IMPT) [55], the authors found significantly lower mean doses to the lungs, resulting in reduced incidence of RP3+ in the IMPT group (2% vs. 17%), which indicates the impact of more advanced and accurate delivery method on reducing treatment-related toxicity, though a straight comparison the state-of-the-art photon vs. proton RT in terms of toxicity burden is still lacking. Aside from the physical dose bath, another important difference between photon and proton delivery is the difference in biological effectiveness of proton compared with photon, which is often captured by the concept of relative biological effectiveness (RBE). In a preliminary study in the early phase of the current trial [56], the authors found correlations between the regions of higher variable RBE-weighted doses inside the lung and higher SUV updates in the re-staging PET. However, a complete study of the potential impact of variable RBE on incidence and patterns of RP is still missing.
Despite its advantages, the limitations of our study have to be acknowledged. First, the limited sample size of our study could jeopardize the generalizability of our predictive model. Although we attempted to account for it using statistical techniques and internal validation (bootstrapping and cross validation), it is hard to foresee the model’s generalizability without applying it to a much larger and ideally multi-institutional dataset. Second, the translation of the model predictions (RP risks) into a single NTCP parameter () is perhaps an oversimplification (which we nevertheless had to make in order to bridge the gap between the Predictive Module and the Adaptation Module), as it reduces the complexity of a multi-factor predictions (and thus patients’ complex radiosensitivity) into a single parameter. Even though this is in line with a traditional way of modeling radiosensitivity in the RT literature (using α/β parameters), a better approach would have been to directly integrate the predictive model into the treatment planning process. This is the subject of our ongoing research and we hope to report on that in a follow-up publication. Another important aspect which was outside the scope of this study but nevertheless is worth mentioning, is the impact of uncertainties on the adaptation. There are three main sources of uncertainties: (i) modeling uncertainties (uncertainties regarding the predictions of the model, i.e., model “accuracy”), and (ii) uncertainties arising while translating the risk into NTCP parameter, and (iii) biomarker uncertainties contained within the FDG SUV signals. The latter can be further classified into inherent uncertainties of FDG PET scans to assess patients’ metabolism, and the registration-related uncertainties. We attempted to quantify the impact of the registration uncertainties on the results of our algorithm by introduced systematic error of up to 5mm on x-y-z directions (the estimated error of our image registration) and assessing the impact on model predictions and plan adaptation part. The results showed no significant impact introduced by the image registration (p > 0.05); in particular, the average change in the adapted mean lung dose changed on average was estimated at 0.35Gy (95% CI: 0.12–0.64), presumably because in the prediction model, only aggregate metrics (SUVmean, SUV5%, etc.) were used (which did not significantly get changed as the result of the introduced error), and the prediction only partially relies on imaging features. Nonetheless, taking all (or some) of these uncertainties into account would require robust optimization. We had previously researched the impact of some robust optimization methods on reducing parameter and model’s uncertainties [57, 58, 59, 60]. Lastly, we only included four OARs in the Adaptation Module, which inevitably lead to oversimplification of the optimization problem and overestimating the extent to which the plan can be adapted. However, our aim here was not to present a fully clinical version of our methodology, but to investigate its feasibility and potential clinical impact. Of course, the full examination of the clinical impact requires running a full-on clinical trial.
Despite these limitations, this study, for the first time, proposes a rather simple method for bridging the gap between machine learning and optimization, and offers a biologically-informed and systematic approach for adapting the treatment course of NSCLC patients which does not require physicians to pre-specify the adaptation dose level [21, 49]. In our future works, we aim at combining our approach with our previous [41] TCP-based plan adaptation scheme to provide a full TCP-NTCP-based treatment personalization framework.
5. Conclusions
In this project, we have implemented a three-component framework to adapt the RT treatment plans of NSCLC patients according to individually predicted risk of radiation pneumonitis, using FDG PET images acquired during the course of RT. We have shown that a personalized adaptation plans can be derived by using mid-treatment FDG PET scans and a novel machine learning-based predictive model. This work can be seen as a proof-of-concept for future development of such personalized treatment planning model which, if implemented, might make a significant contribution towards enhancing the existing “one-size-fits-all” methodologies in treatment planning in radiotherapy. The proposed methodology could help the design of personalized clinical trials for NSCLC patients.
Supplementary Material
Acknowledgments
The authors would like to express their gratitude to Drs. Nadya Shusharina (Massachusetts General Hospital & Harvard Medical School), Uwe Titt and Dragan Mirkovic (both from University of Texas’ MD Anderson Cancer Center) for their help in extracting treatment and imaging data. This study was partially funded by the National Cancer Institute of the United States under grant number R01CA266275, the Therapy Imaging Program (TIP) funded by the Federal Share of program income earned by Massachusetts General Hospital on C06CA059267, Proton Therapy Research and Treatment Center, and by Philips Medical Systems.
6. Appendices
A. Fractionation-corrected NTCP
In order to adjust the NTCP in Eq. (2.7) to the change in fractionation as the result of adaptation (i.e., delivering two distinct dose distribution (pre- and post-adaptation), we resort to the concept of biologically-effective dose (BED) proposed by [28]. For an organ receiving Dpre and Dpost during the first N1 = (T − 1) and the second N2 = (N − T +1) fractions, the fractionation-corrected BED is calculated as
| (A.1) |
where α/β is the OAR radiosensitivity parameter [28]. Further, since all NTCP parameters are estimated for a standard fractionation (2 Gy/fraction), we need to convert the dose to an equivalent 2-Gy-per-fraction dose. This can be accomplished converting BED to the modified equivalent uniform dose [61], as recommended by AAPM Report 166 [62]:
| (A.2) |
Therefore, the fractionation-corrected version of NTCPBN in Eq. (2.7) can be calculated as
| (A.3) |
B. Convexity of the fractionation-corrected NTCP
The convexity of can be proven by following the deductive steps given below:
The log-transformation , where is dervied by setting in (A.3), is convex (see [29] for proof of convexity).
According to the composition rule of convexity [34], a composite function H = g ∘ f = g(f(x)), where , is convex if g is convex and nondecreasing (nonincreasing), and f is convex (concave).
If we set (which is both convex and nondecreasing) and (which is convex), then will be convex.
The convexity of follows by verifying that .
Footnotes
It can be shown that the set defined by the right-hand-side (RHS) of the inequality attains its supremum (its most restrictive case) when N = 1 and αT → 0, in which case, we have . Thus, for a typical minimum tumor dose of 60 Gy, which will automatically be enforced via Const. (2.14), the convexity of log TCP is guaranteed as long as βT > 1.39 × 10−4, which is known to hold not only for lung tumors, but for virtually all known tumor sites [32, 33].
Note that constraints of the form f(x) ≥ q(x) where f(x) and q(x) are, respectively, concave and affine functions, are convex [34].
Given that for fixed combinations of , TD50, and m, minimizing NTCPBN is equivalent to minimizing , the NTCP term in (2.25) can be replaced by the gEUD function of Eq. (2.5), which, since it is a norm and therefore convex [34], can speed up the optimization. This could further be improved for n ≈ 1 (a typical value for a parallel organ such as lung), in which case the gEUD formulation reduces to mean dose, which would subsequently result in a linear constraint.
Ethical Statement
This was a retrospective secondary study of a previously-published clinical trial #NCT00915005. All the requirements of the institutional Internal Review Board was met. All participants (or their parent or legal guardian in the case of children under 16) gave written informed consent to participate in the study.
References
- [1].Bradley Jeffrey D., Paulus Rebecca, Komaki Ritsuko, Masters Gregory, Blumenschein George, Schild Steven, Bogart Jeffrey, Hu Chen, Forster Kenneth, Magliocco Anthony, Kavadi Vivek, Garces Yolanda I., Narayan Samir, Iyengar Puneeth, Robinson Cliff, Wynn Raymond B., Koprowski Christopher, Meng Joanne, Beitler Jonathan, Gaur Rakesh, Curran Walter, and Choy Hak. Standard-dose versus high-dose conformal radiotherapy with concurrent and consolidation carboplatin plus paclitaxel with or without cetuximab for patients with stage IIIA or IIIB non-small-cell lung cancer (RTOG 0617): a randomised, two-by-two factorial p. Lancet Oncol, 16(2):187–199, feb 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Martel Mary Kaye, Haken Randall K. Ten, Hazuka Mark B., Kessler Marc L., Strawderman Myla, Turrisi Andrew T., Lawrence Theodore S., Fraass Benedick A., and Lichter Allen S. Estimation of tumor control probability model parameters from 3-D dose distributions of non-small cell lung cancer patients. Lung Cancer, 24(1):31–37, 1999. [DOI] [PubMed] [Google Scholar]
- [3].Willner Jochen, Baier Kurt, Caragiani Ekaterini, Tschammler Axel, and Flentje Michael. Dose, volume, and tumor control prediction in primary radiotherapy of non-small-cell lung cancer. Int. J. Radiat. Oncol. Biol. Phys, 52(2):382–389, feb 2002. [DOI] [PubMed] [Google Scholar]
- [4].Bradley Jeffrey, Graham Mary V., Winter Kathryn, Purdy James A., Komaki Ritsuko, Roa Wilson H., Ryu Janice K., Bosch Walter, and Emami Bahman. Toxicity and outcome results of RTOG 9311: A phase I-II dose-escalation study using three-dimensional conformal radiotherapy in patients with inoperable non-small-cell lung carcinoma. Int. J. Radiat. Oncol. Biol. Phys, 61(2):318–328, feb 2005. [DOI] [PubMed] [Google Scholar]
- [5].Kong Feng Ming, Haken Randall K. Ten, Schipper Matthew J., Sullivan Molly A., Chen Ming, Lopez Carlos, Kalemkerian Gregory P., and Hayman James A. High-dose radiation improved local tumor control and overall survival in patients with inoperable/unresectable non-small-cell lung cancer: Long-term results of a radiation dose escalation study. Int. J. Radiat. Oncol. Biol. Phys, 63(2):324–333, oct 2005. [DOI] [PubMed] [Google Scholar]
- [6].van Baardwijk Angela, Geert Bosmans, Boersma Liesbeth, Wanders Stofferinus, Dekker André, Dingemans Anne Marie C., Gerben Bootsma, Wiel Geraedts, Cordula Pitz, Jean Simons, Philippe Lambin, and Ruysscher Dirk De. Individualized Radical Radiotherapy of Non–Small-Cell Lung Cancer Based on Normal Tissue Dose Constraints: A Feasibility Study. Int. J. Radiat. Oncol, 71(5):1394–1401, aug 2008. [DOI] [PubMed] [Google Scholar]
- [7].Reymen Bart, Van Baardwijk Angela, Rinus Wanders, Borger Jacques, Dingemans Anne Marie C., Bootsma Gerben, Pitz Cordula, Lunde Ragnar, Geraedts Wiel, Lambin Philippe, and Ruysscher Dirk De. Long-term survival of stage T4N0–1 and single station IIIA-N2 NSCLC patients treated with definitive chemo-radiotherapy using individualised isotoxic accelerated radiotherapy (INDAR). Radiother. Oncol, 110(3):482–487, mar 2014. [DOI] [PubMed] [Google Scholar]
- [8].Zhang Qin, Cai Xu Wei, Wen Feng, Yu Wen, and Fu Xiao Long. Dose-escalation by hypofractionated simultaneous integrated boost IMRT in unresectable stage III non-small-cell lung cancer. BMC Cancer, 22(1), dec 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Hallqvist Andreas, Bergström Stefan, Hedvig Björkestrand, Svärd Anna Maja, Simon Ekman, Lundin Erik, Holmberg Erik, Johansson Mikael, Friesland Signe, and Nyman Jan. Dose escalation to 84 Gy with concurrent chemotherapy in stage III NSCLC appears excessively toxic: Results from a prematurely terminated randomized phase II trial. Lung Cancer, 122:180–186, aug 2018. [DOI] [PubMed] [Google Scholar]
- [10].Van Diessen Judi, De Ruysscher Dirk, Sonke Jan-Jakob, Damen Eugène, Sikorska Karolina, Reymen Bart, Van Elmpt Wouter, Gunnar Westman, Persson Gitte Fredberg, Dieleman Edith, Bjorkestrand Hedvig, Corinne Faivre-Finn, and José Belderbos. The acute and late toxicity results of a randomized phase II dose-escalation trial in non-small cell lung cancer (PET-boost trial). Radiother. Oncol, 131:166–173, 2019. [DOI] [PubMed] [Google Scholar]
- [11].Gillham Charles, Zips Daniel, Pönisch Falk, Carsten Evers, Enghardt Wolfgang, Abolmaali Nasreddin, Klaus Zöphel, Steffen Appold, Hölscher Tobias, Jörg Steinbach, Kotzerke Jörg, Herrmann Thomas, and Baumann Michael. Additional PET/CT in week 5–6 of radiotherapy for patients with stage III non-small cell lung cancer as a means of dose escalation planning? Radiother. Oncol, 88(3):335–341, sep 2008. [DOI] [PubMed] [Google Scholar]
- [12].Møller Ditte Sloth, Khalil Azza Ahmed, Knap Marianne Marquard, Ludv ig Paul, and Hoffmann Lone. A planning study of radiotherapy dose escalation of PET-active tumour volumes in non-small cell lung cancer patients. Acta Oncol, 50(6):883–888, aug 2011. [DOI] [PubMed] [Google Scholar]
- [13].Cannon Donald M., Mehta Minesh P., Adkison Jarrod B., Khuntia Deepak, Traynor Anne M., Tomé Wolfgang A., Chappell Richard J., Ranjini Tolakanahalli, Pranshu Mohindra, Bentzen Søren M., and Cannon George M. Dose-limiting toxicity after hypofractionated dose-escalated radiotherapy in non-small-cell lung cancer. J. Clin. Oncol, 31(34):4343–4348, dec 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Wanet Marie, Delor Antoine, Hanin François Xavier, Benoît Ghaye, Van Maanen Aline Vincent, Clermont Christian, Goossens Samuel, Lee John Aldo, Guillaume Janssens, Bol Anne, and Geets Xavier. An individualized radiation dose escalation trial in non-small cell lung cancer based on FDG-PET imaging. Strahlenther. Onkol, 193(10):812–822, oct 2017. [DOI] [PubMed] [Google Scholar]
- [15].Wang Xiuying, Cui Hui, Gong Guanzhong, Fu Zheng, Zhou Jianlong, Gu Jiabing, Yin Yong, and Feng Dagan. Computational delineation and quantitative heterogeneity analysis of lung tumor on 18F-FDG PET for radiation dose-escalation. Sci. Rep, 8(1), dec 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Andreas Köthe, Nicola Bizzocchi, Safai Sairos, Lomax Antony John, Weber Damien Charles, and Fattori Giovanni. Investigating the potential of proton therapy for hypoxia-targeted dose escalation in non-small cell lung cancer. Radiat. Oncol, 16(1), dec 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Tucker Susan L., Li Minghuan, Xu Ting, Gomez Daniel, Yuan Xianglin, Yu Jinming, Liu Zhensheng, Yin Ming, Guan Xiaoxiang, Wang Li E., Wei Qingyi, Mohan Radhe, Vinogradskiy Yevgeniy, Martel Mary, and Liao Zhongxing. Incorporating single-nucleotide polymorphisms into the lyman model to improve prediction of radiation pneumonitis. Int. J. Radiat. Oncol. Biol. Phys, 85(1):251–257, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zhongxing Liao, Lee J Jack, Komaki Ritsuko, Gomez Daniel R, O’Reilly Michael S, Fossella Frank V, Blumenschein George R, Heymach John V, Vaporciyan Ara A, Swisher Stephen G, Allen Pamela K, Choi Noah Chan, DeLaney Thomas F, Step hen M, Cox James D, Lu Charles S, and Mohan Radhe. Bayesian Adaptive Randomization Trial of Passive Scattering Proton Therapy and Intensity-Modulated Photon Radiotherapy for Locally Advanced Non-Small-Cell Lung Cancer. J. Clin. Oncol, 36(18):1813–1822, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Edet-Sanson Agathe, Bernard Dubray, Doyeux Kaya, Back Adeline, Hapdey Sebastien, Modzelewski Romain, Bohn Pierre, Gardin Isabelle, and Vera Pierre. Serial assessment of FDG-PET FDG uptake and functional volume during radiotherapy (RT) in patients with non-small cell lung cancer (NSCLC). Radiother. Oncol, 102(2):251–257, feb 2012. [DOI] [PubMed] [Google Scholar]
- [20].Lazzeroni M, Uhrdin J, Carvalho S, van Elmpt W, Lambin P, Dasu A, Wersäll P, and Toma-Dasu I Evaluation of third treatment week as temporal window for assessing responsiveness on repeated FDG-PET-CT scans in Non-Small Cell Lung Cancer patients. Phys. Medica, 46(November 2017):45–51, 2018. [DOI] [PubMed] [Google Scholar]
- [21].Kong Feng Ming, Ten Haken Randall K., Schipper Matthew, Frey Kirk A., Hayman James, Gross Milton, Ramnath Nithya, Hassan Khaled A., Matuszak Martha, Ritter Timothy, Bi Nan, Wang Weili, Orringer Mark, Cease Kemp B., Lawrence Theodore S., and Kalemkerian Gregory P. Effect of midtreatment PET/CT-adapted radiation therapy with concurrent chemotherapy in patients with locally advanced non–small-cell lung cancer: A phase 2 clinical trial. JAMA Oncol, 3(10):1358–1365, oct 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Kong Feng Ming (Spring), Li Ling, Wang Weili, Campbell Jeff, Waller Jennifer L., Piert Morand, Gross Milton, Cheng Monica, Owen Dawn, Stenmark Matthew, Huang Ke Colin, Frey Kirk A., Haken Randall K. Ten, and Lawrence Theodore S. Greater reduction in mid-treatment FDG-PET volume may be associated with worse survival in non-small cell lung cancer. Radiother. Oncol, 132:241–249, mar 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Shusharina Nadya, Liao Zhongxing, Mohan Radhe, Liu Amy, Niemierko Andrzej, Choi Noah, and Bortfeld Thomas. Differences in lung injury after IMRT or proton therapy assessed by18FDG PET imaging. Radiother. Oncol, 2018. [DOI] [PubMed] [Google Scholar]
- [24].Pearl Judea. Chapter 12 - Bayesian Inference. Probabilistic Reason. Intell. Syst. (Revised Second Printing), pages 29–75, 1988.
- [25].Sarkar Sudeep and Boyer Kim L. Integration, Inference, and Management of Spatial Information Using Bayesian Networks: Perceptual Organization. IEEE Trans. Pattern Anal. Mach. Intell, 15(3):256–274, 1993. [Google Scholar]
- [26].Hartemink A. Principled Computational Methods for the Validation and Discovery of Genetic Regulatory Networks. PhD thesis, Massachusetts Institute of Technology, 2001. [Google Scholar]
- [27].Tucker Susan L., Liu H. Helen, Liao Zhongxing, Wei Xiong, Wang Shulian, Jin Hekun, Komaki Ritsuko, Martel Mary K., and Mohan Radhe. Analysis of Radiation Pneumonitis Risk Using a Generalized Lyman Model. Int. J. Radiat. Oncol. Biol. Phys, 72(2):568–574, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Fowler John F. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol, 62(740):679–694, aug 1989. [DOI] [PubMed] [Google Scholar]
- [29].Hoffmann Aswin L., Hertog Dick Den, Siem Alex Y.D., Kaanders Johannes H.A.M., and Henk Huizenga. Convex reformulation of biologically-based multi-criteria intensity-modulated radiation therapy optimization including fractionation effects. Phys. Med. Biol, 53(22):6345–6362, 2008. [DOI] [PubMed] [Google Scholar]
- [30].Saberian Fatemeh, Ghate Archis, and Kim Minsun. A two-variable linear program solves the standard linear–quadratic formulation of the fractionation problem in cancer radiotherapy. Oper. Res. Lett, 43(3):254–258, may 2015. [Google Scholar]
- [31].Edwin Romeijn H, Ahuja Ravindra K., Dempsey James F., Arvind Kumar, and Li Jonathan G. A novel linear programming approach to fluence map optimization for intensity modulated radiation therapy treatment planning. Phys. Med. Biol, 48(21):3521–3542, nov 2003. [DOI] [PubMed] [Google Scholar]
- [32].Williams MV, Denekamp J, and Fowler JF A review of alpha/beta ratios for experimental tumors: implications for clinical studies of altered fractionation. Int. J. Radiat. Oncol. Biol. Phys, 11(1):87–96, 1985. [DOI] [PubMed] [Google Scholar]
- [33].van Leeuwen CM, Oei AL, Crezee J, Bel A, Franken NAP, Stalpers LJA, and Kok HP The alfa and beta of tumours: A review of parameters of the linear-quadratic model, derived from clinical radiotherapy studies. Radiat. Oncol, 13(1):1–11, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Boyd Stephen and Vandenberghe Lieven. Convex Optimization, volume 25. Cambridge University Press, New York, NY., 7th edition, 2010. [Google Scholar]
- [35].Nagarajan Radhakrishnan, Scutari Marco, and Sophie Lèbre. Bayesian Networks in R. Springer New York, New York, NY, 1st edition, 2013. [Google Scholar]
- [36].Wieser Hans Peter, Eduardo Cisternas, Wahl Niklas, Ulrich Silke, Stadler Alexander, Mescher Henning, Muller Lucas Raphael, Thomas Klinge, Gabrys Hubert, Burigo Lucas, Mairani Andrea, Ecker Swantje, Ackermann Benjamin, Ellerbrock Malte, Parodi Katia, Jakel Oliver, and Bangert Mark. Development of the open-source dose calculation and optimization toolkit matRad. Med. Phys, 44(6):2556–2568, 2017. [DOI] [PubMed] [Google Scholar]
- [37].Bortfeld Thomas, Schlegel Wolfgang, and Rhein Bernhard. Decomposition of pencil beam kernels for fast dose calculations in three-dimensional treatment planning. Med. Phys, 20(2 Pt 1):311–318, 1993. [DOI] [PubMed] [Google Scholar]
- [38].Hong Linda, Goitein Michael, Bucciolini Marta, Comiskey Robert, Gottschalk Bernard, Rosenthal Skip, Serago Chris, and Urie Marcia. A pencil beam algorithm for proton dose calculations. Phys. Med. Biol, 41(8):1305–1330, aug 1996. [DOI] [PubMed] [Google Scholar]
- [39].Marks Lawrence B., Yorke Ellen D., Jackson Andrew, Ten Haken Randall K., Constine Louis S., Eisbruch Avraham, Bentzen Søren M., Nam Jiho, and Deasy Joseph O. Use of Normal Tissue Complication Probability Models in the Clinic. Int. J. Radiat. Oncol. Biol. Phys, 76(3 SUPPL.):S10, mar 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Wächter Andreas and Biegler Lorenz T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program, 57:25–57, 2006. [Google Scholar]
- [41].Ten Eikelder SCM, Ferjančič P, Ajdari A, Bortfeld T, Den Hertog D, and Jeraj R Optimal treatment plan adaptation using mid-treatment imaging biomarkers. Phys. Med. Biol, 65(24), 2020. [DOI] [PubMed] [Google Scholar]
- [42].Oh Jung Hun, Jeffrey Craft, Lozi Rawan Al, Manushka Vaidya, Meng Yifan, Deasy Joseph O., Bradley Jeffrey D., and Issam El Naqa. A Bayesian network approach for modeling local failure in lung cancer. Phys. Med. Biol, 56(6):1635–1651, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lee Sangkyu, Ybarra Norma, Jeyaseelan Krishinima, Seuntjens Jan, Naqa Issam El, Sergio Faria, Kopek Neil, Brisebois Pascale, Bradley Jeffrey D., and Robinson Clifford. Bayesian network ensemble as a multivariate strategy to predict radiation pneumonitis risk. Med. Phys, 42(5):2421–2430, 2015. [DOI] [PubMed] [Google Scholar]
- [44].Luo DL, El Naqa y., McShan I Unraveling Biophysical Interactions of Radiation Pneumonitis in Non-Small-Cell Lung Cancer via Bayesian Network Analysis. Radiother. Oncol, 123(1):85–92, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Luo Yongfeng, Li Nan, Chen Hui, G Esteban Fernandez David Warburton, Moats Rex, Robert P Mecham Daria Krenitsky, Pryhuber Gloria S, and Wei Shi. Spatial and temporal changes in extracellular elastin and laminin distribution during lung alveolar development. Sci. Rep, (May):1–12, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Yue Jinbo, Matthew McKeever Terence T. Sio, Xu Ting, Huo Jinhai, Shi Qiuling, Nguyen Quynh-Nhu, Komaki Ritsuko, Gomez Daniel R., Pan Tinsu, Wang Xin Shelley, and Zhongxing Liao. Association of lung fluorodeoxyglucose uptake with radiation pneumonitis after concurrent chemoradiation for non-small cell lung cancer. Clin. Transl. Radiat. Oncol, 4:1–7, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Ajdari A, Shusharina N, Liao Z, Mohan R, and Bortfeld T Mid-Treatment [18]F-FDG PET Uptakes Can Predict Symptomatic Radiation Pneumonitis in Non-Small Cell Lung Cancer Patients. Int. J. Radiat. Oncol, 105(1):S224, sep 2019. [Google Scholar]
- [48].Vera Pierre, Mezzani-Saillard Sandrine, Agathe Edet-Sanson, Ménard Jean François, Romain Modzelewski, Thureau Sebastien, Meyer Marc Etienne, Khadija Jalali, Bardet Stéphane, Lerouge Delphine, Houzard Claire, Mornex Françoise, Olivier Pierre, Faure Guillaume, Rousseau Caroline, Mahé Marc André, Philippe Gomez, Brenot-Rossi Isabelle, Salem Naji, and Dubray Bernard. FDG PET during radiochemotherapy is predictive of outcome at 1 year in non-small-cell lung cancer patients: a prospective multicentre study (RTEP2). Eur. J. Nucl. Med. Mol. Imaging 2014. 416, 41(6):1057–1065, feb 2014. [DOI] [PubMed] [Google Scholar]
- [49].Ma Li, Men Yu, Feng Lingling, Kang Jingjing, Sun Xin, Yuan Meng, Jiang Wei, and Hui Zhouguang. A Current Review of Dose-escalated Radiotherapy in Locally Advanced Non-small Cell Lung Cancer. Radiol. Oncol, 53(1):6, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Tandberg Daniel J., Tong Betty C., Ackerson Bradley G., and Kelsey Chris R. Surgery versus stereotactic body radiation therapy for stage I non-small cell lung cancer: A comprehensive review. Cancer, 124(4):667–678, feb 2018. [DOI] [PubMed] [Google Scholar]
- [51].Giuliani Meredith, Mathew Ashwathy S., Bahig Houda, Bratman Scott V., Filion Edith, Glick Daniel, Louie Alexander V., Raman Srinivas, Swaminath Anand, Warner Andrew, Yau Vivian, and Palma David. SUNSET: Stereotactic Radiation for Ultracentral Non-Small-Cell Lung Cancer-A Safety and Efficacy Trial. Clin. Lung Cancer, 19(4):e529–e532, jul 2018. [DOI] [PubMed] [Google Scholar]
- [52].Moore Casey, Hsu Ching Cheng, Chen Wei Min, Chen Benjamin P.C., Han Chuanhui, Story Michael, Aguilera Todd, Pop Laurentiu M., Hannan Raquibul, Fu Yang Xin, Debabrata Saha, and Timmerman Robert. Personalized Ultrafractionated Stereotactic Adaptive Radiotherapy (PULSAR) in Preclinical Models Enhances Single-Agent Immune Checkpoint Blockade. Int. J. Radiat. Oncol. Biol. Phys, 110(5):1306, aug 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Ten Eikelder SCM, Ajdari A, Bortfeld T, and Den Hertog D Conic formulation of fluence map optimization problems. Phys. Med. Biol, 66(22):225016, nov 2021. [DOI] [PubMed] [Google Scholar]
- [54].Breedveld Sebastiaan, Storchi Pascal R.M., Voet Peter W.J., and Heijmen Ben J.M. iCycle: Integrated, multicriterial beam angle, and profile optimization for generation of coplanar and noncoplanar IMRT plans. Med. Phys, 39(2):951–963, 2012. [DOI] [PubMed] [Google Scholar]
- [55].Gjyshi Olsi, Xu Ting, Elhammali Adnan, Boyce-Fappiano David, Chun Stephen G., Gandhi Saumil, Lee Percy, Chen Aileen B., Lin Steven H., Chang Joe Y., Tsao Anne, Gay Carl M., Zhu X. Ronald, Zhang Xiaodong, Heymach John V., Fossella Frank V., Lu Charles, Nguyen Quynh Nhu, and Zhongxing Liao. Toxicity and Survival after Intensity-Modulated Proton Therapy (IMPT) versus Passive Scattering Proton Therapy (PSPT) for Non-Small Cell Lung Cancer. J. Thorac. Oncol, 16(2):269, feb 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Mirkovic D, Titt U, Peeler C, Perles L, Liao Z, and Mohan R TU-G-108–08: Variable RBE and Incidence of Radiation Pneumonitis in Lung Patients Treated with Proton Therapy. Med. Phys, 40(6):455, 2013. [Google Scholar]
- [57].Ajdari Ali and Ghate Archis. Robust fractionation in radiotherapy. 2015.
- [58].Ajdari Ali and Ghate Archis. Robust spatiotemporally integrated fractionation in radiotherapy. 2016.
- [59].Ajdari Ali, Ghate Archis, and Kim Minsun. Adaptive treatment-length optimization in spatiobiologically integrated radiotherapy. Phys. Med. Biol, 63(7):075009, mar 2018. [DOI] [PubMed] [Google Scholar]
- [60].Eikelder Stefan C M. Adjustable robust treatment-length optimization in radiation therapy. Master thesis, Tilburg University, 2018. [Google Scholar]
- [61].Park Clinton S., Kim Yongbok, Lee Nancy, Bucci Kara M., Quivey Jeanne M., Verhey Lynn J., and Xia Ping. Method to account for dose fractionation in analysis of IMRT plans: Modified equivalent uniform dose. Int. J. Radiat. Oncol. Biol. Phys, 62(3):925–932, 2005. [DOI] [PubMed] [Google Scholar]
- [62].Allen Li X, Markus Alber, Deasy Joseph O., Jackson Andrew, Jee Kyung Wook Ken, Marks Lawrence B., Martel Mary K., Mayo Charles, Moiseenko Vitali, Nahum Alan E., Niemierko Andrzej, Semenenko Vladimir A., and Yorke Ellen D. The use and QA of biologically related models for treatment planning: Short report of the TG-166 of the therapy physics committee of the AAPM. Med. Phys, 39(3):1386–1409, 2012. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


